A Modeling Study of a Patient-specific Safe Zone for THA: Calculation, Validation, and Key Factors Based on Standing and Sitting Sagittal Pelvic Tilt

Abstract

Background

Lumbar-pelvic stiffness and sagittal imbalance have been reported to increase the risk of dislocation and wear after THA. One potential way to approach this concern is by identifying patient-specific safe zones for THA components based on the standing and sitting sagittal pelvic tilt. However, there is no algorithm to integrate the standing and sitting pelvic tilt into the surgical plan of component orientations.

Questions/purposes

We established a new mathematical algorithm for determining a patient-specific safe zone for THA by integrating the impingement-free ROM requirements of standing and sitting while preventing edge loading while standing. We aimed to determine (1) the accuracy of this new method for predicting the impingement-free ROM for a given component orientation, (2) the sensitivity and specificity of detecting an impingement-free acetabular cup position for standing and sitting, and (3) the influences of key factors including pelvic tilt while standing and pelvic tilt while sitting and implant parameters on patient-specific safe zones.

Methods

A strategy for calculating the intersection of standing and sitting impingement-free safe zones and the zone of a standing radiographic inclination of ≤ 45° was used to develop patient-specific safe zones. We conducted a computer simulation study including the pelvis and THA prosthesis to answer the three study questions. We enrolled 10 patients who underwent robot-assisted THA for avascular necrosis of the femoral head (mean age 49 ± 19 years; five were women) from October 2019 to December 2019. We used a prosthesis model with a conical stem neck and a non-hooded liner, with the femoral head diameter ranging between 28 mm and 40 mm, and the corresponding head-neck ratio ranging between 2.33 and 3.33. We tested 1680 movements for the accuracy of impingement-free ROM (Question 1), and 80 marginal points and 120 non-marginal points of the comprehensive impingement-free safe zone, which combines the standing and sitting postures (Question 2). For Question 3, we explored the influences of standing and sitting pelvic tilt, femoral head diameter, and ROM criteria on the size of the patient-specific safe zone.

Results

With the simulation method as a reference for detecting impingement, the mean absolute error (arithmetic mean of all the absolute errors) of the calculated impingement-free ROM was 1.4° ± 2.3°, and the limit of agreement of errors was between -3.6° and 3.7°. The sensitivity of detecting a safe cup orientation within the comprehensive impingement-free safe zone for a given ROM criterion was 98.9% (95% CI 93.6% to 99.9%), and specificity was 97.1% (95% CI 91.0% to 99.2%). There were no impingement-free safe zones for 29% (pelvic tilt combinations without an impingement-free safe zone and all tested combinations) and no patient-specific safe zones for 46% (pelvic tilt combinations without a patient-specific safe zone and all tested combinations) of the tested combinations of standing and sitting pelvic tilt. The patient-specific safe zone was sensitive to changes in standing and sitting pelvic tilt, femoral head diameter, stem version, and ROM criteria. Stem anteversions beyond 10° to 20° dramatically reduced the size of the patient-specific safe zone to 0 within a change of 10° to 20°.

Conclusion

The patient-specific safe zone algorithm can be an accurate method for determining the optimal orientation for acetabular cups and femoral stems in THA. The patient-specific safe zone is sensitive to changes in standing and sitting pelvic tilt, stem version, ROM criteria, and the femoral head diameter. A narrow zone of 10° to 20° for stem anteversion is recommended to maximize the size of the patient-specific safe zone.

Clinical Relevance

This study suggests the potential of a mathematical algorithm to optimize the orientation of THA components and illustrates how key parameters affect the patient-specific safe zone.

Introduction

Appropriate acetabular component orientation is important for achieving good function and longevity after THA [12, 19, 27, 29, 36]. Accurate acetabular cup and femoral stem orientation is essential for avoiding dislocation, wear, and other complications caused by component malposition after THA [8, 21, 42]. Lewinnek et al. [20] introduced the concept of a safe zone for the acetabular cup: 30° to 50° of inclination and 5° to 25° of anteversion. However, this traditional safe zone is ineffective for predicting dislocation [1, 6, 10, 36]. Pelvic tilt has been recognized as a key reason for the failure of the Lewinnek safe zone because it affects functional component orientation after implantation [22, 31, 35]. Lumbar-pelvic stiffness and sagittal imbalance increase the risk of dislocation and wear after THA, suggesting that the THA component’s safe zone should be individualized [9, 11-13, 35]. Tezuka et al. [34] proposed a new functional safe zone, the combined sagittal index, incorporating the acetabular ante-inclination and sacrofemoral angle into a single parameter to guide the positioning of THA components. Phan et al. [28] recommended classifying patients according to the degree of spine stiffness and imbalance to help surgeons choose an appropriate degree of cup anteversion. Although these qualitative methods provide the basis for recommendations for cup orientation, concrete target angles for cups remain elusive for surgeons wanting to minimize dislocation and wear for specific patients. With the increasing use of robotic THA and three-dimensional preoperative planning, quantitative hip arthroplasty algorithms for defining the proper prosthetic position might reduce the risk of dislocation and wear.

Impingement is an important mechanism leading to dislocation, wear, and loosening [3, 32]. Impingement-free ROM has been used to examine whether a given component orientation is safe [37, 38, 41]. Some authors [15] reported a mathematical algorithm to calculate impingement-free component alignments that are based on pelvic tilt, using the formula published by Yoshimine and Ginbayashi [41] and Yoshimine [40]. Thus, pelvic tilt could be quantitatively integrated into the THA safe zone. However, because of the dynamic motion of the pelvis, a patient-specific safe zone based on a single instance of pelvic tilt may not cover the functional requirements of other pelvic positions [18, 43].

Edge loading is another important cause of liner wear and component loosening [17, 22]. Edge loading in the anterosuperior aspect of the cup during standing has been reported to be more detrimental than posterior edge loading while sitting because it creates greater local stress [12]. Other authors [4, 19] recommended 45° as the upper limit of abduction to decrease the wear rate of polyethylene. However, to our knowledge, pelvic tilt has not been considered for the calculation of a functional inclination angle, despite its large influence on the functional cup orientation [22]. We thus established a new method for determining a patient-specific safe zone for THA by integrating different pelvic positions into an impingement-free ROM algorithm and using the criterion of a standing functional inclination of ≤ 45° to simultaneously fulfill the ROM requirements of standing and sitting while preventing edge loading while standing.

We aimed to determine (1) the accuracy of this new method for predicting the impingement-free ROM for a given component orientation, (2) the sensitivity and specificity of detecting an impingement-free acetabular cup position for standing and sitting, and (3) the influences of key factors including pelvic tilt while standing and pelvic tilt while sitting and implant parameters on patient-specific safe zones.

Materials and Methods

Overview

Using patient data, we established a computer-aided design model with the Solidworks software (SolidWorks 2012, SolidWorks Corporation), which contains a function of impingement detection and ROM measurement between the stem neck and liner after the model is assembled [42]. A modeling study was conducted to validate the accuracy of the impingement-free ROM prediction algorithm and determine the sensitivity and specificity of predicting impingement in either the standing or sitting position using this algorithm. The influences of key factors impacting the size of safe zones were further explored according to the validated algorithm (Fig. 1).

Fig. 1.

This flowchart shows the study design. PSSZ = patient-specific safe zone. A color image accompanies the online version of this article.

Patients

To evaluate the accuracy of the algorithm, we prospectively enrolled 10 patients from our center. The inclusion criteria were patients waiting for robot-assisted primary THA, patients with a diagnosis of avascular necrosis, and those with a planned cup diameter larger than 52 mm to accommodate a 36-mm femoral head. Patients with a prosthesis in situ, planned cup diameter less than 52 mm, deformities in the femur and pelvis, and contralateral lower limb deformities leading to coronal-plane pelvic tilting were excluded. We selected heads that were 36 mm in diameter because we wanted to maximize the safe zone size available for evaluation; no patient-specific safe zone might be available if a head smaller than 36 mm is used. Between October 1, 2019, and December 31, 2019, we performed 16 robot-assisted THAs for avascular necrosis of the femoral head. Ten of these patients were included in the current study, five of whom were women. The average age was 49 ± 19 years. Four patients were excluded because the planned cup diameter was smaller than 52 mm, and the other two patients were excluded because of severe arthritis of the contralateral hip.

Definition of the Pelvic Coordinate System and Hip ROM

We used the pelvic coordinate system of the International Society of Biomechanics [39]. The origin was defined as the upper center of the S1 vertebral body, with the x-axis pointing laterally, the y-axis anteriorly, and the z-axis superiorly. The femoral coordinate system was defined similarly using the rotation center of the hip as the origin, with the z-axis along the mechanical axis of the femur (Fig. 2A). Hip ROM was defined as the rotation angles of the femoral coordinate system from the neutral position [23]. Femoral motion was determined in the following order [33]: The first rotation (external and internal rotation) occurred on the z-axis of the femur (Fig. 2B), the second rotation (abduction and adduction) occurred on the y-axis of the pelvis (Fig. 2C), and the third rotation (flexion and extension) occurred on the x-axis of the pelvis (Fig. 2D). Internal rotation, flexion, and adduction were defined as positive values. We converted leg motions to prosthetic ROM using the method described by Hsu et al. [15, 16].

Fig. 2.

These drawings show the pelvic coordinate system, order of movement, and algorithm for detecting impingement. (A) The femoral coordinate system and pelvic coordinate system are shown. (B) In the first step, internal and external rotation around the z-axis of the femur are determined. (C) In the second step, abduction and adduction around the y-axis of the femur are determined. (D) In the third step, flexion and extension around the x-axis of the pelvis are determined. (E) This diagram shows the algorithm for detecting impingement, with R1 as the radius of the femoral head, R2 as the radius of the prosthetic stem neck at the level of impingement, angle A as the technical ROM of the prosthesis, and θ as the femoral position angle between the central axes of the stem neck and the acetabular cup. A color image accompanies the online version of this article.

Mathematical Algorithm for a Patient-specific Safe Zone

We deduced the impingement-free safe zone of the acetabular cup by comparing the femoral position angle (θ) with the technical ROM (A) using the mathematical algorithm reported by Yoshimine and Ginbayashi [41] and Hsu et al. [15]. The femoral position angle θ was defined as the angle between the central axes of the stem neck and the acetabular cup (Fig. 2E). We simplified the stem neck so that it was conical and the liner edge was not chamfered [14] (Table 1):

$$\text{A}=180°-2\times \text{ arcsin}\mathrm{}\frac{R2}{R1}\mathrm{}$$

where A is again the technical ROM, R1 is the radius of the femoral head, and R2 is the radius of the cross-section of the stem neck (Fig. 2E). Impingement was considered positive in both the standing and sitting pelvic positions at 14 extreme positions of hip ROM when θ ≥ A/2 (Fig. 2). Cup orientations were defined using radiologic anteversion and radiographic inclination in reference to Lewinnek’s plane [20, 24]. The algorithm for determining impingement is as follows:

$${\text{θ}}_{standing}=\text{arccos}(R_{cup2pelvis}\left(\text{RA},\text{RI},{\text{PT}}_{standing}\right)(:,3),R_{femur}(:,3))$$

$${\text{θ}}_{sitting}=\text{arccos}(R_{cup2pelvis}\left(\text{RA},\text{RI},{\text{PT}}_{sitting}\right)(:,3),R_{femur}(:,3))$$

$$\text{θ}=\min \left({\text{θ}}_{standing},{\text{θ}}_{sitting}\right)\{\begin{array}{c}>A\to impingement \\ \le A\to no impingement \end{array}$$

where (:,3) indicates the third column of the matrix, RA is radiologic anteversion, RI is radiographic inclination, PT_standing is pelvic tilting in the standing position, and PT_sitting is pelvic tilting in the sitting position (Appendix 1; Supplemental Digital Content 1, http://links.lww.com/CORR/A612).

Table 1.

Parameters of prosthesis design for calculating the IFSZ and PSSZ

Parameter	Model options
Cup outer diameter in mm	44-60 with 1-mm increment
Cup inner diameter in mm	28	32	36	40
Head design	Modular monopolar
Neck geometry	Cylindrical
Cup design	Hemispherical shell
Liner hood	Non-hooded
Head diameter in mm	28	32	36	40
Head-neck ratio	2.33	2.67	3.00	3.33
Neck-shaft angle in °	132
Neck diameter in mm	12
Cup radiographic inclination in °	0-60
Cup radiographic anteversion in °	-20 to 50
Stem anteversion in °	15

IFSZ = impingement-free safe zone; PSSZ = patient-specific safe zone.

The impingement-free ROM in each direction can be calculated as the maximal impingement-free angle of θ with given values of PT_standing and PT_sitting (Fig. 3), which is then compared with the predetermined ROM criteria of 14 positions in the corresponding direction to detect whether a cup orientation is impingement-free for standing and sitting [2, 25] (Table 2). Acetabular cup orientations between 0° and 60° of radiographic inclination and between -10° and 50° of radiologic anteversion underwent ergodic testing in three steps to form patient-specific safe zones (Fig. 4). First, we calculated the pelvic tilt–specific impingement-free safe zones for standing and sitting according to the impingement-free ROM algorithm (Fig. 4A-D). Second, we obtained the intersection area between the standing and sitting impingement-free safe zones to form a comprehensive impingement-free safe zone (Fig. 4E). Third, we excluded points with a standing radiographic inclination of > 45° for a functional acetabular cup, preserving the residual points in the comprehensive impingement-free safe zone to form a patient-specific safe zone (Fig. 4F).

Fig. 3.

This schematic drawing illustrates the algorithm for calculating the impingement-free safe zone. The cup orientation is judged to be safe if the calculated impingement-free ROM fulfills the ROM criteria (Table 2) in both the (A) standing position and (B) sitting position. A color image accompanies the online version of this article.

Table 2.

ROM criteria for the 14 hip positions for calculating the IFSZ

Motion category	Type of motion	Standing in °	Sitting in °
Single-axis movement	Flexion	120	145
	Extension	20	-
	Internal rotation	80	40
	External rotation	40	40
	Abduction	50	50
	Adduction	50	50
Compound flexion movement	Flexion	60	90
	Extension
	Internal rotation	30	15
	External rotation
	Abduction
	Adduction	30	15
Compound extension movement	Flexion
	Extension	30
	Internal rotation
	External rotation	30
	Abduction	0
	Adduction

There are six single-axis and two compound-axis movements for standing, and five and one corresponding movements for the sitting axis types. Extension in sitting was not considered in the current model. IFSZ = impingement-free safe zone.

Fig. 4.

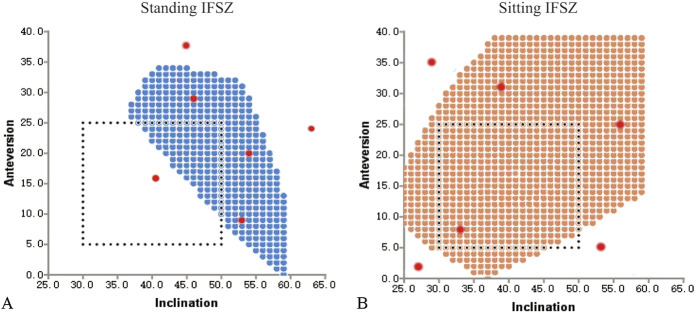
This figure shows the algorithm for calculating the patient-specific safe zone. (A) A full-length standing lateral image was used to obtain a standing pelvic tilt value, which was imputed into the formula to calculate (B) the standing impingement-free safe zone (IFSZ). (C) A full-length sitting lateral image was similarly used to determine (D) the sitting impingement-free safe zone. The standing and sitting impingement-free safe zones were integrated to obtain the intersection and form (E) the comprehensive impingement-free safe zone. (F) A zone with a standing radiographic inclination of ≤ 45° was maintained to form the patient-specific safe zone (PSSZ). Pelvic incidence is defined as the angle between the line connecting the midpoint of the bilateral femoral head’s center and the midpoint of the S1 endplate and the line perpendicular to the S1 upper endplate. The prosthesis model included in this figure was a 36-mm-diameter femoral head with other parameters identical to that in Table. 2.

The size of a safe zone was defined as the number of points (1° resolution for radiologic anteversion and radiographic inclination) within an impingement-free safe zone or a patient-specific safe zone, and it was calculated using the area formula for irregular polygons [37].

Computer-aided Design Simulation Model

To examine the accuracy of the patient-specific safe zone algorithm, we used data from preoperative standing and sitting biplanar digital radiographs (EOS Imaging System, EOS Imaging SA) and supine CT images of the pelvises and femurs of the 10 enrolled patients. Pelvic tilt in the sagittal plane was measured by an angle subtended by a vertical line and the line joining the midpoint of the bilateral hip center and the midpoint of the upper endplate of the S1 vertebral body on standing and sitting EOS images. For each patient, we calculated the standing and sitting impingement-free safe zone, the comprehensive impingement-free safe zone, and the patient-specific safe zone (Table 3).

Table 3.

Patient demographic information and size of the IFSZ, comprehensive IFSZ, and PSSZ

Patient number	Demographic information						Size of the safe zone
	Age in years	Sex	Standing PT in °	Sitting PT in °	PI in °	Femoral head diameter in mm	Standing IFSZ	Sitting IFSZ	Comprehensive IFSZ	PSSZ
1	51	M	3	60	53	36	434	910	261	43
2	53	F	15	44	65	36	905	1278	503	232
3	21	F	12	23	41	36	820	438	179	27
4	52	M	-1	43	44	36	673	1008	332	54
5	38	F	16	32	58	36	636	349	228	47
6	40	M	1	21	39	36	1010	1920	324	145
7	57	M	1	58	41	36	554	1032	302	59
8	62	F	-9	61	70	36	729	1884	265	49
9	58	M	-4	25	30	36	734	1400	261	66
10	57	F	10	26	39	36	742	567	227	38

IFSZ = impingement-free safe zone; PSSZ = patient-specific safe zone; PT = pelvic tilt; PI = pelvic incidence.

A simulation experiment using computer-aided design software (SolidWorks 2012, SolidWorks Corporation) was conducted to evaluate the accuracy of the impingement-free safe zone algorithm (Fig. 5A). Ten pelvic models were created from patients’ CT images and mounted with cup and liner models that had diameters identical to those that were implanted. The pelvis was rotated to the corresponding standing and sitting positions. Acetabular cup orientations were modulated according to radiologic anteversion and radiographic inclination, with the anterior pelvic plane used as the reference plane (Fig. 5B). The original position of the femur was defined as the neutral position, with the stem model mounted into the femoral canal along the femoral anatomic axis and with anteversion set at 15°. The impingement-free ROM for a given cup position and pelvic tilt was then simulated by the SolidWorks software with the same order of movement.

Fig. 5.

The CAD model for the validation experiment is shown. (A) Impingement was detected by simulated 53° of extension, 0° of internal rotation, and 0° of abduction. (B) The anterior pelvic plane was determined by the bilateral anterior superior iliac spine and the pubic symphysis; the radiographic anteversion and radiographic inclination were defined based on the orthogonal coordinate system using the anterior pelvic plane as the coronal plane. The stem position had a compound-axis movement with 30° of internal rotation, 30° of adduction, and 93° of flexion, and single-axis movement with 0° of internal rotation, 58° of abduction, and 0° of flexion. A color image accompanies the online version of this article.

Pelvic Tilt–specific Validation of the Impingement-free ROM Algorithm

The algorithm of the pelvic tilt–specific impingement-free ROM was validated using the computer-aided design simulation. For the impingement-free safe zone, we randomly selected 12 orientations for each of the 10 patients, all evenly distributed within and outside the standing (Fig. 6A) and sitting (Fig. 6B) impingement-free safe zone. The 14 movements of the ROM criteria were simulated (Table 2). A total of 120 cup positions with 14 ROM movements for each position (1680 movements in total) were tested. The accuracy of the ROM prediction by the algorithm was then calculated.

Fig. 6.

The design of the impingement-free ROM validation experiment is shown. (A) The standing-position impingement-free safe zone was calculated, and three points within and three points outside (red dots) the impingement-free Safe Zone (blue dots) were randomly selected for examining the accuracy of the impingement-free ROM algorithm for the standing position for corresponding single-axis and compound-axis movement. (B) Six points (red dots) were similarly selected for the sitting-position impingement-free safe zone (orange dots) for examining the algorithm for the sitting position. A color image accompanies the online version of this article.

Validation of the Comprehensive Impingement-free Safe Zone

The sensitivity and specificity of the comprehensive impingement-free safe zone to predict a safe cup orientation in the standing and sitting positions were evaluated with the computer-aided design model experiment as the reference. Points were marked as “predicted safe” if they were within the comprehensive impingement-free safe zone or as “predicted unsafe” if outside it. Eight borderline cup positions of the comprehensive impingement-free safe zone were tested, with four on the margin of the safe zone (Fig. 7A) and the other four as adjacent outlier points with 1 deviation (Fig. 7B). There were 12 other non-marginal points, six of them within (Fig. 7A) and six of them outside (Fig. 7B) the comprehensive impingement-free safe zone, randomly selected to test sensitivity and specificity. We tested 200 cup positions with 80 marginal points and 120 non-marginal points. The ROM criteria of the nine directions were then implemented for each of the positions using the computer-aided design models, and each cup position was marked as “tested safe” if no impingement was detected or as “tested unsafe” if there was a positive finding for any movement.

Fig. 7.

The design of the comprehensive impingement-free safe zone validation experiment is shown. (A) Ten points within the comprehensive impingement-free safe zone (blue dots) were chosen, with four marginal points (yellow dots) and six non-marginal points (red dots) to assess the sensitivity. (B) Ten points outside the comprehensive impingement-free safe zone (blue dots) were similarly chosen, with four marginal points (yellow dots) immediately adjacent to the margins of the comprehensive impingement-free safe zone (blue dots) and six non-marginal points (red dots) to assess the specificity. A color image accompanies the online version of this article.

Key Factors Influencing the Patient-specific Safe Zone

We explored the influences of standing and sitting pelvic tilt variations on the patient-specific safe zone using a given model of the pelvis (pelvic incidence = 70°; normal bilateral hip rotation centers) and prosthesis (femoral head diameter = 36 mm; head-neck ratio = 3.0) (Table 1). Testing produced standing pelvic tilt values ranging from -30° to 40° and sitting pelvic tilt values ranging from -20° to 70°. The influence of standing pelvic tilt on the patient-specific safe zone was explored, and the sitting pelvic tilt values were fixed at -20°, 0°, 10°, 20°, 40°, and 60°. In addition, the effect of sitting pelvic tilt on the patient-specific safe zone was explored, with the standing pelvic tilt values fixed at -20°, 0°, 10°, 20°, and 40°. The patient-specific safe zone sizes for each combination of standing and sitting pelvic tilt were calculated to check the combined influences of standing and sitting pelvic tilt on the patient-specific safe zone. The influences of femoral stem version, femoral head size, and ROM criteria on the size of the patient-specific safe zone were explored with different combinations of standing and sitting pelvic tilt values.

Primary and Secondary Study Outcomes

Our primary study goal was to validate the accuracy of the mathematic algorithm. To achieve this, we used patient data including standing and sitting pelvic tilt and pelvic anatomy, and combined it with THA prosthesis models as the modeling reference to determine the accuracy of the pelvic tilt–specific impingement–free ROM algorithm as well as the sensitivity and specificity of the comprehensive impingement-free safe zone.

Our secondary study goals were to explore the influences of multiple key factors on the patient-specific safe zone based on the algorithm validated above. Changes in standing and sitting pelvic tilt, stem version, ROM criteria, and femoral head diameter were explored using an ergodicity approach for their influences on the size of safe zone.

Ethical Approval

Ethical approval for this study was obtained from our institution.

Statistical Analysis

We used the computer-aided design simulation model as the standard for determining the accuracy of the patient-specific safe zone algorithm. The mean absolute error for ROM prediction by the patient-specific safe zone algorithm was calculated with a 95% CI. A Bland-Altman analysis was used to calculate the 95% limits of agreement, within which the theoretical ROM estimation errors fell within 95% probability. The sensitivity and specificity of detecting a safe acetabular cup orientation in the comprehensive impingement-free safe zones were calculated. All statistical analyses were performed using SPSS software, version 15.0 (IBM Corp.) and MedCalc software.

Results

Accuracy of the Pelvic Tilt–specific Impingement-free ROM Algorithm

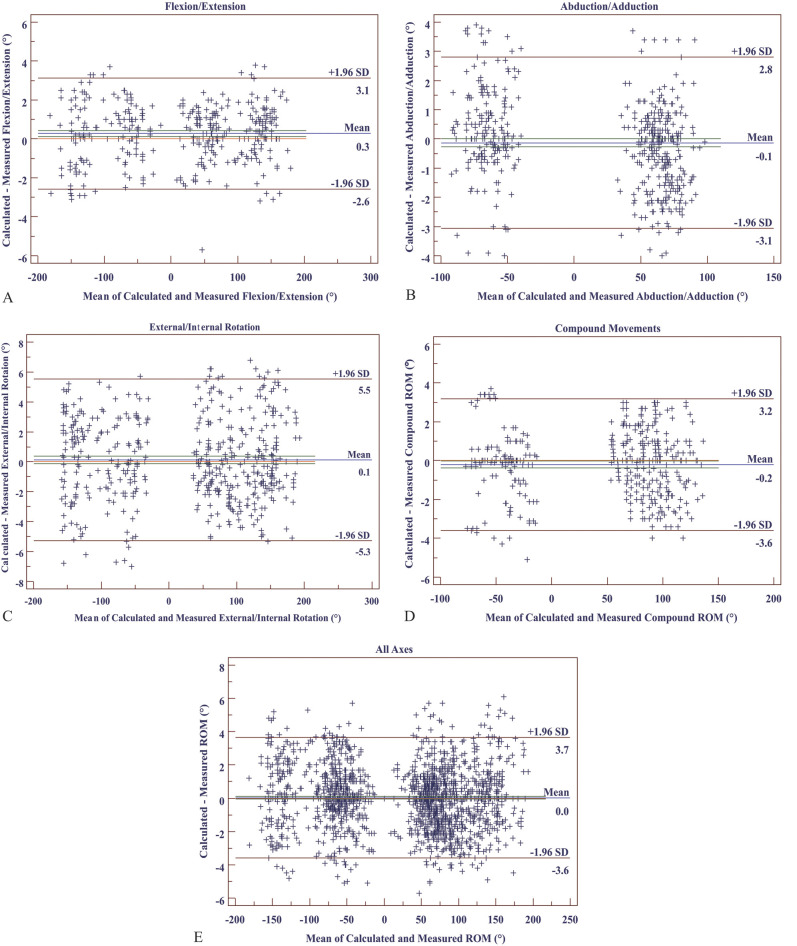
The overall 95% CI for the mean absolute error of the calculated impingement-free ROM compared with the computer-aided design measurements was 1.4° ± 2.3° and ranged from 1.1° to 1.9° for single-axis and compound-axis movements (Table 4). The Bland-Altman analysis indicated that the mean errors for the calculated single-axis impingement-free ROM were 0.3° for flexion and extension (Fig. 8A), -0.1° for abduction and adduction (Fig. 8B), 0.1° for external and internal rotation (Fig. 8C), and -0.2° for compound movements (Fig. 8D), with an overall mean of error of 0.0° and limit of agreement of errors of between -3.6° and 3.7° for all movements (Fig. 8E).

Table 4.

Mean absolute error for impingement-free ROM calculated with the PSSZ algorithm

Parameter	Number of tests	Mean absolute error in °, mean ± SD
All axes	1680	1.4 ± 2.3
Flexion and extension	360	1.2 ± 1.8
Abduction and adduction	480	1.1 ± 1.9
External and internal rotation	480	1.9 ± 2.8
Compound movements	360	1.3 ± 2.2

PSSZ = patient-specific safe zone.

Fig. 8.

This figure shows the results of the Bland-Altman analysis of the accuracy of the ROM predicted by the impingement-free ROM algorithm, including (A) single-axis movement of flexion and extension, (B) single-axis movement of abduction and adduction, (C) single-axis movement of external and internal rotation, (D) compound movement with three axes involved, and (E) accuracy for all movements. The green line represents the CI of the mean of difference line, and the orange represents the zero line.

Sensitivity and Specificity of the Comprehensive Impingement-free Safe Zone

The sensitivity of detecting a safe cup orientation within the comprehensive impingement-free safe zone for a given ROM criterion was 98.9% (95% CI 93.6% to 99.9%), and specificity was 97.1% (95% CI 91.0% to 99.2%), with a positive predictive value of 97.0% (95% CI 90.9% to 99.2%) and negative predictive value of 99.0% (95% CI 93.8% to 99.9%) (Appendix 2; Supplemental Digital Content 2, http://links.lww.com/CORR/A613).

Key Factors Influencing the Patient-specific Safe Zone

The shape of the comprehensive impingement-free safe zone was sensitive to changes in standing (Fig. 9A) and sitting pelvic tilt (Fig. 9B), and so was the size of the comprehensive impingement-free safe zone (Fig. 9C) and patient-specific safe zone (Fig. 9D). Among all pelvic tilt combinations tested, there were no impingement-free safe zones available for 29% (pelvic tilt combinations without an impingement-free safe zone and all tested combinations) and no patient-specific safe zones available for 46% (pelvic tilt combinations without a patient-specific safe zone and all tested combinations) of the tested combinations for the given model of prosthesis and pelvic tilt. With an increase in standing pelvic tilt from -20° to 40°, the impingement-free safe zone size first increased and then decreased. The peak size of patient-specific safe zones as well as the corresponding standing pelvic tilt values increased with increases in sitting pelvic tilt values (Fig. 9E). Qualitatively, there was an increase in the size of the impingement-free safe zone, which reached a plateau when sitting pelvic tilt values increased from -20° to 60°. The turning point gradually increased with an increase in standing pelvic tilt values (Fig. 9F).

Fig. 9.

The influences of PT_standing and PT_sitting on the impingement-free safe zone and the patient-specific safe zone are shown, including (A) the influence of PT_standing on the comprehensive impingement-free safe zone with PT_sitting set constant at 30°; (B) the influence of PT_sitting on the comprehensive impingement-free safe zone with PT_standing set constant at 10°, with each different color showing a cross-section of the three-dimensional space of the safe zone; (C) the influences of PT_standing and PT_sitting on the size of the comprehensive impingement-free safe zone; (D) the influences of PT_standing and PT_sitting on the size of the patient-specific safe zone, with the red color indicating large size of safe zone and the blue color indicating the small size of safe zone; (E) the influences of PT_standing with different PT_sitting values on the size of the impingement-free safe zone; and (F) the influence of PT_sitting with different PT_standing values on the size of the impingement-free safe zone. PT_standing = pelvic tilt in the standing position; PT_sitting = pelvic tilt in the sitting position.

The patient-specific safe zone was also sensitive to changes in femoral stem version, ROM criteria, and femoral head diameter. The size of the impingement-free safe zone and patient-specific safe zone varied greatly with changes in stem anteversion for a given standing and sitting pelvic tilt value (Fig. 10A). The size of the patient-specific safe zone reached a stable plateau between 10° and 20° of stem version and decreased dramatically beyond this region to 0 within 10° to 20° of alteration in stem version, with changes in pelvic tilt while standing (Fig. 10B) or changes in pelvic tilt while sitting (Fig. 10C). Changes in the femoral head size and ROM criteria can dramatically affect the size of the comprehensive impingement-free safe zone to a maximum of seven-fold (Fig. 11).

Fig. 10.

This figure shows the influence of stem version on the impingement-free safe zone and patient-specific safe zone. (A) Excessively small or large stem anteversion reduces the size of the impingement-free safe zone and patient-specific safe zone. The size of the patient-specific safe zone is sensitive to stem version for different (B) PT_standing values and (C) PT_sitting values, and there is a zone between 10° and 20° of stem anteversion at which the patient-specific safe zone size is maximized. PT_standing = pelvic tilt in the standing position; PT_sitting = pelvic tilt in the sitting position. A color image accompanies the online version of this article.

Fig. 11.

This figure shows the influences of the ROM criteria and femoral head diameter on the patient-specific safe zone. The four ROM criteria gradually decreased for the ROM required for single-axis movement for both standing and sitting, and the compound-axis movement remained the same, as shown in Table 2. A color image accompanies the online version of this article.

Discussion

The traditional universal safe zone fails to prevent dislocation and wear after THA. Spinal-pelvic motion is one of the major reasons, and its patient-specific nature necessitates a quantitative, individualized safe zone to solve the problem. Our study established and validated a mathematical strategy to calculate patient-specific safe zones for THA to fulfill the ROM requirements of the standing and sitting positions while preventing impingement and edge loading. Our data showed that the impingement-free ROM prediction algorithm is highly accurate and that detecting safe cup orientations has a high sensitivity and specificity when the patient-specific safe zone algorithm is used. The patient-specific safe zone is sensitive to changes in standing and sitting pelvic tilt, ROM criteria, and prosthetic design and implantation parameters. With the rapid growth of robot-assisted THA, the algorithm reported here could guide the accurate placement of primary THA components in a patient-specific way. In addition, the current work may also help improve the quantitative assessment of component orientations for dislocation after THA.

Limitations

Our study has several limitations. First, because the current algorithm only simulates a simplified prosthesis, further improvements, including femoral head offset, neck-shaft angle, bone-to-bone impingement, hooped liners, and types of bearing surface, should be further integrated into the mathematical algorithm to improve prediction accuracy [15, 37, 41]. To our understanding, the influences of these factors will not jeopardize the validity of our findings, because spinal-pelvic motions play a fundamental role in the in vivo behavior of THA prostheses. Second, the biomechanical criterion of standing radiographic inclination cannot preclude edge loading while sitting. However, because edge loading in the anterosuperior aspect while standing is more detrimental than posterior edge loading while sitting [12], the criterion of standing radiographic inclination < 45° may substantially reduce wear. Third, other dynamic activities such as climbing stairs, squatting, and running must be integrated into the analysis. This can be solved by introducing more pelvic tilt positions and associated ROM criteria to the algorithm, which can be modified according to the culture- or gender-specific requirements of the hip.

Accuracy of the Pelvic Tilt–specific Impingment-free ROM Algorithm

Our data show that the current patient-specific safe zone strategy of obtaining an impingement-free safe zone accurately resolves the problem of adapting a prosthesis to mobile pelvic tilt. The low mean absolute error (0.9°-1.7°) for each direction of ROM calculation and the high sensitivity and specificity for predicting impingement in the standing or sitting position indicate that the algorithm for calculating pelvic tilt–based impingement-free ROM might be highly accurate for clinical use. The small errors at the margins of a patient-specific safe zone might be due to the slight difference in the model mounting in the computer-aided design software.

Intersection Algorithm of the Standing and Sitting Impingement-free Safe Zone

The intersection algorithm of the standing and sitting impingement-free safe zone is one major contribution of this study. Spinopelvic motion influences the sagittal inclination of acetabular cups, increases hip flexion, and renders the Lewinnek safe zone ineffective [11, 15, 35, 41]. Several authors have reported qualitative strategies to modulate the optimal cup orientation according to spinopelvic motion, but these authors could not identify any accurate component targets for specific patients [28, 36]. Previous quantitative studies were primarily focused on the design or implantation parameters of the prosthesis that affect the impingement-free ROM of THA [14, 37]. Additionally, Hsu et al. [15] integrated pelvic tilt into the mathematical formulas for impingement-free safe zones.

However, because pelvic movement is dynamic, a safe zone for a single pelvic position may not fulfill the requirements of other pelvic positions. To our knowledge, no reports have explored an algorithm of the cup’s safe zone that considers pelvic tilt in the standing and sitting positions. The introduction of standing and sitting pelvic tilt into the patient-specific safe zone algorithm substantially narrows the safe zone (see Fig. 4). The validated mathematical algorithm we used might allow surgeons to plan THA while quantitatively considering standing and sitting. Other positions can be added to the algorithm according to patient-specific needs. We are developing a commercially available software tool; in the meantime, we are open to an analysis of a patient-specific safe zone for patients on request, with the data provided.

Key Factors Influencing the Patient-specific Safe Zone

This study revealed that the patient-specific safe zone is sensitive to changes in standing and sitting pelvic tilt values (Fig. 9A-F). The size of the patient-specific safe zone tends to decrease with either too-small (< -5°) or too-large (> 10°) standing pelvic tilt values (Fig. 9E), just as there is an increase in the size of the patient-specific safe zone with increases in sitting pelvic tilt values that plateau after roughly 40° (Fig. 9F). The combinations with the largest patient-specific safe zones are those with standing pelvic tilt values between 0° and 10° and those with sitting pelvic tilt values between 40° and 50°, which corresponds to a balanced and flexible spine [28] (Fig. 9E-F).

Among the tested pelvic tilt combinations, there were no impingement-free safe zones available for 29% and no patient-specific safe zones available for 46%. Thus, we recommend a routine assessment of standing and sitting pelvic positions in clinical practice. For patients for whom there are no impingement-free safe zones or patient-specific safe zones, other methods might be required to allow for a workable safe zone, such as bipolar arthroplasty or osteotomy of the spine before THA to improve pelvic positioning.

Our data also indicate that stem version plays a vital role in determining the size of the impingement-free and patient-specific safe zones (Fig. 10). This is consistent with Widmer’s [37] finding that stem anteversion between 10° and 20° maximizes the impingement-free safe zone. Our data further validated that the patient-specific safe zone, in which the standing and sitting pelvic tilt are considered, is also sensitive to stem version. The femur-first technique, with cup adaptation to the stem version, is recommended because of its reverse correlation with cup anteversion [7, 21, 26], and our data indicate that excessively aberrant stem version must be adjusted to allow for the creation of a reasonably large patient-specific safe zone for the cup, instead of always adapting the acetabular cup to the femoral stem version. Similar to the concept of redundancy design in the aviation industry [30], individualizing stem version helps to improve the calculated tolerance of THA implants to spinopelvic disturbances by providing a larger patient-specific safe zone [7] (Fig. 10).

The ROM criteria and femoral head size also have a great influence on the size of the patient-specific safe zone (Fig. 11). Similarly, the impingement-free safe zone has been reported to be sensitive to the ROM criteria and head-neck ratio set for calculation [5, 15]. Our study validated that the ROM criteria and femoral head diameter sensitively affect the patient-specific safe zone, in which the standing and sitting pelvic motions are considered. Therefore, we recommend an individualized ROM criterion for the clinical application of this algorithm that is based on the functional requirements of each patient.

Conclusion

Our study showed that the patient-specific safe zone algorithm can be an accurate tool for optimizing the acetabular cup and femoral stem orientations. The patient-specific safe zone is sensitive to changes in standing and sitting pelvic tilt, stem version, ROM criteria, and femoral head diameter. We recommend using a narrow safe zone of stem anteversion between 10° and 20° to maximize the size of the patient-specific safe zone. A patient-specific approach to planning target component orientations may maximize the benefits of robot-assisted THA. Future studies should integrate the traits of the prosthesis in clinical use, such as a hooped liner, shape of the femoral neck, and neck offset, to improve the algorithm’s prediction accuracy. Prospective multicenter clinical studies are required to validate its clinical efficacy for reducing dislocation and wear after THA.