CleftNet: Augmented Deep Learning for Synaptic Cleft Detection from Brain Electron Microscopy

Abstract

Detecting synaptic clefts is a crucial step to investigate the biological function of synapses. The volume electron microscopy (EM) allows the identification of synaptic clefts by photoing EM images with high resolution and fine details. Machine learning approaches have been employed to automatically predict synaptic clefts from EM images. In this work, we propose a novel and augmented deep learning model, known as CleftNet, for improving synaptic cleft detection from brain EM images. We first propose two novel network components, known as the feature augmentor and the label augmentor, for augmenting features and labels to improve cleft representations. The feature augmentor can fuse global information from inputs and learn common morphological patterns in clefts, leading to augmented cleft features. In addition, it can generate outputs with varying dimensions, making it flexible to be integrated in any deep network. The proposed label augmentor augments the label of each voxel from a value to a vector, which contains both the segmentation label and boundary label. This allows the network to learn important shape information and to produce more informative cleft representations. Based on the proposed feature augmentor and label augmentor, We build the CleftNet as a U-Net like network. The effectiveness of our methods is evaluated on both external and internal tasks. Our CleftNet currently ranks #1 on the external task of the CREMI open challenge. In addition, both quantitative and qualitative results in the internal tasks show that our method outperforms the baseline approaches significantly.

I. Introduction

Synapses are fundamental biological structures that transmit signals across neurons. A synapse is composed of several pre-synaptic neurons, a pro-synaptic neuron, and a synaptic cleft between these two types of neurons [1]–[3]. Detecting synapses and synaptic clefts is a key step to reconstruct synapses and investigate synaptic functions [4]–[11]. Currently, the volume electron microscopy (EM) is recognized as the most reliable technique for reconstruction of neural circuits [12]–[17]. It can provide 3D EM images with high resolution and sufficient details for synaptic cleft detection and synaptic structure analysis [18], [19].

The manual annotation of synaptic clefts is time-consuming and requires heavy labor from domain experts [20]. This raises the need of constructing computational models to automatically detect synaptic clefts from EM images. Machine learning approaches [4], [11], [18], [21] have been employed to learn relationships between EM images and the annotated clefts. Then for any newly obtained EM image, the synaptic clefts it contains could be directly predicted by the trained models. Earlier studies [4], [11] create hand-crafted features to train machine learning models for synaptic cleft detection. The features are carefully designed based on the prior knowledge of synapses and EM images.

With the rapid development of deep learning, recent methods [18], [21] automatically learn features from EM images using deep neural networks. Thus, hand-crafted features are avoided and models can be learned end-to-end. Importantly, synaptic cleft detection is formulated as an image dense prediction problem, where each voxel in the input volume is predicted as a cleft voxel or not. There exist several deep architectures for the dense prediction of biological images [22]–[27], among which networks based on the U-Net architecture [24], [28]–[30] are commonly employed. Existing studies [18], [21] apply vanilla U-Nets for cleft detection. However, they do not consider the unique properties of clefts, e.g., morphological patterns and geometrical shapes of clefts.

In this work, we propose the CleftNet, a novel deep learning model for improving synaptic cleft detection from brain EM images. Our CleftNet contains two novel components, known as the feature augmentor (FA) and the label augmentor (LA), to augment features and labels by considering and learning important properties of clefts. The feature augmentor is essentially a modified attention operator [31], [32] to generate augmented feature representations. The feature representation of each output position in the FA is dependent on features of all positions in the input. Hence, global information is captured effectively to improve cleft features. Importantly, a learning-based query tensor is used to learn common morphological patterns of all synaptic clefts. The query is fully trainable and updated by all input EM images. Thus, it can capture common patterns and learn topological structures in clefts, leading to augmented feature representations. Note that our proposed FA is flexible in terms of generating outputs of different sizes. Thus, it can simulate any commonly-used operations, like pooling, convolution, or deconvolution, and can be easily integrated into any deep neural network.

In addition to augmenting features using the FA, we propose the label augmentor to augment labels for voxels. Our label augmentor essentially employs multi-task learning using boundary information and a novel coherence loss. Existing methods mainly use original segmentation labels, which is demonstrated to be biased towards learning image textures while ignoring shape information [33], [34]. However, such information is important to circuit reconstruction based on biological images [21]. To this end, We proposed the LA to augment the label of each voxel from a scalar to a vector, which contains the segmentation label and the boundary label for the voxel. Hence, the whole network contains two streams and is trained with multi-task learning. In addition to the segmentation loss and boundary loss, we propose a novel coherence loss to suppress inconsistency between segmentation and boundary representations. By doing this, the network is encouraged to learn inherent high-level features for both texture and shape information from inputs, leading to more informative representations. Finally, we build the CleftNet, an augmented deep learning model with feature augmentors and label augmentors based on the U-Net architecture. We replace all the pooling layers, deconvolution layers, and the bottom block with the appropriately sized FAs to generate augmented features. A novel loss function based on the LA is used in the CleftNet for learning more powerful cleft representations.

We conduct comprehensive experiments to evaluate our methods. First, we apply our methods to the MICCAI Challenge on Circuit Reconstruction from Electron Microscopy Images (CREMI). Our CleftNet now ranks #1 on the synaptic cleft detection task of the CREMI open challenge. Next, we compare our methods with several baseline methods on both the validation set and the test data. Quantitative and qualitative results show that our methods achieve significant improvements over the baselines. In addition, we conduct ablation studies to demonstrate the effectiveness of the important network components including the FA, LA and the learnable query. Overall, our contributions are summarized as below:

• We propose the feature augmentor that improves cleft features through fusing global information from inputs and learning shared patterns in clefts. It can generate outputs with varying dimensions and can be adapted to any deep network with high flexibility.

• We design the label augmentor that augments the label for each voxel from a scalar to a vector. The LA enables the network to prioritize the learning of shape information, which is important for identifying synaptic clefts.

• We develop the CleftNet, an augmented deep learning method considering and learning specific morphological patterns and shape information in clefts. CleftNet generates improved cleft representations by incorporating the proposed feature augmentor and label augmentor.

• CleftNet is the new state-of-the-art model for synaptic cleft detection. It not only ranks #1 on the external task of the CREMI open challenge, but also outperforms other baseline methods significantly on internal tasks.

II. Related Work

A. Synaptic Cleft Detection

Machine learning methods have been explored for synaptic cleft detection. Earlier studies [4], [11] use carefully-designed features to train machine learning models. The work in [4] designs features for synapses by considering similar texture cues shared by clefts. The constructed features are then taken by an AdaBoost-based classifier to identify synapses and clefts. The work in [11] applies a random-forest classifier to hand-crafted features that constructed based on the geometrical information in EM volumes. Recently, deep learning methods [18], [21] are used to automatically learn features from EM images. Synaptic cleft detection is formulated as an image dense prediction problem in these methods. The work in [18] uses the 3D residual U-Net [35] to detect cleft voxels from a newly obtained large EM dataset. The misalignment issue of adjacent patches is tackled by designing a training strategy that is robust to misalignments. The work in [21] employs the vanilla 3D U-Net with an auxiliary task to detect clefts and uses the CREMI [36] dataset. Both approaches apply well-studied deep architectures and obtain state-of-the-art detection performance on the used datasets. In this work, we propose a novel deep model, known as CleftNet, to improve synaptic cleft detection by augmenting cleft features and labels of clefts.

B. Attention on Images

We summarize the attention-based methods on images in this section. Generally, there exist two categories of attention methods for images in literature; those are, gated-attention (GateAttn) methods and self-attention (SelfAttn) methods. We start by defining annotations for clear illustration. Given an input image tensor $\mathcal{M}$, we convert it to a matrix $M\in {\mathbb{R}}^{c\times s}$ following appropriate modes as introduced in [37], where s denotes the spatial dimensions, and c denotes the channel dimension. For instance, s = dhw if the input is a 3D image, where d, h and w denote the depth, height, and the width, respectively.

1). Gated-attention Methods:

The GateAttn aims at selecting important features from inputs using a trainable vector inspired by [38], [39]. This trainable vector can be treated as the context vector representing the contextual meaning of the input image. It is shared by all feature vectors and updated during the whole training process. Hence, the importance score for each feature vector is computed by inner product of itself and the trainable vector. The selection could be conducted along the spatial direction, namely spatial-wise attention (SWA), as used in the spatial attention module in CBAM [40] and the attention U-Net [31]. In the SWA, the matrix $M\in {\mathbb{R}}^{c\times s}$ could be treated as a set of vectors as ${\left\{m_i\in {\mathbb{R}}^c\right\}}_{i=1}^s$, where each m_i, is a vector representation for the pixel or voxel i, and i = 1, …, s. If the selection is performed along the channel direction, it is known as the channel-wise attention (CWA) and is used in the channel attention module in CBAM [40] and the squeeze and excitation networks [41]. We use the matrix $M^T\in {\mathbb{R}}^{s\times c}$ in CWA and it could be treated as a set of vectors as ${\left\{{\tilde{\mathbf{m}}}_j\in {\mathbb{R}}^s\right\}}_{j=1}^c$, where each ${\tilde{\mathbf{m}}}_j$ is a vector representation for the channel j, and j = 1, …, c.

Let ${\mathbf{\text{q}}}_s\in {\mathbb{R}}^c$ and ${\mathbf{q}}_c\in {\mathbb{R}}^s$ denote the learnable vectors for the SWA and the CWA. The corresponding importance vectors a_s and a_c are computed as

$$\begin{gathered} {\mathbf{\text{a}}}_s=\text{Softmax}\left(M^T{\mathbf{\text{q}}}_s\right)\in {\mathbb{R}}^s, \\ {\mathbf{\text{a}}}_c=\text{Softmax}\left(M{\mathbf{\text{q}}}_c\right)\in {\mathbb{R}}^c, \end{gathered}$$ (1)

where Softmax() denotes the element-wise softmax operation. Essentially, each $a_s^i$ in a_s indicates the important score for m_i and it is similar to $a_c^j$. Finally, in SWA, each m_i is scaled by its important score $a_s^i$, resulting in the output matrix N_s as a set of vectors as ${\left\{a_s^i{m}_i\in {\mathbb{R}}^c\right\}}_{i=1}^s$. Similarly, in CWA, the generated matrix N_c could be treated as ${\left\{a_c^j{\tilde{m}}_j\in {\mathbb{R}}^s\right\}}_{i=1}^c$. The obtained N_s or N_c can be converted back to the output tensor that has the same dimensions as the input $\mathcal{M}$. Importantly, the GateAttn highlights important pixels/voxels or channels using the commonly shared learnable vector. However, it fails in capturing global information to the output. In addition, using a trainable vector constraints the network’s capability to learn complicated patterns, such as the common morphological patterns shared by all clefts.

2). Self-attention Methods:

The SelfAttn is firstly introduced in the work [32] and then applied to images [42] and videos [43]. It first performs linear transformation on the $\mathcal{M}$ three times and generates three tensors; those are, the query $\mathcal{Q}$, the key $\mathcal{K}$, and the value $\mathcal{V}$. These three tensors are converted to three matrix Q, K, and V along the appropriate modes [37]. Each matrix has the dimensions of c × s same as M. SelfAttn is then performed as

$$N=V·\text{Softmax}\left(K^{T}Q\right)\in {\mathbb{R}}^{c\times s},$$ (2)

where Softmax() denotes the column-wise softmax operation. N is then converted back to the tensor $\mathcal{N}$ that has the same dimensions as $\mathcal{M}$. By performing SelfAttn, Each pixel/voxel feature in the output $\mathcal{N}$ is dependent on features of all the pixels/voxels in the input $\mathcal{M}$. To this end, SelfAttn is used to capture long-range dependencies and aggregate global information from inputs. However, all the three tensors $\mathcal{Q}$, $\mathcal{K}$, and $\mathcal{V}$ are generated from inputs, making them input-dependent, which may not able to capture the common patterns shared by all clefts. In addition, SelfAttn preserves the dimensions from inputs, which leads to its nature of low flexibility. For instance, we can only replace a convolution with a stride of 1 with SelfAttn. It can not simulate other operations that change the input dimensions, such as pooling or deconvolution. In this work, we propose a novel attention-based method, known as feature augmentor, using learnable query to capture common patterns in clefts and generating outputs with arbitrary dimensions.

III. The Proposed Methods

A. Feature Augmentation

The gated-attention and self-attention methods introduced in II have achieved great success in various domains, including natural language processing [38], [39] and computer vision [29], [30], [44]. Based upon these methods, we propose a novel method, known as the feature augmentor (FA), to improve cleft feature representations. our proposed FA not only aggregates global information from the whole feature space of inputs, but also captures shared patterns of all synaptic clefts in the whole dataset, thereby leading to augmented and improved feature representations.

An illustration of our proposed FA is provided in Figure 1. Formally, let $\mathcal{M}\in {\mathbb{R}}^{d\times h\times w\times c}$ denote the input tensor to the FA, where d is the depth, h is the height, w is the width, and c is the number of channels. We first generate the key tensor $\mathcal{K}$ and the value tensor $\mathcal{V}$ from the input tensor M by performing two separate 3D convolutions, each of which has a kernel size of 1 × 1 × 1 and a stride of 1. The used convolutions retain the spatial sizes of the input tensor but generate varying numbers of feature maps. Assuming the first convolution above produces c_k feature maps, thus, we have $\mathcal{K}\in {\mathbb{R}}^{d\times h\times w\times c_k}$. Similarly, we obtain $\mathcal{V}\in {\mathbb{R}}^{d\times h\times w\times c_v}$ assuming the second convolution generates c_v feature maps. Note that $\mathcal{K}$ and $\mathcal{V}$ are both generated from M, hence, they are input-dependent.

Fig. 1.

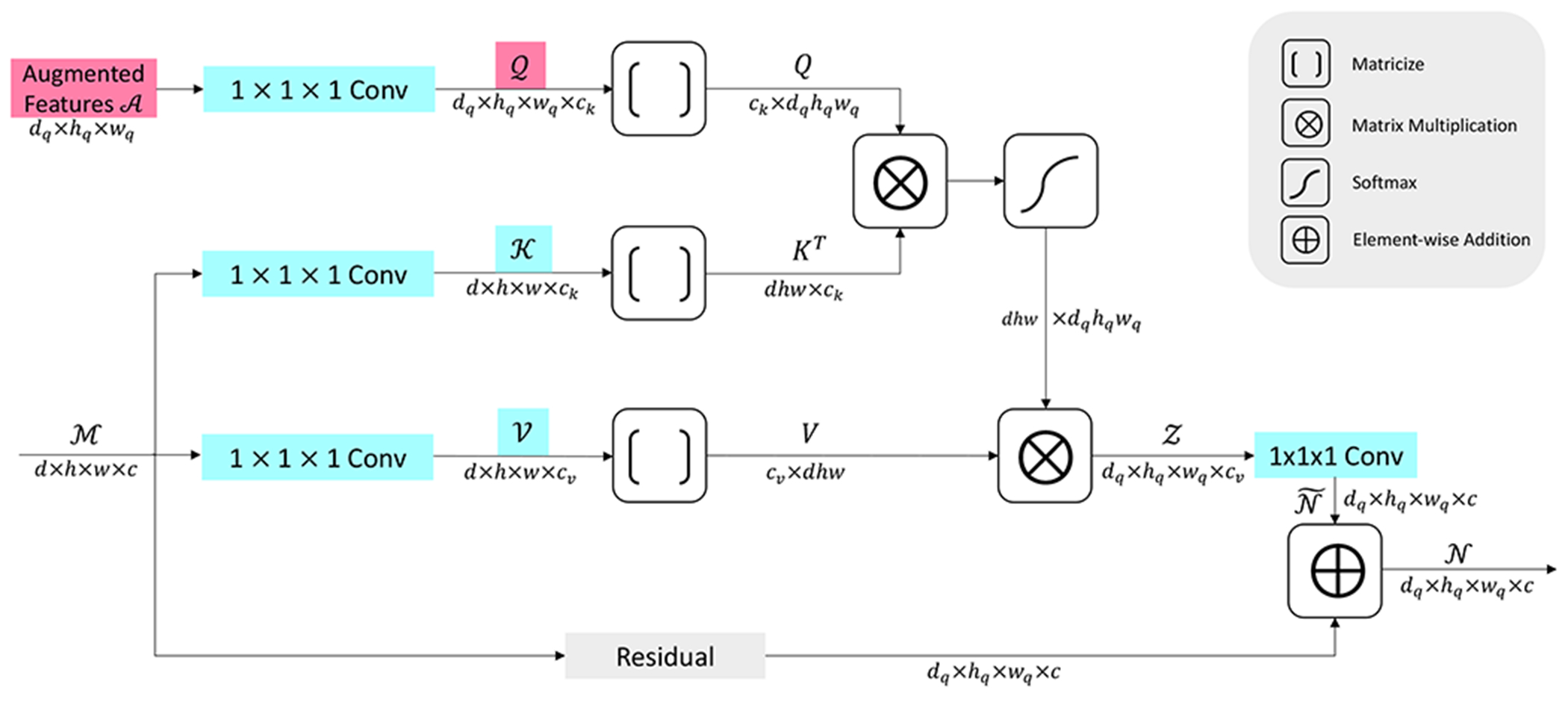
An illustration of the proposed feature augmentor (FA) as detailed in Section III-A. For each operation, the generated tensor/matrix and the dimensions are marked aside the corresponding arrow. The operations for converting tensors back to matrices are not included for simplification. The augmented features tensor $\mathcal{A}$ contains free parameters and is trained during the whole learning process to capture shared patterns of cleft features. The query tensor $\mathcal{Q}$ is obtained by performing a 1 × 1 × 1 convolution on $\mathcal{A}$. The depth, height, and the width of the output tensor $\mathcal{N}$ are determined by those of $\mathcal{A}$ or $\mathcal{Q}$. These dimensions can be flexibly adapted per design requirements. Hence, the proposed FA can replace any commonly-used operation like pooling or deconvolution, and can be integrated to any deep architecture with high flexibility.

Next, we consider the query tensor $\mathcal{Q}$ in our proposed FA. Existing studies [29], [30], [44] use the same strategies to generate $\mathcal{Q}$ as $\mathcal{K}$ and $\mathcal{V}$, making it to be input-dependent. In this work, we instead produce Q from a learnable tensor $\mathcal{A}\in {\mathbb{R}}^{d_q\times h_q\times w_q}$ containing free parameters, where d_q, h_q, w_q denote the depth, height, and width respectively. The parameters in $\mathcal{A}$ are randomly initialized and trained along with other parameters during the whole learning process. The output feature map number c_q in $\mathcal{Q}\in {\mathbb{R}}^{d_q\times h_q\times w_q\times c_q}$ needs to be equal to c_k as required by the attention mechanism.

The main purpose of using a learnable tensor $\mathcal{A}$ generating $\mathcal{Q}$ is to capture shared patterns of all synaptic clefts. Even though different synaptic clefts exhibit distinct shapes, they share common morphological patterns. Such patterns are important for learning structural topology and improving cleft feature representations. Existing studies [29], [30], [44] obtain the query tensor by imposing a linear transformation on the input $\mathcal{M}$. However, they suffer from two limitations when learning cleft features. First, the input-dependent query fails to capture the common patterns shared by all clefts. In addition, the shared patterns are complicated, and it is difficult to explicitly capture them by performing a linear transformation on the input. To this end, inspired by the gated-attention, we use a learning-based query $\mathcal{Q}$ to automatically learn such complicated and shared patterns. As $\mathcal{A}$ is shared and updated by all input volumes in the dataset, it is expected to grasp common patterns and help to augment cleft features.

After obtaining the tensors $\mathcal{K}$, $\mathcal{V}$, and $\mathcal{Q}$, we perform attention by first converting them to three matrices. Formally, we have

$$\begin{gathered} K=\text{Matricize}(\mathcal{K})\in {\mathbb{R}}^{c_k\times dhw}, \\ V=\text{Matricize}(\mathcal{V})\in {\mathbb{R}}^{c_v\times dhw}, \\ Q=\text{Matricize}(\mathcal{Q})\in {\mathbb{R}}^{c_k\times d_q{h}_q{w}_q}, \end{gathered}$$ (3)

where Matricize() denotes the mode-4 matricization of an input tensor [37]. The attention is then performed as

$$Z=V·\text{Softmax}\left(K^{T}Q\right)\in {\mathbb{R}}^{c_v\times d_q{h}_q{w}_q},$$ (4)

where Softmax() denotes the column-wise softmax operation. The Z is then converted back to the tensor $\mathcal{Z}\in {\mathbb{R}}^{d_q\times h_q\times w_q\times c_v}$ along mode-4 [37]. Another 1 × 1 × 1 3D convolution is performed on $\mathcal{Z}$ to produce $\tilde{\mathcal{N}}\in {\mathbb{R}}^{d_q\times h_q\times w_q\times c}$ to match the number of feature maps of the input $\mathcal{M}$. Then the final output $\mathcal{N}$ of the proposed FA is computed as

$$\mathcal{N}=\tilde{\mathcal{N}}+\text{Residual}(\mathcal{M})\in {\mathbb{R}}^{d_q\times h_q\times w_q\times c},$$ (5)

where Residual() denotes the residual operations that directly map the input to the output with the purpose of reusing features and accelerating training [45]. It is obvious that the depth, height, and width of $\mathcal{N}$ are determined by $\mathcal{Q}$. Theoretically, d_q, h_q, and w_q can be any positive integers. In practice, we consider three scenarios to be corresponding to other commonly-used operations. For instance, we set d_q = 1/2d, h_q = 1/2h, w_q = 1/2w to correspond with a 2 × 2 × 2 pooling or a convolution with a stride of 2; we set d_q = 2d, h_q = 2h, w_q = 2w to match up with a deconvolution with a stride of 2; we can also preserve the spatial dimensions from the input to simulate a convolution with a stride of 1. For the residual operations, accordingly, we simply use a 2 × 2 × 2 max pooling, a trilinear interpolation with a factor of 2, and an identical mapping for these three scenarios.

Generally, the matrix Q in Eq. 4 can be treated as a set of query vectors ${\left\{q_i\in {\mathbb{R}}^{c_q}\right\}}_{i=1}^{d_q{h}_q{w}_q}$, and it is similar to K, V and the produced Z. K^T Q enables each query q_i to attend each key vector k_j, generating an attention map as a matrix (a_ji), where i = 1, …, d_qh_qw_q, and j = 1, …, dhw. This matrix is further normalized by performing the column-wise softmax operation. Next, by multiplying V at the left side, each output vector z_h in Z is obtained as a weighted sum of all the value vectors in V, with each v_g scaled by the weight a_gh in the attention map matrix. By doing this, the feature vector of each voxel in the tensor $\mathcal{Z}$ is dependent on feature vectors of all the voxels in the input. Hence, global information from the whole feature space of the input is captured effectively. In addition, we use a learnable tensor $\mathcal{A}$ to produce the query tensor $\mathcal{Q}$, thus automatically learning shared pattern features of all synaptic clefts. The query $\mathcal{A}$ is randomly initialized and trained during the whole learning process. As $\mathcal{A}$ is shared and updated by all input volumes, it is expected to grasp common patterns and shape structural relationships in clefts. Notably, our FA with learnable $\mathcal{A}$ is based on gated-attention methods introduced in Sec. II-B1. Similarly, the optimized $\mathcal{Q}$ is obtained in training and then fixed in inference. Even though Q represents high-level cleft patterns and is not spatially specific, $\mathcal{K}$ and $\mathcal{Q}$ are input-dependent and contain spatial information. By performing two matrix multiplications in Eq. (4), the spatial information is effectively preserved in outputs of FA. Interestingly, in inference, if the input tensor $\mathcal{K}$ and $\mathcal{Q}$ contain cleft features, $\mathcal{Q}$ with augmented cleft patterns would help recognize such cleft features, leading to more powerful models. In opposite, if there are no cleft features in $\mathcal{K}$ and $\mathcal{Q}$, the generated output would not contain clefts due to the nature of multiplication that zero times anything remains zero. Overall, the basic computing procedures in the attention mechanism ensure that our FA with learnable query still generate spatially precise outputs.

B. Label Augmentation

Deep neural networks (DNNs) have achieved state-of-the-art performance on the tasks of dense prediction for 3D images [28], [30], [46] Existing methods mainly perform voxel-wise classification and the label information only contains the category for each voxel. In this work, we propose the label augmentor (LA) to augment labels and explicitly consider shape information of clefts.

Generally, an image contains color, shape, and texture information. These information is combined together to DNNs for pixel/voxel-wise classification [33], [47]. The work in [34] demonstrates that DNNs have strong biases towards learning textures but pay little attention to shapes. In biological-image analysis, however, manual annotations from domain experts are usually conducted with the prior knowledge of boundary and shape identification. For instance, segmenting clefts from tissue volumes would entail following cleft boundaries and consequently narrowing the region of interest. Hence, it is natural to leverage shape information to enhance the capability of the networks. To this end, we propose to prioritize the learning of boundary information by augmenting labels. Specifically, for each voxel, we augment its label from a scalar to a vector, which consists of both the segmentation category and the corresponding boundary information. The proposed label augmentor enables the multi-task learning that captures ample information from input EM images.

There exist several methods to compute and incorporate boundary information [33], [48]–[50]. In this work, we use tanh distance map (TDM) to represent the boundary information. TDM computes the tanh of the Euclidean distance of each voxel from the nearest boundary voxel [51]. To enable the accurate learning of both texture and boundary information, we design three loss functions, including the segmentation loss ${\mathcal{L}}_s$, boundary loss ${\mathcal{L}}_b$, and the coherence loss ${\mathcal{L}}_c$. ${\mathcal{L}}_c$ is proposed to suppress the inconsistency between texture and boundary. The final loss of the network is the combination of these three loss functions.

Formally, let Λ denote the set of cleft voxels for one synaptic cleft, and let ∂Λ represent the set of boundary voxels for this synaptic cleft. Then the TDM y_b is defined as

$$y_b^i=\{\begin{array}{ll}\tanh \left(\underset{j\in \partial \text{Λ}}{\min }\text{d}(i,j)\right)& i\in \text{Λ}\\ 0& i\notin \text{Λ}\end{array},$$ (6)

where i is the index of any voxel in the input volume, d( , ) denotes the Euclidean distance for any two voxels, and tanh() is the element-wise tanh operation. Apparently, $y_b^i$ is in the range of (0, 1) based on the definition. Essentially, TDM reveals how each voxel contributes to the shape of the corresponding cleft. Let $y_s^i$ denote the original segmentation category of the voxel i. To this end, we augment the label for each voxel i to a vector ${\ell }^i={\left[y_s^i,y_b^i\right]}^T$.

Let $y_s^i=1$ indicate the voxel i is a cleft voxel. For the segmentation steam, a weighted binary cross-entropy loss is proposed as

$${\mathcal{L}}_s=-{\beta }_s\sum _{i\in y_s^{+}}\log P\left(y_s^i=1\right)-\left(1-{\beta }_s\right)\sum _{i\in y_s^{-}}\log P\left(y_s^i=0\right),$$ (7)

where ${\beta }_s$ is the ratio of non-cleft voxels to all voxels in the volume, $P\left(y_s^i\right)$ is the probability of the predicted class for the voxel i, and $y_s^{+}$, $y_s^{-}$ are the sets of indexes of voxels whose segmentation labels are clefts, non-clefts, respectively. As the data is imbalanced and the non-clefts are overwhelmingly dominant in the volume, β_s is close to one while 1 − β_s is close to zero. Intuitively, we use larger penalties for cleft voxels in the loss function to tackle the imbalance issue.

Essentially, the segmentation stream is a voxel-wise classification problem, while the boundary stream is a voxel-wise regression problem. We use the weighted L2 loss for the boundary stream as

$${\mathcal{L}}_b={\beta }_b\sum _{i\in y_b^{+}}{\left(y_b^i-{\widehat{y}}_b^i\right)}^2+\left(1-{\beta }_b\right)\sum _{i\in y_b^{-}}{\left(y_b^i-{\widehat{y}}_b^i\right)}^2,$$ (8)

where β_b is the ratio of voxels whose boundary labels are larger than zero to all voxels in the volume, ${\widehat{y}}_b^i$ is the predicted boundary distance of the voxel i, and $y_b^{+}$, $y_b^{-}$ are the sets of indexes of voxels whose boundary labels are positive, and zeros, respectively.

We augment the label of each voxel i to a vector ${\ell }^i={\left[y_s^i,y_b^i\right]}^T$, and the boundary label $y_b^i$ is computed based on the provided segmentation label $y_s^i$. Importantly, there exists correspondence between these two scalars. Specifically, the segmentation label $y_s^i=1$ is in line with the boundary label $y_b^i>0$, and $y_s^i=0$ corresponds to $y_b^i=0$. By augmenting labels and employing the same network with weight sharing, the texture and shape information are jointly learned together in the training phase. However, there may still exist mismatch in the predicted segmentation map and shape map. Here, we propose a coherence loss as a regularizer as

$${\mathcal{L}}_c=-\sum _{i\in {\widehat{y}}_b^{+}}\left(1-{\widehat{y}}_s^i\right)\log {\widehat{y}}_b^i-\sum _{i\in {\widehat{y}}_b^{-}}\left(1-{\widehat{y}}_b^i\right)\log P\left(y_s^i=1\right),$$ (9)

where ${\widehat{y}}_b^{+}$, and ${\widehat{y}}_b^{-}$ denote the sets of voxels whose predicted boundary values are positive, and non-positive, respectively. Intuitively, we impose a penalty to voxel i if the two predicted values ${\widehat{y}}_s^i$ and ${\widehat{y}}_b^i$ are not consistent with each other. Specifically, there are two terms in Eq. 9. The former penalizes the voxel i whose predicted boundary value is positive while the predicted segmentation value is zero. We use the function −log to impose heavier penalties for the voxels close to the boundary. For the latter, the voxel is penalized if the predicted boundary value is zero but the predicted segmentation value is one. Note that ${\widehat{y}}_b^i$ ranges from 0 to 1 in the former. Correspondingly, we use $P(y_s^i=1)$ to produce a probability that also ranges from 0 to 1 in the latter.

The final loss is computed as the weighted sum of the above three loss functions as

$$\mathcal{L}={\mathcal{L}}_s+{\alpha }_1{\mathcal{L}}_b+{\alpha }_2{\mathcal{L}}_c,$$ (10)

where the weights α₁ and α₂ are hyper-parameters. Notably, we use the same network to produce outputs for both segmentation and boundary streams, and the parameters are shared across both streams. By doing this, the network is forced to learn high-level features for both texture and shape information. The strategy of weight sharing not only helps ${\mathcal{L}}_s$ and reduces the inconsistency between the segmentation and boundary outputs, but also accelerates the training through involving less parameters. As a result, shape information is precisely considered in LA without increasing the computational cost. Experimental studies in Sec. IV-I also show that the weight sharing achieves better performance than using different decoders for two streams. In addition, all of the ${\mathcal{L}}_s$, ${\mathcal{L}}_b$, and ${\mathcal{L}}_c$ are demonstrated to make contributions to final performance.

C. CleftNet

Deep architectures have been intensively studied for dense prediction of biological images [23], [24], [29], among which networks based on the U-Net architecture are shown to achieve superior performance [24], [28], [29]. Essentially, the U-Net consists of an encoder and a decoder, which are connected by the bottom block and several skip connections. In this work, we propose the CleftNet, an augmented U-Net like network with the proposed feature augmentors and label augmentors, for improving synaptic cleft detection from EM images.

Specifically, we replace all the downsampling layers in the encoder, all the upsampling layers in the decoder, and the bottom block of the vanilla U-Net with the corresponding FAs as introduced in Section III-A. An illustration of producing query tensors in all FAs on the U-Net architecture is provided in Fig. 3. Importantly, we only formulate one learnable augmented features tensor $\mathcal{A}$ in the first FA that replaces the first downsampling layer of the U-Net architecture. Thus, the augmented features tensor $\mathcal{A}$ has the same dimensions as the input image. The query tensor in the first FA is produced by performing a 1 × 1 × 1 3D convolution on $\mathcal{A}$. To be clearer, we denote the query tensor in Fig. 1 as ${\mathcal{Q}}^0$. Query tensors in following FAs are directly computed based on ${\mathcal{Q}}^0$ to capture hierarchical shared patterns and accelerate training. For example, when replacing the second downsampling layer with a FA, the corresponding query ${\mathcal{Q}}^1$ is obtained by performing a 3 × 3 × 3 convolution with stride 2 on ${\mathcal{Q}}^0$. Hence, the depth, height, and width of ${\mathcal{Q}}^1$ are all set to be half of those of the input tensor to this FA. The number of channels ${\mathcal{Q}}^1$ should match the key tensor of the current FA. In addition, the residual operation used in this FA is a 2 × 2 × 2 max pooling. It is similar in the decoder that the query tensor in one FA is achieved by performing a 3 × 3 × 3 deconvolution with stride 2 on the query tensor of the previous FA. By doing this, shared patterns are learned in a hierarchical fashion while the number of parameters is kept acceptable. Essentially, The proposed FA augments cleft features by aggregating global information from the whole input volume and capturing commonly shared patterns of all clefts in a hierarchical manner.

Fig. 3.

An illustration of generating query tensors in all FAs on the U-Net architecture. We use a U-Net with depth 3 for simplification. Fig. 1 essentially shows how to obtain the query tensor in the first FA. We denote this query tensor as ${\mathcal{Q}}^0$ and it is obtained by performing a 1 × 1 × 1 convolution on the augmented features tensor $\mathcal{A}$. In the encoder, each of the query tensor in other FAs is achieved by performing a 3 × 3 × 3 convolution with stride 2 on the previous query tensor. In the decoder, each of the query tensor in FAs is produced by performing a 3 × 3 × 3 deconvolution with stride 2 on the previous query tensor. Hence, shared patterns in clefts are learned in a hierarchical fashion.

By incorporating the proposed LA as described in Section III-B, the CleftNet outputs a vector with two elements for each voxel corresponding to its label vector containing the segmentation label and the boundary label. The final loss function of the CleftNet is the weighted sum of the three loss functions as mentioned in Eq. 10. By doing this, the network is forced to learn both the texture and the shape information for synaptic clefts, thereby leading to more powerful cleft representations.

IV. Experimental Studies

A. Dataset

We use the dataset from the MICCAI Challenge on Circuit Reconstruction from Electron Microscopy Images (CREMI) [36]. The CREMI dataset was obtained from the adult Drosophila using serial section transmission electron microscopy (ssTEM) with the resolution 40nm × 4nm × 4nm. The training data is consist of three volumes A, B, and C, each of which has the spatial sizes of 125 × 1250 × 1250. The original segmentation label for the training data indicates whether a voxel is a background voxel or a cleft voxel. There are also three volumes A+, B+, and C+ with the same dimensions as the training volumes in the test data, but the label is not publicly provided. The CREMI challenge requires the submitting of predicted results to conduct unbiased comparisons among different methods. Generally, the data is sparse regarding the ratio of cleft voxels to total voxels.

B. Network Settings

Our proposed CleftNet follows the general settings in the 3D U-Net architecture [28] and ResUnet [35] with integrating our proposed FAs and LAs. Both the encoder and decoder contain 4 blocks, and the numbers of output channels of the 4 block are 32, 64, 96, 128, respectively. The bottom block outputs 160 channels. We replace the second convolution block in each of the 9 blocks in the original 3D U-Net architecture [28] with a residual block. By doing this, each of the 9 blocks contains a convolution block, a residual block, and a corresponding FA, sequentially. Each of the 4 used FAs in the encoder serves as a downsampling layer such that the spatial sizes are halved along the depth, height, and the width directions. In the decoder, the FA can be used for performing upsampling and recovering the spatial sizes of inputs. For c_k and c_v in each FA, we set them to be quarter of the number of channels of the input tensor. Similar to the work [32], each FA is followed by layer normalization [52]. Convolution layers and residual blocks in the encoder and decoder are used for extracting features. Each convolution block is consist of a convolution layer with kernel 3 × 3 × 3 and stride 1, followed by a batch normalization (BN) layer and ELu with α equal to 1 [53]. For each residual block, we employ the original version of ResNets in [54] that addition is performed after the second BN layer and before the second Elu. The output block integrates our proposed LA and generates two channels for both the textual and shape learning. The weights in Eq. 10 are α₁ = 0.5, α₂ = 0.2, respectively.

C. Training and Inference

Each of the three volumes A, B, C in the training data contains 125 slices. We use the first 100 slices of all the A, B, C as the training set. The last 25 slices of A, B, C are used as the validation set. In this way, the training set contains three volumes with sizes of 100 × 1250 × 1250, while the validation set contains three volumes with sizes of 25 × 1250 × 1250.

We compute the augmented label vector based on the original segmentation label for each voxel of the input volumes. The input sizes of the network are set to be 8 × 256 × 256. During training, a 3D patch with sizes 8 × 256 × 256 is randomly cropped from the any of the three volumes as input to the network to train the weights. During inference, we first perform prediction for each patch and then stack all the predicted patches together to generate the final prediction map for each volume. As the data is sparse, we further tackle the imbalance issue by counting the number of cleft voxels in an input patch. Specifically, we reject a patch with a high probability of 95% if it contains less than 200 cleft voxels. Our data augmentation techniques include rotation with probability 0.5, flip with probability 0.5, and grayscale with probability 0.2. We run 10e5 iterations in total, and inference on the validation set is performed per 100 iterations. Four NVIDIA GeForce RTX 2080 Ti GPUs are used in both training and inference. We employ the Adam optimizer [55] with a fixed learning rate. Batch size and learning rate are tuned on the validation set using grid search. Search space for batch size is {4, 8, 16} and for learning rate is {1e-2, 1e-3, 1e-4}. Based on inference performance on the validation set, we set the batch size to be 16 and learning rate to be 1e-3 for all optimized models. We do not use weight decay or dropout for all models.

After obtaining the optimized model, we conduct inference on the test data, which contains three volumes A+, B+, and C+ with sizes of 125 × 1250 × 1250. We use the same input patch sizes 8 × 256 × 256 and generate predicted patches then stack them together as the final predictions. As the ground truth of the test data is not publicly provided, we submitted the predictions to CREMI open challenge to compute the model performance.

D. Metrics

As data is imbalanced regarding the ratio of cleft voxels to total voxels in three volumes, we use F1-score, AUC, and CREMI-score for evaluation. Note for experiments on the internal tasks on the validation set, we use all of these three metrics. For external tasks on the test set, The CREMI organizers only provide results for F1-score and CREMI-score at their website. The CREMI-score is computed as

$$\text{CREMI-score}=\frac{\text{ADGT}+\text{ADF}}{2},$$ (11)

where ADGT represents the average distance of any predicted cleft voxel to the closest ground truth cleft voxel, which is related to FPs in predictions. ADF denotes the average distance of any ground truth cleft voxel to the closest predicted cleft voxel, which is related to FNs in predictions. Essentially, CREMI-score measures the overall distance between a predicted cleft and a true cleft. Note that CREMI-score is used as the primary ranking metric on the leaderboard of synaptic cleft detection of the CREMI open challenge.

E. CREMI Open Challenge Task

The MICCAI Challenge on Circuit Reconstruction from Electron Microscopy Images (CREMI) [36] started from the year of 2016 and has become one of the most well-known open challenges on EM data. There are totally three tasks in the CREMI challenge including neuron segmentation, synaptic cleft detection, and synaptic partner identification. We focus on the task of synaptic cleft detection and the used data is described in Section IV-A. As the label for the test data is not publicly provided, we submitted the predicted results of our CleftNet to the task of synaptic cleft detection of the CREMI challenge, where CREMI-score is used as the primary ranking metric. There are at least 15 groups participating in this task. We summarize the results of the best models for the top 5 groups in Table I. Our best model CleftNet ranks the first with the CREMI-score of 57.73 and F1-score of 0.831.

TABLE I.

Results on the task of synaptic cleft detection of the CREMI open challenge. We summarize the results of the best models for the top 5 groups. Our group is DIVE, and our best models is CleftNet. A DOWNWARD ARROW ↓ is used to indicate that a lower metric value corresponds to better performance. An upward arrow ↑ is used to indicate that a higher metric value corresponds to better performance. These results are provide at the CREMI website [36].

Rank	Group	Model	CREMI-score(↓)	F1-score(↑)
1	DIVE	CleftNet	57.73	0.831
4	CleftKing	CleABC1	58.02	0.821
6	lbdl	lb_thicc	59.04	0.810
9	3DEM	BesA225	59.34	0.823
15	SDG	Unet2	63.92	0.744

F. Comparison with Baselines

We compare our methods with several state-of-the-art architectures including SegNet [56], V-Net [22], 3D U-Net [28], ResUnet [35], and AttnUnet [31]. To ensure fair comparisons, we use similar architectures for all methods, including number of blocks for the encoders and decoders, numbers of output features of each block, etc. In addition, we integrate their official code for specific components (like residual blocks and attention units) to the architectures.

For the validation set, we directly report the computed values for all metrics from the optimized models. The comparison results are provided in Table II. We can observe from the table that our proposed CleftNet consistently outperforms other baseline methods on all the three metrics. Specifically, compared with the best baseline method AttnUnet, CleftNet refines the CREMI-score by a large margin of 6.84, which is a considerable value of 13.5% of our current CREMI-score 50.50. CleftNet reduces the CREMI-score by an average margin of 13.76 when considering all the five baseline methods, which is an incredible percentage of 27.2% of our current score. In addition, CleftNet outperforms the baselines on the other two metrics by average margins of 4.25% in terms of AUC and 3.72% in terms of F1-score. All of these results demonstrate the effectiveness of CleftNet with the proposed feature augmentors and label augmentors.

TABLE II.

Comparison among different models in terms of CREMI-score, F1-Score, and AUC on the validation set. The best performance is in bold.

Model	CREMI-score(↓)	AUC(↑)	F1-score(↑)
SegNet	72.32	0.883	0.842
3D U-Net	64.27	0.875	0.837
V-Net	65.73	0.896	0.858
ResUnet	59.64	0.909	0.874
AttnUnet	57.34	0.914	0.878
CleftNet	50.50	0.938	0.895

For the test data, we submitted the predicted volumes from all the optimized models to the CREMI open challenge for evaluation. The results in terms of CREMI-score and F1-score are provided at the CREMI website [36] and summarized in Table III. We draw similar conclusions that CleftNet performs the best on the test data. Specifically, CleftNet outperforms the other five methods by an average margin of 15.33 in terms of CREMI-score, which is 26.6% of the current score 57.73. In addition, CleftNet achieves an average improvement of 3.12% in terms of F1-score. The CREMI open challenge does not provide results for AUC.

TABLE III.

Comparison among different models in terms of CREMI-score and F1-Score on the test data. The best performance is in bold.

Model	CREMI-score(↓)	F1-score(↑)
SegNet	82.46	0.794
V-Net	76.12	0.744
3D U-Net	75.02	0.800
ResUnet	66.50	0.813
AttnUnet	65.19	0.812
CleftNet	57.73	0.831

G. Ablation Studies

We conduct ablation study to investigate the effectiveness of our proposed components feature augmentor (FA) and label augmentor (LA). We remove the FAs from CleftNet which we denote as CleftNet w/o FA, and we remove the LAs from CleftNet which we denote as CleftNet w/o LA. If we remove both the FAs and LAs then CleftNet would simply become ResUnet. We also include the results of AttnUnet to compare the attention units used in AttnUnet and our proposed FA. Experimental results on the validation set is provided in Table IV. We can observe from the table that CleftNet outperforms ResUnet by large margins of 9.14, 2.7%, and 2.1% in terms of CREMI-score, AUC, and F1-score, respectively. As we use ResUnet as the backbone architecture, the better performance achieved by CleftNet compared with ResUnet indicates the effectiveness of our proposed FA ans LA. In addition, the contribution of FAs can be shown from two comparisons; these are, the better results of CleftNet w/o LA over ResUnet, and the better results of CleftNet over CleftNet w/o FA. Similarly, both the better performances of CleftNet w/o FA over ResUnet and CleftNet over CleftNet w/o LA reveal the effectiveness of LAs.

TABLE IV.

Comparison among ResUnet, AttnUnet, CleftNet without feature augmentors (FAs), CleftNet without lable augmentor (LAs), and CleftNet in terms of CREMI-score, F1-Score, and AUC on the validation set.

Model	CREMI-score(↓)	AUC(↑)	F1-score(↑)
ResUnet	59.64	0.909	0.874
AttnUnet	57.34	0.914	0.878
CleftNet w/o FA	53.37	0.922	0.883
CleftNet w/o LA	52.65	0.930	0.890
CleftNet	50.50	0.938	0.895

Notably, the only difference of CleftNet w/o LA from AttnUnet is the use of the FAs rather that the attention units proposed in AttnUnet. Table IV shows that compared with AttnUnet, CleftNet w/o LA induces improvements of 6.99, 2.1%, and 1.6% in terms of CREMI-score, AUC, and F1-score, respectively. This reveals the superior capability of our proposed FA than the attention unit. Essentially, the used attention unit in AttnUnet employs a query vector to highlight more important voxels in the input. The inner product between the query vector and each voxel vector produces a scalar as the importance score of the corresponding voxel. However, it fails to aggregate global context information from the whole input to the output, imposing natural constraints to the network’s capability. In addition, a single vector may not sufficient to store and learn the commonly shared patterns of all clefts in the dataset. Our FA uses a learnable query tensor with high dimensions and generates response of each voxel by considering all the voxels in the input. By doing this, FA not only extracts global information from the whole input volume, but also captures the complicated shared patterns of all clefts in the dataset, leading to augmented and improved cleft features.

We summarize the results on the test data in Table V. For CREMI score, CleftNet w/o LA reduces the score by 7.47 compared with ResUnet, and CleftNet reduces the score by 1.38 compared with CleftNet w/o FA. Both of these demonstrate the contribution of the proposed FA. Similarly, the effectiveness of the LA can be demonstrated by either the improvement of 7.39 induced by CleftNet w/o FA over ResUnet, or the the improvement of 1.30 induced by CleftNet over CleftNet w/o LA. Essentially, we draw consistent conclusions that both the FA and LA make considerable contributions for learning better cleft representations.

TABLE V.

Comparison among ResUnet, AttnUnet, CleftNet without feature augmentor (FA), CleftNet without lable augmentor (LA), and CleftNet in terms of CREMI-score and F1-Score on the test data.

Model	CREMI-score(↓)	F1-score(↑)
ResUnet	66.50	0.813
AttnUnet	65.19	0.812
CleftNet w/o FA	59.11	0.820
CleftNet w/o LA	59.03	0.823
CleftNet	57.73	0.831

H. Investigating Different Queries

We investigate the effectiveness and efficiency of the learnable query in FA compared the input-dependent query in self-attention [32]. The studies [29], [30] use similar strategies to integrate attention-based methods in U-Net, but the query tensor is achieved by performing a linear transformation on the input. By doing this, the query is similar as the key and value that to be input-dependent. For clear illustration, we denote our method as CleftNet w FA, and the methods in [29], [30] as CleftNet w SelfAttn. Note that SelfAttn here is not exactly the self-attention in the work [32], but based on our investigation in Sec. III-A that output spatial dimensions are the same as those of the query tensor. Hence, we perform max pooling or trilinear interpolation on query tensors to achieve downsampling or upsampling. In addition, the original self-attention in the work [32] uses $\sqrt{c_k}$ to scale the dot product between the key and query matrices. We set another two networks CleftNet w FA (scale) and CleftNet w SelfAttn (scale) to study the effect of such scaling.

Experiments are conducted to compare these four methods and the results on the validation set are reported in Table VI. We can observe from the table that our method induces improvements based on CleftNet w SelfAttn with and without scaling. Specifically, CleftNet w FA outperforms CleftNet w SelfAtt by margins of 1.48, 0.6%, and 2.1% in terms of CREMI-score, AUC, and F1-score, respectively. CleftNet w FA (scale) outperforms CleftNet w SelfAtt (scale) by margins of 1.38, 1.4%, and 1.4% in terms of CREMI-score, AUC, and F1-score, respectively. This indicates that compared with using self-attention, integrating our proposed FA in U-Net generates better cleft representations. The performance improvements are achieved by purely using the learnable query rather than the input-dependent query. Note that our FA can achieve one similar goal as self-attention that capturing global context information. The output response of each voxel fuses information from all the voxels in the whole input volume. However, commonly shared patterns for clefts are complicated, and it is difficult to obtain these patterns by performing a linear transformation on the input. The self-attention used in [29], [30] designs the query to be input-dependent, failing to store and learn complicated inherent patterns shared by all the clefts in the dataset. Instead, in our FA, we design a trainable augmented features tensor $\mathcal{A}$ to generate query tensors for automatically learning such complex patterns during the whole training process and produce better cleft representations. We can also observe from the table that the scaling does not affect final performance significantly. This maybe because $\sqrt{c_k}$ is set to be quarter of the input channels and is relatively small. Hence, the dot product would not generate extremely large values then it is not necessary to perform scaling.

TABLE VI.

Comparison between CleftNet w SelfAtt and CleftNet w FA with ans without scaling in terms of CREMI-score, F1-Score, AUC, number of parameters, and parameter ratio on the validation set.

Model	CREMI-score(↓)	AUC(↑)	F1-score(↑)	* of Parameters	Parameter Ratio
CleftNet w SelfAttn	51.98	0.932	0.874	6,602,785	0.00%
CleftNet w FA	50.50	0.938	0.895	6,843,126	3.64%
CleftNet w SelfAttn (scale)	51.95	0.930	0.874	6,602,785	0.00%
CleftNet w FA (scale)	50.57	0.944	0.888	6,843,126	3.64%

Importantly, compared with CleftNet w SelfAttn, additional parameters in CleftNet w FA come from the only learnable tensor $\mathcal{A}$ in the first FA, and several convolution and deconvolution layers to generate query tensors in all FAs, as shown in Fig. 3 and introduced in Sec. III-C. Table VI shows CleftNet w FA only induces 3.64% additional parameters. Hence, FAs will not significantly increase the number of trainable parameters or cause the over-fitting.

I. Investigating Three Loss Functions

In LA, we use the strategy of weight sharing to generate outputs for both streams when computing ${\mathcal{L}}_s$ and ${\mathcal{L}}_b$. This aims to force the network to learn high-level feature for both texture and shape information, and to accelerate the training using less parameters. In addition, the final loss of the network is the combination of three loss functions. In this section, we conduct experiments to evaluate the effectiveness of the weight sharing and different loss functions. we first set a network with two different decoders (without weight sharing) for the two streams, which we denote as CleftNet w/o WS. Table VII shows that CleftNet consistently outperforms CleftNet w/o WS on all the three metrics. In addition, we only use ${\mathcal{L}}_s$ in CleftNet which we denote as CleftNet w ${\mathcal{L}}_s$, and we only use ${\mathcal{L}}_b$ which we denote as CleftNet w ${\mathcal{L}}_s$. To demonstrate the function of ${\mathcal{L}}_c$, we remove it from CleftNet which we denote as CleftNet w/o ${\mathcal{L}}_c$. Experimental results in Table VII shows the removal of any of the ${\mathcal{L}}_s$, ${\mathcal{L}}_s$, and ${\mathcal{L}}_s$ results in performance reduction. Existing studies [57], [58] also utilize boundary representations to learn rich shape information and improve predictions. However, they fail to consider the inconsistency between segmentation and boundary representations. Thus, they can be categorized into CleftNet w/o ${\mathcal{L}}_c$, which is demonstrated less powerful than the proposed CleftNet. In addition, these two methods use separate decoders for predicting segmentation and boundary outputs. By doing this, the network is incapable of capturing relations between high-level texture and shape features. The strategy without weight sharing also involves more parameters and may induce the overfitting.

TABLE VII.

Comparison among different strategies for the final loss in terms of CREMI-score, F1-Score, and AUC on the validation set.

Model	CREMI-score(↓)	AUC(↑)	F1-score(↑)
CleftNet w/o WS	51.32	0.933	0.886
CleftNet w ${\mathcal{L}}_s$	52.16	0.921	0.873
CleftNet w ${\mathcal{L}}_b$	53.04	0.915	0.857
CleftNet w/o ${\mathcal{L}}_c$	51.65	0.930	0.882
CleftNet	50.50	0.938	0.895

J. Efficiency Study of CleftNet

One concern regarding FA is the efficiency as it performs attention. Given the input with the same dimensions, a FA usually takes more time and computational memory than other operators like convolution or pooling. However, the use of FAs will not necessarily make the CleftNet more inefficient than the baseline 3D U-Net. As we mentioned, FAs are capable of extracting global information in one step and capturing shared patterns in all clefts. With such advances of FAs, the architecture of CleftNet can be more compressed. For example, CleftNet can use a shallower architecture with less intermediate output channels. In top methods on the learderborad of the CREMI open challenge, only the method DTU-2 is published [21] and it employs a basic 3D U-Net architecture. We reimplement the method then calculate the number of parameters as well as inference time on the test set. The overall performance and efficiency are reported in Table VIII. We can observe from the table that CleftNet outperforms 3D U-Net significantly with much less parameters as well as slightly less inference time.

TABLE VIII.

Comparison between 3D U-Net in [21] and CleftNet in terms of performance and efficiency on the test set.

Model	Rank	CREMI-score(↓)	* of Parameters	Inference Time (min)
3D U-Net (DTU-2) [21]	31	67.56	8,392,644	3.72
CleftNet	1	57.73	6,843,126	3.08

K. Qualitative Results

We compare the four best methods among six qualitatively by showing visualization results in Figure 4. Specifically, we compare 3D U-Net, ResUnet, AttnUnet, and CleftNet on the validation set for clear comparisons as the validation set has labels. We show the predicted results for three slices, and each of them is from the volume A, B, and C, respectively. The figure evidently shows that CleftNet generates best cleft predictions among the four methods. Generally, some non-cleft cracks in tissues appear to be similar as clefts, and it is possible that these voxels are predicted as cleft voxels, thereby resulting in false positives. In addition, some clefts have small sizes that the contained voxels can be easily predicted as background voxels, which inducing false negatives. Our CleftNet produces the least false positives or false negatives, generating predictions that are closest to the ground truth. This again demonstrates the effectiveness of the proposed feature augmentor and label augmentor in CleftNet.

Fig. 4.

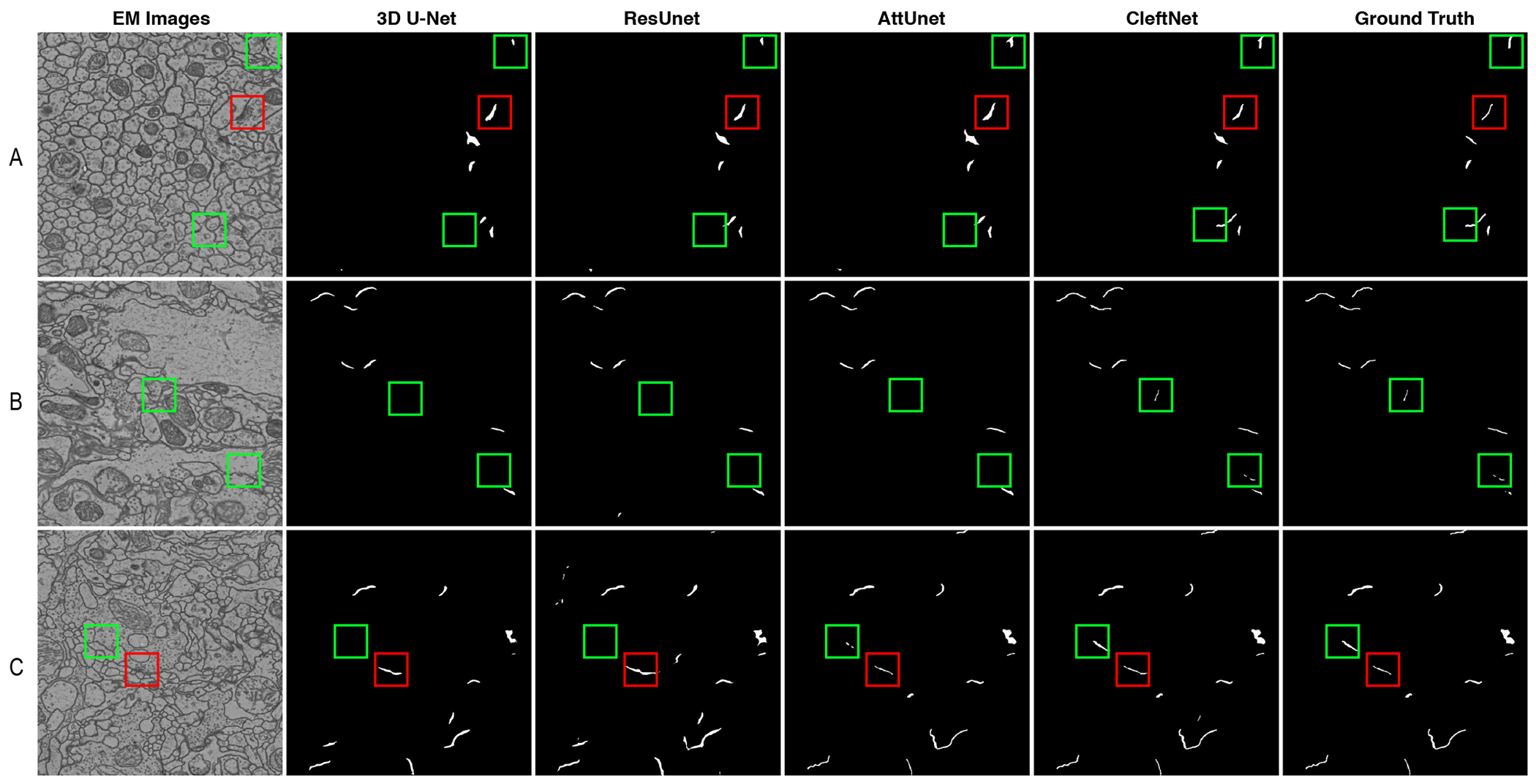
Qualitative results for 3D U-Net, ResUnet, AttnUnet, and CleftNet on the validation set. Each row shows results for a slice from the corresponding volume A, B or C. The red boxes mark the regions where false positives are easily produced in predictions. The green boxes mark the regions where false negatives could be easily generated in predictions.

V. Conclusion

In this work, we propose a novel deep network, known as CleftNet, for synaptic cleft detection from brain EM images. Our CleftNet is a U-Net like network with the purpose of learning specific properties of synaptic clefts, such as common morphological patterns and shape information of clefts. We achieve this goal by augmenting the network with two network components, the feature augmentor and the label augmentor. The feature augmentor is designed based on the gated-attention and self-attention, using a learning-based query and generates outputs with arbitrary spatial dimensions. It can not only capture global information from inputs, but also learn complicated morphological patterns shared by all clefts, leading to aumgmented cleft features. The feature augmentor can replace any commonly-used operation, such as convolution, pooling, or deconvolution. Hence, it can be integrated into any deep model with high flexibility. The original label for each input voxel is the segmentation label purely, and we propose the label augmentor to augment it to a vector, which contains both the segmentation label and boundary label. This essentially enables the multi-task learning, and the network is capable of learning both the texture and shape information of clefts, generating more informative representations. We integrate these two components and propose the CleftNet, the new state-of-the-art model for synaptic cleft detection. CleftNet not only ranks first on the external task of the CREMI challenge, but also performs much better than the baseline methods on internal tasks.

Fig. 2.

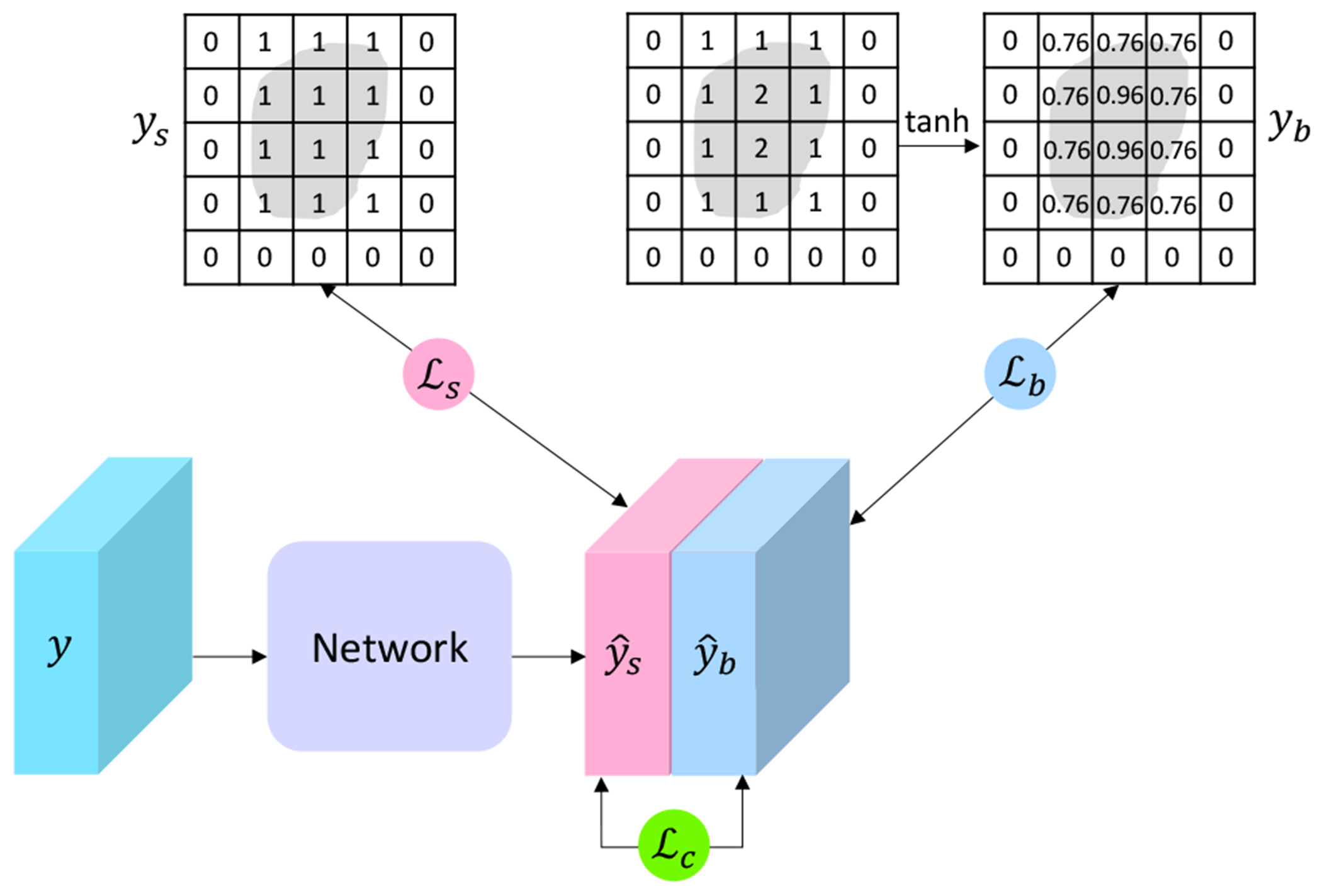
An illustration of the proposed label augmentor (LA) as detailed in Section III-B. For each voxel i of the input volume y, LA augments its label to a vector ${\left[y_s^i,y_b^i\right]}^T$, where $y_s^i$ is the segmentation label and $y_b^i$ is the boundary label. The gray areas indicate the same cleft. The boundary labels y_b are computed using tanh distance map (TDM) as shown in the figure. The same network with weight sharing is employed to learn predictions on the two sets of labels. The segmentation loss ${\mathcal{L}}_s$ for the volume y is achieved from the segmentation predictions ${\widehat{y}}_s$ and segmentation labels y_s. The boundary loss ${\mathcal{L}}_b$ is calculated from the boundary predictions ${\widehat{y}}_b$ and boundary labels y_b. The coherence loss ${\mathcal{L}}_c$ is computed based on the divergences between predictions ${\widehat{y}}_s$ and ${\widehat{y}}_b$.