Modeling the number of people infected with SARS-COV-2 from wastewater viral load in Northwest Spain

Abstract

The quantification of the SARS-CoV-2 RNA load in wastewater has emerged as a useful tool to monitor COVID–19 outbreaks in the community. This approach was implemented in the metropolitan area of A Coruña (NW Spain), where wastewater from a treatment plant was analyzed to track the epidemic dynamics in a population of 369,098 inhabitants. Viral load detected in the wastewater and the epidemiological data from A Coruña health system served as main sources for statistical models developing. Regression models described here allowed us to estimate the number of infected people (R² = 0.9), including symptomatic and asymptomatic individuals. These models have helped to understand the real magnitude of the epidemic in a population at any given time and have been used as an effective early warning tool for predicting outbreaks in A Coruña municipality. The methodology of the present work could be used to develop a similar wastewater-based epidemiological model to track the evolution of the COVID–19 epidemic anywhere in the world where centralized water-based sanitation systems exist.

Graphical abstract

1. Introduction

During the last decade, wastewater–based epidemiology (WBE) has emerged as a highly relevant discipline with the potential to provide objective information by combining the use of cutting-edge analytical methodologies with the development of ad hoc modeling approaches. WBE has been extensively used in the last years to predict with high accuracy the consumption patterns of numerous substances (EMCDDA, 2020). Several examples from the literature showed different approaches and strategies to tackle the uncertainty associated with WBE studies. For example, Goulding and Hickman assumed three main sources of uncertainty and, using Bayesian statistics, fitted the data to linear regression hierarchical models (Goulding et al., 2020). Other modeling approaches (Croft et al., 2020) considered Monte Carlo simulations to deal with uncertainties such as wastewater inflow variability or stability of the substances in wastewater and their pharmacokinetics. In general, WBE studies showed that despite the wide number of parameters involved in predicting the consumption rate of a specific substance, a correct selection of assumptions combined with a thoughtful modeling process will overcome such uncertainty, leading to accurate results.

Previous studies have evaluated the presence in wastewater of other viruses (Ehlers et al., 2005; Hellmér et al., 2014; Hovi et al., 2012; Lizasoain et al., 2018; Mancini et al., 2019). During the present global COVID–19 pandemic, processes to monitor SARS–CoV–2 in wastewater were first developed in the Netherlands (Medema et al., 2020), followed by other countries (Nemudryi et al., 2020; Wurtzer et al., 2020; Ahmed et al., 2020; La Rosa et al., 2020; Randazzo et al., 2020b; Peccia et al., 2020; Balboa et al., 2021; Weidhaas et al., 2021; Pillay et al., 2021; Kumar et al., 2021; Hart and Halden, 2020).

A range varying from one third to four fifths of patients infected with SARS–CoV–2 are asymptomatic (Bi et al., 2020; Day, 2020; Pollán et al., 2020); a condition that depends on many factors such as the mean age in the population and that promotes the undetected spread of COVID–19. A systematic literature review found that at least an important proportion of COVID–19 infected persons, including symptomatic and asymptomatic people, tested for fecal viral RNA were positive from initial steps of infection (Gupta et al., 2020) and persistently tested positive on rectal swabs even after nasopharyngeal testing was negative (Chen et al., 2020; Xing et al., 2020; Xu et al., 2020; Zhang et al., 2020; Cevik et al., 2021; Miura et al., 2021). For example, it has been reported that excretion of viral RNA in the stool of people infected occurs during a mean prolonged period of 27.9 days after the person has tested negative in their respiratory samples (Y. Wu et al., 2020). Therefore, genetic material of SARS–CoV–2 can be found in wastewater (Lodder and de Roda Husman, 2020), which has made monitoring of viral RNA load in sewage an excellent tool for the epidemiological tracking of the actual pandemic as well as an extremely efficient early warning tool for outbreaks detection (Randazzo et al., 2020a; Ahmed et al., 2020; Medema et al., 2020; Peccia et al., 2020; F. Wu et al., 2020; Wurtzer et al., 2020).

These studies showed the potential of monitoring SARS–CoV–2 levels in wastewater and sewage sludge to track and even pre-empt outbreaks in the community. The works of Lahrich et al. (2021) and Bandala et al. (2021) are two comprehensive monographs on the subject.

Previous studies estimated the number of SARS–CoV-2 infected patients in a community using simple equations and Monte Carlo simulation (Ahmed et al., 2020; Curtis et al., 2020; Hasan et al., 2021). A similar study was made in Barcelona elaborating a simple model to predict the total number of SARS-CoV-2 shedders during the first wave of the pandemic, showing a high proportion of asymptomatic individuals (Chavarria-Miró et al., 2021). In addition, Saththasivam et al. (2021) developed a suitable WBE mathematical model for monitoring the trend in the numbers of infected people in Qatar. The Susceptible-Exposed-Infectious-Removed (SEIR) model based on mass rate of SARS–CoV–2 RNA in wastewater was also used to estimate the number of infected patients in the state of South Carolina (McMahan et al., 2021). Regarding the forecasting of the prevalence of virus shedders within a community, Cao and Francis (2021) have proposed the fitting of VAR models, whereas Li et al. (2021) have used multiple linear regression, artificial neural network, and adaptive neuro fuzzy inference systems.

On March 9th 2020, the city of A Coruña, in the region of Galicia, Northwest of Spain, reported circulation of SARS–CoV–2 for the first time, with data of a COVID–19 outbreak in a civic center that affected 11 people (GCiencia, 2020, GCiencia, 2020). At that point, a surveillance phase on approximately 250 people began, and the recommendations from the Health Department on cleaning and mobility restrictions were followed (GCiencia, 2020a). During these initial days of the COVID–19 epidemic in Galicia, most of the cases were in the municipality of A Coruña. Thus, at noon on March 13th, the Xunta de Galicia (Government of the Autonomous Community of Galicia) reported 90 confirmed cases of COVID–19 in Galicia, 43 of them in the A Coruña area (GCiencia, 2020b). The Spanish Government declared a state of alarm on March 14th throughout the country, at which point the Galician community still had few cases. Despite this, in a few days the region went from a monitored and controlled situation to an exponential growth of cases (Rey, 2020), reaching a peak of 1667 active cases. The cases were distributed in an area that covers 37 municipalities in the health area of A Coruña–Cee, as shown by the data provided by SERGAS (Galician Health Service) in https://www.datawrapper.de/_/QrkrZ (SERGAS, 2021).

In this context, the main objective of the present work was to develop parametric and nonparametric statistical models useful to determine the entire SARS–CoV–2 infected population, including symptomatic and asymptomatic people, by tracking the viral load present in the wastewater of the Bens wastewater treatment plant that serves the metropolitan area of A Coruña with near 370,000 residents, without the need of health system data or the number of positive people reported, and obtaining information from population-based seroepidemiological surveys developed in Spain (this represents a contribution with respect to other models). The pursuit of this objective has a public service motivation. At this regard, it is important to note that this research, in the framework of the COVIDBENS project, had high social impact and it was one of the precursors of this type of monitoring in Spain, for the surveillance of SARSCoV–2 in wastewater. COVIDBENS currently provides a public service through weekly reports to municipalities, public health and regional administrations (SERGAS, Xunta de Galicia) for surveillance and early warning tasks.

2. Materials and methods

2.1. Sample collection

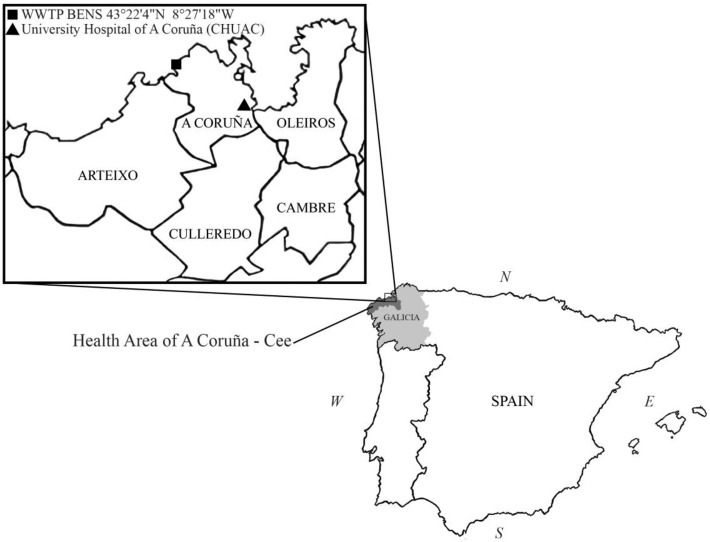
The wastewater treatment plant (WWTP) Bens (43° 22′ 8.4″ N 8° 27′ 10.7″ W, A Coruña, Spain) serves the metropolitan area of A Coruña. It includes the municipalities of A Coruña, Oleiros, Culleredo, Cambre and Arteixo, which correspond to a geographical area of 277.8 km² and to a population of 369,098 inhabitants (Fig. 1). The wastewater samples were collected by automatic samplers installed both at the entrance of the WWTP Bens and in a sewer collecting sewage from COVID–19 patients housed on 7 floors of the University Hospital of A Coruña (CHUAC). At the WWTP Bens, 24-h composite samples were collected from April 15th until June 4th, while at CHUAC 24–h composite samples were collected from April 22nd to May 14th 2020. Dataset S1 includes the dates when each sample was collected in the two locations considered: the WWTP Bens and the CHUAC. A total of 33 24–h composite samples were collected from the WWTP and 19 from CHUAC. In addition, samples were collected at 2–h intervals for 24 h on specific days at the WWTP Bens and at CHUAC. A total of 36 2–h intervals samples were collected from the WWTP and 12 from CHUAC. The 24–h composite samples were collected by automatic samplers taking 150 mL of wastewater every 15 min in 24 bottles (1 h per bottle) and, when the 24-h collection ended, the 24 bottles were integrated and a representative sample of 100 mL was collected. For the collection of 2 h intervals, 2 bottles obtained every 2 h were integrated, finally providing 12 bottles per day.

Fig. 1.

Map showing Galicia region in Spain, the metropolitan area of A Coruña including Oleiros, Cambre, Culleredo, Arteixo and A Coruña municipalities, and the Health Area of A Coruña-Cee, as well as the specific locations of the University Hospital of A Coruña (CHUAC) and WWTP Bens.

2.2. Sample processing

Samples of 100 mL were processed immediately after collection at 4 °C. Firstly, 100 mL samples were centrifuged for 30 min at 4000 ×g and then filtered through 0.22 μm membranes (Merck Millipore). Regenerated cellulose Amicon Ultra Filters of 30 kDa (Merck Millipore) were used to concentrate and dialyze, keeping the fraction retained, in 500 μL of a buffer containing 50 mM Tris-HCL, 100 mM NaCl and 8 mM MgSO₄. Samples were preserved in RNAlater reagent (Sigma-Aldrich) at −80 °C.

2.3. RNA extraction and qRT-PCR assays

RNA was extracted from 100 μL of the concentrated samples using the QIAamp Viral RNA Mini Kit (Qiagen, Germany) according to manufacturer's instructions. Briefly, the sample was lysed under highly denaturing conditions to inactivate RNases and to ensure isolation of intact viral RNA. Then, the sample was loaded in the QIAamp Mini spin column where RNA was retained in the QIAamp membrane. Samples were washed twice using washing buffers. Finally, RNA was eluted in 70 μL of RNase-free water. The quality and quantity of the RNA was checked using a Nanodrop Instrument and an Agilent Bioanalyzer. Samples were kept at −80 °C until use. RT-qPCR assays were done in a CFX 96 System (BioRad, USA) using the qCOVID–19 kit (GENOMICA, Spain) through N gene (coding for nucleocapsid protein N) amplification. Hard–Shell 96–well PCR plates (BioRad, USA) were used and sealed with microseal ‘B’ PCR Plate Sealing Film (BioRad, USA). Recommendations given by Ahmed et al. (2022) were followed for minimizing errors in RT–PCR detection. RT–qPCR reactions were done following the manufacturer's instructions (GENOMICA, Spain). This kit provided two reaction mixes; Mix A contained DNA polymerase, nucleotides, polymerase buffer and an internal control and Mix B contained primers and probe for N gene. The final reaction contained 5 μL of Mix A, 1 μL of Mix B, 0.2 μL of reverse transcriptase, 5 μL of template and 8.8 μL of water. The internal control allowed discarding the presence of inhibitors. Nuclease–free water was used as negative-control template. The cycling parameters were 50 °C for 20 min for the retrotranscription step, followed a PCR program consisting of a preheating cycle of 95 °C for 2 min, 50 cycles of amplification at 95 °C for 5 s and finally one cycle of 60 °C for 30 s. RT-qPCR assays were done in sextuplicate.

For RNA quantification, a reference pattern was standardized using the Human 2019-nCoV RNA standard from European Virus Archive Glogal (EVAg) (Fig. S1). To build the calibration curve, the decimal logarithm of SARS–CoV–2 RNA copies per μL of control material ranging from 5 to 500 were plotted against Cq (quantification cycle) values. Calibration was done amplifying the N gene. Viral load was defined as number of copies of RNA of SARS–CoV–2 per L.

The analytical efficiency of the RT–qPCR was calculated following the criteria recommended by the MIQE guidelines (Bustin et al., 2009). The limit of detection (LOD) of the RT–qPCR was analyzed using serial dilutions of Human 2019-nCoV RNA standard (EVAg). Detection rates are shown in Table S1 (in Supplementary material section), where the LOD was established in 25 copies per reaction and limit of quantification (LOQ) was between 25 and 15 copies per reaction. The slope of the standard curve was -3.56, the R² was 0.9984 and the amplification efficiency was above 90%.

2.4. Data collection

In the present work a COVID–19 case was defined as a person with COVID–19 virus infection laboratory-confirmed by RT-PCR of SARS–CoV–2 regardless of clinical signs and symptoms. Active cases mean living persons confirmed with COVID–19 whose symptom onset date is less than or equal to 14 days from the date of the current report.

Data gathered from different sources were used for the present study. Dataset S2 integrates daily observations at the meteorological station of Coruña-Bens, including rainfall, temperature, and humidity, for the period March 1st–May 31st, 2020, obtained from the Galician Meteorology Agency (METEOGALICIA, 2021). Dataset S3 includes cumulative and active number of COVID–19 cases in the metropolitan area of A Coruña and the health area A Coruña–Cee for the period March 1st–May 31st, 2020, reported by the Galician Health Service (SERGAS), the General Directorate of Public Health (Autonomous Government of Galicia) and the University Hospital of A Coruña (CHUAC). Since flow may be an important variable when determining the viral load in the wastewater, an exploratory data analysis for the volume of water pumped at the WWTP Bens during the lockdown period has been performed using flow data. Dataset S4 includes two-minute flow measurements (m³·s⁻¹) at WWTP Bens for the period January 1st–May 14th. An additional flow study is described in the Supplementary material section.

2.5. Backcasting of COVID–19 active cases

Preliminary statistical methods have been devised to backcast the number of COVID–19 active cases based on reported official cases. Follow-up times (available only until May 7th) for anonymized individual reported COVID–19 cases in Galicia (NW Spain where the WWTP Bens is located, Fig. 1) have been used to count the number of cases by municipality based on patient zip codes. Since the epidemiological discharge date is missing, the number of active cases in the metropolitan area of A Coruña could not be obtained but the cumulative number of cases was computed. On the other hand, the main epidemiological series for COVID–19 were publicly available daily in Galicia at the level of health areas. However, the definition of one of the series changed from cumulative cases to active cases in April 29th. Thus, the epidemiological series for COVID–19 in the health area of A Coruña – Cee (population 551,937) was used to estimate the epidemiological series for COVID–19 for the metropolitan area of A Coruña (population 369,098). To do this, a linear regression model was used to relate the relative cumulative and active cases (cases per million) of COVID–19 for the health area of A Coruña – Cee. Predicting the rate of active cases and considering the population size in the metropolitan area gives the estimated total number of official active cases in the five municipalities. The previous approach is only possible until May 7th, our database update date. To estimate the number of official active cases from May 8th onwards, another linear regression model has been used to relate the number of active cases in the health area of A Coruña – Cee and in the metropolitan area of A Coruña. Since the number of active cases in the health area has been reported until June 5th, the series of estimated official active cases could be backcasted from May 8th until June 5th. Finally, to transform the official number of COVID–19 cases into the real number, the ratio mean of real cases/mean of official cases was estimated using the official figures of cumulative cases. The Spanish seroepidemiological survey made by the National Center of Epidemiology in Spain, ENECOVID (Pollán et al., 2020), included representative samples within the metropolitan area of A Coruña during the period, April–June 2020. These data have been used to quantify the real proportion of population infected during the period April–June in the area corresponding to WWTP Bens. Accordingly, the number of actual active cases in Galicia was: 56,713 for April 27th–May 11th (prevalence 2.1%) and 59,414 for May 18th–June 1st (prevalence 2.2%). Confronting these numbers with the official numbers in May 11th (10,669) and June 1st (11,308) gives estimated ratios of 5.316 and 5.254 in these two periods, with an average of around 5.29. This conversion factor was used to backcast the series of real active cases based on the estimated daily official COVID–19 cases in the metropolitan area of A Coruña. Some of these series, including the backcasted series of real active cases, are included in the Dataset S3.

2.6. Nonparametric fitting of viral load overtime

In order to properly interpret the results of fitting models applied aiming understand the viral load evolution, a brief description of them is included as follows, namely of the Generalized Additive Models and the Locally Estimated Scatterplot Smoothing (LOESS). In fact, GAM using a basis of cubic regression splines (Hastie and Tibshirani, 1990) and LOESS (Cleveland, 1979) nonparametric regression models have been used to fit the viral load along the day on May 5th, 6th, 11th and 12th, and as a function of time at CHUAC from April 22nd to May 12th and at WWTP Bens from April 16th to June 3rd. Several outliers, showing very small viral load (some of them under the level of detection), have been removed from the data, corresponding to unexpected and intensive pipeline cleaning episodes (8-hour 70 °C water cleaning during Thursday-Friday nights) carried out in April 23rd-24th, April 30th - May 1st and May 7th–8th.

Nonparametric methods do not assume any parametric form (Maity, 2017), allowing us to model complex nonlinear functions (Shokrzadeh et al., 2014). There is a wide range of nonparametric regression models, such as local polynomial regression (Fan and Gijbels, 2018; Breidt and Opsomer, 2000), kernel smoothing (Wand and Jones, 1994), regression splines (Wood, 2017), and LOESS (Cleveland, 1979), among others.

There is other group of models, called semiparametric regression models, that allow the inclusion of linear parametric and flexible nonparametric effects of the predictors on the response, such as the GAM models. In this work, GAM models are applied to define the relation between the viral load and the date, by using penalized regression splines (Wood, 2017) to estimate the smooth effect of date on the viral load. But this type of models can include linear effects in addition to smooth effects. For instance, a GAM model expression consisting in one linear, X ₁, and two smooth predictors, T ₁ and T ₂, can be defined by

$$Y={\beta }_0+{\beta }_1{X}_1+s_1\left(T_1\right)+s_2\left(T_2\right)+s_{12}\left(T_1,T_2\right)+\epsilon ,$$

whereby β ₀ and β ₁ are the parameters that define the linear effect of X ₁ on the response Y, s ₁(T ₁) and s ₁(T ₁) are the smooth effects of T ₁ and T ₂ variables, S(T ₁,  T ₂) accounts for the smooth effect of their interaction, and ε is the random error, i.e. the difference between Y and its conditional mean provided by the model. In the present case, Y is assumed to be Gaussian distributed, but instead it could be assumed, for instance, Binomial or Poisson distributed, in which case Y should be replaced by g(η). In the framework of this section, Y = Viral Load and X = Time, thus:

$$E\left(\mathit{Viral\hspace{0.17em}Load}|\mathit{Time}\right)={\beta }_0+s_{\mathit{Time}}\left(\mathit{Time}\right).$$

s accounts for the smooth effects of the predictors (T) and are usually estimated by using penalized regression splines. Splines are piecewise polynomial functions of a specific degree that are continuous in a set of knots a < t ₁ < t ₂ < ⋯ < t _L < b (up to L − 1 degree) defined in an interval [a,  b]. Thus, the smooth effect of T can be expressed by means a splines basis composed of L + degree elements,

$$s_j\left(t\right)=\sum _{k=1}^{L+\mathit{degree}}{\beta }_{\mathit{jk}}{\varphi }_{\mathit{jk}}\left(t\right)={\beta }_{j^{\prime }}^{\prime }{\varphi }_j,$$

where ϕ _jk are the splines functions and L accounts for the number of knots. In this work degree = 3 (cubic regression splines) was chosen.

2.7. Viral load models

In order to find a useful statistical model to estimate the number of real infected cases, including symptomatic and asymptomatic people, well-known regression models, such as simple and multivariate linear models, and more flexible models, such as nonparametric (e.g. local linear polynomial regression) and semiparametric (GAM and LOESS) models, have been formulated.

As in the previous section, in order to be able to correctly interpret the results of the application of the models, a brief introduction from a statistical point of view is provided beforehand.

Parametric models such as linear regression, the simplest one, show a transfer function that defines the relation of dependence between two or more variables involved in a specific process. This function depends on the value of some parameters that can be interpreted from physical or chemical point of views, among others. We can define a simple parametric model by

$$Y=m\left(X\right)+\epsilon ,\text{with}\mathrm{E}\left(\epsilon \right)=0,$$

where Y is the response variable to be modeled, and m is the parametric function, depending on X, the independent variable. In the present case, Y is the number of real infected people, X accounts for the values of the logarithm of viral load in wastewater, while ε are the model random errors. The regression function is assumed to be an element of a set of parametric functions ℳ = {m_θ/θ ∈ ⊖}, whereby θ is the vector of parameters that defines the regression model and ⊖ is a subset of ℝ ^k.

On the other hand, the semiparametric models used are flexible ones that allow the introduction of linear and smooth effects of the predictors on the response. All these models have been successfully used to predict the number of COVID–19 active cases based on the measured viral load (number of SARS–CoV–2 RNA copies/L) at WWTP Bens, daily flow in the sewage network as well as other environmental variables, such as rainfall, temperature and humidity. Diagnostic tests (Q-Q plots, residuals versus fitted values plots and Cook's distance) were used for outlier detection, which improved the models fit. The R statistical software was used to perform statistical analyses (R Core Team, 2021). Namely, the mgcv library (Wood, 2017) was applied to fit GAM models and ggplot2 and GGally (Schloerke et al., 2020; Ginestet, 2011) to perform correlation analysis, obtain graphical output and fit LOESS models, respectively. The caret R package was used to fit and evaluate regression models (Kuhn et al., 2008).

Although some RT-qPCR replicates could not be measured when the viral load was scarce, due to the limitation of the detection technique (errors randomly occur when the number of copies/L is under 10,000), 74% of the assays led to three or more measured replications. Conditional mean imputation (Enders, 2010) was used for unmeasured replications. In those cases, the missing values along the replications were imputed with the sample mean of the non-missing values of the replications. When all the replications were missing, they were imputed as the lowest value of all the observed measurements along the whole dataset.

2.8. Public dissemination

With the aim of helping in the awareness of the population and in the management of the pandemic, the data obtained were disseminated at first through private reports to the political and health authorities. Later, data were disseminated through social networks, press, radio, TV and finally a public web page was created in order to inform weekly the society about the COVID–19 pandemic situation in the metropolitan area of A Coruña city assessed by COVIDBENS (COVIDBENS, 2021). The web site can be found in the link https://edarbens.es/covid19/.

3. Results

3.1. Estimated COVID–19 positive cases in the metropolitan area of A Coruña

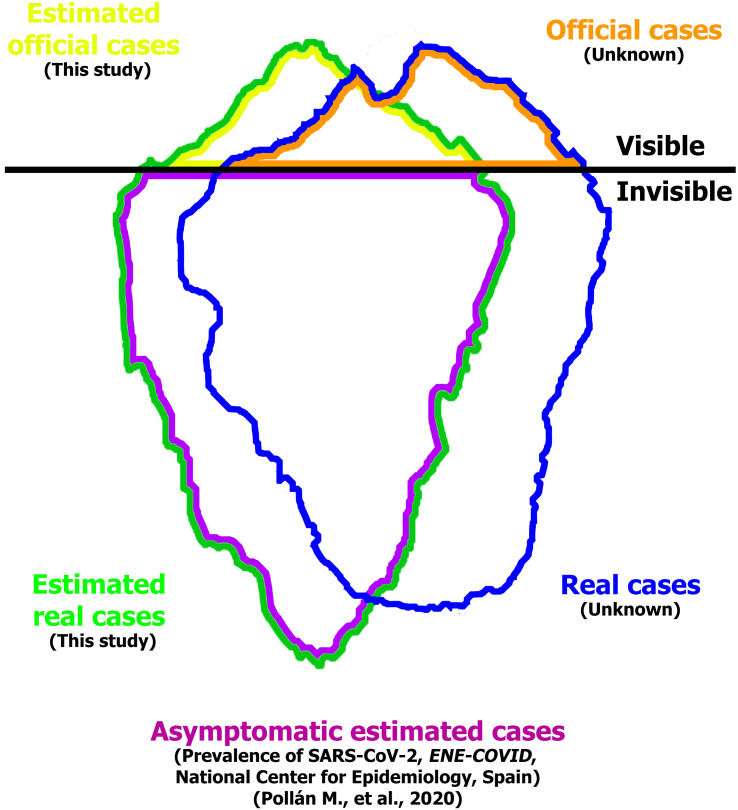
To model the viral load, the number of COVID–19 positive cases need to be estimated (Fig. 2 ). Iceberg on Fig. 2 represents the global health of the population of the metropolitan area of A Coruña based in our study, where visible cases are differentiated from the invisible ones separated by a black line. The real (and unknown) iceberg is represented in blue, which includes real cases with or without symptoms, visible and invisible. The iceberg represented in green corresponds to the number of people infected estimated using the statistical models presented here. The green iceberg has been drawn with a slightly different shape and size but very similar to blue, taking into account the 10% margin of error of our models. Visible cases estimated in this study (in yellow) against the real (and unknown) ones (in orange) are also represented in Fig. 2. Finally, the asymptomatic cases known thanks to the national seroprevalence study (Pollán et al., 2020) are represented in purple.

Fig. 2.

Iceberg representing the overall health of the population of the metropolitan area of A Coruña infected by SARS–CoV–2, showing the real and official cases estimated in this study. (For interpretation of the references to color in this figure, the reader is referred to the web version of this article.)

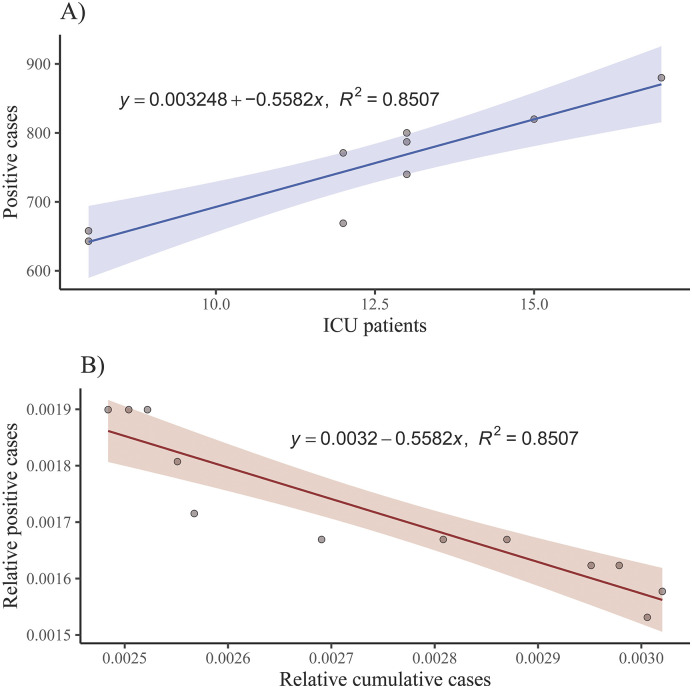
However, due to difficulties in determining the exact number of positive cases, mathematical models had to be developed based on data recovered in Dataset S3. Thus, linear regression models (Fig. 3) were successfully used to estimate COVID–19 positive cases in the A Coruña – Cee health area, where the region of this study is located (Fig. 1). This was based on Intensive Care Unit (ICU) patients before April 29th (Fig. 3A) and, from this date on, on positive cases reported by health authorities in Galicia. A linear regression trend was fitted to predict the proportion of positive cases in the health area of A Coruña – Cee based on the proportion of cumulative cases (Fig. 3B). This linear regression fit was finally used to estimate the positive cases in the metropolitan area of A Coruña served by the WWTP Bens, by means of the proportion of cumulative positive cases in the same area, which was directly obtained from the individual patient data.

Fig. 3.

Estimation of the COVID–19 positive cases using simple linear regression models. A) ICU patients versus COVID–19 positive cases in A Coruña – Cee health area, and its linear fit for the period April 29th on. B) Relative cumulative cases versus relative positive cases in the health area of A Coruña – Cee and their linear fit.

3.2. Daily variation of SARS-CoV-2 RNA load in the metropolitan area of A Coruña and hospital

The evolution of the viral load along the day both at the A Coruña metropolitan area and at the University Hospital Complex of A Coruña (CHUAC) was monitored in order to discern which amount of the viral load detected in the WWTP Bens came from the CHUAC and which from the community. An analysis of the viral load of the 24–h and 2-h samples collected at the WWTP Bens and CHUAC, as reflected in sampling schedule presented in Dataset S1, was performed. Dataset S5 includes RT–qPCR results in viral load (number of SARS–CoV–2 RNA copies/L) and Cq values obtained from the 24–h samples. Dataset S6 includes viral load and Cq values obtained from the 2–h samples. Because of the small sample size, nonparametric LOESS models were used in order to prevent the possible overfitting of alternatives such as GAM. Fig. S2 (in Supplementary material) shows the viral load trends at CHUAC (Fig. S2A) and at WWTP Bens (Fig. S2B) depending on the hour of the day, during four different days. Fig. S2A shows the hourly trend at CHUAC, with a maximum around 08:00, whereas the viral load curves at WWTP Bens (Fig. S2B) attained a minimum around 05:00 and a maximum between 14:00 and 15:00. As a consequence of these trends, 24-hour integrated samples are fully justified.

3.3. Lockdown de-escalation in the metropolitan area of A Coruña

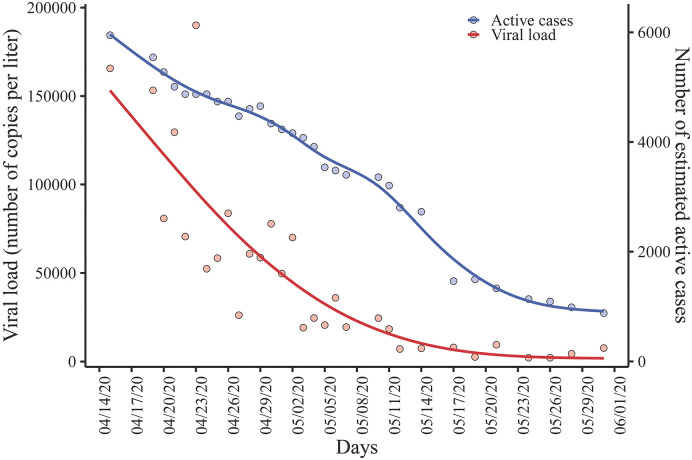
As expected, the mean viral load decreased with time when measured at CHUAC (Fig. S3A of Supplementary material, late April–mid May) and at WWTP Bens (Fig. S3B, mid April–early June) following an asymptotic trend (fitted using GAM with cubic regression splines). Time course quantitative detection of SARS–CoV–2 in WWTP Bens correlated with the estimated number of COVID–19 positive cases, as shown in Fig. 4 . The number of copies of viral RNA per liter decreased from around 500,000 to less than 1000, while the estimated cases of patients infected by SARS–CoV–2 decreased approximately 6–fold in the same period, reaching in both cases the lowest levels in the metropolitan area at the beginning of June 2020.

Fig. 4.

Viral load detected in the influent of the WWTP Bens (red line) and the estimated number of COVID–19 positive cases (blue line) in the metropolitan area of A Coruña.

3.4. Wastewater epidemiological models based on viral load for COVID–19 real active cases prediction

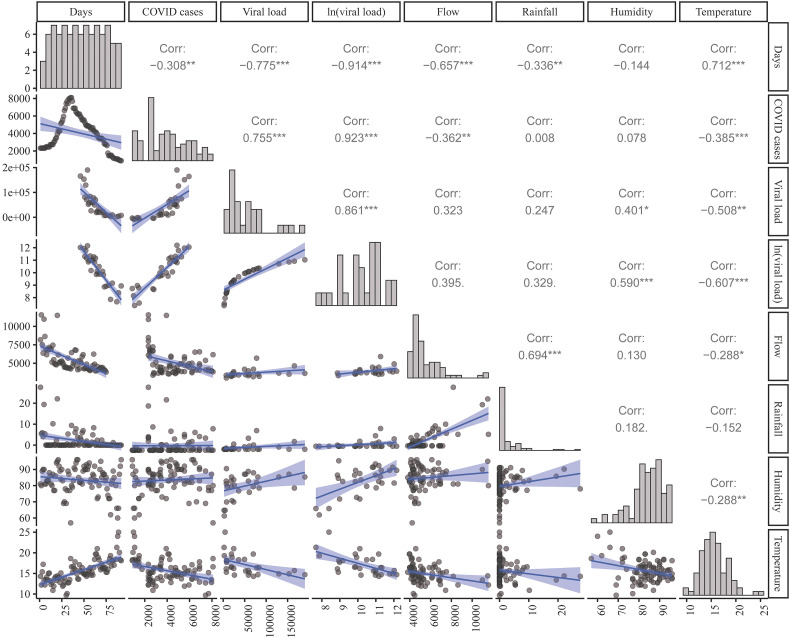
Firstly, a correlation analysis (Fig. 5 ) was done finding that estimated number of COVID–19 cases strongly correlated linearly with the logarithm of daily mean viral load at Bens (R = 0.923) and with the mean flow (R = − 0.362). Nonetheless, a strong inverse linear relationship between estimated COVID–19 positive cases and time was found (R = − 0.99).

Fig. 5.

Correlation analysis between estimated COVID–19 positive cases and different variables. Scatterplot matrix shows fitted linear models and linear correlation coefficients of each pair of variables: time (measured in days from the beginning of reported COVID–19 cases), estimated COVID–19 positive cases (positive cases), daily mean viral load measured in Bens, mean flow of sewage water in Bens, mean rainfall, daily mean humidity and daily mean temperature.

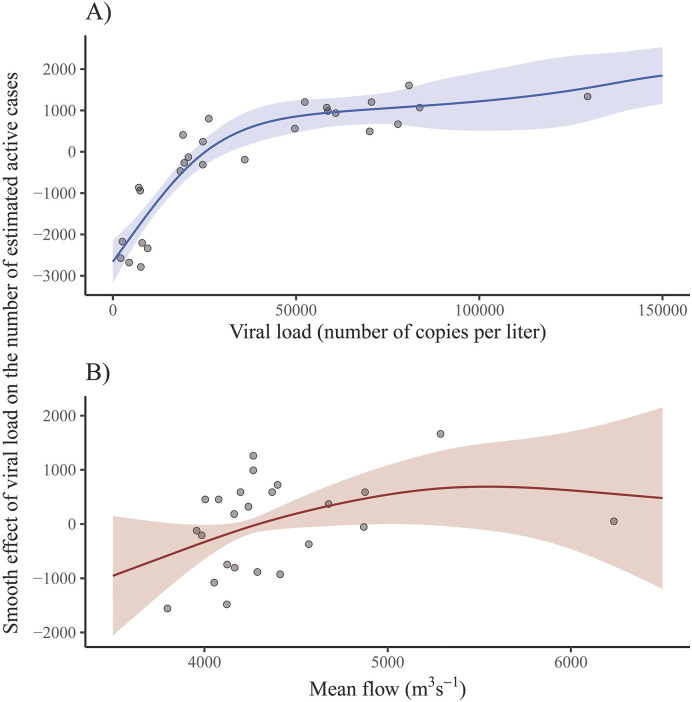
Then, different regression models were tested to predict the real number of COVID–19 active cases based on the viral load and the most relevant atmospheric variables. The best results were obtained using GAM models depending on the viral load and the mean flow (Fig. 6 ). The effect of the viral load on the COVID–19 estimated active cases showed a logarithmic shape (Fig. 6A), which suggested that the number of COVID–19 real active cases could be modeled linearly as a function of the logarithm of the viral load. On the other hand, the shape of the effect of the mean flow on the estimated number of COVID–19 real active cases appears to be quadratic (Fig. 6B), but its confidence band was wide and contained the horizontal line with height zero, which means that the effect of the mean flow was not significant (p-value = 0.142). Therefore, the only significant independent variable was the viral load, with R ² = 0.86.

Fig. 6.

Smooth effect (solid line) and confidence band (shaded area) for the viral load (A) and for the mean flow (B) on the number of estimated COVID–19 active cases when fitting a GAM.

Since the nonparametric estimation of the viral load effect had a logarithmic shape, a multiple linear model was fitted using the logarithmic transformation of the viral load, daily flow, rainfall, temperature, and humidity. The best option to explain the number of COVID–19 cases is a simple linear model as a function of the as a function of the natural logarithm of viral load. In fact, the R² hardly change when adding Flow, Rainfall, Humidity and Temperature variables (see Fig. S4 in Supplementary material that shows the most explanatory models for different number of predictors using the R ² maximization criterion). In fact, when a multivariate linear model depending on three predictors (viral load, daily flow, and rainfall) was fitted, data showed that the only significant explanatory variable was the viral load (p-value = 1.32 × 10⁻⁸). Table 1 shows that the effect of the other two predictors, daily flow (p-value = 0.186525) and rainfall (p-value = 0.099239), were not clearly significant.

Table 1.

Signification analysis of the multivariate linear model to explain the number of active cases as a function of viral load, and mean temperature.

	Estimate	Standard error	t value	Test p-value
Intercept	−5433.37	1805.63	−3.009	0.00562
ln(Viral load)	1008.25	107.32	9.395	5.33e−10
Mean Temperature	−72.66	52.97	−1.372	0.18144

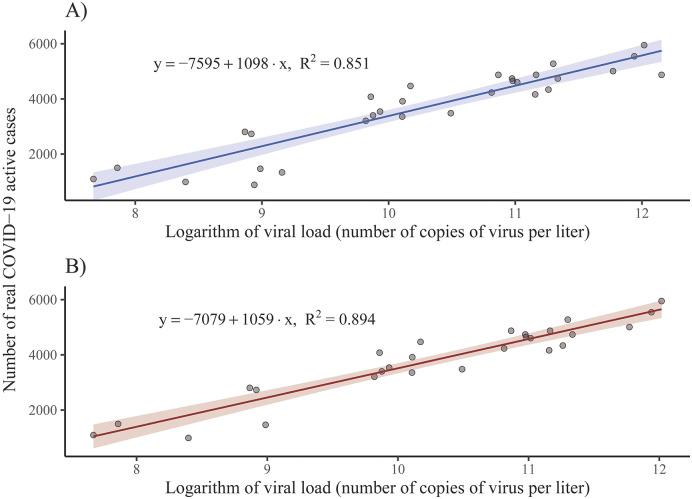
Finally, ignoring the rest of the explanatory variables, only the natural logarithm of the viral load gave a good linear model fit (R ² = 0.851) that was useful to predict the real number of active COVID–19 cases (Fig. 7A). After removing three outliers, the fit improved slightly (R ² = 0.894), as shown in Fig. 7B.

Fig. 7.

Estimation of the number of COVID–19 real active cases using a linear regression model. Scatterplot represents the logarithm of the viral load measured in WWTP Bens and the estimated number of COVID–19 real active cases before (A) and after (B) removing the three outliers detected. The linear fit (solid line) and the confidence band (shaded area) are also included.

The final fitted linear model became:

$$Y=-7079+1059\times lnX$$

where Y denotes the real number of active COVID–19 cases, X is the viral load (number of RNA copies per L) and ln stands for the natural logarithm.

For instance, a viral load of X = 150,000 copies per liter would lead to an estimated number of Y = 5543 active cases.

The prediction ability of this fitted linear model, the GAM, and the linear and quadratic LOESS models has been evaluated using a 6-fold cross validation procedure, to prevent overfitting. In all cases, the response variable was the estimated number of real COVID–19 active cases in the metropolitan area (Fig. 2), and the explanatory variable, the natural logarithm of the viral load. Table 2 shows the corresponding prediction R ² for each one of the four models, along with the root mean squared prediction error (RMSPE). The smaller this error, the better the predictive ability of the model was. All the models provided quite accurate predictions for the real number of COVID–19 active cases using the viral load, with an error of around 10% of the response range. The model with the lowest prediction error, 9.5%, was the quadratic LOESS model. Flexible models, such as LOESS and GAM, slightly improved the predictive performance when compared with the linear model, which has a prediction error of around 11.4% of the response range. The quadratic LOESS model was also the one with the largest value for R ². Therefore, it provided the best predictive results.

Table 2.

R² and root mean squared prediction error (RMSPE) corresponding to different regression models explaining the number of real active cases in the metropolitan area as a function of the natural logarithm of the viral load. RMSPE was obtained using a 6-fold cross validation procedure.

Model	R2	RMSPE
Linear	0.8515	581.94
GAM	0.8767	508.62
LOESS (linear)	0.8695	487.97
LOESS (quadratic)	0.8833	478.33

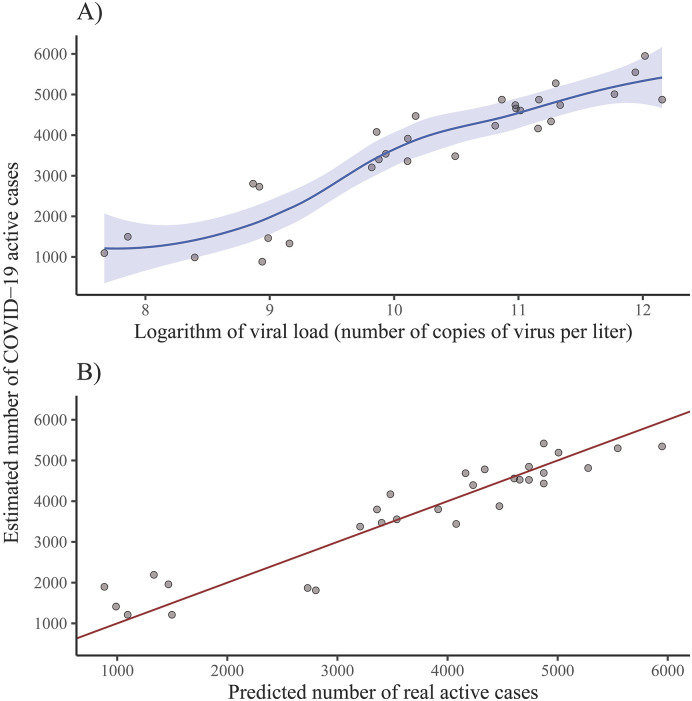
A scatterplot of the estimated number of COVID–19 active cases in the metropolitan area versus the natural logarithm of the viral load, along with the quadratic LOESS fitted curve show the linear relationship between these two variables (see Fig. 8A). The actual and predicted values of real number of COVID–19 active cases are very close to the diagonal line, which represents perfect model prediction (see Fig. 8B).

Fig. 8.

Estimation of number of real COVID–19 active cases using the quadratic LOESS model. A) Estimated COVID–19 active cases in the metropolitan area vs the natural logarithm of the viral load. B) Estimated number of COVID–19 active cases in the metropolitan area vs the predicted number of COVID–19 real active cases.

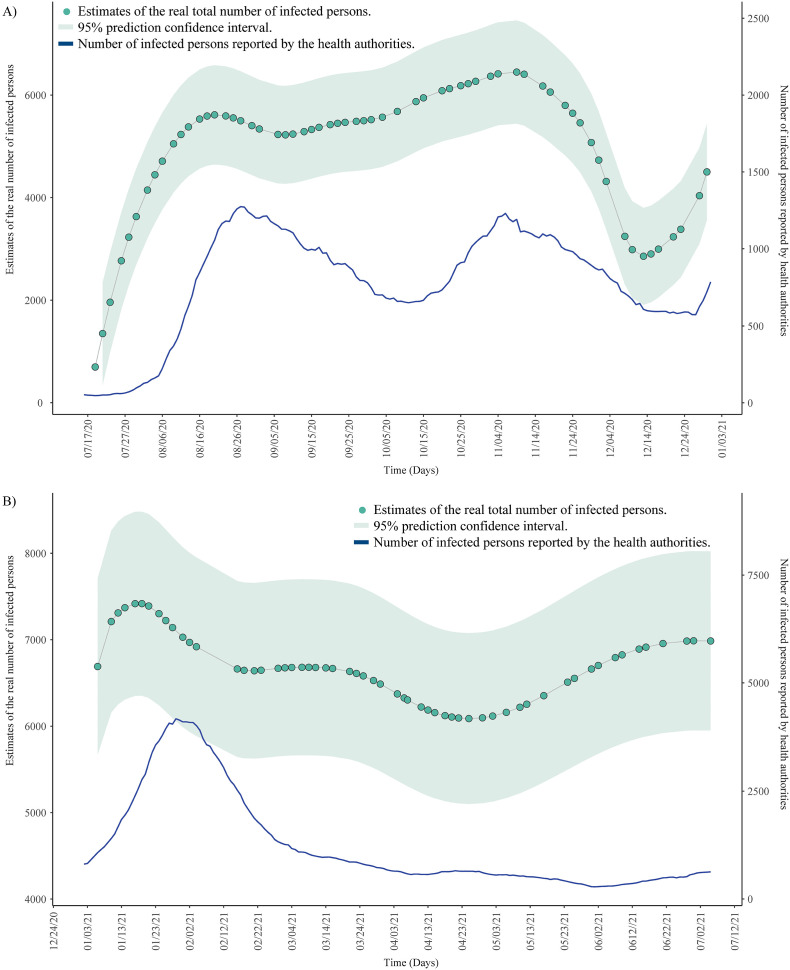
The above mentioned linear model has been used to make estimates of the total number of infected population with COVID–19 in the A Coruña metropolitan area from April 2020 on. In this regard, it is worth mentioning that the correlation coefficient between the logarithm of the viral load and the number of reported active cases 9 days after by the health authorities was 0.87 in the period July–December 2020. Thus, both the number of COVID–19 active cases for each day reported by the health services of Galicia (SERGAS) and the estimates of the number of infected persons (symptomatic and asymptomatic) obtained by the proposed model have been monitored in the framework of the COVIDBENS, so that the estimates can serve as an early warning indicator of possible outbreaks. Fig. 9A shows the trends of reported active cases and estimates of active cases for 2020 (from 17/07/2020), whereas Fig. 9B shows the trends corresponding to 2021 (until 07/04/2020). This figure is split in two panels taking into account that the dominant SARS-CoV-2 variants in A Coruña during 2020 were replaced by SARS-CoV-2 Alpha variant at the beginning of 2021. The evolution of variants can be followed at the link of the website of the Spanish Ministry of Health, Consumer Affairs and Social Welfare (Spanish Health Ministery, 2021), https://www.mscbs.gob.es/profesionales/saludPublica/ccayes/alertasActual/nCov/situacionActual.htm.

Fig. 9.

Estimation of number of real COVID–19 active cases using the linear model (in green), including the prediction confidence intervals. These estimates are compared with the number of cases of infected persons reported by the Galician health services (in blue). A) Trends corresponding to 2020. B) Trends corresponding to 2021. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

4. Discussion

In the pandemic context described above, 24–h composite samples from WWTP Bens were continuously analyzed from April 19th until early June, although surveillance has continued until now. The data from wastewater obtained from April 19th to June 1st has confirmed the decrease in COVID–19 incidence. We showed that time course quantitative detection of SARS–CoV–2 in wastewater from WWTP Bens correlated with COVID–19 confirmed cases, which backs up the plausibility of our approach. The previous seroprevalence studies carried out by the Spanish Centre for Epidemiology showed that cases in A Coruña represented about 1.8% of the local population (Pollán et al., 2020). This means that, for a population of about 369,098 inhabitants, the number of people infected with SARS–CoV–2 contributing their sewage into the WWTP Bens would be around 6644, which includes people with symptoms and those who are asymptomatic. Considering that the ratio between people with symptoms (reported by the health service) and the total infected population (including asymptomatic people) was estimated to be 1:5, we estimated that reported cases contributing their wastewater into WWTP Bens would be around 1661, which is close to the maximum number of cases reported in the A Coruña-Cee area (1667 cases on April 28th) therefore these data support our study. Of course, as reflected above, this ratio presents uncertainty and can be discussed. It should be noted that the criteria used by the authorities to report cases varied over time, so this may explain the gap between the graphs reported in the media throughout the epidemic and our Fig. 4, where both a decrease in the viral load and in the estimated COVID–19 cases can be observed from mid–April to early–June. However, the level of the curve at WWTP Bens at the beginning of May was much higher than that corresponding to May 11th. This is due to the effectiveness of the lockdown measures applied in Spain. The May 12th daily curve at CHUAC showed a higher viral load than the one corresponding to May 11th at WWTP Bens, showing that the viral load measured at the hospital tends to be higher than at WWTP Bens due to a lower dilution effect, as expected. One of the key points of this work is the use of statistical regression models for the estimation of real cases of COVID–19 from the information provided by wastewater, in the specific framework of the metropolitan area of A Coruña. In fact, in the present work, nonparametric and even simple parametric regression models have been shown to be useful tools to estimate the real number of COVID–19 active cases as a function of the viral load. This is a pioneering approach in the context of the SARS-CoV-2 pandemic, specifically in the framework of Spain. To our knowledge, the WBE studies available before the performance of our proposal (Vallejo et al., 2020) tended to be limited to reporting the occurrence of SARS–CoV–2 RNA in WWTPs and sewer networks, in order to establish a direct comparison with declared COVID–19 cases (Randazzo et al., 2020b; Medema et al., 2020; Nemudryi et al., 2020; La Rosa et al., 2020; Randazzo et al., 2020a; Polo et al., 2020). However, there are a number of studies that at similar dates proposed mathematically based models for estimating the number of COVID–19 cases. In this line, Hart and Halden (2020) is one of the precedent works that combines computational analysis and modeling with a theoretical approach in order to identify useful variables and confirm the feasibility and cost-effectiveness of WBE as a prediction tool. We have to mention also the studies of Ahmed et al. (2020) and Curtis et al. (2020) that proposed parametric transfer functions depending on WBE variables to estimate the number of persons infected. In addition, recently, new works focused on providing and comparing regression and time series models for the prediction of active cases have been developed (Cao and Francis, 2021; Li et al., 2021). The present methodology is characterized by focusing on a particular region and studying carefully all the steps, from sample collection to the estimation of the actual number of infected persons. This significantly differentiates our method, and the resulting predictive model, from other valid and useful alternatives. In addition, it is important to note that we focus on estimating the actual number of infected people rather than the number of cases reported by health authorities, as other methodologies do. For this task, the present approach uses the seroprevalence studies carried out by the Spanish Centre for Epidemiology. Moreover, the statistical regression models included in this methodology range from parametric to non-parametric approaches such as GAM or LOESS, which allow much more flexible data fitting, not subject to a fixed parametric expression relating the response variable and predictors. Other WBE models have been applied to previous outbreaks of other infectious diseases. For example, during a polio outbreak detected in Israel in 2013–2014, a disease transmission model was optimized incorporating environmental data (Brouwer et al., 2018). Given the availability of clinical information on poliovirus, the developed infectious disease model incorporated fully validated parameters such as the transmission and vaccination rates, leading to accurate estimations of incidence. This type of study highlights one of the main challenges we have faced developing our model: the SARS-CoV-2 novelty and the very few epidemiologic information available at the early stage of the pandemic. Considering this, our proposed model has minimized the uncertainty implementing a complete set of hydraulic information from the sewer network of the city of A Coruña. This ad hoc model can be adapted to other scenarios as long as similar hydraulic information can be obtained from the region where it will be implemented. Relevant possible explanatory variables (such as rainfall or the mean flow) did not enter the model. Although this is a bit counterintuitive (dilution should affect the viral load measured), it is important to point out that rainfall fluctuated little during the data collection period from mid-April to early–June 2020: its median was 0, its mean was 2.88 L/m² and its standard deviation was 6.59 L/m². Obviously, flow is an important factor to consider in WBE. In our case, before starting to model, the study correlations study between several variables was done, of course including flow. Since this work was done at time of drought, it was found that, contrary to expectations, flow was not a variable that entered the model. The strongest correlation was established between the log of the viral load and the number of active cases (R ² = 0.93). Of course, our models can be affected in the rainy season. However, as soon as the rainy season came, large distortions in our models were detected caused by the appearance of the Alpha and Delta variants (data not shown). Also, the water temperature remains stable in our geographical area and never raises enough to cause excessive degradation of viral RNA, so this variable does not enter the models either, as expected. It is important to highlight that, as a consequence of the results of the GAM fit, a simple linear model was considered to fit the estimated number of COVID–19 active cases as a function of the logarithm of the viral load. The log-linear relationship between viral concentration and the number of active cases of COVID–19 can be explained by exponential degradation of SARS–CoV–2 RNA during transportation through the sanitary network. As pointed out by Deagle et al. (2006) for DNA samples, if RNA damage occurs according to a random Poisson process, then an exponential decline in the amount of amplifiable product with increasing product size is expected. If this is the case and the logarithm of the amount of amplifiable product is linearly related with the original amount of SARS–CoV–2 RNA material on excretion. The percentage of variability explained by this linear model was reasonably high (85.1%) increasing up to 89.4% when three outliers detected were excluded. Some outliers were data obtained from samples collected during cleaning episodes, where viral RNA was almost totally degraded, leading to discordant data. Alternative, more flexible models, such as GAM and LOESS, were also fitted. They produced slightly better results in terms of R ² and RMSPE. The quadratic LOESS model avoided overfitting and showed a good predictive ability (R ² = 0.88, RMS   PE = 478), the best among all the considered models. However, similar results were found for the linear model that also brings the advantage of simplicity. Therefore, both models, linear and LOESS quadratic, could be successfully used to estimate the number of infected people in a given region based on viral load data obtained from wastewater.

The proposed models, as described, are only applicable to the metropolitan area of A Coruña, the region for which they have been developed, although can be adapted to any other location. This area has Atlantic weather and it may rain substantially in autumn and winter, which could lead to explanatory variables such as rainfall and/or mean flow becoming significant for those seasons and needing to enter the prediction model. Thus, when applying these models to the same location but in seasons with different climatic behavior, they might need to be reformulated.

In addition, the methodology used to build these statistical models could be used at other locations for epidemiological COVID–19 outbreak detection, or even for other epidemic outbreaks caused by other microorganisms. Of course, in that case a detailed data analysis would have to be carried out as well, since specific features of the sewage network or the climate may affect the model itself.

Overall results showed that the estimations of the real total number of infected persons are significantly higher than the number of reported infected persons. Both curves are very different in terms of scale. However, regarding the shape of both trends, it is very similar, providing relevant information of the evolution of the pandemic in Spain. Moreover, it is important to note that the curve of estimates is slightly out of phase with respect to the number of active cases reported by health authorities. In fact, it is slightly ahead (around two weeks) contributing to early information about the beginning of each outbreak, such as those corresponding to August 2020, November 2020 or January 2021 (data not shown). This information has provided support for decision making to the public authorities, involving decisions such as confinement, mobility and time restrictions. In addition, the model estimates have given an idea of the real progress of the pandemic in our region, complementing the information on active cases reported by public administrations. This work has proposed a methodology to estimate the real number of infected persons of COVID–19 (symptomatic and asymptomatic) in A Coruña metropolitan area from the viral load measured in its wastewater. It is a comprehensive and multidisciplinary procedure that includes all the steps from the wastewater sample collection to the estimation of actual infected persons by parametric or nonparametric regression models. The close collaboration between the public wastewater company and an interdisciplinary research team of microbiologists, chemists, engineers, statisticians and computer scientists has resulted in the implementation of an alert system in the metropolitan area of A Coruña. The results have been weekly delivered since July 2020 up to now to public authorities of A Coruña metropolitan area, Galicia and Spain to support their decision making during the pandemic, being one of the pioneer systems in Spain. The usefulness of this work has transcended the administrative sphere to provide a service open to all citizens of the metropolitan area, initially through the media (La Voz de Galicia, 2021; La Opinión de A Coruña, 2021; Bravo, 2021) and then through its own website (COVIDBENS, 2021) with an important social impact. The successive web reports have helped citizens to know about the evolution of the pandemic in our metropolitan area, even anticipating each of the successive outbreaks, also facilitating decision making at personal, family and business level.

5. Study limitations

The first serious limitation to start this work was the beginning of the total confinement of the first outbreak decreed by the national government when the COVIDBENS research team was created on purpose for this work. This limited, of course, interaction between the researchers. We had to ask for special permits to be able to carry out the laboratory work in the hospital and do the sample collection. Then the lack of reagents came; for RNA purification, for PCR, for suitable devices and personal protective material such as masks, gloves, etc. The lack of reagents did not allow us to make replicates at the very first time, which could only be done later. The control of recovery efficient was also impossible due to the unavailability of marker viruses at that moment. Also, the lack of reliable data of COVID–19 cases was an important limitation, therefore statisticians had to create a statistical model to be able to estimate the real number of cases, since the information at that first moment of the pandemic was very biased and incomplete. Moreover, some periodically cleaning events made with hot water in the wastewater collection system of the hospital originated confusing data during the first weeks of the study, since hot water practically eliminates viral RNA. Due to lack of several materials and reagents a great effort in sample collection and processing had to be done and finally the number of samples was enough to develop the statistical models as soon as possible. Variability found in data obtained by PCR when viral load was very low was another important limitation, which has been partially solved by making six replications of each RT-qPCR. Also, ratios fixed for the calculation of symptomatic cases and total cases are another source of uncertainties that should be taken into account. The mean ratio between real COVID–19 cases and official COVID–19 cases was estimated using the Spanish sero–epidemiological survey, which age a mean ratio estimation of 5.29. The mean ratio was rather stable over the time in our study since it ranged between 5.316 (May 11th) and 5.254 (June 1st). However, this mean ratio may be quite different in further periods of the pandemic. The statistical models described in the present study were done with data recovered only during the first epidemic outbreak. This is a limitation but, nevertheless, this fact allowed having early statistical models that, since July 2020 were able to estimate the number of infected people in the population and collaborate with the public health system. Other important limitation is that the models described here did not depend on rainfall, probably because the data were obtained in spring, a season of little rain in NW Spain. So in order for the models to be used in rainy seasons, they must be adapted. Also adaptation has to be done for using this type of models in other locations. However, the authors believe they could be of help to adapt these models to any other place in the world where there is a wastewater sanitation system. Finally, despite the serious limitations, we decided to exploit the statistical models as soon as possible to help in the fight against the pandemic.

6. Conclusions

This work aimed to evaluate the viral load measured in wastewater as a predictor of the real number of COVID–19 active cases. Different regression models were fitted to predict the real number of COVID–19 active cases based on the viral load, flow and the most relevant atmospheric variables. These statistical models have been able to provide estimates, from April 2020 up to now, of the real magnitude of the epidemic at the metropolitan area of A Coruña. These estimates have been weekly reported to the local public authorities. A variable selection method based on the maximization of the adjusted R ² was used. The only predictor with a significant effect on the real number of infected persons was the viral load, both when GAM and multivariate linear models were fitted. In the GAM model, the effect of the viral load on the real number of active cases had a logarithmic shape. Thus, the viral load was introduced in the multivariate linear model using its logarithmic transformation. As a result, very explanatory GAM (R ² = 0.86) and linear (R ² = 0.851) models were fitted. Their goodness-of-fit increased when outliers are removed (R ² = 0.894). It is important to stress that this simple model, Y = − 7079 + 1059 × ln X, is valid for this specific case of the metropolitan area of A Coruña. In other locations, with different weather, or in other seasons, the role of the other potential explanatory variables could be more important. In addition, the reliability of the model predictions could change during time due to different causes such as the change of SARS–CoV–2 variants. Moreover, the prediction ability of the linear, the GAM, and the linear and quadratic LOESS models has been evaluated using a 6–fold cross validation through the prediction R ² and the RMSPE index. The prediction errors of all the models were relatively small, supporting their use for prediction tasks. The lowest prediction error corresponded to the quadratic LOESS model. Finally, we have used the linear model to predict the number of real active cases using viral load. The reasons are its low prediction error, its simplicity, and the fact that it provides a parametric function that defines the relationship between variables. The present methodology, including the fitting of the parametric linear or nonparametric statistical models (GAM, LOESS), can be extended to estimate the real number of infected people at other locations. In addition, it is important to note that their sampling cost–effectiveness and speed can help to early alert health authorities about potential new outbreaks, thereby helping to protect the local population.

The following are the supplementary data related to this article.

Dataset S1

Data about sample collection. This document includes the dates when each sample was collected in the two locations considered: the WWTP Bens and the University Hospital of A Coruña (CHUAC). They all correspond to 24–h composite samples. Additional 2–h samples were collected during some of those days (marked as “each 2h”).

Dataset S2

Daily observations at the meteorological station of Coruña-Bens, for the period March 1st–May 31st, 2020, obtained from the Galician Meteorology Agency, MeteoGalicia (https://www.meteogalicia.gal/observacion/estacionshistorico/historico.action?idEst=14010). It contains measures for daily rainfall (L/m²), average humidity (%), and average temperature (°C).

Dataset S3

Cumulative and active number of COVID–19 cases in the metropolitan area of A Coruña and from the health area A Coruña – Cee for the period March 1st–May 31st, 2020. It contains: date; ma_cumulative_cases, which is the cumulative number of confirmed COVID–19 cases in the metropolitan area according to the records provided by the General Directorate of Public Health (Autonomous Government of Galicia) of individual patients with domicile in one of the following municipalities: A Coruña, Arteixo, Cambre, Oleiros, Culleredo; ha_reported_active_cases, which is the number of active COVID–19 cases in the health area reported by SERGAS (Galician Health Service) and extracted from https://galiciancovid19.info/; ma_real_active_cases, corresponds to the series of real active cases based on the estimated daily official COVID–19 cases in the metropolitan area of A Coruña; and ICU_patients, which is the number of ICU patients with COVID–19 at University Hospital of A Coruña (CHUAC).

Dataset S4

Two–minute flow measurements (m³·s⁻¹) at WWTP Bens for the period January 1st–May 14th. It includes the following columns: date, hour, UR–MC–01, UR–MC–02, UR–MC–03. The last three columns are different flow measurements, namely: UR–MC–01 corresponds to the flow meter at the first pumping line; UR-MC-02 corresponds to the flow meter at the second pumping line; and UR–MC–03 corresponds to the flow meter found in the auxiliary rainwater pumping. For this article, the total flow rate pumped from the raw water well at WWTP Bens is computed as the sum of the three measurements (UR–MC-01 + UR–MC–02 + UR–MC–03).

Dataset S5

Viral load and Cq values obtained from the 24–h samples, measured in number of SARS–CoV–2 RNA copies/L. The measurements for six RT–PCR replicates are included. The data contains: date, number of copies/L and location (WWTP_Bens or CHUAC). Measurements marked with an asterisk (*) in the fourth column mean that the RT-PCR failed and the value had to be imputed as the lowest value of the rest of the replicates.

Dataset S6

Viral load and Cq values obtained from the 2–h samples, measured in number of SARS–CoV–2 RNA copies/L. The measurements for three RT-PCR replicates are included. The data contains: date, hour of the day, number of copies/L and location (WWTP_Bens or CHUAC). Measurements marked with an asterisk (*) in the fourth column mean that the RT-PCR failed and the value had to be imputed as the lowest value of the rest of the replicates. The document includes the measurements for three days in the case of WWTP Bens (May 5th, 6th, and 11th, 2020) and for one day in the case of CHUAC (May 12th, 2020).

Table

Summary table of used datasets.

Supplementary material: Description of supplementary datasets, straight pattern done with the human 2019-nCoV RNA standard (EVAg) for viral load quantification through RT-qPCR assays, determination of the lower limit of viral load detected by RT-qPCR, nonparametric fitting of viral load overtime, multivariate linear model selection using the R² maximization criterion for estimating the number of COVID-19 cases, and flow study before, during and after lockdown.

Funding

This work was supported by EDAR Bens S.A., A Coruña, Spain [grant references INV04020, INV12120 and INV05921 to MP], the National Plan for Scientific Research, Development and Technological Innovation 2013-2016 funded by the ISCIII, Spain - General Subdirection of Assessment and Promotion of the Research-European Regional Development Fund (FEDER) “A way of making Europe” [grant numbers PI15/00860 to GB, PI17/01482 and PI20/00413 to MP], the GAIN, Xunta de Galicia, Spain [grant number IN607A 2016/22 to GB, ED431C-2016/015 and ED431C-2020/14 to RC, ED431C 2017/58 to SL, ED431G 2019/01 to RC and SL, and ED431C 2017/66 to MCV], MINECO, Spain [grant number MTM2017-82724-R to RC], Ministerio de Ciencia e Innovación, Spain [grant number PID2020-113578RB-100 to RC], and the Spanish Network for Research in Infectious Diseases [REIPI RD16/0016/006 to GB]. The work was also supported by the European Virus Archive Global (EVA-GLOBAL) project that has received funding from the European Union's Horizon 2020 - Research and Innovation Framework Programme under grant agreement no 871029. SR-F was financially supported by REIPI RD16/0016/006, KC-P by IN607A 2016/22 and the Spanish Association against Cancer (AECC) and JAV by IN607A 2016/22. Funding for open access charge: Universidade da Coruña/CISUG.

Data availability

The authors declare that all data supporting the findings of this study are available within the article and Supplementary information files, and also are available from the corresponding authors on reasonable request.

CRediT authorship contribution statement

MP, RC, CL, JAV, JT-S and RR conceived and designed the study. MP, JAV, NT, SR-F, MN and KC-P performed wastewater processing and viral analysis, RC, AL-O, IB, MV and JT-S performed statistical models and data analysis, SL managed and analyzed data, BKR-J assisted in the study design and analysis, AA assessed in data collection, AC supervised the wastewater analysis, MCV assessed in wastewater sampling, GB and MP supervised the microbiology team, MP, JAV, RC, RR and JT-S wrote the manuscript. MP, JT-S and RC supervised the team and coordinated all tasks.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Editor: Warish Ahmed