A broadly applicable method for characterizing the slope of the electrically evoked compound action potential amplitude growth function

Abstract

Objective:

Amplitudes of electrically evoked compound action potentials (eCAPs) as a function of the stimulation level constitute the eCAP amplitude growth function (AGF). The slope of the eCAP AGF (i.e., rate of growth of eCAP amplitude as a function of stimulation level), recorded from subjects with cochlear implants (CIs), has been widely used as an indicator of survival of cochlear nerve fibers. However, substantial variation in the approach used to calculate the slope of the eCAP AGF makes it difficult to compare results across studies. In this study we developed an improved slope fitting method by addressing the limitations of previously used approaches and ensuring its application for the estimation of the maximum slopes of the eCAP AGFs recorded in both animal models and human listeners with various etiologies.

Design:

The new eCAP AGF fitting method was designed based on sliding window linear regression. Slopes of the eCAP AGF estimated using this new fitting method were calculated and compared to those estimated using four other fitting methods reported in the literature. These four methods were nonlinear regression with a sigmoid function, linear regression, gradient calculation and boxcar smoothing. The comparison was based on the fitting results of 72 eCAP AGFs recorded from 18 acutely implanted guinea pigs, 46 eCAP AGFs recorded from 23 chronically implanted guinea pigs, and 2,094 eCAP AGFs recorded from 200 human CI users from four patient populations. The effect of the choice of input units of the eCAP AGF (linear vs logarithmic) on fitting results was also evaluated.

Results:

The slope of the eCAP AGF was significantly influenced by the slope fitting method and by the choice of input units. Overall, slopes estimated using all five fitting methods reflected known patterns of neural survival in human patient populations and were significantly correlated with speech perception scores. However, slopes estimated using the newly developed method showed the highest correlation with spiral ganglion neuron density among all five fitting methods for animal models. In addition, this new method could reliably and accurately estimate the slope for four human patient populations, while the performance of the other methods was highly influenced by the morphology of the eCAP AGF.

Conclusions:

The novel slope fitting method presented in this study addressed the limitations of the other methods reported in the literature and successfully characterized the slope of the eCAP AGF for various animal models and CI patient populations. This method may be useful for researchers in conducting scientific studies and for clinicians in providing clinical care for CI users.

INTRODUCTION

The functional status of the cochlear nerve (CN) (i.e., number and responsiveness of CN fibers) has been suggested to be important for hearing outcomes in cochlear implant (CI) users (e.g., Kim et al., 2010; Teagle et al., 2010; Garadat et al., 2012; Long et al., 2014; Zhou & Pfingst, 2014; Schvartz-Leyzac & Pfingst, 2018; Skidmore et al., 2021). However, the number of surviving CN fibers cannot be directly measured in human CI users. Therefore, animal models have been used to identify indicators of CN survival that could potentially be generalized to human listeners (e.g., Prado-Guitierrez et al., 2006; Ramekers et al., 2014, 2015; Pfingst et al., 2015a,b, 2017; Schvartz-Leyzac et al., 2019, 2020a).

Several potential indicators of CN survival have been derived from results of the electrically evoked compound action potential (eCAP). The eCAP is a near-field recorded neural response that is generated by electrically stimulated CN fibers. Its amplitude, which is defined as the difference in electrical potential between the positive and negative peaks of the eCAP waveform, increases with increasing electrical stimulation until it reaches an asymptote. A series of eCAP amplitudes recorded at corresponding stimulation levels is referred to as the eCAP amplitude growth function (AGF). In animal models, the eCAP AGF generally follows a monotonic “S”-shaped (i.e., sigmoid) curve. However, in some CI animals, and also in awake human CI users, the upper asymptote at the “true” maximum eCAP amplitude (i.e., saturation) may not be reached due to loudness discomfort, compliance limits, or non-auditory responses at high stimulation levels.

The slope of the eCAP AGF has repeatedly been shown to be associated with the density of spiral ganglion neurons (SGNs) in both acutely and chronically implanted animals, with steeper slopes indicating greater SGN density (Ramekers et al., 2014; Pfingst et al., 2015a,b; Pfingst et al., 2017; Schvartz-Leyzac et al., 2019, Vink et al., 2020). The slope of the eCAP AGF has been shown to account for 47–67% of the variance in SGN density (Ramekers et al., 2014; Pfingst et al., 2017), which suggests that it can serve as a potential biomarker for CN survival. Results from studies with human CI users agree with the results from these animal studies and show that steeper slopes are associated with presumed better neural function. Specifically, children with cochlear nerve deficiency (CND) have shallower AGF slopes than age-matched children with normal-sized cochlear nerves (He et al., 2018, 2020b), and older CI users have shallower slopes than younger CI users (Jahn & Arenberg, 2020a,b; Mussoi & Brown, 2020). However, inconsistent results have been shown by studies evaluating the association between the slope of the eCAP AGF and speech perception scores. Steeper slopes were associated with better speech perception scores in some studies (Brown et al., 1990; Gantz et al., 1994; Kim et al., 2010), while no association was found between these two measures in other studies (Franck & Norton, 2001; Turner et al., 2002). The inconsistency in results may, at least partially, be due to the differences in how speech perception was evaluated (words vs sentence, in quiet vs in noise, etc) and/or the differences in how the slope of the eCAP AGF was calculated.

One challenge in comparing the slope of the eCAP AGF across studies is the difference in input/output (I/O) units used to create the AGF. The stimulation level (i.e., input) has been specified in terms of charge in nanocoulombs (nC) (e.g., Ramekers et al., 2014; Adenis et al., 2018; He et al., 2020a,b; Xu et al., 2020; Vink et al., 2020), current in mA or μA (e.g., Gantz et al., 1994; Miller et al., 1998; Pfingst et al., 2015a,b, 2017; Schvartz-Leyzac et al., 2018, 2019, 2020b), current normalized to the threshold current (Miller et al., 1998) or logarithmic units in dB or current level (CL) (e.g., Abbas et al., 1999; Brown et al., 2010; Kim et al., 2010; Hughes at al., 2001, 2018; Nehmé et al., 2014; Cafarelli-Dees et al., 2005; Jahn & Arenberg, 2020a,b; Luo et al., 2020). The eCAP amplitude (i.e., output) is typically specified in terms of voltage in mV or μV (e.g., Abbas et al., 1999; Nehmé et al., 2014; Ramekers et al., 2014; Cafarelli-Dees et al., 2005; Pfingst et al., 2015a,b, 2017; Schvartz-Leyzac et al., 2018, 2019, 2020b; Jahn & Arenberg, 2020a,b; Luo et al., 2020 He et al., 2020b), or normalized to the maximum eCAP (e.g., He et al., 2018, 2020a, Xu et al., 2020). Slopes calculated in different units can dramatically affect the study results. This is exemplified in Miller et al (1998) in which an opposite polarity effect on the slope of the eCAP AGF was reported when the input units changed from linear current (i.e., mA) to normalized current.

Another challenge is the difference in the methods/algorithms used to calculate the slope of the eCAP AGF. The vast majority of studies have used linear regression to estimate the slope (e.g., Abbas et al., 1999; Nehmé et al., 2014, Kim et al., 2010, Franck & Norton, 2001; Turner et al., 2002; Cafarelli-Dees et al., 2005; Pfingst et al., 2015a,b, 2017; Adenis et al., 2018; Luo et al., 2020; Xu et al., 2020). However, eCAP AGFs reported in many studies are not linear (e.g., Hughes et al., 2001, 2018; Abbas et al., 2003; Lai & Dillier, 2007; Cohen, 2009; Abbas & Brown, 2015; Adenis et al., 2018). Some studies have excluded specific data points in the eCAP AGF from the linear regression analysis in order to account for this non-linearity (e.g., Franck & Norton, 2001; Pfingst et al., 2015a,b, 2017; Adenis et al., 2018). Sigmoidal functions have also been used to characterize the eCAP AGF (Ramekers et al., 2014; Jahn & Arenberg, 2020a; Van de Heyning et al., 2016; He et al., 2018, 2020a,b; Vink et al., 2020) because simulation and animal studies have shown that sigmoidal functions accurately characterize the neural response versus stimulation-level function of CN fibers (Galambos & Davis, 1943; Sachs & Abbas, 1974; Wen et al., 2009; Heil et al., 2011). However, sigmoidal regression often creates an unreasonable estimate of the slope when the AGF does not approach an asymptote of the maximum eCAP amplitude at the highest stimulation levels. This asymptote frequently cannot be obtained due to subject discomfort or device limitations. For example, eCAP AGFs recorded in awake guinea pigs, where the upper limit of stimulation has been based on evidence of facial nerve stimulation, seldom demonstrate a clear asymptote at the highest stimulation levels tested (Pfingst et al., 2015a; 2017). Customized methods have been used in a few studies to estimate the slope of the eCAP AGF in order to account for the nonlinear nature of the eCAP AGF (Schvartz-Leyzac et al., 2019, 2020b; Hughes et al., 2001). However, these methods were designed for specific datasets and are not broadly applicable because the underlying algorithm in each method is highly influenced by the number and spacing of the data points in the eCAP AGF. In general, none of the methods is able to reliably and accurately estimate the maximum slope of the eCAP AGF, which greatly limits the clinical application of this eCAP measure. In order to address these limitations of existing slope fittings methods, we recently developed a new method for estimating the maximum linear slope of the eCAP AGF.

In this paper, we present our newly developed slope fitting method, compare slopes estimated using different fitting methods and input units, and discuss four features that distinguish the newly developed method from the other fitting methods. These four features include broad application, total automaticity, easy implementation, and meaningful results. This study also tested the hypothesis that the maximum slope of the eCAP AGF provides the best estimate of SGN density and speech perception compared to shallower slope measures.

METHODS AND MATERIALS

Data

This study is based on previously reported eCAP results measured in acutely implanted guinea pigs (Ramekers et al., 2014), chronically implanted guinea pigs (Pfingst et al., 2017; Schvartz-Leyzac et al., 2019, 2020a), and human CI users (He et al., 2020a,b; Luo et al., 2020; Skidmore et al., 2021). In the present study, the SGN density measured in guinea pigs was defined as the averaged SGN density across four transections of Rosenthal’s canal in the basal and middle turns of the cochlea.

Acutely Implanted Guinea Pigs

Detailed information regarding these animals, experimental design and procedures can be found in Ramekers et al. (2014). Briefly, animals were implanted with a 4-contact electrode array connected to a MED-EL PULSARCI¹⁰⁰ cochlear implant (MED-EL GmbH, Innsbruck, Austria). Under anesthesia, eCAPs were recorded in six normal-hearing guinea pigs and 12 guinea pigs that were deafened two or six weeks prior to data collection (i.e., six animals in each study group). Both stimulating and recording of eCAPs were done with a monopolar configuration. Pulse parameters tested included either a pulse phase duration (PPD) of 30 or 50 μs and an inter-phase gap (IPG) of 2.1 or 30 μs. In the present study, eCAP AGFs were re-analyzed for the same animals and four stimuli. Example eCAP waveforms recorded in one normal-hearing animal and one deafened animal included in the present study can be seen in Figure 1 of Ramekers et al. (2014).

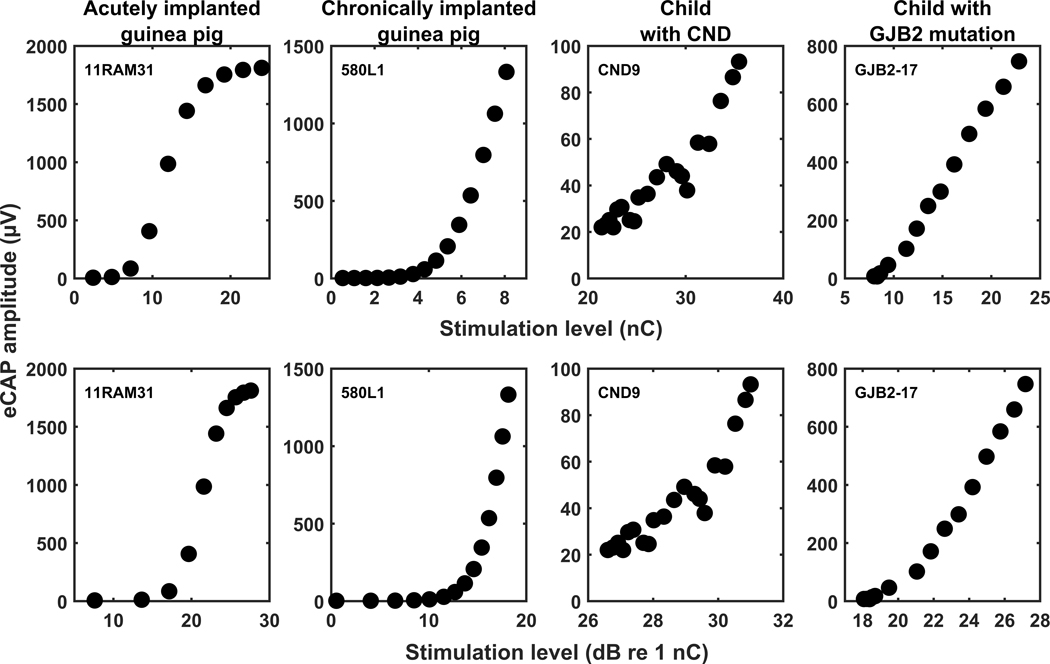
Figure 1.

Electrically evoked compound action potential amplitude growth functions (AGFs) for an acutely implanted anesthetized guinea pig, a chronically implanted awake guinea pig, a child with cochlear nerve deficiency, and a child with a GJB2 genetic mutation in two sets of input/output units. The AGFs are shown on different input and output scales to maximize the display of each AGF. In general, the chronically implanted awake guinea pigs were not stimulated at levels where an upper asymptote was reached in acutely implanted anesthetized guinea pigs. The subject identification number is also presented in each panel.

Chronically Implanted Guinea Pigs

Detailed information regarding these animals, experimental design and procedures can be found in Schvartz-Leyzac et al. (2019) and Schvartz-Leyzac et al. (2020a). Briefly, animals were implanted with an 8 electrode CI (Cochlear Corporation, Englewood, CO). While awake, eCAPs were recorded in normal-hearing guinea pigs and deafened guinea pigs that received various treatments with neurotrophins via gene therapies. The various deafening, treatment and implantation paradigms provided a wide range of SGN densities in this dataset. Both stimulating and recording of eCAPs were done with monopolar electrode configurations. Pulse parameters were a PPD of 45 μs and an IPG of either 2.1 or 30 μs. eCAPs were recorded over the course of each animal’s experimental test period, which ranged from 4.5 to 15.4 months post-implantation. Figure 2 of Schvartz-Leyzac et al. (2019) shows eCAP waveforms at various stimulation levels for one animal (580L1) included in the present study.

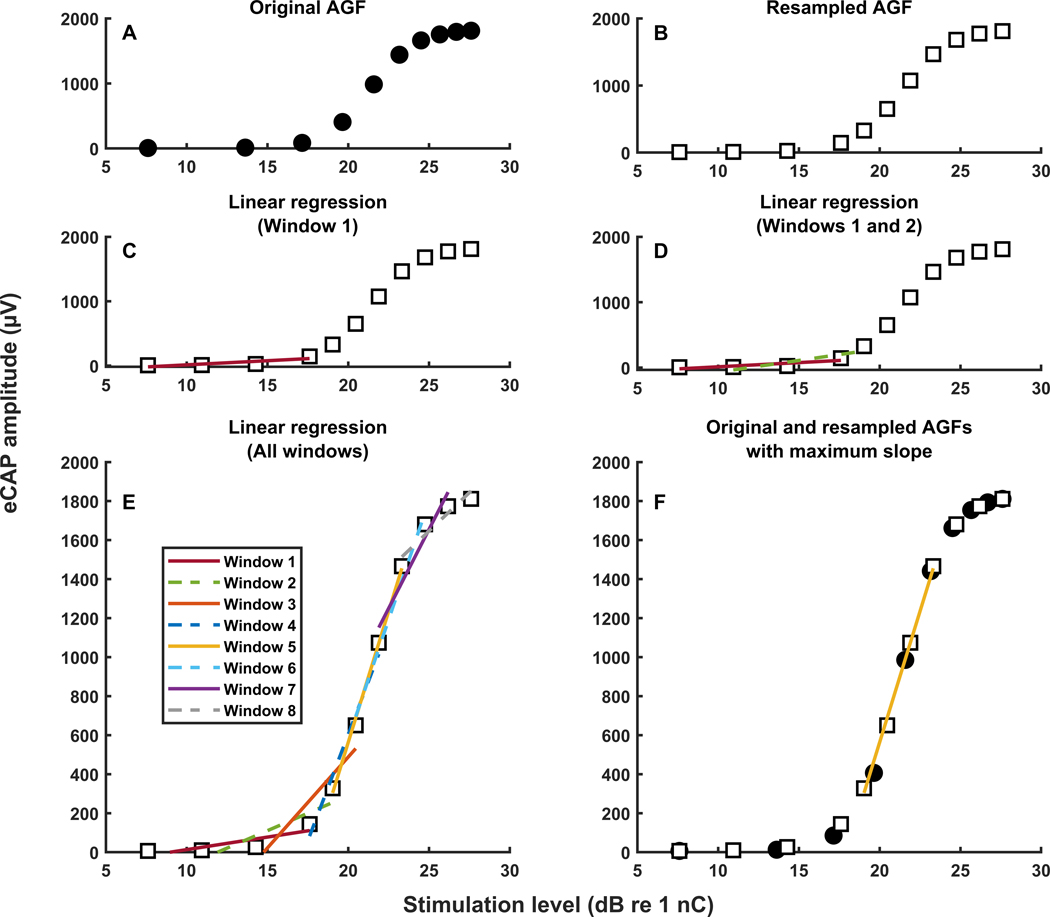
Figure 2.

A visual representation of the window method for calculating the maximum slope of the electrically evoked compound action potential amplitude growth function.

In the present study, eCAPs AGFs for a subset of the normal-hearing guinea pigs (N = 6) and deafened guinea pigs (N = 17) and the two stimulus configurations were reanalyzed. Only eCAP AGFs on or closest to the day that the animal was euthanized for histological examination were used.

Human Cochlear Implant Users

Details of eCAP recording methods and participant demographic information can be found in He et al. (2020a,b), Luo et al. (2020), and Skidmore et al. (2021). Briefly, all participants were implanted with a Cochlear Nucleus CI (Cochlear Ltd., Macquarie, NSW, Australia) in the ear tested. A total of 2094 eCAP AGFs from four different CI patient populations were reanalyzed for this study: 963 AGFs from 61 children with CND, 755 AGFs from 73 children with normal-sized CNs and various etiologies of hearing loss (non-CND study group), 59 AGFs from 20 children with biallelic Gap Junction Beta-2 (GJB2) genetic mutations, and 317 AGFs from 46 adults with various etiologies of hearing loss. Example eCAP waveforms recorded in participants who were included in the present study can be seen in Figure 2B of Luo et al. (2020) and Figure 2 of Skidmore et al. (2021).

Participants from these four patient populations were included in this study because of generally different CN functional statuses between these patient populations. Specifically, CND refers to a small or absent CN as indicated by results of high-resolution magnetic resonance imaging scans (Glastonbury et al., 2002; Adunka et al., 2006). As a group, children with CND have been shown to have significantly worse CN function and CI outcomes than age-matched CI patients with normal-sized CNs (Kang et al., 2010; Wei et al., 2017; He et al., 2018). Additionally, CI patients with GJB2 mutations have excellent CI outcomes (e.g., Reinert et al., 2010; Yan et al., 2013; Yoshida et al., 2013) and have been shown to have better CN function than children with idiopathic hearing loss (Luo et al., 2020). Finally, data from adults of various ages was included in this study because CN function deteriorates with advanced age and/or long duration of deafness (e.g., Hellstrom & Schmiedt, 1996; McFadden et al., 1997; Makary et al., 2011). Therefore, these four patient populations were included in this study to compare the slope fitting methods across a large range of CN functions.

The eCAP AGFs were recorded for all participants using a monopolar-coupled configuration at multiple electrode locations along the length of the cochlea. The number of electrodes tested ranged from 3 to 7 for each participant. Pulse parameters were a variety of PPDs (25, 37, 50, 62, 75, 88 or 100 μs) and IPGs (7, 14, 21, 28, 35, 42 or 45 μs). One eCAP AGF was recorded for each set of pulse parameters.

For comparison to eCAP AGF slopes, speech perception was tested in quiet and in noise (+5 dB signal-to-noise ratio) for a subset (In quiet: N = 33, In noise: N = 27) of the 46 adult CI users using Consonant-Nucleus-Consonant (CNC) word lists (Peterson & Lehiste, 1962). All testing was performed in a soundproof booth and followed the procedure outlined in the new Minimum Speech Test Battery (MSTB, 2011). For any bilateral CI users, speech perception was measured separately for each test ear.

Amplitude Growth Functions

The eCAP AGF was created by plotting the amplitudes of the eCAP response (i.e., output) as a function of stimulation level (i.e., input). In the present study, the slope fitting methods were compared with linear output units (μV) and both linear and logarithmic input units (i.e., nC and dB re 1 nC, respectively). Logarithmic output units (i.e., dB re 1 μV) were included in the initial analyses, but there was not a significant correlation between slope and SGN density when the slope was calculated with logarithmic output units. Therefore, logarithmic output units were not used in this study. Representative AGFs randomly selected from the dataset for an acutely implanted guinea pig, a chronically implanted guinea pig, a child with CND, and a child with a GJB2 genetic mutation are shown in Figure 1 for each set of I/O units used in this study, with linear input units used in the panels on the top row and logarithmic input units used in the panels on the bottom row. The axes in each panel have been independently scaled to best display the morphology of each AGF despite differences in stimulation levels and response amplitudes across species and patient populations. Factors that contribute to these differences include, but are not limited to, stimulation level that can be used in anesthetized animals versus awake animals and human listeners, anatomy, electrode geometry, distance from electrode to neural tissue, and size of neural population.

Slope Fitting Methods

In this study, we developed an improved fitting method (window method) and compared its fitting results with those obtained using nonlinear regression with a Boltzmann sigmoid function (sigmoid method), linear regression (linear method), gradient calculation (gradient method) and boxcar smoothing (boxcar method). Details of each method are reported below.

Sigmoid Method:

In the sigmoid method, the eCAP AGF was fitted with a Boltzmann sigmoid function in the form of

$$y=a+\frac{b}{1+e^{-\left(\frac{x-c}{d}\right)}}$$ (1)

where $y$ was a vector of output measurements (i.e., eCAP amplitudes), $x$ was a vector of input magnitudes (i.e., stimulation levels), and $a-d$ were fitting parameters. The maximum slope of the function was calculated as $b/\left(4d\right)$, where $b$ represented the estimated maximum eCAP amplitude and $4d$ represented the estimated dynamic range. Slopes calculated with this method were removed as outliers when the estimated maximum eCAP amplitude (i.e., fitting parameter $b$) was more than five times greater than the recorded maximum eCAP amplitude. With the sigmoid method described here, the slope of the eCAP AGF can be reasonably estimated only when the measured AGF approaches an asymptote.

Linear Method:

In the linear method, the eCAP AGF was fitted with a linear function in the form of

$$y=a\mathrm{*}x+b$$ (2)

where $y$ and $x$ were vectors of output and input values, respectively, $a$ represented the slope of the eCAP AGF, and $b$ represented the intercept of the linear function with the vertical axis.

Several studies that used the linear method excluded eCAP amplitudes from the fitting function that were below a defined threshold and/or were near saturation in order to improve estimation of the maximum slope (e.g., Franck & Norton, 2001; Pfingst et al., 2015a,b, 2017; Adenis et al., 2018). However, this requires subjective decisions and thus is difficult to replicate across studies. For the data reported in the current paper, it was infeasible to identify a uniform exclusion criterion due to the thousands of AGFs included from multiple species and patient populations. Additionally, any manual pre-processing of the AGF could introduce unwanted subjectivity into the results. Therefore, linear regression was applied to all of the data points recorded in each AGF for the linear method in the present study, even though it did not necessarily reflect how the linear method had been applied in previous studies. Thus, the linear method implemented in this study represented the overall slope of the AGF (i.e., the linear slope calculated with all recorded data points) and was highly dependent on the number of data points collected in the nonlinear portions of the AGF.

Gradient Method:

The gradient method was introduced in Schvartz-Leyzac et al. (2019). This custom algorithm removed outlying data points from the AGF before performing linear regression. First, all data points below the noise floor were removed. The algorithm then estimated the instantaneous slope of the AGF at each data point using the ‘gradient’ function implemented in the MATLAB software package (MathWorks Inc., version 2019b). The data points with instantaneous slopes that deviated by more than 20% of the maximum instantaneous slope were subsequently removed. Finally, the overall slope of the AGF was calculated using the linear method (above) with all of the remaining data points. Like the linear method, this method requires selection of the data points that fall in the linear portion of the AGFs and thus can be difficult to apply uniformly across studies.

Boxcar Method:

The boxcar method was utilized by Hughes et al (2001). This method first smoothed the eCAP AGF by using a 3-point boxcar filter on all of the data points between the lowest and highest stimulation levels. The steepest slope between the two adjacent points of the smoothed function was then used to represent the slope of that AGF. Due to the nature of the boxcar filter, the boxcar method is highly influenced by the number and spacing of the data points in the AGF, which limits the robustness of this method across datasets.

Window Method:

The window method was developed to address the limitations of the other slope fitting methods reviewed above. This method included three main steps. The first step was to resample the original eCAP AGF (i.e., the recorded data points) at 11 data points in order to handle missing data points or non-uniformly sampled data in the original AGF. The second step was to perform a series of eight linear regression analyses on sequential subsets of four data points (i.e., sliding window linear regression). The final step was to select the maximum slope from among all subsets of data points (i.e., windows). The number of resampled data points (i.e., 11) and the length of the window (i.e., 4) were determined by maximizing the correlation of the slope of the AGF with SGN density for the acutely implanted guinea pigs (i.e., training dataset). Data from the chronically implanted guinea pigs were not included in the optimization of those parameters in order to test the performance of the method on data that was not used to identify the method parameters (i.e., testing dataset). Each step of the method is detailed below and illustrated in Figure 2 for an eCAP AGF recorded in an acutely implanted guinea pig.

Step 1: Resampling the original AGF.

The original AGF (Figure 2A) was resampled at 11 points with the first point and the last point measured at the lowest and the highest stimulation level, respectively (Figure 2B), in either linear or logarithmic input units. There were four points equally distributed in the first half of the AGF and seven points equally distributed in the second half of the AGF. Approximately one-third of the total number of points were included in the first half of the AGF to filter this part of the function due to a low signal-to-noise ratio. An eCAP amplitude was calculated at each of the 11 resampled stimulation level points by linearly interpolating between the eCAP amplitude data points of the original AGF.

Step 2: Sliding window linear regression.

Linear regression was then performed eight times on sequential windows that each contained four different data points from the resampled AGF. In other words, linear regression was first performed with only the first four data points (i.e., first window) from the resampled AGF (Figure 2C). The window then ‘slid’ by one data point to contain the second through fifth data points (i.e., second window), and linear regression was again performed (Figure 2D). This process continued until linear regression had been performed on all eight windows (Figure 2E).

Step 3: Selecting maximum slope.

The slope was calculated from each instance of linear regression performed in Step 2. The maximum value of all of the slopes was selected as the slope of the AGF (Figure 2F).

Statistical Analysis

Statistical modeling and analysis for this study was performed using MATLAB (MathWorks Inc., version 2019b) software. Parameters of the mathematical functions used in statistical modeling were estimated using the trust-region-reflective algorithm. The one-way repeated measures analysis of variance (ANOVA) with the Tukey’s honest significant difference (HSD) post-hoc test was used to compare slopes of the eCAP AGF estimated using the five slope fitting methods. The Greenhouse-Geisser correction was applied in all ANOVA tests because the assumption of sphericity was violated as indicated by the Mauchly Sphericity Test (Mauchly, 1940). The one-tailed Pearson correlation analysis was used to evaluate the association between the slope of the eCAP AGF and the SGN density in guinea pigs. The $R^2$ resulting from the correlation analyses were compared between slopes calculated with linear and logarithmic input units using a one-tailed, paired sample t-test. The effect of the slope fitting method on $R^2$ was evaluated using one-way, repeated measures ANOVA with Greenhouse-Geisser correction and HSD post-hoc testing.

Outliers of the slope estimated from eCAP AGFs recorded in human CI users were excluded using the three scaled median absolute deviations criterion (Leys et al. 2013). The one-tailed Pearson correlation analysis was used to evaluate the association between the slope of the eCAP AGF averaged across all electrode locations and CNC word scores measured in adult participants. All statistical analyses were performed at the 95% confidence level.

RESULTS

Effect of Units and Fitting Method on Calculated eCAP AGF Slope using Data from Animal Models

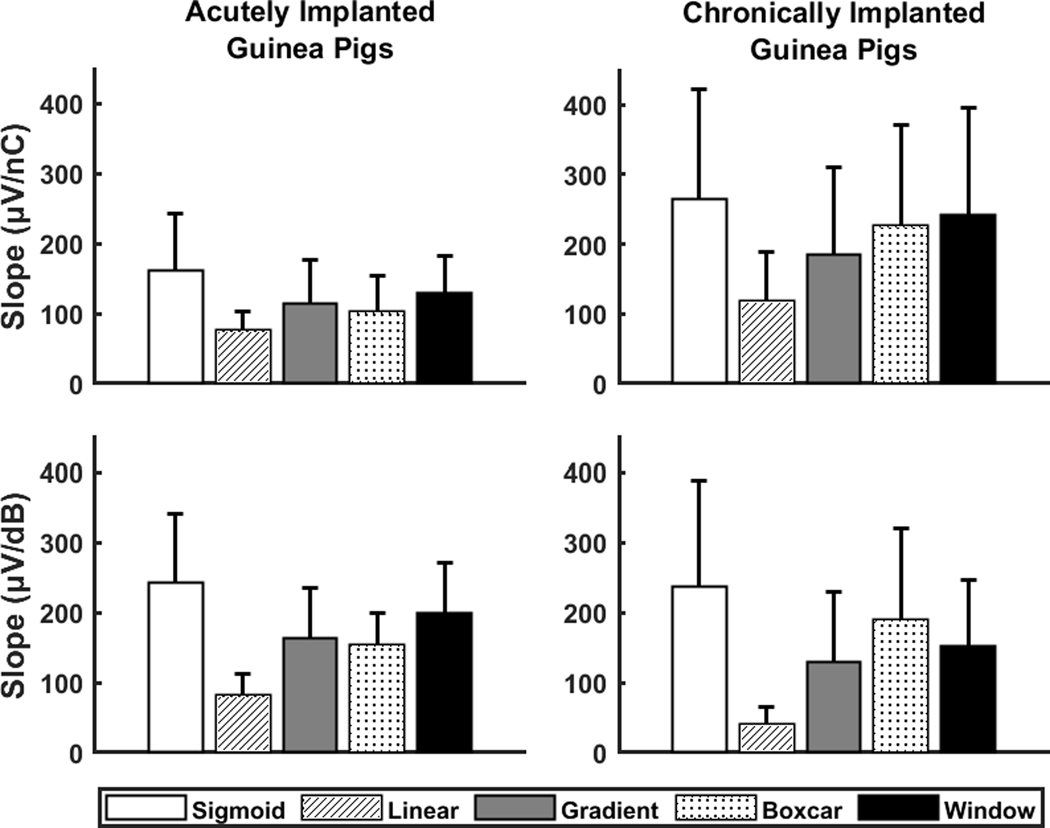
The means and standard deviations of the slope of the eCAP AGF calculated in two sets of I/O units with five methods are shown in Figure 3 for both acutely implanted and chronically implanted guinea pigs. The sigmoid method estimated extremely high slopes for seven of the 92 AGFs (7.6%) from chronically implanted guinea pigs because those seven AGFs did not approach an upper asymptote. Therefore, for the sigmoid method, those seven AGFs were excluded from the mean and standard deviation calculations shown in Figure 3 and from further data analyses (e.g., correlation of slope with SGN density). Those seven AGFs were not excluded from analyses with the other four slope fitting methods.

Figure 3.

The means and standard deviations of the slope of the electrically evoked compound action potential amplitude growth function calculated in two sets of input/output units (top row: linear input units, bottom row: logarithmic input units) with five slope fitting methods for acutely implanted (left column) and chronically implanted (right column) guinea pigs. The sample size (N = 92) was the same for all calculations except for the sigmoid method (nC: N = 89, dB: N = 88) due to removal of extreme estimates of the slope from the sigmoid method.

As observed in the figure, there was a large variability in the magnitude of slopes estimated using different methods, even within the same group of guinea pigs. Slopes were the highest when estimated with the sigmoid method and the lowest when estimated with the linear method for both animal groups and sets of I/O units. Results of one-way, repeated measures ANOVA analyses indicated a significant effect of method on the slope of the eCAP AGF for both acutely implanted [μV/nC: F_(1,71) = 303.8, p<0.001; μV/dB: F_(1,71) = 471.9, p<0.001] and chronically implanted [μV/nC: F_(1,43) = 125.0, p<0.001; μV/dB: F_(1,40) = 117.6, p<0.001] guinea pigs. All post-hoc comparisons were significant except for the slopes calculated with the gradient and boxcar methods in units of μV/dB for acutely implanted guinea pigs. Results of all post-hoc comparisons with Tukey’s HSD are provided in Table 1.

TABLE 1.

Statistical results from multiple comparisons using Tukey’s honest significance difference post-hoc test when comparing slope fitting methods in two sets of input/output units for acutely implanted and chronically implanted guinea pigs.

Units	Comparison	Acutely implanted			Chronically implanted
		Difference	Standard Error	p-value	Difference	Standard Error	p-value
$\frac{\mathrm{\mu }\mathrm{V}}{\mathrm{n}\mathrm{C}}$	S vs L	76.9	6.2	<0.001	136.1	14.8	<0.001
	S vs G	43.1	3.0	<0.001	68.4	6.1	<0.001
	S vs B	52.5	4.2	<0.001	28.5	2.9	<0.001
	S vs W	26.9	3.4	<0.001	14.2	2.4	<0.001
	L vs G	−33.8	3.6	<0.001	−67.8	9.7	<0.001
	L vs B	−24.4	2.6	<0.001	−107.7	13.1	<0.001
	L vs W	−50.0	3.1	<0.001	−121.9	13.8	<0.001
	G vs B	9.4	1.7	<0.001	−39.9	4.4	<0.001
	G vs W	−16.2	1.9	<0.001	−54.2	5.4	<0.001
	B vs W	−25.6	2.0	<0.001	−14.3	2.4	<0.001
$\frac{\mathrm{\mu }\mathrm{V}}{\mathrm{d}\mathrm{B}}$	S vs L	158.8	8.6	<0.001	200.8	23.6	<0.001
	S vs G	71.8	4.4	<0.001	99.2	13.3	<0.001
	S vs B	81.1	6.8	<0.001	37.2	7.7	<0.001
	S vs W	42.5	3.2	<0.001	82.1	14.9	<0.001
	L vs G	−87.0	5.2	<0.001	−101.6	12.0	<0.001
	L vs B	−77.7	3.7	<0.001	−163.5	17.7	<0.001
	L vs W	−116.3	5.6	<0.001	−118.7	10.9	<0.001
	G vs B	9.3	3.9	0.142	−61.0	7.0	<0.001
	G vs W	−29.3	2.6	<0.001	−17.1	4.3	0.002
	B vs W	−38.5	4.1	<0.001	44.8	8.2	<0.001

S: sigmoidal method, L: linear method, G: gradient method, B: boxcar method, W: window method.

Correlation of eCAP AGF Slope and Histology

The strength of correlation between SGN density and the slope of the eCAP AGF calculated in two sets of I/O units with five slope fitting methods is shown in Table 2 for multiple PPDs and IPGs. All correlations were statistically significant (p < 0.003). The $R^2$ varied from 0.34 to 0.77 across all methods, units, and animal groups. As shown in the bottom row of Table 2, the strongest correlation was obtained with the window method in units of μV/dB for all pulse parameters and animal groups.

TABLE 2.

R-squared values resulting from Pearson correlation analyses with SGN density and slope of the eCAP AGF calculated with five methods and two sets of input/output units for acutely implanted and chronically implanted guinea pigs. Maximum values in each column are shown in bold. All correlations were significant (p<0.003).

		Acutely implanted				Chronically implanted
		30 μs PPD		50 μs PPD		45 μs PPD
Units	Method	2.1 μs IPG	30 μs IPG	2.1 μs IPG	30 μs IPG	2.1 μs IPG	30 μs IPG
$\frac{\mathrm{\mu }\mathrm{V}}{\mathrm{n}\mathrm{C}}$	Sigmoid	0.61	0.63	0.61	0.67	0.43	0.45
	Linear	0.56	0.73	0.59	0.71	0.48	0.48
	Gradient	0.58	0.58	0.63	0.63	0.55	0.52
	Boxcar	0.61	0.60	0.56	0.58	0.45	0.47
	Window	0.64	0.69	0.61	0.72	0.46	0.48
$\frac{\mathrm{\mu }\mathrm{V}}{\mathrm{d}\mathrm{B}}$	Sigmoid	0.66	0.71	0.66	0.71	0.34	0.44
	Linear	0.53	0.69	0.56	0.68	0.46	0.44
	Gradient	0.62	0.63	0.63	0.67	0.56	0.51
	Boxcar	0.64	0.73	0.62	0.72	0.54	0.53
	Window	0.68	0.74	0.68	0.77	0.63	0.59

SGN: spiral ganglion neuron; eCAP: electrically evoked compound action potential; AGF: amplitude growth function

Results of a one-tailed, paired sample t-test confirmed that the $R^2$ was significantly higher for slopes calculated with logarithmic input units across all slope fitting methods and pulse parameters [t₍₂₉₎ = −3.28, p = 0.001]. Results of a one-way, repeated measures ANOVA analysis indicated a significant effect of the slope fitting method on the $R^2$ obtained with slopes calculated with logarithmic input units [F_(1,5) = 383.9, p<0.001]. Results from post-hoc comparisons showed significant differences in $R^2$ between the window method and the linear, gradient, and boxcar methods (p = 0.006, p = 0.002, p = 0.025, respectively). There was not a significant difference in $R^2$ between the window method and the sigmoid method (p = 0.322). As previously mentioned, seven slope estimates obtained from the sigmoid method were removed prior to conducting these correlation and ANOVA analyses. Therefore, the sigmoid and window methods provide slope estimates that similarly reflect neural survival, except for when the sigmoid method fails to provide a reasonable estimate of the slope.

Unreasonable Slope Estimates with Sigmoid Method using Data from Human Patient Populations

The sigmoid method created an unreasonable estimate (i.e., estimated maximum eCAP amplitude was more than five times greater than the recorded maximum eCAP amplitude) for the slope of the eCAP AGF for 31.6% of the AGFs recorded in the human participants. The total number of slope estimates considered as outliers are provided in Table 3 for both sets of I/O units and the four patient populations. The fraction of AGFs with unreasonable slope estimates were the highest for AGFs from children with CND, closely followed by children with normal-sized cochlear nerves and various etiologies of hearing loss (i.e., non-CND study group). While the fraction of outliers was less for children with GJB2 genetic mutations and adults, at least 17% of the slope estimates for AGFs from these patient populations were unreasonable.

TABLE 3.

The number of unreasonable estimates for the slope of the eCAP AGF using the sigmoid method for two sets of I/O units and four patient populations.

Units	Patient population	Number of AGFs	Number of outliers	Fraction of outliers
$\frac{\mathrm{\mu }\mathrm{V}}{\mathrm{n}\mathrm{C}}$	CND	963	335	0.35
	Non-CND	755	242	0.32
	GJB2	59	10	0.17
	Adult	317	64	0.20
$\frac{\mathrm{\mu }\mathrm{V}}{\mathrm{d}\mathrm{B}}$	CND	963	342	0.36
	Non-CND	755	247	0.33
	GJB2	59	12	0.20
	Adult	317	73	0.23

eCAP: electrically evoked compound action potential; I/O: input/output; AGF: amplitude growth function; CND: cochlear nerve deficiency; GJB2: Gap Junction Beta-2 mutations

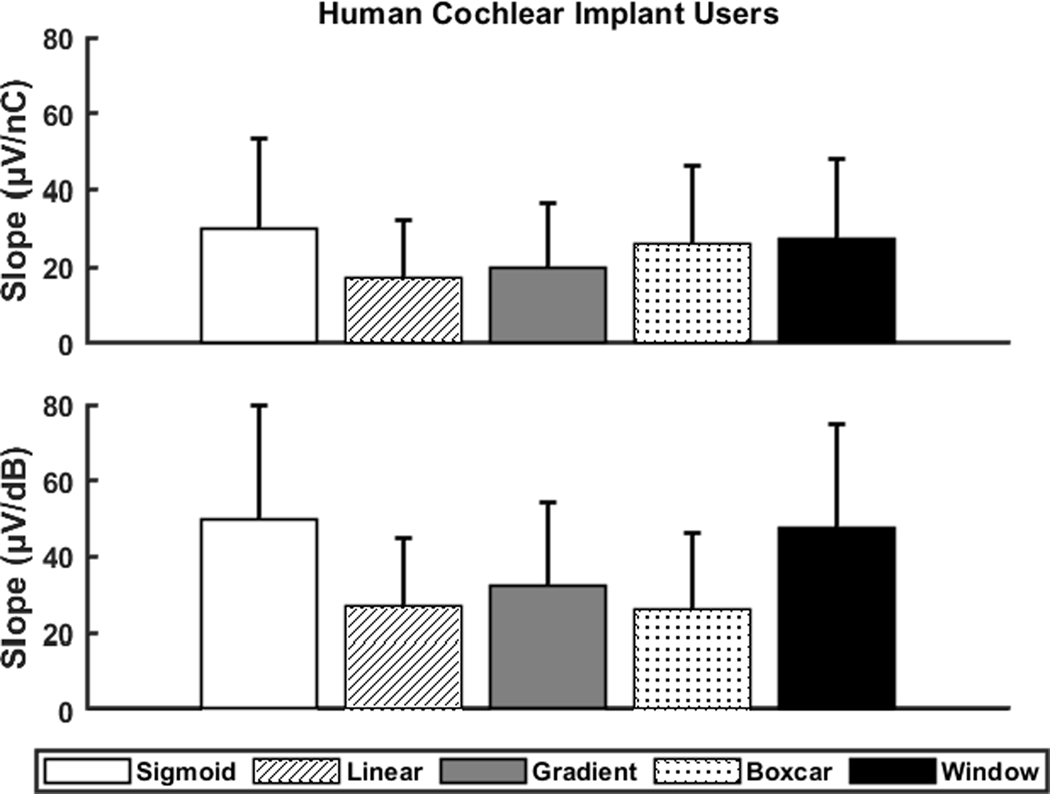
Effect of Units and Fitting Method on Calculated eCAP AGF Slope using Data from Human Patient Populations

Examples of the slope estimated using each of the five methods for one randomly selected AGF that was representative of AGFs recorded from each patient population are shown in Figure 4. As observed in all panels of Figure 4, the linear and gradient methods estimated slopes that were smaller than the slope estimates from the other methods. For the AGFs that trended toward an upper asymptote (Panels A, B and D), the sigmoid and window methods provided similar estimates for the slope. The sigmoid method estimated an extremely large slope (190000 μV/dB) for the AGF from the child with CND (Panel C) in which the maximum recorded eCAP amplitude was a small fraction of the estimated maximum eCAP amplitude. In contrast, the other methods estimated a slope of less than 100 μV/dB, with the window method estimating the highest slope among those four methods.

Figure 4.

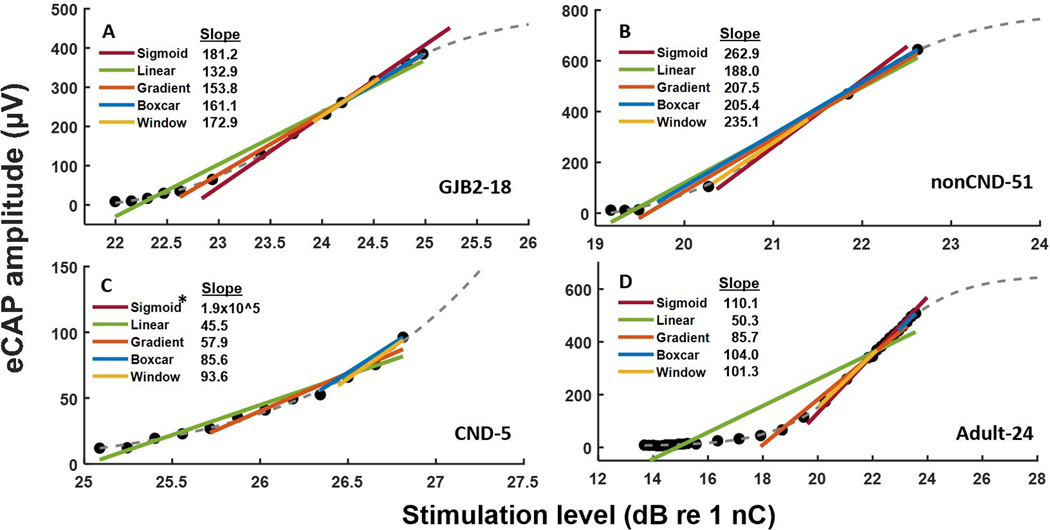
Representative electrically evoked compound action potential amplitude growth functions (filled circles) with slope estimates (colored lines) from five slope fitting methods for a child with a GJB2 genetic mutation (Panel A), a child with a normal-sized cochlear nerve and idiopathic hearing loss (Panel B), a child with cochlear nerve deficiency (Panel C), and an adult (Panel D). The participant identification number is provided in the bottom right-hand corner of each panel. Each panel also shows the best fit line from sigmoidal regression (gray dashes). *The slope estimate from the sigmoid method was extremely large for the child with cochlear nerve deficiency and did not fit within the display of Panel C.

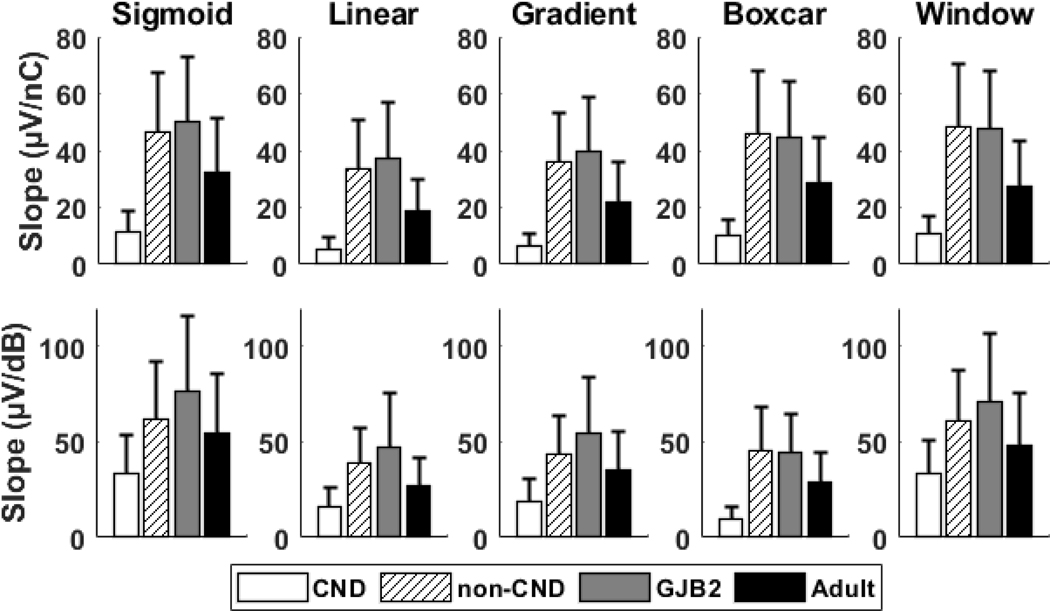
The means and standard deviations of the slope of the eCAP AGF calculated in two sets of I/O units with five methods for four patient populations are shown in Figure 5. The unreasonable slopes estimated with the sigmoid method (see Table 3) are not included in the data shown in Figure 5. Overall, the differences in slope between the four patient populations were similar across both sets of I/O units and all slope fitting methods. Specifically, children with CND had the smallest average slopes for each set of I/O units and slope fitting method. Additionally, children with normal-sized CNs (i.e., non-CND and GJB2 study groups) had the largest average slopes. The average slopes for the adult participants were between the children with CND and children with normal-sized CNs for each set of I/O units and slope fitting method.

Figure 5.

The means and standard deviations of the slope of the electrically evoked compound action potential amplitude growth function calculated in two sets of input/output units (top row: linear input units, bottom row: logarithmic input units) with five slope fitting methods for four patient populations. The sample size varied across input/output units, methods and patient populations due to removing outliers of the slope estimations using the three scaled median absolute deviations criterion.

Figure 6 shows the means and standard deviations of the slope of the eCAP AGFs across all patient populations estimated by the five slope fitting methods in two sets of I/O units. There was large variability in the magnitude of the slopes estimated using different slope-fitting methods, similar to the results obtained in guinea pigs (see Figure 3). Specifically, slopes were the highest when estimated with the sigmoid method and lowest when estimated with the linear method. Results of one-way ANOVA analyses indicated a significant effect of method on the slope of the eCAP AGF in both sets of I/O units [μV/nC: F_(4,9275) = 138.5, p<0.001; μV/dB: F_(4,9311) = 420.2, p<0.001]. Post-hoc comparisons indicated that there were no significant differences in slope estimates when comparing the boxcar and window methods in units of μV/nC (p=0.300), or when comparing the linear and boxcar methods (p=0.779) and window and sigmoid methods (p=0.064) in units of μV/dB. The remaining 17 post-hoc comparisons were all significant (p<0.001).

Figure 6.

The means and standard deviations of the slope of the electrically evoked compound action potential amplitude growth function calculated in two sets of input/output units (top row: linear input units, bottom row: logarithmic input units) with five slope fitting methods for all eCAPs recorded in human cochlear implant users. The sample size varied across input/output units and methods due to removing outliers of the slope estimations using the three scaled median absolute deviations criterion.

Correlation of eCAP AGF Slope with Speech Perception

Table 4 shows the results of correlation analyses between CNC word scores (measured in quiet and in noise) and the slope of the eCAP AGF averaged across all electrodes tested for each adult participant. Results are shown for eCAP AGF slopes calculated with five methods in two sets of I/O units. Overall, the correlations were significant for all slope fitting methods, I/O units, and speech testing conditions (p ≤ 0.045). Within each testing condition, the strength of correlation was similar across methods and units, ranging from 0.30 to 0.37 in quiet and from 0.37 to 0.58 in noise. All correlations were positive which indicated that higher average slopes were associated with better performance on speech perception tests, with stronger correlations observed for the in-noise test condition. Results of a one-tailed, paired sample t-test confirmed that the correlation between averaged slope and speech perception score was significantly stronger for the in-noise test condition than the in-quiet test condition [t₍₉₎ = −13.48, p < 0.001]. Results of a one-way ANOVA analysis indicated that there was not a significant effect of the slope fitting method on the strength of correlation between averaged slope and performance on speech perception tests [F_(4,15) = 0.33, p=0.85].

TABLE 4.

Pearson correlation coefficients from correlation analyses between CNC word scores in quiet and in noise (+5 dB SNR) and the averaged slope of eCAP AGFs calculated with five methods and two sets of input/output units.

Units	Method	In Quiet (N=33)	In Noise (N=27)
$\frac{\mathrm{\mu }\mathrm{V}}{\mathrm{n}\mathrm{C}}$	Sigmoid	0.30*	0.52**
	Linear	0.37*	0.58**
	Gradient	0.36*	0.58**
	Boxcar	0.34*	0.57**
	Window	0.33*	0.55**
$\frac{\mathrm{\mu }\mathrm{V}}{\mathrm{d}\mathrm{B}}$	Sigmoid	0.30*	0.37*
	Linear	0.33*	0.53**
	Gradient	0.33*	0.54**
	Boxcar	0.34*	0.57**
	Window	0.30*	0.52**

CNC: Consonant-Nucleus-Consonant; eCAP: electrically evoked compound action potential; AGF: amplitude growth function; SNR: signal-to-noise ratio;

^*: p<0.05;

^**: p<0.01

DISCUSSION

The goal of this study was to develop a robust method for calculating the slope of the eCAP AGF. The following discussion focused on four features that distinguish the newly developed method from the other four fitting methods evaluated in two sets of I/O units in this study.

Feature 1: Broad Application

The ideal method for calculating the slope of the eCAP AGF would be broadly applicable to data from humans and animals obtained in a variety of clinical and scientific studies. This is not trivial due to the variability in the morphology of eCAP AGFs between and within species (Figures 1 and 4). While eCAP AGFs generally follow the “S”-shaped sigmoidal curve, there are large differences in how close the maximum recorded eCAP amplitude is to the “true” maximum eCAP amplitude. This discrepancy can be influenced by subject comfort level, CN health, and the positions and impedances of the stimulating and recording electrodes, all of which are highly variable among subjects.

The lack of an upper asymptote in many eCAP AGFs is the primary factor that prevents the sigmoid method from being broadly applicable. For AGFs that reached a saturation plateau (Figure 1A), the sigmoid method provided slopes that were similarly correlated with SGN density as the window method (Table 2). However, for non-saturating AGFs (Figure 1B), the sigmoid method yielded a weaker correlation with SGN density than all of the other methods (Table 2). More importantly, for human CI users in which the AGF rarely reached saturation (Figure 1C, D and Figure 4), the sigmoid method produced a large fraction of unreasonable estimates (Table 3).

The linear, gradient, and boxcar methods typically do not produce unreasonable estimates because they do not extrapolate beyond the recorded AGF like the sigmoid method. However, in the present study, they yielded significantly smaller slopes than the window method (Table 1) which also resulted in significantly weaker correlations with SGN density in guinea pigs (Table 2). Similarly, in human CI users, these three methods resulted in estimates of shallower slopes than the window method (Figures 4, 5, and 6). This result was most pronounced with the linear method, which was expected because the slope estimate calculated with the linear method in this study was based on all eCAP data points, including many points that were near threshold.

In comparison, the window method did not produce any unreasonable estimates, and could accurately estimate the maximum linear slope of the measured portion of any AGF (Figure 4). Slopes estimated with the window method had the strongest correlation with SGN density across all stimuli and animal models (Table 2). Therefore, the window method can appropriately be applied to AGFs from animal models or human patients.

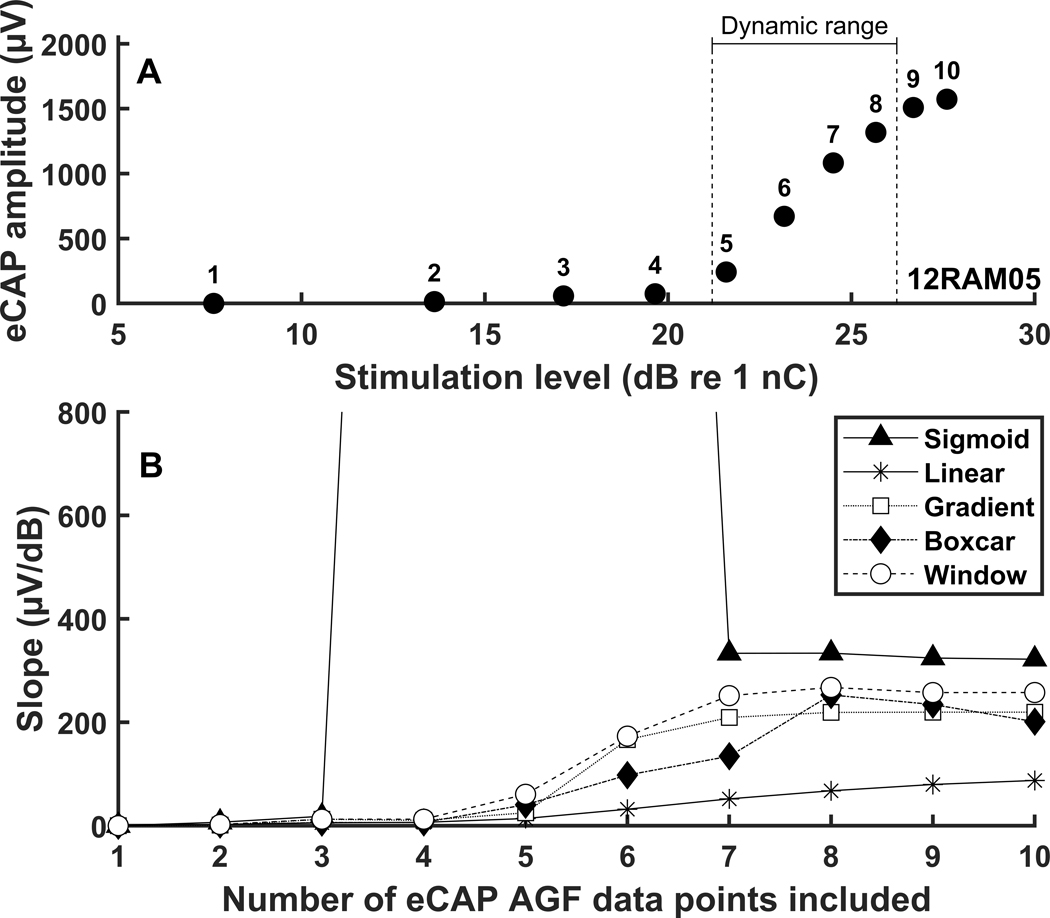
One caveat of any slope fitting method investigated in this study, including the window method, is the need to record eCAPs at sufficiently high stimulation levels in order to estimate the maximum slope of the eCAP AGF. In other words, the measured dynamic range must include the point of maximum slope in order to calculate the “true” maximum slope. This caveat is illustrated in Figure 7 in which the slope estimate is shown as a function of the range of stimulation level over which eCAPs are recorded.

Figure 7.

Panel A: An electrically evoked compound action potential amplitude growth function (AGF) from an acutely implanted guinea pig with an indication of the dynamic range estimated by sigmoidal regression. Each data point of the AGF is numbered, and the subject identification is presented in the lower right-hand corner. Panel B: Slope estimates from five slope-fitting methods calculated with various numbers of sequential data points included in the AGF. The slopes were estimated iteratively as data points were systematically excluded from the slope calculation, starting with data point 10 and proceeding downward one at a time.

As observed in the figure, the slope estimated while systematically removing the eCAP measurements at the highest stimulation levels remained fairly constant for the sigmoid and window methods until only six data points remained in the AGF. With six total data points, and only two data points in the steepest region of the AGF between threshold and saturation (i.e., dynamic range), the sigmoid method estimated an extremely large slope and the window method estimated a smaller slope than the “true” maximum slope estimated with all ten data points. Therefore, measuring eCAPs at increasing stimulation levels until the point of maximum slope (which can be estimated as the point when the slope is larger than at threshold and no longer increasing as a function of stimulation level) will improve the accuracy of the estimate of the maximum slope for any of the slope fitting methods. However, this may not always be possible due to patient discomfort and/or device limitations. Nevertheless, the slope may still provide useful information even if it is smaller than the “true” slope. Slopes estimated with the linear, gradient, and boxcar methods were generally smaller than slopes estimated with the window method (Figures 3 and 6), but they were still correlated with SGN density (Table 2) and speech perception (Table 4). This suggests that an approximation of the “true” slope is still useful, even if not ideal.

Results presented in Figure 7 indicated that with only one or two data points in the measured dynamic range (i.e., five or six total data points in the AGF), the window method provided the closest estimate to the “true” maximum slope among all of the slope fitting methods evaluated in this study. Therefore, the window method may provide the closest approximation to the “true” maximum slope when eCAPs cannot be recorded at stimulation levels sufficiently high to reach the point of maximum slope.

Feature 2: Total Automaticity

Another feature of the ideal slope fitting method is that it does not require data preprocessing or subjective judgements by the researcher or clinician (i.e., total automaticity). In this study, all of the methods/algorithms were evaluated based on their automatic implementation. However, several studies excluded data points before applying the slope fitting algorithm with a user-defined threshold (e.g., Pfingst et al., 2015a,b, 2017, Schvartz-Leyzac et al., 2019) or by visual inspection (Franck & Norton, 2001). These subjective judgments are 1) unique to the specific dataset in the study, 2) susceptible to unintentional bias by removing data points to improve the fit, and 3) time consuming. In contrast, the window method presented in this study does not require any subjective judgments or preprocessing, assuming all of the data points in the AGF are confirmed to be valid. Rather, the window method takes all of the validated eCAP measurements and objectively calculates the maximum slope for that AGF.

Feature 3: Easy Implementation

As a companion to feature 2, the ideal method would be easily implemented in a variety of scientific and clinical contexts (i.e., foolproof). The features of the window method were designed with this in mind. Specifically, the resampling of the AGF (Figure 2B) allows the slope to be calculated in a consistent manner, independent of the number, spacing, and uniformity of data points collected for the AGF. This means that the method does not dictate the exact data collection process needed for calculating the slope. In contrast, the other methods are highly influenced by the number and spacing of AGF data points because each data point influences the least squares minimization of error during the fitting process. As an example, multiple data points collected near threshold (Figure 4A, 4D) provide more ‘weight’ to that area of the AGF and flattens the slope estimated with the linear method. Additionally, the sigmoid method, applied without supervision, could lead to very large and incorrect estimates of the slope (Table 3 and Figure 4C). However, even with the window method, it is important to have a sufficient number of recorded data points to capture the morphology of the AGF.

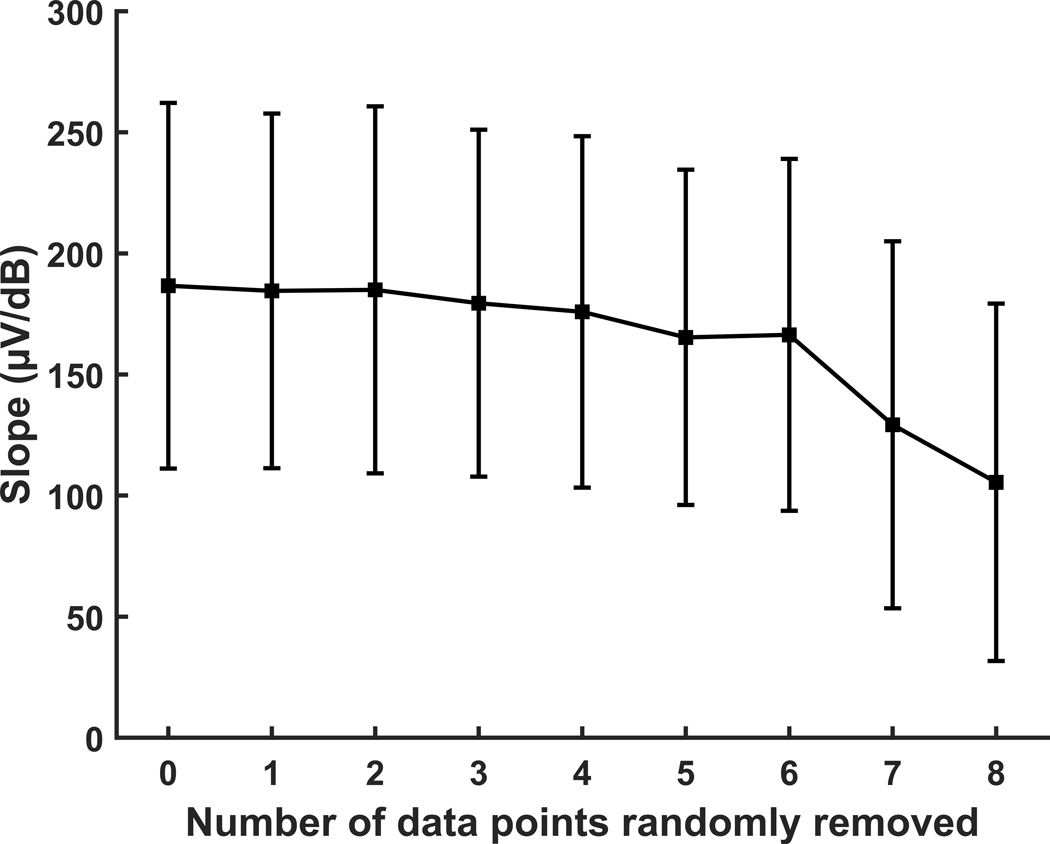
We investigated the effect of the number of recorded data points on the slope estimated with the window method by systematically removing zero to eight randomly selected data points from the ten original data points in each of the eCAP AGFs recorded from the acutely implanted guinea pigs. The means and standard deviations of the slope estimated with the window method are shown in Figure 8 for each condition (i.e., number of data points removed). It is readily observed that the average slope estimate decreased as more data points were removed from the eCAP AGF. However, there was not a significant difference in estimated slope from the baseline condition (i.e., zero points removed) until seven points were removed (p<0.001), based on results of one-way ANOVA [F_(8,639) = 10.69, p<0.001] with multiple comparisons using Tukey’s HSD criterion. Therefore, the window method provided a fairly consistent estimate of the slope when including four to ten data points in the AGF. Due to these results, we recommend that an absolute minimum of four data points be recorded in each eCAP AGF that span from near the threshold for eliciting an eCAP to the upper limit of stimulation that is safe, comfortably tolerable for the subject, and within compliance limits of the stimulator. However, a greater number of data points is advisable to ensure accuracy of the slope estimate, especially in situations with a limited dynamic range and/or measurement noise.

Figure 8.

The means and standard deviations of the slope of the electrically evoked compound action potential amplitude growth function (AGF) from 18 acutely implanted guinea pigs calculated with the window method as a function of the number of data points randomly removed from the ten data points in the original AGF.

Feature 4: Meaningful Results

Finally, and perhaps most importantly, the ideal method for calculating the slope of the eCAP AGF should provide scientifically and clinically meaningful results. All of the methods in this study yielded slopes that were significantly correlated with SGN density, with the window method providing the strongest correlation (Table 2). This suggests that the slope of the eCAP AGF has potential to be used as an objective measure of CN function. Indeed, results from each of the methods compared in this study provide support for the hypothesis that the slope of the eCAP AGF reflects, at least in part, the density of surviving SGN cell bodies in laboratory animals. In addition, all methods produced slope estimates that reflected general patterns of neural survival in human patient populations (Figure 5) and were significantly correlated with speech perception scores (Table 4). Therefore, the slope of the eCAP AGF provides scientifically and clinically meaningful results, regardless of the method used to estimate the slope.

Summary

While each of the methods presented in this study have some of the four features of the ideal slope fitting method discussed, only the window method meets the criteria of each feature. The most distinguishing feature is that the window method is the only method that can accurately and reliably estimate the slope for the eCAP AGF for various AGF morphologies and dynamic ranges. The window method addresses the crucial need for a broadly applicable slope fitting method by providing a method that can easily and automatically be applied to any dataset.

Association between Slope of the eCAP AGF and SGN Density or Speech Perception

This study also tested the hypothesis that the maximum slope of the eCAP AGF provides the best estimate of SGN density and speech perception compared to shallower slope estimates. The study results partially support this hypothesis and suggest that maximum slope provides the best estimate of SGN density, but does not provide a superior estimate for speech perception. Specifically, the sigmoid and window methods, which estimate the maximum slope, yielded the strongest correlation with SGN density in guinea pigs (Table 2). In contrast, the slope estimated with the linear method used in this study represented the overall slope and was significantly less correlated with SGN density than the sigmoid and window methods. However, all methods yielded slopes that were similarly correlated with speech perception and slopes estimated using the window method did not yield the highest correlation with CNC words scores (Table 4). The exact reason for this result remains unknown. We speculate that the large effects of central auditory and cognitive functions on speech perception could have masked the potential difference among correlation results for different slope fitting methods.

Effect of Input/Output Units on Calculated eCAP AGF Slope

The present study showed a significant effect of the input/output units on the results for animal subjects, but not for human subjects. Specifically, slopes estimated with linear output units and logarithmic input units (μV/dB) were more strongly correlated with SGN density in guinea pigs than slopes estimated with linear output and linear input units (μV/nC; Table 2). However, in human subjects, slopes estimated with linear output units, and either linear or logarithmic input units, did not significantly differ (Figure 6) and were similarly correlated with speech perception (Table 4). Additionally, slopes estimated with any of the five methods using logarithmic output units (dB re 1 μV), and either input units, were not significantly correlated with SGN density or speech perception ability. This suggests that calculating the slope with logarithmic output units is unlikely to provide scientifically or clinically meaningful results. Therefore, based on the overall results of the present study, it is recommended that the slope of the eCAP AGF be calculated with linear output units and logarithmic input units (μV/dB).

Study Limitations

One potential study limitation is the lack of a gold standard for quantifying CN function in human CI users. Therefore, we must rely, in part, on comparisons between patient populations and the results of speech perception to validate our slope fitting method. While substantial literature supports the importance of peripheral neural function for speech perception (e.g., Kim et al., 2010; Garadat et al., 2012; Long et al., 2014; Zhou & Pfingst, 2014; Schvartz-Leyzac & Pfingst, 2018), cognition and other central factors likely make important contributions to speech perception as well (Moberly et al., 2016, O’Neill et al., 2019). The relative contributions of peripheral and central factors to speech perception have not been well established. Therefore, speech perception can provide useful, but not conclusive, information about CN function. Nevertheless, a slope fitting method that is broadly applicable to animal and human data, such as is presented in this study, allows for direct comparisons of results across studies, which is important for identifying reliable biomarkers for CN function.

CONCLUSIONS

This study presented a novel method for calculating the slope of the eCAP AGF. This fully automated and robust method is broadly applicable to eCAP AGF data from animals and humans. Slopes estimated using the newly developed method had stronger correlation with SGN density in animal models than slopes estimated with any of the methods that we found in the literature. A slope-fitting approach that can be utilized across studies (both animal and human), such as the method presented in this study, can greatly improve comparisons across studies. This method may be useful for researchers in conducting scientific studies and for clinicians in providing clinical care for CI users.