Machine Learning-Enabled High-Resolution Dynamic Deuterium MR Spectroscopic Imaging

Abstract

Deuterium magnetic resonance spectroscopic imaging (DMRSI) has recently been recognized as a potentially powerful tool for noninvasive imaging of brain energy metabolism and tumor. However, the low sensitivity of DMRSI has significantly limited its utility for both research and clinical applications. This work presents a novel machine learning-based method to address this limitation. The proposed method synergistically integrates physics-based subspace modeling and data-driven deep learning for effective denoising, making high-resolution dynamic DMRSI possible. Specifically, a novel subspace model was used to represent the dynamic DMRSI signals; deep neural networks were trained to capture the low-dimensional manifolds of the spectral and temporal distributions of practical dynamic DMRSI data. The learned subspace and manifold structures were integrated via a regularization formulation to remove measurement noise. Theoretical analysis, computer simulations, and in vivo experiments have been conducted to demonstrate the denoising efficacy of the proposed method which enabled high-resolution imaging capability. The translational potential was demonstrated in tumor-bearing rats, where the Warburg effect associated with cancer metabolism and tumor heterogeneity were successfully captured. The new method may not only provide an effective tool to enhance the sensitivity of DMRSI for basic research and clinical applications but also provide a framework for denoising other spatiospectral data.

I. Introduction

DEUTERIUM (²H) is a stable and non-radioactive isotope of hydrogen. By introducing deuterium-labeled substrate (e.g., deuterated glucose (Glc)) into laboratory animals or the human body, one can noninvasively image and monitor the substrate and its down-stream labeled metabolites (e.g., glutamate + glutamine (Glx) and lactate (Lac)) using deuterium (²H) magnetic resonance spectroscopic (DMRS) imaging (DMRSI). This capability enables noninvasive measurement of key cellular energy metabolism (e.g., glycolysis in cytosol and oxidative phosphorylation in mitochondria) and their metabolic rates such as cerebral Glc consumption rate, Lac production rate, and tricarboxylic acid (TCA) cycle rate [1–4]. These measurements are essential for evaluating the Warburg effect, a hallmark of cancer biology, and for studying the metabolic reprograming between elevated glycolytic metabolism associated with the Warburg effect and inhibited oxidative metabolism including the impaired TCA cycle flux in tumors [5], [6].

Using deuterium as an indicator to study tissue metabolism dates back to 1935 [7]; earlier studies also applied in vivo DMRS to study ²H turnover of different ²H-labeled substrates in live animals [8–12]. Later, in vivo assessment of brain energy metabolism using DMRS/DMRSI was proposed and its feasibility was demonstrated in both rat and human brains [1], [3], [13]. The potential of using DMRSI for metabolic imaging of tumors was also investigated [3], [14]–[16]. Particularly, steady-state DMRSI was used to image the Warburg effect in preclinical and human brain tumors [3], [14]. Dynamic DMRSI experiments were also successfully carried out, albeit in low spatiotemporal resolution, for assessment of metabolic rates and the metabolic shift between glycolysis and oxidation in brain tumors [15], [16].

However, in spite of the encouraging progress, clinical and research applications of DMRSI have been impeded by its low sensitivity due to deuterium’s low gyromagnetic ratio (about a factor of 7 lower than hydrogen) and very low concentrations of deuterated metabolites (about 4 orders of magnitude lower than tissue water molecule used for proton MRI) [1], [2], [17]. Obtaining reliable dynamic DMRSI data with sufficient temporal and spatial resolution to study metabolic kinetics and its spatial variation is particularly challenging, even at ultrahigh field (UHF) and/or with existing denoising methods [1], [3], [16], [18], [19]. As a result, most DMRSI studies were carried out to obtain steady-state measurements [3], [14] or with low spatial (80-250 μL) [16], [19] and temporal (10-20 min) [16], [19] resolutions. Low spatial resolution limits the capability of DMRI for detecting focal changes in tissue metabolism; and metabolic kinetics information is lost in steady-state measurements or measurements with low temporal resolution.

This work presents a new machine learning-based method to overcome the current technical barriers and make high-resolution dynamic DMRSI possible. The proposed method has two key novel features. First, a novel signal model was used to represent the desired image function of dynamic spatiospectral variations as a union of low-dimensional subspaces; the subspace structures were pre-learned via machine learning, absorbing both physics and data-based priors. This subspace model offered up to 200-fold reduction of degrees-of-freedom, thus enabling substantial sensitivity enhancement. Second, statistical distributions of practical DMRSI signal variations were learned via deep neural networks. The trained networks captured the nonlinear manifolds embedded in the training data and were used synergistically with the subspace model to enable additional sensitivity gain.

The improved sensitivity was analyzed using both theoretical performance analysis and computer simulations. The proposed method has been evaluated for dynamic metabolic imaging of brain tumors in a rat model, where substantial improvement of spatiotemporal resolution over the existing DMRSI methods were obtained owing to the enhanced sensitivity. The improved imaging capability enabled detection of metabolic alterations in small tumors as well as intra-tumor metabolic heterogeneities, which were not feasible using the current DMRSI methods.

II. Proposed Method

A. Learning-Based Dynamic DMRSI

The proposed DMRSI method contains two components: a) a data acquisition scheme to obtain DMRSI data with high spatiotemporal resolution, and b) a novel machine learning-based data processing scheme to greatly enhance the signal-to-noise ratio (SNR) of the DMRSI data and make high-resolution deuterium-based dynamic imaging possible.

The proposed data acquisition scheme uses the chemical shift imaging (CSI) based pulse sequence. To achieve high spatiotemporal resolution, we used extended k-space coverage (to achieve high spatial resolution) and reduced the number of signal averages (to achieve high temporal resolution). For rat brain-tumor imaging with a field-of-view of 28 × 28 × 24 mm³, we covered k-space with 17 × 17 × 5 spatial encodings and only 1-2 averages. Dynamic DMRSI signals were acquired with unprecedented spatial resolution (~10 μL voxel size) and 0.9-1.8 min temporal resolution, which represents a factor of 7 improvement in spatial resolution and a factor of 6 improvement in temporal resolution over the existing methods [16].

The proposed data processing scheme is the key component that enables high-resolution DMRSI. As illustrated in Fig. 1, our processing scheme exploits two types of signal structures for SNR improvement: a) physics-based linear subspaces, and b) data-driven nonlinear manifolds. More specifically, we explicitly represented the spectral-temporal, spatial-spectral, and spatial-temporal distributions of each ²H-labelled molecule using low-dimensional subspaces. The subspace structures were pre-learned absorbing prior information from both spin physics (to determine the resonance structures) and training data (to determine the feasible spectral and temporal variations). In addition, the spectral and temporal distributions of practical dynamic DMRSI data reside in low-dimensional manifolds; we pre-learned these manifolds from training data using deep neural networks. The learned linear subspaces and nonlinear manifolds were synergistically integrated to remove the measurement noise. The following sections describe the proposed linear subspace model, learning the nonlinear manifolds of signal distributions, and integration of linear subspaces and nonlinear manifolds.

Fig. 1.

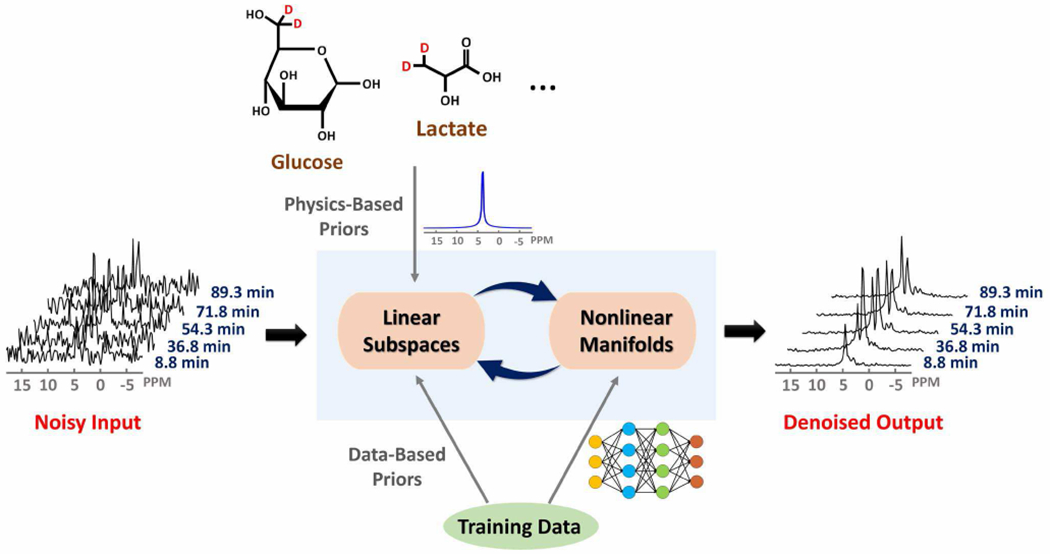
Schematic overview of the proposed learning-based processing framework that enables high-resolution dynamic DMRSI. This framework exploits linear subspace structures and nonlinear manifold structures of dynamic DMRSI signals. These structures are synergistically integrated to provide an effective computational framework to reduce the measurement noise, thus enabling substantial sensitivity enhancement and improving resolution.

B. Linear Subspace Model

We used a novel subspace model to represent the spatial-spectral-temporal function of L detectable ²H-labelled molecules (e.g., deuterated Glc, water, Glx, and Lac):

$$\begin{gathered} \rho (\mathit{x},f,T)={\sum }_{\ell =1}^L{\rho }_{\ell }(\mathit{x},f,T) \\ ={\sum }_{\ell =1}^L{s}_{\ell }(\mathit{x},f)g_{\ell }(\mathit{x},T) \\ \text{subject to}{s}_{\ell }(\mathit{x},f)={\sum }_{r=1}^{R_{\ell }}{a}_{r,\ell }(\mathit{x}){\varphi }_{r,\ell }(f) \\ {g}_{\ell }(\mathit{x},T)={\sum }_{q=1}^{Q_{\ell }}{b}_{q,\ell }(\mathit{x}){\phi }_{q,\ell }(T), \end{gathered}$$ (1)

where $\rho (\mathit{x},f,T)$ denotes the overall dynamic spectroscopic image of spatial (x), spectral (f), and temporal (T) variations, and ${\rho }_{\ell }(\mathit{x},f,T)$ is the signal component from the ℓ^th molecule. The proposed model was designed to effectively exploit the spatial-spectral-temporal correlation that exists in DMSRI data. More specifically, for each molecule, its spectral-temporal distribution was represented by a rank-1 subspace: ${\rho }_{\ell }(\mathit{x},f,T)=s_{\ell }(\mathit{x},f)g_{\ell }(\mathit{x},T)$, its spatial-spectral distribution by a rank-R_ℓ subspace: $s_{\ell }(\mathit{x},f)={\sum }_{r=1}^{R_{\ell }}{a}_{r,\ell }(\mathit{x}){\varphi }_{r,\ell }(f)$, and its spatial-temporal distribution by a rank-Q_ℓ subspace: $g_{\ell }(\mathit{x},T)={\sum }_{q=1}^{Q_{\ell }}{b}_{q,\ell }(\mathit{x}){\phi }_{q,\ell }(T)$.

The proposed low-rank subspace representation was motivated by the characteristics of the DMRSI signals. Particularly, the spectroscopic signal from a specific molecule (or an isochromat, or often called a spectral component) can be expressed as $s(t)=a_{\ell }{e}^{-t/T_{2,\ell }+i2\pi f_{\ell }t}h(t)$, where $a_{\ell }$, $f_{\ell }$, and $T_{2,\ell }$ represent concentration, resonance frequency and spin-spin relaxation constant of the ℓ^th spectral component, respectively, and h(t) accounts for non-Lorentzian spectral lineshape variations introduced by non-ideal experimental conditions (e.g., field drift, field inhomogeneity, etc.). For biological tissue, there are only a small number of those spectral components. Therefore, the measured DMRSI data, after correction of field drift and field inhomogeneity, can be expressed as a partially separable function [20]. Partially separable functions lead to low-rank matrices and tensors (or low-dimensional subspace representation), which have been successfully used in various applications [20–29].

In the proposed method, we pre-learned the spectral basis functions ${\varphi }_{r,\ell }(f)\}$ incorporating prior information. Specifically, we recognized that a general model expresses the spectral signal as a mixture of Lorentzian [30]:

$$s_{\ell }(f;f_{\ell }^{\prime },{\theta }_{\ell })={\sum }_{n=-N_s}^{N_s}{a}_{n,\ell }\frac{T_{2,\ell }}{1+i2\pi T_{2,\ell }(f-f_{\ell }^{\prime }-\text{Δ}{f}_{\ell }-n\text{Δ}f)}$$ (2)

where N_s is the order of the mixture model and the model parameters include $f_{\ell }^{\prime }$, representing the resonance frequency, and ${\theta }_{\ell }=\left({\left\{a_{n,\ell }\right\}}_{n=-N_s}^{N_s},\text{Δ}{f}_{\ell },T_{2,\ell }\right)$, representing the spectral lineshape parameters. Conventional methods determine $f_{\ell }^{\prime }$ and ${\theta }_{\ell }$ directly from noisy imaging data point by point, resulting in large estimation variations [30], [31]. We overcame this problem by exploiting physics-based and data-based prior information. First, based on spin physics, we pre-determined $f_{\ell }^{\prime }$ for each molecule, for example, water: 4.8 ppm; Glc: 3.8 ppm; Glx: 2.4 ppm; Lac: 1.4 ppm [18]. Second, we represented the variations of $s_{\ell }(f;f_{\ell }^{\prime },{\theta }_{\ell })$ due to different practical values of ${\theta }_{\ell }$ using a subspace model and determined the basis functions of the subspace model from training data. Specifically, from the acquired training data, we obtained ${\text{Θ}}_{\ell }=\{{\theta }_{\ell }^1,{\theta }_{\ell }^2,\dots ,{\theta }_{\ell }^N$ that represents the set of possible values for ${\theta }_{\ell }$ encountered in practice. We then used ${\left\{s_{\ell }\left(f;f_{\ell }^{\prime },{\theta }_{\ell }^n\right)\right\}}_{n=1}^N$ to form the following Casorati matrix:

$$C_{{\varphi }_{\ell }}=\left[\begin{array}{cccc}{s}_{\ell }\left(f_1;f_{\ell }^{\prime },{\theta }_{\ell }^1\right)& s_{\ell }\left(f_2;f_{\ell }^{\prime },{\theta }_{\ell }^1\right)& \dots & s_{\ell }(f_{N_f};f_{\ell }^{\prime },{\theta }_{\ell }^1)\\ s_{\ell }\left(f_1;f_{\ell }^{\prime },{\theta }_{\ell }^2\right)& s_{\ell }\left(f_2;f_{\ell }^{\prime },{\theta }_{\ell }^2\right)& \dots & s_{\ell }(f_{N_f};f_{\ell }^{\prime },{\theta }_{\ell }^2)\\ ⋮& ⋮& \ddots & ⋮\\ s_{\ell }\left(f_1;f_{\ell }^{\prime },{\theta }_{\ell }^N\right)& s_{\ell }\left(f_2;f_{\ell }^{\prime },{\theta }_{\ell }^N\right)& \dots & s_{\ell }(f_{N_f};f_{\ell }^{\prime },{\theta }_{\ell }^N)\end{array}\right].$$ (3)

We applied singular value decomposition (SVD) to Eq. (3) to obtain the singular values and right-singular vectors of $C_{{\varphi }_{\ell }}$. Based on the singular value distributions (as shown in Fig. S1), we determined the subspace model order $R_{\ell }$ such that the rank-$R_{\ell }$ approximation of $C_{{\varphi }_{\ell }}$ had error below 5% in the L₂ sense. In this study, we chose $R_{\ell }$ to be 4, 4, 3 and 3 for water, Glc, Glx, and Lac, respectively. Then, we chose the R_ℓ principal right-singular vectors to be the spectral basis functions ${\left\{{\varphi }_{r,\ell }(f)\right\}}_{r=1}^{R_{\ell }}$ [20], [29], [32–34].

We also pre-learned the temporal basis functions ${\phi }_{q,\ell }(T)$ from high-SNR training data. Similarly to the determination of spectral basis, we obtained a set of representative temporal signals ${\left\{g_{\ell }\left({\mathit{x}}_p,T\right)\right\}}_{p=1}^P$ for each molecule from training data and then ${\left\{{\phi }_{q,\ell }(T)\right\}}_{q=1}^{Q_{\ell }}$ using SVD of the following Casorati matrix:

$$C_{{\phi }_{\ell }}=\left[\begin{array}{cccc}{g}_{\ell }({\mathit{x}}_1,T_1)& g_{\ell }({\mathit{x}}_1,T_2)& \dots & g_{\ell }({\mathit{x}}_1,T_{N_T})\\ g_{\ell }({\mathit{x}}_2,T_1)& g_{\ell }({\mathit{x}}_2,T_2)& \dots & g_{\ell }({\mathit{x}}_2,T_{N_T})\\ ⋮& ⋮& \ddots & ⋮\\ g_{\ell }({\mathit{x}}_P,T_1)& g_{\ell }({\mathit{x}}_P,T_2)& \dots & g_{\ell }({\mathit{x}}_P,T_{N_T})\end{array}\right].$$ (4)

As in spectral subspace learning, we determined the model order $Q_{\ell }$ based on the singular value distributions of $C_{{\phi }_{\ell }}$ (Fig. S1); our current study chose $Q_{\ell }$ to be 3, 7, 6 and 6 for water, Glc, Glx, and Lac, respectively. Then, we chose the $Q_{\ell }$ principal right-singular vectors to be the temporal basis functions ${\left\{{\phi }_{q,\ell }(T)\right\}}_{q=1}^{Q_{\ell }}$.

The proposed subspace model offers several advantages over the conventional Fourier series model. First, the model explicitly exploits the low-rank structures of DMRSI data [20]; as a result, the overall spatial-spectral-temporal function $\rho (\mathit{x},f,T)$ expressed in a union-of-subspaces has a significantly reduced number of degrees of freedom as compared to the conventional Fourier series model (up to 200-fold reduction, as calculated in Supplementary Materials). Second, the model uses pre-learned subspace structures from prior information, which further reduced the number of unknowns, thereby reducing the uncertainty of the estimate spatial-spectral-temporal function.

C. Nonlinear Manifolds of Signal Distributions

The spectral and temporal signal variations of dynamic DMRSI signals reside in low-dimensional manifolds [35], [36]. We used deep autoencoders to capture these structures. We built one deep autoencoder to capture the manifold underlying overall spectral variations (denoted as S_α with parameters α); we also built another four deep autoencoders, one for each molecule, to capture the manifolds underlying temporal variations (denoted as ${\mathbb{G}}_{\ell ,\gamma }$ with parameters γ).

In this work, we used different network architectures for S_α and ${\mathbb{G}}_{\ell ,\gamma }$ as illustrated in Fig. S2. The network of S_α was a fully connected autoencoder modified from [35]; the network architecture consisted of an encoding path and a decoding path. Both paths were stacks of 4 fully connected layer activated by rectified linear units (ReLUs) except for the last layers. The network of ${\mathbb{G}}_{\ell ,\gamma }$ was modified from the U-Net [37], which also consisted of an encoding path and a decoding path. The encoding path was a stack of 4 convolutional blocks, each consisting of 4 convolutional layers; all convolutional layers were activated by ReLUs and followed by max pooling with stride 2 for down-sampling. The decoding path was a stack of 3 convolutional blocks; each block consisted of an upsampling operation followed by convolution, a concatenation with the corresponding feature map from the encoding path, and 4 successive convolutional layers activated by ReLUs.

Training these deep autoencoders often requires large amount of high-quality training data. We addressed this by using a physics-based generative model to generate spectral and temporal training data. Specifically, we first determined the empirical distribution of spectral variations by fitting Eq. (2) to our training data to obtain parameter sets ${\text{Θ}}_{\ell }=\{{\theta }_{\ell }^1,{\theta }_{\ell }^2,\dots ,{\theta }_{\ell }^P\}$. We then fit ${\mathrm{\Theta }}_{\ell }$ with a parametric mixture of Gaussian (MoG) model to obtain its empirical distribution [38], [39]. To determine the empirical distribution of temporal variations, we fit our training data with the following parametric dynamic model:

$$g_{\ell }(T;{\beta }_{\ell })=b_{1,\ell }\left(1-e^{-\frac{T-T_{0,\ell }}{{\tau }_{1,\ell }}}\right)u(T-T_{0,\ell })-b_{2,\ell }\left(1-e^{-\frac{T-T_{0,\ell }}{{\tau }_{2,\ell }}}\right)u(T-T_{0,\ell }),$$ (5)

where the parameters ${\beta }_{\ell }$ include amplitudes $(b_{1,\ell },b_{2,\ell })$, time constants $({\tau }_{1,\ell },{\tau }_{2,\ell })$, and start time $(T_{0,\ell })$; u(⋅) denotes the step function. The resulting parameter values $B_{\ell }=\{{\beta }_{\ell }^1,{\beta }_{\ell }^2,\dots ,{\beta }_{\ell }^P\}$ were fit with another MoG model to yield its empirical distribution. Then, we generated 100k random samples of ${\theta }_{\ell }$ and ${\beta }_{\ell }$ based on the learned MoG models, from which we generated spectral and temporal training data based on Eqs. (2) and (5). More details about the acquisition of training data are provided in the Results section.

After training data were prepared, we trained the deep networks using the mean-squared-error (MSE) loss and stochastic gradient descent with ADAM optimizer [40], with a batch size of 256, learning rate 10⁻⁴, and 300 training epochs.

D. Integration of Linear Subspaces and Nonlinear Manifolds

The proposed method synergistically integrates the learned linear subspaces and nonlinear signal manifolds for denoising. More specifically, the proposed method determines the optimal solution with the following properties. First, it resides in a subspace with the pre-learned subspace structures, i.e.,

$$\begin{gathered} \text{P}=\{\rho (\mathit{x},f,T):\rho (\mathit{x},f,T) \\ ={\sum }_{\ell =1}^L{s}_{\ell }(\mathit{x},f)g_{\ell }(\mathit{x},T)\} \\ \text{where}{s}_{\ell }(\mathit{x},f)={\sum }_{r=1}^{R_{\ell }}{a}_{r,\ell }(\mathit{x}){\varphi }_{r,\ell }(f) \\ {g}_{\ell }(\mathit{x},T)={\sum }_{q=1}^{Q_{\ell }}{b}_{q,\ell }(\mathit{x}){\phi }_{q,\ell }(T) \end{gathered}$$ (6)

Second, it has small squared Euclidean distance to the spectral and temporal manifolds:

$$\begin{gathered} D_s={\sum }_T{\Vert \rho (\mathit{x},f,T)-S_{\alpha }(\rho (\mathit{x},f,T))\Vert }_2^2\le {\sigma }_s^2 \\ {D}_T={\sum }_{\ell }\Vert {\sum }_{q=1}^{Q_{\ell }}{b}_{q,\ell }(\mathit{x}){\phi }_{q,\ell }(T) \\ -G_{\ell ,\gamma }{\left({\sum }_{q=1}^{Q_{\ell }}{b}_{q,\ell }(\mathit{x}){\phi }_{q,\ell }(T)\right)\Vert }_2^2\le {\sigma }_T^2 \end{gathered}$$ (7)

Third, it satisfies the data consistency constraints:

$${\Vert {\rho }_n(\mathit{x},f,T)-\rho (\mathit{x},f,T)\Vert }_2^2\le {\sigma }_n^2,$$ (8)

where ${\rho }_n$ denotes the noisy data and ${\sigma }_n^2$ reflects the noise level.

It is worth to note that Eq. (7) enforces the solution to be close to the learned manifolds. This is based on our assumption that anything far away from these manifolds is not a meaningful signal component (e.g., generated by noise) and should be excluded. By imposing Eq. (7), we effectively incorporate the prior information captured by the deep learning models to constrain the signal variations allowed, which is complementary to the subspace-based priors.

Mathematically, the constraints in Eqs. (6–8) lead to the following regularized reconstruction problem:

$$\begin{gathered} \underset{\{a_{r,\ell }\},\{b_{q,\ell }\}}{\min }{\Vert {\rho }_n(\mathit{x},f,T)-\rho (\mathit{x},f,T)\Vert }_2^2 \\ +{\lambda }_f{\sum }_T{\Vert \rho (\mathit{x},f,T)-{\mathbb{S}}_{\alpha }(\rho (\mathit{x},f,T))\Vert }_2^2 \\ +{\lambda }_T{\sum }_{\ell }\Vert {\sum }_{q=1}^{Q_{\ell }}{b}_{q,\ell }(\mathit{x}){\phi }_{q,\ell }(T) \\ -{\mathbb{G}}_{\ell ,\gamma }{\left({\sum }_{q=1}^{Q_{\ell }}{b}_{q,\ell }(\mathit{x}){\phi }_{q,\ell }(T)\right)\Vert }_2^2 \end{gathered}$$

where

$$\rho (\mathit{x},f,T)={\sum }_{\ell =1}^L\left\{{\sum }_{r=1}^{R_{\ell }}{a}_{r,\ell }(\mathit{x}){\varphi }_{r,\ell }(f)\right\}\left\{{\sum }_{q=1}^{Q_{\ell }}{b}_{q,\ell }(\mathit{x}){\phi }_{q,\ell }(T)\right\}.$$ (9)

In Eq. (9), ${\lambda }_f$ and ${\lambda }_T$ are regularization parameters chosen based on the noise level. The optimization problem in Eq. (9) can be solved using the following alternating minimization algorithm, which iteratively performed the following two steps:

1. Update $a_{r,\ell }$ with fixed $b_{q,\ell }^{(i)}$ (i denotes the iteration index):

   $$\begin{gathered} \{{\widehat{a}}_{r,\ell }^{(i+1})\}=\underset{\{a_{r,\ell }\}}{\arg \min }{\Vert {\rho }_n(\mathit{x},f,T)-\rho (\mathit{x},f,T)\Vert }_2^2 \\ +{\lambda }_f{\sum }_T{\Vert \rho (\mathit{x},f,T)-S_{\alpha }(\rho (\mathit{x},f,T))\Vert }_2^2 \end{gathered}$$

   where

   $$\begin{gathered} \rho (\mathit{x},f,T)={\sum }_{\ell =1}^L\left\{{\sum }_{r=1}^{R_{\ell }}{a}_{r,\ell }(\mathit{x}){\varphi }_{r,\ell }(f)\right\} \\ \times \left\{{\sum }_{q=1}^{Q_{\ell }}{\widehat{b}}_{q,\ell }^{(i)}(\mathit{x}){\phi }_{q,\ell }(T)\right\} \end{gathered}$$ (10)
2. Update $b_{q,\ell }$ with fixed $a_{r,\ell }^{(i)}$:

   $$\begin{gathered} \left\{b_{q,\ell }^{(i+1})\right\}=\underset{\{b_{q,\ell }\}}{\arg \min }{\Vert {\rho }_n(\mathit{x},f,T)-\rho (\mathit{x},f,T)\Vert }_2^2 \\ +{\lambda }_f{\sum }_T{\Vert \rho (\mathit{x},f,T)-{\mathbb{S}}_{\alpha }(\rho (\mathit{x},f,T))\Vert }_2^2 \\ +{\lambda }_T{\sum }_{\ell }\Vert {\sum }_{q=1}^{Q_{\ell }}{b}_{q,\ell }(\mathit{x}){\phi }_{q,\ell }(T) \\ {-{\mathbb{G}}_{\ell ,\gamma }\left({\sum }_{q=1}^{Q_{\ell }}{b}_{q,\ell }(\mathit{x}){\phi }_{q,\ell }(T)\right)\Vert }_2^2 \end{gathered}$$

   where

   $$\begin{gathered} \rho (\mathit{x},f,T)={\sum }_{\ell =1}^L\left\{{\sum }_{r=1}^{R_{\ell }}{\widehat{a}}_{r,\ell }^{(i+1)}(\mathit{x}){\varphi }_{r,\ell }(f)\right\} \\ \times \left\{{\sum }_{q=1}^{Q_{\ell }}{b}_{q,\ell }(\mathit{x}){\phi }_{q,\ell }(T)\right\} \end{gathered}$$ (11)

The subproblems in Eqs. (10) and (11) were solved using ADAM optimization algorithm [40]. With $\{{\widehat{a}}_{r,\ell }\}$ and $\{{\widehat{b}}_{q,\ell }\}$ determined, the denoised data were generated based on the proposed subspace model:

$$\overline{\rho }(\mathit{x},f,T)={\sum }_{\ell =1}^L\left\{{\sum }_{r=1}^{R_{\ell }}{\widehat{a}}_{r,\ell }(\mathit{x}){\varphi }_{r,\ell }(f)\right\}\left\{{\sum }_{q=1}^{Q_{\ell }}{\widehat{b}}_{q,\ell }(\mathit{x}){\phi }_{q,\ell }(T)\right\}.$$ (12)

After solving Eq. (9), the proposed method further incorporated spatial constraints into the subspace model for additional denoising effect. The spatial constraints were in the form of statistical distributions on $a_{r,\ell }(\mathit{x})$ and $\{b_{q,\ell }(\mathit{x})\}$ shared by all the voxels, denoted as $P\left(\left\{a_{r,\ell }\right\}\right)$ and $P\left(\left\{b_{q,\ell }\right\}\right)$. These distributions were derived by fitting MoG models to $\left\{{\widehat{a}}_{r,\ell }(\mathit{x})\right\}$ and $\left\{{\widehat{b}}_{q,\ell }(\mathit{x})\right\}$ obtained from different spatial locations. Then, the desired spatial-spectral-temporal functions were determined via:

$$\begin{gathered} \underset{\{a_r,\ell \},\{b_{q,\ell }\}}{\min }\parallel \overline{\rho }(\mathit{x},f,T) \\ -{\sum }_{\ell =1}^L\left\{{\sum }_{r=1}^{R_{\ell }}{a}_{r,\ell }(\mathit{x}){\varphi }_{r,\ell }(f)\right\} \\ {\times \left\{{\sum }_{q=1}^{Q_{\ell }}{b}_{q,\ell }(\mathit{x}){\phi }_{q,\ell }(T)\right\}\Vert }_2^2 \\ -\lambda \log \left(P\left(\left\{a_{r,\ell }\right\}\right)P\left(\left\{b_{q,\ell }\right\}\right)\right), \end{gathered}$$ (13)

where λ was chosen based on the noise level. Eq. (13) was solved using the majorization-minimization algorithm [41].

III. Results

A. Performance Analysis

We used the Cramér-Rao lower bound (CRLB) analysis to validate and quantify the sensitivity enhancement provided by the proposed method. Specifically, we calculated the CRLB of the proposed subspace model in comparison with the conventional model. The reduction in CRLB can be viewed as a quantitative index for sensitivity enhancement.

1. Spectral-temporal subspace constraint:

   The conventional model expresses the spectral-temporal signal as [30]:

   $${\rho }_{\ell }(f,T)=h_{\ell }(f;g_{\ell }(T),{\theta }_{\ell }(T))+\xi ,$$ (14)

   with time-dependent concentration $g_{\ell }(T)$ and lineshape parameter ${\theta }_{\ell }(T)$. In contrast, the proposed method represents ${\rho }_{\ell }(f,T)$ using a rank-1 subspace model as:

   $${\rho }_{\ell }(f,T)=g_{\ell }(T)s_{\ell }(f;{\theta }_{\ell })+\xi .$$ (15)

   This results in about 30% reduction of the square root of CRLB for concentration, as calculated based on the derivation in [42].

2. Spatial-spectral subspace constraint:

   The conventional model expresses the spatial-dependent lineshape function as [30]:

   $$s_{\ell }(\mathit{x},f)=s_{\ell }(f;{\theta }_{\ell }(\mathit{x}))+\xi ,$$ (16)

   with spatial-dependent spectral parameters ${\theta }_{\ell }(\mathit{x})$. In contrast, the proposed method expresses $s_{\ell }(\mathit{x},f)$ as:

   $$s_{\ell }(\mathit{x},f)={\sum }_{r=1}^{R_{\ell }}{a}_{r,\ell }(\mathit{x}){\varphi }_{r,\ell }(f)+\xi .$$ (17)

   The spatial-independent subspace constraint results in about 11% reduction of the square root of CRLB for the lineshape function, as calculated based on the derivation in [42], [43].

3. Spatial-temporal subspace constraint:

   The conventional model expresses the spatial and temporal-dependent concentration as:

   $$g_{\ell }(\mathit{x},T)={\sum }_p{b}_{\ell }(p\text{Δ}\mathit{k},T)e^{-i2\pi p\text{Δ}\mathit{k}\mathit{x}}+\xi ,$$ (18)

   which assumes no spatial and temporal correlations. In contrast, the proposed method expresses $g_{\ell }(\mathit{x},T)$ as:

   $$g_{\ell }(\mathit{x},T)={\sum }_{q=1}^{Q_{\ell }}{b}_{q,\ell }(\mathit{x}){\phi }_{q,\ell }(T)+\xi .$$ (19)

   The enforced subspace model results in about a factor of 3.2 reduction of the square root of CRLB for the concentration, as calculated based on the derivation in [43].

4. Statistical distributions on model coefficients:

   The proposed method also imposes statistical distributions on the model coefficients: $a_{r,\ell }\sim P\left(\left\{a_{r,\ell }\right\}\right)$ and $b_{q,\ell }\sim P\left(\left\{b_{q,\ell }\right\}\right)$. These distribution-based constraints reduce the square roots of CRLB for the lineshape function and concentration by about 16% and a factor of 1.5, as quantified using Bayesian CRLB [44].

B. Simulation Study

The proposed method was also evaluated using Monte-Carlo simulations to compare the performance of the proposed method with the state-of-the-art methods. A numerical phantom was constructed to simulate the rat brain with a small tumor (~60 μL), based on the standard spectral model (Eq. (2)) with parameters determined from in vivo data. Gaussian noise was added to match the SNR of high-resolution in vivo DMRSI data (~6 dB). We compared the proposed scheme with two traditional model-based methods: the Fourier-based method and the Tucker decomposition-based denoising scheme [16], and a modern denoising neural network (details can be found in the Supplementary Materials).

Figure 2 compares the quality of spatial, spectral, and temporal estimation achieved by the traditional methods and the proposed method, respectively, in one of the Monte-Carlo trials. As can be seen, the proposed method produced the most accurate quantification results with the smallest noise-induced fluctuations and errors, especially for the low-concentration metabolites such as Glx and Lac. As a result, the tumor contrast in both the Glx and Lac maps could be best reproduced by the proposed method. Figure S3 compares the results from the denoising neural networks and the ones from the proposed method. While the neural networks can significantly reduce the spatial and temporal signal fluctuations, it introduced large estimation biases for Glx and Lac measurements, which could be problematic for kinetic analysis and quantification.

Fig. 2.

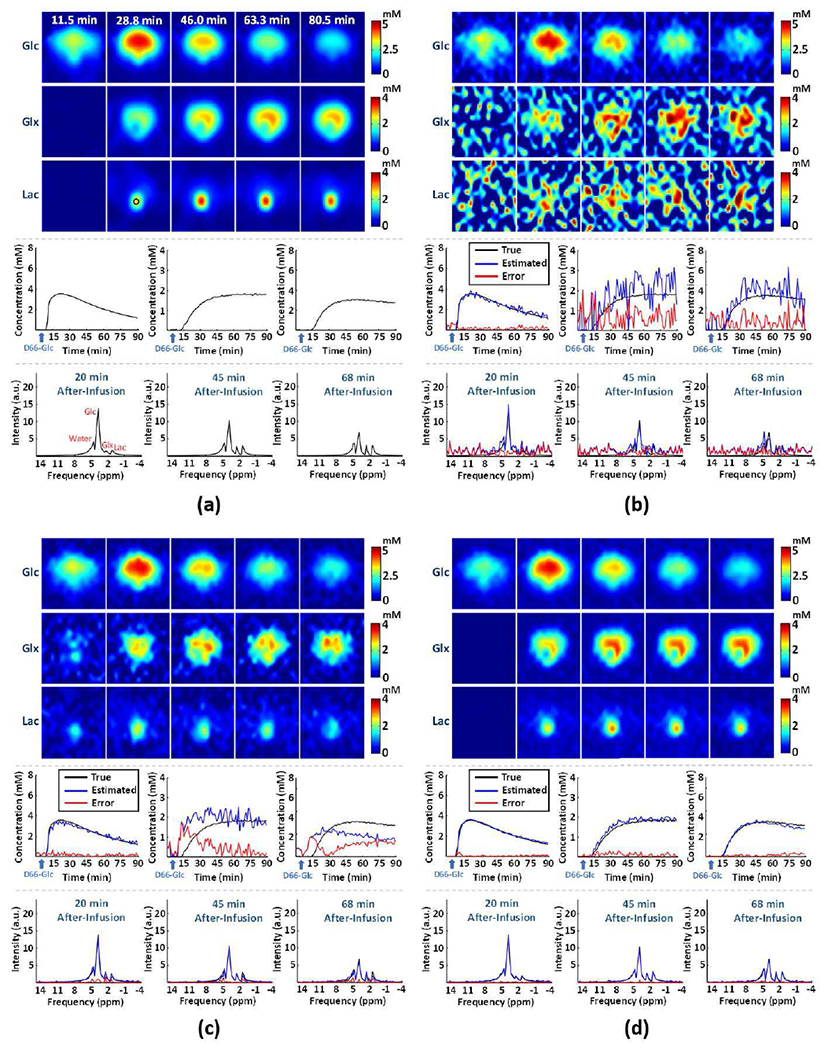
Simulation-based performance analysis. Simulation results in one of the Monte-Carlo trials: (a) ground truth, (b-d) results obtained by the Fourier-based scheme, Tucker decomposition with rank reduction, and the proposed method, respectively. On the top panels are concentration maps of deuterated Glc, Glx and Lac at five time points; on the middle panels are time courses of dynamic concentration changes of deuterated Glc, Glx, and Lac from one representative imaging voxel (at the center of the tumor marked by a black circle in (a)); on the bottom panels are representative spectra from the same voxel obtained at 20 min, 45 min and 68 min after the infusion.

For a more quantitative analysis, we determined the quantification accuracy and estimation variances of different methods based on 250 Monte-Carlo trials, as summarized in Table I, Table II, and Fig. S4. The analysis shows that the proposed method achieved excellent quantification accuracy and low estimation uncertainty even for small signals of Glx (fitting error = 13.5%; standard deviation = 7.1%) and Lac (fitting error = 11.3%; standard deviation = 9.6%) at the pre-determined SNR level. Compared to the traditional methods, the improvement of reliability and sensitivity was substantial; for example, the fitting errors and standard deviations for Glx were reduced by factors of 5.8 and 9.7, respectively, as compared to the Fourier-based scheme. Compared to the denoising neural networks, the proposed method led to slightly higher standard deviations (Table I). This happened because the data consistency constraint in Eq. (8) re-introduced some measurement noise back. Enforcing data consistency reduces estimation bias (Table I), and significantly improves the estimation accuracy for Glx and Lac (Table II), which is important for application of dynamic DMRSI in cancer imaging.

TABLE I.

Estimation Biases and Standard Deviations (STD) from Monte-Carlo Simulation^*

Bias±STD (%)	Glc	Glx	Lac**
Fourier	9.0±16.5	31.4±68.6	21.0±36.8
Tucker Decomposition	3.2±9.2	12.3±21.7	41.7±7.2
Machine learning	3.3±2.2	14.7±4.3	51.0±2.4
Proposed	2.8±3.3	10.1±7.1	5.0±9.6

^*All the values were averaged over different spatial and temporal points.

^**Lac was considered only within the tumor region

TABLE II.

Estimation Relative Mean Square Errors (RMSE)^*

RMSE (%)	Glc	Glx	Lac**
Fourier	19.2	78.0	42.8
Tucker Decomposition	10.0	26.4	42.7
Machine learning	4.2	16.0	51.1
Proposed	4.6	13.5	11.3

^*All the values were averaged over different spatial and temporal points.

^**Lac was considered only within the tumor region

We have also investigated the denoising effect of the linear subspace and the nonlinear manifold individually. As shown in Fig. 3, both modules had noticeable denoising effect. However, subspace-based denoising had relatively large residual noise (Fig. 3b) because the signal subspace still contains significant noise. Denoising using the nonlinear manifold could significantly reduce the noise-induced signal fluctuations. However, the denoising results are heavily biased, especially for the small signals from Glx and Lac (Fig. 3c), making the outcomes unreliable for practical DMRSI applications. Synergistic integration of the two modules made the proposed method more robust and consistent (Fig. 3d).

Fig. 3.

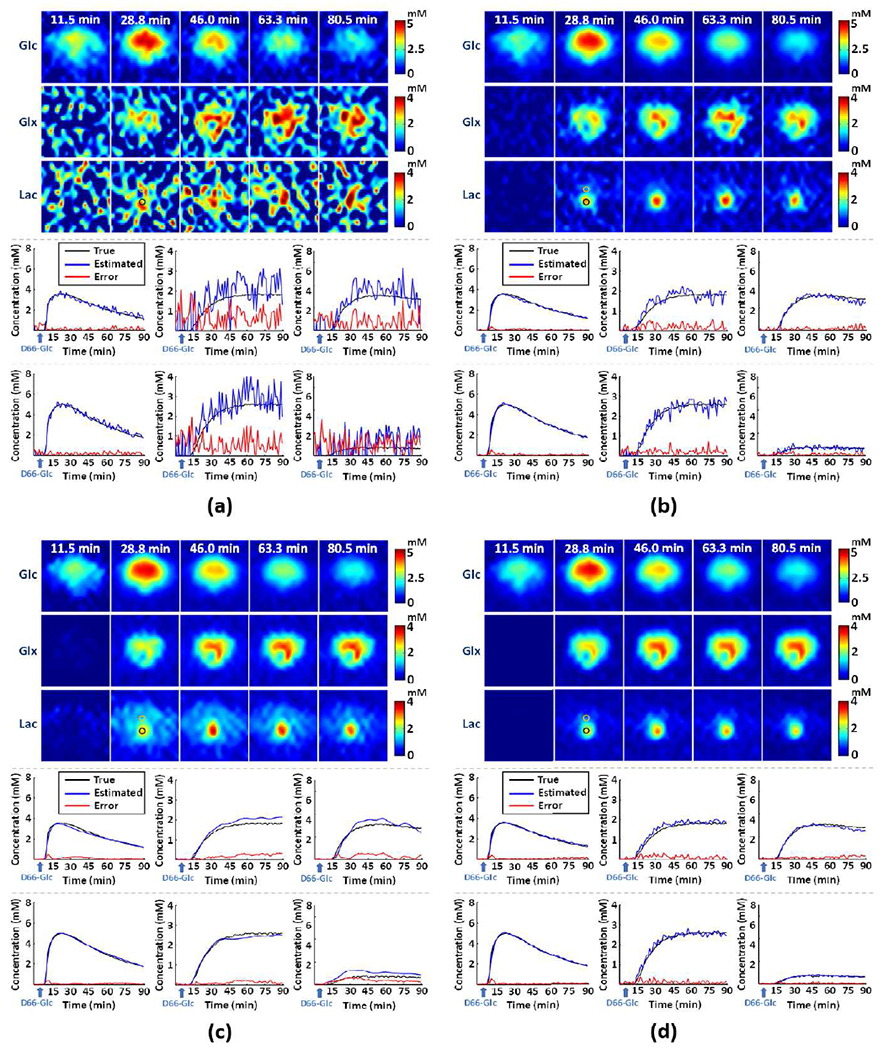
Simulation-based study on the denoising effects provided by the individual modules. The subfigures include results obtained from (a) Fourier-based scheme, (b) linear subspace-based denoising, (c) nonlinear manifold-based denoising, and (d) the proposed method. On the top panels are concentration maps of deuterated Glc, Glx and Lac at five time points; on the middle and bottom panels are time courses of dynamic concentration changes of deuterated Glc (left panels), Glx (middle panels), and Lac (right panels) from two representative imaging voxel (marked by the black and yellow circles).

C. In Vivo Study

We have also evaluated the proposed method using in vivo DMRS imaging data acquired from rat brains. In this study, male and female rats (body weight: 335±126 g) were used, including both healthy (n = 5, Sprague Dawley) and tumor (n = 5, Fischer) subjects. Among these rats, 3 healthy and 2 tumor subjects were scanned for training the learning-based processing model; the remaining rats were scanned for high-resolution dynamic DMRS imaging. Details of animal preparation can be found in the Supplementary Materials.

All the in vivo MR experiments were conducted at 16.4 T/26 cm scanner (Varian/VNMRJ; USA) using a passively decoupled ¹H/²H dual surface coil. For high-resolution dynamic DMRSI data acquisition, repeated 3D ²H-CSI data were acquired from the rat brains before, during and after the 2.5-minute intravenous infusion of D-Glucose-6,6-d₂ (D66-Glc, Sigma-Aldrich, 1.3 g/kg body weight and dissolved in 2.5 mL saline). The imaging parameters included: field of view (FOV) = 28 × 28 × 24 mm³, matrix size = 17 × 17 × 5, cylindrical voxel with a nominal voxel size of 10μL, repetition/echo time (TR/TE) = 45/0.2 ms, 4.11 kHz readout bandwidth, 175 points for each FID signal, total number of phase encodings = 1172 or 2344, 0.9 or 1.8 min acquisition time per CSI volume, and a total of 60 CSI volumes. For training data acquisition, the imaging protocol was the same as used in high-resolution dynamic DMRSI scan except for the following parameters: matrix size = 9 × 9 × 5, total number of phase encodings = 1533, 1.2 min per CSI volume, and a total of 90 CSI volumes. For all the acquired dynamic DMRSI data, the B₀ inhomogeneity was handled as described in the Supplementary Materials. The ¹H anatomical image was also acquired using a fast spin echo (FSE) sequence with the following acquisition parameters: TE = 21 ms; TR = 2 sec; FOV = 2.8 × 2.8 cm; imaging matrix size = 192 × 192; slice thickness = 1 mm; 8 echoes train length.

Figure 4 summarizes the experimental results obtained from one rat with a relatively small tumor (~60 μL) located in one hemisphere (see Fig. S5a); and dynamic DMRSI data were acquired with 10 μL spatial resolution and 1.8 min temporal resolution. As can be seen from Fig. 4a, our proposed imaging method was able to detect elevated Lac labeling (reflecting enhanced glycolysis activity) and reduced Glx labeling (reflecting suppressed TCA cycle activity) in the gliosarcoma tumor, a clear sign of the Warburg effect and underlying cancer metabolic reprograming [5], [6]. The results also showed normal Glc metabolism with higher ²H-labeled Glx and negligible ²H-labeled Lac in the normal-appearing brain tissue in the contralateral hemisphere as expected. In addition, the time course of ²H-labeled Glc signal changes (middle panel in Fig. 4a) clearly indicated a fast decline of ²H-labeled Glc in tumor compared to normal-appearing brain tissue, revealing high glycolysis activity associated with the tumor Warburg effect, which is consistent with a higher Lac turnover observed in the tumor. To quantitatively characterize the metabolic alterations in the tumor, we also conducted a regional analysis to quantify the [Lac]/[Glx] ratio differences and dynamics between the tumor and contralateral normal-appearing tissues (regions of interest (ROIs) are illustrated in Fig. S5b). As shown in Fig. 4b, a large difference in [Lac]/[Glx] ratio (> 5 times) between the tumor and normal-appearing tissue was observed with high statistical significance (2.32 ± 0.58 in tumor versus 0.38 ± 0.19 in normal-appearing brain tissue; P < 0.001). This result indicates that [Lac]/[Glx] ratio could be used as a sensitive index of the tumor severity reflecting the degree of the Warburg effect and the metabolic shift between largely elevated glycolysis activity (i.e., increasing Lac labeling) and suppressed TCA cycle activity (i.e., reducing Glx labeling) associated with the brain tumor.

Fig. 4.

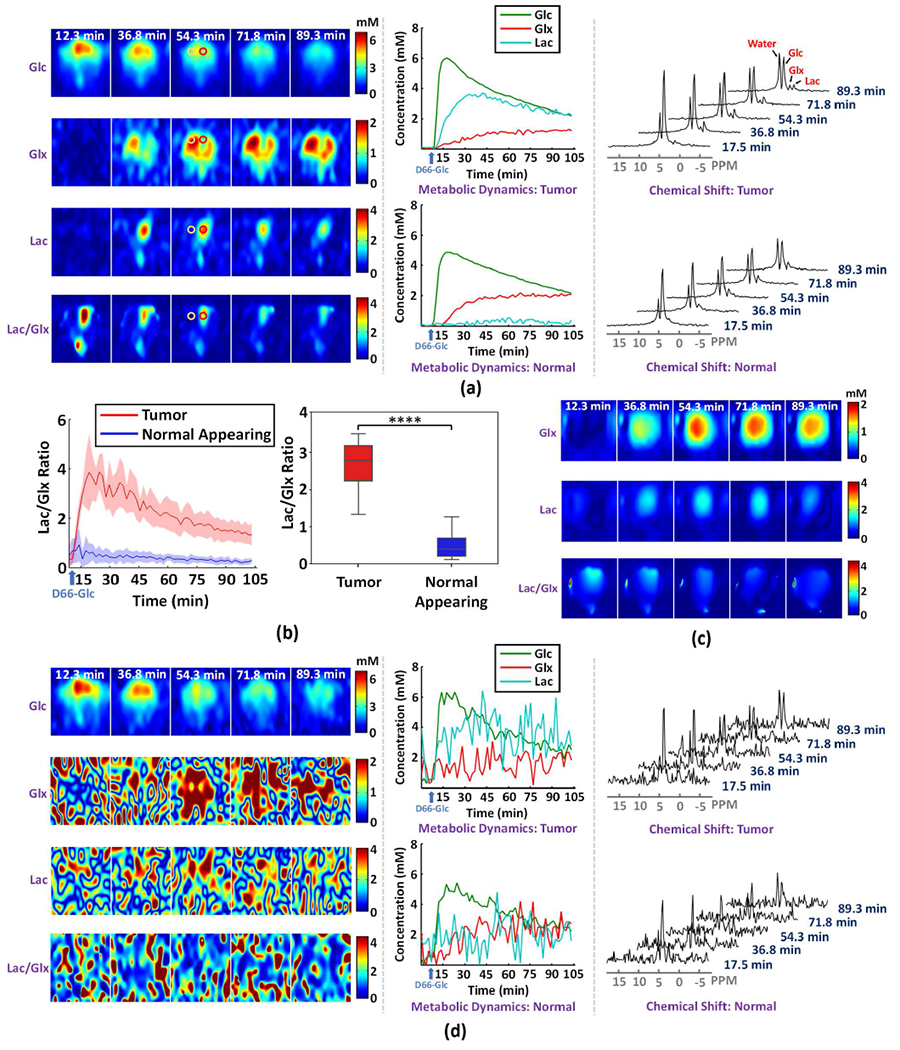
High-resolution dynamic DMRSI results of rat brain with a small tumor. (a) Results obtained by the proposed imaging scheme, including time-dependent concentration maps (left panel), metabolic time courses (middle panel), and the time evolution of ²H-spectra (right panel); here, the metabolic time courses and spectra are from voxels at the center of the red and yellow circles within tumor and normal-appearing tissues, respectively. (b) Dynamic change and statistical comparison of [Lac]/[Glx] ratio between tumor and normal-appearing tissues; the left panel illustrates the time-dependent regional comparison, where the solid line and shaded area indicate the mean and standard deviation, respectively; the right panel shows [Lac]/[Glx] ratio averaged over 15 to 105 minutes after the infusion of deuterated glucose (tumor: 2.32 ± 0.58; normal appearing: 0.38 ± 0.19); **** indicates P < 0.0001. (c) Results obtained from retrospectively sampled low-resolution data (spatial resolution: 5.6 × 5.6 × 8.0 mm³). (d) Results obtained by the Fourier-based scheme with the same layout as (a).

To illustrate the significance of our high-resolution imaging capability in detecting altered metabolism in small brain tumors, we retrospectively sampled a set of low-resolution data (~250 μL voxel size) from the original DMRSI data. The low-resolution DMRSI results (Fig. 4c) failed to separate the tumor from the normal-appearing tissues clearly due to severe spatial blurring (or partial volume) effect. To further demonstrate the advantage of the enhanced sensitivity offered by the proposed method, we compared the metabolic images produced by the traditional Fourier-based scheme and our method. As shown in Fig. 4d, the Fourier-based scheme generated large temporal fluctuations and very noisy Glx, Lac and [Lac]/[Glx] ratio maps, from which detection of the brain tumor was not possible (left panel in Fig. 4d). We also quantitatively calculated the SNR improvement and found the SNR value was increased by about a factor of 8 (SNR_original = 5.9 dB vs. SNR_proposed = 23.5 dB). We have also compared the proposed method to the Tucker decomposition-based denoising scheme as shown in Fig. S6. As can be seen, the traditional low-rank denoising method failed to detect the Warburg effect within the tumor tissues.

Figure 5 illustrates the experimental results from another rat with a relatively large tumor. Figure 5a shows the anatomical images and the metabolic images of steady-state deuterated Glx and Lac concentration and their ratio generated using the proposed method. As can be seen at the location of the tumor, abnormal metabolic activities were clearly captured in the form of reduced Glx and increased Lac levels, which is consistent with that observed in a different rat brain tumor (see Figs. 4a and 4b). The imaging results also show largely varied metabolite concentrations and [Lac]/[Glx] ratio within the tumor, indicating spatial inhomogeneity of the underlying metabolic reprogramming related to tumor aggressiveness. To better characterize the intra-tumor metabolic variations, we segmented the tumor into 12 sub-regions based on their anatomical images (top panel in Fig. 5b) and the [Lac]/[Glx] ratio maps (bottom panel in Fig. 5b); 4 normal-appearing brain regions were also identified in the contralateral hemisphere as the reference. Figure 5c quantitatively compares steady-state [Lac]/[Glx] from different ROIs. As can be seen, clear heterogeneity among different ROIs was confirmed (P < 0.001). Moreover, all tumor regions had higher [Lac]/[Glx] ratio than the normal-appearing tissues (P < 0.001). In particular, based on the anatomical images, the two ROIs (i.e., R_T5a and R_T5b) located inside the tumor necrotic core showed the highest labeled Lac, indicating that glycolysis was greatly elevated. Interestingly, the [Lac]/[Glx] ratio in R_T5b was statistically significantly higher than that in R_T5a (Fig. 5c), which may partially be due to a relatively low Glx labeling in R_T5b (Fig. 5d). Figure 5d displays the metabolic dynamics of Glx and Lac from ROIs. Distinct temporal characteristics of metabolic changes were observed in different ROIs, demonstrating the capability of the proposed method to image the heterogeneous metabolic dynamics within the same tumor. For example, the labeled Lac turnover rate were higher in R_T8c than in R_T8a, while the labeled Glx turnover rate were much lower in R_T8c than in R_T8a, resulting in a much high [Lac]/[Glx] ratio in R_T8c (Fig. 5c). These results again demonstrate the high-resolution imaging capability of the proposed method, which may provide a new and sensitive tool to investigate and characterize metabolic heterogeneity of brain tumors. We have also compared the proposed method with two existing methods usng this dataset. As can be seen from the results in Fig. S7, the proposed method achieved the good denoising performance, while the existing methods failed to detect the metabolic abnormality within the tumor tissues.

Fig. 5.

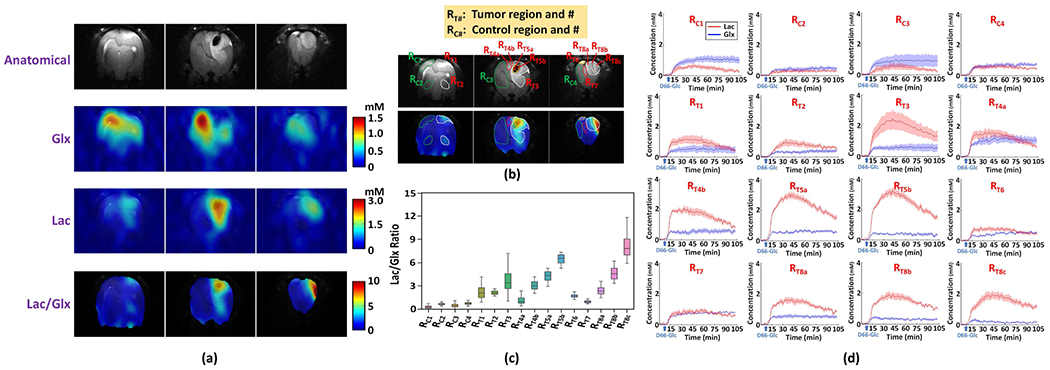
In vivo DMRSI results of intra-tumor metabolic heterogeneity. (a) Anatomical images (top panel) and steady-state metabolite (ratio) maps (bottom panels) at 3 different slices obtained by averaging the DMRSI signals obtained after the infusion of deuterated glucose. (b) Segmentation of the intra-tumor subregions and contralateral normal-appearing region based on anatomical images (top panel) and [Lac]/[Glx] ratio maps (bottom panel). (c) Statistical comparison of [Lac]/[Glx] ratio at steady state among different ROIs (R_C1 0.31 ± 0.17, 362 voxels; R_C2: 0.70 ± 0.13, 236 voxels; R_C3: 0.51 ± 0.23, 1239 voxels; R_C4: 0.77 ± 0.18, 367 voxels; R_T1: 2.23 ± 0.80, 328 voxels; R_T2: 2.15 ± 0.26, 236 voxels; R_T3: 3.67 ± 1.44, 1081 voxels; R_T4a: 1.17 ± 0.46, 140 voxels; R_T4b: 3.09 ± 0.58, 55 voxels; R_T5a: 4.31 ± 0.65, 74 voxels; R_T5b: 6.48 ± 0.62, 121 voxels; R_T6: 1.75 ± 0.23, 62 voxels; R_T7: 1.00 ± 0.16, 131 voxels; R_T8a: 2.40 ± 0.51, 274 voxels; R_T8b: 4.63 ± 0.80, 164 voxels; R_T8c: 8.10 ± 1.42, 185 voxels). (d) Metabolic dynamics of Glx and Lac from different ROIs; the solid line and shaded area indicate the mean and standard deviation, respectively.

In this study, we have also acquired dynamic DMRSI data from a special rat that experienced remission of cancer. Despite the tumor implantation was confirmed by a pre-study MRI scan (7 days in advance), the tumor in this rat brain had disappeared at the time of dynamic DMRSI experiment, as indicated by the anatomical images (Fig 6a). We hypothesized that after the disappearance of tumor, the tissue metabolism should have less abnormality and reduced Warburg effect, which was confirmed by the proposed method. As shown in Fig. 6, no significantly reprogramed metabolic fingerprints of tumor (e.g., elevated [Lac]/[Glx] ratio, Fig. 6b) and metabolic dynamics (Fig. 6c) could be observed at the site of previously implanted tumor, which was consistent with that of anatomical images (Fig. 6a). Quantitative regional analysis was performed to confirm this by calculating the steady-state metabolite concentrations or ratios (averaged over 30 to 105 minutes after the infusion of deuterated Glc). The results indicate that the differences of the metabolite ratios between the ROI of tumor implantation and contralateral normal tissue were much smaller (i.e., Ratio_[Lac] = 0.91, Ratio_[Glx] = 1.09 and Ratio_[Lac]/[Glx] = 0.84) as compared to those shown in Figs. 4 and 5, which is expected since the glycolysis activity associated with tumor growth had been significantly reduced after tumor regression. This finding further demonstrates the potential of proposed method for metabolic imaging of cancer regression and perhaps more importantly for assessing therapeutic vulnerabilities and predicting treatment outcomes.

Fig. 6.

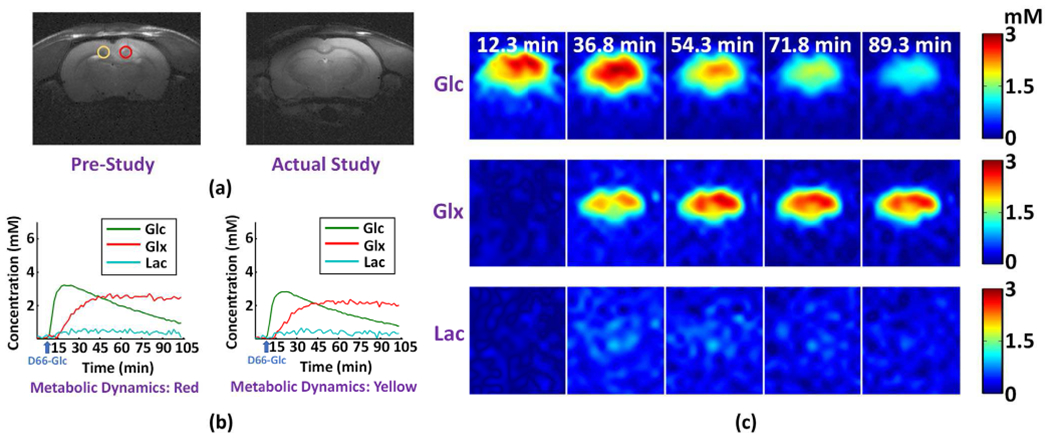
In vivo DMRSI results of rat brain showing spontaneous tumor remission. (a) Anatomical images acquired at one week before (left panel; red circle in tumor and yellow circle in normal-appearing tissue) and on the same day (right panel) of the high-resolution dynamic DMRSI experiment; the tumor disappeared at the time of this study. (c) Metabolic time courses from two voxels at the center of red and yellow circles in (a), respectively. (c) Time-dependent concentration maps of deuterated Glc, Glx and Lac. Note the dynamic DMRSI results showed no significant Warburg effect, which was consistent to the corresponding anatomical image.

D. Reproducibility Assessment

The reproducibility of the proposed method was assessed using in vivo data acquired from both tumor-bearing (n = 3; one with remitted tumor at the scan time) and healthy rat (n = 2) brains. Each of these data was divided into two sets of equal size based on the odd/even number in the time series. Each pair of data sets had identical imaging acquisition parameters and animal conditions but was processed independently. Figure 7 shows the reproducibility results from two representative tumor-bearing rat brains that had clear tumors at the time of DMRSI experiments; Figure S8 shows the results from the other rat brains. As can be seen, voxel-wise comparison showed that concentrations of different voxels in the “odd” and “even” datasets were reasonably repeatable (Glc: slope = 1.00±0.02, n = 5; Glx: slope = 0.99±0.03, n = 5; Lac: slope = 1.06±0.08, n = 2). The metabolic images reconstructed from the paired datasets were almost identical for Glc. Note that the reconstruction of Lac signals was not as reproducible as other molecules (e.g., Fig. 7e) because its SNR was significantly lower. Lac signal is barely detectable by MRS in normal brain tissues and became detectable in cancerous tissue [14]. In this experiment, we pushed for high spatial resolution at the expense of SNR. By lowering the spatial resolution, the reproducibility of the results became much better, as shown in Fig. S9.

Fig. 7.

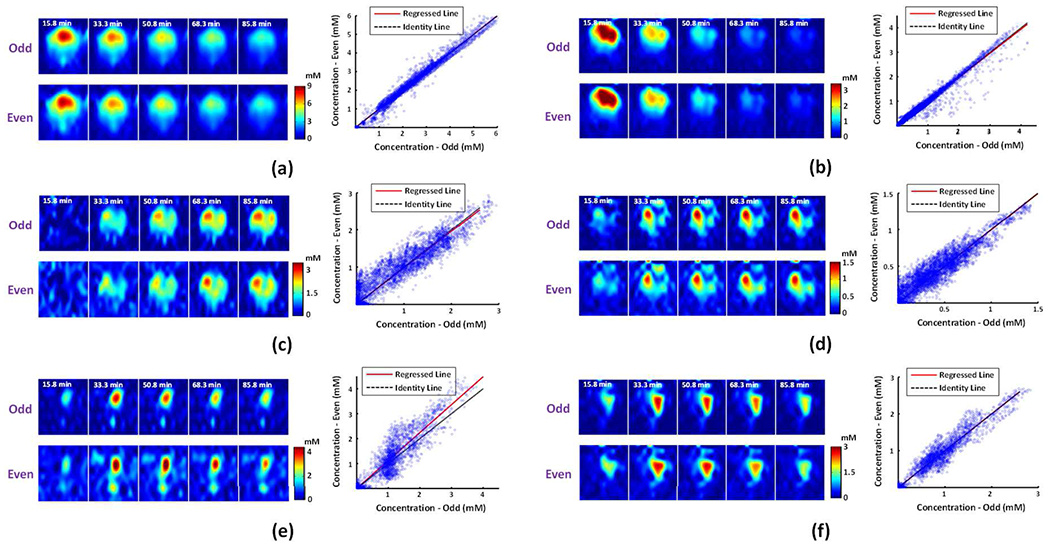
In vivo reproducibility assessment on rat brains with clear tumors. Reproducibility results for (a-b) deuterated Glc, (c-d) Glx, and (e-f) Lac, including concentration maps (left panel) and voxel-wise comparison of the estimates inside the brain obtained in “odd” and “even” datasets (right panel). The results in (a), (c), and (e) were obtained from the 1^st rat (Glc: slope = 1.00, R² = 0.98; Glx: slope = 0.98, R² = 0.82; Lac: slope = 1.12, R² = 0.81). The results in (b), (d), and (f) were obtained from the 2^nd rat (Glc: slope = 0.99, R² = 0.97; Glx: slope = 1.00, R² = 0.85; Lac: slope = 1.00, R² = 0.91).

IV. Discussion

This paper presents a machine learning-based method for high-resolution DMRSI. The theoretical analysis, computer simulations and in vivo experiments demonstrate that the new method can successfully capture the reprogramed energy metabolism associated with elevated glycolysis activity (i.e., the Warburg effect) and suppressed TCA cycle activity in brain tumors and resolve the inter-subject variability and intra-tumor metabolic heterogeneity.

The high-resolution [Lac]/[Glx] map generated by the proposed method provides a sensitive biomarker of the Warburg effect in brain tumor. It has several advantages over the existing tumor biomarkers. First, as compared to ¹⁸F-2-fluoro-2-deoxy-D-glucose (¹⁸F-FDG) in ¹⁸F-FDG PET, the [Lac]/[Glx] ratio can provide a superior image contrast reflecting the reprogramed energy metabolism in brain tumors. Due to the high brain glycolytic activity, ¹⁸F-FDG inherently shows a large difference in the Glc uptake between gray matter (GM) and white matter (WM) and a high baseline uptake in the brain, resulting in a poor tumor contrast [45]. On the contrary, the [Lac]/[Glx] ratio imaged by DMRSI is quite uniform in normal brain tissue as well as between GM and WM, and it becomes larger in tumor as demonstrated in Figs. 4a and 5a. second, as compared to anatomical biomarkers (e.g., T2-weight MRI), the [Lac]/[Glx] ratio could reflect early tumor progression before morphology changes are clearly visible (see Fig. 5). Therefore, the proposed method has a potential to significantly advance the metabolic imaging capability for early detection and diagnosis of brain tumors.

Several existing model-based denoising methods in NMR also exploit the low-rank property of spectroscopic signals to remove data noise. For example, the methods proposed in [21], [46] take advantage of the linear predictability of the NMR signals and use low-rank approximation of the Hankel structured matrices for denoising. As compared to these existing low-rank denoising schemes, the proposed method has a number of novel features desired for denoising MR spectroscopy data with low sNR. First, the existing methods determine the signal subspace and noise subspace directly from the noisy imaging data [21], [47], [48]. Separation of the signal subspace and the noise subspace often requires relatively high sNR data. Otherwise, weak spectral components could be lost in subspace decomposition [49]. The proposed method overcomes this problem by pre-learning the structures of the signal subspace using high-SNR training data; incorporation of physics-based spectral priors also further improves the estimation accuracy. Second, the current subspace methods determine the model coefficients by directly projecting the noisy measured data onto the signal subspace. The proposed method incorporates additional constraints through the learned nonlinear manifolds to reduce estimation uncertainty, thus improving denoising effectiveness.

More recently, deep learning was also used for denoising signal denoising MR spectroscopy data. Many of them use end-to-end neural networks to map noisy signals to their high-SNR counterparts [50], [51]. Although those methods have produced impressive empirical results, they also have several known limitations, such as estimation bias as demonstrated in Refs. [52] and [53] and in Fig. S3, The proposed method treats the output of the deep denoisers as priors, which reduced estimation bias, as shown in Tables I and II, as well as Figs. S3 and S4.

In this study, we learned the subspace structures from acquired training data that have about 1000 samples (one from each voxel). The number of training samples is comparable to what was used in the published works [22], [32], [48]. We also confirmed that this number was adequate for our study using computer simulation, as shown in Fig. S10. For manifold learning, we generated large amounts of training data (100k) using a physics-based generated model (Eqs. (2) and (5)). The parameters and their distributions were estimated from in vivo training data. While the computational framework of our proposed method is independent of the number of training samples available, we expect its practical performance would improve with more training data available, which should be determined for specific applications.

The proposed method may also provide a useful framework for denoising other dynamic magnetic resonance spectroscopic imaging (MRSI) data as the proposed model can represent a large class of dynamic spatiospectral variations. For example, in application of dynamic ³¹P-MRSI for mapping the mitochondrial function and metabolic rate change, one key issue is low-SNR which impedes accurate kinetic quantification of adenosine triphosphate (ATP), phosphocreatine (PCr) and inorganic phosphate (Pi) [27]. This issue could be addressed using the same strategy developed in this work. Specifically, a subspace model can be used to reduce the degrees of freedom in representing the signal variations of ATP, PCr, and Pi; their underlying nonlinear manifolds can also be learned and integrated for additional SNR gain. We expect a similar level of sensitivity improvement can be achieved as observed in the current study. Extension of the proposed method to other dynamic MRSI applications will be investigated in future research.

V. Conclusion

This work presents a new machine learning-based method for high-resolution dynamic DMRSI. The proposed method overcomes the low-sensitivity issue by synergistically integrating physics-based subspace modeling and data-driven deep learning, thus making dynamic DMRSI with high spatiotemporal resolution possible. Its performance has been evaluated using theoretical analysis, computer simulations, and in vivo experiments. Significantly improved sensitivity has been observed over the conventional methods. The proposed method is expected to be useful for dynamic DMRSI applications, in particular, for imaging the Warburg effect.