基于系统动力学模型的 2019冠状病毒病早期防控机制研究

Abstract

目的：

探讨各国2019冠状病毒病（COVID-19）暴发早期防控的效果，为传染病疫情暴发早期的防控提供对策。

方法：

以世界卫生组织公开的中国、美国、英国、澳大利亚、塞尔维亚和意大利COVID-19疫情暴发早期数据为样本，建立广义易感-暴露-感染-恢复（SEIR）模型，对其参数进行最优化求解。然后，根据基本传染数表达式中的参数，利用系统动力学模型中的敏感性分析，定量分析各国保护率、感染率和平均检疫时间对疫情暴发早期的影响。最后，根据分析结果提出COVID-19暴发早期的防控对策。

结果：

广义SEIR模型对六国COVID-19暴发早期的预测和评估具有较好的拟合性，实际数据与拟合数据高度重合。COVID-19扩散主要受保护率、感染率和平均检疫时间影响：从保护率来看，前10 d的保护率提高最为重要，保护率越大，确诊人数越少；从感染率来看，前5 d的感染率最为关键，感染率越小，确诊人数越少；从平均检疫时间来看，前5 d的平均检疫时间至关重要，平均检疫时间越短，确诊人数越少。通过对六国关键参数对比发现，澳大利亚和中国由于实行严格的防疫政策，保护率较高，平均检疫时间较短，因而防疫效果较好。

结论：

在COVID-19暴发早期，需要实行提高保护率、缩短平均检疫时间的措施，以及严格的隔离政策，抑制COVID-19传播及扩散。

2019冠状病毒病（coronavirus disease 2019，COVID-19）;易感-暴露-感染-恢复（susceptible-exposed-infectious-recovered，SEIR）;世界卫生组织（World Health Organization，WHO）;

2020年初，COVID-19在中国迅速蔓延，但随着严格防疫政策的实施，疫情在2020年2月中下旬已被基本抑制。之后，COVID-19在我国部分地区虽有零星散发，但均较快得到控制，对居民健康和日常生活未构成持续威胁，而这均得益于疫情早期的防控。因此，如何在疫情暴发早期迅速采取有效的防控措施，对于COVID-19这类传染病疫情的防控具有重要作用。

目前，国内外学者从微观防控机制与宏观防控体系两个方面对COVID-19疫情防控进行了研究。在微观防控机制方面，部分学者以省份和地区为样本，建立疫情微观防控机制，例如精准的智控机制、针对特大城市的全流程疫情防控机制、集中医疗观察点和控制感染源 ^{[ 1- 3]} ；有学者针对工作场所提出防控机制 ^[4] ，还有学者通过MH参数估计法、SEIR模型模拟和预测干预场景来建立隔离患者、实时追踪密切接触者等一系列防控机制 ^[5] 。在宏观防控体系方面，有研究制订了有关交通运输部门的防控应对机制，提出应完善交通运输应急预案体系，指导交通部门疫情防控决策 ^{[ 6- 7]} ；还有学者提出国家治理现代化背景下的防控策略，将国家层面的疫情防控体系和卫生健康的理念引入政府防控机制中 ^{[ 8- 10]} 。但上述研究主要是定性研究，基于系统建模方法的定量研究较少。

现有的传染病系统建模方法中，SEIR模型是体系独立且理论完善的理想模型，可以在建立微分方程组的基础上按照一般的传播机制进行系统建模分析。已有学者基于SEIR模型在COVID-19传播预测与防控方面进行了研究：范如国等 ^[11] 将复杂网络理论引入SEIR模型，通过SEIR模型对3种不同病毒潜伏期的拐点进行了预测，并提出对应的防控建议；张宇等 ^[12] 将人口迁徙强度与SEIR模型相结合，建立交通工具内部疫情传播模型，并模拟了疫情沿交通工具线路传播的过程。基于SEIR模型考虑因素较少的缺陷，一些研究对SEIR模型做出了改进。曹盛力等 ^[13] 结合潜伏期传播能力和追踪隔离干预措施，基于修正SEIR模型预测和评估了湖北省COVID-19疫情的走向；游光荣等 ^[14] 将建模仿真和因果推断方法相结合，利用修正后的SEIR模型，对COVID-19在中国的传播趋势进行建模，并评估武汉采取防疫政策的重要性。但这些研究所采用的SEIR模型并没有考虑到COVID-19的多种状态，忽略了不易感人群和隔离人群，参数相对固定、单一，且只分析了COVID-19疫情在中国的情况。广义的SEIR模型考虑到易感人群、不易感人群、暴露人群等多个状态，且治愈率和病死率等参数处于动态变化中。为了研究样本在防控政策上具有区别性和代表性，且满足区域研究的广泛性，本研究以中国、美国、英国、澳大利亚、塞尔维亚和意大利COVID-19暴发早期数据为研究样本，通过广义SEIR模型，基于动力学模型中的敏感性分析，对基本传染数表达式中的保护率、感染率和平均检疫时间进行对比分析，为COVID-19和其他流行病早期防控提出针对性的防控建议。

1资料与方法

1.1数据来源与假设

本文数据来源于WHO每日公布的COVID-19情况报告（ https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports），数据时长约为30 d， 各国数据采集时间段为其COVID-19暴发早期，即累计确诊人数处于快速上升期，具体时间段如下：中国为2020年1月22日—2月20日，美国为2020年3月19日—4月17日，英国为2020年3月16日—4月14日，澳大利亚为2020年3月18日—4月16日，塞尔维亚为2020年3月20日—4月18日，意大利为2020年3月10日—4月8日。根据WHO公开的数据，6个国家COVID-19暴发早期每日累计确诊病例数见 图1。

图 1 .

六国2019冠状病毒病暴发早期每日累计确诊病例数

1.2基于广义SEIR模型的参数估计

本研究以广义SEIR模型为基础，引入7个不同的状态，即 S（ t）、 P（ t）、 E（ t）、 I（ t）、 Q（ t）、 R（ t）、 D（ t），分别表示在时间 t内的易感人群、不易感人群、暴露人群（已感染但尚不具有传染性，处于潜伏状态）、感染人群（具有传染性，尚未隔离）、隔离人群（已感染和确诊）、恢复人群和死亡人群的数量，并用微分方程式表征，见 图2。新的隔离状态由数据驱动，死亡与恢复状态一起取代了经典SEIR模型中的原始 R状态。常数 N是某个区域的总人口，计算公式为 N＝ S+ P+ E+ I+ Q+ R+ D。系数 α、 β、 γ ^–1、 δ ^–1、 λ（ t）、 κ（ t）分别表示保护率、感染率、平均潜伏时间（d）、平均检疫时间（d）、治愈率和病死率。

图 2 .

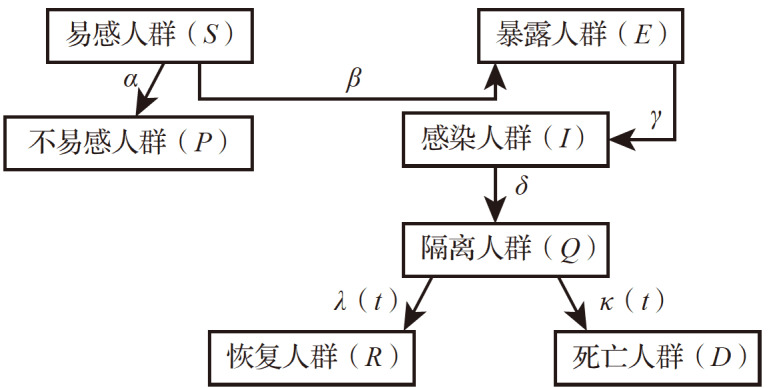
广义易感-暴露-感染-恢复模型的架构

广义SEIR模型 ^[15] ：

$$\begin{array}{cr}\{\begin{array}{l}\frac{dS(t)}{dt}=-\alpha S(t)-\beta \frac{S(t)I(t)}{N}\\ \frac{dE(t)}{dt}=-\gamma E(t)+\beta \frac{S(t)I(t)}{N}\\ \frac{dI(t)}{dt}=\gamma E(t)-\delta I(t)\\ \frac{dQ(t)}{dt}=\delta I(t)-\lambda (t)Q(t)-\kappa (t)Q(t)\\ \frac{dR(t)}{dt}=\lambda (t)Q(t)\\ \frac{dD(t)}{dt}=\kappa (t)Q(t)\\ \frac{dP(t)}{dt}=\alpha S(t)\end{array}& \text{(1)}\end{array}$$

由于治愈率和病死率具有时间依赖性 ^[16] ，需要一些经验系数来调整其时间依赖性。病死率分为两个阶段，治愈率分为三个阶段，其思路是以明确的指数时间相关趋势进行调整，病死率应随着时间的增加而接近于零，而治愈率则趋于恒定。

广义SEIR模型中的病死率：

$$\begin{array}{cr}\kappa (t)={\kappa }_0{e}^{-{\kappa }_{1}t}& \text{(2)}\end{array}$$

广义SEIR模型中的治愈率：

$$\begin{array}{cr}\lambda (t)=\frac{{\lambda }_0}{1+e^{[-{\lambda }_1(t-\tau )]}}& \text{(3)}\end{array}$$

1.3系统动力学模型的参数敏感性分析

利用系统动力学模型的敏感性分析分析COVID-19传播中的参数。敏感性分析的主要参数来源于基本传染数（ R ₀），即在没有特殊外力的干预下，种群都不具备免疫力时，某个病原体会把疾病传染给他人的平均数。 R ₀数值愈大，传染病的控制愈难 ^[17] 。在没有防疫的情况下：若 R ₀<1，传染病会逐渐消失；若 R ₀>1，传染病会以指数分布的方式爆炸式增长，上升为流行病；若 R ₀=1，传染病会变成种群中的地域性流行病。为讨论参数对疫情传播的影响，需要分析 R ₀与 α、 β、 γ ^–1、 δ ^–1、 λ（ t）、 κ（ t）的关系，式（4）为基本传染数 R ₀的计算公式：

R ₀= β× δ ^–1×（1– α） ^T （4）

其中 T为疫情传播的天数。由式（4）可知， R ₀的值仅受 α、 β以及 δ ^–1的影响。同时平均潜伏时间 γ ^–1在某种疫情传播过程中一般为稳定的值，且治愈率 λ（ t）和病死率 κ（ t）对疫情传播过程影响较小，因此本文仅对 α、 β以及 δ ^–1的值进行分析，从而得出这些参数对疫情传播的影响。

2结果

2.1COVID-19暴发早期参数估计结果

基于六国COVID-19暴发早期的确诊人数、死亡人数、治愈人数和总人口，通过SEIQRDP函数表达广义SEIR模型，选用MATLAB软件中非线性拟合函数lsqcurvefit对模型的参数进行拟合，得到六国模型的最优参数（ 表1）。中国和澳大利亚的原始感染率分别为1.1332和1.1830，因感染率范围应为0~1.0，故将感染率修订为最大值1.0000 ^[15] 。COVID-19疫情早期，各项医疗技术、设施和防控手段未快速提高，故保护率、感染率、平均检疫时间和平均潜伏时间在短时间内未发生显著变化。本文主要研究保护率、感染率、平均检疫时间等单一参数对病毒传播的影响，故设定其参数为固定值，而对治愈率和病死率的参数估计采取动态变化方式。

表 1 六国广义易感-暴露-感染-恢复模型最优参数值

Table 1 Optimal parameters of generalized susceptible-exposed-infectious-recovered model in six countries

国家	保护率（ α）	感染率（ β）	平均潜伏时间（ γ –1）	平均检疫时间（ δ –1）	治愈率（ λ）	病死率（ κ）	总人口数（ N）
美国	0.0331	0.5995	1.0096	3.126 0	0.013000/0.019 3/0.0088	0.007400/0.0210	329466283
中国	0.0335	1.0000	1.0000	1.622 1	0.692700/0.0888/59.6739	0.005 200/0.0296	1404676330
意大利	0.0934	0.9660	7.0028	3.4614	0.016700/0.9424/40.4657	0.021700/0.0380	60461828
英国	0.0356	0.5906	1.7126	4.3290	0.000688/0.9420/40.2121	0.024300/0.0158	67886004
澳大利亚	0.2883	1.0000	2.6042	5.1256	0.033300/0.2120/11.8151	0.000 605/0.000056	25459700
塞尔维亚	0.026 3	0.5208	2.2665	4.5455	0.066000/5.0000/26.8389	0.007 900/0.0704	8737370

将六国参数估计值代入模型中，计算得到的拟合数据与实际数据的对比如 图3所示，其中死亡者与治愈者为累计数据，当前感染者为累计确诊人数减去死亡人数和治愈人数 ^[13] 。由 图3可知，美国、英国、意大利和塞尔维亚的感染者、治愈者、死亡者人数的拟合曲线与实际数据曲线高度重合；中国和澳大利亚的感染者人数的拟合曲线与实际数据曲线略有差别，但基本重合，死亡者人数的拟合曲线与实际数据曲线高度重合。各国感染者、治愈者、死亡者的拟合曲线与实际曲线重合说明了广义SEIR模型的拟合效果较好。

图 3 .

六国感染者、治愈者、死亡者的拟合数据与实际数据对比

2.2关键参数敏感性分析结果

根据广义SEIR模型，利用MATLAB软件，通过单一改变保护率、感染率和平均检疫时间，分析六国COVID-19疫情在暴发早期的变化趋势，得到相应参数对COVID-19疫情传播的影响。

2.2.1保护率对感染人数的影响

保护率 α指从易感人群转变为不易感人群的概率。保护率的变化对各国感染者人数的影响如 图4所示。从六国COVID-19感染人数随保护率变化的趋势来看，以实际曲线为基准，前10 d保护率对COVID-19感染人数的变化影响不大，但随着时间推移，保护率对感染人数变化的影响增大。当保护率变化为较小值时，除澳大利亚外，各国感染人数在短期内几乎都成指数增长；当保护率变化为较大值时，感染人数开始变少，到最后几乎变成了水平直线，感染人数逐渐清零。结果提示，在前10 d采取有效、合理的措施增大保护率，感染人数将急速减少，甚至出现拐点，反之将导致感染人数迅速增加。

图 4 .

保护率对六国2019冠状病毒病患者例数的影响

2.2.2感染率对感染人数的影响

感染率 β指由非感染人群变为感染人群的概率。感染率的变化对各国感染者人数的影响如 图5所示。从各国感染人数随感染率变化趋势可知，以实际曲线为基准，除中国和澳大利亚外，前5 d的感染率对感染人数变化的影响不大，但随着时间推移，感染率对感染人数变化的影响增大，且成倍数变化。当感染率变化为较大值时，短期内感染人数呈现指数增长，若控制不当，会直线上升；当感染率降低时，感染人数逐渐减少，曲线也趋于平滑，感染人数逐渐清零。结果提示，在前5 d采取有效、合理的措施降低感染率，感染人数将急速减少，甚至出现拐点，反之将导致感染人数成倍增长。

图 5 .

感染率对各国2019冠状病毒病患者例数的影响

2.2.3平均检疫时间对感染人数的影响

平均检疫时间 δ ^–1是指确诊者从患病到收治进医院隔离或居家自我隔离的时间。平均检疫率 δ为平均检疫时间 δ ^–1的倒数，即平均检疫率越小，平均检疫时间越长。平均检疫率的变化对六国感染人数的影响如 图6所示。以实际曲线为基准，前5 d的平均检疫时间对感染人数的变化影响不大，但随着时间推移，平均检疫时间对感染人数的影响增大。当平均检疫率变化为较小值时，检测周期加长，导致感染者接触人群的时间变长，进而导致感染人数短期内呈现暴发式增长；当平均检疫率变化为较大值时，感染人数逐渐减少，曲线也趋于平稳，感染人数逐渐清零。结果提示，在前5 d采取有效、合理的措施缩短平均检疫时间，感染人数将急速减少，甚至出现拐点，反之将导致感染人数爆炸式增长。

图 6 .

平均检疫率对六国2019冠状病毒病患者例数的影响

2.3不同的保护率平均检疫时间每日感染占比国家早期防控结果

为了进一步对比各国COVID-19暴发早期防控的效果，需要对三个重要参数进行比较分析。澳大利亚由于在COVID-19暴发早期实行严格的防疫政策，对来自重点疫情国家的人流实行限制管控，实现了较高的保护率；而中国的平均检疫时间最短（ 图7）。结合各国COVID-19疫情发展态势，说明COVID-19暴发早期实行提高保护率、缩短平均检疫时间的政策可以抑制COVID-19疫情的传播与扩散。

图 7 .

六国2019冠状病毒病暴发早期保护率与平均检疫时间比较

因COVID-19暴发早期的感染与各国人口有关，故本文采用30 d内的日确诊人数除以总人口数计算每日感染占比。 图8为各国以5 d为时间段的感染占比，可以看出中国在COVID-19暴发早期感染占比最低，且由于实行严格的隔离政策与实时追踪感染者行踪，导致感染占比逐渐下降；澳大利亚也是如此，通过严格的隔离防疫措施，加大对感染人群的隔离管控，致使感染占比逐渐下降，说明COVID-19暴发早期需要实行严格的隔离防控政策来降低感染占比。

图 8 .

六国2019冠状病毒病暴发早期感染占比变化趋势

3讨论

针对COVID-19疫情，各国在考察本国国情后采取的一系列防控措施大致可分为两类 ^[18] 。第一类是以中国、澳大利亚和意大利为代表的政府集中管控模式。政府统筹全国各地疫情管控，国家成立疫情专项工作小组，跟踪疫情进展，对COVID-19疫情进行每天通报，对重点疫情地区实行“封闭”，限制人员流动。通过这些措施的实施，这些国家迅速切断了病毒传播途径，降低病毒传播率，有效遏制了病毒蔓延。第二类是以英国、美国和塞尔维亚为代表的有限防控模式。此模式兼顾疫情防控和社会秩序的平衡，期望整个社会经济正常运转；鼓励轻症患者居家隔离自愈，对重症患者实行集中资源重点治疗；倡导减少外出活动，不强制限行，不实行全面的感染监测和跟踪政策。此模式对社会经济活动的影响限制在有限范围，避免对医疗资源的挤兑，但高度依赖民众的自觉性，一旦感染者未能自觉居家隔离，疫情将会蔓延并逐步超过防控力度，给国家带来巨大的防控压力。

本文根据中国、美国、英国、澳大利亚、塞尔维亚和意大利COVID-19暴发早期的历史数据，基于广义SEIR模型，得出六国的最优参数；进而根据基本传染数表达式中的保护率、感染率和平均检疫时间，利用系统动力学模型的敏感性分析，结合各国COVID-19暴发早期的防控政策，得到如下主要结论：①广义SEIR模型对各国COVID-19暴发早期的预测和评估具有较好的拟合性，实际数据与拟合数据高度重合，且本文模型主要适用于疫情发展早期增长段的分析。②COVID-19扩散主要受保护率、感染率和平均检疫时间的影响，从保护率来看，前10 d保护率提高最为重要，保护率越大，确诊人数越少；从感染率来看，前5 d感染率降低最为关键，感染率越小，确诊人数越少；从平均检疫时间来看，前5 d的平均检疫时间至关重要，平均检疫时间越短，确诊人数越少。③通过关键参数对比发现，澳大利亚和中国由于实行严格的防疫政策，致使其防疫效果更好。因此，在COVID-19 暴发早期，实行提高保护率、缩短平均检疫时间的措施及严格的隔离政策可以抑制COVID-19疫情的传播及扩散。

根据关键参数的敏感性分析以及各国成功的防控政策，本研究从个人行为、政府管理和未来防控三个层次对防控措施进行如下建议：

（1）提高保护率。个人备好生活物资和防疫物资，尽量少扎堆，增加社交距离，甚至不出门。国家卫生系统加强基本要素的投资，如医生使用远程医疗手段对易感人群提供远程医疗咨询；限制高风险地区人流外出，如限制出入境、停飞航班等 ^[19] ，有效切断病毒传播途径，遏制病毒蔓延 ^[20] ；对不同社区进行分层分类管理，如运用七色管理法实施COVID-19社区分级分类分层防控的实践方案 ^[21] ；建立易感人群大数据平台和医疗档案，定期对易感人群进行排查和走访，必要时采取隔离手段等。

（2）降低感染率。个人佩戴好口罩，规范洗手并对衣物、鞋子进行消毒，降低个人感染概率，对接触患者的隔离工作人员和治疗人员定期检测病毒并记录相关症状；政府管理部门追踪感染者的行径，对感染者行迹过的区域进行详细排查 ^{[ 22- 23]} ；充分发挥政府主导协调优势，集中医疗卫生资源支援重点疫区；建立个人和单位防控流感流程，定期抽查企业和高校的防控体系。

（3）缩短平均检疫时间。个人积极配合检测，若有发热、咳嗽等症状，须尽快就医；国家成立疫情专项工作小组，跟踪疫情进展，对COVID-19疫情进行每日通报；增大检测力度，在必要的情况下对高风险地区进行全民检测，其他中低风险区域可抽样检测，另外可以根据污水病毒RNA浓度推算人群中的感染人数 ^[24] ；在疫情高发期要严格排查，定期检查以往COVID-19患者情况。

Funding Statement

国家重点研发计划（2016YFE0111000）