Automatic Localization of Landmarks in Craniomaxillofacial CBCT Images Using a Local Attention-Based Graph Convolution Network

Abstract

Landmark localization is an important step in quantifying craniomaxillofacial (CMF) deformities and designing treatment plans of reconstructive surgery. However, due to the severity of deformities and defects (partially missing anatomy), it is difficult to automatically and accurately localize a large set of landmarks simultaneously. In this work, we propose two cascaded networks for digitizing 60 anatomical CMF landmarks in cone-beam computed tomography (CBCT) images. The first network is a U-Net that outputs heatmaps for landmark locations and landmark features extracted with a local attention mechanism. The second network is a graph convolution network that takes the features extracted by the first network as input and determines whether each landmark exists via binary classification. We evaluated our approach on 50 sets of CBCT scans of patients with CMF deformities and compared them with state-of-the-art methods. The results indicate that our approach can achieve an average detection error of 1.47mm with a false positive rate of 19%, outperforming related methods.

1. Introduction

Craniomaxillofacial (CMF) surgeries aim to correct congenital or acquired deformities of the head and face [10]. Due to the complexity of CMF anatomy, detailed surgical planning is often carried out with the help of cone-beam computed tomography (CBCT) images. CMF landmark localization, also called “landmark digitization”, is an important step to quantify deformities for surgical planning. An automated landmark digitization method is highly valuable for effective and efficient surgical planning.

Deep learning-based methods, such as convolutional neural networks have been proposed to learn task-specific features for anatomical landmark localization in medical images. For example, Payer et al. [6] applied fully convolutional network (FCN) [4,5,7] to predict a non-linear mapping from input image patches to the respective heatmap patches. Zhang et al. [13] employed a cascade of two FCNs to detect multiple anatomical landmarks simultaneously, where the 3D displacements generated by the first FCN are used in combination with the image patches in the second FCN to regress the respective landmark heatmaps. Wang et al. [8] developed a multi-task network for segmentation and landmark localization in prenatal ultrasound volumes.

Although yielding promising prediction results in landmark localization, the above methods suffer from a number of limitations. First, for patients with facial trauma or post-ablative surgery, some anatomical landmarks might be missing due to deformities. Failure to consider this will lead to false-positive detections, affect deformity quantification, and mislead surgical planning. Second, these methods localize each landmark independently without considering the inter-dependency between landmarks. Most CMF landmarks are located on bony boundaries and are related via a relatively fixed geometrical structure. Explicitly modeling this kind of inter-dependency can reduce misdetections.

In this paper, we focus on localizing CMF landmarks and at the same time determine their existence. We propose a coarse-to-fine two-stage approach to gradually detect CMF landmarks in CBCT images. In the first stage, a cascade of two networks is employed for coarse but reliable landmark localization. The first network is derived from U-Net, which takes a down-sampled 3D image as input, and outputs a set of attention maps. To model the dependence between landmarks, we first group all landmarks according to 7 pre-defined anatomical regions and encode their spatial relationships in an adjacency matrix. We then employ a second network based on a graph convolution network (GCN) with the adjacency matrix and features extracted from the attention maps as inputs to determine the existence of each landmark. In the second stage, image patches with a higher resolution are sampled in the vicinity of the landmark locations estimated in the first stage. These patches are used to train a high-accuracy network [3] to further refine landmark localization.

The contribution of our paper is two-fold. First, we introduce a new attention feature extraction mechanism for feature learning. Second, we encode the dependency of all landmarks in the form of a graph to be adopted in a GCN to predict the existence of each landmark. The accuracy of this method will be demonstrated via quantitative evaluation.

2. Method

To improve the accuracy of CMF landmark localization on CBCT images, we use a coarse-to-fine framework that adopts a proposed network to gradually and jointly refine the predicted locations of all landmarks. Specifically, we adopt GCN to solve the problem of landmark existence determination. The proposed network is shown in Fig.1 (a), (b). Different from other GCN networks in [2], we use a feature extraction network to automatically learn the features used as inputs for GCN. Moreover, we design an adjacent matrix to model the dependencies of landmarks in the same anatomic region. Details of our proposed network is introduced in the following sections.

Fig. 1.

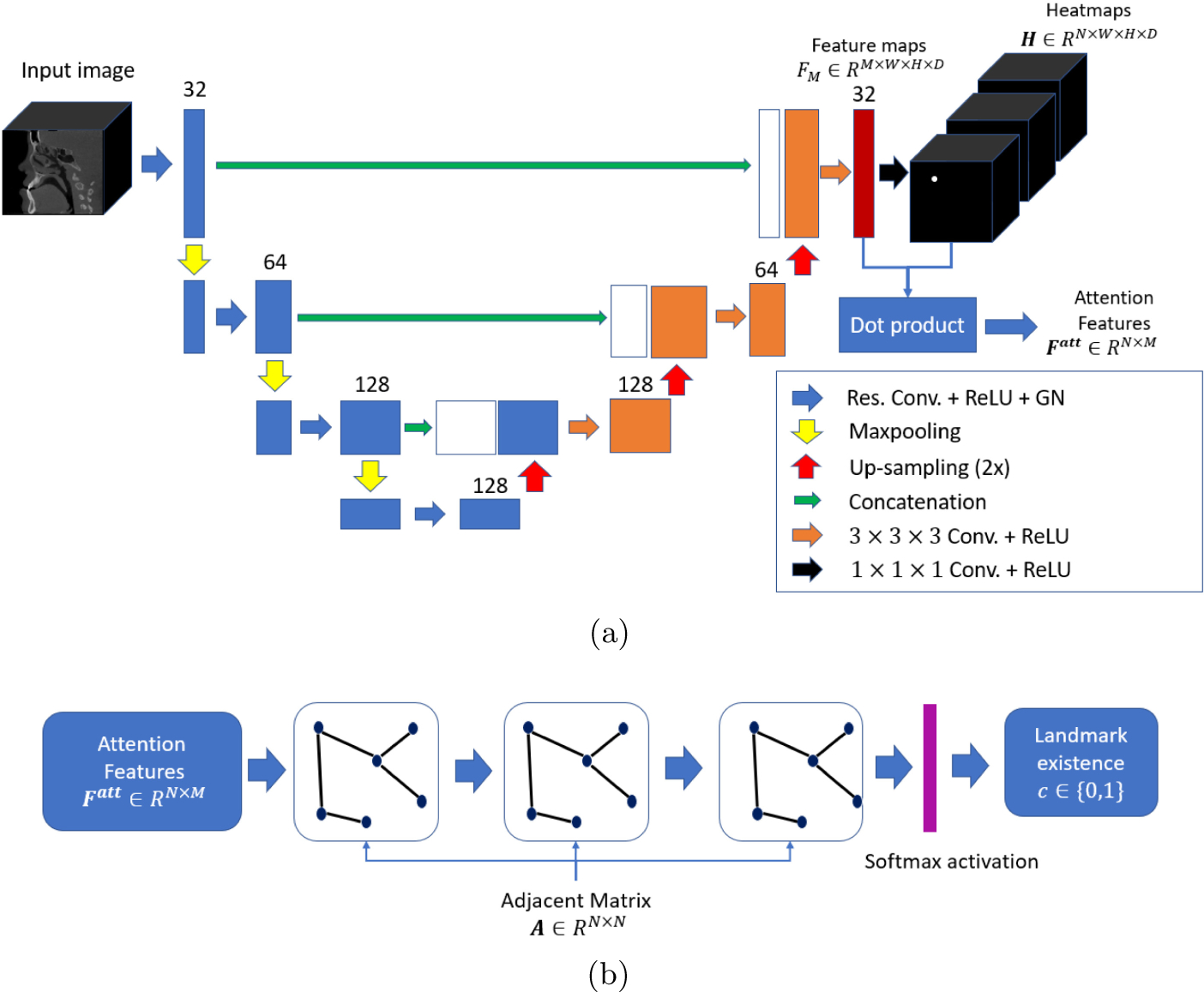
The proposed network for CMF landmarks detection. (a) Attention feature extraction network for localizing landmarks and generating attention features. (b) GCN for determining landmark existence (0 for negative and 1 for positive).

2.1. Attention Feature Extraction Network

The purpose of Attention Feature Extraction Network (AFEN) is to generate N numbers of feature vectors for the subsequent GCN, and to predict landmark locations by heatmap regression. Each landmark is represented by a heatmap, where the landmark location has the highest intensity. As shown in Fig. 1(a), AFEN is constructed as a U-Net, with a contraction path consisting of four residual blocks [1], and an expansion consisting of three expansive blocks. Each residual block consists of two 3 × 3 × 3 convolutional (conv) layers, and each conv layer is followed by Rectified Linear Units (ReLU) activation and Group Normalization (GN) [9]. Between two subsequent residual blocks, a max pooling layer is used to down-sample feature maps and increase receptive field. In the expansive path, each expansive block consists of two 3 × 3 × 3 conv layers, each followed by a ReLU activation. N numbers of heatmaps are generated after a 1 × 1 × 1 convolutional layer. The training loss of AFEN is:

$$L_{\mathit{\text{AFEN}}}\left(H_i,{\widehat{H}}_i\right)=\frac{1}{N}\sum _{i=1}^N{\left(H_i-{\widehat{H}}_i\right)}^2$$ (1)

where H_i is the regressed heatmap for landmark i, and ${\widehat{H}}_i$ is the corresponding ground-truth heatmap. N is the number of landmarks.

The generated heatmap should be a probability distribution map with large probability value around the location of each landmark. Meanwhile, probability values are close to zero at other locations far away from the landmark. Therefore, in this work, we use the regressed heatmap as attention map rather than activating the features maps by Softmax or Sigmoid functions as introduced in the conventional attention mechanisms [14,15]. Each element of the attention feature $F_i^{att}$ for the i-th landmark is calculated by:

$$F_{i_j}^{att}=H_i*F_{M_j}$$ (2)

where * is the dot product. $F_{M_j}$ is the j-th feature map in the last layer of U-Net as shown in Fig.1(a). H_i is the i-th regressed heatmap. $F_i^{att}$ gathers all the information from each feature map near the landmark locations.

2.2. Graph Convolution Network

Due to the fact that the locations of CMF landmarks follow a stable structure, a graph is formed by all landmarks, where each node represents one landmark. The edge between each pair of landmarks is determined by whether the two landmarks are in the same anatomical regions. All 60 landmarks are pre-defined to be located in 7 non-overlapped regions: Midface-left (MF-L), Midface-Central (MF-C), Midface-Right (MF-R), Maxilla (MAX), Mandible-Left (MD-L), Mandible-Right (MD-R), and Mandible-Central (MD-C), as shown in Fig.2(a)–(d) using different colors. The landmark dependency is represented by an adjacent matrix defined as:

$$A=\left[\begin{array}{ccc}{a}_{11}& \cdots & a_{1N}\\ ⋮& a_{ij}& ⋮\\ a_{N1}& \cdots & a_{NN}\end{array}\right]$$ (3)

where a_ij is the value of the edge between landmark i and j defined as:

$$a_{ij}=\{\begin{array}{ll}1,\hfill & \text{if }i=j,\mathit{\text{ or }}i,j\in R_k\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$ (4)

where R_k is the k-th anatomical region.

Fig. 2.

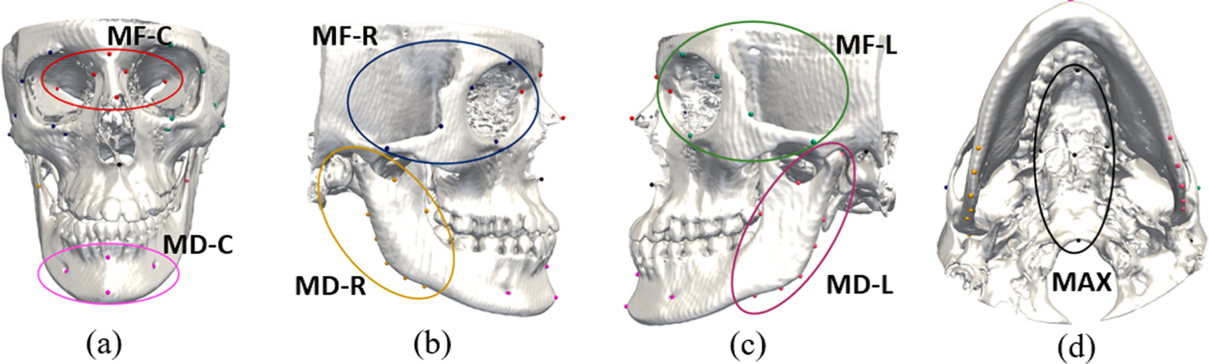
The illustrations of landmarks in 7 predefined anatomical regions shown in (a)–(d).

Our GCN consists of three graph convolutional layers as shown in Fig.1(b). Each layer takes feature $F_i\in R^{N\times M_i}$ and the adjacent matrix A as input, and outputs a high level feature $F_i^{\prime }\in R^{N\times M_i^{\prime }}$, where M_i and $M_i^{\prime }$ is the numbers of input and output feature channels, respectively. The output of each layer $F_i^{\prime }$ is calculated by the definition in [2]. Specially, the number of output feature channels $M_i^{\prime }$ is set to be 32, 16 and 2 for each layer. The first layer takes F₁ = F^att ∈ R^N×M and A as input, and the output of the last layer is $F_3^{\prime }=F^o\in R^{N\times 2}$, followed by a softmax activation layer. The training loss of GCN is defined as:

$$L_{GCN}=-\sum _{i=1}^N{\widehat{c}}_{i}log(\sigma \left(F_i^o\right)+\left(1-{\widehat{c}}_i\right)log\left(1-\sigma \left(F_i^o\right)\right)$$ (5)

where $\widehat{c_i}\in \left\{0,1\right\}$ is the ground truth of the existence of the i-th landmark, σ is the softmax activation. The total training loss of our network is:

$$L={\lambda }_A{L}_{\mathit{\text{AFEN}}}+{\lambda }_G{L}_{GCN}$$ (6)

where λ_A and λ_G are the training weights.

2.3. Implementation and Inference Procedure

At each stage, our detection network was trained by back-propagation and stochastic gradient descend (SGD) in an end-to-end manner. The initial learning rate was set to 0.001, decaying by 20% after every 5 epochs. The total number of training epochs was 20, and each epoch contained 12,000 iterations. For the first stage, to simplify the training, at the first 5 epochs, a large weight (λ_A = 1.0,λ_G = 0.3) was assigned for heatmap regression losses (i.e., (1)) to produce reliable attention maps. After that, we reduced the heatmap regression weights and increased the landmark existence classification weights, such as λ_A = 0.3,λ_G = 1.0. We first pre-trained our models using randomly selected 50 sets of normal spiral CT images (scanning matrix: 0.488×0.488 mm²; and slice thickness: 1.25mm) provided by clinic. After the pre-training, we subsequently trained our network using CBCT images of patient subjects. For training the network in the second stage, the training parameters were set exactly same as described in [3] with the size of input image patch as 64 × 64 × 64.

During the inference procedure, all landmarks on a testing CBCT image were jointly detected using the trained two-stage coarse-to-fine framework. From the second stage, we only sampled image patches centered at the algorithm-localized landmark positions from the previous stage (with the size of 64×64×64), that is, totally 60 image patches for each testing image, which can significantly reduce the time for testing. The trained model only takes around 1–3 min to process a CBCT volume (size: 536 × 536 × 440) for the joint prediction of 60 landmarks.

3. Experiments

3.1. Experimental Data and Methods

Our method was evaluated quantitatively using randomly selected 50 sets of CBCT images (resolution: 0.3 or 0.4 mm³ isotropically) from patients with non-syndromic jaw deformities from our digital archive of Oral and Maxillofacial Surgery Department at Houston Methodist Hospital. IRB approval was obtained prior to the study (Pro00013802). Each volume was larger than 536×536×440. Figure 3 shows an example. For each dataset, the midface and the mandible were manually segmented and 60 landmarks, with 33 on the midface and 27 on the mandible, were digitized and verified by two experienced CMF surgeons using the AnatomicAligner system [11]. 40% of our CBCT dataset are patients with defect due to imcompleted scaning or trauma. Using 5-fold cross-validation, we orderly selected 35 sets of data for training, 5 for validation, and the remaining 10 for testing. Prior to the training, the resolution of each dataset was resampled to 0.4 mm³ isotropically, and the intensity was normalized to the same distribution by histogram matching and Gaussian normalization constant (GNC). For training in the first stage, each image was down-sampled to a resolution of 1.6 mm³ and then padded to the size of 128×128×128. Resolution and size of image patch in the second stage is 0.4 mm³ and 64×64×64, respectively. Data augmentation (e.g. rotation, flipping) was also used to increase the training set and the robustness of our models. The landmark localization was completed under an environment of Intel Core i7–8700K CPU with a 12GB GeForce GTX 1080Ti graphics processing unit (GPU).

Fig. 3.

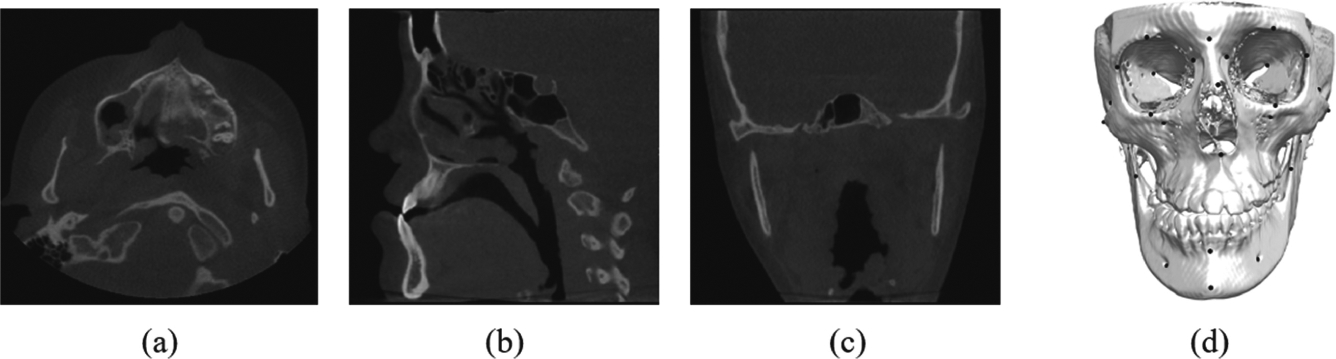
The illustrations of (a)–(c) the original image and (d) 60 landmarks on bony structure from a random subject in our dataset.

We quantitatively compared our method to three baseline deep-learning methods: 1) a basic U-Net proposed in [7]; 2) an extended Mask R-CNN proposed in [3]; and 3) a joint bone segmentation and landmark digitization (JSD) network proposed in [13]. The details of each method are described below.

1. U-Net: We used the same two-stage training strategy to train this network. The networks in the first and the second stages were trained with 128 × 128 × 128 images (resolution: 1.6 mm³ isotropically) and 96 × 96 × 96 image patches (resolution: 0.4 mm³ isotropically), respectively. Each landmark position was decided by the coordinates of the highest-value voxel in the predicted heatmap. All 60 landmarks were compared.

2. Extended Mask R-CNN: We used the same parameters and the three-stage coarse-to-fine training strategy introduced in [3] to train this network. The size of image (or image patches) in the three stages is 128×128×128 (resolution: 1.6 mm³ isotropically), 64 × 64 × 64 (resolution: 0.8 mm³ isotropically) and 64×64×64 (resolution: 0.4 mm³ isotropically), respectively. We also used the same predefined anatomical regions to model landmark dependencies. All 60 landmarks were compared.

3. JSD. We trained the network for landmark localization by using 96×96×96 image patches (resolution: 0.4 mm³ isotropically) as inputs. Network architecture and training parameters were set as those described in [13]. However, JSD method required a large amount of GPU memories for restoring displacement maps, which made it infeasible for detecting all 60 landmarks. Therefore, in JSD comparison, we only detected and compared 15 most clinically relevant landmarks, which were evenly located in 7 regions.

Root mean squared errors (RMSEs) and 95% of confidence intervals (95% Cis) were calculated. The false positive rate was also calculated by FP/(FP + TN), where FP and TN is the numbers of false positives and true negatives, respectively.

3.2. Results

Table 1 shows the comparison of the RMSEs and their 95% CIs between the algorithm-localized and ground-truth landmarks, where negative landmarks (the landmarks not existing) were also taken part into calculation (the ground truth of missing landmark location is set to be [0.0, 0.0, 0.0]). RMSE of using our proposed method was 1.47 mm, which was well within the clinical tolerance of 2 mm [12]. It also had the lowest FP rate of 19%, which showed the effectiveness of the proposed mechanism in determining the existence of negative landmarks by using GCN with the explicit modeling of local dependencies between landmarks and the attention features extraction.

Table 1.

Root mean squared error (mm) of landmark detection (on top) and the corresponding confidence intervals (on bottom) in the predefined 7 regions.

	MF-L	MF-C	MF-R	MAX	MD-L	MD-R	MD-C	Overall
U-Net in [7]	2.05 [1.66, 2.44]	1.54 [1.16,1.92]	3.83 [3.42, 4.24]	1.42 [1.08, 1.76]	3.85 [3.48, 3.92]	3.91 [3.53, 4.22]	2.04 [1.67, 2.41]	2.67 [2.33, 3.01]
M R-CNN in [3]	1.86 [1.73, 1.99]	1.58 [1.31, 1.85]	1.61 [1.45, 1.77]	1.57 [1.34, 1.79]	2.05 [1.74, 2.36]	2.41 [2.11, 2.71]	1.67 [1.34, 1.99]	1.82 [1.57, 2.17]
JSD in [13]	1.42 [1.32, 1.52]	1.38 [1.20, 1.56]	1.61 [1.50, 1.72]	1.32 [1.17, 1.47]	2.43 [2.15, 2.71]	2.37 [2.16, 2.58]	1.31 [1.23, 1.39]	1.69 [1.46, 1.92]
Our approach	1.63 [1.51, 1.74]	1.36 [1.16, 1.56]	1.58 [1.49, 1.67]	1.37 [1.19, 1.56]	1.41 [1.30, 1.52]	1.37 [1.24, 1.50]	1.35 [1.28, 1.42]	1.47 [1.26, 1.68]

In contrast, the results achieved with the U-Net had the largest RMSE of 2.67 mm, and reached the highest FP rate of 100% since this network was not capable of determining the landmark existence. The extended Mask R-CNN had a better accuracy than U-Net. However, the false positive rate was still very high (95%). For both methods, RMSEs in MF-L, MF-R, MD-L and MD-R were relatively higher than those in other regions due to the high FP. The results achieved with JSD method reached the accuracy of 1.69mm, and in some regions (MAX, MD-C) the accuracy is higher than those obtained by our approach. However, FP in MD-L and MD-R is still high (100%). Meanwhile, the high GPU memory cost made it difficult to be used for large-scale landmark detection. Nonetheless, this network was also not able to determine the missing landmarks.

Our approach took 1–3 min to jointly localize 60 landmarks from a large CBCT volume with the size of 536 × 536 × 440, while U-Net took 1–2 min, and the extended Mask R-CNN took 2–6 min. It took less than 1 min for JSD to detect 15 landmarks.

Figure 4 illustrates the results of three different subjects whose condition severity ranged from slight deformity, severe deformity, to discontinuity defects (partial anatomy was missing) using our method. No missing landmark was miss-detected.

Fig. 4.

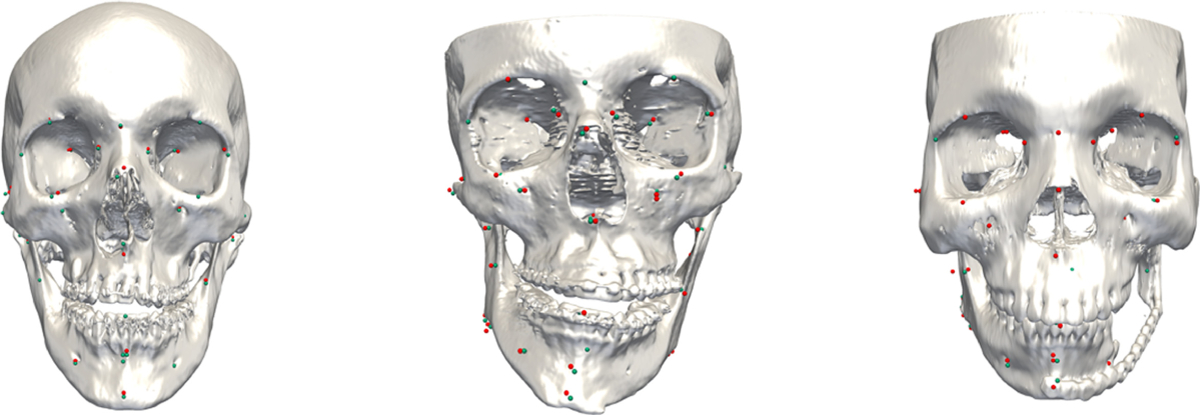
The results of landmark localization using our method. Condition severity of patients ranged from mild deformity, severe deformity, to discontinuity defect (partially missing anatomy). The detected landmarks are shown as red points, with the ground-truth landmarks shown as green points.

4. Discussion and Conclusion

In this work, we have proposed a two-cascade-network for digitizing 60 anatomical craniomaxillofacial landmarks on CBCT images. Specially, the first network, the U-Net, outputs the regressed heatmaps for localizing the landmark locations, as well as attention features extracted by a proposed extraction mechanism. The second network, Graph Convolution Network, takes the attention features with a designed adjacent matrix as input and outputs the existence of each landmark as a binary classification. The results of quantitative evaluation have proven the location accuracy and also the reduced false positive rate when our method was used. The proposed network can be trained in an end-to-end manner and output large-scale landmarks simultaneously.