A two‐stage neural network prediction of chronic kidney disease

Abstract

Accurate detection of chronic kidney disease (CKD) plays a pivotal role in early diagnosis and treatment. Measured glomerular filtration rate (mGFR) is considered the benchmark indicator in measuring the kidney function. However, due to the high resource cost of measuring mGFR, it is usually approximated by the estimated glomerular filtration rate, underscoring an urgent need for more precise and stable approaches. With the introduction of novel machine learning methodologies, prediction performance is shown to be significantly improved across all available data, but the performance is still limited because of the lack of models in dealing with ultra‐high dimensional datasets. This study aims to provide a two‐stage neural network approach for prediction of GFR and to suggest some other useful biomarkers obtained from the blood metabolites in measuring GFR. It is a composite of feature shrinkage and neural network when the number of features is much larger than the number of training samples. The results show that the proposed method outperforms the existing ones, such as convolutionneural network and direct deep neural network.

1. INTRODUCTION

Chronic kidney disease (CKD) has been an underestimated disease in the past decades. It has drawn the attention of researchers since it became a globally existing health issue, which leads to an outcome of severe kidney failure and other subsequent diseases [1]. In most clinical laboratories or medical institutions, a commonly used standard of assessment of the stage of CKD is via the measured glomerular filtration rate (mGFR, by iohexol plasma clearance), which is nearly equal to the total filtration rates of the functioning nephrons in the kidney [2]. However, mGFR is difficult to be used widely as an index of assessment of the level of CKD since its measurement is not only expensive but also time consuming. In clinical practice, it is usually approximated by estimated glomerular filtration rate (eGFR), which is a response variable fitted by other features collected from patients, such as age, weights, and serum or plasma indicators. Inker et al. [3] proposed the CKD‐EPI creatinine‐cystatin C equation, which improves the classical estimation of GFR from using creatinine or cystatin C alone as an explanatory variable. Other further research works, synthesise new attributes into this benchmark equation attempting to improve the estimation accuracy [4, 5, 6].

Machine learning methods have been introduced to detect the stage of CKD. Krishnamurthy et al. [7] found that the Convoluted Neural Network outperforms other existing machine learning approaches when predicting the tendency that a patient may suffer from CKD in the coming 6 to 12 months. Salekin and Stankovic [8] implemented a feature selection by both state‐space search algorithm and least absolute shrinkage and selection operator (LASSO) before predicting by the neural network. Similarly, Chimwayi et al. [9] predicted the risk that a patient may have CKD by Neuro‐Fuzzy and Hierarchical Clustering algorithm associated with random‐forest feature selection preprocessing. Chen et al. [10] proposed an adaptive hybridised deep convolutional neural network (CNN) to detect the early stage of CKD. Instead of selecting a subset of most important features, they conducted a dimensional reduction before plugging data into the Neural Network. Some tried to modify the one‐step algorithm to avoid the over‐fitting issue. For instance, Zhang et al. [11] chose to learn the data by a so‐called LASSO Preset Neural Network, which is a multi‐layer problem associated with a Lasso regulariser.

The modern machine learning approaches, although attractive, impose a common assumption that the sample size should be much greater than the number of attributes. Those works consider an appropriate range of 20–30 features, which induces a subjective pre‐selection issue. When thousands of features are extracted from a blood sample and limited samples are available within a region, a method to deal with an ultra‐high dimensional prediction problem is imperative. To address this issue, this study provides empirical evidence by adopting a two‐stage machine learning approach on an ultra‐dimensional training data‐set. The methodologies for preprocessing feature selection include LASSO, smoothly clippedabsolute deviations (SCAD), iterative sure independent screening (ISIS), robust rank correlation‐based screening (RRCS) and partial least squares (PLS). We use the one‐layer Neural Network structure to train our processed data. In fact, many modifications help in prediction performance, such as dropout‐layer. We leave a more complex design for future investigation since our emphasis here is to evaluate the improvement by two‐stage setting from a direct application of machine learning.

2. MATERIAL AND METHODS

2.1. Data

A total of 198 participants (96 females, 48.5%), in Macau SAR, China, with varying degrees of renal dysfunction were tested using Ultra‐High Performance Liquid Chromatography‐Tandem Mass Spectroscopy. Mean age was 58.2 ± 18.5 years (range 18–96 years). The mean body‐mass index was 24.2 ± 4.2 kg/m² (range 15.0–48.6 kg/m²). Mean serum creatinine was 1.82 ± 2.01 g/L (range 0.42–10.79 mg/L). An analysis of blood metabolites was conducted in the Calibra‐Metabolon Joint Laboratory, Hangzhou, China, using Metab‐olon's HD4 Discovery untargeted metabolomics platform in the early 2021.

These collections include 1094 features in the form of peak areas obtained from blood metabolites. In contrast with other studies using concentrations as attributes, the introduction of peak area data provides new insight into the prediction of CKD. Moreover, although we exclude some basic features such as age, sex, weight, and height, for reasons that we believe a large enough feature set could potentially capture all basic individual information, we hope their statistics to locate at a similar range.

Considering the uncertainty induced by small sample data, we fit the models and carry out prediction by a fivefold cross‐validation setting. That is, the original data‐set is divided into five partitions with sizes 39 or 40. A selected partition is treated as a test set while the remaining four partitions are combined as a training set, and this process will be repeated five times until each partition is used as the test set exactly once. In Table 1, we list an example of their statistics by cross‐validation for reference. Finally, all metrics obtained from test sets are averaged as prediction errors.

TABLE 1.

Summary of mGFR and basic features

Target variable and basic information	Training and validation set	Test set
mGFR – ml/min/1.73 m2 of body‐surface area	59.1 ± 32.0	60.8 ± 33.6
Age – years	59.0 ± 18.5	56.2 ± 18.4
Weight – kg	63.5 ± 14.1	65.4 ± 11.7
Height – cm	161.9 ± 9.4	162.1 ± 8.8
Male sex – no. (%)	82 (51.9)	20 (50.0)

Note: Values associated with plus‐minus sign are sample mean ± sample standard deviation.

Abbreviation: mGFR, measured glomerular filtration rate.

Before plugging data in feature selectors, we have to deal with missing data and data preprocessing. We excluded the features with more than 20 percent of missing data, finally 1012 features are included for in the model fitting. Besides, the missing data of the remaining features are filled by the training sample mean. Then, the training sample is standardised by training sample mean and standard deviation. In particular, to avoid using out‐of‐sample information, data preprocessing does not involve any information from the test sample.

2.2. Methodologies

In this section, we provide detailed descriptions of the machine learning methodologies, for both the feature selection stage and the prediction stage, respectively. Before proceeding to a specific methodology, we exhibit a general model for the prediction of mGFR.

Denote X as an N × p matrix of collected input variables that contains N samples with p individual features information. Namely, X _i,j denotes the j ^th explanatory feature of the i ^th sample. Additionally, an N‐dimensional vector Y is denoted as the corresponding set of the response variables. To distinguish the test set and training set, we further denote τ ₁ and τ ₂ as the training and test samples, respectively. Define |⋅| to be the cardinal number of the given set. Clearly, |τ ₁| + |τ ₂| = N.

In our study, |τ ₁| ∈ {158, 159}, |τ ₂| ∈ {39, 40}, depending on the division by cross‐validation, and p = 1012, which implies a fact of ultra‐high dimensional problem, that is, the size of samples available for training is much smaller than the number of features (|τ ₁| ≪ p). To address this issue, our first step is to filter less useful features and to reduce the dimension of input features, that is, reduce p to p* so that p* ≤ |τ ₁|. We denote the new set of input features after selection by $Z\in {\mathbb{R}}^{N\times p^{*}}$ with corresponding k ^th column $Z_{\cdot ,k}\in {\mathbb{R}}^N$, k = 1, …, p*. Thus, we express the process of feature selection by Z _i,. = g(X _i,⋅), where i ∈ τ ₁ and g(⋅) is the feature selector. Considering the tradeoff between model complexity and out‐of‐sample performance, we choose p* = 20. We will provide an empirical explanation of our choice of p* in Section 3.

The second step is to predict the value of mGFR by plugging the remaining ‘useful’ features obtained in the first step into the fitted model. In summary, our fitted model can be expressed as follows:

$$Y_i=f(Z_{i,\cdot })+{ϵ}_i=f(g(X_{i,\cdot }))+{ϵ}_i,$$ (1)

where f is the prediction function describing either the linear or non‐linear relationship between the input features in Z and the response variable Y. Subscript (i, ⋅) denotes the corresponding i ^th row of matrices, and Y _i is the i ^th element in Y with i ∈ τ ₁. ϵ _i is the random error assumed to have zero mean. Our target is to find a prediction function $\widehat{f}$ conditional on feature selector g with the given initial input features in X _i,⋅, so that the in‐sample error is minimised. The general form of prediction model is then written as follows:

$${\widehat{Y}}_i=\widehat{f}(g(X_{i,\cdot })).$$ (2)

A detailed pictorial illustration of our proposed two‐stage methodology is exhibited in Figure 1. In the following subsections, we provide statistical models for the machine learning methods.

FIGURE 1.

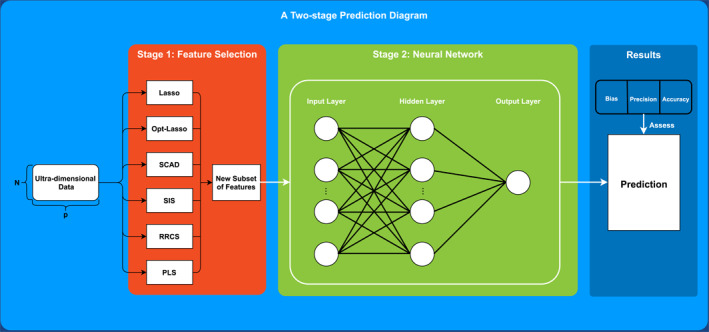
A methodology workflow which illustrates how a two‐stage neural network prediction is implemented. An ultra‐high dimensional data will be inputted into the first stage and reformed into matrices of lower dimensions by a feature selection approach. Then, predictions are obtained from a neural network in the second stage fed by the new subset of features. Finally, all predictions are assessed by three metrics

2.2.1. Lasso

Lasso, proposed by Tibshirani [12], has become one of the most well‐known methods that perform with both variable selection and regularisation. The classic Lasso approach is expressed as the following optimisation problem:

$$\begin{array}{c}\widehat{\beta }=\underset{\beta }{\mathrm{argmin}}\left\{\frac{1}{2}\sum _{i\in {\tau }_1}{\left(Y_i-X_{i,\cdot }\cdot \beta \right)}^2\right\},\\ \text{subject}\text{to}\Vert \beta {\Vert }_1\le C,\end{array}$$ (3)

where, β is a p‐dimensional vector of feature loadings which is identical to all samples indexed by i ∈ τ ₁, and ‖⋅‖₁ is the L ¹−norm of the given vector. C ≥ 0 is a tuning parameter determining the magnitude of shrinkage on features. The problem can be equivalently rewritten as the form of a Lagrange equation

$$\begin{array}{c}\widehat{\beta }=\underset{\beta }{\mathrm{argmin}}\left\{\frac{1}{2}\sum _{i\in {\tau }_1}{\left(Y_i-X_{i,\cdot }\cdot \beta \right)}^2+\lambda \Vert \beta {\Vert }_1\right\},\end{array}$$ (4)

where, the second term is associated with a Lagrange multiplier λ ≥ 0 that is called the penalty term playing a similar role as the parameter C in Equation (3). By solving Equation (4), the absolute value of solution $\widehat{\beta }$ is the desired variable importance. We set λ to vary from 0.001 to 1 with equal step size 0.001. The larger the λ, the more features are shrunk to zero. In this article, we employ two different ways to implement the Lasso algorithm as introduced in Section 1. One is the Lasso with preset hyper‐parameter λ, so that the number of features is directly shrunk to p* = 20. In our study, λ is finally set to be 0.04. The other way is using the Optimal‐Lasso that allows Lasso reach its optimisation automatically without pre‐determining the value of λ. Thus, the number of features surviving from this selection procedure is subsequently either smaller or larger than p*. We choose the top 20 features with largest variable importance if more than 20 features are left, or all features otherwise.

2.2.2. Smoothly clipped absolute deviation

SCAD, proposed by Fan and Li [13], provides a parametric Lasso‐type framework of feature regularisation with a non‐convex penalty. Given two constants γ > 2 and λ > 0, the SCAD uses a composite penalty for β as follows:

$$Q(\beta |\gamma ,\lambda )=\left\{\begin{array}{cc}\lambda |\beta |,\hfill & \text{if}\beta \le \lambda \hfill \\ \frac{2\gamma \lambda |\beta |-{\beta }^2-{\lambda }^2}{2(\gamma -1)},\hfill & \text{if}\lambda <|\beta |<\gamma \lambda \hfill \\ \frac{{\lambda }^2(\gamma +1)}{2},\hfill & \text{if}|\beta |\ge \gamma \lambda \hfill \end{array}\right..$$ (5)

In particular, Q(β|γ, λ) is differentiable on $\mathbb{R}/0$ with derivative vanishing when |β|≥ γλ. The SCAD penalty remains an identical shrinkage intensity when coefficients are smaller than tuning parameter λ, but processes a sparse and unbiased estimator for large coefficients. For the SCAD, we also obtained 20 most important features.

2.2.3. Sure independence screening

When p ≫ N, penalised feature selection, such as Lasso and SCAD, may work poorly, see Wang and Leng [14]. An efficient approach to reduce the dimensionality, called Sure Independent Screening (SIS), has been developed by Fan and Lv [15], aiming at selecting features in the scenario of ultra‐high dimensional data. Instead of shrinking insignificant features, SIS ranks features by their marginal correlation with the target variable, which is associated with the Pearson correlation. The construction of SIS for selecting p* features is as follows:

$${\mathcal{M}}_{p^{*}}=\{1\le i\le p:|{\omega }_i|\text{is}\text{among}\text{the}\text{first}p*\text{largest}\text{of}\text{all}\},$$

where, p* is the number of feature subset after selection, ω _i is the i ^th entry of vector ω = X ^⊤ Y. SIS is rather simple to implement. In the meantime, it easily omits some important features from the true sub‐model, as pointed out by Fan and Lv [15]. To avoid this issue, an extension of SIS is also provided by Fan and Lv [15] named Iterative SIS (ISIS). ISIS conducts a large‐scale screening to select a relatively larger subset of survival features in advance, and obtains the in‐sample residuals by regressing response over those features. Then, it is followed by a moderate‐scale screening as a second step, in which residuals are regressed over a new smaller subset of features. This process is repeated until we obtain 20 survival features as the result of selection. Specifically, we set the number of iterations to be at most 10 to avoid oversize iteration.

2.2.4. Robust rank correlation‐based screening

Similar to SIS, RRCS adopts the same idea of non‐parametric feature selection. SIS‐type selection is not robust against outliers, and additionally, fails to depict the non‐linearity between target and explanatory variables. Motivated by SIS, RRCS, proposed by Li et al. [16], provides an alternative feature screening method associated with a non‐parametric correlation coefficient based on Kendall's τ. The term ‘Robust’ implies its advantage of handling noise made by outliers, which is especially beneficial to data with a limited sample size. Rather than Pearson correlation, the RRCS ranks the following statistics:

$${\omega }_j=\frac{1}{|{\tau }_1|(|{\tau }_1|-1)}\sum _{i\ne m}{\mathbb{1}}_{\{X_{i,j}<X_{m,j}\}}{\mathbb{1}}_{\{Y_i<Y_m\}}-\frac{1}{4},$$ (6)

for j = 1, …, p, where ${\mathbb{1}}_{\{A\}}$ defined the indicator function, namely, 1 if the event A is true and 0 if false. Given a predefined threshold value ${\gamma }_{p^{*}}$, p* features satisfying $|{\omega }_j|\ge {\gamma }_{p^{*}}$ are selected, and we chose p* = 20.

2.2.5. Partial least squares

PLS method is famous for its efficiency when the number of features exceeds the number of available training subsamples, proposed by Wold et al. [17]. It is similar to the principal component analysis (PCA). The PCA reduces dimension merely on explanatory variables, but PLS selects components considering both response and explanatory variables.

According to Wold's PLS algorithm, we first compute the projection of Y on each feature X _⋅,j , j = 1, …, p, to compute the coefficient φ _j , and repeat this procedure for all features. Then, the solution of PLS, proposed by Hastie et al. [18], is an iterative procedure, the m ^th PLS direction α _m solves:

$$\begin{array}{ll}\hfill \underset{\alpha }{\max }& {\text{Corr}}^2(Y,X\alpha )\text{Var}(X\alpha )\hfill \\ \hfill & \text{subject}\text{to}\Vert \alpha \Vert =1,{\alpha }^{\top }{X}^{\top }X{\alpha }_k=0,k=1,\text{…},m-1.\hfill \end{array}$$ (7)

The optimal solution within the training sample returns a p × K matrix Ω _K with columns α ₁, …, α _K collecting K directions. In addition, we allow for the preset parameter K to vary from 1 to 10 and determined by validation performance. Identical to Lasso and SCAD, we choose the first 20 features with the highest absolute value of coefficients.

The next subsection is a brief introduction of the Single‐layer Perceptron Network, which is the second stage of our algorithm. In the case of an ultra‐high dimensional feature data being reformed into a new subset through effective feature selection, we plug subset into this easy‐to‐be‐implemented neural network and compare their performance against a benchmark of direct neural network approach.

2.2.6. Prediction: Neural network

On both classifications of the stage of CKD and prediction of mGFR, Neural Network is the most popular machine learning methodology [7, 19, 20, 21]. Existing works, however, all equip neural network with structural modifications with predetermined feature data. To exhibit a straightforward improvement in performance by the two‐stage method, we use the simplest single‐layer perceptron network without any modification for reducing overfitting such as dropout layer and penalisation.

In the following sections, we provide a brief description of the neural network with one hidden layer. Suppose that a single hidden layer network includes p input units and N _h hidden units; the input and output of hidden layer, denoted by h _input and h _output, respectively, are calculated by the following:

$$h_{input}=w_{input}{X}^{\top },h_{output}=f(h_{input}),$$ (8)

where $w_{input}\in {\mathbb{R}}^{N_h\times p}$ is the weight matrix mapping from input layer to hidden layer, and f(⋅) represents the pre‐determined logistic activation function. Then, the prediction of response, $\widehat{Y}\in {\mathbb{R}}^N$, can be modelled by

$$\widehat{Y}=g(w_{output}{h}_{output}),$$ (9)

where $w_{output}\in {\mathbb{R}}^{N_h}$ is the hidden‐to‐output weight matrix and g(⋅) is an output function that transforms the linear combination of the hidden layer's outputs into predicted values.

This neural network can be easily realised by the R package neurualnet [22]. In specific, the algorithm chosen to compute the network is the resilient back‐propagation with weight backtracking. In each iteration, the components in the weight matrix are updated according to the consecutive sign of activation's partial derivative. We set the maximum number of iterations as 10⁵, and the threshold of stopping criteria is set to be 0.01. That is, the training will stop either when the gradient descent updated is less than the threshold, or when the number of steps reaches the maximum.

In the next section, we will show our empirical results of prediction performance by the two‐stage Neural Network approach associated with all feature selection methods mentioned above.

3. RESULTS

The overarching result is feature selection. We present all features selected in form of a heat plot in Figure 2. Names placed in the left column are features surviving from the procedure of selection. The colours in blocks imply corresponding variable importance. Creatinine is the most frequently selected biomarker with the highest average feature importance among all methodologies. This result coincides with many previous biological and medical researches such as Inker et al. [3]. Other features, among which are seldom or even never discovered their significance in previous studies, contribute to the variation of response as well.

FIGURE 2.

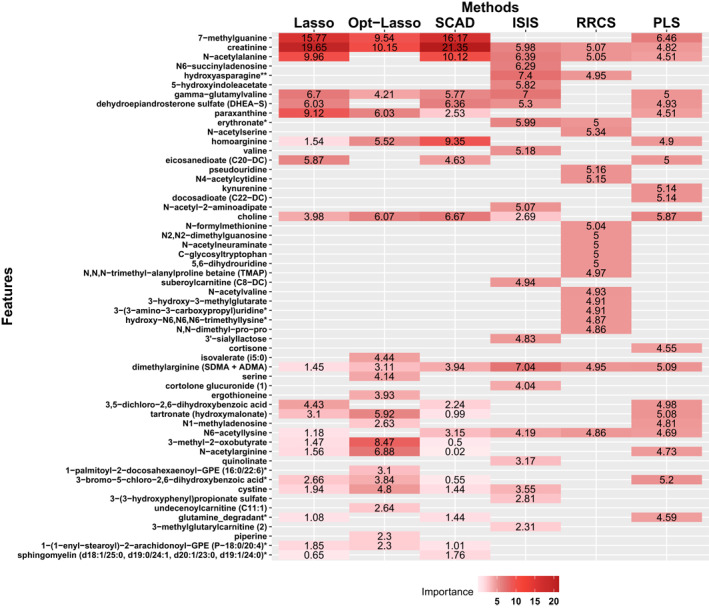
Result of feature selection by all mentioned methodologies, where the y‐axis collects all included features' name and the x‐axis lists all feature selection methods. Feature placed in the y axis is in the order of their average importance among all methods, in which features on top carry out relatively higher importance while those on the bottom have the less influence

Before proceeding to the comparison of prediction performance, we briefly introduce our metrics from three dimensions that includes bias, precision, and accuracy. It is worth reminding that all metrics are computed within the test subsamples in cross‐validation, which measures models' out‐of‐sample explanatory power. Bias is calculated as the median of the difference between eGFRs and mGFRs where negative values imply overestimation, measuring the degree of central tendency of prediction performance. The second metric of our interest is the precision, calculated by interquartile range (IQR), which is the difference between upper and lower quartiles of difference of the eGFRs and mGFRs. The final metric is the accuracy (RMSE) which is the squared root of mean squared error.

All results are shown in Tables 2 and 3. Table 2 reports the RMSE induced by model with different tuning parameters p* and N _h . The estimation results is obtained from a fivefold cross‐validation. It is clear that among all feature selection methods, N _h  = 1 is a superior choice. For p*, when p* = 10 and p* = 15, the average RMSE is relatively higher than others. By letting p* = 20 and p* = 25, we receive a similar error in average. For convenience and lower computational cost, we choose p* = 20 eventually.

TABLE 2.

This table reports the results of root mean squared errors obtained from the fivefold cross‐validations, allowing hyper‐parameter p* to take values of either 10, 15, 20 or 25 and the number of neurons to vary from 1 to 10

Number of features	Number of neurons	Lasso	Opt‐Lasso	SCAD	ISIS	RRCS	PLS	Average
p* = 10	1	13.45	13.88	13.61	14.11	14.02	16.06	14.19
	2	14.22	14.60	13.89	15.38	13.21	16.79	14.68
	3	16.01	16.05	13.93	16.26	14.38	18.58	15.87
	4	16.79	16.71	17.12	17.98	13.82	19.23	16.94
	5	19.16	18.88	18.86	18.07	13.89	22.48	18.56
	6	19.40	19.75	18.49	18.77	14.75	20.47	18.60
	7	20.90	22.05	20.07	17.73	15.35	23.69	19.97
	8	20.95	25.21	21.53	18.97	14.59	25.08	21.06
	9	23.40	24.88	23.19	20.02	15.10	25.82	22.07
	10	23.81	24.45	24.51	21.11	15.05	27.00	22.65
p* = 15	1	12.61	14.00	14.84	11.95	13.43	14.85	13.61
	2	14.67	16.41	17.08	16.11	13.49	16.40	15.69
	3	14.99	17.80	18.79	33.59	13.92	17.95	19.51
	4	18.36	19.19	19.83	14.05	13.99	21.67	17.85
	5	20.29	19.30	19.73	15.50	13.57	21.04	18.24
	6	19.12	22.52	25.30	16.63	13.86	22.37	19.97
	7	22.13	21.83	23.51	20.71	14.89	24.87	21.32
	8	22.58	27.18	27.93	19.64	14.20	27.56	23.18
	9	23.70	24.30	26.81	19.23	32.70	27.15	25.65
	10	25.86	23.65	28.75	23.78	14.88	27.15	24.01
p* = 20	1	13.18	12.53	14.79	11.62	13.46	14.01	13.27
	2	15.00	14.15	16.92	11.77	14.25	14.92	14.50
	3	16.97	15.41	20.40	14.27	14.70	17.99	16.62
	4	18.98	17.86	22.78	14.51	13.74	19.45	17.89
	5	19.78	23.64	23.30	16.64	16.54	20.53	20.07
	6	24.12	25.05	25.56	18.36	16.21	22.26	21.93
	7	22.29	24.40	27.99	22.96	16.60	24.90	23.19
	8	22.89	22.32	26.23	20.51	17.13	25.07	22.36
	9	24.55	26.13	31.14	23.81	18.65	22.84	24.52
	10	22.95	22.10	27.20	24.27	20.42	24.96	23.65
p* = 25	1	12.34	11.59	15.38	12.04	13.62	14.19	13.19
	2	15.29	14.22	16.81	13.70	13.79	17.06	15.15
	3	16.28	15.64	22.77	14.05	14.19	19.13	17.01
	4	19.23	19.37	23.38	19.38	15.72	20.76	19.64
	5	22.13	22.32	27.89	17.99	16.89	24.15	21.89
	6	25.09	21.34	25.46	19.56	16.25	23.51	21.87
	7	26.03	24.94	29.91	20.42	18.29	23.60	23.86
	8	26.20	24.63	30.52	20.43	16.87	27.11	24.29
	9	26.20	23.07	27.97	21.03	19.59	25.96	23.97
	10	24.45	23.46	24.52	22.00	20.14	25.12	23.28

Abbreviations: ISIS, iterative sure independent screening; PLS, partial least squares; RRCS, robust rank correlation‐based screening; SCAD, smoothly clippedabsolute deviations.

TABLE 3.

This table shows the results of prediction performance by fivefold cross‐validation estimations

Metrics	Lasso	Opt‐Lasso	SCAD	ISIS	RRCS	PLS	CNN	Direct DNN
Bias	−0.23	−0.57	−0.43	−0.59	−0.98	−0.11	−0.56	−1.96
IQR	10.06	10.81	12.17	9.66	8.95	10.79	13.46	21.51
RMSE	13.18	12.53	14.79	11.62	13.46	14.01	16.65	25.52

Abbreviations: CNN, convolutional neural network; DNN, deep neural network; IQR, interquartile range; ISIS, iterative sure independent screening; PLS, partial least squares; RRCS, robust rank correlation‐based screening; SCAD, smoothly clippedabsolute deviations.

We then turn to the prediction performance in Table 3, in which we evaluate the superiority of the two‐stage approach over the existing methods. We choose the neural network without feature selection (deep neural network [DNN]) as a benchmark. In the meantime, based on the latest study by Krishnamurthy et al. [7] exhibiting that CNN outperforms other machine learning methods, we also include CNN as a benchmark for comparison. To be specific, we allow DNN to automatically choose the number of neurons in validation. We follow the setting of CNN in Krishnamurthy et al. [7], that is, letting numbers of filters = 3, filter size = 1, and keeping 32 units in the dense layer. All results of metrics are estimated by cross‐validation as well.

For specifically chosen one hidden neuron and 20 input variables, feature selection by PLS carries out a lowest bias of −0.11 ml per minute per 1.73 m². According to precision, RRCS outperforms other approaches with 8.95 per minute per 1.73 m² IQR, exhibiting its advantage of dealing with ultra‐high dimensional feature data. In addition, ISIS also performs competitively. It carries out the lowest RMSE of 11.62 per minute per 1.73 m², and performs with the second lowest IQR. In general, a two‐stage algorithm outperforms a direct application of Neural Network and CNN prediction.

4. DISCUSSION

In this study, we employ some commonly used feature screening methods in machine learning, in detecting the effective and useful features obtained from the blood metabolism, to measure the mGFR.

Traditional models in biological and medical studies are usually built based on researchers' prior knowledge, regarding an expensive cost in learning either linear or non‐linear relationship between response variable and attributes. On the contrary, machine learning techniques do not need human specialists in characterising different properties from distinct sources of data. It automatically filters the less useful information and learns from their complex situation. Machine learning approaches have been extensively employed under this framework. Almansour et al. [19] predicted CKD by Neural Network and Support Vector Machine. Kriplani et al. [20] predicted CKD by Neural Network. Pasadana et al. [23] summarised some commonly used decision tree algorithms and evaluated their performances of predicting CKD. Recently, on the topic of CKD prediction and classification, many studies have shown the improved prediction ability of using various machine learning techniques, compared with the traditional models [7, 8, 9, 10, 11, 19, 20, 21, 23]. Most of them, compared with the traditional CKD detection equations, also present superior in the accuracy of classification.

Since each of the feature screening method has its advantages, as we see in the results, the six methods yield different ranks of the important features; this creates a difficulty to get an overall rank which accounts for the results from all methods. To cope with this issue, we suggest a novel score‐based approach to further rank the important features. According to the final results, this score‐based ranking approach indeed exhibits a satisfactory performance. By doing this, we want to keep as few as important features in predicting the GFR to improve the predictability in the neural networks. In fact, since the neural network is also capable of dealing with many features simultaneously, one may also apply the neural networks to all of the features, or to the combined features detected by six feature screening methods, without using the score‐based approach. Nevertheless, according to our experience and also shown by other literature, the full model usually does not perform well, particularly if many features are redundant in explaining the output. This is indeed true for our dataset, we can see that most of the features have a very low correlation with the eGFRs.

This is the first attempt of combining feature screening in the ultra‐high dimensional framework and deep learning approach, there are many possible extensions based on this work. First, besides the score‐based feature selection method, one may also employ the idea of boosting approach to directly combine many feature screening methods. Second, because of the success of the random forest method, particularly in the medical studies, we can consider the combination of the feature screening and random forest method.

5. CONCLUSION

In this research, we study the prediction of mGFR, which is a key problem in the diagnosis and treatment of CKD. Among the 1012 features obtained from the blood metabolome of about 200 people in South China, we proposed a new two‐stage prediction method for mGFR, which is a combination of the feature screening method in the ultra‐high dimensional framework and deep learning approach. The proposed approach is able to assist to detect the stage of CKD and identify potentially useful biomarkers. The two‐stage method consists of six different feature selection approaches and demonstrates the superiority over direct machine learning without feature selection. Among the six feature screening methods, we recommend the partial least squares and ISIS approaches, since the features detected by these two approaches are more robust to the peculiar data points. Moreover, our findings also suggest some extra biomarkers (7‐methylguanine, creatinine, N‐acetylalanine) that are useful in measuring the glomerular filtration rate.

CONFLICT OF INTEREST

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Peng, H. , et al.: A two‐stage neural network prediction of chronic kidney disease. IET Syst. Biol. 15(5), 163–171 (2021). 10.1049/syb2.12031