Anisotropic nanomechanical properties of bovine horn using modulus mapping

Abstract

Bovine horns are durable that they can withstand an extreme loading force which with special structures and mechanical properties. In this study, the authors apply quasi‐static nanoindentation and modulus mapping techniques to research the nanomechanical properties of bovine horn in the transverse direction (TD) and longitudinal direction (LD). In quasi‐static nanoindentation, the horn's modulus and hardness in the inner layer and the outer layer demonstrated a gradual increase in both TD and LD. Laser scanning confocal microscopy revealed microstructure in the horn with wavy morphology in the TD cross‐section and laminate in the LD cross‐section. When using tensile tests or quasi‐static nanoindentation tests alone, the anisotropy of the mechanical properties of bovine horn were not obvious. However, when using modulus mapping, storage modulus (E ′), loss modulus (E ″) and loss ratio (tan δ) are clearly different depending on the position in the TD and LD. Modulus mapping is proposed as accurately describing the internal structures of bovine horn and helpful in understanding the horn's energy‐absorption, stiffness and strength that resists forces during fighting.

1 Introduction

The continuous evolution of an animal is a way for the animal to adapt itself to the nature of environmental change. The existence of a horn is an important product of the evolution of Bovidae. Typically, the horns are not shed annually but grow continuously by the proliferation of germinal layer cells [1]. Because of this mode of formation, horn has special structures and distinguishing functions. Bovine horn is a keratinised structure [2]; keratin is the main constituent of vertebrate skin, hair, horns, feathers and feet and has a greater toughness compared with other natural biological materials [3]. These keratinised tissues are typically responsible for the protecting epithelial cells against mechanical stress [4]. However, the horn is different from other structural biological materials, such as bones, tusks, teeth, antlers and mollusk shells. It is composed of α‐keratin crystalline filaments embedded in an amorphous protein (mostly non‐crystalline keratin) matrix [5]. State the reasons why horn is different to other structures.

For most bovid animals, the horns must be strong and durable, as they are subjected to extreme loading impacts during the life of the animal and, unlike antlers, will not grow back if broken. From the analysis of optical micrographs of cross‐sections perpendicular and parallel to the growth directions, the tubules appear to extend continuously in the growth direction and are shaped to form small delaminated regions between the lamellae [6]. Over the past few decades, in addition to the study of structure, researchers have performed a series of uniaxial tension, three‐point bending, and fracture tests to investigate the structural and mechanical properties of the horn sheaths of cattle [5, 7, 8, 9]. The effects of the water content, sampling position and the orientation of a bovid horn on the mechanical properties have been systematically investigated, and the bending properties, flexural moduli and yield strength of the samples varied along the length of the horn [8]. The Young's modulus and tensile strength of the specimens increases threefold from a 19% water content to a 0% water content calculated from the load/displacement curve [10]. Static and dynamic compression tests have shown that the compressive moduli and the yield strengths of horn pieces decrease from the distal end to the proximal end of the horn [11]. These techniques provide valuable information on the bulk mechanical properties of an individual horn and have helped to characterise the strength, extensive ability, and toughness of many different horns; taken together, these findings further deepen our understanding of the relationships between optimal structures, properties and functions of cattle horns.

Nanoindentation is a novel technique originally developed to measure the mechanical properties of biomaterials. Because of its small probe size, this technique can be used to measure local material properties in small, thin, and heterogeneous samples and has been used to measure the mechanical properties of microstructural features, to investigate variations in mechanical properties with changes in tissue and to spatially map mechanical properties in complex biomaterials [12, 13, 14, 15, 16]. Static indents can be analysed to enable the determination of the viscoelastic response by setting different loading functions, which produce responses that vary according to the viscoelasticity of the biomaterial, but these tests are affected by the surface size and the indenter shape [17]. Dynamic nanoindentation is another approach used to determine the viscoelastic properties that permits measurement of the storage modulus (E ′), the loss modulus (E ″) and the loss tangent (tan δ) at frequent intervals during the test [18, 19]. The storage and loss moduli in viscoelastic materials measure the stored energy, which represents the elastic portion and the energy dissipated as heat. These measures describe the changes in the properties of the biomaterials either in terms of the effect of changing the frequency [20] or of changing the dynamic and static force. Modulus mapping is a method of dynamic testing by superimposing a sinusoidal force onto the quasi‐static force and recording the displacement amplitude and phase as the surface is scanned with a piezo scanner and a force modulation system [21, 22]. The frequency of the sinusoidal force is selected to be greater than the response of the feedback loop controller to prevent the feedback loop system from affecting the measured displacement [23]. This force modulation technique is used to map the local variation of the nano‐mechanical properties of the sample. The properties are shown in topographic information, the storage and loss stiffness, E ′ and E ″, and the tan δ maps obtained from a single scan. Therefore, this method allows for the measurement of mechanical characteristics in the vicinity of individual interfaces [24]. Modulus mapping has also been used to study the surface topography and mechanical properties of the junctions between and hard tissues adjacent to teeth [25]; to characterise the elasticity of extremely thin soft layers of a biological composite, specifically the anchor spicule of the glass sponge Monorhaphis chuni [26]; and to perform nanomechanical characterisations of living cells (human osteoblasts) and cell–substrate constructs under physiological conditions [27].

Most biomaterials are anisotropic, hence in this study, the viscoelastic properties of bovine horn in the transverse direction (TD) and the longitudinal direction (LD) were measured using quasi‐static and dynamic nanoindentation techniques (Fig. 1). Herein, the localised quasi‐static and dynamic nanomechanical properties are discussed in relation to the microstructure and the function of bovine horn. The goal was to map the two‐dimensional spatial distribution of E ′ and E ″ as a function of the indent position along different directions in a bovine horn. Determining the distribution of these properties should shed further light on the nanomechanical properties of key structural features. In fact, future high‐energy absorption materials could simulate the distribution of nanomechanical properties exhibited by the bovine horn.

Fig. 1.

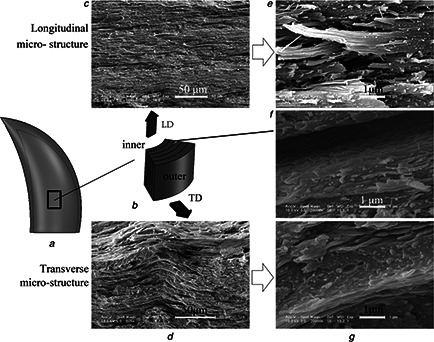
Most biomaterials are anisotropic, hence in this study, the viscoelastic properties of bovine horn in the TD and the LD were measured using quasi‐static and dynamic nanoindentation techniques

a Captured specimen position in the horn

b Schematic of the micro‐structure of the specimen

c –f LSCM images in the TD and the LD

g Micro‐structure of the layer interface in the TD

2 Materials and methods

2.1 Specimens

The horn specimens from male bovines (Bos taurus L.) approximately 2 years in age (shown in Fig. 1 a) were collected from a slaughter house in the city of Changchun, Jilin Province. The horns samples were prepared in Experimental Animal Center of Jilin University. The thickness of the keratin shell decreased from the tip to the base of the horn. We obtained specimens 7 mm above the base and away from the cutting point to avoid the structures that were affect by the cutting operation. The thicknesses of specimens were 3 to 8 mm. The specimens were initially cut into small pieces in both the TD and the LD using a precision cutting machine (IsoMet^® 1000, Buehler Inc.).

After air drying, the keratin sheath and the bone core naturally detached from each other. Laser scanning confocal microscopy (LSCM, OLYMPUS OLS3000) was used to investigate the microstructure of the bovine horn cross‐sectioned in the TD and the LD.

Appropriate grinding and polishing of specimens can reduce the effect of roughness for nanoindentation testing. The sliced specimens were then embedded in resin and were subsequently polished using a Grinder‐Polisher (MetaServ 250, Buehler Inc.). First, using 1000 grit SiC paper, the specimen surface was roughly ground for approximately 5 min until completely exposed. Subsequently, polishing cloths with different diamond suspensions as small as 0.3 μm were used and were followed by a mixed polishing liquid containing silicon oxide abrasive (0.05 μm) and alumina abrasive (0.02 μm) (at a ratio of 2:3) applied using a polishing micro‐cloth. Distilled water was used as the coolant, and deionised water was used for 10 min ultrasonic treatments. The final step of specimens preparation was drying the specimens in a low‐temperature oven, and all measurements were conducted under dry conditions.

2.2 Nanoindentation

The indentation technique was carried out using a nanoindenter (TriboIndenter, Hysitron Inc.) with a triangular pyramidal diamond Berkovich indenter (the tip radius was 100 nm).

Initially, it was necessary to calibrate the nanoindenter transducer with the indenter tip before each experiment. For the quasi‐static nanoindentation tests, a controlled load was applied to the specimens, and the resulting E _r and H were analysed from the slope of the unloading segment of the load‐displacement curve using the Oliver–Pharr indentation measurement principle [28]. E _s of the tested materials are obtained by the E _r which is called reduced modulus [29]. The equation of E _r as follow

$$E_{\mathrm{r}}=\frac{\sqrt{\pi }}{2\beta }\frac{S}{\sqrt{A}}$$ (1)

Where A is the indenter tip contact area, S is the slope of the upper portion of the unloading curve and β is related to the shape of indenter tip which Berkovich indenter tip is 1.034 as constant. E _s is related to the reduced modulus E _r of a test specimen through the following relationship derived from contact mechanics: $1/E_{\mathrm{r}}=\left(1-{\upsilon }_{\mathrm{s}}^2\right)/E_{\mathrm{s}}+\left(1-{\upsilon }_i^2\right)/E_i$ (where E_i and υ_i are the elastic modulus and Poisson's ratio for a diamond tip and are equal to 1114 GPa and 0.07, respectively). That is, E _s ≃ E _r.

In the quasi‐static nanoindenation experiments, the indenter was driven into the surface at a constant loading rate of 500 µN/s until a peak load (P _max) of 1500 µN was achieved. A 20 s hold period was applied to allow for suitable viscoelastic settling of the indenter in contact with the composite surface. In the nanoindentation experiment, six indentation measurements were conducted, and the mean value was used as the nanomechanical parameter for each corresponding measurement position.

Nano‐dynamic mechanical analysis applies a cycle of sinusoidal manner to the surface of a sample in nanoindentation. With the help of a lock‐in amplifier, the alternating displacement response is measured at a determinate frequency during the test. It is loss modulus, storage modulus, and tan δ that were calculated from the values of the load amplitude, displacement amplitude, and the phase lag which were measured during the test. Properties of materials can be expressed by modulus, stiffness and a mechanical damping by dynamic nanoindentation. Damping indicates the dissipation of energy in a material under sinusoidal load, which is reported as the tangent of the phase angle, telling mechanical properties of a material about absorbing energy. Stiffness is another value used to describe behaviours of material, which is a measure of the resistance offered by an elastic deformation. The complex modulus that is a measure of the materials resistance to deformation performances both in‐phase and out‐of phase response of the sample, from which the storage modulus (E ′) and the loss modulus (E ″) can be calculated, respectively. While, the storage modulus (E ′) and the loss modulus (E ″) are a measurement of the elastic energy stored and energy lost severally. The relevant equation are given below [30].

$$E^{\ast }=E^{\mathrm{\prime }}+i{E}^{\mathrm{\prime }\mathrm{\prime }}$$ (2)

$$E^{\mathrm{\prime }}=\frac{k_{\mathrm{S}}\sqrt{\pi }}{2\sqrt{A_{\mathrm{C}}}},E^{\mathrm{\prime }\mathrm{\prime }}=\frac{\omega C_{\mathrm{S}}\sqrt{\pi }}{2\sqrt{A_{\mathrm{C}}}}$$ (3)

$$\tan \delta =\frac{E^{\mathrm{\prime }\mathrm{\prime }}}{E^{\mathrm{\prime }}}=\frac{\omega C_{\mathrm{S}}}{k_{\mathrm{S}}}$$ (4)

Here k _s is the stiffness of the specimen, C _s is the damping coefficient of the specimen, and A _c is the projected contact area of indent on the surface of the specimen.

Modulus mapping allows quantitative nanoscale mapping of the elastic moduli by means of a hybrid nanoindentation and force modulation instrument [23]. A dynamic test was performed at each point on the image, and these tests resulted in a high‐resolution, two‐dimensional map of the storage and loss moduli for different material systems, which resolved sub‐micron sized structural features with dissimilar elastic and viscoelastic characteristics [22, 23, 24]. Modulus mapping can perform nanomechanical characterisations of living cells (human osteoblasts) and cell–substrate constructs under physiological conditions [27].

In this study, modulus mapping measurements were taken using a Hysitron TriboIndenter with a diamond Berkovich tip (the same equipment that was used in the quasi‐static experiment). A lock‐in amplifier analysed the signal coming from the displacement transducer and determined the amplitude and phase shift relative to the sinusoidal excitation force signal. These data were sent to the acquisition and analysis software, which calculated the contact stiffness and the damping using a dynamic model. The sample was brought into contact with the diamond tip at a constant contact force of 1–2 µN, the indentation depths for this force are 6–8 nm, and scanning area is 5 × 5 µm. To obtain the stiffness image, the indenter tip was modulated with a sinusoidal force of 2 µN at 200 Hz and a scanning rate of 0.1 Hz.

3 Results and discussion

Bovine horn is not entirely homogeneous, as observed by LSCM (Fig. 1). Fig. 1 a shows a schematic of the cross‐sectional morphology of the horn. Fig. 1 b shows extensive parallel wavy laminates. Some laminates form one layer, and there are some tubules among the laminates in the TD. The thickness of the layers is similar. In the LD, the microstructure shows primarily parallel laminates and layers (Fig. 1 c). Fig. 1 d shows details in the TD, and there are many truncations, which are possibly residues of fibres after being stretched and breaking. Similar phenomena can be observed in Fig. 1 e. Therefore, bovine horn fibres can be concluded to be laminated in one direction and intersected in a different direction. In the TD, because the specimens were dry before being measured using LSCM, there was a peeling phenomenon between lamellae, which means the structures between the laminates are relatively loose. In the interface of the layers, as shown in Fig. 1 f, there are fewer truncations compared with the TD as well as an irregular fringe ridge distribution. It can be deduced that, because the possibility exists that the interfaces are strong but some phases lose considerable amounts of water that cause significant volume decreases, resulting in extremely high interfacial shear stresses; the relatively low strength plays a role in buffer structure, which is compounded with the buffer material matrix organisation of this high‐strength fibre bundle with good elasticity, which makes the horn difficult to break. In addition to friction between the layers will also dissipate a portion of the energy.

Quasi‐static nanoindentation testing results in the TD and the LD are shown in Fig. 2. In Figs. 2 a and b, the abscissa shows the spacing of the testing points from the inner layer to the outer layer in the TD. Fig. 2 a shows that reduced modulus (E _r) and hardness (H) of the horn in the TD demonstrate a gradual increase from the inner layer to the outer layer. E _r ranges from 8.42 to 12.99 GPa, and H ranges from 0.41 to 1.02 GPa from the innermost layer to the outermost layer, respectively, which is an increase of 54.28 and 148.78%. Under the same experimental parameters, the change in E _r and H in the LD have a similar trend as in the TD (Fig. 2 b).

Fig. 2.

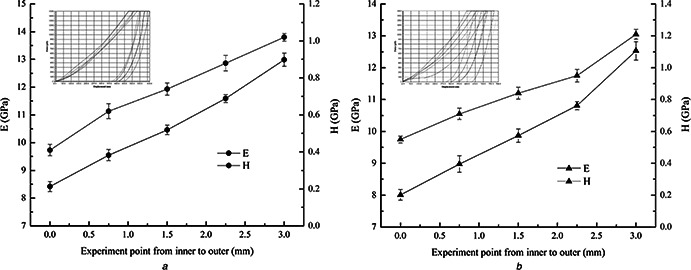
Quasi‐static nanoindentation testing results in

a TD

b LD, respectively

Table 1 summarises the mean storage modulus (E ′), loss modulus (E ″) and loss ratio (tan δ) obtained from the modulus mapping technique in the TD and the LD. The mean E ′, E ″ and tan δ were calculated from the value of each image (5 × 5 μm scan size, 256 × 256 indents). E ′ and E ″ in the TD were 28.80 ± 14.85 GPa and 0.41 ± 0.09 GPa, and in the LD, E ′ and E ″ were 27.30 ± 19.58 GPa and 0.13 ± 0.04 GPa, respectively. Tan δ is the ratio of E ″ to E ′, where δ is the phase angle between the sinusoidally varying stress and strain. This measure represents the internal friction. The value of tan δ was 0.052 ± 0.04 and 0.020 ± 0.01 in the TD and the LD, respectively.

Table 1.

Modulus mapping results (frequency of 200 Hz) of the bovine horn cross‐sections in the TD and the LD. E ′, E ′′ and tan δ are reported as the means ± standard deviation

Specimens	E ′, Gpa	E ′′, Gpa	tan δ
TD	28.80 ± 14.85	0.41 ± 0.09	0.052 ± 0.04
LD	27.30 ± 19.58	0.13 ± 0.04	0.020 ± 0.01

Fig. 3 shows images from the modulus mapping in the TD and the LD (5 × 5 µm scan size, 256 × 256 indents). The various distributions of E ′, E ″ and tan δ values correspond to the position in the TD and the LD. As shown in Fig. 3, the microstructure of the fracture surfaces is different in the TD (Figs. 3 a –c) and in the LD (Figs. 3 e –f). Fig. 3 a clearly demonstrates that the bovine horn has dense laminates and wavy structures in the TD, which is further shown in Fig. 1 c.

Fig. 3.

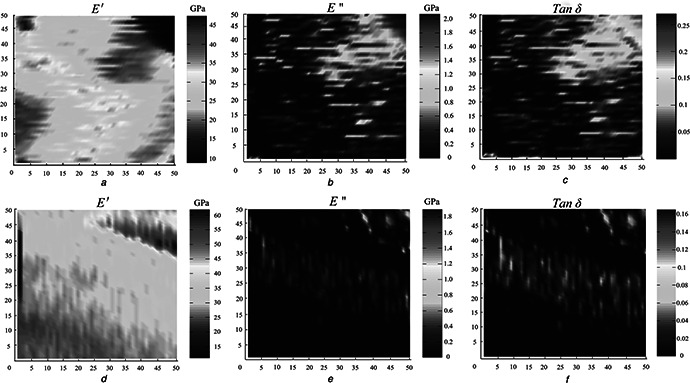
E′, E″ and tan δ in the

a –c TD

d –f LD for the horn section collected using modulus mapping at 200 Hz

From the inner layer to the outer layer in the LD, both E _r and H demonstrate a linear growth trend and increase at 56.43 and 120%, respectively. E _r ranges from 8.01 to 12.53 GPa, and H ranges from 0.55 to 1.21 GPa from the innermost layer to the outermost layer, respectively. E _r and H from the inner layer and the outer layer in the TD and the LD are similar. The anisotropy of the mechanical properties of the horn is not clear. From the quasi‐static indentation, these experimental data demonstrate that the mechanical properties of the horn are different in different directions; however, the values are closely related to the measurement positions. When the measurement position is the innermost layer, E _r and H are minimal and increase as the measurements extend outward. This is not the case in the TD, but it is the case in the LD.

The mean Young's modulus of the samples at 0% water content was approximately 2.34 ± 0.12 GPa, which is significantly greater than when the horn had an 8% water content (1.56 ± 0.06 GPa) or a 19% water content (0.85 ± 0.09 GPa). These moduli were determined using uniaxial tension tests [7]. These values are less than the values captured during nanoindentation. The mechanical characteristic values of cattle horn gradually increase from the base of the horn to the tip [8]. In other words, the modulus of the specimen is related to measurement position in the horn. This relationship is a possible reason why the values determined from macroscopic testing are less than the values determined through nanoindentation, or the larger samples taken into account larger structural levels when there are any compliant interfaces or porosity this would lead to lower modulus (this is similar in bone). The results obtained from the tensile tests of the horn may be subject to the composite effects of multiple layers. However, in the nanoindenation tests, we can clearly determine the gradient effect of the mechanical properties of the horn in TD. This difference may be related to the energy absorption. We know that horns are sometimes used for fighting, hence the horn must be adequate to absorb and dissipate energy during a collision. As shown in Fig. 1, there are fibres that form a layer, and the thickness of the outer layer is greater than the thickness of the inner layer. Under an external load, the greater mechanical properties in the lateral portion of the horn can bear a greater load whereas the inner smaller parts can act as a buffer to avoid inner bone core damage. Increasing the amount of material away from the neutral axis of the horn, increases its structural stiffness. The mechanical structure can improve the light load resistance properties of the horn.

The water content of the horn can also affect the horn's mechanical properties [7]. Dry horn keratin is more sensitive to the presence of cracks and may rupture at a relatively low strain level. Furthermore, an increase in the moisture content increases the rate of wear [31]. A greater modulus and hardness, which is perhaps caused by the dry horn keratin, can decrease the bovine horn durability and decrease the modulus and the hardness. Keratin with a greater moisture content, compared with the outer layer, may protect the horn from fracture. The specimens used in the nanoindentation tests were dry, hence the E _r values were slightly greater.

E ′ is greater than E _r in both directions (8.42 GPa vs. 12.99 GPa). The value of E ′ is a measure of how elastic a material is and is ideally equivalent to elastic modulus (E _s) (E _s ≃ E _r); however, this relation does not hold in actuality. For materials with insignificant damping, E ′ is equivalent to E _s [32]; for a viscoelastic material, E ′ is certainly different from E _s. Therefore, it can be deduced that there is damping in a horn. The elastic properties in the TD are similar to the elastic properties in the LD and were 5.49% greater. E ″ is related to the damping behaviour of a material and can be acquired from the time lag between the maximum force and the maximum displacement. This damping is the amount of energy applied to the sample during indentation that is dissipated by various processes that facilitate energetic loss, which is mostly plastic deformation. This property, E ″, is shown in Table 1. E ″ is 215.38% greater in the TD than in the LD. The damping characteristics in the TD are greater than in the LD, which means the energy absorption is greater. In addition, the greater E ″ in the TD compared with the LD could be due to a different concentration of lamellae. The high value of tan δ indicates that vibrational damping is high; conversely, a low value indicates a highly elastic behaviour with minimal energy losses [33]. As shown in table 1, the values in the TD and LD are 0.052 and 0.020, respectively, which means that the tan δ value in the TD was 160% greater than in the LD. A greater value of this ratio suggests that the material response in the LD was more elastic with a minimal energy loss, which means that the ability of the horn to bear stress in the TD is greater than in the LD. As a result, the TD is more viscoelastic than the LD. This difference is a result of greater energy dissipation as heat when the TD is deformed compared with the LD. The higher loss modulus of intertubular dentin compared to enamel and peritubular dentin is due to high concentration of collagen fibrils in the dentin matrix and more viscoelastic than both enamel and peritubular dentin which results in dentin less prone to fracture [25]. Hence the greater loss modulus makes the TD less prone to fracture, which result is the reason that the horn can resist high stress without breaking, which allows the animal to use the horn to attack and for protection.

Because of the wide distributional range of the values of E ′, E ″ and tan δ, as shown in Table 1, we compared these values with the images from the modulus mapping. At the centre of the wavy structure, the value of E ′ is greater. This result means that the interfaces between layers play a buffering role. The horn forms a stable progressive failure mode under pressure, can absorb energy through plastic buckling, and is a buffering absorption structure. In addition, because the smallest E ′ existed at the interfaces, these areas are easily fractured, which agrees with Fig. 1 f, as this result is closely related to the water content. In the upper right‐hand side corner, there is a portion of a tubule, as shown in Figs. 3 b and c, and the maximum of E ″ and tan δ are on the edge of the tubule. In the upper left‐hand side corner of Fig. 3 d, there is a fractured lamella that is irregular and crowded together in the LD. Figs. 3 e and f reveal a layer in the LD. The modulus mapping revealed anisotropy in the mechanical properties of the bovine horn. It is clear to see that the micro‐structures and mechanical properties are different in the TD and the LD. This technique will be accurate in describing the internal structures of the horn and will be helpful in understanding the horn's energy‐absorbing mechanism.

4 Conclusions

This work used nanoindentation techniques to study the mechanical and structural properties of the bovine horn in two orientations. In the quasi‐static nanoindentation tests, E _r and H of the horn gradually increased from the inner layer to the outer layer in both the TD and the LD. This gradient effect helps absorb and dissipate energy. In addition to determining the mechanical properties, modulus mapping can also illustrate the micro‐structural features of the bovine horn in the TD and the LD. Furthermore, from the modulus mapping images of the surface morphology of the horn in the TD and the LD, some internal details of the horn were clearly observed. These data cannot be obtained by quasi‐static nanoindentation test alone and have clearly demonstrated the anisotropy of the bovine horn. Further, accurate description of the horn's internal structures will be helpful in understanding its energy‐absorbing mechanism.