Abstract
Color polymorphism—two or more heritable color phenotypes maintained within a single breeding population—is an extreme type of intraspecific diversity widespread across the tree of life. Color polymorphism is hypothesized to be an engine for speciation, where morph loss or divergence between distinct color morphs within a species results in the rapid evolution of new lineages, and thus, color polymorphic lineages are expected to display elevated diversification rates. Multiple species in the lizard family Lacertidae are color polymorphic, making them an ideal group to investigate the evolutionary history of this trait and its influence on macroevolution. Here, we produce a comprehensive species-level phylogeny of the lizard family Lacertidae to reconstruct the evolutionary history of color polymorphism and test if color polymorphism has been a driver of diversification. Accounting for phylogenetic uncertainty with multiple phylogenies and simulation studies, we estimate an ancient origin of color polymorphism (111 Ma) within the Lacertini tribe (subfamily Lacertinae). Color polymorphism most likely evolved few times in the Lacertidae and has been lost at a much faster rate than gained. Evolutionary transitions to color polymorphism are associated with shifts in increased net diversification rate in this family of lizards. Taken together, our empirical results support long-standing theoretical expectations that color polymorphism is a driver of diversification.[Color polymorphism; Lacertidae; state-dependent speciation extinction models; trait-dependent diversification.]
Understanding how diversity is generated and maintained within and across species is a fundamental goal of evolutionary biology. Color polymorphism, or the presence of two or more distinct genetically determined color phenotypes within a breeding population (Huxley 1955; Gray and McKinnon 2007), exemplifies extraordinary intraspecific phenotypic diversity. Despite its usefulness in developing population genetic theory (Ford 1945; Huxley 1955; Svensson 2017), relatively little is known about the evolutionary origins and macroevolutionary consequences of color polymorphism (Gray and McKinnon 2007; Jamie and Meier 2020). A longstanding hypothesis is that the presence of different genetically based color morphs within populations may promote speciation (West-Eberhard 1986; Jonsson 2001; Gray and McKinnon 2007; Corl et al. 2010a, 2010b; Hugall and Stuart-Fox 2012; McLean et al. 2014). In this scenario, a group of distinct morphs is established within a population, phenotypic variation among morphs gradually accumulates, and over time isolated populations with different morphs diverge, facilitating speciation (West-Eberhard 1986). Studies of color polymorphisms spanning fish (Jonsson 2001; Seehausen and Schluter 2004; Allender et al. 2003), birds (Hugall and Stuart-Fox 2012), and reptiles (Corl et al. 2012) all suggest the evolution of multiple variable morphs as an impetus for speciation. However, after more than 50 years of research, few comparative studies exist that test this claim (but see Hugall and Stuart-Fox 2012).
The origins and maintenance of color polymorphism have long been subjects of fascination in evolutionary biology (Huxley 1955; West-Eberhard 1986; Roulin 2004; Stuart-Fox et al. 2020). Understanding the evolution of stable color polymorphisms has been difficult because the processes involved seem to operate across multiple biological scales—ranging from within and among population processes within species (reviewed in Gray and McKinnon 2007) to convergence and divergence in color polymorphisms among species (reviewed in Stuart-Fox et al. 2020). Theoreticians have argued that evolutionary branching events (e.g., population divergence, speciation) provide a useful framework for generating predictions and testing alternative hypotheses regarding the likelihood that phenotypic polymorphisms evolve, persist, or diverge (West-Eberhard 1986; Leimar 2005). Leimar (2005) posited that multiple genetically determined phenotypes, or morphs, are less likely to persist within one lineage at an evolutionary branching event because a polymorphic system is inherently less stable than a monomorphic one. Indeed, studies of color polymorphic species have consistently found that some form of balancing selection is required for multiple discrete phenotypes to persist over evolutionary timescales (Sinervo and Lively 1996; Pérez i de Lanuza et al. 2017). Further, empirical studies have found that geographic variation in the number and types of morphs among populations is usually explained by morph loss from populations, with little evidence for gaining morphs back (Corl et al. 2010b; Sacchi et al. 2007). In a phylogenetic context, we would thus expect novel gains of color polymorphism to evolve at a slower rate than monomorphism and that color polymorphism is lost at a faster rate than monomorphism across a phylogeny of species or populations (Corl et al. 2010b; Hugall and Stuart-Fox 2012). Given this, on a phylogenetic tree, we would expect ancestral state reconstructions of the evolutionary history of color polymorphism to produce a pattern of ancestral polymorphic lineages diversifying and giving rise to monomorphic lineages.
A phylogenetic comparative approach can be leveraged to test the hypothesis that color polymorphism is a driver of diversification (Morlon 2014; Morlon et al. 2020). First proposed by Huxley (1955), many theoretical (West-Eberhard 1986; Forsman et al. 2008) and empirical studies (Boughman 2001; Corl et al. 2010b) in groups across the tree of life have followed that also suggest multiple color morphs within species should lead to faster formation of new species (reviewed in Gray and McKinnon 2007). Forsman et al. (2008) present a series of ecological and evolutionary scenarios where color polymorphic species should have the greater evolutionary potential for speciation compared to monomorphic species. According to Forsman et al. (2008), the evolution of multiple color forms within a population may increase the evolutionary potential for speciation through increased utilization of diverse habitats and resources, and greater ability to successfully colonize and expand their range relative to monomorphic populations. Coupled with divergent selection, either natural, sexual, or their combination, alternative morph phenotypes spread across variable geographic contexts may increase the chance for unbalanced morph frequencies, rapid phenotypic divergence, and speciation (reviewed in McLean and Stuart-Fox 2014). Most well-studied color polymorphic species, from moths to lizards, exhibit population differences in the number and frequency of morphs (Grant et al. 1998; Corl et al. 2010b; Stuart-Fox et al. 2020; Chelini et al. 2021). Consensus from field studies of natural populations suggest that the disruption of balancing selection for multiple color morphs usually results in morph loss, and divergence in remaining morphs may progress quickly toward speciation (Galeotti et al. 2003; Corl et al. 2010b). If color polymorphic species are engines of speciation, then net diversification rates (speciation–extinction) should be greater within color polymorphic lineages compared to monomorphic lineages. To date, the claim that color polymorphism promotes diversification has largely gone untested at the macroevolutionary level. A single study by Hugall and Stuart-Fox (2012) found that in three of five families of nonpasserine birds investigated, speciation rates were higher in color polymorphic lineages than monomorphic lineages. More comparative studies of speciose groups that have multiple independent origins of color polymorphism are needed to evaluate hypotheses of color polymorphism maintenance and its role in diversification.
Lizards from at least seven different families have repeatedly and independently evolved a similar color polymorphism on the head, throat, and/or ventral region (Stuart-Fox et al. 2020), which makes this trait ideal for comparative analysis. The lizard family Lacertidae (Oppel 1811) is an excellent group for a comparative study on the evolution of color polymorphism as the group is relatively speciose and multiple species spanning several genera are known to be color polymorphic (Vercken and Clobert 2008; Huyghe et al. 2009a, 2009b; Runemark et al. 2010; Brock et al. 2020). Biologists have identified a similar throat color polymorphism in several genera across the family Lacertidae (Fig. 1), including Iberolacerta monticola (López et al. 2009), Podarcis species (P. erhardii, Brock et al. 2020; P. gaigeae, Runemark et al. 2010; P. melisellensis, Huyghe et al. 2009a, 2009b; P. muralis, Pérez i de Lanuza et al. 2019), and Zootoca vivipara (Vercken and Clobert 2008). The Lacertidae is the most speciose family of squamates in the Western Palearctic comprising around 320 species distributed across Africa, Asia, and Europe (Arnold et al. 2007). While lacertids share a relatively similar body plan, they occur in a variety of habitats from xeric desert lands to montane forests, range widely in their geographic distributions, and exhibit diverse ecologies (Edwards et al. 2012; Garcia-Porta et al. 2019). The family currently comprises two major taxonomic subgroups, the Gallotiinae and the Lacertinae. Lacertinae is further divided into two tribes, the Eremiadini and the Lacertini. There is likely some undescribed taxonomic diversity in both the Eremiadini and Lacertini tribes. This undescribed diversity is due to lack of molecular data and undersampling in the Eremiadini and under-reported species-level diversity in the Lacertini which contains many geographically isolated subspecies and species with extraordinarily large geographic distributions, some on the order of several continents (Herczeg et al. 2003). These factors, combined with short internal branches and gene tree discordance, have made family-wide species-level phylogenetic inference for the Lacertidae difficult (Fu 2000; Arnold et al. 2007; Pyron et al. 2013; Baeckens et al. 2015; Garcia-Porta et al. 2019). However, the opportunity to leverage new data (Garcia-Porta et al. 2019) and analytical approaches mean the Lacertidae is now an ideal group for a comparative study on the evolution of color polymorphism.
Figure 1.
Throat color polymorphism in Podarcis erhardii (Brock et al. 2020), a Mediterranean lacertid species. In lacertid lizards, 43 species spanning several genera exhibit a similar color polymorphism. Across all lacertid species in our study, color polymorphism is expressed at adulthood as colorful badges ventrally on the throat or belly region.
In this study, we infer the evolutionary relationships among species in the family Lacertidae to reconstruct the evolutionary history of color polymorphism and test whether the evolution of this trait is associated with diversification rate shifts. We build a comprehensive species-level phylogeny of the Lacertidae, including 262 species from all 42 described genera. We apply a multispecies coalescent approach that accounts for potential individual gene histories among species (in contrast to approaches used in previous studies, Fu 2000; Arnold et al. 2007; Pavlicev and Mayer 2009). Using this species-level tree, a distribution of possible trees from the posterior, a recently inferred time tree from Garcia-Porta et al. (2019), and trait simulations, we conduct the first family-wide investigation of color polymorphism in lizards. We identify previously undescribed color polymorphic lacertids and assess long-standing hypotheses concerning the evolutionary origins and consequences of this trait. Specifically, we address the following questions: 1) What is the evolutionary history of color polymorphism in the Lacertidae? 2) Do color polymorphic lineages have elevated rates of diversification compared to noncolor polymorphic lineages?
Materials and Methods
Phylogenetic Inference of the Lacertidae
GenBank data
We used publicly available sequence data from GenBank to build our tree (Clark et al. 2016). We first pulled all Lacertidae single gene sequences from GenBank and identified five genetic markers for which there were at least 100 species with data for that marker. This filtering resulted in three mitochondrial genes (12s:  species; 16s:
species; 16s:  species; cytochrome b: 239 species) and two nuclear genes (mos proto-onco gene:
species; cytochrome b: 239 species) and two nuclear genes (mos proto-onco gene: 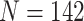 species; recombination activating gene (RAG) 1:
species; recombination activating gene (RAG) 1: 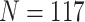 species). Genes selected from the mitochondrial genome have been used extensively for phylogenetic reconstruction of Lacertidae in the past (Fu 2000; Edwards et al. 2012; Pyron et al. 2013; Baeckens et al. 2015; Baeckens et al. 2017), and the RAG-1 nuclear gene has been shown to evolve at a greater rate than other commonly used nuclear markers, which may allow for greater confidence both deep within the tree and at the tips (Portik et al. 2012; Edwards et al. 2012). To ensure taxonomic validity, sequences were georeferenced to verify they fell within species distributions as described on the regularly updated lacertid database, AG Lacertiden (www.lacerta.de, maintained by The Arbeitsgemeinschaft Lacertiden within the Deutsche Gesellschaft für Herpetologie und Terrarienkunde). Overall, we retrieved gene sequences for 262 lacertid species—approximately 82% of described lacertid diversity according to the AG Lacertiden database, covering all currently described genera (Arnold et al. 2007). Details of genetic data used per species and GenBank accession numbers for each genetic marker are provided in Supplementary Table S1 available on Dryad at https://doi.org/10.5061/dryad.k0p2ngf68. Sequences were aligned separately in AliView (v.1.25) using MUSCLE (v.3.8.425) with default parameters. Gene sequence alignments were then assessed for appropriate models of molecular evolution for tree inference using the Akaike Information Criterion in jModelTest (v.2.1.10) using default parameters (Darriba et al. 2012).
species). Genes selected from the mitochondrial genome have been used extensively for phylogenetic reconstruction of Lacertidae in the past (Fu 2000; Edwards et al. 2012; Pyron et al. 2013; Baeckens et al. 2015; Baeckens et al. 2017), and the RAG-1 nuclear gene has been shown to evolve at a greater rate than other commonly used nuclear markers, which may allow for greater confidence both deep within the tree and at the tips (Portik et al. 2012; Edwards et al. 2012). To ensure taxonomic validity, sequences were georeferenced to verify they fell within species distributions as described on the regularly updated lacertid database, AG Lacertiden (www.lacerta.de, maintained by The Arbeitsgemeinschaft Lacertiden within the Deutsche Gesellschaft für Herpetologie und Terrarienkunde). Overall, we retrieved gene sequences for 262 lacertid species—approximately 82% of described lacertid diversity according to the AG Lacertiden database, covering all currently described genera (Arnold et al. 2007). Details of genetic data used per species and GenBank accession numbers for each genetic marker are provided in Supplementary Table S1 available on Dryad at https://doi.org/10.5061/dryad.k0p2ngf68. Sequences were aligned separately in AliView (v.1.25) using MUSCLE (v.3.8.425) with default parameters. Gene sequence alignments were then assessed for appropriate models of molecular evolution for tree inference using the Akaike Information Criterion in jModelTest (v.2.1.10) using default parameters (Darriba et al. 2012).
Species tree inference and divergence dating estimation
We employed a multilocus coalescent approach for species tree inference as individual gene histories can vary within closely related species (Maddison 1997; McCormack et al. 2009). To do this with our five locus alignments, we used the full Bayesian method of species tree estimation in BEAST2 using the *BEAST template (v.2.5.1) (Heled and Drummond 2010; Bouckaert et al. 2014). We unlinked all site and molecular clock models and linked the gene tree models for mtDNA alignments only. We used the GTR I site model for each gene according to model comparison results from jModelTest with all frequencies set to empirical and no additional parameters estimated for computational efficiency. For all genes, we specified an uncorrelated relaxed molecular clock with a log-normal distribution that assumes each branch has its own independent rate (Drummond et al. 2006). The species tree population size function was set to linear with constant root and population mean set to 1.0. We set the species tree prior to a Yule Model (pure-birth) with a log-normal distribution on the species birth rate. Prior distributions for all gene clock-rate priors were set to exponential, and the population mean prior was set to log-normal. To time-calibrate the phylogeny, we used the “Sampled Ancestors” package in BEAUti2 to generate monophyletic taxon set hyperpriors according to fossil information from the literature (Hipsley et al. 2009). Time-calibrated outgroup nodes following Hipsley et al. (2009) include: 1) Sphenodon punctatus—Cnemidophorus tigris, 228.0 Ma (Sues and Olsen 1990), 2) Cnemidophorus tigris—Rhineura floridana, 113.0 Ma (Nydam and Cifelli 2002), and 3) Rhineura floridana—Gallotia galloti, 64.2 Ma (Sullivan 1985). All fossil hyperpriors were offset by the above dates, given a log-normal distribution with a mean of 1.0 and standard deviation of 1.25, and constrained to be monophyletic. We ran two independent species tree analyses with the same data and XML configuration for 1 billion MCMC generations and stored every 30,000th sampled tree. Posterior distributions of trees for the two independent BEAST2 runs were combined in BEAST2’s logCombiner (v.2.5.1) with the first 20% of trees discarded as burn-in and the rest of the trees resampled at a lower frequency for a total posterior sample of 12,000 trees. A final maximum clade credibility tree, the tree from the reduced posterior sample that had the maximum sum of posterior probabilities on its
I site model for each gene according to model comparison results from jModelTest with all frequencies set to empirical and no additional parameters estimated for computational efficiency. For all genes, we specified an uncorrelated relaxed molecular clock with a log-normal distribution that assumes each branch has its own independent rate (Drummond et al. 2006). The species tree population size function was set to linear with constant root and population mean set to 1.0. We set the species tree prior to a Yule Model (pure-birth) with a log-normal distribution on the species birth rate. Prior distributions for all gene clock-rate priors were set to exponential, and the population mean prior was set to log-normal. To time-calibrate the phylogeny, we used the “Sampled Ancestors” package in BEAUti2 to generate monophyletic taxon set hyperpriors according to fossil information from the literature (Hipsley et al. 2009). Time-calibrated outgroup nodes following Hipsley et al. (2009) include: 1) Sphenodon punctatus—Cnemidophorus tigris, 228.0 Ma (Sues and Olsen 1990), 2) Cnemidophorus tigris—Rhineura floridana, 113.0 Ma (Nydam and Cifelli 2002), and 3) Rhineura floridana—Gallotia galloti, 64.2 Ma (Sullivan 1985). All fossil hyperpriors were offset by the above dates, given a log-normal distribution with a mean of 1.0 and standard deviation of 1.25, and constrained to be monophyletic. We ran two independent species tree analyses with the same data and XML configuration for 1 billion MCMC generations and stored every 30,000th sampled tree. Posterior distributions of trees for the two independent BEAST2 runs were combined in BEAST2’s logCombiner (v.2.5.1) with the first 20% of trees discarded as burn-in and the rest of the trees resampled at a lower frequency for a total posterior sample of 12,000 trees. A final maximum clade credibility tree, the tree from the reduced posterior sample that had the maximum sum of posterior probabilities on its  internal nodes, was generated in BEAST2’s TreeAnnotator for use in comparative analyses.
internal nodes, was generated in BEAST2’s TreeAnnotator for use in comparative analyses.
The Evolutionary History of Color Polymorphism and Diversification in the Lacertidae
Color polymorphism data
We scored the presence or absence of color polymorphism for all described extant lacertid species ( ), including those not represented in our phylogeny. Examination of all extant taxa, including species lacking available genetic data and not represented in our phylogeny, was necessary to account for trait estimation proportions downstream in our state-dependent speciation and extinction (SSE) models. We scored color polymorphism from several georeferenced sources to ensure taxonomic validity, including online databases with photographs (www.inaturalist.org, www.lacerta.de), scientific literature (Huyghe et al. 2009a, 2009b; López et al. 2009; Runemark et al. 2010; Brock et al. 2020), and field guides (Valakos et al. 2008; Speybroeck et al. 2016). We a priori restricted our investigation to color polymorphism defined as species with multiple coexisting color morphs in the same geographic location. Further, we focused on color polymorphism in the same trait on the same region of the body, as this is likely to share both a similar underlying genetic mechanism and be subject to similar selective pressures across species (Andrade et al. 2019). In lacertid lizards, color polymorphism is expressed as colorful badges on the throat and colors vary from species to species (Runemark et al. 2010; Brock et al. 2020). Species were coded as color polymorphic if we could adequately identify they met al. of the following criteria: 1) variation in color located on the throat, 2) variation in throat color is not the result of ontogenetic color change and is present in adults, 3) individuals from the same location exhibit at least two different throat colors, and 4) all sexes exhibit at least two different color types. We were able to collect color polymorphism data for all described lacertids and thus had no missing trait data for both our MCC species tree and the Garcia-Porta et al. (2019) tree. Altogether, we identified 43 color polymorphic lacertid species spanning 10 genera.
), including those not represented in our phylogeny. Examination of all extant taxa, including species lacking available genetic data and not represented in our phylogeny, was necessary to account for trait estimation proportions downstream in our state-dependent speciation and extinction (SSE) models. We scored color polymorphism from several georeferenced sources to ensure taxonomic validity, including online databases with photographs (www.inaturalist.org, www.lacerta.de), scientific literature (Huyghe et al. 2009a, 2009b; López et al. 2009; Runemark et al. 2010; Brock et al. 2020), and field guides (Valakos et al. 2008; Speybroeck et al. 2016). We a priori restricted our investigation to color polymorphism defined as species with multiple coexisting color morphs in the same geographic location. Further, we focused on color polymorphism in the same trait on the same region of the body, as this is likely to share both a similar underlying genetic mechanism and be subject to similar selective pressures across species (Andrade et al. 2019). In lacertid lizards, color polymorphism is expressed as colorful badges on the throat and colors vary from species to species (Runemark et al. 2010; Brock et al. 2020). Species were coded as color polymorphic if we could adequately identify they met al. of the following criteria: 1) variation in color located on the throat, 2) variation in throat color is not the result of ontogenetic color change and is present in adults, 3) individuals from the same location exhibit at least two different throat colors, and 4) all sexes exhibit at least two different color types. We were able to collect color polymorphism data for all described lacertids and thus had no missing trait data for both our MCC species tree and the Garcia-Porta et al. (2019) tree. Altogether, we identified 43 color polymorphic lacertid species spanning 10 genera.
Ancestral state reconstruction of color polymorphism in the Lacertidae
To understand the evolutionary history of color polymorphism in lacertids, we used ancestral state reconstructions jointly estimated with character transitions and diversification rates in the HiSSE package with the “MarginRecon” function (Beaulieu and O’Meara 2016). We present ancestral state reconstructions for both our MCC species tree and a recently published lacertid tree inferred in a maximum likelihood (ML) framework by Garcia-Porta et al. (2019) that differed somewhat in taxon representation and topology to test if our results were robust to phylogenetic uncertainty (Fig. 2).
Figure 2.
Phylogenetic reconstructions of evolutionary relationships and color polymorphism in the lizard family Lacertidae. a) Phylogeny is the maximum clade credibility (MCC) tree calculated from the posterior of a full-Bayesian species tree inference from three mitochondrial and two nuclear loci. b) Phylogeny is the ML time tree inferred by Garcia-Porta et al. (2019). In both trees, genera are labelled and separated by blue and yellow bars. Branches of the phylogeny are painted with ancestral state reconstructions of color polymorphism (black and white) and net diversification rates from the best fit HiSSE model (blue to red gradient), and indicate the estimated evolutionary history of color polymorphism and tempo of net diversification, respectively. On each tree, an asterisk denotes the oldest common ancestor with 99% probability of being color polymorphic. c) Model-averaged net diversification rates extracted from the tips of the Brock et al. MCC tree (a). d) Model-averaged net diversification rates extracted from the tips of the Garcia-Porta et al. ML tree (b). d) Model-averaged net diversification rates extracted from the tips of the Garcia-Porta et al. (2019) (b). Model-averaged results are from all 11 SSE models.
State-dependent diversification models
To test our hypothesis that evolutionary transitions to color polymorphism are associated with elevated diversification rates, we used state-dependent speciation and extinction (SSE) models (Maddison et al. 2007). An advantage of SSE models is joint estimation of trait transitions and diversification rates (Maddison et al. 2007; Beaulieu and O’Meara 2016). The original binary state-dependent speciation and extinction (BiSSE) model calculates the probability that a group of extant species evolved as observed at the tips given a phylogenetic tree and a binary character under a simple model of evolution with six parameters (Maddison et al. 2007). The parameterization of a basic BiSSE model specifies two speciation rates (a rate for when a lineage is in state 0, and a rate for when a lineage is in state 1), two extinction rates (for lineages in state 0 and state 1), and two rates of character state transition (from state 0 to state 1 and vice versa). The hidden-state speciation and extinction (HiSSE) model framework is an extension of BiSSE that specifies additional parameters to account for diversification rate heterogeneity that is not associated with the observed trait (Beaulieu and O’Meara 2016). These “hidden states” represent unmeasured characters that could affect diversification rate estimates for the measured observed character (Beaulieu and O’Meara 2016). Thus, including hidden states allows us to estimate the effect of color polymorphism while controlling for other unmeasured correlated traits on diversification rate. The SSE model framework is statistically advantageous because BiSSE models are nested within HiSSE models, and maximum likelihood inference can be used to estimate a suite of alternative models and their parameters for subsequent hypothesis tests (see below). Biologically, SSE models are desirable for our study because we are interested in both the evolutionary history of color polymorphism (historic transitions to and from color polymorphism) and if this character, or something unmeasured, is associated with increased speciation and extinction or not at all.
We performed BiSSE and HiSSE model tests on both our maximum clade credibility (MCC) species tree and the Garcia-Porta et al. maximum likelihood (ML) time tree in R with the “HiSSE” package (Beaulieu and O’Meara 2016). We constructed a suite of character-dependent (BiSSE and HiSSE), character-independent models (CID-2 and CID-4), and null models that vary in the number of distinct transition rates, extinction parameters, and hidden states to test alternative hypotheses related to the evolution of color polymorphism and diversification rates in the family Lacertidae (Table 1). Briefly, the CID-2 and CID-4 models are BiSSE and HiSSE character-independent models, respectively. The CID-2 and CID-4 models contain the same number of distinct turnover and extinction fraction parameters that can vary across the tree as their analogous BiSSE and HiSSE models, but CID-2 and CID-4 explicitly specify that diversification is not linked to the observed character state (Beaulieu and O’Meara 2016). The BiSSE and HiSSE null models also contain the same number of transition rates as the BiSSE and HiSSE models, but the null models specify a constant rate of diversification across the tree (number of distinct turnover rates  ). For all 11 SSE models run on our time-calibrated MCC species tree (Fig. 2a), we used the same estimated proportion of extant species (82% of all noncolor polymorphic and 100% of color polymorphic extant species are represented in our tree) and did not constrain the root character state. For the Garcia-Porta et al. (2019) ML tree (Fig. 2b), we specified a slightly different estimated proportion of extant species due to differences in taxonomic representation (73% of all noncolor polymorphic and 93% of color polymorphic extant species represented in the tree), otherwise, all other SSE model specifications are identical. Full SSE model parameterizations are given in Supplementary material available on Dryad. Nested SSE models were compared using AICc scores,
). For all 11 SSE models run on our time-calibrated MCC species tree (Fig. 2a), we used the same estimated proportion of extant species (82% of all noncolor polymorphic and 100% of color polymorphic extant species are represented in our tree) and did not constrain the root character state. For the Garcia-Porta et al. (2019) ML tree (Fig. 2b), we specified a slightly different estimated proportion of extant species due to differences in taxonomic representation (73% of all noncolor polymorphic and 93% of color polymorphic extant species represented in the tree), otherwise, all other SSE model specifications are identical. Full SSE model parameterizations are given in Supplementary material available on Dryad. Nested SSE models were compared using AICc scores,  AIC scores, and Akaike weights (Table 1) (Burnham and Anderson 2002).
AIC scores, and Akaike weights (Table 1) (Burnham and Anderson 2002).
Table 1.
Summary of color polymorphism SSE hypotheses and associated model fits from diversification analyses performed on the Brock et al. maximum clade credibility (MCC) species tree, averaged results for 1000 trees from the posterior of Brock et al. species tree inference, and the Garcia-Porta et al. (2019) maximum likelihood tree
| Model | AIC |
 AIC
AIC |
Akaike weights | Trait dependent diversification | N distinct turnover rates | N distinct extinction fractions | N distinct transition rates |
|---|---|---|---|---|---|---|---|
| Brock et al. maximum clade credibility tree and 1000 trees from posterior | |||||||
| HiSSE | 2478.605 | 0 | 0.913 | Yes | 4 | 4 | 8 |
(2500  58.1) 58.1) |
(0) | ||||||
| HiSSE No 1B | 2483.477 | 4.872 | 0.079 | Yes | 3 | 3 | 4 |
| HiSSE No 0B | 2489.169 | 10.564 | 0.001 | Yes | 3 | 3 | 4 |
| BiSSE 1 extinct frac | 2491.563 | 12.958 | 0.0005 | Yes | 2 | 1 | 2 |
| BiSSE | 2493.563 | 14.958 |
 0.0001
0.0001 |
Yes | 2 | 2 | 2 |
| 2 extinct frac | (2504  57.3) 57.3) |
(3) | |||||
| BiSSE null | 2511.294 | 32.689 |
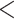 0.0001
0.0001 |
No | 1 | 1 | 2 |
(2519  57.5) 57.5) |
(20) | ||||||
| CID-4 | 2515.252 | 36.647 |
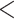 0.0001
0.0001 |
No | 4 | 4 | 3 |
| 3 trans rate CID-2 | 2517.294 | 38.689 |
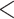 0.0001
0.0001 |
No | 2 | 2 | 3 |
| 3 trans rate HiSSE null | 2528.909 | 50.304 |
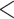 0.0001
0.0001 |
No | 2 | 2 | 1 |
(2512  57.5) 57.5) |
(12) | ||||||
| CID-2 | 2541.242 | 62.637 |
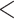 0.0001
0.0001 |
No | 2 | 2 | 1 |
(2539  59.1) 59.1) |
(46) | ||||||
| CID-4 | 2544.542 | 65.937 |
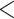 0.0001
0.0001 |
No | 4 | 4 | 1 |
(2538.1 59) 59) |
(45) | ||||||
| Garcia-Porta et al. maximum likelihood tree | |||||||
| HiSSE | 2049.914 | 0 | 0.999 | Yes | 4 | 4 | 8 |
| HiSSE No 1B | 2064.018 | 14.104 |
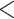 0.0001
0.0001 |
Yes | 3 | 3 | 4 |
| HiSSE No 0B | 2066.914 | 17 |
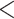 0.0001
0.0001 |
Yes | 3 | 3 | 4 |
| BiSSE 1 extinct frac | 2076.788 | 26.866 |
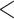 0.0001
0.0001 |
Yes | 2 | 1 | 2 |
| BiSSE 2 extinct frac | 2078.788 | 28.874 |
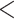 0.0001
0.0001 |
Yes | 2 | 2 | 2 |
| BiSSE null | 2081.417 | 31.503 |
 0.0001
0.0001 |
No | 1 | 1 | 2 |
| CID-4 3 trans rate | 2081.879 | 31.965 |
 0.0001
0.0001 |
No | 4 | 4 | 3 |
| CID-2 3 trans rate | 2083.417 | 33.503 |
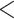 0.0001
0.0001 |
No | 2 | 2 | 3 |
| CID-4 | 2100.142 | 50.228 |
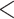 0.0001
0.0001 |
No | 4 | 4 | 1 |
| CID-2 | 2114.789 | 64.875 |
 0.0001
0.0001 |
No | 2 | 2 | 1 |
| HiSSE null | 2116.559 | 66.645 |
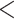 0.0001
0.0001 |
No | 2 | 2 | 1 |
Notes: For the Brock et al. and Garcia-Porta et al. phylogenies, models are listed in best-fit order according to AIC value. Average AIC and  AIC score results from the six models run on the posterior are given in parentheses under the corresponding model run on the Brock et al. MCC tree. A trait-dependent diversification HiSSE model best explained the data for both phylogenies and the posterior.
AIC score results from the six models run on the posterior are given in parentheses under the corresponding model run on the Brock et al. MCC tree. A trait-dependent diversification HiSSE model best explained the data for both phylogenies and the posterior.
Trait simulations and SSE model adequacy
The main disadvantage of SSE models is the potential issue of choosing between model A and model B when model C is true (Caetano et al. 2018). To address this potential issue, we conducted a simulation study (similar to Portik et al. 2019) to identify the rate at which a character-dependent model of diversification (BiSSE or HiSSE) is falsely chosen as the correct model out of a subset of six different SSE models with uncorrelated simulated-color polymorphism trait data on our empirical phylogeny. To simulate color polymorphism character data on our species tree and the Garcia-Porta et al. ML tree, we used the “phytools” (v.0.6-60) “sim.history” function (Revell 2012). For trait data simulation, we used the parameter estimations from the transition matrix from the best fit HiSSE model run on the empirical data. We extracted the root state probabilities from our fitted models and used them to specify simulation root states. We then simulated character data on the empirical trees 10,000 times and randomly selected 1000 simulations where at least 10% of tips were color polymorphic for SSE model adequacy investigation. We then ran a subset of six SSE models from our empirical study on our 1000 simulations and extracted AIC scores for model comparison and adequacy evaluation (Fig. 3). Given that the simulated trait data are uncorrelated, we expect character-independent (CID-2 and CID-4) or null models (BiSSE null and HiSSE null) to have the lowest AIC scores most of the time on both trees.
Figure 3.
Distributions of Akaike model weights for six state-speciation extinction (SSE) models run on 1000 simulated color polymorphism trait data sets (uncorrelated trait data run on true trees) and a posterior distribution of possible trees (real data run on 1000 posterior trees). For a) and b), all simulations and models were performed with empirical phylogenies. The horizontal axis (Akaike weight) refers to the relative probability of that SSE model compared to the other five competing SSE models run on the same uncorrelated simulated color polymorphism trait data. The dotted vertical lines indicate model weights from our empirical phylogeny and observed color polymorphism trait data for that same SSE model. Low model weight indicates relatively low support for the hypothesis, and high model weight indicates greater support. c) Distributions of Akaike model weights for six SSE models run on 1000 phylogenetic trees randomly selected from posterior distribution of possible trees and our empirical color polymorphism trait data set. A higher model weight indicates greater relative support for that state-speciation extinction hypothesis.
Phylogenetic uncertainty and SSE model comparison
A phylogenetic tree represents one hypothesis of evolutionary relatedness. Biological conclusions drawn from phylogenetic comparative methods are influenced by uncertainty in the timing and topology of those relationships, with the potential for misleading conclusions based on misestimating the true diversification history (Louca and Pennell 2020). To understand the robustness of our conclusions based on phylogenetic comparative analyses carried out on our MCC species tree we performed a sensitivity analysis using 1000 randomly selected trees from the posterior distribution of 12,000 trees from our Bayesian tree inference. Here, we ran the same subset of six SSE models from trait simulation analyses with the same parameterizations (Table 1) on 1000 possible phylogenies with our observed color polymorphism trait data. We extracted AIC scores for SSE models run on each tree for model comparison (Fig. 3). Finally, we extracted model parameter estimates from a subset of phylogenies from the posterior sample of 1000 trees to understand how uncertainty in phylogeny affects net diversification and extinction fraction estimates (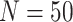 phylogenies, Table 2). A similar analysis was not possible for the Garcia-Porta et al. (2019) ML tree because no posterior is generated from ML tree inference.
phylogenies, Table 2). A similar analysis was not possible for the Garcia-Porta et al. (2019) ML tree because no posterior is generated from ML tree inference.
Table 2.
SSE model parameter estimates from comparative analyses on the Brock et al. maximum clade credibility (MCC) species tree from Bayesian inference, a posterior subsample of 100 species trees from Bayesian inference by Brock et al., and the maximum likelihood (ML) tree from Garcia-Porta et al. (2019)
| Model | Net turnover (1A) | Net turnover (0A) | Net turnover (1B) | Net turnover (0B) | Extinction turnover (1A) | Extinction turnover (0A) | Extinction turnover (1B) | Extinction turnover (0B) |
|---|---|---|---|---|---|---|---|---|
| HiSSE | MCC | MCC | MCC | MCC | MCC | MCC | MCC | MCC |
| 0.055 | 0.025 | 0.146 | 0.019 | 2.06e-09 | 2.06e-09 | 2.06e-09 | 1.177 | |
| Posterior | Posterior | Posterior | Posterior | Posterior | Posterior | Posterior | Posterior | |
| 0.078 | 0.032 | 0.265 | 0.120 | 0.469 | 0.066 | 0.388 | 0.192 | |
| (0.025) | (0.0.347) | (0.321) | (0.139) | (1.09) | (0.277) | (0.455) | (0.555) | |
| ML | ML | ML | ML | ML | ML | ML | ML | |
| 0.011 | 2.06e-09 | 0.093 | 0.011 | 3.000 | 2.08e-09 | 2.06e-09 | 2.06e-09 | |
| HiSSE No 1B | MCC | MCC | MCC | MCC | MCC | MCC | ||
| 0.080 | 0.020 | 0.025 | 0.433 | 0.065 | 2.06e-09 | |||
| Posterior | Posterior | Posterior | Posterior | Posterior | Posterior | |||
| 0.078 | 0.022 | N/A | 0.035 | 0.414 | 0.055 | N/A | 2.06e-09 | |
| (0.031) | (0.022) | (0.042) | (0.050) | (0.032) | (0.003) | |||
| ML | ML | ML | ML | ML | ML | |||
| 0.045 | 0.010 | 0.012 | 2.06e-09 | 2.06e-09 | 0.007 | |||
| HiSSE No 0B | MCC | MCC | MCC | MCC | MCC | MCC | ||
| 0.063 | 0.026 | 0.042 | 2.06e-09 | 2.06e-09 | 2.06e-02 | |||
| Posterior | Posterior | Posterior | Posterior | Posterior | Posterior | |||
| 0.106 | 0.026 | 0.038 | N/A | 3.79e-03 | 6.03e-04 | 6.75e-02 | N/A | |
| (0.072) | (0.003) | (0.013) | (0.015) | (0.004) | (0.421) | |||
| ML | ML | ML | ML | ML | ML | |||
| 0.127 | 0.053 | 2.06e-09 | 2.06e-09 | 2.06e-09 | 3.000 | |||
| BiSSE 1 extinct fraction | MCC | MCC | MCC | MCC | ||||
| 0.050 | 0.026 | 1.374e-08 | 1.374e-08 | |||||
| Posterior | Posterior | Posterior | Posterior | |||||
| 0.050 | 0.026 | N/A | N/A | 1.00e-08 | 1.00e-08 | N/A | N/A | |
| (0.006) | (0.003) | (0.002) | (0.002) | |||||
| ML | ML | ML | ML | |||||
| 0.067 | 0.054 | 2.06e-09 | 2.06e-09 | |||||
| BiSSE 2 extinct fractions | MCC | MCC | MCC | MCC | ||||
| 0.050 | 0.026 | 2.06e-09 | 2.35e-09 | |||||
| Posterior | Posterior | Posterior | Posterior | |||||
| 0.053 | 0.027 | N/A | N/A | 0.007 | 2.51e-09 | N/A | N/A | |
| (0.002) | (0.006) | (0.019) | (1.70e-09) | |||||
| ML | ML | ML | ML | |||||
| 0.067 | 0.054 | 2.06e-09 | 2.06e-09 | |||||
| BiSSE null | MCC | MCC | MCC | MCC | ||||
| 0.031 | 0.031 | 2.061e-02 | 2.061e-02 | |||||
| Posterior | Posterior | Posterior | Posterior | |||||
| 0.032 | 0.032 | N/A | N/A | 1.23e-08 | 1.23e08 | N/A | N/A | |
| (0.003) | (0.003) | (1.50e-08) | (1.50e-08) | |||||
| ML | ML | ML | ML | |||||
| 0.057 | 0.057 | 2.06e-09 | 2.06e-09 | |||||
| HiSSE null | MCC | MCC | MCC | MCC | MCC | MCC | MCC | MCC |
| 0.183 | 0.183 | 0.028 | 0.028 | 0.673 | 0.673 | 2.064e-09 | 2.064e-09 | |
| Posterior | Posterior | Posterior | Posterior | Posterior | Posterior | Posterior | Posterior | |
| 0.671 | 0.671 | 0.647 | 0.647 | 0.343 | 0.343 | 0.420 | 0.420 | |
| (0.305) | (0.305) | (0.159) | (0.159) | (0.411) | (0.411) | (0.426) | (0.426) | |
| ML | ML | ML | ML | ML | ML | ML | ML | |
| 2.06e-09 | 2.06e-09 | 0.060 | 0.060 | 3.01e-09 | 3.01e-09 | 2.06e-09 | 2.06e-09 | |
| CID-2 | MCC | MCC | MCC | MCC | MCC | MCC | MCC | MCC |
| 0.014 | 0.014 | 0.032 | 0.032 | 2.06e-09 | 2.06e-09 | 2.06e-09 | 2.06e-09 | |
| Posterior | Posterior | Posterior | Posterior | Posterior | Posterior | Posterior | Posterior | |
| 0.073 | 0.073 | 0.183 | 0.183 | 0.119 | 0.119 | 0.134 | 0.134 | |
| (0.029) | (0.029) | (0.651) | (0.651) | (0.306) | (0.306) | (0.323) | (0.323) | |
| ML | ML | ML | ML | ML | ML | ML | ML | |
| 2.06e-09 | 2.06e-09 | 0.061 | 0.061 | 3.17e-09 | 3.17e-09 | 2.06e-09 | 2.06e-09 |
| Model | Net turnover (1A) | Net turnover (0A) | Net turnover (1B) | Net turnover (0B) | Extinction fraction (1A) | Extinction fraction (0A) | Extinction fraction (1B) | Extinction fraction (0B) |
| CID-2 3 trans rates | MCC | MCC | MCC | MCC | MCC | MCC | MCC | MCC |
| 0.031 | 0.031 | 0.031 | 0.031 | 2.061e-09 | 2.061e-09 | 2.061e-09 | 2.061e-09 | |
| Posterior | Posterior | Posterior | Posterior | Posterior | Posterior | Posterior | Posterior | |
| 0.074 | 0.074 | 0.186 | 0.186 | 0.121 | 0.121 | 0.137 | 0.137 | |
| (0.155) | (0.155) | (0.658) | (0.658) | (0.309) | (0.309) | (0.326) | (0.326) | |
| ML | ML | ML | ML | ML | ML | ML | ML | |
| 9.26e-04 | 9.26e-04 | 0.083 | 0.083 | 2.06e-09 | 2.06e-09 | 2.06e-09 | 2.06e-09 | |
| CID-4 | MCC | MCC | MCC | MCC | MCC | MCC | MCC | MCC |
| 0.031 | 0.031 | 0.009 | 0.009 | 2.061e-09 | 2.061e-09 | 2.061e-09 | 2.061e-09 | |
| Posterior | Posterior | Posterior | Posterior | Posterior | Posterior | Posterior | Posterior | |
| 0.024 | 0.024 | 0.004 | 0.004 | 2.08e-09 | 2.08e-09 | 2.08e-09 | 2.08e-09 | |
| (0.031) | (0.031) | (0.014) | (0.014) | (0.017) | (9.29e-11) | (9.29e-11) | (9.29e-11) | |
| ML | ML | ML | ML | ML | ML | ML | ML | |
| 0.008 | 0.008 | 0.002 | 0.002 | 2.06e-09 | 2.06e-09 | 2.06e-09 | 2.06e-09 | |
| CID-4 3 trans rates | MCC | MCC | MCC | MCC | MCC | MCC | MCC | MCC |
| 0.020 | 0.020 | 0.042 | 0.042 | 2.061e-09 | 2.061e-09 | 2.061e-09 | 2.061e-09 | |
| Posterior | Posterior | Posterior | Posterior | Posterior | Posterior | Posterior | Posterior | |
| 0.021 | 0.021 | 0.125 | 0.125 | 2.06e-09 | 2.06e-09 | 2.06e-09 | 2.06e-09 | |
| (0.006) | (0.006) | (0.259) | (0.259) | (0.005) | (0.005) | (0.005) | (0.005) | |
| ML | ML | ML | ML | ML | ML | ML | ML | |
| 0.099 | 0.099 | 0.003 | 0.003 | 2.19e-09 | 2.19e-09 | 2.06e-09 | 2.06e-09 |
Notes: Net diversification parameter estimates from the MCC species tree (Fig. 2a) are given for each SSE model under Spp. MCC. SSE model parameter estimates from all 11 models run on 50 phylogenies extracted from the posterior are given under Posterior where the first value is the average and the value in parentheses is the standard deviation of the estimate. SSE model parameter estimates from the Garcia-Porta et al. (2019) tree (Fig. 2b) are given under ML.
Results
Phylogeny of the Lacertidae
Phylogenetic inference from the combined two independent MCMC runs with 20% burn-in converged well (ESS values for posterior, species tree height, 12S gene tree, 16S gene tree, cmos gene tree, and cyt-b gene tree 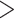 200). ESS values for the likelihood (117), species coalescent (175), and rag-1 (193) were slightly lower but over 100. We estimated the most recent common ancestor (MRCA) of all lacertids occurred 98.3–148.9 Ma (95% HPD
200). ESS values for the likelihood (117), species coalescent (175), and rag-1 (193) were slightly lower but over 100. We estimated the most recent common ancestor (MRCA) of all lacertids occurred 98.3–148.9 Ma (95% HPD  –148.988, average age
–148.988, average age 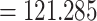 Ma). Evolutionary relationships presented in our maximum clade credibility tree (Fig. 2a), recovered from our multilocus full Bayesian species tree inference had some disagreements with other family-wide phylogenies (Hipsley et al. 2009; Garcia-Porta et al. 2019). The subfamily Gallotiinae, comprising Gallotia and Psammodromus genera, grouped together monophyletically consistent with previous studies (Arnold et al. 2007; Garcia-Porta et al. 2019). However, our inference placed Gallotiinae nested within Lacertinae with low node support (posterior probability
Ma). Evolutionary relationships presented in our maximum clade credibility tree (Fig. 2a), recovered from our multilocus full Bayesian species tree inference had some disagreements with other family-wide phylogenies (Hipsley et al. 2009; Garcia-Porta et al. 2019). The subfamily Gallotiinae, comprising Gallotia and Psammodromus genera, grouped together monophyletically consistent with previous studies (Arnold et al. 2007; Garcia-Porta et al. 2019). However, our inference placed Gallotiinae nested within Lacertinae with low node support (posterior probability 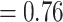 ), which follows results from Fu (2000), but is in contrast to the hypothesis that the Gallotiinae and Lacertinae are two separate monophyletic subfamilies that comprise the Lacertidae (Arnold et al. 2007; Garcia-Porta et al. 2019). The two tribes within the subfamily Lacertinae (as most recently reviewed with 620 bp of mtDNA and 64 morphological characters from 59 nominal species by Arnold et al. 2007), the Lacertini and Eremiadini, were not reciprocally monophyletic. The Lacertini tribe (Oppel 1811; Arnold et al. 2007) that usually comprise 18 genera from Europe, northwest Africa, and southwest and east Asia largely grouped together, with 15 of 18 genera forming a monophyletic clade containing Algyroides, Anatololacerta, Apathya, Archaeolacerta, Dalmatolacerta, Dinarolacerta, Hellenolacerta, Iberolacerta, Lacerta, Parvilacerta, Phoenicolacerta, Podarcis, Teira, Timon, and Zootoca. The Darevskia and Iranolacerta genera that belong to the Lacertini tribe grouped monophyletically sister to the aforementioned Lacertini, but also include the Eremias, which are traditionally placed in the Eremiadini tribe. The last Lacertini genus, the Takydromus, which contains 24 species that have a far east distribution spanning eastern China, Japan, and southeast Asia grouped monophyletically but separate from the other Lacertini. The Eremiadini tribe diverge from other lacertids deep in our phylogeny, with the speciose Acanthodactylus and Meroles genera forming a monophyletic clade, the Afrotropical genera Pedioplanis, Nucras, Poromera, Latastia, Pseuderemias, Heliobolus, Meroles, Ichnotropis, Vhembelacerta, and Australolacerta forming a monophyletic clade. The remaining Eremiadini genera from Equatorial Africa, Adolfus, Gastropholis, Holaspis, Congolacerta, Atlantolacerta, and Omanosaura form a separate clade similar to Arnold et al. (2007). Most genera formed monophyletic groups with the exception of Algyroides, Eremias, and Ophisops.
), which follows results from Fu (2000), but is in contrast to the hypothesis that the Gallotiinae and Lacertinae are two separate monophyletic subfamilies that comprise the Lacertidae (Arnold et al. 2007; Garcia-Porta et al. 2019). The two tribes within the subfamily Lacertinae (as most recently reviewed with 620 bp of mtDNA and 64 morphological characters from 59 nominal species by Arnold et al. 2007), the Lacertini and Eremiadini, were not reciprocally monophyletic. The Lacertini tribe (Oppel 1811; Arnold et al. 2007) that usually comprise 18 genera from Europe, northwest Africa, and southwest and east Asia largely grouped together, with 15 of 18 genera forming a monophyletic clade containing Algyroides, Anatololacerta, Apathya, Archaeolacerta, Dalmatolacerta, Dinarolacerta, Hellenolacerta, Iberolacerta, Lacerta, Parvilacerta, Phoenicolacerta, Podarcis, Teira, Timon, and Zootoca. The Darevskia and Iranolacerta genera that belong to the Lacertini tribe grouped monophyletically sister to the aforementioned Lacertini, but also include the Eremias, which are traditionally placed in the Eremiadini tribe. The last Lacertini genus, the Takydromus, which contains 24 species that have a far east distribution spanning eastern China, Japan, and southeast Asia grouped monophyletically but separate from the other Lacertini. The Eremiadini tribe diverge from other lacertids deep in our phylogeny, with the speciose Acanthodactylus and Meroles genera forming a monophyletic clade, the Afrotropical genera Pedioplanis, Nucras, Poromera, Latastia, Pseuderemias, Heliobolus, Meroles, Ichnotropis, Vhembelacerta, and Australolacerta forming a monophyletic clade. The remaining Eremiadini genera from Equatorial Africa, Adolfus, Gastropholis, Holaspis, Congolacerta, Atlantolacerta, and Omanosaura form a separate clade similar to Arnold et al. (2007). Most genera formed monophyletic groups with the exception of Algyroides, Eremias, and Ophisops.
The Evolutionary History of Color Polymorphism in the Lacertidae
We identified 43 color polymorphic extant lacertid species spanning 10 out of 42 currently described genera. The 10 genera containing color polymorphic species are all within the subfamily Lacertinae: Algyroides (2 of 4 spp.), Anatololacerta (5 of 5 spp.), Apathya (1 of 2 spp.), Darevskia (8 of 30 spp.) Dinarolacerta (1 of 2 spp.), Hellenolacerta (1 of 1 sp.), Iberolacerta (3 of 8 spp.), Phoenolacerta (2 of 4 spp.), Podarcis (19 of 23 spp.), and Zootoca (1 of 1 sp.). All 43 color polymorphic lacertid species are represented in the MCC species tree (Fig. 2a) and comparative analyses, and 40 color polymorphic species are contained in the ML tree (Fig. 2b). We present ancestral state reconstructions estimated with HiSSE for both our MCC species and the ML tree proposed by Garcia-Porta et al. (2019) (Fig. 2a,b, indicated on the branches of the tree in black and white).
Ancestral state reconstructions on both the MCC and ML trees estimated that the most recent common ancestor of all lacertids was most likely not color polymorphic (Fig. 2a,b). Results from ancestral state reconstructions also suggest that color polymorphism is an ancient trait within lacertids and is likely to have evolved by the most recent common ancestor of the Lacertini around 111 Ma (Fig. 2a,b, denoted with an asterisk).
State-Dependent Diversification in the Lacertidae
Results from SSE analyses on the MCC species tree support a character state-dependent diversification model with hidden states, or HiSSE model (Akaike weight 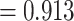 , Fig. 2, Table 1). For the best fit model, turnover parameter estimates were asymmetrical between color polymorphic and noncolor polymorphic lineages (MCC parameter estimates, Table 2). Estimated net diversification rates were higher in observed color polymorphic lineages (HiSSE model, Table 2). Parameter estimates for character transitions from color polymorphism to monomorphism were much higher than transitions from monomorphism to color polymorphism, providing further evidence that color polymorphism is more easily lost than gained (HiSSE model transition rate CP-1A to NotCP-0A
, Fig. 2, Table 1). For the best fit model, turnover parameter estimates were asymmetrical between color polymorphic and noncolor polymorphic lineages (MCC parameter estimates, Table 2). Estimated net diversification rates were higher in observed color polymorphic lineages (HiSSE model, Table 2). Parameter estimates for character transitions from color polymorphism to monomorphism were much higher than transitions from monomorphism to color polymorphism, providing further evidence that color polymorphism is more easily lost than gained (HiSSE model transition rate CP-1A to NotCP-0A 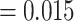 , NotCP-0A to CP-1A
, NotCP-0A to CP-1A  2.061e-09, CP-1B to NotCP-0B
2.061e-09, CP-1B to NotCP-0B  , NotCP-0B to CP-1B
, NotCP-0B to CP-1B  ). The other state-dependent diversification models had lower AIC values and greater Akaike model weights than trait-independent and null models of diversification (Table 1).
). The other state-dependent diversification models had lower AIC values and greater Akaike model weights than trait-independent and null models of diversification (Table 1).
Parameter estimates from trait-dependent diversification SSE models also detected higher rates of net diversification at evolutionary transitions to color polymorphism (Table 2). We estimated much higher character transition rates from color polymorphism to monomorphism (MCC HiSSE transition rates from poly- to monomorphism  , mono- to polymorphism
, mono- to polymorphism  2.06e-09; ML HiSSE transition rates from poly- to monomorphism
2.06e-09; ML HiSSE transition rates from poly- to monomorphism 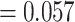 , mono- to polymorphism
, mono- to polymorphism  2.06e-09). All null and character-independent SSE models received very little support relative to state-dependent diversification SSE models, accounting for less than 0.1% of the Akaike model weight (Table 1). Complete details of all SSE model net diversification and extinction fraction parameter estimates are given in Table 2. Overall, for diversification analyses on the MCC species tree, the HiSSE model accounted for more than 91% of the Akaike model weight, and model-averaged net diversification rate estimates extracted from tree tips (Fig. 2d) support our hypothesis that evolutionary transitions to color polymorphism are associated with elevated diversification rates.
2.06e-09). All null and character-independent SSE models received very little support relative to state-dependent diversification SSE models, accounting for less than 0.1% of the Akaike model weight (Table 1). Complete details of all SSE model net diversification and extinction fraction parameter estimates are given in Table 2. Overall, for diversification analyses on the MCC species tree, the HiSSE model accounted for more than 91% of the Akaike model weight, and model-averaged net diversification rate estimates extracted from tree tips (Fig. 2d) support our hypothesis that evolutionary transitions to color polymorphism are associated with elevated diversification rates.
Model selection results from the same set of eleven SSE analyses performed on the Garcia-Porta et al. (2019) ML time tree are also given in Table 1. Again, we find the greatest support for a HiSSE model with hidden states (Akaike weight 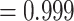 ) and that trait-dependent diversification models have lower AIC values and greater Akaike model weights than trait-independent and null models. Estimated transition rates from color polymorphism to monomorphism were much higher than evolutionary transitions from monomorphism to color polymorphism (HiSSE model transition rate CP-1A to NotCP-0A
) and that trait-dependent diversification models have lower AIC values and greater Akaike model weights than trait-independent and null models. Estimated transition rates from color polymorphism to monomorphism were much higher than evolutionary transitions from monomorphism to color polymorphism (HiSSE model transition rate CP-1A to NotCP-0A  , NotCP-0A to CP-1A
, NotCP-0A to CP-1A  2.061e-09, CP-1B to NotCP-0B
2.061e-09, CP-1B to NotCP-0B  , NotCP-0B to CP-1B
, NotCP-0B to CP-1B  2.066e-09). Model-averaged net diversification rate estimates extracted from the ML tree tips (Fig. 2c) also suggest that color polymorphic lineages experience elevated diversification rates.
2.066e-09). Model-averaged net diversification rate estimates extracted from the ML tree tips (Fig. 2c) also suggest that color polymorphic lineages experience elevated diversification rates.
Trait Simulations on Empirical MCC and ML Phylogenies and SSE Model Adequacy
When we compared AIC values of six SSE models run on 1000 trait data sets simulated with no correlation to diversification rates on the empirical MCC and ML Lacertidae phylogenies, we found that trait-dependent diversification models were chosen as the best fit model less than 2% of the time. For uncorrelated trait simulations performed on the MCC species tree, the BiSSE null model was selected as the best fit model most often (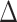 AIC score
AIC score  , 58.3% of simulations for BiSSE null model), followed by the HiSSE null model (
, 58.3% of simulations for BiSSE null model), followed by the HiSSE null model ( AIC score
AIC score  , 36.8% of simulations). Character-independent models, CID-2 and CID-4, were rarely the best fit models on simulated trait data and also had low Akaike model weights compared to other models (3.4% of simulations CID-2
, 36.8% of simulations). Character-independent models, CID-2 and CID-4, were rarely the best fit models on simulated trait data and also had low Akaike model weights compared to other models (3.4% of simulations CID-2 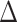 AIC score
AIC score 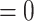 , 1.1% of simulations CID-4
, 1.1% of simulations CID-4 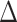 AIC score
AIC score  , Fig. 3a). Character-dependent diversification models, BiSSE and HiSSE, were rarely the best fit models on simulated uncorrelated color trait data (
, Fig. 3a). Character-dependent diversification models, BiSSE and HiSSE, were rarely the best fit models on simulated uncorrelated color trait data ( AIC score
AIC score  , 0.1% of simulations for BiSSE model, 1.1% for HiSSE model, Fig. 3a).
, 0.1% of simulations for BiSSE model, 1.1% for HiSSE model, Fig. 3a).
For 1000 uncorrelated trait simulations performed on the Garcia-Porta et al. (2019) ML tree, we produce similar results. Here, the HiSSE null model was chosen as the best fit model most often (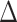 AIC score
AIC score  , 99% of simulations) (Fig. 3b). A trait-dependent diversification model was identified as the best fit model only 7 times (0.7% of simulations, HiSSE
, 99% of simulations) (Fig. 3b). A trait-dependent diversification model was identified as the best fit model only 7 times (0.7% of simulations, HiSSE  AIC score
AIC score  ). Ultimately, we recover a Type I error rate (trait-dependent diversification when there should be none) less than 1% of the time when we run a subset of six SSE models from our observed data on uncorrelated simulated trait data.
). Ultimately, we recover a Type I error rate (trait-dependent diversification when there should be none) less than 1% of the time when we run a subset of six SSE models from our observed data on uncorrelated simulated trait data.
SSE Model Selection and Parameter Estimation from Posterior Distribution of Trees
SSE model selection using the empirical color polymorphism data performed on a posterior distribution of 1000 trees identified trait-dependent diversification models, HiSSE and BiSSE, as the best fit models 99.4% of the time (Fig. 3c), which largely supports a color polymorphism-dependent diversification scenario in the Lacertidae. The HiSSE and BiSSE models also had greater Akaike model weights than null or character-independent diversification models (Fig. 3c). The HiSSE model was identified as the best fit model most of the time (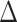 AIC score
AIC score  , 60.6% of sampled trees). The BiSSE model, trait-dependent diversification with no hidden states was selected as the best fit model second-most often (
, 60.6% of sampled trees). The BiSSE model, trait-dependent diversification with no hidden states was selected as the best fit model second-most often (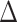 AIC score
AIC score  , 38.8% of sampled trees). Of the six times the HiSSE null model was selected as the best fit model, it achieved a
, 38.8% of sampled trees). Of the six times the HiSSE null model was selected as the best fit model, it achieved a 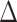 AIC score
AIC score  1 only once. Out of 1000 potential evolutionary histories of the Lacertidae, the BiSSE null model and character-independent models (CID-2 and CID-4) of diversification were never selected as best fit models.
1 only once. Out of 1000 potential evolutionary histories of the Lacertidae, the BiSSE null model and character-independent models (CID-2 and CID-4) of diversification were never selected as best fit models.
SSE model net diversification parameter estimates extracted from a subset of 50 phylogenetic trees overlapped with the estimates obtained from the maximum clade credibility tree (Table 2).
Discussion
Color polymorphism research has often suggested that multiple genetically based phenotypes can be a precursor to speciation, but with few comparative studies there has been a limited ability to test this hypothesis. We generated a comprehensive family-wide multilocus species tree of the Lacertidae to elucidate the evolutionary history and macroevolutionary consequences of color polymorphism. Phylogenetic ancestral state reconstructions of the family from two different tree inferences of the relationships in the Lacertidae suggests the most recent common ancestor of all lacertids was most likely not color polymorphic, and there were probably multiple independent evolutionary transitions to color polymorphism throughout the family tree. We found that the evolution of color polymorphism from monomorphism happens at a much slower rate than evolutionary transitions from color polymorphism to monomorphism. This macroevolutionary-level finding follows empirical results from species-specific case studies that color polymorphism is more easily lost than gained from populations (Corl et al. 2010b; Runemark et al. 2010). We explored macroevolutionary dynamics within the Lacertidae using two summary phylogenies and a posterior distribution of possible trees to test the theory that color polymorphism is a driver of diversification. Amongst several alternative hypotheses that simultaneously consider evolutionary history, unsampled hidden states, and trait transitions, we found multiple lines of support for the hypothesis that color polymorphic lineages diversify at a higher rate than monomorphic lineages.
The Lacertidae: Evolutionary History and Color Polymorphism
Phylogenies are essential for addressing macroevolutionary hypotheses that use interspecific data, and a long-contested phylogeny has limited our understanding of the evolutionary history and macroevolutionary dynamics of the Lacertidae (Fu 2000). Molecular investigations of the entire family Lacertidae at the species level are rare, and topological relationships in the family tree remain controversial (Fu 1998; Harris et al. 1998; Fu 2000; Arnold et al. 2007; Mayer and Pavlicev 2007; Garcia-Porta et al. 2019). Phylogenetic uncertainty in the Lacertidae likely stems from a combination of early and recent bursts of diversification (Fu 2000; Garcia-Porta et al. 2019). Family-level phylogenies of lacertids usually recover low support deep within the tree and at nodes connecting short branches near the tips (Fu 2000; Arnold et al. 2007; Garcia-Porta et al. 2019). We find a similar pattern in our data, with an early period of rapid diversification deep within the tree and low support or nontraditional placement of short branch taxa. Fossils and genetic data from Europe help resolve relationships among morphologically convergent European lacertids, but limited genetic data and poor fossil records in other areas where lacertids currently occur, such as the Middle East, Africa, and Asia, hinder our ability to generate phylogenies with strong support deep in the tree and between subgroups in these lineages (Hipsley et al. 2009). In particular, Eurasian lacertids and Lacertini species with expansive geographic distributions tend to have uncertain placement in phylogenetic reconstructions (Fu 2000; Garcia-Porta et al. 2019). Twenty years later, and with far more molecular markers, we echo Fu’s (2000) sentiment that to resolve nodes with low support in the lacertid family tree, future investigations should focus on interrogating species-level evolutionary relationships between a few widely distributed and contested genera that are probably not monophyletic (e.g., the highly polyphyletic former Lacerta genus; Arnold et al. 2007).
Accommodating phylogenetic uncertainty is essential to evolutionary studies. Indeed, the one true evolutionary history escapes us due to missing data from past processes such as extinction and an incomplete fossil record, and from limitations in the present from missing data, taxonomic uncertainty, and the continuous and ephemeral nature of speciation (Huelsenbeck et al. 2000; Rosenblum et al. 2012; Louca and Pennell 2020). We account for phylogenetic disagreement and uncertainty with trait simulation studies, test suites of alternative hypotheses on 1000 sampled trees from our Bayesian posterior, and run parallel comparative methods analyses on our own lacertid tree inference and that of others (Garcia-Porta et al. 2019). Through these methods, we find multiple lines of evidence all in agreement with regard to the evolutionary history of color polymorphism in the Lacertidae. Whether the Gallotinae truly belong sister to all Lacertinae (Arnold et al. 2007; Garcia-Porta et al. 2019), or somewhere nested within (Fu 2000), the phylogenetic structure of the evolution of color polymorphism across extant lacertids places the first instances of color polymorphism deep within the tree, though most likely in the tribe Lacertini and not at the common ancestor of all lacertids (Fig. 2a,b).
The Lacertidae exhibit a high degree of color polymorphism, spanning 10 genera and comprising 43 species that share a similar throat color polymorphism. Phylogenetic and ancestral state reconstruction analyses coestimated with diversification rates revealed that the ancestor of all lacertids was probably not color polymorphic, and that color polymorphism has been gained few times and lost many times throughout the evolutionary history of the Lacertidae. That the ancestor of all lacertids was most likely not color polymorphic is not surprising, given that the closest relatives of lacertids used as outgroup taxa are themselves not color polymorphic. Color polymorphism, however, appears to have evolved relatively early in the history of lacertids, during or shortly after an initial early period of diversification in the family. Color polymorphism seems to be a trait restricted to the Lacertini tribe, and most likely evolved in the group. Our results that recover an ancient origin of color polymorphism in the group also underline recent findings from a study of the highly polymorphic Podarcis group, which found patterns of molecular evolution at the color polymorphism pigmentation loci that indicate the alleles are of ancient origin (Andrade et al. 2019). We estimate that color polymorphism evolved fewer times than it has been lost throughout the evolutionary history of the Lacertidae, and that evolutionary transition rates from monomorphism to color polymorphism are much lower than transitions from color polymorphism to monomorphism, by up to seven times. This result is not surprising given that empirical studies of color polymorphic taxa at the species level report that morph loss in populations represents lost genetic variation that cannot likely be regained (Corl et al. 2010b). Our estimates indicate the rate of loss far exceeds the rate of gain of color polymorphism, which aligns with our expectations. The tendency for color polymorphism to be lost faster than it evolves follows from theory on morphic speciation (West-Eberhard 1986; Gray and McKinnon 2007). If color polymorphic species have highly variable or large geographic ranges where gene flow between populations is infrequent, populations that experience morph loss may diverge quickly genetically and phenotypically (Corl et al. 2010a,b), setting the stage for speciation. This scenario would generate a phylogenetic pattern where color polymorphic lineages give rise to daughter lineages that are monomorphic, which we see in our ancestral state reconstruction in the Apathya, Darevskia, Dinarolacerta, Iberolacerta, and Phoenicolacerta generic groups (Fig. 2).
An unexpected pattern emerges in the speciose Podarcis clade, where 19 out of 23 extant species are color polymorphic. If color morph loss or divergence progresses to speciation, we would expect to see polymorphic lineages give rise to monomorphic descendant lineages (Jamie and Meier 2020). Further, the only other comparative study on color polymorphism and diversification we are aware of found that color polymorphic lineages tend to be younger than monomorphic lineages (Hugall and Stuart-Fox 2012), which also aligns with early theoretical models of morphic speciation driven by morph loss and fixation (West-Eberhard 1986). However, the Podarcis group is not particularly young compared to other groups in the Lacertidae, nor does it exhibit many short branches like the color polymorphic Darevskia clade. So, what might explain persistent polymorphism in Podarcis? A recent genomic study that identified genes controlling color differences amongst morphs in Podarcis muralis also found some evidence for interspecific color allele sharing with other Podarcis species (Andrade et al. 2019). To retain color polymorphism after speciation, the alleles for different morphs must be present, either ancestrally or arising again through a novel mutation. Ancestral genetic variation may persist past speciation via introgression or standing ancestral variation (Andrade et al. 2019; Jamie and Meier 2020). If speciation rates are high, and genetic barriers between species are porous, there may be opportunities for introgressed morph alleles and morph persistence beyond complete speciation if a color polymorphic lineage comes into secondary contact with a monomorphic lineage (Jamie and Meier 2020). Taken together, these genomic and phylogenetic investigations of the Podarcis clade raise interesting implications for the role of hybridization and introgression in the evolution and long-term maintenance of color polymorphism and its relationship to speciation rates (Jamie and Meier 2020).
Color Polymorphism is Associated With Rapid Diversification Rates
Theory suggests that dramatic intraspecific phenotypic diversity and the underlying processes that maintain it may promote rapid speciation in color polymorphic lineages (West-Eberhard 1986; Gray and McKinnon 2007; Forsman et al. 2008). We find evidence for this in the Lacertidae, where diversification rates are substantially faster in lineages in the color polymorphic state. Across many possible phylogenetic reconstructions of the Lacertidae, we consistently estimate that net diversification is almost double the rate in color polymorphic lineages than monomorphic lineages. Indeed, lacertids also exhibit faster character transition rates from color polymorphism to monomorphism, which is consistent with the theory that suggests speciation occurs by morph loss and fixation of remaining morphs (West-Eberhard 1986). Trait simulations and state-speciation extinction models run on many possible trees, including a ML time tree inferred with a large phylogenomic data set (Garcia-Porta et al. 2019), suggest that it is unlikely that the shape of the Lacertidae phylogeny produces false estimates of trait-dependent diversification. These findings are also supported by empirical studies that show repeated loss, fixation, and rapid divergence of morph types among populations of color polymorphic species (Corl et al. 2010b).
Animal color and pattern are important traits involved in processes such as mate choice, species recognition, and sexual selection, which can all play a role in accelerating speciation (Houde and Endler 1990; Roulin 2004). Across many color polymorphic species, morph color is often involved in intraspecific visual signaling to communicate myriad messages in a variety of social and environmental contexts (Gray and McKinnon 2007). In social contexts, morph color can indicate reproductive strategy (Sinervo and Lively 1996) and morph color is often a factor in mate choice (Pryke and Griffith 2007). In birds, reptiles, and fish, the prevailing environment and lighting conditions affect the efficacy and transmission of signals displayed by different color morphs (Gray and McKinnon 2007), and color morphs may segregate microhabitat to optimize signal transmission (Endler 1984). Thus, if sexual and/or natural selection pressures shift away from balancing color polymorphism toward favoring the phenotype of one or several morphs over another, divergent or directional selection could result in morph loss from a population. Because color polymorphic species inherently possess extreme variation, there exists increased opportunity for selection or drift to operate against any one of several distinct color morph phenotypes, which may explain elevated diversification rates in color polymorphic lineages. Theoretical expectations and empirical studies of populations show that morph loss and fixation can result in rapid divergence (West-Eberhard 1986; Corl et al. 2010a, 2010b), but the microevolutionary processes operating within and between populations that disrupt balanced color polymorphisms and generate divergence remain less understood and generalizable (Chelini et al. 2021). Further study is needed to quantify the relative roles of natural selection, sexual selection, and drift in color polymorphism maintenance and speciation (Chunco et al. 2007).
Ultimately, we show the color polymorphic condition in lacertids is associated with elevated diversification rates. Species have many traits, and it is unlikely that a single trait is the only factor that accounts for increased or decreased diversification rates. Indeed, the best fit model was trait-dependent diversification that included additional unobserved “hidden states” that are correlated with color polymorphism. The inclusion of hidden states in the HiSSE framework ameliorates confounding effects of unmeasured correlated traits on diversification by allowing for greater rate heterogeneity (Caetano et al. 2018; Patton et al. 2020), and thus alternative SSE models in our study measure the effect of color polymorphism while controlling for other correlated traits on diversification rates in the Lacertidae. Color polymorphism is usually accompanied by alternative morph-specific ecological, morphological, physiological, and behavioral syndromes, or correlated traits (Lattanzio and Miles 2016; Huyghe et al. 2009a, 2009b; Sinervo and Lively 1996; Sinervo and Svensson 2002). Here, color and other heritable traits are likely subject to multivariate selection, wherein correlational selection builds up genetic correlations through linkage disequilibrium at loci underlying the traits (Sinervo and Svensson 2002). Correlation between color morphs and traits related to fitness, such as reproductive strategy (Sinervo and Lively 1996; Galeotti et al. 2013), or reproductive hormone levels (Huyghe et al. 2009b), or body size (Brock et al. 2020 in press), can produce color morphs with alternative adaptations that occupy different adaptive peaks (West-Eberhard 1986). When a color polymorphic lineage with multiple balanced adaptive peaks faces strong or novel selective forces, one or more of the peaks may shift, and a morph or morphs must cross “valleys” of selection to persist else they are lost. Another interesting possibility to explore in future studies is the relationship of habitat diversity to color polymorphism and diversification dynamics. Conceptual models suggest that habitat heterogeneity may promote color polymorphism, and divergent selection between populations could drive morph divergence and speciation (Forsman et al. 2008) and have also been shown to be related to sexual selection in lizards (Östman and Stuart-Fox 2011). Thus, the nature of color polymorphism and correlated traits could increase the potential for color polymorphism to contribute to the divergence amongst morphs and speciation.
Color Polymorphism: Linking Microevolutionary Process and Macroevolutionary Pattern
Color polymorphism is widespread throughout the tree of life, but our understanding of the mechanisms underlying morph evolution and the processes that influence the shape of the tree remain fragmented. The evolutionary mechanisms that maintain alternative color phenotypes within a population are also likely involved in morph loss, divergence, and speciation (Harris et al. 1998). These population-level processes, particularly the effects of natural and sexual selection and their relative roles within and between populations, are of utmost interest (Jamie and Meier 2020). Color polymorphism is often studied at the level of a single species (Huyghe et al. 2009a,b; Corl et al. 2010a,b; Runemark et al. 2010), but macroevolutionary perspectives will provide deeper insights into the origin, duration of maintenance, and interspecific persistence of color polymorphism (Harris et al. 1998; Jamie and Meier 2020). Very few empirical studies link population-level evolutionary processes and the evolution of color polymorphism at the macroevolutionary scale (Hugall and Stuart-Fox 2012; Willink et al. 2019). Studies that investigate trait variation within species and use biologically meaningful versions of those inputs at the between-species level with the use of comparative methods are needed (Gray and McKinnon 2007). Such investigations will illuminate the connection between the evolutionary process and macroevolutionary pattern. Color polymorphisms offer ideal model systems to study how microevolutionary dynamics shape macroevolutionary patterns of diversification. Our results show that the Lacertidae, in particular, offer a promising avenue for interrogating the relative contributions of different forms of selection on alternative phenotypes, and how population-level color morph dynamics scale up to influence macroevolutionary patterns.
Acknowledgments
We would like to thank Jessica Blois, Jeremy Beaulieu, and Jeffrey McKinnon for their helpful comments during the preparation of our manuscript and Indiana Madden for her assistance in compiling phenotypic data for this project. Computation for phylogenetic analyses was made possible with assistance from Sarvani Chadalapaka and the many cores of the MERCED cluster (National Science Foundation Grant No. ACI-1429783). We would also like to thank the Herpetology Collections at the Zoologisches Forschungmuseum Alexander Koenig (Morris Flecks) and the University of Michigan Museum of Zoology (Gregory Schneider) for access to lacertid specimens.
Funding
This work was supported by a Graduate Student Research Award from the Society of Systematic Biologists awarded to K.M.B.
Supplementary Material
Data available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.k0p2ngf68.
References
- Allender C.J., Seehausen O., Knight M.E., Turner GF, Maclean N. 2003. Divergent selection during speciation of Lake Malawi cichlid fishes inferred from parallel radiations in nuptial coloration. Proc. Natl. Acad. Sci. USA 100:14074–14079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrade P., Pinho C., Pérez i de Lanuza G., Alfonso S., Brejcha J., Rubin C.-J., Wallerman O., Pereira P., Sabatino S.J., Bellati A., Pellitteri-Rosa D., Bosakova Z., Bunikis I., Carretero M.A., Feiner N., Marsik P., Paupério F., Salvi D., Soler L., While G.M., Uller T., Font E., Andersson L., Carneiro M. 2019. Regulatory changes in pterin and carotenoid genes underlie balanced color polymorphisms in the wall lizard. Proc. Natl. Acad. Sci. USA 116:5633–5642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arnold E.N. 1989. Towards the phylogeny and biogeography of the Lacertidae: relationships within an old-world family of lizards derived from morphology. Bull. Br. Museum Natural Hist. (Zool.) 55:209–237. [Google Scholar]
- Arnold E.N., Arribas O., Carranza S. 2007. Systematics of the Palaearctic and Oriental lizard tribe Lacertini (Squamata: Lacertidae: Lacertinae), with descriptions of eight new genera. Zootaxa 1430:1–86. [Google Scholar]
- Baeckens S., Edwards S., Huyghe K., Van Damme R. 2015. Chemical signaling in lizards: an interspecific comparison of femoral pore numbers in Lacertidae. Biol. J. Linnean Soc. 114:44–57. [Google Scholar]
- Baeckens S., Martín J., García-Roa R., Pafilis P., Huyghe K., Van Damme, R. 2017. Environmental conditions shape the chemical signal design of lizards. Funct. Ecol. 32(2):566–580. [Google Scholar]
- Beaulieu J.M., O’Meara B.C. 2016. Detecting hidden diversification shifts in models of trait-dependent speciation and extinction. Syst. Biol. 65(4):584–601. [DOI] [PubMed] [Google Scholar]
- Bouckaert R., Heled J., Kühnert D., Vaughan T., Wu C.-H., Xie D., Suchard M.A., Rambaut A., Drummond A. 2014. BEAST 2: a software platform for Bayesian evolutionary analysis. PLoS Comput. Biol 10(4):e1003537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boughman J.W. 2001. Divergent sexual selection enhances reproductive isolation in sticklebacks. Nature 411(6840):944–948. [DOI] [PubMed] [Google Scholar]
- Brock K.M., Baeckens S., Donie C.M., Martín J., Pafilis P., Edwards D.L. 2020. Trait differences among discrete morphs of a color polymorphic lizard, Podarcis erhardii. PeerJ 8:e10284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caetano D.S., O’Meara B.C., Beaulieu J.M. 2018. Hidden state models improve state-dependent diversification approaches, including biogeographical models. Evolution 72(11):2308–2324. [DOI] [PubMed] [Google Scholar]
- Chelini M.C., Brock K.M., Yeager J., Edwards D.L. 2021. Environmental drivers of sexual dimorphism in a lizard with alternative mating strategies. J. Evol. Biol. [DOI] [PubMed] [Google Scholar]
- Chunco A.J., McKinnon J.S., Servedio M.R. 2007. Microhabitat variation and sexual selection can maintain male color polymorphisms. Evolution 61(11):2504–2515. [DOI] [PubMed] [Google Scholar]
- Clark K., Karsch-Mizrachi I., Lipman D.J., Ostell J., Sayers E.W. 2016. GenBank. Nucleic Acids Res. 44(Database issue):D67-D72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corl A., Davis A.R., Kuchta S.R., Comendant T., Sinervo B. 2010a. Alternative mating strategies and the evolution of sexual size dimorphism in the side-blotched lizard, Uta stansburiana: a population-level comparative analysis. Evolution 64(1):79–96. [DOI] [PubMed] [Google Scholar]
- Corl A., Davis A.R., Kuchta S.R., Sinervo B. 2010b. Selective loss of polymorphic mating types is associated with rapid phenotypic evolution during morphic speciation. Proc. Natl. Acad. Sci. USA 107:4254–4259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corl A., Lancaster L.T., Sinervo B. 2012. Rapid formation of reproductive isolation between two populations of side-blotched lizards, Uta stansburiana. Copeia 2012(4):593–602. [Google Scholar]
- Darriba D., Taboada G.L., Doallo R., Posada D. 2012. jModelTest 2: more models, new heuristics and parallel computing. Nat. Methods 9(8):772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drummond A.J., Ho S.Y., Phillips M.J., Rambaut A. 2006. Relaxed phylogenetics and dating with confidence. PLoS Biol. 4(5):e88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards S., Vanhooydonck B., Herrel A., Measey G.J., Tolley K.A. 2012. Convergent evolution associated with habitat decouples phenotype from phylogeny in a clade of lizards. PLoS One 7(12):e51636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Endler J.A. 1984. Natural and sexual selection on color patterns in poeciliid fishes. In: Zaret T.M., editors. Evolutionary ecology of neotropical freshwater fishes. Developments in environmental biology of fishes, vol. 3. Dordrecht: Springer. p. 95–111. [Google Scholar]
- Felsenstein J. 1985. Phylogenies and the comparative method. Am. Nat., 125: 1–15. [Google Scholar]
- Ford E.B. 1945. Polymorphism. Biol. Rev. 20:73–88. [Google Scholar]
- Forsman A, Ahnesjö J, Caesar S, Karlsson M. 2008. A model of ecological and evolutionary consequences of color polymorphism. Ecology 89:34–40. [DOI] [PubMed] [Google Scholar]
- Fu J. 1998. Toward the phylogeny of the family Lacertidae: implications from mitochondrial DNA 12S and 16S gene sequences (Reptilia: Squamata). Mol. Phylogenet. Evol. 9:118–130. [DOI] [PubMed] [Google Scholar]
- Fu J. 2000. Toward the phylogeny of the family Lacertidae —- why 4708 base pairs of mtDNA sequences cannot draw the picture. Biol. J. Linnean Soc. 1: 203–21. [Google Scholar]
- Galeotti P., Rubolini D., Dunn P.O., Fasola M. 2003. Colour polymorphism in birds: causes and functions. J. Evol. Biol. 16:635–646. [DOI] [PubMed] [Google Scholar]
- Galeotti P., Sacchi R., Pellitteri-Rosa D., Bellati A., Cocca W., Gentilli A., Scali S., Fasola M. 2013. Colour polymorphism and alternative breeding strategies: effects of parent’s colour morph on fitness traits in the Common wall lizard. Evol. Biol. 40: 385–394. [Google Scholar]
- Garcia-Porta J., Irisarri I., Kirchner M., Rodríguez A., Kirchhof S., Brown J.L., MacLeod A., Turner A.P., Faraham A., Albaladejo G., Crnobrnja-Isailovic J., Göçmen B., Harris D.J., Jiménez-Robles O., Joger U., Glavas O.J., Karis M., Koziel G., Künzel S., Lyra M., Miles D., Nogales M., Oguz M.A., Pafilis P., Rancilhac L., Rodríguez N., Concepción B.R., Sanchez E., Salvi D., Slimani T., S’khifa A., Qashqaei A.T., Zagar A., Lemmon A., Lemmon E.M., Carretero M.A., Carranza S., Philippe H., Sinervo B., Müller J., Vences M., Valero C.W. 2019. Environmental temperatures shape thermal physiology as well as diversification and genome-wide substitution rates in lizards. Nat. Commun. 10(1):1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grant B.S., Cook A.D., Clarke C.A., Owen D.F. 1998. Geographic and temporal variation in the incidence of melanism in peppered moth populations in America and Britain. J. Heredity 89:465–471. [Google Scholar]
- Gray S.M., McKinnon J.S. 2007. Linking color polymorphism maintenance and speciation. Trends Ecol. Evol. 22(2):71–79. [DOI] [PubMed] [Google Scholar]
- Harris D.J., Arnold E.N., Thomas R.H. 1998. Relationships of lacertid lizards (Reptilia: Lacertidae) estimated from mitochondrial DNA sequences and morphology. Proc. R. Soc. Lond. B 265:1939–1948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heled J., Drummond A. 2010. Bayesian inference of species trees from multilocus data. Mol. Biol. Evol. 27(3):570–580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hipsley C.A., Himmelmann L., Metzler D., Müller J. 2009. Integration of Bayesian molecular clock methods and fossil-based soft bounds reveals early Cenozoic origin of African lacertid lizards. BMC Evol. Biol. 9:151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Houde A.E., Endler J.A. 1990. Correlated evolution of female mating preferences and male color patterns in the guppy Poecilia reticulata. Science 248(4961):1405–1408. [DOI] [PubMed] [Google Scholar]
- Huelsenbeck J., Rannala B., Masly J.P. 2000. Accommodating phylogenetic uncertainty in evolutionary studies. Science 5475:2349–2350. [DOI] [PubMed] [Google Scholar]
- Hugall A.F., Stuart-Fox D. 2012. Accelerated speciation in colour polymorphic birds. Nature 485:631–634. [DOI] [PubMed] [Google Scholar]
- Huxley J. 1955. Morphism and evolution. Heredity 9(1):1–52. [Google Scholar]
- Huyghe K., Herrel A., Adriaens D., Tadiæ Z., Van Damme R. 2009a. It is all in the head: morphological basis for differences in bite force among colour morphs of the Dalmatian wall lizard. Biol. J. Linnean Soc. 96(1):13–22. [Google Scholar]
- Huyghe K., Husak J.F., Herrel A., Tadić Z., Moore I.T., Van Damme R., Vanhooydonck B. 2009b. Relationships between hormones, physiological performance and immunocompetence in a color-polymorphic lizard species, Podarcis melisellensis. Hormones Behav. 55:488–494. [DOI] [PubMed] [Google Scholar]
- Jamie G.A., Meier J.I. 2020. Persistence of polymorphisms across species radiations. Trends Ecol. Evol. 35(9):795–808. [DOI] [PubMed] [Google Scholar]
- Jonsson B. 2001. Polymorphism and speciation in Arctic charr. J. Fish Biol. 58:605–638. [Google Scholar]
- Lattanzio M.S., Miles D.B. 2016. Trophic niche divergence among colour morphs that exhibit alternative mating tactics. R. Soc. Open Sci. 3(4):150531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leimar O. 2005. The evolution of phenotypic polymorphisms: randomized strategies versus evolutionary branching. Am. Nat. 165(6):669–681. [DOI] [PubMed] [Google Scholar]
- López P., Moreira P.L., Martín J. 2009. Chemical polymorphism and chemosensory recognition between Iberolacerta monticola lizard color morphs. Chem. Senses 34(8):723–731. [DOI] [PubMed] [Google Scholar]
- Louca S., Pennell M.W. 2020. Extant timetrees are consistent with a myriad of diversification histories. Nature 580:502–505. [DOI] [PubMed] [Google Scholar]
- Maddison W.P. 1997. Gene trees in species trees. Syst. Biol. 46(3):523–536. [Google Scholar]
- Maddison W.P., Midford P.E., Otto S.P. 2007. Estimating a binary character’s effect on speciation and extinction. Syst. Biol. 64:127–136. [DOI] [PubMed] [Google Scholar]
- Mayer W., Pavlicev M. 2007. The phylogeny of the family Lacertidae (Reptilia) based on nuclear DNA sequences: convergent adaptations to arid habitats within the subfamily Eremiainae. Mol. Phylogenet. Evol. 44:1155–1163. [DOI] [PubMed] [Google Scholar]
- McCormack J.E., Huang H., Knowles L.L. 2009. Maximum likelihood estimates of species trees: how accuracy of phylogenetic inference depends upon the divergence history and sampling design. Syst. Biol. 58(5):501–508. [DOI] [PubMed] [Google Scholar]
- McLean C.A., Stuart-Fox D., Moussalli A. 2014. Phylogeographic structure, demographic history and morph composition in a colour polymorphic lizard. J. Evol. Biol. 27(10):2123–2137. [DOI] [PubMed] [Google Scholar]
- Morlon H. 2014. Phylogenetic approaches for studying diversification. Ecol. Lett. 17:508–525. [DOI] [PubMed] [Google Scholar]
- Morlon H., Hartig F., Robin S. 2020. Prior hypotheses or regularization allow inference of diversification histories from extant timetrees. bioRxiv, doi: 10.1101/2020.07.03.185074. [DOI] [Google Scholar]
- Nydam R.L., Cifelli R.L. 2002. Lizards from the lower cretaceous (Aptian-Albian) antlers and cloverly formations. J. Vertebr. Paleontol. 22:286–298. [Google Scholar]
- O’Meara B.C., Beaulieu J.M. 2016. Past, future, and present of state-dependent models of diversification. Am. J. Bot., 103(5):7972–7975. [DOI] [PubMed] [Google Scholar]
- Oppel M. 1811. Die Ordnungen, Familien und Gattungen der Reptilien, als Prodrom einer Naturgeschichte derselben. Munchen: Joseph Lindauer, xii. p. 87. [Google Scholar]
- Östman Ö., Stuart-Fox D. 2011. Sexual selection is positively associated with ecological generalism among Agamid lizards. J. Evol. Biol. 24:733–740. [DOI] [PubMed] [Google Scholar]
- Paradis E., Schliep K. 2018. ape 5.0: an environment for modern phylogenetics and evolutionary analyses in R. Bioinformatics 35:526–528. [DOI] [PubMed] [Google Scholar]
- Patton A.H., Margres M.J., Epstein B., Eastman J., Harmon L.J., Storfer A. 2020. Hybridizing salamanders experience accelerated diversification. Sci. Rep. 10(1):1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pavlicev M., Mayer W. 2009. Fast radiation of the subfamily Lacertinae (Reptilia: Lacertidae): history or methodological artefact? Mol. Phylogenet. Evol. 52:727–734. [DOI] [PubMed] [Google Scholar]
- Pérez i de Lanuza G., Bellati A., Pellitteri-Rosa D., Font E., Carretero M.A. 2019. Colour variation between different lineages of a colour polymorphic lizard. J. Zool. 308(3):175–187. [Google Scholar]
- Pérez i de Lanuza G., Carretero M.A., Font E. 2017. Intensity of male-male competition predicts morph diversity in a color polymorphic lizard. Evolution 71(7):1832–1840. [DOI] [PubMed] [Google Scholar]
- Portik D.M., Bell R.C., Blackburn D.C., Bauer A.M., Barratt C.D., Branch W.R., Burger M., Channing A., Colston T.J., Conradie W., Dehling J.M., Drewes R.C., Ernst R., Greenbaum E., Gvozdík V., Harvey J., Hillers A., Hirschfeld M., Jongsma G.F.M., Kielgast J., Kouete M.T., Lawson L.P., Leaché A.D., Loader S.P., Lötters S., Van Der Meiden A., Menegon M., Müller S., Nagy Z.T., Ofori-Boateng C., Ohler A., Papenfuss T.J., Rößler D., Sinsch U., Rödel M.O., Veith M., Vindum J., Zassi-Boulou A.G., McGuire J. 2019. Sexual dichromatism drives diversification within a major radiation of African amphibians. Syst. Biol. 68(6):859–875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Portik D.M., Wood P.L., Grismer J.L., Stanley E.L., Jackman T.R. 2012. Identification of 104 rapidly-evolving nuclear protein-coding markers for amplification across scaled reptiles using genomic resources. Conserv. Genet. Resour. 4:1–10. [Google Scholar]
- Pryke S.R., Griffith S.C. 2007. The relative role of male vs female mate choice in maintaining assortative pairing among discrete colour morphs. J. Evol. Biol. 20(4):1512–1521. [DOI] [PubMed] [Google Scholar]
- Pyron R.A., Burbrink F.T., Wiens J.J. 2013. A phylogeny and revised classification of Squamata, including 4161 species of lizards and snakes. BMC Evol. Biol. 13: 1–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rabosky D.L., Grundler M., Anderson C., Title P., Shi J.J., Brown J.W., Huang H., Larson J.G. 2014. BAMMtools: an R package for the analysis of evolutionary dynamics on phylogenetic trees. Methods Ecol. Evol. 5(7):701–707. [Google Scholar]
- Revell L.J. 2012. phytools: an R package for phylogenetic comparative biology (and other things). Methods Ecol. Evol. 3:217–223. [Google Scholar]
- Rosenblum E.B., Sarver B.A.J., Brown J.W., Des Roches S., Hardwick K.M., Hether T.D., Eastman J.M., Pennell M.W., Harmon L.J. 2012. Goldilocks meets Santa Rosalia: an ephemeral speciation model explains patterns of diversification across time scales. Evol. Biol. 39:255–261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roulin A. 2004. The evolution, maintenance and adaptive function of genetic colour polymorphism in birds. Biol. Rev. 79:815–848. [DOI] [PubMed] [Google Scholar]
- Runemark A., Hansson B., Pafilis P., Valakos E., Svensson E. 2010. Island biology and morphological divergence of the Skyros wall lizard Podarcis gaigeae: a combined role for local selection and genetic drift on color morph frequency divergence? BMC Evol. Biol. 10(269):1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sacchi R., Scali S., Gentilli A., Fasola M. 2007. Microgeographic variation of colour morph frequency and biometry of common wall lizards. J. Zool. 273(4):389–396. [Google Scholar]
- Seehausen O., Schluter D. 2004. Male-male competition and nuptial-color displacement as a diversifying force in Lake Victoria cichlid fishes. Proc. R. Soc. Lond. Ser. B 271:1345–1353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinervo B., Lively C.M. 1996. The rock-paper-scissors game and the evolution of alternative male strategies. Nature 380:240–243. [Google Scholar]
- Sinervo B., Svensson E. 2002. Correlational selection and the evolution of genomic architecture. Heredity 89:329–338. [DOI] [PubMed] [Google Scholar]
- Speybroeck J., Beukema W., Bok B., Van Der Voort J. 2016. Field guide to the amphibians and reptiles of Britain and Europe. London, UK: Bloomsbury Publishing Plc. [Google Scholar]
- Stuart-Fox D., Aulsebrook A., Rankin K.J., Dong C.M., McLean C.A. 2020. Convergence and divergence in lizard colour polymorphisms. Biol. Rev. 96(1):289–309. [DOI] [PubMed] [Google Scholar]
- Sues H.D., Olsen P.E. 1990. Triassic vertebrates of Gondwanan aspect from the Richmond Basin of Virginia. Science 249:1020–1023. [DOI] [PubMed] [Google Scholar]
- Sullivan R.M. 1985. A new middle Paleocene (Torrejonian) rhineurid amphisbaenian Plesiorhineura tsentasi new genus, new species, from the San Juan Basin, New Mexico. J. Paleontol. 59:1481–1485. [Google Scholar]
- Svensson E. 2017. Back to basics: using colour polymorphisms to study evolutionary processes. Mol. Ecol. 26(8):2204–2211. [DOI] [PubMed] [Google Scholar]
- Valakos E., Pafilis P., Sotiropoulos K., Lymberakis P., Maragou P., Foufopoulos J. 2008. The amphibians and reptiles of Greece. Edition Chimaira, Frankfurt, Germany. [Google Scholar]
- Vercken E., Clobert J. 2008. Ventral colour polymorphism correlates with alternative behavioural patterns in female common lizards (Lacerta vivipara). Ecoscience 15:320–326. [Google Scholar]
- West-Eberhard M.J. 1986. Alternative adaptations, speciation, and phylogeny (a review). Proc. Natl. Acad. Sci. USA 83:1388–1392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White T.E., Kemp D.J. 2016. Colour polymorphism. Curr. Biol. 26:R515-R522. [DOI] [PubMed] [Google Scholar]
- Willink B., Duryea M.C., Svensson E. 2019. Macroevolutionary origin and adaptive function of a polymorphic female signal involved in sexual conflict. Am. Nat. 194(5):707–724. [DOI] [PubMed] [Google Scholar]





