Abstract
This paper suggests values or probability distributions for a variety of parameters used in estimating internal doses from radioactive fallout due to ingestion of food. Parameters include those needed to assess the interception and initial retention of radionuclides by vegetation, translocation of deposited radionuclides to edible plant parts, root uptake by plants, transfer of radionuclides from vegetation into milk and meat, transfer of radionuclides into non-agricultural plants and wildlife, and transfer from food and drinking water to mother's milk (human breast milk). The paper includes discussions of the weathering half-life for contamination on plant surfaces, biological half-lives of organisms, food processing (culinary factors), and contamination of drinking water. As appropriate, and as information exists, parameter values or distributions are specific for elements, chemical forms, plant types, or other relevant characteristics. Information has been obtained from the open literature and from publications of the International Atomic Energy Agency. These values and probability distributions are intended to be generic; they should be reviewed for applicability to a given location, time period, or season of the year, as appropriate. In particular, agricultural practices and dietary habits may vary considerably both with geography and over time in a given location.
Key words: fallout, environmental transport, food chain, ingestion
INTRODUCTION
The present paper provides parameter values and distributions for use in estimating radionuclide activity concentrations in foodstuffs and drinking water following deposition of radioactive fallout. The activity concentrations in foodstuffs and drinking water are based on estimated deposition densities (Beck et al. 2022) and are used to estimate internal doses due to ingestion of the foodstuffs (Anspaugh et al. 2022) as part of an overall dose assessment for a given nuclear fallout event (Simon et al. 2022). Anspaugh et al. (2022) describe two methods for estimation of the internal dose from ingestion of contaminated foods: an aggregated approach based on a time-integrated intake of radionuclides per unit deposition and the traditional method based on examination of individual processes. The parameters presented here are intended for use with the relevant individual processes considered in the traditional method. This paper is part of a proposed comprehensive schema for dose assessments for exposures to radioactive fallout from nuclear detonations (Simon et al. 2022).
Processes included
This paper includes parameters commonly used for assessment of the following processes: interception of radionuclides by plants and initial retention of the radionuclides on the plants (for both dry and wet deposition); weathering losses from vegetation; translocation of radionuclides into edible plant parts; transfer of radionuclides from soil to vegetation (root uptake); transfer of radionuclides from vegetation to milk and meat; transfer of radionuclides into non-agricultural food products; transfer of radionuclides into human breast milk; biological half-lives and corrections for non-equilibrium situations; processing of plant and animal products (culinary factors); and treatment of drinking water. The most important of these processes (interception and initial retention on plants, weathering losses from plants, transfer from soil to vegetation, transfer from vegetation to milk and meat, and transfer to mother's milk) are described by Anspaugh et al. (2022) as part of the "traditional" method for calculation of ingestion doses attributable to individual exposure pathways; other processes can be included as needed for specific assessments. Migration and fixation of radionuclides in soil, and consequent time-dependence of root uptake, are not addressed in this paper.
Anspaugh et al. (2022) also provide ingestion rates for key food types by age group. Dose coefficients by age group are provided by Anspaugh et al. (2022) and Melo et al. (2022). The approaches are generic, and thus the parameter values and distributions provided are generic. Parameters found to be important in estimation of ingestion doses for a given deposition event should be carefully evaluated for applicability of the values or distributions for the specific situation.
Several types of information should be site-specific to the extent possible. For example:
Did it rain during the period of deposition, and if so, how much rainfall was there? Whether wet deposition was involved or only dry deposition affects both the amount of deposition at a location and the efficiency of initial interception and retention on plant surfaces.
For dry deposition, were leaf surfaces wet or dry at the time of deposition? This affects the efficiency of initial interception and retention on plant surfaces.
During what stage of the growing season did deposition occur? The stage of growth (which might be different for different crops) affects the amount of standing plant biomass available for interception of the deposition, whether edible parts of some plants received direct deposition, the time to harvest (the time available for translocation of deposited materials to edible plant parts), and the time between deposition and consumption of food or animal feed.
What local crops and food products are important in the local diet, and what are the ingestion rates? Ingestion rates of local crops and food products determine most of the ingestion dose; these rates might differ for various subsets of the local population. The importance of local food production may also affect the ability to replace the local food supply with uncontaminated food.
Plants, animals, and food types
Food types and food groups are commonly categorized for a specific assessment or fallout event, depending primarily on the agricultural and food-consumption practices for the given location and time of year. A general preliminary categorization includes plants and plant products (both cultivated and wild), milk and dairy products, domestic meat and animal products, wild meat and animal products, and fish and seafood.
The plants can be further subdivided by types, most commonly including leafy vegetables, non-leafy vegetables, legumes, grains and cereals, fruits, root crops, and tubers. Animal feed typically includes grasses and leguminous fodder and may be either fresh or stored (e.g., hay). In general, parameters such as soil-to-vegetation transfer factors (Fv) have been reported by plant type (a group of similar plants), rather than by individual species. Plants may be further characterized by description (e.g., tree vs. shrub vs. herbaceous), type of root system, typical harvest season, the parts of the plant used for food or fodder, and how the plant was typically used (e.g., fresh, dried, cooked, etc.). This information may be useful in selecting transfer coefficients, considering whether to include translocation, or estimating the time between the deposition event and harvest.
Plant or food types that are generally not consumed by people or livestock (at least not in the location of interest) can usually be excluded from an assessment, as can plant or food types that are generally imported from noncontaminated locations into the area of interest. For some crop plants (e.g., corn or wheat), it is possible that some fraction of the food consumed in the area of interest is grown locally and the remaining fraction is grown elsewhere; these fractions likely are different for different crops.
For plant-based items that are processed in some way from the plant as it is grown or harvested (e.g., dried foods, bread or other cereal products, local alcoholic beverages), the time necessary for processing these foods would permit additional radioactive decay between the time of harvest and the time of consumption. In addition, some types of processing may result in either lower or higher radionuclide activity concentrations in the processed food.
For milk and dairy products, important considerations are the time between milking and consumption (including time to make and age a milk product), any partitioning of radioactivity during processing (e.g., into butter or cheese), and backyard vs. commercial sources of milk. Important considerations for meat and meat products are the time between harvest and consumption (including time to make a product), and any partitioning of radioactivity during preparation and processing.
Radionuclides and elements
A list of 34 radionuclides (including primary radionuclides and key progeny of some primary radionuclides) likely to be most important for assessments of internal dose due to radioactive fallout is provided in Table 1 (Simon et al. 2022; Anspaugh et al. 2022).6 Where appropriate, element-specific information is provided in this report for the corresponding 17 elements. For some parameters, information is not available for all of the elements; however, radionuclides of these elements are generally of minor importance for internal doses from ingestion.
Table 1.
Radionuclides likely to be important contributors to internal dose following a fallout event.a
| Radionuclide | Half-lifeb | Decay constantc (d−1) | Radionuclide | Half-lifeb | Decay constantc (d−1) |
|---|---|---|---|---|---|
| 89Sr | 50.6 d | 1.37 × 10−2 | 132Te | 3.20 d | 2.16 × 10−1 |
| 90Sr | 28.9 a | 6.57 × 10−5 | 131I | 8.03 d | 8.64 × 10−2 |
| 91Sr | 9.65 h | 1.72 × 100 | 132I | 2.30 h | 7.25 × 100 |
| 92Sr | 2.66 h | 6.25 × 100 | 133I | 20.8 h | 7.99 × 10−1 |
| 90Y | 64.1 h | 2.60 × 10−1 | 135I | 6.58 h | 2.53 × 100 |
| 91Y | 58.5 d | 1.18 × 10−2 | 137Cs | 30.1 a | 6.31 × 10−5 |
| 92Y | 3.54 h | 4.70 × 100 | 140Ba | 12.8 d | 5.44 × 10−2 |
| 93Y | 10.2 h | 1.63 × 100 | 140La | 1.68 d | 4.13 × 10−1 |
| 97Zr | 16.7 h | 9.93 × 10−1 | 141La | 3.92 h | 4.24 × 100 |
| 97Nb | 72.1 m | 1.38 × 101 | 142La | 91.1 m | 1.10 × 101 |
| 99Mo | 66.0 h | 2.52 × 10−1 | 143Ce | 33.0 h | 5.04 × 10−1 |
| 99mTc | 6.01 h | 2.77 × 100 | 144Ce | 285 d | 2.43 × 10−3 |
| 103Ru | 39.2 d | 1.77 × 10−2 | 143Pr | 13.6 d | 5.11 × 10−2 |
| 105Ru | 4.44 h | 3.75 × 100 | 144Pr | 17.3 m | 5.78 × 101 |
| 106Ru | 372 d | 1.86 × 10−3 | 145Pr | 5.98 h | 2.78 × 100 |
| 103mRh | 56.1 m | 2.64 × 101 | 239Np | 2.36 d | 2.94 × 10−1 |
| 105Rh | 35.4 h | 4.70 × 10−1 | 239Pu | 24,100 a | 7.88 × 10−8 |
aIncludes radionuclides expected in fallout plus key decay products (see Simon et al. 2022; Anspaugh et al. 2022).
bFrom the National Nuclear Data Center (www.nndc.bnl.gov), rounded to 3 significant digits.
cThe decay constant λ = ln 2 / T1/2, where T1/2 is the unrounded half-life from the National Nuclear Data Center (www.nndc.bnl.gov).
Probability distributions vs. point estimates
For most parameters described in this paper, we provide both a probability distribution representing uncertainty about the true but unknown parameter value and the arithmetic mean of that distribution. The true but unknown value of a parameter refers to the single value that could, in theory, be identified if the data were available, but in the absence of complete data remains unknown and is represented by a probability distribution based on what data are available. In most cases, the probability distributions in this paper are based on reported geometric mean values of available measurements, with the bounds of the distribution based on reported ranges, when available. The arithmetic mean of each distribution is provided for use as a point estimate. For key processes, recommended single values or distributions are suggested by Anspaugh et al. (2022). For parameters that are important in a specific assessment, we recommend that information specific to the situation of concern be obtained and evaluated to select a value and/or distribution appropriate for that event and location.
To address uncertainty in the dose estimation or for more in-depth analyses, use of probabilistic methods (e.g., Monte Carlo analyses) is recommended, together with probability distributions for parameters associated with uncertain values. However, calculations based on point estimates of parameters may be useful as rapid first estimates or for screening estimates. Use of an arithmetic mean of the probability distribution as a point estimate for a parameter will generally be appropriate in such assessments, especially for those parameters used in equations that are either a multiplicative or additive series of uncertain variables (NCRP 2007a and b, 2012; Hoffman et al. 2011; UNSCEAR 2015). For multiplicative equations, the input of arithmetic mean values will produce the expectation value of the product of the multiplication. For those parameters that are highly uncertain and appear in the denominator of an otherwise multiplicative equation, the harmonic mean rather than the arithmetic mean should be considered to produce the expected value of the quotient (Kocher et al. 2018; Ferger 1931). For equations that are an additive series of uncertain parameters, input of arithmetic mean values for each parameter will produce the expectation value of the sum.
INTERCEPTION AND INITIAL RETENTION OF RADIONUCLIDES BY VEGETATION
Interception and initial retention of radionuclides by vegetation can be characterized in several different ways (Pröhl 2009; IAEA 2009, 2010). The simplest is the interception fraction fv, defined as the ratio of the activity of a given radionuclide initially retained on the vegetation per unit ground area (Bq m−2) and the total activity of that radionuclide deposited per unit ground area (Bq m−2) (Chadwick and Chamberlain 1970; Chamberlain 1970; Hoffman et al. 1992, 1995; Pröhl 2009). Because the interception fraction depends on the stage of plant development, it is often normalized for either the standing plant biomass (B, kgdry weight plant per m2 soil) or the leaf area index (LAI, m2 leaf surface per m2 soil). The interception fraction normalized for the standing plant biomass (fv/B) is often referred to as the mass interception factor (m2 kg−1dry weight). The interception fraction normalized for the leaf area index (fv/LAI) is sometimes referred to as the leaf area interception fraction (LAIF, unitless); this value can also be obtained by dividing the mass interception factor by the leaf surface area-to-mass ratio. Anspaugh et al. (2022) describe the use of fv,dry/B for deposition and initial retention of radionuclides on vegetation.
Both wet and dry conditions should be included in an assessment of vegetation interception of fallout particles, depending on the actual weather conditions at the time of a deposition event and for several days following the event. For purposes of an initial assessment, Anspaugh et al. (2022) assume that fv,wet/B for wet deposition is equal to fv,dry/B (based on Whicker and Kirchner 1987); however, as described later in this paper, retention of radionuclides may be different for wet deposition than for dry deposition, and dry deposition onto wet surfaces may result in higher values of vegetation interception than when dry deposition occurs onto dry surfaces. Thus, it is useful to assess wet deposition separately from dry deposition.
The main considerations with respect to element or radionuclide are the chemical form—primarily cations (most of the elements) vs. anions (e.g., iodine) vs. insoluble particles (plutonium)—and (as relevant) the particle size. Other main considerations are the type of plant in terms of its ability to intercept contamination and the parts of the plant that are consumed by humans or animals.
Interception of radionuclides by vegetation and initial retention on vegetation depend on the amount of standing vegetation (in turn dependent on the type of plant and the stage of growth), usually described in terms of B or LAI; whether the deposition is wet or dry; and the properties of the radionuclide (chemical form, charge, particle size). Wet deposition (deposition during a precipitation event) depends on the capacity of the plant canopy to retain water, the amount of rainfall, and the charge and size of the deposited particles; it is less dependent on the intensity of rainfall and the species of plant. For dry deposition, small particles tend to be retained better than large particles. Initial retention is higher on wet surfaces (at the time of deposition) than on dry surfaces, and cations are retained better than anions. The primary concern is particles less than about 50 μm in size, which are most readily retained by vegetation (Gordeev et al. 2006; Anspaugh et al. 2022; Beck et al. 2022). In the deposition model described by Beck et al. (2022), it is assumed that, for the most part, only particles < 50 μm in size will be intercepted and retained on vegetation. Thus, the activity of a given radionuclide i intercepted and initially retained by vegetation of a particular type is defined as the deposition density of radionuclide i on particles < 50 μm in size, DDi,veg (Bq m−2).
Experimental data for interception and initial retention are available for several specific plant types (mostly grasses and grains), radionuclide types, and particle sizes. Some more recent data for a few selected radionuclides (e.g., 131I, 134Cs, 137Cs) were collected following the Chernobyl and Fukushima nuclear power plant accidents. The approaches used for analyses of Trinity and Nevada Test Site (NTS) fallout are summarized below, followed by a discussion of general equations for dry and wet deposition.
Nevada Test Site fallout
The PATHWAY model (Whicker and Kirchner 1987) developed for assessments of NTS fallout estimated the partitioning of fallout deposition between the soil and vegetation surfaces but did not distinguish between dry and wet deposition. The fraction of fallout deposited on soil was estimated as
 |
and the fraction deposited on vegetation surfaces as
 |
where
fs = the fraction of fallout deposited on soil (unitless);
fv = the fraction of fallout deposited on vegetation surfaces (unitless);
α = the foliar interception constant (m2 kg−1dry weight); and
B = the above-ground biomass of vegetation (kgdry weight m−2).
The term α is empirical, with lower values for larger particle sizes (Whicker and Kirchner 1987; Whicker et al. 1990). A value of 2.8 m2 kg −1 was used for gases and small particles (less than a few microns), and a value of 0.39 m2 kg −1 was used for large fallout particles (Whicker and Kirchner 1987).
Trinity fallout
For the Trinity dose assessment (Bouville et al. 2020), separate calculations were used for dry and wet deposition, based on the general approaches described in following sections. The parameter values used to estimate dry and wet deposition in the Trinity assessment are summarized in Tables 2 and 3, respectively. For dry deposition, the approach was used only for the fraction of activity associated with particles < 50 μm in size; particles > 50 μm were assumed to be poorly intercepted and ineffectively retained by vegetation.
Table 2.
Summary of parameter values used in the Trinity assessment for estimation of activity concentrations on vegetation due to dry deposition of particles < 50 μm (from Bouville et al. 2020).
| Maximum interception | Foliar interception constant | Standing plant biomass | Interception fractiona | |
|---|---|---|---|---|
| Vegetation type | M (unitless) | α (m2 kg−1dry weight) | Ydry (kgdry weight m−2) | fdry (unitless) |
| Vegetables grown in gardens for local consumption | 0.85 | 2.8 | 0.3 | 0.48 |
| Fruit, berries, etc., directly exposed to fallout | 1 | 2.8 | 1 | 0.94 |
| Pasture grasses and vegetation grazed by livestock | 1 | 2.8 | 0.3 | 0.57 |
aCalculated from the information in the preceding columns, using eqn (3). The foliar interception constant α and standing plant biomass Ydry used by Bouville et al. (2020) are the same as the absorption coefficient μ and the standing plant biomass B, respectively, in eqn (3).
Table 3.
Summary of parameter values used in the Trinity assessment for estimation of activity concentrations on vegetation due to wet deposition (from Bouville et al. 2020).
| Parameter | Applicable situation | Value or distribution |
|---|---|---|
| Leaf area index LAI (unitless) | Depends on the plant canopy | Range from 0 (bare ground) to 10 (dense conifer forests) |
| Constant for chemical type k (unitless) | Anions (Br, I) | 0.5 |
| Monovalent cations (Rb, Cs) | 1 | |
| Polyvalent cations (Sr, Ba) | 2 | |
| Other elements (Fe, Co, Cu, As, Y, Zr, Nb, Mo, Tc, Ru, Rh, Pd, Ag, Cd, In, Sn, Sb, Te, La, Ce, Pr, Nd, Pm, Sm, U, Np, Pu) | 1.25 (uniform distribution from 0 to 2.5) | |
| Water storage capacity S (mm) | Grasses, cereals, corn (maize) | 0.2 |
| All other crops | 0.3 | |
| Constant for plant type and weather conditions c (unitless) | All situations | 3 (log-triangular distribution with modeb = 3, lower bound = 0.5, upper bound = 5) |
| Interception fractionafwet (unitless) | Iodine on grass | 0.36 |
| Iodine on other crops | 0.47 | |
| Cesium on grass | 0.55 | |
| Cesium on other crops | 0.64 | |
| Strontium on grass | 0.70 | |
| Strontium on other crops | 0.77 | |
| Uranium on grass | 0.60 | |
| Uranium on other crops | 0.69 |
aSample calculations for R = 1 mm, LAI = 4, using eqn (9) and values (or modes or midpoints of distributions) in this table.
bMode in logarithmic space.
General approach for dry deposition
Interception of dry deposition may be characterized by the original filtration model of Chamberlain (1970) as modified by Vandecasteele et al. (2001):
 |
where
fv,dry = the interception fraction for dry deposition (unitless);
M = the maximum interception (unitless);
μ = the absorption coefficient (m2 kg−1dry weight); and
B = the standing plant biomass (kgdry weight m−2).
The interception fraction fv,dry from eqn (3) is used to estimate the radionuclide activity concentrations on plants due to dry deposition:
 |
and
 |
where
DDi,veg,dry = the deposition density of radionuclide i initially intercepted and retained on vegetation due to dry deposition (Bq m−2);
Cveg,i,dry = the activity concentration of radionuclide i intercepted and initially retained on vegetation due to dry deposition (Bq kg−1dry weight);
DDi,dry = the total deposition density of radionuclide i deposited by dry deposition (Bq m−2);
fv,dry = the interception fraction (unitless) from eqn (3), calculated for the specific radionuclide and vegetation type; and
B = the standing plant biomass (kgdry weight m−2);
Suggested parameter distributions and point estimates are described below and summarized in Table 4.
Table 4.
Suggested probability distributions and arithmetic means for parameters used to calculate the interception fraction (fv,dry, unitless) for dry deposition.
| Parameter | Applicable situation | Distribution type | Distribution parameters | Arithmetic meana |
|---|---|---|---|---|
| M, maximum interception (unitless)b | crop plants | uniform | minimum 0.8; maximum 0.9 | 0.85 |
| non-crop plants | uniform | minimum 0.9; maximum 1.0 | 0.95 | |
|
B, standing plant biomass (kg m−2 dry weight)c |
grasses | log-uniform | minimum 0.005; maximum 0.8 | 0.16 |
| cereals/grains | log-uniform | minimum 0.01; maximum 2 | 0.38 | |
| herbaceous plants (small) | log-uniform | minimum 0.01; maximum 1.5 | 0.30 | |
| shrubs | log-uniform | minimum 0.05; maximum 3 | 0.72 | |
| treesd | log-uniform | minimum 2; maximum 20 | 7.8 | |
| cactus/succulents | log-uniform | minimum 0.05; maximum 20 | 3.3 | |
|
μ, absorption coefficient (m2 kg−1 dry weight)e |
dry surface | |||
| iodine vapor | log-triangularf | minimum 0.3; mode 3; maximum 10 | 2.6 | |
| methyl iodide | log-triangularf | minimum 0.001; mode 0.01; maximum 0.03 | 0.0084 | |
| particles 1–50 μm | log-triangularf | minimum 0.3; mode 3; maximum 10 | 2.6 | |
| wet surface | ||||
| iodine vapor | log-triangularf | minimum 1; mode 10; maximum 100 | 15 | |
| methyl iodide | log-triangularf | minimum 0.003; mode 0.03; maximum 0.1 | 0.026 | |
| particles, all sizes | log-uniform | minimum 0.1; maximum 10 | 2.1 |
aThe arithmetic mean of the indicated distribution; this value can be used as a point estimate in deterministic assessments.
bBased primarily on Chamberlain (1970) and Vandecasteele et al. (2001). Crop plants are generally set in rows, while non-crop plants (e.g., grass) could cover more of the ground surface area.
cBased on a review of the literature; sources included Scott and Billings (1964); Witherspoon and Taylor (1970); Dwyer (1971); Hufstader (1976); Lauenroth and Whitman (1977); Cunningham et al. (1979); Heinemann and Vogt (1980); Sharifi et al. (1982); Acevedo et al. (1983); Coppock et al. (1983); Millard et al. (1983); McLeod et al. (1984); Cox (1985); Cully and Cully (1989); Garcia de Cortázar and Nobel (1992); Owensby et al. (1993); Cassels et al. (1995); Gibbens et al. (1996); Han and Felker (1997); Vandecasteele et al. (2001); Choi et al. (2002); Stavast et al. (2005); Muldavin et al. (2008); Robertson et al. (2009); Bengtsson et al. (2012); Newingham et al. (2013); WELC (2013); Pearson et al. (2014); Moreno-de las Heras et al. (2015).
dAll above-ground parts (trunks, branches, leaves).
eBased on Martin (1965); Heinemann and Vogt (1980); Pinder et al. (1988); Madoz-Escande et al. (2005); Pröhl (2009).
fParameter values are for the log-triangular distribution as plotted in logarithmic space.
The maximum interception M has a default value of 1 (100% interception), consistent with Chamberlain's original model (Chamberlain 1970), but may have an empirical value less than 1, depending on plant type. Vandecasteele et al. (2001) reported an empirical value of 0.85 for spring wheat (cultivated in rows), but suggested that for pasture grass (not in rows), M would be more likely to reach a value of 1.
Values of the standing plant biomass B have been reported for a number of plant types and can vary with the season or stage of growth or the planting density. In principle, the standing plant biomass could be readily measured for specific plant types or ecosystems if necessary.
The absorption coefficient μ is the same as α, the foliar interception constant, in eqns (1) and (2); the value of μ depends on whether the plant surface is wet or dry (with generally higher values for dry deposition onto wet surfaces), the chemical form of the radionuclide (e.g., vapor vs. particle), and the particle size. A variety of experimentally obtained values of μ are available (reviewed by Pröhl 2009; see also Heinemann and Vogt 1980; Pinder et al. 1988).
Examples of point estimates for fv,dry and fv,dry/B based on eqn (3) and Table 4 are provided in Table 5 for pasture grass and herbaceous plants for both dry and wet vegetation surfaces and for both iodine vapor and particles < 50 μm in size. For purposes of the example, M (the maximum interception) is assumed to be 1.
Table 5.
Examples of estimates of the interception fraction (fv,dry, unitless) and the mass interception factor (fv,dry/B, m2 kg−1dry weight) for dry deposition, based on eqn (3) and Table 4.
| Parameter | Pasture grass | Herbaceous plants | ||
|---|---|---|---|---|
| M (unitless) | 1 | 1 | ||
| B (kg m−2 dry weight) | 0.16 | 0.3 | ||
| Dry vegetation surfaces | ||||
| Iodine vapor | Particles < 50 μm |
Iodine vapor | Particles< 50 μm | |
| μ (m2 kg−1 dry weight) | 2.6 | 2.6 | 2.6 | 2.6 |
| fv,dry (unitless) | 0.34 | 0.34 | 0.54 | 0.54 |
| fv,dry/B (m2 kg−1dry weight) | 2.1 | 2.1 | 1.8 | 1.8 |
| Wet vegetation surfaces | ||||
| Iodine vapor | Particles < 50 μm |
Iodine vapor | Particles < 50 μm |
|
| μ (m2 kg−1 dry weight) | 15 | 2.1 | 15 | 2.1 |
| fv,dry (unitless) | 0.91 | 0.29 | 0.99 | 0.47 |
| fv,dry/B (m2 kg−1dry weight) | 5.7 | 1.8 | 3.3 | 1.6 |
Empirical approach for dry deposition
An empirical approach for obtaining values for μ was proposed by Simon (1990) and Simon et al. (1990), based on previously published measurements for Nevada Test Site fallout. That approach estimated the absorption coefficient (called the vegetation interception parameter by Simon 1990 and Simon et al. 1990) as a function of either the distance from ground zero or the time of arrival (TOA) of the fallout at a point of interest using data over the TOA range from a few minutes to 25+ h and over a distance ranging from a few tens of km to about 300 km (Simon 1990):
 |
or
 |
where
μ = the absorption coefficient (m2 kg−1dry weight) for pasture grass and agricultural crops;
d = the distance from ground zero (km); and
TOA = the time of arrival of the fallout at the point of interest (h).
Simon (1990) also provided a functional relationship specifically for native range vegetation at similar distances:
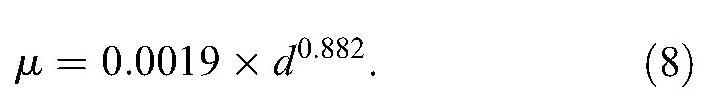 |
Based on empirically derived relationships, eqns (6), (7), and (8) are intended to account for changes in particle size and the corresponding interception and initial retention on vegetation (for a given vegetation type) with increasing distance or increasing time from the detonation site. These equations are based on the concept that close-in fallout will have a substantial fraction of large particles that are poorly retained (or quickly lost), while fallout at more distant locations will have a greater proportion of smaller (finer) particles that are better retained on the vegetation. However, the Simon model for μ depends only on distance or TOA and does not explicitly account for changes in the relative activity of specific fission and activation products in fallout due to fractionation with increasing distance or time of arrival; nor does it account for the change in particle sizes, and thus μ, as a function of distance from the plume centerline for the same TOA.
General approach for wet deposition
For a single deposition event, Pröhl (2009) proposed an equation for the interception fraction fv,wet based on the leaf area index, the amount of rainfall, the type of radionuclide, and the water storage capacity of the plant, with a maximum value of 1 (100% interception):
 |
where
fv,wet = the interception fraction for wet deposition (unitless);
LAI = the leaf area index (unitless);
k = a unitless constant dependent on the type of radionuclide;
S = the water storage capacity of the plant (mm);
R = the total amount of rainfall during a single event (mm); and
c = a unitless constant dependent on the type of plant and ambient conditions (e.g., evaporation).
The interception fraction fv,wet from eqn (9) is used to estimate the radionuclide activity concentrations on plants due to wet deposition:
 |
and
 |
where
DDi,veg,wet = the deposition density of radionuclide i initially intercepted and retained on vegetation due to wet deposition (Bq m−2);
Cveg,i,wet = the activity concentration of radionuclide i intercepted and initially retained on vegetation due to wet deposition (Bq kg−1dry weight);
DDi,wet = the total deposition density of radionuclide i deposited by wet deposition (Bq m−2);
fv,wet = the interception fraction (unitless) from eqn (9), calculated for the specific radionuclide, vegetation type, and rainfall amount; and
B = the standing plant biomass (kgdry weight m−2).
Suggested parameter distributions and point estimates are described below and summarized in Table 6.
Table 6.
Suggested probability distributions and arithmetic means for parameters used to calculate the interception fraction (fv,wet, unitless) for wet deposition.
| Parameter | Applicable situation | Distribution type | Distribution parameters | Arithmetic meana |
|---|---|---|---|---|
| k, dependent on element (unitless)b | anions (I) | triangular | minimum 0; mode 0.5; maximum 1 | 0.5 |
| monovalent cations (Cs) | triangular | minimum 0.5; mode 1; maximum 1.5 | 1 | |
| polyvalent cations (Sr, Ba) | triangular | minimum 1.5; mode 2; maximum 2.5 | 2 | |
| other elements (Y, Zr, Nb, Mo, Tc, Ru, Rh, Te, La, Ce, Pr, Np, Pu) | uniform | minimum 0; maximum 2.5 | 1.25 | |
| S, water storage capacity (mm)c | grasses, cereals, maize | log-uniform | minimum 0.1; maximum 6 | 1.44 |
| other crops, herbaceous plants (broad-leaved species), shrubs | log-uniform | minimum 0.1; maximum 10 | 2.15 | |
| trees | log-uniform | minimum 0.05; maximum 10 | 1.88 | |
| c (unitless)d | all plant types | log-triangulare | minimum 0.5; mode 3; maximum 5 | 2.19 |
aThe arithmetic mean of the indicated distribution; this value can be used as a point estimate in deterministic assessments.
bBased on Pröhl (2009) and Müller and Pröhl (1993). See also Bengtsson et al. (2014).
cBased on Pröhl (2009), IAEA (2009), and a review of the literature. Information was reported by or estimated from Clark (1940); Grah and Wilson (1944); Hamilton and Rowe (1949); Stoltenberg and Wilson (1950); Slatyer (1965); Corbett and Crouse (1968); Rutter et al. (1971/1972, 1975); West and Gifford (1976); Rutter and Morton (1977); Gash and Morton (1978); Gash (1979); Massmann (1983); Thompson (1986); Thurow et al. (1987); Scatena (1990); Návar and Bryan (1994); Domingo et al. (1998); Klaassen et al. (1998); Llorens and Gallart (2000); Liu (2001); Breuer et al. (2003); Kang et al. (2005); Toba and Ohta (2005); Keim et al. (2006); Pryet et al. (2012); Zhang et al. (2016). The water storage capacity was variously reported as water storage capacity, interception storage capacity, residual interception storage, residual storage, canopy interception, interception, water storage, adherent storage capacity, canopy storage capacity, surface storage capacity, canopy saturation, quantity of water on canopy when all surfaces are wet, wetting coefficient, or total interception loss.
eParameter values are for the log-triangular distribution as plotted in logarithmic space.
The constant k quantifies the ability of an element to attach to the vegetation (Pröhl 2009). Pröhl (2009) proposed values for k of 0.5 for anions (e.g., iodide, sulfate), 1 for monovalent cations (e.g., cesium), and 2 for polyvalent cations (e.g., strontium). The water storage capacity of the plant S depends on the type of plant; Pröhl (2009) proposed a value of 0.2 mm for grass, cereals, and corn (maize) and a value of 0.3 mm for all other crops. An earlier paper (Müller and Pröhl 1993) incorporated both k and S into a single retention coefficient. The distributions of k and S in Table 6 are based on these two papers, with additional elements added, plus additional information on water storage by vegetation. The available information for many elements is very sparse, hence the wide uniform distribution of k for "other elements."
Klaassen et al. (1998) define the water storage capacity S (mm) as "the maximum possible water storage after quick drainage has stopped" and point out that the exact definition of S may vary with different methods of estimating S. In principle, the total intercepted rainfall equals the water storage at the end of a rain event plus the water evaporated during the rain event (Klaassen et al. 1998), but Klaassen et al. consider evaporation during rain to be of lesser importance than water storage, at least for dense forest and continuous rain. Klaassen et al. (1998) also reported that indirect methods of estimating water storage (based on rainfall measurements inside and outside the forest) may underestimate by a factor of 2, in comparison with direct methods (direct observations of water storage and evaporation). The value of S also depends on whether it is estimated for the whole plant canopy (leaves, stems) or just part of the plant (e.g., leaves); values of S limited to edible portions of the plant are generally not available. Some information indicates that cactus may actively take up water droplets from fog (Ju et al. 2012; Liu et al. 2015), suggesting that, for a few plant types, rainwater could be taken up into the plant and not simply intercepted on the surface of the plant.
Grah and Wilson (1944) and Hamilton and Rowe (1949) specifically distinguish between the interception storage capacity (the total intercepted rainfall) and the water depth on the plant surface (the thickness of the water film on the vegetation). The total intercepted rainfall is a function of the depth of the water film on the vegetation and of the total surface area of the vegetation. In the studies by Grah and Wilson (1944) and Hamilton and Rowe (1949), the depth of the water film (mm) was approximately 1/10 of the total interception storage capacity (mm).
In effect, fv,wet in eqn (9) is a function of how much water the vegetation can hold (S, mm), divided by the rainfall (R, mm), i.e., the maximum fraction of rainfall (for a given rainfall event) that can be intercepted and retained on the vegetation. This in turn is multiplied by LAI, which accounts for density of the plant cover. For many purposes, the total water storage capacity (interception capacity) is the important parameter, because all of the water on the plant contributes to the radioactivity deposited on the plant. However, water storage capacity of vegetation may require further attention for a given assessment; e.g., with respect to the depth of water film on specific plant parts of interest.
Müller and Pröhl (1993) and Pröhl (2009) use the term ln(2)/3 rather than ln(2)/c. The term ln(2)/3 is based on an assumption that one-half of the storage capacity S of the vegetation is reached when the total rainfall R is equal to 3S (explained by Kinnersley and Scott 2001). However, for the present purpose, it is useful to consider this as ln(2)/c, where c is an uncertain constant that probably depends on the characteristics of the plant, the evaporative conditions, and the amount and intensity of the rainfall. For example, under some conditions (e.g., low rainfall, no wind), water loss from the plant could be minimal, in which case one-half the storage capacity may be reached when the rainfall equals one-half the assumed storage capacity (R = 0.5S, or c = 0.5). Or, in other situations (e.g., high rainfall, high wind), water loss from the plant could be higher than that assumed by Müller and Pröhl (1993) and Pröhl (2009), such that one-half the storage capacity is reached only when the rainfall is equal to 4 or 5 times the assumed storage capacity (R = 4S or R = 5S). Therefore, the proposed distribution for c (Table 6) ranges from 0.5 to 5.
Site-specific values of the rainfall amount R should be used. If that information is not available, a distribution of rainfall amounts for days in the relevant month during which rainfall actually occurs could be developed from available meteorological data for specific sites of interest.
Values of the leaf area index LAI depend on the crop or plant type and the stage of plant growth. LAI should be estimated for a given assessment, depending on the time of year and the local crops or plant types of importance. In an extensive literature review for temperate climates, Breuer et al. (2003) report a mean LAI of 6.2 (range, 0.4–16.2) for herbs, forbs, and grasses (pasture), and a mean of 3.8 (range, 1.8–10) for crops. These values are provided here as examples; they represent the mean and range of reported values of LAI across a variety of species, stages of plant growth, crop densities, and types of management (e.g., fertilization). Breuer et al. (2003) also provide LAI by plant species along with additional information (as available) and the original references. Other sources of information include Clark (1940); Witherspoon and Taylor (1970); Owensby et al. (1993); Han and Felker (1997); Vandecasteele et al. (2001); Kang et al. (2005); and Bengtsson et al. (2014).
Examples of point estimates for fv,wet and fv,wet/B based on eqn (9) and Table 6 are provided in Table 7 for pasture grass and other crops, for selected elements (iodine, cesium, strontium, plutonium), and for several rainfall amounts. For these examples, LAI = 6 for pasture grass and 4 for other crops; S = 1.4 mm for pasture grass and 2.2 mm for other crops; B = 0.16 kgdry weight m−2 for pasture grass and 0.3 kgdry weight m−2 for other crops; and c = 2.2 for all plant types.
Table 7.
Examples of estimates of the interception fraction (fv,wet, unitless) and the mass interception factor (fv,wet/B, m2 kg−1dry weight) for wet deposition, based on eqn (9) and Table 6.
| Parameter | Pasture grass | Other crops | ||||||
|---|---|---|---|---|---|---|---|---|
| LAI (unitless) | 6 | 1 | ||||||
| S (mm) | 1.4 | 2.2 | ||||||
| B (kg m−2 dry weight) | 0.16 | 0.3 | ||||||
| c (unitless) | 2.2 | 2.2 | ||||||
| Iodine | Cesium | Strontium | Plutonium | Iodine | Cesium | Strontium | Plutonium | |
| k (unitless) | 0.5 | 1 | 2 | 1.25 | 0.5 | 1 | 2 | 1.25 |
| R = 1 mm | ||||||||
| fv,wet (unitless) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| fv,wet/B (m2 kg−1dry weight) | 6.3 | 6.3 | 6.3 | 6.3 | 3.3 | 3.3 | 3.3 | 3.3 |
| R = 3 mm | ||||||||
| fv,wet (unitless) | 1 | 1 | 1 | 1 | 0.8 | 1 | 1 | 1 |
| fv,wet/B (m2 kg−1dry weight) | 6.3 | 6.3 | 6.3 | 6.3 | 2.8 | 3.3 | 3.3 | 3.3 |
| R = 10 mm | ||||||||
| fv,wet (unitless) | 0.4 | 0.8 | 1 | 0.9 | 0.4 | 0.7 | 0.9 | 0.8 |
| fv,wet/B (m2 kg−1dry weight) | 2.6 | 4.7 | 6.3 | 5.5 | 1.4 | 2.2 | 3.0 | 2.5 |
| R = 20 mm | ||||||||
| fv,wet (unitless) | 0.2 | 0.4 | 0.8 | 0.5 | 0.2 | 0.4 | 0.7 | 0.5 |
| fv,wet/B (m2 kg−1dry weight) | 1.3 | 2.6 | 4.7 | 3.2 | 0.7 | 1.4 | 2.2 | 1.6 |
A much simpler model for wet deposition has recently been proposed by Cristina et al. (2020). This model estimates f as a function of standing biomass (B) or both B and radionuclide type (anion vs. cation). For crops with horizontally oriented leaves (e.g., leafy vegetables, spinach, radishes), and for low values of LAI (i.e., early growth stages), good agreement with experimental data was obtained. Information on the wider utility of this simpler model (e.g., for other vegetation types, for later growth stages or higher values of B, or for a wider range of rainfall amounts) is not yet available.
Weathering half-life
Following initial interception and retention, activity concentrations of radionuclides deposited on plants can decrease over time due to growth dilution. In addition, some fraction of deposited radioactivity is lost from vegetation surfaces over time by means other than radioactive decay. The major processes by which radioactivity can be lost from above-ground vegetation include translocation to the roots, volatilization, evaporation, removal by rain or wind (or other disturbances), grazing by animals, and weathering of leaves or leaf surfaces (Chamberlain 1970; Chadwick and Chamberlain 1970; Miller and Hoffman 1983; Choi et al. 2002; IAEA 2009). Gordeev (2000) attributed all losses other than radioactive decay to growth dilution and preferential consumption of fresh grass by grazing animals. The amount of weathering loss is dependent on the radionuclide (e.g., its solubility), plant characteristics, and stage of plant development (e.g., growth dilution), as well as weather. Weathering loss may be substantially reduced for dormant vegetation (e.g., in winter; Chamberlain 1970; Chadwick and Chamberlain 1970; Miller and Hoffman 1983).
The weathering loss (reduction in activity concentration for any reason other than radioactive decay) is typically described in terms of a weathering half-life, Tw (d; Miller and Hoffman 1983; Choi et al. 2002; IAEA 2009) or an environmental loss constant (λenv, d−1) derived from the weathering half-life [λenv = ln(2)/Tw]. The weathering half-life, Tw, can be obtained from measurements of radionuclide activity concentration per unit mass of plant or per unit ground area (Miller and Hoffman 1983); for use with normalized estimates of deposition and interception, use of Tw values obtained on a unit mass basis (rather than a unit area basis) is suggested (Miller and Hoffman 1983). Miller and Hoffman (1983) also report generally larger values of Tw (slower weathering) for dormant vegetation as opposed to growing vegetation.
Some authors have reported short-term (fast component) and long-term (slow component) values of Tw, or values of Tw dependent on stage of plant growth (e.g., Russell 1965; Witherspoon and Taylor 1970; Millard et al. 1983; IAEA 2009; Bengtsson et al. 2014). This type of information could be used for time-dependent estimation of radionuclide activity concentrations. However, given the relative scarcity of information on weathering half-lives for different time periods or growth stages, together with the expectation that a fallout event would be an acute deposition event, use of a single weathering half-life for the whole event is probably adequate.
Reported values of the weathering half-life for various elements and vegetation types were reviewed by Miller and Hoffman (1983) and IAEA (2009). In general, values tend to be a bit lower for iodine and a bit higher for cesium compared with other elements. However, the reported information comes from a variety of studies, and the same set of plant types is not available for every element. Table 8 provides suggested probability distributions and point estimates of the weathering half-life for use for fallout events for both growing vegetation and dormant vegetation.
Table 8.
Suggested probability distributions and arithmetic means for the weathering half-life (Tw, d).a
| Element | Modeb | Minimum | Maximum | Arithmetic meanc |
|---|---|---|---|---|
| Growing vegetation | ||||
| I | 10 | 3 | 30 | 10.8 |
| Cs | 14 | 4 | 50 | 16.1 |
| Sr | 13 | 4 | 40 | 14.2 |
| All others | 15 | 4 | 60 | 17.8 |
| Dormant vegetation | ||||
| I | 22 | 5 | 50 | 19.7 |
| All others | 30 | 8 | 100 | 32.9 |
aAll distributions are log-triangular distributions (as plotted in logarithmic space) and are applicable for all plant types. Information sources included Martin (1965); Witherspoon and Taylor (1970); Heinemann and Vogt (1980); Simmonds and Linsley (1982); Millard et al. (1983); Miller and Hoffman (1983); Pinder and Doswell (1985); Pinder et al. (1987); Choi et al. (2002); IAEA (2009); Bengtsson et al. (2014).
bParameter values are for the log-triangular distribution as plotted in logarithmic space.
cThe arithmetic mean of the indicated distribution; this value can be used as a point estimate in deterministic assessments.
Translocation into edible plant parts
Over time, some fraction of radioactivity deposited on vegetation surfaces may be translocated to edible parts of the plant that were not themselves directly contaminated (IAEA 2009, 2010). This is of particular concern for cereals and grains, root vegetables and tubers, and fruits (including some vegetables). This process is commonly reported in terms of a translocation factor (ftr), defined here as the ratio of the activity in the edible part at harvest to the activity initially deposited, and expressed as a percentage, although several other methods have also been used (Choi et al. 2002; IAEA 2009). The translocation factor so defined includes the effects of weathering and growth dilution. Values of translocation factors depend on the plant characteristics, the element (particularly its mobility in the plant), the stage of plant growth at the time of deposition, and characteristics of the deposition (e.g., wet or dry). For example, available data for 137Cs and 90Sr indicate that maximum translocation to grain occurs when the deposition event is 30 d (strontium) or 45 d (cesium) before harvesting (IAEA 2009).
Table 9 provides suggested probability distributions and point estimates for the translocation factor (ftr, %) for six elements based on reported information summarized by element and plant type (IAEA 2009, 2010). For cereals and grains, some information is available by stage of plant growth, but information on stage of plant growth is generally not available for root vegetables, tubers, or fruits (IAEA 2009, 2010). The distributions presented in Table 9 include considerable uncertainty, due both to limitations in the available data and to allowing for differences in plant types and growth stages.
Table 9.
Suggested probability distributions and arithmetic means for the translocation factor (ftr, %).a
| Element | Plant types | Distribution type | Distribution parameters | Arithmetic meanb |
|---|---|---|---|---|
| Cs | all plant types | log-uniform | minimum 0.5; maximum 50 | 10.7 |
| Ce | all plant types | log-uniform | minimum 0.1; maximum 10 | 2.15 |
| Sr, Ba | all plant types | log-uniform | minimum 0.01; maximum 10 | 1.45 |
| Ru, Te | all plant types | log-uniform | minimum 0.01; maximum 1 | 0.215 |
aBased on information summarized in IAEA (2010). The distributions are intended to include all growth stages.
bThe arithmetic mean of the indicated distribution; this value can be used as a point estimate in deterministic assessments.
TRANSFER OF RADIONUCLIDES FROM SOIL TO VEGETATION (ROOT UPTAKE)
Over time, radionuclides initially deposited on soil, or on plants that are eventually added to the soil layer, can be taken up by plants. This process is typically not important in the early period after a deposition event, but it contributes to the long-term exposure of humans through ingestion of the contaminated plants and ingestion of milk and meat from animals consuming contaminated plants. For most radionuclides, depending on the time of year that a deposition event occurs, direct deposition and possibly translocation would be expected to dominate in terms of the radionuclide activity concentrations in or on vegetation during the current growing season, while soil-to-plant uptake is unlikely to be important until time periods later in the growing season or after the first harvest of vegetation initially contaminated by direct deposition (dry or wet) of fallout.
Table 10 provides suggested probability distributions and point estimates for the soil-to-vegetation transfer coefficient (Fv, Bq kg−1dry weight plant tissue per Bq kg−1 dry soil) for a variety of plant types (as information is available) for all 17 elements. Where possible, geometric means (GM) were obtained from a review by the IAEA (2009, 2010); these were used as the modes of log-triangular distributions (in logarithmic space),7 and the minimum and maximum are the reported minimum and maximum values.
Table 10.
Suggested probability distributions and arithmetic means for the soil-to-vegetation transfer coefficient (Fv, Bq kg−1dry weight plant tissue per Bq kg−1 dry soil).a
| Element | Plant type | Plant compartment | Modeb | Minimum | Maximum | Arithmetic meanc |
|---|---|---|---|---|---|---|
| Sr | Cereals | Grain | 1.1 × 10−1 | 3.6 × 10−3 | 1.0 × 100 | 1.3 × 10−1 |
| Cereals | Stems and shoots | 1.1 × 100 | 1.5 × 10−1 | 9.8 × 100 | 1.7 × 100 | |
| Maize | Grain | 3.2 × 10−1 | 2.0 × 10−3 | 2.6 × 100 | 2.9 × 10−1 | |
| Maize | Stems and shoots | 7.3 × 10−1 | 1.2 × 10−1 | 3.0 × 100 | 7.9 × 10−1 | |
| Leafy vegetables | Leaves | 7.6 × 10−1 | 3.9 × 10−3 | 7.8 × 100 | 7.6 × 10−1 | |
| Non-leafy vegetables | Fruits, heads, berries, buds | 3.6 × 10−1 | 7.1 × 10−3 | 7.9 × 100 | 6.7 × 10−1 | |
| Leguminous vegetables | Seeds and pods | 1.4 × 100 | 1.3 × 10−1 | 6.0 × 100 | 1.4 × 100 | |
| Root crops | Roots | 7.2 × 10−1 | 3.0 × 10−2 | 4.8 × 100 | 7.6 × 10−1 | |
| Tubers | Tubers | 1.6 × 10−1 | 7.4 × 10−3 | 1.6 × 100 | 2.1 × 10−1 | |
| Grasses | Stems and shoots | 9.1 × 10−1 | 2.5 × 10−1 | 2.8 × 100 | 9.7 × 10−1 | |
| Leguminous fodder | Stems and shoots | 3.7 × 100 | 1.3 × 100 | 1.8 × 101 | 5.1 × 100 | |
| Pasture | Stems and shoots | 1.3 × 100 | 5.6 × 10−2 | 7.3 × 100 | 1.3 × 100 | |
| Herbs | Stems and shoots | 4.5 × 100* | 4.5 × 10−1 | 4.5 × 101 | 6.9 × 100 | |
| Other crops | Not specified | 8.8 × 10−1 | 2.0 × 10−2 | 8.2 × 100 | 1.0 × 100 | |
| Y | Cereals | Grain | 5.0 × 10−4* | 5.0 × 10−5 | 5.0 × 10−3 | 7.6 × 10−4 |
| Leafy vegetables | Leaves | 2.0 × 10−3* | 2.0 × 10−4 | 2.0 × 10−2 | 3.1 × 10−3 | |
| Non-leafy vegetables | Fruits, heads, berries, buds | 2.0 × 10−3* | 2.0 × 10−4 | 2.0 × 10−2 | 3.1 × 10−3 | |
| Root crops | Roots | 2.0 × 10−3* | 2.0 × 10−4 | 2.0 × 10−2 | 3.1 × 10−3 | |
| Tubers | Tubers | 1.0 × 10−3* | 1.0 × 10−4 | 1.0 × 10−2 | 1.5 × 10−3 | |
| Pasture | Stems and shoots | 5.0 × 10−3* | 5.0 × 10−4 | 5.0 × 10−2 | 7.6 × 10−3 | |
| Zr | Cereals | Grain | 1.0 × 10−3* | 1.0 × 10−4 | 1.0 × 10−2 | 1.5 × 10−3 |
| Leafy vegetables | Leaves | 4.0 × 10−3* | 4.0 × 10−4 | 4.0 × 10−2 | 6.1 × 10−3 | |
| Non-leafy vegetables | Fruits, heads, berries, buds | 4.0 × 10−3* | 4.0 × 10−4 | 4.0 × 10−2 | 6.1 × 10−3 | |
| Root crops | Roots | 4.0 × 10−3* | 4.0 × 10−4 | 4.0 × 10−2 | 6.1 × 10−3 | |
| Tubers | Tubers | 2.0 × 10−3* | 2.0 × 10−4 | 2.0 × 10−2 | 3.1 × 10−3 | |
| Pasture | Stems and shoots | 1.0 × 10−2* | 1.0 × 10−3 | 1.0 × 10−1 | 1.5 × 10−2 | |
| Nb | Cereals | Grain | 1.4 × 10−2* | 1.4 × 10−3 | 1.4 × 10−1 | 2.1 × 10−2 |
| Leafy vegetables | Leaves | 1.7 × 10−2* | 1.7 × 10−3 | 1.7 × 10−1 | 2.6 × 10−2 | |
| Non-leafy vegetables | Fruits, heads, berries, buds | 8.0 × 10−3* | 8.0 × 10−4 | 8.0 × 10−2 | 1.2 × 10−2 | |
| Root crops | Roots | 1.7 × 10−2* | 1.7 × 10−3 | 1.7 × 10−1 | 2.6 × 10−2 | |
| Tubers | Tubers | 4.0 × 10−3* | 4.0 × 10−4 | 4.0 × 10−2 | 6.1 × 10−3 | |
| Pasture | Stems and shoots | 2.0 × 10−2* | 2.0 × 10−3 | 2.0 × 10−1 | 3.1 × 10−2 | |
| Mo | Cereals | Grain | 8.0 × 10−1* | 8.0 × 10−2 | 8.0 × 100 | 1.2 × 100 |
| Maize | Stems and shoots | 7.3 × 10−1 | 1.0 × 10−1 | 3.8 × 101 | 3.1 × 100 | |
| Leafy vegetables | Leaves | 5.1 × 10−1* | 5.1 × 10−2 | 5.1 × 100 | 7.8 × 10−1 | |
| Root crops | Roots | 3.2 × 10−1 | 2.3 × 10−2 | 9.6 × 10−1 | 2.5 × 10−1 | |
| Leguminous fodder | Stems and shoots | 5.4 × 100* | 5.4 × 10−1 | 5.4 × 101 | 8.2 × 100 | |
| Tc | Cereals | Grain | 1.3 × 100* | 1.3 × 10−1 | 1.3 × 101 | 2.0 × 100 |
| Maize | Grain | 3.8 × 100 | 5.0 × 10−1 | 5.2 × 101 | 7.2 × 100 | |
| Maize | Stems and shoots | 6.4 × 100 | 8.4 × 10−1 | 3.7 × 101 | 7.8 × 100 | |
| Leafy vegetables | Leaves | 1.8 × 102 | 4.5 × 100 | 3.4 × 103 | 3.2 × 102 | |
| Leguminous vegetables | Seeds and pods | 4.3 × 100 | 1.1 × 100 | 3.0 × 101 | 6.6 × 100 | |
| Root crops | Roots | 4.6 × 101* | 4.6 × 100 | 4.6 × 102 | 7.0 × 101 | |
| Tubers | Tubers | 2.3 × 10−1 | 1.3 × 10−2 | 6.5 × 10−1 | 1.7 × 10−1 | |
| Pasture | Stems and shoots | 7.6 × 101 | 7.9 × 100 | 4.7 × 102 | 9.1 × 101 | |
| Ru | Cereals | Grain | 3.0 × 10−3 | 6.0 × 10−4 | 1.0 × 10−2 | 3.1 × 10−3 |
| Cereals | Stems and shoots | 1.6 × 10−1 | 3.0 × 10−2 | 1.0 × 100 | 2.2 × 10−1 | |
| Leafy vegetables | Leaves | 9.0 × 10−2 | 2.0 × 10−2 | 2.3 × 10−1 | 8.4 × 10−2 | |
| Non-leafy vegetables | Fruits, heads, berries, buds | 2.0 × 10−2* | 2.0 × 10−3 | 2.0 × 10−1 | 3.1 × 10−2 | |
| Leguminous vegetables | Seeds and pods | 1.5 × 10−2* | 1.5 × 10−3 | 1.5 × 10−1 | 2.3 × 10−2 | |
| Root crops | Roots | 1.0 × 10−2* | 1.0 × 10−3 | 1.0 × 10−1 | 1.5 × 10−2 | |
| Tubers | Tubers | 5.0 × 10−3* | 5.0 × 10−4 | 5.0 × 10−2 | 7.6 × 10−3 | |
| Rh | Not specified | Not specified | 9.0 × 10−1* | 9.0 × 10−2 | 9.0 × 100 | 1.4 × 100 |
| Te | Cereals | Grain | 1.0 × 10−1* | 1.0 × 10−2 | 1.0 × 100 | 1.5 × 10−1 |
| Leafy vegetables | Leaves | 3.0 × 10−1* | 3.0 × 10−2 | 3.0 × 100 | 4.6 × 10−1 | |
| Non-leafy vegetables | Fruits, heads, berries, buds | 3.0 × 10−1* | 3.0 × 10−2 | 3.0 × 100 | 4.6 × 10−1 | |
| Root crops | Roots | 3.0 × 10−1* | 3.0 × 10−2 | 3.0 × 100 | 4.6 × 10−1 | |
| Tubers | Tubers | 2.0 × 10−1* | 2.0 × 10−2 | 2.0 × 100 | 3.1 × 10−1 | |
| Pasture | Stems and shoots | 1.0 × 100* | 1.0 × 10−1 | 1.0 × 101 | 1.5 × 100 | |
| I | Cereals | Grain | 6.3 × 10−4 | 1.0 × 10−4 | 1.1 × 10−2 | 1.4 × 10−3 |
| Cereals | Stems and shoots | 5.2 × 10−2 | 7.0 × 10−3 | 7.5 × 10−1 | 1.0 × 10−1 | |
| Leafy vegetables | Leaves | 6.5 × 10−3 | 1.1 × 10−3 | 1.0 × 10−1 | 1.4 × 10−2 | |
| Non-leafy vegetables | Fruits, heads, berries, buds | 1.0 × 10−1* | 1.0 × 10−2 | 1.0 × 100 | 1.5 × 10−1 | |
| Leguminous vegetables | Seeds and pods | 8.5 × 10−3 | 2.0 × 10−4 | 1.4 × 10−1 | 1.4 × 10−2 | |
| Root crops | Roots | 7.7 × 10−3 | 1.4 × 10−3 | 4.7 × 10−2 | 1.0 × 10−2 | |
| Tubers | Tubers | 1.0 × 10−1* | 1.0 × 10−2 | 1.0 × 100 | 1.5 × 10−1 | |
| Pasture | Stems and shoots | 3.7 × 10−3 | 9.0 × 10−4 | 5.0 × 10−1 | 3.1 × 10−2 | |
| Cs | Cereals | Grain | 2.9 × 10−2 | 2.0 × 10−4 | 9.0 × 10−1 | 5.9 × 10−2 |
| Cereals | Stems and shoots | 1.5 × 10−1 | 4.3 × 10−3 | 3.7 × 100 | 3.2 × 10−1 | |
| Maize | Grain | 3.3 × 10−2 | 3.0 × 10−3 | 2.6 × 10−1 | 4.4 × 10−2 | |
| Maize | Stems and shoots | 7.3 × 10−2 | 3.0 × 10−3 | 4.9 × 10−1 | 7.7 × 10−2 | |
| Leafy vegetables | Leaves | 6.0 × 10−2 | 3.0 × 10−4 | 9.8 × 10−1 | 7.9 × 10−2 | |
| Non-leafy vegetables | Fruits, heads, berries, buds | 2.1 × 10−2 | 7.0 × 10−4 | 7.3 × 10−1 | 5.6 × 10−2 | |
| Leguminous vegetables | Seeds and pods | 4.0 × 10−2 | 1.0 × 10−3 | 7.1 × 10−1 | 6.8 × 10−2 | |
| Root crops | Roots | 4.2 × 10−2 | 1.0 × 10−3 | 8.8 × 10−1 | 7.8 × 10−2 | |
| Root crops | Leaves | 3.5 × 10−2 | 6.0 × 10−3 | 4.5 × 10−1 | 6.8 × 10−2 | |
| Tubers | Tubers | 5.6 × 10−2 | 4.0 × 10−3 | 6.0 × 10−1 | 8.4 × 10−2 | |
| Grasses | Stems and shoots | 6.3 × 10−2 | 4.8 × 10−3 | 9.9 × 10−1 | 1.2 × 10−1 | |
| Leguminous fodder | Stems and shoots | 1.6 × 10−1 | 1.0 × 10−2 | 1.8 × 100 | 2.4 × 10−1 | |
| Pasture | Stems and shoots | 2.5 × 10−1 | 1.0 × 10−2 | 5.0 × 100 | 4.9 × 10−1 | |
| Herbs | Stems and leaves | 6.6 × 10−2 | 4.8 × 10−3 | 2.8 × 100 | 2.2 × 10−1 | |
| Other crops | Not specified | 3.1 × 10−1 | 3.6 × 10−2 | 2.2 × 100 | 4.1 × 10−1 | |
| Ba | Cereals | Grain | 1.0 × 10−3* | 1.0 × 10−4 | 1.0 × 10−2 | 1.5 × 10−3 |
| Leafy vegetables | Leaves | 5.0 × 10−3* | 5.0 × 10−4 | 5.0 × 10−2 | 7.6 × 10−3 | |
| Non-leafy vegetables | Fruits, heads, berries, buds | 5.0 × 10−3* | 5.0 × 10−4 | 5.0 × 10−2 | 7.6 × 10−3 | |
| Root crops | Roots | 5.0 × 10−3* | 5.0 × 10−4 | 5.0 × 10−2 | 7.6 × 10−3 | |
| Tubers | Tubers | 5.0 × 10−3* | 5.0 × 10−4 | 5.0 × 10−2 | 7.6 × 10−3 | |
| Grasses | Stems and shoots | 1.8 × 100 | 6.0 × 10−1 | 5.4 × 100 | 2.0 × 100 | |
| Leguminous fodder | Stems and shoots | 6.0 × 10−1 | 2.0 × 10−1 | 2.1 × 100 | 7.1 × 10−1 | |
| La | Cereals | Grain | 2.0 × 10−5* | 2.0 × 10−6 | 2.0 × 10−4 | 3.1 × 10−5 |
| Maize | Stems and shoots | 8.8 × 10−5* | 8.8 × 10−6 | 8.8 × 10−4 | 1.3 × 10−4 | |
| Leafy vegetables | Leaves | 5.7 × 10−3 | 1.1 × 10−3 | 1.5 × 10−2 | 5.2 × 10−3 | |
| Non-leafy vegetables | Fruits, heads, berries, buds | 6.0 × 10−3* | 6.0 × 10−4 | 6.0 × 10−2 | 9.2 × 10−3 | |
| Leguminous vegetables | Seeds and pods | 4.2 × 10−4 | 1.6 × 10−4 | 1.8 × 10−3 | 5.6 × 10−4 | |
| Root crops | Roots | 1.6 × 10−3 | 4.5 × 10−4 | 6.0 × 10−3 | 1.9 × 10−3 | |
| Tubers | Tubers | 3.9 × 10−4 | 7.0 × 10−5 | 4.0 × 10−3 | 6.8 × 10−4 | |
| Grasses | Stems and shoots | 1.8 × 10−5 | 6.0 × 10−6 | 5.4 × 10−5 | 2.0 × 10−5 | |
| Pasture | Stems and shoots | 2.0 × 10−2* | 2.0 × 10−3 | 2.0 × 10−1 | 3.1 × 10−2 | |
| Ce | Cereals | Grain | 3.1 × 10−3 | 2.4 × 10−4 | 2.0 × 10−2 | 3.6 × 10−3 |
| Cereals | Stems and shoots | 3.9 × 10−2 | 3.0 × 10−3 | 6.8 × 10−1 | 7.8 × 10−2 | |
| Leafy vegetables | Leaves | 6.0 × 10−3* | 6.0 × 10−4 | 6.0 × 10−2 | 9.2 × 10−3 | |
| Leguminous vegetables | Seeds and pods | 1.3 × 10−2* | 1.3 × 10−3 | 1.3 × 10−1 | 2.0 × 10−2 | |
| Root crops | Roots | 6.0 × 10−3* | 6.0 × 10−4 | 6.0 × 10−2 | 9.2 × 10−3 | |
| Tubers | Tubers | 4.0 × 10−3* | 4.0 × 10−4 | 4.0 × 10−2 | 6.1 × 10−3 | |
| Grasses | Stems and shoots | 2.0 × 10−2* | 2.0 × 10−3 | 2.0 × 10−1 | 3.1 × 10−2 | |
| Leguminous fodder | Stems and shoots | 8.0 × 10−3 | 3.0 × 10−3 | 2.4 × 10−2 | 9.1 × 10−3 | |
| Pasture | Stems and shoots | 3.7 × 10−1 | 2.0 × 10−2 | 3.5 × 100 | 4.9 × 10−1 | |
| Pr | Cereals | Grain | 2.0 × 10−2* | 2.0 × 10−3 | 2.0 × 10−1 | 3.1 × 10−2 |
| Leafy vegetables | Leaves | 2.0 × 10−2* | 2.0 × 10−3 | 2.0 × 10−1 | 3.1 × 10−2 | |
| Root crops | Roots | 2.0 × 10−2* | 2.0 × 10−3 | 2.0 × 10−1 | 3.1 × 10−2 | |
| Np | Cereals | Grain | 2.9 × 10−3 | 2.3 × 10−5 | 7.1 × 10−2 | 5.2 × 10−3 |
| Maize | Grain | 4.8 × 10−3* | 1.0 × 10−4 | 1.4 × 10−2 | 3.0 × 10−3 | |
| Maize | Stems and shoots | 1.9 × 10−2 | 1.4 × 10−3 | 1.1 × 10−1 | 2.1 × 10−2 | |
| Leafy vegetables | Leaves | 2.7 × 10−2 | 5.0 × 10−3 | 8.0 × 10−2 | 2.6 × 10−2 | |
| Non-leafy vegetables | Fruits, heads, berries, buds | 1.8 × 10−2 | 4.0 × 10−3 | 5.7 × 10−2 | 1.8 × 10−2 | |
| Leguminous vegetables | Seeds and pods | 1.7 × 10−2 | 4.0 × 10−3 | 3.8 × 10−2 | 1.5 × 10−2 | |
| Root crops | Roots | 2.2 × 10−2 | 5.0 × 10−3 | 6.6 × 10−2 | 2.2 × 10−2 | |
| Tubers | Tubers | 5.7 × 10−3 | 7.1 × 10−4 | 2.7 × 10−2 | 6.2 × 10−3 | |
| Grasses | Stems and shoots | 3.1 × 10−2 | 7.2 × 10−3 | 8.6 × 10−2 | 3.0 × 10−2 | |
| Leguminous fodder | Stems and shoots | 2.5 × 10−2 | 2.0 × 10−3 | 1.2 × 10−1 | 2.5 × 10−2 | |
| Pasture | Stems and shoots | 6.1 × 10−2 | 1.3 × 10−2 | 4.7 × 10−1 | 9.4 × 10−2 | |
| Pu | Cereals | Grain | 9.5 × 10−6 | 2.0 × 10−7 | 1.1 × 10−3 | 5.3 × 10−5 |
| Cereals | Stems and shoots | 4.4 × 10−5 | 4.4 × 10−7 | 9.0 × 10−4 | 7.2 × 10−5 | |
| Maize | Grain | 3.0 × 10−6* | 3.0 × 10−7 | 3.0 × 10−5 | 4.6 × 10−6 | |
| Maize | Stems and shoots | 5.2 × 10−5 | 2.0 × 10−6 | 3.2 × 10−4 | 5.2 × 10−5 | |
| Leafy vegetables | Leaves | 8.3 × 10−5 | 1.0 × 10−5 | 2.9 × 10−4 | 7.8 × 10−5 | |
| Non-leafy vegetables | Fruits, heads, berries, buds | 6.5 × 10-5 | 6.0 × 10−6 | 2.0 × 10−4 | 5.4 × 10−5 | |
| Leguminous vegetables | Seeds and pods | 6.3 × 10−5 | 2.0 × 10−5 | 2.0 × 10−4 | 7.1 × 10−5 | |
| Root crops | Roots | 3.9 × 10−4 | 7.0 × 10−5 | 5.8 × 10−3 | 8.2 × 10−4 | |
| Root crops | Leaves | 1.2 × 10−3 | 2.5 × 10−4 | 4.9 × 10−3 | 1.4 × 10−3 | |
| Tubers | Tubers | 1.1 × 10−4 | 3.8 × 10−6 | 5.0 × 10−3 | 3.5 × 10−4 | |
| Grasses | Stems and shoots | 1.6 × 10−4* | 1.6 × 10−5 | 1.6 × 10−3 | 2.4 × 10−4 | |
| Leguminous fodder | Stems and shoots | 4.9 × 10−4 | 1.1 × 10−4 | 2.9 × 10−3 | 6.7 × 10−4 | |
| Pasture | Stems and shoots | 5.5 × 10−4 | 6.3 × 10−5 | 3.9 × 10−3 | 7.2 × 10−4 |
aAll distributions are log-triangular distributions (as plotted in logarithmic space). Values of Fv were obtained from IAEA 2010 (Tables 17–18 and corrigendum) and IAEA 2009 (pp. 139–206) and represent all soil types for which information is available. For most cases, the mode (in logarithmic space) represents the geometric mean of the available data, and the minimum and maximum are the reported minimum and maximum values. If the reported minimum and maximum values differed by less than a factor of 10, the minimum and maximum values of the distribution were set at a factor of 3 below and above the mode. Mode values (in logarithmic space) with an asterisk (*) represent only one reported value or the arithmetic mean of two reported values (IAEA 2009), and the minimum and maximum values represent a factor of 10 below and above the mode (in logarithmic space), respectively.
bParameter values are for the log-triangular distribution as plotted in logarithmic space.
cThe arithmetic mean of the indicated distribution; this value can be used as a point estimate in deterministic assessments.
The values in Table 10 are provided for all plant types for which information was included in the IAEA's review. For some elements and plant types, it might be necessary to use the suggested probability distribution for a different plant type, if the plant type of interest is not in the table.
Values in Table 10 correspond to "all" soil types in IAEA (2009, 2010); this should be understood to mean all soil types for which information was available. Where possible, the IAEA review (IAEA 2009, 2010) provided information by soil group, as well as for "all" soil types.
The information in Table 10 corresponds to a standardized rooting depth (root zone) of 10 cm for grass and 20 cm for all other crops (IAEA 2010). Note that actual root uptake can vary with growing conditions such as fertilization and irrigation (IAEA 2010).
The values of Fv in Table 10 are given in terms of dry weight of plants for all plant types. The dry matter content for many specific plant types can be obtained from Appendix I of the IAEA's review (IAEA 2010). Typical ranges of dry matter content are as follows: seeds and grain, 83–90%; fruits and wild berries, 7–18%; vegetative mass of agricultural plants, 5–40%; pasture and silage, 20–34%; and hay and concentrated feeds, 86–88% (IAEA 2010).
The soil-to-vegetation transfer factors in Table 10 are intended for equilibrium conditions (IAEA 2009; Choi et al. 2009). Following a fallout event, an approximate equilibrium between soil and vegetation could reasonably be assumed for the longest-lived radionuclides in the soil (90Sr, 137Cs, 239Pu) after the first months following the deposition. For an acute deposition, the direct deposition of radionuclides on vegetation will dominate the radionuclide activity concentrations in the vegetation during the first weeks or months, the potential exceptions being for plant parts not receiving direct deposition and some radionuclides that are readily taken up by plants (e.g., strontium). In addition, soon after an acute deposition event, the radionuclides will not be mixed in the top layer of soil (one of the assumptions for the transfer coefficients). The IAEA (2009) and Choi et al. (2009) have suggested the use of aggregated transfer factors for the time period of interest, in terms of the ratio of the radionuclide activity concentration in the plant at harvest to the deposited radionuclide activity per unit area of soil. However, this information does not exist for very many radionuclides, plants, or time periods (IAEA 2009; Choi et al. 2009). Approaches to account for non-equilibrium situations are provided later in this paper.
TRANSFER OF RADIONUCLIDES FROM VEGETATION TO MILK AND MEAT
Dairy cows and goats can consume contaminated vegetation, with subsequent transfer of radionuclides into milk. In principle, animals could consume contaminated plants within hours of a deposition event, and contaminated milk could be consumed by humans within a few more hours. Beef cattle, goats, sheep, swine, and poultry can also consume contaminated vegetation, with subsequent transfer of radionuclides into the meat or into the eggs of poultry. In principle, animals could consume contaminated plants within one or more days of a deposition event, and contaminated meat could be consumed by humans within a few hours or days of a deposition event. Dairy cows (commercial and backyard), dairy goats, and beef cattle are the animals most commonly considered in radiological assessments.
The most commonly used approach for model-based estimation of radionuclide activity concentrations in milk and meat due to consumption by animals of contaminated vegetation has been through the use of transfer coefficients, defined as either the equilibrium ratio of the fresh weight activity concentration in milk or meat to the daily dietary radionuclide intake of the animal (Howard et al. 2009b; Bq L−1 milk per Bq d−1 ingested or Bq kg−1 meat per Bq d−1 ingested) or the ratio of infinite time-integrated concentrations to the ingested activity (Bq d L−1 per Bq ingested or Bq d kg−1 per Bq ingested). Either definition provides a transfer coefficient in units of d L−1 for milk and d kg−1 for meat. Use of the feed-to-milk transfer coefficient (Fm, d L−1) or the feed-to-meat transfer coefficient (Ff, d kg−1) requires the amount of feed consumed per day (kgdry weight d−1) as well as the radionuclide activity concentration in the feed (Bq kg−1dry weight). This approach is easily adapted for use with more than one feed source or for consumption of contaminated water as well as feed. Transfer coefficients for milk and meat are discussed in the following sections.
A more recent approach is the use of concentration ratios (CR), defined as the equilibrium ratio between the radionuclide activity concentration in the animal food product (Bq kg−1fresh weight) and the radionuclide activity concentration in the feedstuff (Bq kg−1dry weight) (Howard et al. 2009b) or as the ratio of infinite time-integrated concentrations (Bq d kg−1 per Bq d kg−1). Use of CR values avoids the need to estimate the intake of the feedstuff; more importantly, the CR is much less variable across animal species and does not seem to depend on body sizes or milk yield (Howard et al. 2009b). However, concentration ratios may be less useful if there is more than one feed source or if both drinking water and feed are contaminated. Information on concentration ratios for milk can be obtained from Howard et al. (2016, 2017).
Both transfer coefficients and concentration ratios are intended either for equilibrium conditions or for estimation of an infinite time-integrated amount of activity following an acute deposition event. For a single deposition event, estimation of an ingestion dose involves a time-integration (either of the intake of activity or of the dose during the time following the deposition event), and thus use of transfer coefficients or concentration ratios is appropriate. Approaches to account for non-equilibrium or time-dependent situations and non-infinite time-integrated concentrations are provided later in this paper.
Transfer from vegetation to milk (cows and goats)
Tables 11 and 12 provide suggested probability distributions and point estimates for the feed-to-milk transfer coefficient (Fm, d L−1) for cow's milk (17 elements) and goat's milk (11 elements). Where possible, geometric means (GM) were obtained from Howard et al. (2016, 2017) and used as the modes of log-triangular distributions (in logarithmic space); reported minimum and maximum values were used as the minimum and maximum values of the probability distributions. The summaries of Howard et al. (2016, 2017) are updates of earlier information summarized by the IAEA (2009, 2010) and Howard et al. (2009a).
Table 11.
Suggested probability distributions and arithmetic means for the feed-to-milk transfer coefficient for cow's milk (Fm, d L−1).a
| Element | Modeb | Minimum | Maximum | Arithmetic meanc |
|---|---|---|---|---|
| Sr | 1.3 × 10−3 | 1.5 × 10−5 | 4.3 × 10−3 | 7.9 × 10−4 |
| Y | 1.0 × 10−4 | 1.0 × 10−5 | 1.0 × 10−3 | 1.5 × 10−4 |
| Zr | 3.6 × 10−6 | 5.5 × 10−7 | 1.7 × 10−5 | 4.1 × 10−6 |
| Nb | 4.1 × 10−7* | 4.1 × 10−8 | 4.1 × 10−6 | 6.3 × 10−7 |
| Mo | 1.2 × 10−3 | 2.8 × 10−4 | 5.9 × 10−3 | 1.5 × 10−3 |
| Tc | 2.5 × 10−4 | 2.5 × 10−5 | 2.5 × 10−3 | 3.8 × 10−4 |
| Ru | 9.4 × 10−6 | 6.7 × 10−7 | 1.4 × 10−4 | 1.7 × 10−5 |
| Rh | 1.0 × 10−4 | 1.0 × 10−5 | 1.0 × 10−3 | 1.5 × 10−4 |
| Te | 3.2 × 10−4 | 7.8 × 10−5 | 1.0 × 10−3 | 3.3 × 10−4 |
| I | 6.0 × 10−3 | 4.0 × 10−4 | 4.4 × 10−2 | 7.2 × 10−3 |
| Cs | 4.9 × 10−3 | 6.0 × 10−4 | 5.7 × 10−2 | 8.4 × 10−3 |
| Ba | 1.8 × 10−4 | 3.8 × 10−5 | 7.3 × 10−4 | 2.0 × 10−4 |
| La | 1.0 × 10−4 | 1.0 × 10−5 | 1.0 × 10−3 | 1.5 × 10−4 |
| Ce | 1.5 × 10−5 | 1.0 × 10−6 | 1.3 × 10−4 | 2.0 × 10−5 |
| Pr | 1.0 × 10−4 | 1.0 × 10−5 | 1.0 × 10−3 | 1.5 × 10−4 |
| Np | 1.0 × 10−4 | 1.0 × 10−5 | 1.0 × 10−3 | 1.5 × 10−4 |
| Pu | 3.6 × 10−5 | 7.5 × 10−6 | 5.0 × 10−4 | 7.5 × 10−5 |
aAll distributions are log-triangular distributions (as plotted in logarithmic space). Where possible, Fm for cow's milk was obtained from Howard et al. 2017 (Tables 2a, 5a). For most cases, the mode (in logarithmic space) represents the geometric mean of the available data, and the minimum and maximum are the reported minimum and maximum values. If the reported minimum and maximum values differed by less than a factor of 10, the minimum and maximum values of the distribution were set at a factor of 3 below and above the mode (in logarithmic space). The mode value (in logarithmic space) with an asterisk (*) represents only one reported value (Howard et al. 2017). Mode values (in logarithmic space) in italics were obtained from the IAEA (in press) and represent professional judgment based (in most cases) on gastrointestinal absorption of the element. For mode values (in logarithmic space) with an asterisk or in italics, the minimum and maximum values represent a factor of 10 below and above the mode (in logarithmic space), respectively.
bParameter values are for the log-triangular distribution as plotted in logarithmic space.
cThe arithmetic mean of the indicated distribution; this value can be used as a point estimate in deterministic assessments.
Table 12.
Suggested probability distributions and arithmetic means for the feed-to-milk transfer coefficient for goat's milk (Fm, d L−1).a
| Element | Modeb | Minimum | Maximum | Arithmetic meanc |
|---|---|---|---|---|
| Sr | 1.5 × 10−2 | 5.8 × 10−3 | 8.1 × 10−2 | 2.2 × 10−2 |
| Y | 2.0 × 10−5* | 2.0 × 10−6 | 2.0 × 10−4 | 3.1 × 10−5 |
| Zr | 5.5 × 10−6* | 5.5 × 10−7 | 5.5 × 10−5 | 8.4 × 10−6 |
| Nb | 6.4 × 10−6* | 6.4 × 10−7 | 6.4 × 10−5 | 9.8 × 10−6 |
| Mo | 1.1 × 10−2 | 3.6 × 10−3 | 3.3 × 10−2 | 1.2 × 10−2 |
| Te | 4.4 × 10−3* | 4.4 × 10−4 | 4.4 × 10−2 | 6.7 × 10−3 |
| I | 2.1 × 10−1 | 2.7 × 10−2 | 7.7 × 10−1 | 2.0 × 10−1 |
| Cs | 1.1 × 10−1 | 9.0 × 10−3 | 3.3 × 10−1 | 8.9 × 10−2 |
| Ba | 3.3 × 10−3* | 3.3 × 10−4 | 3.3 × 10−2 | 5.0 × 10−3 |
| Ce | 4.0 × 10−5* | 4.0 × 10−6 | 4.0 × 10−4 | 6.1 × 10−5 |
| Np | 5.3 × 10−5* | 5.3 × 10−6 | 5.3 × 10−4 | 8.1 × 10−5 |
aAll distributions are log-triangular distributions (as plotted in logarithmic space). Values of Fm for goat's milk were obtained from Howard et al. 2016 (Table 2). Where possible, the mode (in logarithmic space) represents the geometric mean (or median) of the available data, and the minimum and maximum are the reported minimum and maximum values. If the reported minimum and maximum values differed by less than a factor of 10, the minimum and maximum values of the distribution were set at a factor of 3 below and above the mode (in logarithmic space). Mode values (in logarithmic space) with an asterisk (*) represent only one reported value or the arithmetic mean of two reported values (Howard et al. 2016), and the minimum and maximum values are set at a factor of 10 below and above the mode (in logarithmic space).
bParameter values are for the log-triangular distribution as plotted in logarithmic space.
cThe arithmetic mean of the indicated distribution; this value can be used as a point estimate in deterministic assessments.
Tables 11 and 12 include probability distributions for iodine from Howard et al. (2016, 2017). The National Cancer Institute (NCI) has probability distributions for iodine in cow's milk (backyard and commercial) and goat's milk (backyard) that are used in the updated NCI fallout calculator (https://radiationcalculators.cancer.gov/fallout/). These distributions are provided in Table 13.
Table 13.
Probability distributions for Fm for iodine, as used in the updated NCI fallout calculator.a
| Animal | Distribution type | Distribution parameters |
|---|---|---|
| Backyard cow | log-normal | GMb = 6.0 × 10−3; GSDc = 2.1 |
| Commercial cow | log-normal | GM = 4.0 × 10−3; GSD = 1.5 |
| Backyard goat | triangular | minimum = 0.04; mode = 0.22; maximum = 0.9 |
bGM = geometric mean.
cGSD = geometric standard deviation.
Transfer from vegetation to meat (domestic animals)
Tables 14 and 15 provide suggested probability distributions and point estimates for the feed-to-meat transfer coefficient (Ff, d kg−1) for beef for all 17 elements, and for pork, mutton (sheep meat), goat meat, poultry, and eggs (contents) as data are available. Beef can be considered as a surrogate for other types of meat when specific transfer coefficients are not available. Where possible, geometric means (GM) were obtained from Howard et al. (2009a), which summarizes a review by the IAEA (2009, 2010).
Table 14.
Suggested probability distributions and arithmetic means for the feed-to-meat transfer coefficient for beef (Ff, d kg−1).a
| Element | Modeb | Minimum | Maximum | Arithmetic meanc |
|---|---|---|---|---|
| Sr | 1.3 × 10−3 | 2.0 × 10−4 | 9.2 × 10−3 | 1.8 × 10−3 |
| Y | 7.5 × 10−4 | 7.5 × 10−5 | 7.5 × 10−3 | 1.2 × 10−3 |
| Zr | 1.2 × 10−6* | 1.2 × 10−7 | 1.2 × 10−5 | 1.8 × 10−6 |
| Nb | 2.6 × 10−7* | 2.6 × 10−8 | 2.6 × 10−6 | 4.0 × 10−7 |
| Mo | 1.0 × 10−3* | 1.0 × 10−4 | 1.0 × 10−2 | 1.5 × 10−3 |
| Tc | 1.0 × 10−2 | 1.0 × 10−3 | 1.0 × 10−1 | 1.5 × 10−2 |
| Ru | 3.3 × 10−3 | 1.1 × 10−3 | 1.0 × 10−2 | 3.7 × 10−3 |
| Rh | 1.0 × 10−2 | 1.0 × 10−3 | 1.0 × 10−1 | 1.5 × 10−2 |
| Te | 7.0 × 10−3* | 7.0 × 10−4 | 7.0 × 10−2 | 1.1 × 10−2 |
| I | 6.7 × 10−3 | 2.0 × 10−3 | 3.8 × 10−2 | 9.6 × 10−3 |
| Cs | 2.2 × 10−2 | 4.7 × 10−3 | 9.6 × 10−2 | 2.6 × 10−2 |
| Ba | 1.4 × 10−4* | 1.4 × 10−5 | 1.4 × 10−3 | 2.1 × 10−4 |
| La | 1.3 × 10−4* | 1.3 × 10−5 | 1.3 × 10−3 | 2.0 × 10−4 |
| Ce | 2.0 × 10−3 | 2.0 × 10−4 | 2.0 × 10−2 | 3.1 × 10−3 |
| Pr | 1.0 × 10−3 | 1.0 × 10−4 | 1.0 × 10−2 | 1.5 × 10−3 |
| Np | 1.0 × 10−3 | 1.0 × 10−4 | 1.0 × 10−2 | 1.5 × 10−3 |
| Pu | 1.1 × 10−6 | 8.8 × 10−8 | 3.0 × 10−4 | 1.3 × 10−5 |
aAll distributions are log-triangular distributions (as plotted in logarithmic space). Where possible, Ff was obtained from Howard et al. 2009a (Table 4). For most cases, the mode (in logarithmic space) represents the geometric mean (or median) of the available data, and the minimum and maximum are the reported minimum and maximum values. If the reported minimum and maximum values differed by less than a factor of 10, the minimum and maximum values of the distribution were set at a factor of 3 below and above the mode (in logarithmic space). Mode values (in logarithmic space) with an asterisk (*) represent only one reported value or the arithmetic mean of two or three reported values (Howard et al. 2009a). Mode values (in logarithmic space) in italics were obtained from the IAEA (in press) and represent professional judgment based (in most cases) on gastrointestinal absorption of the element. For mode values (in logarithmic space) with an asterisk or in italics, the minimum and maximum values represent a factor of 10 below and above the mode (in logarithmic space).
bParameter values are for the log-triangular distribution as plotted in logarithmic space.
cThe arithmetic mean of the indicated distribution; this value can be used as a point estimate in deterministic assessments.
Table 15.
Suggested probability distributions and arithmetic means for the feed-to-meat transfer coefficient for pork, mutton, goat meat, and poultry, and the transfer coefficient for feed to poultry eggs (Ff, d kg−1).a
| Element | Modeb | Minimum | Maximum | Arithmetic meanc |
|---|---|---|---|---|
| Pork | ||||
| Sr | 2.5 × 10−3 | 5.0 × 10−4 | 8.0 × 10−3 | 2.5 × 10−3 |
| Ru | 3.0 × 10−3* | 3.0 × 10−4 | 3.0 × 10−2 | 4.6 × 10−3 |
| I | 4.1 × 10−2* | 4.1 × 10−3 | 4.1 × 10−1 | 6.3 × 10−2 |
| Cs | 2.0 × 10−1 | 7.0 × 10−2 | 6.0 × 10−1 | 2.2 × 10−1 |
| Mutton | ||||
| Sr | 1.5 × 10−3 | 3.0 × 10−4 | 4.0 × 10−3 | 1.4 × 10−3 |
| Ru | 2.1 × 10−3* | 2.1 × 10−4 | 2.1 × 10−2 | 3.2 × 10−3 |
| I | 3.0 × 10−2* | 3.0 × 10−3 | 3.0 × 10−1 | 4.6 × 10−2 |
| Cs | 1.9 × 10−1 | 5.3 × 10−2 | 1.3 × 100 | 2.9 × 10−1 |
| Ce | 2.5 × 10−4* | 2.5 × 10−5 | 2.5 × 10−3 | 3.8 × 10−4 |
| Goat meat | ||||
| Sr | 2.9 × 10−3 | 1.0 × 10−3 | 1.0 × 10−2 | 3.4 × 10−3 |
| Y | 5.4 × 10−2* | 5.4 × 10−3 | 5.4 × 10−1 | 8.2 × 10−2 |
| Zr | 2.0 × 10−5* | 2.0 × 10−6 | 2.0 × 10−4 | 3.1 × 10−5 |
| Nb | 6.0 × 10−5* | 6.0 × 10−6 | 6.0 × 10−4 | 9.2 × 10−5 |
| Te | 2.4 × 10−3* | 2.4 × 10−4 | 2.4 × 10−2 | 3.7 × 10−3 |
| Cs | 3.2 × 10−1 | 1.2 × 10−1 | 1.9 × 100 | 4.9 × 10−1 |
| Ba | 1.3 × 10−5* | 1.3 × 10−6 | 1.3 × 10−4 | 2.0 × 10−5 |
| Poultry | ||||
| Sr | 2.0 × 10−2 | 7.0 × 10−3 | 4.1 × 10−2 | 1.9 × 10−2 |
| Zr | 6.0 × 10−5* | 6.0 × 10−6 | 6.0 × 10−4 | 9.2 × 10−5 |
| Nb | 3.0 × 10−4* | 3.0 × 10−5 | 3.0 × 10−3 | 4.6 × 10−4 |
| Mo | 1.8 × 10−1* | 1.8 × 10−2 | 1.8 × 100 | 2.7 × 10−1 |
| Te | 6.0 × 10−1* | 6.0 × 10−2 | 6.0 × 100 | 9.2 × 10−1 |
| I | 8.7 × 10−3 | 4.0 × 10−3 | 1.5 × 10−2 | 8.4 × 10−3 |
| Cs | 2.7 × 100 | 9.0 × 10−1 | 8.1 × 100 | 3.0 × 100 |
| Ba | 1.9 × 10−2* | 1.9 × 10−3 | 1.9 × 10−1 | 2.9 × 10−2 |
| Eggs (contents) | ||||
| Sr | 4.9 × 10−1 | 2.5 × 10−1 | 4.8 × 100 | 1.0 × 100 |
| Zr | 2.0 × 10−4* | 2.0 × 10−5 | 2.0 × 10−3 | 3.1 × 10−4 |
| Nb | 1.0 × 10−3* | 1.0 × 10−4 | 1.0 × 10−2 | 1.5 × 10−3 |
| Mo | 6.4 × 10−1 | 2.1 × 10−1 | 2.0 × 100 | 7.2 × 10−1 |
| Ru | 4.0 × 10−3* | 4.0 × 10−4 | 4.0 × 10−2 | 6.1 × 10−3 |
| Te | 5.1 × 100* | 5.1 × 10−1 | 5.1 × 101 | 7.8 × 100 |
| I | 2.4 × 100 | 1.9 × 100 | 3.2 × 100 | 2.5 × 100 |
| Cs | 4.0 × 10−1 | 1.0 × 10−1 | 1.2 × 100 | 4.1 × 10−1 |
| Ba | 8.7 × 10−1* | 8.7 × 10−2 | 8.7 × 100 | 1.3 × 100 |
| Ce | 3.1 × 10−3* | 3.1 × 10−4 | 3.1 × 10−2 | 4.7 × 10−3 |
| Pu | 1.5 × 10−4† | 9.9 × 10−6 | 2.3 × 10−3 | 2.7 × 10−4 |
aAll distributions are log-triangular distributions (as plotted in logarithmic space). Where possible, Ff was obtained from Howard et al. 2009a (Tables 5–9). Where possible, the mode (in logarithmic space) represents the geometric mean (or median) of the available data, and the minimum and maximum are the reported minimum and maximum values. If the reported minimum and maximum values differed by less than a factor of 10, the minimum and maximum values of the distribution were set at a factor of 3 below and above the mode (in logarithmic space), respectively. Mode values (in logarithmic space) with an asterisk (*) represent only one reported value or the arithmetic mean of two reported values (Howard et al. 2009a), and the minimum and maximum values represent a factor of 10 below and above the mode (in logarithmic space), respectively. The mode value (in logarithmic space) with a dagger (†) represents the geometric mean of two values (the reported minimum and maximum values), and the minimum and maximum are the reported minimum and maximum values.
bParameter values are for the log-triangular distribution as plotted in logarithmic space.
cThe arithmetic mean of the indicated distribution; this value can be used as a point estimate in deterministic assessments.
TRANSFER OF RADIONUCLIDES INTO NON-AGRICULTURAL PRODUCTS
Consumption of non-agricultural plants and wildlife could also contribute to internal doses to humans following a fallout event. The importance of these contributions will depend on site-specific situations and practices. Radionuclide transfer from soil into wildlife and non-agricultural plants is typically estimated in terms of a concentration ratio (CR), defined as the equilibrium ratio between the radionuclide activity concentration in the whole organism (Bq kg−1fresh weight) and the radionuclide activity concentration in the soil (Bq kg−1dry weight) or water (Bq L−1) (IAEA 2014).
The concentration ratios described below are intended for equilibrium conditions or for estimation of infinite time-integrated activities after an acute deposition event. Approaches to account for non-equilibrium situations are provided later in this paper.
An alternative to the use of concentration ratios (CR) is the use of aggregated transfer factors (Tag), defined as the ratio of the radionuclide activity concentration in a plant or animal (Bq kg−1, fresh weight or dry weight) to the total deposition on the soil per unit area (Bq m−2) (commonly reported as m2kg − 1, either dry weight or fresh weight; Calmon et al. 2009). Aggregated transfer factors have been reported for a variety of forest products for a few radionuclides (Duff and Ramsey 2008; Calmon et al. 2009). This approach might be useful for some specific products (e.g., mushrooms, berries, game).
Direct deposition on non-agricultural plants
Estimation of radionuclide activity concentrations on non-agricultural plants due to direct deposition of radionuclides on the vegetation should be handled as described above for pasture and crops. Relevant parameter values should be selected by plant characteristics (e.g., type and size) as appropriate.
Transfer into non-agricultural plants (root uptake)
The concentration ratio (CR) for non-agricultural plants is defined as the equilibrium ratio between the radionuclide activity concentration in the whole plant (Bq kg−1fresh weight) and the radionuclide activity concentration in the soil (Bq kg−1dry weight) (IAEA 2014), or the ratio of infinite time-integrated activity concentrations (Bq d kg−1fresh weight plant per Bq d kg−1dry weight soil). CR values have been summarized for a limited number of plant groups and species (IAEA 2014; Guillén et al. 2018). Suggested probability distributions and point estimates for CR values for non-agricultural plants are based on the available data and are summarized in Table 16.
Table 16.
Suggested probability distributions and arithmetic means for the concentration ratios (CR) for non-agricultural plants (whole organism) with respect to soil (Bq kg−1fresh weight per Bq kg–1dry weight).a
| Element | Plant type | Modeb | Minimum | Maximum | Arithmetic meanc |
|---|---|---|---|---|---|
| Sr | grasses and herbs | 4.7 × 10−1 | 6.7 × 10−3 | 8.8 × 100 | 7.6 × 10−1 |
| grasses | 9.5 × 10−1 | 5.0 × 10−2 | 6.3 × 100 | 1.0 × 100 | |
| herbs | 2.2 × 100 | 3.2 × 10−1 | 5.0 × 100 | 1.8 × 100 | |
| shrubs | 2.5 × 10−1 | 4.7 × 10−3 | 6.7 × 100 | 5.2 × 10−1 | |
| trees | 2.0 × 10−1 | 1.2 × 10−3 | 5.3 × 100 | 3.6 × 10−1 | |
| trees-broad leaf | 2.3 × 10−1 | 1.2 × 10−3 | 3.1 × 100 | 2.7 × 10−1 | |
| trees-coniferous | 2.0 × 10−1 | 1.5 × 10−3 | 5.3 × 100 | 3.7 × 10−1 | |
| Zr | shrubs | 7.2 × 10−5† | 7.2 × 10−6 | 7.2 × 10−4 | 1.1 × 10−4 |
| Mo | shrubs | 8.7 × 10−1 | 2.9 × 10−1 | 4.0 × 100 | 1.2 × 100 |
| Tc | grasses and herbs | 1.0 × 101 | 6.2 × 10−3 | 2.0 × 101 | 3.2 × 100 |
| grasses | 1.3 × 101 | 8.3 × 10−2 | 2.0 × 101 | 5.0 × 100 | |
| shrubs | 8.4 × 10−3 | 6.3 × 10−4 | 3.3 × 10−2 | 7.6 × 10−3 | |
| Ru | shrubs | 3.2 × 10−1 | 1.1 × 10−1 | 1.0 × 100 | 3.6 × 10−1 |
| I | grasses | 5.3 × 10−2† | 5.3 × 10−3 | 5.3 × 10−1 | 8.1 × 10−2 |
| Cs | grasses and herbs | 5.1 × 10−1 | 1.9 × 10−3 | 3.7 × 101 | 1.7 × 100 |
| grasses | 8.5 × 10−1 | 3.6 × 10−3 | 3.7 × 101 | 2.0 × 100 | |
| herbs | 5.0 × 10−1 | 3.0 × 10−3 | 2.2 × 101 | 1.3 × 100 | |
| shrubs | 1.1 × 100 | 9.8 × 10−3 | 1.6 × 101 | 1.4 × 100 | |
| trees | 7.5 × 10−2 | 1.2 × 10−3 | 1.8 × 100 | 1.4 × 10−1 | |
| trees-broad leaf | 7.5 × 10−2 | 1.2 × 10−3 | 1.3 × 100 | 1.2 × 10−1 | |
| trees-coniferous | 7.5 × 10−2 | 1.2 × 10−3 | 1.8 × 100 | 1.4 × 10−1 | |
| Ba | grasses and herbs | 5.4 × 10−2 | 1.8 × 10−2 | 1.6 × 10−1 | 5.9 × 10−2 |
| shrubs | 2.2 × 100 | 1.3 × 10−2 | 9.8 × 100 | 1.4 × 100 | |
| trees-coniferous | 1.6 × 10−1 | 5.0 × 10−2 | 5.0 × 10−1 | 1.8 × 10−1 | |
| La | grasses and herbs | 6.0 × 10−3 | 2.0 × 10−3 | 2.0 × 10−2 | 6.9 × 10−3 |
| shrubs | 9.9 × 10−3 | 3.3 × 10−3 | 3.7 × 10−2 | 1.2 × 10−2 | |
| trees | 3.6 × 10−3 | 1.2 × 10−3 | 1.1 × 10−2 | 4.0 × 10−3 | |
| Ce | grasses and herbs | 3.6 × 10−3 | 1.2 × 10−3 | 1.1 × 10−2 | 4.0 × 10−3 |
| shrubs | 9.9 × 10−3 | 1.8 × 10−3 | 3.2 × 10−1 | 3.3 × 10−2 | |
| trees-coniferous | 3.3 × 10−3* | 3.3 × 10−4 | 3.3 × 10−2 | 5.0 × 10−3 | |
| Pu | grasses | 9.4 × 10−3 | 3.1 × 10−3 | 2.8 × 10−2 | 1.0 × 10−2 |
| shrubs | 4.3 × 10−2 | 4.4 × 10−5 | 3.3 × 10−1 | 3.0 × 10−2 |
aAll distributions are log-triangular distributions (as plotted in logarithmic space). Values of CR were obtained from IAEA 2014 (Table 5). Values represent all relevant plant types for which information is available. For most cases, the mode (in logarithmic space) represents the geometric mean of the available data, and the minimum and maximum are the reported minimum and maximum values. If the reported minimum and maximum values differed by less than a factor of 10, the minimum and maximum values of the distribution were set at a factor of 3 below and above the mode (in logarithmic space), respectively. The mode value (in logarithmic space) with an asterisk (*) represents only one reported value (IAEA 2014); for this case, the minimum and maximum have been set to a factor of 10 below and above the mode (in logarithmic space), respectively. Mode values (in logarithmic space) with a dagger (†) represent a geometric mean for which minimum and maximum values were not available; the minimum and maximum have been set to a factor of 10 below and above the mode (in logarithmic space), respectively.
bParameter values are for the log-triangular distribution as plotted in logarithmic space.
cThe arithmetic mean of the indicated distribution; this value can be used as a point estimate in deterministic assessments.
Transfer into wildlife—mammals and birds
The concentration ratio (CR) for terrestrial wildlife is defined as the equilibrium ratio between the radionuclide activity concentration in a whole organism (Bq kg−1fresh weight) and the radionuclide activity concentration in the soil (Bq kg−1dry weight) (IAEA 2014), or the ratio of infinite time-integrated activity concentrations (Bq d kg−1fresh weight animal per Bq d kg−1dry weight soil). CR values have been summarized for a limited number of wildlife types (Sheppard et al. 2010b; IAEA 2014). Suggested probability distributions and point estimates for CR values for wildlife based on the available data are summarized in Table 17.
Table 17.
Suggested probability distributions and arithmetic means for the concentration ratios (CR) for wildlife (birds and mammals, whole organism) with respect to soil (Bq kg−1fresh weight per Bq kg‑1dry weight).a
| Element | Wildlife type | Modeb | Minimum | Maximum | Arithmetic meanc |
|---|---|---|---|---|---|
| Sr | birds | 2.3 × 10−1 | 4.8 × 10−3 | 7.2 × 100 | 5.4 × 10−1 |
| birds-omnivorous | 2.6 × 10−1 | 4.0 × 10−2 | 7.2 × 100 | 7.6 × 10−1 | |
| mammals | 9.5 × 10−1 | 9.9 × 10−3 | 1.7 × 101 | 1.4 × 100 | |
| mammals-carnivorous | 4.3 × 10−1 | 1.3 × 10−2 | 9.8 × 100 | 8.7 × 10−1 | |
| mammals-herbivorous | 1.6 × 100 | 9.9 × 10−3 | 1.7 × 101 | 1.7 × 100 | |
| mammals-omnivorous | 1.1 × 100 | 3.0 × 10−2 | 1.0 × 101 | 1.3 × 100 | |
| mammals-Rangifer spp. | 5.5 × 100 | 4.8 × 10−3 | 1.5 × 101 | 2.2 × 100 | |
| Tc | birds | 1.7 × 10−1* | 1.7 × 10−2 | 1.7 × 100 | 2.6 × 10−1 |
| Cs | birds | 2.7 × 10−1 | 1.4 × 10−3 | 1.6 × 101 | 8.1 × 10−1 |
| birds-herbivorous | 5.4 × 10−1 | 2.3 × 10−2 | 5.8 × 100 | 7.4 × 10−1 | |
| birds-omnivorous | 1.7 × 10−1 | 9.4 × 10−3 | 1.6 × 101 | 9.2 × 10−1 | |
| mammals | 1.3 × 100 | 2.8 × 10−3 | 1.4 × 102 | 5.4 × 100 | |
| mammals-carnivorous | 1.4 × 10−1 | 2.8 × 10−3 | 2.3 × 101 | 9.9 × 10−1 | |
| mammals-herbivorous | 1.5 × 100 | 1.0 × 10−2 | 1.4 × 102 | 6.3 × 100 | |
| mammals-omnivorous | 1.7 × 100 | 1.7 × 10−2 | 3.6 × 101 | 2.8 × 100 | |
| mammals-Rangifer spp. | 1.3 × 101 | 1.2 × 10−1 | 8.1 × 101 | 1.1 × 101 | |
| Ba | mammals-omnivorous | 4.8 × 10−3 | 1.6 × 10−3 | 1.4 × 10−2 | 5.2 × 10−3 |
| Pu | birds | 9.8 × 10−4 | 3.3 × 10−5 | 1.5 × 10−2 | 1.6 × 10−3 |
| birds-omnivorous | 1.3 × 10−3 | 3.3 × 10−5 | 1.5 × 10−2 | 1.7 × 10−3 | |
| mammals | 9.3 × 10−3 | 1.6 × 10−4 | 2.6 × 100 | 9.4 × 10−2 | |
| mammals-carnivorous | 3.1 × 10−3 | 7.1 × 10−4 | 2.2 × 10−2 | 4.7 × 10−3 | |
| mammals-herbivorous | 9.2 × 10−3 | 1.6 × 10−4 | 2.8 × 10−1 | 2.1 × 10−2 | |
| mammals-omnivorous | 1.1 × 10−2 | 2.2 × 10−4 | 2.6 × 100 | 1.0 × 10−1 | |
| mammals-Rangifer spp. | 3.5 × 10−3 | 3.3 × 10−3 | 7.6 × 10−3 | 4.5 × 10−3 |
aAll distributions are log-triangular distributions (as plotted in logarithmic space). Values of CR were obtained from IAEA 2014 (Table 5). Values represent all relevant wildlife types for which information is available. For most cases, the mode (in logarithmic space) represents the geometric mean (or median) of the available data, and the minimum and maximum are the reported minimum and maximum values. If the reported minimum and maximum values differed by less than a factor of 10, the minimum and maximum values of the distribution were set at a factor of 3 below and above the mode (in logarithmic space), respectively. The mode value (in logarithmic space) with an asterisk (*) represents the arithmetic mean of two reported values (IAEA 2014); for this case, the minimum and maximum have been set to a factor of 10 below and above the mode (in logarithmic space), respectively.
bParameter values are for the log-triangular distribution as plotted in logarithmic space.
cThe arithmetic mean of the indicated distribution; this value can be used as a point estimate in deterministic assessments.
The CR values are for the whole body of the organism, which in some cases may be used as an estimate for individual tissues or organs. For some elements, a whole-body-to-tissue concentration ratio is available for selected tissues (muscle, liver, kidney, and bone; Yankovich et al. 2010; IAEA 2014). Table 18 provides the mean whole-body-to-tissue concentration ratios for muscle (meat) and liver for four elements for mammals, and for liver for two elements for birds. These values should be used together with the whole-body concentration ratios (Table 17) to estimate the radionuclide concentrations in the wildlife tissues likely to be consumed by humans.
Table 18.
Mean whole-body to tissue concentration ratios for mammals and birds, for tissues likely to be consumed by humans.a
| Element | Whole body to muscle | Whole body to liver |
|---|---|---|
| Mammals | ||
| Ru | 1.1 | 0.12 |
| Cs | 0.97 | 0.97 |
| Ce | 34 | 0.29 |
| Pu | 5.3 (2.1–33)b | 0.24 (0.027–9.2) |
| Birds | ||
| Cs | –c | 1.4 (0.090–2.3) |
| Ce | – | 0.33 (0.16–0.78) |
aValues were obtained from Table 6 (mammals) and Table 5 (birds) of Yankovich et al. (2010).
bValues in parentheses indicate the minimum and maximum reported values (Yankovich et al. 2010).
cNot reported.
Transfer into wildlife—locusts, bee honey
The concentration ratio (CR) for terrestrial arthropods (e.g., locusts) is defined as the equilibrium ratio between the radionuclide activity concentration in a whole organism (Bq kg−1fresh weight) and the radionuclide activity concentration in the soil (Bq kg−1dry weight) (IAEA 2014). CR values for arthropods have been summarized for a limited number of elements (IAEA 2014). Suggested probability distributions and point estimates for CR values for arthropods based on the available data are summarized in Table 19. For cesium, a CR value for herbivorous arthropods is also available.
Table 19.
Suggested probability distributions and arithmetic means for the concentration ratios (CR) for arthropods (whole organism) with respect to soil (Bq kg−1fresh weight per Bq kg‑1dry weight).a
| Element | Wildlife type | Modeb | Minimum | Maximum | Arithmetic meanc |
|---|---|---|---|---|---|
| Sr | arthropods | 8.4 × 10−2 | 6.3 × 10−2 | 1.9 × 100 | 3.0 × 10−1 |
| Ru | arthropods | 4.1 × 10−3† | 4.1 × 10−4 | 4.1 × 10−2 | 6.3 × 10−3 |
| I | arthropods | 2.8 × 10−1 | 9.0 × 10−2 | 8.4 × 10−1 | 3.1 × 10−1 |
| Cs | arthropods | 2.4 × 10−2 | 2.0 × 10−3 | 1.7 × 100 | 1.1 × 10−1 |
| arthropods-herbivorous | 4.7 × 10−3 | 3.0 × 10−3 | 7.1 × 10−2 | 1.3 × 10−2 | |
| Ba | arthropods | 3.8 × 10−2* | 3.8 × 10−3 | 3.8 × 10−1 | 5.8 × 10−2 |
| Pu | arthropods | 1.6 × 10−2 | 4.2 × 10−4 | 2.5 × 10−1 | 2.5 × 10−2 |
aAll distributions are log-triangular distributions (as plotted in logarithmic space). Values of CR were obtained from IAEA 2014 (Table 5). For most cases, the mode (in logarithmic space) represents the geometric mean (or median) of the available data, and the minimum and maximum are the reported minimum and maximum values. If the reported minimum and maximum values differed by less than a factor of 10, the minimum and maximum values of the distribution were set at a factor of 3 below and above the mode (in logarithmic space), respectively. The mode value (in logarithmic space) with an asterisk (*) represents only one reported value (IAEA 2014), and the mode value (in logarithmic space) with a dagger (†) represents a geometric mean for which minimum and maximum values were not available. For these cases, the minimum and maximum have been set to a factor of 10 below and above the mode (in logarithmic space), respectively.
bParameter values are for the log-triangular distribution as plotted in logarithmic space.
cThe arithmetic mean of the indicated distribution; this value can be used as a point estimate in deterministic assessments.
Concentration ratios (CR) for honey (produced by honeybees) can be defined with respect to the flowers that the bees utilize (Bq kg−1 honey per Bq kg−1dry weight flowers) or with respect to the soil in which the flowers grow (Bq kg−1 honey per Bq kg−1dry weight soil). Based on very limited information (Molzahn and Assmann-Werthmüller 1993; Djuric et al. 1996; Fisk and Sanderson 1999; Sheppard et al. 2010a), a log-uniform distribution from 0.001 to 0.20 (arithmetic mean, 0.038) is suggested for the honey to soil CR, and a log-uniform distribution from 0.0001 to 0.10 (arithmetic mean, 0.015) for the honey to plant CR for all radionuclides.
Transfer into freshwater fish
The concentration ratio (CR) for aquatic wildlife is defined as the equilibrium ratio between the radionuclide activity concentration in a whole organism (Bq kg−1fresh weight) and the radionuclide activity concentration in the water (Bq L−1) (IAEA 2014), or the ratio of infinite time-integrated activity concentrations (Bq d kg−1fresh weight fish per Bq d L−1).
CR values have been summarized for broad types for freshwater fish (Yankovich et al. 2013; IAEA 2014). Suggested probability distributions and point estimates for CR values for freshwater fish are based on the available data and are summarized in Table 20. In most cases, the suggested distribution for "fish" is likely to be adequate. If the type of fish is known (benthic feeding fish, forage fish, piscivorous fish), the corresponding distribution can be used if available.
Table 20.
Suggested probability distributions and arithmetic means for the concentration ratios (CR) for freshwater fish (whole organism) with respect to water (Bq kg−1fresh weight per Bq L‑1).a
| Element | Type of fish | Modeb | Minimum | Maximum | Arithmetic meanc |
|---|---|---|---|---|---|
| Sr | fish | 1.5 × 102 | 3.8 × 100 | 1.2 × 105 | 3.5 × 103 |
| fish-benthic | 3.3 × 102 | 3.8 × 100 | 4.8 × 104 | 2.0 × 103 | |
| fish-forage | 2.9 × 102 | 1.7 × 101 | 2.8 × 103 | 4.0 × 102 | |
| fish-piscivorous | 1.1 × 102 | 5.3 × 100 | 1.2 × 105 | 3.4 × 103 | |
| Y | fish | 2.8 × 10−1 | 9.0 × 10−2 | 8.4 × 10−1 | 3.1 × 10−1 |
| Zr | fish | 5.4 × 101 | 9.2 × 100 | 6.9 × 102 | 1.0 × 102 |
| fish-piscivorous | 6.3 × 101 | 1.2 × 101 | 6.9 × 102 | 1.1 × 102 | |
| Mo | fish | 8.9 × 100 | 1.8 × 10−1 | 1.9 × 102 | 1.6 × 101 |
| fish-benthic | 5.3 × 100 | 1.8 × 10−1 | 9.8 × 101 | 9.6 × 100 | |
| fish-piscivorous | 1.0 × 101 | 3.8 × 10−1 | 1.9 × 102 | 1.9 × 101 | |
| Tc | fish-forage | 7.1 × 101 | 5.3 × 100 | 2.0 × 102 | 5.5 × 101 |
| Ru | fish | 2.9 × 101 | 1.7 × 10−1 | 1.4 × 103 | 7.7 × 101 |
| Te | fish-piscivorous | 2.8 × 102 | 9.6 × 101 | 8.9 × 102 | 3.2 × 102 |
| I | fish | 2.6 × 102 | 9.0 × 100 | 1.3 × 103 | 2.3 × 102 |
| fish-piscivorous | 2.9 × 102 | 1.0 × 101 | 1.3 × 103 | 2.4 × 102 | |
| Cs | fish | 1.6 × 103 | 1.3 × 101 | 8.2 × 104 | 4.6 × 103 |
| fish-benthic | 4.6 × 102 | 1.8 × 101 | 2.0 × 104 | 1.4 × 103 | |
| fish-forage | 4.7 × 102 | 1.7 × 101 | 8.6 × 103 | 8.5 × 102 | |
| fish-piscivorous | 2.7 × 103 | 1.3 × 101 | 8.2 × 104 | 5.2 × 103 | |
| Ba | fish | 4.3 × 101 | 3.0 × 10−1 | 8.8 × 102 | 6.7 × 101 |
| fish-benthic | 5.7 × 101 | 1.4 × 100 | 6.6 × 102 | 7.5 × 101 | |
| fish-piscivorous | 3.9 × 101 | 3.0 × 10−1 | 8.8 × 102 | 6.6 × 101 | |
| La | fish | 6.0 × 101 | 3.3 × 10−1 | 1.3 × 103 | 9.5 × 101 |
| fish-benthic | 1.8 × 102 | 3.8 × 100 | 1.3 × 103 | 1.8 × 102 | |
| fish-piscivorous | 5.0 × 101 | 7.3 × 10−1 | 4.4 × 102 | 5.2 × 101 | |
| Ce | fish | 6.5 × 101 | 1.8 × 100 | 2.3 × 103 | 1.7 × 102 |
| fish-benthic | 2.9 × 102 | 3.4 × 100 | 2.3 × 103 | 2.8 × 102 | |
| fish-piscivorous | 4.5 × 101 | 1.8 × 100 | 1.3 × 103 | 1.1 × 102 | |
| Pu | fish | 3.8 × 101 | 4.0 × 10−2 | 7.0 × 102 | 4.5 × 101 |
| fish-forage | 3.4 × 101 | 1.5 × 100 | 5.9 × 102 | 6.2 × 101 |
aAll distributions are log-triangular distributions (as plotted in logarithmic space). Values of CR were obtained from IAEA 2014 (Table 6). Values represent all types of freshwater fish for which information is available. For most cases, the mode (in logarithmic space) represents the geometric mean (or median) of the available data, and the minimum and maximum are the reported minimum and maximum values. If the reported minimum and maximum values differed by less than a factor of 10, the minimum and maximum values of the distribution were set at a factor of 3 below and above the mode (in logarithmic space), respectively.
bParameter values are for the log-triangular distribution as plotted in logarithmic space.
cThe arithmetic mean of the indicated distribution; this value can be used as a point estimate in deterministic assessments.
The CR values are for the whole body of the fish. For some elements, a whole-body-to-tissue concentration ratio is available for selected tissues (muscle, liver, kidney, and bone; Yankovich 2010; IAEA 2014). Table 21 provides reported mean whole-body-to-tissue concentration ratios for muscle (meat) and liver for freshwater fish. These values should be used together with the whole-body concentration ratios (Table 20) to estimate the radionuclide concentrations in the fish tissues likely to be consumed by humans.
Table 21.
Mean whole-body to tissue concentration ratios for freshwater fish, for tissues likely to be consumed by humans.a
| Element | Whole body to muscle | Whole body to liver |
|---|---|---|
| Sr | 38 (3.6–560)b | 27 (1.2–530) |
| Y | 1.8 (1.0–4.2) | 0.42 (0.13–2.6) |
| Zr | 1.2 (1.0–1.9) | 0.83 (0.20–2.5) |
| Nb | 1.1 (1.0–1.2) | –c |
| Mo | 1.4 (0.91–6.7) | 0.16 (0.036–0.83) |
| Ru | 1.2 (0.91–2.9) | – |
| Te | 1.2 (0.91–1.5) | 1.3 |
| I | 1.0 (0.91–1.1) | – |
| Cs | 1.1 (1.0–1.3) | 2.6 (1.9–5.0) |
| Ba | 5.6 (0.83–140) | 6.7 (0.91–120) |
| La | 1.9 (0.91–11) | 0.43 (0.13–0.91) |
| Ce | 2.0 (0.91–6.3) | 0.53 (0.30–1.0) |
aValues were obtained from Table 3 of Yankovich et al. (2010).
bValues in parentheses indicate the minimum and maximum reported values (Yankovich et al. 2010).
cNot reported.
Transfer into saltwater fish and seafood
Available information for marine (saltwater) fish and seafood (shellfish, aquatic plants or macroalgae) is generally in the form of concentration factors (CF), defined as the equilibrium ratio of radionuclide activity concentration in the edible part of the organism (Bq kg−1fresh weight) to the radionuclide activity concentration in the seawater (Bq L−1) (IAEA 2004). Suggested probability distributions and point estimates for CF values for 13 elements are summarized in Table 22 for marine fish, crustaceans, mollusks (gastropods and lamellibranchs but not cephalopods), and macroalgae. Table 23 provides reported mean whole-body-to-tissue concentration ratios for muscle (meat) and liver for marine fish. These values should be used together with the whole-body concentration ratios (Table 22) to estimate the radionuclide concentrations in the fish tissues likely to be consumed by humans.
Table 22.
Suggested probability distributions and arithmetic means for the concentration factors (CF) for marine fish and seafood (edible parts of organisms) with respect to water (Bq kg–1fresh weight per Bq L‑1).a
| Element | Type of fish | Modec | Minimum | Maximum | Arithmetic meand |
|---|---|---|---|---|---|
| Sr | fish | 3 × 100 | 3 × 10−1 | 3 × 101 | 4.6 × 100 |
| crustaceans | 5 × 100 | 5 × 10−1 | 5 × 101 | 7.6 × 100 | |
| mollusksb | 1 × 101 | 1 × 100 | 1 × 102 | 1.5 × 101 | |
| macroalgae | 1 × 101 | 1 × 100 | 1 × 102 | 1.5 × 101 | |
| Y | fish | 2 × 101 | 2 × 100 | 2 × 102 | 3.1 × 101 |
| crustaceans | 1 × 103 | 1 × 102 | 1 × 104 | 1.5 × 103 | |
| mollusksb | 1 × 103 | 1 × 102 | 1 × 104 | 1.5 × 103 | |
| macroalgae | 1 × 103 | 1 × 102 | 1 × 104 | 1.5 × 103 | |
| Zr | fish | 2 × 101 | 2 × 100 | 2 × 102 | 3.1 × 101 |
| crustaceans | 2 × 102 | 2 × 101 | 2 × 103 | 3.1 × 102 | |
| mollusksb | 5 × 103 | 5 × 102 | 5 × 104 | 7.6 × 103 | |
| macroalgae | 3 × 103 | 3 × 102 | 3 × 104 | 4.6 × 103 | |
| Nb | fish | 3 × 101 | 3 × 100 | 3 × 102 | 4.6 × 101 |
| crustaceans | 2 × 102 | 2 × 101 | 2 × 103 | 3.1 × 102 | |
| mollusksb | 1 × 103 | 1 × 102 | 1 × 104 | 1.5 × 103 | |
| macroalgae | 3 × 103 | 3 × 102 | 3 × 104 | 4.6 × 103 | |
| Tc | fish | 8 × 101 | 8 × 100 | 8 × 102 | 1.2 × 102 |
| crustaceans | 1 × 103 | 1 × 102 | 1 × 104 | 1.5 × 103 | |
| mollusksb | 5 × 102 | 5 × 101 | 5 × 103 | 7.6 × 102 | |
| macroalgae | 3 × 104 | 3 × 103 | 3 × 105 | 4.6 × 104 | |
| Ru | fish | 2 × 100 | 2 × 10−1 | 2 × 101 | 3.1 × 100 |
| crustaceans | 1 × 102 | 1 × 101 | 1 × 103 | 1.5 × 102 | |
| mollusksb | 5 × 102 | 5 × 101 | 5 × 103 | 7.6 × 102 | |
| macroalgae | 2 × 103 | 2 × 102 | 2 × 104 | 3.1 × 103 | |
| Te | fish | 1 × 103 | 1 × 102 | 1 × 104 | 1.5 × 103 |
| crustaceans | 1 × 103 | 1 × 102 | 1 × 104 | 1.5 × 103 | |
| mollusksb | 1 × 103 | 1 × 102 | 1 × 104 | 1.5 × 103 | |
| macroalgae | 1 × 104 | 1 × 103 | 1 × 105 | 1.5 × 104 | |
| I | fish | 9 × 100 | 9 × 10−1 | 9 × 101 | 1.4 × 101 |
| crustaceans | 3 × 100 | 3 × 10−1 | 3 × 101 | 4.6 × 100 | |
| mollusksb | 1 × 101 | 1 × 100 | 1 × 102 | 1.5 × 101 | |
| macroalgae | 1 × 104 | 1 × 103 | 1 × 105 | 1.5 × 104 | |
| Cs | fish | 1 × 102 | 1 × 101 | 1 × 103 | 1.5 × 102 |
| crustaceans | 5 × 101 | 5 × 100 | 5 × 102 | 7.6 × 101 | |
| mollusksb | 6 × 101 | 6 × 100 | 6 × 102 | 9.2 × 101 | |
| macroalgae | 5 × 101 | 5 × 100 | 5 × 102 | 7.6 × 101 | |
| Ba | fish | 1 × 101 | 1 × 100 | 1 × 102 | 1.5 × 101 |
| crustaceans | 7 × 10−1 | 7 × 10−2 | 7 × 100 | 1.1 × 100 | |
| mollusksb | 1 × 101 | 1 × 100 | 1 × 102 | 1.5 × 101 | |
| macroalgae | 7 × 101 | 7 × 100 | 7 × 102 | 1.1 × 102 | |
| Ce | fish | 5 × 101 | 5 × 100 | 5 × 102 | 7.6 × 101 |
| crustaceans | 1 × 103 | 1 × 102 | 1 × 104 | 1.5 × 103 | |
| mollusksb | 2 × 103 | 2 × 102 | 2 × 104 | 3.1 × 103 | |
| macroalgae | 5 × 103 | 5 × 102 | 5 × 104 | 7.6 × 103 | |
| Np | fish | 1 × 100 | 1 × 10−1 | 1 × 101 | 1.5 × 100 |
| crustaceans | 1 × 102 | 1 × 101 | 1 × 103 | 1.5 × 102 | |
| mollusksb | 4 × 102 | 4 × 101 | 4 × 103 | 6.1 × 102 | |
| macroalgae | 5 × 101 | 5 × 100 | 5 × 102 | 7.6 × 101 | |
| Pu | fish | 1 × 102 | 1 × 101 | 1 × 103 | 1.5 × 102 |
| crustaceans | 2 × 102 | 2 × 101 | 2 × 103 | 3.1 × 102 | |
| mollusksb | 3 × 103 | 3 × 102 | 3 × 104 | 4.6 × 103 | |
| macroalgae | 4 × 103 | 4 × 102 | 4 × 104 | 6.1 × 103 |
aAll distributions are log-triangular distributions (as plotted in logarithmic space). Values of CF were obtained from IAEA (2004; Tables III, IV, V, VI) and represent edible parts of the organism. The mode (in logarithmic space) represents the "recommended value" from the indicated tables; the minimum and maximum were set to a factor of 10 below and above the mode (in logarithmic space), respectively, as suggested by the IAEA (2004; pp. 29–30).
bMollusks include gastropods and lamellibranchs, but not cephalopods.
cParameter values are for the log-triangular distribution as plotted in logarithmic space.
dThe arithmetic mean of the indicated distribution; this value can be used as a point estimate in deterministic assessments.
Table 23.
Mean whole-body to tissue concentration ratios for marine fish, for tissues likely to be consumed by humans.a
| Element | Whole body to muscle | Whole body to liver |
|---|---|---|
| Sr | 3.1 (1.1–67)b | 0.91 (0.53–4.8) |
| Zr | 2.4 | 8.3 |
| Ru | 1.8 | 0.13 |
| Cs | 0.91 (0.71–1.1) | 2.8 (2.0–3.8) |
| Pu | 36 | 0.51 |
aValues were obtained from Table 3 of Yankovich et al. (2010).
bValues in parentheses indicate the minimum and maximum reported values (Yankovich et al. 2010).
TRANSFER OF RADIONUCLIDES INTO HUMAN BREAST MILK
Radionuclides in food or drinking water consumed by a lactating woman are transferred into breast milk, with the fraction transferred depending on the element. The most commonly used approach to estimation of radionuclide activity concentrations in mother's milk due to contaminated food and drinking water has been the use of transfer coefficients, defined as the equilibrium ratio of the fresh weight activity concentration in mother's milk to the daily dietary radionuclide intake of the mother. Use of the intake-to-mother's milk transfer coefficient (Fmm, Bq L−1 mother's milk per Bq d−1 ingested, or d L−1) requires estimation of the mother's total intake of each radionuclide from all sources. The transfer coefficients are intended for equilibrium conditions or for estimation of infinite time-integrated activities following an acute deposition event. Approaches to account for non-equilibrium or time-dependent situations and non-infinite time-integrated concentrations are provided later in this paper. Table 24 provides suggested probability distributions and point estimates for Fmm for each element, based on the values used for the Trinity assessment by Bouville et al. (2020, see also ICRP 2004, Simon et al. 2002).
Table 24.
Suggested probability distributions and arithmetic means for the intake-to-mother's milk transfer coefficient (Fmm, d L−1).a
| Element | Modeb | Minimum | Maximum | Arithmetic meanc |
|---|---|---|---|---|
| Sr | 6.1 × 10−2 | 6.1 × 10−3 | 6.1 × 10−1 | 9.3 × 10−2 |
| Y | 4.1 × 10−6 | 4.1 × 10−7 | 4.1 × 10−5 | 6.3 × 10−6 |
| Zr | 4.7 × 10−4 | 4.7 × 10−5 | 4.7 × 10−3 | 7.2 × 10−4 |
| Nb | 2.8 × 10−4 | 2.8 × 10−5 | 2.8 × 10−3 | 4.3 × 10−4 |
| Mo | 1.2 × 10−2 | 1.2 × 10−3 | 1.2 × 10−1 | 1.8 × 10−2 |
| Tc | 1.0 × 10−1 | 1.0 × 10−2 | 1.0 × 100 | 1.5 × 10−1 |
| Ru | 2.2 × 10−3 | 2.2 × 10−4 | 2.2 × 10−2 | 3.4 × 10−3 |
| Rh | 3.4 × 10−3 | 3.4 × 10−4 | 3.4 × 10−2 | 5.2 × 10−3 |
| Te | 2.9 × 10−3 | 2.9 × 10−4 | 2.9 × 10−2 | 4.4 × 10−3 |
| I | 3.3 × 10−1 | 3.3 × 10−2 | 3.3 × 100 | 5.0 × 10−1 |
| Cs | 1.2 × 10−1 | 1.2 × 10−2 | 1.2 × 100 | 1.8 × 10−1 |
| Ba | 5.8 × 10−3 | 5.8 × 10−4 | 5.8 × 10−2 | 8.9 × 10−3 |
| La | 2.3 × 10−3 | 2.3 × 10−4 | 2.3 × 10−2 | 3.5 × 10−3 |
| Ce | 2.1 × 10−5 | 2.1 × 10−6 | 2.1 × 10−4 | 3.2 × 10−5 |
| Pr | 2.3 × 10−5 | 2.3 × 10−6 | 2.3 × 10−4 | 3.5 × 10−5 |
| Np | 4.1 × 10−5 | 4.1 × 10−6 | 4.1 × 10−4 | 6.3 × 10−5 |
| Pu | 2.4 × 10−5 | 2.4 × 10−6 | 2.4 × 10−4 | 3.7 × 10−5 |
aAll distributions are log-triangular distributions (as plotted in logarithmic space). Modes (in logarithmic space) were taken from Bouville et al. (2020). The minimum and maximum values were set to a factor of 10 below and above the mode (in logarithmic space), respectively.
bParameter values are for the log-triangular distribution as plotted in logarithmic space.
cThe arithmetic mean of the indicated distribution; this value can be used as a point estimate in deterministic assessments.
BIOLOGICAL HALF-LIVES AND CORRECTIONS FOR NON-EQUILIBRIUM SITUATIONS
The transfer coefficient approaches described above are intended for equilibrium conditions (i.e., long-term situations where activity concentrations in the soil or the animal feed do not vary appreciably with time) or for estimation of infinite time-integrated activity concentrations. Concentration ratios for domestic animal products and for non-agricultural plants and wildlife are also intended for equilibrium situations. Some aggregated transfer coefficients are available in the literature for specific growth stages of vegetation (e.g., Choi et al. 2009), but most information on environmental transfer of radionuclides is still intended for equilibrium or infinite time-integrated situations.
An assumption of equilibrium is reasonable for a longer-term situation, where radioactivity in animal feed and animal products is dependent primarily on long-lived radionuclides in the soil that are taken up into the vegetation. For a short-term situation (e.g., the duration of the growing season during which a fallout event occurs), including both short-lived radionuclides and radioactivity deposited on vegetation from a single event, several approaches are needed.
Reduction of soil-to-plant transfer factor for deposition during the growing season
For a fallout event during the growing season, soil-to-plant transfer will probably not be as important that year as in subsequent years (for long-lived radionuclides) and generally will be less important than direct deposition onto vegetation for that growing season. However, the contribution of root uptake during the remaining part of the growing season after the fallout event can be crudely estimated, especially for plant types for which the edible parts did not receive direct deposition. Time-dependent aggregated transfer factors (specified for the time between deposition and harvest) are available for a few radionuclides and account for temporary localization of acutely deposited radionuclides on the soil surface (IAEA 2009, 2010). Müller and Pröhl (1993) suggest using a reduced value for the soil-to-plant transfer coefficient for the partial growing period. The reduction factor is the ratio of the time period between the deposition and harvest to the length of the whole growing season (e.g., the length of time between the fallout event and a typical harvest date for a given crop, divided by the total length of the growing season for that crop). The reduction factor likely differs among crops and types of edible wild plants.
Use of equilibrium transfer coefficients in time-dependent calculations
Müller and Pröhl (1993) provide an equation for time-dependent estimation of the transfer of radionuclides from animal feed to meat and milk. Their general equation uses one or more biological loss terms, the fraction of radionuclide corresponding to each term, and an integration to the time of interest. This equation can be simplified to use a single biological loss term:
 |
where
Cp(T) = the radionuclide activity concentration in product p (e.g., milk or meat) at time T (Bq kg−1 or Bq L−1);
Fp = the transfer coefficient for product p [e.g., Fm (d L−1) or Ff (d kg−1)];
Ap(t) = the activity intake rate of the animal producing product p (Bq d−1);
λb,p = the biological loss constant (transfer rate) for product p (d−1);
λi = the rate constant for radioactive decay (decay constant) of radionuclide i (d−1); and
T and t are time (d).
The biological loss constant λb,p is derived from the biological half-life for product p (λb,p = ln(2)/Tb,p, where Tb,p is the biological half-life for product p). The biological half-life accounts for loss of radionuclides from an animal product due to processes other than radioactive decay (Table 25; described below). Values of λi for the radionuclides considered in this paper are provided in Table 1.
Table 25.
Suggested probability distributions and arithmetic means for the biological half-life (Tp, d) in various food products or environmental compartments (for all elements).
| Product or compartment | Distribution type | Distribution parameters | Arithmetic meana |
|---|---|---|---|
| Milkb | log-triangularg | minimum = 0.5; mode = 2; maximum = 5 | 1.9 |
| Meat (muscle)c and wildlife | log-triangularg | minimum = 3; mode = 30; maximum = 300 | 46 |
| Plantsd | log-triangularg | minimum = 1; mode = 10; maximum = 100 | 15 |
| Fishe | log-triangularg | minimum = 3; mode = 30; maximum = 300 | 46 |
| Arthropodsf | log-triangularg | minimum = 3; mode = 30; maximum = 300 | 46 |
aThe arithmetic mean of the indicated distribution; this value can be used as a point estimate in deterministic assessments.
bDistribution based on information reviewed or summarized by Fesenko et al. (2015).
cDistribution based on information reviewed or summarized by Fesenko et al. (2015). The distribution is intended for use for beef, pork, mutton, goat, poultry, and eggs.
dDistribution based on a central value of 10 d (IAEA in press); see also Heinemann and Vogt (1980).
eDistribution based on a central value of 30 d (NCRP 1996).
fDistribution based on a central value of 30 d (Dragovic et al. 2010).
gParameter values are for the log-triangular distribution as plotted in logarithmic space.
Correction of transfer coefficients for short-lived radionuclides
For estimation of the transfer of short-lived radionuclides, it is necessary to use a correction factor for the transfer coefficients (NCRP 1996):
 |
where
CFi,p = the correction factor for the transfer of radionuclide i to product p (e.g., milk or meat);
λi = the rate constant for radioactive decay (decay constant) of radionuclide i (d−1);
λb,p = the rate constant for biological loss from product p (d−1), where λb,p = ln (2)/Tb,p; and
Tb,p = the biological half-life for product p (d).
This correction factor corrects for either radioactive decay of short-lived radionuclides or biological turnover of long-lived radionuclides. The biological half-life (Table 25; described below) accounts for the loss of radionuclides from an animal product or tissue (e.g., milk or meat) or from vegetation, due to processes other than radioactive decay. Values of λi for the radionuclides considered in this paper are provided in Table 1.
Biological half-lives
The biological half-life describes the loss over time of radionuclides from an animal product or tissue (e.g., milk or meat) or from vegetation, due to processes other than radioactive decay. Suggested probability distributions and point estimates for various products are provided in Table 25 and described below.
The probability distributions for the biological half-life of radionuclides in milk and meat are based largely on a recent review of Russian-language literature (Fesenko et al. 2015), which includes some comparisons with other published information; no other comprehensive review is available. The reported biological half-life depends, in principle, on the tissue or product of interest, the element, the nature of the exposure (e.g., single administration vs. chronic exposure), and the species, age, and size of the animals. In practice, experimental procedures (e.g., timing of sampling) also affect the results. Concentration or retention of some elements in specific organs or tissues (e.g., iodine in thyroid, strontium in bones) affects the biological half-life as well. Some studies report two or more loss components (e.g., a short-term half-life and a longer-term half-life); use of a two-component loss model would also require information on the fraction of radionuclide lost in each compartment (Fesenko et al. 2015). Available data do not presently permit detailed descriptions of biological half-lives by element and animal species, although for a few elements more specific probability distributions could be described if this parameter is sufficiently important. Sources of further information include Fesenko et al. (2015) and the database described by Beresford et al. (2015).
For milk, data for a number of elements in cows are relatively consistent, with reported biological half-lives of about 2 d and most values within the range of 0.6–3.5 d (Fesenko et al. 2015); similar values are found for goats (Fesenko et al. 2015). A log-triangular distribution from 0.5 to 5 d, with a mode (in logarithmic space) at 2 d, is suggested for the biological half-life of all radionuclides in milk.
For meat (muscle tissue), a single probability distribution is suggested for all elements and animal species (beef, pork, mutton, goat, poultry, eggs) for a single-component loss model. This can be revisited for some elements (primarily cesium and strontium), if necessary. A log-triangular distribution is suggested, with a range from 3 to 300 d, with a mode (in logarithmic space) at 30 d. This would account for both short-term and longer-term losses and for continuing exposure to a one-time release event. In the absence of information specific to wildlife, this distribution is also suggested for wildlife (mammals and birds).
Suggested probability distributions for the biological half-life of radionuclides in plants and in fish (Table 25) are based on single values previously suggested for screening analyses (NCRP 1996; IAEA in press; Heinemann and Vogt 1980) and should be revisited if they prove to be sufficiently important.
From a review of the limited literature, Dragovic et al. (2010) report a biological half-life for cesium in invertebrates of 4 d to 1 mo and expect a much longer biological half-life for actinides. In the absence of further information, the suggested distribution for arthropods is the same as that proposed for meat, wildlife, and fish, centered on a value of 30 d.
PROCESSING OF PLANT AND ANIMAL PRODUCTS (CULINARY FACTORS)
Processing of plant and animal products can affect the activity concentrations of radionuclides present in the products at the time of their consumption by humans in several ways (IAEA 2009, 2010). First, the additional time between harvest of the plant or animal and consumption of the product allows for additional radioactive decay. Second, the processing itself can affect the fraction of an element retained in the product. This could be either a loss of activity from the plant or animal (e.g., loss of activity when a vegetable is washed or peeled; extraction of a radionuclide during boiling) or an increase in activity concentration in the product compared with the plant or animal at harvest (e.g., activity concentration of a radionuclide in a dried product). The effect of processing has to be considered on a case-by-case basis for processed plant and animal products that are consumed in substantial quantities. Some information on food processing is available in recent IAEA reviews (IAEA 2009, 2010). Information on the dry matter content of various plants and animals (e.g., Appendix I of IAEA 2010; Appendix I of IAEA 2014) can be used to estimate the resulting radionuclide activity concentrations in dried products.
The IAEA (2009, 2010) has summarized available information on food processing, in terms of the activities remaining in food after the food has been processed or prepared for consumption. Additional information on the fraction of contaminant remaining in plant products is also available in the general literature (e.g., Simmonds and Linsley 1982; McLeod et al. 1984; Pinder et al. 1987; Carini et al. 1999; Rosen and Vinichuk 2016). Specific information is not available for many elements or for all types of food processing and preparation.
In general, the IAEA (2010) reports a food processing retention factor Fr, defined as the fraction of radionuclide activity retained in the food after processing (e.g., Fr = 0.3 indicates that 30% of the activity remains; Fr = 1 indicates that 100% of the activity remains and that the processing had no effect in terms of reducing the radionuclide activity in the food). The IAEA (2010) also defines Pe, the processing efficiency (the ratio of the fresh weight of the processed food to the weight of the original raw food), and Pf, the processing factor (the ratio of the radionuclide activity concentrations, analogous to a concentration ratio), with the following relationship:
 |
Pe and Pf are important when the yield of processed food is a fraction of the raw food, e.g., a 12% yield of cheese from goat's milk (IAEA 2010). For the example of cheese, Fr = 0.6 for strontium, so accounting for both the retention of strontium in the processed goat's milk and the yield of cheese from goat's milk gives Pf = Fr / Pe = 0.6 / 0.12 = 5, indicating that the activity concentration of strontium in cheese is 5 times the activity concentration of strontium in fresh goat's milk (IAEA 2010). Table 26 in this paper provides values for Fr and Pe for a variety of culinary processes. Note that Fr is dependent on the element in many cases, while Pe is not dependent on the element.
Table 26.
Examples of estimated food processing losses, reported in terms of the processing efficiency (Pe) and the fraction of contamination remaining in the food (Fr).a,b
| Type of processing | Pe | Elements | Fr |
|---|---|---|---|
| Washing of vegetables, berries, and fruits (direct contamination) | 1.0 | I, Cs Sr Ru |
0.1–0.9 0.1–0.5 0.2–0.8 |
| Washing of vegetables, berries, and fruits (total contamination) | 1.0 | Cs I Sr Ru |
0.6–1.0 0.8 0.4–1.0 0.7–0.9 |
| Boiling in water of vegetables and berries (direct contamination) | 0.8–1.0 | I, Cs Sr Ru, Te Ba Zr |
0.1–0.5 0.1–0.2 0.3–0.7 0.6–0.9 1.0 |
| Boiling in water of vegetables and berries (total contamination) | 0.8–1.0 | Cs Sr Ru, Pu |
0.4–0.9 0.6–1.0 0.3–1.0 |
| Peeling of vegetables (total contamination) | 0.7–0.9 | Sr, Cs Pu |
0.5–0.9 0.1–1.0 |
| Canning, blanching, and pickling of vegetables (total contamination) | 0.5–0.9 | Cs Sr |
0.1–1.0 0.3–1.0 |
| Milling of grain to flour | 0.6–0.8 | Cs Sr Pu |
0.2–0.6 0.1–0.6 0.1–0.2 |
| Milling of grain to bran | 0.1–0.4 | Cs Sr |
0.4–0.7 0.6–0.9 |
| Berries and fruits to juice | 0.3–0.9 | Cs Pu |
0.2–0.9 0.5 |
| Grapes to wine | 0.6–0.8 | Cs Sr |
0.3–0.7 0.2–0.6 |
| Tea, brewed 2–8 minutes (direct contamination) | 1.0 | Cs | 0.9 |
| Tea, brewed 2–8 minutes (total contamination) | 1.0 | Cs | 0.4–0.6 |
| Herbal tea, brewed (total contamination) | 1.0 | Cs | 0.4–0.6 |
| Medicinal plants (infusions and broths)c | 1.0 | Cs Sr |
0.1–0.9 0.1–0.8 |
| Milk to cream | 0.08 (0.03–0.24) | Cs Sr I |
0.05 (0.03–0.16) 0.04 (0.02–0.25) 0.06 (0.006–0.19) |
| Milk to skim milk | 0.92 (0.76–0.97) | Cs Sr I |
0.95 (0.85–0.99) 0.93 (0.75–0.96) 0.81–0.94 |
| Milk to sour cream | 0.1 (0.1–0.2) | Cs Sr |
0.1 (0.1–0.2) 0.1 (0.1–0.13) |
| Milk to butter | 0.04 (0.03–0.05) | Cs Sr I |
0.01 (0.003–0.02) 0.006 (0.0025–0.012) 0.02 (0.01–0.035) |
| Goat's milk to cheese | 0.12 (0.08–0.17) | Cs Sr I |
0.07–0.15 0.61 0.08–0.14 |
| Cow's milk to cheese (rennet process) | 0.12 (0.08–0.18) | Cs Sr I |
0.07 (0.05–0.23) 0.7 (0.025–0.8) 0.2 (0.11–0.53) |
| Cow's milk to cheese (acid process) | 0.1 (0.08–0.12) | Cs Sr I |
0.06 (0.01–0.12) 0.08 (0.04–0.08) 0.22–0.27 |
| Cow's milk to cottage cheese (rennet process) | 0.1 | Cs Sr |
0.01–0.05 0.07–0.17 |
| Cow's milk to cottage cheese (acid process) | 0.12 (0.1–0.14) | Cs Sr |
0.1 0.2–0.7 |
| Boiling of meat | 0.5–0.7 | Cs Sr I Ru |
0.4 (0.2–0.7) 0.5 (0.4–0.9) 0.6 0.3 |
| Frying, roasting, or grilling of meat | 0.4–0.7 | Cs Sr I |
0.7 (0.5–0.8) 0.8 0.2–0.6 |
| Pickling, salting, or marinating of meat (curing) | 0.9–1.0 | Cs | 0.5 (0.1–0.7) |
| Sausage production | 1.0 | Cs | 0.4–1.0 |
| Cooking of poultryd | 0.4–0.7 | Cs Sr I |
0.7–0.8 0.5 0.5–1.0 |
| Boiling of fish | 0.5–0.9 | Cs Sr |
0.2–0.9 0.9 |
| Frying or grilling of fish | 0.7–0.8 | Cs | 0.8–0.9 |
aInformation from IAEA (2010). Where a range is given, the values may be used to define a uniform distribution; where a single value and a range are given, the single value is the recommended value from the IAEA (2010) and may be used with the range to define a triangular distribution.
bThe processing efficiency (Pe) is independent of element and is defined as the ratio of processed food (fresh weight) to raw food (fresh weight). The retention factor (Fr) is the fraction of radionuclide activity retained in the processed food. The processing factor (Pf) is the ratio of the radionuclide activity concentration in the processed food to the radionuclide activity concentration in the raw food and can be calculated from Pe and Fr as follows: Pf = Fr / Pe [see eqn (14) in the main text].
cIAEA (2010, Table 79) gives more detailed information by plant parts for Cs and Sr.
dValues for Cs are for baking; for Sr, for boiling; for I, for roasting (IAEA 2010, Table 76).
It is important to distinguish between contamination on a plant surface due to direct deposition and total contamination of a plant due to uptake from the soil or to translocation from contaminated foliage, in addition to (or instead of) direct contamination. For many fallout events, direct deposition of contamination on edible parts of plants is likely to be more important than contamination of edible plant parts due to translocation or uptake from soil. For example, removal of outer leaves or peels will be more effective in reducing direct contamination than indirect contamination; values of Fr for "washing of vegetables, berries, and fruits" therefore can be lower for direct contamination than for indirect contamination.
Where single values are given in Table 26, they are likely to be conservative. Where ranges are given, they may be used as the minimum and maximum of uniform distributions, or an appropriate value may be selected from the range based on project-specific information. In some cases, the IAEA (2010) provided a recommended value and a range; these may be used to define a triangular distribution, or the recommended value may be used, but modified as needed based on location-specific information.
Radioactive decay during processing and storage is not included in the retention factors. Instead, the time required for processing of foods is included in the estimates of total time between harvest and consumption of the foods (delay in consumption due to processing, storage, etc.). Time between harvesting and consumption is discussed later in this report.
MANUFACTURE OF ALCOHOLIC BEVERAGES
There is a limited amount of information on the transfer of radionuclides from plants or fruits into alcoholic beverages made from the plants or fruits. Pröhl et al. (1997) reported that about 10% of 137Cs in barley was in the final beer (processing factor of 0.11 Bq L−1 beer per Bq kg−1 barley). Okuda et al. (2012, 2013) report that about 5% of cesium in brown rice is present in sake produced from the rice (processing factor around 0.03–0.05 Bq kg−1 sake per Bq kg−1 rice). Hellmuth et al. (1989) reported transfer factors from soil to grapes of 0.027 for 90Sr and 0.0057 for 137Cs (units not given). On average, the 137Cs content of wine compared with grapes was about 0.40 (0.40 Bq L−1 wine per Bq kg−1 grapes), and the 90Sr content of wine compared with grapes was about 0.23 (0.23 Bq L−1 wine per Bq kg−1 grapes) (Hellmuth et al. 1989). Okuda et al. (2016) reported that about 80% of cesium in the fruit of Japanese apricot was retained in the liqueur made from the fruit; this corresponded to a cesium concentration in the liqueur of approximately 20–25% of that in the fruit (processing factor about 0.25 Bq L−1 liqueur per Bq kg−1 fruit).
While very limited, these data suggest that radionuclide activity concentrations (at least for cesium and strontium) in alcoholic beverages made from the fruit of a plant could be 20–40% of the radionuclide activity concentration in the fruit, while radionuclide activity concentrations in alcoholic beverages made from grain could be 5-15% of the radionuclide activity concentration in the grain.
DRINKING WATER
Rainfall soon after an event producing radioactive fallout could contaminate the drinking water for area residents using surface water sources or cisterns collecting rainwater. Radionuclide activity concentrations in drinking water from a surface water source or from cisterns would reflect the deposition in the catchment area, the solubility of the radionuclides or radioactive particles, the amount of rainwater in the reservoir or cistern prior to the arrival of fallout, and the amount of rain collected in the reservoir or cistern in the days or weeks following the deposition of the fallout.
All soluble radionuclides can be assumed to remain in the drinking water if there is no further treatment. Boiling of water (e.g., for disinfection) would result in higher concentrations of solutes (e.g., dissolved radionuclides) in the water actually consumed due to the loss of water volume during boiling (Grimaldo et al. 1995; Tagami and Uchida 2011).
For municipal drinking water, a limited amount of information is available on the removal of radionuclides by water treatment (Lindsten et al. 1965; Denham and Soldat 1975; Goossens et al. 1989; Napier 1993; Brown and Hammond 2009).
TIME BETWEEN HARVEST AND CONSUMPTION
Radioactive decay during processing and storage is not included in the retention factors. Instead, the time required for processing of foods is included in the estimates of total time between harvest and consumption of the foods (delay in consumption due to processing and storage), and concentrations in foods can be adjusted for radioactive decay during that time. The reduction in radionuclide concentrations in foods due to a delay in consumption is especially important for shorter-lived radionuclides. For some radionuclides, it is also necessary to account for build-up of radioactive decay products (progeny) during the time between harvest and consumption.
Table 27 summarizes information on delay times for a variety of food products in terms of a typical delay time and the minimum and maximum delay times (IAEA 2010). These values are intended to represent average delay times for long-term assessments of routine releases under modern conditions of agriculture and food handling. Delay times following a single deposition event could be much shorter, as many types of foods can be eaten very soon after harvest (e.g., fresh fruits and vegetables, fresh milk from backyard animals, fresh fish). Delay times for local food sources should be evaluated for a given situation.
Table 27.
Examples of delay times between harvest and consumption of food products (duration of processing and storage).
| Delay timea | |||
|---|---|---|---|
| Food type | Typical | Minimum | Maximum |
| Leafy vegetables | 4 days | 1 day | 7 days |
| Fruit vegetables | 7 days | 2 days | 14 days |
| Root vegetables | 10 days | 7 days | 14 days |
| Potatoes and beets | 3 months | 7 days | 6 months |
| Cereals and cereal products | 6 months | 45 days | 1 year |
| Fresh apples and pears | 3.5 months | 0 | 8 months |
| Fresh drupe fruits, soft fruit, rhubarb | 4 days | 0 | 8 days |
| Canned fruit | 1 year | 14 days | 2 years |
| Frozen fruit | 6 months | 7 days | 1 year |
| Jams and jellies | 1 year | 1 day | 2 years |
| Milkb | 2 days | 1 day | 6 days |
| Butter | 1 month | 3 days | 3 months |
| Cream | 5 days | 2 days | 10 days |
| Skim milk | 2 days | 1 day | 6 days |
| Cheese (rennet process) | 1.5 months | 30 days | 3 months |
| Cheese (acid process) | 1 month | 7 days | 2 months |
| Fresh beef | 20 days | 14 days | 28 days |
| Fresh pork, veal | 4 days | 2 days | 7 days |
| Fresh chicken | 4 days | 2 days | 7 days |
| Fresh lamb | 10 days | 7 days | 14 days |
| Fresh game | 10 days | 2 days | 20 days |
| Eggs | 14 days | 2 days | 28 days |
aFrom IAEA (2010, Table 81).
bIAEA (2010) does not distinguish between backyard and commercial dairy animals or between cows and goats.
FEED CONSUMPTION BY LIVESTOCK
Feed consumption rates for local livestock should be evaluated for the given location and agricultural situation, including the time of year that a fallout event occurs. Typically, dairy animals fed fresh pasture are of the highest concern, as the radioactivity deposited directly on vegetation could be consumed immediately, transfer of radioactivity to milk can be substantial, and consumption of milk can occur within days. For backyard cows and for dairy goats, transfer of radioiodine is typically higher than for commercial dairy cows (Table 13; see also Simon et al. 1990; NCI 1997; Apostoaei et al. 1999), and the milk may be consumed much sooner after collection than is the case for commercially produced milk. Other livestock that may need to be considered include beef cattle, swine, sheep, goats, and poultry.
For example, for estimation of doses from NTS fallout, consumption by dairy cows of fresh pasture and stored feed was estimated by geographical area and time of year (NCI 1997). For assessment of doses from the Trinity test in July 1945, it was necessary to compile information on New Mexico agricultural practices in the 1940s (Bouville et al. 2020). It may also be necessary to account for the animals' consumption of contaminated soil and contaminated drinking water.
Sources of local agricultural information include state and local agricultural stations and colleges, as well as local farmers, dairies, and livestock producers. Feeding practices are generally considered in terms of fresh pasture, feed consumed soon after harvest (e.g., green chop; feed cut and immediately fed to animals kept indoors), contaminated feed that is stored for later use (e.g., hay, grain), and uncontaminated stored feed from a previous season or imported from outside the affected area. Both the types and the amounts of feed may vary seasonally or with the type of farm.
INGESTION RATES
Ingestion rates of various local foods by people should be evaluated for a local contamination situation. Due to the importance of direct deposition of radioactivity onto pasture vegetation and gardens, and because both milk and leafy vegetables may be consumed very soon after harvest, locally produced milk and leafy vegetables are typically of highest concern; Anspaugh et al. (2022) provide suggested ingestion rates for fruits, vegetables, dairy products, and meat. For a given food type, consumption rates may vary by age and sex, time of year, and population subgroup. For example, the assessment of the Trinity test evaluated ingestion rates for six age groups and six population groups described in terms of location, urban vs. rural conditions, and ethnicity (Bouville et al. 2020).
General information on ingestion rates can be found in publications by the US EPA (e.g., US EPA 2004, 2008, 2011, 2019, and updates). For important local food sources, consultation with members of the public and with state and local authorities (agricultural, health, wildlife) could be valuable, along with literature reviews. Many general sources report per capita consumption or average ingestion rates for the whole population; for this type of assessment, it is better to estimate average consumption by people who actually consume the item. It is generally important to distinguish between long-term average consumption rates and short-term consumption rates, especially for foods that are produced seasonally.
Previous assessments have used an intake rate for nursing infants of 0.8 L d−1 for the first year of life and assumed exclusive breastfeeding (Simon et al. 2010; Bouville et al. 2020). Currently in the US, many infants are never breastfed, and only about 25% are exclusively breastfed for 6 mo (CDC 2020); in addition, breastfeeding rates vary among population subgroups (Li et al. 2019). Thus, for an actual assessment, it would be necessary to obtain local information on breastfeeding rates, exclusivity of breastfeeding, and other sources of infant nutrition. Use of contaminated local water for preparation of infant formula could also be important; estimates of water intake by formula-fed infants are available (US EPA 2019; Kahn et al. 2013).
ADDITIONAL TYPES OF INFORMATION
Additional types of information could be useful for a particular assessment. These would generally be site-specific or situation-specific. This information could include typical planting and harvest dates, irrigation practices, sources of irrigation water and drinking water, and the distribution of crops and livestock products (sources of locally consumed food and animal feed). For example, for the Trinity assessment, the milk sources for each local area were estimated in terms of the source and amount of milk consumed in each area: locally produced, brought in from the major milk-producing areas, or some of both (Bouville et al. 2020). Collection of this information will generally require consultation with state and local authorities and agricultural specialists, as well as members of the affected public.
CONCLUDING REMARKS
In this paper, we have reviewed a number of parameters that are necessary for model-based estimation of internal doses from fallout due to a nuclear detonation, and we have suggested both probability distributions and point estimates for these parameters. Numerous processes may result in contamination of edible food products. While a detailed understanding of site-specific contamination and loss processes is desirable, in many cases generic information may have to be used in the absence of site-specific information and should be presented with appropriate caveats.
In general, the probability distributions in this paper reflect uncertainty about a true but unknown value of a parameter for a specific assessment, based on available information. However, some of these data might not be fully relevant for a specific event and location. The point estimates suggested in this paper are the arithmetic means of the corresponding probability distributions; use of the arithmetic means is intended to provide reasonable estimates for screening calculations or initial assessments without introducing excessive conservatism into estimates of internal dose. It is the responsibility of the assessor to understand and appropriately use both the point estimates and the distributions presented.
The assessor should also carefully consider the presence of equilibrium or non-equilibrium conditions, especially for estimation of appropriate time-dependent concentrations in foods of importance for decisions to intervene.
The summary of model parameters and parameter values presented here represents a detailed synthesis of past and recent published data and is believed to be appropriate for retrospective or prospective assessments of internal doses from ingestion of radioactive fallout. The values and probability distributions presented here can be readily updated and modified, both to allow for event- and location-specific conditions and to accommodate new data that may be acquired after the event has occurred.
Acknowledgments
This research was primarily supported by the Intra-Agency Agreement between the National Institute of Allergy and Infectious Diseases and the National Cancer Institute, NIAID agreement #Y2-Al-5077 and NCI agreement #Y3-CO-5117 with additional support from the Intramural Research Program of the NCI, NIH. The authors acknowledge the extensive work of many investigators who preceded them and contributed to our present-day understanding of exposure to radioactive fallout. No conflicts of interest are declared.
This list is based on the results of previous studies of important radionuclides in fallout (Ng et al. 1990; Simon et al. 2020). These radionuclides are believed to account for > 95% of the dose from ingestion and inhalation (Simon et al. 2022). Additional radionuclides are included in the estimation of external dose (Bouville et al. 2022).
Throughout this paper, the "mode" of a log-triangular distribution is the value of the mode given in arithmetic units when the triangular distribution is plotted on a logarithmic scale. For a symmetrical log-triangular distribution, the mode is equidistant in logarithmic space from the minimum and maximum values and equal to the median value. For an asymmetrically skewed log-triangular distribution, the mode in logarithmic space will be a different value from the median value or mode plotted in arithmetic (linear) space.
The authors declare no conflicts of interest.
(Manuscript accepted 5 August 2021)
Contributor Information
F. Owen Hoffman, Email: fohoff3084@aol.com.
André Bouville, Email: abouville@aol.com.
Lynn R. Anspaugh, Email: lanspaugh@aol.com.
Harold L. Beck, Email: hbeck5@verizon.net.
Steven L. Simon, Email: ssimon@mail.nih.gov.
REFERENCES
- Acevedo E, Badilla I, Nobel PS. Water relations, diurnal acidity changes, and productivity of a cultivated cactus, Opuntia ficus-indica. Plant Physiol 72:775–780; 1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anspaugh LR, Bouville A, Thiessen KM, Hoffman FO, Beck HL, Gordeev K, Simon SL. A methodology for calculation of internal dose following exposure to radioactive fallout from the detonation of a nuclear fission device. Health Phys 122(1):84–124; 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Apostoaei AI, Burns RE, Hoffman FO, Ijaz T, Lewis CJ, Nair SK, Widner TE. Iodine-131 releases from radioactive lanthanum processing at the X-10 site in Oak Ridge, Tennessee (1944–1956): an assessment of quantities released, off-site radiation doses, and potential excess risks of thyroid cancer. Reports of the Oak Ridge Dose Reconstruction, Vol. 1. The Report of Project Task 1. Oak Ridge, TN: Tennessee Department of Health, Oak Ridge Health Studies, Oak Ridge Dose Reconstruction; 1999. [Google Scholar]
- Beck HL, Bouville A, Simon SL, Anspaugh LR, Thiessen KM, Shinkarev S, Gordeev K. A method for estimating the deposition density of fallout on the ground and on vegetation from a low-yield, low-altitude nuclear detonation. Health Phys 122(1):21–53; 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bengtsson SB, Eriksson J, Gärdenäs AI, Rosén K. Influence of development stage of spring oilseed rape and spring wheat on interception of wet-deposited radiocaesium and radiostrontium. Atmos Environ 60:227–233; 2012. [Google Scholar]
- Bengtsson SB, Gärdenäs AI, Eriksson J, Vinichuk M, Rosén K. Interception and retention of wet-deposited radiocaesium and radiostrontium on a ley mixture of grass and clover. Sci Tot Environ 497–498:412–419; 2014. [DOI] [PubMed] [Google Scholar]
- Beresford NA, Beaugelin-Seiller K, Burgos J, Cujic M, Fesenko S, Kryshev A, Pachal N, Real A, Su BS, Tagami K, Vives i Batlle J, Vives-Lynch S, Wells C, Wood MD. Radionuclide biological half-life values for terrestrial and aquatic wildlife. J Environ Radioact 150:270–276; 2015. [DOI] [PubMed] [Google Scholar]
- Bouville A, Beck HL, Thiessen KM, Hoffman FO, Potischman N, Simon SL. The methodology used to assess doses from the first nuclear weapons test (Trinity) to the populations of New Mexico. Health Phys 119:400–427; 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouville A, Beck HL, Anspaugh LR, Gordeev K, Shinkarev S, Thiessen KM, Hoffman FO, Simon SL. A methodology for estimating external doses to individuals and populations exposed to radioactive fallout from nuclear detonations. Health Phys 122(1):54–83; 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breuer L, Eckhardt K, Frede H-G. Plant parameter values for models in temperate climates. Ecol Modelling 169:237–293; 2003. [Google Scholar]
- Brown J, Hammond D. UK recovery handbook for radiation incidents: drinking water supplies. Version 3. Chilton, Didcot, UK: Health Protection Agency; HPA-RPD-064: Part 3; 2009. [Google Scholar]
- Calmon P, Thiry Y, Zibold G, Rantavaara A, Fesenko S. Transfer parameter values in temperate forest ecosystems: a review. J Environ Radioact 100:757–766; 2009. [DOI] [PubMed] [Google Scholar]
- Carini F, Scotti A, D'Alessandro PG. 134Cs and 85Sr in fruit plants following wet aerial deposition. Health Phys 77:520–529; 1999. [DOI] [PubMed] [Google Scholar]
- Cassells DM, Gillen RL, McCollum FT, Tate KW, Hodges ME. Effects of grazing management on standing crop dynamics in tallgrass prairie. J Range Manage 48:81–84; 1995. [Google Scholar]
- Centers for Disease Control and Prevention . Results: breastfeeding rates. Breastfeeding among U.S. children born 2010–2017, CDC National Immunization Survey [online]. 2020. Available at https://www.cdc.gov/breastfeeding/data/nis_data/results.html. Accessed 29 June 2021.
- Chadwick RC, Chamberlain AC. Field loss of radionuclides from grass. Atmos Environ 4:51–56; 1970. [DOI] [PubMed] [Google Scholar]
- Chamberlain AC. Interception and retention of radioactive aerosols by vegetation. Atmos Environ 4:57–78; 1970. [DOI] [PubMed] [Google Scholar]
- Choi YH, Lim KM, Yu D, Park HG, Choi YG, Lee CM. Transfer pathways of 54Mn, 57Co, 85Sr, 103Ru and 134Cs in rice and radish plants directly contaminated at different growth stages. Ann Nuclear Energy 29:429–446; 2002. [Google Scholar]
- Choi Y-H, Lim K-M, Jun I, Park D-W, Keum D-K, Lee C-W. Root uptake of radionuclides following their acute soil depositions during the growth of selected food crops. J Environ Radioact 100:746–751; 2009. [DOI] [PubMed] [Google Scholar]
- Clark OR. Interception of rainfall by prairie grasses, weeds, and certain crop plants. Ecol Monographs 10:243–277; 1940. [Google Scholar]
- Coppock DL, Detling JK, Ellis JE, Dyer MI. Plant-herbivore interactions in a North American mixed-grass prairie. I. Effects of black-tailed prairie dogs on intraseasonal aboveground plant biomass and nutrient dynamics and plants species diversity. Oecologia 56:1–9; 1983. [DOI] [PubMed] [Google Scholar]
- Corbett ES, Crouse RP. Rainfall interception by annual grass and chaparral. Losses compared. Berkeley, CA: Pacific Southwest Forest and Range Experiment Station. USDA Forest Service Research Paper PSW-48; 1968. [Google Scholar]
- Cox JR. Above-ground biomass and nitrogen quantities in a big sacaton [Sporobolus wrightii] grassland. J Range Manage 38:273–276; 1985. [Google Scholar]
- Cristina A, Samson R, Horemans N, Van Hees M, Wannijn J, Bruggeman M, Sweeck L. Interception of radionuclides by planophile crops: a simple semi-empirical modelling approach in case of nuclear accident fallout. Environ Pollut 266:115308; 2020. [DOI] [PubMed] [Google Scholar]
- Cully AC, Cully JF, Jr. Spatial and temporal variability in perennial and annual vegetation at Chaco Canyon, New Mexico. Great Basin Naturalist 49:113–122; 1989. [Google Scholar]
- Cunningham GL, Syvertsen JP, Reynolds JF, Willson JM. Some effects of soil-moisture availability on above-ground production and reproductive allocation in Larrea tridentata (DC) Cov. Oecologia 40:113–123; 1979. [DOI] [PubMed] [Google Scholar]
- Denham DH, Soldat JK. A study of selected parameters affecting the radiation dose from radionuclides in drinking water downstream of the Hanford project. Health Phys 28:139–144; 1975. [DOI] [PubMed] [Google Scholar]
- Djuric G, Popovic D, Todovic D. Activity variations and concentration factors for natural radionuclides in a "soil-plant-honey" system. Environ Int 22(Suppl 1):S361–S363; 1996. [Google Scholar]
- Domingo F, Sánchez G, Moro MJ, Brenner AJ, Puigdefábregas J. Measurement and modelling of rainfall interception by three semi-arid canopies. Agric Forest Meteorol 91:275–292; 1998. [Google Scholar]
- Dragovic S, Howard BJ, Caborn JA, Barnett CL, Mihailovic N. Transfer of natural and anthropogenic radionuclides to ants, bryophytes and lichen in a semi-natural ecosystem. Environ Monit Assess 166:677–686; 2010. [DOI] [PubMed] [Google Scholar]
- Duff MC, Ramsey ML. Accumulation of radiocesium by mushrooms in the environment: a literature review. J Environ Radioact 99:912–932; 2008. [DOI] [PubMed] [Google Scholar]
- Dwyer DD. Nitrogen fertilization of blue grama range in the foothills of south-central New Mexico. Las Cruces, NM: New Mexico State University. Agricultural Experiment Station Bulletin 585; 1971. [Google Scholar]
- Ferger WF. The nature and use of the harmonic mean. J Am Stat Assoc 26:36–40; 1931. [Google Scholar]
- Fesenko S, Isamov N, Barnett CL, Beresford NA, Howard BJ, Sanzharova N. Review of Russian language studies on radionuclide behaviour in agricultural animals: biological half-lives. J Environ Radioact 142:136–151; 2015. [DOI] [PubMed] [Google Scholar]
- Fisk S, Sanderson DCW. Chernobyl-derived radiocesium in heather honey and its dependence on deposition patterns. Health Phys 77:431–435; 1999. [DOI] [PubMed] [Google Scholar]
- Garcia de Cortázar V, Nobel PS. Biomass and fruit production for the prickly pear cactus, Opuntia ficus-indica. J Amer Soc Hort Sci 117:558–562; 1992. [Google Scholar]
- Gash JHC. An analytical model of rainfall interception by forests. Quart J R Met Soc 105:43–55; 1979. [Google Scholar]
- Gash JHC, Morton AJ. An application of the Rutter model to the estimation of the interception loss from Thetford Forest. J Hydrol 38:49–58; 1978. [Google Scholar]
- Gibbens RP, Hicks RA, Dugas WA. Structure and function of C3 and C4 Chihuahuan Desert plant communities. Standing crop and leaf area index. J Arid Environ 34:47–62; 1996. [Google Scholar]
- Goossens R, Delville A, Genot J, Halleux R, Masschelein WJ. Removal of the typical isotopes of the Chernobyl fall-out by conventional water treatment. Wat Res 23:693–697; 1989. [Google Scholar]
- Gordeev KI. Radiation exposure to the population of the Semipalatinsk Region from Semipalatinsk weapons tests. Part II. Experimental data and justification of functional connections and relationships determining radioactive contamination of milk of cows and of other dairy cattle with taking into account nonradiation processes of elimination of radionuclides from pasture grass on the traces of local fallout from nuclear explosions. Moscow, Russia: Report to the National Cancer Institute; 2000. [Google Scholar]
- Gordeev K, Shinkarev S, Ilyin L, Bouville A, Hoshi M, Luckyanov N, Simon SL. Retrospective dose assessment for the population living in areas of local fallout from the Semipalatinsk Nuclear Test Site. Part II: Internal exposure to thyroid. J Radiat Res 47(Suppl):A137–A141; 2006. [DOI] [PubMed] [Google Scholar]
- Grah RF, Wilson CC. Some components of rainfall interception. J Forestry 24:890–898; 1944. [Google Scholar]
- Grimaldo M, Borja-Aburto VH, Ramírez AL, Ponce M, Rosas M, Díaz-Barriga F. Endemic fluorosis in San Luis Potosi, Mexico. I. Identification of risk factors associated with human exposure to fluoride. Environ Res 68:25–30; 1995. [DOI] [PubMed] [Google Scholar]
- Guillén J, Beresford NA, Baeza A, Izquierdo M, Wood MD, Salas A, Muñoz-Serrano A, Corrales-Vázquez JM, Muñoz-Muñoz JG. Transfer parameters for ICRP's Reference Animals and Plants in a terrestrial Mediterranean ecosystem. J Environ Radioact 186:9–22; 2018. [DOI] [PubMed] [Google Scholar]
- Hamilton EL, Rowe PB. Rainfall interception by chaparral in California. Berkeley, CA: State of California and U.S. Forest Service, California Forest and Range Experiment Station; 1949. [Google Scholar]
- Han H, Felker P. Field validation of water-use efficiency of the CAM plant Opuntia ellisiana in south Texas. J Arid Environ 36:133–148; 1997. [Google Scholar]
- Heinemann K, Vogt KJ. Measurements of the deposition of iodine onto vegetation and of the biological half-life of iodine on vegetation. Health Phys 39:463–474; 1980. [DOI] [PubMed] [Google Scholar]
- Hellmuth KH, Wagner A, Fisher E. The radioecology of the grapevine. 1. The transfer of nuclear weapons fallout from the soil into wine. Z Lebensm Unters Forsch 188:317–323; 1989. (in German, abstract in English). [DOI] [PubMed] [Google Scholar]
- Hoffman FO, Thiessen KM, Frank ML, Blaylock BG. Quantification of the interception and initial retention of radioactive contaminants deposited on pasture grass by simulated rain. Atmos Environ 26A:3313–3321; 1992. [Google Scholar]
- Hoffman FO, Thiessen KM, Rael RM. Comparison of interception and initial retention of wet-deposited contaminants on leaves of different vegetation types. Atmos Environ 29:1771–1775; 1995. [Google Scholar]
- Hoffman FO, Kocher DC, Apostoaei AI. Beyond dose assessment: using risk with full disclosure of uncertainty in public and scientific communication. Health Phys 101:591–600; 2011. [DOI] [PubMed] [Google Scholar]
- Howard BJ, Beresford NA, Barnett CL, Fesenko S. Radionuclide transfer to animal products: revised recommended transfer coefficient values. J Environ Radioact 100:263–273; 2009a. [DOI] [PubMed] [Google Scholar]
- Howard BJ, Beresford NA, Barnett CL, Fesenko S. Quantifying the transfer of radionuclides to food products from domestic farm animals. J Environ Radioact 100:767–773; 2009b. [DOI] [PubMed] [Google Scholar]
- Howard BJ, Wells C, Barnett CL. Improving the quantity, quality and transparency of data used to derive radionuclide transfer parameters for animal products. 1. Goat milk. J Environ Radioact 154:34–42; 2016. [DOI] [PubMed] [Google Scholar]
- Howard BJ, Wells C, Barnett CL, Howard DC. Improving the quantity, quality and transparency of data used to derive radionuclide transfer parameters for animal products. 2. Cow milk. J Environ Radioact 167:254–268; 2017. [DOI] [PubMed] [Google Scholar]
- Hufstader RW. Precipitation, temperature, and the standing crop of some southern California grassland species. J Range Manage 29:433–435; 1976. [Google Scholar]
- International Atomic Energy Agency . Sediment distribution coefficients and concentration factors for biota in the marine environment. Vienna: International Atomic Energy Agency; IAEA Technical Reports Series No. 422; 2004. [Google Scholar]
- International Atomic Energy Agency . Quantification of radionuclide transfer in terrestrial and freshwater environments for radiological assessments. Vienna: International Atomic Energy Agency; IAEA-TECDOC-1616; 2009. [Google Scholar]
- International Atomic Energy Agency . Handbook of parameter values for the prediction of radionuclide transfer in terrestrial and freshwater environments. Vienna: International Atomic Energy Agency; IAEA Technical Reports Series No. 472; 2010. [Google Scholar]
- International Atomic Energy Agency . Handbook of parameter values for the prediction of radionuclide transfer to wildlife. Vienna: International Atomic Energy Agency; IAEA Technical Reports Series No. 479; 2014. [Google Scholar]
- International Atomic Energy Agency . Assessment of the impact of radioactive discharges to the environment, volume 2: generic models for use in screening assessment of public exposure for planned exposure situations. Vienna: International Atomic Energy Agency; (in press). [Google Scholar]
- International Commission on Radiological Protection . Doses to infants from radionuclides ingested in mothers' milk. Oxford: ICRP; ICRP Publication 95; 2004. [Google Scholar]
- Ju J, Bai H, Zheng Y, Zhao T, Fang R, Jiang L. A multi-structural and multi-functional integrated fog collection system in cactus. Nature Commun 3:1247; 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kahn HD, Stralka K, White PD. Estimates of water ingestion in formula by infants and children based on USDA's 1994–1996 and 1998 Continuing Survey of Food Intakes by Individuals. Human Ecol Risk Assess 19:888–899; 2013. [Google Scholar]
- Kang Y, Wang Q-G, Liu H-J. Winter wheat canopy interception and its influence factors under sprinkler irrigation. Agric Water Manage 74:189–199; 2005. [Google Scholar]
- Keim RF, Skaugset AE, Weiler M. Storage of water on vegetation under simulated rainfall of varying intensity. Adv Water Res 29:974–986; 2006. [Google Scholar]
- Kinnersley RP, Scott LK. Aerial contamination of fruit through wet deposition and particulate dry deposition. J Environ Radioact 52:191–213; 2001. [DOI] [PubMed] [Google Scholar]
- Klaassen W, Bosveld F, de Water E. Water storage and evaporation as constituents of rainfall interception. J Hydrol 212-213:36–50; 1998. [Google Scholar]
- Kocher DC, Apostoaei AI, Hoffman FO, Trabalka JR. Probability distribution of dose and dose-rate effectiveness factor for use in estimating risks of solid cancers from exposure to low-LET radiation. Health Phys 114:602–622; 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauenroth WK, Whitman WC. Dynamics of dry matter production in a mixed-grass prairie in western North Dakota. Oecologia 27:339–351; 1977. [DOI] [PubMed] [Google Scholar]
- Li R, Perrine CG, Anstey EH, Chen J, MacGowan CA, Elam-Evans LD. Breastfeeding trends by race/ethnicity among US children born from 2009 to 2015. JAMA Pediatrics 173:e193319; 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindsten DC, Hasuike SK, Friend AG. Removal of radioactive contaminants from a seminatural water source with U.S. Army water purification equipment. Health Phys 11:723–729; 1965. [DOI] [PubMed] [Google Scholar]
- Liu S. Evaluation of the Liu model for predicting rainfall interception in forests world-wide. Hydrol Process 15:2341–2360; 2001. [Google Scholar]
- Liu C, Xue Y, Chen Y, Zheng Y. Effective directional self-gathering of drops on spine of cactus with splayed capillary arrays. Nature Sci Rep F:17757; 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Llorens P, Gallart F. A simplified method for forest water storage capacity measurement. J Hydrol 240:131–144; 2000. [Google Scholar]
- Madoz-Escande C, Garcia-Sanchez L, Bonhomme T, Morello M. Influence of rainfall characteristics on elimination of aerosols of cesium, strontium, barium and tellurium deposited on grassland. J Environ Radioact 85:1–20; 2005. [DOI] [PubMed] [Google Scholar]
- Martin WE. Interception and retention of fallout by desert shrubs. Health Phys 11:1341–1354; 1965. [DOI] [PubMed] [Google Scholar]
- Massmann WJ. The derivation and validation of a new model for the interception of rainfall by forests. Agric Meteorol 28:261–286; 1983. [Google Scholar]
- McLeod KW, Alberts JJ, Adriano DC, Pinder JE, III. Plutonium contents of broadleaf vegetable crops grown near a nuclear fuel chemical separations facility. Health Phys 46:261–267; 1984. [DOI] [PubMed] [Google Scholar]
- Melo DR, Bertelli L, Ibrahim SA, Anspaugh LR, Bouville A, Simon SL. Dose coefficients for internal dose assessments for exposure to radioactive fallout. Health Phys 122(1):125–235; 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Millard GC, Fraley L, Jr, Markham OD. Deposition and retention of 141Ce and 134Cs aerosols on cool desert vegetation. Health Phys 44:349–357; 1983. [DOI] [PubMed] [Google Scholar]
- Miller CW, Hoffman FO. An examination of the environmental half-time for radionuclides deposited on vegetation. Health Phys 45:731–744; 1983. [DOI] [PubMed] [Google Scholar]
- Molzahn D, Assmann-Werthmüller U. Caesium radioactivity in several selected species of honey. Sci Tot Environ 130/131:95–108; 1993. [DOI] [PubMed] [Google Scholar]
- Moreno-de las Heras M, Díaz-Sierra R, Turnbull L, Wainwright J. Assessing vegetation structure and ANPP dynamics in a grassland-shrubland Chihuahuan ecotone using NDVI-rainfall relationships. Biogeosciences 12:2907–2925; 2015. [Google Scholar]
- Muldavin EH, Moore DI, Collins SL, Wetherill KR, Lightfoot DC. Aboveground net primary production dynamics in a northern Chihuahuan Desert ecosystem. Oecologia 155:123–132; 2008. [DOI] [PubMed] [Google Scholar]
- Müller H, Pröhl G. ECOSYS-87: a dynamic model for assessing radiological consequences of nuclear accidents. Health Phys 64:232–252; 1993. [DOI] [PubMed] [Google Scholar]
- Napier BA. Determination of key radionuclides and parameters related to dose from the Columbia River pathway. Richland, WA: Pacific Northwest Laboratory; BN-SA-3768 HEDR; 1993. [Google Scholar]
- National Cancer Institute . Estimated exposures and thyroid doses received by the American people from iodine-131 in fallout following Nevada atmospheric nuclear bomb tests. Washington, DC: US Department of Health and Human Services, National Institutes of Health; 1997. [Google Scholar]
- National Council on Radiation Protection and Measurements . Screening models for releases of radionuclides to atmosphere, surface water, and ground. Bethesda, MD: National Council on Radiation Protection and Measurements; NCRP Report No. 123I; 1996. [Google Scholar]
- National Council on Radiation Protection and Measurements . Uncertainties in the measurement and dosimetry of external radiation. Bethesda, MD: National Council on Radiation Protection and Measurements; NCRP Report No. 158; 2007a. [Google Scholar]
- National Council on Radiation Protection and Measurements . Uncertainties in internal radiation dose assessment. Bethesda, MD: National Council on Radiation Protection and Measurements; NCRP Report No. 164; 2007b. [Google Scholar]
- National Council on Radiation Protection and Measurements . Uncertainties in the estimation of radiation risks and probability of disease causation. Bethesda, MD: National Council on Radiation Protection and Measurements; NCRP Report No. 171; 2012. [Google Scholar]
- Návar J, Bryan RB. Fitting the analytical model of rainfall interception of Gash to individual shrubs of semi-arid vegetation in northeastern México. Agric Forest Meteorol 68:133–143; 1994. [Google Scholar]
- Newingham BA, Vanier CH, Charlet TN, Ogle K, Smith SD, Nowak RS. No cumulative effect of 10 years of elevated [CO2] on perennial plant biomass components in the Mojave Desert. Global Change Biol 19:2168–2181; 2013. [DOI] [PubMed] [Google Scholar]
- Ng YC, Anspaugh LR, Cederwall RT. ORERP internal dose estimates for individuals. Health Phys 59:693–713; 1990. [DOI] [PubMed] [Google Scholar]
- Okuda M, Joyo M, Tokuoka M, Hashiguchi T, Goto-Yamamoto N, Yamaoka H, Shimoi H. The transfer of stable 133Cs from rice to Japanese sake. J Biosci Bioeng 114:600–605; 2012. [DOI] [PubMed] [Google Scholar]
- Okuda M, Hashiguchi T, Joyo M, Tsukamoto K, Endo M, Matsumaru K, Goto-Yamamoto N, Yamaoka H, Suzuki K, Shimoi H. The transfer of radioactive cesium and potassium from rice to sake. J Biosci Bioeng 116:340–346; 2013. [DOI] [PubMed] [Google Scholar]
- Okuda M, Akao T, Sumihiro M, Mizuno M, Goto-Yamamoto N. Transfer of caesium and potassium from Japanese apricot (Prunus mume Sieb. et Zucc.) to Japanese apricot liqueur (Ume liqueur). J Inst Brew 122:473–479; 2016. [Google Scholar]
- Owensby CE, Coyne PI, Ham JM, Auen LM, Knapp AK. Biomass production in a tallgrass prairie ecosystem exposed to ambient and elevated CO2. Ecological Appl 3:644–653; 1993. [DOI] [PubMed] [Google Scholar]
- Pearson CH, Williams M, Rock CD. Agricultural production of prickly pear cactus for biomass in the Intermountain West. Fruita, CO: Colorado State University, Agricultural Experiment Station; Technical Report TR15-03; 2014. [Google Scholar]
- Pinder JE, III, Doswell AC. Retention of 238Pu-bearing particles by corn plants. Health Phys 49:771–776; 1985. [DOI] [PubMed] [Google Scholar]
- Pinder JE, III, Adriano DC, Ciravolo TG, Doswell AC, Yehling DM. The interception and retention of 238Pu deposition by orange trees. Health Phys 52:707–715; 1987. [DOI] [PubMed] [Google Scholar]
- Pinder JE, III, Ciravolo TG, Bowling JW. The interrelationships among plant biomass, plant surface area and the interception of particulate deposition by grasses. Health Phys 55:51–58; 1988. [DOI] [PubMed] [Google Scholar]
- Pröhl G. Interception of dry and wet deposited radionuclides by vegetation. J Environ Radioact 100:675–682; 2009. [DOI] [PubMed] [Google Scholar]
- Pröhl G, Müller H, Voigt G, Vogel H. The transfer of 137Cs from barley to beer. Health Phys 72:111–113; 1997. [DOI] [PubMed] [Google Scholar]
- Pryet A, Domínguez C, Tomai PF, Chaumont C, d'Ozouville N, Villacís M, Violette S. Quantification of cloud water interception along the windward slope of Santa Cruz Island, Galapagos (Ecuador). Agric Forest Meteorol 161:94–106; 2012. [Google Scholar]
- Robertson TR, Bell CW, Zak JC, Tissue DT. Precipitation timing and magnitude differentially affect aboveground annual net primary productivity in three perennial species in a Chihuahuan Desert grassland. New Phytol 181:230–242; 2009. [DOI] [PubMed] [Google Scholar]
- Rosén K, Vinichuk M. Interception and transfer of wet-deposited 134Cs to potato foliage and tubers. J Environ Radioact 151:224–232; 2016. [DOI] [PubMed] [Google Scholar]
- Russell RS. An introductory review. Interception and retention of airborne material on plants. Health Phys 11:1305–1315; 1965. [DOI] [PubMed] [Google Scholar]
- Rutter AJ, Morton AJ. A predictive model of rainfall interception in forests. III. Sensitivity of the model to stand parameters and meteorological variables. J Appl Ecol 14:567–588; 1977. [Google Scholar]
- Rutter AJ, Kershaw KA, Robins PC, Morton AJ. A predictive model of rainfall interception in forests. I. Derivation of the model from observations in a plantation of Corsican pine. Agric Meteorol 9:367–384; 1971/1972. [Google Scholar]
- Rutter AJ, Morton AJ, Robins PC. A predictive model of rainfall interception in forests. II. Generalization of the model and comparison with observations in some coniferous and hardwood stands. J Appl Ecol 12:367–380; 1975. [Google Scholar]
- Scatena FN. Watershed scale rainfall interception on two forested watersheds in the Luquillo Mountains of Puerto Rico. J Hydrol 113:89–102; 1990. [Google Scholar]
- Scott D, Billings WD. Effects of environmental factors on standing crop and productivity of an alpine tundra. Ecol Monographs 34:243–270; 1964. [Google Scholar]
- Sharifi MR, Nilsen ET, Rundel PW. Biomass and net primary production of Prosopis glandulosa (Fabaceae) in the Sonoran Desert of California. Am J Botany 69:760–767; 1982. [Google Scholar]
- Sheppard SC, Long JM, Sanipelli B. Verification of radionuclide transfer factors to domestic-animal food products, using indigenous elements and with emphasis on iodine. J Environ Radioact 101:895–901; 2010a. [DOI] [PubMed] [Google Scholar]
- Sheppard SC, Long JM, Sanipelli B. Measured elemental transfer factors for boreal hunter/gatherer scenarios: fish, game and berries. J Environ Radioact 101:902–909; 2010b. [DOI] [PubMed] [Google Scholar]
- Simmonds JR, Linsley GS. Parameters for modelling the interception and retention of deposits from atmosphere by grain and leafy vegetables. Health Phys 43:679–691; 1982. [DOI] [PubMed] [Google Scholar]
- Simon SL. An analysis of vegetation interception data pertaining to close-in weapons test fallout. Health Phys 59:519–626; 1990. [DOI] [PubMed] [Google Scholar]
- Simon SL, Lloyd RD, Till JE, Hawthorne HA, Gren DC, Rallison ML, Stevens W. Development of a method to estimate thyroid dose from fallout radioiodine in a cohort study. Health Phys 59:669–691; 1990. [DOI] [PubMed] [Google Scholar]
- Simon SL, Luckyanov N, Bouville A, VanMiddlesworth L, Weinstock RM. Transfer of 131I into human breast milk and transfer coefficients for radiological dose assessments. Health Phys 82:796–806; 2002. [DOI] [PubMed] [Google Scholar]
- Simon SL, Bouville A, Melo D, Beck HL, Weinstock RM. Acute and chronic intakes of fallout radionuclides by Marshallese from nuclear weapons testing at Bikini and Enewetak and related internal radiation doses. Health Phys 99:157–200; 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simon SL, Bouville A, Beck HL, Melo DR. Estimated radiation doses received by New Mexico residents from the 1945 Trinity nuclear test. Health Phys 119:428–477; 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simon SL, Bouville A, Beck HL, Anspaugh LR, Thiessen KM, Hoffman FO, Shinkarev S. Dose estimation for exposure to radioactive fallout from nuclear detonations. Health Phys 122(1):1–20; 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slatyer RO. Measurements of precipitation interception by an arid zone plant community (Acacia aneura F. Muell). In: Eckardt FE, ed. Methodology of plant eco-physiology. Proceedings of the Montpellier Symposium. Paris: UNESCO; 1965: 181–192. [Google Scholar]
- Stavast LJ, Baker TT, Ulery AL, Flynn RP, Wook MK, Cram DS. New Mexico blue grama rangeland response to dairy manure application. Rangeland Ecol Manage 58:423–429; 2005. [Google Scholar]
- Stoltenberg NL, Wilson TV. Interception storage of rainfall by corn plants. Trans Am Geophys Union 31:443–448; 1950. [Google Scholar]
- Tagami K, Uchida S. Can we remove iodine-131 from tap water in Japan by boiling? Experimental testing in response to the Fukushima Daiichi Nuclear Power Plant accident. Chemosphere 84:1282–1284; 2011. [DOI] [PubMed] [Google Scholar]
- Thompson GL. Rainfall interception by mesquite on the rolling plains of Texas. Lubbock, TX: Texas Tech University; 1986. Dissertation. [Google Scholar]
- Thurow TL, Blackburn WH, Warren SD, Taylor CA, Jr. Rainfall interception by midgrass, shortgrass, and live oak mottes. J Range Manage 40:455–460; 1987. [Google Scholar]
- Toba T, Ohta T. An observational study of the factors that influence interception loss in boreal and temperate forests. J Hydrol 313:208–220; 2005. [Google Scholar]
- United Nations Scientific Committee on the Effects of Atomic Radiation . 2012 report to the General Assembly: sources and effects and risks of ionizing radiation. Scientific Annex B: uncertainties in risk estimates for radiation-induced cancer. New York: United Nations; 2015. [Google Scholar]
- US Environmental Protection Agency . Estimated per capita water ingestion and body weight in the United States—an update. Washington, DC: US Environmental Protection Agency; EPA-822-R-00-001; 2004. [Google Scholar]
- US Environmental Protection Agency . Child-specific exposure factors handbook. Washington, DC: US Environmental Protection Agency; EPA/600/R-06/096F; 2008. [Google Scholar]
- US Environmental Protection Agency . Exposure factors handbook: 2011 edition. Washington, DC: US Environmental Protection Agency; EPA/600/R-090/052F; 2011. [Google Scholar]
- US Environmental Protection Agency . Update for Chapter 3 of the Exposure Factors Handbook: ingestion of water and other select liquids. Washington, DC: US Environmental Protection Agency; EPA/600/R-18/259F; 2019. [Google Scholar]
- Vandecasteele CM, Baker S, Förstel H, Muzinsky M, Millan R, Madoz-Escande C, Tormos J, Sauras T, Schulte E, Colle C. Interception, retention and translocation under greenhouse conditions of radiocaesium and radiostrontium from a simulated accidental source. Sci Total Environ 278:199–214; 2001. [DOI] [PubMed] [Google Scholar]
- West NE, Gifford GF. Rainfall interception by cool-desert shrubs. J Range Manage 29:171–172; 1976. [Google Scholar]
- Western Environmental Law Center . Chama healthy forest and wood utilization study. Prepared by the Chama Peak Land Alliance and Ecosphere Environmental Services. Eugene, OR: Western Environmental Law Center; 2013. Available at https://chamapeak.org/landowner-resources. Accessed 30 June 2021. [Google Scholar]
- Whicker FW, Kirchner TB. PATHWAY: a dynamic food-chain model to predict radionuclide ingestion after fallout deposition. Health Phys 52:717–737; 1987. [DOI] [PubMed] [Google Scholar]
- Whicker FW, Kirchner TB, Breshears DD, Otis MD. Estimation of radionuclide ingestion: the "PATHWAY" food-chain model. Health Phys 59:645–657; 1990. [DOI] [PubMed] [Google Scholar]
- Witherspoon JP, Taylor FG, Jr. Interception and retention of a simulated fallout by agricultural plants. Health Phys 19:493–499; 1970. [DOI] [PubMed] [Google Scholar]
- Yankovich TL, Beresford NA, Wood MD, Aono T, Andersson P, Barnett CL, Bennett P, Brown JE, Fesenko S, Fesenko J, Hosseini A, Howard BJ, Johansen MP, Phaneuf MM, Tagami K, Takata H, Twining JR, Uchida S. Whole-body to tissue concentration ratios for use in biota dose assessments for animals. Radiat Environ Biophys 49:549–565; 2010. [DOI] [PubMed] [Google Scholar]
- Yankovich T, Beresford NA, Fesenko S, Fesenko J, Phaneuf M, Dagher E, Outola I, Andersson P, Thiessen K, Ryan J, Wood MD, Bollhöfer A, Barnett CL, Copplestone D. Establishing a database of radionuclide transfer parameters for freshwater wildlife. J Environ Radioact 126:299–313; 2013. [DOI] [PubMed] [Google Scholar]
- Zhang Z-S, Zhao Y, Li X-R, Huang L, Tan H-J. Gross rainfall amount and maximum rainfall intensity in 60-minute influence on interception loss of shrubs: a 10-year observation in the Tengger Desert. Sci Rep 6:26030; 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]


