Sample Design and Estimation in the National Social Life, Health, and Aging Project: Round 3 (2015–2016)

Abstract

Objectives

This article, and corresponding articles for the earlier rounds of the National Social Life, Health, and Aging Project (NSHAP), provide the scientific underpinning for the statistical analysis of NSHAP data. The 2015–2016 round of data collection for NSHAP comprised the third wave of data collection for the original cohort born 1920–1947 (C1) and the first wave of data collection for a second cohort born 1948–1965 (C2). Here we describe (a) our protocol for reinterviewing C1; (b) our approach to the sample design for C2, including the frame construction, stratification, clustering, and within-household selection; and (c) the construction of cross-sectional weights for the entire 2015–2016 sample when analyzed at the individual level or when analyzed as a sample of cohabiting couples. We also provide guidance on computing design-based standard errors.

Methods

The sample for C2 was drawn independently of the C1 sample using the NORC U.S. National Sampling Frame. A probability sample of households containing at least one individual born 1948–1965 was drawn, and from these, each age-eligible individual was included together with their cohabiting spouse or partner (even if not age-eligible). This C2 sample was combined with the C1 sample to yield a sample representative of the U.S. population of adults born 1920–1965.

Results

Among C1, we conducted 2,409 interviews corresponding to a 91% conditional response rate (i.e., among previous respondents); the unconditional three-wave response rate for the original C1 sample was 71%. Among C2, we conducted 2,368 interviews corresponding to a response rate of 76%.

Discussion

Together C1 and C2 permit inference about the U.S. population of home-dwelling adults born from 1920 to 1965. In addition, three waves of data from C1 are now available, permitting longitudinal analyses of health outcomes and their determinants among older adults.

The National Social Life, Health, and Aging Project (NSHAP) was originally designed as a cohort study (O’Muircheartaigh et al., 2009). Our objective was to recruit and follow a nationally representative probability sample of older American adults (aged 57–85 in 2005) until they were no longer able to participate in the study; we refer to this original group as Cohort 1 (C1), which was recruited and initially interviewed in 2005–2006. A second wave (W2) of data was then collected from C1 in 2010–2011. At that time, we recruited the coresident spouses or romantic partners of W1 respondents, thereby substantially increasing the sample size while enabling analysis of couples (these newly recruited individuals are considered part of C1). We also returned to originally sampled individuals who did not respond in W1 in order to maximize the cross-sectional response rate and the panel retention rate. Procedures and results for the W2 sample are described in the work of O’Muircheartaigh et al. (2014).

In 2015–2016 NSHAP returned to C1 for a third wave (W3) of data collection. At the same time, we also refreshed the sample by adding a new, younger cohort (aged 50–67 in 2015), which we refer to as Cohort 2 (C2). This cohort was recruited from a probability sample of U.S. adults born 1948–1965. As with C1, cohabiting spouses or partners were also recruited regardless of age.

The NSHAP team has agreed upon a new standardized terminology to refer to the time points at which NSHAP data are collected. Authors of publications, proposals, and other materials using NSHAP data are asked to adopt this terminology moving forward. This is presented in the inset below.

Inset 1—Standardized Terminology for Time Points and Scope of Data Collection.

Rounds

The term “Round” will refer to each of NSHAP’s major periodic data collection efforts. So far, NSHAP has completed three rounds of data collection:

• Round 1 [R1], conducted in 2005–2006

• Round 2 [R2], conducted in 2010–2011

• Round 3 [R3], conducted in 2015–2016

The current round, Round 4 [R4] will be conducted in 2021–2022.

Cohorts

The term “Cohort” will refer to the category of persons deemed eligible at successive recruitment rounds. These are birth cohorts (e.g., born 1920–1947) together with coresident spouses or partners (who themselves may have been born outside the range of the cohort).

• Cohort 1 [C1] covers those born 1920–1947 (sampled in Round 1) and their coresident spouses or partners (recruited in Round 2).

• Cohort 2 [C2] covers those born 1948–1965 and their coresident spouses or partners (sampled in Round 3).

Waves

The term “Wave” is a within-cohort term and will refer to the sequence of observations for each cohort.

• C1 C2

• In Round 1 we collected Wave 1 [W1] data for Cohort 1: C1W1

• In Round 2 we collected Wave 2 [W2] data for Cohort 1: C1W2

• In Round 3 we collected Wave 3 [W3] data for Cohort 1: C1W3

• we collected Wave 1 [W1] data for Cohort 2: C2W1

• In Round 4 we will collect Wave 4 [W4] data for Cohort 1: C1W4

• we will collect Wave 2 [W2] data for Cohort 2: C2W2

The purpose of this article is to describe the sampling procedure for C2 and the response rates and construction of weights for Round 3. In addition, we also provide guidance regarding the calculation of design-based standard errors.

Recap of Cohort 1 Sample Design

The sample for C1, recruited in 2005–2006, was an area-based national probability sample of older home-dwelling adults living in the United States, as described in the work of O’Muircheartaigh et al. (2009). Geographic areas were selected with probability proportional to size (PPS), and a sample of households was selected in each area following a classic multistage design (Kish, 1965; Harter et al., 2010). Selected households were screened (see Smith et al. (2009) for a discussion of survey screening operations and ascertaining eligibility) to determine whether they contained any age-eligible adults in collaboration with the Health and Retirement Study (HRS) to share costs. At the time, HRS was screening for recruitment of their 2004 and 2010 cohorts, consisting of adults born 1948–1953 and 1954–1959, respectively. To avoid overlap (a minor overlap, described in the work of O’Muircheartaigh et al. (2009), persisted) with the HRS target populations, we defined the target population for C1 to be adults born between 1920 and 1947. We fielded 4,400 sampled addresses yielding a sample size for C1W1 of 3,005 with a weighted response rate of 75.5%.

Recap of Round 2

In 2010–2011, we returned to all previous respondents as well as those sampled individuals who did not respond in R1, the latter helping to maintain a high overall response rate. In addition, we recruited coresident spouses or romantic partners, regardless of age, to increase the sample size and to permit couple-level analyses. Respondents approached in R1 are designated as prime respondents, while their coresident spouses or romantic partners recruited at R2 are designated as partners. Because we were concerned that the introduction of partners might lead to biases in the responses of the primes, we performed a randomized field experiment within the R2 data collection, whereby prime respondents with a coresident spouse or partner were randomized to one of the three conditions: (a) they were told about the participation of their spouse/partner before their own interview (50%); (b) they were told after they had completed their interview (30%); or (c) their spouse/partner was not recruited (see O’Muircheartaigh et al. (2014) for details). Reassuringly, there was no evidence that the recruitment of partners negatively affected response rates for the primes, or that it introduced any bias into their responses (O’Muircheartaigh et al., 2019). The conditional response rate among R1 respondents was 89%, with a conversion rate among R1 nonrespondents of 26%; the conditional response rate among partners was 84%. A total of 3,377 interviews were performed in R2 yielding an overall weighted response rate of 74%.

Recontacting Cohort 1 in R3

In 2015–2016, we returned to all C1 sample members who had responded in either R1 or R2. Cases that were determined to have been ineligible in R2 due to erroneous age information or those classified as hostile refusals in R2 were excluded. Overall, there were 3,499 respondents identified from R1 and R2 who were eligible for contact at R3. Ten cases responded with a hostile refusal to an initial postcard mailing and so were removed from consideration, leaving us with a prefield C1 sample size of 3,489 respondents.

Final results for C1 are given in Table 1, both overall and separately for four sample groups: primes who responded in R1 and R2, spouses or partners recruited in R2, primes who did not respond in R1 (i.e., not interviewed respondents [NIRs]) but did respond in R2, and R1 respondents who did not respond in R2. Those who responded in R1 and R2 and partners recruited in R2 had response rates of 93% and 94%, respectively. In addition, R1 nonrespondents (NIRs) converted in R2 had an encouragingly high retention rate (78%). However, only 40% of surviving R1 respondents who did not respond in R2 responded in R3, perhaps in some cases reflecting a considered decision in R2 no longer to participate based on their experience in R1.

Table 1.

NSHAP Cohort 1 Survival and Yields by Sample Group at Round 3 (C1W3)

Sample group	Returning respondent sample	Survival rate	Responsea rate	Yield rateb	Completed interviews
R1 and R2	2,253	80%	93%	69%	1,554
Spouse/partner	951	87%	94%	77%	731
R2 (R1 NIR)	161	80%	78%	53%	86
R1 (R2 NIR)	132	85%	40%	28%	38
Total	3,497	82%	91%	69%	2,409

Note: NSHAP = National Social Life, Health, and Aging Project.

^aCompleted interviews/eligible respondents contacted (rounding may cause small differences).

^bCompleted interviews/total respondents contacted (rounding may cause small differences).

Cohort 2 Wave 1 (C2W1) Sample Design in R3

In 2015, we selected a probability sample of households to generate a nationally representative sample of adults aged 50–67, together with their cohabiting romantic partners (whether age-eligible or not), for C2W1. The sample was based on the NORC 2010 National Sampling Frame. The primary component of the sampling frame is a version of the United States Postal Service (USPS) Computerized Delivery Sequence file (CDS) acquired from a vendor. The CDS is the comprehensive list of household mailing addresses maintained by the USPS. This file has been used as a sampling frame for surveys of the household-dwelling population of the United States in recent decades and contains almost all residential addresses in urban areas. The file has less than 90% coverage in some rural areas (Harter et al., 2016); in these areas, the CDS is supplemented by an in-person listing of all housing units in the selected block groups. This in-person listing improves the coverage of the NORC National Sampling Frame to about 97% (Pedlow & Zhao, 2016). As a further enhancement, we used a Missed Housing Unit (MHU) procedure (Eckman & O’Muircheartaigh, 2011) to supplement the frame in the field.

The 2010 NORC National Sampling Frame uses a two-stage clustered probability sample design to select a representative sample of areas in the United States as described in the work of Harter et al. (2010). Primary sampling units (PSUs; metropolitan areas or counties) were selected with PPS, with second-stage sampling units (tracts or block groups) selected within these. Four hundred second-stage units, each of which represents 0.25% of the U.S. population, are the basis of the NSHAP C2W1 sample.

In order to oversample Hispanic and non-Hispanic Black households, the 400 second-stage areas were divided into 50 high Hispanic areas (>33% of the population is Hispanic and >non-Hispanic Black population), 47 high non-Hispanic Black areas (>33% of the population is non-Hispanic Black and >Hispanic population), and 303 Other areas (neither). The high Hispanic and high non-Hispanic Black areas were sampled at roughly twice the rate of the other areas. Within selected housing units, all age-eligible adults and their coresident spouses or romantic partners were included in the sample.

Our plan to refresh the NSHAP sample with approximately 2,500 new respondents (including 900 couples) involved screening approximately 8,000 housing units from NORC’s 2010 National Sampling Frame and conducting an interview in all households with at least one eligible respondent. With a target total sample size of 1,700 households and 2,500 individuals interviewed within 400 second-stage units, this produced a low-average cluster size of 4.25 interviewed households per second-stage unit. This modest degree of clustering contributes to a low design effect and smaller standard errors than we would have with a more heavily clustered sample.

The C2W1 fieldwork was extremely successful and closely matched our targets; Table 2 displays the outcome. We had assumed a housing unit eligibility rate of 87% on the frame, which we obtained. We had a target screener completion rate of 92%, which we exceeded slightly. We were a little below our assumed household eligibility rate (34% vs. 36%). The eligibility rate of identified (in the screener) household members was 94% (the occupancy and eligibility rates used above were both estimated using the 2010 American Community Survey Public Use Microdata Sample). The interview completion rate for eligible household members (the interview response rate) was 76% (75% anticipated), yielding 2,368 completed interviews in total. The interview response rate was particularly impressive as it matched the response rate for C1W1 achieved 10 years earlier, despite a general decrease in survey response rates in the interim.

Table 2.

Realized Screener and Member Sample for NSHAP Cohort 2 at Round 3

Selected housing units		7,667
Housing unit-level eligibility ratea	86.6%
Eligible housing units		6,809
Screener completion rate	92.5%
Completed screeners		6,100
Household eligibility rate	33.8%
Eligible households		2,051
Spawned members		3,339
Member-level eligibility rate	93.7%
Eligible members		3,127
Interview completion rate	75.7%
Completed interviews		2,368

Note: NSHAP = National Social Life, Health, and Aging Project.

^aUnoccupied housing units are ineligible; a small number of occupied households are ineligible due to nonsupported languages.

Following our approach in C1W2, we intend to return in C2W2 not only to all respondents from C2W1 but also to nonrespondents from C2W1 in order to maximize our unconditional response rate for C2W2. This strategy in C1 (for both W2 and W3) has enabled us to maintain an exceptionally high unconditional response rate for the NSHAP panel thus far.

Weight Construction

The complex design of NSHAP requires that the data be weighted in order to provide unbiased estimates of population parameters. In this section, we use the names given to the weighting variables in the public use data set, so that analysts can easily connect this narrative to their analyses. The NSHAP public use data set contains one weight (weight_adj) that can be used for all analyses of all R3 respondents (those from both cohorts). As described earlier, those consist of 1,678 C1 prime respondents (those who were selected into the W1 sample and responded in W3), 731 C1 partners (the cohabiting spouses or romantic partners of prime respondents), and 2,368 C2 respondents. Two additional weights were created for special uses: weight_sel (this weight adjusts for selection probabilities, but not for nonresponse) and weight_couple (for analyses of the 1,389 couples from either cohort who both completed a W3 interview). The couple weight is designed for analyses where the unit is the dyad, a couple with at least one age-eligible member from C1 or C2.

The steps involved in calculating the weights for the W3 respondents are the same for both cohorts, but were generally carried out separately.

For C1, the 2015 base weight is the weight for W2 before the nonresponse adjustment, which already includes the addition of partners’ adjustment in W2. The partners’ adjustment was necessary in W2, because in W1, if there were two age-eligible residents, one was selected at random. In W2, the other was added so the within-household probability had to be adjusted in W2.

The C2 sample is a nationally representative equal-probability sample of housing units in the United States. Therefore, the base weight for the C2 sample is equal for all households except two that were added through the MHU procedure. Then, we adjusted the weights for households who were eligible for the other cohort. The remaining adjustments are done in parallel for the two cohorts: an adjustment for eligibility at the time of interviewing, an adjustment for nonresponse, and a final scale adjustment so that the sum of the weights is equal to the total number of respondents. We now provide more details on these steps:

Base Weight

For C1, we start with the weight from W2 before nonresponse adjustment. As described in the work of O’Muircheartaigh et al. (2014), the variable weight_adj from W2 includes the original household selection probability for HRS, the subsequent selection probability for NSHAP, an additional factor to prevent overlap with the HRS, the within-household probability that was originally calculated in W1 the adjustment to the within-household probability calculated during W2 due to the addition of partners, and the W2 adjustment for eligibility at the time of interviewing.

For C2, as described above, a new nationally representative sample of housing units was drawn from the 2010 NORC National Sampling Frame. NSHAP C2 selected housing units from 400 areas across the country. Within selected housing units, all age-eligible adults and their coresident spouses or romantic partners were included in the sample. The base weight for C2 is the inverse of the selection probability for the selected housing units.

The most complex aspect of weighting (though it has only a modest effect on the weights overall) is the possible overlap in partners across the cohorts. In C1, all prime respondents were age-eligible, but some of their nonage-eligible partners are age-eligible for C2, not C1. Similarly, for C2, at least one respondent from every responding household was eligible for C2, but partners of C2 age-eligible respondents could be eligible for C1 rather than C2. Households with one member eligible for C1 and one member eligible for C2 therefore could have entered the NSHAP R3 sample through either cohort, giving them two probabilities that must be combined in the base weight step.

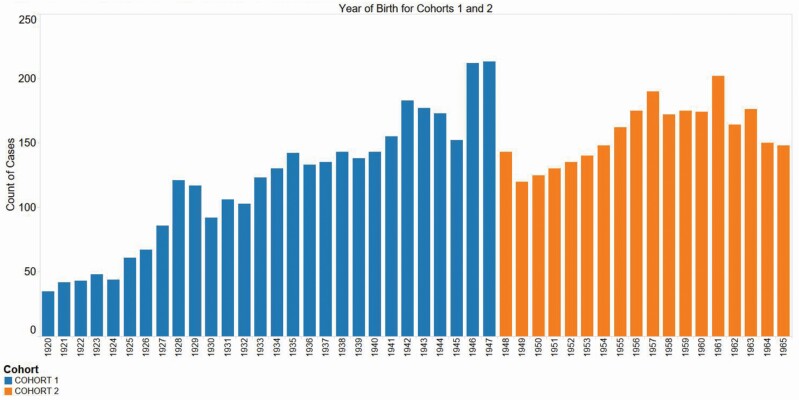
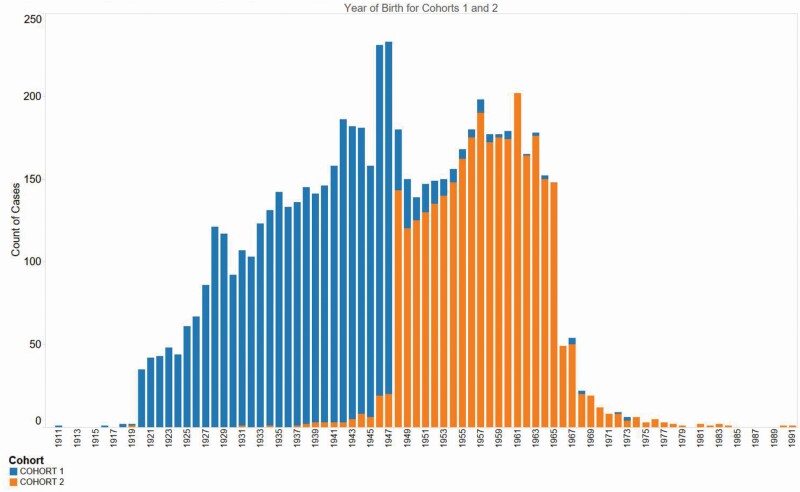
Figure 1 shows that among the age-eligible respondents in C1 and C2, there is no overlap in the year of birth; Figure 2, including all respondents, shows that among the age-ineligible partner respondents in C1 and C2, there is an overlap in the year of birth. Comparing Figures 1 and 2, it is easy to spot the age-ineligible partners who were age-eligible for the other cohort. Figure 2 shows that there are 177 C1 partners who were age-ineligible for C1 (blue cases outside of 1920–1947). Of these 177 “age-ineligible” C1 partners, 170 would have been eligible for Cohort 2 (blue cases in 1948–1965). Similarly, there are 175 “age-ineligible” C2 partners (orange cases outside of 1948–1965), of whom 75 would have been eligible for C (orange cases in 1920–1947). These 245 partners (170 + 75) had a nonzero selection probability in the other cohort, so we calculated that selection probability. As the samples are otherwise independent, we can add the two selection probabilities (for each cohort) to determine the combined selection probability, of which the inverse is the revised base weight.

Figure 1.

Year of birth for age-eligible respondents in Cohorts 1 and 2.

Figure 2.

Year of birth for all respondents in Cohorts 1 and 2.

The base weights for R3 need to be adjusted for eligibility because some households or persons given a base weight became ineligible prior to the fieldwork. From C1, these include (a) C1W2 respondents who died and (b) some partners newly screened in during W3 who left the household, became incapacitated, or died.

For C2, some selected housing units were vacant or otherwise ineligible (vacation homes, for example). For unknown eligibility cases in C2, we used the observed eligibility rate within its first-stage sampling unit (the metropolitan area or county to which it belongs) to adjust their weights. Because C2 consists of housing units that must be screened for eligibility, there were instances where we were not able to determine whether any resident was age-eligible for NSHAP. Such households would be considered of “unknown eligibility.” For both cohorts, ineligible cases are not included in the final data set (their base weights disappear so that the sum of the eligible weights is the estimate of the eligible population). The weights for eligible cases were unchanged in this step.

Nonrandom nonresponse of any magnitude threatens the basis of inference from the survey data to the population of interest. We provide an adjustment to the weights to account for nonrandom nonresponse. All nonresponse adjustments rely on a model that makes assumptions about the nonrespondents. The method we used, which Kalton and Kasprzyk (1986) call “sample-based weighting,” assumes that, once we control for key characteristics, nonrespondents are like respondents. The only variables that can be used to control for nonresponse are those that are observed for both the responding and the nonresponding cases. For C1, nonresponse analyses using the sampling unit-level variables (types of secondary sampling units [SSU]) and the screener variables determined that the urbanicity (measured at the sampling unit level) and age (of the screened individuals) provided the greatest discrimination in response rates (O’Muircheartaigh et al., 2009). For consistency, we used the same variables for C2; we created nonresponse adjustment cells for each cohort using these variables. Due to the two-phase design of C1 (the addition of partners only at C1W2), we separated the two sample types (primary respondent/partner); two additional cells were used for younger age-ineligible partners in C1 (there were not enough older age-ineligible partners to be given an additional age cell). In each of the 20 adjustment cells, weights for responding cases were increased by the reciprocal of the cell-level response rate such that the responding cases take on the weight of the nonresponding cases. To the extent that the correspondence between respondents and nonrespondents is closer within these adjustment classes than it is overall, adjusting the weights separately within these classes will improve the validity of our estimates (Kish, 1992).

While C1 has many additional variables that could be used to adjust for differential conditional nonresponse between C1W1, C1W2, and C1W3, we consider it inappropriate to include such adjustments in the base weight. Weighting inevitably implies assumptions about relevance and all of these variables are made available to analysts as part of the public use data sets. We prefer to leave it to users either to incorporate such additional weights in their analyses or to include the variables explicitly in their analytic models.

The use of the couple weight—weight_couple—is appropriate when the unit of analysis is the couple. Such analyses may involve measures derived from both partners’ responses. The couples in NSHAP are defined by the age eligibility of at least one partner and their being a couple at the time of the NSHAP W3 fieldwork. The inference population is therefore the population of R3 couples, at least one of whom is NSHAP age-eligible; the NSHAP sample is a probability sample from this population.

Adjusted and unadjusted weights have nonzero values for all Round 3 respondents including spouses or partners outside the cohort’s age range; analysts who wish to make inferences to the population of U.S. adults born 1920–1947 and/or 1948–1965 should exclude spouses and partners who are age-ineligible.

Scale Adjustment

As a final step to the weighting procedure, weights are rescaled so that they sum to the total number of completed interviews for that cohort.

Use of Weights

Sample designs with unequal probabilities of selection such as those used by NSHAP require the use of weights to obtain unbiased estimates of population parameters (Kish & Frankel, 1974). In addition, potential nonresponse bias may be reduced through the use of a nonresponse adjustment such as the one described above. For these reasons, we recommend use of the nonresponse-adjusted weights (weight_adj) included with the data set for most analyses. For those analysts who wish to make their own nonresponse adjustment, we have also provided an unadjusted weight (weight_sel) representing the inverse probability of selection that should be used as the base weight.

Calculation of Design-Based Standard Errors

Using a sample to make inferences about a population also involves estimating the variability across hypothetical repeated samples. This variability depends critically on the sample design. Ignoring the design by using methods that assume simple random sampling can lead to incorrect variance estimates and therefore yield incorrect inferences (Wolter, 2007; Kish, 1965; Lee & Forthofer, 2006; Verma et al., 1980). While calculating design-based standard errors once required specialized programs, it is now straightforward to obtain these using standard analytic software (e.g., Stata’s svy prefix, the survey package written for R, and SAS’s survey analysis procedures; Kreuter & Valliant, 2007).

Several aspects of the sample design can affect the variance, including the sampling fraction, selection probabilities, stratification, and clustering. Stratification involves dividing the population into relatively homogenous subgroups (or strata) and sampling within each stratum, a procedure that reduces the variability across samples. Clustering involves sampling entire groups (or clusters) of individuals at a time, typically by sampling geographic areas. Clustered samples are easier to draw and cheaper to field; however, in contrast to stratification, clustering increases the variability across samples to the extent that the clusters contain individuals who are similar to one another. It is important to note that while both stratification and clustering are properties of the sample design, their impact on the variance is specific to the variable(s) being studied; specifically, the extent to which those variables are similar within strata and clusters. This is summarized via the design effect (DEFF) that is the ratio of the estimated design-based variance divided by the variance of a hypothetical simple random sample of the same size (Kish, 1965). Design effects will typically exceed one, though most survey studies including NSHAP try to minimize design effects by limiting differences in the selection probabilities and through effective stratification.

Because the sample designs for both NSHAP cohorts used systematic sampling, exact variance formulas are not available. Instead, NSHAP follows the common practice among other national surveys of creating so-called pseudo-strata containing pseudo-PSUs that may be used to approximate the variance (e.g., Current Population Survey, Survey and Consumer Finances, National Survey of Family Growth; Wolter, 1984). Specifically, NSHAP creates pseudo-strata each containing a pair of PSUs; the resulting variables (called stratum and cluster) are provided with the data set and can be specified, together with the weights, when using analytic software. Note that because each pseudo-stratum contains exactly two pseudo-PSUs, it is possible to use either the linearized variance estimator (Binder 1983) or balanced repeated replication (McCarthy, 1966, 1969).

Finally, while the NSHAP sample design involved selection at multiple, nested stages, NSHAP relies on the “ultimate cluster” method to estimate variance by which only the variation among the highest level units is considered (Kalton, 1979). This yields a reasonable approximation to the variance, regardless of the correlation among units at lower levels of sampling. Thus, for example, a possible correlation between spouses or partners within a household is automatically accommodated by this method. Despite this, in certain contexts, analysts may wish to model such correlation explicitly to improve efficiency or when it is of substantive interest.

Funding

This article was published as part of a supplement supported by funding for the National Social Life, Health, and Aging Project from the National Institute on Aging, National Institutes of Health (R01 AG043538 and R01 AG048511) and NORC at the University of Chicago. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute on Aging, National Institutes of Health, or NORC.

Conflict of Interest

None declared.

Data Availability

NSHAP data for Rounds 1–3 are publicly available via the Inter-University Consortium for Politics and Social Research (Waite et al., access listed in references).