Graph-convolutional-network-based interactive prostate segmentation in MR images

Abstract

Purpose:

Accurate and robust segmentation of the prostate from magnetic resonance (MR) images is extensively applied in many clinical applications in prostate cancer diagnosis and treatment. The purpose of this study is the development of a robust interactive segmentation method for accurate segmentation of the prostate from MR images.

Methods:

We propose an interactive segmentation method based on a graph convolutional network (GCN) to refine the automatically segmented results. An atrous multiscale convolutional neural network (CNN) encoder is proposed to learn representative features to obtain accurate segmentations. Based on the multiscale feature, a GCN block is presented to predict the prostate contour in both automatic and interactive manners. To preserve the prostate boundary details and effectively train the GCN, a contour matching loss is proposed. The performance of the proposed algorithm was evaluated on 41 in-house MR subjects and 30 PROMISE12 test subjects.

Result:

The proposed method yields mean Dice similarity coefficients of 93.8 ± 1.2% and 94.4 ± 1.0% on our in-house and PROMISE12 datasets, respectively. The experimental results show that the proposed method outperforms several state-of-the-art segmentation methods.

Conclusion:

The proposed interactive segmentation method based on the GCN can accurately segment the prostate from MR images. Our method has a variety of applications in prostate cancer imaging.

1. INTRODUCTION

Prostate cancer is one of the most common types of cancer among American men. In 2020, it was estimated that there were 191,930 new cases of prostate cancer, and 33,330 deaths from prostate cancer in the United States.¹ Magnetic resonance imaging (MRI) is being increasingly used for prostate cancer diagnosis and treatment planning.^2,3 Accurate segmentation of the prostate from MR images has many applications in the management of this disease. Manual segmentation of each prostate image is a time-consuming and subjective task. The accuracy of the segmentation depends on the experiences of the radiologists and on the intra-reader and inter-reader variations. Therefore, numerous studies have focused on prostate MR image segmentation in recent years.^4–6

Deep-learning-based automatic segmentation methods have achieved improved medical image segmentation performance.^4,7–9 However, it is difficult to develop a fully automatic prostate segmentation method that can address various issues, such as cases with low-contrast prostate boundaries, large shape variations, and variations of the appearance pattern in basal and apical regions. Therefore, these automatic segmentation methods are not adequately accurate and robust for routine clinical use. To solve this problem, user interventions are often needed to refine the automatic segmentation issues.

To-this-date, many interactive image segmentation methods have been proposed.^10–14 In this study, we propose an interactive segmentation method based on a graph convolutional network (GCN) for prostate on MR images. The interactivity of the proposed method is similar to GrabCut,¹⁰ wherein a bounding box is drawn around the object to obtain an initial segmentation. GrabCut further improves the initial segmentation by drawing points on background and foreground regions, respectively. In contrast, we present a different interactive scheme that is better suited for a GCN-based algorithm by dragging a point on the prostate contour to the appropriate position. This manner can reduce user interactions during segmentation refinement to achieve higher accuracy. The user can intervene whenever an inaccurate segmentation occurs by correcting the erroneously predicted points. The proposed method continues its prediction based on the corrections.

In this study, we consider prostate segmentation as a regression problem, whereby the locations of all the vertices/points of the prostate contour are predicted simultaneously. These vertices are represented as a graph with a fixed topology. We perform predictions of these vertices based on the use of a GCN that can be optimized for interactive segmentation.

To the best of our knowledge, this is the first study that has explored GCN-based interactive methods for prostate MR segmentation. The contributions of the proposed method are as follows. (a) A GCN is adopted to extract prostate contours from MR images automatically. The GCN is also used in an interactive manner to further improve the accuracy by correcting the points on the prostate contour. (b) We propose an atrous multiscale convolutional neural network encoder to obtain representative features for prostate from MR images that could help GCN to generate more accurate prostate contours. (c) The proposed method outperforms several state-of-the-art methods on both PROMISE12 dataset and in-house dataset.

The remainder of the study is organized as follows. In Section 2, related works are reviewed. In Section 3, we introduce the GCN-based interactive prostate segmentation method followed by the details of each part. In Section 4, we describe the evaluations based on the experimental results. In Section 5, we summarize the proposed method and outline the study’s conclusions.

2. RELATED WORKS

Interactive segmentation methods provide an effective way wherein a human and a machine interact. According to the interaction type, interactive segmentation methods can be classified into three categories, including the bounding box, click/scribble, and contour-interaction-based methods.

In bounding-box-based methods, a bounding box is supposed to be placed around a target object to present the object’s range. Lempitsky¹⁵ mentioned that the bounding box is not only used to exclude the background information, but also to prevent the segmentation from shrinking. MILCut¹⁶ proposed the use of a sweeping-line strategy to perform segmentation tasks based on the bounding box provided by users that converts the interactive image segmentation into a multiple-instance learning problem. Rother¹⁰ proposed a GrabCut method for interactive object segmentation based on the graph-cut algorithm.¹⁷ GrabCut only requires the user to draw a bounding box loosely around the object. Wang¹² presented an interactive medical image segmentation method based on a bounding box that adds an image-specific adaptation model for CNNs to obtain accurate segmentation. However, the segmentation results of these bounding box-based interactive methods cannot be further refined by users.

In the cases of click/scribble-based methods, users usually draw scribbles/points on foreground and background regions. Interactive graph cuts¹⁸ is a seminal scribble-based interactive segmentation method that marks several seed pixels that belong to the background or foreground. It then uses a max-flow/min-cut algorithm to provide a global optimal solution for segmentation. Papadopoulos¹⁹ and Maninis²⁰ proposed a clicking strategy to replace the traditional bounding box method that lets users to click on the top, bottom, left, and right-most points of an object to achieve the desired segmentation results. In the field of medical image segmentation, Wang²¹ proposed an interactive method for two-dimensional (2D) and three-dimensional (3D) medical image segmentations. A CNN is used to obtain an initial automatic segmentation on which user click/scribble interactions were added to indicate mis-segmentations to refine the results. Although these click/scribble-based interactive methods can obtain more accurate segmentation results by drawing scribbles or seed points multiple times on the foreground and background regions, these methods cannot obtain accurate and smooth object boundaries. In addition, the segmentation boundary cannot be fine-tuned in a click/scribble interactive manner.

Contour interaction methods are usually used to present an object boundary and refine it. Castrejon²² and Acuna²³ proposed a contour-interaction-based segmentation method. They considered the segmentation task as a contour prediction problem that predicted the vertices of a contour that outlined the object. Ling²⁴ proposed an interactive segmentation method to predict all the vertices of the object’s contour based on a GCN. The aforementioned methods could yield promising segmentation results. However, there is no method that combines deep learning and user interaction in a seamless way that is trained end-to-end. In addition, the methods ignore the multiscale feature that limits the representative feature extraction capability and restricts the segmentation performance.

In this study, we propose a GCN based interactive segmentation method to segment the prostate. GCN is a deep-learning method that handles non-Euclidean data within the graph domain. Therefore, it is suitable for contour-interaction-based segmentation methods. Because of convincing performance and high interpretability, GCN has been receiving increased attention recently. Motivated by the above descriptions, an interactive method is proposed for prostate segmentation by combining GCN and user interactions that are trained end-to-end.

3. MATERIALS AND METHODS

In this study, we propose an interactive MR image segmentation algorithm for prostate based on GCN. The algorithm accepts user interactions based on the interaction points (nodes or vertices) on the prostate contour. The proposed method consists of three parts, namely, the CNN feature encoder, automatic GCN module, and interactive GCN module.

In this study, we assume that the prostate shape can be accurately represented by N interaction points (also called vertices). The neighboring points/vertices are connected with spline curves to form the prostate contour. The locations of the vertices are considered as random variables and can be predicted based on the GCN in the non-Euclidean domain.

The GCN takes the output feature from the last convolutional layer of the CNN encoder applied on the cropped image as its input. We denote the CNN encoder feature as X_cnn. To observe the contour of prostate, a contour block is proposed. The output feature of the contour block is concatenated with X_cnn to produce an enhanced feature X_cnnEnh.

The enhanced feature is followed by four 3 × 3 convolutional layers that aim to form a GCN feature X_gcn. To encode the locations of the interaction vertices, the initial coordinates of the interaction vertices are concatenated with the GCN feature to form a location-aware feature X_gcnLoc. The feature X_gcnLoc is fed to a GCN block to predict the locations of the vertices that could obtain the output of the automatic GCN module. The generation of the location-aware feature X_gcnLoc is shown in Fig. 1.

Fig. 1.

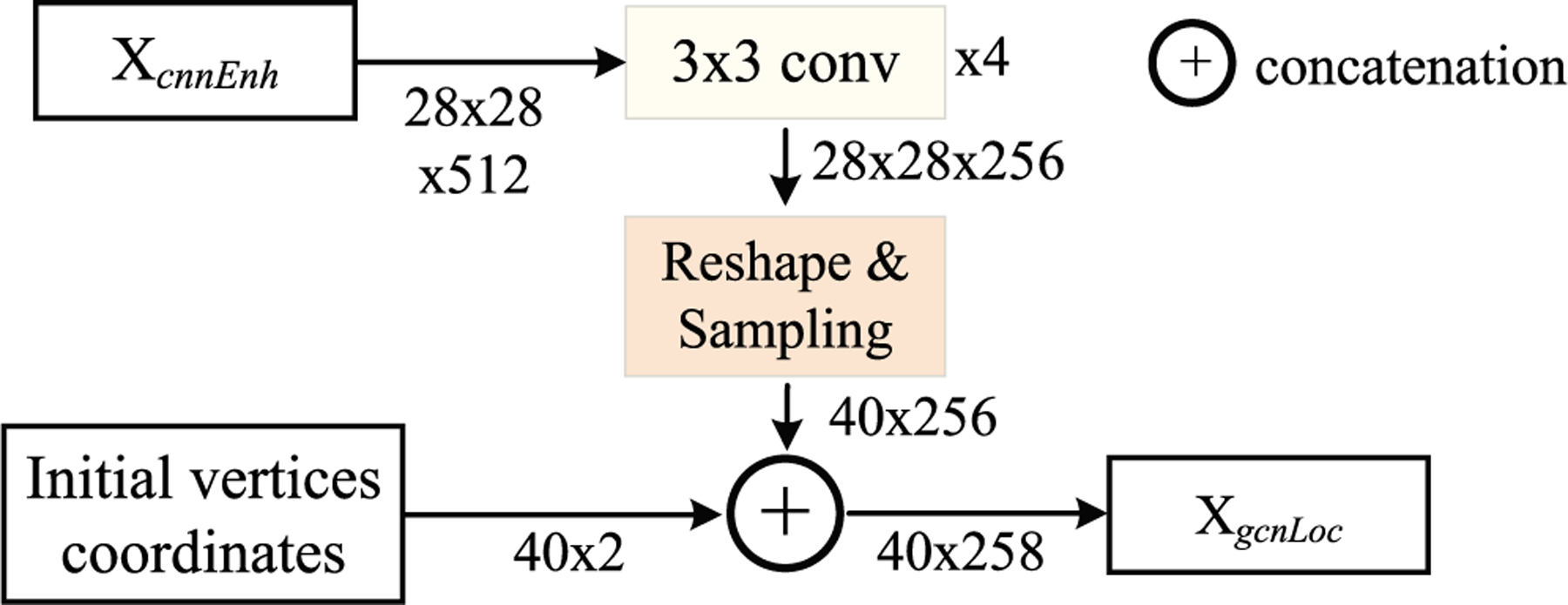
The generation of the location-aware feature X_gcnLoc. The number of vertices is 40 in our method.

The interactive GCN module follows the automatic GCN module. The interactive GCN aims to improve the segmentation accuracy by introducing user interactions. The users select inaccurate interaction points and drag them to the correct positions. The shifts of these points are concatenated with feature X_gcnLoc to produce a shift-encoded feature X_gcnLocS. The feature X_gcnLocS is fed into the GCN block to obtain the shifts of k neighboring vertices of the current interaction point. Fig. 2 presents an overview of the proposed method.

Fig. 2.

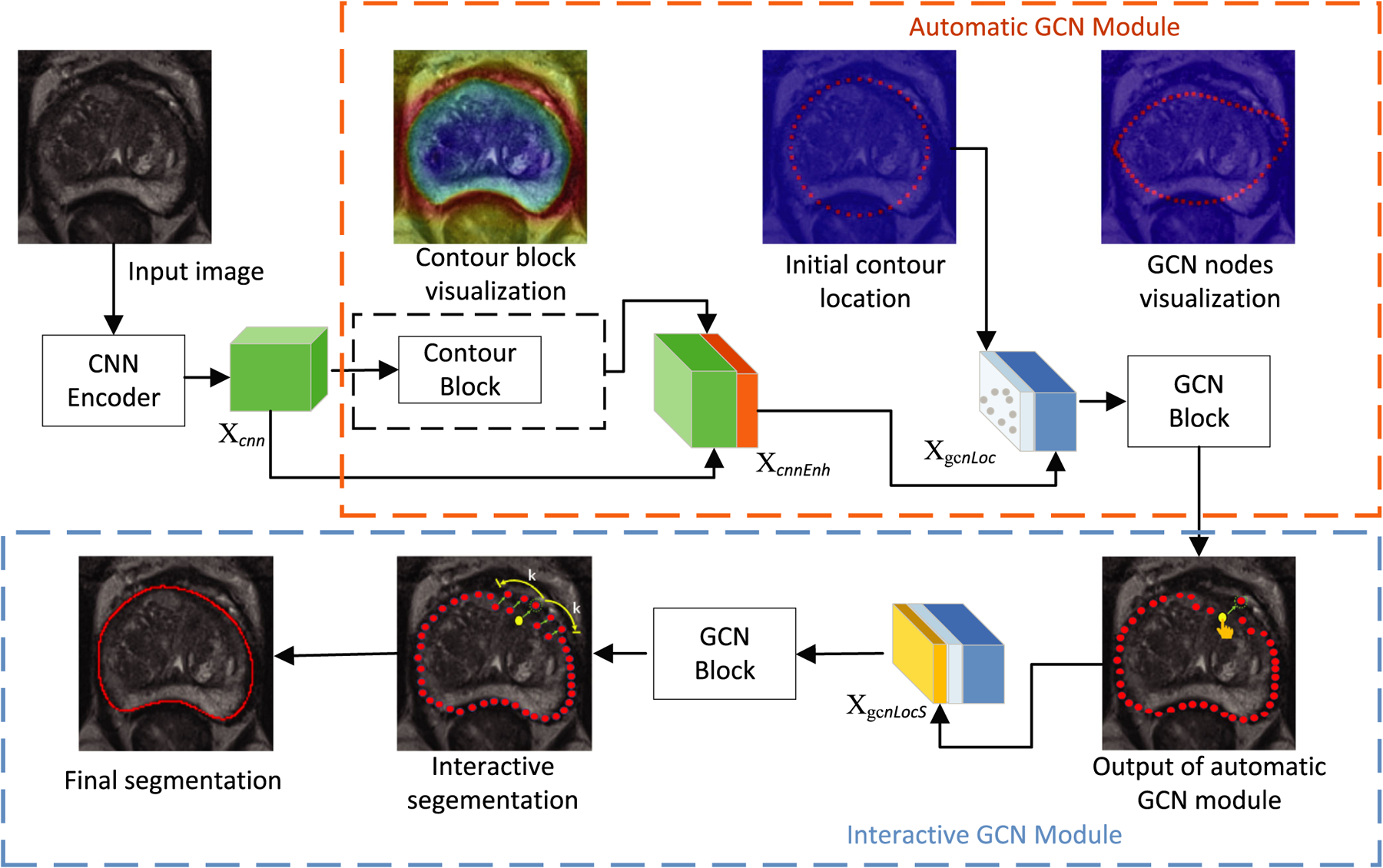
Overview of the proposed graph convolutional network (GCN) segmentation method. The proposed method consists of three parts: (a) CNN feature encoder, (b) automatic GCN module, and (c) interactive GCN module. In the interactive GCN module, the users select interaction points (e.g. yellow vertex) and drag them to their correct locations. Subsequently, the new locations of 2k neighboring vertices (k neighbors on either side) will be predicted. The green arrow indicates the movement of the vertex from the current location to a new location.

3.A. CNN feature encoder

Owing to the use of the repeated downsampling operations in traditional CNN networks, it is difficult to obtain an adequately large output feature resolution for the image segmentation task.^25,26 ResNet²⁷ is a commonly used backbone network in the semantic segmentation domain. However, the empirical receptive field of ResNet is smaller than the input image. In addition, it lacks multiscale features in the output feature map that is very important for the representation of the objects. To address these problems, an atrous/dilated multiscale CNN feature encoder is proposed. A dilated convolutional operation²⁵ and a spatial pyramidal pooling module²⁸ are introduced in ResNet to obtain multiscale features. In addition, a skip-layer architecture is used to obtain an effective output resolution and a multiscale feature. The dilated convolution aims to extract multiscale features and increase the receptive field of the kernel when the network depth increases. Meanwhile, it does not introduce any extra parameters into the network. The spatial pyramid pooling module can obtain both local information and global context information. At the same time, the skip-layers concatenate different feature levels that can incorporate both shallow and deep-layer feature maps. By combining dilated convolutions, spatial pyramid pooling module, and the skip-layer architecture, the proposed CNN feature encoder can capture high-level semantic information, low-level detailed information, and multiscale features.

In the proposed multiscale CNN encoder, we removed first the fully connected layers and the last average pooling layer of ResNet-101. In addition, the convolutional operations in the last two blocks of ResNet-101 were replaced by dilation convolution with two and four dilated rates respectively. A 3 × 3 convolution layer was applied after four layers, including the first 7 × 7 convolution layer, the first residual layer, the second residual layer, and the last residual layer with dilated convolution. To obtain multiscale spatial features, the output features of four 3 × 3 convolutions were concatenated. Three bilinear upsampling operations were performed to ensure that they achieve the same spatial sizes. The concatenated features were then fed to two consecutive 3 × 3 convolution layers. Global prior representations have proven to be effective ways to produce high-quality results on object instance segmentations. Therefore, a pyramid scene parsing network (PSPNet)²⁸ was adopted as a final pixel-level CNN feature extractor. The proposed dilated multiscale CNN encoder is shown in Fig. 3.

Fig. 3.

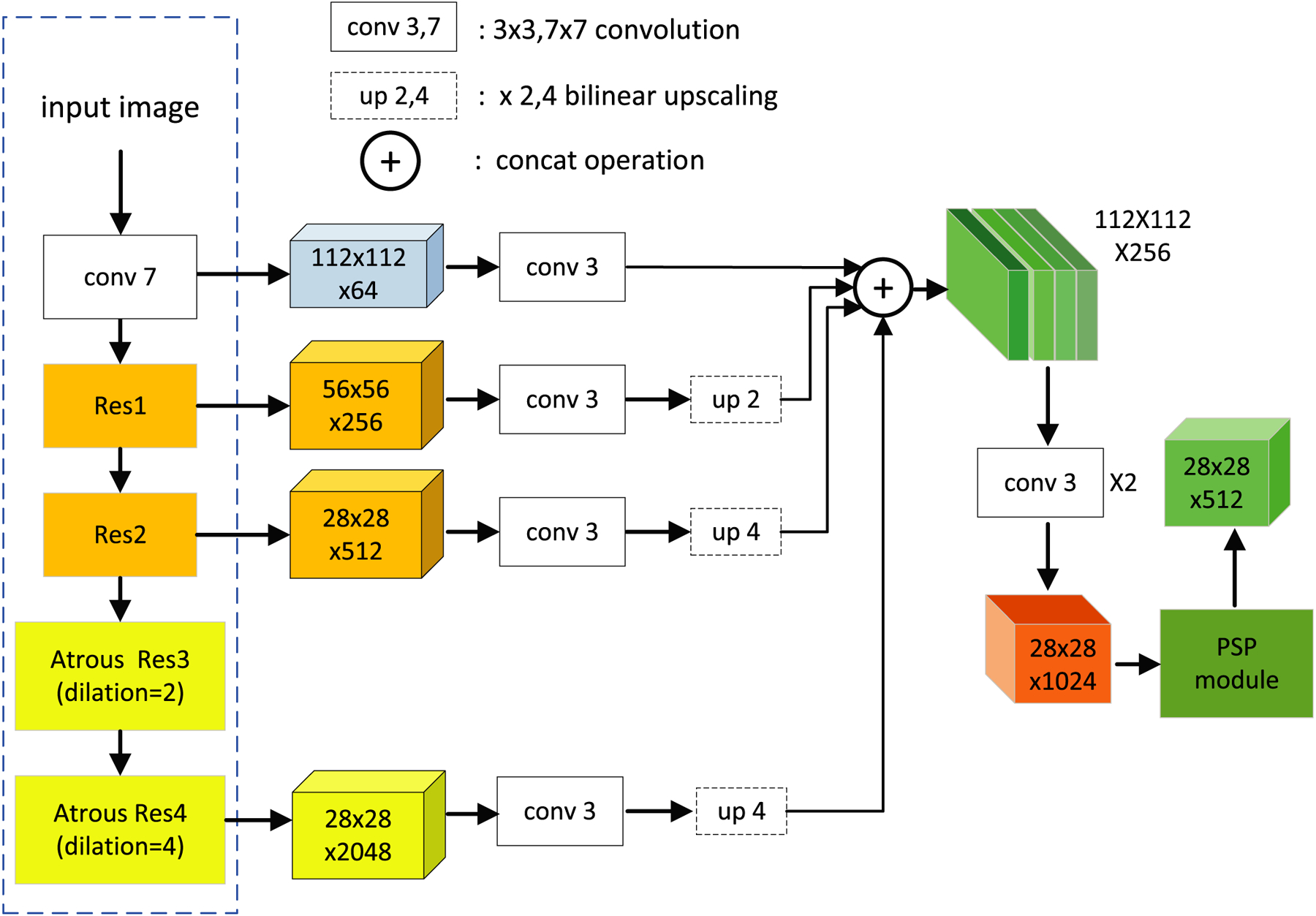
Overview of the multiscale convolutional neural network feature encoder.

3.B. Automatic GCN module

Automatic GCN module consists of two blocks, namely, contour and GCN blocks.

3.B.1. Contour block

The CNN feature does not encode boundary information explicitly. It is difficult to be directly used to extract the prostate boundary. Therefore, the feature X_cnn obtained from the CNN encoder cannot allow the direct visualization of the prostate contour. To solve this problem, a contour block is proposed to help the model visualize the prostate contour. The contour block is trained to predict the probability of existence of a prostate contour that consists of a 3 × 3 convolutional layer and a fully connected layer. A cross entropy loss is used to train the contour block. The output of the contour block is a 2 × 28 × 28 feature that encodes the boundary features of the prostate. The visualization of the contour block is shown in Fig. 2.

3.B.2. GCN block

While the CNN has achieved great success in processing Euclidean data, it has been associated with an increasing number of tasks whereby data are non-uniformly sampled in the non-Euclidean domain, and are presented as graphs with complex relationships between data. It is a major challenge for CNN-based methods to handle the complexity of graph data.²⁹ The data (location of the vertex) used in our method are graph data. Therefore, the GCN is adopted (instead of CNN-based methods) for prostate segmentation.

In this study, a graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$, is defined on a prostate MR image that consists of vertices $\mathcal{V}$ and edges $\mathcal{E}$. $\mathcal{V}=\left\{v_i,i=1,2,\dots ,N\right\}$ is the set of N vertices in the graph. Let v_i = (x_i, y_i) denote the location of the i-th interaction-point. $\mathcal{E}=\left\{e_j,j=1,2,\dots ,M\right\}$ is the set of M edges with each of its elements connecting two vertices. This graph structure defines how the information propagates in the GCN. The nodes of the GCN are initialized at a static central position in the cropped prostate image. The aim of the GCN is to predict the offsets for all points that could be used to shift these points to the true prostate contour locations.

In the GCN model, $X^{(l)}\in {ℝ}^{N\times d_l}$ is the output feature of the l^th layer of the graph convolution that is also the input of the (l + 1)^th layer. N is the number of the vertices on the prostate contour, while d_l is the feature dimension of each vertex. $X^{(l+1)}\in {ℝ}^{N\times d_{l+1}}$ is the output feature of the (l + 1)^th layer of the graph convolution, whereby d_l+1 is the dimension of the output feature. The graph convolution operation (GCO) is defined as follows,

$$X^{(l+1)}=\sigma \left({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{X}^{(l)}{W}^{(l)}\right)$$ (1)

where $\tilde{A}=A+I_N$ is the adjacency matrix of the graph $\mathcal{G}$ with self-connections. The self-connections are implemented by adding the identity matrix I_N. The element of the adjacency matrix $\tilde{A}$ denotes whether an edge exists between two vertices of the prostate contour. $\tilde{D}$ is the degree matrix of $\tilde{A}$. W^(l) is a layer-specific trainable weight matrix, and σ(·) is an activation function.

The GCN generalizes the convolutional operation from a grid data to a non-Euclidean graph data. The graph convolutional operation aims to generate representations for vertices by aggregating its own feature and the features of its neighboring vertices. Based on multiple graph convolutional layers, the high-level vertex representations can be obtained. This representation generation methodology is also called information propagation. From this point-of-view, Eq. (1) can be considered as an information propagation rule. The high-level representations of vertices are very important for vertex classification or regression. Based on the high-level vertex representations, the locations of the vertices can be predicted accurately. Therefore, an accurate prostate contour can be predicted by the GCN.

Information propagation in GCN is the main distinction from a CNN that also constitutes an important concept in GCN. Similar to CNNs, GCNs learn a new feature representation for each vertex in a graph over multiple layers.³⁰ The feature of each vertex at the beginning is averaged with the features of its neighboring vertices. The feature will be updated based on different layers. This update can be expressed over the entire graph as a matrix multiplication between $\tilde{A}$ and X.

The proposed GCN module is shown in Fig. 4.

Fig. 4.

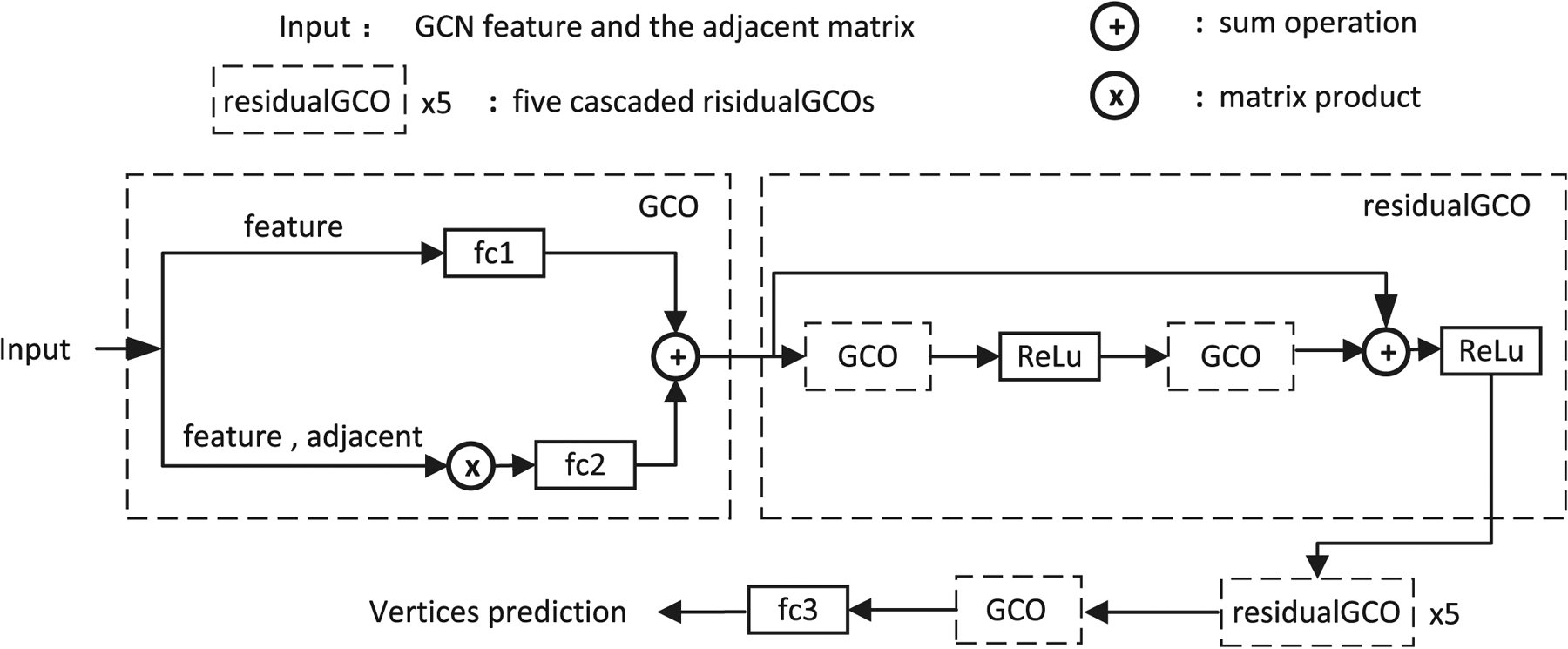
Overview of the graph convolutional network (GCN) block. The GCN block consists of two types of operations, namely the graph convolutional operation (GCO) and the residual graph convolutional operations (residual GCO). The GCO is used at the beginning and ending of the GCN block for the adjustment of the feature dimensions. The residual GCO is used to learn more representative features for interactive segmentation. Additionally, fc1, fc2, and fc3, are three fully connected layers. The CNN feature and the adjacent matrix are the inputs of the graph convolution operation. The convolutional neural network feature is a 40 × 258 feature map, while the adjacent is a 40 × 40 matrix.

In our method, the GCN block consisted of two graph convolutional operations (GCOs) and six cascaded residual GCOs. Therefore, the GCN block is a multilayer architecture. In each layer, the vertex feature is obtained by aggregating the features of its neighbors that are one hop away. This implies that after multiple layers, a vertex obtains feature information from all vertices that are multiple-hops away in the graph. This multilayer architecture is similar to CNNs, wherein the depth can increase the receptive field of the internal features.³¹ The proposed GCN block can also increase the receptive field by using multiple GCOs and residual GCOs. The fc1, fc2, and fc3 in Fig. 4 denote the fully connected layers that have different output dimensions. The residual GCO consists of two GCOs with two nonlinear activation rectified linear functions (ReLUs) and a skip connection. A graph convolution operation and a fully connected layer are added after the output feature of the cascaded residual GCOs.

3.B.3. Loss function

The proposed model is trained with a contour matching loss, which is used for the evaluation of the accuracy of the predicted interaction points. We assume that the points have a well-defined order. Therefore, the vertices of the ground truth and those of the prediction should be well matched to calculate the loss. The contour vertices of ground truth are defined as gt = {gt₀, gt₁, ⋯, gt_T−1}, and interaction points of the prediction are defined as ip = {ip₀, ip₁, ⋯, ip_N−1}. N is the number of the interaction points. The contour matching loss L_cm is defined as follows.

$$L_{\text{cm}}(ip,gt)=\underset{j\in [0\cdots ,N-1]}{\text{min}}\sum _{i=0}^{N-1}{\Vert i{p}_i-g{t}_{(j+i)\text{\%}N}\Vert }_1$$ (2)

where i and j are the indices of the vertices of the prediction and ground truth, respectively. To calculate the loss function L_cm, the sum of the distances between two sets of vertices $\sum _{i=0}^{N-1}{\Vert i{p}_i-g{t}_i\Vert }_1$ should be calculated. However, there is no one-to-one match between the two point sets. Therefore, we should calculate the sum of the distances of all the possible N matches. The minimum sum distance is then selected as the loss. The subscript of gt is used to implement all the possible N matches.

3.C. Interactive GCN module

To mimic the processing of user interactions, we simulated an annotator that shifted the predicted incorrect vertex to its correct location (ground truth). The model was trained to predict the shifts of 2k neighboring vertices (k neighbors on either side) of the current interaction point. In our experiment, we set k = 2. This parameter can be changed during the test to control the neighborhood range. The shifting of the vertex (x_i, y_i) is denoted as (Δx_i, Δy_i).

We added two extra channels to the GCN feature X_gcnLoc, namely, (Δx_i, Δy_i). Therefore, the input feature of the interactive GCN module X_gcnLocS is presented as follows,

$$X_{\mathit{\text{gcnLocS}}}=\text{concat}\left\{X_{cnn},\left(\Delta x_i,\Delta y_i\right),\left(x_i,y_i\right)\right\}$$ (3)

where i = 1, ⋯, N, N is the number of interaction points. We set the value of (Δx_i, Δy_i) to zero for other vertices that did not belong to the 2k neighboring vertices. During the training, we let the annotator choose to correct the vertex with the worst accuracy. This was achieved based on the identification of the maximum Manhattan distance between the predicted and ground truth vertices. The interactive GCN module chose the worst prediction and re-predicts its 2k neighbors iteratively. At each iteration, the interactive GCN module predicted the new locations of neighbors of the current interaction point, and then corrected the next vertex with the worst prediction. To allow the model to learn the user’s interactive ability, we performed the aforementioned operations in an iterative manner.

3.D. Evaluation metrics

To quantitatively evaluate the proposed methods, four popular metrics were used in our experiments. Two metrics were region-based, namely, the Dice similarity coefficient (DSC) and the relative volume difference (RVD). The other two metrics were distance-based, namely, the Hausdorff distance (HD) and the average symmetric surface distance (ASD). The DSC was obtained with the following equation,

$$DSC=\frac{2\left|R_{gt}\cap R_{pre}\right|}{\left|R_{gt}\right|+\left|R_{pre}\right|}\times 100\text{\%},$$ (4)

where R_gt and R_pre are the prostate ground truth and predicted regions, respectively. The operator |*| represents the number of pixels in a region. The metric RVD is used to evaluate the prediction irrespective of whether it tends to cause under-segmentation or over-segmentation. The RVD is defined as follows.

$$RVD=\frac{\left|R_{pre}\right|-\left|R_{gt}\right|}{\left|R_{gt}\right|}\times 100\text{\%}.$$ (5)

The HD metric is defined as follows.

$$HD=\text{max}\left(\underset{i\in {\text{B}}_{\text{pre}}}{\text{max}}\left(\underset{j\in B_{gt}}{\text{min}}(d(i,j))\right),\underset{j\in B_{gt}}{\text{max}}\left(\underset{i\in {\text{B}}_{\text{pre}}}{\text{min}}(d(i,j))\right)\right),$$ (6)

where B_gt is the boundary of the ground truth, and B_pre is the boundary of prediction. d(i,j) is the Euclidean distance between pixel i (prediction) and pixel j (ground truth). The ASD is defined as follows,

$$\begin{gathered} ASD=\frac{1}{\left|B_{pre}\right|+\left|B_{gt}\right|} \\ \times \left(\sum _{i\in B_{pre}}d\left(i,B_{gt}\right)+\sum _{j\in B_{gt}}d\left(j,B_{pre}\right)\right), \end{gathered}$$ (7)

where d is the distance from a point to a boundary.

4. EXPERIMENTAL RESULTS AND DISCUSSION

4.A. Data

In total, 140 subjects of prostate MRI from three datasets were used for the training model in our experiments. These included PROMISE12 (50 subjects),³² International Symposium on Biomedical Imaging 2013 (ISBI2013) (49 subjects), and in-house (41 subjects) datasets. Our in-house MR subject dataset included transversal T2-weighted MR images which were scanned at 1.5 T and 3.0 T. The voxel size varied from 0.4 to 1 mm. The matrix sizes of the transverse images ranged from 512 × 512 to 320 × 320. To evaluate the proposed method, we used the ground truths of 30 test subjects from PROMISE12 and 41 in-house subjects which were labeled by the radiologists. Each slice was manually labeled by two radiologists who had 15 yr and 3 yr of experience, respectively. In addition, each radiologist labelled the slices three times. To avoid the situation in which the two radiologists would remember previous labelled examples, successive manual segmentations were performed one week apart with respect to each other. Majority voting was adopted to fuse the labels segmented by the two radiologists.

4.B. Implementation details

The algorithm was implemented in Python with developed codes subject to the PyTorch framework. The algorithm ran on an Ubuntu system with an Intel Xeon E5-2620 CPU (2.1 GHz) and with a 64 GB memory. Our code used a GTX 1080 Ti GPU with 11 GB memory. The implementation was not optimized and did not use multithread and parallel programming.

During the training, a learning rate was set as 1×10⁻³. The weights of the CNN encoder were initialized with the use of the pre-trained model based on natural images.

4.C. Qualitative results

The segmentations of six subjects obtained from the PROMISE12 test dataset are shown in Fig. 5. The prostatic apex and base are not easily segmented. Therefore, a subdivision scheme was used to compute values of four metrics on three subregions of the prostate. All prostate slices were divided into three parts that included the apex subregion, mid-gland subregion, and base subregion (30%, 40%, and 30%, respectively).

Fig. 5.

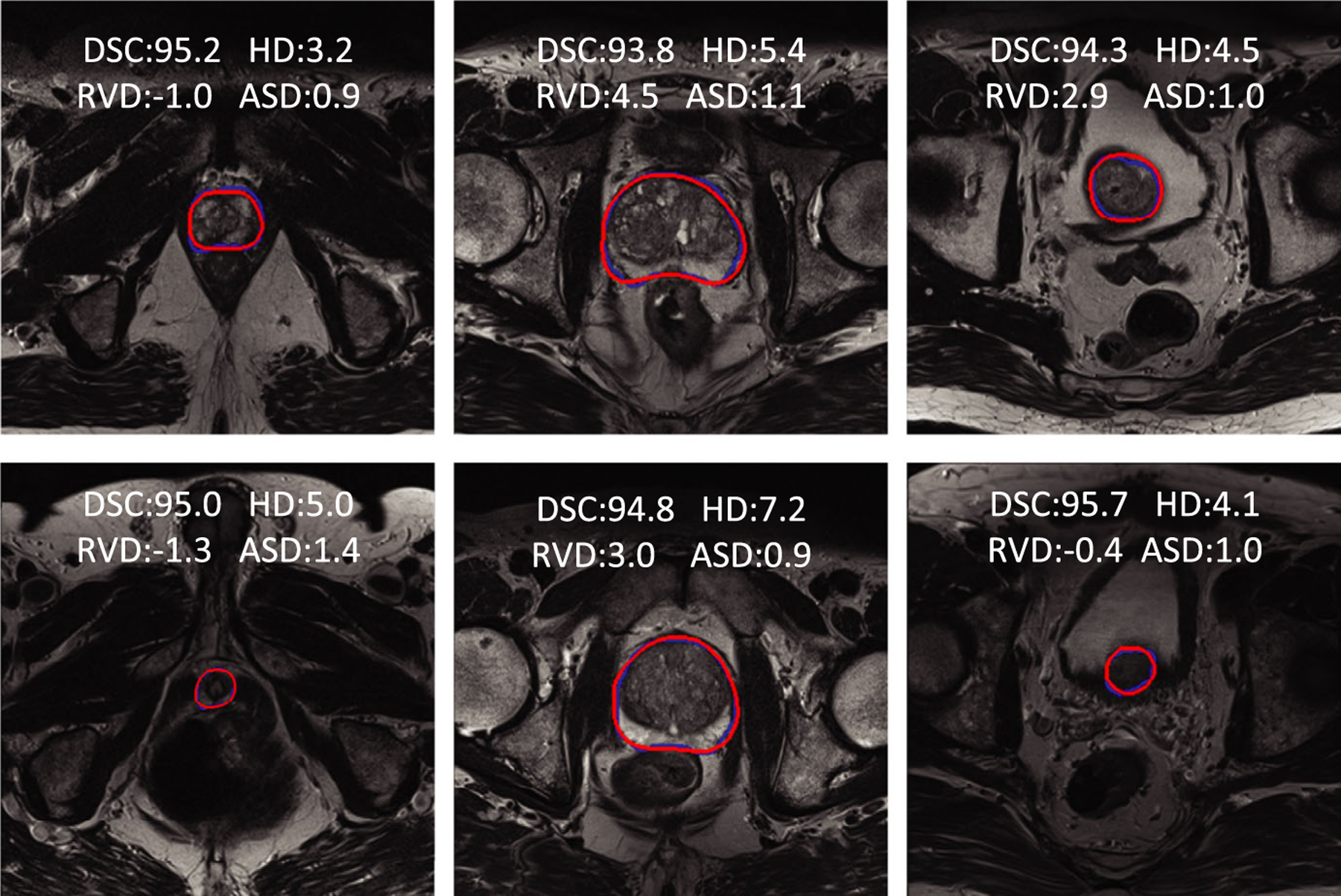
Qualitative results of six prostate MR cases from the PROMISE12 test dataset. The red curves are the results of the proposed method. The blue curves are the manually labeled ground truth. The first column shows the results of the apex subregion. The middle column shows the results of the mid-gland subregion. The last column shows the base subregion. Four metric values are presented on the MR images, including the DSC (%), RVD (%), HD (mm), and ASD (mm). DSC is a Dice similarity coefficient (%). RVD is a relative volume difference (%). HD is the Hausdorff distance (mm), and ASD is the average symmetric surface distance (mm).

The images from the three subregions of the prostate were chosen for qualitative evaluation. Each subregion presented two result images from different subjects. In Fig. 5, three columns showed the apex, mid-gland, and base images, respectively. The values of the evaluation metrics were overlaid on the resulting images. Blue contours included the ground truth manually labelled by the radiologists, while the red contours were the results obtained from the proposed method. From the figure, we can observe that the proposed method could obtain accurate results from all three subregions.

4.D. Quantitative results

The quantitative segmentation results of the proposed automatic mode on in-house dataset are shown in Table I. Five-fold cross validation was adopted in this experiment. The proposed method yielded a DSC of 93.8% ± 1.2%, a HD of 5.8 mm ± 2.4 mm, and an ASD of 1.0 mm ± 0.3 mm on the entire gland. The results show that the proposed method could yield a relatively accurate segmentation with a low standard deviation. In addition, it could yield a RVD of −4.0% × 4.0%. This value indicates that the proposed method achieves an effective tradeoff between the under-segmentation and over-segmentation. Meanwhile, the proposed method could respectively yield a DSC of 92.9% ± 2.1%, 94.9% ± 1.4%, and 93.1% ± 1.6% on base, mid-gland, and apex subregions, respectively. The results of the apex and base are comparable with those of the mid-glands.

Table I.

Quantitative segmentation results from a 41 in-house dataset

CaseID	Whole Gland				Base				Mid-gland				Apex
	DSC	RVD	HD	ASD	DSC	RVD	HD	ASD	DSC	RVD	HD	ASD	DSC	RVD	HD	ASD
01	93.6	−4.5	4.6	1.0	92.2	−0.3	4.6	1.1	95.0	−6.7	4.5	0.9	92.9	−4.9	3.6	0.9
02	93.8	−5.9	4.1	0.8	91.4	−9.9	4.1	1.0	96.0	−2.8	3.0	0.7	93.2	−8.7	3.3	0.9
03	93.8	−7.2	4.0	0.9	94.8	−4.6	4.0	0.9	93.8	−9.8	3.6	1.1	93.0	−4.9	3.2	0.8
04	94.5	0.8	5.0	0.9	94.1	1.0	5.0	0.9	95.7	0.0	4.1	0.9	93.1	2.7	3.6	0.9
05	93.4	1.0	8.1	0.9	91.6	−4.3	8.1	1.0	95.8	2.6	3.0	0.8	92.0	6.1	4.1	0.9
06	92.5	−4.1	7.3	0.9	87.1	−9.7	7.3	1.4	95.8	−1.1	3.7	0.7	93.1	−1.3	3.2	0.8
07	93.5	−4.4	3.7	0.7	94.5	−0.9	3.0	0.7	95.2	−3.1	2.0	0.6	90.0	−11.6	3.7	0.9
08	94.9	−5.4	5.7	0.8	93.8	−6.7	5.7	0.9	96.1	−4.9	2.8	0.7	94.4	−3.8	2.8	0.6
09	94.5	−4.3	9.8	1.1	95.3	−6.1	12.1	1.0	96.0	−3.2	8.9	1.1	91.5	−4.9	9.8	1.3
10	93.8	−6.5	6.4	0.9	94.1	−6.0	3.6	0.9	95.0	−6.7	4.0	0.9	91.9	−6.7	6.4	0.9
11	92.3	−8.8	6.2	1.0	89.1	−15.0	6.2	1.3	93.7	−9.0	4.2	1.0	93.8	1.8	3.2	0.8
12	92.0	−8.1	9.1	1.5	89.8	−12.2	9.1	1.8	92.6	−9.5	8.6	1.5	93.5	3.2	4.2	1.0
13	94.4	−1.0	5.0	0.7	93.2	0.0	5.0	0.8	95.3	−0.9	2.8	0.6	94.4	−2.7	2.2	0.6
14	93.9	−9.2	5.4	0.8	93.8	−9.4	5.4	0.8	94.3	−9.7	3.0	0.8	93.5	−7.8	2.4	0.7
15	94.4	−6.5	4.7	1.0	95.3	−5.0	4.1	1.0	94.5	−9.0	5.0	1.0	93.4	−3.6	3.7	0.9
16	95.4	−1.4	5.2	1.0	95.8	−4.7	4.1	0.9	96.2	−0.8	5.1	1.0	94.1	0.0	5.2	1.0
17	95.1	−3.4	3.6	0.7	95.2	−4.9	3.0	0.7	96.0	−2.1	3.6	0.7	93.9	−5.1	3.2	0.8
18	94.9	−1.2	6.0	1.0	92.9	1.7	6.3	1.3	96.5	−1.7	5.4	0.9	94.8	−2.9	4.1	0.9
19	92.5	−5.9	4.1	0.9	92.0	1.2	4.0	0.9	95.7	−4.9	3.0	0.8	88.9	−14.2	4.1	1.2
20	95.1	−1.2	3.6	0.7	96.0	0.9	3.0	0.7	95.0	−2.2	3.6	0.8	94.4	−2.5	2.2	0.6
21	94.2	7.3	6.2	1.2	92.6	12.7	6.2	1.5	95.0	4.6	4.2	1.1	95.0	1.9	4.0	0.8
22	93.1	1.7	7.3	1.4	92.3	11.3	6.6	1.6	95.1	1.5	6.4	1.3	91.3	−8.6	7.3	1.4
23	93.7	−7.2	4.0	0.9	94.4	−5.8	3.6	0.8	94.6	−8.0	4.0	1.1	92.0	−6.5	3.6	0.9
24	94.2	−5.1	4.5	0.8	92.2	−3.7	5.0	0.8	95.7	−5.9	3.6	0.8	94.2	−4.3	4.5	0.8
25	94.3	−4.4	6.2	1.1	92.6	−1.2	7.2	1.2	95.8	−4.1	8.0	1.1	94.1	−6.7	5.8	1.2
26	92.2	−7.8	6.0	1.0	90.4	−6.8	4.5	1.2	94.3	−7.3	4.1	1.0	91.1	−10.4	6.0	1.1
27	92.5	−6.8	7.1	1.1	88.3	−13.6	7.2	1.7	95.7	−2.2	5.1	0.9	92.6	−7.3	3.7	0.9
28	93.3	3.3	8.5	1.4	92.4	−6.2	7.8	1.5	93.1	9.0	8.5	1.6	94.4	2.7	4.0	1.0
29	93.1	0.9	16.0	2.0	93.8	−3.6	9.7	1.6	93.8	8.1	11.7	2.3	91.5	−8.6	16.0	1.9
30	93.5	−2.8	6.4	1.1	89.6	−9.4	6.4	1.7	95.1	0.6	4.2	1.0	95.3	−1.9	3.7	0.8
31	95.0	−3.5	3.5	0.8	94.6	−3.1	3.0	0.8	95.4	−3.0	3.5	0.8	94.6	−5.9	2.4	0.7
32	95.0	−0.2	3.6	0.7	94.8	−1.6	3.6	0.8	95.6	4.3	3.0	0.7	94.3	−5.0	3.3	0.7
33	95.3	1.5	5.0	0.9	95.1	0.7	5.0	1.0	95.9	3.0	3.2	0.8	94.7	0.1	4.1	0.9
34	92.8	0.3	11.4	1.7	92.0	−11.4	11.4	2.0	94.5	6.7	6.4	1.4	91.2	7.4	8.6	1.7
35	94.7	−6.3	5.7	1.0	92.7	−12.0	6.1	1.4	96.6	−4.7	9.1	0.9	94.3	−3.3	4.1	1.0
36	91.6	−9.6	5.1	1.0	93.1	−2.5	4.0	0.9	89.8	−15.2	8.0	1.3	92.0	−9.0	3.2	0.8
37	93.5	−6.4	5.1	1.1	93.1	−6.5	5.2	1.2	93.6	−6.3	4.6	1.1	93.8	−6.4	4.1	1.0
38	91.0	−11.9	4.1	1.0	91.5	−12.0	3.6	0.9	91.8	−10.3	4.1	1.0	89.4	−14.5	4.2	1.2
39	92.3	−9.2	4.1	1.0	92.7	−7.5	3.0	0.9	92.5	−8.7	4.1	1.1	91.4	−11.7	4.0	1.0
40	95.4	−5.9	5.0	1.0	94.9	−6.6	4.0	1.0	95.9	−5.1	4.4	1.1	95.2	−6.7	5.0	1.1
41	95.6	−4.3	3.2	0.7	94.9	−6.1	2.4	0.6	96.5	−3.3	3.2	0.7	95.0	−4.8	3.0	0.7
Avg.	93.8	−4.0	5.8	1.0	92.9	−4.6	5.4	1.1	94.9	−3.2	4.8	1.0	93.1	−4.4	4.5	1.0
Std.	1.2	4.0	2.4	0.3	2.1	5.8	2.3	0.3	1.4	5.3	2.2	0.3	1.6	5.0	2.4	0.3

The values of the four metrics of the whole gland and the three gland subregions (base, mid-gland, and apex) are shown. Four metrics are used to evaluate the performance, including the Dice similarity coefficient (%), relative volume difference (%), Hausdorff distance (mm), and ASD (mm).

Besides the experiment on the in-house dataset, the quantitative results on the PROMISE12 test dataset are also presented. These achieved a DSC of 94.44% ± 1.03%, a RVD of 0.03% ± 3.59%, a HD of 8.66mm ± 3.47 mm, and an ASD of 1.36mm ± 0.33 mm.

To evaluate the effectiveness of the proposed multiscale CNN encoder, an ablation experiment was performed on 30 test subjects of PROMISE12 and in-house dataset. The evaluation results of the four metrics of each subregion are shown in Table II and III. The results show that the proposed multiscale CNN feature encoder could improve the segmentation accuracy.

Table II.

Quantitative prostate segmentation results obtained from a PROMISE12 test dataset

	DSC (%)	RVD (%)	HD (mm)	ASD (mm)
Whole Gland
Baseline w/o multiscale CNN encoder	93.79	0.25	8.61	1.47
Baseline with multiscale CNN encoder	94.44	0.03	8.66	1.36
Apex
Baseline w/o multiscale CNN encoder	93.01	−0.65	7.75	1.61
Baseline with multiscale CNN encoder	93.80	0.04	7.69	1.54
Mid-gland
Baseline w/o multiscale CNN encoder	95.68	1.11	6.96	1.38
Baseline with multiscale CNN encoder	96.37	0.13	6.23	1.21
Base
Baseline w/o multiscale CNN encoder	92.85	−0.65	8.75	1.92
Baseline with multiscale CNN encoder	93.99	−0.82	8.57	1.76

The results of the whole gland, base, apex, and mid-gland regions are shown.

Table III.

Quantitative prostate segmentation results obtained from an in-house dataset

	DSC (%)	RVD (%)	HD (mm)	ASD (mm)
Whole Gland
Baseline w/o multiscale CNN encoder	92.47	−4.72	7.66	1.16
Baseline with multiscale CNN encoder	93.77	−3.99	5.84	1.01
Apex
Baseline w/o multiscale CNN encoder	92.19	−5.40	5.76	1.02
Baseline with multiscale CNN encoder	93.09	−4.42	4.47	0.95
Mid-gland
Baseline w/o multiscale CNN encoder	93.24	−3.56	6.24	1.20
Baseline with multiscale CNN encoder	94.90	−3.22	4.82	0.98
Base
Baseline w/o multiscale CNN encoder	91.73	−5.78	6.56	1.27
Baseline with multiscale CNN encoder	92.93	−4.63	5.45	1.10

The results of the whole gland, base, apex, and mid-gland regions are shown.

4.E. Comparison with other methods

A set of eight state-of-the-art image segmentation methods^{3,10,20,28,33–36} were chosen as the benchmark to evaluate the proposed method. The reported results in the tables were obtained based on the application of publicly available codes of these methods on the datasets. The comparisons of these eight methods with our method are listed in Tables IV and V. Four metrics are chosen to evaluate the performances of these methods. The results are reported as average ± standard deviation.

Table IV.

Comparison results of eight previously published state-of-the-art segmentation methods applied on a PROMISE12 test set

	Type	DSC(%)	RVD(%)	HD(mm)	ASD(mm)
PSPNet28	auto	75.49 ± 9.41	4.71 ± 20.52	24.58 ± 15.26	2.89 ± 0.72
FCN33	auto	82.37 ± 5.56	6.07 ± 10.59	19.64 ± 19.79	2.39 ± 0.71
U-Net34	auto	84.71 ± 6.52	2.40 ± 7.98	15.92 ± 6.85	1.89 ± 0.42
V-Net35	auto	85.29 ± 6.82	3.49 ± 8.79	16.78 ± 6.60	2.02 ± 0.46
DeepLabV3+36	auto	86.45 ± 5.09	−6.17 ± 7.09	23.08 ± 19.07	2.20 ± 0.42
Superixel3	semi-auto	87.03 ± 3.21	4.28 ± 9.27	5.04 ± 1.03	2.14 ± 0.35
Grab-Cut10	semi-auto	78.41 ± 15.62	12.22 ± 21.52	21.52 ± 11.27	2.93 ± 1.70
ExtremeCut20	semi-auto	90.78 ± 2.45	−3.44 ± 2.22	10.94 ± 2.22	1.93 ± 0.14
Ours	semi-auto	94.44 ± 1.03	0.03 ± 3.59	8.66 ± 3.47	1.36 ± 0.33

TABLE V.

Comparison results of eight previously published state-of-the-art segmentation methods applied on in-house dataset

	Type	DSC(%)	RVD(%)	HD(mm)	ASD(mm)
PSPNet28	auto	83.96 ± 8.90	8.82 ± 19.40	16.06 ± 14.46	2.04 ± 1.00
FCN 33	auto	80.33 ± 10.67	6.73 ± 46.33	13.24 ± 5.64	2.79 ± 1.54
U-Net34	auto	86.73 ± 6.87	−1.78 ± 19.28	31.71 ± 27.75	2.03 ± 1.13
V-Net35	auto	81.77 ± 9.74	6.15 ± 25.13	19.01 ± 17.33	2.47 ± 1.31
DeepLabV3+36	auto	82.86 ± 6.99	−5.76 ± 13.58	13.29 ± 6.51	1.96 ± 0.63
Superixel3	semi-auto	89.25 ± 1.90	0.81 ± 8.20	8.75 ± 2.70	1.71 ± 0.41
Grab-Cut10	semi-auto	74.86 ± 17.80	14.53 ± 48.87	15.70 ± 5.76	1.92 ± 0.89
ExtremeCut20	semi-auto	88.78 ± 1.41	−19.79 ± 2.54	10.35 ± 3.51	1.85 ± 0.42
Ours	semi-auto	93.77 ± 1.15	−3.99 ± 4.03	5.84 ± 2.45	1.01 ± 0.27

To emphasize the superiority of the proposed method, a statistical significance experiment was performed on the whole gland in terms of the DSC and ASD. We did a t-test for reporting the improvements. The analyses of the tests showed that there was a statistically significant difference on the entire gland (P < 0.05) both in terms of DSC and ASD.

4.F. Evaluation of interactions

To evaluate the performance of the interactive mode, the mean intersection over union (IoU) scores³⁷ were computed according to the number of clicks. Fig. 6 shows the IoU score vs the number of clicks on PROMISE12 test set. From the figure, we can observe that the segmentation accuracies of three subregions increase along with the number of clicks increases. The performance of the proposed method has no much improvement after eight clicks. This helps the users decide how much effort should be input to obtain the best segmentation results. In our experiment, the DSC increases from 94.4% to 95.7% with three interactions on PROMISE12 test set. Meanwhile, the DSC increases from 93.8% to 95.3% with three interactions on in-house dataset.

Fig. 6.

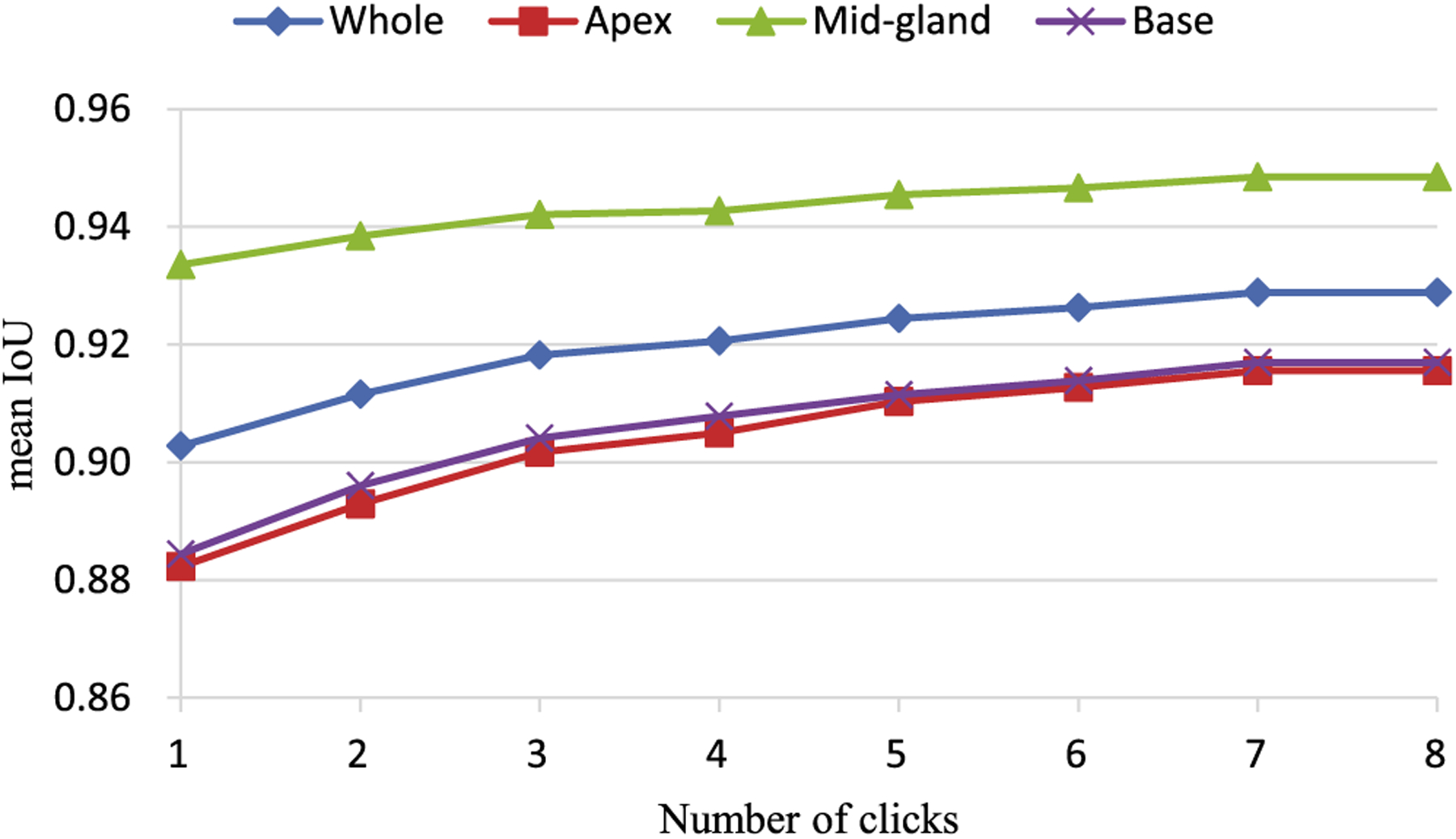
Effects attributed to the number of clicks.

4.G. Evaluation of robustness

To evaluate the influence of the neighborhood range k of the interaction point, the DSC values obtained from experiments with five different parameters k are reported. From the Fig. 7, we can see that the DSC varies within a small range. This proves that the proposed method is robust to the parameter k.

Fig. 7.

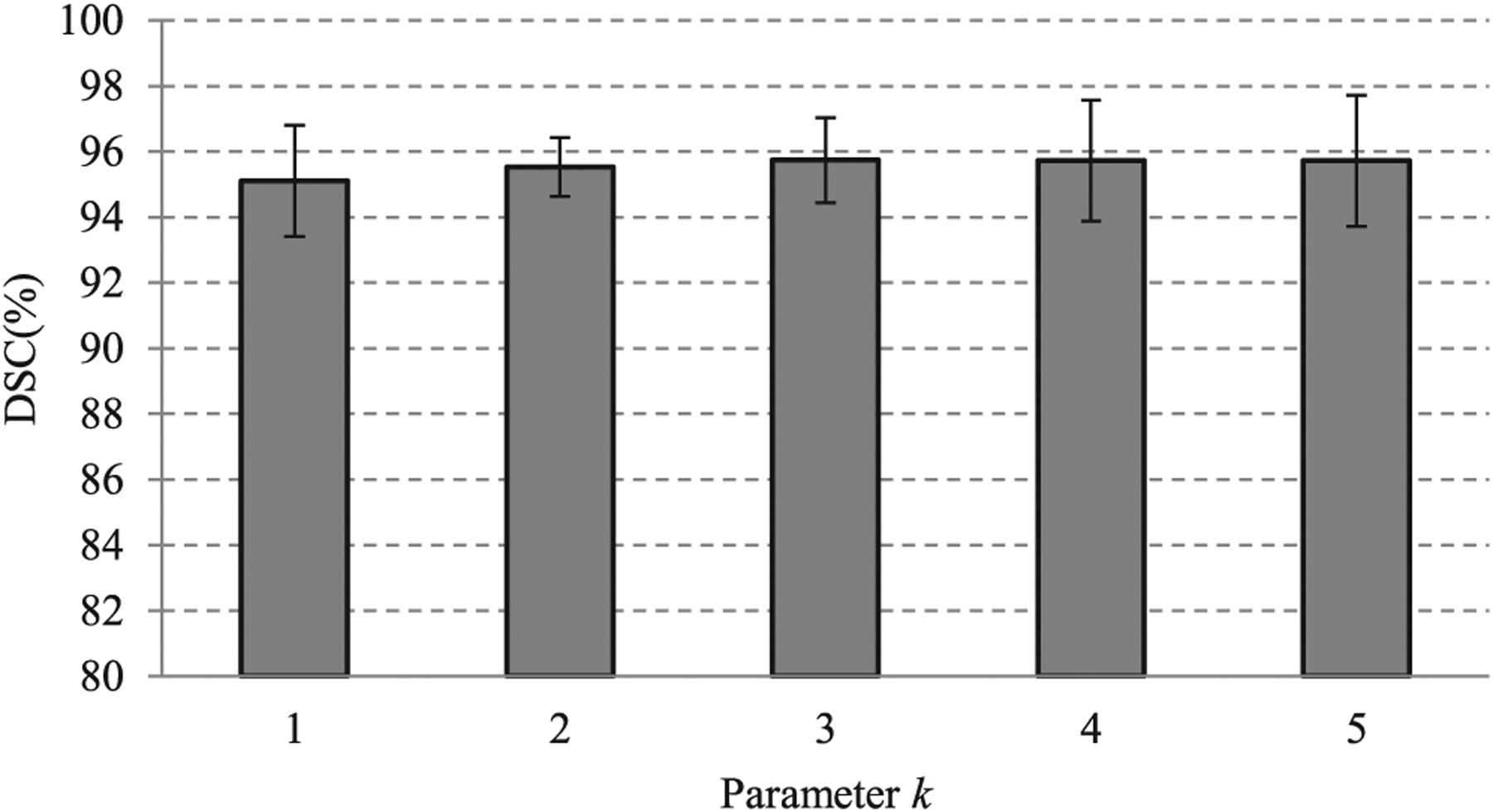
Effects of parameter k on the segmentation performance. When the value of the parameter k varies from 1 to 5, the Dice similarity coefficient does not exhibit considerable change. This shows that the proposed method is robust to the neighborhood range of the interaction point.

Different users may yield different variations by clicking and dragging the interaction points. To evaluate the user variability of the proposed interactive segmentation method, two radiologists were recruited to use the proposed interactive method. The DSC metric and in-house dataset were used to evaluate the user variability. The DSC obtained from the first user was 95.7%, while the second user obtained a DSC of 93.4%. The experimental results showed that the proposed interactive segmentation method achieved a high DSC and considerable user variability. Therefore, the high DSC of our method is associated with an increased cost of user variability.

4.H. Evaluation of loss function

To evaluate the performance of L1 contour matching loss that used in the proposed method, three popular loss functions were chosen for comparison. These three loss functions are earth mover loss, chamfer loss, and L2 contour matching loss. PROMISE12 dataset was adopted for the comparison experiment. The results are shown in Table VI. From the table, we can observe that the L1 contour matching loss performs best among these loss functions.

TABLE VI.

Comparison with three loss functions on PROMISE12 dataset

	DSC(%)	RVD(%)	HD(mm)	ASD(mm)
Earth mover loss	92.17	2.66	9.86	1.76
Chamfer loss	93.54	−0.75	10.23	1.49
L2 contour matching loss	93.78	0.36	9.20	1.48
L1 contour matching loss	94.44	0.03	8.66	1.36

4.I. Ablation study

We conducted an ablation study to show the superiority of the proposed multiscale encoder (ME) and multiple residual GCO blocks (MRG). A bare-bone adaption of Ling’s method²⁴ was chosen as baseline in this ablation study. PROMISE12 dataset was adopted in the experiment. The ablation results are show in Table VII. Compared with the baseline, the DSC of only using multiscale encoder or the multiple residual GCO blocks increases 1.14% and 2.53%, respectively. The DSC of both using two modules increases from 91.26% to 94.44%.

Table VII.

The effects of the proposed multiscale encoder (ME) and the proposed multiple residual GCO (MRG)

	DSC(%)	RVD(%)	HD(mm)	ASD(mm)
Baseline	91.26	2.32	11.89	1.93
Baseline + ME	92.40	0.19	9.76	1.72
Baseline + MRG	93.79	0.25	8.61	1.47
Baseline + ME + MRG	94.44	0.03	8.66	1.36

PROMISE12 dataset was adopted for this ablation study. Baseline is bare-bone adaption of Ling’s method.²⁴

4.J. Computation time

The training time of the proposed model was approximately 6 h, while the inference time of the automatic GCN approach required 56 ms for one MR image. In the interactive approach, the proposed model re-used the CNN feature of the automatic approach that only consumed 13 ms to generate an inference after the onset of the interaction operation Table VIII.

Table VIII.

Computation time required by the proposed method after its application on a magnetic resonance image

Methods	Time (ms)
Extreme-Cut20	164
Ours(automatic module)	56
Ours(interactive module)	13

ExtremeCut was used for comparison.

The total interaction time of the segmentation of a prostate was 1.5 min on average. This included 20 s for drawing bounding boxes, 70 s for correcting erroneously predicted vertices to the proper locations.

5. CONCLUSION AND DISCUSSIONS

In this study, we developed and evaluated a GCN for the segmentation of the prostate gland from MR images. To allow learning of more representative features for improved accuracy, a multiscale CNN feature encoder was proposed. To effectively train the GCN for prostate segmentation, we proposed a contour matching loss function. The contour matching loss was preferred to preserve boundary details that are useful for the contour-based interactive segmentation method. The proposed method could yield more accurate segmentation compared with several other popular methods. We defined the interactive prostate segmentation from a novel point-of-view based on the use of the GCN. Our segmentation method benefitted from GCN from two perspectives: (a) the segmented contour can be further improved by correcting the interaction points based on GCN that yielded more accurate segmentation results, (b) the GCN-based segmentation method could obtain the segmented prostate segmentation efficiently. We believe that the proposed method can be extensively used for different image modalities and different regions-of-interests in medical images.

Most current CNN-based prostate segmentation methods treat prostate segmentation as a pixel-wise labeling problem and define the segmentation model at the pixel-level. Accordingly, each pixel of the input image needs to be classified.^38,39 In this way, it is very difficult to incorporate the shape priors of the prostate. In addition, ambiguous regions, image saturation, and low-resolution prostate images will seriously affect the performance of the pixel-level prostate-segmentation methods. In this study, the proposed method considered the segmentation of prostate images as a prostate contour prediction problem. The contour of the prostate was represented with several vertices. Compared with other CNN-based prostate segmentation methods, the proposed GCN-based method does not need to classify each pixel of the image, but only predicts the vertices on the contour of the prostate by the GCN. The proposed GCN-based method can produce accurate prostate segmentation. In addition, the proposed GCN-based method can refine the segmentation result in an interactive manner. Furthermore, the time required by the proposed interactive module to formulate an inference was only 13 ms. The reduced time required to formulate an inference is very important for the responsive user interfaces. Traditional and CNN-based methods require 700–4000 ms to draw inferences.^11,38 Therefore, the proposed GCN-based algorithm is more suitable for interactive segmentations.

Although the proposed method achieves accurate segmentation, there are still some limitations. The proposed method is a deep-learning-based method that depends on the number of MR volumes. More MR volumes could yield more accurate results based on deep-learning methods. Although we have collected 140 volumes from three datasets, the amount and diversity of the data can be increased to improve accuracy. The automatic GCN approach required only 56 ms to segment an MR image, and has many clinical applications in prostate cancer diagnosis and therapy. The costs associated with a semi-automatic algorithm are the interaction time and the observer variability. In our interactive segmentation method, the user interaction time is 1.5 min on average for one patient case that is less efficient than the fully automated methods. In addition, owing to the involvement of humans, the method yields higher observer variability than the fully automated methods.

The proposed method aims to segment the whole gland of the prostate. However, the segmentation of the peripheral and transition zones of the prostate⁴⁰ would be more useful as cancerous lesions have different appearances in the two zones. Therefore, the proposed method will be extended in our future work to achieve the zonal segmentation of the prostate.

The proposed GCN-based segmentation method can be extended to handle 3D segmentations. In these cases, the predicted 3D segmentation masks are considered as 3D shapes composed of triangular meshes. The vertices of the triangular meshes are considered as graph nodes in the GCN. These nodes incorporated with CNN features can be input to GCN for 3D segmentation.