ANNORE: genetic fine-mapping with functional annotation

Abstract

Genome-wide association studies (GWASs) have successfully identified loci of the human genome implicated in numerous complex traits. However, the limitations of this study design make it difficult to identify specific causal variants or biological mechanisms of association. We propose a novel method, AnnoRE, which uses GWAS summary statistics, local correlation structure among genotypes and functional annotation from external databases to prioritize the most plausible causal single-nucleotide polymorphisms (SNPs) in each trait-associated locus. Our proposed method improves upon previous fine-mapping approaches by estimating the effects of functional annotation from genome-wide summary statistics, allowing for the inclusion of many annotation categories. By implementing a multiple regression model with differential shrinkage via random effects, we avoid reductive assumptions on the number of causal SNPs per locus. Application of this method to a large GWAS meta-analysis of body mass index identified six loci with significant evidence in favor of one or more variants. In an additional 24 loci, one or two variants were strongly prioritized over others in the region. The use of functional annotation in genetic fine-mapping studies helps to distinguish between variants in high LD and to identify promising targets for follow-up studies.

Introduction

Large-scale genotyping studies have great potential to enhance our understanding of the genetic etiology of human complex traits. Genome-wide association studies (GWASs), in which a large number of single-nucleotide polymorphisms (SNPs) are individually tested for association with an outcome of interest, have been the primary study design for such investigations (1). However, the findings from such analyses typically suggest genomic loci with hundreds of kilobases in size, often containing hundreds of SNPs that exceed the genome-wide significance threshold.

Patterns of linkage disequilibrium (LD) within such loci present a challenge for researchers seeking to identify the true causal variants. Functional validation in experimental organisms is necessary to confirm findings from epidemiological studies, but these experiments are costly and time-consuming. Statistical fine-mapping methods can be useful to prioritize variants for follow-up. There is a demand for methods that use only summary association statistics rather than individual-level data, to take advantage of large sample sizes available by meta-analysis of GWAS across cohorts (2,3).

Functional annotation, which describes both protein-coding genes and genomic regulatory elements, provides additional information about the potential biological relevance of SNPs within a trait-associated locus. Several methods have been proposed to integrate functional annotation into fine-mapping of loci identified by GWAS. These methods attempt to jointly model the influence of functional annotation categories and the individual-level SNP effects, requiring computationally demanding iterative algorithms or resampling procedures and limiting the number of functional categories that can be modeled simultaneously. Of these methods, only PAINTOR uses summary statistics as input and incorporates both functional annotation and LD structure into the fine-mapping analysis (4).

We propose AnnoRE, a random effects model for genetic fine-mapping that integrates the genome-wide heritability attributable to each functional annotation category to prioritize the most likely causal SNPs within GWAS loci. This approach is motivated by the omnigenic model for complex heritable traits, which posits that a large number of causal SNPs influence the phenotype. From a GWAS perspective, this implies that the true SNP effect is non-zero for a substantial fraction of variants. We model the distribution of these genetic effects as a function of the annotations, where higher values of the random effects variance correspond to greater probability of effects with large magnitude.

Simulation studies compare the performance of AnnoRE to previously published fine-mapping methods. Finally, we apply AnnoRE to a large-scale GWAS meta-analysis of body mass index (BMI) (5). A software implementation in R is available at https://github.com/vafisher/AnnoRE/.

Results

Simulation study

AnnoRE was compared to four other fine-mapping approaches (naïve GWAS, LASSO, GenoWAP and PAINTOR) in 20 simulated scenarios each with one true causal SNP selected from a range of annotation priority, in high or low LD with other SNPs in the locus. Because the alternative approaches use a range of estimands that are not directly comparable, performance was summarized by ranking all SNPs in the locus by their relative evidence of effect on the simulated phenotype and comparing the ranking obtained for the causal SNP from the various approaches. AnnoRE gave a higher ranking on average across 1000 replicates to the true causal SNP than comparison methods for all selected causal SNPs, except in three scenarios where the causal SNP was in at least the 90th percentile of functional annotation, and PAINTOR gave a higher average ranking (Table 1 and Fig. 1). The causal SNPs that PAINTOR ranked higher than AnnoRE were located in three or four of the annotation categories considered in the PAINTOR estimation, suggesting that PAINTOR is powerful when the selected annotations contain the true causal SNPs, but it is sensitive to the choice of annotation categories included in the model. In fact, PAINTOR often failed to converge entirely for SNPs not included in any of the annotation categories it considered. AnnoRE is more robust to scenarios of moderate evidence from annotation because it summarizes the effects of a large number of annotation categories which are estimated from genome-wide summary statistics.

Table 1.

Selected causal SNP characteristics for simulated studies: minor allele frequency (MAF), overall LD 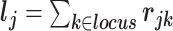in the bottom quartile (low) or top quartile (high) within the locus, and percentile of annotation score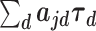

Causal SNP	MAF	Overall LD	Annotation Percentile	Average rank at causal SNP
				GWAS	LASSO	GenoWAP	PAINTOR	AnnoRE
rs9974258	0.413	Low	10	69.2	55.3	1191.3	NA	23.0
rs77960433	0.037	Low	20	1602.2	48.1	2076.9	2129.2	14.4
rs433893	0.381	Low	30	42.1	52.5	1466.8	NA	13.5
rs2830795	0.278	Low	40	1931.4	49.8	946.1	2142.6	13.9
rs2830794	0.493	Low	50	1414.6	52.1	1003.7	2098.7	19.3
rs189506146	0.305	Low	60	52.1	50.6	1333.0	28.3	6.8
rs235952	0.193	Low	70	59.0	45.2	1201.8	13.8	6.6
rs235938	0.467	Low	80	59.9	50.8	1212.5	18.6	6.8
rs235936	0.495	Low	90	54.4	50.9	1040.7	4.1	7.0
rs2830854	0.393	Low	100	53.7	49.7	1704.9	1.8	6.5
rs381814	0.286	High	10	70.5	67.7	1090.4	2044.7	29.9
rs229093	0.299	High	20	75.0	22.6	981.3	NA	52.1
rs7281968	0.33	High	30	77.4	NA	32.7	NA	49.5
rs229087	0.303	High	40	72.0	NA	27.2	1938.1	53.8
rs229061	0.305	High	50	88.4	NA	505.6	NA	58.3
rs229060	0.305	High	60	72.6	NA	99.4	146.6	34.1
rs162497	0.331	High	70	76.1	58.4	86.3	154.2	28.3
rs229063	0.305	High	80	81.5	NA	473.9	165.8	30.7
rs371445	0.292	High	90	82.5	72.9	327.0	78.7	15.9
rs162508	0.282	High	100	72.3	NA	73.2	5.2	25.4

Methods used to evaluate simulated data are compared in terms of average rank of the true causal variant across 1000 replicates. Rankings of ‘NA’ appear where LASSO was unable to estimate several SNPs due to high collinearity with other variants in the locus, and where the PAINTOR algorithm did not converge for four scenarios where the causal SNP was not located in any of the most relevant annotations included in the PAINTOR model.

Figure 1.

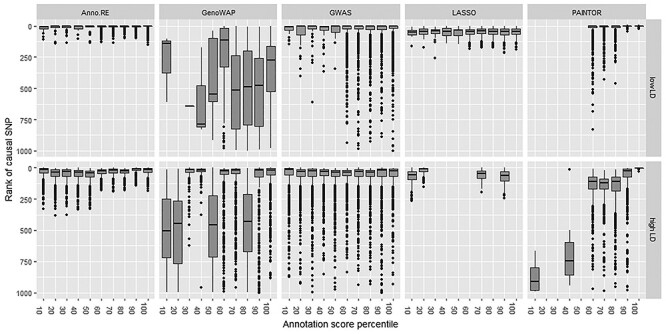
Box plots depicting the quartiles of ranking of simulated causal SNP within fine-mapping locus by all methods under comparison, and whiskers extending 1.5 times the interquartile range, truncated to only show rankings in the top 500 SNPs. Note that LASSO was unable to obtain estimates in six high LD scenarios due to extreme collinearity, and PAINTOR estimation did not converge when the causal SNP was not included in any of the five annotation categories considered by that analysis.

All methods performed better in scenarios where the simulated causal variant was in low LD with all other SNPs in the locus than in patterns of high LD (top row of Fig. 1), except for GenoWAP, which does not model LD. However, the improved performance of GenoWAP at high LD variants is not consistent across scenarios. The prior probabilities of causality used by GenoWAP are different from the annotations used by AnnoRE and PAINTOR in these analyses, possibly accounting for the discrepancy. Additionally, the EM algorithm used by PAINTOR to estimate simultaneously the annotation-level heritability enrichment and the SNP-level effects was unable to converge in simulation scenarios where the true causal SNP was not located in any of the top five most highly enriched annotation categories, which were the only annotation data provided to PAINTOR. The developers of PAINTOR, in showing its application to practical data, used a stepwise selection procedure to choose a set of annotations for inclusion in the final model based on goodness-of-fit statistics from 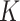fine-mapping models, each with only one annotation category included. However, the annotation feature selection step is outside the scope of this project, so PAINTOR results are presented based only on the scenarios that reached convergence.

Real-data analysis

In the analysis of summary statistics from 77 loci with genome-wide significant associations with BMI in the GIANT consortium meta-analysis of European ancestry studies, 6 loci contained results exceeding the locus-specific significance threshold. In each of these cases, the top SNP selected by fine-mapping was different from the SNP with lowest GWAS P-value, though all of the top fine-mapping SNPs did exceed genome-wide significance in the GWAS results (Table 2).

Table 2.

Top-ranked SNPs for BMI from random effects fine-mapping (AnnoRE) and GWAS analysis in each of the loci with AnnoRE results attaining locus-wide significance

SNP	Chr: position	Nearest gene	L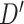D and	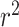MAF	GWAS	GWA.pval	AnnoRE	Wald scores	AnnoRE pval	GWA rank	AnnoRE rank
rs1477196	16:53808258	FTO	1.0	0.28	−0.058	3.22E−72	−0.147	348.049	1.13E−77	50	1
rs1558902	16:53803574		0.41	0.45	0.082	7.51E−153	0.014	2.930	0.087	1	31
rs34358	5:74965122	ANKDD1B	0.96	0.35	0.023	2.31E−12	0.037	37.200	1.07E−09	11	1
rs2112347	5:75015242		0.87	0.38	−0.026	6.19E−17	−0.001	0.368	0.544	1	56
rs988748	11:27724745	BDNF	0.99	0.22	−0.041	5.90E−23	−0.027	33.935	5.70E−09	16	1
rs11030104	11:27684517		0.89	0.20	0.041	5.56E−28	0.003	0.729	0.393	1	43
rs11676272	2:25141538	ADCY3	1.0	0.48	0.032	1.12E−21	0.031	28.952	7.42E−08	3	1
rs10182181	2:25150296		0.99	0.50	−0.031	8.78E−24	−0.009	5.028	0.025	1	4
rs1048932	11:115044850	CADM1	0.90	0.50	−0.019	9.43E−10	−0.019	17.367	3.08E−05	2	1
rs12286929	11:115022404		0.57	0.43	0.022	1.31E−12	0.002	1.884	0.170	1	7
rs1800437	19:46181392	QPCTL	0.99	0.18	0.035	1.73E−17	0.022	12.912	3.27E−04	3	1
rs2287019	19:46202172		0.89	0.15	0.036	4.59E−18	0.002	1.159	0.282	1	10

LD measures D′ and 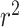quantify association between the top SNPs identified by the two methods.

The strongest fine-mapping signal, rs1477196, identified by the AnnoRE is in the FTO locus on chromosome 16 (Fig. 2), which has been studied extensively in the genetics of obesity (6). Identified in association with obesity in previous publications (7,8), this SNP is located in a haplotype block with two other highly associated SNPs, rs17817449 and rs9939609. However, the random effect variance for rs1477196 is higher than that of the other SNPs on the haplotype due to its inclusion in the super enhancer and H3K27ac histone mark annotation categories, both of which were estimated to contain enriched heritability signal for BMI by LD score regression.

Figure 2.

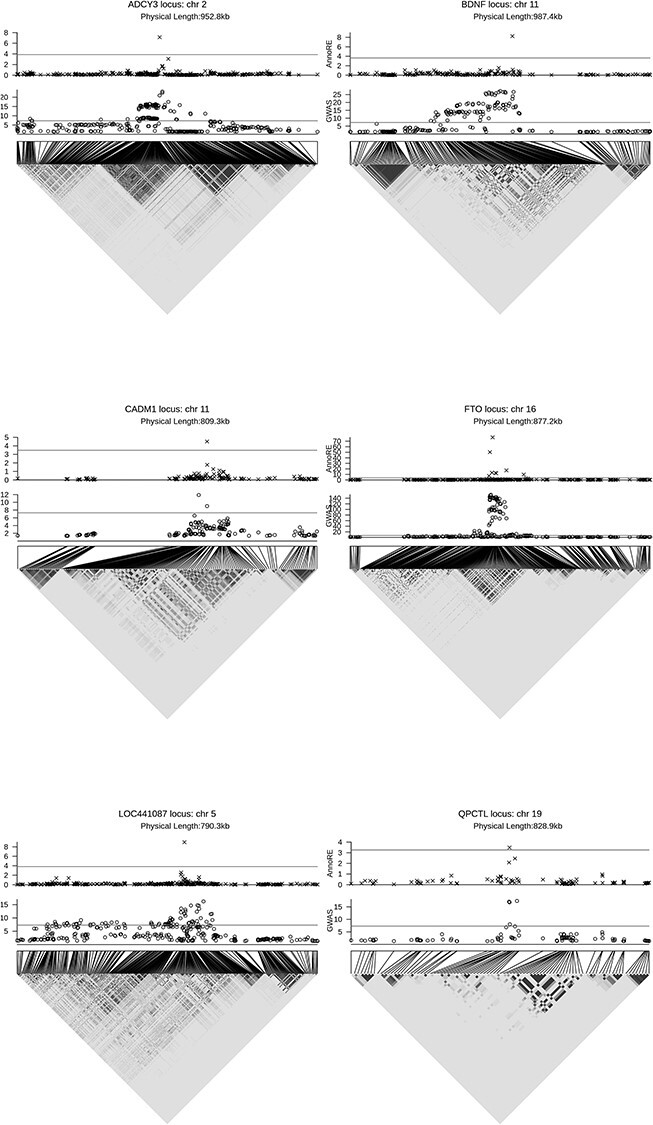
Plots of local LD structure, −log₁₀ GWAS P-values and –log₁₀ AnnoRE P-values in six loci with significant fine-mapping results. Horizontal lines in each scatter plot show genome-wide (GWAS) and locus-wide (AnnoRE) significance thresholds, respectively. Physical length in kilobase (kb) refers to the number of base pairs (in 1000s) from beginning to end of locus, defined by nominally associated SNPs less than 500 kb from the strongest GWAS association.

In the ANKDD1B locus on chromosome 5, the top GWAS signal is located in an intron of the gene, while the top SNP selected by AnnoRE, rs34358, is a stop gain mutation in an exon of the gene, located in a highly conserved region across vertebrate species, a ChIP-seq peak and DNaseI hypersensitive site.

The BDNF (brain-derived neurotrophic factor) gene on chromosome 11 has been implicated in numerous psychiatric and neurological diseases (9,10). Both the top GWAS hit in this locus, rs11030104, and the top SNP selected by AnnoRE fine-mapping, rs988748, are located in conserved regions in introns of this gene. The SNP selected by AnnoRE fine-mapping is included in the super enhancer, fetal DNaseI hypersensitive site, and H3K4me3 peak annotation categories, while the SNP with lowest GWAS P-value is not in these important categories.

AnnoRE identified the SNP with lowest GWAS P-value as the most likely causal variant in 13 (16.8%) of the 77 loci analyzed. Among the remaining loci, the median GWAS ranking of the top fine-mapping SNPs was 14, and the median AnnoRE fine-mapping ranking of the top GWAS SNP was 9. Remarkably, only 39 (51%) of the top SNPs identified by AnnoRE attained genome-wide significance (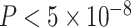) in univariate GWAS analysis.

To assess the ability of our fine-mapping method to discriminate between SNPs in the locus, we computed the ratio between the random effect Wald statistics of the top-ranked SNP, and the second- and third-ranked SNPs. In 17 (22%) of the loci, the signal at the top-ranked SNP was more than twice as strong as the second ranked, and in 30 (39%) of loci, the top-ranked signal was more than twice the third-ranked signal.

Discussion

This paper presents AnnoRE, a method for genetic fine-mapping incorporating functional annotation. This model uses random effects to perform multiple regression with smoothing of the SNP effect estimates dependent on their functional annotation, so that SNPs in categories with enriched heritability receive less shrinkage relative to those without evidence of biological function. This method performed favorably in comparison with existing approaches for genetic fine-mapping with functional annotation in simulated trait-associated genomic loci. In real-data analysis of a GWAS of BMI, AnnoRE identified candidate causal SNPs with plausible biological function.

AnnoRE makes no assumptions regarding the number of true causal signals, because all SNPs in a given locus are included as predictors in the random effects model. This approach is compatible with the omnigenic or infinitesimal models of inheritance, which hypothesize that complex traits are influenced by large numbers of genetic variants with small effect magnitudes (11,12). Under this model, we assume that a locus containing functional elements that affect trait outcomes may contain several causal SNPs modifying the protein product of genes or regulatory elements that control gene expression. However, existing fine-mapping methods generally assume a model of inheritance in which only a few SNPs are truly causal, and all other association signals are artifacts of confounding due to LD. In regions of high LD, the tagging effect of numerous weak signals may substantially influence test statistics, in ways that cannot be captured by a model that assumes zero effect sizes at all but a few SNPs.

Using a two-stage procedure for the estimation of the annotation-level effects and the SNP-level effects allows for improvements in computational efficiency while exploiting information about the annotation effects from all genome-wide test statistics. Thus, AnnoRE is able to account for systematic enrichment of association signal below the genome-wide significance level to identify functional categories that are more likely to contain causal SNPs. On the other hand, the AnnoRE approach assumes that the relative enrichment of trait heritability among functional categories is consistent genome-wide. If a given annotation category is important only in specific genomic locations, AnnoRE may fail to identify causal SNPs in that category. All implementations in this paper have used estimates of the annotation-specific heritability enrichment parameter 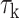from LD score regression, but alternative estimators, such as SumHer (13), could be substituted without modification of the fine-mapping model.

The repeated use of summary statistics from the same GWAS to generate 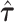to define random effect distributions and also the association statistics within a given locus could lead to inflated Type 1 error, arising when a SNP with strong trait association increases the estimated heritability of its own annotations, thus giving itself an advantage in the fine-mapping model. This risk will be greatest when few loci contribute a majority of the trait heritability or when few SNPs per annotation strongly influence the estimates 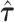. For complex traits with large numbers of causal variants distributed across the genome, the estimates of heritability enrichment will be less sensitive to the association statistics within any specific locus, reducing the risk of bias. We demonstrate that the estimates from the GWAS of BMI in our real data application do not depend strongly on the summary statistics in any specific locus. However, if external estimates of heritability enrichment are available, these could also be used in AnnoRE to eliminate this source of potential bias entirely.

The AnnoRE method shows superior performance to naïve GWAS ranking, LASSO penalized regression and GenoWAP (14) in simulation studies across a range of LD structures and annotation scenarios. PAINTOR (4) showed superior performance when the five annotation categories provided for its model included at least three containing the causal variant. Because PAINTOR is only capable of considering a few annotation categories simultaneously, it is at a disadvantage for causal variants outside of those annotations and must be conduct several times to build a small set of strongly enriched annotations, requiring substantial computation time. AnnoRE ranked the true causal variant in the top 10% by ordering of the fine-mapping statistics, on average across the 1000 simulation replicates, even in simulation scenarios where LASSO and PAINTOR were unable to obtain estimates at all.

In our analysis of loci identified by a large GWAS meta-analysis of BMI, we found six loci where the top variant identified by random effects fine-mapping exceeded a locus-wide significance threshold. In all of these cases, the top SNP selected during fine-mapping was in very high LD with the most significant GWAS signal, with 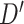statistic greater than 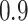in all six loci. The 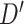statistic accounts for differences in allele frequency, whereas the standard correlation statistic 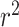cannot attain its maximum value of one between SNP genotypes with different allele frequencies. In these six loci, the SNPs selected as most significant by AnnoRE fine-mapping are located in annotation categories with greater plausible functional relevance than the top SNPs selected by GWAS. In 25 additional loci, the AnnoRE test statistic at the top SNP is more than twice the magnitude at the third-ranked SNP. These loci are promising candidates for further exploration, as the fine-mapping analysis distinguishes one or two SNPs with stronger evidence of causality relative to others in the locus.

Our proposed method addresses the problem of collinearity due to high LD among sets of SNPs within a locus by defining random effect variances that depend on SNP annotation. The resultant estimator is similar to a penalized method such as ridge regression (15), with the smoothing penalty differing by SNP annotation. Thus, even if two SNPs are in perfect LD, the one with stronger annotation evidence will receive a larger effect estimate. For this reason, it is desirable to include many annotation categories in the estimation of variance components to ensure that differences in annotation allow the estimator to prioritize the genetic variants within LD blocks. However, the variance component estimates may be unstable when there is high correlation among the annotation marks themselves, as may be the case for tissue-specific annotation of the same signal across similar tissues. Further work is required to identify optimal sets of annotation categories for use in fine-mapping studies.

One limitation of AnnoRE is the fact that the distribution of the test statistics is conditional upon the variance components estimated by LD score regression and does not account for the uncertainty in these estimates. Large GWAS sample sizes reduce the variability of these estimates, making this simplifying assumption more acceptable. This method is designed to identify causal SNPs in common allele frequency ranges and may be less powerful in the case of rare variants, as is also the case for other existing fine-mapping methods.

Another limitation is that the incorporation of LD structure assumes that the study sample is drawn from a population with homogeneous ancestry. If a study contains multiple ancestry groups, AnnoRE could be performed in each group separately, with different ancestry-specific LD matrices, then combined through meta-analysis. Extension of this method to admixed populations, where patterns of LD cannot be summarized in a single static matrix, remains a potential direction for future work.

As a linear function of the GWAS summary statistics, AnnoRE is computationally efficient relative to other fine-mapping approaches that incorporate genomic annotations. Its most demanding procedure is the inversion of a matrix with dimension equal to the number of nominally significant SNPs in a given fine-mapping locus, usually at most a few hundred. In contrast, the best-performing comparator method, PAINTOR, uses an iterative expectation–maximization algorithm to jointly estimate the effect enrichment per annotation category and the individual SNP effects, which can be computationally prohibitive with many loci or many annotation categories.

In summary, we have proposed a framework to prioritize variants with known biological relevance that are associated with the phenotype independently of other variants in the locus. Integrating local LD structure and functional annotation, this proposed approach can either be applied to individual-level data or to GWAS summary statistics data. The resulting SNPs are promising candidates for the functional follow-up studies that are necessary to translate findings from genetic epidemiology towards increased understanding of human biology and clinical applications.

Materials and Methods

Random effects model

We estimate the AnnoRE model from GWAS summary statistics and local LD in a population-matched reference panel as an approximation of the genetic correlation structure. Suppose that a given fine-mapping locus contains M SNPs, with allelic effect estimates 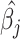, standard errors 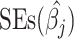and allele frequencies 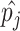available from a study with 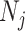unrelated subjects contributing to analysis at SNP j. Additionally, suppose that the LD matrix 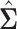of pairwise Pearson correlations between all M SNPs is available from a reference panel of the same ancestral population as the GWAS sample.

These summary statistics are calculated in terms of the SNP genotypes 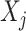, the length-N column vectors of the matrix X, with a simple linear regression model at each SNP j:

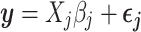By assumption, the subjects are unrelated, so .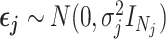

If all genotypes were independent, i.e. if there was no tagging due to LD and the GWAS effect estimates at a given SNP represented only the causal effect of that SNP and independent residual error, the asymptotic distributions of the least squares estimators 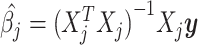would give rise to the GWAS test statistics:

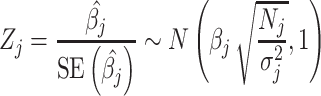Following the CAVIAR model (16), define the non-centrality parameter 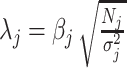, which is related to the statistical power to detect a significant association between genotype j and the trait of interest.

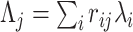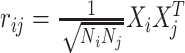Allowing for genotype correlation within the locus yields the LD-induced non-centrality parameter where is the LD (Pearson correlation) between SNPs i and j.

Then, the multivariate distribution of the vector Z of Wald statistics across the locus is

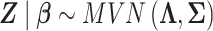where 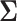is the LD matrix, which may be approximated from a reference panel. Define 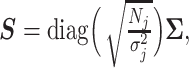so that 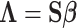, yielding a multiple regression model

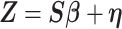where .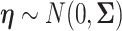

We define the effect distribution of each SNP by annotation-specific functional variance components. For the implementation presented here, we estimate annotation-specific functional variance components by the LD score regression method of partitioning heritability (17), but other estimators may be substituted. This method uses GWAS summary statistics to estimate enrichment of association signals across a large number of functional categories. Annotation describing C functional categories is summarized in a matrix 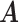of binary indicators 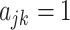if SNP j is included in functional category k and zero otherwise.

We define a random effect for each standardized SNP by a Gaussian distribution with mean zero and variance 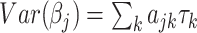where the sum is taken over all annotation categories containing SNP j. The annotation-specific variance component 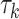represents the coefficient of expected per-SNP heritability in category k. These variance components may be estimated by the LD score regression method for partitioning heritability, with negative estimates truncated at zero. The factor 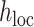is defined as the expected heritability per SNP within each fine-mapping locus, relative to the genome-wide heritability per SNP. Inclusion of this factor adjusts the random effect variances for the strength of the observed genetic association within the locus.

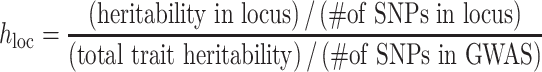The vector of SNP effects 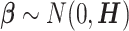is modeled as random effects with independent Gaussian distributions, where 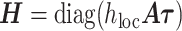. The best linear unbiased predictor (BLUP) is obtained by maximizing the joint distribution of Y and 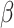conditional on H and the residual variance 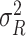. This estimator is given by

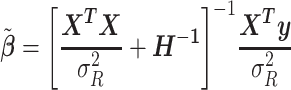and its variance–covariance matrix, conditionally on the matrix H that specifies random effect variances as a function of the annotation coefficients tau

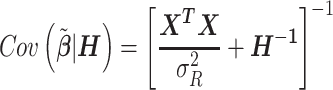This is a well-known result in the theory of random effects models and coincides with the estimator implemented in SAS PROC MIXED (18).

Note that, under this model, genotype vector standardization encodes the assumption that less frequent variants will have larger effect sizes, as we would expect due to negative selection.

From the diagonal elements of this covariance matrix, we may construct a Wald test statistic, conditional on 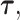for the effect of each SNP in the locus: 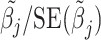. The BLUP for this regression is

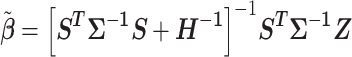Variances of the individual SNP effect estimates are given by the diagonal elements of the matrix 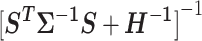, which may be used to define Wald statistics for the estimators. These test statistics 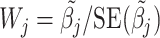follow an asymptotic standard normal distribution under the null hypothesis 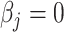, conditional on the random effect variances 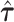(19).

This model formulation accommodates heterogeneous SNP effects in such a way that variants in biologically active genomic elements are more likely to be causal and avoids assumptions on the number of true causal variants per locus. The random effects distribution here refers to the distribution across all SNPs in the genome, rather than individuals in the population, so that two subjects with the same genetic profile are assumed to have the same predisposition to the phenotype of interest.

Simulation study

We simulated GWAS results in a 1 megabase region from 28 000 000 to 29 000 000 base pairs on chromosome 21. This locus was selected as subjectively representative of GWAS results, which are commonly defined as a 500 kilobase region around a a lead SNP with smallest p-value. The simulation locus contains the genes ADAMTS1 and ADAMTS5, and numerous GWAS variants associated with diverse traits including Alzheimer’s disease (20), bone mineral density (21) and blood protein levels (22). Four recombination hotspots divide the region into distinct LD blocks, and a majority of the GWAS variants in the locus are located in blocks that contain regulatory elements but no gene coding regions. Using HAPGEN2 (23), we constructed synthetic samples of size N = 10 000 from haplotypes of the 379 individuals of European ancestry included in the Phase 1 of the 1000 Genomes Project (24). This reference panel contained M = 2159 SNPs in the locus of interest.

Annotation-specific variance components 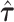were estimated from the GIANT Consortium GWAS of BMI (5) for 52 regulatory annotation categories from the ENCODE project (25), to define the random effect distributions for all SNPs in the locus. Negative estimates 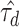were truncated at zero, effectively removing 28 annotation categories from the model, representing no evidence of enriched heritability in these categories. To assess the sensitivity of fine-mapping within the locus to the repeated use of the same data set in estimating the variances of the SNP effects and predicting the joint effects conditional on those variances, we repeated the LD score regression procedure with a subset of the GWAS results excluding all variants in the fine-mapping locus.

We defined 20 simulation scenarios, each with one causal SNP chosen to explore a range of genetic architectures. For each causal SNP scenario, we created 1000 phenotype replicates, fixing SNP-specific heritability at 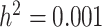and calculating the genetic effect size to account for different allele frequencies between the scenarios.

Causal SNPs were selected in scenarios of both high and low total LD with other variants in the region. High and low LD SNPs were defined as those with total LD 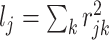in the top or bottom quartile for the locus. To assess the contribution of annotation across methods, we considered scenarios with one causal SNP near the deciles of the distribution of random effects variances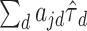, where the sum is taken over all annotation categories in the model. Table 1 presents the characteristics of the selected causal variants.

In these simulated samples, we compared the ranking by AnnoRE with (1) a naïve GWAS approach based solely on marginal association P-values, (2) LASSO regression using subject level genotype and phenotype data, (3) PAINTOR (4) with the top five most highly enriched annotation categories [conserved regions, extended H4K5me1 peaks, extended H3K9ac peaks, H3K9ac peaks and extended Super Enhancers (26)] and (4) GenoWAP, using prior probabilities of causality pre-computed from NHGRI GWAS catalog training data (27,28).

Real-data analysis

BMI is an important risk factor for numerous diseases, such as Type 2 diabetes, hypertension and heart disease. It is highly heritable, with twin study estimates of the genetic contributions accounting for 49–90% of trait variance (29). The Genetic Investigation of ANthropometric Traits (GIANT) consortium is an international collaboration studying the genetic basis of anthropometric phenotypes including BMI. We performed AnnoRE analysis fine-mapping with summary statistics from the GIANT GWAS meta-analysis of BMI in 322 154 subjects of European ancestry (5). This study reported 77 loci with the strongest signals separated by at least 500 kb and reaching genome-wide significance (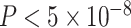) in the European ancestry sample. Summary statistics for all reported SNPs within a 500 kb radius of the most significantly associated markers were extracted for fine-mapping, with LD information from the 1000 Genomes Project Phase 1 European ancestry reference panel.

We assessed the impact of repeated use of GWAS summary statistics for estimation SNP effect variances obtained from LD score regression and fine-mapping analysis. For each locus attaining genome-wide significance, we performed LD score regression with a subset of GWAS summary statistics excluding the SNPs at that locus, then calculated the Pearson correlation between the random effect variance estimates per SNP from LD scores including and excluding that locus. The mean correlation across the 77 genome-wide significant loci was 0.9994, and the minimum value was 0.9773 at the rs13021737 locus. From this sensitivity analysis, it is concluded that the results within each locus would not be affected by this repeated use of the GWAS statistics, supporting the use of genome-wide heritability partition estimates for all fine-mapping.

Within each locus, we defined a locus-specific significance threshold by Bonferroni correction based on the number of SNPs included in the fine-mapping analysis, to adjust for multiple testing of the BLUP Wald statistics.

Funding

National Institutes of Health (R01DK089256 to V.F., L.A.C. and C.-T.L., R01DK122503 to L.A.C. and C.-T.L., R01AR072199 to C.T.L.).