Actomyosin dynamics modulate microtubule deformation and growth during T-cell activation

Abstract

Activation of T-cells leads to the formation of immune synapses (ISs) with antigen-presenting cells. This requires T-cell polarization and coordination between the actomyosin and microtubule cytoskeletons. The interactions between these two cytoskeletal components during T-cell activation are not well understood. Here, we elucidate the interactions between microtubules and actin at the IS with high-resolution fluorescence microscopy. We show that microtubule growth dynamics in the peripheral actin-rich region is distinct from that in the central actin-free region. We further demonstrate that these differences arise from differential involvement of Arp2/3- and formin-nucleated actin structures. Formin inhibition results in a moderate decrease in microtubule growth rates, which is amplified in the presence of integrin engagement. In contrast, Arp2/3 inhibition leads to an increase in microtubule growth rates. We find that microtubule filaments are more deformed and exhibit greater shape fluctuations in the periphery of the IS than at the center. Using small molecule inhibitors, we show that actin dynamics and actomyosin contractility play key roles in defining microtubule deformations and shape fluctuations. Our results indicate a mechanical coupling between the actomyosin and microtubule systems during T-cell activation, whereby different actin structures influence microtubule dynamics in distinct ways.

INTRODUCTION

T-cells play a major role in the adaptive immune system. Upon stimulation of the T-cell receptors (TCRs) by engagement of antigens presented by antigen-presenting cells (APCs), T-cells spread over the APCs. The junction formed between the two cells is known as the immune synapse (IS). This process is characterized by polarization of T-cells and dramatic remodeling of the actin cytoskeleton with accumulation of filamentous actin at the periphery of the cell–cell contact (Martín-Cófreces et al., 2008; Morgan et al., 2013; Ritter et al., 2017). T-cell polarization is accompanied by reorganization of the microtubule cytoskeleton and reorientation of the centrosome towards the contact zone, a process that occurs within minutes of TCR stimulation. Centrosome reorientation requires coordination of the actin and microtubule cytoskeletons and is important both for the release of cytolytic granules in cytotoxic T-cells and for the secretion of cytokines in T-helper cells (Le Floc’h et al., 2013; Choudhuri et al., 2014; Ritter et al., 2017).

The formation of the T-cell immune synapse (IS) has been studied extensively using antigen-coated flat substrates to mimic the APC, facilitating the use of fluorescence microscopy. A remarkable feature of the immune synapse is the bull’s-eye pattern produced by the spatial reorganization of several signaling and associated proteins. This pattern manifests as three concentric rings of membrane receptors with their underlying cytoskeletal and signaling proteins (Alarcón et al., 2011). At the center lies the central supramolecular activation cluster (cSMAC), which is depleted in actin and concentrates the TCR and signaling co-receptors such as CD28. The next region is the peripheral SMAC (pSMAC) with integrins and sarcomeric acto-myosin structures. Most peripheral is the distal SMAC (dSMAC), which contains large ectodomain proteins such as CD45 and is characterized by a lamellipodial actin meshwork. These different regions appear to be differentially regulated by actin regulatory proteins. The Arp2/3 complex, which nucleates branched actin networks, is largely localized in the dSMAC, while the pSMAC is rich in formin-mediated actin linear structures that associate with myosin bipolar filaments to generate a contractile ring (Yi et al., 2012; Fritzsche et al., 2017; Hong et al., 2017). Arp2/3 and formin have been found to compete for the available pool of actin monomers in several cell types (Lomakin et al., 2015; Rotty and Bear, 2015). In Jurkat T-cells, inhibition of Arp2/3 leads to an increase of formin-mediated actin arcs or cables, while inhibition of formins abolishes actin arcs and enhances the Arp2/3-generated lamellipodial actin meshwork (Murugesan et al., 2016). Thus, these actin-nucleating proteins mutually regulate each other.

While the role of actin in the IS has been studied extensively, the role of microtubule dynamics during IS formation has been less examined. The microtubule end-binding protein 1 (EB1) has been shown to interact directly with the CD3 immunotyrosine-associated motifs. EB1 knockdown alters TCR dynamics and prevents propagation of the TCR activation signal to linker for activation of T-cells (LAT; Martín-Cófreces et al., 2012). Ezrin and discs-large 1(Dlg1) control MT positioning at the immune synapse and regulate the movement of SLP-76 (Lasserre et al., 2010). Dynein motors colocalize with TCRs, and TCR microclusters move along MTs toward the center of the immune synapse in a dynein-dependent manner (Hashimoto-Tane et al., 2011), providing an additional mechanism to reorganize TCR microclusters along with the better known drag forces produced by actin flows (Varma et al., 2006; Beemiller et al., 2012; Murugesan et al., 2016). Hui and Upadhyaya (2017) found that the traction force generated by T-cells is regulated by dynamic MTs through suppression of RhoA activation, myosin bipolar filament assembly, and actin retrograde flow. MTs are also involved in centrosome reorientation toward the activation surface, which occurs within the first 5 min of cell activation and is known to require the coordination of myosin and dynein motors (Martín-Cófreces et al., 2008; Liu et al., 2013; Yi et al., 2013). Interestingly, formin is also required for centrosome polarization in T-cells (Gomez et al., 2007; Andrés-Delgado et al., 2013), and IQGAP1 (a protein that binds directly to actin and MT associated proteins) plays a major role in centrosome repositioning in B cells after signaling activation (Wang et al., 2017). These findings point to an interesting connection between actin and microtubules and highlight the importance of cross-talk between these two cytoskeletal systems.

Despite extensive research on signaling events at the IS, how different cytoskeletal components coordinate to establish the immune synapse upon T-cell activation is not well understood. Moreover, the impact of actin dynamics and myosin contractility on MT stability and shape remains unclear. In this work, we studied the interactions between microtubules and actin at the IS with high-resolution fluorescence microscopy of Jurkat T-cells. In particular, we investigated the role of Arp2/3 and formin-generated actin structures in MT growth and dynamics using chemical perturbations. We characterized MT dynamics (growth rates and filament shapes) in the different regions of the immune synapse. We found that MT growth is slower in the distal actin-rich region and MT tip trajectories were less radial and more likely to change direction. Formin inhibition led to a moderate decrease in MT growth rates. Integrin engagement did not have any visible effects on MT growth dynamics. However, formin inhibition upon integrin engagement caused a strong reduction in MT growth rates, while Arp2/3 inhibition resulted in an increase in MT tip speeds. We also found that microtubule filaments are more highly deformed and more dynamic in the peripheral actomyosin-rich region of the cell–substrate contact than in the central actin-depleted zone. Inhibition of formin and Arp2/3, as well as ROCK kinase, resulted in decreased deformations and shape fluctuations of MT filaments, suggesting that actin dynamics and actomyosin contractility play an important role in defining MT shapes. Our results indicate an important mechanical coupling between the actomyosin and microtubule systems, where different actin structures influence microtubule growth and shape dynamics in distinct ways.

RESULTS

Spatial distribution of cytoskeletal components in the immune synapse

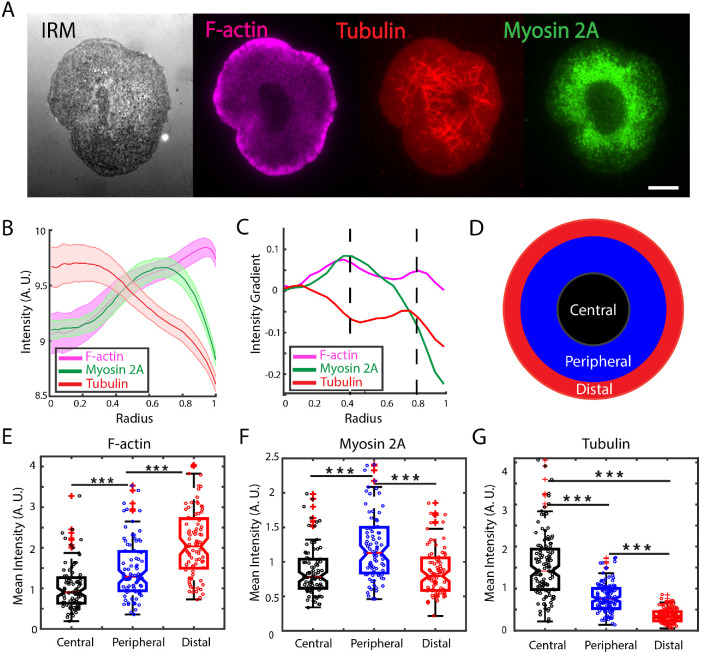
The T-cell immune synapse characteristically forms three concentric regions (cSMAC, pSMAC, and dSMAC), which are distinguished by the accumulation of distinct sets of membrane proteins (TCR, co-receptors, integrins, and phosphatases; Huppa and Davis, 2003; Hammer et al., 2018). Actin dynamics and architecture also exhibit spatial variations across these different regions of the IS. Actin retrograde flow decreases from the periphery toward the center of the cell—fastest at the lamellipodium (distal region), slower across the lamella (peripheral region), and there is no directed motion in the central region (Babich et al., 2012).

To characterize the distribution of cytoskeletal components at the contact zone, we allowed Jurkat T-cells to spread on anti-CD3–coated coverslips and fixed them 10 min after activation. The cells were stained for f-actin (with rhodamine phalloidin), nonmuscle myosin 2A (with an antibody for the heavy chain of NM2A), and tubulin (with an antibody for beta-tubulin) and imaged using total internal reflection fluorescence (TIRF) microscopy as shown in Figure 1A. For all cells, an interference reflection microscopy (IRM) image was taken to identify the contact zone of the cell and detect the cell contour and centroid. Fifty lines were drawn radially across the cell and the intensity profile for each line was obtained for each of the cytoskeletal proteins (for more details see Material and Methods). Averaging the intensity profiles reveals patterns of intensity variation across the contact zone for all three cytoskeletal elements (Figure 1B). We next calculated the gradient of the intensity for each protein as shown in Figure 1C. Based on the inflection points found, we characterized the IS by three regions as shown in Figure 1D (also marked by the dashed lines in Figure 1C). These regions are roughly consistent with earlier studies (Babich et al., 2012). The central region (radius < 0.4) is largely depleted in actin and myosin, the peripheral region (0.4 < radius < 0.8) is enriched in myosin and formin-nucleated actin filaments (Murugesan et al., 2016), and the distal region (radius > 0.8) is enriched in branched actin networks. The mean intensities were obtained by dividing the sum of pixel intensities within a region by the area of that region for F-actin (Figure 1E), myosin (Figure 1F), and tubulin (Figure 1G). For these three cytoskeletal proteins, the amount of protein represented by the fluorescence intensity was significantly different across these regions.

FIGURE 1:

Cytoskeletal proteins are differentially distributed across the immune synapse. (A) IRM and representative TIRF images of WT Jurkat T-cells fixed 10 min after being activated on anti-CD3–coated glass coverslips. Cells were stained for filamentous actin (magenta), tubulin (red), and nonmuscle myosin 2A (green). Scale bar is 5 μm. (B) Average intensity profiles of cytoskeletal proteins derived from N = 90 cells. Shaded region represents the standard error. (C) Intensity gradient for each of the proteins shown in B. The dashed lines mark inflection points that demarcate regions with different characteristics of these cytoskeletal proteins. (D) Schematic showing the three regions: the central region largely depleted in actin and myosin, the peripheral region enriched in myosin- and formin-nucleated actin filaments, and the distal region enriched in Arp2/3-nucleated actin meshworks. (E) Mean intensity of F-actin at the contact zone measured in fixed cells for the regions defined in C: central (black), peripheral (blue), and distal (red) regions. (F) Nonmuscle myosin 2A mean intensity measured in fixed cells for the regions defined in C. (G) Mean intensity of tubulin measured in fixed cells for the same regions. Significance of differences was tested using the Kruskal–Wallis test (***p < 0.001). N = 90 cells for all panels.

Microtubule growth rates are differentially modulated across different regions and by Arp2/3 and formin-mediated actin architectures

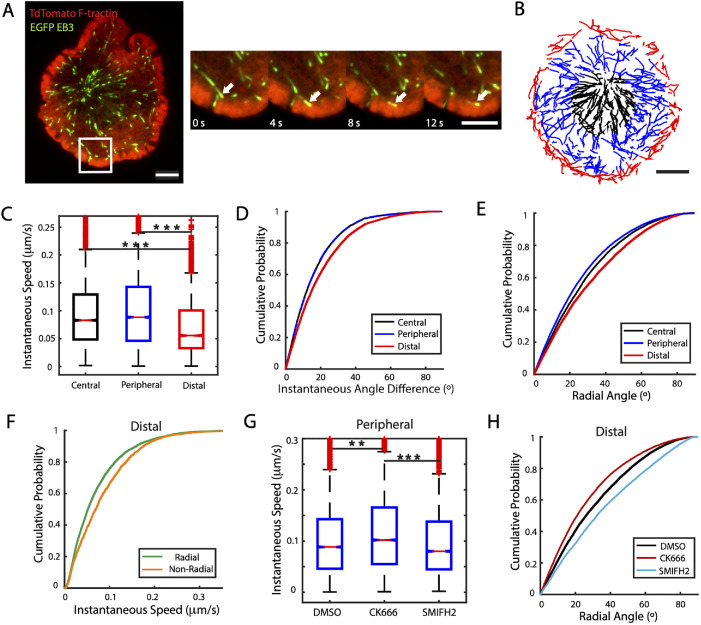
Having defined specific regions at the IS, we next investigated whether microtubule growth rates are affected by the presence of different actin structures. We transiently transfected Jurkat T-cells with EGFP-EB3, a microtubule-plus-end binding protein, and tdTomato-F-tractin, which labels polymerized actin filaments (Brehm et al., 2004) to correlate MT growth and actin dynamics. The cells were activated on anti-CD3–coated coverslips and imaged with TIRF microscopy 5 min after being activated (Figure 2A and Supplemental Movie 1). Cells were imaged for 5 min at 2-s intervals. We observed that the EB3 comets slowed down as they reached the actin-dense lamellipodial region (white arrow in the zoomed region of Figure 2A). To quantify the growth rates of MTs we tracked EB3 comets (see Supplemental Movie 2) using the MATLAB-based tracking routine U-track (Jaqaman et al., 2008). To correlate EB3 dynamics with different IS regions, the interframe displacements were assigned to specific regions based on the coordinates of the final position at the second frame (Figure 2B).

FIGURE 2:

Microtubule growth rates are differentially modulated across different regions and by Arp2/3- and formin-mediated actin architectures. (A) Representative two-color image of a Jurkat cell transiently transfected with tdTomato-F-tractin (red) and EGFP-EB3 (green). Scale bar is 5 μm. Higher magnification views at different time points of the region enclosed by the white square in the left-hand image are shown on the right. The white arrow points to a microtubule tip, whose movement is drastically reduced once it reaches the actin-rich distal region. Scale bar is 3 μm. (B) EB3 tracks from a different cell than the one shown in A, color coded for the region of the synapse where they occurred: central (black), peripheral (blue), and distal (red). (C) Comparison of instantaneous speeds of EB3 across the three regions considered. N = 11 cells. (D) Cumulative distribution of instantaneous angle differences of EB3 tracks as a measure of directionality persistence, defined as the angle difference between two consecutive displacements, in different regions. (E) Cumulative distribution of radial angles calculated from interframe displacements of EB3 tracks for the different regions. (F) Cumulative distribution of instantaneous EB3 speeds in the distal region classified as radial (radial angle ≤ 45°) or nonradial (radial angle > 45°). (G) Box plot of EB3 instantaneous speeds measured in the peripheral region cells treated with the actin nucleation inhibitor CK666 (Arp2/3) or SMIFH2 (formin) compared with DMSO control. N = 11 cells for DMSO, N = 11 for CK666 and N = 16 for SMIFH2. (H) Cumulative distribution of radial angles in the distal region for cells treated with CK666 or SMIFH2 compared with DMSO. Significance of differences was tested using the Kruskal–Wallis test (***p < 0.001, **p < 0.01, *p < 0.05). Number of data points: C, Cen 12930, Per 23962, Dist 9579. D and E, Cen 11563, Per 21964, Dist 8206. F, Rad 6047, Non Rad 2159. G, DMSO 23962, CK666 19909, SMIFH2 21128. H, DMSO 8206, CK666 17316, SMIFH2 9186.

Movie S1.

Download video file ^{(3.4MB, mov)}

Time lapse movie of an activated Jurkat T cell double transfected with tdTomato-F-tractin (red) and EGFP-EB3 (green). Scale bar is 5 μm.

Movie S2.

Download video file ^{(7MB, mov)}

Time lapse showing EB3 trajectories (labeled in red) detected using the MATLAB routine Utrack.

We defined the instantaneous speed as the displacement between two consecutive frames divided by the time elapsed (2 s). We found that the instantaneous speeds of EB3 are similar in the central and peripheral regions (Figure 2C), but MT tips slow down as they reach the distal region, with significantly lower instantaneous speed than in the central and peripheral regions (median speed: 0.053 μm/s in distal region, 0.082 μm/s in central region, 0.086 μm/s in peripheral region). From the time-lapse movies (Supplemental Movie 1), we additionally observed qualitative changes in the direction of the EB3 tracks in the distal region. To quantify the directionality persistence of growing MT tips, we defined the “instantaneous angle difference” (Supplemental Figure 1A) as the difference in angle between two consecutive displacements (as defined from an arbitrary line of reference). Figure 2D shows the cumulative probability of the instantaneous angle difference measured in each region. We found the distribution of angles in the central and peripheral regions to be nearly identical. However, the distal region showed significantly larger angles, indicating that EB3 was more likely to change direction in the extreme periphery of the cell, leading to more curved tracks.

To examine how MT growth is correlated with local actin dynamics in each region, we quantified the degree to which MT growth is radial. We defined the radial angle as the difference between the angle formed during an interframe displacement and the angle formed by a line connecting the centroid of the cell with the initial position of that displacement (Supplementary Figure 1B). Small angles correspond to largely radial interframe displacements while larger angles correspond to nonradial displacements. Figure 2E shows the cumulative probability distribution of the radial angle in the three regions. The distal region shows the largest angles, indicating that MT growth is least radial in this region. We next investigated whether EB3 instantaneous speed depends on its direction. We classified the instantaneous speed as “radial” whenever its radial angle was less than or equal to 45° and “nonradial” for radial angles larger than 45°. We found that the nonradial speeds were significantly higher than the radial speeds in the distal region (Figure 2F), while the radial and nonradial speeds were similar in the central and peripheral regions (Supplemental Figure 1, C and D). The lower EB3 radial speeds, as well as the higher directionality change, observed in the distal region may be attributed to the opposing force produced by the centripetal actin retrograde flow, which is highest in this region (Babich et al., 2012).

We next investigated how perturbing actin network dynamics affected EB3 instantaneous speeds (see Supplemental Movie 3). We used the small-molecule inhibitors CK666 (5-min incubation at 50 μM) for Arp2/3 inhibition and SMIFH2 (5-min incubation at 25 μM) for formin inhibition. The cumulative distribution of EB3 instantaneous speeds (for all regions) shows no significant differences for these different treatments (Supplemental Figure 1E). We then examined the effect of these inhibitors in the previously defined regions. We found that, in the peripheral region, inhibition of Arp2/3 caused a moderate, but significant, increase of speeds and that formin inhibition led to a modest decrease in EB3 speeds (Figure 2G) but did not significantly change the speeds in the central or in the actin-dense distal region (Supplemental Figure 1, F and G). Interestingly, the inhibition of these actin nucleators had opposing effects on MT growth orientation: formin inhibition led to a significant increase in radial angles, while Arp2/3 inhibition led to decreased radial angles (Figure 2H). This effect was strongest in the distal region but qualitatively similar to the effect in the peripheral region, while the effect on the central region was negligible (Supplemental Figure 1, H and I). Finally, we found that neither formin nor Arp2/3 inhibition had an effect on the distribution of instantaneous angle differences for any of the regions (Supplemental Figure 1, J–L).

Movie S3.

Download video file ^{(10MB, mov)}

Activated Jurkat T cells double transfected with tdTomato-Ftractin (red) and EGFP-EB3 (green) treated with DMSO (left), CK666 50 μM (center) and SMIFH2 25 μM (right). Scale bar is 5 μm.

Integrin engagement enhances the effect of formin inhibition on MT growth

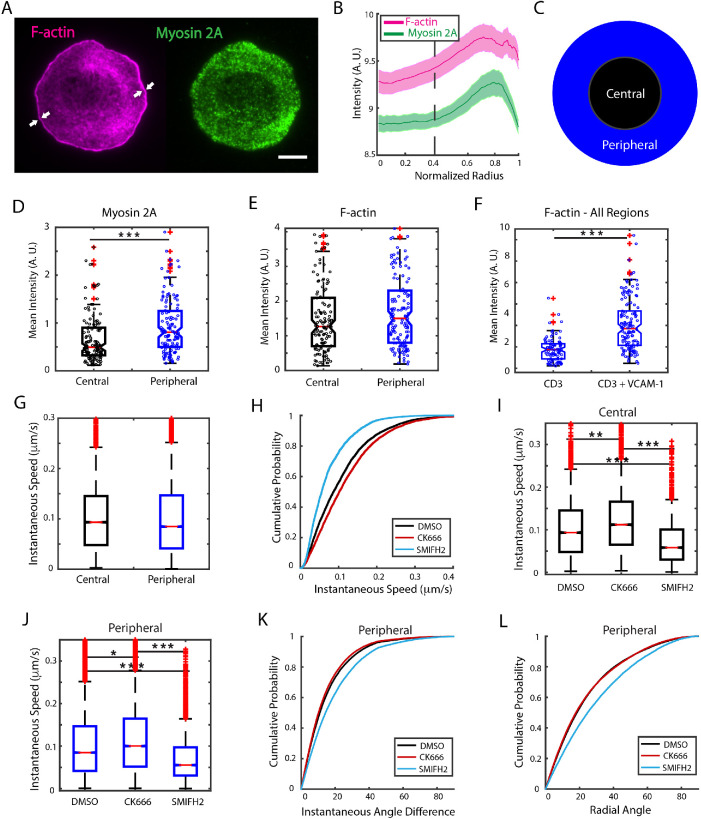
Motivated by the observation that nonradial EB3 instantaneous speeds were higher than the radial speeds in the distal region, where actin retrograde flow speed is highest, we next examined whether actin retrograde flow modulates MT growth. Integrin engagement, by linking the integrin VLA-4 with VCAM-1, is known to reduce the speed of actin retrograde flow in Jurkat T-cells (Lam Hui et al., 2014; Jankowska et al., 2018) without disrupting the actin cytoskeleton. We thus studied the effect of integrin engagement and subsequent slowdown of actin flow on EB3 dynamics and how this was influenced by different actin architectures. We activated Jurkat T-cells on coverslips coated with anti-CD3 and VCAM-1 and fixed the cells 10 min after activation (Figure 3A). Analysis of the IRM images showed that integrin coating did not affect the spread area of the cells as compared with cells on anti-CD3–only substrate (Supplemental Figure 2A). We characterized the actin and myosin distributions by immunostaining and found that the dense lamellipodial region had shrunk significantly, as indicated by the white arrows in Figure 3A. The average actin and myosin intensity profiles along the normalized cell radius (Figure 3B) show a loss of the previously defined actin-rich distal region. We therefore classified the contact zone into two regions: the central region, defined as before (radius < 0.4, dashed line in Figure 3B), and the peripheral region (radius > 0.4, which combines the previously defined peripheral and distal regions, Figure 3C). Myosin is significantly more abundant in the peripheral region (Figure 3D), while F-actin accumulation is not significantly different between the two regions (Figure 3E), in contrast to the case for anti-CD3 coating alone, which showed significant differences for all three proteins in the different regions. Interestingly, the presence of VCAM-1 on the activating substrate induced a significant increase in the amount of F-actin over the entire contact zone (Figure 3F).

FIGURE 3:

Integrin engagement enhances the effect of formin inhibition on MT growth. (A) Representative TIRF images of WT Jurkat cells fixed 10 min after activation on a glass substrate coated with anti-CD3 and VCAM-1 and immunostained for filamentous actin (magenta) and nonmuscle myosin 2A (green). White arrows point to the narrow lamellipodial region typically displayed by cells under these conditions. Scale bar is 5 μm. (B) Average intensity profile derived from N = 134 cells for cytoskeletal proteins similar to that shown in A. The dashed line denotes the empirical choice of boundary between the central and peripheral regions and the shaded region represents the standard error. (C) Schematic showing two regions: the central region depleted in myosin and the peripheral region enriched in myosin and actin. (D) Mean fluorescence intensity of myosin at the contact zone for central (black) and peripheral (blue) regions. (E) Comparison of the F-actin mean intensity for central (black) and peripheral (blue) regions. (F) Comparison of the level of F-actin at the contact zone of the whole cell as measured by rhodamine–phalloidin mean intensity for cells activated with anti-CD3 alone and activated with anti-CD3 + VCAM-1. N = 90 cells for CD3 and N = 134 cells for CD3+VCAM-1. (G) Comparison of EB3 instantaneous speeds measured at central and peripheral regions in cells activated on CD3+VCAM-1 substrates. (H) Cumulative distribution of instantaneous speeds of EB3 across all regions for cells treated with CK666 or SMIFH2 compared with DMSO control. N = 12 cells for DMSO, N = 16 cells for CK666, and N = 20 cells for SMIFH2. (I) EB3 instantaneous speeds in the central and (J) peripheral region for cells treated with actin nucleation inhibitors CK666 and SMIFH2. (K) Cumulative distribution of instantaneous angle differences and (L) radial angles in the peripheral region for cells treated with CK666 and SMIFH2 as compared with DMSO (carrier control). Significance of differences was tested using the Kruskal–Wallis test (***p < 0.001, **p < 0.01, *p < 0.05). For H, SMIFH2 is significantly different from DMSO (p < 0.0001) and CK666 is different from DMSO (p < 0.01). For K and L, SMIFH2 is significantly different from DMSO and CK666 (p < 0.001).

We next imaged live cells activated on coverslips coated with anti-CD3 and VCAM-1 and tracked EB3 tips as described before. We found that the instantaneous speed distribution of EB3 across all regions was similar for CD3 and CD3+VCAM-1 cases (Supplemental Figure 2B). Furthermore, comparison of instantaneous speeds between the central and peripheral regions also showed no significant difference (Figure 3G). We next investigated the influence of actin nucleation inhibitors on MT growth rates for cells activated on anti-CD3 + VCAM-1–coated coverslips. Figure 3H shows the cumulative probability distribution of EB3 instantaneous speeds across all regions for cells treated with CK666 or SMIFH2 compared with DMSO control. Cells treated with CK666 displayed slightly but significantly higher speeds than those treated with DMSO, while SMIFH2 caused a strong reduction in the speeds as compared with controls (Supplemental Movie 4). The effect described was also observed for both central and peripheral regions, as shown in Figures 3I and 3J, respectively. We had observed an 8% reduction in the median speed for SMIFH2-treated cells in the peripheral region for cells on anti-CD3 coated substrates (DMSO median speed 0.086 μm/s, SMIFH2 median speed 0.079 μm/s; see summary statistics in Supplemental Table 1). Upon integrin engagement with VCAM, we found that SMIFH2 treatment resulted in a significantly larger reduction (34%—DMSO median speed 0.084 μm/s, SMIFH2 median speed 0.055 μm/s; see summary statistics in Supplemental Table 1). Our results thus suggest that integrin engagement enhances the effect of formin inhibition on MT tip dynamics. We also found that formin inhibition led to larger changes in direction and less radial trajectories, as measured by instantaneous angle differences and radial angle distributions respectively for both peripheral (Figure 3, K and L) and central regions (Supplemental Figure 2, C and D). Taken together, these results suggest that integrin engagement, upon addition of VCAM-1 to the activating surface, leads to significantly larger changes in speed and directionality with Arp2/3 or formin inhibition, in contrast to cells engaged with anti-CD3 alone.

Movie S4.

Download video file ^{(10.5MB, mov)}

Jurkat T cells double transfected with tdTomato-F-tractin (red) and EGFP-EB3 (green) activated on glass slide coated with anti-CD3 and VCAM-1 treated with DMSO (left) and SMIFH2 25 μM (right). Scale bar is 5 μm.

Actomyosin dynamics regulates MT filament dynamics

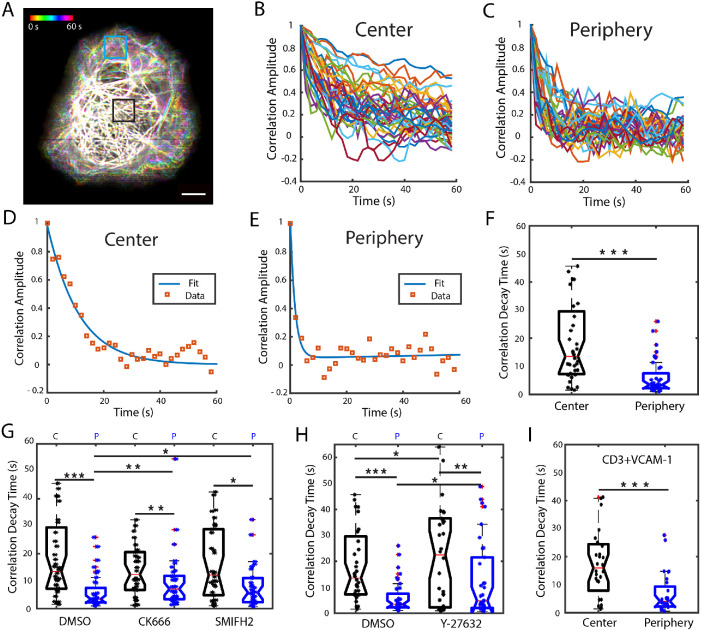
Previous work suggests that fluctuations induced by actomyosin forces on MT tip growth lead to overall fluctuations and shape changes of MT filaments (Brangwynne et al., 2007, 2008). These forces may in turn be dependent on the local architecture of the actin networks induced by different nucleating proteins. To better understand the interaction between the different actin networks and microtubules, we visualized microtubule filament shape and dynamics and examined the effect of perturbing specific actin network architectures. Jurkat T-cells were transiently transfected with EGFP-EMTB (ensconsin microtubule-binding domain), a microtubule-associated protein that does not modulate MT dynamics (Bulinski et al., 2001). Cells were activated on anti-CD3 coated coverslips and imaged 5 min after activation at 2-s intervals using instant structured illumination microscopy (iSIM; York et al., 2013) to obtain highly resolved images of MT filaments in living cells (Supplemental Figure 3 and Supplemental Movie 5). We observed that MTs at the periphery of the cell (equivalent to the peripheral plus distal regions defined in Figure 1C) were more dynamic than those at the center (equivalent to the central region in Figure 1C). Figure 4A shows the maximum-intensity projection of a 30-frame time-lapse movie of MTs color coded for time. In the central region of the cell, the filaments appear white due to the superposition of the filaments at different time points, while the filaments at the periphery appear at different positions and colors, indicating their higher dynamics.

FIGURE 4:

Actomyosin dynamics regulate MT filament dynamics. (A) Maximum intensity projection of a 30-frame time-lapse movie, taken at 2-s intervals, color coded for time. Scale bar is 5 μm. (B) Representative plots of the correlation amplitude decay of the fluorescence intensity per pixel row over time for the region enclosed in black in panel A corresponding to the central region and (C) for the peripheral region (blue square in A). (D) Ensemble average correlation values calculated from a sample ROI in a cell (red squares) from the center and (E) from the periphery. Solid lines show double-exponential fits to the data. (F) Comparison of correlation decay times, obtained from the fits, for the central and peripheral regions. N = 18 cells, 2 ROIs per cell for each region. (G) Comparison of the distribution of correlation decay times for central and peripheral regions in cells treated with CK666 and SMIFH2 with DMSO (vehicle control). N = 18 for DMSO, N = 19 for CK666, and N = 15 for SMIFH2. (H) Box plots of correlation decay times comparing cells treated with the Rho-kinase inhibitor Y-27632 and with DMSO (vehicle control). N = 18 for DMSO, N = 17 cells for Y-27632. C: central region; P: peripheral region. (I) Comparison of correlation decay times in the center and periphery for cells in CD3+VCAM-1 substrates. N = 14 cells. Significance of differences was tested using the Kruskal–Wallis test (***p < 0.001, **p < 0.01, *p < 0.05).

Movie S5.

Download video file ^{(2.2MB, mov)}

Instant structured illumination microscopy (iSIM) timelapse of an activated Jurkat T cell transfected with EMTB-EGFP. Scale bar is 5 μm.

To quantify MT filament dynamics, we chose two ROIs of 3 × 3 μm at the center and at the periphery of each cell (as indicated by the boxes in Figure 4A). We computed the temporal autocorrelation of the intensity profile along each row of pixels in the boxed region. Supplemental Figure 4A shows a sample pixel row selected and the corresponding intensity profile for that line in consecutive frames. The temporal autocorrelation is computed by comparing the intensity signal of the first frame with itself and with every consecutive frame (Supplemental Figure 4B). The typical correlation amplitude curves obtained for a central ROI are shown in Figure 4B and those for a peripheral ROI in Figure 4C. For all curves obtained, the correlation amplitude decays over time, reaching roughly zero (no correlation) at later times. We noticed that the correlation amplitude decays faster at the periphery, which is consistent with the visually observed higher dynamics of the filaments in this region. To characterize the correlation decay, we calculated the average correlation curve for an ROI and fit the curve to a double exponential of the form C(t) = αe^–bt + ce^–dt. We constrained the value of the fit parameter α to a range close to 1, since it corresponds to the correlation at time zero (short times). The parameter b corresponds to the correlation decay rate at short times, and the parameters c and d correspond to the correlation amplitude and decay rate at later times. Our data were well fit by this relation, as shown by sample fits in Figure 4, D and E, corresponding to individual ROIs and as evaluated by the distribution of fit residuals, which is normal, narrow, and centered on zero (Supplemental Figure 4C), in contrast to the right-skewed residuals obtained from a single exponential fit (Supplemental Figure 4D). We found that the correlation decay time (as evaluated for two ROIs per region of each cell) was significantly longer in the central region of the cell than in the peripheral region, as shown by the distribution of values of the parameter b^–1 in Figure 4F. The distribution of values for fit parameters c and d, which correspond to the correlation amplitude and decay rate at later times, was very similar for central and peripheral regions and across all the conditions explored (Supplemental Figure 4, E and F). We next investigated the effect of the actin nucleation inhibitors CK666 (Arp2/3 inhibition) and SMIFH2 (formin inhibition) on MT filament dynamics as shown in Figure 4G. We found that perturbing either actin network induces a significant increase in the correlation decay time (implying decreased dynamics) for ROIs at the periphery of the cell, with little effect on MT dynamics in the central region. This indicates that both Arp2/3 and formin mediated networks are important to sustain MT filament dynamics. Notably, while the correlation decay time at the periphery was increased for CK666- and SMIFH2-treated cells, in both cases the correlation decay time at the periphery was still shorter than that at the center, indicating that MT filaments are more dynamic at the cell periphery even after inhibition of either actin nucleator. To explore the role of myosin in MT filament dynamics, we used the ROCK kinase inhibitor Y27632, which prevents myosin phosphorylation and associated cell contractility. Cells treated with Y27632 also displayed less dynamic microtubules, particularly at the periphery, as measured by the significant increase in correlation decay time (Figure 4H), indicating that myosin contractility modulates MT dynamics. Finally, we asked whether actin retrograde flow influences MT filament dynamics. We applied the same analysis to time-lapse movies of activated cells on anti-CD3+VCAM-1 coated coverslips and found that the correlation decay time was significantly lower for MTs at the periphery than for MTs in the central region (Figure 4I). Interestingly, the MT dynamics in both regions, as assayed by correlation time, was very similar to that observed in the corresponding regions of cells on anti-CD3 coated coverslips. Thus integrin engagement does not appear to alter MT filament dynamics.

MT filament deformation is modulated by actin dynamics and myosin contractility

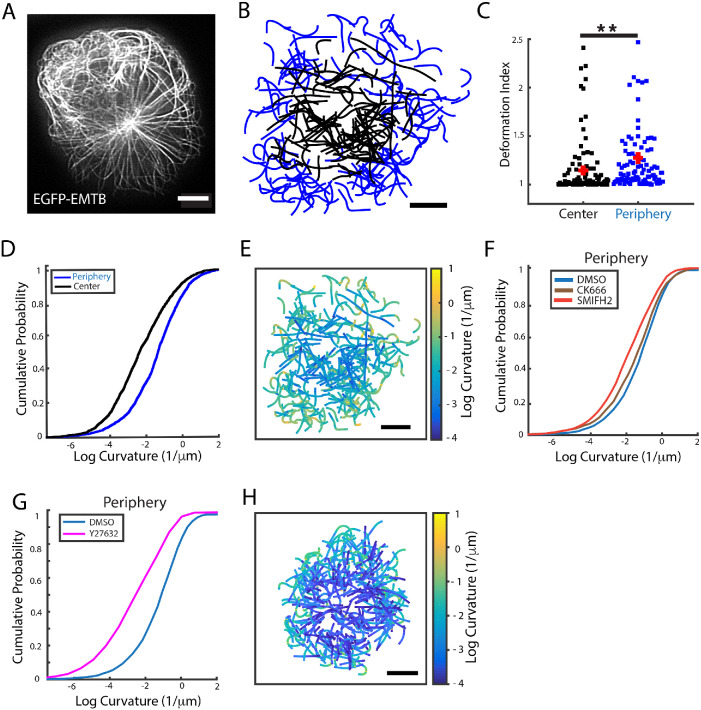
From the movies taken for the filament dynamics analysis (Supplemental Movie 5), it was evident that the filaments in the peripheral region exhibited more deformed shapes than those at the center. We therefore investigated the spatial distribution of microtubule filament deformations at different regions and under different perturbations to elucidate the role of actomyosin dynamics on filament shapes. For this analysis we used time-lapse iSIM images, as shown in Figure 5A. For each cell, we manually traced individual MT filaments from three image frames taken 30 s apart, to ensure that MT shapes were uncorrelated (see Materials and Methods). Each filament traced was assigned to the central or peripheral region of the cell based on the coordinates of its center of mass. Figure 5B shows a collection of filaments traced from different superimposed cells with the peripheral filaments shown in blue and the central ones shown in black. The filaments traced in both regions have a similar distribution of lengths (Supplemental Figure 5A). To quantify MT deformations, we first calculated the deformation index, which is the ratio of the filament contour length to the end-to-end distance. We found that filaments at the periphery have a significantly higher deformation index than those at the center as shown in Figure 5C. To examine in more detail the filament shapes in both regions, we quantified the local curvature (see Materials and Methods) over segments ∼0.4 μm in length. The distribution of local curvatures is shown in Figure 5D and confirms our qualitative observations that MTs at the periphery display greater deformation than those at the center. A visual representation highlighting this difference is shown in Figure 5E, where the filaments in Figure 5B have been plotted with each segment color coded for the local curvature value. Greater deformations (yellow) are observed mostly at the periphery, while lower curvature values (blue) are observed at the center.

FIGURE 5:

MT filament deformation is modulated by actin dynamics and myosin contractility. (A) Representative iSIM image of a Jurkat T-cell transiently transfected with EGFP-EMTB. (B) Segmented MT filament traces from different cells color coded for the region to which they belong: black for center and blue for periphery. (C) Comparison of the deformation index (ratio of contour length to end-to-end distance) for filaments in the center and periphery. (D) Cumulative probability plots of local curvature distributions of central and peripheral filaments. (E) Plot of the filaments shown in panel B color coded for the local curvature. (F) Cumulative probability plots of local curvature distribution of peripheral filaments in cells treated with CK666 (brown) and SMIFH2 (red) as compared with DMSO control (blue). N = 18 for DMSO, N = 19 for CK666, and N = 15 for SMIFH2. (G) Cumulative distribution plot comparing the local curvature of peripheral filaments in cells treated with Rho-kinase inhibitor Y27632 (magenta) with DMSO control cells (blue). N = 17 for Y27632. (H) Plot of filaments traced in cells treated with Y27632 color coded for the local curvature. All scale bars are 5 μm. Significance of differences was tested using the Kruskal–Wallis test (**p < 0.01). For D, curvatures in the periphery and center are significantly different (p < 0.0001). For F, the difference between curvatures in DMSO and CK666 is significant (p < 0.05) and the difference between DMSO and SMIFH2 is significant (p < 0.001). For G, the curvatures in DMSO and Y-27632 are significantly different (p < 0.0001). All scale bars are 5 μm.

We then investigated the effect of CK666 and SMIFH2 treatments on filament shapes. We found that both inhibitors reduced the local curvature for filaments at the periphery, with SMIFH2 showing a stronger effect (Figure 5F), indicating that both types of actin networks play a role in modulating MT filament shape. Central microtubule shapes were largely unaffected by these inhibitions, though CK666 caused a small but significant increase in deformation (Supplemental Figure 5B).

Given the known role of myosin in the generation and maintenance of formin-mediated cable-like actin filaments (Murugesan et al., 2016), we next investigated the role of myosin in filament deformation. We inhibited myosin activity using the ROCK kinase inhibitor Y27632 which prevents myosin phosphorylation. We found that inhibition of myosin activity significantly reduced the local curvature distribution of filaments at the periphery (Figure 5G) and to a lesser extent at the center (Supplemental Figure 5C) as compared with DMSO control. Figure 5H shows the collection of filaments traced in cells treated with Y27632, color coded for curvature. The filaments exhibit lower local curvature (as seen from the greater fraction of blue in the plot) than those in Figure 5E. An alternate approach to quantify filament deformations is to calculate the average of the cosines of the tangent angles along the filament segments, which decays with segment distance and is analogous to a correlation (Supplemental Figure 5D and Materials and Methods). For deformed microtubules, the average cosines decay faster than for more straight filaments. We found that this quantity decayed faster for filaments at the periphery than for filaments at the center of the cell (Supplemental Figure 5E) and that inhibitors of actin nucleators (Supplemental Figure 5, F and G) and inhibitors of ROCK kinase (Supplemental Figure 5, H and I) reduced the distance-dependent decay in correlations, particularly for filaments at the periphery—indicating more straight microtubules as a result of actin nucleator inhibition. The length scale over which the correlations decay (a measure of the deformation of the microtubules) is summarized in Supplemental Table 2.

Post-translational modification of microtubules can influence their physical properties and dynamics. TCR activation leads to detyrosination of the α-tubulin subunit, which requires the formin INF2. Detyrosinated microtubules are more stable and facilitate centrosome repositioning (Andrés-Delgado et al., 2012). TCR signaling also induces transient deacetylation of MTs at early times (2–5 min) and enhanced acetylation at later times (Serrador et al., 2004). Tubulin acetylation is performed by acetyltransferase TAT1 in the lumen of filaments. Acetylated microtubules are mechanically more resistant due to their higher plasticity (Xu et al., 2017). We found that the ratio of acetylated tubulin to total tubulin was not significantly different (Supplemental Figure 6, A and B) across the different regions of the cell (central, peripheral, and distal). Thus microtubule acetylation is uniform across the cell and unlikely to be responsible for the differences in curvatures between peripheral and central microtubules. Our results suggest that filament deformation is highly influenced by actomyosin contractility.

DISCUSSION

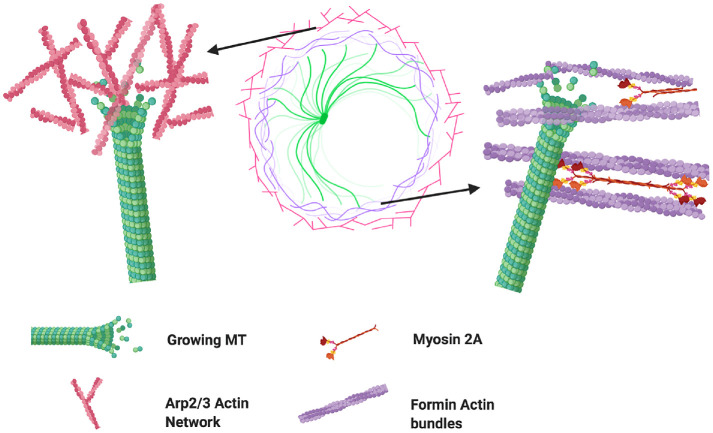
Here, we used high-resolution fluorescence microscopy and quantitative image analysis to characterize the growth and shape deformation dynamics of microtubules across the different regions of the immune synapse and under chemical perturbation of specific actin architecture networks. The spatially segregated cytoskeletal architecture displayed by activated T-cells makes them an ideal model system to explore the influence of different actin networks on microtubule dynamics. We found that microtubule growth rates were reduced in the actin-dense distal region. Additionally, MTs growing in this region showed lower directional persistence and were less radial. The actin cortex of Jurkat cells is about 200 nm thick (Clausen et al., 2017) and TCR activation induces actin polymerization and enrichment in the contact zone, particularly in the lamellipodial (distal) region, further increasing the actin density. It is thus likely that the slowdown of MT tips in this region is the result of crowding by the actin meshwork, leading to spatial and temporal constraints on MT filament growth and possibly reducing the diffusivity of tubulin dimers and other proteins involved in MT filament polymerization. Furthermore, the fact that neither formin nor Arp2/3 inhibition caused changes in MT tip speeds in this region suggests that crowding or confinement is the dominant factor, independent of the prevalence of either actin architecture. Interestingly, MT growth rates were differentially modulated by the actin nucleators formin and Arp2/3 in the peripheral region of the cell. Arp2/3 inhibition caused a moderate increase in MT growth rates while formin inhibition led to slower rates. There exists a balance between the actin networks produced by Arp2/3 and formin, whereby inhibition of one of these nucleators leads to enrichment in actin structures formed by the other. Thus, formin inhibition leads to an increase in branched actin meshworks produced by Arp2/3 (Murugesan et al., 2016) resulting in a more intricate network that may enhance the physical barrier to microtubule growth (Figure 6). The FH2 and DAD domains of formins allow them to interact directly with microtubules and MT-associated proteins (Breitsprecher and Goode, 2013). Indeed, MT growth can be guided along actin bundles (López et al., 2014) and formins can nucleate actin from growing microtubule ends (Henty-Ridilla et al., 2016). It is thus possible that the observed increase in MT growth rates after Arp2/3 inhibition is not only caused by the removal of a physical barrier but also due to a synergistic interaction between MTs and formin-nucleated actin cables.

FIGURE 6:

Microtubule growth encounters different barriers through distinct actin architectures. The lamellipodium of T-cells is characterized by a dense network of actin filaments nucleated mostly by Arp2/3 (left side). These branched networks may constitute a physical barrier for MT growth. Formins contain domains that allow them to bind directly to microtubules, allowing them to guide their growth as reported [37], but also potentially allowing them to transmit forces generated by myosin motors associated with formin nucleated filaments (see right). Created with BioRender.com.

We found that integrin engagement changed the morphology of the actin cytoskeleton in activated T-cells. Jurkat cells activated on VCAM-1 coated substrates displayed a much thinner lamellipodial region, a more homogeneous actin distribution across the contact zone, and higher F-actin density than cells activated on anti-CD3-only substrates. The inhibition of formin upon integrin engagement with VCAM caused a greater reduction in MT tip speeds (higher than the effect of formin inhibition in cells on anti-CD3-only substrates), fewer radial EB3 trajectories, and decreased persistence in directionality. This effect was evident across both regions (central and peripheral) of the cell. We note that formin inhibition on anti-CD3+VCAM-1 substrates did not completely disrupt the actin arcs in all cells tested, suggesting that the overall reduction in tip speeds that we observed might be an underestimate.

On the other hand, Arp2/3 inhibition of integrin-engaged cells led to faster-growing tips, again showing an opposite effect to formin inhibition. It is intriguing that integrin engagement enhances the effect of formin inhibition in MT growth dynamics. The higher actin density may play a role; however, because the increased actin density did not affect overall growth dynamics in untreated cells, this suggests that the balance between the two actin architectures and their spatiotemporal organization may be the most relevant factor in determining MT growth speeds. A number of proteins have been shown to mediate the synergy between actin polymerization and MT tip dynamics (Seetharaman and Etienne-Manneville, 2020) modulating focal adhesion assembly and disassembly and contact guidance in migrating cells (Stehbens and Wittmann, 2012; Tabdanov et al., 2018). These include adenomatous polyposis coli (APC), EB1, CLIP-170, and IQGAP, all of which have also been shown to play important roles in early T-cell signaling (Martín‐Cófreces et al., 2012; Agüera-González et al., 2017; Lim et al., 2018). The differential distribution of these adaptors between the two actin networks may contribute to our observed differences in MT growth and fluctuations.

We also found that microtubule filaments in the peripheral actomyosin-rich region were more dynamic and displayed more deformed shapes than those located in the central region. MT density is highest in the central region, which is likely due to the docking of the centrosome near the center of the contact zone. Microtubules in this region appeared more bundled and their proximity to the centrosome is likely to restrict their movement. However, we qualitatively observed similar spatial effects on the dynamics and deformations of peripheral and central filaments even in cells for which the centrosome had not polarized (the centrosome was not near the contact zone—”unpublished data”). This suggests that the differences in MT dynamics cannot be attributed only to centrosome positioning. Furthermore, the inhibition of actin nucleators and myosin affected the dynamics and shapes of peripheral microtubules but not central ones. Thus, the deformation of MTs and their shape fluctuations are modulated by the actomyosin cytoskeleton. The inhibition of Arp2/3 and formin had similar effects on MT dynamics, resulting in less dynamic microtubules at the periphery, as indicated by the increase in correlation times. Interestingly, integrin engagement and the associated reduction in actin retrograde flow did not have an impact on the correlation times of fluctuating MTs. This suggests that a different dynamic property of the actin cytoskeleton modulates MT fluctuations. Actomyosin contractility is likely to be responsible, since inhibition of myosin activity led to significantly less deformed microtubules and a reduction in their fluctuations in the peripheral region and to a lesser extent in the central region. Actin architecture plays an important role in the transmission of forces produced by associated myosin motors, and the spatial arrangement and physical properties of the actin network are key to tension regulation (Chugh et al., 2017; Koenderink and Paluch, 2018). Thus, the reduction in MT fluctuations caused by inhibition of formin or Arp2/3 is likely associated with an overall disruption of actin network connectivity and a resultant decrease in myosin-generated tension and contractility.

The high curvature displayed by peripheral MTs was decreased upon inhibition of Arp2/3 and formin. The latter had a stronger effect, suggesting that the deformation is associated with the contractility produced by actomyosin arcs. This hypothesis is supported by the even stronger reduction in curvatures produced by the inhibition of myosin activation. The dense actin network surrounding microtubules allows them to withstand compressive forces (Brangwynne et al., 2006). Our results indicate that there is a mechanical balance between the microtubule and actin cytoskeleta and that different actin architectures modulate microtubule dynamics in distinct ways.

MATERIALS AND METHODS

Substrate preparation

Coverslips attached to eight-well Labtek chambers were incubated in poly-l-lysine (PLL) at 0.01% W/V (Sigma Aldrich, St. Louis, MO) for 10 min. PLL was aspirated and the slide was left to dry for 1 h at 37°C. T-cell activating antibody coating was performed by incubating the slides in a 10 μg/ml solution of anti-CD3 antibody (Hit-3a, eBiosciences, San Diego, CA) for 2 h at 37°C or overnight at 4°C. For VCAM-1 coating, the coverslip was first washed with 1X PBS to remove excess antibody and then incubated with VCAM-1 solution (Sino Biological, Chesterbrook, PA) at 2 μg/ml concentration for 2 h at 37°C. Excess anti-CD3 or VCAM-1 was removed by washing with L-15 imaging media right before the experiment.

Cell culture and transient transfections

E6-1 Jurkat cells were cultured in RPMI 1640 supplemented with 10% fetal bovine serum (FBS) and 1% Penn-Strep antibiotics. For transient transfections we used the Neon (ThermoFisher Sci.) electroporation system 2 days before the experiment. The protocol was as follows: 2 × 10⁵ cells were resuspended in 10 μl of R-buffer with 0.5–2 μg of the plasmid. The cells were exposed to three pulses of amplitude 1325 V and duration 10 ms in the electroporator. Cells were then transferred to 500 μl of RPMI 1640 supplemented with 10% FBS and kept in the incubator at 37°C. EMTB–3 × EGFP was a gift from William Bement (Addgene plasmid # 26741). The tdTomato-F-tractin plasmid was a gift from John A. Hammer and the EGFP-EB3 plasmid was a gift from Robert Fisher.

Immunofluorescence

Cells were activated on anti-CD3–coated coverslips, fixed after 10 min of activation using 4% paraformaldehyde for 10 min at room temperature, and then washed thoroughly with 1X PBS. Cells were then permeabilized for 5–10 min with a 0.15% Triton X solution and blocked with BSA (0.02 g/ml) and glycine (0.3 M) in 1× PBS solution for 1 h at room temperature. For incubation periods and concentrations of primary and secondary antibodies, we followed the manufacturers recommendations. For F-actin labeling, we used Acti-stain 670 phalloidin from Cytoskeleton (Denver CO). For labeling Myosin 2A, we used the heavy-chain nonmuscle myosin 2A antibody from Biolegend (San Diego, CA). For microtubule labeling, we used beta-tubulin antibody from Invitrogen (Carlsbad, CA).

Microscopy

TIRF imaging was performed on an inverted microscope (Nikon Ti2000 PFS, Melville, NY) equipped with a 1.49 numerical aperture 100× lens for TIRF imaging and a Prime BSI camera (Photometrics, Tucson, AZ). Imaging protocols were implemented using the software Elements from Nikon and images were cropped using Fiji before further analysis using MATLAB scripts. Imaging of EGFP–EMTB–expressing Jurkat cells was performed using a homebuilt iSIM (York et al., 2013), with a 1.42 numerical aperture 60× lens (Olympus), a 488-nm laser for excitation with 200-ms exposure times, and a PCO Edge scientific CMOS camera. Cells were added to the activating substrate and allowed to spread for 5 min and time-lapse images were taken at 2-s intervals. Images obtained were postprocessed with background subtraction and deconvolution. The final lateral resolution for deconvolved images was between 140 and 150 nm. The Richardson–Lucy algorithm was used for deconvolution and run for 10 iterations. The point spread function (PSF) used was simulated by a Gaussian function but based on parameters obtained from measurement—that is, the full width at half maximum (FWHM) of the PSF used is the same as the FWHM measured.

Inhibitor experiments

For all inhibitor experiments, cells were incubated for 5 min in an inhibitor and L-15 solution at 37°C and at the indicated concentration. After the incubation period, cells were added to the imaging chamber, which had L-15 and the inhibitor at the same concentration. Cells were allowed to spread for 5 min before imaging. CK666 (Calbiochem, Millipore-Sigma, Darmstadt, Germany) was used at 50 μM, SMIFH2 (Sigma-Aldrich, Millipore-Sigma, Darmstadt, Germany) was used at 25 μM, and Y27632 (Calbiochem, Millipore-Sigma, Darmstadt, Germany) was used at 100 μM. For vehicle control experiments, cells were incubated for 5 min in a DMSO and L-15 solution at 0.01% concentration and the same concentration was kept in the imaging chamber.

Data analysis

For image analysis, all cell images were cropped using Fiji and then postprocessed and analyzed using MATLAB (Mathworks, Natick MA) custom scripts. For cytoskeletal profile analysis, the IRM image was used to generate a mask and detect the cell contour. Based on this mask, the fluorescence intensity in the other channels (corresponding to F-actin, tubulin, and myosin) was quantified. To determine the intensity per region, we assigned each pixel to a region based on its location relative to the centroid and the closest point along the cell contour (Supplemental Figure 7A). The distance between each pixel within the mask and the cell centroid was computed. Then we computed the distance between the cell centroid and a point along the cell contour that was closest to the pixel in question to obtain an effective radius. The pixel is then assigned to a region based on the ratio of the pixel-to-centroid distance and the effective radius. The mean intensity was obtained by dividing the sum of pixel intensities within a region by the total number of pixels in that region. To generate the intensity profiles (pixel intensities as a function of spatial coordinate), 50 lines were drawn radially across the cell and the intensity profile for each line was obtained (see dashed lines in Supplemental Figure 7A and corresponding intensity profiles in Supplemental Figure 7B). A representative intensity profile for each cell was obtained by averaging the 50 profiles. The individual cell profile was later used to compute the population intensity profile as shown in Figures 1B and 3B. To quantify the F-actin levels in Figure 3F, the fluorescence intensity of the pixels within the cell contour was summed and divided by the total number of pixels in the cell to obtain a mean intensity.

EB3 speeds were analyzed using the MATLAB-based routine U-track (Jaqaman et al., 2008), which links particles between consecutive frames using a global combinatorial optimization strategy to identify the most likely set of trajectories in a movie. We used a search radius range of 3–8 pixels (0.18–0.48 μm) for frame-to-frame linking. The instantaneous speeds obtained from interframe displacements were assigned to a region based on the coordinates of the particle position using the criteria described above for pixel assignment to a region (Supplemental Figure 7A).

For microtubule shape analysis from each cell, we manually traced individual MT filaments from three image frames taken 30 s apart. We selected this time interval because microtubules displaying short-wavelength bends (∼6 μm) become uncorrelated within 10 s (Brangwynne et al., 2007), and we found that the time correlation of the microtubule intensity pattern dropped to zero (became uncorrelated) within 10–30 s (Figure 4F). Filaments were traced by hand using the segmented line tool in Fiji. The spline fit option was selected to obtain a smoothed filament and the coordinates of the filament were imported to MATLAB. To assign a filament to a region, the image from which the filaments were traced was segmented and processed to obtain the cell contour and centroid. The distance between the centroid of the cell and the filament centroid, D_C-MT, was calculated (Supplemental Figure 7C). Then the distance between the centroid of the cell and the closest point to the MT centroid along the cell edge, D_C-CE, was calculated. If the ratio D_C-MT/ D_C-CE is equal to or less than 0.4, the filament is assigned to the central region; otherwise it is assigned to the peripheral region (Supplemental Figure 7D). To calculate the curvature of microtubules, the filament coordinates were coarse-grained to an average spacing of seven pixels using a custom algorithm to reduce the contributions from errors during data collection procedures (Bicek et al., 2007). Filament curvature was calculated using the equation 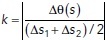, where κ is the local curvature, Δθ(s) is the angle between two adjacent filament segments, and Δs₁, Δs₂ are the segment contour lengths (Bicek et al., 2009).

For the cosine correlation analysis, the angle between a line tangent to the first segment of the filament and a line tangent to each consecutive segment was calculated for each filament. Next, the average cosines of all angles N segments apart were calculated (Supplemental Figure 5D), where N = 0, 1, 2…. The average cosines were fitted to the function (Rivetti et al., 1996):

where θ_N is the angle between tangents to the segments, x_N is the distance between the segments, and l_p is the persistence length. For straight filaments, the angle difference between segments is close to zero, resulting in a slowly decreasing curve of the average cosine with segment distance, with values close to 1 (Supplemental Figure 5D). For highly deformed microtubules, the average cosines decrease faster with segment distance. Only segments less than 3 μm apart were considered due to the high noise observed in the data for larger distances.

Statistical analysis

For statistical comparisons, the Kruskal–Wallis test was used to assess the difference between data distributions corresponding to different conditions. For tip speed distributions, the test was implemented over 500–1000 values randomly extracted from the original dataset using the Kruskal–Wallis test in MATLAB and Bonferroni correction was applied for multiple pairwise comparisons. The size of the data subsets chosen were such that they overlapped qualitatively with the original distributions.

Data and code availability

All data and analysis scripts will be made available upon request.

Abbreviations used:

EB1/3

end-binding protein 1/3

IS

immune synapse

MT

microtubule

ROCK

Rho-associated protein kinase

SMAC

supramolecular activation complex

SMIFH2

small molecule inhibitor of formin homology 2 domains

TCR

T-cell receptor

VCAM

vascular cell adhesion molecule.