Skip to main content
PMC home page
Molecular Biology of the Cell logoLink to Molecular Biology of the Cell
. 2021 Aug 19;32(18):1624–1633. doi: 10.1091/mbc.E20-08-0502

Valproic acid-induced changes of 4D nuclear morphology in astrocyte cells

Alexandr A Kalinin a,b,c, Xinhai Hou a,b,d, Alex S Ade b, Gordon-Victor Fon b, Walter Meixner b, Gerald A Higgins b, Jonathan Z Sexton e,f,g, Xiang Wan a, Ivo D Dinov b,c,h, Matthew J O’Meara b, Brian D Athey b,h,i,*
Editor: Jennifer Lippincott-Schwartzj
PMCID: PMC8684733  PMID: 33909457

Abstract

Histone deacetylase inhibitors, such as valproic acid (VPA), have important clinical therapeutic and cellular reprogramming applications. They induce chromatin reorganization that is associated with altered cellular morphology. However, there is a lack of comprehensive characterization of VPA-induced changes of nuclear size and shape. Here, we quantify 3D nuclear morphology of primary human astrocyte cells treated with VPA over time (hence, 4D). We compared volumetric and surface-based representations and identified seven features that jointly discriminate between normal and treated cells with 85% accuracy on day 7. From day 3, treated nuclei were more elongated and flattened and then continued to morphologically diverge from controls over time, becoming larger and more irregular. On day 7, most of the size and shape descriptors demonstrated significant differences between treated and untreated cells, including a 24% increase in volume and 6% reduction in extent (shape regularity) for treated nuclei. Overall, we show that 4D morphometry can capture how chromatin reorganization modulates the size and shape of the nucleus over time. These nuclear structural alterations may serve as a biomarker for histone (de-)acetylation events and provide insights into mechanisms of astrocytes-to-neurons reprogramming.

INTRODUCTION

Multicellular organisms regulate their cell type and state by selectively exposing portions of their genome for transcription through the spatial and temporal organization of chromatin—dubbed the 4D nucleome (Chen et al., 2015; Cremer et al., 2015; Higgins et al., 2015, 2017a). Structurally, 3D conformation of the genome involves 1.65 turns of DNA wrapped onto a histone octamer, creating nucleosomes linked as beads-on-a-string, which are then wrapped into chromatin fibers and higher-order loops, organizing into topologically associating domains (TADs). Finally, TADs collect into a diploid set of chromosome territories (Higgins et al., 2015, 2017a). Histones accommodate a range of posttranslational modifications, which are controlled by epigenetic proteins that ultimately regulate the transcriptional state of the cell and mediate mechanical protection of genome by chromatin rigidity (Yang and Seto, 2007; Stephens et al., 2019). Chemicals that target these proteins can be used to modulate chromatin states and the concomitant cell and nuclear morphology changes observed in human diseases (Marchion et al., 2005; Stephens et al., 2019). For example, valproic acid (VPA) is a histone deacetylase inhibitor used clinically to treat epilepsy, bipolar disorders, social phobias, and neuropathic pain (Göttlicher et al., 2001; Ganai et al., 2015). Mechanistically, VPA shifts the balance toward greater histone acetylation, DNA exposure, and chromatin decondensation; activating transcriptional programs that regulate cellular processes related to cancer (Göttlicher et al., 2001; Eckschlager et al., 2017), traumatic brain injury (Higgins et al., 2017b), ischemia (Pickell et al., 2020), as well as cellular reprogramming (Huangfu et al., 2008). An outstanding question, however, is to characterize how mesoscale nuclear structures such as TADs mediate the effects of VPA and other epigenetic modulators on cellular morphology. However, limitations of the emerging technologies that can capture these nanoscale (histone marks) and mesoscale (nuclear architecture) phenomena, including optical microscopy, ATACseq, and single cell RNAseq, make it difficult to simultaneously monitor macroscale (cellular morphology) cellular state.

Recent mechanobiology studies revealed the role of chromatin as a key regulator of nuclear shape (Uhler and Shivashankar, 2018; Stephens et al., 2019). VPA induces increased euchromatin, which results in weakened nuclear rigidity and morphology changes that occur independently of lamins (Stephens et al., 2017, 2018). Here we aim to leverage this effect for assessing how the epigenetic and mesoscale nuclear state can be characterized by the overall nuclear size and shape to probe VPA’s mechanism of action. Importantly, we show that nuclear morphology can be captured in standard microscopy experiments to relate epigenetic regulators with phenotypic measurements of a cell and its organelles.

Toward this goal, we present a detailed characterization of the size and shape of astrocyte nuclei in the context of VPA treatment. We chose astrocytes because they developmentally originate from the same precursor cells as neurons and proliferate in response to brain damage (Amamoto and Arlotta, 2014), but also can be directly reprogrammed into functional neurons by sets of small molecules—often including VPA—in the lab (Cheng et al., 2015; Zhang et al., 2015; Gao et al., 2017; Qin et al., 2017). These studies, however, are not always congruent. Some reports demonstrated that VPA inhibits (Yin et al., 2019) or increases reprogramming efficiency (Cheng et al., 2015; Zhang et al., 2015), while others suggest that VPA alone induces astrocyte reprogramming into neurons (Cheng et al., 2015). The treatment protocols, concentrations, and combinations of small molecules differ between these studies, indicating that underlying mechanisms driving the transdifferentiation process are not well understood.

Existing studies that have focused on astrocyte-to-neuron reprogramming observed changes only in cellular morphology, presented in a qualitative manner. Others quantified VPA-induced nuclear morphological changes in non-astrocyte cells, reporting time-, dose-, and cell type–dependent responses. Their results ranged from no observed changes in nuclear geometry (Ganai et al., 2015); to altered nuclear shape (“blebbing”), but not size (Stephens et al., 2017, 2018); to increased nuclear size, either after 1 h (Felisbino et al., 2011, 2014, 2016) or not earlier than after 7–14 d (Kortenhorst et al., 2009) of VPA treatment. Moreover, these approaches were limited to basic 2D surrogates of geometric measures, often reporting few features such as cross-sectional nuclear area or maximum diameter. Given that chromatin is highly organized in 3D, the effects of chromatin remodeling on nuclear morphology can only be fully described in three dimensions. Supporting this assumption, there is growing practical evidence that 3D representations allow for more accurate characterizations of cell and nuclear morphology, compared with 2D measures (Choi and Choi, 2007; Meyer et al., 2009; Depeursinge et al., 2014; Kalinin et al., 2018a; Medyukhina et al., 2020). Because single-perspective 2D images depend on an object’s orientation and the focal plane, they provide only a sample of its real geometry. For example, cell nuclei that differ in volume and shape can appear similarly small and circular in optically sectioned images, thus leading to lower discriminative performance of a classifier (Choi and Choi, 2007). In addition, a more comprehensive morphological representation of nuclei in 3D is more informative than resolution as a determining factor for classification performance (Meyer et al., 2009). Our previous results also indicated that 3D size and shape descriptors outperform their 2D counterparts in the task of nuclear morphological classification (Kalinin et al., 2018a).

Even when the 3D object is perfectly aligned with the focal plane, only the first two out of three principal axes (major, median, minor) can be measured from its 2D representation. This reduces the accuracy of shape measures computed from size features. For example, sphericity assesses the compactness of the object, that is, it measures how closely the global object shape resembles that of a perfect sphere, which is computed via volume and surface area or approximated using principal axes (Xu et al., 2009). The extent (ratio of the object volume to the bounding box volume) and solidity (ratio of the object volume to the convex hull volume) of nuclear surfaces are useful measures of the amount and size of concavities (or protrusions) in an object boundary. Other shape descriptors rely on the notion of the curvature that describes how bent the curve is around each point of a surface. They allow for measuring local shape alterations that are observed on the nuclear surface and would not be exhibited in 2D projection. Mean curvature is an extrinsic measure of 3D shape that provides a balanced measure between shape morphology and curvature magnitude (Tsagkrasoulis et al., 2017; Kalinin et al., 2018b). Gaussian curvature is an intrinsic (scale-invariant) measure of curvature that depends only on distances that are measured on the surface. Shape index and curvedness are morphometric descriptors that can capture local shape features, independently or in relation to the size of an object (Koenderink and Van Doorn, 1992). Fractal dimension is the measure of the object’s boundary complexity (Metze et al., 2019). Together, these features allow one to measure various aspects of shape and provide a detailed quantitative characterization of 3D object morphology.

To address the limitations of previous studies, we quantified VPA-induced changes in the 4D nuclear morphology of primary human astrocyte cells. Our findings show that geometric descriptors extracted from voxel and surface-modeled representations of 3D nuclear shapes enabled accurate and interpretable characterization of time-dependent morphological changes in VPA-treated astrocytes. This allowed us to distinguish between nuclear morphological profiles of treated and normal astrocytes over time with a time-average accuracy of 82%. We showed that VPA treatment induced a time-dependent increase in nuclear size and nuclear shape irregularity in astrocytes over the course of treatment.

RESULTS AND DISCUSSION

Experiment and data

To determine how VPA-induced alterations of chromatin structure are reflected in 4D nuclear morphology, we treated human astrocyte cells with 1.5 mM of VPA at multiple time points (days 1, 3, and 5) and obtained volumetric images of DAPI-labeled nuclei using confocal microscopy at three time points (days 3, 5, and 7). This provided us with 4D images (3D + time) in the following conditions: normal human astrocytes (NHAs) and cells treated with VPA (Figure 1A). First, we used deconvolution to correct for background noise and spherical aberrations in original image volumes (Supplemental Figure 1). Then, we segmented individual nuclei into 3D binary voxel masks (Figure 1B). The number of nuclei identified after segmentation and quality control are listed in Table 1 for each day and treatment condition. Higher numbers of untreated nuclei compared with the treated group might be due to significant inhibition of astrocyte cell growth by VPA at concentrations over 1 mM (Sasai et al., 2007). Details of the deconvolution, segmentation, and quality control protocols can be found in the Materials and Methods section.

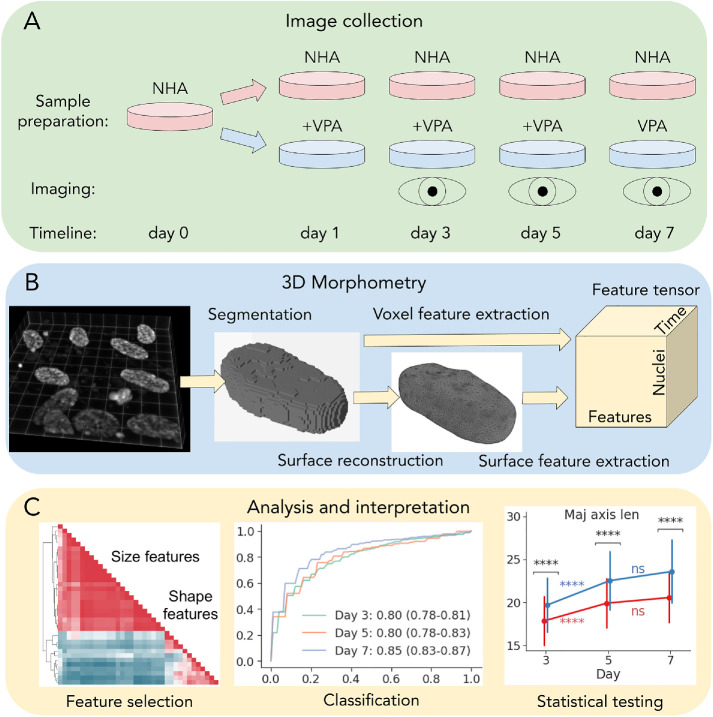
FIGURE 1:

FIGURE 1:

Open in a new tab

A schematic overview of the experiment, data collection, and analysis. (A) Sample preparation, treatment, and imaging. (B) 3D nuclear segmentation, shape modeling, and feature extraction. (C) Feature selection, and univariate statistical and machine learning analysis.

TABLE 1:

Number of segmented astrocyte nuclear 3D binary masks per day for each treatment condition after QC (number of nuclei filtered by quality control is in parentheses).

Day
Treatment 3 5 7
NHA 186 (−23) 163 (−18) 101 (−10)
VPA 128 (−18) 67 (−6) 78 (−15)
Total 314 (−41) 230 (−24) 179 (−35)
Open in a new tab

A simple approach to 3D morphometry is to extract features from binary object masks represented as voxel volumes (Dufour et al., 2015). From each voxel binary mask (Figure 1B), we computed the total of 11 geometric features: volume, bounding box and convex hull volumes, extent, solidity, lengths of main axes, and inertia tensor principal components. However, voxel-based representations can be noisy and may lose fine local geometric detail or even misrepresent the object’s global topological structure. We have previously shown that nuclear surfaces obtained via shape modeling are more informative and reliable for nuclear morphometry when compared with alternatives (Kalinin et al., 2018b). Here, we extended that approach by extracting 16 different size and shape descriptors that can characterize morphological changes in more detail, compared with just 6 in our previous study (Kalinin et al., 2018b). We obtained nuclear surface representations from 3D binary masks (Figure 1B) and measured the same descriptors as extracted from voxels, with the addition of bounding cylinder and sphere volumes, sphericity, fractal dimension, mean and Gaussian curvatures, curvedness, and shape index. The combined feature tensor containing nuclear morphological profiles (Figure 1B) was used for model and feature selection, statistical and machine learning–based analysis, and interpretation (Figure 1C).

Surface modeling provided compact and accurate characterization of 3D nuclear morphology

To evaluate the utility of different representations of nuclear morphology, we asked how well they facilitate morphological classification of NHA versus VPA cells, using time point–averaged area under the receiving operator characteristic curve (AUC) as the performance metric. Because the performance of classification algorithms varies across bioinformatics problems and datasets (Olson et al., 2018) and not all models have a feature weighting mechanism, we compared the performance across eight standard classifiers that enable feature importance estimation (Supplemental Figure S2). At each timepoint, we used random subsampling of the prevalent class due to high class imbalance (Table 1). First, because voxel and surface features have not been directly compared before in terms of nuclear morphological classification, we trained each model on sets of voxel-based (V) and surface-based features (S). As a baseline, we defined 2D voxel features extracted from 3D binary mask maximum intensity projections (V2D). To facilitate a fairer comparison between V and S, we also evaluated the subsets Vsub and Ssub that consisted of the 10 features that are captured by both representations (Supplemental Figure S2). As expected, the 2D feature set performed the worst (73% AUC), confirming that 3D measures provide more discriminative power. The performance was higher on the subset of voxel features (77% vs. 74% AUC on Vsub vs. Ssub), but not with full sets (77% AUC on V and on S). The best overall performance was achieved when using the combination of both voxel and surface-based features (78% AUC on V + S). Among tested classifiers, the support vector machine (SVM) model (Cortes and Vapnik, 1995) outperformed other classifiers averaged across all feature sets (81% AUC), so we chose to use this model going forward.

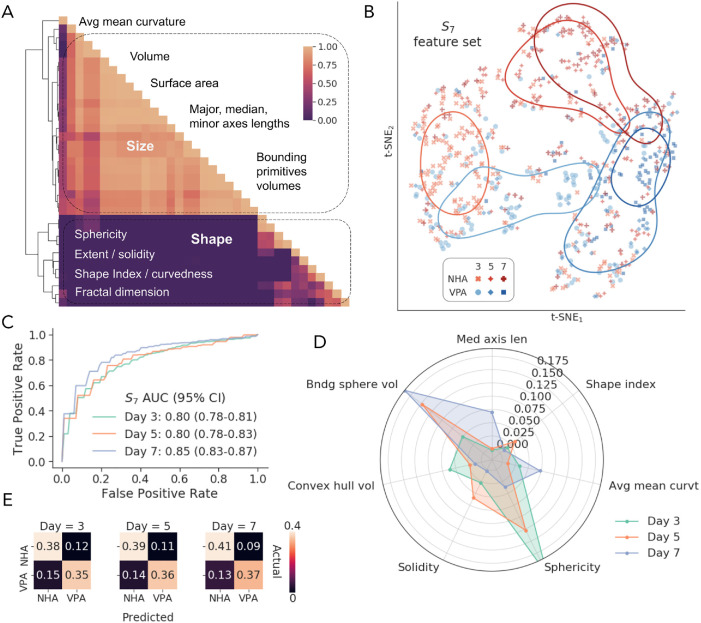
Clustering of the complete V + S feature set revealed two major groups, roughly corresponding to size and shape descriptors (Figure 2A). To reduce redundancy and aid interpretability, we selected seven features (S7) from smaller subclusters that maximized SVM classification performance (82% AUC). These features included surface-based median axis length, convex hull volume, bounding sphere volume, sphericity, average mean curvature, shape index, and voxel-based solidity. S7 provided distinctive representations of nuclear morphological profiles at different time points, as shown by the t-distributed stochastic neighbor embedding (t-SNE; van der Maaten and Hinton, 2008) 2D projection in Figure 2B. The SVM classifier demonstrated robust performance with AUCs of 80%, 80%, and 85% on days 3, 5, and 7, respectively (Figure 2C), with classification errors that were only slightly shifted toward false negatives at each day, indicating the effectiveness of the prevalent class subsampling (Figure 2D). Relative feature ranking from the trained SVM model (Figure 2E) revealed that sphericity was the most important feature for day 3, followed by convex hull and bounding sphere volumes. On day 5, bounding sphere volume, sphericity, and solidity were the top-3 important descriptors. Bounding sphere volume was again the most important measure on day 7, followed by average mean curvature, median axis length, and sphericity. Our findings showed that both size and shape features were important for discrimination of treated and untreated nuclei, demonstrating that a combination of 3D descriptors aids in accurate morphological classification.

FIGURE 2:

FIGURE 2:

Open in a new tab

Morphological classification performance. (A) hierarchical clustering of the Pearson correlations among all voxel and surface features (V + S), showing representative size and shape descriptors. (B) 2D t-distributed stochastic neighbor embedding (t-SNE) of the selected feature space, showing corresponding conditions (NHA or VPA) at every time point (day 3, 5, or 7). The lines denote clusters identified by kernel density estimation. (C) Receiver operating characteristic (ROC) curves for the SVM classifier with S7 features on days 3, 5, and 7. (D) Average normalized confusion matrices for the SVM classifier on the S7 features. (E) SVM-estimated permutation importance of S7 features for distinguishing nuclear morphologies on each day.

VPA induced increased nuclear size

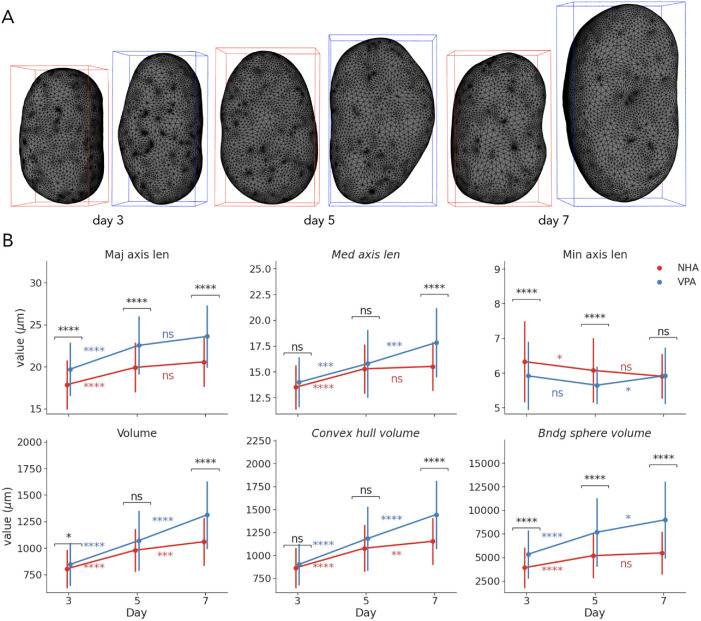
We observed time-dependent alterations in astrocyte nuclear sizes as demonstrated by examples of NHA and VPA-treated reconstructed nuclear surfaces shown in Figure 3A, with the latter having increasingly longer major axis length and higher volume. To provide a more detailed characterization of changes in 3D nuclear size, we chose six size descriptors for further study; three of which were selected as a part of S7 (median axis length, convex hull, and bounding sphere volumes), while major and minor axes lengths and nuclear volume were chosen manually for interpretability (Figure 3B). Measuring the three principal axes also allowed for the generation of inferences about the global shape of nuclei, as described in the next section. We reported each relative difference as the percentage change from the mean of the control group (NHA), along with a p value obtained using a two-sided Mann-Whitney U test with Holm–Šidák multiple testing correction, and AUC that in the case of the Mann-Whitney U test is equivalent to the common language effect size statistic (Mason and Graham, 2002).

FIGURE 3:

FIGURE 3:

Open in a new tab

Visualization and univariate statistical analysis of size changes under VPA treatment. (A) Reconstructed surfaces of representative NHA and VPA nuclei on days 3, 5, and 7. (B) Time-dependent changes in morphometric measures of nuclear sizes (points show mean; error bars show SD; *, p < 0.05; **, p < 0.01; ***, p < 0.001; ****, p < 0.0001).

By day 3, the average major axis length of VPA-treated nuclei compared with controls had increased by 10% (p < 0.0001, 70% AUC), the average minor axes length had decreased by 7% (p < 0.0001, 67% AUC), while there was no significant difference in median axis lengths (Figure 3B). Despite more subtle changes in nuclear (+5%, p < 0.05, 58% AUC) and convex (+4%, p > 0.05, 57% AUC) hull volumes, the volume of the bounding sphere was 36% larger (p < 0.0001, 74% AUC) in the VPA group. Between days 3 and 5, measures of major and median axes lengths indicated intragroup changes for both NHA (+12%, p < 0.0001 for major; +13%, p < 0.0001 for median) and VPA nuclei (+14%, p < 0.0001 for major; +13%, p < 0.001 for median), along with a slight shortening of minor axes. Nuclear, convex hull, and bounding sphere volumes also increased in both groups, correspondingly. As a result, the treated nuclei differed from controls on day 5 by having a 13% longer major axis (p < 0.0001, 73% AUC) and a 4% shorter minor axis (p < 0.0001, 67% AUC), along with 48% larger bounding sphere volumes (p < 0.0001, 74% AUC).

Between days 5 and 7, there were no significant changes in axes lengths in the control group, while the median axis length in the treated group increased by 13% (p < 0.001) and the minor increased by 5% (p < 0.05; Figure 3B). By day 7, VPA-treated nuclei had 15% larger major axes (p < 0.0001, 75% AUC) and 15% larger median axes (p < 0.0001, 70% AUC), while the minor axis length was comparable to that of the untreated nuclei. Nuclear volume and convex hull volume increased in both groups from day 5 to 7, but the change in the VPA-treated nuclei was more dramatic (+23%, p < 0.0001 for volume; +22%, p < 0.0001 for convex hull) than in the NHA group (+8%, p < 0.001 for volume; +7%, p < 0.01 for convex hull). As a result, the treated nuclei had 24% larger volume (p < 0.0001, 77% AUC), 25% larger convex hull (p < 0.0001, 76%), and 64% larger bounding sphere volume (p < 0.0001, 80% AUC), when compared with controls on day 7.

Our findings highlight a transition point between two phases of morphological changes. Before day 5, nuclear sizes in both the VPA and the NHA groups significantly increased in all reported measures, except for the minor axis length. VPA-treated nuclei demonstrated more prominent elongation and flattening, along with the slightly more rapid increase of the volume, compared with controls. NHA nuclear volumes increased less between days 5 and 7, while measures of VPA-treated nuclear size continued to increase, mostly due to longer median axes, demonstrating biggest differences by the last day, as illustrated by visualizations in Figure 3A. Finally, all individual feature AUCs were lower than those of the SVM model at each time point (Figure 2C), which highlighted the ability of a combination of 3D linear and volumetric features to capture size alterations that are difficult to ascertain when using solely individual measures.

VPA induced nuclear shape irregularity

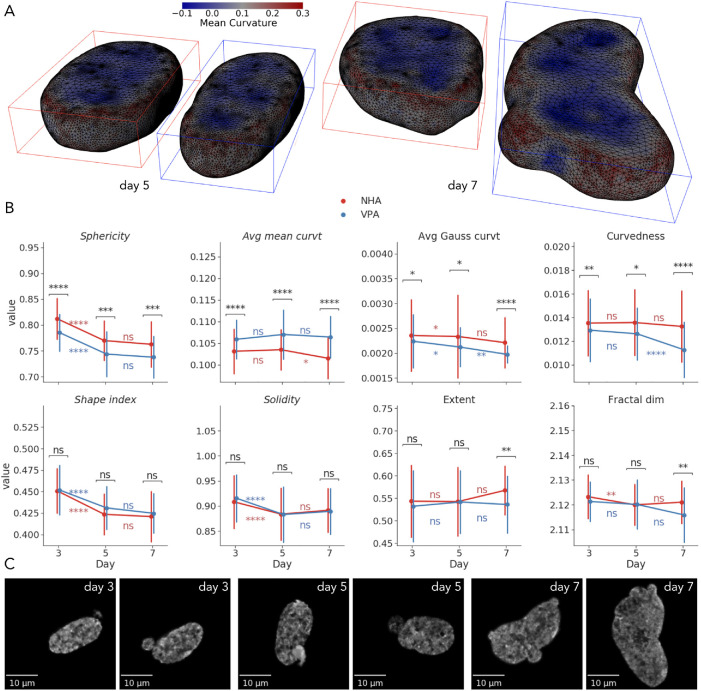
Consistent with VPA decondensing the chromatin to reduce nuclear rigidity (Stephens et al., 2018), we observed more globally irregular surface shapes (Figure 4, A and C) and occasional blebbing (Figure 4C). As reported by the size measures (Figure 3B), VPA induced nuclear elongation and flattening that were reflected in more ellipsoidal and less spherical shape. To quantify, by day 3, VPA-treated nuclei demonstrated lower sphericity (−3%, p < 0.0001, 72% AUC) and higher average mean curvature (+3%, p < 0.0001, 71% AUC), compared with the NHA group (Figure 4B), which indicated the presence of more convex and less concave points on the surface (Figure 4A). Average Gaussian curvature and curvedness of VPA-treated nuclei were slightly lower (−5%, p < 0.05, 58% AUC for Gaussian curvature; −5%, p < 0.01, 59% AUC for curvedness) than those of controls, which also corresponded to overall less spherical objects. Between days 3 and 5, there were similar intragroup decreases in sphericity, shape index, and solidity that corresponded to an increase in size of both treated and untreated nuclei at the same time point. More subtle alterations also included a decrease in average Gaussian curvature in both the NHA (−1%, p < 0.05) and the VPA (−5%, p < 0.05) groups, along with the decrease of fractal dimension of the untreated nuclei (−0.2%, p < 0.01; Figure 4B). Differences between shape descriptors extracted from two conditions on day 5 were similar to those from day 3. While the difference in solidity and shape index were not identified as “statistically significant” at the chosen p-value cutoffs, they contributed to the discriminative ability of the SVM classifier on both days 3 and 5 (Figure 2D), indicating their importance.

FIGURE 4:

FIGURE 4:

Open in a new tab

Visualization and univariate statistical analysis of shape changes under VPA treatment. (A) Reconstructed surfaces of a representative NHA and VPA nuclei on days 5 and 7, annotated with per-vertex mean curvature. (B) Time-dependent changes in morphometric measures of nuclear shapes (points show mean; error bars show SD; *, p < 0.05; **, p < 0.01; ***, p < 0.001; ****, p < 0.0001). (C) XY maximum intensity projections of VPA-treated nuclei with irregular shapes and blebbing.

By day 7, NHA nuclei only demonstrated a 2% decrease in average mean curvature (p < 0.05) from the previous time point across all shape features. The VPA group exhibited an 11% decrease in curvedness (p < 0.0001) and a 7% decrease in average Gaussian curvature (p < 0.01; Figure 4B). As on days 3 and 5, treated nuclei were still less spherical and had higher average mean curvature on day 7 compared with controls. However, decreases in curvedness (−15%, p < 0.0001, 74% AUC) and average Gaussian curvature (−10%, p < 0.0001, 71% AUC) were also more prominent at the last time point. Moreover, VPA-treated nuclei had 6% lower extent (p < 0.01, 64% AUC), and 0.2% lower fractal dimension (p < 0.01, 66% AUC), which indicated an overall higher global shape irregularity and less intensively folded and wrinkled nuclear surfaces, respectively.

Overall, we showed that VPA robustly induced more elongated and less spherical nuclear shapes with higher mean curvature from day 3. Toward day 7, these nuclei demonstrated more prominent deformations characterized, for example, by a kidney-like form and blebbing (Figure 4C). At the same time, the decrease in curvedness and fractal dimension reflected nuclear surfaces with lower local border complexity that has also been suggested to be indicative of chromatin decondensation, reduced tumorigenesis, and neuroprotection (Metze et al., 2019). Combined with the size features, these 3D shape descriptors enable more accurate characterization of time-dependent morphological changes than their 2D counterparts or any single measure used individually.

Together, our findings described the dynamics of VPA-treated nuclear morphological profiles characterized by the increased sizes and progressively more irregular, complex shapes that can be attributed to altered histone modifications and chromatin decondensation. These observations represent a first step to studying time-dependent morphological effects of chromatin reorganization in the astrocyte-to-neuron reprogramming process and relating them to underlying molecular mechanisms. In future studies, this approach can be extended to label additional subnuclear components or organelles, such as nucleoli, chromosome territories, TADs, transcriptional condensates, and other compartments using, for example, cell painting assay(s) for high-content morphological profiling (Bray et al., 2016). While tracking the overall cellular phenotype, this extension will allow us to include many other features in the models and assess their variability, association with cellular and nuclear shape morphology, disease state, and treatment conditions. All of this will set the stage to evaluate the effects of VPA and other small molecules measured with different concentrations and temporal sampling. Correlating these phenotypical cell and nuclear profiles with data from other assays, such as Hi-C (Lieberman-Aiden et al., 2009), will likely provide useful insights into how altered functional properties of the genome are correlated with TAD structure, nuclear and cellular morphology, and whether it can be used for training machine learning models to more accurately predict treatment response in model systems and in humans (Kalinin et al., 2018c).

MATERIALS AND METHODS

Request a protocol through Bio-protocol.

Sample preparation and image acquisition

Primary human astrocyte cells were purchased from ScienCell (human astrocytes hippocampal, catalog #1830).

Day 0:

Replace media with 50% growth media and 50% N2 media (DMEM/F12 + 1X pen/strep, 1X N2 supplements).

Day 1:

Control samples (NHA): for 30 ml of N2 media add 36 µl dimethyl sulfoxide (DMSO).

VPA-treated (1.5 mM VPA): for 30 ml of N2 media add 450 µl VPA

Day 3:

Collect day 3 control and VPA samples:

  1. Fix samples in 4% paraformaldehyde (PFA) for 10 min.

  2. Rinse three times for 5 min each in phosphate-buffered saline (PBS).

  3. Store samples in PBS at 4°.

Control samples (NHA): for 30 ml of N2 media add 187.5 µl DMSO.

VPA-treated (1.5 mM VPA): for 30 ml of N2 media add 450 µl VPA.

Day 5:

Collect day 5 control and VPA samples:

  1. Fix samples in 4% PFA for 10 min.

  2. Rinse three times for 5 min each in PBS.

  3. Store samples in PBS at 4°.

Control samples (NHA): for 30 ml of N2 media add 37.5 µl DMSO.

VPA-treated (1.5 mM VPA): for 30 ml of N2 media add 450 µl VPA.

Day 7:

Collect day 7 control and VPA samples:

  1. Fix samples in 4% PFA for 10 min.

  2. Rinse three times for 5 min each in PBS.

  3. Store samples in PBS at 4°.

Cells in both collections were labeled with DAPI (4′,6-diamidino-2-phenylindole), a common stain for the nuclear DNA. 3D imaging employed a Zeiss LSM 710 laser scanning confocal microscope with a 63× PLAN/apochromat 1.4 NA DIC objective. Each original 3D volume was then resliced into a 1024 × 1024 × Z lattice (Z = {30,50}), where regional subvolumes facilitate the alignment with the native tile size of the microscope. For every subvolume, accompanying vendor metadata was extracted from the original data.

Image preprocessing and segmentation

To correct for imaging artifacts, including the effect of axial smearing on volumetric measures, we deconvolved the obtained images. Theoretical 3D point spread functions for each individual image volume were modeled using the Richards and Wolf algorithm from the PSFGenerator plugin for Fiji (Kirshner et al., 2013). We then used estimated point spread functions and imaging metadata to apply Lucy-Richardson deconvolution (10 iterations) to the original 3D image volumes using the DeconvolutionLab2 software (Sage et al., 2017). Deconvolution reduced axial smearing and improved segmentation and classification results (Supplemental Figure S1).

We performed the automatic 3D segmentation of nuclei from deconvolved images using the Nuclear Segmentation algorithm from the Farsight toolkit (Al-Kofahi et al., 2010; Kalinin et al., 2018a). The main advantage of this tool is that it was created specifically to segment DAPI-stained nuclei in 2D or 3D. Unlike other learning-based segmentation algorithms, it does not require a labeled training set. It demonstrated stable results in our previous project (Kalinin et al., 2018a) and on these data. The algorithm implements multiple steps, which include a graph-cut algorithm to binarize the subvolumes, a multiscale Laplacian of Gaussian filter to convert the nuclei to blob masks, fast clustering to delineate the nuclei, and nuclear contour refinement using graph cuts with α expansions (Al-Kofahi et al., 2010).

After segmentation of the DAPI channel subvolumes, data were converted to 16-bit 3D TIFF files; each segmented nucleus was represented as a binary mask, and given a unique index value. Postsegmentation processing of nuclear masks included 3D hole filling and a filtering step that removed the objects if they span the edge of a tile or are connected to other objects. This quality control protocol filtered out most of the artifacts and the remaining were removed by visual inspection.

3D morphometry

3D binary nuclear masks were then used for voxel-based feature extraction using the scikit-image Python library (van der Walt et al., 2014), obtaining feature set V. For each binary mask, we measured nuclear volume, bounding box and convex hull volumes, extent, solidity, lengths of principal axes, inertia tensor principal components, and diameter of the sphere with the same volume as the nucleus. To compare the performance of 2D versus 3D features, we also extracted 2D features from maximum intensity projections of binary masks.

First, we model the boundaries of nuclear 3D masks extracted from the microscopic images as genus zero two-dimensional manifolds that are embedded as triangulated surfaces in ℝ3 (Kalinin et al., 2018b). 3D surface modeling uses an iterative Laplace-Beltrami eigenprojection and a topology-preserving boundary deformation algorithm (Shi et al., 2010). This algorithm performs robust reconstruction of the objects’ surfaces from their segmented masks using an iterative mask filtering process. We used Mask2Mesh implementation of this algorithm from the MOCA framework (Shi et al., 2010) and then applied mesh simplification and subdivision to 40,000 triangles, following the shape analysis protocol in Kalinin et al. (2018b). The next step included the extraction of geometric characteristics of the 3D nuclear surfaces (e.g., mesh volume, surface area, curvedness, shape index, and fractal dimension), implemented in Laboratory of Neuro Imaging Pipeline v7.0.3 (Dinov et al., 2009; Kalinin et al., 2018b). To provide a comprehensive morphological characterization, we expanded the list of six metrics previously reported in Kalinin et al. (2018b). The additional surface features were extracted using the trimesh library (Dawson-Haggerty and GitHub open-source software contributors, 2019) and included average mean curvature, convex hull and bounding primitive (box, oriented box, cylinder, sphere) volumes, convex hull surface area, inertia tensor eigenvalues, and principal axes lengths. Surface-based extent and solidity were computed from trimesh-derived measures as the ratio of the object volume to the bounding box volume and the ratio of the object volume to the convex hull volume, correspondingly. Sphericity of the nucleus was computed as the ratio of the surface area of a sphere with the same volume as the given nucleus to the surface area of the nucleus: 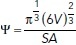Inline graphic, where V is the volume of the nucleus and SA is the surface area of the nucleus (Wadell, 1935). All surface descriptors were combined into the feature set S.

Both volumetric and surface features we merged by inner join on the per-nucleus basis, filtering out those individual cells, for which feature extraction failed or voxel volume measure exceeded the empirically estimated threshold of 150,000 voxels. Nuclei were also considered outliers and removed if any feature value computed over all cells was out of the [P5 – 1.5(P95 – P5); P95 + 1.5(P95 – P5)] range, where P5 and P95 are 5th and 95th percentiles, correspondingly. All extracted features were aggregated into per-nucleus feature vectors, from which we constructed a feature table per each day of treatment with the labels corresponding to phenotypic conditions (NHA and VPA).

Feature and model selection, and analysis

To handle multicollinear features, we performed hierarchical clustering on the Spearman rank-order correlations between all features and then used averaged SVM classification performance to select a threshold for defining feature clusters, while controlling for overfitting with fivefold statistical cross-validation repeated from five different random seeds. From each cluster, we selected one feature according to the highest value for the χ2 statistic, while ignoring inertia tensor eigenvalues, as they were highly correlated with other features that are easier to directly interpret, such as volume or minimal principal axis length. This process yielded the final set S7 consisting of the following seven descriptors: surface-based median axis length, convex hull and bounding sphere volumes, sphericity, average mean curvature, shape index, and voxel-based solidity. t-SNE embedding was generated using the scikit-learn library (Pedregosa et al., 2011) with PCA initialization, perplexity of 13, and cosine distance as a metric. Clusters for each condition at every time point were identified using kernel density estimation in the seaborn library (Waskom et al., 2020) with 0.75 threshold. It should be noted that cluster sizes and intercluster distances should be interpreted with care when using t-SNE (Wattenberg et al., 2016).

The following sets of features were used to compare volumetric and surface-based shape representations: V2D, V, S, Vsub, Ssub, V+S, S7, where Vsub and Ssub were subsets of equivalent voxel and surface feature sets correspondingly (nuclear volume, convex hull and bounding box volumes, extent, solidity, inertia eigenvalues, and major axis length). We assessed the classification performance of those classifiers with the scikit-learn library (Pedregosa et al., 2011) that provided feature weights as an output. These included Gaussian naïve Bayes, k-nearest neighbors, logistic regression, linear SVM, random forest, extremely randomized trees, AdaBoost and gradient boosting machine. They were trained using default hyperparameter values and evaluated at each time point using the AUC. AUCs, confusion matrices, and feature ranking were averaged from 10 repetitions of the internal statistical fivefold stratified cross-validation with different random seeds. We averaged the performance of each model over time points and over all feature sets. To compare feature sets, we averaged the AUCs over all models and days. Random subsampling of the prevalent class by the total number of per-fold training samples from an underrepresented class at each iteration of the cross-validation procedure was used to combat class imbalance. To rank features by their relative importance, we employed the permutation importance strategy that reflects the decrease in a model performance when a single feature value is randomly shuffled (Breiman, 2001). This breaks the relationship between the feature and the outcome, while being model agnostic and can be calculated many times with different permutations of the feature. We computed permutation importance on a held-out set on each cross-validation cycle, highlighting which features contribute the most to the generalization power of the trained model. Permutation feature importance was computed using the “coef” property of the trained SVM model at each time point.

Univariate statistical analysis of individual features was performed using the SciPy package (Virtanen et al., 2020) with multiple testing correction using statsmodels (Seabold and Perktold, 2010). We reported each relative difference as the percentage change from the control group, along with a p value obtained using a two-sided Mann-Whitney U test with Holm–Šidák multiple testing correction (α = 0.05), and the common language effect size statistic that in the case of the Mann-Whitney U test is equivalent to the AUC (Mason and Graham, 2002).

For all analysis tasks we used Python 3.8.3 from the Anaconda distribution (Continuum Analytics and others, 2020), with the numpy (van der Walt et al., 2011), pandas (McKinney, 2010), and iPython (Perez and Granger, 2007) packages. Image processing was done using scikit-image (van der Walt et al., 2014). Visualizations and charts were built with the matplotlib (Hunter, 2007), seaborn (Waskom et al., 2020), trimesh (Dawson-Haggerty and GitHub open-source software contributors, 2019), and SOCRAT (Kalinin et al., 2017) libraries.

The documentation supporting the conclusions of this article together with the derived data, pipeline workflows, and underlying source code is made publicly available online on the project webpage: SOCR 3D Cell Morphometry Project, https://socr.umich.edu/projects/3d-cell-morphometry.

Supplementary Material

Click here for additional data file. (1.3MB, pdf)
Click here for additional data file. (241.9KB, pdf)

Acknowledgments

The authors thank Ari Allyn-Feuer, Samuel Handelman, and Gilbert Omenn for thoughtful discussions and helpful suggestions. We thank colleagues at the Laboratory of Neuro Imaging (LONI), Keck School of Medicine, University of Southern California, for providing technical support for the LONI Pipeline environment. This work is supported by Chinese Key-Area Research and Development Program of Guangdong Province (2020B0101350001). This work was also partially supported by the National Science Foundation Grants no. 1916425, no. 1734853, no. 1636840, no. 1416953, no. 0716055, and no. 1023115; the National Institutes of Health Grants no. P20 NR-015331, no. P30 DK-089503, no. UL1TR-002240, no. R01CA-233487, and no. R01MH-121079. Xin Rong of the University of Michigan donated NVIDIA TITAN X GPU used for this research, and the NVIDIA Corporation donated the TITAN Xp GPU used to execute the computationally intensive protocol.

Abbreviations used:

AUC

area under the receiving operator characteristic curve

NHAs

normal human astrocytes

SVM

support vector machine

TADs

topologically associating domains

VPA

valproic acid.

Footnotes

This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E20-08-0502) on April 28, 2021.

REFERENCES

  1. Al-Kofahi Y, Lassoued W, Lee W, Roysam B (2010). Improved automatic detection and segmentation of cell nuclei in histopathology images. IEEE Trans Biomed Eng 57, 841–852. [DOI] [PubMed] [Google Scholar]
  2. Amamoto R, Arlotta P (2014). Development-inspired reprogramming of the mammalian central nervous system. Science 343, 1239882. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bray M-A, Singh S, Han H, Davis CT, Borgeson B, Hartland C, Kost-Alimova M, Gustafsdottir SM, Gibson CC, Carpenter AE (2016). Cell painting, a high-content image-based assay for morphological profiling using multiplexed fluorescent dyes. Nat Protoc 11, 1757–1774. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Breiman L (2001). Random forests. Mach Learn 45, 5–32. [Google Scholar]
  5. Chen H, Chen J, Muir LA, Ronquist S, Meixner W, Ljungman M, Ried T, Smale S, Rajapakse I (2015). Functional organization of the human 4D nucleome. Proc Natl Acad Sci USA 112, 8002–8007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Cheng L, Gao L, Guan W, Mao J, Hu W, Qiu B, Zhao J, Yu Y, Pei G (2015). Direct conversion of astrocytes into neuronal cells by drug cocktail. Cell Res 25, 1269. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Choi H-J, Choi H-K (2007). Grading of renal cell carcinoma by 3D morphological analysis of cell nuclei. Comput Biol Med 37, 1334–1341. [DOI] [PubMed] [Google Scholar]
  8. Continuum Analytics and others (2020). Anaconda software distribution. Computer software version 2-2.4.0, https://docs.anaconda.com. [Google Scholar]
  9. Cortes C, Vapnik V (1995). Support-vector networks. Mach Learn 20, 273–297. [Google Scholar]
  10. Cremer T, Cremer M, Hübner B, Strickfaden H, Smeets D, Popken J, Sterr M, Markaki Y, Rippe K, Cremer C (2015). The 4D nucleome: evidence for a dynamic nuclear landscape based on co-aligned active and inactive nuclear compartments. FEBS Lett 589, 2931–2943. [DOI] [PubMed] [Google Scholar]
  11. Dawson-Haggerty and GitHub open-source software contributors (2019). trimesh (software). https://github.com/mikedh/trimesh
  12. Depeursinge A, Foncubierta-Rodriguez A, Van De Ville D, Müller H (2014). Three-dimensional solid texture analysis in biomedical imaging: Review and opportunities. Med Image Anal 18, 176–196. [DOI] [PubMed] [Google Scholar]
  13. Dinov I, Van Horn J, Lozev K, Magsipoc R, Petrosyan P, Liu Z, MacKenzie-Graha A, Eggert P, Parker DS, Toga AW (2009). Efficient, distributed and interactive neuroimaging data analysis using the LONI pipeline. Frontiers Neuroinf 3, 22. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Dufour AC, Liu T-Y, Ducroz C, Tournemenne R, Cummings B, Thibeaux R, Guillen N, Hero AO, Olivo-Marin J-C (2015). Signal processing challenges in quantitative 3-d cell morphology: more than meets the eye. IEEE Signal Process Mag 32, 30–40. [Google Scholar]
  15. Eckschlager T, Plch J, Stiborova M, Hrabeta J (2017). Histone deacetylase inhibitors as anticancer drugs. Int J Mol Sci 18, 1414. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Felisbino MB, Costa TA, Gatti MSV, Mello MLS (2016). Differential response of human hepatocyte chromatin to HDAC inhibitors as a function of microenvironmental glucose level. J Cell Physiol 231, 2257–2265. [DOI] [PubMed] [Google Scholar]
  17. Felisbino MB, Gatti MSV, Mello MLS (2014). Changes in chromatin structure in NIH 3T3 cells induced by valproic acid and trichostatin A. J Cell Biochem 115, 1937–1947. [DOI] [PubMed] [Google Scholar]
  18. Felisbino MB, Tamashiro W, Mello MLS (2011). Chromatin remodeling, cell proliferation and cell death in valproic acid-treated HeLa cells. PLoS One 6, e29144. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Ganai SA, Malli Kalladi S, Mahadevan V (2015). HDAC inhibition through valproic acid modulates the methylation profiles in human embryonic kidney cells. J Biomol Struct Dyn 33, 1185–1197. [DOI] [PubMed] [Google Scholar]
  20. Gao L, Guan W, Wang M, Wang H, Yu J, Liu Q, Qiu B, Yu Y, Ping Y, Bian X, et al. (2017). Direct generation of human neuronal cells from adult astrocytes by small molecules. Stem Cell Rep 8, 538–547. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Göttlicher M, Minucci S, Zhu P, Krämer OH, Schimpf A, Giavara S, Sleeman JP, Coco FL, Nervi C, Pelicci PG, et al. (2001). Valproic acid defines a novel class of HDAC inhibitors inducing differentiation of transformed cells. EMBO J 20, 6969–6978. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Higgins GA, Allyn-Feuer A, Georgoff P, Nikolian V, Alam HB, Athey BD (2017a). Mining the topography and dynamics of the 4D Nucleome to identify novel CNS drug pathways. Methods 123, 102–118. [DOI] [PubMed] [Google Scholar]
  23. Higgins GA, Allyn-Feuer A, Handelman S, Sadee W, Athey BD (2015). The epigenome, 4D nucleome and next-generation neuropsychiatric pharmacogenomics. Pharmacogenomics 16, 1649–1669. [DOI] [PubMed] [Google Scholar]
  24. Higgins GA, Georgoff P, Nikolian V, Allyn-Feuer A, Pauls B, Higgins R, Athey BD, Alam HE (2017b). Network reconstruction reveals that valproic acid activates neurogenic transcriptional programs in adult brain following traumatic injury. Pharm Res 34, 1658–1672. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Huangfu D, Maehr R, Guo W, Eijkelenboom A, Snitow M, Chen AE, Melton DA (2008). Induction of pluripotent stem cells by defined factors is greatly improved by small-molecule compounds. Nat Biotechnol 26, 795–797. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Hunter JD (2007). Matplotlib: a 2D graphics environment. Comput Sci Eng 9, 90–95. [Google Scholar]
  27. Kalinin AA, Allyn-Feuer A, Ade A, Fon GV, Meixner W, Dilworth D, De Wet JR, Higgins GA, Zheng G, Creekmore A, et al. (2018a). 3D cell nuclear morphology: microscopy imaging dataset and voxel-based morphometry classification results. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, 2272–2280.
  28. Kalinin AA, Allyn-Feuer A, Ade A, Fon GV, Meixner W, Dilworth D, Husain SS, Jeffrey R, Higgins GA, Zheng G, et al. (2018b). 3D shape modeling for cell nuclear morphological analysis and classification. Sci Rep 8, 13658. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Kalinin AA, Higgins GA, Reamaroon N, Soroushmehr S, Allyn-Feuer A, Dinov ID, Najarian K, Athey BD (2018c). Deep learning in pharmacogenomics: from gene regulation to patient stratification. Pharmacogenomics 19, 629–650. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Kalinin AA, Palanimalai S, Dinov ID (2017). SOCRAT platform design: a web architecture for interactive visual analytics applications. In: Proceedings of the 2nd Workshop on Human-In-the-Loop Data Analytics, New York: ACM, 8:1–8:6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Kirshner H, Aguet F, Sage D, Unser M (2013). 3-D PSF fitting for fluorescence microscopy: implementation and localization application. J Microsc 249, 13–25. [DOI] [PubMed] [Google Scholar]
  32. Koenderink JJ, Van Doorn AJ (1992). Surface shape and curvature scales. Image Vis Comput 10, 557–564. [Google Scholar]
  33. Kortenhorst MSQ, Isharwal S, van Diest PJ, Chowdhury WH, Marlow C, Carducci MA, Rodriguez R, Veltri RW (2009). Valproic acid causes dose- and time-dependent changes in nuclear structure in prostate cancer cells in vitro and in vivo. Mol Cancer Ther 8, 802–808. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Lieberman-Aiden E, Van Berkum NL, Williams L, Imakaev M, Ragoczy T, Telling A, Amit I, Lajoie BR, Sabo PJ, Dorschner MO, et al. (2009). Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science 326, 289–293. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Marchion DC, Bicaku E, Daud AI, Sullivan DM, Munster PN (2005). Valproic acid alters chromatin structure by regulation of chromatin modulation proteins. Cancer Res 65, 3815–3822. [DOI] [PubMed] [Google Scholar]
  36. Mason SJ, Graham NE (2002). Areas beneath the relative operating characteristics (ROC) and relative operating levels (ROL) curves: statistical significance and interpretation. Q J R Meteorol Soc 128, 2145–2166. [Google Scholar]
  37. McKinney W (2010). Data structures for statistical computing in Python. In: Proceedings of the 9th Python in Science Conference, 56–61.
  38. Medyukhina A, Blickensdorf M, Cseresnyés Z, Ruef N, Stein JV, Figge MT (2020). Dynamic spherical harmonics approach for shape classification of migrating cells. Sci Rep 10, 6072. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Metze K, Adam R, Florindo JB (2019). The fractal dimension of chromatin—a potential molecular marker for carcinogenesis, tumor progression and prognosis. Expert Rev Mol Diagn 19, 299–312. [DOI] [PubMed] [Google Scholar]
  40. Meyer MG, Fauver M, Rahn JR, Neumann T, Patten FW, Seibel EJ, Nelson AC (2009). Automated cell analysis in 2D and 3D: a comparative study. Pattern Recogn 42, 141–146. [Google Scholar]
  41. Olson RS, Cava WL, Mustahsan Z, Varik A, Moore JH (2018). Data-driven advice for applying machine learning to bioinformatics problems. In: Biocomputing 2018, Kohala Coast, Hawaii: World Scientific, 192–203. [PMC free article] [PubMed] [Google Scholar]
  42. Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, et al. (2011). Scikit-learn: machine learning in Python. J Mach Learn Res 12, 2825–2830. [Google Scholar]
  43. Perez F, Granger BE (2007). IPython: a system for interactive scientific computing. Comput Sci Eng 9, 21–29. [Google Scholar]
  44. Pickell Z, Williams AM, Alam HB, Hsu CH (2020). Histone deacetylase inhibitors: a novel strategy for neuroprotection and cardioprotection following ischemia/reperfusion injury. J Am Heart Assoc 9, e016349. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Qin H, Zhao A, Fu X (2017). Small molecules for reprogramming and transdifferentiation. Cell Mol Life Sci 74, 3553–3575. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Sage D, Donati L, Soulez F, Fortun D, Schmit G, Seitz A, Guiet R, Vonesch C, Unser M (2017). DeconvolutionLab2: an open-source software for deconvolution microscopy. Methods 115, 28–41. [DOI] [PubMed] [Google Scholar]
  47. Sasai K, Akagi T, Aoyanagi E, Tabu K, Kaneko S, Tanaka S (2007). O6-methylguanine-DNA methyltransferase is downregulated in transformed astrocyte cells: implications for anti-glioma therapies. Mol Cancer 6, 36. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Seabold S, Perktold J (2010). statsmodels: econometric and statistical modeling with Python. In: 9th Python in Science Conference.
  49. Shi Y, Lai R, Morra JH, Dinov I, Thompson PM, Toga AW (2010). Robust surface reconstruction via Laplace-Beltrami eigen-projection and boundary deformation. IEEE Trans Med Imag 29, 2009–2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Stephens AD, Banigan EJ, Adam SA, Goldman RD, Marko JF (2017). Chromatin and lamin A determine two different mechanical response regimes of the cell nucleus. Mol Biol Cell 28, 1984–1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Stephens AD, Banigan EJ, Marko JF (2019). Chromatin’s physical properties shape the nucleus and its functions. Curr Opin Cell Biol 58, 76–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Stephens AD, Liu PZ, Banigan EJ, Almassalha LM, Backman V, Adam SA, Goldman RD, Marko JF (2018). Chromatin histone modifications and rigidity affect nuclear morphology independent of lamins. Mol Biol Cell 29, 220–233. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Tsagkrasoulis D, Hysi P, Spector T, Montana G (2017). Heritability maps of human face morphology through large-scale automated three-dimensional phenotyping. Sci Rep 7, 45885. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Uhler C, Shivashankar GV (2018). Nuclear mechanopathology and cancer diagnosis. Trends Cancer 4, 320–331. [DOI] [PubMed] [Google Scholar]
  55. van der Maaten L, Hinton G (2008). Visualizing data using t-SNE. J Mach Learn Res 9, 2579–2605. [Google Scholar]
  56. van der Walt S, Colbert SC, Varoquaux G (2011). The NumPy array: a structure for efficient numerical computation. Comput Sci Eng 13, 22–30. [Google Scholar]
  57. van der Walt S, Schönberger JL, Nunez-Iglesias J, Boulogne F, Warner JD, Yager N, Gouillart E, Yu T (2014). scikit-image: image processing in Python. PeerJ 2, e453. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Virtanen P, Gommers R, Oliphant TE, Haberland M, Reddy T, Cournapeau D, Burovski E, Peterson P, Weckesser W, Bright J, et al. (2020). SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat Methods 17, 261–272. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Wadell H (1935). Volume, shape, roundness of quartz particles. J Geol 43, 250–280. [Google Scholar]
  60. Waskom M, Botvinnik O, Ostblom J, Gelbart M, Lukauskas S, Hobson P, Gemperline DC, Augspurger T, Halchenko Y, Cole JB, et al. (2020). mwaskom/seaborn: v0.10.1 (April 2020), Zenodo. [Google Scholar]
  61. Wattenberg M, Viégas F, Johnson I (2016). How to use t-SNE effectively. Distill 1, e2. [Google Scholar]
  62. Xu D, Cui J, Bansal R, Hao X, Liu J, Chen W, Peterson BS (2009). The ellipsoidal area ratio: an alternative anisotropy index for diffusion tensor imaging. Magn Reson Imaging 27, 311–323. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Yang X-J, Seto E (2007). HATs and HDACs: from structure, function and regulation to novel strategies for therapy and prevention. Oncogene 26, 5310–5318. [DOI] [PubMed] [Google Scholar]
  64. Yin JC, Zhang L, Ma NX, Wang Y, Lee G, Hou XY, Lei ZF, Zhang FY, Dong FP, Wu GY, et al. (2019). Chemical conversion of human fetal astrocytes into neurons through modulation of multiple signaling pathways. Stem Cell Rep 12, 488–501. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. Zhang L, Yin JC, Yeh H, Ma NX, Lee G, Chen XA, Wang Y, Lin L, Chen L, Jin P, et al. (2015). Small molecules efficiently reprogram human astroglial cells into functional neurons. Cell Stem Cell 17, 735–747. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Click here for additional data file. (1.3MB, pdf)
Click here for additional data file. (241.9KB, pdf)

Articles from Molecular Biology of the Cell are provided here courtesy of American Society for Cell Biology

RESOURCES