Cdc42 GTPase-activating proteins (GAPs) regulate generational inheritance of cell polarity and cell shape in fission yeast

Abstract

The highly conserved small GTPase Cdc42 regulates polarized cell growth and morphogenesis from yeast to humans. We previously reported that Cdc42 activation exhibits oscillatory dynamics at cell tips of Schizosaccharomyces pombe cells. Mathematical modeling suggests that this dynamic behavior enables a variety of symmetric and asymmetric Cdc42 activation distributions to coexist in cell populations. For individual wild-type cells, however, Cdc42 distribution is initially asymmetrical and becomes more symmetrical as cell volume increases, enabling bipolar growth activation. To explore whether different patterns of Cdc42 activation are possible in vivo, we examined S. pombe rga4∆ mutant cells, lacking the Cdc42 GTPase-activating protein (GAP) Rga4. We found that monopolar rga4∆ mother cells divide asymmetrically leading to the emergence of both symmetric and asymmetric Cdc42 distributions in rga4∆ daughter cells. Motivated by different hypotheses that can mathematically reproduce the unequal fate of daughter cells, we used genetic screening to identify mutants that alter the rga4∆ phenotype. We found that the unequal distribution of active Cdc42 GTPase is consistent with an unequal inheritance of another Cdc42 GAP, Rga6, in the two daughter cells. Our findings highlight the crucial role of Cdc42 GAP localization in maintaining consistent Cdc42 activation and growth patterns across generations.

INTRODUCTION

Cell polarization is an important process that enables essential cellular functions such as morphogenesis, cell migration, and asymmetric cell division (Johnson et al., 2011). In particular, asymmetric cell division, which produces cells with different cellular fates, is crucial for embryo development and stem cell differentiation. Disruption of these functions contributes to tumorigenesis, fostering the onset of disease (Geiger and Zheng, 2014; MacDonald, 2014).

The conserved GTPase Cdc42 is a master regulator of polarized cell growth in eukaryotes ranging from yeast to humans (Johnson, 1999; Etienne-Manneville, 2004). Targets of active Cdc42 promote growth by enabling functions such as cytoskeletal organization, membrane recycling, and polarized secretion (Etienne-Manneville, 2004; Heasman and Ridley, 2008; Perez and Rincon, 2010). Transitions in Cdc42 activity are regulated by guanine-nucleotide exchange factors (GEFs) that promote the activation of Cdc42, GTPase-activating proteins (GAPs) that inhibit Cdc42 by accelerating GTP hydrolysis and guanine dissociation inhibitors (GDIs) that extract GDP-Cdc42 from the cell membrane (Koch et al., 1997; Cole et al., 2007; Sinha and Yang, 2008). Once activated, Cdc42 associates with cell membranes via its prenylated C-terminus (Choy et al., 1999), where it then undergoes autocatalytic activation, thus enabling symmetry breaking (Butty et al., 2002; Irazoqui et al., 2003; Kozubowski et al., 2008).

Several experimental as well as mathematical modeling studies have examined the mechanism of Cdc42 amplification and symmetry breaking during bud-site selection in the budding yeast Saccharomyces cerevisiae (Irazoqui et al., 2003; Wedlich-Soldner et al., 2004; Kozubowski et al., 2008; Slaughter et al., 2009; Chiou et al., 2018). In the model of Goryachev and Pokhilko (2008), this is realized through a winner-takes-all mechanism that ensures selection of a single bud site (Goryachev and Pokhilko, 2008). These studies suggest that stochastic activation of Cdc42 at the cell membrane recruits a GEF-associated complex consisting of the scaffold protein Bem1 and the GEF Cdc24, which then promotes further activation of Cdc42 in a positive feedback loop (Bender and Pringle, 1989; Chant and Herskowitz, 1991). The emergence of activated Cdc42 clusters exhibits characteristics of activator-inhibitor Turing models. These models typically rely on slow diffusion of an activator coupled with fast diffusion of an inhibitor (Goryachev and Pokhilko, 2008; Bendezu et al., 2015), thus enabling concentration of the activator and inhibition of nearby activator clusters. In this self-organizing system, symmetry breaking can occur in the absence of polarity landmarks as a dynamic process that initially consists of multiple small clusters of active Cdc42. These clusters compete with one another for regulators until the largest cluster with the most robust positive feedback eventually wins (Howell et al., 2009, 2012).

In many complex cell types, such as neurons, symmetry breaking is followed by the organization of multiple sites of growth. An excellent model system for the study of symmetry breaking that allows polarization of multiple sites of Cdc42 activation is the fission yeast Schizosaccharomyces pombe. These cells are rod-shaped with two defined growth zones at the cell poles, which allows for straightforward measurement of changes in cell polarity, growth, and cellular dimensions. In addition, the life cycle of S. pombe cells includes both symmetric and asymmetric growth patterns. S. pombe cells divide in the cell center with each new daughter cell inheriting one cell tip that was previously growing (Streiblova and Wolf, 1972; Mitchison and Nurse, 1985). On cell division, the old cell end (OE) activates Cdc42-dependent growth first in a process termed old-end takeoff (Streiblova and Wolf, 1972; Mitchison and Nurse, 1985). The cell continues in this asymmetric growth pattern until it reaches a length of approximately 9 μm, when growth begins in the new end (NE) of the cell in a process called new-end takeoff (NETO) (Mitchison and Nurse, 1985). From this point, cell growth proceeds symmetrically at both cell tips.

During this process, the activation level of Cdc42 GTPase changes dynamically at the two cell tips. We previously showed that the activation of Cdc42 in S. pombe exhibits oscillations that are anticorrelated between the two cell tips (Das et al., 2012). Mathematical modeling using delay differential equations for three populations (at the two cell tips and the cytoplasm) described this oscillatory behavior as resulting from both positive and delayed negative feedbacks as well as competition for active Cdc42 or its regulators (Das et al., 2012). More recent models of Cdc42 oscillations further explored the effects of diffusion through the cell and incorporated explicit molecular mechanisms for the positive feedback (Xu and Bressloff, 2016; Xu et al., 2019; Khalili et al., 2020). Feedback mechanisms have been experimentally described in S. pombe. For example, the Cdc42 GEF Scd1 (bound to the scaffold protein Scd2) generates a positive feedback loop of Cdc42 activation, analogous to the Cdc24–Bem1 complex in S. cerevisiae (Chang et al., 1994; Endo et al., 2003; Wheatley and Rittinger, 2005; Das et al., 2012; Lamas et al., 2020a;). The Cdc42 effector Pak1 functions in a positive feedback loop that amplifies positional cues (Chang et al., 1999; Lamas et al., 2020a). Conversely, Pak1 kinase activity functions as a negative regulator of Cdc42, generating a delayed negative feedback (Das et al., 2012; Kuo et al., 2014).

Bifurcation analysis of the differential equations governing our mathematical model revealed that the progression from an asymmetric to a symmetric growth pattern travels through a landscape allowing symmetric or asymmetric distribution of active Cdc42 at the cell tips (Das et al., 2012). As the cells grow, our model predicts that saturation of polarity factors at the OE enables the NE to compete more effectively for Cdc42 regulators and exceeds the threshold of Cdc42 activation required for cell growth (Das et al., 2012).

The transition from asymmetric to symmetric Cdc42 activation distribution, however, involves traversing a coexistence region, in which either an asymmetric or a symmetric distribution is possible (Das et al., 2012). Prior models also predicted the role of coexistence and competition in fission yeast cell polarization, modeling actin rather than Cdc42 (Csikasz-Nagy et al., 2008), or modeling the polarisome (Cerone et al., 2012). All models are consistent with the idea that wild-type cells initially exhibit monopolar growth until the levels of Cdc42 regulators are sufficient to activate growth at the second cell tip. Intriguingly, the presence of a coexistence region suggests that subtle changes to the system, driven by regulatory or environmental perturbations, may readily alter active Cdc42 distribution in the cell, enabling alternative growth patterns to emerge.

To experimentally determine if different states of Cdc42 activation distribution are possible in a biological context, and to identify novel molecular mechanisms that control morphological differentiation, we analyzed mutants that display alternative Cdc42 distributions in cells of similar size. Here we describe the role of the Cdc42 GAP Rga4 in determining the initial state of Cdc42 GTPase activation distribution in daughter cells. We find that rga4∆ mother cells divide asymmetrically leading to the emergence of both symmetric and asymmetric Cdc42 distributions in rga4∆ daughter cells. We interpret results of genetic screening to identify mutants that alter the rga4∆ phenotype by comparison to predictions of variations of our computational model for wild-type cells, which suggested three alternative hypotheses to reproduce the unequal fate of rga4∆ daughter cells. Our results suggest that the inheritance of Cdc42 regulators, and in particular of Cdc42 GAP proteins, has a crucial role in determining the morphological fate of daughter cells and also in ensuring consistent growth patterns from generation to generation.

RESULTS

rga4Δ sister cells display divergent Cdc42 dynamics and distribution

We previously showed that the solutions of our model of delay differential equations describing the evolution of the concentration of Cdc42 or its regulators at the two cell tips allow for a transition from asymmetric to symmetric states through a coexistence region, where different Cdc42 distributions between the cell tips are possible, leading to different patterns of cell growth (Supplemental Figure S1A) (Das et al., 2012). This coexistence region is encountered as the cell grows and the availability of active Cdc42 or its regulators increases. In the model, the coexistence region arises when cells are around 7.6–8.0 μm long (Das et al., 2012). Since Cdc42 GTPase activation promotes bipolar cell growth when a threshold activity level has been achieved at the new cell end (Das et al., 2012), the timing of bipolar growth activation reflects the timing of the transition to a more symmetrical distribution of active Cdc42.

One prediction of the mathematical model is that the shape of the dynamical landscape, as well as the initial state of the newly born cell, specifies the trajectory of Cdc42 dynamics as the cell grows (Supplemental Figure S1A). Thus, we searched experimentally for molecular mechanisms that affect the coexistence region of Cdc42 activation and have a role in establishing the initial state of Cdc42 activation distribution and dynamics following cell division.

To this end, we searched for gene mutations that alter Cdc42 dynamics in newly born fission yeast daughter cells. We previously reported that a mutant strain lacking the Cdc42 GAP Rga4 displays asymmetric cell division, in which divergent growth patterns are observed in daughter cells (Das et al., 2007, 2012). Thus, we examined the spatial distribution and activity of Cdc42 in rga4∆ daughter cells, as compared with rga4+ control cells. We used the CRIB-GFP bioreporter (Tatebe et al., 2008) to visualize the localization and dynamics of the active form of Cdc42 (Cdc42-GTP) (Figure 1A).

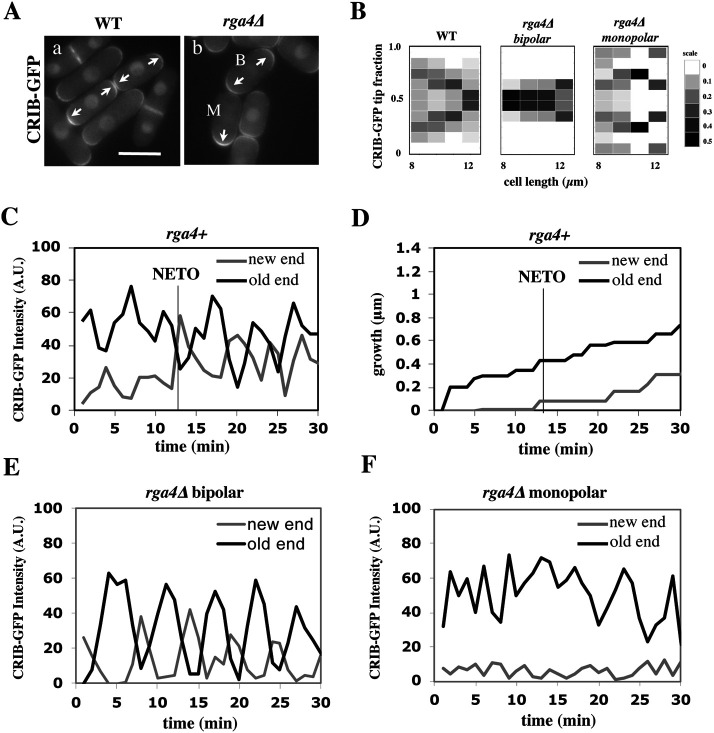
FIGURE 1:

Loss of Cdc42 GAP Rga4 leads to divergent patterns of Cdc42 dynamics in daughter cells. (A) CRIB-GFP intensity in wild-type sister cells and rga4∆ sister cells. Scale bar = 5 μm. (B) Heat map of CRIB-GFP distribution as a function of cell length in wild-type (N = 61), rga4∆ bipolar (N = 45), and rga4∆ monopolar (N = 61) cells. (C) CRIB-GFP intensity (A.U.) over time in the OE (black) and NE (gray) of a representative bipolar wild-type cell measured in 1-min intervals (N = 5). (D) Growth at the old (black) and new (gray) cell ends for the wild-type cell measured in C. The black line denotes the time at which the rate of growth changes in the new cell end (NETO). (E) CRIB-GFP intensity over time in the OE (black) and NE (gray) of a representative bipolar rga4Δ cell (N = 7) measured in 1-min intervals. (F) CRIB-GFP intensity (A.U.) over time in the OE (black) and NE (gray) of a representative monopolar rga4Δ cell (N = 7) measured in 1-min intervals.

As previously shown (Das et al., 2012), following cell division, wild-type cells initially exhibit an asymmetric distribution of active Cdc42, where most of the active Cdc42 is localized at the OE. As the cell increases in size, total levels of active Cdc42 are assumed to increase, allowing Cdc42-GTP to accumulate at the new cell end (NE), resulting in a more symmetrical distribution of active Cdc42 (Figure 1, Aa and B). Both wild-type daughter cells display similar behaviors. Conversely, in cells lacking rga4, daughter cells exhibit different Cdc42 distributions after cell division, consistent with one daughter cell remaining monopolar and one daughter cell activating bipolar growth (Figure 1, Ab and B). In monopolar rga4∆ daughter cells, active Cdc42 remains more asymmetrically enriched at one cell end as the cell grows (Figure 1, Ab cell M, and B), whereas bipolar rga4∆ daughter cells display a more symmetrical distribution of Cdc42-GTP (Figure 1, Ab cell B, and B).

According to our model, active Cdc42 intensities oscillate at the cell tips due to a process of autoamplification, time-dependent negative feedbacks, and competition between cell tips. Wild-type cells initially display asymmetric oscillations of Cdc42-GTP, with most of the active Cdc42 at the OE. As the cell grows and levels of active Cdc42 increase, Cdc42-GTP oscillations become more symmetrical (Figure 1C), allowing the cell to transition from monopolar to bipolar growth (Figure 1D). Consistent with rga4Δ cells remaining competent for Cdc42 oscillations (Das et al., 2012), we found that rga4Δ daughter cells that activate bipolar growth display anticorrelated oscillatory dynamics of Cdc42-GTP at both cell ends (Figure 1E), while rga4Δ daughter cells that are destined to remain monopolar exhibit Cdc42-GTP oscillations mainly at the OE (Figure 1F). This variability indicates that the initial state of the cell may be different among rga4Δ daughter cells, allowing for more or less symmetrical distributions of active Cdc42.

rga4Δ sister cells display divergent patterns of cell growth that are dependent on the growth pattern of the mother cell

Following cell division, wild-type daughter cells grow from the OE, the site that was previously growing in the mother cell (Figure 2, A and B). Activation of growth at the NE occurs later in the cell cycle, typically after the cell is longer than 9 μm in length (NETO) (Figure 1D; Supplemental Movie S1) (Mitchison and Nurse, 1985). In contrast to wild-type cells, newly born rga4∆ daughter cells exhibit divergent growth patterns (Das et al., 2007) (Figure 2A; Supplemental Movies S2 and S3). Some rga4∆ cells grow mainly from the OE, whereas other rga4∆ cells grow immediately from both ends, creating a population of rga4∆ mutant cells composed of both monopolar and bipolar cells (Figure 2A) (Das et al., 2007). When we followed the growth rate of divergent rga4∆ daughter cells, we found that the bipolar cells increase in cell volume faster than monopolar cells (Supplemental Figure 2, A–C).

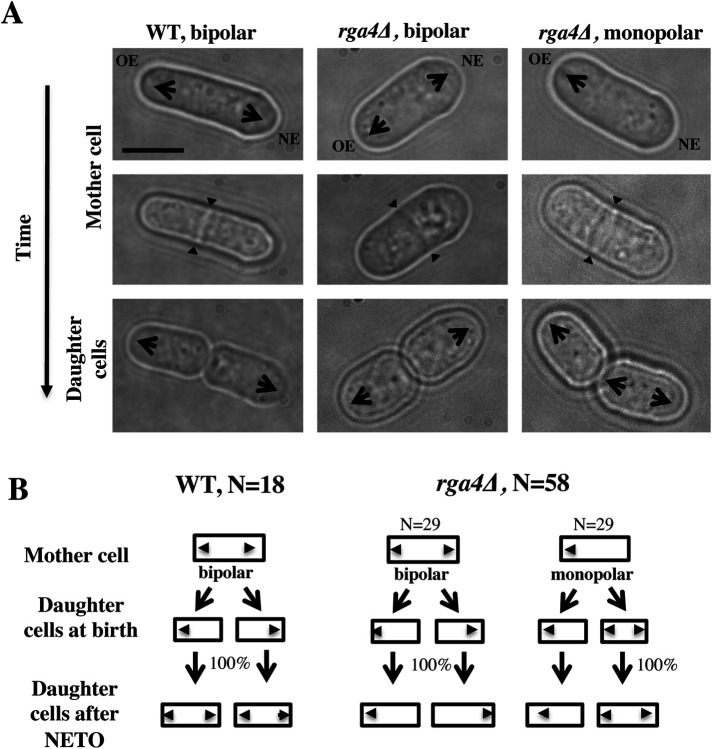
FIGURE 2:

Loss of Rga4 leads to divergent patterns of growth in daughter cells. (A) Time-lapse images showing initial growth patterns of daughter cells from bipolar wild-type, bipolar rga4∆, and monopolar rga4∆ mother cells. Scale bar = 5 μm. (B) Diagram of the growth pattern of bipolar wild-type, monopolar rga4Δ, and bipolar rga4Δ mother cells and their respective daughter cells (showing the initial pattern of growth for daughter cells soon after birth).

Movie S1.

Download video file ^{(6.8MB, mov)}

cell growth pattern of wild-type cells

Movie S2.

Download video file ^{(21.6MB, mov)}

cell growth pattern of rga4∆ cells (Movie 1)

Movie S3.

Download video file ^{(5.1MB, mov)}

cell growth pattern of rga4∆ cells (Movie 2)

To test if specific growth conditions in the mother cell affect polarized cell growth in the daughter cells, we performed a pedigree analysis in wild-type and rga4∆ cells by following cells in time by time-lapse microscopy. Wild-type mother cells generally grow in a bipolar manner as they approach mitosis. Newly born wild-type daughter cells first grow from the previously growing cell end (the “old” end) and then activate growth at the “new” end once they reach a minimal cell length (Mitchison and Nurse, 1985). This pattern of growth is similar in both daughter cells and is consistent from generation to generation (Figure 2B). When we examined the growth patterns of rga4Δ daughter cells arising from monopolar or bipolar mother cells, we found that the specific pattern of growth of daughter cells depends on the history of the mother cells: rga4Δ monopolar mothers always give rise to one monopolar cell that inherited the previously growing tip and one bipolar cell that inherited a tip that did not previously grow (Figure 2, A and B). On the other hand, daughters of bipolar mother cells, which both inherited a previously growing tip, remain monopolar throughout the cell cycle. Thus, our observations indicate that the presence of a previously growing cell tip alters Cdc42 dynamics and cell growth in the daughter cell that inherits it.

Mathematical modeling predicts different mechanisms of divergent Cdc42 dynamics in rga4∆ daughter cells

Since different distributions of active Cdc42 promote specific patterns of observed cell growth, we turned to mathematical modeling to explain the divergent Cdc42 dynamics observed in rga4∆ daughter cells. Our delay differential equation mathematical model for Cdc42 distribution and growth behavior of wild-type cells (Das et al., 2012) (Figure 3A) is the simplest model that contains the main elements needed to describe the polarity transition: saturated autoamplification, time-dependent negative feedbacks, and competition between cell tips. As a guide in the design and mechanistic interpretation of experiments, we thus sought the simplest generalization of this model able to reproduce the growth pattern of rga4∆ cells without attributing it to more subtle effects, such as difference in stochastic noise. We concluded there are three different possible modifications to explain the growth pattern of rga4∆ cells (Figure 3, B–D). For all three cases, we were led to assume an increase in the parameter C_sat that sets the maximum (saturating) amount of Cdc42 activation at each tip resulting from a balance between activation and inactivation (compared with the parameter used for wild-type cells; see Materials and Methods for details). This increase is anticipated in cells lacking GAP Rga4 that ought to be able to recruit larger concentrations of active Cdc42 and its regulators at the cell tip. The experimental observation of large amplitude oscillations for bipolar rga4∆ cells (Supplemental Figure S1B) further indicates a stronger competition between tips, despite the larger saturation threshold. This effect can be accounted by assuming an increase in parameter ε describing the strength of the delayed negative feedback deactivation rate. These changes are consistent with a lack of Rga4 enabling stronger Cdc42 activation at both tips. Given these parameter changes, our model suggests three hypotheses that can be formulated mathematically (see Supplemental Material for details):

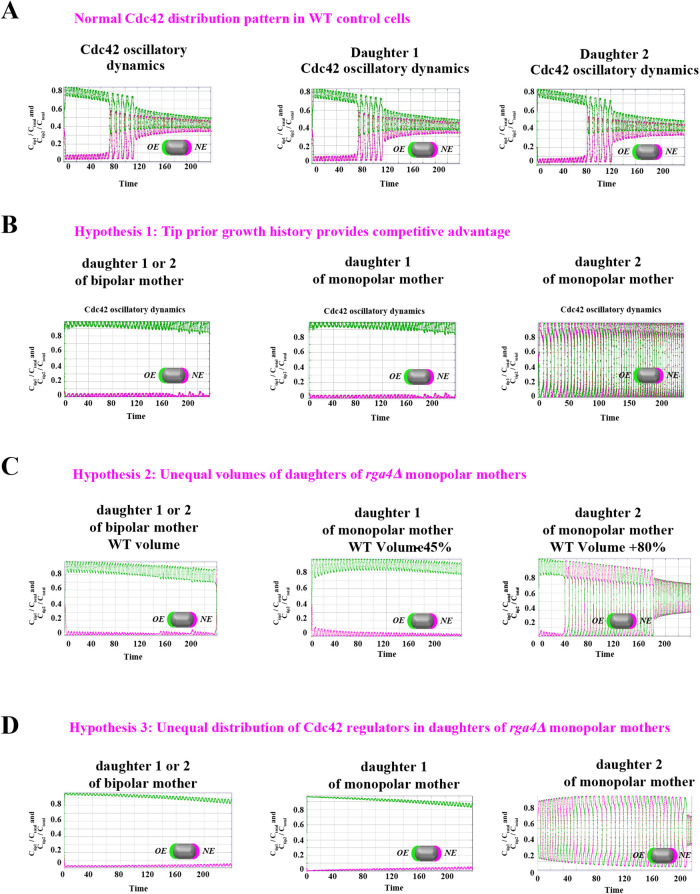
FIGURE 3:

Model describing the determinants of divergent Cdc42 dynamics in daughter cells. (A) Model results for WT cells. The levels of active Cdc42 are indicated by a ratio between the tip bound Cdc42 over the total Cdc42 in the cell (C_tip/C_total). The plot shows WT control results of model with tip aging, which match the results of a model by Das et al. (2012) without tip aging; Cdc42 is shown at the old (green) and new (red) cell ends. Following cell division, both wild-type daughter cells inherit a Cdc42 history that results in cells having similar Cdc42 dynamics. The tip-aging parameter time is shown in Supplemental Figure S3A. A difference to the model of (Das et al., 2012) without tip aging is that oscillations in the latter case are precisely symmetric, unlike the graphs in this panel in which the OE is stronger. (B) Diagram showing the predicted effect of previous history of Cdc42 activation on the symmetry of Cdc42 activation in rga4∆ daughter cells (Hypothesis 1). The mathematical model that describes Cdc42 dynamics (Das et al., 2012) was modified by 1) increasing the saturation constant and oscillation amplitude and 2) incorporating a tip-aging parameter based on the history of Cdc42 activation at the cell tips. The tip-aging parameter vs. time is shown in Supplemental Figure S3A. (C) Plots showing the effect of initial cell volume in rga4∆ cells (Hypothesis 2). Cells that start with half the volume of the mother or less (the first two graphs; the first graph has an initial value 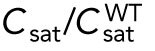= 6.5 as in A and B; the second graph has an initial value 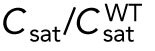= 2.925) remain asymmetric, while those that start with larger volume (the third graph, starting with 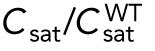= 11.7) encounter the coexistence region and exhibit symmetric oscillations for most part of their growth, corresponding to bipolar growth. (D) Results of a model with unequal distribution of Cdc42 regulators, represented by a growth-dependent rate constant (Hypothesis 3). The corresponding dependence of 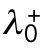on time is shown in Supplemental Figure S3B. Units of time are minutes.

1. The ability of each tip to activate Cdc42 depends on its prior growth history (Figure 3B: Tip Prior Growth History) (Supplemental Figure S3A). In the model of Figure 3B, this was implemented by introducing a tip-aging parameter that describes the rate of Cdc42 recruitment at a given cell tip. This parameter is a function of the history of prior Cdc42 accumulation at the tip and it represents permanent features acquired by cell tips over long growth periods (such as stable membrane-associated macromolecular complexes or cell-wall mechanical properties). According to this model, daughters that inherit a tip that has experienced prior growth remain monopolar because the nonaged new tip cannot compete to accumulate Cdc42 and thus cannot age to the same extent as the dominant tip. By contrast, the daughter of a monopolar mother that inherits the tip that did not grow prior to division starts with two nonaged tips that compete equally and thus enter a bipolar oscillatory state in which they exchange Cdc42 and age together. According to Hypothesis 1, the reason why wild-type cells do not exhibit the rga4∆ growth pattern is that despite aging occurring in wild-type cells, the resulting dynamics are similar to the original model without aging (Das et al., 2012): in wild-type cells, reduced competition between the two cells tips as compared with rga4∆ (quantified in terms of different parameters for C_sat, ε) allows for NETO, after which both tips can grow and age prior to division (Figure 3A; Supplemental Figure S3A). Thus, following cell division, each wild-type daughter cell inherits similar Cdc42 histories, resulting in similar Cdc42 dynamics and growth patterns (Figure 3A; Supplemental Figure S3A).

2. Cell volume is a dominant factor in the rga4∆ growth pattern (Figure 3C; Unequal Volumes of Daughter Cells). We assume that asymmetric cell growth of monopolar rga4∆ cells, persisting through the cell cycle to the point of cell division, could result in asymmetric cell shape or septum localization, generating daughters of unequal volume (but with approximately equal concentrations of Cdc42 and regulators otherwise). In the model, cell volume is assumed proportional to the total amount of Cdc42, or its regulators (parameter C_tot). Because of the larger amount of Cdc42 or regulators (larger initial C_tot), the larger daughter could already be closer to the coexistence region and thus start bipolar growth, exhibiting tip-to-tip oscillations, while the daughter with the smaller volume (smaller initial C_tot), remains in the monopolar oscillatory region (Supplemental Figure S1A). By contrast, daughters of bipolar mothers would divide in the middle, thus generating two daughters of equal volume, both growing in a monopolar manner. Figure 3C shows this is also a possible mechanism, though we note that this mechanism requires large volume differences between daughter cells (a 45% volume decrease for monopolar cells and an 80% volume increase for bipolar cells, as compared with wild-type cells; Figure 3C), and may only partly explain the rga4∆ growth pattern: since wild-type cells go through the coexistence region in the process of doubling their volume, either avoiding (small cells), or directly entering (large cells) this region, the striking rga4∆ phenotype requires starting from very divergent daughter cell volumes, as compared with the initial volume of wild-type cells (Figure 3C).

3. Unequal inheritance of Cdc42 regulators after division is the main contributor to the rga4∆ growth pattern (Figure 3D; Unequal Distribution of Cdc42 Regulators) (Supplemental Figure S3B). According to this hypothesis, the asymmetric growth of monopolar rga4∆ cells persists through the cell cycle to the point of cell division and thus the daughters of monopolar rga4∆ cells inherit different amounts of Cdc42 regulators (this is similar to Hypothesis 2, except that the difference between the two daughters is concentrations instead of volume). One daughter could thus start and stay in the bipolar oscillatory region while the other remains in the monopolar region. By contrast, daughters of bipolar mothers generate two daughters with equal concentrations of Cdc42 regulators (either positive or negative), both of which could grow in a monopolar manner. While we don’t specify the mechanism by which regulators of Cdc42 might be inherited unequally, unequal inheritance resulting from a monopolar growth pattern could be due to long-lived protein-bound states within or around the Cdc42 growth zone. One realization of this mechanism is illustrated in Figure 3D, where we assumed that parameter 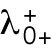starts at different levels in the two daughters of monopolar mothers. Parameter 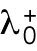describes the linear rate of Cdc42 activation, i.e., the activation rate without positive feedback, which enables the lagging tip to more easily accumulate enough active Cdc42 to trigger the positive feedback (for this reason, in Hypothesis 3, a change in parameter ε compared with wild-type cells was not needed to provide stronger competition). In this model, cell growth results in the relaxation of concentrations toward a reference value, which thus allows the pattern to repeat itself (Supplemental Figure S3B). Daughters of bipolar mothers maintain the reference concentrations inherited from their mothers during growth (Supplemental Figure S3B).

The three hypotheses cannot yet uniquely specify mechanisms at a molecular scale, are not mutually exclusive, and do not rule out more complex possibilities. However, by being simple generalizations of the wild-type model, our mathematical analysis demonstrates the minimum level of additional complexity that must be considered. It also provides us with a framework within which to examine the effects of experimental perturbations of rga4∆ cells in our effort to narrow down the mechanisms. As a background to testing the three hypotheses, we first cast a wide net using genetic screening methods to identify factors that alter the growth patterns and Cdc42 distribution in rga4∆ daughter cells.

A genome-wide screen identifies determinants of Cdc42 dynamics in rga4∆ daughter cells

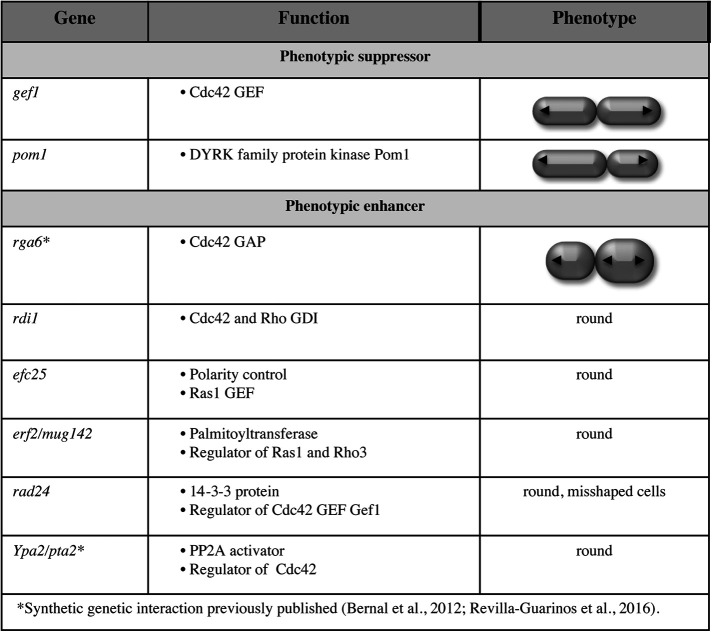
To identify polarity regulators that may functionally interact with Rga4, we performed a synthetic genetic array (SGA) screen to identify mutations that suppress or enhance the polarity and growth pattern defects observed in rga4Δ mutants. We crossed the rga4Δ strain (FV1529) with the Bioneer fission yeast deletion library (Kim et al., 2010) and visually screened the double mutants for changes in morphology or colony growth. This analysis identified several regulators of polarity and cytokinesis as functionally interacting with Rga4 (Figure 4). Gene functions that normalize the growth pattern of rga4∆ mutants, when deleted, include a regulator of Cdc42 activation, the Cdc42 GEF Gef1 (Das et al., 2015), and a factor involved in division site placement, the DYRK family protein kinase Pom1 (Tatebe et al., 2008). Conversely, loss of other Cdc42 regulators enhanced the morphological defects of rga4∆ mutants; these include the Cdc42 GDI Rdi1 (Bendezu et al., 2015), the Cdc42 GAP Rga6 (Revilla-Guarinos et al., 2016), and the PP2A activator, Ypa2/Pta2 (Bernal et al., 2012). Loss of efc25, a Ras1 GEF that controls Ras1 GTPase activity and promotes Cdc42 polarization, produced round cells in the rga4∆ background. The functional interaction of Rga4 with Ypa2/Pta2 and with Cdc42 regulator Rga6 have been previously reported (Bernal et al., 2012; Revilla-Guarinos et al., 2016). Thus, gene functions that normalize the pattern of growth of the bipolar daughter cell, preventing precocious bipolar growth activation, when mutated, decrease Cdc42 activity (gef1∆) or affect the placement of the site of division (pom1∆), while gene mutations that enhance the morphological asymmetry of rga4∆ cells lead to increased Cdc42 activity (rga6∆).

FIGURE 4:

Polarity factors that alter the growth pattern or cell morphology of rga4∆ cells. SGA screen to identify factors that alter the growth pattern of rga4∆ cells. Loss of the Cdc42 GEF Gef1 and the DRCK kinase Pom1 suppress aspects of the rga4∆ phenotype. Loss of the Cdc42-negative regulators, the GDI Rdi1, and the Cdc42 GAP Rga6 worsen the morphology of rga4∆ bipolar cells. The functional genetic interactions of rga4 with rga6 and ypa2/pta2 have been previously published (Bernal et al., 2012; Revilla-Guarinos et al., 2016).

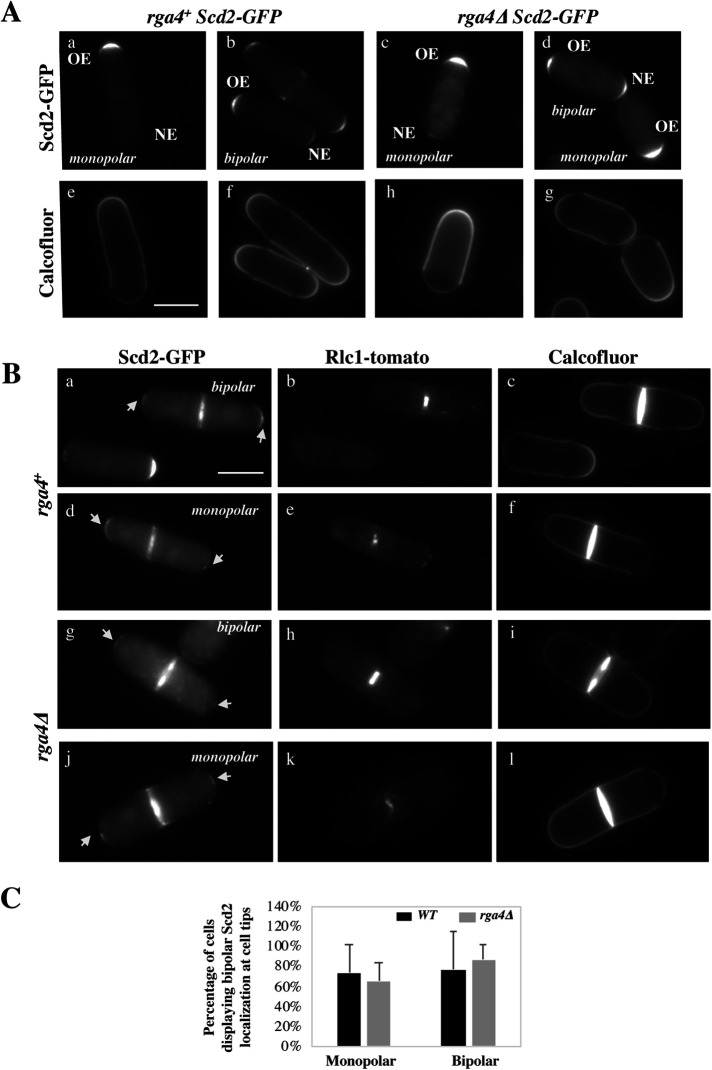
Localization of the Cdc42 scaffold Scd2 is not altered in rga4∆ daughter cells

The asymmetric Cdc42 dynamics and growth patterns observed in rga4Δ daughter cells can be explained by the presence of a “tip aging” factor that accumulates as each tip grows (Hypothesis 1 in Figure 3B). An attractive candidate for this function is the scaffold Scd2, a component of the polarisome, that has an important role in Cdc42 autoamplification (Lamas et al., 2020a). Scd2 average distribution correlates with Cdc42 levels and cell growth at the tips: during interphase, Scd2-GFP localizes asymmetrically in monopolar wild-type cells, whereas in bipolar wild-type cells, Scd2-GFP is distributed more symmetrically (Figure 5A; Supplemental Figure S4A). Conversely, in rga4∆ daughter cells, Scd2-GFP distribution is very symmetrical even in small bipolar cells, while it is mostly asymmetrical in monopolar rga4∆ cells (Supplemental Figure S4A).

FIGURE 5:

Small amounts Scd2-GFP remain at both cell tips during cell division in wild-type and rga4∆ cells. (A) Scd2-localization in wild-type and mutant rga4∆ monopolar and bipolar cells. (B) Images of Scd2-GFP (arrows) in septated cells during constriction of the actomyosin ring, visualized using Rlc1-tomato. Scd2-GFP is present at the tips in wild-type and rga4Δ mother cells during actomyosin ring constriction. (C) Scd2-localization at the cell tips during cell division in wild-type and mutant rga4∆ monopolar and bipolar cells (percentage of either total monopolar or total bipolar cells is shown, where Scd2 is visible).

Thus, to test if Scd2 has a role as a “tip aging” factor that “marks” the previously growing tip, we analyzed the distribution of the Cd42 scaffold Scd2 during cell division in wild-type and rga4∆ cells. We stained the cells with Calcofluor to better visualize the pattern of cell growth (monopolar or bipolar), and we used cells expressing Rlc1-GFP (a septation marker; Naqvi et al., 2000) to identify cells in later stages of cell division. Remarkably, we observed that a small amount of Scd2 remains localized to the cell tips in wild-type cells undergoing mitosis and cytokinesis (Figure 5Ba–f), albeit at a much lower level as compared with interphase cells (Figure 5A). Both bipolar and the few monopolar wild-type cells display Scd2 markings at the tips. This novel finding indicates that Scd2 may indeed serve as a tip marker, conferring memory of the history of Cdc42 activation at previously growing cell tips.

Thus, we hypothesized that monopolar rga4∆ cells may exhibit asymmetric localization of Scd2-GFP between previously growing and nongrowing tips, and that this imbalance may account for the different growth patterns and Cdc42 dynamics in rga4∆ daughter cells. When we analyzed monopolar and bipolar mother cells, however, we found no significant difference in the levels of Scd2-GFP during cell division at the two tips in monopolar and bipolar cells from both wild-type and rga4Δ mutant cell cultures (Figure 5, Bg–l, and C).

These results suggest that, while Scd2 permanence at the cell tips may have a role in “marking” growing cell tips and promoting cell polarization after mitosis, the divergent Cdc42 dynamics observed in rga4Δ sister cells do not arise from asymmetric inheritance of the Scd2 complex at the cell tips.

Does decreasing the initial cell size of bipolar rga4∆ daughter cells abolish bipolar growth?

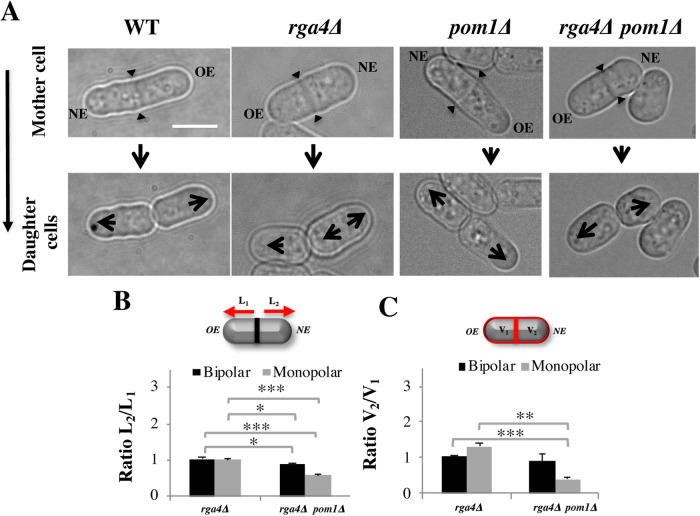
We identified the kinase Pom1 as a suppressor of the rga4∆ phenotype. The DYRK kinase Pom1 is an established regulator of the placement of the division site (Bahler et al., 1998; Rincon et al., 2014), possibly revealing the effects of initial volume (Hypothesis 2). In cells that lack pom1, the cell septum forms closer to the new cell end, generating daughter cells with different volumes (Bahler et al., 1998). Loss of pom1 in rga4∆ mutant cells indeed shifted the site of cell division toward the new cell end, particularly in monopolar rga4∆ mother cells (Figure 6A). This shift decreased the initial volume of the daughter cell inheriting the nongrowing NE, which would normally be destined to be bipolar (Figure 6C). When we followed the growth pattern of daughter cells, we found that all monopolar pom1∆ rga4∆ mother cells gave rise to daughter cells that started growing in a monopolar manner (Figure 6A) (n = 15), whereas all monopolar control rga4∆ mother cells gave rise to one monopolar and one bipolar cell (n = 18). These observations are consistent with the idea that decreasing the initial size of the cell that inherits a nongrowing tip prevents precocious bipolar growth activation. However, it should be noted that pom1∆ cells display decreased percentages of bipolar cells (Koyano et al., 2010) to a similar extent (3:1 monopolar to bipolar ratio) as what was found in our experiments for rga4∆ pom1∆ cells. Pom1 kinase has a variety of substrates, several of which have a role in cell polarity, such as Mod5, Tea4, and GTPases with a role in morphogenesis (Kettenbach et al., 2015). So while it is intriguing that loss of Pom1 restores normal growth (such as OE dominance) in the bipolar rga4∆ cell, it is also possible that the suppression of the rga4∆ phenotype is mediated by decreased phosphorylation of these polarity factors, rather than a decrease in cell volume in one of the daughter cells.

FIGURE 6:

Loss of DYRK-family kinase Pom1 suppresses precocious bipolar cell growth in rga4∆ mutant cells. (A) Pattern of growth in WT, rga4∆, and rga4∆ pom1∆ cells. Scale bar = 5 μm. Large arrows indicate direction of mono- or bipolar growth. Small triangular arrows indicate sites of septation. (B) Quantification of the ratio of the distances between the septum to the cell tip in septated rga4∆ (bipolar N = 10, monopolar N = 10) and pom1∆ rga4∆ (bipolar N = 5, monopolar N = 19) cells. Statistical analysis was done using analysis of variance (ANOVA) followed by Tukey HSD post hoc test (p = 0.011; p = 000; p = 0.018; p = 000) based on three independent experiments. (C) The quantification of the ratio of the volume in the two compartments in septated cells. Statistical analysis was done using ANOVA followed by a Tamhane post hoc test based on three independent experiments (p = 0.000; p = 0.006).

Cdc42 GTPase regulators control the cell growth pattern of rga4∆ daughter cells

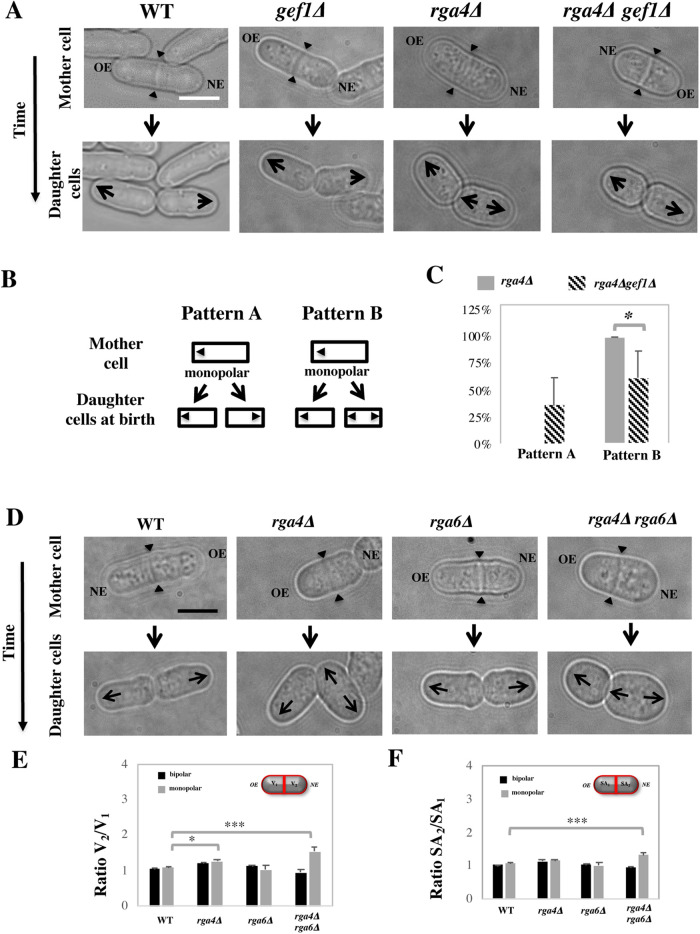
The presence of different amounts of Cdc42 regulators can also account for divergent Cdc42 dynamics in rga4∆ daughter cells (Hypothesis 3). SGA analysis revealed a suppressor interaction between Rga4 and Cdc42 GEF Gef1 (Figure 4). We have previously shown that Gef1 and Rga4 have opposing effects in the control of Cdc42 activation at the cell tips and cell diameter (Das et al., 2015). Cells expressing a mutated form of gef1 (gef1S112A) that increases Gef1 cortical localization exhibit precocious bipolar growth activation (Das et al., 2015). Thus, we tested if loss of gef1 suppresses the distinct growth pattern of rga4∆ daughter cells by reducing the activity of Cdc42 in the bipolar cell. Indeed, we found that cell growth in rga4∆ gef1∆ daughter cells was normalized, with a significantly increased percentage of daughter cells from monopolar rga4∆ mother cells growing in a monopolar manner, as compared with control gef1+ rga4∆ cells (Figure 7, A–C). Hence, decreased levels of Cdc42 activity suppresses the precocious cell growth at the NE of rga4∆ daughter cells destined to be bipolar.

FIGURE 7:

(A–C) Loss of Cdc42 GEF Gef1 partially suppresses precocious bipolar cell growth in rga4∆ mutant cells. (A) Time-lapse DIC images of wild-type, monopolar gef1∆, monopolar rga4∆, and monopolar rga4∆ gef1∆ cells showing the growth patterns of daughter cells. (B) Diagram showing two alternative growth patterns of daughter cells born from monopolar cells. In pattern A, both daughter cells were grown in a monopolar manner after birth, whereas in pattern B, one daughter cell grows in a monopolar manner and the other daughter cells exhibit bipolar growth after birth. (C) Quantification of the proportion of rga4∆ (N = 29) and rga4∆ gef1∆ (N = 14) monopolar mother cells exhibiting either growth pattern A (two monopolar daughter cells) or growth pattern B (one monopolar and one bipolar daughter cell). Statistical analysis was done using an independent T test with SPSS statistics package 22.0 based on six independent experiments (p = 0.013). (D–F) Loss of rga4∆ and rga6∆ produces daughter cells with different cell volumes. (D) Time-lapse DIC images of wild-type, rga4∆, rga6∆, and rga4∆ rga6∆ cells undergoing cell division. Arrowheads indicate the position of the cell septum. Scale bar = 5 μm. (E) Quantification of the ratio of the cell volumes of the two compartments in septated cells in wild-type (bipolar N = 63, monopolar N = 12), rga4∆ (bipolar N = 52, monopolar N = 17), rga6∆ (bipolar N = 58, monopolar N = 5), and rga4∆ rga6∆ (bipolar N = 21, monopolar N = 43) strains. Statistical analysis was done using ANOVA with SPSS statistics package 22.0, followed by Tukey HSD post hoc test based on three independent experiments (p = 0.018; p = 0.000; p = 018; p = 0.000). (F) Quantification of the ratio of the surface area in the two compartments as previously done in B. Statistical analysis was done using ANOVA followed by Tukey HSD post hoc test based on three independent experiments (p = 0.022; p = 0.000)

SGA analysis also revealed a functional interaction between Rga4 and another Cdc42 GAP in S. pombe, Rga6 (Revilla-Guarinos et al., 2016) (Figure 4). We found that, consistent with the partially overlapping functions of Rga4 and Rga6 (Revilla-Guarinos et al., 2016), loss of rga6 in the rga4∆ mutant exacerbates the asymmetric morphology observed in rga4∆ daughter cells (Figure 7D). Using the Pombe Measurer ImageJ plugin (F. Chang, University of California, San Francisco [UCSF]), we calculated the volume (Figure 7E) and surface area (Figure 7F) of the two cell compartments in septated monopolar and bipolar mother cells from WT, rga4∆ and rga4∆ rga6∆ cell cultures. We found that loss of Rga6 significantly increased the volume (V₂/V₁) (Figure 7E) and surface area (SA₂/SA₁) (Figure 7F) ratios of the two compartments in the rga4∆ background, as compared with wild-type cells (where V₁ or SA₁ are the OE compartment and V₂ or SA₂ are the NE compartment). These results suggest that daughter cells from monopolar mothers inherit divergent starting cell morphologies and cell volumes: the rga4∆ cell inheriting the previously growing end is generally slightly smaller, a phenotype exacerbated by loss of rga6 (Figure 7D). As rga4∆rga6∆ daughter cells continue to grow, they display a growth pattern similar to that of rga4∆ single mutant cells; however, loss of Rga6 further enhances the divergent growth rates of rga4∆rga6∆ daughter cells, leading to much larger bipolar cells than monopolar cells (Supplemental Figure 3B). Thus, loss of the second Cdc42 GAP, Rga6, reveals that the “bipolar” daughter cell that inherits the NE has different morphological properties than the “monopolar” daughter cell that inherits the OE.

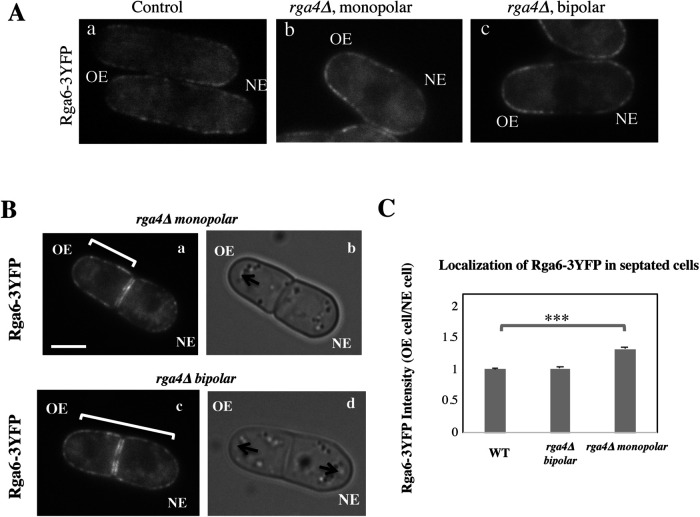
Cdc42 GAP Rga6 distribution is asymmetrically inherited during cell division in rga4∆ cells

Since loss of Cdc42 GAP Rga6 exacerbated the asymmetric phenotype of rga4∆ mutants, we investigated whether loss of Rga4 alters the distribution of Rga6 at the cell membrane. To test this, we measured the intensity of Rga6-3YFP throughout the cell membrane in interphase wild-type and rga4∆ cells. We found that monopolar rga4∆ cells exhibit an asymmetric distribution of Rga6-3YFP which is increased near the OE and depleted from the NE of the cell (Figure 8Ab). Conversely, wild-type cells (Figure 8Aa) and bipolar rga4∆ cells (Figure 8Ac) display a more symmetrical Rga6 distribution, enriched near both the OE and the NE. Importantly, we found that this distribution is maintained throughout mitosis and is inherited by the daughter cells (Figure 8, B and C). In dividing monopolar rga4∆ cells, the daughter cell that inherits the growing end (OE cell, Figure 8C) also acquires increased amounts of Rga6 (Figure 8Ba,b), as compared with the daughter cells that inherit the nongrowing end (NE cell). Conversely, this asymmetric inheritance is not found in wild-type cells (Figure 8C) or in rga4∆ bipolar cells (Figure 8, Bc,d and C). Rga6 localization is likely determined by the specific pattern of growth of cells during interphase (Figure 8A), where we find Rga6 localization to be more asymmetrical early in the cell cycle in monopolar cells to become more symmetrically distributed once NETO occurs.

FIGURE 8:

Distribution of Cdc42 GAP Rga6 to daughter cells is different in monopolar or bipolar rga4∆ mother cells. (A) Distribution of Rga6-3YFP in interphase control, monopolar rga4∆ and bipolar rga4∆ cells. (B) Localization of Rga6-3YFP in rga4∆ dividing cells. Scale bar = 5 μm. (C) Ratio of Rga6-3YFP intensities at the cell membrane, in the OE containing compartment over the NE containing compartment, in septated cells; in bipolar wild-type (N = 25), rga4∆ bipolar (N = 25), and rga4∆ monopolar (N = 31) cells. Statistical analysis was done using ANOVA followed by Tukey HSD post hoc test based on three independent experiments (p = 0.000). (C) Distribution of Rga6 in interphase control, monopolar rga4∆, and bipolar rga4∆ cells.

The localization of two other Cdc42 regulators, the GEFs Scd1 and Gef1, do not display visible differences in dividing monopolar or bipolar rga4∆ mother cells (Supplemental Figure S5A). The third Cdc42 GAP, Rga3 (Gallo Castro and Martin, 2018), displays a very faint localization at the cell tips of dividing cells (Supplemental Figure S5B). Rga3 likely has a role in cell polarization following cell division (Supplemental Figure S6B), since loss of all three Cdc42 GAP proteins leads to almost complete loss of polarity (Gallo Castro and Martin, 2018). While Rga3 localization does not appear significantly altered in dividing monopolar rga4∆ cells (Supplemental Figure 5B), in rga4∆rga6∆ cells, however, Rga3 localization appears more disrupted, particularly in monopolar dividing cells (Supplemental Figure 6A).

These observations, showing that daughter cells of rga4∆ monopolar cells inherit different amounts of Cdc42 GAP Rga6 at the membrane, may explain how different distributions of active Cdc42-GTP are present in rga4∆ sister cells immediately following cytokinesis. Taken together, our results support the notion that divergent rga4∆ daughter cells are born with distinct initial conditions, resulting in different growth patterns. We show that negative regulators of Cdc42 activation, the Cdc42 GAPs Rga4 and Rga6, have a crucial role in ensuring that S. pombe daughter cells follow similar morphological destinies. Since Rga6 localization becomes more biased toward the growing cell end in monopolar rga4∆ cells, these findings suggest that Cdc42 GAP proteins provide a link between the history of cell growth in the mother cell and the initial state of Cdc42 activation distribution in daughter cells.

DISCUSSION

The pattern of growth in the mother cell determines the Cdc42 oscillatory dynamics and distribution in daughter cells

We previously showed that Cdc42 exhibits oscillatory dynamics, and that the relative amounts of active Cdc42 at the cell tips determines the pattern, either monopolar or bipolar, of cell growth (Das et al., 2012). We proposed a mathematical model that describes the distribution of active Cdc42 GTPase at the cell tips in fission yeast cells (Das et al., 2012), and one of the predictions of this model is that the initial state of Cdc42 activation distribution in newly born daughter cells has an important role in defining the future behavior of the system. Thus, in this paper, we asked the question: what determines the initial state of Cdc42 dynamics in newly born daughter cells? To answer this question, we analyzed Cdc42 dynamics in rga4∆ cells that are missing one of the three fission yeast Cdc42 GAPs, Rga4. We previously reported that loss of rga4 confers divergent patterns of growth in daughter cells, where one cell remains monopolar, while the other displays precocious activation of bipolar growth (Das et al., 2007). Here we show that, consistent with their mode of growth, rga4∆ daughter cells show divergent Cdc42 dynamics: one daughter displays highly asymmetric while the other displays highly symmetric, active Cdc42 dynamics and distribution. Further, we find that the particular Cdc42 dynamics of rga4∆ cells are determined by the mode of growth, either monopolar or bipolar, of the mother cell. Thus, these observations reveal a link between the mode of cell growth in the previous cell cycle and the morphological fate of daughter cells.

In wild-type cells, cells start to grow from the “New” end, and thereby activate bipolar growth, in a process called “NETO” (Mitchison and Nurse, 1985) usually later in the cell cycle, during the G2 phase. Thus, once the mother cell divides, both daughter cells inherit one end that had previously been growing (the “old” ends), and following cell division, both daughter cells behave similarly, activating the OEs first. The functional purpose of this process has been relatively elusive. In rga4Δ cells, the consequences of not activating NETO become more evident: if the mother cell is monopolar, the daughter cell that inherits the never-activated cell tip displays symmetric Cdc42 activation and grows symmetrically from both cell ends, generating a different morphology than its sister cell. Our observations suggest a novel function for NETO, in enabling cells to maintain consistent Cdc42 dynamics and cell polarization, across generations.

A mathematical model of Cdc42 oscillations predicts different mechanisms for divergent Cdc42 dynamics in daughter cells

The distinct oscillatory dynamics of Cdc42 in monopolar and bipolar rga4Δ cells can be explained by three different minimal variations of our mathematical model (Das et al., 2012), which represent three possible mechanisms reproducing Cdc42 dynamics observed in the rga4∆ daughter cells.

The first hypothesis invokes a tip-aging parameter that produces an asymmetry in the Cdc42 history between the two cell tips. In this hypothesis, the divergent behavior of rga4∆ sister cells results from inheriting different levels of an “end marker” that accumulates with cell growth. Mathematically, this model was implemented by introducing tip-aging dimensionless parameters 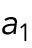and 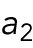, which describe how the rate of Cdc42 recruitment at either tip increases as a result of a history of prior growth. Following cell division, active Cdc42 is predicted to oscillate around different averages at the two cell ends, as we observe in monopolar rga4∆ cells, that have inherited one “marked” end. Conversely, the lack of previous Cdc42 activation at both cell tips, and thus a more symmetric Cdc42 history, yields similar average Cdc42 activation at the two cell ends and more symmetric Cdc42 oscillations, as we observe in bipolar rga4Δ cells (Das et al., 2012).

The second hypothesis involves asymmetric cell division, whereby the rga4∆ daughter cells inherit different cell volumes. Cdc42 dynamics are affected by the concentrations of Cdc42 regulators available to activate Cdc42. Larger cell volumes, which increase the availability of cytoplasmic Cdc42 regulators, lead to increased Cdc42 activity at the NE and thus to more symmetrical Cdc42 oscillations at both ends (Das et al., 2012). Mathematically, daughters of monopolar rga4∆ mothers cells start with different total amounts of Cdc42 or regulators (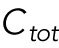) in proportion to the differences in volume. The equations for this model are the same as the ones in Das et al. (2012).

Finally, the third hypothesis invokes the asymmetric inheritance of Cdc42 regulators, which could be GEFs or GAPs in the two daughter cells. Mathematically, parameter 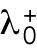(linear rate of Cdc42 activation) starts at different levels in the two daughters of monopolar mothers; cell growth results in the relaxation of concentrations represented by 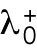toward a reference value. This effect would lead to different Cdc42 dynamics in the two daughter cells; indeed, increasing the level or availability of the Cdc42 activator Gef1 by overexpression, or by specific mutations, leads to more symmetrical Cdc42 oscillations at both ends (Das et al., 2012; Das et al., 2015).

Mutant alleles of Cdc42 regulators functionally interact with rga4, modulating Cdc42 dynamics and growth pattern in rga4∆ daughter cells

To search for clues for distinguishing among the different hypotheses of the model, we first used a SGA screen to search for gene functions that modulate the pattern of cell growth in rga4∆ daughter cells. We identified several suppressors that drive the bipolar daughter cell to grow in a monopolar manner when deleted in the rga4∆ background, including gef1 (encoding a Cdc42 GEF; Coll et al., 2003), and pom1 (encoding a DYRK kinase that controls the placement of the septum; Bahler and Nurse, 2001). Our SGA screen also revealed functional interactions that enhanced the morphological phenotypes of rga4∆ cells, in particular other negative regulators of Cdc42, including the Cdc42 GDI Rdi1, and the Cdc42 GAP Rga6. Overall, this screen indicated that precocious bipolar growth and shape asymmetry of rga4∆ daughter cells could be ameliorated by decreasing Cdc42 activation (gef1∆) and it could be enhanced by loss of a second Cdc42 GAP, Rga6.

Genetic analysis to analyze the different hypotheses of the model

To establish which of the three alternative model hypotheses are most consistent with experimental observations in live cells, we followed the localization of Cdc42 complex components in both rga4∆ cells and cells with additional gene mutations identified by SGA analysis.

Hypothesis 1 invokes the presence of a tip-aging parameter. When introduced into our mathematical model, this tip-aging parameter models how cell growth progressively “marks” the cell tip in the mother cell. The “mark” accumulates at higher values at the tips that grow for the longest time (OE) and then remains at the cell tips throughout mitosis. In the following generation, the “mark” promotes the activation of Cdc42, thus affecting the pattern of cell growth. Cells that never activated the NE (such as rga4∆ monopolar mother cells) produce one daughter cell that is born without any mark, causing symmetrical Cdc42 activation and bipolar cell growth. We considered the possibility that a growth-dependent marker directs the organization of the Scd1/Scd2 GEF complex that activates Cdc42 at the cell tips. Because the organization and amplification of Scd1 at the cortex depends on the scaffold protein Scd2, we asked whether Scd2 remains at the tips during mitosis. We measured the intensity of Scd2-GFP at the cell tips of septated cells and found that while most Scd2-GFP is redistributed to the site of cell division, small amounts of Scd2-GFP can also be observed at the cell tips in WT and rga4Δ cells during cell division. This interesting finding suggests that Scd2 may indeed have a function in WT cells to promote Cdc42 amplification at the OE following mitosis. However, we found Scd2-GFP is similarly present at both tips in either rga4∆ monopolar or rga4∆ bipolar cells undergoing cell division, suggesting that the divergent Cdc42 dynamics observed in daughters of monopolar rga4Δ mother cells do not depend on asymmetric inheritance of the Scd2 complex. While the mechanism of Hypothesis 1 might be realized in a more complex manner in cells, neither our SGA analysis nor analysis of our best candidate, Scd2, provided hints to support it.

The second hypothesis invokes the effects of asymmetric cell division of the monopolar mother cell, leading to daughter cells of different cell volumes. This hypothesis requires the bipolar daughter cell to be significantly larger than the monopolar cell. The cell born with a larger cell volume or larger surface area would then display initial conditions that favor bipolar growth, because it contains larger amounts of Cdc42 activators or a higher concentration of polarity factors at the cell cortex. Thus, we analyzed the dimensions of the two rga4∆ daughter cells. We found that the rga4∆ bipolar daughter cell is indeed larger than the monopolar rga4∆ daughter cell. Consistent with volume affecting the levels of Cdc42 activation, decreasing the volume of the bipolar cell by introduction of the pom1∆ mutation restores the normal, monopolar pattern of growth in young daughter cells that would otherwise be bipolar. A caveat of the rga4∆ pom1∆ experiments is that the normalization of the growth pattern of the bipolar cells (which now grow in a monopolar manner) could be also explained by other functions of the Pom1 kinase, such as direct phosphorylation of polarity control substrates (Kettenbach et al., 2015). Nevertheless, the difference in volumes between rga4∆ monopolar and rga4∆ bipolar daughter cells at birth is rather small (approximately 20%), much smaller than the volume differences that our mathematical model requires to induce a significant change in the behavior of the system. Furthermore, we found that a small volume asymmetry is also sometimes observed in daughters of bipolar mothers that continue to grow in a monopolar way. Thus, these observations suggest that volume asymmetries are not sufficient to generate divergent Cdc42 dynamics in the rga4∆ daughter cells.

Finally, the third hypothesis implicates an asymmetric inheritance of Cdc42 regulators in rga4∆ daughter cells to explain divergent Cdc42 dynamics. Gef1 and Rga4 cooperate to regulate the active Cdc42 distribution at the cell ends (Das et al., 2015). Manipulating the levels of Gef1 and Rga4 controls cell diameter and bipolar cell growth (Das et al., 2015). This finding suggested that divergent growth patterns present in rga4∆ mutant cells may be a consequence of cells having different levels of Cdc42-GTP. Indeed, we found that loss of Cdc42 GEF gef1 partially suppresses the divergent growth patterns observed in rga4∆ mutant cells, suggesting bipolar rga4∆ cells may have different initial levels of Cdc42 activity, as suggested by the model predictions of hypothesis three. However, we did not find evidence for asymmetrical localization of Cdc42 GEF Scd1 (which displays a similar localization as Scd2) or Cdc42 GEF Gef1 (which is normally not visible at cell tips; Das et al., 2015) in rga4∆ newly born daughter cells, indicating that asymmetric inheritance of Cdc42 GEFs is likely not the reason for divergent Cdc42 dynamics.

In our SGA screen, we found that in cells that lack rga4 or both rga4 and rga6, the daughter cell that lacks a previously growing end is born with a greater volume than the daughter cell that inherits a previously growing end. This asymmetry in cell volume is not due to misplacement of the septum along the center axis of the cell (not shown). Rather, monopolar rga4∆ cells and rga4∆ rga6∆ cells have a broader tip at the nongrowing end than at the growing end, an effect that is more dramatic in the double mutant. This difference in tip shape alters the overall shape and surface area of the cell, which becomes broader near the nongrowing cell end. Thus, rga4∆ cells display an irregular cell shape, dividing asymmetrically even when the septum is placed in the middle of the center axis of the cell. This morphological asymmetry is further amplified by loss of a second Cdc42 GAP protein, Rga6. It is only with the loss of the third Cdc42 GAP, Rga3, that both daughter cells display a similar, almost complete loss of polarization. Indeed, Rga4, Rga6, and Rga3 perform roles that are redundant in the control of cell polarization (Revilla-Guarinos et al., 2016; Gallo Castro and Martin, 2018; Lamas et al., 2020b), where progressive loss of one or more Cdc42 GAPs leads to more profound loss of cell polarity. Thus, collectively, our findings indicate that changes in daughter cells’ pattern of growth are due to altered inheritance of Cdc42 regulators, and in particular Cdc42 GAP proteins, at the time of division.

A role for Cdc42 GAP proteins in linking the pattern of cell growth in the mother cell to Cdc42 dynamics in the daughter cells

Rga4 is a negative regulator of Cdc42-GTP, and its lateral localization helps to define a dynamic border that limits the extent of Cdc42 activation to the cell tips (Das et al., 2015; Lamas et al., 2020b). Consistent with this function, rga4Δ cells have broader distribution of active Cdc42 and a wider cell diameter (Kelly and Nurse, 2011; Das et al., 2015; Lamas et al., 2020b). Rga6, a second Cdc42 GAP in fission yeast, cooperates with Rga4 in the control of Cdc42 dynamics, cell dia­meter, and polarized cell growth (Lamas et al., 2020b; Revilla-Guarinos et al., 2016). Here we show that Rga6 localization is more asymmetrically localized toward the single growing cell tip in rga4∆ monopolar mother cells: this asymmetry reflects the pattern and history of cell growth of the mother cell.

Thus, immediately following cell division, newly born rga4∆ cells inherit different levels of Rga6 at the cell membrane in a manner that depends on the pattern of growth of the mother cell. Loss of rga4, by altering the distribution of Rga6, further reduces the negative regulation of Cdc42 in cells that do not inherit a previously growing OE; in these cells, Cdc42 oscillations are immediately symmetrical and cell growth bipolar (Figure 9).

FIGURE 9:

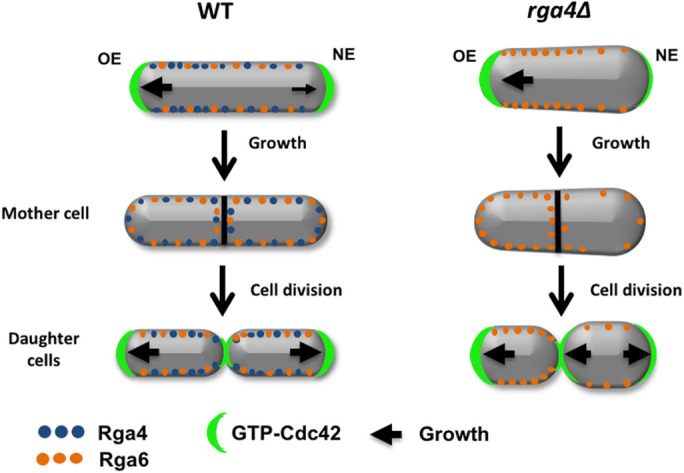
Role of Cdc42 GAP proteins in the inheritance of cell polarity and growth patterns. Cdc42 GAP Rga4 displays a distribution with a bias toward the old growing end in wild-type cells (Das et al., 2007; Tatebe et al, 2008). In mutants that lack rga4, Cdc42 GAP Rga6 distribution becomes more asymmetrical in monopolar cells, resulting in daughter cells with different initial volumes and Cdc42 activity. Different levels of active Cdc42 between the two daughter cells lead to divergent growth patterns.

Overall, our experimental observations support Hypothesis 3 of our mathematical model, which predicts how the presence of different amounts of Cdc42 regulators can generate different Cdc42 dynamics in rga4∆ daughter cells. Additionally, rga4∆ daughter cells display subtly different cell volumes, which may also contribute to divergent Cdc42 dynamics, as predicted by Hypothesis 2 of our mathematical model. Thus, it is also possible that the rga4∆ phenotype derives by a combinatorial effect of asymmetric inheritance of Cdc42 regulators (Hypothesis 3) and a subtle difference in initial cell volumes at the start (Hypothesis 2).

Conversely, we did not find experimental evidence to support the idea of a tip-aging “marker” that promotes Cdc42 activation in daughter cells (Hypothesis 1). Interestingly, we find mathematically that the presence of a tip-aging marker renders the system less able to switch to more symmetrical oscillations, when the time-dependent growth of a wild-type cell is modeled, in the presence of noise (Supplemental Figure S7). This suggests that the presence of a “mark” could actually be detrimental to Cdc42 redistribution in the cell and impede bipolar growth activation. Indeed, the robustness of the third mathematical hypothesis is also supported by the fact that the addition of noise reproduces the transient transitions to bipolar oscillations, sometimes observed in time-lapse images of monopolar rga4∆ cells. Such transient transitions that do not result in permanent growth pattern change, together with all demonstrated differences in concentrations and size between rga4∆ daughter cells, indicate that the growth pattern of rga4∆ cannot be fully explained by rga4∆ daughter cells finding themselves into either monopolar or bipolar valleys of attraction of a coexistence region that maintains itself through the cell cycle (Cerone et al., 2012). We instead suggest that the coexistence region may be encountered at different growth stages for different daughter cells. The observation of transient transitions indicates that noise and stochastic transitions might be important to consider in future experimental and modeling efforts. For example, the addition of noise to rate the model’s constants facilitates NETO (Das et al., 2012) while in the model of (Xu et al., 2019) fluctuations due to finite protein numbers can cause random switching among dynamical states or extinguish oscillations altogether. Both smaller rga4∆ daughters of monopolar mothers (that should generally contain smaller number of Cdc42 and regulators, besides Rga6) as well as larger daughters (that contain fewer Rga6) could be impacted by small protein copy number fluctuations.

Having identified the asymmetric inheritance of Rga6 as a key in the complex growth pattern of rga4∆ cells, a next step for quantitative investigations could be to develop models that explicitly account for GAP distribution in the cell, going beyond the reduced model used in this work (where parameters reflect a combination of molecular processes). The postulated differences of the initial value of 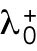among daughters in Hypothesis 3 helped to illustrate the concept of asymmetric inheritance leading to different growth patterns and to design experiments checking for asymmetric inheritance of positive or negative Cdc42 regulators. However, how the concentration of Rga6 might be captured by a reduced parameter such as 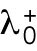(in fact a parameter more easily associated with a positive rather than negative regulator) cannot be fully addressed at this level of description. Such models would require additional experimental information on the mechanisms of GAP recruitment and aggregation on the plasma membrane. A recent spatial reaction-diffusion model of Cdc42 oscillations postulated that GAPs are recruited at the activated tip through active Cdc42 (Khalili et al., 2020). In this spatial model, reducing the concentration of GAPs that accumulate at the cell side promoted symmetric oscillations at the expense of asymmetric oscillations. This result would be consistent with our experimental finding that rga4∆ daughters inheriting less (more) of Rga6 becoming bipolar (monopolar). Accounting for additional complexities, such as changes in cell diameter and cell size, and differences in the diffusion of Cdc42 regulators at the membrane, might be needed in such modeling efforts to understand how deletion of Rga4 leads to an increase in parameter C_sat that was important in our reduced model.

In conclusion, our analysis of rga4∆ cells, by genetic and mathematical approaches, uncovered a possible biological significance of bipolar growth activation (NETO) (Figure 9, hypothetical model). Although NETO is not required for cell growth, we find that NETO may function to ensure that all cells are born with similar initial conditions to enable consistent growth patterns among a population of cells. The activation of NETO and bipolar growth in the mother cell is instrumental to allow localization of Cdc42 GAPs around both cell ends to ensure symmetrical inheritance of these Cdc42-negative regulators in the daughter cells. Overall, our work revealed an unexpected and important role for Cdc42 GAPs in maintaining consistent Cdc42 dynamics from generation to generation. Because the mechanisms of Cdc42 control are highly conserved in higher organisms, this work may contribute to our understanding of asymmetric cell division in higher eukaryotes, with implications for development, stem cell maintenance, and human disease.

MATERIALS AND METHODS

Request a protocol through Bio-protocol.

Strains and cell culture

All S. pombe strains used in this study are isogenic to the original strain 972 and are listed in Supplemental Table S1. Cells were cultured in yeast extract (YE) or in Edinburgh minimal medium (EMM) plus required supplements at 32°C or at 30°C and grown exponentially for at least eight generations before analysis. Standard techniques were used for genetic manipulation and analysis (Moreno et al., 1991).

Fluorescence microscopy and image analysis

Live cell imaging was performed using a Zeiss Axiophot microscope (connected to an Orca-ER Hamamatsu cooled high-resolution digital camera, a shutter, and a MAC 5000 shutter controller box), or an Olympus fluorescence BX61 microscope (Center Valley, PA) (equipped with Nomarski differential interference contrast [DIC] optics, a 100× objective, a Roper Cool-SNAP HQ camera [Tucson, AZ], Sutter Lambda 10 + 2 automated excitation and emission filter wheels [Novato, CA], and a 175 W Xenon remote source lamp with liquid light guide), or an Olympus BX71 inverted microscope (equipped with DIC optics, a 150× objective, a DG4 rapid wavelength switcher, and a Hamamatsu EM CCD camera). Images were acquired using either Intelligent Imaging Innovations SlideBook image analysis software (Denver, CO) or Micromanager (version 1.4.15) from the Ron Vale laboratory at UCSF. ImageJ 1.48 g software (National Institutes of Health) was used to measure fluorescence intensities.

Analyses of cell growth, CRIB-GFP intensities dynamics were performed by spreading 5 μl of exponentially growing cells onto 35-mm glass-bottom culture dishes underneath a premade slab of YE or EMM with 0.6% agarose and 1 mM ascorbic acid. The cells were then incubated at room temperature (25°C) for 30 min to allow cells to adapt. Cells were then visualized from the culture dishes using a Zeiss Axiophot microscope or BX71 inverted microscope. Correlation of growth and CRIB-GFP signal was performed as described in Das et al. (2012). Cell growth was measured as the increase in cell length from the birth scar to either cell tip. The localization of Scd2-GFP and Pom1-GFP was analyzed using either a Zeiss Axiophot microscope or an Olympus fluorescence BX61 microscope. One milliliter of exponentially growing cells was pelleted, and the majority of the supernatant was removed leaving approximately 10 µl. Then, 1 µl of cells was spread onto a 25 × 75 mm 1.0 mm-thick microslide and covered with a 22 × 22 mm microcover glass. For Calcofluor staining, 1–2 µl of Calcofluor solution (1 mg/ml) was added to freshly pelleted cells, and the staining was visualized using epifluorescence.

Heatmaps display a distribution of CRIB-GFP at the two ends of a population of cells. The y-axis shows the relative distribution of CRIB-GFP at the two tips for each cell (where 0.5 value means that same amounts of CRIB-GFP are present at both tips). The x-axis places cells in different bins according to their length. Heatmaps were generated using the R software (http://www.r-project.org/) as previously done (Das et al., 2015).

Fitting of growth profiles

Growth parameters in Supplemental Figure S2 and Supplemental Movies S1–S3 were obtained in the following manner. Briefly, 1 μl of concentrated cells were spread on slides over a thin layer (50 μl) of YE medium plus 1% agar and covered with a coverslip. Cells were then cultured for two generations and imaged using time-lapse microscopy with an interval of 10 min. Tip growth for the new and OE, defined as the distance from the birth scar, was measured using Openlab 3.0.2 software and averaged for each population of cells, excluding data points after stop of growth or t > 160 min. Average time profiles of tip growth were fitted with linear, exponential, and bilinear models using the Excel implementation previously described (Buchwald and Sveiczer, 2006; Buchwald, 2007).

SGA screen

To identify mutations that suppress or worsen the polarity and growth pattern defects observed in rga4Δ mutants, we crossed the rga4Δ strain with the Bioneer fission yeast deletion library (Kim et al., 2010) and visually screened the double mutants for morphology and colony growth phenotypes. Visual analysis of cell morphology was performed by looking at cells from each double-mutant colony under the microscope and recording which double mutants exhibited polarity or shape deviations compared with normal S. pombe cell morphology. Colony growth phenotype analysis was performed by using ScreenMill software, which analyzes images of double-mutant colonies and evaluates colony size as a readout for cell viability.

MATHEMATICAL MODEL

To model the polarization pattern of rga4∆ cells, we started from the model of Das et al. (2012). We first present a brief summary of this model. For more details and for method of numerical solution, see Das et al. (2012). The model considers a population of a limiting component (that could represent Cdc42, Cdc42-GTP, or Cdc42 GEFs) distributed among three subpopulations: a population in the cell middle (cytoplasmic or membrane-bound with total number 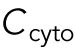) and one at each tip (total numbers , 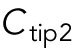). The total amount is 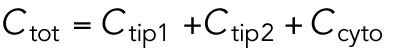and is assumed to increase in proportion to cell volume with constant rate 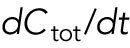. The cytoplasmic population is considered to be well mixed because cytoplasmic or membrane-bound proteins typically diffuse across the cell over a shorter time compared with the time required for significant change of tip concentration (∼ minutes). The dynamical equations in (Das et al., 2012) were the same for each tip:

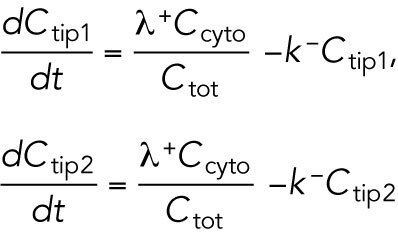1

The cell volume is included in the model through parameter 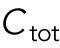, which is assumed to be proportional to cell volume and thus appears in the denominator of the association term because the cytoplasmic concentration interacts with the tip surface, a fixed area. Symmetry breaking was introduced through autocatalytic activation:

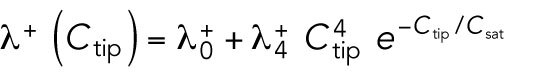2

where 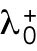and 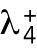are constants. This nonlinear term represents positive feedback and generates asymmetry in short cells by allowing one tip to deplete the cytoplasmic pool and preventing the other tip from accumulating Cdc42. Saturation at level allows long cells to become bipolar. Asymmetric and symmetric oscillations result by assuming Cdc42 accumulation triggers its own removal (delayed negative feedback):

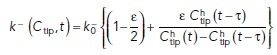3

Here, 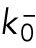is a constant, 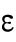determines the delayed dissociation strength, 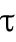is delay time, and exponent h gives the nonlinearity of the effect.

As a simple mechanism to implement concentration fluctuations, Gaussian white noise of amplitude 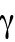can be introduced to both 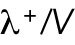and 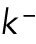without allowing them to fall below zero. This method keeps mass conservation, and concentration amounts cannot become negative.

A limitation of the model of Eqs. (1–3) is that it assumes cytoplasmic and membrane-bound populations to be well mixed. In a spatial model of Cdc42 oscillations that accounted for measured Cdc42 membrane diffusion coefficients, Cdc42-GDP was partly but not fully depleted from cell tips (Khalili et al., 2020). We thus performed our analysis with the current model that neglects concentration gradients within the three pools, but still includes in the simplest form the basic mechanisms of competition, saturation, and positive and negative feedback.

Model for Hypothesis 1. Cdc42 activation rate depends on the tip’s prior growth history. This model was implemented by introducing tip-aging dimensionless parameters 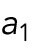and 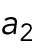, which describe how the rate of Cdc42 recruitment at either tip increases as a result of a history of prior growth. The following equations replace Eq. (1):

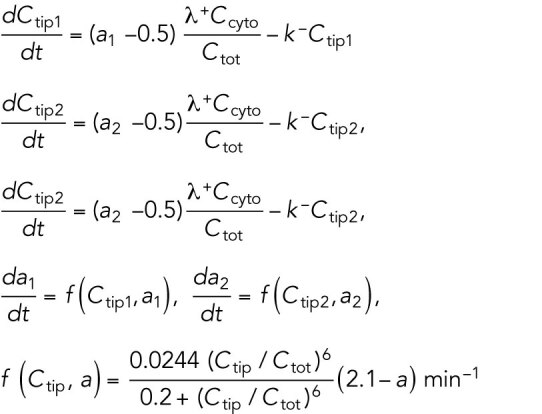4

Here, both tips obey the same equations, but the aging parameter increases faster for the tip that happens to have the highest C_tip, reaching up to a maximum plateau value assumed to be a = 2.1. A new tip formed at the division site is assumed to have a value (= 1 for simulations of rga4∆ cells). The functional dependence of the rate of tip aging parameter increase is chosen such that the aging parameter can reach the plateau smoothly through the cell doubling time under conditions when the tip accumulates a significant fraction of Cdc42 over the cell doubling time, assumed to be 240 min. Each daughter is assumed to start with half of the volume the mother has at division. A daughter inherits one aged tip carrying the aging parameter of one of the two mother tips, and a new tip that starts with aging parameter .

Model for Hypothesis 2. Daughters of monopolar rga4∆ mothers inherit unequal volumes. The equations for this model are the same as the ones in Das et al. (2012). We study the behavior of cells that start with different initial total amounts , changed in proportion to the differences in volume, over a time equal to 4 h (the doubling time of wild-type cells). Thus, the three cases of Hypothesis 2 in Figure 3 correspond to different initial conditions for .

Model for Hypothesis 3. Daughters of monopolar rga4∆ mothers inherit unequal Cdc42 regulators. This model is described by Eqs. (1–3), but we further assume that 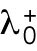is a dynamic global parameter (i.e., has the same value for both tips and varies over time). This parameter relaxes toward a reference value 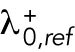over the course of the cell doubling time (assumed to be 4 h):

5

This model was explored as a function of the initial value of that is assumed to be different in the two daughters of monopolar rga4∆ mothers, each inheriting a 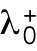at birth above and below 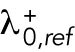, respectively.

Model parameter values and initialization

In all cases, the amount at tips and cell middle measured with respect to the saturation parameter in the model of wild-type cells without tip aging is .

Initialization. We initialized the delay differential equation system of each model by selecting initial values for and 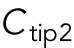as well as for their values at times t between 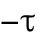and 0. Since the system executes many oscillations within each asymmetric or symmetric state, and since we do not typically start within a coexistence region, the results are not sensitive to the precise choice of these initial values. 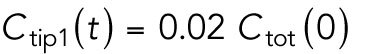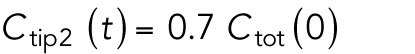This was checked for the results of Figure 3 for which we either had and for 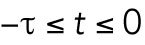or the same but with 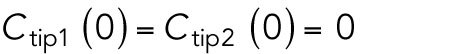for both mother and daughter cells.

TABLE 1:

Model parameters for wild-type cells are the same as Das et al. (2012).

Parameter	Value	Reason
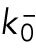
	4 min–1	Affects oscillation shape and anticorrelation between tips. Set to match observed oscillatory behavior.
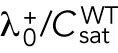
	9 min–1	Enable asymmetric to symmetric transition during cell growth.
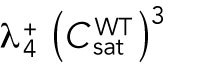
	25.87 min–1
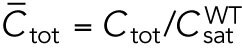
	6.5 (initial at birth) 13 (final at division)
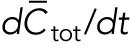
	.0271 min–1	Cells double in approximately 4 h.
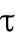
	2 min	Tuned so that oscillations match observed period.
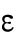
	0.5375	Set to match oscillation size.
h	40	Set to be sufficiently nonlinear to see significant oscillations.
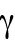
	0	Noise amplitude.

TABLE 2:

Modified parameters for rga4∆. cells, Hypothesis 1 (Figure 3B; Supplemental Figure S3A).

Parameter	Value	Reason
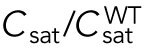
	1.6	Effect of Rga4 deletion (see main text).
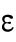
	1.85
	1	Low aging for new tips.

TABLE 3: .

Modified parameters for which model with tip aging history (Hypothesis 1) reproduces wild-type polarity pattern (Figure 3A; Supplemental Figure S3A).

Parameter	Value	Reason
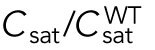
	1	Close to value of model without tip aging.
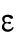
	0.64
	1.7	Low aging for new tips.

TABLE 4:

Modified parameters for rga4∆ cells, Hypothesis 2 (Figure 3C).

Parameter	Value	Reason
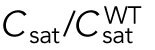
	1.501	Effect of Rga4 deletion (see main text).
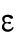
	1.35

TABLE 5:

Modified parameters for rga4∆ cells, Hypothesis 3 (Figure 3D; Supplemental Figure S3B).

Parameter	Value	Reason
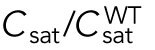
	1.6	Effect of Rga4 deletion (see main text).
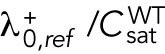
	20 min–1

Abbreviations used:

ANOVA

analysis of variance

DIC

differential interference contrast

EMM

Edinburgh minimal medium

GAP

GTPase-activating protein

GDI

guanine dissociation inhibitor

GEF

guanine-nucleotide exchange factor

NE

new end

NETO

new-end takeoff

OE

old cell end

SGA

synthetic genetic array

YE

yeast extract.