Patient-specific computational analysis of hemodynamics in adult pulmonary hypertension

Abstract

Pulmonary hypertension (PH) is a progressive disease characterized by elevated pressure and vascular resistance in the pulmonary arteries. Nearly 250,000 hospitalizations occur annually in the U.S. with PH as the primary or secondary condition. A definitive diagnosis of PH requires right heart catheterization (RHC) in addition to a chest computed tomography, a walking test, and others. While RHC is the gold standard for diagnosing PH, it is invasive and posseses inherent risks and contraindications. In this work, we characterized the patient-specific pulmonary hemodynamics in silico for diverse PH WHO groups. We grouped patients on the basis of mean pulmonary arterial pressure (mPAP) into three disease severity groups: at-risk (18 mmHg ≤ mPAP < 25 mmHg, denoted with A), mild (25 mmHg ≤ mPAP < 40 mmHg, denoted with M), and severe (mPAP ≥ 40 mmHg, denoted with S). The pulsatile flow hemodynamics was simulated by evaluating the three-dimensional Navier–Stokes system of equations using a flow solver developed by customizing OpenFOAM libraries (v5.0, The OpenFOAM Foundation). Quasi patient-specific boundary conditions were implemented using a Womersley inlet velocity profile and transient resistance outflow conditions. Hemodynamic indices such as spatially averaged wall shear stress (SAWSS), wall shear stress gradient (WSSG), time-averaged wall shear stress (TAWSS), oscillatory shear index (OSI), and relative residence time (RRT), were evaluated along with the clinical metrics pulmonary vascular resistance (PVR), stroke volume (SV) and compliance (C), to assess possible spatiotemporal correlations. We observed statistically significant decreases in SAWSS, WSSG, and TAWSS, and increases in OSI and RRT with disease severity. PVR was moderately correlated with SAWSS and RRT at the mid-notch stage of the cardiac cycle when these indices were computed using the global pulmonary arterial geometry. These results are promising in the context of a long-term goal of identifying computational biomarkers that can serve as surrogates for invasive diagnostic protocols of PH.

3. INTRODUCTION

Pulmonary hypertension (PH) is a vascular condition characterized by high blood pressure in the pulmonary arteries, which typically affects 15 – 50 persons per million [1]. Currently, PH diagnosis requires multiple sessions of a six-minute walk test, trans-thoracic echocardiography, and right heart catheterization (RHC) [2]. While RHC is the gold standard for diagnosing PH, it is invasive and limits the cardiologist’s ability to safely diagnose and monitor the disease. A definitive, non-invasive alternative for RHC would be of profound benefit for the clinical management of this disease. Efforts to develop non-invasive diagnostic methods have extensively characterized pulmonary hemodynamics using MRI-derived blood flow patterns [3], 4D MRI [4, 5], and computational fluid dynamics (CFD) modeling [6–10].

CFD simulations offer superior spatial and temporal flow resolutions, and the capability to resolve pathological hemodynamic challenges [11]. Nevertheless, modeling the hemodynamics in the adult pulmonary vasculature invariably requires certain reasonable approximations. Kheyfets et al. [6], Bordones et al. [12], and Tang et al. [13] used a rigid wall, no-slip boundary condition for the pulmonary arterial walls. At the inlet, the volume flow rate was constant in time and parabolic in space. These studies, albeit useful in gaining insights on the hemodynamics of PH, overlooked the contributions made by the compliant wall of the pulmonary vasculature. This limitation was resolved by coupling the hemodynamics with enclosing wall motion using fluid-structure interaction (FSI) simulations [14–18]. One FSI method involved a coupled-momentum model with the assumption of linearized stiffness for the arterial wall [16, 17, 19], while Gutierrez et al. [20] used small deformation theory. Su and colleagues [14, 15] employed idealized geometries.

A vast majority of modeling studies [6, 11, 12, 16–18, 21] have dealt with pulmonary arterial hypertension (PAH, WHO group I). However, left heart disease (WHO group II) and lung disease (WHO group III) are causative factors for PH in the majority of diagnosed cases [22]. In this work, we quantified the pulmonary hemodynamics in PH patients belonging to diverse WHO groups. We hypothesize that irrespective of WHO classification, pulmonary hemodynamics is strongly associated with PH disease severity. We also investigated the feasibility of using hemodynamic measures for developing a reliable non-invasive PH diagnosis protocol. In doing so, we attempted to address the following research questions:

1. Is disease severity highly associated with specific hemodynamic measures in PH patients?

2. If this association exists, is it affected by the spatiotemporal distribution of the hemodynamic measures?

4. METHODS

All abbreviations used in this manuscript are described in Table 1, which includes mathematical formulations used to calculate hemodynamic measures, if applicable. Following Institutional Review Board approval at Allegheny General Hospital (Pittsburgh, PA), patient-specific geometries of the pulmonary vasculatures were reconstructed from standard of care chest CT angiography (CTA) images obtained retrospectively from 32 adult PH patients. Of these, three patients belonged to WHO group I, six to WHO group II, twenty to WHO group III, one to WHO group IV, and two patients’ WHO group was unknown (see Table 2). Each patient underwent the electrocardiogram-gated chest CTA exam and RHC with a Swan-Ganz standard thermo-dilution catheter. Table 2 details the patient-specific clinical data collected or calculated during the retrospective review of medical records. In this investigation, we categorized the patients on the basis of disease severity following the recommendations described in Simonneau et al. [23] and Kolte et al. [24], as follows: at-risk (18 mmHg ≤ mPAP < 25 mmHg, denoted with A in Table 2), mild (25 mmHg ≤ mPAP < 40 mmHg, denoted with M), and severe (40 mmHg ≤ mPAP, denoted with S).

Table 1:

Abbreviations used in this manuscript with the mathematical expression used for calculations wherever applicable.

Abbreviation	Descriptive form	Remarks
WHO	World Health Organization
RHC	Right heart catheterization
SV	Stroke volume
PVR	Pulmonary vascular resistance	PVR = (mPAP - PCWP)/CO
mPAP	Mean pulmonary arterial pressure	mPAP = (sPAP + 2dPAP)/3
sPAP	Systolic pulmonary arterial pressure
dPAP	Diastolic pulmonary arterial pressure
PCWP	Pulmonary capillary wedge pressure
C	Compliance	C = CO/(sPAP − dPAP)
CO	Cardiac output	CO = HR × SV
HR	Heart rate
SV	Stroke volume
SAWSS	Spatially averaged wall shear stress
WSSG	Wall shear stress gradient
TAWSS	Time averaged wall shear stress
OSl	Oscillatory shear index
RRT	Relative residence time
RV	Right ventricle
PA	Pulmonary arteries
PH	Pulmonary hypertension

Table 2:

Individual clinical data measured or calculated, retrospectively, from the existing medical records. Refer to Table 1 for a description of all abbreviations. Disease severity is designated as A to signify the at-risk (n = 6), M to denote mild (n = 13), and S to represent the severe (n = 13) PH categories.

Patient No.	Age (yrs)	Sex (M/F)	Height (m)	Weight (kg)	WHO group	PVR (N · s/m5) × 105	C (m3/Pa) × 10−3	mPAP (Pa) × 10−3	SV (m3) × 10−5	Severity
1	80	F	1.5	92.0	III	153.0	0.4	2.4	8.2	A
2	42	F	1.6	75.0	II	136.0	2.0	2.5	7.4	A
3	68	F	1.7	77.0	II	151.0	2.3	2.5	8.8	A
4	50	M	1.8	65.0	II	158.0	2.9	2.8	5.6	A
5	71	M	1.7	95.0	I	120.0	2.8	2.8	7.4	A
6	44	F	1.7	90.7	I	143.0	0.0	3.1	7.0	A
7	44	F	1.6	104.0	III	285.0	2.0	3.5	7.0	M
8	55	F	1.7	95.0	NA	109.0	2.1	3.5	7.2	M
9	62	M	1.8	104.0	III	262.0	1.3	3.9	7.6	M
10	66	F	1.6	88.0	I	214.0	2.2	3.9	8.8	M
11	64	F	1.6	93.0	III	334.0	1.2	3.9	6.7	M
12	50	M	1.8	90.0	II	204.0	1.6	4.0	10.5	M
13	59	F	1.6	59.0	III	196.0	2.2	4.0	10.8	M
14	50	M	1.8	112.0	III	180.0	2.3	4.4	7.4	M
15	56	M	1.9	91.0	II	777.0	0.9	4.7	5.4	M
16	78	F	1.6	63.0	III	421.0	1.4	4.8	5.8	M
17	59	M	1.8	89.0	III	245.0	1.5	5.1	9.5	M
18	62	F	1.6	89.0	III	188.0	1.2	5.1	7.7	M
19	65	F	1.6	89.0	III	318.0	1.1	5.2	10.1	M
20	74	F	1.7	156.0	III	172.0	1.6	5.5	9.0	S
21	64	F	1.6	100.0	II	165.0	1.5	5.6	7.4	S
22	71	F	1.5	98.0	III	285.0	1.4	5.7	10.5	S
23	58	F	1.6	88.0	III	465.0	0.2	5.9	7.2	S
24	63	F	1.5	101.0	III	408.0	0.7	6.1	7.1	S
25	60	F	1.6	124.0	III	534.0	0.8	6.4	5.9	S
26	60	F	1.7	64.0	III	778.0	0.2	6.8	5.1	S
27	67	M	1.8	88.0	IV	1316.0	0.4	6.9	4.2	S
28	70	M	1.7	67.0	III	906.0	0.7	6.9	5.0	S
29	65	M	1.8	82.0	III	745.0	0.5	7.7	6.4	S
30	80	M	1.8	93.0	III	830.0	0.2	8.0	6.3	S
31	43	M	1.8	63.0	NA	402.0	1.0	8.9	7.5	S
32	76	F	1.7	91.0	III	1186.0	0.2	9.3	5.5	S

The simulation domain extends from the proximal MPA up to seven generations of branching pulmonary arteries. To avoid boundary-based instabilities, the inflow and outflow surfaces were extended ten times their hydraulic diameters. Figure 1a illustrates the simulation domain for an exemplary PH patient, whereas Fig. 1b shows a magnified view of the same reconstructed pulmonary vasculature. Each patient-specific domain was discretized with nearly 6.5 ± 1.5 million tetrahedral mesh elements in ICEM (Ansys Inc., Canonsburg, PA). Grid convergence studies were previously undertaken by monitoring changes in spatially varying instantaneous wall shear stress (WSS) [15]. The CFD solver was developed in-house by customizing open-source C++ libraries available in OpenFOAM (The OpenFOAM Foundation Ltd, London, U.K.) – v5.0 distribution. Robertson et al. [25], and the references therein, offer an impressive account of notable CFD-based studies conducted using OpenFOAM. Appendix A of the Supplementary Material provides additional details on the infrastructure for the CFD simulations and the governing equations used for them. Blood was considered an incompressible, Newtonian fluid. The finite volume formulation implemented in the solver evaluates the integral form of the incompressible Navier-Stokes system of equations. Appendix B of the Supplementary Material describes the experimental validation of computational results and third-party verification studies conducted for the OpenFOAM solver.

Figure 1:

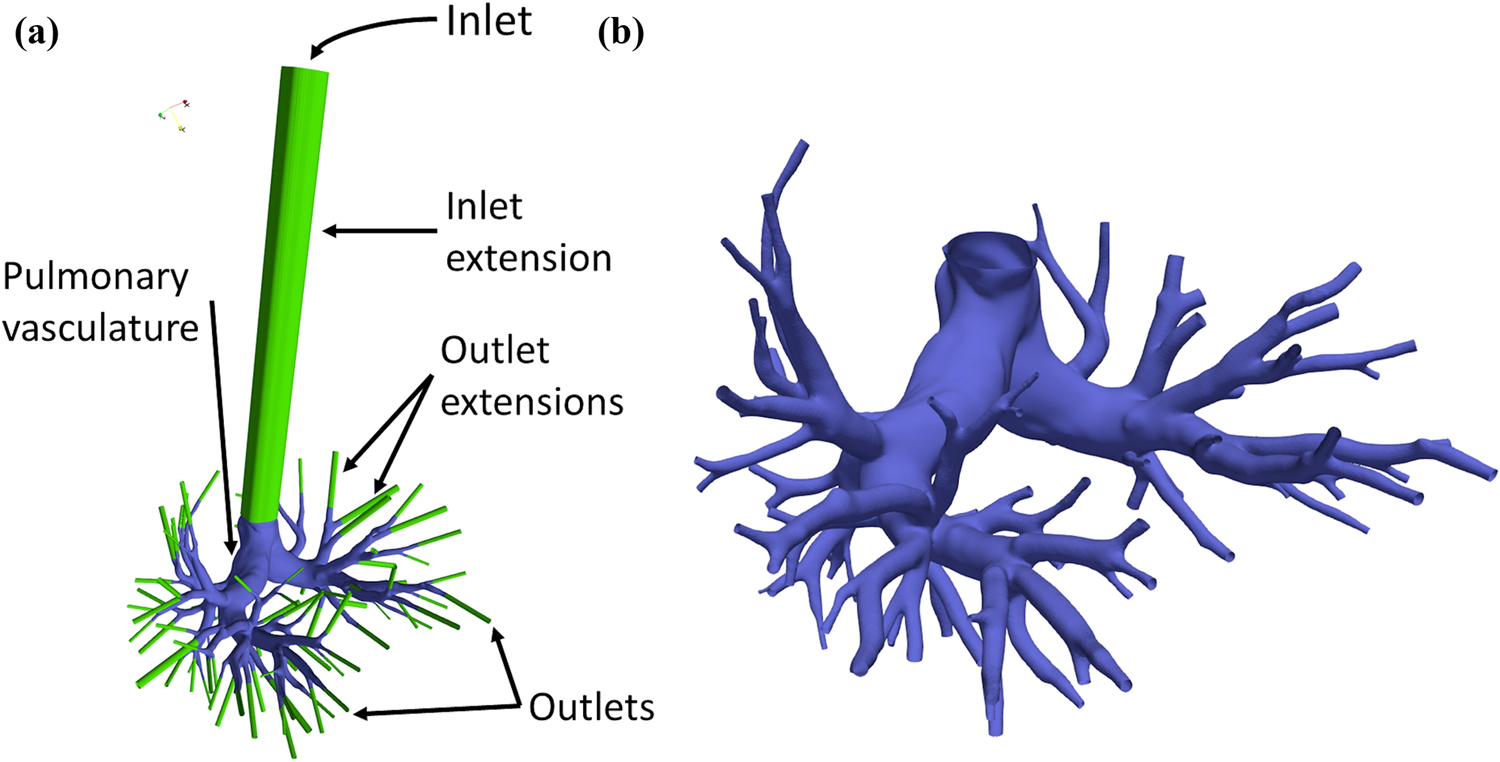
(a) Schematic of an exemplary patient-specific geometry indicating the inlet, outlet, and wall boundaries. (b) Magnified view of the reconstructed pulmonary vasculature.

4.1. Inflow boundary conditions

Velocity and pressure waveforms were recorded in the proximal MPA for five adult PH patients with a ComboWire XT catheter. This subject group was separate from the one described in Table 2. The raw patient-specific velocity and pressure data were post-processed and normalized against cardiac output (CO) and mean pulmonary arterial pressure (mPAP), respectively. Dimensionless waveforms of velocity (see Fig. 2a) and pressure (see Fig. 2b) were evaluated against a normalized timescale.

Figure 2:

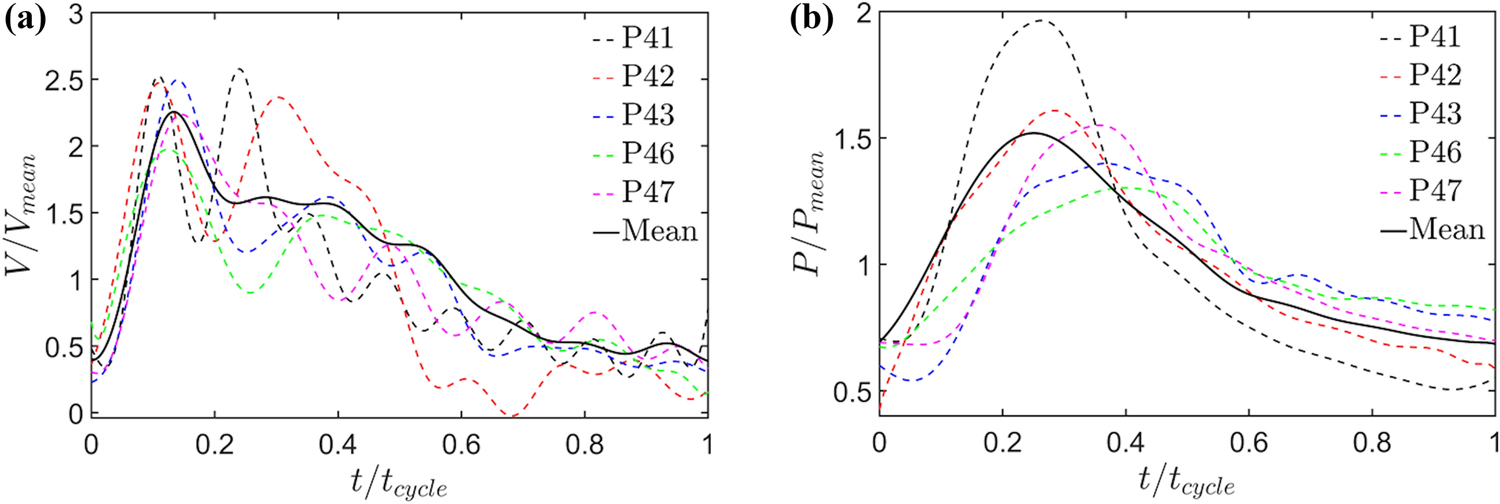
Normalized centerline (a) velocity, and (b) pressure profiles simultaneously recorded in the proximal MPA for a group of five adult PH patients (labeled as P41, P42, P43, P46, and P47). These patients do not belong to the group of 32 subjects described in Table 2.

Subsequently, quasi-patient specific inflow velocities were calculated for the 32 vascular models (Table 2) using their respective CO and mPAP as dimensional factors. A fully developed pulsatile velocity profile (according to the Womersley pulsatile flow solution) was used for the inflow boundary condition during one cardiac cycle. A protocol based on Schwartz–Christoffel mapping was implemented to specify the velocity values on the non-circular inlets [26]. The simulations were run for three cardiac cycles to obtain periodic convergence.

4.2. Outflow boundary conditions

A resistance structured-tree outflow boundary condition, proportional to the respective outlet radius, was applied at each extended outlet boundary. We emulated the algorithm described in the work of Kheyfets et al. [6] to isolate a unique polynomial equation for each patient-specific geometry. For example, Eq. (1) defines the outlet resistances for the CFD model of patient No. 5,

$$\begin{gathered} R_i=-\left(5.04\times {10}^5\right)r_i^7+\left(3.041\times {10}^6\right)r_i^6 \\ -\left(7.582\times {10}^6\right)r_i^5+\left(1.009\times {10}^7\right)r_i^4 \\ -\left(7.727\times {10}^6\right)r_i^3+\left(3.4\times {10}^6\right)r_i^2 \\ -\left(8.028\times {10}^5\right)r_i+\left(8.136\times {10}^4\right) \end{gathered}$$ (1)

where R_i and r_i denote the resistance and radius at outlet i, respectively. In this work, we introduced a variable coefficient, α, to adjust the outlet resistances within each time iteration, as shown in Eq. (2),

$$R_i^{n+1}=\underset{\alpha }{\underbrace{\left[\frac{p_{wf}(t)}{p_{in}(t)}\right]}}{R}_i^n$$ (2)

where p_in(t) is the inlet pressure at the current iteration, p_wf(t) is the quasi-patient specific pressure obtained from the inlet pressure waveform described in section 4.1, and n is the inner iteration counter within a time iteration. The constant, α, is the same for the resistances of all outlets. A subroutine (see Fig. 3a) iteratively modifies α, and by extension, the outlet resistances within every time step until the condition expressed by Eq. (3) is satisfied.

Figure 3:

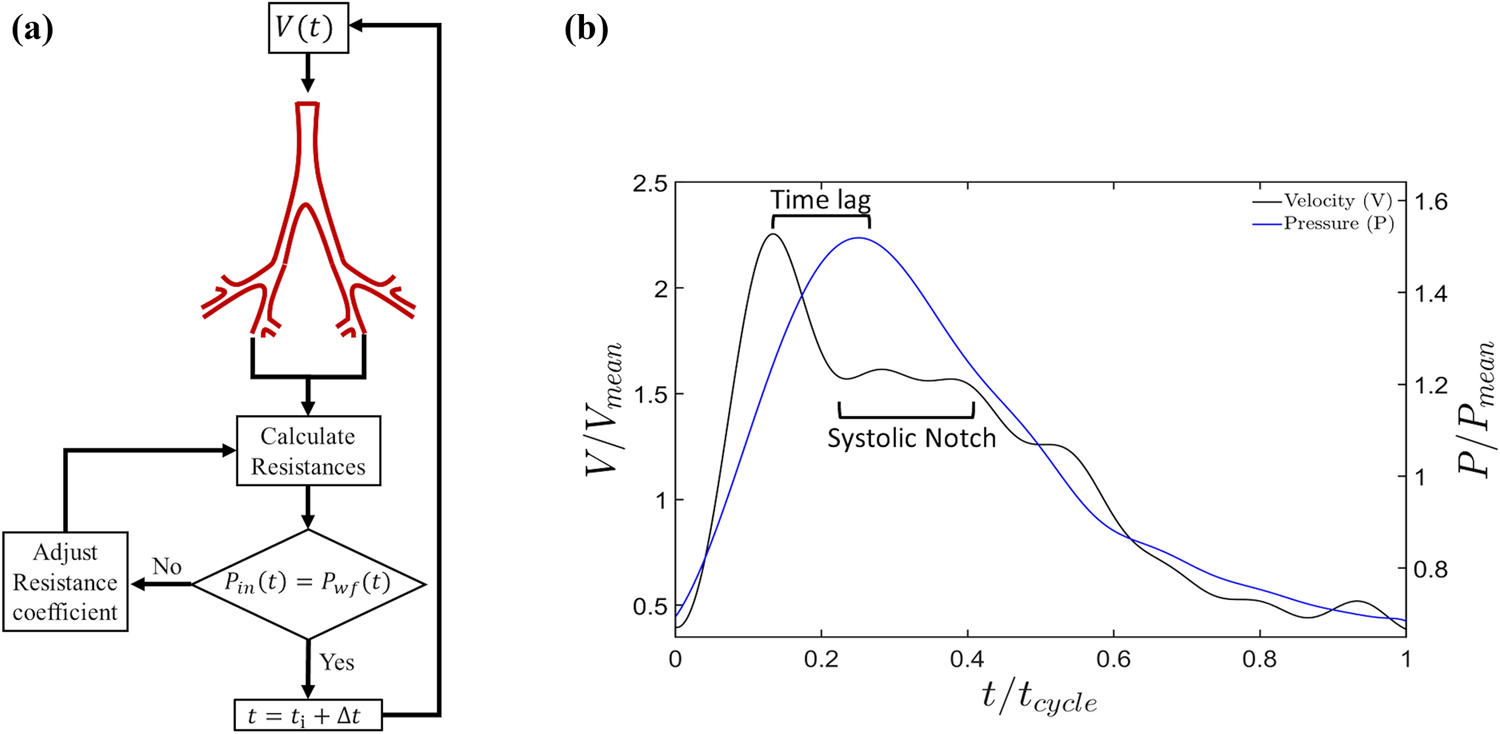
(a) Schematic of subroutine implemented for simultaneously applying quasi-patient-specific velocity and pressure at the inflow boundary based on imposing outflow resistances. (b) Normalized pressure and velocity waveforms; the velocity waveform distinctively shows the systolic notch characteristic of a PH patient.

$$0.99p_{wf}(t)\le p_{in}(t)\le 1.01p_{wf}(t)$$ (3)

The rationale for using this subroutine is to simultaneously achieve quasi-patient specific velocity and pressure at the inflow boundary. In addition, the subroutine yields the time-lag between pressure and velocity waveforms measured during RHC (see Fig. 3b). This time difference primarily exists on account of the inertia and viscosity of blood [27].

4.3. Hemodynamic Indices

The three dimensional flow fields were post-processed using ParaView (Kitware Inc., Clifton Park, NY). This consisted in quantifying the following hemodynamic indices for each pulmonary vasculature:

1. Spatially averaged wall shear stress (SAWSS):

   $$\mathit{\text{SAWS}}S=\frac{1}{A}{\int }_A\left|{\tau }_w\right|dA$$ (4)

   where τ_w is the wall shear stress (WSS) vector field computed as the tangential component of the traction on the luminal surface and A is the discretized vascular luminal area. The limited in-plane resolution of the CTA images results in isolated regions of the distal vasculature that yield non-physiological, high focal WSS. Based on the findings of Tang et al. [7], facets with WSS magnitude greater than 50 dyn/cm² were considered an anomalous product of the image resolution and thus were not included in the SAWSS calculation. Increasing this threshold beyond 50 dyn/cm² revealed insignificant changes in SAWSS.
2. Wall shear stress gradient (WSSG):

   $$\mathit{\text{WSSG}}=\sqrt{{\left(\frac{\partial {\tau }_w}{\partial \xi }\right)}^2+{\left(\frac{\partial {\tau }_w}{\partial n}\right)}^2}$$ (5)

   where ξ and n represent local tangential and normal directions to the luminal surface. The tangential direction comprises two in-plane components; the unit vector parallel to the resultant of these components was used to calculate the directional derivative of the WSS vector. The unit vector ξ retains the direction of the local instantaneous WSS vector.
3. Time averaged wall shear stress (TAWSS):

   $$\mathit{\text{TAWS}}S=\frac{1}{T}{\int }_T\left|{\tau }_w\right|dt$$ (6)

   where T represents the time period for one cardiac cycle, which is achieved in increments of time interval dt.
4. Oscillatory shear index (OSI):

   $$OSI=\frac{1}{2}\left[1-\frac{\left|{\int }_T{\tau }_{w}dt\right|}{{\int }_T\left|{\tau }_w\right|dt}\right]$$ (7)
5. Relative residence time (RRT):

   $$RRT=\frac{1}{[(1-2\times OSI)\times \mathit{\text{TAWS}}S]}$$ (8)

4.4. Statistical analysis

A one-way analysis of variance was performed to determine if statistically significant differences exist in the aforementioned hemodynamic indices among the three severity groups. This was followed by Tukey’s multiple comparison tests to compare the simulation-based indices among all possible pairs of severity groups. A probability value less than 0.05, i.e p < 0.05, was considered statistically significant. In addition, a Pearson’s correlation analysis with Bonferroni correction was performed with all the calculated indices vs. the following clinical metrics: pulmonary vascular resistance (PVR), compliance (C), and stroke volume (SV). For this analysis, a probability value less than 0.01, i.e p < 0.01, was considered statistically significant.

5. RESULTS

5.1. Simulation-based hemodynamic indices

Figure 4 illustrates the TAWSS distribution obtained for all the patient-specific geometries. Qualitatively, all patient-specific vasculatures exhibited elevated TAWSS in the distal ends. We observed a concomitant reduction in regions with TAWSS > 10 dyn/cm² in relation to the severity of the disease, i.e. with S vasculatures having the least number of regions with elevated TAWSS.

Figure 4:

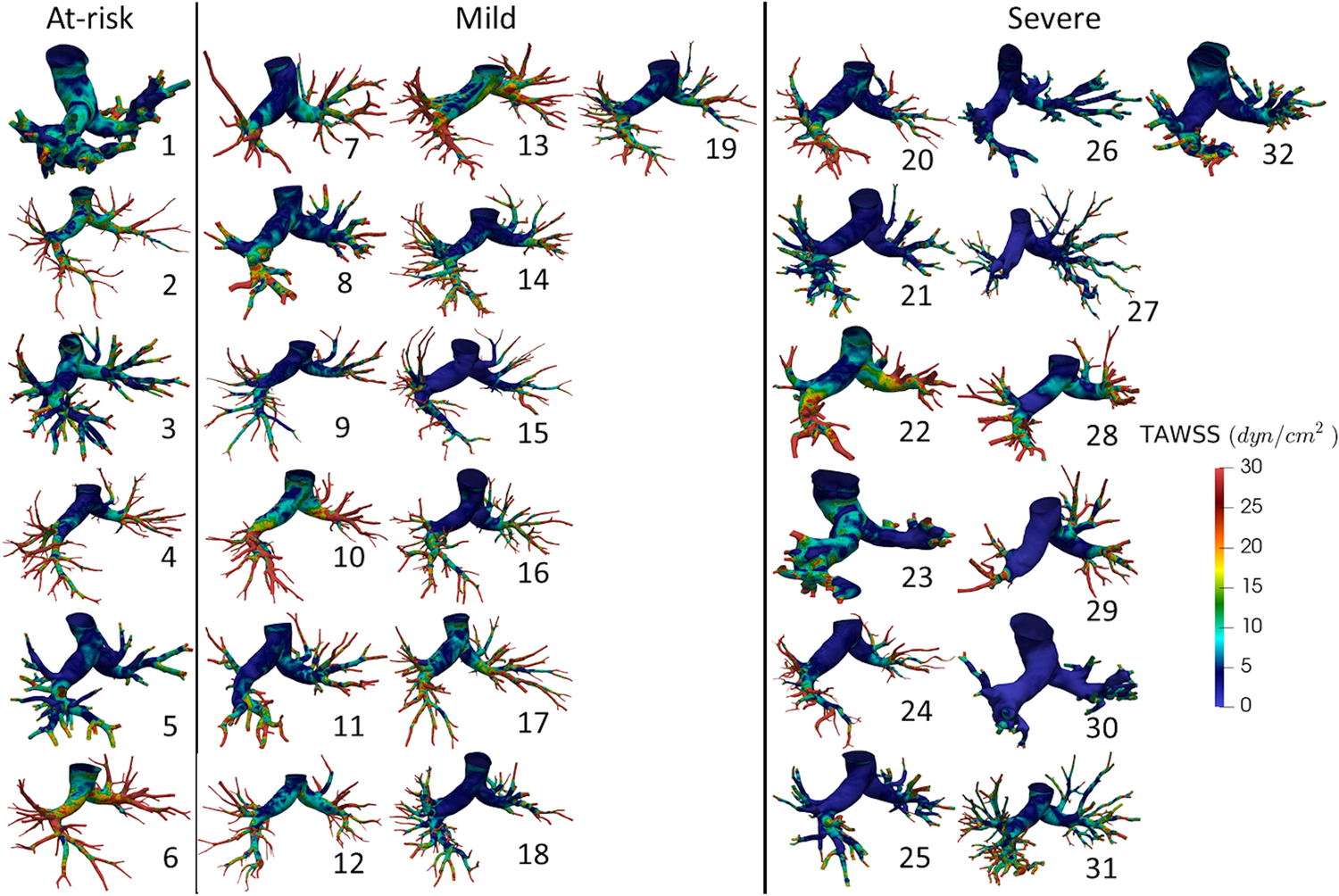
Time averaged wall shear stress (TAWSS) distributions for all patient-specific geometries. Patient numbers are specified next to each stress map. Refer to the corresponding patient number in Table 2 for clinical data collected on each patient.

Figure 5 shows SAWSS at peak systole (Figs. 5a, 5d, 5g, and 5j), mid-notch (Figs. 5b, 5e, 5h, and 5k), and mid-diastole (Figs. 5c, 5f, 5i, and 5l). To examine the regional dependence of SAWSS, the patient-specific geometries were divided into three regions: MPA, left and right pulmonary arteries (LR), and the distal vasculature (D), based on the Weibel system [28]. The spatial averaging is conducted globally (G), i.e. on the complete geometry, in addition to the aforementioned regions. In Figs. 5–7, peak systole is designated with the subscript PS, the mid-notch with the subscript MN, and mid-diastole with the subscript MD. All measures of SAWSS demonstrated significant differences among the three groups, except SAWSS_MPA,MD. The mean SAWSS_G,PS for the A group exceeded that of the M group by 14.5%, whereas SAWSS_G,PS for the M group exceeded the S group by 36.3% (mean SAWSS_G,PS: 21.50 dyn/cm² (A), 18.37 dyn/cm² (M), 11.71 dyn/cm² (S), p = 0.007). The A and M groups exhibited less than 5% disparity for SAWSS_G,MN (p = 0.002) and SAWSS_G,MD (p = 0.011). However, the S group exhibited 37.9% lower SAWSS_G,MN and 43.3% lower SAWSS_G,MD, compared to the M group. Figure 6 shows the percentage decreases computed in regionally averaged SAWSS at the said time instants. SAWSS_MPA,PS, SAWSS_MPA,MN, SAWSS_MPA,MD, SAWSS_LR,PS, SAWSS_LR,MN, and SAWSS_LR,MD yielded percentage deacreases in the range of 20–40%. However, in the distal vasculature, the percentage decreases for SAWSS_D,PS, SAWSS_D,MN, and SAWSS_D,MD were small (< 5%) between the A and M groups, and large (30 – 45%) between the M and S groups.

Figure 5:

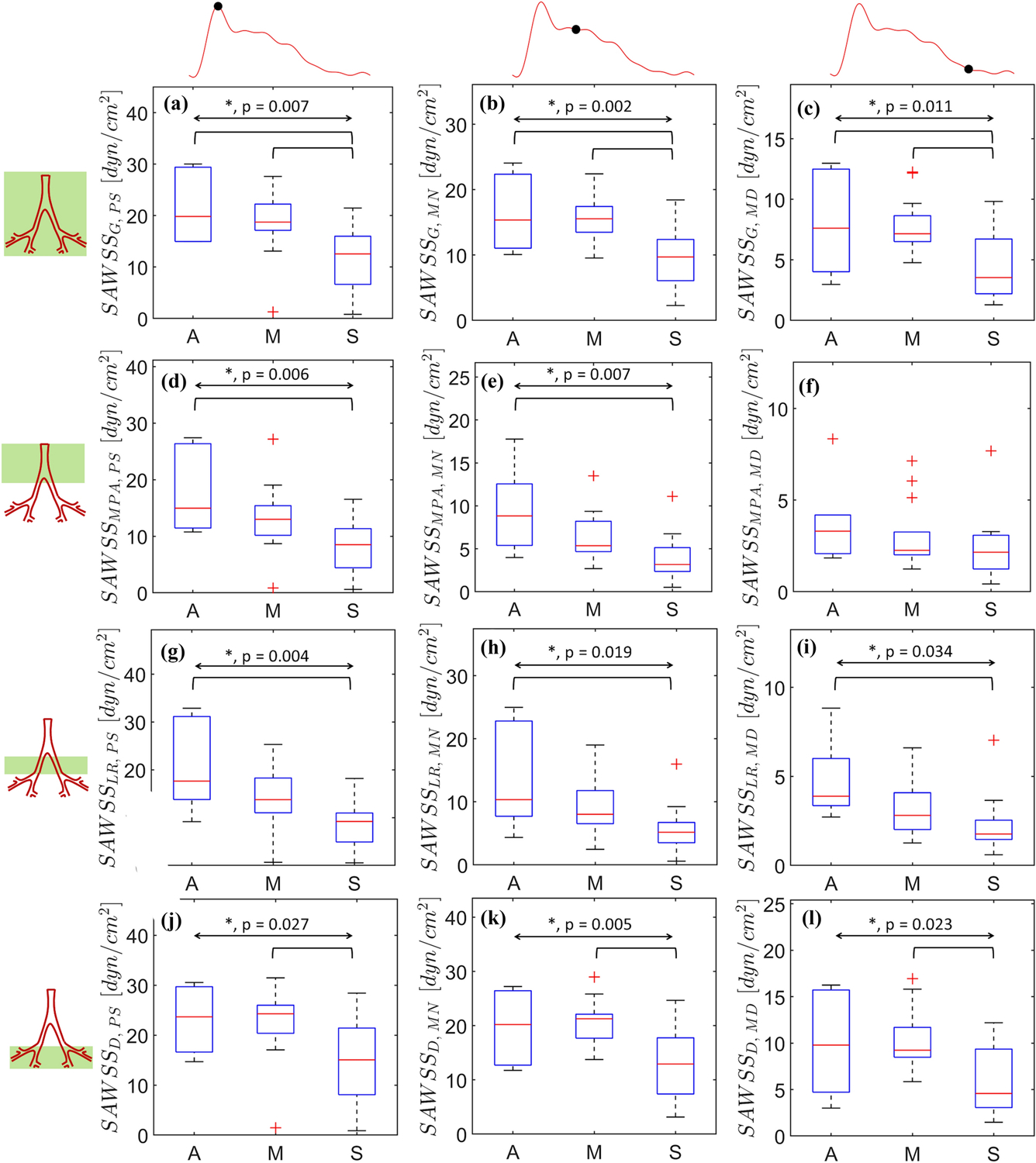
Spatially averaged wall shear stress (SAWSS) calculated at peak systole (a, d, h, j), mid-notch (b, e, h, k), and mid-diastole (c, f, i, l). Region-based spatial averaging is performed in three distinct regions: MPA (d, e, f), LPA+RPA (g, h, i), and the distal vasculature (j, k, l). The overall and pairwise statistical significances are represented by the topmost bidirectional arrow and square brackets underneath, respectively. The crosses represent outliers in each group (A, M, or S).

Figure 7:

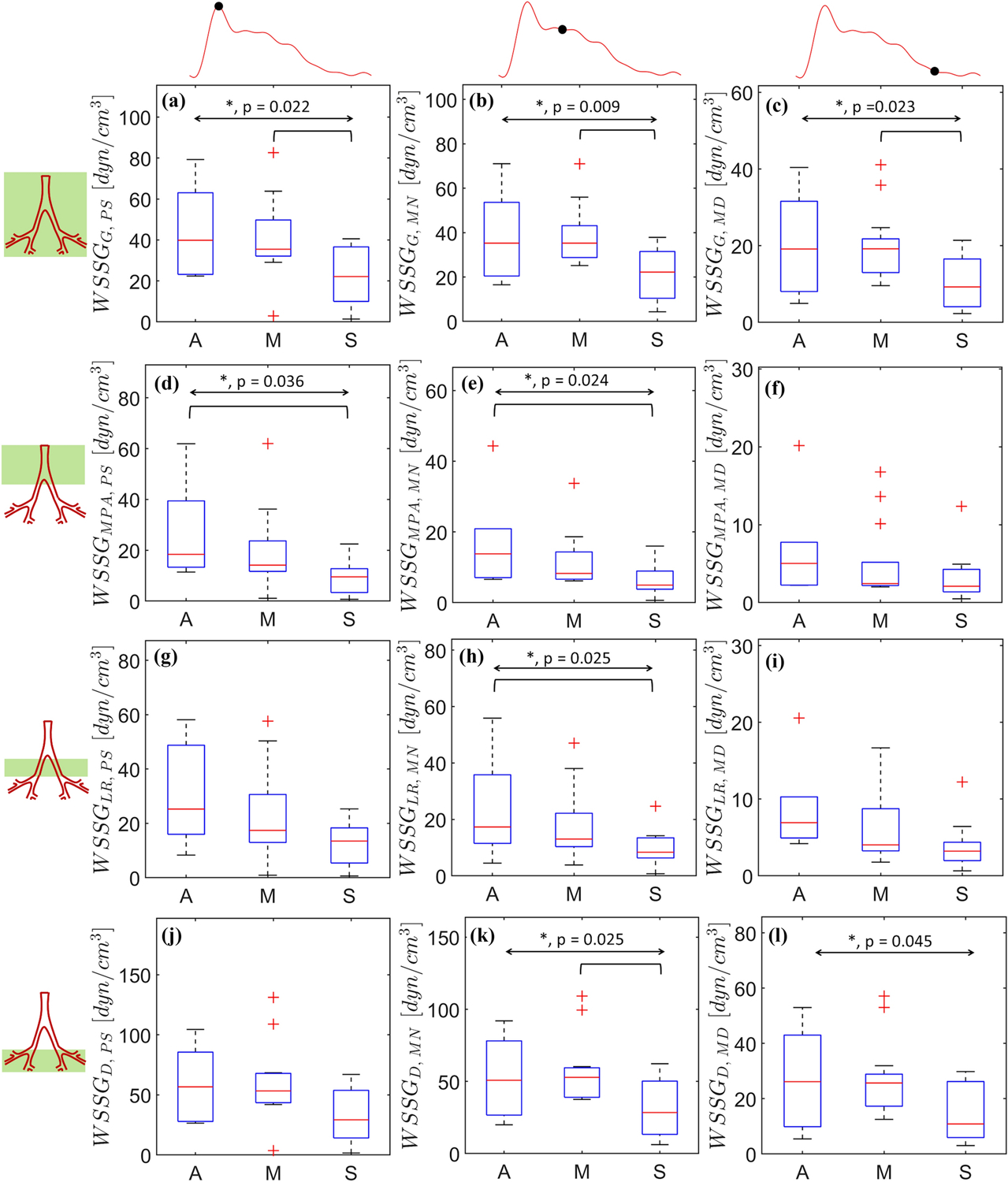
Spatially averaged wall shear stress gradients (WSSG) calculated at peak systole (a, d, h, j), mid-notch (b, e, h, k), and mid-diastole (c, f, i, l). Region based spatial averaging is performed in three distinct regions: MPA (d, e, f), LPA+RPA (g, h, i), and the distal vasculature (j, k, l). The overall and pairwise statistical significances are represented by the topmost bidirectional arrow and square brackets underneath, respectively. The crosses represent outliers in each group (A, M, or S).

Figure 6:

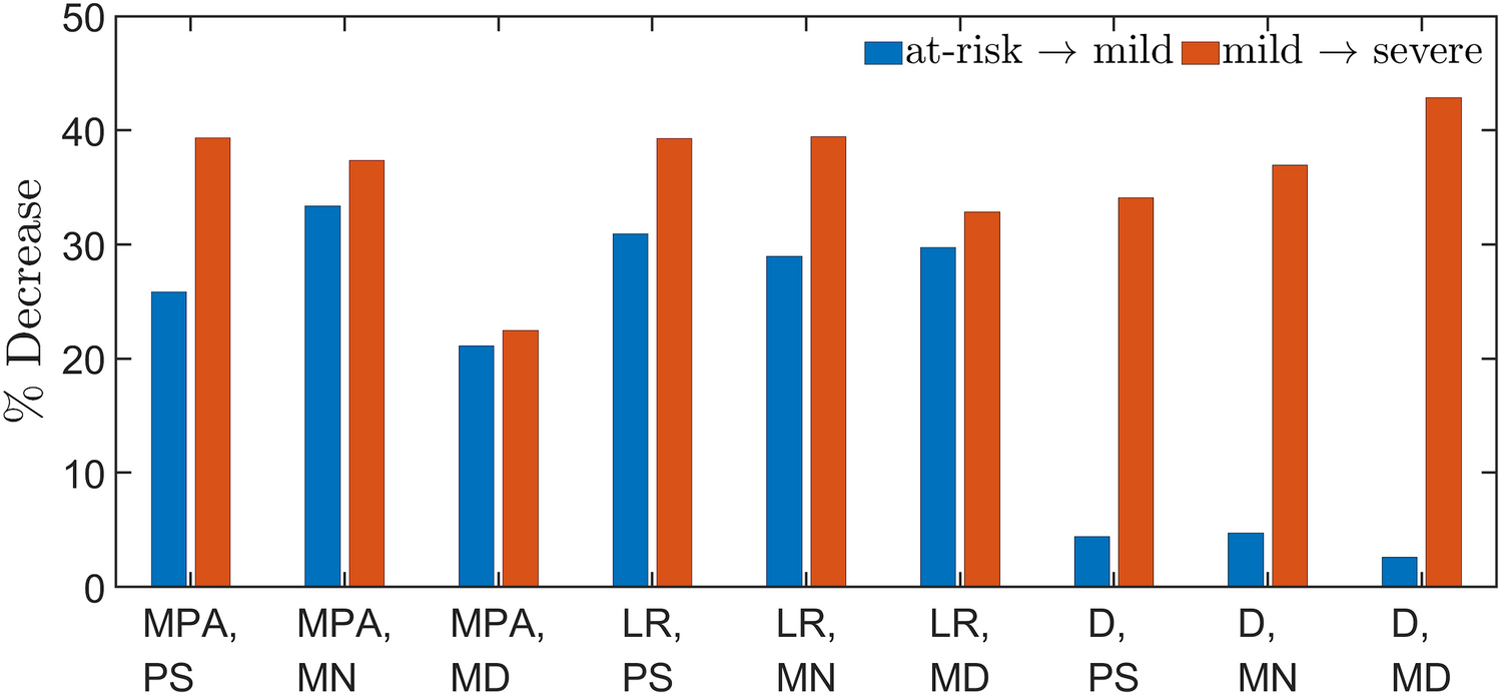
Percentage decrease in region-wise SAWSS between the at-risk (A) and mild (M) groups, and the M and severe (S) groups.

WSSG was calculated at PS, MN, and MD for each of the severity groups, as shown in Figs. 7a through 7l with global and regional spatial averages of WSSG. WSSG_MPA,MD, WSSG_LR,MN, WSSG_LR,MD, and WSSG_D,PS did not exhibit any statistically significant differences among the severity groups. For all groups, the differences between WSSG_G,PS (p = 0.022) and WSSG_G,MN (p = 0.009) were less than 10%. WSSG_G,PS, WSSG_G,MN, and WSSG_G,MD demonstrated significant pairwise differences between the M and S groups. Pairwise differences were also observed between the A and S groups for WSSG_MPA,PS, WSSG_MPA,MN, and WSSG_LR,PS. WSSG in the distal vasculatures, i.e. WSSG_D,PS, WSSG_D,MN, and WSSG_D,MD, were found to be nearly double their counterparts in the MPA and LR regions.

Figure 8 illustrates the spatially averaged TAWSS distributions calculated for the three severity groups. TAWSS_G showed pairwise statistical significance between the A and S groups, and the M and S groups (Fig. 8a, p = 0.002). TAWSS_MPA was 40.0% lower (A vs. M) and 34.4% lower (M vs. S) (Fig. 8b, p = 0.011). Similar trends were observed for TAWSS_LR with decreases of 34.0% (A vs. M) and 41.3% (M vs. S) (Fig. 8c, p = 0.010). Collectively, TAWSS_D was the highest amongst all groups (Fig. 9d, p = 0.008), whereas TAWSS_MPA was observed to be the lowest.

Figure 8:

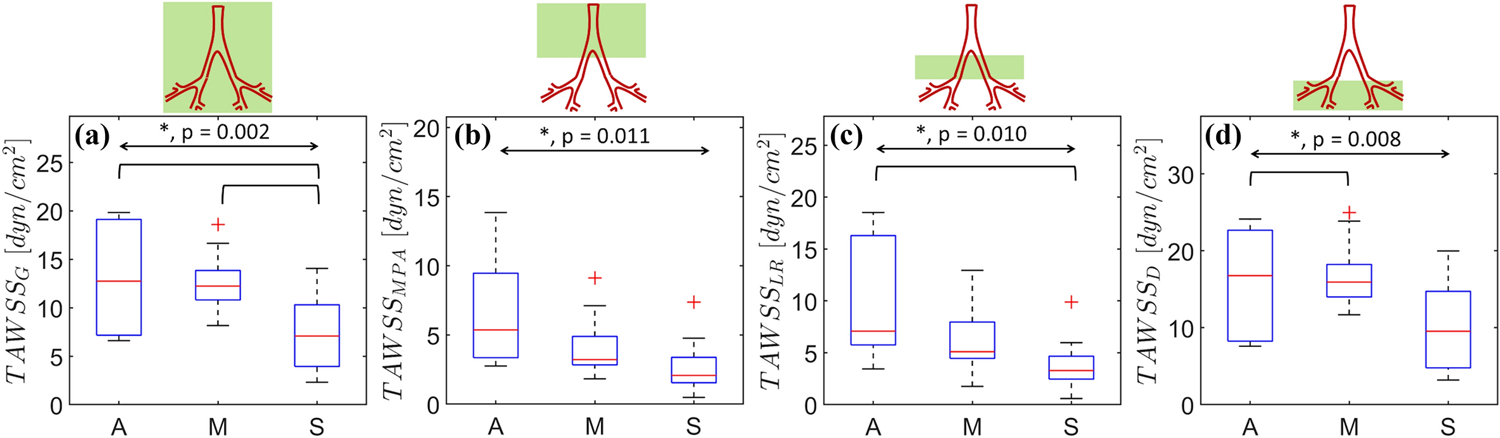
Time averaged wall shear stress (TAWSS) spatially averaged for the (a) complete domain (G), (b) MPA, (c) LPA+RPA (LR), and (d) the distal vasculature (D). The overall and pairwise statistical significances are represented by the topmost bidirectional arrow and square brackets underneath, respectively. The crosses represent outliers in each group (A, M, or S).

Figure 9:

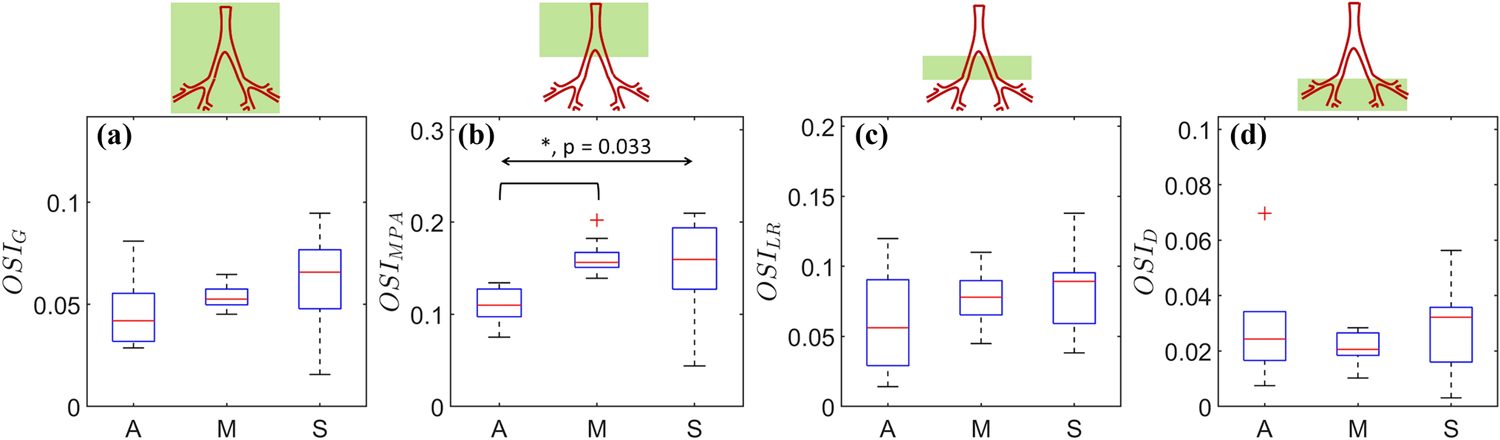
Oscillatory shear index (OSI) spatially averaged for the (a) complete domain (G), (b) MPA, (c) LPA+RPA (LR), and (d) the distal vasculature (D). The overall and pairwise statistical significances are represented by the topmost bidirectional arrow and square brackets underneath, respectively. The crosses represent outliers in each group (A, M, or S).

OSI represents a fusion of the low and oscillatory shear theories into a single, nondimensional measure of WSS relevant for regions of the vasculature with significant flow reversal. Figure 9 shows the spatial averages of OSI. OSI_G increases concomitantly with disease severity: A (0.047 ± 0.02), M (0.053 ± 0.006), and S (0.060 ± 0.021), although the differences between the groups were statistically insignificant (p = 0.231), as shown in Fig. 9a. Similar increases were obtained for OSI_MPA (Fig, 9b, p = 0.033) between the A (0.109 ± 0.021) and M (0.160 ± 0.017) groups, and a decrease from the M to the S group (0.148 ± 0.054). No statistically significant differences were obtained amongst the severity groups for OSI_LR and OSI_D (Figs. 9c and 9d). For all severity groups, the mean OSI follows the inequality OSI_MPA > OSI_LR > OSI_D, suggesting attenuation of the flow pulsatality in the downstream direction.

RRT is a measure used to characterize near-wall stagnation. Figure 10 shows the spatially averaged normalized RRT for each severity group, where the normalization is with respect to the maximum RRT amongst the 32 CFD models. All spatial averages demonstrated statistically significant differences for the three severity groups. The normalized RRT_G, RRT_MPA, and RRT_LR were highest for the S group and lowest for the A group (Figs. 10a – 10c; p = 0.006, p = 0.029, and p = 0.027, respectively). However, in the distal vasculature, the lowest normalized RRT_D was obtained for the M group: A (0.186 ± 0.022), M (0.148 ± 0.005), and S (0.425 ± 0.015), as shown in Fig. 10d (p = 0.008).

Figure 10:

Normalized relative residence time (RRT) spatially averaged for the (a) complete domain (G), (b) MPA, (c) LPA+RPA (LR), and (d) the distal vasculature (D). The overall and pairwise statistical significances are represented by the topmost bidirectional arrow and square brackets underneath, respectively. The crosses represent outliers in each group (A, M, or S).

5.2. Correlations between hemodynamic indices and clinical metrics

The association between the simulation-based indices and clinical metrics (PVR, C, and SV) was investigated by means of linear regression analysis. Pearson’s correlation coefficients, with Bonferroni correction, were calculated for all possible pairs of hemodynamic indices and clinical metrics. Tables 3 and 4 describe the statistically significant (p < 0.01) Pearson’s correlation coefficients between SAWSS and WSSG, and the clinical metrics; no other time-dependent hemodynamic indices yielded statistically significant correlations. Tables 5 and 6 illustrate the significant associations between TAWSS and RRT, and the clinical metrics; no other time-averaged hemodynamic indices yielded statistically significant correlations. PVR correlated significantly with all time-dependent indices except WSSG_MPA,PS, WSSG_MPA,MD, WSSG_D,PS, and WSSG_D,MD. Moreover, moderate correlations (ρ) were observed for PVR with SAWSS_G,MN (ρ = −0.67), SAWSS_G,MN (ρ = −0.67), SAWSS_D,MN (ρ = −0.62), TAWSS_G (ρ = −0.62), RRT_G (ρ = 0.68), RRT_LR (ρ = 0.67), and RRT_D (ρ = 0.65). C weakly correlated with SAWSS_D,MN (ρ = 0.50), while it yielded either insignificant correlations or correlations with |ρ| < 0.50 with all other indices. SV had moderate correlations with SAWSS_MPA,MD (ρ = 0.63) and SAWSS_LR,MD (ρ = 0.62). Its associations with other indices (SAWSS_G,PS, SAWSS_LR,PS, WSSG_G,PS, WSSG_D,PS, SAWSS_D,PS) were insignificant (p > 0.01) or weak (|ρ| < 0.5).

Table 3:

Statistically significant Pearson’s correlation coefficients (with Bonferroni correction) obtained between spatially averaged wall shear stress (SAWSS) and pulmonary vascular resistance (PVR), compliance (C), and stroke volume (SV).

Simulation based Indices	Pulmonary Vascular Resistance (PVR)	Compliance (C)	Stroke Volume (SV)
SAWSS G,PS	−0.52	-	-
SAWSS G,MN	−0.67	0.49	0.59
SAWSS G,MD	−0.54	-	0.51
SAWSS MPA,PS	−0.53	-	0.46
SAWSS MPA,MN	−0.57	-	0.61
SAWSS MPA,MD	−0.48	-	0.63
SAWSS LR,PS	−0.53	-	-
SAWSS LR,MN	−0.54	-	0.55
SAWSS LR,MD	−0.52	-	0.62
SAWSS D,PS	−0.46	0.45	-
SAWSS D,MN	−0.62	0.50	0.55
SAWSS D,MD	−0.49	-	0.45

Table 4:

Statistically significant Pearson’s correlation coefficients (with Bonferroni correction) obtained between spatially averaged wall shear stress gradient (WSSG) and pulmonary vascular resistance (PVR), compliance (C), and stroke volume (SV).

Simulation based Indices	Pulmonary Vascular Resistance (PVR)	Compliance (C)	Stroke Volume (SV)
WSSG G,PS	−0.46	-	-
WSSG G,MN	−0.55	0.47	0.55
WSSG G,MD	−0.48	-	0.50
WSSG MPA,PS	-	-	0.49
WSSG MPA,MN	−0.46	-	0.53
WSSG MPA,MD	-	-	0.55
WSSG LR,PS	−0.46	-	-
WSSG LR,MN	−0.46	-	0.53
WSSG LR,MD	−0.45	-	0.59
WSSG D,PS	-	-	-
WSSG D,MN	−0.50	0.46	0.52
WSSG D,MD	-	-	0.47

Table 5:

Statistically significant Pearson’s correlation coefficients (with Bonferroni correction) obtained between time averaged wall shear stress (TAWSS) and pulmonary vascular resistance (PVR), compliance (C), and stroke volume (SV).

Simulation based Indices	Pulmonary Vascular Resistance (PVR)	Compliance (C)	Stroke Volume (SV)
TAWSS G	−0.62	0.47	0.51
TAWSS MPA	−0.51	-	0.51
TAWSS LR	−0.52	-	0.49
TAWSS D	−0.56	0.46	0.48

Table 6:

Statistically significant Pearson’s correlation coefficients (with Bonferroni correction) obtained between relative residence time (RRT) and pulmonary vascular resistance (PVR), compliance (C), and stroke volume (SV).

Simulation based Indices	Pulmonary Vascular Resistance (PVR)	Compliance (C)	Stroke Volume (SV)
RRT G	0.68	−0.44	−0.51
RRT MPA	0.51	-	-
RRT LR	0.67	-	−0.51
RRT D	0.65	−0.49	−0.47

6. DISCUSSION

In the present work, we developed patient-specific pulmonary aterial models for a group of 32 adult PH patients classified as (A) at-risk (18 mmHg ≤ mPAP < 25 mmHg), (M) mild (25 mmHg ≤ mPAP < 40 mmHg) and (S) severe (mPAP ≥ 40 mmHg). Each patient’s chest CTA images were segmented to obtain the pulmonary endoluminal boundary followed by 3D reconstruction of the patient-specific vasculature. The distal regions of the vasculature extended up to seven generations of branching pulmonary arteries. Pulsatile blood flow simulations were completed by means of an in-house CFD solver using quasi-patient specific inflow/outflow boundary conditions that achieved the mPAP measured at the proximal MPA during RHC. From these, we computed six hemodynamic indices and interrogated their potential association with three standard of care clinical metrics indicative of PH prognosis.

Five hemodynamic indices were derived from the spatiotemporal distribution of WSS. Multiple investigations have been reported on the use of WSS magnitude [6], direction [29], gradients [30, 31], and topological features [29, 32, 33] to characterize arterial hemodynamics. To this end, we calculated SAWSS at three salient stages of the cardiac cycle (peak systole, mid-notch, and mid-diastole). The mild patient group exhibited a SAWSS lower than that of the at-risk group for the three stages at the MPA, LR, and D regions, although such differences were statistically insignificant. Conversely, the lower SAWSS obtained for the severe group was statistically significant compared to the mild group. Noteworthy is that the percentage differences in SAWSS for the distal vasculature comparing the severe and mild groups were at least 6 times larger than the corresponding differences between the mild and at-risk groups. We infer from this outcome that low WSS at peak systole, mid-notch, and mid-diastole could be a consequence of PH disease severity. Such concomitant decrease in SAWSS with disease severity is in agreement with previous CFD studies [6, 7] and MRI-based measurements [4, 34, 35] in the pulmonary vasculature with PH. A similar result was obtained for the WSSG prediction of the global pulmonary geometry, where groupwise differences and the mild vs. severe group differences were statistically significant at the three stages of the cardiac cycle. WSSG decreased with disease severity irrespective of spatiotemporal location, although pairwise group differences were not significant. Flow through complex and tortuous blood vessel geometries results in significant spatial variations of WSS and local vortex structures [36]. WSSG is a hemodynamic measure used to explain flow-induced arterial wall pathology and morphological changes in the intima [30]. It is believed that sustained hemodynamic abnormalities, explained in part by WSSG distributions, may bring irreversible changes to the endothelium.

TAWSS reflected the inter-group variations in a pattern similar to SAWSS and WSSG for the global and regional distributions. For the global pulmonary geometry, groupwise differences and the mild vs. severe group differences were statistically significant. Analogous to SAWSS and WSSG, TAWSS decreased with disease severity and increased distally. OSI accounts for the temporal oscillations in WSS magnitude. An increase in OSI is often accompanied by a reduced TAWSS and together they provide evidence of abnormal hemodynamics on account of either arterial remodeling or vascular injury [37]. OSI increased with disease severity and decreased distally. This may be explained in part by the more evident flow separation in the MPA leading to elevated fluctuations in flow directionality, which become diminished in the distal vasculature. However, we observed statistical significance of OSI only within the MPA and for the pairwise relationship between the at-risk and mild groups. Yang et al. [8] reported similar results for pediatric PH patient groups. In an MRI-based study of 5 adult PH patients, Terada et al. [5] reported OSI_MPA = 0.214 ± 0.026, which is 47% higher than the OSI we obtained in this work (OSI_MPA = 0.146 ± 0.041). This difference could be attributed to the methods used for MRI data acquisition, the limited resolution for near-wall flow characteristic of MRI, and the small number of participants. Our CFD simulations lack individual inflow velocity profiles and are based on a rigid wall assumption, which can also explain the discrepancies in OSI_MPA relative to [10]. Regions with low TAWSS and high OSI experience large RRT, which is indicative of nearly stagnant blood flow. Lee et al. [38] proposed using RRT to characterize low and oscillatory shear. Elevated RRT can also signify constriction or obstruction within a blood vessel, and has been used as a strong indicator of thrombus formation in aneurysms [36, 39]. To the best of our knowledge, our study is the first to investigate RRT as an indicator of a progressing PH condition. We observed an increase in normalized RRT with disease severity and the groupwise differences were statistically significant for the global and regional distributions. The higher mean RRT in the distal vasculature suggests a more steady and unidirectional flow in the small pulmonary branches compared to the MPA.

One of the objectives of this investigation was to examine the potential relationship between simulation-based hemodynamic indices and clinically measured or calculated metrics. The statistical correlations, described in Tables 3 and 4, proved to be dependent on the space and time windows in which the indices were evaluated. The global spatial averages of the indices were predominantly predicted by the values in the distal vasculature. Moderate correlations were obtained between PVR and most indices. The time-dependent indices (SAWSS and WSSG) demonstrated relatively strong associations with PVR and SV at the mid-notch. The highest correlation coefficient for these indices was obtained for SAWSS_G,MN vs. PVR (ρ = −0.67). The time-averaged indices (TAWSS, OSI, and RRT) demonstrated relatively strong associations with PVR, with the highest correlation coefficient found between RRT_G and PVR (ρ = 0.68). We infer from this outcome that a clinical relevant measure such as PVR, which is used for PH diagnosis and patient follow up, can be predicted with global WSS-derived metrics, such as SAWSS and RRT, when calculated from in silico models of the pulmonary vasculature. Our hypothesis was partially proven in that pulmonary hemodynamics, when quantified by means of SAWSS, WSSG, TAWSS, OSI, and RRT, is strongly associated with PH disease severity if using in silico models of the global pulmonary geometry.

Our work is subject to several important limitations. The relatively low number of patients in each disease severity category with no corresponding control group is one such limitation. The absence of control subjects can be explained in part by the difficulty of exposing healthy individuals to a redundant RHC procedure that they do not need. The available patient-specific data for each severity group restricted our ability to postulate a universally applicable hypothesis on the existence of non-invasively diagnosable disease markers. To this end, a follow up computational study with a larger patient population is warranted. The CFD simulations assumed the blood to be a continuum and Newtonian fluid. Though Arzani et al. [40] provided a strong justification in favor of a Newtonian fluid assumption, blood is inherently a colloidal medium. Therefore, a particulate flow simulation with Lagrangian tracking would provide a superior model for pulmonary blood flow simulations. Furthermore, our CFD simulations assumed rigid wall boundaries, which might have led to an overestimation of the regional shear stress distributions. In the absence of vessel compliance, all the pulse pressure energy is transferred to the distal vessels and the reactive component of impedance in the flow dynamics is neglected. The lack of available patient-specific inflow and outflow boundary conditions is a formidable hurdle in studies such as ours. We were successful in partially overcoming this obstacle by means of quasi-patient specific boundary conditions calculated from clinical measurements obtained during RHC. Nonetheless, we acknowledge the limitation of lacking individual velocity and pressure profiles as boundary conditions to match the patient-specific geometries. To this end, a longitudinal study that quantifies changes in MPA diameter with disease progression would be valuable, as such changes would likely result in variations in the inlet velocity waveform used for the CFD simulations.

Spatiotemporal localization of simulation-based hemodynamic indices representative of pulmonary arterial blood flow in adult PH proved to be a valuable method for identifying the inter-group variations of such indices. We observed statistically significant decreases in SAWSS, WSSG, and TAWSS, and increases in OSI and RRT with disease severity. PVR was moderately correlated with SAWSS and RRT at the mid-notch stage of the cardiac cycle when these indices were computed using the global pulmonary arterial geometry. Regional distributions of these indices for the MPA, LPA+RPA, and the distal vasculature revealed moderate to weak associations with the clinical metrics, signifying the need for in silico models based on multiple generations of pulmonary aterial branches. These findings further our understanding of the pulsatile blood flow dynamics in the pulmonary arterial circulation in adult PH and the corresponding relationships between simulation-based hemodynamic indices and standard of care clinical metrics used in the diagnosis and follow up of PH patients.