The microdynamics of spatial polarization: A model and an application to survey data from Ukraine

Significance

We advance our understanding of changes in polarization over time and across space by highlighting how the nature and structure of social interactions shape changes in attitudinal polarization. We show how including geographical information in adaptive voter models improves their predictive accuracy for both individual-level attitude change and for aggregate patterns of spatial polarization. By applying the model to panel survey data from Ukraine, we address the dearth of empirical applications with real-world data in the agent-based modeling literature. This article also demonstrates the importance of a key mechanism underlying earlier findings about the importance of local effects in shaping individual attitudes, namely the role of political discussion in locally rooted networks.

Abstract

Although spatial polarization of attitudes is extremely common around the world, we understand little about the mechanisms through which polarization on divisive issues rises and falls over time. We develop a theory that explains how political shocks can have different effects in different regions of a country depending upon local dynamics generated by the preexisting spatial distribution of attitudes and discussion networks. Where opinions were previously divided, attitudinal diversity is likely to persist after the shock. Meanwhile, where a clear precrisis majority exists on key issues, opinions should change in the direction of the predominant view. These dynamics result in greater local homogeneity in attitudes but at the same time exacerbate geographic polarization across regions and sometimes even within regions. We illustrate our theory by developing a modified version of the adaptive voter model, an adaptive network model of opinion dynamics, to study changes in attitudes toward the European Union (EU) in Ukraine in the context of the Euromaidan Revolution of 2013 to 2014. Using individual-level panel data from surveys fielded before and after the Euromaidan Revolution, we show that EU support increased in areas with high prior public support for EU integration but declined further where initial public attitudes were opposed to the EU, thereby increasing the spatial polarization of EU attitudes in Ukraine. Our tests suggest that the predictive power of both network and regression models increases significantly when we incorporate information about the geographic location of network participants, which highlights the importance of spatially rooted social networks.

Spatial polarization is a crucial element of political polarization across the globe, but the microdynamics of how attitudes on important issues become more or less polarized across space are not well understood. In this article, we focus on the spatial polarization of attitudes on a key political issue and use a modified version of the adaptive voter model (AVM) to show how social learning from other individuals in discussion networks can explain growing local consensus while at the same time exacerbating spatial differences in attitudes. Specifically, we argue that individuals who hold political attitudes that deviate from the predominant opinion in their local network will be under social pressure to adjust either their attitudes or their network and that these changes can lead to divergent patterns of attitudinal polarization across different parts of a country.

We test these predictions using data from a panel survey of Ukrainian citizens, which focuses on the dynamics of attitudes toward European Union (EU) integration between late 2012 and mid-2015. In the context of Ukraine (1), and of Eastern Europe more broadly (2), the issue of EU integration is not a simple or minor foreign policy question but instead is a central political cleavage that both reflects and shapes competing visions of the future and can even threaten the unity of the country. Using a two-wave panel survey, we show that the Euromaidan Revolution of 2013 to 2014, in which President Viktor Yanukovych was overthrown by protests following his decision to suspend talks with the EU on an Association Agreement for Ukraine, led to changes in the extent of attitudinal polarization toward EU integration in different parts of the country, resulting in large part from local dynamics in which citizens changed their attitudes on this “hot question” to conform more with the local majority opinion.

We build and implement two different types of models to study changes in EU integration attitude in the aftermath of the Euromaidan Revolution. The first uses geographically weighted regression models to show the association between observed EU support (based on responses to the second survey wave) and previous attitudes, frequency of political discussion, and a measure of (first wave) local opinion. Our second model type is the AVM, whose goal is to study individual-level processes and, in particular, how varying the parameters guiding these processes can explain and influence the observed outcomes. Accordingly, the AVM, unlike the regression model, does not incorporate any information about the final outcomes. Instead, it takes as input data from the first round of the panel survey and makes predictions about the final attitudes.

This article makes three types of contributions. From a theoretical perspective, our focus on local discussion networks helps us understand how, in the context of preexisting spatial differences in political attitudes, political shocks can lead to increased spatial polarization of attitudes even without significant residential sorting. We generate clear expectations about when a shock that increases the salience of an issue will increase polarization as a result of the initial distribution of attitudes and subsequent discussion within local networks, as well as unpacking how local or regional pockets of political dissent cannot only survive but even grow despite an increasing national consensus. Thus, our article theorizes and documents an important mechanism underlying earlier findings about the role of local influence on individual attitudes (3, 4).

In modeling terms, we build an extension of the AVM, an adaptive network model used in opinion dynamics. This model allows for changes to occur within the network at both the opinion level and the network structure level. Our extension of the AVM combines geographic information and political discussion frequency (i.e., “political talkativeness”) from the survey data in order to build representative social networks for each node without explicit microlevel social network information about the respondents. We use this data-informed model to study the local and global dynamics that are driven by attitude and social network changes. By exploring different relative probabilities of these changes, we are able to see how interpersonal interactions can drive the divergent dynamics in polarization that we observe in our survey data. Combining network models and individual-level data without (notoriously difficult to collect) social network information is a challenging problem and one that is of interest to both social scientists and network scientists. We hope that our approach takes a step toward helping these communities think about how models and data collection can complement each other and how they can be used together to make predictions and propose mechanisms to describe observed behavior.

Finally, by examining in detail attitude change in Ukraine on the issue of joining the EU, we contribute both to the literature on the Euromaidan Revolution in Ukraine and its aftermath and to the literature on attitudes towards the EU. In nuancing our understanding of the political effects of the Euromaidan, we are able to shed light on the durability and, in some cases, the deepening of divides in Ukrainian society despite a successful revolution that triggered a break with Russia and a move toward embracing Europe and its values. This is important from a policy perspective, as Ukrainian leaders and their international supporters seek to find ways to overcome the past and unify the country. We also contribute a clear social dimension to our understanding of EU attitude formation in which the existing literature has focused heavily on individual-level material and cultural factors (5).

Theory.

How spatial polarization changes over time.

In this article, we focus on the spatial dimension of attitudinal polarization (i.e., the extent to which political attitudes differ systematically across different regions or areas of a country). While much of the recent work on spatial polarization has focused on debates about the importance of residential sorting (6–8), in many parts of the world (including Ukraine), residential mobility is considerably lower than in the United States. Therefore, in this article, we demonstrate a complementary phenomenon: the fact that spatial polarization can increase even without people moving their residence if they adapt their political attitudes to match those of the local majority. Here, we do not try to explain either the relationship between different types of political attitudes or how this attitudinal polarization affects the related but distinct phenomena of partisan polarization (9, 10) and affective polarization (11), though we do address the connection between attitudes and other aspects of polarization in the discussion section.

To understand the temporal and spatial dynamics of this type of attitudinal change, we draw on two distinctive strands of social science research. The first strand, which Beissinger (12) calls the “eventful” perspective, explains the timing of attitudinal change. It focuses on the role of revolutions and other dramatic political events in driving significant increases in the degree of spatial polarization (13). This is particularly true when “hot questions” (14) or “takeoff questions” (15) that are especially divisive become the focus of current political attention. Indeed, very significant divergence on important and topical political questions can occur rapidly without much divergence in underlying attitudes on other issues (16). The second strand of research, which goes back more than sixty years (17) but has often been neglected in favor of individualist explanations, highlights the role of local context on issues as diverse as party identification (9, 18), attitudes to immigration (19), and constitutional issues (20). Work in this tradition shows that opinions tend to change in the direction of the community majority position.

Combining these two strands, we would expect that when political crises raise the salience of a particular political issue, we should observe an increase in pressure toward social conformity and a resulting increase in attitudinal homogeneity within discussion networks. When such discussion networks are embedded in local contexts and these local environments in turn reflect preexisting geographic differences in attitudes, then we expect to see a growing spatial polarization of political attitudes even in the absence of residential sorting. In other words, in regions where there is a preexisting majority opinion, we expect to see attitudinal variation within localities diminish. This means greater local homogeneity but, potentially, growing attitudinal differences between geographic units if the preexisting majorities are on different sides of the issue. By contrast, where local attitudes were fairly evenly divided, we should expect to see continued heterogeneity in attitudes.

Data and Context.

To test our theoretical predictions, we use data from a nationally representative public opinion panel survey fielded through in-person interviews in Ukraine between 2012 and 2015. Of the 1,800 respondents interviewed in the first survey wave in December 2012, we were able to reinterview 924 individuals in June 2015.* By focusing on respondents interviewed in both survey waves, we can analyze attitudinal change at the individual level. Moreover, since the surveys collected information on the locality where respondents resided at the time of the interviews and since respondents are clustered in localities such that we have multiple respondents per locality^†, we can use this information, along with data on political talkativeness, to capture probabilistically the informational nature of individual networks (21).

For our main attitudinal outcome, we use a survey question that measures support for Ukraine’s integration into the EU using a three-point scale (oppose, neutral, and support). In addition to its intrinsic interest to debates about the drivers of support for EU integration, focusing on EU support in Ukraine has two important advantages for testing the dynamics of attitudinal change in social networks.^‡

The first advantage is that during the time period covered by our surveys, Ukrainian citizens experienced a (largely exogenous) increase in the salience of attitudes toward EU integration. This rising salience was due to the fact that in November 2013, the Ukrainian government (under pressure from Russia) abruptly reversed its prior commitment to sign the EU Association Agreement, which would have continued Ukraine’s gradual process of European integration. The announcement triggered a series of mass protests, which spread from the capital to large parts of the country, and eventually brought down President Yanukovych in February 2014. While the revolution, widely known as the Euromaidan or the Revolution of Dignity, featured a broader and evolving set of demands (22), one of its central themes was the debate about Ukraine’s foreign policy orientation and particularly about whether the country should be joining the EU or a Russian-led Customs’ Union (23, 24). The salience of foreign policy attitudes was further heightened by the fact that the overthrow of the Yanukovych government was swiftly followed by the Russian annexation of Crimea and the secession of parts of eastern Ukraine under the leadership of Russian-backed rebels, triggering a lengthy military conflict with high human costs. Therefore, we expect that the likelihood of people discussing EU integration and the costs of holding minority views on this issue would have increased significantly between the two survey waves.

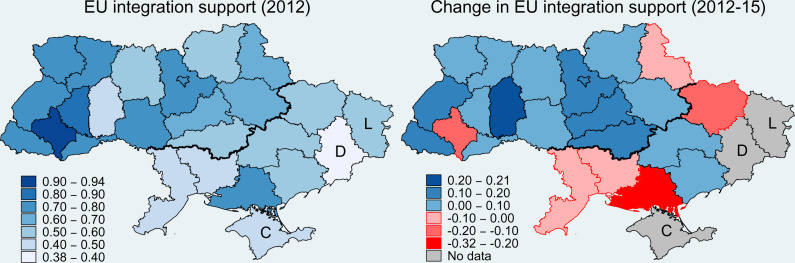
The second advantage of focusing on EU integration attitudes is that there was considerable heterogeneity in the geographic distribution of EU preferences. In western and central Ukraine, a clear majority (57.6%) of the respondents to the 2012 survey supported EU integration (with only 15% opposed). By contrast, in southern and eastern Ukraine, EU opponents slightly outnumbered EU supporters (by 32.8 to 29%). This heterogeneity is also illustrated in Fig. 1, Left, which shows the oblast-level^§ averages in EU integration preferences derived from the individual data in our December 2012 survey and highlights the contrast between the clear EU support in most of the west and center and the much more mixed picture in oblasts located in the south and east.

Fig. 1.

Spatial patterns in EU integration support in Ukraine (2012 to 2015). The figure shows the average EU support at the oblast level in the 2012 survey (Left) and the change in support from 2012 to 2015 (Right) is shown. The index on Left ranges from 0 (universal opposition) to 1 (universal support), while 0.5 indicates an even balance between supporters and opponents. For Right, positive values (in blue) indicate an increase in EU support, while negative values (in red) indicate reductions in EU support. Right has no estimates for Crimea (C), Donetsk (D), or Lugansk (L) because of missing/truncated data following Russian occupation. The thick black line on each map demarcates the oblasts of the western and central regions from those of the south and east to facilitate the interpretation of results but has no administrative or political meaning in Ukraine.

Following the Euromaidan revolution and the subsequent Russian aggression, Ukrainians overall became more supportive of EU integration. However, as scholars have noted (25, 26), this broad trend masks important regional variation: whereas in the west and center, roughly two thirds (66.4%) of respondents supported EU integration by 2015 (with only 9.4% opposed), in the south and east, the shares of both EU supporters and opponents increased from 2012 to 2015 (to 36.8 and 32.8% respectively). Moreover, while support for EU membership rose in the face of war and annexation, this did not necessarily foster national unity. Instead, identities actually became more predictive of political opinions than before (27). Fig. 1, Right shows these dynamics using our individual-level data aggregated to the oblast level: in 15 of the 17 oblasts of western and central Ukraine, EU support increased further between 2012 and 2015. By contrast, four of the six oblasts in southern and eastern Ukraine actually experienced at least slight declines in EU support among our respondents during that time period.^¶

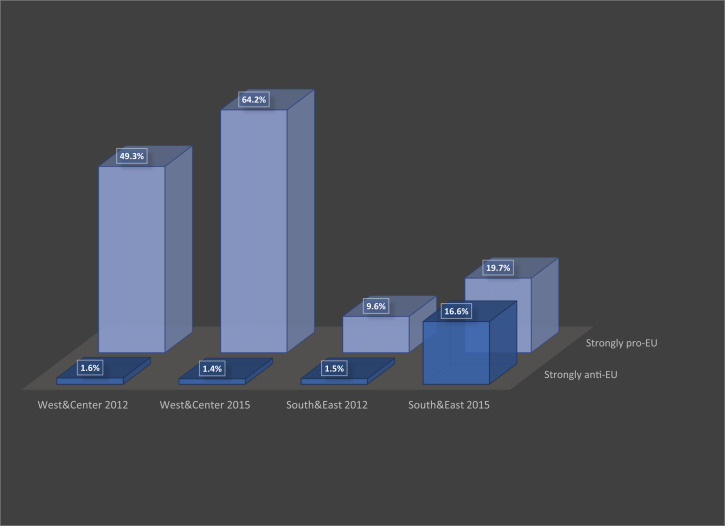
In Fig. 2, we zoom in closer to show attitudinal dynamics at the locality level^#, which are closer to our theoretical focus on locally grounded discussion networks. To illustrate these dynamics, we defined types of locality based on the relative share of EU supporters and opponents. We defined a locality as strongly pro-EU if the share of supporters was at least 50% larger than the share of opponents and as strongly anti-EU if the proportions were reversed. Fig. 2 shows variation in the extent to which localities in different parts of the country either follow the national level trend or, in fact, move in the opposite direction. In the west and center, the proportion of strongly pro-EU towns increased from 49% in 2012 to 64% in 2015 (while the share of strongly anti-EU localities was negligible throughout). Meanwhile, in the south and east, the share of strongly pro-EU towns also grew but more slowly and from a much lower base. Even more importantly, the share of towns with large anti-EU majorities increased more substantially, illustrating increased local divergence even in the context of a national pro-EU bandwagon.

Fig. 2.

Regional differences in local EU attitudes (2012 to 2015). The proportion of respondents by macroregion who lived in localities that were either strongly pro-EU or strongly anti-EU in the 2012 and 2015 surveys are shown.

Overall, both Figs. 1 and 2 suggest that in areas where clear majorities of respondents had already favored EU integration in 2012, the size of the pro-EU majority further increased by 2015. However, in areas that were evenly split or had anti-EU majorities in 2012, attitudes either remained divided, or anti-EU sentiment increased. While these aggregate patterns are compatible with the general idea that increased polarization is the result of attitudinal change driven by local contextual dynamics, we need to avoid the dangers of ecological fallacy inherent in drawing individual-level conclusions based on aggregate-level data. Therefore, in testing the network model presented in Model, we turn our attention to the interplay between individual attitude change, local context, and discussion networks.

Model.

Motivation and background.

Computational models of social influence have been widely studied to understand the processes influencing opinion dynamics, albeit with weak links to specific cases and empirical data (28). In this work, we contribute to filling this gap in the intersection of real-world data analysis and modeling. In order to investigate and disentangle the factors shaping polarization in post-Euromaidan Ukraine, we use a specifically tailored extension of the AVM proposed by Holme and Newman (29) that is informed by our detailed, individual-level survey data. The AVM is an adaptive network model, a broad class of stochastic multiagent models that explores the dynamic relationship between node properties and network topology or structure (30–32). Specifically, the AVM is a network-based model of opinion dynamics in which individuals are nodes, and edges between these nodes denote some kind of connection or interaction (33). Each individual holds exactly one of several possible opinions.

In the specific case of the standard AVM, changes can occur within the network in one of two ways: first, through homophily, an edge forms between two individuals who already agree (while an edge between individuals who either agree or disagree is cut); second, through social learning, an individual adopts one of their neighbor’s opinions. This model controls the balance of these two processes using only one variable, ϕ. As this parameter is varied, we see several resulting dynamics from one giant component of individuals who all share the same opinion (which can be thought of as a state of high consensus) to a fragmentation into “islands” in which the individuals on each fully separated island share the same opinion and do not interact with those who have different opinions (which can be thought of as polarization of a sort, as individuals converge into single-opinion clusters). We often see similar dynamics play out in the real world, for example, on Twitter (34) and, more generally, when networks demonstrate assortative mixing (35) in which individuals more frequently attach to those who are similar to them. This results in social networks that partition into groups of individuals who are largely likeminded.

While we might often encounter a snapshot of a network in time and observe some degree of polarization in opinions, it is not always immediately clear from where this polarization arose and which processes may have led to this state (36–38). Indeed, a fundamental question in (social) network dynamics is whether the dynamics on the network govern the network structure or, conversely, whether the network structure governs the dynamics or both as is the case in a dynamic feedback process (30).

In this article, we propose an adapted AVM specifically taking into account the effects of spatial organization and the tendency of individuals to engage in political discussions^ǁ in order to better understand how small-scale, individual-level mechanisms led to the large-scale postrevolution changes in EU integration opinions that we see in our survey data. Given its integration of empirical data in addition to more realistic update rules (see Materials and Methods), our AVM is well suited to studying questions of how interpersonal connections and communication shape individual opinions and how the interplay between these factors can lead to polarization. We show computationally the importance of local discussion networks in driving opinion and social network changes and demonstrate that our modified AVM can explain the qualitative changes in polarization that we see in our survey data.

Our analysis is unique due to the integration of the survey data into the model. First, we extend standard AVMs by initializing the model with more realistic adjacency matrices created from the data that reflect the spatial constraints of the underlying social network,^** and we vary the number of political ties based on individuals’ self-reported political discussion frequency. In addition, we add geographically informed constraints to homophilic rewiring events to ensure that when cutting a tie, individuals preferentially create new edges to likeminded individuals in their spatial (i.e., geographical) neighborhood, particularly making sure that links are not lost from the network at excessive rates. This choice ensures that the underlying geographic integrity of the modeled social network (in terms of its link distance distribution and higher-order correlations between link distance and attitudes) is not quickly destroyed by random link rewiring steps (39). We compare the performance of our tailored AVM to that of a standard AVM.

Results

We present the results in a series of steps. We use both the AVM and spatially weighted regressions to show the importance of the distribution of local attitudes in explaining individual-level changes. We then show how the geographically informed AVM performs well in modeling our main outcome of interest—the increasing local homogenization of opinion—demonstrating the role of discussion networks as a mechanism. Finally, we show the extent to which different modeling approaches capture the growing role of geography in explaining patterns of attitudinal change between 2012 and 2015 as attitudes become more homogenous in some parts of the country and more polarized in others.

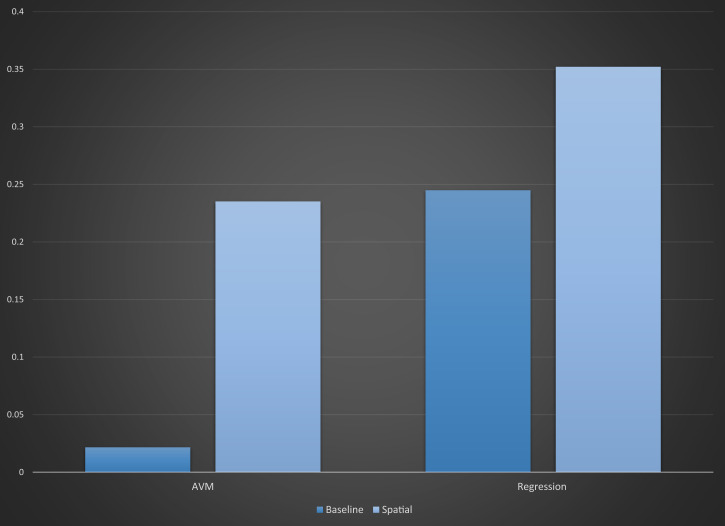
As a first step, we compare the performance of different modeling approaches in predicting individual-level attitudinal change between the two survey waves. To do so, in Fig. 3, we show the correlation between the actual EU attitudes in the second survey wave (from 2015) and predictions from four different types of models. The left cluster uses the output from different versions of the AVM, while the right cluster uses geographically weighted spatial autoregressive models with the same informational inputs as the corresponding AVMs.^†† Within each of the clusters, we first show the results of a baseline model, which only incorporates individual characteristics (initial levels of EU support and a political discussion index), followed by a model that incorporates information about the balance of attitudes in the local context/networks.

Fig. 3.

Individual predictions–model comparisons. The correlation between the actual individual-level EU support (based on the 2015 survey) and predicted attitudes based on the four different modeling approaches are shown. The AVM results are for a snapshot taken at 10⁵ time steps with ϕ = 0.2 and p_SL = 0.6 for an effective ϕ_e = 0.12.

The most important finding from Fig. 3 is that incorporating information about the local attitudinal context is important in explaining individual-level attitudinal change in polarized societies. The explanatory boost of incorporating local context is strongest for the AVMs, but it is still quite strong for the regression models and suggests that analyses that ignore the role of local effects may suffer from significant omitted variable bias.^‡‡

It is worth noting that the overall explanatory power of the regression-based models is consistently higher than for the AVM predictions. This is to be expected because the purpose of the regressions is to use both rounds of the survey data to develop a model that fits changes in the outcome (EU support) between rounds one and two (with or without information about the nature of the local attitudinal context). The AVM does not do this. Instead, it only uses the initial distribution of opinions and political discussion frequency to predict the patterns of individual change.

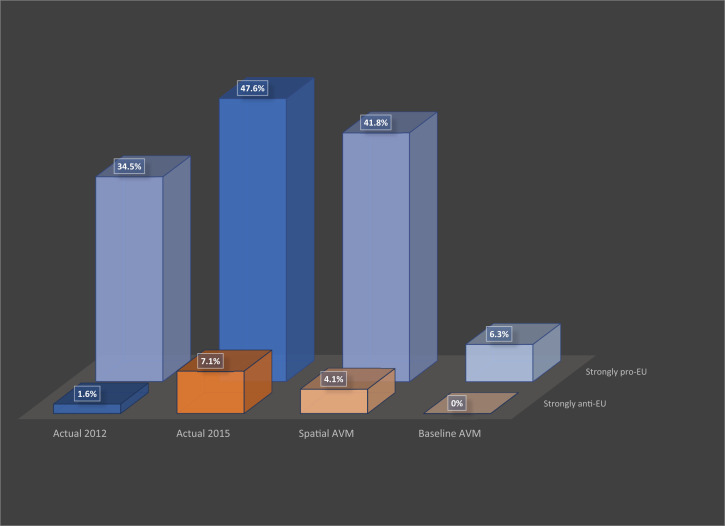
Consequently, what matters more than the individual-level predictive power is the extent to which different models can capture and shed light on the dynamics of spatial polarization we described in the introduction. To capture the extent of local attitudinal homogenization, we use the same metric from Fig. 2: the share of individuals who live in localities with overwhelming majorities either for or against EU integration. The first two columns in Fig. 4 are based on the raw data of the responses in the 2012 and 2015 survey waves and reflect the significant increase in “mono-attitudinal” localities from 2012 and 2015. The last two columns in Fig. 4 compare the predictive power of the standard AVM to the modified network model with geographically clustered ties. The results clearly confirm that whereas the standard AVM performs poorly on this measure, the geographically informed model captures much of the increase in locality-level attitudinal uniformity in Ukraine between 2012 and 2015.^§§

Fig. 4.

Locality-level homogenization of EU attitudes. The proportion of respondents who lived in localities that were either strongly pro-EU or strongly anti-EU based on actual responses to the 2012 and 2015 surveys (in the left two sets of columns) and on predictions from the AVM (in the right two sets of columns) are shown. The AVM results are for a snapshot taken at 10⁵ time steps with ϕ = 0.2 and p_SL = 0.6 for an effective ϕ_e = 0.12.

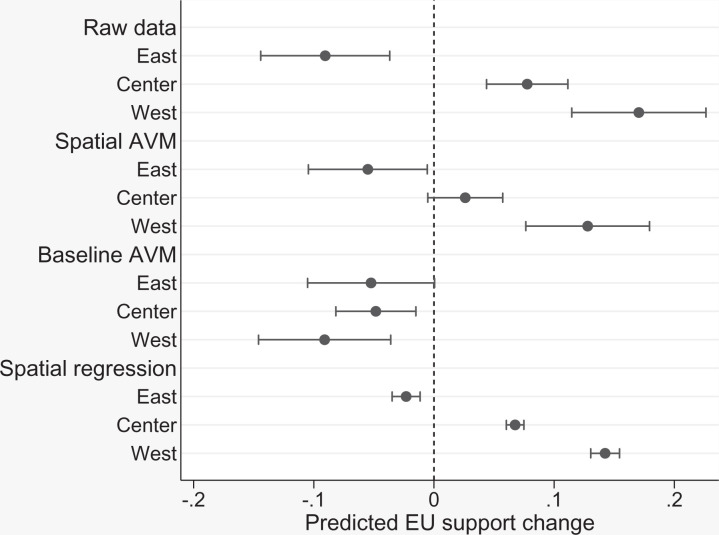
While Fig. 4 captures the trend of increasing local homogenization, it does not tell us anything about the implications for spatial polarization. In particular, a large literature on Ukrainian politics (40–43) has highlighted the historical, developmental, and political differences between the western and central regions, which have tended to favor closer Western integration, and the more pro-Russian south and east Ukraine. To capture this important geographic gradient, we ran a set of static score regressions in which we regressed changes in EU attitudes on the geographic latitude and longitude of survey respondents’ location.^¶¶ To evaluate the extent to which the geographic differences in attitudinal change are captured by different modeling approaches, we report in Fig. 5 the predicted attitude change from 2012 to 2015 for respondents located in the eastern, central, and western parts of Ukraine for each model type.^##

Fig. 5.

Geographic patterns in EU support change–model comparisons. The predicted changes in EU support (along with 95% CIs) for respondents located at the 5th, 50th, and 95th percentile of longitude (corresponding to the west, center, and east of Ukraine) based on the raw data from the 2015 survey as well as predicted attitudes from three types of models (spatial AVM, baseline AVM, and spatial regression) are shown. For regression results, see SI Appendix, Table S2.

The patterns in the raw data reflected at the top of the figure confirm the patterns in the maps in Fig. 1: whereas in the west and center, EU support increased significantly from 2012 to 2015, in the east, the trend was actually negative (and statistically significant). When comparing the predictions of the other models in Fig. 5 to the trends in the raw data, two findings are worth highlighting. First, the geographically informed AVM clearly outperforms the baseline AVM. Second, unlike for the individual-level predictions, it appears that the spatial AVM captures the geographic patterns in the raw data at least as accurately as the spatial regressions, especially with respect to the predicted change among respondents from eastern Ukraine.

Discussion and Next Steps

In this article, we developed a modified version of the AVM and applied it to an original two-wave panel survey to try to explain the dynamics of spatial polarization in EU support in Ukraine in the aftermath of the Euromaidan Revolution. The model emphasized the importance of spatially constrained discussion networks for understanding why over time opinion becomes more pro-EU in western and central Ukraine but more anti-EU in much of the south and east and why, overall, location becomes a better predictor of attitudes even as there is a nationwide increase in support for EU integration.

One important question that arises from focusing on a single attitude in a very specific geographic and temporal context is how our findings should be expected to generalize beyond the dynamics of EU support in Ukraine. While space constraints prevent us from theorizing and testing the broader systemic implications of the two phenomena—increasing local uniformity and spatial differentiation—for Ukrainian politics, we tested the extent to which our findings about EU support applied to other issues. As we show in SI Appendix, Table S3, the role of local context in explaining the dynamics of change applied to a fairly broad range of attitudes, including, but not limited to, other foreign policy preferences, language policy, and democracy support. Moreover, we also found that local context affected attitudes about the desirability of Russian neighbors (a potential proxy of affective polarization) as well as home language and ethnicity (as proxies of identity). Meanwhile, in SI Appendix, Table S4, we show that the degree of spatial differentiation (as measured by the predictive power of geographic coordinates) increased for a smaller subset of issues generally more closely related to the ongoing conflict with Russia (support for NATO membership, desirability of Russian neighbors, and home language). From this perspective, it appears that the dynamics we discuss with respect to EU attitudes affected a broader set of attitudes and identity-related indicators but did not result in the wholesale spatial polarization of the broader political landscape in Ukraine.

More broadly, from a theoretical perspective, we would expect the phenomenon of increasing local uniformity to be stronger for issues that are more salient—since salience increases the likelihood that a particular issue would be discussed and that dissenting from the majority would be costly—and where the local balance is more skewed in either direction. The dynamics of growing spatial polarization hinge on the combination of high/growing salience and preexisting differences in the spatial distribution of particular attitudes or traits. Taken together, this suggests that our model will be particularly useful for understanding political change dynamics in the context of political upheavals or crises in societies with deep geographic cleavages.

In terms of extensions, we have shown the importance of tendencies toward conformity within discussion networks without being able to unpack the nature of the social pressures at work given the limitations of space. There are a number of aspects to this question including understanding both the nature of the incentives at play and the extent to which different kinds of people in the population may be more or less likely to respond to those incentives. Both of these represent potentially fruitful avenues for extensions to the model.

Another potentially interesting extension, which is suggested by the Ukrainian case, would be to allow for external information shocks. Such shocks, which in the Ukrainian case would be a pro-EU shock due to the Russian aggression, could either be uniform (randomly chosen individuals could receive a one-step pro-EU push at certain times) or they could be geographically uneven (44). These uneven shocks could happen as a function of distance to Western Europe or as a function of proximity to the pro-EU protests that took place in 2013/2014 (24).

Finally, while our focus has been on geographically bounded networks, future research could allow for people who are active on social media to transcend geographic constraints and link up to other people who are also active online.

Materials and Methods

An Adaptive Network Model of Attitudinal Change.

Model setup.

We start with a population of n = 1,522 individuals (nodes) (the difference between the size of the first wave sample and the one used in the present analysis is due to excluding respondents from territories that were not under control of the Ukrainian government at the time of the second survey wave and could therefore neither be reinterviewed nor, for the most part, interact normally with respondents from other parts of Ukraine), with a one-to-one correspondence between survey respondents and nodes. Each node i inherits the following measures from the empirical data: 1) EU integration opinion, g_i: each individual starts out with one of G = 3 possible opinions corresponding to their EU integration attitude (pro-, anti-, or neutral) in 2012 and 2) discussion frequency, d_i: a self-reported aggregate measure reflecting the amount of political discussion a respondent engages in across multiple social groups. For mathematical convenience, we rescale d_i to the open unit interval, (0,1). There is a small amount of missing data in the EU support and political discussion frequency responses in the 2012 wave: to address this, we impute missing EU support values with the most common attitude in the oblast in which each individual with a missing attitude resides and impute missing political discussion frequencies with the mean frequency across all individuals surveyed. In addition, we keep track of each respondent’s locality and oblast (in addition to the corresponding latitude and longitude coordinates).

In order to study the individual and combined effects of discussion frequencies and local geography on the opinion dynamics, we build a two-tiered model: a baseline model, which is geographically uninformed but takes into account political discussion frequencies, and a geographically informed version in which we add a layer to the political discussion frequencies by incorporating the pairwise geographical distances between the nodes.

Creating the initial adjacency matrix.

We assign initial edges between individuals by building realistic NxN adjacency matrices, A_NxN. While many models of opinion dynamics are initialized with random networks, we build data-informed adjacency matrices (corresponding to undirected networks) to faithfully reflect each node’s ties, which are influenced both by political discussion tendencies as well as geography. First, we apply a linear rescaling of the political discussion frequencies in order to assign each node i a k_i,max or maximum initial degree (i.e., number of connections) based on their political talkativeness. We apply this rescaling so that the average over the k_i,max is between 10 and 15, which is reasonable for a network of our size (35, 45).

In the baseline, geographically uninformed model, edges are formed between nodes based on discussion frequencies only. The edges are assigned as follows: first, a random node is chosen and connects to a random sample (across the entire population) of k_i,max nodes. Then, a new random node is chosen and attempts to do the same and so on. Since our networks are undirected, an individual may, after this edge building is executed enough times, try to connect to a node whose connections have already been exhausted in the sense that their degree is already equal to k_i,max. In this case, the edge is not formed, and the individual moves on to another randomly chosen node until they find one who has less than their maximum number of ties. This process repeats until all nodes have been sampled and given the opportunity to form up to k_i,max links. This process results in an NxN symmetric adjacency matrix A with zeros along the diagonal, reflecting the lack of self-interaction.

In the geographically informed models, we incorporate geographic distance into the initial network formation (on top of talkativeness). Each survey respondent has a corresponding longitude and latitude coordinate. In the data, each locality is represented by the same longitude and latitude coordinates. In order to adjust for this, we add uniform medium Gaussian noise to these coordinates to reflect more realistic pairwise distances (we experimented with uniform low and high Gaussian noise as well as variable Gaussian noise based on locality size and found that uniform medium noise produced the best results). To compute the raw distance between each pair of individuals, we use the standard Haversine formula, which gives the great-circle distance between two points on a sphere given latitude and longitude coordinates.

Edges in the geographically informed model are assigned as follows: first, a random node is chosen and connects to its k_i,max closest geographic neighbors (based on distance as computed from the noisy latitude and longitude coordinates). Then, a new random node is chosen and attempts to do the same, and this repeats until all nodes have been sampled and allowed to form edges. As with the geographically uninformed model, an individual may try to connect to a geographically close neighbor whose connections have already been exhausted in the sense that their degree is already equal to k_i,max. In this case, the edge is not formed, and the individual moves on to the next closest neighbor and retries. By doing this, we allow individuals to make longer-range connections (46) while keeping the degree distribution in the desired range (by not allowing individuals who have reached their k_i,max connections to gain new ones).

This results in an initial link distance distribution consistent with typical empirical spatial networks describing human activities such as communication, friendship, or travel (47, 48). Individuals are mostly connected to others in their local surroundings but can also maintain longer distance contacts to individuals in different localities across Ukraine (SI Appendix, Fig. S1). Finally, we sample nodes randomly across the population instead of in the order in which they appear in the survey data in order to eliminate the bias that would occur because of the respondents being roughly sorted by oblast and locality (sampling in order would give the first respondents chosen to make ties the advantage of having their pick of local connections before individuals begin reaching their k_i,max). Note that this process may result in nodes who have degrees less than k_i,max.

Creating these initial adjacency matrices is a challenge in general due to the constraints of the data and our desire to make the matrices realistic. In making these matrices, we aim to capture a realistic distribution of initial ties while preserving a reasonable correlation between the number of total initial ties per individual and their discussion frequencies. For example, a representative initial adjacency matrix that we use has a mean degree of 11 (and a correlation of 0.65 with discussion frequency), an average local transitivity of 0.5, and an average path length of 5.5—all values within reasonable ranges for real social networks (45, 49). In the geographically informed models, we additionally need the initial ties to reflect the effect that geographical distance between individuals has on their probability of connecting to each other (i.e., that individuals should have the majority of their ties within their oblast).

Running the model.

We run computer simulations of our models, which take as input the data-informed adjacency matrix. Each simulation consists of sequential, discrete time steps. At each of these time steps, an edge between two individuals i and j, denoted (i,j), is chosen at random across the entire population. We sample edges and not nodes (which are often sampled in such models) because we would like to “observe” a political conversation between interacting individuals proportional to how many conversations they are having (and sampling a random node would not take into account the degree or number of conversations the individual has). A random individual among i and j is then chosen to be the “learner,” while the other is the “role model”; for simplicity, we call i the learner and j the role model. Then, one of two things can happen: social learning or homophily. With probability ϕ (a global parameter), we end up on the social learning branch of our process, and with probability 1- ϕ, we end up on the homophily branch.

Social learning and homophily.

Geographically uninformed model.

In the standard AVM, an update (either social learning or homophily) occurs at each time step. However, in real-world conversations and situations, individuals do not always change their attitude or social connections as a result of every interaction. Therefore, for social learning, we introduce a new tunable parameter, p_SL, which is the probability that social learning will actually take place once on the social learning branch. This creates an effective social learning rate, ϕ·p_SL.

In addition, we introduce graded attitude changes, which reflect that individuals’ attitudes often change gradually over the course of weeks, months, or even years (50). We are able to incorporate this into the model because of the option of having an intermediate (neutral) EU integration attitude in the survey. More precisely, if j has an anti- (pro-) EU attitude and i has a pro- (anti-) attitude, then with probability ϕ·p_SL, i will adopt the neutral attitude rather than completely switching to the opposite attitude in a single time step. If i is already neutral and j is anti- (or pro-), then i will directly adopt j’s attitude with probability ϕ·p_SL. In practice, then, individual i (the learner) will change their opinion in the direction of j (the role model) with probability ϕ·p_SL. Note that this allows for the possibility of no discernible change in the population-level distribution of opinions, as i and j could have already had the same opinion at the time of the update.

For homophily, if i and j already have the same opinion, we leave this homogeneous edge between them (this is not done automatically in the standard AVM; indeed, edges between individuals who agree can be cut in a homophily update step) and move to the next time step. Otherwise, we introduce a new parameter, p_H, the homophily analog of p_SL. With probability p_H, i keeps their heterogeneous tie with j; this is more realistic than what is done in the standard AVM, as it is often the case that an individual will keep a tie with a social connection even if they disagree with them (particularly if it is only on one issue). Then, with probability 1-p_H, individual i cuts their tie with j and forms a new edge with an individual (chosen randomly across the entire population) who has their opinion. While unrealistic to the real world, particularly in a country as large as Ukraine, this is in line with the geographically uninformed nature of our baseline model.

We introduce these additional parameters p_SL and p_H to avoid having social learning or homophilic rewiring events following from each discussion event, which leads to unrealistically high social learning or network fragmentation that is inconsistent with the empirical survey data. Incorporating these homophilic rewiring update rules leads to good overall predictions, particularly for the locality-level homogenization of attitudes (see Results), which demonstrates the value of making realistic assumptions in the homophily branch of the model and suggests that this step is a promising place in which to incorporate real-world processes (51).

Geographically informed models.

In the geographically informed model, social learning remains the same as in the baseline. For homophily, if i and j have the same opinion, they again keep the tie between them. Otherwise, we cut the edge, and i attempts to connect to a close geographical neighbor, who has the same opinion as they do, and to whom they are not already connected (in the network sense). If no such individual exists, j attempts to do the same but with their nearest geographical neighbors. If this also fails, we choose a random individual k in the population who again attempts the same. If this is not possible, the edge is not replaced (the joint probability of all these events occurring is very small, and we therefore do not need to worry about excessive edge loss, which would result in the breakdown of the network, and many degree 0 nodes).

To render the modeling results comparable to the empirical survey data, we roughly estimate the number of political discussion events that may have taken place between the individuals in the survey data and run the model until a comparable number of discussion events has taken place therein, between 10⁵ and 1.5 × 10⁵ time steps. For details on robustness checks and parameter exploration, see SI Appendix, Fig. S2.

Data Availability

A repository containing our data and adaptive voter model implementation files is available at GitHub, https://github.com/oliviachu/ukraine-polarization (53). The replication data (including anonymized survey data) for the figures and regression analyses is available at the Harvard Dataverse, https://doi.org/10.7910/DVN/Q4HFRS (54).