Significance
How can a pluralistic republic combat dangers of tyrannical factions? In Federalist No. 10, James Madison proposed that the problem of factions could be mitigated by expanding the political sphere. Over 200 y later, however, polarization plagues the United States, despite the likely greater diversity of issues considered in the realm of politics. To tackle this puzzle, we explore how, in a partisan context, interactions among regular citizens can lead to collective-level factionalization via diversity collapse, as issues/opinions become increasingly segregated by party. We find that, while Madison was right that issue diversity can promote both individual cooperation and societal cohesion, extreme partisanship can introduce tension between the two, so that interindividual cooperation thrives at the cost of increased polarization.
Keywords: polarization, interest diversity, evolutionary game theory, dynamic networks
Abstract
Political theorists have long argued that enlarging the political sphere to include a greater diversity of interests would cure the ills of factions in a pluralistic society. While the scope of politics has expanded dramatically over the past 75 y, polarization is markedly worse. Motivated by this paradox, we take a bottom–up approach to explore how partisan individual-level dynamics in a diverse (multidimensional) issue space can shape collective-level factionalization via an emergent dimensionality reduction. We extend a model of cultural evolution grounded in evolutionary game theory, in which individuals accumulate benefits through pairwise interactions and imitate (or learn) the strategies of successful others. The degree of partisanship determines the likelihood of learning from individuals of the opposite party. This approach captures the coupling between individual behavior, partisan-mediated opinion dynamics, and an interaction network that changes endogenously according to the evolving interests of individuals. We find that while expanding the diversity of interests can indeed improve both individual and collective outcomes, increasingly high partisan bias promotes a reduction in issue dimensionality via party-based assortment that leads to increasing polarization. When party bias becomes extreme, it also boosts interindividual cooperation, thereby further entrenching extreme polarization and creating a tug-of-war between individual cooperation and societal cohesion. These dangers of extreme partisanship are highest when individuals’ interests and opinions are heavily shaped by peers and there is little independent exploration. Overall, our findings highlight the urgency to study polarization in a coupled, multilevel context.
Two hundred and twenty-five years ago, George Washington, in his farewell address, predicted that factions—or monolithic parties—would yield precisely the political sectarianism that the United States now experiences. As party sectarianism has increased, democratic norms have eroded, and the United States seems to be at a breaking point. However, a decade prior to Washington’s speech, James Madison argued that the “mischiefs of faction” could be prevented by expanding the sphere of politics: In a society with diverse interests, no faction could act as a monolith and agendas could be pursued only by negotiating across differences and forming alliances toward shared goals.
The scope of politics has dramatically increased over the past 75 y. Potentially driven by increases in educational attainment, the nationalization of politics, and changes to the information environment (1, 2), the number of issues people care about and consider within the realm of national politics has markedly increased (3–5). Despite this trend, and the consequent expectation that an abundance of issues will improve the collective cohesion by decreasing the likelihood of monoliths, polarization is markedly worse.
A potential explanation for this paradox is the decreasing dimensionality of the issue space. In other words, although the number of issues may have increased, individuals’ opinions on these issues might be so strongly correlated with their political ideology that, in effect, there are only one or two issue dimensions (6, 7). While some papers have argued that the decreasing dimensionality of issue attitudes (8, 9) is at the core of current political tensions, any demonstrated relationship between dimensionality reduction and polarization has been merely correlational. In fact, some have argued that “[a]lthough polarization and the reduction in dimensionality tend to coincide, there is no necessary logical connection between the two trends” (ref. 10, p. 42).
Here we propose a bottom–up mechanism that might offer a resolution for the paradox of polarization in the face of rising issue diversity. In particular, we focus on individual-level interactions that are influenced by issue stances, coupled with social learning that is mediated by partisan bias. The issues individuals care about (political or otherwise) and the stances they take on these issues have become both increasingly visible to others (e.g., via social media) and strong determinants of individual behaviors (11): How trustful, forgiving, or helpful we are—even in quotidian, pairwise interactions with neighbors, colleagues, friends, or strangers (12–15)—can hinge on our respective views on a variety of issues, from preferred sports teams to art tastes (16) to gun control or to favored political candidates [even in a primary election (12)]. Simultaneously, the stronger the perceived partisan bias, the less likely it is that individuals leaning toward one end of the political spectrum will embrace issues or opinions held by those at the opposite end (e.g., mask wearing in the COVID-19 pandemic) (17–19).
We propose that the interplay between individual-level behavior on the one hand and the degree of partisanship on the other hand mediates the effect of issue dimensionality both on individual-level dynamics and on emergent collective-level factioning. To investigate this proposition, we extend an evolutionary game theoretic (20, 21) model of cultural evolution (22) that allows the coevolution of individual states and social networks (23): Individuals imitate others—i.e., adopt their interests, opinions, and strategies—depending on their relative success in a pairwise donation game (also known as a simplified Prisoner’s Dilemma). Our choice of game is motivated by previous behavioral studies that have used similar pairwise games, such as the dictator game or the trust game, to measure cooperation between individuals with different political or other attitudes (12–15). However, our framework is sufficiently versatile to allow multiplayer interactions, such as public goods games, or even multilevel interactions, in which individuals can not only cooperate with peers but also contribute to their party.
Finally, but importantly, we assume that the imitation process is influenced by political affiliations and partisan bias, a mesolevel societal organization—intermediate between the individual and the collective—that governs the extent of a politically mediated reduction in issue dimensionality (24). Because we focus on the United States, where third parties have minimal influence (25), we model a two-party system (, ) with individuals distributed equally between the parties. We also ignore unaffiliated independents since a majority of independents admit to leaning Democrat or Republican and act much like their partisan counterparts, at least in their voting behavior (26). However, because independents may perceive partisan bias differently in their day-to-day pairwise interactions, future work should extend this model to consider an independent class.
Model Description
Population.
Building on ref. 22, we consider a population of individuals distributed over potentially overlapping groups, each representing a political issue of interest (e.g., climate change, gun control; Fig. 1A). A priori, we do not assume any relationship among the issues; i.e., we assume that all issues are independent, so that gives the dimensionality (or diversity) of the issue space. Individuals can care about (or have an interest in) any nonzero number of issues. Individual cares about issue if individual i takes either a liberal () or a conservative () position on it; future extensions could explore different strengths of interest by allowing values along a scale (e.g., 1–7). We say that individual i does not care about issue if takes a neutral position () on it. We define the opinion vector of as and the corresponding issue interest vector as , where if cares about issue and 0 otherwise. For simplicity, we assume that every individual cares about exactly issues, but the set of issues can differ among individuals.
Fig. 1.
Schematic illustration of the model. (A) individuals (nodes) are distributed over groups (black ovals), each representing a political issue. Colors represent behavioral strategies as indicated; shapes represent party affiliations (circle, diamond). Individual cares about all three issues and has opinion vector , where and correspond to liberal and conservative positions, respectively. Individual cares only about issue 3 and takes a liberal position; hence, . In each round, every pair plays one-shot donation games as many times as they have issues in common. Edges represent the interactions of focal individual ; widths are proportional to the number of interactions. Opinions determine interaction patterns: Whether cooperates with in a given group depends on whether they agree on that issue. (B) Once all games in a round are played, a learner is chosen uniformly at random to imitate a role model , chosen proportional to fitness. Strategies and issues/opinions can both be imitated but not party affiliation, which is fixed. (C) Whether learner imitates role model depends on party bias () and on the pair’s party affiliations: An imitation event occurs with probability if and belong to different parties and with probability 1 otherwise. In an imitation event, adopts ’s strategy with probability or a random strategy with probability ; independently, abandons k’s issues and adopts ’s issues and opinions with probability ; with probability , picks a random set of issues and adopts opinions on those issues that are biased toward ’s party with probability .
Individuals also have political affiliations, but their opinions on issues are not necessarily perfectly correlated with their political label. In other words, someone who identifies as a member of a left-leaning party can hold right-leaning opinions and vice versa (e.g., an American might identify as a Democrat based on stances on economic issues but still oppose the party on some social issues). The strength of correlation between one’s party label and opinions is subject to model dynamics as described below in Imitation Dynamics.
Pairwise Interactions.
In our model, an interaction takes the form of a one-shot pairwise donation game. In a game, the donor must choose whether to cooperate with the recipient. A cooperating donor (“cooperator,” ) incurs a cost to provide a benefit to the recipient; a defecting donor (“defector,” ) incurs no cost and provides no benefit to the recipient.
Interactions are entirely determined by issues and are not influenced by party affiliation. Specifically, individuals and (independent of their party labels) interact if and only if there is at least one issue that they are both interested in, and they interact as many times as they have shared interests (Fig. 1A). This dynamic reflects, for instance, social media interactions, where an individual will respond to someone else only if they have a mutual interest in the issue and will do so regardless of whether they have the same opinion on that issue. How they choose to respond will, however, be determined by their opinions. In our model, an individual can employ one of four strategies depending on the individual’s own opinion and that of the donor: unconditional defector (), unconditional cooperator (), homophilous cooperator (; cooperates with those who share the same opinion but defects against those who have the opposite opinion), or heterophilous cooperator (; defects against those who share the same opinion but cooperates with those who have the opposite opinion).
Fitness.
After all pairwise games for a given round have been played, the fitness of individual is computed as , where denotes the total payoff accumulated by individual and denotes the intensity of selection, a quantity employed in evolutionary game theory to capture the impact of the dynamics under study on relative fitness. Most often, and in our case, the assumption is that selection is weak (i.e., ), to reflect the fact that most peer interactions represent only a tiny fraction of an individual’s overall fitness. This limit also facilitates analytical insights.
Imitation Dynamics.
The population updates dynamically according to a frequency-dependent Moran process (27–29), a standard approach in models of cultural evolution (Fig. 1B). This framework describes a social learning process in which individuals preferentially copy the traits of successful others. In our model, both the strategy and the issues and associated opinions are subject to this updating process. However, we assume that individual party affiliations are fixed over time because empirical evidence suggests that Americans rarely change their party affiliations (30)—although future work can relax this assumption to explore the dynamics of party affiliations, possibly on longer timescales. This imitation process plays out at the individual level (i.e., individuals imitate peers). However, it mirrors the influence of political leaders and campaigns on public discourse (31), as exemplified by the empirically documented follow-the-leader phenomenon (32); i.e., voters tend to first pick a political leader they deem successful and then adopt their policies, rather than choosing a leader whose policies match the voters’ own preferences.
Once fitness is computed for all individuals, a learner is chosen uniformly at random from the population. The learner then selects a role model randomly with probability proportional to fitness (Fig. 1B). Importantly, the learner and the role model do not have to share any issues in common prior to the imitation event; i.e., the imitation network is the complete graph and there is a breaking in symmetry (33) between the interaction network (which is local) and the imitation network (which is global). Whether the learner proceeds to imitate the role model or not depends on their party affiliations (Fig. 1C), so that an imitation event is initiated with probability 1 if and belong to the same party, but only with probability otherwise. When , the imitation graph completely segregates into two modules according to party affiliations. The exogenous parameter —which, for simplicity, we assume to be the same for both parties—thus captures partisan bias: A larger means that individuals are less willing to imitate across party lines, consistent with cognitive dissonance theory and partisan-mediated reasoning (34); if , individuals imitate only those in their own party.
An imitation event also allows for the possibility of errors (e.g., incorrectly assessing someone’s strategy or opinions) and for nonsocial learning or exploration (e.g., learning about new issues from sources other than peers) (Fig. 1C). Let and be the strategy mutation rate and the issue and opinion exploration rate, respectively. Learner adopts either role model ’s strategy with probability or a random strategy with probability . Similarly, with probability , adopts ’s opinion vector ; with probability , however, explores a new and random set of issues and opinions, . The lower the exploration rate, the more reliant individuals are on their peers as sources of information. When an individual explores a completely new and random set of issues, party affiliation can still play a role in determining what opinions that individual will take on the newly adopted issues: With probability , learner adopts a random set of opinions. With probability , however, learner adopts a biased set of opinions aligned with party membership.
Individual- and Collective-Level Metrics.
We define the following metrics to characterize the three phenomena of interest: cooperation, opinion alignment, and interest alignment. See Materials and Methods for full mathematical definitions.
Cooperation.
To quantify the amount of interindividual cooperation in the population, we define the effective cooperation to be the population-level mean fraction of cooperative interactions averaged over the stationary distribution of the dynamical process. To characterize individual behaviors in more detail, we also measure the steady-state strategy distribution, i.e., the frequency (or relative abundance) of each of the four possible behavioral strategies averaged over the stationary distribution.
Opinion alignment.
We use as a measure of factionalization the ability of a party to act as a monolith on issues of interest, i.e., the extent to which within-party opinions are aligned. Although this metric has been primarily used to describe party unity, some have argued that it can be used to characterize the degree of societal polarization (35).
To quantify opinion alignment, we define the average opinion distance in a given subpopulation as the average city block distance—also known as Manhattan distance or norm—between pairs of opinion vectors. The opinion distance between individuals and thus represents the total magnitude of their opinion differences across all issues and is computed as . We define average opinion distance for three subpopulations: among members of the same party (within party), among members of different parties (between party), and among all individuals (population level). A lower average opinion distance in a subpopulation indicates greater opinion alignment within that subpopulation.
Interest alignment.
Interest alignment refers to the degree to which individuals share overlapping interests and therefore interact with one another. To quantify it, we define the average interest distance within a given subpopulation as the average pairwise Hamming distance between pairs of issue interest vectors. The interest distance between and thus measures the number of issues they do not have in common (i.e., issues that either or cares about but not both) and is computed as . We define average interest distance within parties, between parties, and within the whole population. A lower average interest distance within a subpopulation indicates greater interest alignment within that subpopulation.
To illustrate how opinion distance and interest distance work in tandem, consider a population in which each individual cares about three of five available issues (i.e., , ). Suppose individuals , , and have opinion vectors , , and , respectively. Even though both pairs and have the largest possible divergence in issues for the given and (pairwise interest distance 4, since they share only one issue of interest), the opinion distance for pair (given by ) is greater than that for pair (given by ) because and have the same opinion on the one issue that they do have in common. Thus, the two quantities together capture not only the overlap in issues but also the divergence in opinion on those overlapping issues.
Results and Discussion
We conducted computational simulations (Materials and Methods) and, where possible, analytical calculations (SI Appendix).
Regardless of Political Bias, Increasing the Number of Available Issues () but Decreasing the Number of Issues That Each Individual Cares About () Promotes Interindividual Cooperation and Reduces Polarization.
At the individual level, pairwise cooperation tended to increase when there were more available issues (higher ; Fig. 2A) or when individuals cared about fewer issues (lower ; Fig. 2B). The latter had a stronger effect on cooperation, particularly when individuals were not exploratory (), but the effect of the former became clear as increased to an intermediate level (see effect sizes in SI Appendix, Tables S2 and S3). Analytical calculations provide insight into the relative effects of and (SI Appendix, Eqs. 21 and 22): Whereas affects the frequencies of both unconditional () and conditional (, ) cooperators, affects only the former and only positively (SI Appendix, Eq. 22). Consequently, effective cooperation always increases with the number of available issues, consistent with the simulations. However, impacts the frequency of via a term proportional to , and therefore the positive effect of increasing is vanishingly small. In contrast, impacts all frequencies at least linearly, and therefore the effects of varying are much stronger than those of varying .
Fig. 2.
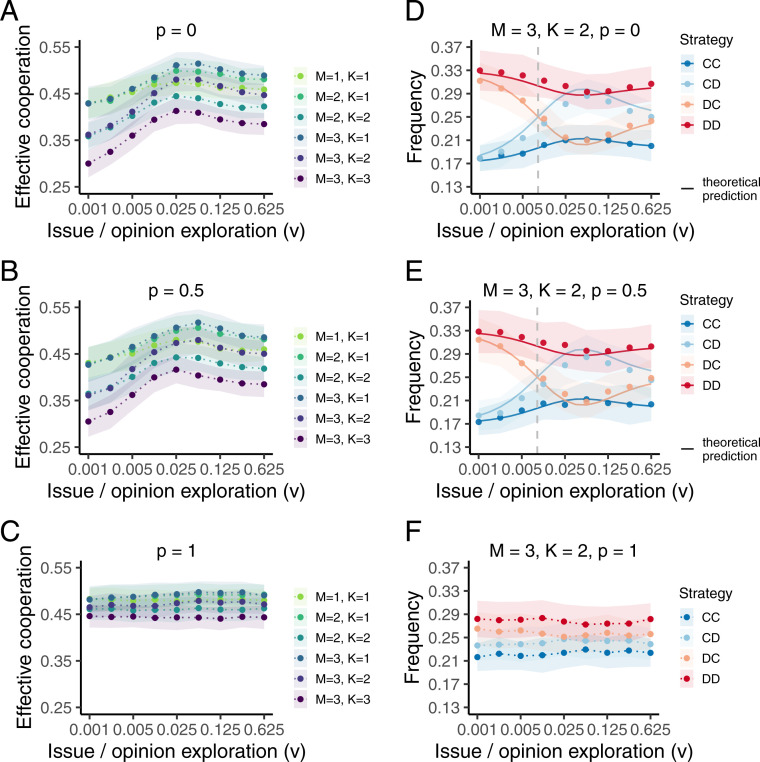
Cooperation increases with increasing number of available issues () and decreasing number of issues individuals care about (). For each parameter setting, we ran an ensemble of 150 simulations with population size , each lasting generations, the first 10% of which were disregarded to account for potential initialization effects. (A and B) Effective cooperation as a function of and in the absence of partisan bias ( = 0), grouped by (A) or by (B). Within a simulation, effective cooperation was measured as the fraction of cooperative actions among all interactions in a generation, averaged across generations. Each circle represents the mean effective cooperation ( SD) averaged across the ensemble. Colors indicate issue/opinion exploration rates (). (C and D) Steady-state strategy distributions as a function of and in the absence of partisan bias ( = 0). Each circle represents the average frequency ( SD) of the corresponding strategy (indicated by its color) across generations, averaged across the ensemble; error bars indicate SD within the ensemble. Parameter is as indicated. (E and F) Effective cooperation as a function of partisan bias across combinations of and . Color indicates degree of effective cooperation, from low (yellow) to high (purple). Parameter is as indicated. See SI Appendix, Table S1 for other parameter values and SI Appendix, Tables S2 and S3 for the effect sizes corresponding to A–D.
Consistent with previous work (22), these findings capture the essence of why structured populations promote cooperation: The greater the possibility is for assortment with like-minded individuals, the higher the chance for cooperation to thrive (22, 36–39). Having more available issues but few of those issues claimed by any one individual increases the possibility for cooperators to find refugia from free riders (i.e., unclaimed issues that cooperators can make their own and thrive). This increased assortment leads to a lower frequency of unconditional defection () relative to unconditional cooperation () (Fig. 2 C and D).
At the collective level, within-party average opinion distance increased (and the potential for a party to act as a monolith decreased) with increasing and decreasing (see Fig. 4A). When there are more issues to explore, individuals have the possibility to adopt a wider variety of opinions and therefore are less confined to a small cluster of opinions. This reduces the chances of high within-party opinion alignment and the potential for polarization.
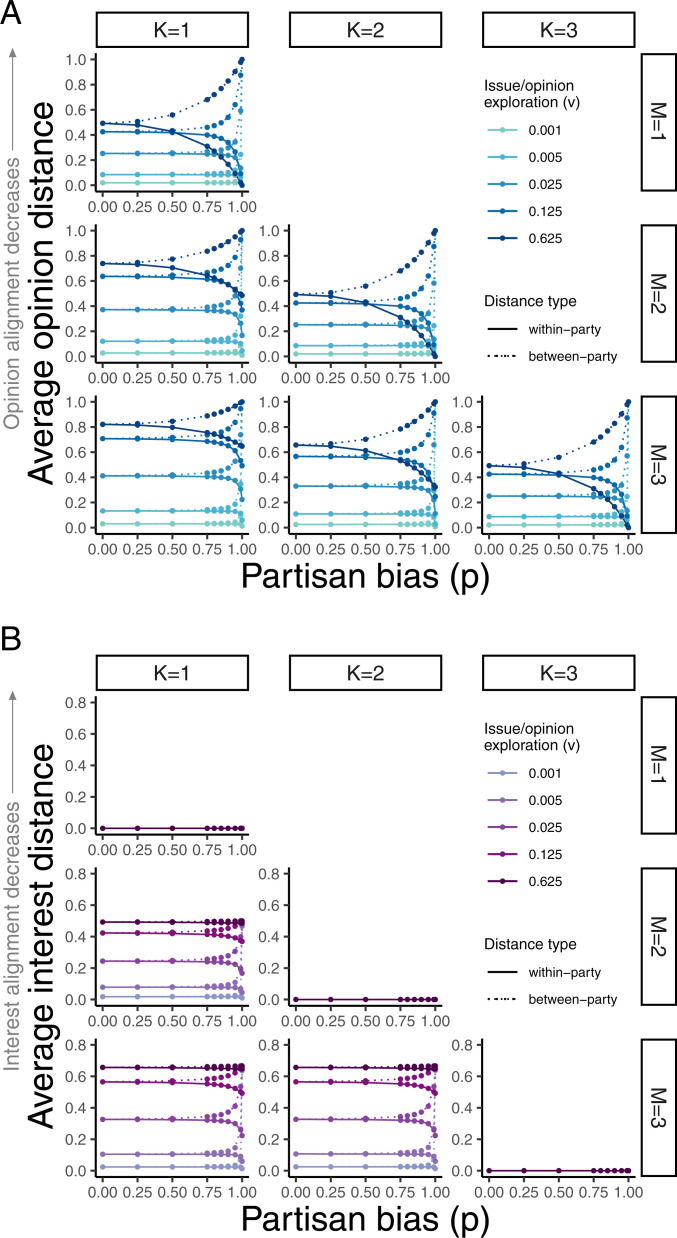
Fig. 4.
Opinion and interest alignment as a function of partisan bias. For each parameter setting, we ran an ensemble of 150 simulations with population size , each lasting generations, the first 10% of which were disregarded to account for potential initialization effects. Each circle within a panel represents the mean value ( SD) of the corresponding metric averaged across generations and across the ensemble. Dotted and dashed lines indicate values within and between parties, respectively. Values of and are as indicated; the values of between 0.75 and 1.00 are = 0.8, 0.85, 0.9, 0.95, 0.99. (A) Opinion alignment as measured by normalized average opinion distance. Opinion alignment decreases with increasing average opinion distance. (B) Interest alignment as measured by normalized average interest distance. Interest alignment decreases with increasing average interest distance. See Materials and Methods for definitions and the normalization procedure; SI Appendix, Fig. S5 for population-level values; and SI Appendix, Table S1 for other parameter values.
A Moderate Rate of Issue/Opinion Exploration Optimally Promotes Cooperation While Also Reducing Polarization Relative to a Rigid Population.
At the individual level, relative to our low-exploration baseline (), effective cooperation tended to be higher as the exploration rate increased up to a moderate rate of issue/opinion exploration (), after which it began to decrease (Figs. 2 A and B and 3A). These results are consistent with previous work showing that an intermediate level of stochasticity in the imitation of the population structure optimally promotes cooperation (22, 38). That such an intermediate optimum also arises in our system is to be expected, since too little exploration limits the cooperators’ ability to take advantage of “empty” issues while too much exploration scrambles the population structure and renders it virtually well mixed.
Fig. 3.
Moderate rates of issue/opinion exploration promote cooperation. For each parameter setting, we ran an ensemble of 150 simulations with population size , each lasting generations, the first 10% of which were disregarded to account for potential initialization effects. (A–C) Mean effective cooperation ( SD) across the ensemble as a function of issue/opinion exploration rate (log scale). Colors indicate combinations of and . (D–F) Steady-state strategy distributions for , as a function of issue/opinion exploration rate (log scale). Each circle represents the average frequency ( SD) of the corresponding strategy (indicated by color), averaged across the ensemble. Solid curves in D and E show the corresponding theoretical predictions in the limit of small (SI Appendix, Eqs. 17 and 18) and dashed gray lines show the critical exploration rate computed from Eq. 1, both showing excellent agreement with the simulation results. Partisan bias is as indicated in each panel. See SI Appendix, Table S1 for other parameter values and SI Appendix, Fig. S3 for an expanded figure with and .
To understand how changes in individual behavior drive the rising effective cooperation, we investigated the effect of issue/opinion exploration rate on the steady-state strategy distribution (Figs. 2 C and D and 3D). Notably, while heterophilous cooperators () were more frequent than homophilous cooperators () at low exploration rates (Fig. 2C), this ordering was eventually reversed at intermediate exploration rates (Figs. 2D and 3D). Analytical calculations confirm that these simulation results hold for any benefit-to-cost ratio (), as long as (SI Appendix; fitted to simulation data in Fig. 3D). Selection favors (and simultaneously disfavors ) when the effective population-level exploration rate () satisfies
| [1] |
where is the critical threshold, which is independent of and . Importantly, although selection always favors when Eq. 1 holds, the frequency of has a maximum as a function of (SI Appendix, Fig. S1), which likely contributes to the existence of an optimum exploration rate for the effective cooperation (Fig. 3).
Intuitively, the order reversal in the frequencies of and occurs because, as the exploration rate increases, so does the possibility of assortment with “like” individuals. This favors those who cooperate with others who are the same (share the same opinion) and penalizes those who cooperate with others who are different: Both and are more likely to encounter their own type (same strategy and, importantly, same opinions), but two s with the same opinions will mutually cooperate and gain benefits, whereas two s with the same opinions will mutually defect and forgo benefits.
At the collective level, exploration introduces new issues and opinions into a subpopulation, thus continually increasing opinion diversity. This, in turn, helps shuffle the opinion clusters, thereby mitigating polarization. Unlike at the individual level, where eventually too much scrambling of opinions and issues diminishes the possibility of assortment and reduces cooperation, polarization at the collective level will continue to decrease with increasing shuffling of sets and opinions. We therefore did not expect an intermediate optimum level of exploration, past which polarization would begin to increase again. Accordingly, we found that the average opinion distance increased with the issue/opinion exploration rate , regardless of the subpopulation (Fig. 4A and SI Appendix, Fig. S2A).
Strong Partisan Bias Promotes within-Party Opinion and Interest Alignment at the Cost of Global Alignment.
At the collective level, partisan bias tended to promote stronger opinion alignment by party regardless of and (Fig. 4A and SI Appendix, Fig. S2A), although these trends were more striking with increasing exploration rate (Fig. 4A). Extreme partisan bias () corresponded to maximum alignment among members of the same party (minimum within-party average opinion distance) and minimum alignment among those of different parties (maximum between-party average opinion distance). Within-party alignment decreased nonlinearly and between-party alignment increased nonlinearly as partisan bias declined; at reasonable values of issue/opinion exploration (), the most pronounced change occurred between and . This pattern suggests that, while extreme partisan bias () leads to strong assortment in the opinion space and therefore polarization, a fairly small amount of cross-party imitation can mitigate this adverse effect.
As expected from its definition (Individual- and Collective-Level Metrics), the average interest distance was zero when individuals cared about all available issues (), irrespective of subpopulation, partisan bias, or opinion mutation rate (Fig. 4B). When , partisan bias increased interest alignment within, but not between, parties: Average interest distance rose within parties but declined between parties. As in the opinion case, the within-party and between-party curves quickly converged as decreased. This outcome showed that, while the population strongly tended to fragment into party-based clusters when partisan bias was extreme (), a fairly small likelihood of cross-party imitation made the population more cohesive. Unlike in the opinion case, however, partisan bias had no effect on interest distance at high exploration rates (Fig. 4B).
Extreme Partisan Bias Promotes Pairwise Cooperation While Maximizing Polarization, but Only If Individuals Are Not Sufficiently Exploratory.
At the individual level, there was a marked difference in steady-state behavior between the cases and (extreme bias): While behaved the same as (compare Fig. 3 A vs. B and D vs. E) and this was confirmed by our analytical calculations (SI Appendix, Eqs. 19 and 20), had markedly different dynamics (Fig. 3 C and F). This is because qualitatively modifies the imitation network: When , the imitation network is the complete graph (anyone can imitate anyone else in the population); as increases, the imitation structure becomes modular (according to party label) with an increasingly weak connection between the two modules. Ultimately, when partisan bias is extreme (), the two modules become disconnected, as individuals can only imitate those of their own party. Importantly, when , even if the exploration rate is nontrivial, individuals’ opinions on new issues are perfectly aligned with their party (Fig. 1C). This gives rise to a discontinuity in the system behavior: For , even though individuals continue to interact according to issue membership, the world becomes segregated according to party labels when it comes to learning and exploration (i.e., at = 1, there is zero probability to be influenced by an individual outside of one’s party or to adopt an opinion misaligned with one’s party).
Consequently, this party-based segregation and alignment further boosted spatial assortment by both strategy and opinion, maximizing effective cooperation (Fig. 2E). Unlike when , cooperation was not primarily boosted by a strong positive effect on , but rather by a positive effect on and a negative effect on (Fig. 3 F vs. D and SI Appendix, Fig. S4 C and D vs. Fig. 2 C and D): When assortment by opinion is very high, the second letter of each strategy matters less because individuals will mostly encounter others of the same opinion. However, this trend largely disappeared around the optimum issue/opinion exploration rates (Fig. 2F and compare Fig. 3 A–C), where the moderate exploration sufficiently boosts cooperation at low to match the positive effect of extreme bias. Moreover, when , the effect of extreme bias overshadowed the effect of exploration: Effective cooperation changed minimally with increasing (Fig. 3C; SI Appendix, Fig. S4 A and B; and see also SI Appendix, Fig. S4 C and D for corresponding steady-state strategy distributions).
These results—together with the fact that, at the collective level, extreme partisan bias maximized both opinion and interest alignment among members of the same party and minimized alignment among those of different parties—suggest a potential tension between the individual and collective levels when the population is away from the optimum issue/opinion exploration rate. This tension disappears when the issue/opinion exploration rate is around the optimum: Then, extreme bias still increases polarization but without increasing effective cooperation.
Conclusion
Our results demonstrate that partisan bias interacts in unexpected ways with the diversity of issues that people care about. If partisan bias is not too high, increasing issue diversity both increases interindividual cooperation and prevents a monolithic majority. Interestingly, decreasing the number of issues that any given individual cares about has an even stronger positive effect than increasing the total number of available issues, suggesting that the extent to which individuals engage with available issues can dramatically impact cooperation and cohesion even when the scope of issues considered in the society stays the same. Thus, when partisanship is not too high, our results support Madison’s argument that a diverse set of issues can prevent a monolithic majority, but they further suggest that, counter to some contemporary democratic theories (40), the splintering of attention driven by information abundance could, in fact, further improve outcomes.
However, increasingly high partisan bias induces party-based assortment of issues and opinions, thereby reducing issue diversity and making the collective worse off. When bias is extreme (), individuals become completely closed off to influence from ideologically divergent peers, and the emergent tribalism boosts interindividual cooperation at the cost of a weakened, polarized collective. This suggests that, in a highly polarized state, there will be an emergent tension between the individual and the collective levels, with little incentive for individuals to reduce the collective polarization. This emergent tension could hinder bottom–up efforts to reduce polarization endogenously until, eventually, the cost of living in a polarized, dysfunctional society outweighs the high individual benefits of tribalism (41, 42). But our results offer a silver lining: Not only do the boost to cooperation and associated appeal of tribalism occur only when partisanship is extreme, they are also substantial only in a society whose members are primarily learning from peers and are limited in their independent exploration.
Although, a priori, issues in our model are completely independent of each other (i.e., uncorrelated), high partisanship leads to emergent alignment of issues according to party labels and, thus, to emergent correlations among them (e.g., if and are both left leaning and cares about issue X, there is a very high likelihood that does too). The associated dimensionality reduction is, as hypothesized, a driver of the observed factioning. However, it is not the sole driver. Even when individuals care about all available issues and therefore cannot sort themselves across issues by party affiliation, we still observe between-party divergence in opinions when partisanship is high (i.e., if holds a right-leaning position on issue X, then i is likely to also be right leaning on issue Y). This latter scenario seems to capture the current state of US politics: Democrats and Republicans care about the same set of hot-button issues, such as gun control and immigration, but they hold opposing views (43). To understand how the waxing and waning of a society’s interest in politics affect both individual and collective-level dynamics, future work could allow individuals to dynamically change the number of issues they care about and/or their party memberships. Such extensions would further our understanding of how independents or the politically indifferent might impact polarization (44).
Given well-known differences in openness to experience between the right and the left (45) and documented patterns of asymmetric polarization in the United States, wherein the right is more polarized than the left (46–49), future work needs to explore individual-level or party-level differences in partisan bias, openness to experience, and other attributes that might affect issue exploration and social learning. A simple extension would have be party dependent (i.e., individuals of different parties could perceive different levels of partisan bias), with independents experiencing an altogether different level. To study the endogenous evolution of partisanship, individuals could exhibit different levels of partisanship independent of their party labels and partisanship could be subject to learning and imitation, just as the issues and opinions are. If individual fitnesses then depend both on pairwise interaction payoffs and on the collective-level factioning, this approach could allow the study of endogenous waxing and waning of partisanship and polarization.
While our model focuses on two major parties because third parties have minimal influence in the United States—they typically get 5% of the popular vote in a presidential election (25)—it can be extended to include three or more parties. This would allow one to explore dynamics of coalition formation, including the possibility of logrolling (“I will cooperate with you on issue 1 if you cooperate with me on issue 2”), which would constitute a key step toward understanding polarization in multiparty parliamentary systems. Here, an important question would be whether and how the introduction of a third party could destabilize the system. To answer this question, one could consider parties with dynamic memberships, that is, where individuals can migrate from a party to another via social learning or based on shifts in party platforms, among other factors.
Despite the simplicity of our model, the results comport with recent evidence of polarization, factionalization, and party bias. Using data from 1972 to 2004, Baldassarri and Gelman (35) do not find increases in within-group issue alignment. However, since then, factionalism has markedly increased (50), as has partisan bias (51, 52) and subsequent polarization (47). At the same time, the first decades of the 21st century were also accompanied by exponential increases in information production and consumption, driven by digital technology (53). Our study uncovers how these trends may not be in opposition and prompts us to reevaluate the effectiveness of Madison’s suggested cure for the mischiefs of faction. Issue diversity, in the absence of strong partisan bias, promotes individual and collective welfare. Issue diversity, in the presence of extreme partisan bias and a rigid society, promotes individual cooperation while intensifying polarization.
Materials and Methods
Full Model Description.
Opinions and political affiliations.
We consider individuals distributed over potentially overlapping groups, each representing a political issue. As described in Model Description, let denote the -element opinion vector of individual , where represents ’s opinion on issue : liberal (), neutral (0), or conservative (). Individual cares about issue if individual i takes either a liberal or a conservative position on it. Thus, the issue interest vector of is given by , where if cares about issue and 0 otherwise.
Individuals also have political affiliations. Let denote the party affiliation of . For simplicity, we focus on a two-party system () with individuals distributed equally across the parties and, without loss of generality, assume that party 1 is liberal leaning () and that party 2 is conservative leaning ().
Interactions and payoffs.
Opinions determine the patterns of interaction. In each round, two individuals play one-shot pairwise donation games (simplified Prisoner’s Dilemmas) as many times as the number of shared interests. In a given game, the donor can choose to either cooperate ()—incur a cost to provide a benefit to the recipient—or defect ()—incur no cost and provide no benefit to the recipient.
Whether a donor cooperates or defects depends both on the donor’s behavioral strategy and on the agreement between the donor and the recipient. The strategy of individual is given by , where 0 corresponds to defection and 1 to cooperation. When interacts with in group , plays strategy if and agree on issue (e.g., both have opinion ) and plays if they disagree. Thus, an individual can be an unconditional defector (), a homophilous cooperator (), a heterophilous cooperator (), or an unconditional cooperator (). Note that does not interact with in group if does not care (i.e., is neutral) about issue .
In sum, an individual is characterized by three variables: 1) party affiliation [ under our simplifying assumptions], 2) opinions , and 3) behavioral strategy . These, together with benefit and cost , determine the total payoff of in a given round:
| [2] |
with if and agree on issue and 0 otherwise; is ’s payoff when and agree () or disagree ().
Fitness and its nonnegativity.
After all the games for a given round are played, we compute the fitness of as , where denotes the intensity of selection. To guarantee nonnegativity of fitness, we consider the scenario that results in minimum possible fitness and derive the parameter conditions under which . When interacts with every other individual in every issue group and loses in every interaction, ’s fitness is: . Thus, and must satisfy . We chose simulation parameters (, , , and ; SI Appendix, Table S1) satisfying this condition.
Simulation details.
We implemented our model as stochastic agent-based simulations in Julia (54). All code for simulations, analytical calculations, and figures are available at https://github.com/marikawakatsu/CooperationPolarization2 (55). For the simulations, we assumed that every individual cares about exactly issues. Under these assumptions, the population was initialized as follows: Without loss of generality, individuals 1 through were assigned to party and through were assigned to party . To initialize an individual’s opinions, we first selected out of the issues at random. We assigned the individual an opinion corresponding to the individual’s party affiliation ( for party , for party ) for each of these issues and a neutral opinion 0 for the remaining issues. This process was repeated independently for all individuals. Finally, each individual was also assigned a strategy (, , , ) at random.
Measuring opinion alignment.
Polarization was characterized using average opinion distance. The opinion distance between individuals and is defined as the city block distance between their opinion vectors and : Then, population-level, within-party, and between-party average opinion distances are defined as
| [3] |
| [4] |
| [5] |
respectively. Eq. 3 computes the average opinion distance between every pair of individuals and in the population. In Eq. 4, the bracketed term sums the opinion distance between every pair and within party (). In Eq. 5, the bracketed term sums the opinion distance between every pair and whose party affiliations differ ().
Normalization.
The range of possible pairwise opinion distances depends on : Given , the maximum possible opinion distance is . To allow for meaningful comparisons of opinion alignment across values of , we divided each raw average opinion distance by .
Measuring interest distance.
Interest alignment was characterized using average interest distance. The interest distance between and is defined as the Hamming distance between pairs of their issue interest vectors and : Then, population-level, within-party, and between-party average interest distances are defined as
| [6] |
| [7] |
| [8] |
respectively. Eq. 6 computes the average interest distance between every pair of individuals and in the population. In Eq. 7, the bracketed term sums the interest distance between every pair and within party (). In Eq. 8, the bracketed term sums the interest distance between every pair and whose party affiliations differ ().
Normalization.
In contrast to opinion distance, the range of possible pairwise interest distances depends on both and : The maximum possible interest distance is if and if , where is the floor function. To allow for meaningful comparisons of interest alignment across values of , we divided each raw average interest distance by when .
Supplementary Material
Acknowledgments
We thank the anonymous reviewers for their constructive feedback. We also thank Joshua Plotkin, Samuel Wang, and Bernard Grofman for helpful discussions and feedback. M.K. acknowledges support from the Army Research Office Grant W911NF-18-1-0325. S.A.L. thanks The College of Liberal Arts and Sciences at Arizona State University for its support.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission. C.P. is a guest editor invited by the Editorial Board.
Published under the PNAS license.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2102148118/-/DCSupplemental.
Data Availability
All simulation data and code for simulations, figures, and analytical calculations are available at Github (https://github.com/marikawakatsu/CooperationPolarization2) (55).
References
- 1.Chaffee S. H., Wilson D. G., Media rich, media poor: Two studies of diversity in agenda-holding. J. Mass Commun. Q. 54, 466–476 (1977). [Google Scholar]
- 2.Green J., Hobolt S. B., Owning the issue agenda: Party strategies and vote choices in British elections. Elect. Stud. 27, 460–476 (2008). [Google Scholar]
- 3.McCombs M., Zhu J.-H., Capacity, diversity, and volatility of the public agenda: Trends from 1954 to 1994. Public Opin. Q. 59, 495–525 (1995). [Google Scholar]
- 4.Edy J. A., Meirick P. C., The fragmenting public agenda: Capacity, diversity, and volatility in responses to the “most important problem” question. Public Opin. Q. 82, 661–685 (2018). [Google Scholar]
- 5.Jennings W., et al., Effects of the core functions of government on the diversity of executive agendas. Comp. Polit. Stud. 44, 1001–1030 (2011). [Google Scholar]
- 6.Treier S., Sunshine Hillygus D., The nature of political ideology in the contemporary electorate. Public Opin. Q. 73, 679–703 (2009). [Google Scholar]
- 7.Taagepera R., Grofman B., Rethinking Duverger’s Law: Predicting the effective number of parties in plurality and PR systems—Parties minus issues equals one. Eur. J. Polit. Res. 13, 341–352 (1985). [Google Scholar]
- 8.DellaPosta D., Pluralistic collapse: The “oil spill” model of mass opinion polarization. Am. Sociol. Rev. 85, 507–536 (2020). [Google Scholar]
- 9.Webster S. W., Abramowitz A. I., The ideological foundations of affective polarization in the US electorate. Am. Polit. Res. 45, 621–647 (2017). [Google Scholar]
- 10.Barber M., McCarty N., Mansbridge J., Martin C. J.. Causes and consequences of polarization. Polit. Negotiation 37, 39–43 (2015). [Google Scholar]
- 11.Settle J. E., Frenemies: How Social Media Polarizes America (Cambridge University Press, 2018). [Google Scholar]
- 12.Rand D. G., et al., Dynamic remodeling of in-group bias during the 2008 presidential election. Proc. Natl. Acad. Sci. U.S.A. 106, 6187–6191 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Carlin R. E., Love G. J., The politics of interpersonal trust and reciprocity: An experimental approach. Polit. Behav. 35, 43–63 (2013). [Google Scholar]
- 14.Carlin R. E., Love G. J., Political competition, partisanship and interpersonal trust in electoral democracies. Brit. J. Polit. Sci. 48, 115–139 (2018). [Google Scholar]
- 15.Iyengar S., Westwood S. J., Fear and loathing across party lines: New evidence on group polarization. Am. J. Polit. Sci. 59, 690–707 (2015). [Google Scholar]
- 16.Billig M., Tajfel H., Social categorization and similarity in intergroup behaviour. Eur. J. Soc. Psychol. 3, 27–52 (1973). [Google Scholar]
- 17.Guilbeault D., Becker J., Centola D., Social learning and partisan bias in the interpretation of climate trends. Proc. Natl. Acad. Sci. U.S.A. 115, 9714–9719 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Allcott H., et al., Polarization and public health: Partisan differences in social distancing during the coronavirus pandemic. J. Public Econ. 191, 104254 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Milosh M., Painter M., Sonin K., Van Dijcke D., Wright A. L., Political polarisation impedes the public policy response to COVID-19. https://voxeu.org/article/political-polarisation-impedes-public-policy-response-covid-19. Accessed 23 December 2020.
- 20.Hofbauer J., Sigmund K., Evolutionary Games and Population Dynamics (Cambridge University Press, 1998). [Google Scholar]
- 21.Nowak A. M., Evolutionary Dynamics: Exploring the Equations of Life (Harvard University Press, 2006). [Google Scholar]
- 22.Tarnita C. E., Antal T., Ohtsuki H., Nowak M. A., Evolutionary dynamics in set structured populations. Proc. Natl. Acad. Sci. U.S.A. 106, 8601–8604 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Castellano C., Fortunato S., Loreto V., Statistical physics of social dynamics. Rev. Mod. Phys. 81, 591–646 (2009). [Google Scholar]
- 24.Levendusky M. S., Clearer cues, more consistent voters: A benefit of elite polarization. Polit. Behav. 32, 111–131 (2010). [Google Scholar]
- 25.Goff S., Lee D. J.. Prospects for third party electoral success in a polarized era. Am. Polit. Res. 47, 1324–1344 (2019). [Google Scholar]
- 26.Keith B. E., Magleby D. B., Nelson C. J., Orr E. A., Westlye M. C., The Myth of the Independent Voter (University of California Press, 1992). [Google Scholar]
- 27.Nowak M. A., Sasaki A., Taylor C., Fudenberg D., Emergence of cooperation and evolutionary stability in finite populations. Nature 428, 646–650 (2004). [DOI] [PubMed] [Google Scholar]
- 28.Taylor C., Fudenberg D., Sasaki A., Nowak M. A.. Evolutionary game dynamics in finite populations. Bull. Math. Biol. 66, 1621–1644 (2004). [DOI] [PubMed] [Google Scholar]
- 29.Traulsen A., Claussen J. C., Hauert C., Coevolutionary dynamics in large, but finite populations. Phys. Rev. E 74, 011901 (2006). [DOI] [PubMed] [Google Scholar]
- 30.Donald G., Palmquist B., Schickler E., Partisan Hearts and Minds: Political Parties and the Social Identities of Voters (Yale University Press, 2004). [Google Scholar]
- 31.Wang X., Sirianni A. D., Tang S., Zheng Z., Fu F., Public discourse and social network echo chambers driven by socio-cognitive biases. Phys. Rev. X 10, 041042 (2020). [Google Scholar]
- 32.Lenz G. S., Follow the Leader?: How Voters Respond to Politicians’ Policies and Performance (University of Chicago Press, 2013). [Google Scholar]
- 33.Ohtsuki H., Nowak M. A., Pacheco J. M., Breaking the symmetry between interaction and replacement in evolutionary dynamics on graphs. Phys. Rev. Lett. 98, 108106 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bakker B. N., Lelkes Y., Malka A., Understanding partisan cue receptivity: Tests of predictions from the bounded rationality and expressive utility perspectives. J. Polit. 82, 1061–1077 (2020). [Google Scholar]
- 35.Baldassarri D., Gelman A., Partisans without constraint: Political polarization and trends in American public opinion. Am. J. Sociol. 114, 408–446 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Tarnita C. E., Ohtsuki H., Antal T., Fu F., Nowak M. A., Strategy selection in structured populations. J. Theor. Biol. 259, 570–581 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Antal T., Ohtsuki H., Wakeley J., Taylor P. D., Nowak M. A., Evolution of cooperation by phenotypic similarity. Proc. Natl. Acad. Sci. U.S.A. 106, 8597–8600 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Nowak M. A., Tarnita C. E., Antal T., Evolutionary dynamics in structured populations. Philos. Trans. R. Soc. Lond. B Biol. Sci. 365, 19–30 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Cavaliere M., Sedwards S., Tarnita C. E., Nowak M. A., Csikász-Nagy A., Prosperity is associated with instability in dynamical networks. J. Theor. Biol. 299, 126–138 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Sunstein C. R., Republic.com (Princeton University Press, 2001). [Google Scholar]
- 41.Finkel E. J., et al., Political sectarianism in America. Science 370, 533–536 (2020). [DOI] [PubMed] [Google Scholar]
- 42.Fu F., et al., Evolution of in-group favoritism. Sci. Rep. 2, 460 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.McCarty N., Poole K. T., Rosenthal H., Polarized America: The Dance of Ideology and Unequal Riches (Walras-Pareto Lectures, MIT Press, ed. 2, 2016). [Google Scholar]
- 44.Jones M. I., Sirianni A. D., Fu F., Polarization, abstention, and the median voter theorem. arXiv [Preprint] (2021). https://arxiv.org/abs/2103.12847 (Accessed 18 June 2021).
- 45.Malka A., Soto C. J., Inzlicht M., Lelkes Y., Do needs for security and certainty predict cultural and economic conservatism? A cross-national analysis. J. Pers. Soc. Psychol. 106, 1031–1051 (2014). [DOI] [PubMed] [Google Scholar]
- 46.Mann T. E., Ornstein N. J., It’s Even Worse Than It Looks: How the American Constitutional System Collided with the New Politics of Extremism (Basic Books, 2016). [Google Scholar]
- 47.McCarty N., Polarization: What Everyone Needs to Know (Oxford University Press, 2019). [Google Scholar]
- 48.Pierson P., Schickler E., Madison’s constitution under stress: A developmental analysis of political polarization. Annu. Rev. Polit. Sci. 23, 37–58 (2020). [Google Scholar]
- 49.Leonard N. E., Lipsitz K., Bizyaeva A., Franci A., Lelkes Y., The nonlinear feedback dynamics of asymmetric political polarization. Proc. Natl. Acad. Sci. U.S.A. 118, e2102149118 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Kozlowski A. C., Murphy J. P., Issue alignment and partisanship in the American public: Revisiting the ‘partisans without constraint’ thesis. Soc. Sci. Res. 94, 102498 (2021). [DOI] [PubMed] [Google Scholar]
- 51.Iyengar S., Lelkes Y., Levendusky M., Malhotra N., Westwood S. J., The origins and consequences of affective polarization in the United States. Annu. Rev. Polit. Sci. 22, 129–146 (2019). [Google Scholar]
- 52.Donovan K., Kellstedt P. M., Key E. M., Lebo M. J., Motivated reasoning, public opinion, and presidential approval. Polit. Behav. 42, 1201–1221 (2020). [Google Scholar]
- 53.Dhamdhere A., Dovrolis C., Twelve years in the evolution of the internet ecosystem. IEEE/ACM Trans. Netw. 19, 1420–1433 (2011). [Google Scholar]
- 54.Bezanson J., Edelman A., Karpinski S., Shah V. B.. Julia: A fresh approach to numerical computing. SIAM Rev. 59, 65–98 (2017). [Google Scholar]
- 55.Kawakatsu M., Lelkes Y., Levin S. A., Tarnita C. E., Code for “Interindividual cooperation mediated by partisanship complicates Madison’s cure for ’mischiefs of faction.’” GitHub. https://github.com/marikawakatsu/CooperationPolarization2. Deposited 1 August 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All simulation data and code for simulations, figures, and analytical calculations are available at Github (https://github.com/marikawakatsu/CooperationPolarization2) (55).