Sliding ferroelectricity in 2D van der Waals materials: Related physics and future opportunities

Abstract

Near the 100th anniversary of the discovery of ferroelectricity, so-called sliding ferroelectricity has been proposed and confirmed recently in a series of experiments that have stimulated remarkable interest. Such ferroelectricity exists widely and exists only in two-dimensional (2D) van der Waals stacked layers, where the vertical electric polarization is switched by in-plane interlayer sliding. Reciprocally, interlayer sliding and the “ripplocation” domain wall can be driven by an external vertical electric field. The unique combination of intralayer stiffness and interlayer slipperiness of 2D van der Waals layers greatly facilitates such switching while still maintaining environmental and mechanical robustness at ambient conditions. In this perspective, we discuss the progress and future opportunities in this behavior. The origin of such ferroelectricity as well as a general rule for judging its existence are summarized, where the vertical stacking sequence is crucial for its formation. This discovery broadens 2D ferroelectrics from very few material candidates to most of the known 2D materials. Their low switching barriers enable high-speed data writing with low energy cost. Related physics like Moiré ferroelectricity, the ferroelectric nonlinear anomalous Hall effect, and multiferroic coupling are discussed. For 2D valleytronics, nontrivial band topology and superconductivity, their possible couplings with sliding ferroelectricity via certain stacking or Moiré ferroelectricity also deserve interest. We provide critical reviews on the current challenges in this emerging area.

Ferroelectrics with spontaneous switchable electric polarizations are important candidates for realizing nonvolatile random-access memory. Their bistable states with moderate switching barriers may enable memories with room-temperature robustness at nanoscale. A successful combination of ferroelectricity and semiconductors will be highly desirable in the coming era of ferroelectronics (1), which enables ferroelectric field-effect transistor, merging logic, and memory functionalities in a single device, overcoming the interconnect bottleneck in von Neumann architecture.

The field of ferroelectricity continues to grow a century after its discovery by Valasek, with emerging new topics (2). Studies on two-dimensional (2D) van der Waals ferroelectrics since 2013 (3–5) offer a possible solution to the well-known epitaxial compatibility problem with the substrate: If the media of ferroelectricity are 2D materials with atomic thickness, also with a clean van der Waals interface that does not require lattice match with substrates, they should be exempt from the interfacial issues for device integration. Additionally, many of them are high-mobility semiconductors (>1,000 cm²·V⁻¹·s⁻¹) like phosphorene (6), MoS₂ (7), and InSe (8). Similar studies have even been extended to 1D/0D ferroelectricity (9, 10). Nevertheless, successful trials in searching for 2D van der Waals ferroelectrics were once limited to very few cases: The electric polarizations of lV–VI monolayers are strictly in-plane (11–14), and the more favorable vertical ferroelectricity was experimentally confirmed in only CuInP₂S₆ (15, 16), In₂Se₃ (17–19), and MoTe₂ (20) down to the monolayer limit. After all, the vertical ion displacements for ferroelectric switching are limited in a confined 2D layer.

However, the theory of sliding ferroelectricity proposed in 2017 (21) reveals the universal existence of vertical ferroelectricity in 2D layers, which has been confirmed in a series of van der Waals systems within several years. Strikingly, herein the vertical ferroelectric switching is induced by in-plane interlayer sliding without any requisite vertical ion displacements, which was unreported in previous ferroelectrics. Such a unique mechanism gives rise to ultralow switching barriers (approximate millielectron volts per formula unit [f.u.]) that enable high-speed data writing with low energy cost, while the robustness against thermal fluctuations is still ensured. In this perspective, we discuss the research trajectory of sliding ferroelectricity, clarify its origin, and examine its potential and challenges. We suggest promising directions for future research and broader emerging topics like Moiré ferroelectricity, metallic ferroelectricity, and so on.

Theoretical Model

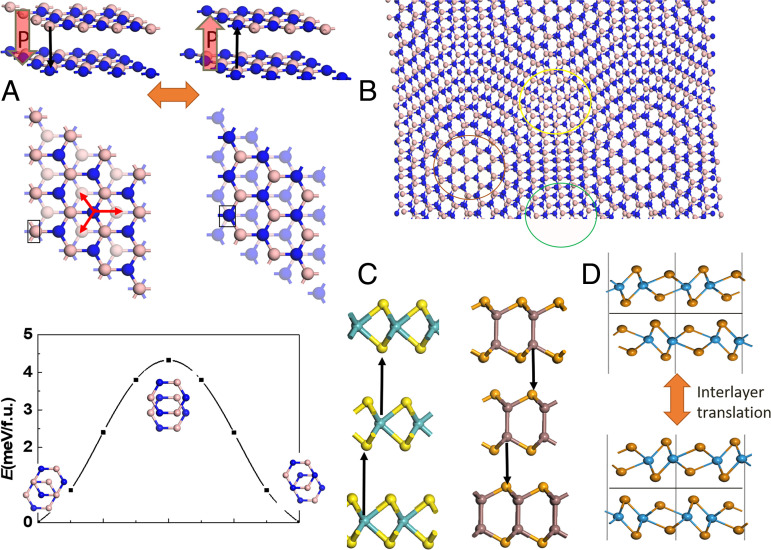
According to the model of sliding ferroelectricity (21, 22), for the van der Waals bilayer of many 2D materials the two layers are actually not identical, and such inequality leads to a net interlayer charge transfer. Taking the AB stacking boron nitride (BN) bilayer displayed in Fig. 1A as an example, the two layers are related by ℳz mirror reflection symmetry and the in-plane translation t_∥ along the B–N bond by a bond length, which places the N atom in the top BN layer atop the hexagon center of the bottom BN layer, while the B atom in the top layer is right over the N atom in the down layer (staggered with B over N marked by the black arrow). Such noncentrosymmetric coordination supports 2D ferroelectricity with an out-of-plane electric polarization, which is estimated to be 2.08 pC/m by first-principles calculations (0.68 μC·cm⁻² in 3D). An important consequence of this symmetry is a possibility to control the lateral alignment between the two monolayers by an applied electric field. This follows from the fact that two opposite polarization orientations in the AB (BA)-stacked BN are distinguished by a 2t_∥ translation along the weakly coupled interface. As a result, the polarization reversal can be regarded as lateral sliding of one BN monolayer with respect to the other, which can be achieved via interlayer translation by one B–N bond length along either one of the three directions marked by the red arrows (three equivalent reversed states), moving the N atoms in the upper layer right over the B atoms of the down layer, as shown in Fig. 1A.

Fig. 1.

Mechanism of sliding ferroelectricity. (A) Ferroelectric switching pathway of BN bilayer via interlayer sliding, where the black arrows point from positively charged B atoms to the nearest N atoms of other layers with negative charges and red arrows denote the polarization directions. (B) Ferroelectric domains of Moiré superlattice in twisted BN bilayer. (C) Ferroelectric 3R bulk MoS₂ and InSe. Reproduced with permission from ref. 21 (Copyright 2017, American Chemical Society). (D) The state obtained via mirror operation with respect to the horizontal plane in the center can also be obtained via interlayer translation for WTe₂ bilayer. Reprinted with permission from ref. 21.

The minimum energy path at the unit-cell level, i.e., the ferroelectric switching pathway, entails an areal energy barrier (q) of only around 9 meV per unit cell, or a few millielectron volts per square angstrom, which indicates a potentially very small energy cost for data writing. Periodic ferroelectric domains with spatially varying polarization signs can also be formed upon a small-angle twist within the bilayer, as shown in Fig. 1B. In such a Moiré superlattice with large-scale modulation of local stacking, the polarization vanished in AA stacking domains (see the red circle), while for AB or BA stacking domains the polarization can be either downward (see the yellow circle) or upward (see the green circle). Similar types of Moiré patterns for graphene/BN hetero-bilayers can be constructed, where periodic n or p doped graphene domains can be generated and the electronic properties of graphene can be tuned.

Similar principles can be applied to a series of 2D materials, including most binary compounds with honeycomb lattices, e.g. the already-synthesized graphitic few-layer GaN (23), SiC (24), and ZnO (25) with much higher computed polarizations, as summarized in Table 1. Van der Waals bilayers and multilayers like MoS₂, InSe, and GaSe, as well as their ground state of 3D bulk phase with R3m symmetry, can also exhibit such sliding ferroelectricity, as shown in Fig. 1C. Meanwhile, they are also semiconductors with suitable bandgaps and high mobility for nanoelectronics, enabling novel in-memory computing device constructs. Aside from honeycomb lattices with three equivalent sliding variants, some other bilayer structures are ferroelectric, but with bistable states, e.g. WTe₂ bilayer with a much smaller computed polarization of ∼0.38 pC/m (22). Actually, most van der Waals bilayers or multilayers can be endowed with sliding ferroelectricity with certain stacking-sequence control, and its existence can be judged by using a general principle, as displayed in Fig. 1D: The van der Waals bilayer or multilayer should be noncentrosymmetric, and the equivalent state obtained via mirror operation with respect to the horizontal plane in the center can also be obtained via interlayer translation, revealing a feasible switching pathway of sliding ferroelectricity.

Table 1.

Computed vertical polarizations of AB stacking van der Waals bilayers ( 21 )

	BN	ZnO	AlN	GaN	SiC	MoS2	InSe	GaSe
Polarization, pC/m	2.08	8.22	10.29	9.72	6.17	0.97	0.24	0.46

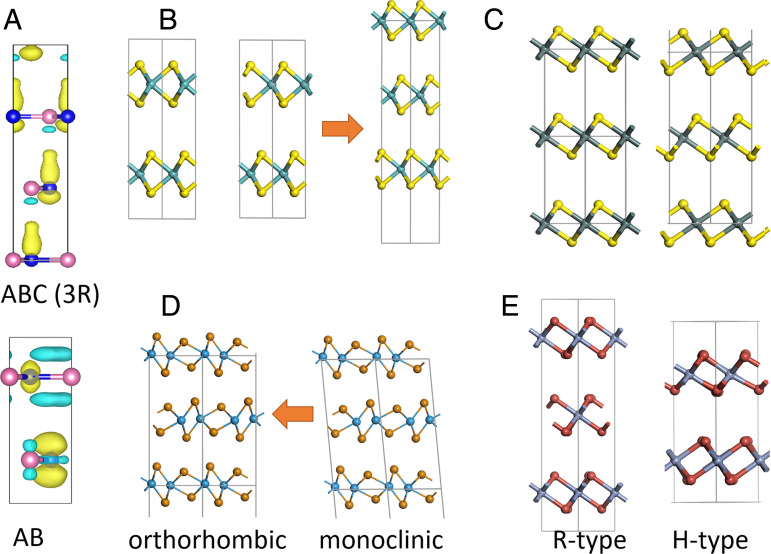
Not all stacking configurations can give rise to ferroelectricity. The aforementioned ferroelectric systems may turn nonpolar when the stacking sequence is altered, e.g. to the nonpolar AA′ stacking for BN bilayer (eclipsed with B over N) that is almost degenerate in energy compared with polar AB stacking. For bulk phase BN, MoS₂ or InSe stacked by honeycomb monolayers, AA′ stacking is nonpolar, and the vertical polarization is also missing for AB stacking: The vertical mirror symmetry is preserved in the AB stacking bulk phase although the AB layers are not identical, either positively or negatively charged, as revealed by the interlayer differential charge density in Fig. 2A. All the planar layers in the ABC stacking bulk phase are identical and neutral, while their nonsymmetric charge density distributions due to the interlayer configuration give rise to vertical polarity. Meanwhile, the AB stacking phase may be transformed to a polar 3R phase (ABC stacking; see 3R MoS₂ in Figs. 1C and 2B) via interlayer translation upon the application of an external electric field. Without limitation by the depolarization field as in 3D ferroelectric material with complex interfaces with the substrate, their bulk polarizations can be greatly enhanced; e.g., the 3R BN possesses a large bulk polarization of 7.6 µC/cm² as listed in Table 2. For 1T/1T′ transition metal dichalcogenides or trihalide monolayers that are centrosymmetric, similarly their corresponding bulk phase can be either polar or nonpolar depending on the stacking phases, e.g. the well-known two phases for SnS₂ and SnSe₂ (trigonal and hexagonal phases in Fig. 2C) (26), WTe₂ and ZrI₂ (orthorhombic and monoclinic phases in Fig. 2D) (27), CrI₃, and CrBr₃ (R-type and H-type in Fig. 2E) (28). The nonpolar monoclinic WTe₂ can be transformed to polar orthorhombic phase via lateral translation, which cannot be applied to transform the nonpolar trigonal SnS₂ to ferroelectric hexagonal phase, or the nonpolar R-type CrI₃ to ferroelectric H-type. Those phases of different stacking are almost degenerate in energy, so phase control during the synthesis is crucial for the realization of sliding ferroelectricity.

Fig. 2.

Polar and nonpolar phases upon different stacking. (A) Interlayer differential charge density of ABC and AB stacking bulk BN, where blue and yellow isosurfaces indicate electron depletion and accumulation after layer stacking, respectively. (B) Bulk MoS₂ of different stacking configurations. (C) Trigonal and hexagonal SnS₂. (D) Orthorhombic and monoclinic WTe₂. (E) R-type and H-type CrI₃/CrBr₃.

Table 2.

Computed vertical polarizations of van der Waals bulk structures

	3R-BN	3R-MoS2	3R-InSe	h-SnS2	h-SnSe2	h-CrI3	ZrI2
Polarization, µC/cm2	2.41	0.52	0.08	0.18	0.42	0.06	0.31

The kinetics of 2D displacive phase transformations (29) deserve careful discussion. When an externally applied forcing F, e.g. applied vertical electric field or shear stress, is below the athermal threshold (30) F_C for domain switching, the transformation will happen heterogeneously and asynchronously, assisted by thermal activation. That is to say, there will be a nucleation event and a subsequent growth process of a particular polarization/sliding domain variant, with a finite characteristic nucleation and/or migration activation energy Q(F < F_C) > 0, that are related to the domain walls [“ripplocations” (30, 31) in the case of 2D sliding ferroelectricity]. On the other hand, if the applied field is strong enough, F ≥ F_C, the transformation will be barrierless and does not need thermal activation (30), Q(F_C) = 0, in which case a nucleation-and-growth sequence is not necessary, and the transformation can take place in the entire region almost instantaneously like in spinodal decomposition. Generally speaking, F_C is proportional to q, so a smaller areal energy barrier (in units of millielectron volts per square angstrom) means a smaller athermal coercive field. On the other hand, when F < F_C and there is a barrier, the relationship between the absolute activation energy Q (in units of electron volts) and q can be somewhat complex and depends on the detailed geometric boundary condition. Here we are talking about one layer sliding over another layer, forming a ripplocation (31) loop as the domain wall, which is both a crystallographic dislocation and potentially a surface ripple in its core region due to out-of-plane buckling. In a free-standing bilayer, trilayer, and so on with some excess area “slack” due to precompression (32), the formation energy of the ripplocation (31) should be much smaller than standard dislocation or martensitic domain walls in a 3D solid, due to the lack of long-range elastic interactions. In fact, it has been shown that the standard Frank’s law for dislocations, dislocation core energy ∝ |b|² (b is the Burgers vector or the sliding displacement in the case of sliding ferroelectricity), no longer works in 2D van der Waals stacked layers, due to the near-complete relaxation of the long-range in-plane elastic energy, by buckling “ripple.” The lattice friction (Peierls barrier) to a gliding 2D ripplocation (31) is also expected to be small when q is small. So, one can expect facile 2D domain nucleation and growth for certain subthreshold F < F_C. In the case of high-field, F > F_C, this issue is largely moot, and the transformation is expected to happen rapidly with appropriate boundary conditions. The nonvolatile memory function of sliding ferroelectricity would work well if and only if 1) Q(F = 0) ≫ 50 k_BT, so when there is zero field a ferroelectric domain variant state can stay “locked in” despite the thermal fluctuations, and 2) for certain achievable F (such as < 10 MV/cm vertical electric field), Q < 5 k_BT, so the transformation can be accomplished within a nanosecond or even picosecond timescale (32). Due to the fundamental difference between 2D and 3D dislocations, we expect sliding ferroelectricity in 2D van der Waals materials to be both facile under field and nonvolatile without field, when appropriate size and geometric boundary condition are implemented to relieve the elastic energy constraints (29) that have long confined 3D martensitic transformations.

Experimental Investigations

The first system where sliding ferroelectricity was experimentally detected was few-layer WTe₂ despite its metallicity and relatively small polarization. In 2018, Fei et al. designed a device using a graphene monolayer as an electrode that can quantify the polarization of WTe₂ bilayer or trilayer below (33). The graphene conductance is measured when a voltage bias is applied to the bottom gate with the intervening WTe₂ grounded. The ferroelectric switching between two vertical polarization states is then revealed by the hysteresis loop in the graphene conductance sensitive to the polarization. The conductance measurements at a series of temperatures indicate its Curie temperature around 350 K, and no bistability is detected in monolayer WTe₂. Such a device is able to estimate the areal polarization density of WTe₂ bilayer (∼1 × 10⁴ e/cm = 0.16 pC/m measured at 20 K), which can be approximately fitted by density functional theory calculations (∼0.38 pC/m) considering the influence of defects, substrate, and thermal fluctuations (22).

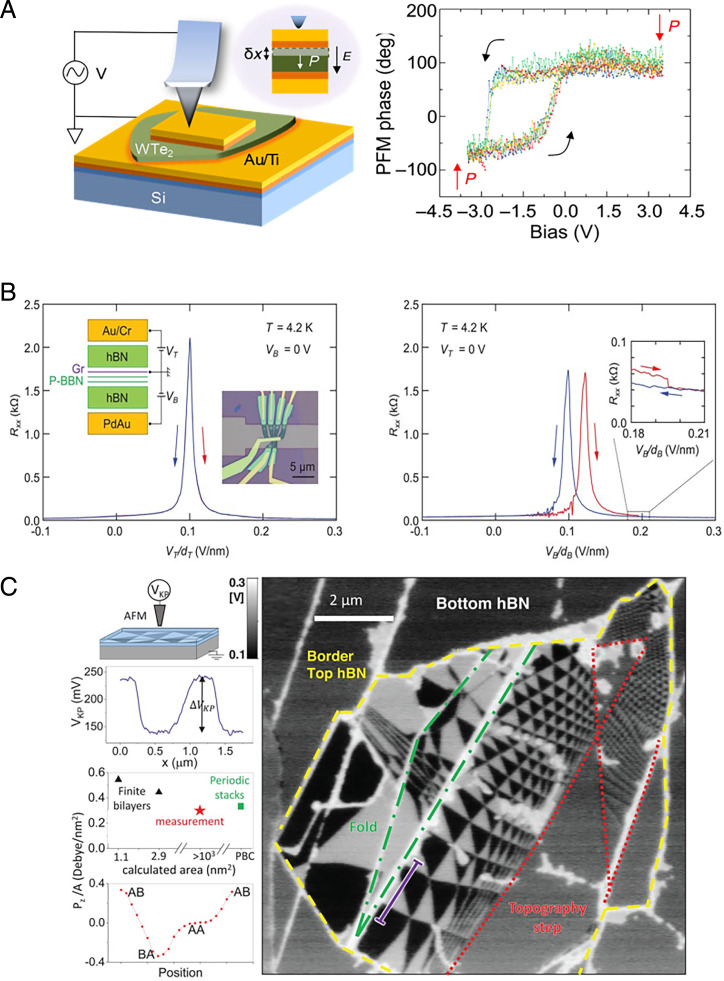
In a later report, the vertical ferroelectricity of bulk WTe₂ was further verified by piezoresponse force microscopy (PFM), where the antiparallel ferroelectric domain can be visualized directly as shown in Fig. 3A, implying the existence of bistable polarization states (34). The domains usually exhibit a distorted circular profile with an average domain size in the range of ∼20 to 50 nm, with domain walls that appear as dark lines in the amplitude image. Spectroscopic PFM measurements were performed through the top electrode in a capacitor geometry with WTe₂ multilayer with a thickness around 15 nm. The acquired piezoresponse as a function of applied bias shows switchable hysteretic behavior, and the bias-driven, oppositely oriented remnant polarization can be clearly seen in the PFM images of different color contrasts, indicating that the polarization of WTe₂ is switchable under an external bias. The stacking transition during ferroelectric switching in few-layer WTe₂ was confirmed via in situ nonlinear Hall transport measurement utilizing its large Berry curvature near the Fermi level, where the transition via interlayer sliding enables synchronized annihilation and switching of ferroelectric polarization and the Berry curvature (35).

Fig. 3.

Detection of ferroelectricity in WTe₂ and BN thin layer. (A) Device setups and images for probing the ferroelectric domains and bias-dependent piezoresponse phase of WTe₂ flake. Reprinted from ref. 34 which is licensed under CC BY 4.0. (B) The design of a dual-gated van der Waals heterostructure device composed of a metal top gate (Au/Cr)/hBN/graphene/0° parallel stacked bilayer BN (P-BBN)/hBN/metal bottom gate (PdAu), and its resistance R_xx of graphene as a function of V_T/d_T, with the top gate voltage V_T divided by the thickness of top hBN d_T and the bottom gate voltage VB divided by the distance between graphene and bottom gate electrode d_B. (C) Atomic force microscope is operated in Kelvin-probe mode to measure the local potential modulation, at the surface of two 3-nm-thick h-BN flakes, which are stacked with a minute twist angle. Reproduced with permission from refs. 36 and 37 (Copyright 2021, American Association for the Advancement of Science).

In 2020, the existence of sliding ferroelectricity in BN thin layers was observed by several research groups. Yasuda et al. designed a dual-gated van der Waals heterostructure device shown in Fig. 3B, using a graphene monolayer as a detector that can quantify the polarization of BN bilayer (36). The resistance of the graphene sensor as a function of top gate voltage (for both forward and backward gate sweep directions) exhibits a typical maximum without hysteresis. In contrast, the forward and backward scans of the resistance versus the bottom gate voltage show hysteresis, revealing the polarization switching of bilayer BN by the applied electric field. Another case in point is the measured carrier density n_H of graphene extracted from Hall resistance measurements that exhibit hysteretic behavior with an abrupt jump of n_H sweeping V_B, which is almost independent of temperature, up to room temperature. They also investigated the Moiré pattern of twisted bilayer BN with different stacking domains, which can expand or shrink through domain wall motion upon a vertical electric field.

In another report, Vizner Stern et al. (37) observed alternating domains of inverted normal polarization around several square micrometers in 3-nm-thick BN layers by atomic force microscope (Fig. 3C) operated in a Kelvin probe mode, which can measure the variations in the electrostatic potential at the surface regions of different stacking configurations. The polarization coupled to lateral sliding can be switched by scanning a biased tip above the surface, where the redistribution of domain walls to orient the local polarization can be visualized by Kelvin-probe maps. The measured polarizations in both reports on BN layers can fit well with the results predicted by first-principles calculations.

Aside from metallic WTe₂ and insulating BN, the possible existence of sliding ferroelectricity in semiconducting van der Waals layers has also been explored. For example, the amplitude-off and bias-on PFM amplitude and phase hysteresis loops were measured on a 7-nm-thick β-InSe nanoflake at room temperature (38). A clear amplitude butterfly loop and phase hysteresis loops were observed, revealing the switching of vertical polarization. In another recent report (39), the authors of ref. 36 successfully detected sliding ferroelectricity in a series of transition-metal dichalcogenides (e.g., MoS₂, WS₂, MoSe₂, and WSe₂) bilayers, all with polarizations almost half as large compared with bilayer BN.

Related Physics

Moiré Ferroelectricity.

The proposed Moiré ferroelectric domain with spatially varying potential upon a twisted angle in Fig. 1B has been observed in both aforementioned reports on ferroelectric BN thin layers (36, 37). In addition, Woods et al. used electrostatic force microscopy for the visualization of local electric charges on twisted BN bilayer by detecting the variations in the surface potential (40). Owing to the large potential variation, the regular ferroelectric domains arranged in triangular superlattice can be clearly visualized, as shown in Fig. 4A.

Fig. 6.

Schematic diagram of the opportunities in sliding ferroelectricity.

Fig. 4.

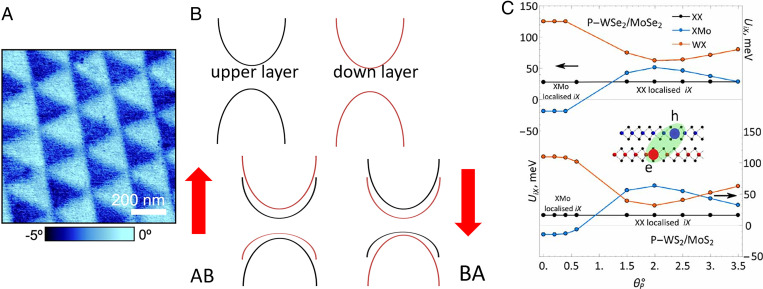
Moiré ferroelectricity. (A) Electrostatic force microscopy image of twisted hBN with triangular potential modulation. Reprinted from ref. 40 which is licensed under CC BY 4.0. (B) Schematic relative shift between the bands of the upper and down layer in different stacking regions of twisted semiconducting bilayer. Reprinted with permission from ref. 41. (C) Twist-angle dependence of interlayer exciton energy in different stacking regions of moiré supercell. Reprinted from ref. 42 which is licensed under CC BY 4.0.

Moiré ferroelectricity not only generates periodic n/p doped domains and shapes the periodicity of the potential energy landscape but also gives rise to a new research focus concerning the coupling between ferroelectricity and twistronic properties, like Moiré flat bands that induce correlation (43) and superconductivity (44) and the spatially varying bandgaps of twisted bilayer semiconductors driving the exciton flow (45). For a semiconducting bilayer, a small twist angle creates an internal stacking translation u(r) varying gently with position r that controls the local bandgap E_g(u(r)). Aside from the spatially varying interlayer hybridizations, the Moiré potential and local band variation can also be induced by the varying potential of Moiré ferroelectricity, which determines the relative shift between the bands of the upper and down layer in different stacking regions. With the band alignment shown in Fig. 4B (41), the twisted semiconducting bilayer combined with Moiré ferroelectricity can mimic a quantum dot array with type-II junctions (both in-plane and out-of-plane), which facilitates exciton trapping. A theoretical study (42) revealed the trapping of electrons, holes, and excitons in twisted WX₂/MoX₂ bilayers (X = S, Se), which is attributed to the domain wall networks of Moiré ferroelectricity, as shown in Fig. 4C. Tong et al. predicted bichromatic Moiré potentials for valley electrons, holes, and interlayer trions in MX₂/M′X′₂/MX₂ trilayers, with two independently configurable triangular superlattices of neutral excitons with opposite electric dipoles (46). In a recent experimental study, unconventional ferroelectricity was observed in bilayer graphene sandwiched between two hexagonal BN layers with a Moiré superlattice potential formed at the graphene/BN interface, which is attributed to the electronic correlation effect of Moiré flat bands (47).

Multiferroicity and Spin-Orbitronics

Multiferroic materials with robust magnetism and ferroelectricity that are strongly coupled have been long sought but remain elusive to date (48). For two ferromagnetic monolayers that are antiferromagnetically coupled, inequivalent stacking may give rise to both sliding ferroelectricity and uncompensated magnetic moments. The total magnetization can be switched with the reversal of polarization and interlayer voltage, rendering a desirable mode of “electrical writing + magnetic reading.” The switchable magnetization for MXene Cr₂NO₂, VS₂, and MoN₂ bilayer are, respectively, 0.008, 0.016, and 0.09 µ_B per unit cell (21), where µ_B is a Bohr magneton, which is already much larger compared with most type-II mutiferroics. In a recent study on VS₂ bilayer (49), the coupling of valley between magnetism and ferroelectricity was noted. Owing to the interaction of interlayer ferrovalleys the splitting values at the bottom of the conduction band and the top of the valence band are not equal at valley K₊ and K₋, which will be exchanged via ferroelectric switching or magnetic reversal for both layers. The predicted manipulations of the couplings between electron charge, spin, and valley degrees of freedom are yet to be experimentally validated. Actually, even for ferroelectric bilayer that is nonmagnetic, its noncentrosymmetricity allows linear in momentum spin-orbit coupling (SOC) which locks the electron’s spin direction to its momentum, resulting in nontrivial spin textures in the reciprocal space. The spin textures are coupled to the ferroelectric polarization and thus can be controlled by its orientation and magnitude for spintronic and valleytronic applications (50), especially for those ferroelectrics with strong SOC-like WSe₂ bilayer. Nontrivial topology in bilayer ferroelectrics with strong SOC also deserves further exploration (51).

Metallic Ferroelectricity

The multiferroic bilayers mentioned above are mostly metallic (and strong ferromagnets are usually metallic). The coexistence of ferroelectricity and metallicity is forbidden in conventional ferroelectrics as polarization switching upon an external electric field should be hindered by free-carrier screening. This principle also applies to the “ferroelectric metals” proposed by Anderson and Blount (52), referred to as “polar metals” with nonswitchable polarization [e.g., LiOsO₃ (53)]. However, the experimentally confirmed sliding ferroelectricity in metallic thin-layer WTe₂ indicates that a thin enough polar metal can be sufficiently penetrated by an electric field for its polarization switching, where the ultralow sliding barrier may also play an important role. It is likely that most 2D metallic layers can be endowed with a switchable polarization via stacking sequence control (which is yet to be confirmed), and for those properties that do not or scarcely coexist in pervious insulator ferroelectrics (plasmon, superconductivity, ferromagnetism, etc.), now their possible couplings or interactions with ferroelectricity can be explored.

Ferroelectric Nonlinear Anomalous Hall Effect

For few-layer WTe₂, Wang and Qian predicted a remarkable ferroelectric nonlinear anomalous Hall effect where nonlinear anomalous Hall current switches in odd-layer WTe₂ (except for 1T′ monolayer) while remaining invariant in even-layer WTe₂ upon ferroelectric transition, which is attributed to the absence and presence of Berry curvature dipole reversal and shift dipole reversal due to distinct ferroelectric transformation in even- and odd-layer WTe₂ (54). It was later confirmed (35) by nonlinear Hall effect measurement, where an applied current flow along the a-axis results in the generation of nonlinear Hall voltage along the b-axis, proportional to the Berry curvature dipole strength at the Fermi level. Although with similar butterfly-shaped hysteresis in longitudinal conductance, the sign of the nonlinear Hall signal was observed to be reversed in the trilayer while remaining unchanged in the four-layer crystal. Such Berry curvature memory based on sliding ferroelectric systems with nondestructive reading is worthy of further investigation for applications.

Potential Applications

Despite the promise of 2D van der Waals materials in nanoelectronics, it is still unclear which of them will prevail like silicon today. The wide existence of sliding FE ensures that no matter which one it can be endowed with nonvolatile ferroelectric memory property via certain stacking. The research on sliding ferroelectricity has greatly broadened the candidates of 2D ferroelectrics from very few cases to most 2D materials, ranging from metals to insulators. Boron nitride is widely used as a substrate and gate insulator with high dielectric constant, metallic NbSe₂ or WTe₂ can be used as 2D electrodes, and InSe and MoS₂ can be high-performance semiconductors with suitable bandgaps and high mobility, so they may all possess the function of nonvolatile memory while playing a vital part in devices like field-effect transistors.

The functional fatigue of current perovskite ferroelectrics has been attributed to their mobile oxygen defects at the interface between ferroelectric oxides and metallic electrodes (55). For sliding ferroelectric layers, however, the clean van der Waals surface are usually free of such defects, while all the ion displacements are strictly in-plane despite the vertical polarizations are tuned by the perpendicular electrodes. Hence, the sliding ferroelectrics should be exempt from this kind of fatigue mechanism.

There is usually a trade-off in optimizing the performance for data storage when considering the intensive switching barrier q (in units of millielectron volts per cubic or square angstrom) between ferroic variants: A low q is favorable to reduce the energy cost and enhance the speed for data writing while also reducing the robustness against thermal fluctuations. For example, the low switching barrier of magnetic memories gives rise to their high-speed writing and thermal instability at nanoscale (like “superparamagnetism”). However, the key quantity for estimating thermal stability is somewhat different from the switching barrier. For the anisotropic Heisenberg model of a ferromagnet with exchange coupling J (usually <∼10 meV) and single-ion anisotropy K (usually <~1 meV),

$$H=-J{\displaystyle \sum }_{<i,j>}{S}_i{S}_j-K{\displaystyle \sum }_j{\left(S_{jz}\right)}^2.$$

For each spin with N nearest neighbors, the thermal stability for nonvolatility is determined by the “isolated” barrier (= NJ + K) for one spin to flip while all other spins around are fixed, while the switching barrier controlling the speed and energy cost is the “collective” barrier (= K) where all spins must “simultaneously” switch to the opposite direction.

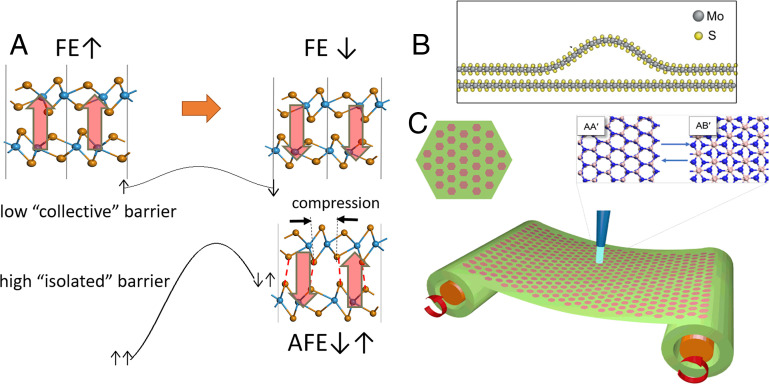
Similar model can be applied for ferroelectricity. The “collective” switching barriers of all room-temperature ferroelectrics, to our knowledge, are higher than 27 meV/f.u. (∼k_BT/f.u. at 300 K), e.g. 0.43 eV/f.u. for BiFeO₃ (56). In comparison, the barriers for interlayer sliding are much lower [4.5 meV/f.u. for BN (21) and 0.15 meV/f.u. for WTe₂ bilayer (22)]. This has to do with the weak van der Waals interaction between adjacent layers. The intralayer rigidity, on the other hand, leads to high “isolated” barrier and high stability against zero-field volatility (see the case of WTe₂ bilayer in Fig. 5A, where the artificial antiferroelectric state formed by in-plane inhomogeneous strain is highly unstable) (22). This is because as the in-plane stretching modulus is much larger than the interlayer shearing modulus, sliding ferroelectricity needs to be quite collective and necessarily involves a relatively large “activation area” and collective defects, namely the ripplocation (31) (Fig. 5B). However, because of the atomic thickness, the total transformed volume and heat dissipation is still small. Such a unique combination enables picosecond-timescale high-speed data writing with experimentally acceptable field strength, as predicted (32, 57) and recently shown with optomechanical light pulses (58). Aside from ferroelectric switching between bistable states from AB to BA, the optical-driven transformation between inequivalent stacking orders from AA′ to AB′ has also been predicted (57) (see Fig. 5C, where the data can be written by laser beam and read by nonlinear Edelstein effect), where low switching barrier and high robustness are similarly ensured.

Fig. 5.

Low switching barrier with high thermal stability. (A) A comparison of ferroelectric switching with a low “collective” barrier, and ferroelectric (FE)-antiferroelectric (AFE) transition with a high “isolated” barrier in WTe₂ bilayer. Reprinted with permission from ref. 22. (B) Ripplocation in MoS₂ bilayer. Reprinted with permission from ref. 31. (C) Optical-driven transition from AA′ to AB′ stacking in BN bilayer. Reprinted with permission from ref. 57.

Finally, we want to comment that interlayer sliding generates large xz or yz plastic strains, so in the “xz/yz” sense sliding ferroelectricity can also be called sliding “ferroelasticity.” However, z is not a Bravais replication direction in 2D van der Waals materials, as only x and y are extensible. So, such a sliding displacement is often considered to be internal shuffling in a 2D Bravais lattice framework. Nonetheless, there will also be in-plane relaxation strains in xx, yy, and zz, and sometimes even xy, slaved to such “internal shuffling” (59) sliding displacement. The coupling between the electric polarization vector, xz/yz plastic strain, xx/yy/xy/zz relaxation (elastic) strain tensor, and the bending curvature inside ripplocation [flexoelectric effect (29)] makes this problem an extremely rich one.

Outlook

In the booming field of 2D ferroelectricity, sliding ferroelectricity is unique in that it exists widely and exists only in 2D van der Waals stacked layers. Without significant vertical ion displacements (except in the ripplocation domain wall core), the vertical polarization can be switched by in-plane interlayer sliding with an ultralow barrier, which can be utilized for high-speed data writing with low heat dissipation. In addition to its unique switching mode, other related new physics like Moiré ferroelectricity, metallic ferroelectricity, ferroelectric nonlinear anomalous Hall effect, sliding multiferroic couplings, and negative piezoelectricity [see the increase in polarizations for BN (21) and ZrI₂ (60) bilayer upon vertical pressure] are emerging. Actually, for many intrinsic physical properties of 2D monolayers (magnetism, excitonics, nontrivial topology, valleytronics, superconductivity, etc.) their potential couplings with sliding ferroelectricity via certain stacking or Moiré ferroelectricity upon a twisted angle can be worthy of further exploration, as summarized in Fig. 6.

There are still challenges to overcome at this early stage. The van der Waals charge transfer due to interlayer inequality is usually weak, leading to a low magnitude in polarizations. Even for the polarization obtained in BN bilayer that is an order of magnitude higher compared with WTe₂ bilayer it is still less than one-half of the computed vertical polarization for thin-layer CuInP₂S₆ and In₂Se₃, almost two orders of magnitude lower compared with the bulk polarization of BiFeO₃. However, it has been shown that even the WTe₂ bilayer with a weak polarization below 0.2 pC/m can give rise to two distinct conductance states when using graphene as a detector (33). Moreover, many systems with much higher polarizations are yet to be explored via high-throughput screening of the material database, noting that the computed polarization of AlN bilayer in Table 1, almost five times higher than that of BN bilayer, is also the highest vertical polarization of current 2D ferroelectrics known to date.

While a free-standing, slightly slacked geometry in a vacuum is theoretically the cleanest to discuss sliding ferroelectricity, in practical applications it might be advantageous to put the 2D van der Waals materials on some solid substrate, and exposed to some gas environment or solid electrode on the top. The issue of mobile ionic impurities and electronic charge puddles that might segregate on top/bottom interfaces and depolarize the vertical electric dipole is something one has to contend with. Covering relatively inert 2D encapsulations like BN on top and bottom to maintain clean interfaces could be a solution, but this will alter the bending modulus and thus the ripplocation domain wall width, and thus the domain kinetics, from the idealized situation.

To conclude, although large-scale applications in nanoelectronics require simultaneous optimization of high ferroelectric polarizations with low switching barriers, moderate bandgaps with high mobility, low materials/manufacturing cost, nontoxicity, and so on, since most 2D materials can be endowed with sliding ferroelectricity via stacking design there are plenty of candidates for such optimizations on different material platforms. The opportunities are vast for both emerging physics and potential applications.

Data Availability

There are no data underlying this work.

Change History

February 25, 2022: Table 2 has been updated. Please see accompanying Correction for details.