Optimal control analysis of hepatocytic-erythrocytic dynamics of Plasmodium falciparum malaria

Abstract

This paper presents an in-host malaria model subject to anti-malarial drug treatment and malaria vaccine antigens combinations. Pontryagin's Maximum Principle is applied to establish optimal control strategies against infected erythrocytes, infected hepatocytes and malaria parasites. Results from numerical simulation reveal that a combination of pre-erythrocytic vaccine antigen, blood schizontocide and gametocytocide drugs would offer the best strategy to eradicate clinical P. falciparum malaria. Sensitivity analysis, further reveal that the efficacy of blood schizontocides and blood stage vaccines are crucial in the control of clinical malaria infection. Futhermore, we found that an effective blood schizontocide should be used alongside efficacious blood stage vaccine for rapid eradication of infective malaria parasites. The authors hope that the results of this study will help accelerate malaria elimination efforts by combining malaria vaccines and anti-malarial drugs against the deadly P. falciparum malaria.

1. Introduction

Malaria is a major leading public health problem, especially in the African continent (Aguilar & Gutierrez, 2020; Yiga, Nampala, & Tumwiine, 2020). In 2019, about 229 million cases and 409 000 deaths due to malaria infections were reported globally (Al-Awadhi, Ahmad, & Iqbal, 2021; WHO, 2020). The (WHO)African Region bore the heaviest burden, accounting for 94% of all reported global malaria cases and deaths in 2019. Existing control measures and treatment therapies have lead to a 1.5 billion and 7.6 million averted malaria cases and malaria-related deaths, respectively, since the year 2000 (WHO, 2020). However, the 2020 world malaria report showed an increase in case incidence in some high burden countries in Africa and Americas (WHO, 2020). Currently, treatment using antimalarial drugs is the main control available for clinical malaria infections (Orwa et al., 2019a). Moreover, artemisinin-based combination therapy (ACT) is the standard of care for uncomplicated P. falciparum malaria worldwide (Arya, Foko, Chaudhry, & Singh, 2020) . Drug resistance against 4-aminoquinolines and sulpha compounds has remained one of the greatest challenge to malaria chemotherapy development (Visser, van Vugt, & Grobusch, 2014). Further evidence of resistance to artemisinins (Dondorp et al., 2009; Noedl et al., 2008) highlights the need for continuous investment in alternative anti-malarial drugs and malaria vaccines.

Combination of anti-malarial drugs have achieved tremendous success in malaria treatment and transmission reduction (NIH, 2019; Visser et al., 2014). Administration of at least two anti-malarial drug regimens with different modes of action and target has been shown to be highly effective compared to monotherapy drugs (WHO, 2015a). A rapidly acting artemisinin drug in ACTs exhibit an extremely short half-life. It is hence combined with a longer-acting monotherapy drug to limit recrudescence and achieve higher clinical response (WHO, 2018). The artemisinin component reduces malaria parasite density by a factor of about 10⁴ within 2 days of asexual cycle (Hodel, Kay, & Hastings, 2016). Furthermore, it is active against blood floating gametocytes that are responsible for infection transmission to mosquito vector. The monotherapy drug with a longer half-life eradicates the rest of the parasites that are not cleared by the artemisinin drug. This further reduces the possible occurrence of resistance due to mutations during treatment. Additionally, the long-acting drug may provide prophylaxis after treatment (WHO, 2015b). In (Okell, Drakeley, Bousema, Whitty, & Ghani, 2008), a combination of an ACT partner drug and a nonartemisinin regimen is shown to have a greater impact in higher-transmission settings. The combination of artesunate and amodiaquine reduced gametocyte density and showed minimal effect on tolerability in P. falciparum patients (Osorio, Gonzalez, Olliaro, & Taylor, 2007). Elsewhere (Smithuis et al., 2010), a combination of artesunate and mefloquine greatly suppressed malaria in Myanmar.

Although malaria drugs and insecticides have helped reduce malaria cases and deaths globally, these two in-host malaria control measures are vulnerable to parasite development of resistance (Chitnis et al., 2015; Duru, Witkowski, & Ménard, 2016). Evidence of P. falciparum resistance to artesunate in Western Cambodia was characterized by slow parasite clearance (Dondorp et al., 2009; Mairet-Khedim et al., 2020). Efficacious malaria vaccine is likely to fill malaria elimination gap (Abdulla et al., 2011; Orwa et al., 2019b). Unfortunately, malaria vaccine development has been impeded by the complex biology of malaria parasites and the many parasites infection cycles (Mahmoudi & Keshavarz, 2018). Several clinical and pre-clinical studies (Bauza, Atcheson, Malinauskas, Blagborough, & Reyes-Sandoval, 2016; Mahmoudi & Keshavarz, 2018; Sherrard-Smith et al., 2018) have demonstrated the significant benefit of combining two or more malaria vaccine antigens. A combination of recombinant PfMSP-1₄₂ and AS02A induced high concentrations of antibody among young children in Western Kenya (Ogutu et al., 2009). In (Chitnis et al., 2015), JAIVAC-1 and Montanide ISA720 induced proportional antibody responses against PfF2 and PfMSP-1₁₉.

In developing response plans to malaria infections, decision makers such as government and public health officers are often faced with trade-offs in choosing among various malaria treatment and control options (Gaff & Schaefer, 2009). The usual challenge, however, is to find the optimal response balancing treatment and vaccination that will minimize incidence and disease-related mortality at an affordable cost (Joshi, Lenhart, Li, & Wang, 2006; Omondi, Orwa, & Nyabadza, 2018). Optimal control theory (Lenhart & Workman, 2007) has been very helpful in identifying optimal control measures against particular diseases. In malaria epidemiology, the application of optimal control theory has for a long time been limited to population level models (Agusto, Marcus, & Okosun, 2012; Makinde & Okosun, 2011; Mwanga, Haario, & Capasso, 2015; Okosun, Ouifki, & Marcus, 2011). In most of these models, the main objective has been to minimize the population of malaria-infected humans at a minimal cost (Mwanga et al., 2015).

In (Okosun et al., 2011), a combination of vaccination and treatment methods is shown to be the optimal control strategy against malaria infection at population level. Moreover, a combination of screening, treatment and use of insecticidals is shown to be highly effective against malaria infections and transmissions among susceptible immigrants (Makinde & Okosun, 2011). In (Silva & Torres, 2013), optimal supervision and educational campaigns on the use of insecticide treated nets (ITNs) are shown to be highly effective in achieving 75% coverage of the host population within a community. Analysis in (Mwanga, Haario, & Nannyonga, 2014), reveal that a combination of three malaria controls: ITNs, indoor residual spraying (IRS) and drug treatment provides the best control measure against malaria transmission and infection within a community. Additionally, control targeting mosquito vector is more effective than personal protection in some cases but not always (Kim et al., 2012). In (Agusto et al., 2012), a combination of insecticides, antimalarial drugs and personal protection are shown to bear the greatest impact on malaria control. In all these dynamical models, optimal control strategies were established based on Pontryagin's Maximum Principle (PMP) (Anita, Capasso, & Arnautu, 2011).

In (Orwa et al., 2018b), a combination of different vaccine antigens are shown to greatly reduce parasitemia and severity of P. falciparum malaria infection. Additionally, a combination of two malaria drugs, fosmidomycin and piperaquine was also established to have higher efficacy, safety and well tolerated (Mombo-Ngoma et al., 2017). Elsewhere (Pukrittayakamee et al., 2004), a combination of artesunate and primaquine resulted in significantly shorter gametocyte clearance times. Although artesunate inhibits gametocyte development, the partner drug, primaquine, is shown to accelerates gametocyte clearance in (Pukrittayakamee et al., 2004). In this paper, we argue that a combination of efficient antimalarial drugs and efficacious malaria vaccines present the best therapeutic strategy to achieving malaria elimination. The theory of optimal control is applied to an in-host malarial model that is characterized by a combination of antimalarial drugs and different vaccine antigens. To the best of our knowledge, this study is the first of its kind to apply optimal control theory to an in-host malaria model with therapeutic control measures. The objective of the paper is to establish an optimal combination therapy for clinical P. falciparum malaria.

The rest of the paper is organized as follows. The in-host malaria model with time-dependent antimalarial drug therapy and malaria vaccine controls is presented in Section 2. Analysis of the model with constant controls is presented in Section 3. The formulation of optimal control problem and the proof of existence and uniqueness of solutions of the optimality system is provided in Section 4. Sensitivity analysis is also performed in Section 4. In Section 5, the optimality system is solved numerically, using the backward-forward sweep algorithm and the 4th order Runge-Kutta scheme in Matlab. This study is finally concluded in Section 6.

2. Mathematical model

An in-host P. falciparum malaria model is formulated to study optimal malaria control strategies within the human host. The deterministic model is an extension of the model in (Orwa et al., 2018a) and comprises of nine compartments of: (i) sporozoites (S), (ii) uninfected hepatocytes (H), (iii) infected hepatocytes (X), (iv) uninfected red blood cells (R), (v) early stage infected red blood cells (blood trophozoites, T), (vi) mature infected red blood cells (blood schizonts, C), (vii) merozoites (M), (viii) gametocytes (G) and (ix) CD8⁺ T cells (Z). The in-host malaria is subjected to a combination of malaria vaccine and anti-malarial drug control strategies. The specific vaccines are: RTS,S/AS01 (a pre-erythrocytic vaccine) (Birkett, 2016)) and merozoite surface protein 3 (MSP3) (blood stage vaccines) (Miura, 2016), which offer direct protection to the human-host. The antimalarial drugs considered here are artemether-lumefantrine (AL) (a blood schizontocide) (Ogutu, 2013)) and primaquine (PQ) (a gametocytocide) (WHO, 2012)). The combined chemotherapy not only target rapid parasite clearance but also reduced parasite transmissibility to mosquito vector. Note that the four malaria control measures considered in this paper, target different sites within the complex malaria parasite life cycle (CDC, 2017) within the human host.

The recruitment of the hepatocytes is assumed to occur at the rate λ_h through self-replication. Sporozoite invasion at the rate β_s results in the formation of infected hepatocytes X. A mature liver schizont burst open to release N merozoites into the blood stream. This marks the start of the erythrocytic cycle. Healthy red blood cells (erythrocytes) are recruited at the rate λ_r from the bone marrow. Merozoite invasion of the uninfected red blood cells at a rate β_r is a complex and ordered process (Cowman, Berry, & Baum, 2012). The infected red blood cells T mature at the rate γ into blood schizonts C that rupture to release more merozoites into blood stream. A proportion π of asexual merozoites commit to form sexual gametocytes G. Human defensive immune cells play a critical role during pathogen invasion. The CD8⁺ T cells are recruited at a constant rate λ_z from the thymus. The production of CD8⁺ T cells is furthermore aggravated by the presence of infected hepatocytes, blood trophozoites and blood schizonts at the rates δ_x, δ_t and δ_c, respectively. Therefore, (δ_x, δ_t, δ_c) represents the immunogenicity of the state variables X, T and C, respectively. The limiting effects of CD8⁺ T cells during parasite invasion is described using a nonlinear bounded Michaelis-Menten-Monod function (Orwa et al., 2018b). The parameters μ_s, μ_m, μ_g represents the death rates of sporozoites, merozoites and gametocytes respective.

The in-host malaria model is further subjected to a combination of malaria vaccine and anti-malarial drug control strategies. These control measures reduce the rates of parasite invasions at the liver and blood stages, respectively. The specific vaccines under our consideration are: (1) RTS,S/AS01 (a pre-erythrocytic vaccine) (Birkett, 2016)) and (2) merozoite surface protein 3 (MSP3) (blood stage vaccines) (Miura, 2016). We also consider two antimalarial drugs (2) artemether-lumefantrine (a blood schizontocide) (Ogutu, 2013)) and (3) primaquine (a gametocytocide) (WHO, 2012)). The combined chemotherapy not only target rapid parasite clearance but also reduced parasite transmissibility to mosquito vector. The gametocytocide considered in this study is a single dose 0.25 mg base/kg of primaquine. This WHO recommended drug (Eziefula et al., 2014; Pukrittayakamee et al., 2004; White, Qiao, Qi, & Luzzatto, 2012; WHO, 2012), mainly targets the blood stage gametocytes. This reduces the probability of parasite transmission to the mosquito vector and hence disease morbidity.

The Pontryagin's Maximum Principle is applied to minimize the population of infected hepatocytes, infected erythrocytes, infective blood stage merozoites and the gametocytes. MSP3 and RTS,S/AS01 reduces the rates of invasion of healthy hepatocytes and healthy erythrocytes, respectively. The hepatocyte invasion rate β_s and the erythrocyte invasion rates β_r are hence, reduced to (1 − u₁(t))β_s and (1 − u₂(t))β_r, respectively. The time dependent controls u₁(t) and u₂(t), therefore represents the efficacies of the pre-erythrocytic vaccine and the blood stage vaccine, respectively. The administration of AL, reduces the average number of merozoites released per bursting blood schizont P to (1 − u₄(t))P, where u₄(t) is the normalized AL dosage efficacy as a function of time (MA, 2019). Similarly, the use of primaquine reduces the average number of merozoites released per bursting infected hepatocyte N to (1 − u₃(t))N, where u₃(t) is the normalized primaquine dosage efficacy as a function of time. Based on these additional assumptions and model dynamics, we have the following optimal control model for in-host P. falciparum malaria:

$$\left(\begin{array}{cc}\frac{\mathrm{d}S}{\mathrm{d}t}& =\mathrm{\Lambda }-{\mu }_{s}S-{\beta }_{s}SH,\\ \frac{\mathrm{d}H}{\mathrm{d}t}& ={\lambda }_h-{\mu }_{h}H-(1-u_1(t)){\beta }_{s}SH,\\ \frac{\mathrm{d}X}{\mathrm{d}t}& =(1-u_1(t)){\beta }_{s}SH-{\mu }_{x}X-\frac{k_{xZX}}{1+{ϵ}_{0}X},\\ \frac{\mathrm{d}R}{\mathrm{d}t}& ={\lambda }_r-\frac{(1-u_2(t)){\beta }_{r}RM}{1+\alpha Z}-{\mu }_{r}R,\\ \frac{\mathrm{d}T}{\mathrm{d}t}& =\frac{(1-u_2(t)){\beta }_{rRM}}{1+\alpha Z}-{\mu }_{t}T-\gamma T-\frac{k_{tZT}}{1+{ϵ}_{1}T},\\ \frac{\mathrm{d}C}{\mathrm{d}t}& =\gamma T-{\mu }_{c}C-\frac{k_{c}ZC}{1+{ϵ}_{2}C},\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =(1-u_3(t))N{\mu }_{x}X+\frac{(1-u_4(t))P(1-\pi ){\mu }_{c}C}{1+\alpha Z}-{\mu }_{m}M-{\beta }_{r}RM,\\ \frac{\mathrm{d}G}{\mathrm{d}t}& =\pi {\mu }_{c}C-(u_3(t)+{\mu }_g)G,\\ \frac{\mathrm{d}Z}{\mathrm{d}t}& ={\lambda }_z+Z\left(\frac{{\delta }_{x}X}{1+{ϵ}_{0}X}+\frac{{\delta }_{t}T}{1+{ϵ}_{1}T}+\frac{{\delta }_{c}C}{1+{ϵ}_{2}C}\right)-{\mu }_{Z}Z.\end{array}\right\},$$ (1)

subject to the initial conditions: S(0) ≥ 0, H(0) > 0, X(0) ≥ 0, R(0) > 0, T(0) ≥ 0, C(0) ≥ 0, M(0) ≥ 0, G(0) ≥ 0, Z(0) > 0.

A brief description of model parameters are presented in Table 1.

Table 1.

Description of model parameters.

Parameter	Description
μs	Death rate of sporozoites
Λ	The rate of injection of sporozoites into liver due to mosquito bites
βs	Rate of invasion of hepatocytes by sporozoites
λh	Rate of supply of hepatocytes from the bone marrow
λr	Rate of supply of erythrocytes from the bone marrow
μh, μx	Death rate of susceptible hepatocyte and infected hepatocyte, respectively
π	Proportion of parasites that become gametocytes per bursting blood schizont C
kx, kt, kc	Immunosensitivity of X, T and C, respectively
δx, δt, δc	Immunogenecity of X, T and C, respectively
μr	Natural mortality rate of healthy RBC
βr	Rate of infection of RBCs by merozoites
μt, μc	Rate of decay of blood trophozoites and blood schizonts, respectively
μm, μg	Rate of decay of merozoites and gametocytes, respectively
P	Average number of merozoites released per bursting blood schizont
N	The average number of merozoites released per bursting infected hepatocytes
γ	Rate of progression from blood trophozoite to schizont stages
α	Rate of inhibition of immune response
λz	Rate of production of CD8+ T-cells
1/ϵ0, 1/ϵ1, 1/ϵ2	Half saturation constants for X, T and C, respectively
μz	Rate of decay of CD8+ T-cells

2.1. Well-posedness of the model

The optimal system (1) is epidemiologically meaningful if all its solutions with non-negative initial conditions remain non-negative for all time t ≥ 0.

Theorem 1

If the initial valuesS(0),H(0),X(0),R(0),T(0),C(0),M(0),G(0) andZ(0) are non-negative, then the solution (S(t), H(t), X(t), R(t), T(t), C(t), M(t), G(t), Z(t)) of system (1) is non-negative for all time t ≥ 0.

Additionally, based on the Theorem by Garrett Birkhoff and Gian-Carlo Rota (Garrett & Rota, 1978), we have

$N_e(t)\le \max \left\{N_e(0),\frac{{\lambda }_r}{{\mu }_e}\right\}$, $N_l(t)\le \max \left\{N_l(0),\frac{{\lambda }_h}{{\mu }_l}\right\}$, $N_p(t)\le \max \left\{N_p(0),\frac{\left(\mathrm{\Lambda }\right)}{{\mu }_p}\right\}$,

$Z(t)\le \max \left\{Z(0),\frac{{\lambda }_z}{{\mu }_z}\right\}$,

whereN_e(t) = R(t) + T(t) + C(t), N_l(t) = H(t) + X(t), N_p(t) = S(t) + M(t) + G(t), μ_e = min{μ_r, μ_t, μ_c}, μ_l = min{μ_h, μ_x} and μ_p = min{μ_s, μ_m, μ_g}.

Furthermore, the region of biological relerance Φ is given by

$$\begin{array}{cc}\mathrm{\Phi }=& \left\{(S,H,X,R,T,C,M,G,Z)\in {\mathbb{R}}_{+}^9:N_e(t)\le \max \left\{N_e(0),\frac{{\lambda }_r}{{\mu }_e}\right\},N_l(t)\le \max \left\{N_l(0),\frac{{\lambda }_h}{{\mu }_l}\right\},\right)\\ & \left(N_p(t)\le \max \left\{N_p(0),\frac{\mathrm{\Lambda }}{{\mu }_p}\right\},Z(t)\le \max \left\{Z(0),\frac{{\lambda }_z}{{\mu }_z}\right\}\right\}.\end{array}$$ (2)

We therefore conclude that the set Φ is positively invariant. Thus, all solutions in Φ remain in Φ for all time t ≥ 0. The optimal system (1) is therefore well-posed mathematically and epidemiologically in the region Φ. It is therefore sufficient to study the dynamics generated by system (1) in Φ. flushleft

3. Analysis of optimal model with constant controls

3.1. Disease-free equilibrium point and effective reproduction number

The optimal system (1) has a disease-free equilibrium state ${\mathcal{E}}_d$ denoted by

$${\mathcal{E}}_d=(S_0,H_0,X_0,R_0,T_0,C_0,M_0,G_0,Z_0)=\left(0,\frac{{\lambda }_h}{{\mu }_h},0,\frac{{\lambda }_r}{{\mu }_r},0,0,0,0,\frac{{\lambda }_z}{{\mu }_z}\right).$$ (3)

At ${\mathcal{E}}_d$, there are no sporozoite recruitment and the human host is free of malaria parasites (sporozoites, merozoites and gametocytes). To eliminate malaria infection, we apply control measures that would reduce the transmission process and ensure stability of ${\mathcal{E}}_d$ (Chiyaka, Garira, & Dube, 2008).

The effective reproduction number R_eff of the P. falciparum malaria is defined as the number of secondary infected erythrocytes generated per primary infected erythrocyte in a human host from the onset of malaria infection (Molineaux & Dietz, 1999) and (Chiyaka et al., 2008). Epidemiologically, if R_eff < 1, then on average a single infected red blood cell produces less than one new infected red blood cell and the within-host infection cannot grow. Conversely, if R_eff > 1, then on average, each infected red blood cell generates at least two new infected erythrocytes and parasitaemia is likely to grow leading to severe malaria case.

Using the next generation matrix approach described in (Van den Driessche & Watmough, 2002) and the notations therein, the matrices F and V⁻¹ are computed as follows:

$$F=\left(\begin{array}{cccccc}0& 0& 0& 0& 0& 0\\ \frac{(1-u_1){\beta }_s{\lambda }_h}{{\mu }_h}& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& \frac{(1-u_2){\beta }_r{\lambda }_r}{{\mu }_r}& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right)$$ (4)

and

$$V^{-1}=\left(\begin{array}{cccccc}\frac{{\mu }_h}{{\beta }_s{\lambda }_h+{\mu }_h{\mu }_s}& 0& 0& 0& 0& 0\\ 0& \frac{1}{{\mu }_x}& 0& 0& 0\\ 0& 0& \frac{1}{\gamma +{\mu }_t}& 0& 0\\ 0& 0& \frac{\gamma }{{\mu }_c(\gamma +{\mu }_t)}& \frac{1}{{\mu }_c}& 0& 0\\ 0& \frac{N(1-u_3){\mu }_r}{{\beta }_r{\lambda }_r+{\mu }_m{\mu }_r}& \frac{P(1-\pi )\gamma (1-u_4){\mu }_r}{({\beta }_r{\lambda }_r+{\mu }_m{\mu }_r)(\gamma +{\mu }_t)}& \frac{P(1-\pi )\gamma (1-u_4){\mu }_r}{({\beta }_r{\lambda }_r+{\mu }_m{\mu }_r)}& \frac{{\mu }_r}{{\mu }_m{\mu }_r+{\beta }_r{\lambda }_r}& 0\\ 0& 0& \frac{\pi \gamma }{(u_3+{\mu }_g)(\gamma +{\mu }_t)}& \frac{\pi }{u_3+{\mu }_g}& 0& \frac{1}{u_3+{\mu }_g}\end{array}\right)$$ (5)

The effective reproduction number is the spectral radius of the next generation matrix (FV⁻¹). Upon computation in Mathematica software, we obtain

$$R_{e\mathit{ff}}=\frac{P(1-\pi )(1-u_2)(1-u_4)\gamma {\mu }_r{\beta }_r{\lambda }_r}{({\beta }_r{\lambda }_r+{\mu }_m{\mu }_r)(\gamma +{\mu }_t)}.$$ (6)

The following theorem results from the existence of the disease effective reproduction number.

Theorem 2

The disease-free equilibrium${\mathcal{E}}_d$is locally asymptotically stable whenR_eff < 1 and unstable when R_eff > 1.

3.2. Global asymptotic stability of the disease-free equilibrium point

If at any time, using appropriate interventions (such as effective antimalarial drugs and or efficacious malaria vaccines) we are able to reduce R_eff to less than unity, then within-host malaria infection may be eliminated.

Theorem 3

The disease-free equilibrium${\mathcal{E}}_d$of system (1) is globally asymptotically stable if the threshold quantity R_eff < 1.

Proof: SeeAppendix A.flushleft

The above result shows that in-host malaria infection would be eliminated provided that the threshold quantity R_eff is less that unity. This is achievable if effective antimalarial drugs are used alongside efficacious malaria vaccines. In-host malaria elimination should hence focus on eradicating infective malaria merozoites and infected erythrocytes.

3.3. Endemic equilibrium point

The stability of the disease-free equilibrium point E_d is violated when R_eff > 1. System (1) therefore assumes an endemic equilibrium ${\mathcal{E}}_e$, where

$${\mathcal{E}}_e=(S^{\ast },H^{\ast },X^{\ast },R^{\ast },T^{\ast },C^{\ast },M^{\ast },G^{\ast },Z^{\ast }).$$ (7)

and

$$\begin{array}{cc}& H^{\ast }=\frac{{\lambda }_h}{{\beta }_s(1-u_1)S^{\ast }+{\mu }_h},X^{\ast }=\frac{{\lambda }_h{\beta }_s(1-u_1)S^{\ast }}{(k_x{Z}^{\ast }+{\mu }_x)({\mu }_h+{\beta }_s(1-u_1)S^{\ast })},S^{\ast }=\frac{b_s+\sqrt{b_s^2-4a_s{c}_s}}{2a_s},\\ & R^{\ast }=\frac{{\lambda }_r(1+\alpha Z^{\ast })}{M^{\ast }(1-u_2){\beta }_r+(1+\alpha Z^{\ast }){\mu }_r},M^{\ast }=\frac{P(1-\pi )(1-u_4){\mu }_c+N{X}^{\ast }(1+\alpha Z^{\ast })(1-u_3){\mu }_3}{(1+\alpha Z^{\ast })({\beta }_r{R}^{\ast }+{\mu }_m)},\\ & G^{\ast }=\frac{\pi {\mu }_c{C}^{\ast }}{u_3+{\mu }_g},Z^{\ast }=\frac{{\lambda }_z}{{\mu }_z-{\mathrm{\Delta }}_z},\text{where}{\mathrm{\Delta }}_z=\frac{{\delta }_x{X}^{\ast }}{1+{\epsilon }_0{X}^{\ast }}+\frac{{\delta }_t{T}^{\ast }}{1+{\epsilon }_1{T}^{\ast }}+\frac{{\delta }_c{C}^{\ast }}{1+{\epsilon }_3{C}^{\ast }},\\ & T^{\ast }=\frac{b_t+\sqrt{b_t^2-4a_t{c}_t}}{-2a_t}\text{and}{C}^{\ast }=\frac{b_c+\sqrt{b_c^2-4a_c{c}_c}}{-2a_c},\end{array}$$

where

$$a_s=(1-u_1){\beta }_s{\mu }_s>0,b_s={\beta }_s({\lambda }_h-\mathrm{\Lambda }(1-u_1))+{\mu }_h{\mu }_s,c_s=-\mathrm{\Lambda }{\mu }_h<0,$$ (8)

$$a_t=-(1+\alpha Z^{\ast }){\epsilon }_1(\gamma +{\mu }_t)<0,b_t=-k_x{Z}^{\ast }+{\epsilon }_1{\beta }_r(1-u_2)M^{\ast }{R}^{\ast }-(1+\alpha Z^{\ast })(\gamma +{\mu }_t),$$ (9)

$$a_c=-{\epsilon }_2{\mu }_c<0,b_c=\gamma {\epsilon }_{2}T-(k_c{Z}^{\ast }+{\mu }_c),c_c=\gamma T^{\ast }\text{and}{c}_t=(1-u_2){\beta }_r{M}^{\ast }{R}^{\ast }.$$ (10)

By Descartes’ “Rule of Signs” (Wang, 2004), it is clear from the coefficients in equations (8), (9), (10) that all the state variables would assume a unitary (single) value at the endemic equilibrium point ${\mathcal{E}}_e$. Effective interventions in the form of antimalarial drugs and efficacious malaria vaccines are necessary to drive the endemic equilibrium state to disease-free state within the human host.

3.4. Sensitivity analysis

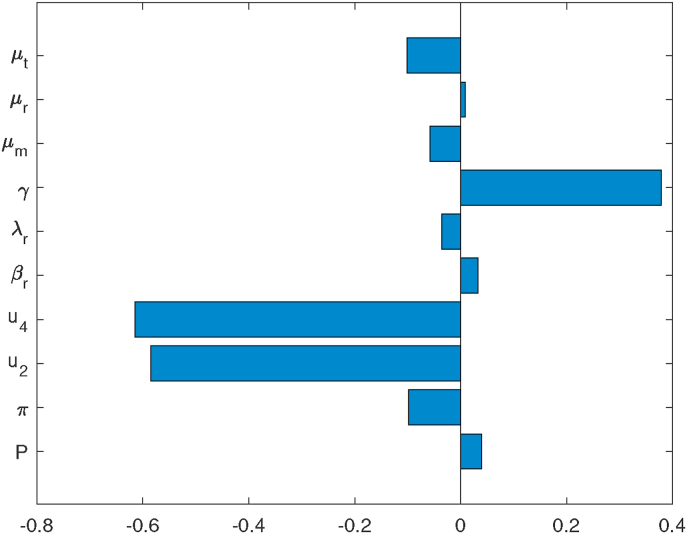
Sensitivity analysis is performed to establish the inherent effect on output variables generated by uncertainties in the input parameters (Iooss and Saltelli, 2017). We determine the contribution of vital model parameters to the progression of in-host malaria infection. Using the technique of Latin Hypercube Sampling and Partial Rank Correlation Coefficient (LHS/PRCC) (Iman & Helton, 1988), we establish the model parameters with significant influence in in-host malaria disease dynamics. Using 1000 simulations per run and parameter baseline values provided in Tabe 2, we determined the PRCCs of the parameters in the disease reproduction number R_eff in equation (6). Results of sensitivity analysis are presented in Fig. 1. Note that parameters with positive (or negative) PRCC increases (or decreases) the disease R_eff when they are increased (or decreased). Subsequently, this increases (or decreases) the levels of parasitaemia within infected human host. Observe that (i) the death rate of blood trophozoites μ_t, (ii) the rate of progression of trophozoites to blood schizont stages γ, (iii) efficacy of blood stage vaccine μ₂ and (iv) efficacy of blood schizontocide μ₄, are the four influential parameters in driving the in-host malaria dynamics. It is further evident that μ₂ and μ₄ are the most sensitive parameters in model system (1). The disease dynamics is hence heavily influenced by the efficacy antimalarial drugs that target blood trophozoites and blood schizonts.

Fig. 1.

Graph showing tornado plots of partial rank correlation coefficients (PRCCs) of the parameters that influence the effective reproduction number R_eff. Parameter values are shown in Table 2.

4. Formulation of optimal control problem

We endevour to reduce malaria disease severity within the human host by reducing parasite invasion of the healthy hepatocytes and erythrocytes. To curtail further transmission, we also aim to reduce the density of sexual gametocytes within the host's blood stream. To achieve these two, we set out to establish the most-effective control strategy drawn from a combination of malaria vaccine antigens and antimalarial drugs regimens described in Section 2. The malaria control measures/strategies under our consideration are u₁(t), u₂(t), u₃(t) and u₄(t) described in Section 2. Therefore, the objective functional J defined over the controls (u₁, …, u₄) and within a finite time interval [0, t_f] is given by

$$J(u_1,\dots ,u_4)={\int }_0^{t_f}(A_{1}X+A_{2}T+A_{3}M+A_{4}G)+\frac{1}{2}\sum _{i=1}^4{B}_i{u}_i^2,$$ (11)

subject to the differential system (1).

In equation (11), A₁, …, A₄ are the costs associated with minimising the infected hepatocyte, infected erythrocytes, the merozoites and gametocytes, respectively. The parameter t_f denotes the time period of intervention. The quantities B₁, …, B₄ represents the weight constants for pre-erythrocytic vaccine, blood stage vaccine, blood schizontocide and gametocytocide, respectively. Additionally, we endevour to minimize the costs associated with the control efforts: pre-erythrocytic vaccines $\frac{1}{2}{B}_1{u}_1^2$, blood stage vaccine $\frac{1}{2}{B}_2{u}_2^2$, blood schizontocide $\frac{1}{2}{B}_3{u}_3^2$ and gametocytocide $\frac{1}{2}{B}_4{u}_4^2$.

Like other disease models (Joshi et al., 2006; Okosun et al., 2011), the costs associated with using antimalarial drugs and malaria vaccines are directly proportional to the rates of implementation of these control measures. Therefore, the coefficients A₁X, A₂T, A₃M and A₄G are linear functions. On the other hand, the cost of administering the listed control measures, $\frac{1}{2}{B}_1{u}_1^2$, $\frac{1}{2}{B}_2{u}_2^2$, $\frac{1}{2}{B}_3{u}_3^2$ and $\frac{1}{2}{B}_4{u}_4^2$ are directly proportional to the square of the corresponding control function. They are hence nonlinear and take quadratic forms.

Numerically, we endevour to establish an optimal control set $(u_1^{\ast },\dots ,u_4^{\ast })$ which minimizes the objective function J in equation (11). That is,

$$J(u_1^{\ast },\dots ,u_4^{\ast })={\min }_{U}J(u_1,\dots ,u_4),$$ (12)

where U = {(u₁, …, u₄) such that {u₁, …, u₄} is a Lebeque measurable control set with 0 ≤ u_i(t) ≤ 1, i = 1, …, 4, for t ∈ [0, t_f]}.

4.1. Existence of optimal solutions to the control problem

An optimal control solution is said to exist provided that the five necessary conditions that define the optimal solutions $J(u_1^{\ast },\dots ,u_4^{\ast })={\min }_{(u_1,\dots ,u_4)\in U}J(u_1,\dots ,u_4)$ of system (1) are satisfied. The resulting optimality problem is solved based on Pontryagin's Maximum Principle (Anita et al., 2011).

Theorem 4

Consider an optimal problem$\mathcal{N}(t,Y(t),u_i(t))$of system (1), subject to initial conditions of state variable $Y(t)\in {\mathbb{R}}_{+}^9$ and boundary condition of control variables u_i(t) ∈ U for i = 1, …, 4. There exists an optimal solution $J(u_1^{\ast },\dots ,u_4^{\ast })$ such that $J(u_1^{\ast },\dots ,u_4^{\ast })={\min }_{(u_1,\dots ,u_4)\in U}J(u_1,\dots ,u_4)$ if the following necessary conditions in (Chuma, Mwanga, & Masanja, 2019) are satisfied:

• (i)Control set U and the corresponding state variables are nonempty,
• (ii)Control set U is convex and closed,
• (iii)The right hand side of the state system is bounded by the linear function in the state and control variables,
• (iv)The integrand of the objective function is convex, and
• (v)There exist constant numbers q₁, q₂ > 0 and ξ > 1 such that the integrand of the objective function is bounded below by $q_1{(|u_1|+|u_2|+|u_3|+|u_4|)}^{\xi /2}-q_2$.

Proof: We verify the existence of an optimal control solution using the conditions provided by Fleming and Rishel (Fleming & Rishel, 1975). Given the optimal problem $\mathcal{N}(t,Y(t),u_i(t))$ of system (1), the set of state variables $Y(t)\in {\mathbb{R}}_{+}^9$ and the control variables {u_i(t) ∈ U|0 ≤ u_i(t) ≤ 1}, t ∈ [0, t_f] are non-negative. By definition, the optimal solution u_i(t) is convex and bounded in U. Hence, the first (i) and second (ii) conditions is satisfied (Mlay, Luboobi, Kuznetsov, & Shahada, 2015; Mpeshe, Luboobi, & Nkansah-gyekye, 2014).

The differential system (1) is bounded. The third condition (iii) therefore holds. Moreover, the integrand in the objective functional in equation (11) is clearly convex on the control set U and the fourth condition also holds. Following the work by Lashara et al., (Lashari, Hattaf, Zaman, & Li, 2013), the integrand in equation (11) is also bounded below by

$$A_{1}X(t)+A_{2}T(t)+A_{3}M(t)+A_{4}G(t)+\frac{1}{2}\left(\sum _{i=1}^4{B}_i{u}_i^2\right)\ge q_1{\left(\sum _{i=1}^4|u_i(t)|\right)}^{\xi /2}-q_2$$ (13)

for i = 1, …, 4. This proves condition (v). The above five conditions are hence satisfied and

$$J(u_1^{\ast },\dots ,u_4^{\ast })={\min }_{U}J(u_1,\dots ,u_4).$$ (14)

4.2. Characterisation of the optimal control

We employ Pontryagin's Maximum Principle (PMP) (Anita et al., 2011) in solving the stated optimal control problem. PMP converts the optimality system (1), objective function (11) and (12) into a problem of minimising a pointwise Hamiltonian H_a, with respect to controls u₁⋯, u₄. The Lagrangian L of the optimal control problem is given by

$$L=A_{1}X+A_{2}T+A_{3}M+A_{4}G+\frac{1}{2}(B_1{u}_1^2+B_2{u}_2^2+B_3{u}_3^2+B_4{u}_4^2).$$ (15)

Clearly, the second derivatives of L in equation (15) with respect to u_i, i = 1, …, 4, are all positive. This confirms that optimal control problem assumes a minimum value at the controls $u_1^{\ast },\dots ,u_4^{\ast }$. We aim at obtaining the Lagrangian minimum value. This is accomplished by defining a Hamiltonian function H_a for the control problem. That is,

$$H_a=L(X,T,M,G,u_1,u_2,u_3,u_4)+{\mathrm{\Upsilon }}_1\dot{S}+{\mathrm{\Upsilon }}_2\dot{H}+{\mathrm{\Upsilon }}_3\dot{X}+{\mathrm{\Upsilon }}_4\dot{R}+{\mathrm{\Upsilon }}_5\dot{T}+{\mathrm{\Upsilon }}_6\dot{C}+{\mathrm{\Upsilon }}_7\dot{M}+{\mathrm{\Upsilon }}_8\dot{G}+{\mathrm{\Upsilon }}_9\dot{Z}=A_{1}X+A_{2}T+A_{3}M+A_{4}G+\frac{1}{2}(B_1{u}_1^2+B_2{u}_2^2+B_3{u}_3^2+B_4{u}_4^2)+{\mathrm{\Upsilon }}_1\left[\mathrm{\Lambda }-{\mu }_{s}S-{\beta }_{s}SH\right]$$ (16)

$$+{\mathrm{\Upsilon }}_2\left[{\lambda }_h-{\mu }_{h}H-(1-u_1(t)){\beta }_{s}SH\right]+{\mathrm{\Upsilon }}_3\left[(1-u_1(t)){\beta }_{s}SH-{\mu }_{x}X-\frac{k_{xZX}}{1+{ϵ}_{0}X}\right]+{\mathrm{\Upsilon }}_4\left[{\lambda }_r-\frac{(1-u_2(t)){\beta }_{r}RM}{1+\alpha Z}-{\mu }_{r}R\right]+{\mathrm{\Upsilon }}_5\left[\frac{(1-u_2(t)){\beta }_{rRM}}{1+\alpha Z}-{\mu }_{t}T-\gamma T-\frac{k_{tZT}}{1+{ϵ}_{1}T}\right]+{\mathrm{\Upsilon }}_6\left[\gamma T-{\mu }_{c}C-\frac{k_{c}ZC}{1+{ϵ}_{2}C}\right]+{\mathrm{\Upsilon }}_7\left[(1-u_3(t))N{\mu }_{x}X+\frac{(1-u_4(t))P(1-\pi ){\mu }_{c}C}{1+\alpha Z}-{\mu }_{m}M-{\beta }_{r}RM\right]+{\mathrm{\Upsilon }}_8\left[\pi {\mu }_{c}C-(u_3(t)+{\mu }_g)G\right]+{\mathrm{\Upsilon }}_9\left[{\lambda }_z+Z\left(\frac{{\delta }_{x}X}{1+{ϵ}_{0}X}+\frac{{\delta }_{t}T}{1+{ϵ}_{1}T}+\frac{{\delta }_{c}C}{1+{ϵ}_{2}C}\right)-{\mu }_{Z}Z\right],$$ (17)

where ϒ_i, for i = 1, …, 9, are the adjoint variables.

Theorem 5

Let (S∗, H∗, X∗, R∗, T∗, C∗, M∗, G∗, Z∗) and $(u_1^{\ast },\dots ,u_4^{\ast })$ be the solutions of the optimal control problem (1) and (12) and the solution of the optimal control measures, respectively. Then there exists adjoint variables ϒ_i, i = 1, 2, …, 9 satisfying

$$\left(\begin{array}{cc}\frac{\mathrm{d}{\mathrm{\Upsilon }}_1}{\mathrm{d}t}& =({\mathrm{\Upsilon }}_2-{\mathrm{\Upsilon }}_3)(1-u_1){\beta }_{s}H+{\mathrm{\Upsilon }}_1({\mu }_s+{\beta }_{s}H),\\ \frac{\mathrm{d}{\mathrm{\Upsilon }}_2}{\mathrm{d}t}& =({\mathrm{\Upsilon }}_1+({\mathrm{\Upsilon }}_2-{\mathrm{\Upsilon }}_3)(1-u_1)){\beta }_s+{\mathrm{\Upsilon }}_2{\mu }_h,\\ \frac{\mathrm{d}{\mathrm{\Upsilon }}_3}{\mathrm{d}t}& =\frac{({\mathrm{\Upsilon }}_3{k}_x-{\mathrm{\Upsilon }}_9{\delta }_x)Z}{{(1+{\epsilon }_{0}X)}^2}-A_1+({\mathrm{\Upsilon }}_3-{\mathrm{\Upsilon }}_{7}N(1-u_3)){\mu }_x,\\ \frac{\mathrm{d}{\mathrm{\Upsilon }}_4}{\mathrm{d}t}& =\frac{{\beta }_r((1+\alpha Z){\mathrm{\Upsilon }}_7+(1-u_2)({\mathrm{\Upsilon }}_4-{\mathrm{\Upsilon }}_5))M}{(1+\alpha Z)}+{\mathrm{\Upsilon }}_4{\mu }_r,\\ \frac{\mathrm{d}{\mathrm{\Upsilon }}_5}{\mathrm{d}t}& =\frac{({\mathrm{\Upsilon }}_5{k}_t-{\mathrm{\Upsilon }}_9{\delta }_t)Z}{{(1+{\epsilon }_{1}T)}^2}+{\mathrm{\Upsilon }}_5(\gamma +{\mu }_t)-(A_2+\gamma {\mathrm{\Upsilon }}_6),\\ \frac{\mathrm{d}{\mathrm{\Upsilon }}_6}{\mathrm{d}t}& ={\mathrm{\Upsilon }}_6\left(\frac{k_{c}Z}{{(1+{\epsilon }_{2}C)}^2}+{\mu }_c\right)-\frac{{\mathrm{\Upsilon }}_9{\delta }_{c}Z}{(1+{\epsilon }_{2}C)}-\pi {\mathrm{\Upsilon }}_8{\mu }_c-\frac{(1-u_4)(1-\pi )P{\mathrm{\Upsilon }}_7{\mu }_c}{(1+\alpha Z)},\\ \frac{\mathrm{d}{\mathrm{\Upsilon }}_7}{\mathrm{d}t}& ={\mathrm{\Upsilon }}_7({\beta }_{r}R+{\mu }_m)-A_3+\frac{({\mathrm{\Upsilon }}_4-{\mathrm{\Upsilon }}_5)(1-u_2){\beta }_{r}R}{1+\alpha Z},\\ \frac{\mathrm{d}{\mathrm{\Upsilon }}_8}{\mathrm{d}t}& ={\mathrm{\Upsilon }}_8(u_3+{\mu }_g)-A_4,\\ \frac{\mathrm{d}{\mathrm{\Upsilon }}_9}{\mathrm{d}t}& =\frac{{\mathrm{\Upsilon }}_3{k}_{x}X}{1+{\epsilon }_{0}X}+\frac{{\mathrm{\Upsilon }}_6{k}_{c}C}{1+{\epsilon }_{2}C}-\frac{{\mathrm{\Upsilon }}_4(1-u_2)\alpha {\beta }_{rMR}}{{(1+\alpha Z)}^2}+\frac{{\mathrm{\Upsilon }}_7(1-\pi )P(1-u_4)\alpha {\mu }_{c}C}{{(1+\alpha Z)}^2}\\ & -{\mathrm{\Upsilon }}_9\left(\frac{{\delta }_{x}X}{1+{\epsilon }_{0}X}+\frac{{\delta }_{t}T}{1+{\epsilon }_{1}T}+\frac{{\delta }_{c}C}{1+{\epsilon }_{2}C}-{\mu }_z\right)+{\mathrm{\Upsilon }}_5\left(\frac{k_{t}T}{1+{\epsilon }_{1}T}+\frac{(1-u_2)\alpha \beta MR}{{(1+\alpha Z)}^2}\right),\end{array}\right\}$$ (18)

with boundary conditions

$${\mathrm{\Upsilon }}_i(t_f)=0,\text{for}i=1,\dots ,9.$$ (19)

The optimal control measures are expressed as

$$u_i^{\ast }=\left\{\begin{array}{ll}0& \text{if }{u}_i\le 0,\\ u_i& \text{if }0<u_i<1,\\ 1& \text{if }{u}_i\ge 1.\end{array}\right)$$ (20)

Additionally, in the interior of the control setU, the optimal control measures$(u_1^{\ast },\dots ,u_4^{\ast })$are given by

$$u_1^{\ast }=\max \left\{\min \left\{\frac{{\beta }_s({\mathrm{\Upsilon }}_3-{\mathrm{\Upsilon }}_2)S^{\ast }{H}^{\ast }}{B_1},1\right\},0\right\}$$ (21)

$$u_2^{\ast }=\max \left\{\min \left\{\frac{{\beta }_r({\mathrm{\Upsilon }}_5-{\mathrm{\Upsilon }}_4)R^{\ast }{M}^{\ast }}{(1+\alpha Z)B_2},1\right\},0\right\}$$ (22)

$$u_3^{\ast }=\max \left\{\min \left\{\frac{{\mathrm{\Upsilon }}_8{G}^{\ast }+{\mathrm{\Upsilon }}_7{\mu }_{x}N{X}^{\ast }}{B_3},1\right\},0\right\}$$ (23)

$$u_4^{\ast }=\max \left\{\min \left\{\frac{{\mathrm{\Upsilon }}_7{\mu }_c(1-\pi )P{C}^{\ast }}{(1+\alpha Z)B_4},1\right\},0\right\}.$$ (24)

Proof: SeeAppendix B.

4.3. Uniqueness of the optimality system

Having proved that both the state variables and the adjoint functions of the optimality system (1) and (12) are bounded and satisfy Lipschitz conditions (Caveny, 1970), the uniqueness of the optimal controls can easily be derived using the technique explained in (Kim et al., 2012).

Theorem 6

The bounded solutions to the optimality system (1) and (12) are unique.

Proof: SeeAppendix C.flushleft

The optimal controls are obtained through numerical simulations in the next section. The optimal control set $u_i^{\ast },i=1,\dots ,4$ gives an optimal control strategy against in-host P. falciparum malaria infection.

5. Numerical simulations

Here, the backward-forward sweep (BFS) algorithm (Lenhart & Workman, 2007) and the 4th-order Runge-Kutta (RK) scheme in Matlab (Ince, 1943) are applied to solve the optimality system. The BFS algorithm has been implemented in several research studies (Joshi et al., 2006; Nakakawa, Mugisha, Shaw, Tinzaara, & Karamura, 2017; Namawejje, Luboobi, Kuznetsov, & Wobudeya, 2014; Okosun et al., 2011; Omondi et al., 2018). The optimal control code presented by Lenhart and Workman (Lenhart & Workman, 2007) was modified to generate numerical solutions to the optimality system (40)–(41). The state variables $\overline{x}=(S,H,X,R,T,C,M,G,Z)$ were solved forward in time using the 4th-order Runge-Kutta scheme in Matlab and the initial conditions (S₀, H₀, X₀, R₀, T₀, C₀, M₀, G₀, Z₀) and ${\overline{u}}_i$. The co-state system ${\overline{\mathrm{\Upsilon }}}_i,i=1,\dots ,9$ was solved backward in time using the boundary conditions ϒ_i(t_f) = 0 and the values of $\overline{x}$ and $\overline{u}$. The control variables $\overline{u}$ were then updated in the second iteration by entering the new values of the state and co-state variables. This procedure is repeated till convergence is achieved.

The parameter values shown in Table 2 were obtained from literature. Other parameter values are however assumed. The retail price of ACTs in sub-Saharan Africa is roughly 5–7 US dollars ($) (Palafox et al., 2015). The median price of AL (the blood schizontocide) is $5.26, $6.03, $4.58, $5.36 and $5.36 in Uganda, Benin, Democratic Republic of the Congo, Nigeria and Zambia, respectively (Palafox et al., 2015). A study on the availability and retail prices of antimalarial drugs in rural Western Kenya revealed that the mean price of AL and DHA-PPQ was $4.5 and $4.39, respectively (Kioko et al., 2016). Penny et al.,(Penny et al., 2016), estimated the cost per dose of RTS,S/AS01 to be $6.52 ($2.69 –$12.9). In this study, and for purposes of this analysis, we shall assume an average retail price of $5 for AL and primaquine per dose. Additionally, the pre-erythrocytic vaccine (RTS,S/AS01) is considered highly cost-effective and is estimated to assume a cost of $5 per dose under a four-dose schedule (Winskill et al., 2017b). This implies a unit cost of $39.25 is incurred per fully vaccinated child (Penny et al., 2016; Winskill et al., 2017b). We further assume the blood-stage vaccine would bear a similar cost of $5 per dose. Therefore, the costs A₁ = A₂ = $39.25. Similarly, A₃ = A₄ = $5.

Table 2.

Table showing parameter values.

Parameter	Value	Range	Units	Source
P	16	(15–20)	Unitless	Diebner et al. (2000)
kx, kt, kc	0.01	(0.001–0.9)	day−1	Chiyaka et al. (2008)
μr	0.083	(0.05–0.1)	day−1	Anderson, May, and Gupta (1989)
βr	2.0 × 10−2	(0.01–0.3)	mm−3day−1	Dondorp, Kager, Vreeken, and White (2000)
βs	1.0 × 10−3	(0.000 1–0.2)	mm−3day−1	Selemani, Luboobi, and Nkansah-Gyekye (2016)
π	0.2	(0.1–0.9)	unitless	Talman, Domarle, McKenzie, Ariey, and Robert (2004)
μh	0.029	(0.01–0.5)	day−1	Estimated
μx	0.02	(0.01–1)	day−1	Selemani et al. (2016)
λr	3 × 103	(3 × 102 − 3 × 108)	cells/ml day−1	Li, Ruan, and Xiao (2011)
λh	3 × 104	(3 × 105 − 3 × 108)	cells μl−1day−1	Tumwiine, Mugisha, and Luboobi (2008)
λz	30	(10–40)	μl−1day−1	Chiyaka (2010)
μm	48	(46–50)	day−1	Li et al. (2011)
Λ	30	(18–35)	sporozoites day−1	Selemani et al. (2016)
μs	1.2	(1.0 − 2.4)	day−1	Selemani et al. (2016)
μt	0.27	(0.01–0.8)	day−1	Magombedze, Chiyaka, and Mukandavire (2011)
μc	0.7	(0.1–0.9)	day−1	Magombedze et al. (2011)
μg	0.000 062 5	(6.0 × 10−5 − 7.0 × 10−5)	day−1	Selemani et al. (2016)
μz	2	(0.5–3)	day−1	Chiyaka (2010)
δx, δt, δc	1e-5	(1e-5-1e-7)	mm−3day−1	Chiyaka (2010)
γ	1.5	(0.1–2)	day−1	Selemani et al. (2016)
ε0, ε1, ε2	1E-5	(1E-6, 1E-4)	day−1	Tumwiine et al. (2008)
α	0.000 5	(0.000 05–0.02)	unitless	Magombedze et al. (2011)
N	10 000	(8000–20 000)	Unitless	Tumwiine et al. (2008)

Malaria treatment using ACTs have made a significant contribution to current success in malaria control efforts. For the period 2014–2017, WHO spent about US $11.71, $13.70, $12.53 and $14.18 per malaria cases averted, respectively. The 2015 World malaria report showed that about 663 million malaria cases were averted for the period 2001–2015 (WHO, 2016); of these cases, 21% (17%, 29%) were averted due to ACT use. Therefore, an average of US $11.90 was spent per year on malaria cases averted by ACTs in the period 2014–2017. Additionally, a report by the President's Malaria Initiative (PMI), estimated that about US $94 (95% CI: $51, $166) was spent per disability adjusted life year (DALY) averted for the period 2005–2017 (Winskill et al., 2017a). This represents about US $7.80 per cases averted per year. Unlike the efficacies of antimalarial drugs (95%), the vaccines considered in this study have a moderate efficacy of 75%. The weight constants B₁, B₂, B₃ and B₄ are hence assigned a slightly lower average value of US $7.50. That is, B₁ = B₂ = B₃ = B₄ = 7.50.

In this section, therefore, we assume that the coefficients A₁ = A₂ = 39.25, A₃ = A₄ = 5.00 and B_i = 7.50, i = 1, …, 4. The initial conditions are also fixed at: S(0) = 3000, H(0) = 3 × 10⁵, X(0) = 5 × 10², R(0) = 5 × 10⁶, T(0) = 5 × 10³, C(0) = 5000, M(0) = 9000, G(0) = 5000, Z(0) = 3000. The results of the effects of various control strategies against in-host P. falciparum malaria infections are as displayed in Fig. 2, Fig. 3, Fig. 4, Fig. 5, Fig. 6, Fig. 7, Fig. 8, Fig. 9, Fig. 10, Fig. 11, Fig. 12, Fig. 13. We chose arbitrary initial conditions because the presented model (with constant vaccine controls) exhibits global stability behaviour. Note that we considered all the possible set of control combinations in this study. However, only those that gave substantial decrease in the populations (of X, T, M and G) as pre-defined in the objective functional (12) are presented. To simplify the analysis, the four control measures are grouped into the following six categories:

• •
  Strategy 1: A combination of two control measures

  • –
    (1A) A combination of blood schizontocide u₃ and gametocytocide u₄ only.
  • –
    (1B) A combination of pre-erythrocytic u₁ and blood stage vaccine antigen u₂ only.
  • –
    (1C) A combination of pre-erythrocytic vaccine u₁ and blood schizontocide drug u₃ only.
• •
  Strategy 2: A combination of three control measures

  • –
    (2A) Pre-erythrocytic vaccine antigen u₁, blood stage vaccine antigen u₂ and blood schizontocide u₃ only.
  • –
    (2B) Pre-erythrocytic vaccine antigen u₁, blood schizontocide u₃ and gametocytocide u₄ only.
• •Strategy 3: A combination of all the four control measures (pre-erythrocytic vaccine antigen u₁, blood stage vaccine antigen u₂, blood schizontocide u₃ and gametocytocide u₄).

Fig. 2.

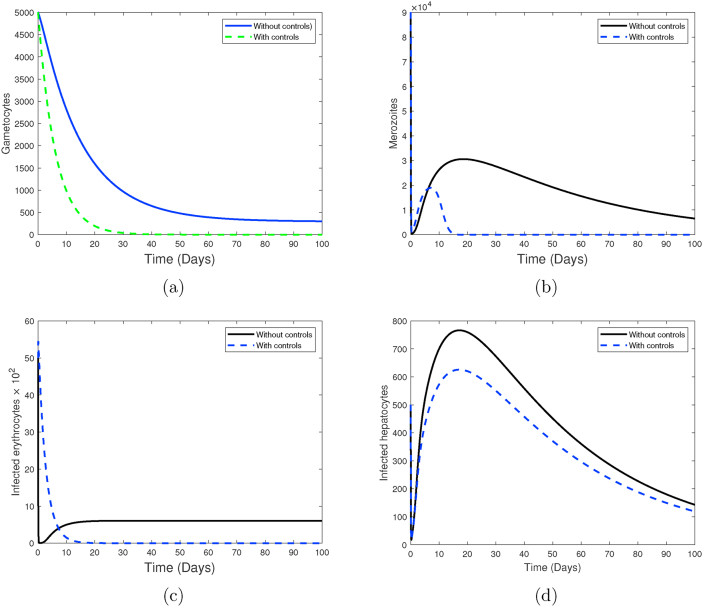
Simulations of system (1), showing the impact of a combination of blood schizontocide u₃ and a gametocitocide u₄ only during clinical P. falciparum malaria infection. Used parameter values are shown in Table 2.

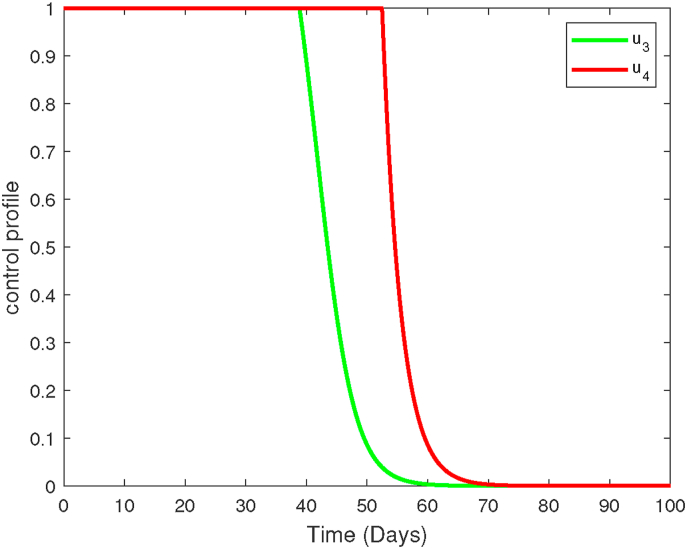
Fig. 3.

Profiles of blood schizontocide u₃ and gametocytocide u₄. Here, u₁ = 0, u₂ = 0.

Fig. 4.

Simulations of system (1), showing the impact of a combination of pre-erythrocytic vaccine antigens u₁ with blood stage vaccine antigens u₂ only. Used parameter values are shown in Table 2.

Fig. 5.

Profiles of pre-erythrocytic vaccine antigen u₁ and blood stage vaccine antigens u₂. Here, u₃ = 0, u₄ = 0.

Fig. 6.

Simulations of system (1), showing the impact of a combining pre-erythrocytic malaria vaccine u₁ and blood schizontocides u₃ only in the control of within-human P. falciparum infection. Used parameter values are shown in Table 2.

Fig. 7.

Profiles of pre-erythrocytic vaccine antigen u₁ and blood schizontocide drug u₃. Here, u₂ = 0, u₄ = 0.

Fig. 8.

Simulations of system (1), showing the impact of a combination of pre-erythrocytic vaccine antigens u₁, blood stage vaccine antigens u₂ and blood schizontocide u₃ only. Used parameter values are shown in Table 2.

Fig. 9.

Profiles of pre-erythrocytic vaccine antigen u₁, blood stage vaccine antigen u₂ and blood schizontocide u₃. Here, u₄ = 0.

Fig. 10.

Simulations of system (1), showing the impact of a combination of pre-erythrocytic malaria vaccine u₁, blood schizontocide u₃ and gametocitocidal drug u₄. Used parameter values are shown in Table 2.

Fig. 11.

Profiles of pre-erythrocytic vaccine antigen u₁, blood schizontocide u₃ and gametocytocide u₄. Here u₂ = 0.

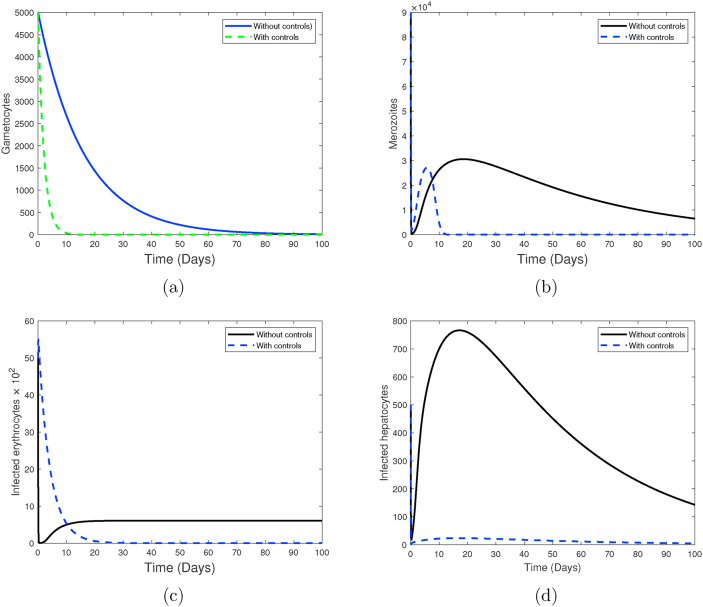
Fig. 12.

Simulations of system (1), showing the impact of combining antigens of pre-erythrocytic malaria vaccine antigen u₁ and blood stage vaccine antigen u₂ together with the administration of combined blood schizontocide u₃ and gametocitocidal drug u₄. Used parameter values are shown in Table 2.

Fig. 13.

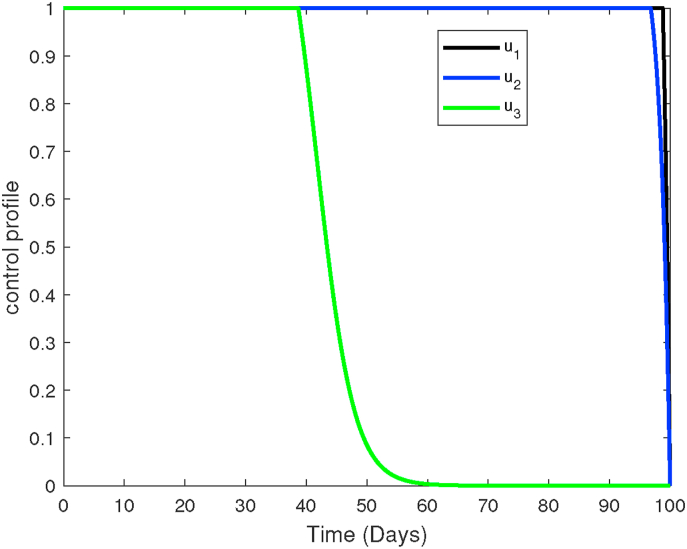
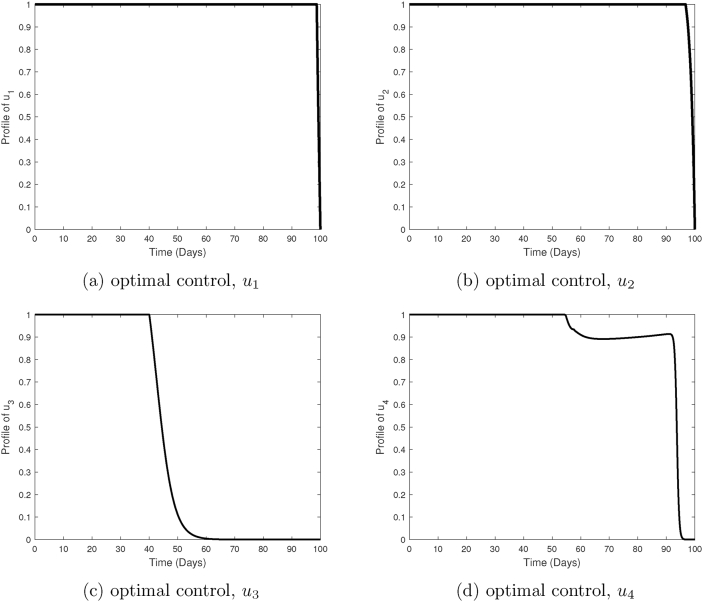
Plots showing the control profiles of pre-erythrocytic vaccine antigen u₁, blood stage vaccine antigen u₂, blood schizontocide u₃ and gametocytocide u₄.

5.1. Simulation results

The impact of employing strategy (1A) (a combination of blood schizontocide and gametocytocide only) in the control of P. falciparum malaria is presented in Fig. 2. It is evident that an antimalarial drug with such a combination is highly effective in eradicating the merozoites and infected erythrocytes as shown in Fig. 2b and c, respectively. However, this combination strategy offers little impact on the population of infected liver hepatocytes (see Fig. 2d). This is because these drugs are not active against the liver stage parasites or schizonts.

Moreover, a moderate decrease in the populations of gametocytes is also observed (see Fig. 2a). Besides effective antimalarial drugs, it is clear that other therapeutic measures maybe necessary to eradicate all parasites and infected hepatocytes and erythrocytes during P. falciparum malaria infections. The control profile of strategy (1A) is shown in Fig. 3. Observe that the concentration of the blood schizontocide and gametocytocide should remain highest for the first three-quarter of the intervention period.

In Fig. 4, a combination of malaria vaccine antigens is considered. This corresponds to strategy (1B). The combination of pre-erythrocytic vaccine antigen u₁ and blood-stage vaccine antigen u₂ is shown to be very effective in decreasing the populations of infected erythrocytes (Fig. 4c) and infected hepatocytes (Fig. 4d). Although the merozoites are eradicated, this takes a slightly longer time, due to low vaccine efficacies (see Fig. 4b). A 100% efficacy of PEV would, however, not require augmenting with BSV. Nevertheless, the efficacies of PEV and BSV is still likely to drop over time as the antibodies decay (Sherrard-Smith et al., 2018). The control profile under this strategy is presented in Fig. 5. We observe that the efficacies of the vaccines should be maintained high for the entire period of intervention.

The combined use of pre-erythrocytic vaccine and blood schizontocide, strategy (1C), is shown to greatly decrease the population of infected erythrocytes and infected hepatocytes in Fig. 6c and d, respectively. Unlike strategies (1A) and (1B), this third strategy (IC) is slightly more effective; it eradicates the merozoites and gametocytes within 30 days of infection (see Fig. 6a and b). Additionally, this strategy has a maximum duration of 11 days before it eradicates all infected erythrocytes from the host. To guarantee total eradication of all infected cells and infective parasites, the used antimalarial drug should be highly effective (efficacy $>$ 95%). The moderate effect of this strategy on the gametocyte population means that the treated malaria patients would facilitate parasite transmission to the mosquito vector, increasing future malaria cases and mortality. Fig. 7 shows the profile of the controls used in this strategy. The efficacy of the pre-erythrocyte vaccine (u₁) should be maintained throughout the control period. Similarly, the effectiveness of blood schizontocide (u₃) should remain high for at least half of the intervention period.

If we combine two or more vaccines and antimalarial drugs, then we observe different outcomes as presented in Fig. 8, Fig. 9, Fig. 10, Fig. 11, Fig. 12, Fig. 13. In Fig. 8, blood schizontocide u₃ is used to treat malaria patients who have received a combination of pre-erythrocytic vaccine antigens u₁ and blood stage vaccine antigens u₂. This defines strategy (2A). The control profiles of u₁ ≠ 0, u₂ ≠ 0 and u₃ ≠ 0 are presented in Fig. 9. A general decline in the populations of infected cells and infective parasite is observed in Fig. 8. However, the rate of decline is moderate and the clearance of gametocytes lasts longer than 20 days. A better result is however, presented in Fig. 10. In this strategy (2B), a combination of blood schizontocide u₃ and gametocytocides u₄ is administered to a malaria patient who is already on a pre-erythrocytic vaccine u₁. We observe a rapid rate of decline in populations of infected erythrocytes, infected hepatocytes, merozoites and gametocytes. The density of gametocytes fall exponentially; within 15 days of blood stage malaria. We also observe total eradication of the merozoite parasites from the human host within two weeks of infection. The profiles of the three controls are as displayed in Fig. 11.

Finally, in Fig. 12, all the four control efforts are employed (strategy 3). Here, antimalarial drugs consisting of blood schizontocides and gametocytocides are administered to malaria patients who are on pre-erythrocytic and blood stage vaccine antigens. Just like in strategy (2B), we observe tremendous decline in the populations of gametocytes, merozoites, infected hepatocytes and infected erythrocytes when all the controls are employed. It takes a much shorter time to eliminate malaria merozoites. Both the merozoites and infected red blood cells get eradicated within 12 days of infection. It is clear that both strategy (2B) and strategy 3 offer the best control options against P. falciparum malaria infection. Moreover, the simulations results in Fig. 10, Fig. 12 reveal that the emergence of clinical malaria would be least likely if either of these control strategies is implemented correctly. Nevertheless, strategy (2B) only needs one highly efficacious malaria vaccine to achieve the same result as that in strategy 3. Additionally, strategy (2B) is likely to be less costly compared to strategy 3, which incorporates all the four controls. We therefore conclude that the optimal control strategy against P. falciparum malaria is strategy (2B): a combination of efficacious pre-erythrocytic vaccine, effective blood schizontocide and a gametocytocide.

The profiles of the four controls employed in strategy 3 are shown in Fig. 13. It is observed that the control profiles of the pre-erythrocytic vaccine (u₁) and blood stage vaccines antigens (u₂) are maintained at highest levels of efficacy (75% in our case) to ensure maximum eradication of asexual sporozoites and infected erythrocytes, respectively. Similarly, the concentrations of blood schizontocides (u₃) and gametocytocides (u₄) should be maintained at the highest levels ($\ge 95\%$ in our case) to maximize eradication of asexual merozoites and infected erythrocytes, respectively. Like in other control strategies already discussed, the effectiveness of the antimalarial drugs is likely to fall after day 45 and this remains lowest till the end of the intervention period.

The best control strategy of an in-host malaria infection should eradicate all infective merozoites, infected hepatocytes and infected red blood cells within the shortest time possible at a minimal cost. Epidemiologically, the best control strategy should ensure no gametocyte parasites are available for transmission to the mosquito vector. Although strategy (2B) is the optimal in-host malaria control strategy (according to our study), it should be implemented alongside existing vector control measures such as ITNs and IRS if malaria elimination goal is to be achieved (WHO, 2015a). This result is crucial for malaria drug development and highlights the urgent need for a highly efficacious pre-erythrocytic malaria vaccine to complement existing ACTs.

6. Conclusion

In this study, the theory of optimal control has been applied to an in-host malaria model. The model incorporates antimalarial drugs and malaria vaccines as control strategies against P. falciparum malaria. The objective was to establish the best combination strategy involving (1) a blood schizontocide (2) a gametocytocide (3), a pre-erythrocytic vaccine antigen and (4) blood stage vaccine antigen against P. falciparum malaria. The Pontryagin's Maximum Principle was used to characterize the control strategies that substantially reduced the populations of infected erythrocytes, infected hepatocytes and malaria parasites. The necessary conditions for the existence of the optimal control solutions were derived and mathematically analyzed. For sufficiently small values of intervention time, we proved the uniqueness of the optimality system.

Numerical results showed that a combination of pre-erythrocytic vaccine, blood schizontocide and gametocytocide drugs would offer the best control strategy against clinical P. falciparum malaria. A combination of all the four controls equally gave a comparatively good results, however, it may be too expensive. Nonetheless, the synergy of malaria vaccine antigens and antimalarial drug regimens is crucial for future malaria chemotherapy control. Moreover, sensitivity analysis revealed that in-host malaria infection dynamics is heavily influenced by the efficacy antimalarial drugs that target blood trophozoites and blood schizonts. To limit or minimize the severity of clinical malaria infections, an effective anti-malarial drug should be used alongside efficacious blood stage vaccine.

Note that the parameter values and weights used in this study are estimated for illustration purposes. Availability of data on the costs of implementation of the four controls is likely to present a much better model outcome. However, the results presented in this paper gives insights on the need to combine effective antimalarial drugs and to use them alongside efficacious malaria vaccine antigens to control P. falciparum malaria infections within the human host. In light of these results, cost effectiveness analysis of the presented controls would form part of our future investigation.

Funding

The authors received no direct funding for this research.

Availability of data and materials

All data used in this study are included in this published article.

Authors’ contributions

All authors contributed to all sections of this manuscript.

Ethical approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Declaration of competing interest

The authors declare that there is no conflict of interest regarding the publication of this article.

Handling editor: Dr Y. Shao

Appendix AProof of Theorem 3

Based on the property of ${\mathcal{E}}_d$ (Kamgang & Sallet, 2005), it is possible to rewrite system (1) in pseudo-triangular form as follows:

$$\begin{array}{cc}{\dot{X}}_1& =B_1(X_1-X_1^{\ast })+B_2{X}_2,\\ {\dot{X}}_2& =B_3{X}_2,\end{array}$$

where X₁ is the vector representing the non-transmitting states (susceptible hepatocytes H, susceptible erythrocytes R and CD8⁺ T cells Z). The populations in these compartments are not infected with malaria parasites and do not therefore transmit malaria infections. So X₁ = (H,R,Z)^t. The vector X₂ represents the compartments that are responsible for disease transmission. These states are infected and or infective. Therefore X₂ = (S,X,T,C,M,G)^t, X = (X₁, X₂) and $X_1^{\ast }=\left(\frac{{\lambda }_h}{{\mu }_h},\frac{{\lambda }_r}{{\mu }_r},\frac{{\lambda }_z}{{\mu }_z}\right)$.

Using the conditions at ${\mathcal{E}}_d$, subsystem X₁ gives

$$B_1(X)=\left(\begin{array}{ccc}-{\mu }_h& 0& 0\\ 0& -{\mu }_r& 0\\ 0& 0& -{\mu }_z\end{array}\right);B_2(X)=\left(\begin{array}{cccccc}\frac{-(1-u_1){\beta }_s{\lambda }_h}{{\mu }_h}& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& \frac{-(1-u_2){\beta }_r{\lambda }_r{\mu }_z}{{\mu }_r(\alpha {\lambda }_z+{\mu }_z)}& 0\\ 0& \frac{{\delta }_x{\lambda }_z}{{\mu }_z}& \frac{{\delta }_t{\lambda }_z}{{\mu }_z}& \frac{{\delta }_c{\lambda }_z}{{\mu }_z}& 0& 0\end{array}\right).$$ (25)

Clearly, the eigenvalues of matrix B₁(X) in (25) are real and negative, showing that system ${\dot{X}}_1=B_1(X)(X_1-X_1^{\ast })+B_2(X)X_2$ is globally asymptotically stable at ${\mathcal{E}}_d$. Moreover, subsystem X₂ gives matrix B₃(X):

$$B_3(X)=\left(\begin{array}{cccccc}\frac{-{\beta }_s{\lambda }_h}{{\mu }_h}-{\mu }_s& 0& 0& 0& 0& 0\\ \frac{(1-u_1){\beta }_s{\lambda }_h}{{\mu }_h}& -{\mu }_x-\frac{k_x{\lambda }_z}{{\mu }_z}& 0& 0& 0& 0\\ 0& 0& -\gamma -{\mu }_t-\frac{k_t{\lambda }_z}{{\mu }_z}& 0& -\frac{(1-u_2){\beta }_r{\lambda }_r{\mu }_z}{{\mu }_r(\alpha {\lambda }_z+{\mu }_z)}& 0\\ 0& 0& \gamma & -{\mu }_c-\frac{k_c{\lambda }_z}{{\mu }_z}& 0& 0\\ 0& 0& 0& \frac{P(1-\pi )(1-u_4){\mu }_c{\mu }_z}{\alpha {\lambda }_z+{\mu }_z}& -{\mu }_m-\frac{{\beta }_r{\lambda }_r}{{\mu }_r}& 0\\ 0& 0& 0& \pi {\mu }_c& 0& -u_3-{\mu }_g\end{array}\right).$$ (26)

Observe that B₃(X) is a Metzler matrix. The equilibrium point ${\mathcal{E}}_d$ is globally asymptotically stable if the matrix B₃(X) is Metzler stable. The stability of B₃(X) is based on the following result:

Lemma 1

LetMbe a square Metzler matrix which is block decomposed:

$$M=\left(\begin{array}{cc}{M}_{11}& M_{12}\\ M_{21}& M_{22}\end{array}\right),$$

whereM₁₁andM₂₂are square matrices. The matrixMis Metzler stable if and only ifM₁₁and$M_{22}-M_{21}{M}_{11}^{-1}{M}_{12}$are Metzler stable.

In this analysis, the matrix M is simply matrix B₃ in (26). We therefore have flushleft

$$\begin{array}{cc}{M}_{11}& =\left(\begin{array}{ccc}\frac{-{\beta }_s{\lambda }_h}{{\mu }_h}-{\mu }_s& 0& 0\\ \frac{(1-u_1){\beta }_s{\lambda }_h}{{\mu }_h}& -{\mu }_x-\frac{k_x{\lambda }_z}{{\mu }_z}& 0\\ 0& 0& -\gamma -{\mu }_t-\frac{k_t{\lambda }_z}{{\mu }_z}\end{array}\right),M_{12}=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& -\frac{(1-u_2){\beta }_r{\lambda }_r{\mu }_z}{{\mu }_r(\alpha {\lambda }_z+{\mu }_z)}& 0\end{array}\right),\\ M_{21}& =\left(\begin{array}{ccc}0& 0& \gamma \\ 0& 0& 0\\ 0& 0& 0\end{array}\right)\text{and}{M}_{22}=\left(\begin{array}{ccc}-{\mu }_c-\frac{k_c{\lambda }_z}{{\mu }_z}& 0& 0\\ \frac{P(1-\pi )(1-u_4){\mu }_c{\mu }_z}{\alpha {\lambda }_z+{\mu }_z}& -{\mu }_m-\frac{{\beta }_r{\lambda }_r}{{\mu }_r}& 0\\ \pi {\mu }_c& 0& -u_3-{\mu }_g\end{array}\right).\end{array}$$ (27)

Upon computation in Mathematica software, we obtain

$$M_{22}-M_{21}{M}_{11}^{-1}{M}_{12}=\left(\begin{array}{ccc}-{\mu }_c-\frac{k_c{\lambda }_z}{{\mu }_z}& 0& 0\\ \frac{P(1-\pi )(1-u_4){\mu }_c{\mu }_z}{\alpha {\lambda }_z+{\mu }_z}& -{\mu }_m-\frac{{\beta }_r{\lambda }_r}{{\mu }_r}& 0\\ \pi {\mu }_c& 0& -u_3-{\mu }_g\end{array}\right).$$ (28)

Clearly, matrix $M_{22}-M_{21}{M}_{11}^{-1}{M}_{12}$ in (28) is Metzler stable matrix whenever R_eff < 1. Results in Lemma (1) yields Theorem 3.

Appendix B. Proof of Theorem 5

The presented adjoint system and the boundary conditions therein are standard results from the PMP (Anita et al., 2011). To obtain the differential equations governing the adjoint or co-state variables, we first set S = S∗, H = H∗, X = X∗, R = R∗, T = T∗, C = C∗, M = M∗, G = G∗ and Z = Z∗, and differentiate (partially) the Hamiltonian function H_a in equation (17) with respect to each of the state variables (S, H, X, R, T, C, M, G and Z). Thus,

$$\frac{\mathrm{d}{\mathrm{\Upsilon }}_1}{\mathrm{d}t}=-\frac{\partial H_a}{\partial X};{\mathrm{\Upsilon }}_1(t_f)=0,$$ (29)

$$\frac{\mathrm{d}{\mathrm{\Upsilon }}_2}{\mathrm{d}t}=-\frac{\partial H_a}{\partial H};{\mathrm{\Upsilon }}_2(t_f)=0,$$ (30)

$$⋮$$

$$\frac{\mathrm{d}{\mathrm{\Upsilon }}_9}{\mathrm{d}t}=-\frac{\partial H_a}{\partial Z};{\mathrm{\Upsilon }}_9(t_f)=0.$$ (31)

To obtain the optimality equations (21), (22), (23), (24), we first differentiate partially the Hamiltonian function H_a with respect to the controls (u₁, …, u₄) and then solve for $u_i^{\ast }$ (optimal control) by equating the derivatives to zero. Thus,

$$\frac{\partial H_a}{\partial u_1}{|}_{u_1^{\ast }}={\beta }_s({\mathrm{\Upsilon }}_2-{\mathrm{\Upsilon }}_3)S^{\ast }{H}^{\ast }+B_1{u}_1^{\ast }=0.$$ (32)

Making $u_1^{\ast }$ the subject of the formula in equation (32), we obtain

$$u_1^{\ast }(t)=\frac{{\beta }_s({\mathrm{\Upsilon }}_3-{\mathrm{\Upsilon }}_2)S^{\ast }{H}^{\ast }}{B_1}.$$ (33)

Application of the above procedure to the rest of the controls yields:

$$u_2^{\ast }=\frac{{\beta }_r({\mathrm{\Upsilon }}_5-{\mathrm{\Upsilon }}_4)R^{\ast }{M}^{\ast }}{(1+\alpha Z)B_2},u_3^{\ast }=\frac{{\mathrm{\Upsilon }}_8{G}^{\ast }+{\mathrm{\Upsilon }}_7{\mu }_{x}N{X}^{\ast }}{B_3},u_4^{\ast }=\frac{{\mathrm{\Upsilon }}_7{\mu }_c(1-\pi )P{C}^{\ast }}{(1+\alpha Z)B_4}.$$ (34)

$$u_1^{\ast }=\left\{\begin{array}{ll}0& \text{if }\frac{{\beta }_s({\mathrm{\Upsilon }}_3-{\mathrm{\Upsilon }}_2)S^{\ast }{H}^{\ast }}{B_1}\le 0,\\ \frac{{\beta }_s({\mathrm{\Upsilon }}_3-{\mathrm{\Upsilon }}_2)S^{\ast }{H}^{\ast }}{B_1}& \text{if }0<u_1<1,\\ 1& \text{if }\frac{{\beta }_s({\mathrm{\Upsilon }}_3-{\mathrm{\Upsilon }}_2)S^{\ast }{H}^{\ast }}{B_1}\ge 1.\end{array}\right)$$ (35)

The solution $u_1^{\ast }$ is therefore expressed as

$$u_1^{\ast }=\max \left\{\min \left\{\frac{{\beta }_s({\mathrm{\Upsilon }}_3-{\mathrm{\Upsilon }}_2)S^{\ast }{H}^{\ast }}{B_1},1\right\},0\right\}.$$ (36)

Similarly, the optimal solutions $u_2^{\ast }$, $u_3^{\ast }$ and $u_4^{\ast }$ are expressed as follows:

$$u_2^{\ast }=\max \left\{\min \left\{\frac{{\beta }_r({\mathrm{\Upsilon }}_5-{\mathrm{\Upsilon }}_4)R^{\ast }{M}^{\ast }}{(1+\alpha Z)B_2},1\right\},0\right\}$$ (37)

$$u_3^{\ast }=\max \left\{\min \left\{\frac{{\mathrm{\Upsilon }}_8{G}^{\ast }+{\mathrm{\Upsilon }}_7{\mu }_{x}N{X}^{\ast }}{B_3},1\right\},0\right\}$$ (38)

$$u_4^{\ast }=\max \left\{\min \left\{\frac{{\mathrm{\Upsilon }}_7{\mu }_c(1-\pi )P{C}^{\ast }}{(1+\alpha Z)B_4},1\right\},0\right\}.$$ (39)

Utilizing the characteristic functions in equations (21), (22), (23), (24), the following optimality system (40)–(41) characterizes the optimal control:

$$\left(\begin{array}{cc}\frac{\mathrm{d}S}{\mathrm{d}t}& =\mathrm{\Lambda }-{\mu }_{s}S-{\beta }_{s}SH,\\ \frac{\mathrm{d}H}{\mathrm{d}t}& ={\lambda }_h-{\mu }_{h}H-\left(1-\max \left\{\min \left\{\frac{{\beta }_s({\mathrm{\Upsilon }}_3-{\mathrm{\Upsilon }}_2)S^{\ast }{H}^{\ast }}{B_1},1\right\},0\right\}\right){\beta }_{s}SH,\\ \frac{\mathrm{d}X}{\mathrm{d}t}& =\left(1-\max \left\{\min \left\{\frac{{\beta }_s({\mathrm{\Upsilon }}_3-{\mathrm{\Upsilon }}_2)S^{\ast }{H}^{\ast }}{B_1},1\right\},0\right\}\right){\beta }_{s}SH-{\mu }_{x}X-\frac{k_{xZX}}{1+{ϵ}_{0}X},\\ \frac{\mathrm{d}R}{\mathrm{d}t}& ={\lambda }_r-\frac{\left(1-\max \left\{\min \left\{\frac{{\beta }_r({\mathrm{\Upsilon }}_5-{\mathrm{\Upsilon }}_4)R^{\ast }{M}^{\ast }}{(1+\alpha Z)B_2},1\right\},0\right\}\right){\beta }_{r}RM}{1+\alpha Z}-{\mu }_{r}R,\\ \frac{\mathrm{d}T}{\mathrm{d}t}& =\frac{\left(1-\max \left\{\min \left\{\frac{{\beta }_r({\mathrm{\Upsilon }}_5-{\mathrm{\Upsilon }}_4)R^{\ast }{M}^{\ast }}{(1+\alpha Z)B_2},1\right\},0\right\}\right){\beta }_{rRM}}{1+\alpha Z}-{\mu }_{t}T-\gamma T-\frac{k_{tZT}}{1+{ϵ}_{1}T},\\ \frac{\mathrm{d}C}{\mathrm{d}t}& =\gamma T-{\mu }_{c}C-\frac{k_{c}ZC}{1+{ϵ}_{2}C},\\ \frac{\mathrm{d}M}{\mathrm{d}t}& =\left(1-\max \left\{\min \left\{\frac{{\mathrm{\Upsilon }}_8{G}^{\ast }+{\mathrm{\Upsilon }}_7{\mu }_{x}N{X}^{\ast }}{B_3},1\right\},0\right\}\right)N{\mu }_{x}X\\ & +\frac{\left(1-\max \left\{\min \left\{\frac{{\mathrm{\Upsilon }}_7{\mu }_c(1-\pi )P{C}^{\ast }}{(1+\alpha Z)B_4},1\right\},0\right\}\right)P(1-\pi ){\mu }_{c}C}{1+\alpha Z}-{\mu }_{m}M-{\beta }_{r}RM,\\ \frac{\mathrm{d}G}{\mathrm{d}t}& =\pi {\mu }_{c}C-\left(\left(\max \left\{\min \left\{\frac{{\mathrm{\Upsilon }}_8{G}^{\ast }+{\mathrm{\Upsilon }}_7{\mu }_{x}N{X}^{\ast }}{B_3},1\right\},0\right\}\right)+{\mu }_g\right)G,\end{array}\right\}$$ (40)

$$\left(\begin{array}{cc}\frac{\mathrm{d}Z}{\mathrm{d}t}& ={\lambda }_z+Z\left(\frac{{\delta }_{x}X}{1+{ϵ}_{0}X}+\frac{{\delta }_{t}T}{1+{ϵ}_{1}T}+\frac{{\delta }_{c}C}{1+{ϵ}_{2}C}\right)-{\mu }_{Z}Z,\\ \frac{\mathrm{d}{\mathrm{\Upsilon }}_1}{\mathrm{d}t}& =({\mathrm{\Upsilon }}_2-{\mathrm{\Upsilon }}_3)\left(1-\max \left\{\min \left\{\frac{{\beta }_s({\mathrm{\Upsilon }}_3-{\mathrm{\Upsilon }}_2)S^{\ast }{H}^{\ast }}{B_1},1\right\},0\right\}\right){\beta }_{s}H+{\mathrm{\Upsilon }}_1({\mu }_s+{\beta }_{s}H),\\ \frac{\mathrm{d}{\mathrm{\Upsilon }}_2}{\mathrm{d}t}& =\left({\mathrm{\Upsilon }}_1+({\mathrm{\Upsilon }}_2-{\mathrm{\Upsilon }}_3)\left(1-\max \left\{\min \left\{\frac{{\beta }_s({\mathrm{\Upsilon }}_3-{\mathrm{\Upsilon }}_2)S^{\ast }{H}^{\ast }}{B_1},1\right\},0\right\}\right)\right){\beta }_s+{\mathrm{\Upsilon }}_2{\mu }_h,\\ \frac{\mathrm{d}{\mathrm{\Upsilon }}_3}{\mathrm{d}t}& =\frac{({\mathrm{\Upsilon }}_3{k}_x-{\mathrm{\Upsilon }}_9{\delta }_x)Z}{{(1+{\epsilon }_{0}X)}^2}-A_1+\left({\mathrm{\Upsilon }}_3-{\mathrm{\Upsilon }}_{7}N\left(1-\max \left\{\min \left\{\frac{{\mathrm{\Upsilon }}_8{G}^{\ast }+{\mathrm{\Upsilon }}_7{\mu }_{x}N{X}^{\ast }}{B_3},1\right\},0\right\}\right)\right){\mu }_x,\\ \frac{\mathrm{d}{\mathrm{\Upsilon }}_4}{\mathrm{d}t}& =\frac{{\beta }_r\left((1+\alpha Z){\mathrm{\Upsilon }}_7+\left(1-\max \left\{\min \left\{\frac{{\beta }_r({\mathrm{\Upsilon }}_5-{\mathrm{\Upsilon }}_4)R^{\ast }{M}^{\ast }}{(1+\alpha Z)B_2},1\right\},0\right\}\right)({\mathrm{\Upsilon }}_4-{\mathrm{\Upsilon }}_5)\right)M}{(1+\alpha Z)}+{\mathrm{\Upsilon }}_4{\mu }_r,\\ \frac{\mathrm{d}{\mathrm{\Upsilon }}_5}{\mathrm{d}t}& =\frac{({\mathrm{\Upsilon }}_5{k}_t-{\mathrm{\Upsilon }}_9{\delta }_t)Z}{{(1+{\epsilon }_{1}T)}^2}+{\mathrm{\Upsilon }}_5(\gamma +{\mu }_t)-(A_2+\gamma {\mathrm{\Upsilon }}_6),\\ \frac{\mathrm{d}{\mathrm{\Upsilon }}_6}{\mathrm{d}t}& ={\mathrm{\Upsilon }}_6\left(\frac{k_{c}Z}{{(1+{\epsilon }_{2}C)}^2}+{\mu }_c\right)-\frac{\left(1-\max \left\{\min \left\{\frac{{\mathrm{\Upsilon }}_7{\mu }_c(1-\pi )P{C}^{\ast }}{(1+\alpha Z)B_4},1\right\},0\right\}\right)(1-\pi )P{\mathrm{\Upsilon }}_7{\mu }_c}{(1+\alpha Z)}\\ & -\frac{{\mathrm{\Upsilon }}_9{\delta }_{c}Z}{(1+{\epsilon }_{2}C)}-\pi {\mathrm{\Upsilon }}_8{\mu }_c,\\ \frac{\mathrm{d}{\mathrm{\Upsilon }}_7}{\mathrm{d}t}& ={\mathrm{\Upsilon }}_7({\beta }_{r}R+{\mu }_m)-A_3+\frac{({\mathrm{\Upsilon }}_4-{\mathrm{\Upsilon }}_5)\left(1-\max \left\{\min \left\{\frac{{\beta }_r({\mathrm{\Upsilon }}_5-{\mathrm{\Upsilon }}_4)R^{\ast }{M}^{\ast }}{(1+\alpha Z)B_2},1\right\},0\right\}\right){\beta }_{r}R}{1+\alpha Z},\\ \frac{\mathrm{d}{\mathrm{\Upsilon }}_8}{\mathrm{d}t}& ={\mathrm{\Upsilon }}_8\left(\left(\max \left\{\min \left\{\frac{{\mathrm{\Upsilon }}_8{G}^{\ast }+{\mathrm{\Upsilon }}_7{\mu }_{x}N{X}^{\ast }}{B_3},1\right\},0\right\}\right)+{\mu }_g\right)-A_4,\\ \frac{\mathrm{d}{\mathrm{\Upsilon }}_9}{\mathrm{d}t}& =\frac{{\mathrm{\Upsilon }}_3{k}_{x}X}{1+{\epsilon }_{0}X}+\frac{{\mathrm{\Upsilon }}_6{k}_{c}C}{1+{\epsilon }_{2}C}-\frac{{\mathrm{\Upsilon }}_4\left(1-\max \left\{\min \left\{\frac{{\beta }_r({\mathrm{\Upsilon }}_5-{\mathrm{\Upsilon }}_4)R^{\ast }{M}^{\ast }}{(1+\alpha Z)B_2},1\right\},0\right\}\right)\alpha {\beta }_{rMR}}{{(1+\alpha Z)}^2}\\ & +\frac{{\mathrm{\Upsilon }}_7(1-\pi )P\left(1-\max \left\{\min \left\{\frac{{\mathrm{\Upsilon }}_7{\mu }_c(1-\pi )P{C}^{\ast }}{(1+\alpha Z)B_4},1\right\},0\right\}\right)\alpha {\mu }_{c}C}{{(1+\alpha Z)}^2}\\ & -{\mathrm{\Upsilon }}_9\left(\frac{{\delta }_{x}X}{1+{\epsilon }_{0}X}+\frac{{\delta }_{t}T}{1+{\epsilon }_{1}T}+\frac{{\delta }_{c}C}{1+{\epsilon }_{2}C}-{\mu }_z\right)\\ & +{\mathrm{\Upsilon }}_5\left(\frac{k_{t}T}{1+{\epsilon }_{1}T}+\frac{\left(1-\max \left\{\min \left\{\frac{{\beta }_r({\mathrm{\Upsilon }}_5-{\mathrm{\Upsilon }}_4)R^{\ast }{M}^{\ast }}{(1+\alpha Z)B_2},1\right\},0\right\}\right)\alpha \beta MR}{{(1+\alpha Z)}^2}\right),\end{array}\right\}$$ (41)

where ϒ_i(t_f) = 0, for i = 1, 2, 3, …, 9 and S(0) ≥ 0, H(0) > 0, X(0) ≥ 0, R(0) > 0, T(0) ≥ 0, C(0) ≥ 0, M(0) ≥ 0, G(0) ≥ 0, Z(0) > 0.

Appendix C. Proof of Theorem 6

Let (S, H, X, R, T, C, M, G, Z, ϒ₁, ϒ₂, ϒ₃, ϒ₄, ϒ₅, ϒ₆, ϒ₇, ϒ₈, ϒ₉) and $(\overline{X},\overline{H},\overline{S},\overline{R},\overline{T},\overline{C},\overline{M},\overline{G},\overline{Z},{\overline{\mathrm{\Upsilon }}}_1,{\overline{\mathrm{\Upsilon }}}_2,{\overline{\mathrm{\Upsilon }}}_3,{\overline{\mathrm{\Upsilon }}}_4,{\overline{\mathrm{\Upsilon }}}_5,{\overline{\mathrm{\Upsilon }}}_6,{\overline{\mathrm{\Upsilon }}}_7,{\overline{\mathrm{\Upsilon }}}_8,{\overline{\mathrm{\Upsilon }}}_9)$ be two different solutions of our optimality system (1) and (12). Suppose S = e^ϒtv₁, H = e^ϒtv₂, X = e^ϒtv₃, R = e^ϒtv₄, T = e^ϒtv₅, C = e^ϒtv₆, M = e^ϒtv₇, G = e^ϒtv₈, Z = e^ϒtv₉, ϒ₁ = e^−ϒtw₁, ϒ₂ = e^−ϒtw₂, ϒ₃ = e^−ϒtw₃, ϒ₄ = e^−ϒtw₄, ϒ₅ = e^−ϒtw₅, ϒ₆ = e^−ϒtw₆, ϒ₇ = e^−ϒtw₇, ϒ₈ = e^−ϒtw₈ and ϒ₉ = e^−ϒtw₉ . Similarly, let $\overline{S}=e^{\mathrm{\Upsilon }t}{\overline{v}}_1$, $\overline{H}=e^{\mathrm{\Upsilon }t}{\overline{v}}_2$, $\overline{X}=e^{\mathrm{\Upsilon }t}{\overline{v}}_3$, $\overline{R}=e^{\mathrm{\Upsilon }t}{\overline{v}}_4$, $\overline{T}=e^{\mathrm{\Upsilon }t}{\overline{v}}_5$, $\overline{C}=e^{\mathrm{\Upsilon }t}{\overline{v}}_6$, $\overline{M}=e^{\mathrm{\Upsilon }t}{\overline{v}}_7$, $\overline{G}=e^{\mathrm{\Upsilon }t}{\overline{v}}_8$, $\overline{Z}=e^{\mathrm{\Upsilon }t}{\overline{v}}_9$, ${\overline{\mathrm{\Upsilon }}}_1=e^{-\mathrm{\Upsilon }t}{\overline{w}}_1$, ${\overline{\mathrm{\Upsilon }}}_2=e^{-\mathrm{\Upsilon }t}{\overline{w}}_2$, ${\overline{\mathrm{\Upsilon }}}_3=e^{-\mathrm{\Upsilon }t}{\overline{w}}_3$, ${\overline{\mathrm{\Upsilon }}}_4=e^{-\mathrm{\Upsilon }t}{\overline{w}}_4$, ${\overline{\mathrm{\Upsilon }}}_5=e^{-\mathrm{\Upsilon }t}{\overline{w}}_5$, ${\overline{\mathrm{\Upsilon }}}_6=e^{-\mathrm{\Upsilon }t}{\overline{w}}_6$, ${\overline{\mathrm{\Upsilon }}}_7=e^{-\mathrm{\Upsilon }t}{\overline{w}}_7$, ${\overline{\mathrm{\Upsilon }}}_8=e^{-\mathrm{\Upsilon }t}{\overline{w}}_8$ and ${\overline{\mathrm{\Upsilon }}}_9=e^{-\mathrm{\Upsilon }t}{\overline{w}}_9$. Further, we let

$$\begin{array}{cc}& u_1^{\ast }(t)=\max \left\{\min \left\{({\beta }_s(w_3-w_2)v_1{v}_2{e}^{\mathrm{\Upsilon }t})/B_1,1\right\},0\right\},\\ & {\overline{u}}_1^{\ast }(t)=\max \left\{\min \left\{({\beta }_s({\overline{w}}_3-{\overline{w}}_2){\overline{v}}_1{\overline{v}}_2{e}^{\mathrm{\Upsilon }t})/B_1,1\right\},0\right\}\text{and}\end{array}$$

$$|u_1^{\ast }(t)-{\overline{u}}_1^{\ast }(t)|\le \frac{e^{\mathrm{\Upsilon }t}{\beta }_s}{B_1}\left|((w_3-w_2)v_1{v}_2-({\overline{w}}_3-{\overline{w}}_2){\overline{v}}_1{\overline{v}}_2)\right|;$$ (42)

$$\begin{array}{cc}& u_2^{\ast }(t)=\max \left\{\min \left\{\frac{{\beta }_r(w_5-w_4)v_5{v}_4{e}^{\mathrm{\Upsilon }t}}{(1+\alpha e^{\mathrm{\Upsilon }t}{v}_9)B_2},1\right\},0\right\},\\ & {\overline{u}}_2^{\ast }(t)=\max \left\{\min \left\{\frac{{\beta }_r({\overline{w}}_5-{\overline{w}}_4){\overline{v}}_5{\overline{v}}_4{e}^{\mathrm{\Upsilon }t}}{(1+\alpha e^{\mathrm{\Upsilon }t}{\overline{v}}_9)B_2},1\right\},0\right\}\text{and}\end{array}$$

$$|u_2^{\ast }(t)-{\overline{u}}_2^{\ast }(t)|\le \frac{e^{\mathrm{\Upsilon }t}{\beta }_r}{B_2}\left|\frac{(w_5-w_4)v_5{v}_4(1+\alpha e^{\mathrm{\Upsilon }t}{\overline{v}}_9)-({\overline{w}}_5-{\overline{w}}_4){\overline{v}}_5{\overline{v}}_4(1+\alpha e^{\mathrm{\Upsilon }t}{v}_9)}{(1+\alpha e^{\mathrm{\Upsilon }t}{v}_9)(1+\alpha e^{\mathrm{\Upsilon }t}{\overline{v}}_9)}\right|;$$ (43)

$$\begin{array}{cc}& u_3^{\ast }(t)=\max \left\{\min \left\{\frac{w_8{v}_8+w_7{v}_3{\mu }_{x}N}{B_3},1\right\},0\right\},\\ & {\overline{u}}_3^{\ast }(t)=\max \left\{\min \left\{\frac{{\overline{w}}_8{\overline{v}}_8+{\overline{w}}_7{\overline{v}}_3{\mu }_{x}N}{B_3},1\right\},0\right\}\end{array}$$

and

$$|u_3^{\ast }(t)-{\overline{u}}_3^{\ast }(t)|\le \frac{1}{B_3}|(w_8{v}_8-{\overline{w}}_8{\overline{v}}_8)+{\mu }_{x}N(w_7{v}_3-{\overline{w}}_7{\overline{v}}_3)|;$$ (44)

$$\begin{array}{cc}& u_4^{\ast }(t)=\max \left\{\min \left\{\frac{w_7{\mu }_c(1-\pi )P{v}_6}{(1+\alpha e^{\mathrm{\Upsilon }t}{v}_9)B_4},1\right\},0\right\},\\ & {\overline{u}}_4^{\ast }(t)=\max \left\{\min \left\{\frac{{\overline{w}}_7{\mu }_c(1-\pi )P{\overline{v}}_6}{(1+\alpha e^{\mathrm{\Upsilon }t}{\overline{v}}_9)B_4},1\right\},0\right\}\end{array}$$

and

$$|u_4^{\ast }(t)-{\overline{u}}_4^{\ast }(t)|\le \frac{{\mu }_c(1-\pi )P}{B_4}\left|\frac{w_7{v}_6(1+\alpha e^{\mathrm{\Upsilon }t}{\overline{v}}_9)-{\overline{w}}_7{\overline{v}}_6(1+\alpha e^{\mathrm{\Upsilon }t}{v}_9)}{(1+\alpha e^{\mathrm{\Upsilon }t}{v}_9)(1+\alpha e^{\mathrm{\Upsilon }t}{\overline{v}}_9)}\right|.$$ (45)

Substituting S = e^ϒtv₁ into the first equation of system (1), (dS/dt), the state equation becomes

$$e^{\mathrm{\Upsilon }t}({\dot{v}}_1+\mathrm{\Upsilon }{v}_1)=\mathrm{\Upsilon }-{\mu }_s{v}_1{e}^{\mathrm{\Upsilon }t}-{\beta }_s{v}_2{v}_1{e}^{2\lambda t}.$$ (46)

Similarly, substituting ϒ₁ = e^−ϒtw₁ into the first equation of system (18), (dϒ₁/dt), the adjoint equation becomes

$$e^{-\mathrm{\Upsilon }t}({\dot{w}}_1-\mathrm{\Upsilon }{w}_1)=(w_2-w_3)(1-u_1^{\ast }(t)){\beta }_s{v}_2+{\mu }_s{w}_1{e}^{-\mathrm{\Upsilon }t}+{\beta }_s{w}_1{v}_2.$$ (47)

Now, subtracting the equations for S and $\overline{S}$ in equation (46), ϒ₁ and ${\overline{\mathrm{\Upsilon }}}_1$ in equation (47) gives

$$\mathrm{\Upsilon }(v_1-{\overline{v}}_1)+({\dot{v}}_1-{\overline{\dot{v}}}_1)=-{\mu }_s(v_1-{\overline{v}}_1)-{\beta }_s{e}^{\mathrm{\Upsilon }t}(v_1{v}_2-{\overline{v}}_1{\overline{v}}_2)\text{and}$$ (48)

$$\mathrm{\Upsilon }(w_1-{\overline{w}}_1)+({\dot{w}}_1-{\overline{\dot{w}}}_1)=(1-u_1^{\ast }){\beta }_s{e}^{\mathrm{\Upsilon }t}\left\{v_2(w_2-w_3)-{\overline{v}}_2({\overline{w}}_2-{\overline{w}}_3)\right\}+{\mu }_s(w_1-w_1)+{\beta }_s{e}^{\mathrm{\Upsilon }t}(w_1{v}_2-{\overline{w}}_1{\overline{v}}_2).$$ (49)

Multiplying each equation by appropriate difference of functions ($(v_1-{\overline{v}}_1)$ and $(w_1-{\overline{w}}_1)$, respectively) and integrating from 0 to t_f yields (for the case of equation (48))

$$\frac{1}{2}{(v_1-{\overline{v}}_1)}^2+\mathrm{\Upsilon }{\int }_0^{t_f}{(v_1-{\overline{v}}_1)}^{2}dt=-{\mu }_s{\int }_0^{t_f}{(v_1-{\overline{v}}_1)}^{2}dt-{\beta }_s{e}^{\mathrm{\Upsilon }t}{\int }_0^{t_f}(v_1{v}_2-{\overline{v}}_1{\overline{v}}_2)(v_1-{\overline{v}}_1)dt.$$ (50)

Applying the above procedure on the rest of the state and adjoint variables, we obtain

$$\frac{1}{2}{(v_2-{\overline{v}}_2)}^2+\mathrm{\Upsilon }{\int }_0^{t_f}{(v_2-{\overline{v}}_2)}^{2}dt=-{\mu }_h{\int }_0^{t_f}{(v_2-{\overline{v}}_2)}^{2}dt-{\beta }_s{\int }_0^{t_f}(1-u_1^{\ast })(v_1{v}_2-{\overline{v}}_1{\overline{v}}_2)(v_2-{\overline{v}}_2)e^{\mathrm{\Upsilon }t}dt,$$ (51)

$$\frac{1}{2}{(v_3-{\overline{v}}_3)}^2+\mathrm{\Upsilon }{\int }_0^{t_f}{(v_3-{\overline{v}}_3)}^{2}dt=-{\mu }_x{\int }_0^{t_f}{(v_3-{\overline{v}}_3)}^{2}dt+{\beta }_s{\int }_0^{t_f}(1-u_1^{\ast })(v_1{v}_2-{\overline{v}}_1{\overline{v}}_2)(v_3-{\overline{v}}_3)e^{\mathrm{\Upsilon }t}dt-k_x{\int }_0^{t_f}\left(\frac{v_3{v}_9}{1+{\epsilon }_0{e}^{\mathrm{\Upsilon }t}{v}_3}-\frac{{\overline{v}}_3{\overline{v}}_9}{1+{\epsilon }_0{e}^{\mathrm{\Upsilon }t}{\overline{v}}_3}\right)(v_3-{\overline{v}}_3)e^{\mathrm{\Upsilon }t}dt,$$ (52)

$$\frac{1}{2}{(v_4-{\overline{v}}_4)}^2+\mathrm{\Upsilon }{\int }_0^{t_f}{(v_4-{\overline{v}}_4)}^{2}dt=-{\beta }_r{\int }_0^{t_f}(1-u_2^{\ast })\left(\frac{v_4{v}_7}{1+\alpha e^{\mathrm{\Upsilon }t}{v}_9}-\frac{{\overline{v}}_4{\overline{v}}_7}{1+\alpha e^{\mathrm{\Upsilon }t}{\overline{v}}_9}\right)(v_4-{\overline{v}}_4)e^{\mathrm{\Upsilon }t}dt-{\mu }_r{\int }_0^{t_f}{(v_4-{\overline{v}}_4)}^{2}dt,$$ (53)

$$\frac{1}{2}{(v_5-{\overline{v}}_5)}^2+\mathrm{\Upsilon }{\int }_0^{t_f}{(v_5-{\overline{v}}_5)}^{2}dt={\beta }_r{\int }_0^{t_f}(1-u_2^{\ast })\left(\frac{v_4{v}_7}{1+\alpha e^{\mathrm{\Upsilon }t}{v}_9}-\frac{{\overline{v}}_4{\overline{v}}_7}{1+\alpha e^{\mathrm{\Upsilon }t}{\overline{v}}_9}\right)(v_5-{\overline{v}}_5)e^{\mathrm{\Upsilon }t}dt-k_t{\int }_0^{t_f}\left(\frac{v_5{v}_9}{1+{\epsilon }_1{e}^{\mathrm{\Upsilon }t}{v}_5}-\frac{{\overline{v}}_5{\overline{v}}_9}{1+{\epsilon }_1{e}^{\mathrm{\Upsilon }t}{\overline{v}}_5}\right)(v_5-{\overline{v}}_5)e^{\mathrm{\Upsilon }t}dt-({\mu }_t+\gamma ){\int }_0^{t_f}{(v_5-{\overline{v}}_5)}^{2}dt,$$ (54)

$$\frac{1}{2}{(v_6-{\overline{v}}_6)}^2+\mathrm{\Upsilon }{\int }_0^{t_f}{(v_6-{\overline{v}}_6)}^{2}dt=\gamma {\int }_0^{t_f}(v_5-{\overline{v}}_5)(v_6-{\overline{v}}_6)dt-{\mu }_c{\int }_0^{t_f}{(v_6-{\overline{v}}_6)}^{2}dt-k_c{\int }_0^{t_f}\left(\frac{v_6{v}_9}{1+{\epsilon }_2{e}^{\mathrm{\Upsilon }t}{v}_6}-\frac{{\overline{v}}_6{\overline{v}}_9}{1+{\epsilon }_2{e}^{\mathrm{\Upsilon }t}{\overline{v}}_6}\right)(v_6-{\overline{v}}_6)e^{\mathrm{\Upsilon }t}dt,$$ (55)

$$\frac{1}{2}{(v_7-{\overline{v}}_7)}^2+\mathrm{\Upsilon }{\int }_0^{t_f}{(v_7-{\overline{v}}_7)}^{2}dt={\mu }_{x}N{\int }_0^{t_f}(1-u_3^{\ast })(v_3-{\overline{v}}_3)(v_7-{\overline{v}}_7)dt-(1-\pi )P{\mu }_c{\int }_0^{t_f}(1-u_4^{\ast })\left(\frac{v_6}{1+\alpha e^{\mathrm{\Upsilon }t}{v}_9}-\frac{{\overline{v}}_6}{1+\alpha e^{\mathrm{\Upsilon }t}{\overline{v}}_9}\right)(v_7-{\overline{v}}_7)dt-{\mu }_m{\int }_0^{t_f}(v_7-{\overline{v}}_7)dt-{\beta }_r{\int }_0^{t_f}(v_4{v}_7-{\overline{v}}_4{\overline{v}}_7)(v_7-{\overline{v}}_7)dt,$$ (56)

$$\frac{1}{2}{(v_8-{\overline{v}}_8)}^2+\mathrm{\Upsilon }{\int }_0^{t_f}{(v_8-{\overline{v}}_8)}^{2}dt=\pi {\mu }_c{\int }_0^{t_f}(v_6-{\overline{v}}_6)(v_8-{\overline{v}}_8)dt-{\int }_0^{t_f}(u_3^{\ast }-{\mu }_g){(v_8-{\overline{v}}_8)}^{2}dt,$$ (57)

$$\frac{1}{2}{(v_9-{\overline{v}}_9)}^2+\mathrm{\Upsilon }{\int }_0^{t_f}{(v_9-{\overline{v}}_9)}^{2}dt={\delta }_x{\int }_0^{t_f}\left(\frac{v_3}{1+{\epsilon }_0{e}^{\mathrm{\Upsilon }t}{v}_3}-\frac{{\overline{v}}_3}{1+{\epsilon }_0{e}^{\mathrm{\Upsilon }t}{\overline{v}}_3}\right)(v_9-{\overline{v}}_9)e^{\mathrm{\Upsilon }t}dt{\delta }_t{\int }_0^{t_f}\left(\frac{v_5}{1+{\epsilon }_1{e}^{\mathrm{\Upsilon }t}{v}_5}-\frac{{\overline{v}}_5}{1+{\epsilon }_1{e}^{\mathrm{\Upsilon }t}{\overline{v}}_5}\right)(v_9-{\overline{v}}_9)e^{\mathrm{\Upsilon }t}dt{\delta }_c{\int }_0^{t_f}\left(\frac{v_6}{1+{\epsilon }_2{e}^{\mathrm{\Upsilon }t}{v}_6}-\frac{{\overline{v}}_6}{1+{\epsilon }_2{e}^{\mathrm{\Upsilon }t}{\overline{v}}_6}\right)(v_9-{\overline{v}}_9)e^{\mathrm{\Upsilon }t}dt-{\mu }_z{\int }_0^{t_f}{(v_9-{\overline{v}}_9)}^{2}dt.$$ (58)

Note that

$$(i)k_x{\int }_0^{t_f}\left(\frac{v_3{v}_9}{1+{\epsilon }_0{e}^{\mathrm{\Upsilon }t}{v}_3}-\frac{{\overline{v}}_3{\overline{v}}_9}{1+{\epsilon }_0{e}^{\mathrm{\Upsilon }t}{\overline{v}}_3}\right)(v_3-{\overline{v}}_3)e^{\mathrm{\Upsilon }t}dt=k_x{\int }_0^{t_f}\left(\frac{v_3{v}_9-{\overline{v}}_3{\overline{v}}_9}{(1+{\epsilon }_0{e}^{\mathrm{\Upsilon }t}{v}_3)\left(1+{\epsilon }_0{e}^{\mathrm{\Upsilon }t}{\overline{v}}_3\right)}\right)(v_3-{\overline{v}}_3)e^{\mathrm{\Upsilon }t}dt+{\epsilon }_0{k}_x{\int }_0^{t_f}\left(\frac{v_3{v}_9{\overline{v}}_3-{\overline{v}}_3{\overline{v}}_9{v}_3}{(1+{\epsilon }_0{e}^{\mathrm{\Upsilon }t}{v}_3)\left(1+{\epsilon }_0{e}^{\mathrm{\Upsilon }t}{\overline{v}}_3\right)}\right)(v_3-{\overline{v}}_3)e^{2\mathrm{\Upsilon }t}dt\le (C_1{e}^{\mathrm{\Upsilon }{t}_f}+C_2{e}^{2\mathrm{\Upsilon }{t}_f}){\int }_0^{t_f}[{(v_3-{\overline{v}}_3)}^2+{(v_9-{\overline{v}}_9)}^2]dt$$ (59)

and

$$(ii){\beta }_s{\int }_0^{t_f}(1-u^{\ast })(v_1{v}_2-{\overline{v}}_1{\overline{v}}_2)(v_3-{\overline{v}}_3)dt\le C_3{e}^{\mathrm{\Upsilon }{t}_f}{\int }_0^{t_f}[{(v_1-{\overline{v}}_1)}^2+{(v_2-{\overline{v}}_2)}^2+{(v_3-{\overline{v}}_3)}^2]dt.$$ (60)

Upon combining the integrals in equations (50), (51), (52), (53), (54), (55), (56), (57), (58) gives

$$\begin{array}{cc}& \frac{1}{2}{(v_1-{\overline{v}}_1)}^2(t_f)+\frac{1}{2}{(v_2-{\overline{v}}_2)}^2(t_f)+\frac{1}{2}{(v_3-{\overline{v}}_3)}^2(t_f)+\frac{1}{2}{(v_4-{\overline{v}}_4)}^2(t_f)+\frac{1}{2}{(v_5-{\overline{v}}_5)}^2(t_f)\\ & +\frac{1}{2}{(v_6-{\overline{v}}_6)}^2(t_f)+\frac{1}{2}{(v_7-{\overline{v}}_7)}^2(t_f)+\frac{1}{2}{(v_8-{\overline{v}}_8)}^2(t_f)+\frac{1}{2}{(v_9-{\overline{v}}_9)}^2(t_f)\\ & +\frac{1}{2}{(w_1-{\overline{w}}_1)}^2(0)+\frac{1}{2}{(w_2-{\overline{w}}_2)}^2(0)+\frac{1}{2}{(w_3-{\overline{w}}_3)}^2(0)+\frac{1}{2}{(w_4-{\overline{w}}_4)}^2(0)\\ & +\frac{1}{2}{(w_5-{\overline{w}}_5)}^2(0)+\frac{1}{2}{(w_6-{\overline{w}}_6)}^2(0)+\frac{1}{2}{(w_7-{\overline{w}}_7)}^2(0)+\frac{1}{2}{(w_8-{\overline{w}}_8)}^2(0)\\ & +\frac{1}{2}{(w_9-{\overline{w}}_9)}^2(0)+\mathrm{\Upsilon }{\int }_0^{t_f}\left[{(v_1-v_1)}^2+{(v_2-v_2)}^2+{(v_3-v_3)}^2+{(v_4-v_4)}^2\right)\\ & +{(v_5-v_5)}^2+{(v_6-v_6)}^2+{(v_7-v_7)}^2+{(v_8-v_8)}^2+{(v_9-v_9)}^2+{(w_1-w_1)}^2\\ & +{(w_2-w_2)}^2+{(w_3-w_3)}^2+{(w_4-w_4)}^2+{(w_5-w_5)}^2+{(w_6-w_6)}^2\\ & \left(+{(w_7-w_7)}^2+{(w_8-w_8)}^2+{(w_9-w_9)}^2\right]\mathrm{d}t\end{array}$$ (61)

$$\le (\mathrm{\Upsilon }-{\overline{D}}_1-{\overline{D}}_2{e}^{3\mathrm{\Upsilon }{t}_f})\times \left\{{\int }_0^{t_f}\left[{(v_1-v_1)}^2+{(v_2-v_2)}^2+{(v_3-v_3)}^2+{(v_4-v_4)}^2+{(v_5-v_5)}^2+{(v_6-v_6)}^2\right)\right)\left(+{(v_7-v_7)}^2+{(v_8-v_8)}^2+{(v_9-v_9)}^2\right]+{\int }_0^{t_f}\left[{(w_1-w_1)}^2+{(w_2-w_2)}^2\right)+{(w_3-w_3)}^2+{(w_4-w_4)}^2+{(w_5-w_5)}^2+{(w_6-w_6)}^2+{(w_7-w_7)}^2\left(\left(+{(w_8-w_8)}^2+{(w_9-w_9)}^2\right]\right\},$$ (62)

where ${\overline{D}}_1$ and ${\overline{D}}_2$ depend on the coefficients and the bounds of v_i and w_i, i = 1, …, 9. If ϒ is chosen such that $\mathrm{\Upsilon }>{\overline{D}}_1+{\overline{D}}_2$ and $t_f<\frac{1}{3\mathrm{\Upsilon }}\ln \left(\frac{\mathrm{\Upsilon }-{\overline{D}}_1}{{\overline{D}}_2}\right)$, then $v_1={\overline{v}}_1$, $v_2={\overline{v}}_2$, $v_3={\overline{v}}_3$, $v_4={\overline{v}}_4$, $v_5={\overline{v}}_5$, $v_6={\overline{v}}_6$, $v_7={\overline{v}}_7$, $v_8={\overline{v}}_8$, $v_9={\overline{v}}_9$, $w_1={\overline{w}}_1$, $w_2={\overline{w}}_2$, $w_3={\overline{w}}_3$, $w_4={\overline{w}}_4$, $w_5={\overline{w}}_5$, $w_6={\overline{w}}_6$, $w_7={\overline{w}}_7$, $w_8={\overline{w}}_8$, $w_9={\overline{w}}_9$. This shows that the solution to the optimality system (1) and (12) is unique.