Fast and Accurate Craniomaxillofacial Landmark Detection via 3D Faster R-CNN

Abstract

Automatic craniomaxillofacial (CMF) landmark localization from cone-beam computed tomography (CBCT) images is challenging, considering that 1) the number of landmarks in the images may change due to varying deformities and traumatic defects, and 2) the CBCT images used in clinical practice are typically large. In this paper, we propose a two-stage, coarse-to-fine deep learning method to tackle these challenges with both speed and accuracy in mind. Specifically, we first use a 3D faster R-CNN to roughly locate landmarks in down-sampled CBCT images that have varying numbers of landmarks. By converting the landmark point detection problem to a generic object detection problem, our 3D faster R-CNN is formulated to detect virtual, fixed-size objects in small boxes with centers indicating the approximate locations of the landmarks. Based on the rough landmark locations, we then crop 3D patches from the high-resolution images and send them to a multi-scale UNet for the regression of heatmaps, from which the refined landmark locations are finally derived. We evaluated the proposed approach by detecting up to 18 landmarks on a real clinical dataset of CMF CBCT images with various conditions. Experiments show that our approach achieves state-of-the-art accuracy of 0.89±0.64mm in an average time of 26.2 seconds per volume.

I. Introduction

Craniomaxillofacial (CMF) deformities include congenital and developmental deformities of the CMF region, such as jaws, face and skull [1], [2]. Digitization (detection and localization) of CMF landmarks is an essential step for accurate deformity quantification and precise surgical planning. Cone-beam computed tomography (CBCT) is routinely used for the diagnosis and surgical planning of CMF deformities, mainly due to its lower radiation and cost in comparison with multi-slice computed tomography (MSCT). However, digitizing landmarks with CBCT images is very challenging, considering the significant noise, severe imaging artifacts (e.g., inhomogeneity and truncation), large inter-subject variation in image appearance, and large image size with hundreds of millions of voxels per image. In clinical practice, landmark digitization is still performed manually, which is time-consuming, error-prone, experience dependent, and susceptible to intra- and inter-observer variability. Therefore, robust algorithms to automate landmark digitization are highly desirable by clinicians.

Conventional landmark detection methods for medical images can be categorized as based on anatomical knowledge [3]-[5], image atlases [6], [7], statistical shape models (SSMs) [8]-[10], and random forest (RF) [11]-[15]. Anatomical knowledge-based methods leverage the geometrical properties of human body parts (e.g., skull and vertebrae symmetry) to locate landmarks. These methods, however, do not work well in cases with abnormalities [4]. Atlas-based [6], [7] and SSM-based [8]-[10] methods usually non-rigidly align template image(s) to target images, achieving relatively good results when object shapes and appearances are similar. However, non-rigid registration is computationally intensive and very sensitive to large shape variations and imaging artifacts [2]. RF-based methods [11]-[14], [16] have been reported to achieve promising accuracy, but they rely heavily on the quality of hand-crafted features and thus require significant feature engineering expertise.

Recently, motivated by the successes of deep learning in the field of medical image analysis, methods based on convolutional neural networks (CNNs) [2], [17]-[20] and deep reinforcement learning (DRL) [21]-[23] have been proposed for landmark detection. Existing CNN-based methods typically formulate landmark detection as a heatmap/coordinate regression problem [17], [19] or voxel-wise classification problem [18]. As 3D medical images (e.g., CMF CBCT) are often too large to fit into the memory of a typical graphical processing unit (GPU), these CNN-based methods are usually implemented in a patch-based fashion, requiring inefficient dense sampling of local patches from an image for inference. However, due to the limited field-of-view, such patch-based implementation may yield considerable false detections. A special case of CNN-based methods is proposed in [20], where an iterative framework is employed to directly regress the coordinates of multiple landmarks. Although efficient, its detection accuracy is hampered by (i) inevitable information loss caused by the 2.5D representation of 3D images, and (ii) high sensitivity to the initialization of potential landmark locations. In summary, existing CNN-based methods are either inefficient during inference or lacking in accuracy, greatly hindering their application in clinical settings.

In contrast to CNN-based methods, DRL-based methods [21], [22] work by allowing intelligent agents to move step-by-step towards the target landmarks. However, the performance of these methods is sensitive to the initial landmark positions, which are often randomly selected in the image space. Moreover, to maximize detection accuracy, a separate model often needs to be trained for each landmark [22]. Recent years have seen some progress towards detecting multiple landmarks jointly using multi-agent DRL [23]. However, due to the high computational complexity of multi-agent systems, the number of landmarks that can be handled simultaneously is still very limited.

In addition to the category-specific limitations, existing methods for automated landmark detection share a common limitation in terms of practical usage. That is, they typically assume that different subjects have the same number and types of landmarks. However, this is not the case in reality due to variations associated with patients (e.g., incomplete CMF bones due to trauma), imaging hardware, and acquisition protocols.

In this paper, we propose a novel coarse-to-fine method to efficiently and accurately detect a varying number of CMF landmarks simultaneously in CBCT images. Our method leverages the benefits of a region-based object detector and a CNN for heatmap regression. In the first stage, approximate landmark locations are predicted by following the generic object detection paradigm proposed in [24]. In the second stage, landmark positions are refined via heatmap regression.

Using generic object detection paradigm as the first step allows us to elegantly handle the challenging scenario where the number of landmarks varies across images. To adapt a generic object detection algorithm for landmark detection, we propose to regard landmarks as virtual, fixed-size objects and represent each landmark by a bounding box. Detecting landmarks is hence equivalent to detecting these virtual objects. Since our aim is to detect landmarks in 3D medical images, a 3D extension of the faster R-CNN framework is proposed here in this paper. However, due to GPU memory constraints, 3D faster R-CNN can only work on down-sampled images and as a result can only predict approximate locations of the landmarks. Therefore, we adopt a lightweight multi-scale UNet (MS-UNet) in the second step for location refinement in the high-resolution image space via heatmap regression. Compared with direct heatmap regression, our method is remarkably more efficient, since location estimation in the first step significantly reduces the search space.

In summary, our contributions are as follows:

1. We propose a coarse-to-fine deep learning method for anatomical landmark detection, combining a 3D faster R-CNN and a lightweight variant of 3D UNet. For landmark detection, we regard the landmarks as fixed-size, virtual objects associated with tight bounding boxes. To work on 3D medical images, we extend the original 2D faster R-CNN to 3D by redesigning the architecture. Also, we integrate a 3D ROI-Align operation [25] into our 3D faster R-CNN to obviate the misalignment issue caused by the ROI pooling operations used in the original 2D faster R-CNN.

2. In contrast to existing methods, our method can deal with the situation where the number of landmarks varies across subjects.

3. We evaluated our method on a challenging CBCT dataset for detecting up to 18 major landmarks. The experiments show that our method achieves better performance than state-of-the-art methods in terms of accuracy.

The rest of the paper is organized as follows. We review related work in Section II, flesh out the details of our method in Section III, report method comparison results in Section IV, and conclude in Section V.

II. Related Work

A. Landmark Detection

1). Knowledge-based approaches:

Anatomical knowledge-based methods [3]-[5] take advantage of the bilateral symmetry of the human body to locate landmarks, for example, in the skull [3], humerus [4] and spine [5]. However, the symmetry assumption does not necessarily hold in abnormal cases.

2). Atlas-based approaches:

Atlas-based methods [6], [7] rigidly or non-rigidly align atlases annotated with landmarks with target images. In practice, their detection accuracy is affected by inaccurate inter-subject registration [11]. Most of these methods are limited by the assumption that strict correspondences exist between the atlas and the target images [26]. This assumption is often violated due to anatomical abnormalities (e.g., missing teeth) and poor image quality (e.g., noise and imaging artifacts). Moreover, non-rigid image registration is time-consuming due to the high computational cost.

3). SSM-based approaches:

SSM-based methods [8]-[10] model the shape mean and variance of an object of interest. Modeling shape statistics requires a set of training shapes with well-defined correspondences usually established via image registration. Therefore, SSM-based methods suffer the same drawbacks as atlas-based methods.

4). RF approaches:

Random forest (RF) is a popular machine learning-based method for anatomical landmark detection in medical images of different modalities [12]-[16]. Although effective, they require hand-crafted features, designing of which is non-trivial and requires domain knowledge.

5). CNN approaches:

Recently, CNN-based methods have achieved great success in landmark detection due to their ability to learn representative, task-oriented features. They can be broadly categorized as based on regression [2], [17], [19], [20], [27] and classification [18], [28].

Most CNN-based approaches formulate landmark detection as a regression problem, including (i) landmark heatmap regression [17], [19], [27] and (ii) landmark coordinate regression [20] in the image space, with the exception of [2], which works in the shape space and regresses geodesic distance maps instead. Using a heatmap, which encodes the likelihood of a voxel/pixel of being a specific landmark, as the target, landmark heatmap regression methods [19], [27] achieve state-of-the-art performance. However, it is unstable when dealing with high-resolution images and is inefficient at inference time due to its reliance on dense sampling of patches. Li et al. [20], proposed a multi-task learning framework to simultaneously locate multiple landmarks in an iterative fashion. This method is very efficient as it only needs to sample a small number of patches during inference but at the cost of much lower accuracy compared with methods based on heatmap regression.

Classification-based methods are also used for landmark detection. For example, Zheng et al. [18] proposed a two-step classification method, in which a shallow network is used to obtain multiple candidates and then a deeper network is used to reduce false positives. Although this method achieves relatively good accuracy, it is inefficient due to the need for voxel-wise classification. Liu et al. [28] formulated landmark detection as segmentation of the local neighborhood of a landmark. A pyramid non-local module is employed to exploit high-level contextual information for better performance. Although effective for 2D images, it is challenging to incorporate non-local modules into neural networks for volumetric data because of memory limitation.

Although existing CNN-based approaches have achieved great success, they are either inaccurate or inefficient, hindering their applications in practice. In addition, they assume that all subjects have the same number and types of landmarks and thus do not generalize well to more practical and complicated scenarios where the assumption is violated.

6). DRL approaches:

Benefitting from both deep learning and reinforcement learning, several DRL methods have been recently proposed for landmark detection. For example, Ghesu et al. [21] introduced an artificial agent that learns to navigate in the image space with fixed-step actions and finds the optimal path from any initial location to the target position to maximize the expected cumulative rewards. In [29], Ghesu et al. extended this approach to exploit multi-scale image representations for better localization. Following [21], [29], Vlontzos et al. [23] proposed a multi-agent system to jointly detect multiple landmarks.

Generally, DRL-based methods have the advantage of being more efficient than most CNN-based methods, as they only need to take a small amount of samples along the search path during inference. However, DRL-based methods often cannot handle more than a few landmarks (e.g., more than 4) simultaneously even with multi-agent systems, since each landmark needs an independent agent, consisting of several fully connected layers, to learn a distinct policy. In addition, our empirical observation is that the detection accuracy tends to degrade when the number of landmarks that need to be detected simultaneously is increased.

B. Object Detection

For generic object detection, the goal is to locate and classify objects in images or videos. Most modern generic object detection frameworks can be broadly divided into two categories: 1) single-stage detectors [30]-[32] and 2) two-stage detectors [24], [25], [33], [34]. Two-stage detectors include a proposal generation stage while single-stage detectors do not. Generally, single-stage detectors are more efficient but two-stage detectors are more accurate.

Our work is highly related to faster R-CNN [24], which is for generic object detection. The first stage of our method shares exactly the same pipeline as faster R-CNN, that is, class-agnostic proposals are first generated and then classified and regressed to the target. However, unlike faster R-CNN, which only works for generic object detection in 2D images, our method is capable of handling 3D volumetric data and, more importantly, is able to deal with the challenging problem of landmark point detection.

Our work also shares some similarities with [35], [36]. Xu et al. [35] proposed a 3D RPN to generate organ-specific proposals to locate multiple organs. However, the method cannot generalize well because it relies on the unrealistic assumption that at most one instance of each organ exists in an image. Liu et al. [36] proposed a method conceptually similar to ours by converting the detection of a landmark to the detection of the local neighborhood patch of the landmark in 2D X-ray images. However, unlike ours, their method is based on a direct adoption of faster R-CNN [37] without taking into account the misalignment issue caused by ROI pooling and the detection of landmarks near image boundaries. More importantly, their method is not designed for detecting a varying number of landmarks.

In this work, we generalize box-wise generic object detection to point-wise landmark detection by regarding landmarks as virtual, fixed-size objects with the aim of detecting a varying number of landmarks in volumetric medical images. This distinguishes the proposed method from all previous methods for object/landmark detection in both natural and medical images.

III. Methods

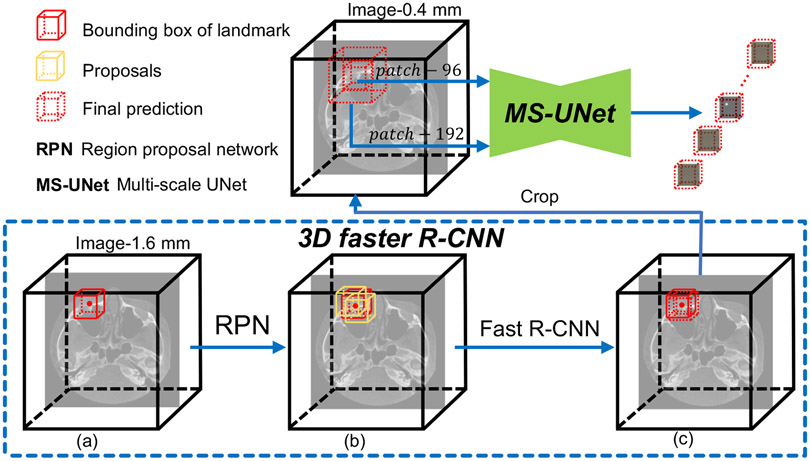
Overall, our method comprises two main steps: 1) landmark location estimation using a 3D faster R-CNN and 2) landmark location refinement using a MS-UNet. The schematic diagram of our method is shown in Fig. 1. In the first step, by denoting landmarks as fixed-size virtual objects, the landmark detection task is formulated as a combination of fixed-size object classification and bounding box regression problems. Multiple class-agnostic candidate regions (i.e., location proposals) are first generated by a RPN. Then, each proposal is consumed by the 3D fast R-CNN to predict its unique class label (i.e., it is associated with a unique landmark) and its offsets to the respective ground-truth box. In the second step, refined landmark locations are determined by the heatmaps generated by the MS-UNet, which is trained using high-resolution images.

Fig. 1:

The proposed landmark detection pipeline. A 3D faster R-CNN is used for landmark location approximation and a MS-UNet is used for landmark location refinement. 3D faster R-CNN works on down-sampled images (1.6 × 1.6 × 1.6 mm³) and consists of two main steps: 1) proposal generation (a→b) via a RPN and 2) proposal classification and regression (b→c) via the Fast R-CNN. The approximate landmark locations are refined based on the heatmaps predicted by the MS-UNet, which is trained using high-resolution images (0.4 × 0.4 × 0.4 mm³).

A. 3D Faster R-CNN

The 3D faster R-CNN unifies a backbone, a 3D RPN and a 3D fast R-CNN for end-to-end training. The backbone acts as the feature extractor and feature maps at multiple levels form a feature pyramid with rich semantics. Based on the feature pyramid, 3D RPN is used to identify a number of class-agnostic proposals (regions where landmarks are located with high probability) from pre-defined anchors (described in detail in Anchors). Next, the proposals are propagated to 3D fast R-CNN where each proposal is further classified into different classes. That is, each proposal is associated with a specific landmark. The 3D fast R-CNN includes an interpolation layer (i.e., ROI-Align) at the very beginning to crop and resize the feature maps confined within each proposal to a fixed size. The resized feature maps are used as inputs to the 3D fast R-CNN to make proposal-specific predictions. In the following, we first describe the definition and usage of anchors and ROI-Align, which are prerequisites for understanding the training details. Then, we present the implementation and training details of the main components of our 3D faster R-CNN, i.e., the backbone, RPN, and fast R-CNN.

Considering that direct processing of high-resolution volumes is computationally infeasible even for modern GPUs, our 3D faster R-CNN works on down-sampled images to predict approximate landmark locations. We re-sample the original images to a uniform spatial resolution of 1.6 × 1.6 × 1.6 mm³, and fix the maximum spatial size of down-sampled images to 112 × 144 × 144. Note that the training images may be zero-padded or randomly cropped before being fed to the neural network, depending on their original sizes. To deal with the practical challenges that different subjects may have varying numbers of landmarks and only limited training data are available, we combine data augmentation methods, such as random cropping and random erasing, to simulate samples with different conditions during training.

a). Anchors:

Anchors are some pre-defined boxes distributed over the input volumes. They serve as candidate bounding boxes for the objects to be detected. Recall that we formulate the point-wise landmark detection problem as a box-wise classification and regression problem, representing each landmark by a cubic fixed-size box. It is natural to choose only one aspect ratio (i.e., 1 : 1 : 1) and one size, matching the ground-truth bounding boxes, for the definition of anchors for our landmark detection task. The choice of the size of the ground-truth bounding boxes is tricky considering two contradicting aspects. On the one hand, the size should be large enough to include enough contextual information for anchor classification and regression. An ROI that is too small may not contain sufficient contextual information and thus leads to mediocre performance. On the other hand, the size of the ground-truth bounding box should ensure reasonable uniqueness and discriminability in landmark representation. For example, a bounding box that encloses all landmarks is clearly not representative of any specific landmark. Empirically, we set the size of ground-truth bounding boxes to be 24 × 24 × 24 according to the two requirements above. To handle the situation that some landmarks could be close to the image boundary, we symmetrically zero-pad all sides of the image region. The final spatial size of the input volumes is 136 × 168 × 168.

b). ROI-Align:

Translating the ROI into fixed-length feature vectors is necessary since proposals may have very different sizes and aspect ratios. In the original faster R-CNN framework, ROI pooling is used for this purpose. However, this approach causes misalignment [25] due to round-off errors associated with coordinates of proposal corners and ROI subdivision. To better locate landmarks, following [25], we replace ROI pooling with ROI-Align in our 3D faster R-CNN implementation. The ROI alignment operation implemented in this paper works directly on 3D images, unlike the original 2D version [25]. Integer quantization is avoided via trilinear interpolation based on the values at the 8 corners of a cell.

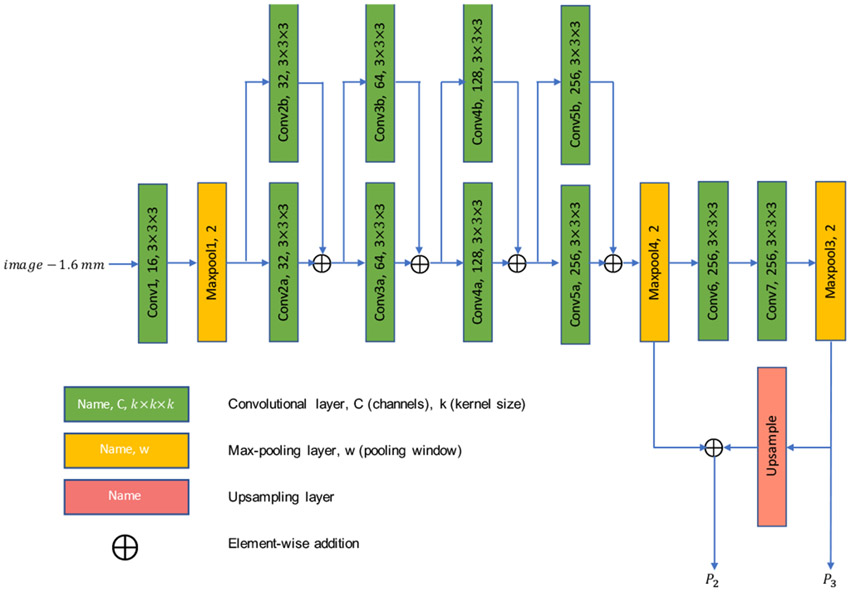
c). Backbone:

The backbone is a feature extractor that learns discriminative features from the input volumes for subsequent classification and regression tasks. Deeper and wider backbones are believed to play an important role in object detection. However, since 3D operations consume significantly larger memory than their 2D counterparts, 3D faster R-CNN cannot be as deep and wide as its 2D counterpart. Therefore, in this work, a backbone is designed specifically for our 3D faster R-CNN. As illustrated in Fig. 2, the backbone is composed of three stages (layers of the same spatial size belong to the same stage) separated by max-pooling layers. Stage 1 consists of only one convolutional layer to reduce memory consumption. Stage 2 has the most number of layers and consists of 4 residual blocks [39]. Stage 3 is designed to enlarge the receptive field.

Fig. 2:

Architecture of the backbone of the 3D faster R-CNN. Batch normalization [38] layer in non-trainable mode and rectified linear unit (ReLU) activation layer are added after each convolutional layer.

Following [33], we adopted a feature pyramid network (FPN, consisting of P₂ and P₃) as a part of the backbone of our 3D faster R-CNN. Note that we do not include the output of the first max pooling layer into the design of FPN, considering that (i) the first max pooling layer is too shallow, and thus its receptive field is too small and the discriminative power of the respective features is limited, and (ii) the number of anchors can be cut down significantly as anchors are actually built on the feature pyramid, greatly reducing the difficulties of the subsequent (positive anchor vs. negative anchor) classification and regression problems.

d). RPN Training & Inference:

The RPN is a small network shared by the feature maps in the feature pyramid. Similar to [24], [33], the RPN takes as input a 3 × 3 × 3 window of the input feature map and each sliding window is mapped to a lower-dimensional feature (we choose 256 as the dimensionality). This feature is then fed into two sibling fully-connected layers for anchor classification and offsets regression, respectively. Finally, the outputs (i.e., classification output and regression output) from the two different feature maps in the feature pyramid are concatenated.

To train the RPN, we assign a binary class label to each anchor. Specifically, we assign a positive label to two kinds of anchors: (i) the ones with the highest Intersection-over-Union (IoU) value with a ground-truth box, and (ii) the ones that have an IoU value higher than 0.5 with any ground-truth box. We assign a negative label to anchors that have IoU values lower than 0.3 with all ground-truth boxes. Anchors that are neither positive nor negative are called neutral anchors and do not contribute to objective classification loss. In addition to the classification of anchors, the offsets from positive anchors to their corresponding ground-truth boxes are also estimated via regression. The correspondence is established by calculating and comparing the IoU values of each positive anchor with all the ground-truth boxes, and the ground-truth box with which a positive anchor has the largest IoU value is associated with that positive anchor. When a tie occurs, the ground-truth box with the smallest class index is associated with the positive anchor. Only positive anchors contribute to the regression loss. The regression target is a triplet for each positive anchor, representing the offsets from the center of the positive anchor to the center of its associated ground-truth box in the three spatial dimensions. During the whole training process, we sample 256 anchors at each iteration and control the ratio between positive anchors and negative anchors to be (roughly) 1 : 1.

To generate proposals for the next stage, we first select the top 6, 000 anchors in terms of the objectness score, which basically represents the probability of an anchor being a positive anchor, and apply the corresponding predicted offsets on them. Note that the offsets are applied to the center of anchors and that the raw proposals all have an equal size of 24 × 24 × 24. The bounding box limits of each raw proposal are computed by using the coordinates of the center and the pre-defined, fixed size for anchors. Proposals are then clipped at the boundary. Finally, we screen out redundant proposals by using non-maximum suppression operation. We use 0.7 as the IoU threshold when generating the final proposals. The maximum number of proposals generated for the next stage during training is set to 1, 200.

During inference, proposal generation is basically identical to the training phase, except that for efficiency only at most 600 proposals are propagated to the next stage.

Even though we have controlled the ratio of positive and negative anchors for classification during training, either positive anchors or negative anchors can still dominate in the computation of classification loss in some cases. To better balance the contributions of the different kinds of anchors, we adopt the class-balanced categorical cross-entropy loss for classification. That is, we first calculate the mean loss values for positive anchors and negative anchors separately and then calculate the mean of the means. For regressing the offsets, we use the mean absolute error as our objective function.

e). Fast R-CNN Training & Inference:

Fast R-CNN is a shared network for all proposals. To train the fast R-CNN, we further assign a binary class label to the proposals generated from the first stage. A positive label is assigned to proposals that have IoU values no less than 0.5 with any ground-truth boxes, whereas a negative label is assigned to those that have IoU values less than 0.5 with all ground-truth boxes. We then sample 120 proposals from them and control the ratio between positive proposals and negative proposals to be (roughly) 1 : 1. We assign label 0 to negative proposals and nonzero class labels (e.g., 1 to N, where N is the total number of landmarks) to positive proposals. Associating proposals with ground-truth boxes is done similarly as associating anchors with ground-truth boxes in the training of the RPN. At the same time, the offsets from the positive proposals to their corresponding ground-truth boxes are calculated as the regression target. Similar to RPN training, the regression target represents the offsets from the center of each positive proposal to the center of its corresponding ground-truth box. For each proposal, we use ROI-Align, instead of ROI pooling used in [24], [33], [37], to resize the ROI to fixed spatial extent of 5 × 5 × 5. We then use a convolutional layer with 1, 024 channels and kernel size of 5 × 5 × 5 to reduce the spatial size of feature maps to 1 × 1 × 1. This convolutional layer is followed by another convolutional layer with 1, 024 channels and kernel size of 1 × 1 × 1 to fully connect all pairs of neurons. Finally, two task specific branches with fully connected layers are used to assign to each proposal a class label (classification subnet) and regress the offsets to its ground-truth box (regression subnet), respectively. The loss functions used for proposal classification and regression are the same as those used in RPN training.

In the inference phase, ROI-Align is first applied to each proposal generated from the RPN, and then Fast R-CNN performs classification and regression in sequence for the proposals. The final predictions are given by performing non-maximum suppression for each class (i.e., landmark) separately.

B. Multi-Scale UNet

Landmarks located at symmetrical locations in medical images (e.g., craniomaxillofacial landmarks in CBCT images) usually have similar local structures. Therefore, it is difficult to differentiate them without leveraging contextual information. We found that using a single-scale patch, which covers limited region in image space, is often insufficient to capture enough contextual information to differentiate similar-looking, symmetrically-located landmarks, especially when they are far apart and/or the image resolution is too high. To deal with this challenging problem, we design a multi-scale variant of UNet [41] at the second stage of our coarse-to-fine framework for accurate landmark localization. The detailed design of MS-UNet is shown in Fig. 3. There are two inputs for MS-UNet: 1) a local patch with the size of 96 × 96 × 96 and 2) a global patch with the size of 192 × 192 × 192. The spatial size of the two patches is mismatched, therefore, we reduce the spatial size of the global patch by a down-sampling factor of 2 using a convolutional layer with the kernel size of 5 and stride of 2 while leave the size of the local patch unchanged using a convolutional layer with the kernel size of 3 and unit stride. In this way, the mismatch in the spatial sizes of the two patches is properly addressed in the feature space, and the resulting feature maps are concatenated across channels and then fed into a variant of UNet for landmark heatmap regression. The last layer of MS-UNet is a convolutional layer with 18 channels, each of which is a predicted heatmap for a specific landmark (i.e., 18 landmarks in total).

Fig. 3:

Architecture of the MS-UNet. All convolutional layers except the last one are followed by instance normalization [40] and ReLU activation.

Note that in the training phase of MS-UNet, only image patches randomly cropped from a small neighborhood of the landmarks are used. In our case, the center of image patches is confined to a region of size 64 × 64 × 64 centered around a specific landmark. That is, we do not use image patches that do not contain any landmarks in training phase. This is because we found that, in this way, the difficulty of the regression problem can be greatly reduced because the network avoids learning from regions that do not contain any landmarks, and therefore the neural network converges faster. We use mean absolute error as the loss function to train the MS-UNet.

C. Inference Procedure

Three steps are involved during inference to obtain precise landmark locations:

1. Feed the down-sampled images into the 3D faster R-CNN and obtain the corresponding class labels and approximate locations of landmarks.

2. Map the derived approximate landmark locations in the down-sampled images to their corresponding high-resolution images.

3. Repeat a), b), and c) for each landmark in each image:

   1. Crop a local patch and a global patch from the high-resolution image with the approximate landmark location (rounded down to the nearest integer) as the common patch center, and then forward them to the MS-UNet to obtain the corresponding heatmaps.
   2. Find the coordinates of the maximum in the heatmap corresponding to the right class label. For example, when the class label shows that the landmark class is #5, just return the location of the maximum in the 5th heatmap patch.
   3. Compute the relative offsets from the maximum in the patch to the position of the center voxel of the heatmap, and then add the offsets to the rounded approximate landmark location to get the final, refined landmark location.

D. Implementation Details

Keras with TensorFlow backend was adopted to implement the proposed method for landmark detection. To train 3D faster R-CNN, we adopted the Stochastic Gradient Descent (SGD) optimizer with momentum 0.9 and weight decay 0.0001. We applied gradient clipping when the gradient norm exceeds 5.0. The convolutional kernels were initialized by the He algorithm [42] and bias terms were initialized as 0. We used the constant learning rate of 0.0005 throughout the whole training process. For MS-UNet training, the Adam algorithm [43] was used as the optimizer. Parameters β₁ and β₂ of the optimizer were set to be 0.9 and 0.999, respectively. The initialization of trainable parameters were the same as the 3D faster R-CNN part. We trained the MS-UNet for 160, 000 steps. The initial learning rate was set to be 0.005 and reduced to 0.002, 0.001, 0.0001, 5e-5 at step 8, 000, 30, 000, 80, 000 and 120, 000, respectively. Batch size was set to 1 in both coarse and fine steps.

IV. Experimental Results

A. Dataset

We evaluated our method using 80 sets of CBCT images that are randomly selected from our clinical digital archive. All the images were acquired from patients with CMF deformities (e.g., jaw deformities, post-traumatic defects and congenital deformities). Personal information was removed. Landmarks were manually digitized by experienced CMF surgeons using AnatomicAligner [44] and the ground truth label is determined via consensus voting. The resolutions of the images varied from 0.3 × 0.3 × 0.3 mm³ to 0.4 × 0.4 × 0.4 mm³ and the intensity range varied from −999 to 20, 000. We normalized the voxel size of the images to 0.4 × 0.4 × 0.4 mm³ and image intensity to the range of [0, 1]. This study was approved by Institutional Review Board (#Pro0009723).

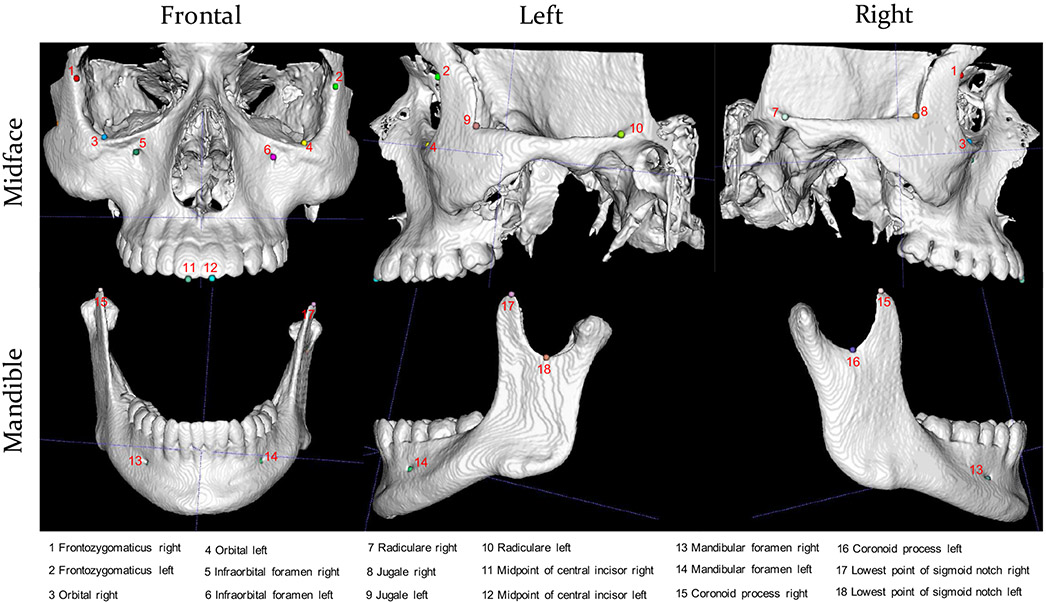
To demonstrate the efficacy of our method, we apply it to jointly detect 18 landmarks with indexes and definitions shown in Fig. 4. It is worth noting that the proposed method can be easily generalized to more landmarks.

Fig. 4:

Skull bones and landmarks. 12 landmarks are on midface and 6 on mandible.

B. Evaluation Metrics

The performance of the algorithms is evaluated from two aspects: localization accuracy and time efficiency. To evaluate localization accuracy, we use the mean value and standard deviation of the Euclidean distances (in millimeter) between the predicted locations and the ground-truth locations of the landmarks. We report the number of failure cases of each method. Following [17], the network is regarded as unsuccessful in predicting a landmark when the distance between the predicted location and the ground-truth location is larger than 10 mm and/or it is a false prediction (false positive and false negative). A false positive (FP) is a landmark that does not exist but is predicted to exist whereas a false negative (FN) is a landmark that exists but is not predicted. For time efficiency evaluation, we report the average processing time (in second) that is needed to get the final output. The time cost is measured on a machine with 64GB RAM, Intel i7 CPU, and GeForce GTX 1080Ti GPU.

C. Competing Methods

To demonstrate the efficacy of our method, we compare it with three deep learning methods: 1) patch-based iterative method (Iterative) [20], 2) deep reinforcement learning method (DQN) [23] and 3) patch-based heatmap regression method (HM). Since no source code is publicly available for the third method, we use the MS-UNet. Notably, in contrast to previous heatmap regression methods that use single-scale patches, the MS-UNet is a more powerful baseline method that takes multi-scale patches as input for more detailed contextual information. We adapt the officially released source code of Iterative [20] and DQN [23] to detect 18 craniomaxillofacial landmarks, without any changes to the default settings except that, in DQN, we split the 18 landmarks into 6 groups and detect 3 landmarks at a time while the default is 2. When training the MS-UNet alone for landmark detection, we use the same way as done in the second step of the proposed method except that samples are randomly taken from the entire high-resolution image space.

D. Experimental Settings

As mentioned in Section I, our method can deal with a varying number of landmarks while the competing methods are not designed with this in mind. For fair comparison, we used a subset of the data with the full 18 landmarks for evaluating the proposed method in comparison with the competing methods. Additional evaluation of the proposed method was performed using images with missing landmarks. For clarity, we report the results from these two different sets of images separately.

Of the 80 images in our dataset, 60 images have all 18 landmarks. When comparing different methods, we randomly split these 60 images into 3 folds and use 3-fold cross validation to evaluate the different methods. When evaluating our method on the entire dataset, we randomly split the entire dataset into 4 folds and use 4-fold cross validation to evaluate the method.

E. Results

a). Comparison with Competing Methods:

The results of different methods on a subset of the CBCT dataset are shown in Table I. We assess all the methods in terms of 1) the number of failure cases (Failure cases), 2) localization accuracy (Accuracy), and 3) inference time (Time). It can be seen that the patch-based iterative method [20] is the most efficient method, being able to detect 18 landmarks in less than 1 second, but has the most failure cases and the worst localization accuracy. DQN [23] achieves better balance between localization accuracy and inference time, with accuracy 2.18 ± 1.48 mm and average inference time 13.5 seconds per image. However, it is worth noting that the actual time efficiency is overestimated. This is because DQN is not robust to the initial seed positions of landmarks and therefore needs to run multiple times (e.g., 10) from different initial positions and takes the average of the predictions from different trials as the final predictions. Therefore, the actual time required is often about an order of magnitude longer. Heatmap regression is a popular method for landmark detection due to its robustness and accuracy. As shown in Table I, the MS-UNet achieves an average accuracy of 1.31 ± 0.78 mm, which is significantly better than Iterative and DQN. However, compared with the proposed coarse-to-fine method (i.e., 3D faster R-CNN + MS-UNet), which achieves an average accuracy of 0.79 ± 0.62 mm, the MS-UNet still shows significantly inferior performance. Moreover, even for a strong baseline method like the MS-UNet, there are still 78 failure cases in the prediction, while our method only has 14 failure cases. One possible reason is that, limited by the discriminative capability of the neural networks, heatmap regression becomes very difficult when a large number of landmarks (e.g., 18) are considered simultaneously and when the image resolution is too high. Furthermore, compared with our method, the MS-UNet takes much longer time to obtain the predictions.

TABLE I:

Method comparison on the images with the complete 18 landmarks, quantified in terms of the number of failure cases, localization accuracy (mean±standard deviation), and average processing time. Failure cases are not taken into account when calculating the accuracy.

	Failure cases	Accuracy (mm)	Time
Iterative [20]	216	6.48 ± 2.89	0.78 second
DQN [23]	56	2.18 ± 1.48	13.5 seconds
HM	78	1.31 ± 0.78	8.3 min
3D faster RCNN	14	2.55 ± 1.40	16.4 seconds
3D faster RCNN + MS-Unet (Proposed)	14	0.79 ± 0.62	26.6 seconds

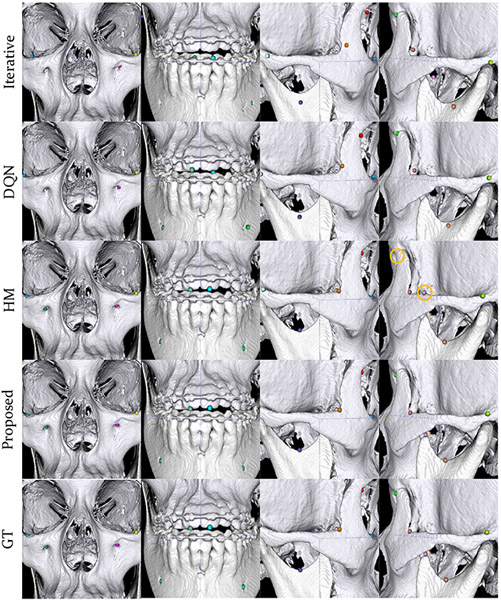
A typical example is shown in Fig. 5 for qualitative comparison. It is clear that the proposed method yields significantly better landmark localization accuracy. In this example, no false predictions occur for Iterative, DQN and the proposed method. In contrast, HM results in two false predictions.

Fig. 5:

Predictions given by our method, the patch-based iterative method (Iterative), DQN, the patch-based heatmap regression method (HM) in comparison with the ground truth (GT) on a case with full landmarks. Landmarks marked by yellow circles are false detection or misdetections. Different landmarks are differentiated by color.

b). Evaluation on Subjects with Varying Numbers of Landmarks:

The results on the entire dataset with varying numbers of landmarks are shown in Table II. We quantitatively evaluated the performance of the proposed method in terms of 1) the mean (Mean) and standard deviation (Std) of the distances between the ground-truth and predicted locations, 2) number of false negatives (FNs) and number of false positives (FPs) and 3) average processing time. Overall, our method achieves an average localization accuracy of 2.34 ± 1.31 mm and 0.89 ± 0.64 mm at the first and second stage, respectively. There are 11 FPs and 20 FNs in the prediction, the total of which takes up about 2.30% of the total number of landmarks. The average processing times to obtain the intermediate results in the first step and the final results in the second step are 15.8 seconds and 26.2 seconds, respectively.

TABLE II:

Intermediate results given by the 3D faster R-CNN and final results after refinement using the MS-UNet on the CBCT dataset, quantified using 4-fold cross validation in terms of detection accuracy (mean±standard deviation), number of FPs and FNs, and average processing time. FPs and FNs are not taken into account when calculating the accuracy.

Method	Accuracy (mm)	#FPs/#FNs	Time
3D faster R-CNN	2.34 ± 1.31	11/20	15.8 seconds
3D faster R-CNN + MS-UNet	0.89 ± 0.64	11/20	26.2 seconds

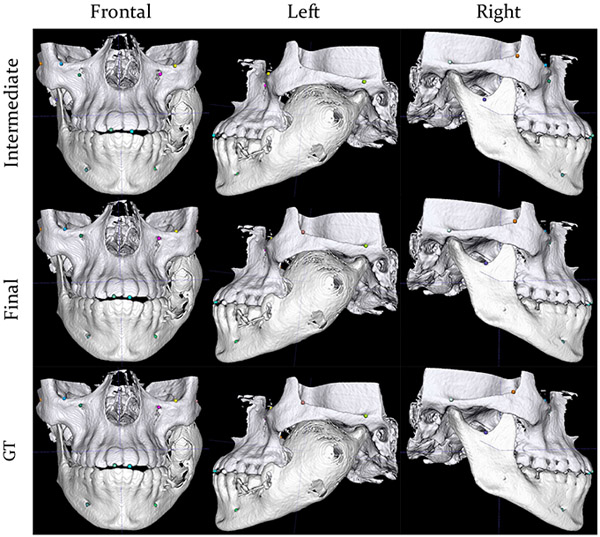
The mean localization accuracy for each landmark are shown in Table III, indicating that the proposed method works fine on all landmarks. The mean localization accuracy lies within the range of 0.75 – 1.15 mm (about 2 – 3 voxels) and standard deviation within the range of 0.28 – 1.08 mm (about 1 – 3 voxels). Results of a patient with incomplete landmarks are shown in Fig. 6 for qualitative assessment.

TABLE III:

Landmark localization accuracy computed in millimeter (mm) in the physical space. Note that not all cases have the full 18 landmarks. FPs and FNs are not taken into account when calculating the mean and standard deviation.

Landmark ID	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
Mean (mm)	1.15	1.12	0.97	0.87	0.90	0.79	0.79	0.75	0.82	0.76	0.77	0.85	0.94	0.79	0.86	1.05	0.88	0.96
Std (mm)	1.08	0.93	0.93	0.40	1.14	0.33	0.40	0.66	0.80	0.53	0.28	0.67	0.30	0.48	0.41	0.54	0.32	0.49

Fig. 6:

Predictions of our method in comparison with the ground truth on a subject with missing landmarks due to a smaller acquisition field of view and jaw deformity. The 1st row shows the intermediate predictions from 3D faster R-CNN with a down-sampled image as input. The intermediate predictions have been mapped to the high-resolution image space. The 2nd row shows the final predictions after landmark location refinement using the MS-UNet. The 3rd row shows the ground-truth locations of the landmarks. Different landmarks are differentiated by color.

F. Ablation Study

We performed experiments by using different anchor size and loss functions to validate our choices described in Section III.

a). Effects of Anchor Size:

We tried anchor sizes 16 and 24 for 3D faster R-CNN. Smaller anchors may result in proposals that may not contain sufficient contextual information for accurate classification and regression. Larger anchors increase memory requirements.

As shown in Table IV, anchor size 16 or 24 has limited effect on the performance. The mean detection accuracy decreases by only 0.04 mm and the number of FPs and FNs increase slightly by 1 and 2, respectively.

TABLE IV:

Effects of anchor size on the performance of 3D faster R-CNN. FPs and FNs are not taken into account when calculating the mean and standard deviation.

Anchor size	Accuracy (mm)	#FPs/#FNs
16	2.38 ± 1.17	12/22
24	2.34 ± 1.31	11/20

b). Effects of Loss Functions:

We compared the class-balanced categorical cross-entropy loss (class-balanced CE) and the naïve categorical cross-entropy loss (naïve CE) as the classification loss. We also compared the mean absolute error (MAE) and the mean squared error (MSE) as the regression loss. When studying the classification loss, we fixed MAE as the regression loss. When studying the regression loss, we fixed class-balanced CE as the classification loss. All hyper-parameters, including anchor size, were fixed.

We can see from Table V that the classification and regression losses have limited effects on the overall accuracy and the number of FPs, but may significantly affect the number of FNs. When naïve CE is used as the classification loss, the number of FNs increases from 20 to 65. Compared with the classification loss, the choice of regression loss has less negative effects on the FNs (increases from 20 to 32). These observations suggest that balanced CE is critical for the performance whereas the choice of regression loss is less important.

TABLE V:

Effects of loss functions on the performance of 3D faster R-CNN. FPs and FNs are not taken into account when calculating the mean and standard deviation.

	Classification Loss		Regression Loss
	naïve CE	class-balanced CE	MSE	MAE
Accuracy (mm)	2.31 ± 1.14	2.34 ± 1.31	2.35 ± 1.22	2.34 ± 1.31
#FPs/#FNs	13/65	11/20	9/32	11/20

G. Discussion

Among the methods listed in Table I, our method yields the best balance between landmark localization accuracy and time efficiency. The high accuracy is largely due to two reasons. First, landmark location estimation is done by taking the global context into account. Second, focusing on localized regions, instead of learning from the entire image, greatly alleviates the difficulties of heatmap regression in high-resolution images. Our method also has good time efficiency, which is attributable to 3D faster R-CNN in the first stage, since only a small number of samples around the approximate landmark locations are needed during inference in the second stage.

V. Conclusions

In this paper, we present a novel, coarse-to-fine method for automated anatomical landmark detection. Our method estimates and refines the location of a landmark by using a 3D faster R-CNN and a 3D MS-UNet, respectively. We formulate the landmark detection problem as a box-wise object detection problem by treating landmarks as virtual, fixed-size objects centered around the landmark locations for coarse predictions. Refined landmark locations are then obtained via heatmap regression. We demonstrate that our method achieves state-of-the-art performance in efficiently localizing a varying number of CMF landmarks on a CBCT dataset. In future, we will explore the application of our method to other imaging modalities, such as ultrasound and magnetic resonance imaging, for localization of dense landmarks.