Single-photon peak event detection (SPEED): a computational method for fast photon counting in fluorescence lifetime imaging microscopy

Abstract

Fluorescence lifetime imaging microscopy (FLIM) characterizes samples by examining the temporal properties of fluorescence emission, providing useful contrast within samples based on the local physical and biochemical environment of fluorophores. Despite this, FLIM applications have been limited in scope by either poor accuracy or long acquisition times. Here, we present a method for computational single-photon counting of directly sampled time-domain FLIM data that is capable of accurate fluorescence lifetime and intensity measurements while acquiring over 160 Mega-counts-per-second with sub-nanosecond time resolution between consecutive photon counts. We demonstrate that our novel method of Single-photon PEak Event Detection (SPEED) is more accurate than direct pulse sampling and faster than established photon counting FLIM methods. We further show that SPEED can be implemented for imaging and quantifying samples that benefit from higher -throughput and -dynamic range imaging with real-time GPU-accelerated processing and use this capability to examine the NAD(P)H-related metabolic dynamics of apoptosis in human breast cancer cells. Computational methods for photon counting such as SPEED open up more opportunities for fast and accurate FLIM imaging and additionally provide a basis for future innovation into alternative FLIM techniques.

1. Introduction

Fluorescence lifetime imaging microscopy (FLIM) was developed in 1993 as a method to examine spatial differences in time-dependent fluorescence emission properties [1]. After absorption, the electron of a fluorescent molecule remains in the excited state for a period of time before returning to the ground state through radiative decay, resulting in the emission of a photon, or through nonradiative decay [2]. The probability distribution of the period of time in the excited state before photon emission follows an exponential decay, and the mean time between excitation and emission is termed the fluorescence lifetime. With enough emitted photons collected, the distribution of photon emission vs. time can be reconstructed for each pixel within an image, and for each pixel the fluorescence lifetime can be estimated. FLIM is often performed with laser-scanning confocal and two-photon microscopy setups, which sequentially excite a focal spot within the sample and collect data for each pixel serially using a single detector. Two-photon absorption has a smaller excitation volume, which allows for less photobleaching, improved depth sectioning, and high spatial resolution, and also enables deeper imaging by using longer excitation wavelengths, making it attractive for FLIM [3]. Furthermore, two-photon FLIM can be simultaneously multiplexed with other nonlinear optical imaging modalities such as harmonic generation [4–6].

Presently, the most common and most accurate FLIM techniques rely on photon counting using analog electronics; generally a detector such as a photomultiplier tube (PMT) is used in conjunction with a constant fraction discriminator (CFD) in order to distinguish the arrival of each photon at the detector. Due to statistical uncertainty introduced during secondary emission at each dynode, PMTs produce a distribution of output amplitudes in response to the arrival of a single photon at the detector [7], and a CFD identifies when the PMT output amplitude has crossed a threshold, defining that as a photon count. If two photons arrive with very little time (on the single ns scale) in between, the PMT signal may not fall to the CFD trigger threshold between photon arrivals, and the second photon arrival will not be counted. The time that a system takes to recover between consecutive photon arrivals is termed the “dead time” and is the main factor limiting acquisition speed for photon counting microscopy systems. Time-correlated single-photon counting (TCSPC) is the gold standard for FLIM acquisition and detection. TCSPC uses analog electronics to time-tag each single photon incident on the detector, commonly a PMT or hybrid photodetector (HPD). However, in addition to the analog photon counting electronics, the time-tagging electronics of TCSPC generally experience a dead time of 10-100 ns after photon arrival, during which additional incident photons cannot be counted [8,9]. For this reason, the photon rate (number of photons incident on the detector per each excitation pulse, typically represented as a percentage) must be low enough that a significant number of photons do not arrive during the dead time, which would result in severely undercounting photons and bias the fluorescence decay curve. To prevent this, the photon rate acceptable in TCSPC has generally been limited to 5-10% or less [8,10,11]. This limitation on the maximum acceptable photon rate is the restricting factor for many key imaging parameters, such as the dynamic range of photon counts that can be collected within a given acquisition time and the maximum frame rate for accurate fluorescence lifetime estimation. Alternatively, to increase the throughput of FLIM systems, single-photon avalanche diode (SPAD) arrays have recently gained interest since they can collect and time-tag photons simultaneously with many parallel channels [12]. SPAD arrays have previously been cited as suffering from relatively lower quantum efficiency (due to low fill factor) and high dark counts [12,13], though recent advancements have shown that high quantum efficiency SPAD arrays are possible [14]. SPAD arrays can be used for time-gated [15] and photon-counting [16] FLIM, though the dead time of single SPAD array pixels in photon-counting mode is often in the range of 10-100 ns, similar to that of a photon-counting PMT [12].

This limitation on acceptable photon rate for photon counting fluorescence microscopy systems has motivated recent innovations aiming to lower the dead time of photon counting and time-tagging electronics, such as the implementation of time-to-digital converter (TDC)- and FPGA- based approaches [17–19]. TDCs greatly lower the electronic dead time of TCSPC systems, and have been implemented in custom FLIM systems with dead times as low as 5.5 ns [17], and commercial systems with dead times as low as 0.650 ns [20,21], enabling maximum count rates of up to 80 Mega-counts-per-second (Mcps). In digital frequency-domain (DFD) FLIM, the dead time is only determined by the detector and CFD, and all counted photons are analyzed by an FPGA, which adds no additional electronic dead time [18,19]. This enables dead times as low as 1.5625 ns and maximum count rates up to 15 Mcps [19]. While these approaches enable higher acquisition capacity, they are still fundamentally limited by the dead time of CFD, which requires the detector output signal to fall to a certain level between consecutive photon arrivals in order to resolve discrete photon arrivals. Other techniques have been employed for photon counting using fast digitization methods with different filters and thresholding. For example, the Leica SP8 FALCON system uses 10 GHz digitization to achieve 80 Mcps with a single detector and up to 225 Mcps with two detectors [22]. Furthermore, thresholding to detect the rising edge of PMT output with digitization at 3.6 GHz has been used for fast stimulated emission depletion (STED) microscopy [23] and digital deconvolution filtering with linear discriminant analysis has also been used to discriminate single photon counts from digitized data, and was specifically used for removing ringing distortions created by impedance mismatch in raw data [24]. While these methods provide improved utility, there is room for improvement for creating customizable, fast, and accurate photon counting for FLIM to broaden the scope of possible applications, especially those that are time-sensitive and/or have a high dynamic range.

Various systems have demonstrated FLIM acquisition via direct pulse sampling, in which the output of the PMT or HPD is amplified and directly sampled by a fast (> 1 GHz) digitizer, thus avoiding any electronic dead time due to photon counting and time-tagging electronics [25–31]. These systems suffer from reduced accuracy due to their lack of single photon precision and relatively long (> 1 ns [25,26]) system impulse response functions (IRFs) which obscure lower fluorescence lifetimes and limit the temporal resolution of the collected fluorescence decays. Previous direct pulse sampling systems have relied on the expectation of collecting multiple fluorescent photons per excitation pulse [27–29]. However, when imaging fluorophores that have a low quantum yield, such as NAD(P)H [11], with 80 MHz two-photon excitation, this assumption may no longer hold, and the maximum number of incident photons on the detector after each excitation pulse may decrease to around one or two; a photon rate of 100-200%. These measurements are also limited by the maximum power that can be incident on biological samples without inducing photodamage.

We have determined that under these conditions, computational methods can be applied to the amplified and directly sampled PMT output to count incident photons. Here, we present a technique we have termed computational single-photon counting that is more accurate than direct pulse sampling and has a shorter dead time than systems that use analog electronics for photon counting, enabling faster imaging. Our hardware is similar to our previously demonstrated direct pulse sampling system [25], however here we employ computational single-photon counting via our Single-photon PEak Event Detection (SPEED) algorithm to discriminate photon counts from single-photon responses from the PMT. We compare the accuracy, precision, and utility of SPEED to computational CFD and our previous direct pulse sampling method, demonstrate the capability of SPEED to accurately calculate the fluorescence lifetime of samples producing photon rates up to 200% (a count rate of 160 Mcps with 80 MHz laser excitation), and employ real-time GPU-accelerated processing to accurately and conveniently characterize the rapid dynamics of apoptosis in a cell culture model and image a variety of biological tissues.

2. Materials and methods

2.1. System design

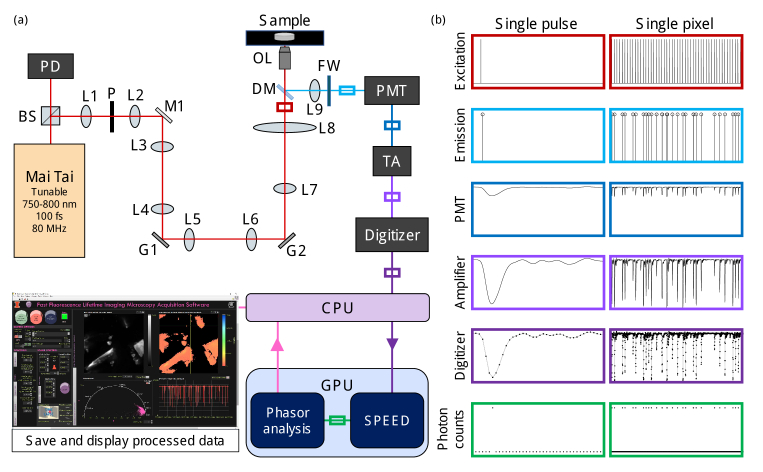
The hardware of our system (Fig. 1(a)) is similar to previous setups [4,25]. Briefly, we use a tunable 80 MHz mode-locked Ti:Sapphire laser (Mai Tai HP, Spectra-Physics) as our source for two-photon excitation; tuned to 750 nm for NAD(P)H excitation. The 80 MHz laser signal is measured by a photodiode (PD, Thorlabs), downsampled to 10 MHz, and used to synchronize the acquisition and scanning electronics [4]. Two galvanometer mirrors (G1, G2, Cambridge Technology) are used for beam scanning. A 1.05 NA objective lens (OL, XLPLN25XWMP2, Olympus) is used to deliver the excitation beam and to collect fluorescence emission. The emitted fluorescence is directed through a bandpass filter, mounted in a filter wheel (FW), incident on the PMT (H10721-210, Hamamatsu), amplified with a transimpedance amplifier (TA, C5594, Hamamatsu), and directly digitized by a 12-bit, 3.2 GHz digitizer (ATS9373, AlazarTech). The PMT was supplied with a control voltage of +1.0 V to achieve optimal pulse linearity, according to manufacturer specifications. Digitized data is streamed from the random-access memory of the computer to the graphics processing unit (GPU, GeForce RTX 2080, NVIDIA), where we implement our SPEED algorithm to count photons and create a single fluorescence decay curve for each pixel (Fig. S1). From this decay curve, phasor components g and s are computed, along with the mean fluorescence lifetime, for each pixel via phasor analysis [32]. Phasor analysis provides fast processing and the additional benefit of examining multi-exponential decay fluorescence lifetime data on a 2D phasor/polar plot. Intensity, fluorescence lifetime, and a pixelwise phasor plot are displayed in real time on a LabVIEW (National Instruments) graphical user interface; GPU processing is visually represented in Fig. S1 and acquisition timing characterizations are given in Table S1. GPU-accelerated processing has been implemented in a variety of imaging modalities [33] including FLIM [25,34,35], but to our knowledge has never before been demonstrated for computational photon counting.

Fig. 1.

Fast fluorescence lifetime imaging microscopy (FLIM) setup with analog output photomultiplier tube (PMT) and graphics processing unit (GPU) accelerated computational photon counting. (a) Optical microscopy and acquisition system diagram including two-photon excitation from a tunable fs laser, laser scanning with galvanometer mirrors, a dichroic mirror to direct emitted fluorescence through a filter wheel (FW) to the PMT. The PMT output is amplified with a transimpedance amplifier (TA) and digitized. The digitized data is copied to the GPU for accelerated computational photon counting via single-photon peak event detection (SPEED) and determination of intensity, phasor components, and mean lifetime for each pixel, which are copied back to the central processing unit (CPU) and displayed in real-time. (b) Signals represented on normalized scales of intensity vs. time in various locations from (a), indicated by the colored boxes. Raw data from a sample of urea crystals is shown in the “Digitizer” column; the signals displayed in the four preceding boxes are estimations based on the digitized data and the “Photon counts” were computed using SPEED. Single pulse (12.5 ns) and single pixel (625 ns) signals are given in the left and right columns, respectively. BS, beam splitter; PD, photodiode; L, lens; P, pinhole; M, mirror; G, galvanometer scanning mirror, G; DM, dichroic mirror; OL, objective lens.

Figure 1(b) shows the excitation, emission, and measured signals in arbitrary units vs. time for a single excitation pulse (12.5 ns, left column), and for a single pixel where 50 excitation pulses in succession were measured (625 ns, right column). As shown in the left column of Fig. 1(b), the response function of the PMT can be clearly visualized when just one photon is incident on the detector within the laser repetition period. The distribution of PMT response peak heights from our system (Fig. S2(a)) matches well with previously presented data [7,11], indicating that these signals are single-photon responses.

2.2. Photon counting algorithms and time resolution

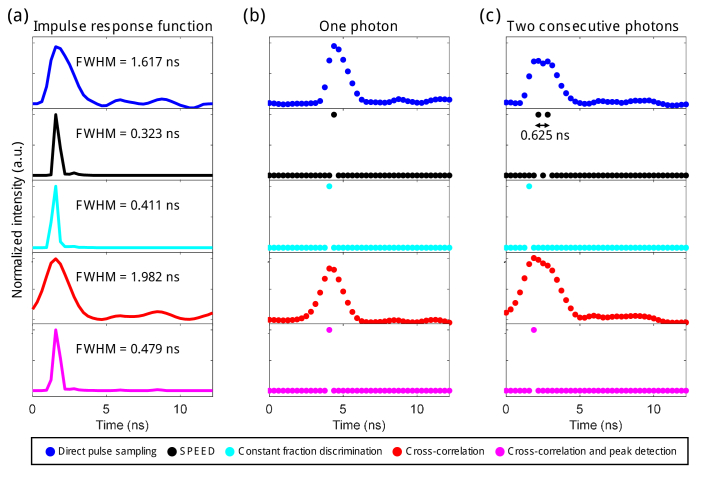
A variety of computational methods were tested for their ability to detect and resolve discrete photon counts from our directly sampled data. For algorithm calibration and sensitivity testing, raw data was saved and then processed in MATLAB 2018a (Mathworks). Figure 2 compares data from direct pulse sampling (blue), SPEED (black), CFD (cyan), cross-correlation with system IRF (red), and cross-correlation with system IRF followed by peak detection (magenta). To implement the algorithms, we examined the distribution of peak heights from our system (Fig. S2(a,b)) and determined the optimal discrimination level as the minima between photon counts and noise (red dashed line, Fig. S2(a-c)) [11], which was validated by examining the effect of peak height on fluorescence intensity and lifetime (Fig. S2(f-i)). The same experimentally determined peak height threshold was used for all presented data calculated using both SPEED and CFD methods. For our SPEED algorithm (Fig. S1), local maxima (a datapoint that has a larger value than the point immediately before and after it, Fig. S2(d)) are considered “peaks”, and peaks that are above the discrimination threshold are considered photon counts (Fig. S1, Fig. S2(e)). The CFD algorithm is meant to mimic the effect of a CFD in the analog electronics of photon counting systems, and counts any cross of the discrimination threshold with a positive derivative to be a photon count. Additionally, cross-correlation with the measured system IRF was used, both with and without peak detection. The full width at half-maximum (FWHM) of the IRF for each of the five techniques was measured (Fig. 2(a)); SPEED yielded the shortest IRF FWHM: 0.323 ns. Examples of the performance of the algorithms on a single-photon response (Fig. 2(b)) and on two consecutive photons separated by less than 1 ns (Fig. 2(c)) are shown; SPEED provided the best time resolution with the ability to resolve two consecutive photons separated by only 0.625 ns (twice the sampling period of the digitizer). In contrast, CFD and cross-correlation with peak detection performed unreliably when consecutive photons were separated by less than several ns, and could only resolve photons separated by 1.56 ns or more (Fig. S3), likely limited by the system IRF of 1.617 ns.

Fig. 2.

Computational single-photon counting methods and time resolution. (a) Impulse response function (IRF), calculated as the average pixel decay resultant from imaging second harmonic generation from a BBO crystal, for five computational analysis techniques performed on the same set of digitized data: direct pulse sampling (blue), SPEED (black), constant fraction discrimination (cyan), cross-correlation with direct pulse sampling IRF (red), and cross-correlation with direct pulse sampling IRF followed by peak detection (magenta). The full width at half-maximum (FWHM) is given in ns for each technique. (b) Example of resultant data from each technique when used to analyze a single photon response of the photomultiplier tube (PMT) from experimental data. (c) Example of resultant data from each technique when used to analyze two photons separated by < 1 ns incident on the PMT from experimental data. The photons are separated by two times the sampling period, or 0.625 ns, using SPEED.

2.3. Cell culture and apoptosis time-lapse sample preparation

Human breast cancer cells, MDA-MB-231 (ATCC HTB-26), were used for investigating Staurosporine (STS)-induced apoptosis. MDA-MB-231 cells were maintained in DMEM supplemented with 10% fetal bovine serum (Hyclone Laboratories) and 1% penicillin streptomycin antibiotic (Thermo Fisher Scientific), and grown in an incubator at 37 °C with 5% CO₂. One day prior to imaging, cells were plated in poly-D-lysine coated 35 mm diameter glass-bottom imaging dishes (P35GC-0-10-C, MatTek) and left to adhere in the incubator overnight in 2 mL of media. For time-lapse imaging, cells were maintained at 37 °C for the duration of the imaging with a stage top incubator (H301-K-Frame, OKOLAB). Three dishes were treated with STS; within 30 s of starting the acquisition, 20 µL of a concentrated STS solution was manually pipetted into the dish, for a final concentration of 1 µM. Three additional dishes were untreated. All samples were imaged continuously at 0.61 frames per second (fps) for up to 45 mins with occasional manual refocusing due to axial focal plane drift. An incident power of 30 mW was used on the cells and a bandpass filter centered at 450 nm (FF01-450/75-25, Semrock) was used to selectively collect NAD(P)H autofluorescence.

2.4. Animal models and in vivo imaging

All animal procedures were performed under a protocol approved by the Institutional Animal Care and Use Committee (IACUC) at the University of Illinois at Urbana-Champaign. Rat mammary adenocarcinoma cells, 13762 MAT B III (ATCC CRL-1666), were grown in McCoy’s medium (Gibco) supplemented with 10% fetal bovine serum (Hyclone Laboratories) and 1% penicillin streptomycin antibiotic (Thermo Fisher Scientific), and grown in an incubator at 37 °C with 5% CO₂. Once enough cells were available, approximately 10 million cells were injected into a rat (Sprague Dawley, ENVIGO) in the right abdomen flank region in order to form a tumor. Once the tumor diameter reached approximately 1 cm, the rat was sacrificed by CO₂ inhalation. The tumor and a kidney were harvested from the recently sacrificed rat and the kidney was bisected to expose the cortex. The fresh kidney and tumor were placed in uncoated glass-bottom imaging dishes (P35G-0-10-C, MatTek) with saline. A lung, liver, and kidney were harvested from a recently sacrificed mouse (Strain #000664, C57/BL/6J, The Jackson Laboratory). The fresh tissue specimens were placed in an uncoated glass-bottom imaging dish (P35G-0-10-C, MatTek) containing saline. All fresh tissue samples were kept on ice for less than 30 min prior to imaging and were then imaged at room temperature. To examine the capability of the system for in vivo imaging, 3D datasets were acquired on the outer layers of skin of an anesthetized mouse. Prior to imaging, hair was manually plucked from a 1 cm diameter area in the dorsal caudal region. The mouse was anesthetized with 1.5% isoflurane-O₂ throughout the imaging session and a heating pad was used to maintain proper body temperature. The duration of the in vivo imaging session was approximately one and a half hours, throughout which the respiration of the animal was monitored. The mouse was sacrificed by CO₂ inhalation while under deep sedation after the imaging session. An incident power of 30 mW or less was used for in vivo and tissue imaging and a bandpass filter centered at 450 nm (FF01-450/75-25, Semrock) was used to selectively collect NAD(P)H fluorescence.

3. Results and discussion

3.1. Comparison of SPEED, CFD, and direct pulse sampling performance

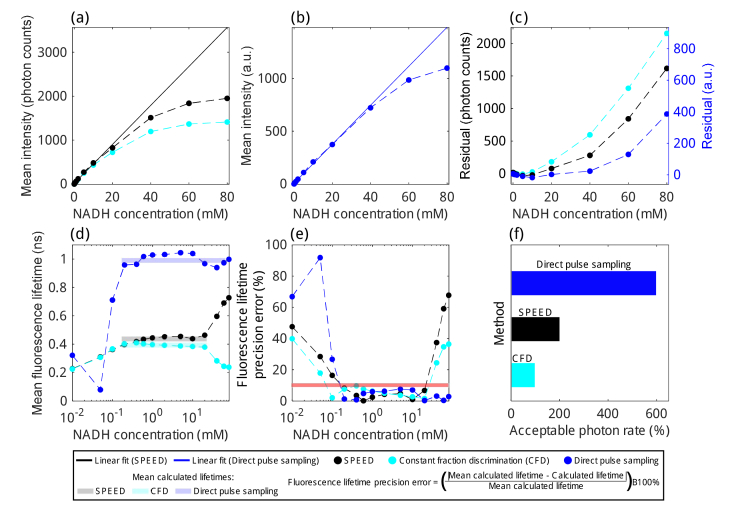
Using various concentrations of NADH in solution, we characterized the mean pixel intensity (Fig. 3(a-c)), mean pixel fluorescence lifetime (Fig. 3(d)), and fluorescence lifetime precision error (Fig. 3(e)) using SPEED, computational CFD, and our previously published direct pulse sampling methods [25]. For this analysis, four frames were acquired sequentially at 0.61 fps with a FOV of 128×128 μm and 256×256 pixels. The same set of raw data was used for all analysis methods. All methods produce linear intensity counts with increasing NADH concentration within a given range, SPEED and CFD provide more linearity in intensity for lower concentrations, whereas for concentrations above 20 mM, direct pulse sampling provides more linearity in intensity. As the photon rate increases, the probability that two photons will arrive at the detector separated by less than 0.625 ns increases, which means the probability that SPEED will undercount photons increases and the probability that CFD will undercount photons increases even more since the effective dead time using computational CFD was determined to be 2–3 times that of SPEED (Fig. 2, Fig. S3). Furthermore, as discrete single-photon responses (Fig. 2(b)) lessen and multiple photons start arriving at the detector more frequently (Fig. 2(c)), the intensity of direct pulse sampling data will still increase, but will not increase as linearly since the PMT response is not a linear, time-invariant function. For both SPEED and direct pulse sampling, linear least squares fits were calculated (solid lines, Fig. 3(a,b)) to enable characterization of intensity linearity with increasing NADH concentrations. The residuals for both SPEED and CFD were calculated from the SPEED linear fit in photon counts (Fig. 3(c), left) and the residuals for direct pulse sampling linear fit were calculated in arbitrary units (a.u., Fig. 3(c), right). As expected, CFD undercounted photons more severely than SPEED. CFD achieved less than 10% loss in photon counts for concentrations up to 10 mM NADH, whereas SPEED maintained less than 10% loss for 20 mM NADH and direct pulse sampling maintained less than 10% error in intensity for 60 mM NADH.

Fig. 3.

Fluorescence lifetime accuracy and precision of SPEED, computational constant fraction discrimination (CFD), and direct pulse sampling determined using concentrations of NADH from 0.01 mM to 80 mM. (a) Mean pixel intensity estimated using SPEED (black dots and dashed line) and CFD (cyan dots and dashed line) with linear least squares fit calculated for SPEED from 0.05 mM to 20 mM (black line). (b) Mean pixel intensity estimated using direct pulse sampling (blue dots and dashed line) and linear least squares fit from 0.01 mM to 60 mM (blue line). (c) Residuals between SPEED and CFD experimental data and the SPEED linear fit (in photon counts, left axis) and residuals between direct pulse sampling experimental data and linear fit (in a.u., right axis). At 20 mM, SPEED has a residual of 78 photons, which corresponds to an error of 8.6% and CFD has a residual of 181 photons, an error of 20%. At 60 mM, direct pulse sampling has a residual of 71 a.u., an error of 6.7%. (d) Mean pixel fluorescence lifetime and (e) fluorescence lifetime precision error using SPEED, CFD, and direct pulse sampling. Horizontal bars in (d) represent the mean lifetime over a range of NADH concentrations. Fluorescence lifetimes calculated using direct pulse sampling may experience a large amount of bias due to the system IRF. For this reason, instead of examining the error from the known fluorescence lifetime of NADH, (e) instead aims to characterize the regions in which the fluorescence lifetime of NADH will be estimated consistently, calculating the % difference relative to the mean fluorescence lifetime in the regions of each technique with approximately linear intensity (SPEED: 0.05 mM to 20 mM, mean calculated lifetime = 0.434 ns; CFD: 0.05 mM to 20 mM, mean calculated lifetime = 0.374 ns; Direct pulse sampling: 0.2 mM to 60 mM, mean calculated lifetime = 0.971 ns). Note that for CFD, there is a fluorescence lifetime precision error of 9.7% at 0.4 mM, which is still below the 10% error line (red). (f) Approximate acceptable photon rate ranges for NADH imaging determined using SPEED, computational CFD, and direct pulse sampling. Ranges were determined to be regions within which there is less than a 10% photon loss due to pile-up and the fluorescence lifetime precision error is less than 10%.

The mean fluorescence lifetime (Fig. 3(d)) and fluorescence lifetime precision error (Fig. 3(e)) were characterized for all three methods. The fluorescence lifetime of NADH dissolved in solution is approximately 0.4 ns [36], so it is clear from Fig. 3(d) that SPEED and CFD provide a significant improvement in the accuracy of fluorescence lifetime estimation compared to direct pulse sampling. Low fluorescence lifetimes, like those of NADH, are biased to higher values by the IRF of the system when using direct pulse sampling methods, consistent with our previous work [25]. However, for concentrations of NADH above 20 mM, the fluorescence lifetime estimated using SPEED rises significantly due to undercounting photons that arrive during the dead time (approximately 0.625 ns for SPEED). This biases the fluorescence lifetime longer when many photons per laser pulse arrive at the detector: the first photon to arrive is counted, the photons arriving within less than 0.625 ns of the first photon are not counted, and later-arriving photons are counted. These later-arriving photons then make up a relatively higher share of the photons used to estimate fluorescence lifetime, which biases estimated lifetimes to higher values. One way this could be corrected is to use a dual-threshold, having one threshold for single photon arrivals and a second threshold for multiple photon arrivals (Fig. S4). This method produced modestly improved results in terms of intensity linearity but did not improve the range of NADH concentrations in which fluorescence lifetime is within 10% error (Fig. S5). A multi-threshold approach would perform much better using a detector with more well-established discrete output levels for simultaneous multiple photon arrival events, such as an HPD [7]. For CFD, fluorescence lifetimes at high photon rates are biased lower since likely only the first photon arriving within each laser period is counted. This is termed the pile-up effect.

For a concentration of 20 mM NADH, the highest concentration with accurate lifetime and intensity estimation using SPEED, the measured photon rate was 206%, and for 0 mM NADH the photon rate was 0.06%, stemming from dark counts and stray light at the detector. Fluorescence lifetimes are estimated consistently within a 10% error for concentrations of 0.2 mM to 20 mM for SPEED, 0.1 mM to 20 mM for CFD, and 0.2 mM to 80 mM for direct pulse sampling (Fig. 3(e)). Since direct pulse sampling does not have a dead time, it is not as susceptible to error in estimated fluorescence lifetimes at high photon rates. With our current setup, SPEED provides optimal performance for photon rates up to approximately 200%, though this also depends on the fluorescence lifetime of the species being investigated. In terms of common fluorophores and autofluorophores, NADH has a relatively low fluorescence lifetime, leading to resultant FLIM data highly susceptible to pile-up, which makes it an ideal candidate for determining maximum allowable photon rates for useful FLIM imaging. The approximate acceptable photon rates for the three techniques were estimated based on the ranges in which they had less than a 10% error in intensity and fluorescence lifetime, with approximate maximum acceptable photon rates determined to be:100% for CFD, 200% for SPEED, and 600% for direct pulse sampling (Fig. 3(f)). Thus, SPEED allows for accurate and precise fluorescence lifetime measurements for photon rates over a large dynamic range, from around 2% to 200%, nearly double the range within which computational CFD can be used. However, for an application that would require consistent fluorescence lifetime estimations over an even larger dynamic range of photon rates, such as from 2% to 600%, direct pulse sampling is better suited. Note that these values were calculated based on data acquired with a pixel dwell time of 5 μs, and that a longer pixel dwell time would decrease the minimum acceptable photon rate for all methods. Additionally, the maximum acceptable photon rates are dependent on the bandwidth of the detection and digitization hardware in addition to pixel dwell time, and may be different if calculated using a different acquisition scheme.

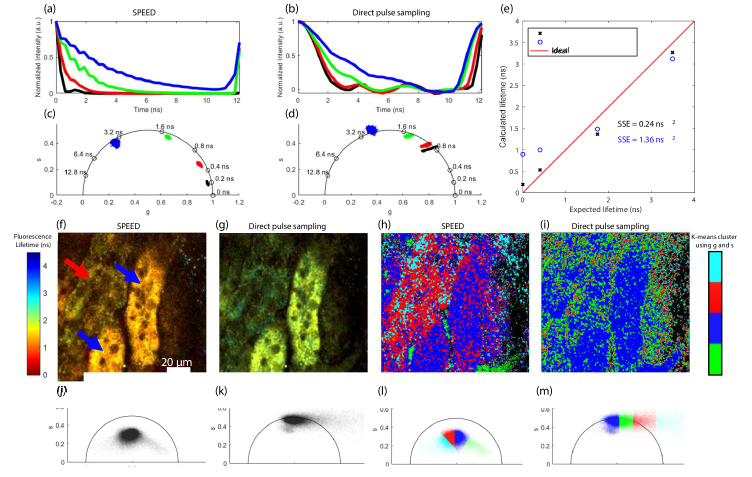
The fluorescence decay curves (Fig. 4(a,b)), phasor plots (Fig. 4(c,d)), and calculated vs. expected fluorescence lifetimes (Fig. 4(e)) were calculated for standard samples using SPEED and direct pulse sampling. The standard fluorophores imaged were Fluorescein in ethanol, Rhodamine B in water, and NADH in 1 mM HEPES with 7.4 pH. SHG from a BBO crystal was used for its instantaneous response to characterize the IRF of the system. The incident power was adjusted so that each standard sample produced a photon rate of <200%. SPEED results in fluorescence decays that more closely resemble the expected exponential decay shape and more accurately estimates fluorescence lifetime (Fig. 4(a-e)). For both methods, the system IRF biases low (sub-ns) lifetimes, as evidenced by the nonzero fluorescence lifetimes calculated from SHG for both methods. As shown in Fig. 2(a,b), the IRF using SPEED is significantly smaller than that using direct pulse sampling. This is additionally visible in the SHG (black) location on the phasor plots (Fig. 4(c,d)), which correspond to mean fluorescence lifetimes of 0.19 ns and 0.90 ns for SPEED and direct pulse sampling, respectively, which represent the biases in fluorescence lifetime introduced by the IRF and clearly shows that direct pulse sampling introduces a significantly larger bias due to the system IRF. The long IRF of direct pulse sampling additionally provides much less separability between low lifetimes, as evidenced by the close proximity of the NADH (red) and SHG (black) populations on the phasor plot in Fig. 4(d). To quantify the relative accuracies of the two methods, the sum of squared error (SSE) was calculated for fluorescence lifetimes estimated with SPEED as 0.24 ns², which is over 5 times less than that using direct pulse sampling, which is 1.36 ns².

Fig. 4.

Fluorescence lifetime accuracy and analysis using SPEED and direct pulse sampling. Average decay curves for second harmonic generation (SHG, black), NADH (red), Rhodamine B (green), and Fluorescein (blue) with analysis using (a) SPEED and (b) direct pulse sampling. Phasor plots of the aforementioned fluorophores with analysis using (c) SPEED and (d) direct pulse sampling. (e) Calculated lifetime vs. expected lifetime for the four known fluorophores with analysis using SPEED (black x) and direct pulse sampling (blue o). The sum of squared error (SSE) for both methods is given. Representative intensity-weighted fluorescence lifetime images of a rat kidney ex vivo with (f) SPEED or (g) direct pulse sampling; two visually different types of tubules are marked in (f) with red and blue arrows. K-means clustering (using MATLAB 2018a) was applied to the two phasor components from each analysis method with K = 4. The images with pixels corresponding to each group are shown in (h) and (i), the pixelwise phasor plots without color coding are shown in (j) and (k), and the K-means coded phasor plots are shown in (l) and (m) for SPEED and direct pulse sampling, respectively.

We further compared the two methods for characterizing biological data by imaging NAD(P)H autofluorescence in an ex vivo rat kidney (Fig. 4(f-m)). The fluorescence lifetime images (Fig. 4(f,g)) and phasor plots (Fig. 4(j,k)) show the bias towards higher lifetimes in direct pulse sampling. To examine the analytical capabilities, K-means clustering using MATLAB 2018a was performed on the phasor components [37] of both methods with K = 4 (Fig. 4(h,i,l,m)). Kidneys have different types of tubules, such as distal tubules, and S1 and S2 proximal tubules, which have previously been investigated and differentiated with two-photon FLIM of NAD(P)H [38]. Without validation we cannot classify the different types of tubules in the image, however visually it is clear there are tubules with two different FLIM signatures; one type of tubule has a lower intensity and longer fluorescence lifetime (Fig. 4(f), red arrow), and the other type of tubule has a higher intensity and slightly shorter fluorescence lifetime (Fig. 4(f), blue arrows). While the SPEED K-means clustering somewhat differentiates two different types of tubules (one red and one blue, Fig. 4(h)) from the background, the direct pulse sampling K-means clustering does not seem to properly segment out the different areas of the image, and both types of tubules appear in the same category (blue, Fig. 4(i)). This example demonstrates that especially for autofluorescence imaging of NAD(P)H, which usually does not produce high photon rates (>200%), SPEED provides more accurate fluorescence lifetime estimations and provides the basis for more useful fluorescence lifetime analysis.

3.2. Label-free dynamic imaging of cell apoptosis

Previous fast FLIM work using direct pulse sampling has contributed to understanding apoptosis dynamics [30,39], but was constrained to using direct pulse sampling techniques, limited in fluorescence lifetime accuracy and data throughput, and was only capable of acquiring 2-3 minutes of continuous data at a time [30,39,40]. In terms of the amount of data that can be collected within an imaging session, our real-time GPU-accelerated SPEED software can acquire over 45 minutes of data continuously with a frame rate of 0.61 fps, similar in capability to our previously published GPU-accelerated direct pulse sampling phasor FLIM [25] and only 23 ms slower for GPU processing time per frame (Table S1). To demonstrate the ability to acquire high-frame rate time-lapse data, the dynamics of STS-induced apoptosis in MDA-MB-231 cells was visualized for up to 45 minutes with a frame rate of 0.61 fps (Visualization 1 ^{(69.9MB, avi)} , Fig. S6).

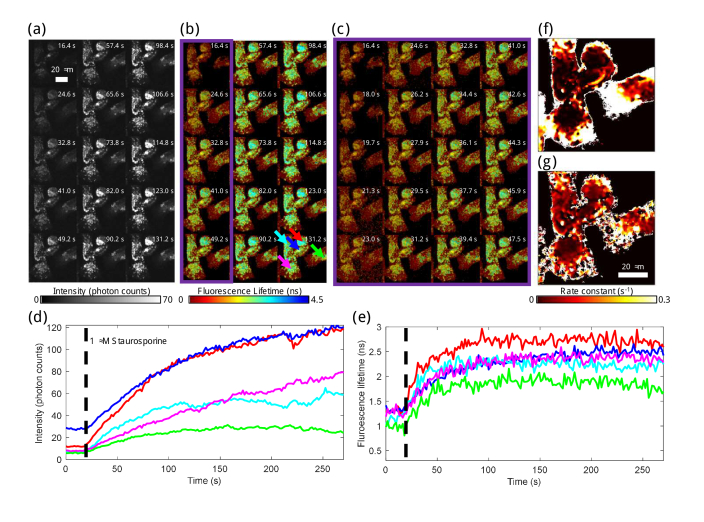
Representative images of dynamics from the first 4.5 mins from one representative STS-treated dish are displayed in Fig. 5; images and analysis for all six dishes can be found in Fig. S6 and Visualization 1 ^{(69.9MB, avi)} . The fluorescence intensity (Fig. 5(a)) and lifetime (Fig. 5(b,c)) over the first two minutes show dramatic increases throughout the cells, and specifically in the mitochondria (Fig. 5(d,e)). The rate constants of fluorescence intensity (Fig. 5(f)) and lifetime (Fig. 5(g)) dynamics for the 4.5 mins following STS treatment were quantified using previously described methods [25]. These data show that the rate constant of fluorescence lifetime is generally higher than the rate constant of fluorescence intensity in the regions of the cells containing mitochondria, which indicates a more rapid change in fluorescence lifetime than in intensity. Metabolically, this suggests that the apoptosis-related increase in NAD(P)H concentration is slightly preceded by an increase in protein-bound NAD(P)H. As shown in Fig. S6, the fluorescence intensity and lifetime in the mitochondria of the STS-treated cells begin to trend slightly downward after 10 mins and by the end of the imaging session, these have nearly reached their original, pre-treatment values. High rate constants around the outer areas of the cells in non-mitochondrial regions (Fig. 5(f,g)) show that a very fast change occurred in the cytosol of cells during apoptosis. Figure 5(a-c) shows that this change, though rapid, was fairly small in magnitude compared to the changes in mitochondrial intensity and lifetime.

Fig. 5.

Label-free apoptosis-induced NAD(P)H dynamic fluorescence lifetime and intensity investigation and quantification. NAD(P)H fluorescence (a) intensity and (b) lifetime from 16.4 to 131.2 s, the beginning of STS-induced apoptosis in one of three dishes examined. Each fifth frame is displayed; frames are displayed with no frame averaging. Fluorescence lifetime is overlaid on intensity, given by the colorbars. (c) Fluorescence lifetime overlay on intensity for every frame from 16.4 to 47.5 s with no frame averaging, representing the first column of (b). For (a-c), a gamma correction of 0.55 was used to rescale fluorescence intensity and balance over the high dynamic range of pixel values. The presented intensity scale corresponds to a minimum of 0 and a maximum of 70 photons per pixel per frame, but the scale is not linear. The given intensity values are estimates of the single-pixel photon counts prior to 3×3 spatial binning, and approximately 9 times the number of photons per pixel per frame is the number of photons used to calculate the fluorescence lifetime in each pixel. The fluorescence (d) intensity and (e) lifetime over 4.5 min for five different areas within in the image are given. Five different areas of 11×11 pixels were manually chosen centered on one mitochondria-rich area of each of the five cells in the image, indicated by arrows in the last frame of (b). The black dashed line indicates when STS was added to the dish. The time constants for fluorescence (f) intensity and (g) lifetime during the first four minutes of apoptosis induction were calculated using previously shown techniques [25].

In the apoptosis dataset, the maximum photon count per pixel per frame was 383, which with 400 laser pulses per pixel corresponds to a photon rate of around 96%. This is higher than the upper limit of photon rate that most commercial TCSPC systems can accept. If this dataset was acquired on a standard TCSPC system capable of a maximum photon rate of 10%, likely the incident power on the sample would have been reduced by about 90% in order to not saturate photon counts, which would have also resulted in the need for an acquisition time that was ten times longer per frame in order to collect enough photons per pixel to accurately calculate fluorescence lifetime. This would additionally lead to decreased SNR since the dark count rate would remain constant while the signal intensity decreased. Thus, the ability to image faster and with a higher dynamics range using SPEED enables FLIM imaging in more diverse situations such as fast dynamic imaging (Fig. 5, Visualization 1 ^{(69.9MB, avi)} , Fig. S6) and higher throughput imaging, as discussed in the following section.

3.3. Towards higher throughput tissue autofluorescence imaging enabled by computational single-photon counting

The traditionally long FLIM acquisition time, limited primarily by low maximum acceptable photon rates of FLIM systems, has been a barrier for FLIM translation into clinical settings and for the application of FLIM imaging to dynamic processes, high dynamic range samples, and samples that logistically benefit from fast, higher throughput imaging. The increased maximum photon rate capacity of SPEED relative to photon counting thus greatly broadens the potential applications for accurate FLIM imaging. Additionally, GPU-accelerated real-time photon counting, phasor analysis, and visualization provides the necessary convenience for imaging scenarios with logistical constraints such as in clinical settings. Presently, various studies have examined fluorescence lifetime imaging of NAD(P)H in clinical and/or in vivo settings [41,42]. The JenLab MPTflex system is one commercially available multiphoton system that is certified for clinical use and has been used for a variety of studies, especially those regarding human skin [43,44], however the TCSPC module in the JenLab MPTflex system has a dead time of 100 ns [45]. By implementing SPEED in conjunction with a high bandwidth detector, amplifier, and digitizer, the dead time of this system could be decreased by a factor of over 100, enabling significantly faster, more convenient, and higher throughput imaging.

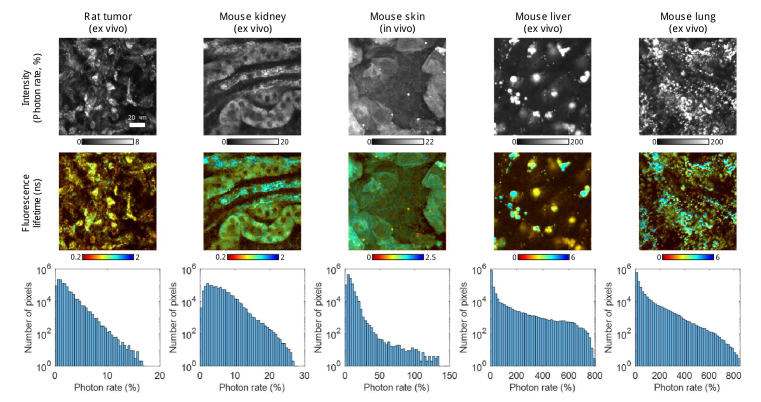
Different rodent tissues were imaged to examine the capabilities of SPEED for rapid characterization of autofluorescence lifetime from samples with a wide variety of fluorescent properties (Fig. 6). Each image consists of 512×512 pixels and was acquired as the average of four frames taken at 0.16 fps, requiring only approximately 25 s per each image. The system is capable of acquiring images of 256×256 pixels approximately four times faster, but for these tissues larger images were acquired to achieve higher quality. For ex vivo tissue imaging, when multiple samples are imaged within one session, faster acquisition enables imaging of more unique fresh samples within one imaging session. Fast acquisition also enables easier acquisition of 3D in vivo datasets (Fig. S7) and large mosaics (Fig. S8) with less concern for motion artifacts within and between frames.

Fig. 6.

Utilizing the high dynamic range capabilities of imaging with SPEED for in vivo and ex vivo rodent tissue autofluorescence imaging. Five different rodent tissues were imaged and analyzed using SPEED using the same acquisition parameters: an average of four 512×512 pixel images, each FOV 128×128 μm, frame rate of 0.16 Hz, two-photon excitation at 750 nm, incident power of 30 mW, and an emission filter centered at 450 nm. The first row shows intensity for each specimen, each represented on its own gamma-corrected (nonlinear) scale in photon rate. The second row shows the fluorescence lifetime in ns overlain on the intensity, each represented on its own scale. The third row provides a histogram of the photon rates present in all four frames acquired at each location, each represented on a semi-log scale with 50 photon rate bins over the dynamic range of the data. While the excitation and emission bands used to acquire these autofluorescence images are traditionally used for NAD(P)H imaging, there may be off-target autofluorescence within the images from other naturally occurring compounds such as lipids.

Though the accuracy of SPEED for both fluorescence lifetime and intensity is limited above a photon rate of 200% (biasing the results for the liver and lung samples), the extremely high dynamic range of autofluorescence intensity (photon rates up to 800%) within biological tissues shows the utility in the ability to acquire at high photon rates. The concentration of NADH varies widely within biological tissues and cell types depending on many factors. Phasor analysis has been used to estimate the concentration of NADH in within each pixel of images for biological samples, for example CHO-K1 cells were estimated to have spatially varying concentrations within them up to 1 mM [46]. Biologically relevant concentrations of NADH in solution, such as those below 1 mM, tended to produce lower photon rates due to the limited sensitivity of our system at a pixel dwell time of 5 μs, however when protein-bound, the quantum yield of NADH can increase by approximately 4 to 5 times [36,47]. However, in Fig. 6, a large amount of extremely bright (>200%) autofluorescence from the liver and lung tissues likely does not originate from NAD(P)H, and instead may be from other autofluorescent molecules such as lipids [48]. Accordingly, applications of SPEED are not limited to NAD(P)H autofluorescence, and could be used to image other autofluorescent molecules and/or bright fluorescent dyes and proteins to fully utilize the full dynamic range and high maximum acceptable photon rate.

By using SPEED, we can collect time-domain FLIM of diverse samples without sacrificing speed or accuracy, bridging the gap between photon counting and direct pulse sampling FLIM techniques. The dead time when using SPEED is 0.625 ns, about 2 to 3 times less than that using CFD (Fig. 2, Fig. S3), and the maximum acceptable photon rate with SPEED is double than that of CFD (Fig. 3). Our computational CFD mimics the performance of an analog electronics-based CFD, and the maximum acceptable photon rate with our computational CFD is similar to (or better than) FLIM systems using analog electronics-based photon counting [17–22]. Thus, for samples that produce high photon rates (100-200%), SPEED enables imaging twice as fast as comparable single-detector photon counting FLIM systems. For samples that do not produce high photon rates, when imaging time is not an important factor, and in scenarios where smaller time bin size is preferred, standard photon counting FLIM systems are more favorable than a fast FLIM setup using either direct pulse sampling or SPEED due to their reliable and precise time-tagging capabilities. Presently, the time bin size of our system (0.3125 ns) is larger than the ps-level time bin size available with TCSPC systems. This may present difficulty in resolving very slight differences in fluorescence lifetime; however it may not be a significant disadvantage in terms of fluorescence lifetime estimation accuracy within acceptable photon rates because previous work has determined that 42 times bins is the optimal amount of temporal binning for FLIM datasets [49]. Furthermore, with techniques like interpolation [35], a stronger capability to more accurately localize photon arrival in time could be possible. Initial work using cubic spline interpolation of raw data showed an improvement in system IRF; interpolation from 40 initial points per laser period to 200 points decreased system IRF FWHMfrom 0.323 ns to 0.183 ns, and to 400 points decreased system IRF FWHM to 0.135 ns (Fig. S9). However, interpolation of raw data showed a decreased range of NADH concentrations in which NADH fluorescence lifetime falls within a 10% error (Fig. S5). Additionally, interpolation of raw data increases the computational burden and the amount of memory needed and was not yet able to be implemented in real-time GPU-accelerated processing. Future work should examine the feasibility and efficacy of different interpolation methods on SPEED performance. There are also many different computational algorithms that could expand upon the current methods.

In addition to computational methods, new hardware would also improve system performance. There are detectors and amplifiers with higher bandwidths that could be used to improve system performance for both direct pulse sampling and SPEED. Presently, our amplifier has the lowest bandwidth of the electronics in our system at 1.50 GHz; the PMT has a rise time of 0.57 ns and the digitizer has a bandwidth of 1.7 GHz. These factors account for the 0.323 ns FWHM of the SPEED IRF, and explain why interpolation of digitized data did not yield more accurate results, since higher frequencies are not resolvable in the raw data prior to digitization. An amplifier with a higher bandwidth and similar or less noise in conjunction with faster digitization would likely improve the capabilities for SPEED, computational CFD, and direct pulse sampling. The choice of detector also affects the quantum efficiency of the system, and so the detector must be carefully chosen to ensure that high photon rates can be collected from the target sample using appropriate incident power. Additionally, faster digitization may not have a huge effect on the direct pulse sampling method but may greatly improve peak localization capabilities in SPEED. Another consideration in system design is the laser repetition rate; a lower repetition rate laser such as 20 MHz will have a higher peak power than our 80 MHz setup for the same average incident power at the sample, which would result in a higher photon rate. Future work will explore new computational methods in addition to hardware implication such as different laser repetition rates, higher bandwidth collection electronics, and faster digitization.

4. Conclusion

FLIM is often limited by either poor accuracy or long acquisition times, depending on the detection method. With computational single-photon counting techniques such as SPEED, fast and accurate imaging can be achieved within a high dynamic range of photon rates, up to 200%, which is much higher than the top single-detector photon counting FLIM systems that rely on analog electronics-based CFD. SPEED was able to accurately estimate fluorescence lifetime and intensity for twice the photon rate range that computational CFD was able to, which enables imaging twice as fast. Compared to our direct pulse sampling methods, SPEED is more accurate and enables better quantitative analysis of fluorescence lifetime. We further demonstrate the ability to examine and quantify the dynamics of apoptosis in human breast cancer cells, showing that the mitochondrial NAD(P)H fluorescence lifetime responds more rapidly than mitochondrial NAD(P)H fluorescence intensity using SPEED. By increasing the maximum acceptable photon rate with SPEED, we enable new possibilities of fast and accurate FLIM measurements, which are of critical importance in biological and clinical applications that require higher throughput, time sensitive analysis techniques, and in studies of dynamic processes. As technologies such as shorter-IRF detectors, faster digitizers, and higher capacity GPUs become available, the capabilities of computational single-photon counting will expand even further.

Funding

National Institutes of Health10.13039/100000002, U. S. Department of Health and Human Services (R01 CA241618, R01 EB023232, R41 GM139528, R43 MH119979); Air Force Office of Scientific Research10.13039/100000181 (FA9550-17-1-0387); National Science Foundation10.13039/100000001 Graduate Research Fellowship Program (DGE-1746047).

Disclosures

The method and apparatus reported here has been disclosed as intellectual property by J.E.S., R.R.I., and S.A.B. to the Office of Technology Management at the University of Illinois at Urbana-Champaign.

Data availability

Data underlying the results presented in this paper are not publicly available at this time, but may be obtained from the authors upon reasonable request, and through a collaborative research agreement. The GPU code for SPEED processing will be made available upon publication at [50].

Supplemental document

See Supplement 1 ^{(5.4MB, pdf)} for supporting content.