1 |. INTRODUCTION
For a typical clinical study comparing two therapies, the investigators identify a target patient population, precisely define the treatments interventions and primary endpoint, then specify a population-level summary to quantify the treatment difference. Collectively, these choices are components of the estimand framework recently set forth by the International Council for Harmonisation of Technical Requirements for Pharmaceuticals for Human Use (ICH).1 In this guideline and various related research publications,2–4 the issue of choosing the study estimand is discussed. Special attention is needed when the study’s primary outcome could foreseeably be affected by intercurrent events, such as treatment discontinuation, which occur after treatment initiation and interfere with the observation or interpretation of the outcome. As an example, in a recent diabetes trial to assess the efficacy of oral semaglutide versus sitagliptin,5 the primary endpoint was the change in hemoglobin A1c from baseline to Week 26. The treatment difference was quantified using the difference in mean changes comparing the two therapies. However, the study treatments could be discontinued for various reasons and patients might be switched to other anti-diabetic regimens. When such unavoidable interruptions of the assigned study therapy are anticipated, it is important to consider at the study design stage how they will be handled when quantifying and interpreting the treatment difference. Here, the treatments of interest need to be precisely defined, and appropriate analytic procedure for handling incomplete observations prespecified.
In this article, we discuss a more fundamental issue of quantifying the treatment difference. In particular, an appropriate population-level summary of the treatment difference preferably has the following features:
The summary is clinically interpretable, ideally in layperson’s terms, and is accompanied by an appropriate summary of the endpoint in each treatment group.
The summary of the treatment difference does not have modeling constraints, and the corresponding inference procedures are robust and model-free.
For feature 1, an intuitive and clinically interpretable treatment summary is essential for allowing clinicians and patients to make better treatment selection decisions at the end of the study. For feature 2, if the treatment difference is defined via a model, but at the interim or final analysis the model does not fit the data well, then it is not clear how to draw conclusions from the study concerning treatment efficacy. Moreover, there are no satisfactory analytic procedures for assessing model appropriateness. The conventional lack-of-fit tests, which use a P-value to evaluate model adequacy, are notoriously uninformative.6 In a large dataset, the lack-of-fit test is likely to report a highly significant P-value, rejecting a fitted model that may provide an acceptable approximation to the truth. On the other hand, in a small to moderate dataset, a lack-of-fit test is typically underpowered for detecting an obvious departure from modeling assumptions, resulting in a large P-value, and leading to claims that a poorly fitted model is acceptable. If possible, one should avoid modeling at the design stage, especially for the primary analysis of the treatment difference, unless one is focused on prediction. For the same reasons, at the analysis stage, the inference procedures for the treatment difference should be model-free.
We present three examples from recent clinical studies for treating patients with COVID-19, cancer, and heart failure. These examples illustrate issues with model-based quantification of the treatment contrast, and present simple, model-free alternatives that are easier to interpret. In each case, the intent is not to draw any new conclusions about the particular study under consideration, but rather to showcase alternative methodology that may be used for the design and analysis of future studies. To the best of our knowledge, there are no publications addressing the issues presented here.
2 |. COVID-19 STUDY WITH AN ORDINAL CATEGORICAL OUTCOME AS THE PRIMARY ENDPOINT
Consider a recent clinical trial evaluating the efficacy of 10-days versus 5-days remdesivir for treating patients hospitalized with confirmed SARS-CoV-2 infection.7 The primary endpoint was clinical status on day 14, assessed on a 7-point ordinal scale, ranging from death at 1 to not hospitalized at 7. The higher the scale, the better a patient’s health status. The population-level summary for quantifying the treatment difference was the odds ratio from an ordinal proportional odds model.8 This model is popular in the statistical literature, and has been applied in other recent trials for COVID-19,9–11 but is not easy to interpret. The difficulty extends beyond interpreting the odds ratio for comparing two treatments. The ordinal proportional odds model additionally assumes that the odds ratio is constant across adjacent outcome categories. The study was designed to have 85% power to detect a common odds ratio of 1.75 and would conclude that 10-day treatment was superior to its 5-day counterpart if the lower bound of the 95% confidence interval (CI) for the odds ratio was greater than 1.7 We use the observed data from the trial to illustrate the issues with this modeling approach.
The study randomized 197 and 200 patients to the 10-day and 5-day groups. On day 14, the observed numbers of patients classified to the seven ordinal categories are presented in Table 1A. For example, in Category 1, there were 21 and 16 deaths for 10-days and 5-days therapies. On the other hand, in Category 7, there were 103 and 120 patients out of hospital, respectively. Table 1B presents the six consecutive 2 × 2 tables. Each table was constructed by dichotomizing the ordinal outcome and combining adjacent categories. The new binary outcome is 1 if the endpoint is beyond a certain category, and 0 if not. For instance, the binary outcome for the third table is 1 when a patient’s health status is in a category higher than 3. The observed odds ratios of the consecutive tables vary from 0.54 to 0.73.
TABLE 1.
Data from the trial comparing 5-day versus 10-day remdesivir among patients with severe COVID-19
| (A) Number of patients in each ordered category | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Category | ||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||||||||
| 10-day (n = 197) | 21 | 33 | 10 | 14 | 13 | 3 | 103 | |||||||
| 5-day (n = 200) | 16 | 16 | 9 | 19 | 11 | 9 | 120 | |||||||
| (B) Consecutive 2 × 2 tables and corresponding odds ratios | ||||||||||||||
| Category | ||||||||||||||
| ≤1 | >1 | ≤2 | >2 | ≤3 | >3 | ≤4 | >4 | ≤5 | >5 | ≤6 | >6 | |||
| 10-day | 21 | 176 | 54 | 143 | 64 | 133 | 78 | 119 | 91 | 106 | 94 | 103 | ||
| 5-day | 16 | 184 | 32 | 168 | 41 | 159 | 60 | 140 | 71 | 129 | 80 | 120 | ||
| Odds Ratio 10-day v. 5-day | 0.73 | 0.54 | 0.54 | 0.65 | 0.64 | 0.73 | ||||||||
The proportional odds model utilized in the study assumed that, conditional on the patient’s baseline clinical status, the six underlying odds ratios were equal, and the empirical summary measure would be the common odds ratio. Even though it may not be a valid estimate, without stratification, the common odds ratio is 0.67 (95% CI, 0.45 to 0.98; P = 0.036), favoring 5-days treatment. However, this pre-specified proposal was abandoned for the final analysis as the investigators determined that the proportional odds assumption was not met when stratifying by baseline clinical status. Instead, the Wilcoxon rank-sum test, stratified by baseline clinical status, was used for the primary analysis. The P-value from this test was 0.14. However, no corresponding estimate for the size of the treatment difference was reported. Note that without stratification, the two-sample Wilcoxon test results in a P-value of 0.036, significantly favoring the 5-days therapy.
The lesson learned from this study is that, even if the assumed model were acceptable, an odds ratio of 0.67 alone is difficult to interpret without a reference event rate from one of the treatment arms. The backup analytic procedure only provided a P-value for the comparison, which does not itself have clinical meaning.6 On the other hand, there is a conventional estimation procedure corresponding to the Wilcoxon test, which is the difference between the Pr(10-day treatment was better than 5-day) and the Pr(5-day treatment was better than 10-day).12 Without stratification, this estimate was −11%, with a 95% CI from −21% to −1%, significantly favoring 5-day treatment. However, this estimate is not ideal because it still does not quantify the extent of clinical improvement. That is, we can conclude that patients in the 5-day arm had better responses on average, but we cannot quantify how much better. Furthermore, abandoning the primary analysis and adopting an alternative analytic procedure may inflate the type I error rate, which highlights the importance of planning a statistical analysis that does not depend on stringent modeling assumptions in the first place.
Instead of using a model for summarizing the 7-point ordinal scale outcomes, we can consider a binary endpoint, “complete response,” defined as being in Category 7, live discharge from the hospital. For this endpoint, the response rates are 60% and 52% for 5-days and 10-days. The difference (5-days minus 10-days) is 8% (95% CI, −1.9% to 17%). Another possible endpoint is to define “partial/complete response” as being in Categories 5, 6, or 7, no longer requiring supplemental oxygen. This results in response rates of 70% and 60%, respectively, and the difference is 10% (95% CI, 0.5% to 18%). These simple binary outcomes have straightforward clinical interpretations, and the analysis does not depend on any model. Ideally, analyses based on dichotomizing the ordinal outcome would be pre-specified, although post hoc analyses may still generate interesting hypotheses for future studies.
If information on the time spent in each disease state across follow-up is available, then an informative summary of the data is the proportion of patients in each state across the entire study period, often depicted by stacking the corresponding multinomial cell probabilities graphically.13 This visual illustrates how disease burden and progression change dynamically across the study period. Moreover, the area between these curves is the mean time spent in each state.13 For study design and analysis, it is important to have a single, clinically interpretable summary measure. One may use a weighted average of the above mean time spans or, specifically, the mean time spent in favorable or recovered states across follow-up.14
3 |. AN IMMUNO-THERAPY CANCER STUDY WITH SURVIVAL TIME AS THE PRIMARY ENDPOINT
Consider the recent CheckMate 227 trial of immune checkpoint inhibitors as first-line treatment for advanced non-small-cell lung cancer (NSCLC).15 The primary endpoint was overall survival (OS), comparing nivolumab/ipilimumab with chemotherapy; 396 patients were randomized to nivolumab/ipilimumab, and 397 patients to chemotherapy. The prespecified summary measure for assessing treatment efficacy was the hazard ratio (HR) from a stratified Cox proportional hazards model. The study was designed to have 90% power to detect a HR of 0.74 and would conclude nivolumab/ipilimumab was superior to chemotherapy, with respect to OS, if the upper bound of the 97.72% CI for the HR was less than 1.
Like the above proportional odds model, the proportional hazards model relies on a strong modeling assumption; namely, that the ratio of the hazard curves for the two study arms is constant across time. Figure 1A presents the reconstructed,16 individual-level survival data from figure 1A15 of the original paper. Since the Kaplan-Meier curves crossed around month 7, the proportional hazards assumption was clearly not met. The authors chose to nonetheless report the hazard ratio (HR) of 0.79 as a summary of treatment efficacy. For this case, the interpretation of the observed HR is unclear. Even if the modeling assumptions had held, the HR is not easy to interpret clinically, since hazard is not a probability measure like “risk.” A 21% reduction in the hazard of death does not translate to a 21% reduction in the risk of death. Lastly, although the log-rank test remains valid for assessing the presence of a treatment difference statistically even when the proportional hazards assumption is not met, a test of significance alone does not convey information regarding the magnitude of the treatment difference or provide the relevant context for evaluating whether the difference is clinically meaningful.6
FIGURE 1.
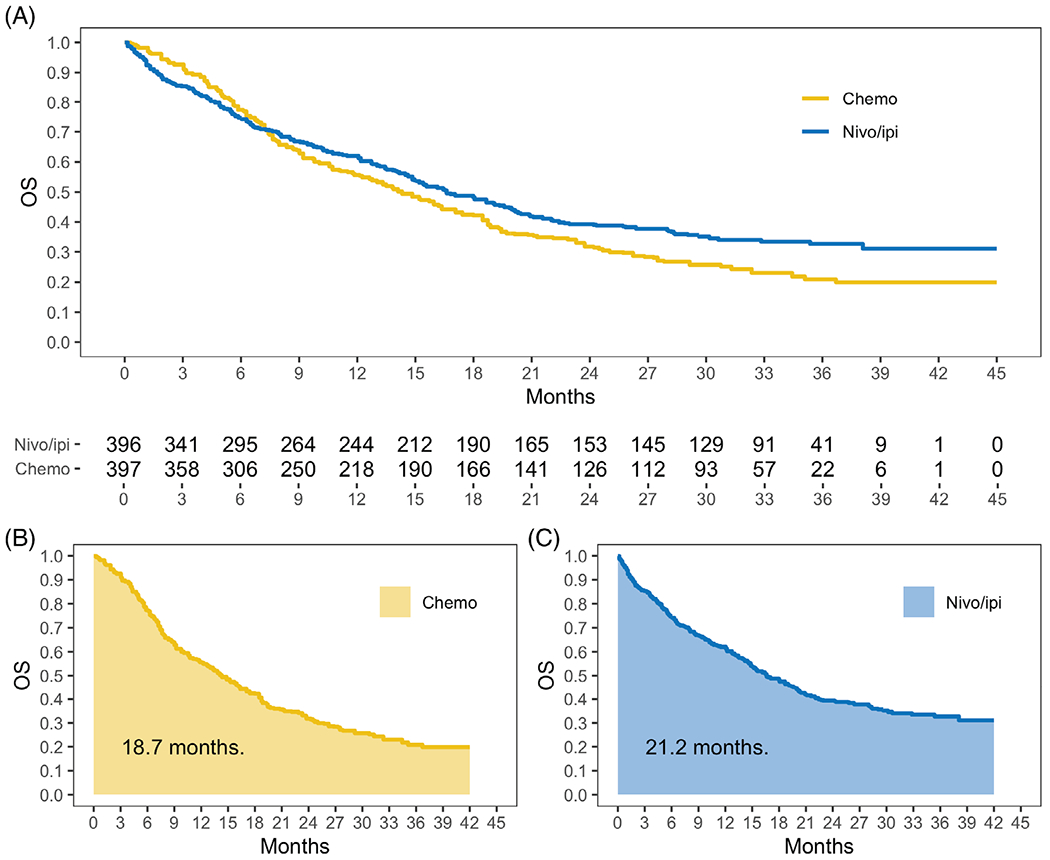
Overall survival curves and restricted mean survival time for the immune checkpoint inhibitor trial among patients with NSCLC [Colour figure can be viewed at wileyonlinelibrary.com]
As secondary analyses in CheckMate 227, the median OS time and the OS rates at landmark time points were reported. Median OS was 17.1 months (95% CI, 15.0 to 20.1) for nivolumab/ipilimumab, and 14.9 months (95% CI, 12.7 to 16.7) for chemotherapy. Since the CIs for the medians overlap, it is unclear whether the difference is statistically significant. With reconstructed data, the median difference was 2.3 months (95% CI, −0.92 to 5.5, P = 0.18). Thus, there was insufficient evidence to conclude that nivolumab/ipilimumab improved median OS. Although interpretable and model-free, the median OS time difference is not an ideal summary. The median is a local measure and cannot capture either the short- or long-term OS profile. Moreover, if the Kaplan-Meier curve does not drop below 50%, then the median cannot be estimated empirically. The OS rate at, for example, 12 months, was 62.6% for nivolumab/ipilimumab, and 56.2% for chemotherapy. The CI for 12-month OS rate difference was not reported. Using reconstructed data, the difference in 12-month OS was 6.4% (95% CI, −0.3% to 13%, P = 0.06). However, like the median, OS at a specific time point only describes the survival curve locally and does not make full use of the time-to-event data.
Visually, in Figure 1A, the higher the Kaplan-Meier curve, the better the treatment. Therefore, the treatment with a larger area under the curve is more effective for that endpoint. This area turns out to be the mean survival time up to a specified time point, for example, 42 months in the figure, and is referred to as the restricted mean survival time (RMST).17–21 As shown graphically in Figure 1B,C, the 42-month RMSTs were 21.2 months for nivolumab/ipilimumab and 18.7 months for chemotherapy. That is, a patient treated with nivolumab/ipilimumab and followed for 42 months survived for 21.2 months on average. These summaries for the OS curves are interpretable, model-free, and make full use of the available data. The treatment difference can be quantified as the difference of two RMSTs.17–21 The difference of 2.5 months (95% CI, 0.3 to 4.6, P = 0.02), across 42 months of follow-up, significantly favored nivolumab/ipilimumab. The difference in RMSTs, accompanied by the individual RMST in each arm, provides an intuitive, robust, and model-free measure for quantifying the time to a survival endpoint. Study design for time-to-event observations using RMST as the summary measure has also been discussed.20,21
4 |. A HEART FAILURE STUDY WITH COUNT OBSERVATION AS A KEY ENDPOINT
Consider the PARADIGM-HF trial, a randomized, double-blind, comparative trial to evaluate the efficacy and safety of sacubitril/valsartan versus enalapril among patients with chronic symptomatic heart failure and reduced ejection fraction.22,23 The primary endpoint was time-to the occurrence of cardiovascular death or first hospitalization due to heart failure; 4187 patients were randomized to sacubitril/valsartan and 4212 to enalapril. Since this primary endpoint may not fully reflect disease progression or burden, a key secondary endpoint was the total number of heart failure hospitalizations and cardiovascular death occurring during follow-up. For this analysis, there were 1409 and 1772 events in the sacubitril/valsartan and enalapril groups.
The negative binomial model is conventionally used for analyzing patient-level count data with corresponding exposure times.24,25 With this model, for each treatment arm, the summary measure is the mean incidence rate per unit time over the entire study period, and the two arms are compared via the ratio of the mean incidence rates.24 This model requires the strong assumption that each patient’s incidence rate is constant across time, even after the patient is informatively off-study. Essentially, the negative binomial assumes that each patient’s incidence rate is independent of their follow-up time. Even if these assumptions are plausible, the negative binomial model may not fit the data, and the capacity of standard lack of fit tests to assess its adequacy is limited. For PARADIGM-HF, in the intention-to-treat analysis, the incidence rate ratio comparing sacubitril/valsartan with enalapril based on the negative binomial model was 0.76 (95% CI, 0.67 to 0.85).24
The assumption that a patient’s exposure time is independent of their incidence rate is questionable for PARADIGM-HF because the exposure time was informatively censored by death. Consequently, the preceding analyses may not be valid. To address this issue, one may consider an assumption-free summary measure for each treatment group. For instance, in each treatment arm, the parameter of interest could be defined as the expectation of the ratio of the individual patient’s observed event counts divided by their exposure time. The relative merits of the two treatments are then assessed using the ratio of these expected rates. This criterion does not require any of the above modeling assumptions. Essentially, we are interested in the individual patient’s incidence rate while they are alive, and treat non-cardiovascular death as a competing risk. Now, the mean incidence rate in each treatment arm can be unbiasedly and nonparametrically estimated by the empirical average of the per-patient incidence rates. For PARADIGM-HF, these were 47.9 and 67.5 events per 100-years for sacubitril/valsartan and enalapril, respectively. The ratio of 0.71 favors sacubitril/valsartan. Using the standard bootstrap with 5000 bootstrap samples, the 95% CI was 0.48 to 1.05. Although the point estimate for the incidence rate ratio is similar to that based on the negative binomial, the corresponding CIs are quite different, suggesting that the parametric CI may not have adequate coverage probability. On the other hand, the nonparametric procedure may not be efficient. For PARADIGM-HF, a number of patients with only short-term follow-up experienced one or more events. This tends to inflate the incidence rate and enlarge the nonparametric CI for the incidence rate ratio.
An alternative definition of the mean incidence rate, which is less sensitive to patients with short-term follow-up, is the mean number of events divided by the mean exposure time. Again, this criterion does not require any assumptions. Using the empirical counterpart of the estimator, this approach results in 15.1 and 19.2 events per 100-years for sacubitril/valsartan and enalapril. The ratio of the mean incidence rates is 0.79 and with 5000 bootstrap samples, the 95% CI is 0.71 to 0.87. Coincidently, the results from this nonparametric analysis are very similar to those from the negative binomial analysis. Note that if the negative binomial model holds and the assumption that the incidence rate is independent of the follow-up time is valid, then two preceding model-free estimators are both unbiased for the same parameter.
The quantifications for recurrent events considered thus far may not be ideal if, for example, there is a definite survival advantage for one treatment arm over the other. A treatment that is effective for extending survival may increase the incidence rate by extending a patient’s exposure period. In other words, a direct comparison of the mean number of recurrent events per unit of exposure time between the treatment arms can be misleading. One approach to deal with this situation is to consider an endpoint that consists of the total event-free survival times summed across all recurrent events that a patient might experience. For example, in cardiovascular studies, this endpoint might include the total time spent free of heart failure hospitalization while the patient is alive. Model-free analytic methods with this endpoint have recently been developed by Claggett et al.26
5 |. DISCUSSIONS
It is important to note that even if we choose a model-free quantification of the treatment difference, it should be accompanied by an appropriate summary of the endpoint in each treatment group. For instance, in the heart failure example, the ratio of the two mean incidence rates has no modeling constraints. However, without estimates of the mean incidence rate for each group, it would be difficult to interpret whether the difference between the groups is clinically meaningful. This parallels the difficulty of presenting a hazard ratio without an estimated hazard curve, as in the second example, or presenting an odds ratio without reference event rates, as in the first example.
One possible reason for choosing a model-based summary of treatment efficacy is to improve statistical power. For instance, in the COVID-19 example, if the proportional odds assumption had held, then an analysis based on the common odds ratio would have provided more power than an analysis based on a binary outcome. However, the improved power is offset by the lack of interpretability of the resulting summary measure. Moreover, when the ordinal proportional odds assumption does not hold, the common odds ratio is even more difficult to interpret, as it does not correspond to the odds ratio comparing any two particular groups. In contrast, the analysis based on the binary “partial response” or “complete response” outcomes is always valid and interpretable. Similarly, for analyzing overall survival in the second example, an analysis based on the hazard ratio is well powered if the hazards of the two treatment arms are in fact proportional across time. Unfortunately, relying on the hazard ratio, whose strong modeling assumption is often not met,27,28 entails an estimate of the treatment difference that may not be valid, and which is difficult to interpret clinically.17–19 Interestingly, by using the difference of restricted mean survival times to quantify treatment efficacy, we do not expect to lose much power relative to an analysis relying on the hazard ratio, even when the proportional hazards assumption is valid.29
It is conventional to select the primary efficacy endpoint separately from the safety endpoints. At the analysis stage, the efficacy and safety analyses are again conducted separately. Clinicians and patients must then weigh the efficacy and safety analyses against one another when making treatment selection decisions. Unfortunately, with this approach, we do not know if the efficacy and risk events occur within the same patients or independently. To emulate clinical practice, in which both efficacy and safety information guide decision making, we may combine the efficacy and safety endpoints, at the individual patient-level, into a single, composite endpoint.30 A treatment that is superior with respect to this endpoint has clear clinical merit.
There are many cases beyond the three examples presented here in which model-based summary measures for the treatment difference are utilized in practice. For example, consider evaluating treatment efficacy longitudinally for an endpoint that consists of repeated measurement of a certain outcome over time, such as the change of hemoglobin A1c from baseline. The conventional parametric approach is to use a repeated measures mixed-effects model to quantify the treatment difference.31 The complexity of such modeling complicates parameter interpretation. Moreover, as for the models discussed previously, it is unclear how to interpret the parameter estimates when the model does not fit the data well. An alternative, model-free summary for this longitudinal endpoint could be the area under the curve constructed, for each group, from the means of the repeated measures. This area can be interpreted as an approximation to the average of the outcome across repeated measures. For the case where the outcome is a binary indicator of whether the patient is responding to treatment, the area under the curve represents the total time, on average, that patients spent responding.32
Finally, when unforeseeable intercurrent events (eg, a widespread, uncontrollable COVID-19 pandemic) prevent us from observing the study endpoints completely during follow-up, the pre-specified statistical analysis may not be able to estimate the target treatment difference. A thorough discussion on unforeseen intercurrent events and their impact on the original trial objectives according to the estimand framework introduced by ICH (2019) is advisable, including the conduct of sensitivity analyses to evaluate the collective evidence on the relative merits between the two treatments.33–36
Footnotes
CONFLICT OF INTEREST
The authors have no competing interests to declare.
DATA AVAILABILITY STATEMENT
The data that support the findings of the study in Section 2 are openly available in Goldman et al.7 at https://www.nejm.org/doi/10.1056/NEJMoa2015301. The data that support the findings of the study in Section 3 are openly available in Hellmann et al.15 at https://www.nejm.org/doi/10.1056/NEJMoa1910231 and Guyot et al.16 at http://doi.org/10.1186/1471-2288-12-9. The data that support the findings of the study in Section 4 are not publicly available.
REFERENCES
- 1.ICH Addendum: Statistical Principles for Clinical Trials. https://www.ich.org/page/efficacy-guidelines#9-2. Accessed August 18, 2020
- 2.Mallinckrodt C, Molenberghs G, Lipkovich I, Ratitch B. Estimands, Estimators and Sensitivity Analysis in Clinical Trials. Boca Raton: Chapman and Hall/CRC; 2020. [Google Scholar]
- 3.Akacha M, Bretz F, Ruberg S. Estimands in clinical trials–broadening the perspective. Stat Med. 2017;36(1):5–19. 10.1002/sim.7033. [DOI] [PubMed] [Google Scholar]
- 4.Permutt T Treatment effects, comparisons, and randomization. Stat Biopharm Res. 2020;12(2):137–141. 10.1080/19466315.2019.1624192. [DOI] [Google Scholar]
- 5.Rosenstock J, Allison D, Brikenfeld AL, et al. Effect of additional oral semaglutide vs sitagliptin on glycated hemoglobin in adults with type 2 diabetes uncontrolled with metformin alone or with sulfonylurea: the PIONEER 3 randomized clinical trial. JAMA. 2019;321(15):1466–1480. 10.1001/jama.2019.2942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wasserstein RL, Lazar NA. The ASA’s statement on p-values: context, process, and purpose. Am Stat. 2016;70(2):129–133. 10.1080/00031305.2016.1154108. [DOI] [Google Scholar]
- 7.Goldman JD, Lye DCB, Hui DS, et al. Remdesivir for 5 or 10 days in patients with severe Covid-19. NEJM. 2020;383:1827–1837. 10.1056/NEJMoa2015301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Agresti A Categorical Data Analysis. Hoboken: John Wiley & Sons; 2003. [Google Scholar]
- 9.Wang Y, Zhang D, Du G, et al. Remdesivir in adults with severe COVID-19: a randomised, double-blind, placebo-controlled, multicentre trial. Lancet. 2020;395(10236):1569–1578. 10.1016/S0140-6736(20)31022-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Beigel JH, Tomashek KM, Dodd LE, et al. Remdesivir for the treatment of Covid-19 - a preliminary report. NEJM. 2020;383:1813–1826. 10.1056/NEJMoa2007764. [DOI] [PubMed] [Google Scholar]
- 11.Cavalcanti AB, Zampieri FG, Rosa RG, et al. Hydroxychloroquine with or without azithromycin in mild-to-moderate Covid-19. N Engl J Med. 2020;383(21):2041–2052. 10.1056/NEJMoa2019014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Thas O, Neve JD, Clement L, Ottoy JP. Probabilistic index models. JRSSB. 2012;74(4):623–671. 10.1111/j.1467-9868.2011.01020.x. [DOI] [Google Scholar]
- 13.Hazard D, Kaier K, von Cube M, et al. Joint analysis of duration of ventilation, length of intensive care, and mortality of COVID-19 patients: a multistate approach. BMC Med Res Methodol. 2020;20(1):206. 10.1186/s12874-020-01082-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.McCaw ZR, Tian L, Vassy JL, et al. How to quantify and interpret treatment effects in comparative clinical studies of COVID-19. Ann Intern Med. 2020;173(8):632–637. 10.7326/M20-4044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hellmann MD, Paz-Ares L, Bernabe CR, et al. Nivolumab plus ipilimumab in advanced non–small-cell lung cancer. NEJM. 2019;381:2020–2031. 10.1056/NEJMoa1910231. [DOI] [PubMed] [Google Scholar]
- 16.Guyot P, Ades AE, Ouwens MJ, et al. Enhanced secondary analysis of survival data: reconstructing the data from published Kaplan-Meier survival curves. BMC Med Res Methodol. 2012;12:9. 10.1186/1471-2288-12-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Uno H, Claggett B, Tian L, et al. Moving beyond the hazard ratio in quantifying the between-group difference in survival analysis. J Clin Oncol. 2014;32(22):2380–2385. 10.1200/JCO.2014.55.2208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kim DH, Uno H, Wei LJ. Restricted mean survival time as a measure to interpret clinical trial results. JAMA Cardiol. 2017;2(11):1179–1180. 10.1001/jamacardio.2017.2922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.McCaw ZR, Orkaby AR, Wei LJ, Kim DH, Rich MW. Applying evidence-based medicine to shared decision making: value of restricted mean survival time. Am J Med. 2019;132(1):13–15. 10.1016/j.amjmed.2018.07.026. [DOI] [PubMed] [Google Scholar]
- 20.Pak K, Uno H, Kim DH, et al. Interpretability of cancer clinical trial results using restricted mean survival time as an alternative to the Hazard ratio. JAMA Oncol. 2017;3(12):1692–1696. 10.1001/jamaoncol.2017.2797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Eaton A, Therneau T, Le-Rademacher J. Designing clinical trials with (restricted) mean survival time endpoint: practical considerations. Clin Trials. 2020;17(3):285–294. 10.1177/1740774520905563. [DOI] [PubMed] [Google Scholar]
- 22.McMurray JJ, Packer M, Desai AS, et al. Dual angiotensin receptor and Neprilysin inhibition as an alternative to angiotensin-converting enzyme inhibition in patients with chronic systolic heart failure: rationale for and design of the prospective comparison of arni with acei to determine impact on global mortality and morbidity in heart failure trial (PARADIGM-HF). Eur J Heart Fail. 2013;15(9):1062–1073. 10.1093/eurjhf/hft052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.McMurray JJ, Packer M, Desai AS, et al. Angiotensin-neprilysin inhibition versus enalapril in heart failure. NEJM. 2014;371(11):993–1004. 10.1056/NEJMoa1409077. [DOI] [PubMed] [Google Scholar]
- 24.Mogensen UM, Gong J, Jhund PS, et al. Effect of sacubitril/valsartan on recurrent events in the prospective comparison of arni with acei to determine impact on global mortality and morbidity in heart failure trial (PARADIGM-HF). Eur J Heart Fail. 2018;20(4):760–768. 10.1002/ejhf.1139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Rogers JK, Yaroshinsky A, Pocock SJ, Stokar D, Pogoda J. Analysis of recurrent events with an associated informative dropout time: application of the joint frailty model. Stat Med. 2016;35(13):2195–2205. 10.1002/sim.6853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Claggett B, Tian L, Fu H, Solomon SD, Wei LJ. Quantifying the totality of treatment effect with multiple event-time observations in the presence of a terminal event from a comparative clinical study. Stat Med. 2018;37(25):3589–3598. 10.1002/sim.7907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Alexander BM, Schoenfeld JD, Trippa L. Hazards of hazard ratios-deviations from model assumptions in immunotherapy. N Engl J Med. 2018;378(12):1158–1159. [DOI] [PubMed] [Google Scholar]
- 28.Rahman R, Fell G, Ventz S, et al. Deviation from the proportional hazards assumption in randomized phase 3 clinical trials in oncology: prevalence, associated factors, and implications. Clin Cancer Res. 2019;25(21):6339–6345. 10.1158/1078-0432.CCR-18-3999. [DOI] [PubMed] [Google Scholar]
- 29.Tian L, Fu H, Ruberg SJ, Uno H, Wei LJ. Efficiency of two sample tests via the restricted mean survival time for analyzing event time observations. Biometrics. 2018;74(2):694–702. 10.1111/biom.12770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Evans SR, Follmann D. Using outcomes to analyze patients rather than patients to analyze outcomes: a step toward pragmatism in benefit:risk evaluation. Stat Biopharm Res. 2016;8(4):386–393. 10.1080/19466315.2016.1207561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Fitzmaurice GM, Laird NM, Ware JH. Applied Longitudinal Analysis. 2nd ed. Hoboken: Wiley; 2011. [Google Scholar]
- 32.Little R, Kang S. Intention-to-treat analysis with treatment discontinuation and missing data in clinical trials. Stat Med. 2015;34(16):2381–2390. 10.1002/sim.6352. [DOI] [PubMed] [Google Scholar]
- 33.Meyer RD, Ratitch B, Wolbers M, et al. Statistical issues and recommendations for clinical trials conducted during the COVID-19 pandemic. Stat Biopharm Res. 2020;17(3):285–294. 10.1177/1740774520905563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Collins SH, Levenson MS. Comment on “statistical issues and recommendations for clinical trials conducted during the COVID-19 pandemic”. Stat Biopharm Res. 2020;12(4):412–413. 10.1080/19466315.2020.1779123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hemmings R Under a black cloud glimpsing a silver lining: comment on statistical issues and recommendations for clinical trials conducted during the COVID-19 pandemic. Stat Biopharm Res. 2020;12(4):414–418. 10.1080/19466315.2020.1785931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Akacha M, Branson J, Bretz F, et al. Challenges in assessing the impact of the COVID-19 pandemic on the integrity and interpretability of clinical trials. Stat Biopharm Res. 2020;12(4):419–426. 10.1080/19466315.2020.1788984. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of the study in Section 2 are openly available in Goldman et al.7 at https://www.nejm.org/doi/10.1056/NEJMoa2015301. The data that support the findings of the study in Section 3 are openly available in Hellmann et al.15 at https://www.nejm.org/doi/10.1056/NEJMoa1910231 and Guyot et al.16 at http://doi.org/10.1186/1471-2288-12-9. The data that support the findings of the study in Section 4 are not publicly available.


