Hybrid CME–ODE method for efficient simulation of the galactose switch in yeast

Abstract

It is well known that stochasticity in gene expression is an important source of noise that can have profound effects on the fate of a living cell. In the galactose genetic switch in yeast, the unbinding of a transcription repressor is induced by high concentrations of sugar particles activating gene expression of sugar transporters. This response results in high propensity for all reactions involving interactions with the metabolite. The reactions for gene expression, feedback loops and transport are typically described by chemical master equations (CME). Sampling the CME using the stochastic simulation algorithm (SSA) results in large computational costs as each reaction event is evaluated explicitly. To improve the computational efficiency of cell simulations involving high particle number systems, the authors have implemented a hybrid stochastic–deterministic (CME–ODE) method into the publically available, GPU‐based lattice microbes (LM) software suite and its python interface pyLM. LM and pyLM provide a convenient way to simulate complex cellular systems and interface with high‐performance RDME/CME/ODE solvers. As a test of the implementation, the authors apply the hybrid CME‐ODE method to the galactose switch in Saccharomyces cerevisiae, gaining a 10–50× speedup while yielding protein distributions and species traces similar to the pure SSA CME.

1 Introduction

Many processes within living cells, especially gene expression, have characteristically low particle numbers and a high degree of randomness that leads to stochastic effects, such as heterogeneity in a population of cells [1–4]. The chemical master equation (CME) is a useful formalism for describing the dynamics of stochastic events in biological systems. It describes a chemical process as a continuous‐time Markov chain on a state space comprising particle numbers of each chemical species; thus, capturing the discreteness of particles and the random nature of individual chemical reactions. The widely used stochastic simulation algorithm (SSA) of Gillespie [5, 6] provides an effective method for obtaining unbiased realisations of these Markov processes. However, the SSA is limited by the fact that reaction events are accounted for explicitly. Systems with high particle counts – those containing metabolites in millimolar concentrations – or those with large reaction rate constants, have a high propensity (probability per unit time) for a reaction event to occur; thus, they evolve on fast time scales and incur large computational cost (e.g. time to solution).

To overcome the computational expense of solving the SSA for high concentration systems, researchers have devised hybrid approaches that decrease time‐to‐solution for stochastic simulations while faithfully capturing the results of stochasticity in important chemical species (e.g. transcription factors). For a brief review of methods that improve computational efficiency by reformulating the original SSA scheme in a more economical fashion, see Jahnke and Kreim [7]. Notably, Cao et al. [8] describe a method by which the chemical system of interest is separated into a set of reactions with fast rates to be simulated deterministically and a set of slow reactions to be simulated stochastically. Alfonsi et al. [9] present a hybrid model in which a CME Markov jump process describing the dynamics of the species with low particle number is coupled to ordinary differential equations (ODEs) representing the highly abundant species. Jahnke and Kriem [7] validated this technique through a rigorous error analysis of the CME–ODE partitioning which was compared to a CME treatment for a small reaction system, Pájaro and Alonso [10] examined the applicability of approximate methods to modelling genetic circuits, and Smith et al. [11] showed the applicability of hybrid methods to metabolic networks. Alternative frameworks exist, for example coupling CME with the chemical Langevin equation [12]. Algorithms to handle stochastic reaction‐diffusion processes typically partition the system into small spatial subvolumes and use the SSA to describe the reaction events within them [1, 2, 13]. The hybrid CME–ODE method discussed in this work will also accelerate spatially resolved simulations of processes described by reaction‐diffusion master equations (RDME) over such subvolumes, where reactions within each compartment are treated by the CME.

A challenging and typical scenario arises when species participating in slow reactions are also changed by firings of one or more fast reactions, making the dynamics of the slow reactions dependent on the fast reactions. While it is tempting to assume a partial thermodynamic limit for the fast reactions involving a large number of species and simply rescale the rate constants so the entire system can be treated stochastically, this assumption cannot be made for genetic switches involving nutrients. During the early phase of sugar/inducer/metabolite uptake, the system evolves quickly and errors in the approximation can compound leading to incorrect switching dynamics and even incorrect switched steady states. The study of nutrient‐induced metabolic switches is of particular importance in understanding survival fitness. As a cell adapts to a change in the composition of its environment, genes that will help in the processing and efficient usage of the new metabolite are upregulated, and genes that are no longer needed are downregulated, in an attempt to optimise its fitness.

2 Test system

We simulate the well‐studied galactose switch in Saccharomyces cerevisiae [14–16]. This system, composed of 37 species and 75 reactions, is summarised in Fig. 1 and provided in Appendix – Section 10.1. The switch has four feedback loops that respond to the presence of the sugar galactose. The transcription factor G80, in dimer form (G80d), binds to the promoters of the genes for several of the proteins (G1, G2, G3 and G80) involved in the galactose switch process, and represses their expression. When galactose binds to G3 it creates an activated complex (G3i) that can bind to G80Cd (G80d in the cytoplasm). The G3i sequesters G80 in the cytoplasm causing the genes to be in an unrepressed, active state. The proteins G2, which transports galactose into the cell, and G1, which metabolises galactose within the cell, also play key roles in the cell's response to changes in the galactose concentration in its environment.

Fig. 1.

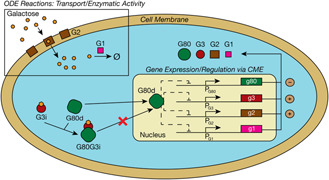
Schematic model of the galactose switch. The reactions depicted in the boxed area are simulated deterministically via an ODE solver, while those outside of this region are simulated stochastically using the SSA. A YFP reporter is under the control of the G1 promoter (PG1), and is not shown in the schematic

The positive (G1, G2, G3) and negative (G80) feedback loops of the system work in the following manner. When exposed to a galactose rich environment the cell begins to take up sugar which subsequently sequesters the transcription factor G80 in the cytoplasm, allowing the expression of the genes for G1, G2, G3 and G80. The associated mRNAs diffuse out of the nucleus into the cytoplasm where they can be translated into their protein products. As G2 transporter proteins accumulate, they subsequently motivate a flood of more galactose into the cell. As a counter‐balance, more G1 proteins are also produced to metabolise the galactose. Increased G3 counts results in the production of more G3i which can sequester the newly formed G80 produced via the lone negative feedback loop of the system. A transcriptional activator G4 is constituitively expressed and dimerises before binding to the each of the genes (G1, G2, G3, G80) in the system to promote transcription. The G4 dimer (G4d) is inactive when G80 is bound at the promoter. To measure the activity of G4d in transcription the expression of a reporter protein under the control of the G1 promoter is quantified. The reporter is a yellow fluorescent protein (YFP) added to each yeast cell whose expression level can be measured experimentally by fluorescence microscopy. The amount of reporter present is used to quantify the overall switching behaviour of the system.

Galactose can exist in up to millimolar concentrations in a yeast cell, therefore, to test our method we examine scenarios ranging from 0.055 to 2.0 mM galactose concentrations (∼1–50 million particles) that mimic the experiments performed by Oudenaarden and co‐workers [14] and Ramsey et al. [15]. We model a yeast cell with a volume of 35.7 fl and set the initial intracellular galactose concentration to zero. These initial conditions allow us to study the dynamics of the genetic switch, while necessitating the use of a deterministic‐stochastic hybrid method to track the millions of sugar particles that rapidly rush into the cell to faithfully capture stochastic gene expression. Simulations were run with a constant concentration of extracellular galactose over the course of a simulation.

The system reactions were treated either by the CME or the ODE (Fig. 1). Transcription, translation and transcription factor–promoter reactions are solved by the CME simulator. Species involved in these reactions were present in (relatively) low copy number throughout the course of a simulation and exhibit high variability, motivating stochastic treatment. Reactions with high propensities, due to highly abundant reactants or high reaction rate constants, such as the transport, binding and metabolisation of galactose, are evolved deterministically using an ODE solver. The choice of this partitioning is crucial in the effectiveness of the hybrid algorithm in capturing the stochastic behaviour seen in the pure CME. In fact, when we began this investigation we had defined the reaction of G3 with the inducer galactose as an ODE reaction and had not considered the relatively low amount of G3 that is biologically present. This assignment led to increased errors in effectively capturing CME distributions especially when the exact SSA‐ODE method (described in Section 5) where CME–ODE communication occurs at every CME reaction event was considered. This is a problem because hybrid simulations will converge to this exact result as smaller timesteps are used. Since the propensities associated with this reaction are not on the order of those for the transport reactions it should be defined as a CME reaction, without a significant deleterious effect on run‐times. A potential flaw that could arise from the above partitioning is that species involved in fast reactions are described by the ODE solver even when they are present in very small numbers (at early simulation times). At early times these species may not have smooth trajectories and can be poorly approximated by differential equations. However, we did not observe these errors playing a noticeable part in simulations of the galactose switch system, as the trajectories of these species seemed to match those obtained from the pure CME, although the hybrid method at times reached steady‐state values slightly sooner than the pure CME (Fig. 2c ).

Fig. 2.

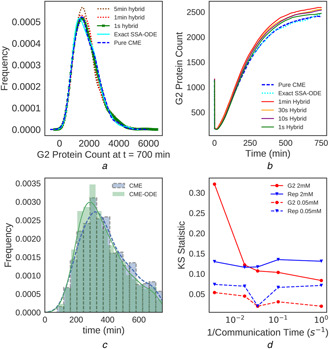
Choice of communication timestep is crucial in recovering the stochastic dynamics of the system

(a) Distributions of the unbound G2 transporter (G2) at 0.055 mM extracellular galactose when the galactose switch system reaches a steady state at 700 min of simulation time, (b) Average species count of G2 as a function of time, with 2 mM extracellular galactose as an initial condition, (c) Kernel density estimate with a histogram below of the times for G2 at 2 mM extracellular galactose to reach 80% of its average steady‐state value. CME–ODE results are given for $\tau =1\mathrm{s}$, (d) KS statistic (showing divergence from pure CME distributions) of the protein distributions for G2 and the reporter protein at 0.05 and 2 mM extracellular galactose at 700 min simulation time

We will now describe the implementation of the hybrid CME–ODE algorithm, its fidelity to pure SSA CME simulations (which we accept as a ground truth) and the relative increase in computational efficiency. We study accuracy relative to the pure CME and computational speedup as a function of sugar concentrations seen in experimental studies of the galactose switch system and provide insight into the differences that are observed. We also examine the effect the choice of interval at which information is exchanged between the CME and ODE solvers (the communication time $\tau$), comparing results and run‐times to the exact SSA‐ODE algorithm where communication occurs between the stochastic and deterministic simulation regimes at every CME reaction event. This hybrid method utilises the lattice microbes (LM) software suite [1], and is implemented using its python interface pyLM [4]. This study showcases the hybrid implementation as a new feature of LM that allows users to easily define and simulate complex biochemical systems and to achieve computational performance that was previously unavailable in LM for systems with chemical species present in millimolar concentrations.

3 Hybrid CME–ODE algorithm description

The hybrid algorithm is implemented such that the states treated by the CME and ODE are distinct and evolve independently over certain time intervals. At intervals set by the user (e.g. the communication timestep $\tau$, shown by thick vertical lines) state data is transferred between treatments. Fig. 3 illustrates the manner in which the hybrid algorithm connects the two descriptions by communicating species count information between them (see pseudocode presented in Fig. 4).

Fig. 3.

Communication scheme of the hybrid algorithm. Filled circles represent reaction events in the CME treatment and ticks represent (adaptively selected) timesteps for the ODE solver. Information is exchanged at every communication timestep

$\tau$

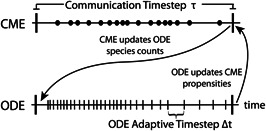
Fig. 4.

Algorithm 1: hybrid CME–ODE algorithm

The communication timestep is the key parameter of the hybrid algorithm. At the conclusion of each communication timestep, the state in the deterministic regime is updated with the species counts obtained from the end of the previous CME timestep. The ODE solver is simulated forward by $\tau$ to evolve the high particle number species in the deterministic regime. The LSODA solver is used to allow for adaptive timesteps. Then, the rates of reactions in the stochastic regime that involve species in the deterministic regime are updated accordingly. In effect the end of the previous timestep and the beginning of the current timestep happen simultaneously since no simulation time elapses between these points in the algorithm. The process then repeats itself until the total user‐defined simulation time is completed.

4 Model modifications

The model of Ramsey et al. [15] adopted for this work contained several Michaelis‐Menten and Hill reactions. To make the model amenable to simulation with the SSA, which is only valid for elementary reactions [5, 6], these reactions were decomposed into first‐ and second‐order reactions. Transport of galactose was originally modelled as a reversible Michaelis‐Menten reaction, which we decomposed into six bimolecular reactions describing the underlying Michealis‐Menten reaction explicitly (see Appendix – Section 10.3.4). Gene repression in the Ramsey et al. model was modelled using Hill functions [15]. These reactions were simplified into four binding or unbinding reactions for each gene. These reactions consist of: (i) binding of G4 dimer to the gene, (ii) unbinding of G4 dimer from the gene, (iii) binding of the G80 dimer to the G4 dimer when it is bound to the gene and (iv) unbinding of the G80 dimer:G4 dimer from the gene (see Appendix – Section 10.3.2). These modifications allow the model (hereafter referred to as the ‘reduced model’) to be directly implemented in a spatially‐resolved stochastic reaction‐diffusion framework (RDME) where the assumptions underlying Hill and Michaelis‐Menten reactions do not always hold [17].

Rate constants for the newly simplified reactions were fit to recapitulate the cooperative behaviour of the more complex rate equations. ODEs of the original and reduced model were simulated for 750 min and used to fit the rate constants. Briefly, during the fitting procedure the sum of squared differences between concentrations of each species in the original and reduced solutions was minimised. The reduced model generally reproduced the results of the original model <5% error.

5 Agreement with pure SSA CME

The communication times between the stochastic and deterministic descriptions as well as the timesteps for each solver must be evaluated to understand under which conditions the hybrid method is appropriate. In this section, we provide insight into the effect the choice of $\tau$ has on the behaviour of different chemical species at varying concentrations of extracellular galactose. The hybrid CME–ODE simulation algorithm effectively captures the stochastic dynamics of the genetic switch process at galactose concentrations ranging from micromolar to millimolar. At a small enough communication timestep, both protein distributions and average traces of key species approach pure SSA CME simulation results, while allowing for sufficient performance enhancement to make the method worthwhile. It is important to note, however, that even in the limit in which the communication timestep approaches zero the results from our hybrid implementation should not converge to the pure CME results, but rather to an exact hybrid SSA‐ODE model, where every time a reaction fires in the CME the ODE solver is called with updated species counts due to the CME reaction.

Significant error arises in the protein distributions of the unbound G2 transporter (hereafter referred to as G2) when large communication timesteps are used (Fig. 2a ). As an example, consider a simulation with an extracellular galactose concentration of 0.055 mM where a 5 min timestep was chosen. This results in an overestimation of the mean and variability in the G2 count. As G2 is affected by reactions in both the CME (gene expression) and ODE (transport), and plays a key role in bringing galactose into the cell, error in the average or the noise in this species could give rise to differences in the switching dynamics or steady‐state copy number distributions. This underscores the importance of choosing an appropriate communication timestep between the simulation regimes. As $\tau$ is decreased from 5 min to 1 s, the protein distribution begins to closely match the pure SSA CME result, with runtime only increasing from ∼25 to 45 min in the worst case.

The optimal communication timestep is dependent on the concentration of the external galactose. At an extracellular galactose concentration of 0.055 mM, a 1 min timestep seems to closely approach the CME distribution results (Fig. 2a ). However, as demonstrated by the G2 average at 2.0 mM galactose (Fig. 2b ), the 1 min timestep is on the order of a few 1000 proteins away from the pure CME result as opposed to hundreds of proteins when using a 1 s timestep at an increase of simulation time from 45 min to ∼1 h. We have observed the trend that a smaller communication timestep is often needed to capture stochastic behaviour at higher inducer concentrations. The exact SSA‐ODE trace (small dashes in Fig. 2b ), which was calculated using 250 replicates, can be used to determine whether moving to a smaller communication timestep will provide an increase in accuracy since smaller timesteps will converge to this result.

The dynamics of a chemical species can also be observed by witnessing the times taken to reach steady‐state values. At an extracellular galactose concentration of 2 mM the CME–ODE hybrid with $\tau =1\mathrm{s}$ takes similar times to reach steady‐state concentration as the pure CME (Fig. 2c ). For G2 the mean and median times to reach 80% of the average steady‐state value were <10 min faster for the CME–ODE than the CME. While the hybrid method did seem to evolve slightly faster than the CME for some of the species with reactions handled by the ODE solver the difference is relatively small (generally on the order of 5–10 min faster and in the worst case ∼20 min faster).

As a quantitative measure of disagreement between the hybrid method and the pure CME, the Kolmogorov–Smirnov (KS) statistic for protein distributions from each method was computed. The KS test calculates the maximum difference in cumulative probability between empirical cumulative distribution functions of two samples (i.e. pure CME and hybrid CME–ODE protein distributions). Therefore, identical distributions give a KS statistic of 0.00 and completely non‐intersecting distributions would give a value of 1.00. The formula for KS statistic is

$$\text{KS}=\underset{x}{\sup }F(x){}_{\text{CME}}-F(x){}_{\text{Hybrid}}$$ (1)

where ${\sup }_x$ is the supremum of the set of distances, $F(x){}_{\text{CME}}$ is the pure CME protein empirical cumulative distribution function and $F(x){}_{\text{Hybrid}}$ is the hybrid CME–ODE protein empirical cumulative distribution function.

For species with reactions in the deterministic regime (i.e. G2) a decrease in communication timestep coincides with a decrease in KS statistic (increase in agreement between protein distributions) although the observed decrease is larger at the higher external galactose concentration of 2 mM as opposed to 0.055 mM (Fig. 2d ). The p‐values associated with the KS test also decrease from 2 × 10⁻³ to 5 × 10⁻⁷ as timestep is decreased from 1 min to 1 s, showing greater agreement at smaller timesteps. However, for species that participate only in reactions in the stochastic regime such as the reporter protein, KS statistic is relatively constant with respect to communication timestep.

6 Computational performance

Having established the fidelity of the hybrid method we now demonstrate the dramatic increase in simulation efficiency it provides. Wall‐time required to simulate 750 min of the galactose switch using the hybrid method, exact SSA–ODE and the pure SSA CME are shown in Table 1 along with the relative speedup.

Table 1.

Hybrid algorithm using a 10 and 1 s communication interval can give 10–50× speedup, respectively, versus a pure CME SSA implementation. The time given is the wall‐time required to simulate 1000 replicates (250 for exact SSA‐ODE) of the system using 1 node per replicate. Simulations were performed on a Cray XE machine (NCSA Blue Waters) containing AMD 6276 ‘Interlagos’ processors

	Galactose, mM
Model	0.055	2.0
CME	2.1	47.4
exact SSA‐ODE	4.7a	47.9
	(0.45)b	(0.99)
hybrid ($\tau =10\mathrm{s}$)	0.4	1.1
	(5.2)	(43.1)
hybrid ($\tau =1\mathrm{s}$)	0.8	1.8
	(2.6)	(26.3)

^aTimes are presented in the number of hours required to simulate 750 min of cell growth.

^bValues in parenthesis indicate the speedup relative to pure CME.

While the pure SSA CME Gillespie direct method takes ∼2 days to simulate a cell introduced to 2 mM external galactose, the hybrid method using $\tau =1\mathrm{s}$ runs in <2 h. Even at the lowest concentration, 0.055 mM external galactose, simulations are executed in 25–45 min instead of 120–130 min. This speedup provides researchers with much higher throughput and can assist informing the design of more complex investigations.

The differences in the simulation times achieved when using a 1 min communication timestep versus a 1 s timestep at 2 mM external galactose demonstrate that at times the user must make a choice between accuracy (see Fig. 2a and d) and simulation speedup. While at the lower galactose concentration a 1 min communication interval appears sufficient, the G2 traces and KS statistic at 2 mM galactose (Fig. 2b and d) show that a 1 s timestep is more appropriate to capture the dynamics of the transporter species. For those considering even coarser timesteps, the run‐time for a simulation using a 5 min communication timestep is ∼50 min compared to ∼110 min for a 1 s timestep at 2 mM external galactose. By choosing a larger timestep the user may lose accuracy in describing the stochastic behaviours in the cell while not gaining a worthwhile decrease in simulation time.

While the exact SSA‐ODE method is an effective tool to determine the accuracy of hybrid methods and the appropriate communication timestep to use, it is much less computationally efficient than comparable fixed timestep runs taking ∼2 days to run at 2 mM external galactose compared to <2 h for $\tau =1\mathrm{s}$. At the lower concentration of 0.055 mM galactose the exact method is still 5–10 times slower than when using 10–1 s timesteps. The increase in simulation time for the exact method is due to the fact that makes orders of magnitude more computationally costly calls to Python to run the ODE Solver than what is made with a fixed timestep. The exact method calls the ODE Solver at every CME reaction and we have observed the time between CME reactions to be on the order of micro to nano seconds at 2 mM external galactose (much smaller than a typical $\tau =1\mathrm{s}$).

7 Conclusion

The hybrid CME–ODE algorithm implementation described in this study, now compatible with LM/pyLM, provides an effective method for the simulation of a genetic switch system containing 37 species, 75 reactions, 4 feedback loops and millions of metabolite particles within a eukaryotic cell. The 10–50‐fold computational performance increase relative to a pure SSA CME simulation for sugar concentrations ranging from micromolar to millimolar makes this simulation method an intriguing option for researchers in the field of computational biology. However, the user must determine a suitable communication timestep between the stochastic and deterministic regimes to ensure that data is passed with enough frequency to maintain the protein distributions and stochastic effects that are observed when using a pure SSA CME implementation. The results gained from these efficient hybrid CME–ODE simulations can be used to inform simulation setup conditions (communication timestep etc.) for hybrid simulations of much more computationally expensive, spatially resolved whole cell RDME studies. Hybrid simulations can utilise LM features developed for RDME simulations, such as multiple‐GPU computation [2] and optimised propensity calculation [18], without any further work on the user's part. LM provides the fastest method for RDME simulations to date and with the addition of this hybrid stochastic–deterministic method, simulations of systems with chemical species present in millimolar concentrations (such as those found in nutrient based genetic switches) are now computationally accessible.

10.1 Galactose switch model

The Python PyLM model for the galactose switch system as well as the code for using the hybrid algorithm through the ‘hookSimulation’ feature of LM is available at http://www.scs.illinois.edu/schulten/software/ODE_CME.tar.gz.

The reaction model is included below for completeness. All rates are stochastic rates (i.e. the volume of the cell has been factored into reaction rate) and are presented in $\text{mi}{\mathrm{n}}^{-1}$ and ${\text{molecules}}^{-1}$ $\text{mi}{\mathrm{n}}^{-1}$

10.2 Species

10.2.1 Genes

$\text{DG}1$	gene encoding Gal1 with nothing bound
$\text{DG}1\_\mathrm{G}4\mathrm{d}$	gene encoding Gal1 bound to G4 dimer
$\text{DG}1\_\mathrm{G}4\mathrm{d}\_\mathrm{G}80\mathrm{d}$	gene encoding Gal1 bound to the Gal4 dimer and Gal80 dimer
$\text{DG}2$	gene encoding Gal2 with nothing bound
$\text{DG}2\_\mathrm{G}4\mathrm{d}$	gene encoding Gal2 bound to G4 dimer
$\text{DG}2\_\mathrm{G}4\mathrm{d}\_\mathrm{G}80\mathrm{d}$	gene encoding Gal1 bound to the Gal4 dimer and Gal80 dimer
$\text{DG}3$	gene encoding Gal3 with nothing bound
$\text{DG}3\_\mathrm{G}4\mathrm{d}$	gene encoding Gal3 bound to G4 dimer
$\text{DG}3\_\mathrm{G}4\mathrm{d}\_\mathrm{G}80\mathrm{d}$	gene encoding Gal4 bound to the Gal4 dimer and Gal80 dimer
$\text{DG}80$	gene encoding Gal80 with nothing bound
$\text{DG}80\_\mathrm{G}4\mathrm{d}$	gene encoding Gal80 bound to G4 dimer
$\text{DG}80\_\mathrm{G}4\mathrm{d}\_\mathrm{G}80\mathrm{d}$	gene encoding Gal80 bound to the Gal4 dimer and Gal80 dimer
$\text{DGrep}$	gene encoding the reporter protein (YFP) with nothing bound
$\text{DGrep}\_\mathrm{G}4\mathrm{d}$	gene encoding reporter protein bound to G4 dimer
$\text{DGrep}\_\mathrm{G}4\mathrm{d}\_\mathrm{G}80\mathrm{d}$	gene encoding reporter bound to the Gal4 dimer and Gal80 dimer

10.2.2 mRNAs

$\mathrm{R}1$	mRNA for Gal1
$\mathrm{R}2$	mRNA for Gal2
$\mathrm{R}3$	mRNA for Gal3
$\mathrm{R}4$	mRNA for Gal4
$\mathrm{R}80$	mRNA for Gal80
reporter_rna	mRNA for the reporter gene

10.2.3 Proteins and metabolites

$\mathrm{G}1$	Gal1; galactokinase that metabolises galactose
$\mathrm{G}2$	Gal2; galactose transporter
$\mathrm{G}3$	Gal3; galactose sensing transcription factor
$\mathrm{G}3\mathrm{i}$	Gal3 bound to a galactose molecule
$\mathrm{G}4$	Gal4; a monomer of the Gal4 transcriptional repressor
$\mathrm{G}4\mathrm{d}$	Gal4 dimer; the transcriptional repressor dimer in the nucleus
$\mathrm{G}80$	Gal80; nuclear; the monomer of the transcriptional repressor
$\mathrm{G}80\mathrm{C}$	Gal80; cytoplasmic; the monomer of the transcriptional repressor in the cytoplasm
$\mathrm{G}80\mathrm{d}$	Gal80 dimer; nuclear; a dimer of the transcriptional repressor
$\mathrm{G}80\text{Cd}$	Gal80 dimer; cytoplasmic; a dimer of the transcriptional repressor in the cytoplasm
$\mathrm{G}80\mathrm{G}3\mathrm{i}$	Gal80 dimer bound to Gal3i; the transcriptional repressor sequestered in the cytoplasm
GAI	intracellular galactose
GAE	extracellular galactose
$\mathrm{G}2\text{GAI}$	galactose bound to the Gal2 transporter on the intracellular side
$\mathrm{G}2\text{GAE}$	galactose bound to the Gal2 transporter on the extracellular side
$\mathrm{G}1\text{GAI}$	galactose bound to the Gal2 transporter on the extracellular side
reporter	a yellow fluorescence reporter protein (YFP)

10.3 Reaction model

10.3.1 Transcription

$$\text{DG}1\_\mathrm{G}4\mathrm{d}\stackrel{k_1=0.7379}{⟶}\mathrm{R}1+\text{DG}1\_\mathrm{G}4\mathrm{d}$$

$$\mathrm{R}1\stackrel{k_2=0.02236}{⟶}\varnothing$$

$$\text{DG}2\_\mathrm{G}4\mathrm{d}\stackrel{k_3=2.54154}{⟶}\mathrm{R}2+\text{DG}2\_\mathrm{G}4\mathrm{d}$$

$$\mathrm{R}2\stackrel{k_4=0.077016}{⟶}\varnothing$$

$$\text{DG}3\_\mathrm{G}4\mathrm{d}\stackrel{k_5=0.426572}{⟶}\mathrm{R}3+\text{DG}3\_\mathrm{G}4\mathrm{d}$$

$$\mathrm{R}3\stackrel{k_6=0.02666}{⟶}\varnothing$$

$$\varnothing \stackrel{k_7=0.009902}{⟶}R4$$

$$\mathrm{R}4\stackrel{k_8=0.0247552}{⟶}\varnothing$$

$$\text{DGrep}\_\mathrm{G}4\mathrm{d}\stackrel{k_9=1.1437}{⟶}\text{reporter}\_\text{rna}+\text{DGrep}\_\mathrm{G}4\mathrm{d}$$

$$\text{reporter}\_\text{rna}\stackrel{k_{10}=0.03466}{⟶}\varnothing$$

$$\text{DG}80\_\mathrm{G}4\mathrm{d}\stackrel{k_{11}=0.6065}{⟶}\mathrm{R}80+\text{DG}80\_\mathrm{G}4\mathrm{d}$$

$$\mathrm{R}80\stackrel{k_{12}=0.028881}{⟶}\varnothing$$

10.3.2 DNA regulation

$$\text{DG}1+\mathrm{G}4\mathrm{d}\stackrel{k_1=0.1}{⟶}\text{DG}1\_\mathrm{G}4\mathrm{d}$$

$$\text{DG}1\_\mathrm{G}4\mathrm{d}\stackrel{k_2=0.384615}{⟶}\text{DG}1+\mathrm{G}4\mathrm{d}$$

$$\text{DG}1\_\mathrm{G}4\mathrm{d}+\mathrm{G}80\mathrm{d}\stackrel{k_3=0.1}{⟶}\text{DG}1\_\mathrm{G}4\mathrm{d}\_\mathrm{G}80\mathrm{d}$$

$$\text{DG}1\_\mathrm{G}4\mathrm{d}\_\mathrm{G}80\mathrm{d}\stackrel{k_4=0.085317}{⟶}\text{DG}1\_\mathrm{G}4\mathrm{d}+\mathrm{G}80\mathrm{d}$$

$$\text{DG}2+\mathrm{G}4\mathrm{d}\stackrel{k_5=0.1}{⟶}\text{DG}2\_\mathrm{G}4\mathrm{d}$$

$$\text{DG}2\_\mathrm{G}4\mathrm{d}\stackrel{k_6=10.101}{⟶}\text{DG}2+\mathrm{G}4\mathrm{d}$$

$$\text{DG}2\_\mathrm{G}4\mathrm{d}+\mathrm{G}80\mathrm{d}\stackrel{k_7=0.1}{⟶}\text{DG}2\_\mathrm{G}4\mathrm{d}\_\mathrm{G}80\mathrm{d}$$

$$\text{DG}2\_\mathrm{G}4\mathrm{d}\_\mathrm{G}80\mathrm{d}\stackrel{k_8=0.134989}{⟶}\text{DG}2\_\mathrm{G}4\mathrm{d}+\mathrm{G}80\mathrm{d}$$

$$\text{DG}3+\mathrm{G}4\mathrm{d}\stackrel{k_9=0.1}{⟶}\text{DG}3\_\mathrm{G}4\mathrm{d}$$

$$\text{DG}3\_\mathrm{G}4\mathrm{d}\stackrel{k_{10}=4.03226}{⟶}\text{DG}3+\mathrm{G}4\mathrm{d}$$

$$\text{DG}3\_\mathrm{G}4\mathrm{d}+\mathrm{G}80\mathrm{d}\stackrel{k_{11}=0.1}{⟶}\text{DG}3\_\mathrm{G}4\mathrm{d}\_\mathrm{G}80\mathrm{d}$$

$$\text{DG}3\_\mathrm{G}4\mathrm{d}\_\mathrm{G}80\mathrm{d}\stackrel{k_{12}=0.530504}{⟶}\text{DG}3\_\mathrm{G}4\mathrm{d}+\mathrm{G}80\mathrm{d}$$

$$\text{DGrep}+\mathrm{G}4\mathrm{d}\stackrel{k_{13}=0.1}{⟶}\text{DGrep}\_\mathrm{G}4\mathrm{d}$$

$$\text{DGrep}\_\mathrm{G}4\mathrm{d}\stackrel{k_{14}=0.384615}{⟶}\text{DGrep}+\mathrm{G}4\mathrm{d}$$

$$\text{DGrep}\_\mathrm{G}4\mathrm{d}+\mathrm{G}80\mathrm{d}\stackrel{k_{15}=0.1}{⟶}\text{DGrep}\_\mathrm{G}4\mathrm{d}\_\mathrm{G}80\mathrm{d}$$

$$\text{DGrep}\_\mathrm{G}4\mathrm{d}\_\mathrm{G}80\mathrm{d}\stackrel{k_{16}=0.085317}{⟶}\text{DGrep}\_\mathrm{G}4\mathrm{d}+\mathrm{G}80\mathrm{d}$$

$$\text{DG}80+\mathrm{G}4\mathrm{d}\stackrel{k_{17}=0.1}{⟶}\text{DG}80\_\mathrm{G}4\mathrm{d}$$

$$\text{DG}80\_\mathrm{G}4\mathrm{d}\stackrel{k_{18}=4.03226}{⟶}\text{DG}80+\mathrm{G}4\mathrm{d}$$

$$\text{DG}80\_\mathrm{G}4\mathrm{d}+\mathrm{G}80\mathrm{d}\stackrel{k_{19}=0.1}{⟶}\text{DG}80\_\mathrm{G}4\mathrm{d}\_\mathrm{G}80\mathrm{d}$$

$$\text{DG}80\_\mathrm{G}4\mathrm{d}\_\mathrm{G}80\mathrm{d}\stackrel{k_{20}=0.530504}{⟶}\text{DG}80\_\mathrm{G}4\mathrm{d}+\mathrm{G}80\mathrm{d}$$

10.3.3 Translation

$$\mathrm{R}1\stackrel{k_1=1.92541}{⟶}\mathrm{G}1+\mathrm{R}1$$

$$\mathrm{G}1\stackrel{k_2=0.003851}{⟶}\varnothing$$

$$\mathrm{R}2\stackrel{k_3=13.4779}{⟶}\mathrm{G}2+\mathrm{R}2$$

$$\mathrm{G}2\stackrel{k_4=0.003851}{⟶}\varnothing$$

$$\mathrm{R}3\stackrel{k_5=55.4518}{⟶}\mathrm{G}3+\mathrm{R}3$$

$$\mathrm{G}3\stackrel{k_6=0.01155}{⟶}\varnothing$$

$$\mathrm{R}4\stackrel{k_7=10.7091}{⟶}\mathrm{G}4+\mathrm{R}4$$

$$\mathrm{G}4\stackrel{k_8=0.0069315}{⟶}\varnothing$$

$$\text{reporter}\_\text{rna}\stackrel{k_9=5.7762}{⟶}\text{reporter}+\text{reporter}\_\text{rna}$$

$$\text{reporter}\stackrel{k_{10}=0.01155}{⟶}\varnothing$$

$$\mathrm{R}80\stackrel{k_{11}=3.67368}{⟶}\mathrm{G}80+\mathrm{R}80$$

$$\mathrm{G}80\stackrel{k_{12}=0.0069315}{⟶}\varnothing$$

10.3.4 Transport and enzymatic

$$\mathrm{G}2\text{GAI}\stackrel{k_1=4350}{⟶}\mathrm{G}2\text{GAE}$$

$$\mathrm{G}2\text{GAE}\stackrel{k_2=4350}{⟶}\mathrm{G}2\text{GAI}$$

$$\mathrm{G}2\text{GAE}\stackrel{k_3=2392.5}{⟶}\mathrm{G}2$$

$$\mathrm{G}2\stackrel{k_4=0.00031353\ast \text{GAE}}{⟶}\mathrm{G}2\text{GAE}$$

$$\mathrm{G}2\text{GAE}\stackrel{k_5=0.003851}{⟶}\varnothing$$

$$\mathrm{G}2+\text{GAI}\stackrel{k_6=0.00031353}{⟶}\mathrm{G}2\text{GAI}$$

$$\mathrm{G}2\text{GAI}\stackrel{k_7=2392.5}{⟶}\mathrm{G}2+\text{GAI}$$

$$\mathrm{G}2\text{GAI}\stackrel{k_8=0.003851}{⟶}\text{GAI}$$

$$\mathrm{G}1+\text{GAI}\stackrel{k_9=0.000402426}{⟶}\mathrm{G}1\text{GAI}$$

$$\mathrm{G}1\text{GAI}\stackrel{k_{10}=1842.5}{⟶}\mathrm{G}1+\text{GAI}$$

$$\mathrm{G}1\text{GAI}\stackrel{k_{11}=3350}{⟶}\mathrm{G}1$$

$$\mathrm{G}1\text{GAI}\stackrel{k_{12}=0.003851}{⟶}\text{GAI}$$

10.3.5 Transcription factor

$$\mathrm{G}3+\text{GAI}\stackrel{k_1=7.45\times {10}^{-7}}{⟶}\mathrm{G}3\mathrm{i}$$

$$\mathrm{G}3\mathrm{i}\stackrel{k_2=890}{⟶}\mathrm{G}3+\text{GAI}$$

$$\mathrm{G}3\mathrm{i}\stackrel{k_3=0.01155}{⟶}\text{GAI}$$

$$\mathrm{G}80\mathrm{G}3\mathrm{i}\stackrel{k_4=0.0159616}{⟶}\mathrm{G}3\mathrm{i}+\mathrm{G}80\text{Cd}$$

$$\mathrm{G}3\mathrm{i}+\mathrm{G}80\text{Cd}\stackrel{k_5=0.025716}{⟶}\mathrm{G}80\mathrm{G}3\mathrm{i}$$

$$\mathrm{G}80\mathrm{G}3\mathrm{i}\stackrel{k_6=0.005775}{⟶}\varnothing$$

$$\mathrm{G}4+\mathrm{G}4\stackrel{k_7=100}{⟶}\mathrm{G}4\mathrm{d}$$

$$\mathrm{G}4\mathrm{d}\stackrel{k_8=0.001}{⟶}\mathrm{G}4+\mathrm{G}4$$

$$\mathrm{G}4\mathrm{d}\stackrel{k_9=0.0069315}{⟶}\varnothing$$

$$\mathrm{G}80+\mathrm{G}80\stackrel{k_{10}=100}{⟶}\mathrm{G}80\mathrm{d}$$

$$\mathrm{G}80\mathrm{d}\stackrel{k_{11}=0.001}{⟶}\mathrm{G}80+\mathrm{G}80$$

$$\mathrm{G}80\mathrm{d}\stackrel{k_{12}=0.0069315}{⟶}\varnothing$$

$$\mathrm{G}80\mathrm{C}+\mathrm{G}80\mathrm{C}\stackrel{k_{13}=100}{⟶}\mathrm{G}80\text{Cd}$$

$$\mathrm{G}80\text{Cd}\stackrel{k_{14}=0.001}{⟶}\mathrm{G}80\mathrm{C}+\mathrm{G}80\mathrm{C}$$

$$\mathrm{G}80\text{Cd}\stackrel{k_{15}=0.0069315}{⟶}\varnothing$$

$$\mathrm{G}80\text{Cd}\stackrel{k_{16}=50}{⟶}\mathrm{G}80\mathrm{d}$$

$$\mathrm{G}80\mathrm{d}\stackrel{k_{17}=50}{⟶}\mathrm{G}80\text{Cd}$$

$$\mathrm{G}80\mathrm{C}\stackrel{k_{18}=50}{⟶}\mathrm{G}80$$

$$\mathrm{G}80\stackrel{k_{19}=50}{⟶}\mathrm{G}80\mathrm{C}$$