Abstract
An improved Hindmarsh–Rose (HR) neuron model, where the memristor is a bridge between membrane potential and magnetic flux, can be used to investigate the effect of periodic signals on autaptic regulation of neurons under electromagnetic radiation. Based on the improved HR model driven by periodic high–low‐frequency current and electromagnetic radiation, the responses of electrical autaptic regulation with diverse high–low‐frequency signals are investigated using bifurcation analysis. It is found that the electrical modes of neurons are determined by the selecting parameters of both periodic high and low‐frequency current and electromagnetic radiation, and the Hamiltonian energy depends on the neuronal firing modes. The effects of Gaussian white noise on the membrane potential are discussed using numerical simulations. It is demonstrated that external high–low‐frequency stimulus plays a significant role in the autaptic regulation of neural firing mode, and the electrical mode of neurons can be affected by the angular frequency of both high–low‐frequency forcing current and electromagnetic radiation. The mechanism of neuronal firing regulated by high–low‐frequency signal and electromagnetic radiation discussed here could be applied to research neuronal networks and synchronisation modes.
Inspec keywords: bioelectric potentials, neural nets, bifurcation, synchronisation, memristors, neurophysiology, numerical analysis, white noise
Other keywords: synchronisation modes, external periodic signals, electromagnetic radiation, improved Hindmarsh–Rose neuron model, membrane potential, periodic high–low‐frequency current, electrical autaptic regulation, diverse high–low‐frequency signals, neuronal firing modes, external high–low‐frequency stimulus, high–low‐frequency forcing current, high–low‐frequency signal, research neuronal networks
1 Introduction
The electrical activities of neurons have various modes which include the quiescent state, spiking state, bursting state, and chaotic state [1]. These modes play an important role in the nervous system, which can achieve different biological functions through information coding and integration [2]. Those processes are useful to adapt to the changes in the internal or external environment. Moreover, the neural network is a complicated network of information which includes a large number of nerve cells [3–5]. In a neuronal network, local heterogeneity occurred in a part of neurons; therefore, ordered waves could emit from the heterogeneity [6, 7]. In previous studies, Hodgkin and Huxley observed abundant electrical modes of neurons in experiments [8–10], and proposed the Hodgkin–Huxley model of neuronal discharge patterns [11]. Subsequently, a great deal of excitable cell models had been built, such as the Hindmarsh–Rose (HR) model, FitzHugh–Nagumo model, Morris–Lecar model, Chay model, and so on [12–21]. These models based on the non‐linear dynamical theory are studied by a single neuron or the neural network [22–25]. In fact, bifurcation analysis and phase synchronisation are used to study the multidimensional HR neuron model [26–29]. It is also confirmed that diverse states of neurons make neurons maintain different Hamilton energy; meanwhile, bursting and chaotic state maintain a lower energy in neuronal firing activities [30]. Wang et al. [31] used the biophysical energy to present the diversification of biological energy in the brain. Ma et al. [32] calculated Hamilton energy on distinct chaotic attractors and found the dependence of oscillating behaviours on Hamilton energy.
Synapse is a part in the information transmission between neurons [33]. An autapse is synaptic connections between neurons and themselves in the nervous system. In recent researches autapse has played an important role in the course of realisation of nervous system function by theoretical and experimental evidences [34–38]. In [39], Yilmaz et al. found that a proper network structure and appropriate coupling strength could make sure the optimal propagation of local rhythm. The autapse not only changes the potential of neurons but also regulates the neural network group activities (similar findings are shown in [40]), and it was described as a feedback current with time delay [41, 42]. Autapses are usually divided into chemical and electrical autapses. Chemical autapses are easier than electrical autapses to guide electrical activities of neurons [43, 44]. It was proved that the connection of autapses is efficacious to advance gamma oscillation. In previous researches, the improved HR model takes the influence of electromagnetic induction into account consisting of the terms under a magnetic flow in the equation of dynamics [45, 46]. The high–low‐frequency signal plays a role in the non‐linear system, for instance, the theories of vibrational resonance that the bistable system uses stimulus as a modulation signal to change the system dynamics by adjusting the amplitude or frequency of the high‐frequency signal under the action of high‐ and low‐frequency signals [47]. In the neuronal system, it is optimal that the response to the membrane potential of low‐frequency signal in the neuronic system under the interaction of high‐ and low‐frequency forcing signals and certain strength of high‐frequency signal [48, 49].
Recently, the improved HR model driven by the external high–low‐frequency stimulant current and electromagnetic radiation had been investigated, and the conversion between different discharge modes was observed [50, 51]. However, the autaptic regulation was not considered in [50, 51]. Although the electrical autaptic regulation was taken into account in the neuronal firing modes [52], the external high–low‐frequency forcing current and the external high–low‐frequency electromagnetic radiation were not considered in the improved HR model. In addition, the effects of autapstic regulation on the membrane potential were not discussed in the previous works [50, 51].
In this paper, the improved HR model is used to study the electrical modes of neurons and the Hamilton energy. First, the improved HR model driven by periodic high–low‐frequency current and by external periodic high–low‐frequency electromagnetic radiation are, respectively, studied; the formulas of Hamilton energy are derived by using the Helmholtz theorem, and the Gaussian white noise on the membrane potential is considered in the improved HR model. Second, the responses of electrical autaptic regulation with diverse high–low‐frequency signals are investigated by using bifurcation analysis, and the effects of Gaussian white noise on the membrane potential are discussed by using the numerical simulation method. Finally, we end with the conclusions.
2 Model and results
The fourth Runge–Kutta algorithm is applied to the flowing numerical calculations, the step of time h is selected as 0.01, and the initial values for the variables of the two models are selected as (0.3, 0.2, 0.1, 0.0). The Gaussian random numbers are generated by the ‘Numerical Recipes’ routine ran2 using the Box–Muller algorithm. Moreover, the flowing results are computed with the tools in C++. The parameters in the equation are taken as a = 1.0, b = 3.0, c = 1.0, d = 5.0, s = 4.0, r = 0.006, k = 0.9, k 1 = 0.4, k 2 = 0.5, α = 0.1, β = 0.02, g = −0.5, and τ = 20.
According to (8), (9), (15), and (16), the Hamilton energy and the Hamilton over time are related to any parameter in the dynamic equation (1). In the following simulations, we focus on the effects of external high–low‐frequency current and electromagnetic radiation signals on the improved HR neuron model by selecting the different parameters with regard to the two kinds of periodic high–low‐frequency signals. In our calculations, the neuron is regarded as quiescent state if the membrane potential of the neuron is lower than zero (a threshold).
2.1 Autaptic regulation on neuronal discharge modes under periodic high–low‐frequency external forcing current
The dynamic equations of the improved HR neuron model driven by periodic high–low‐frequency current are described as follows:
| (1) |
| (2) |
| (3) |
| (4) |
where the variables x, y, z, and φ denote the membrane potential of the neuron, slow current interrelated recovery variable, adaption current, and magnetic flux across the neuronal membrane, respectively. The memory conductance of the memristor depicts the coupling interaction of the neuronic membrane potential, and the expression of magnetic flow is
| (5) |
with the constants α and β.
In (1), the term k 1 ρ(φ)x is an additional induced current. I aut describes the electric autapse current as well as the effects of aynapses on neuronal electrical activities, which is given by
| (6) |
in which g and τ are the feedback gain and the time delay, respectively. The negative value of g would engender the negative feedback and inhibit the electrical activity of neurons. On the contrary, the positive gain g would induce positive feedback and promote neuronal discharge. Therefore, the discharge is further suppressed by the longer time delay if g is taken a negative value, and the discharge is further enhanced by the longer time delay if g is selected as a positive value. The term I ext is the external periodic high‐ and low‐frequency currents given by
| (7) |
where A and B are the amplitudes of external high–low‐frequency current and ω and Nω are the angular frequencies of the mixed external stimulus current.
The transformation of the neuronic discharge patterns can cause the changes of the corresponding energy. Therefore, Hamilton energy and Hamiltonian evolution over time can be calculated by the Helmholtz theorem [53], and the expressions are as follows:
| (8) |
| (9) |
In Fig. 1, the external periodic high–low‐frequency current be exerted after 1000 time units, and the neuron keeps quiescent before adding the forcing current. It is found that the transform of electrical modes of neurons can be observed by changing the angular frequency of the mixed current. When the angular frequency equals 0.001, the neuronal firing state stays in a quiescent state. When the angular frequency is chosen as 0.03, the neuron maintains a spiking state. Moreover, the neuronal state keeps intermittent periodic spiking discharge by exerting an external angular frequency of 0.05. Finally, while the angular frequency keeps 0.05, the electrical mode of the neuron is below the threshold of zero.
Fig. 1.

Time series of membrane potential in a neuron under different angular frequency ω: A = B = 1.0, N = 200, g = −0.5, τ = 20
(a) ω = 0.001, (b) ω = 0.03, (c) ω = 0.05, (d) ω = 0.1
For the sake of representing the effects of angular frequency on the electrical activities of neurons markedly, the inter‐spike interval (ISI) of action potential with the increasing of angular frequency is shown in Fig. 2. When the angular frequency of the high–low‐frequency forcing current is >0.001 and <0.0079, the firing state of the neuron keeps the same period of spiking discharge. When the angular frequency increases to 0.0167, the neuron is in a bursting state. Moreover, when the angular frequency is >0.0167, the neuron maintains a spiking state. Therefore, considering the high–low‐frequency external forcing current with different frequencies, the firing patterns of the neuron are diverse.
Fig. 2.

Bifurcation diagram associated with different angular frequency ω: A = 1.0, B = 1.0, N = 200, g = −0.5, τ = 20. ISI denotes the inter‐spike interval in membrane potential series
Fig. 3 shows the ISI with the increasing amplitude of high‐frequency signal. It can be observed that, although the change of autaptic regulation of neuronal discharge mode is not obvious, the transformation of the neuron electrical pattern is caused by changing the amplitude. When the amplitude is <0.82, the electrical mode maintains a spiking state; however, with increasing the amplitude, the neuronal electrical pattern is in a bursting state. The changing range of ISI is very small when the amplitude varies from 0.82 to 6.52; nevertheless, when the amplitude B is >6.52, the effect of the amplitude of the high‐frequency signal on autaptic regulation is obvious in neuronic electrical activities.
Fig. 3.

Bifurcation diagram associated with amplitude B of the high‐frequency forcing current: A = 1.0, ω = 0.01, N = 200, g = −0.5, τ = 20. ISI denotes the inter‐spike interval in membrane potential series
Fig. 4 shows x and H as a function of time under different condition (B, ω), respectively. The Hamilton energy and the Hamilton energy over time are calculated using (8) and (9). The periodic high–low‐frequency forcing current is exerted on neurons after 1000 time units. As mentioned in the introduction, the changes in Hamilton energy are related to the transformations of electrical pattern of neurons. Our results show that different parameters of angular frequency and amplitude of high–low‐frequency forcing currents can cause the transformation of electrical modes. Meanwhile, the change of modes also can cause the diversification of Hamilton energy. Furthermore, the energy increases with the decrease in the membrane potential. In other words, the energy gradually decreases when the electrical modes of neuron transition from the quiescent state to the spiking state to bursting state and then to chaotic state.
Fig. 4.
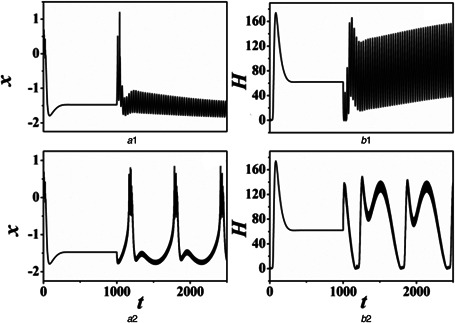
Evolution of action potential and energy function with time are calculated by changing the high–low‐frequency forcing current. The forcing current is triggered at t = 1000 time units. For
(a1, b1) B = 1.0, ω = 0.001, (a2, b2) B = 0.1, ω = 0.01
Fig. 5 shows the various electrical modes (or states) of neuron in the plane of the parameters (B, ω). The results confirm that the stable states rely on the parameter selection of high–low‐frequency forcing current. The transformation can be dominated by frequency and amplitude. The neuronal discharge pattern keeps quiescent state with small frequencies and low amplitude; however, the frequency is too large to make the neuron maintain a quiescent state. With the frequency decreasing, the electrical mode of neuron changes from the quiescent state to the spiking state, and then to the bursting state. Furthermore, for the high–low‐frequency forcing current, the effect of amplitude on the electrical mode is smaller than that of angular frequency on the electrical mode.
Fig. 5.

Distribution of the stable state by high–low‐frequency forcing current: A = 1.0, N = 200, g = −0.5, τ = 20
2.2 Autaptic regulation on neuronal discharge modes under periodic high–low frequency electromagnetic radiation
The dynamic equations of the improved HR neuron model driven by electromagnetic radiation are described by
| (10) |
| (11) |
| (12) |
| (13) |
where the term I ext in (1) is an external constant current. The term φ ext in (13) represents the external periodic high–low‐frequency electromagnetic radiation, which is assumed as
| (14) |
where A and B are the amplitudes of low‐ and high‐frequency electromagnetic radiation, respectively. ω and Nω are angular frequencies of mixed electromagnetic radiation.
The Hamilton energy and the evolution of Hamiltonian energy with time can be derived by the Helmholtz theorem, and the expressions are given by
| (15) |
| (16) |
Fig. 6 shows the effects of high–low‐frequency electromagnetic radiation on electrical modes (or states) of neurons; the high–low‐frequency electromagnetic radiation is applied to the neuron after 1000 time units. The effects of high–low‐frequency electromagnetic radiation on autaptic regulation in electrical activities can be observed by changing the angular frequency of electromagnetic radiation. When the angular frequency is 0.001, the electrical activity of the neuron is modulated by adding the electrical radiation in the period of 1000–4250 time units. Moreover, when the angular frequency is 0.01, the neuronal firing pattern becomes intermittent spiking discharge. When the frequency is chosen as 0.3, the electrical activity of the neuron is enhanced slightly by adding the electromagnetic radiation and present a bursting state. When the frequency is 0.5, the discharge mode of neuron is in the spiking state.
Fig. 6.

Time series of membrane potential in a neuron under different angular frequency ω of high–low‐frequency electromagnetic radiation: A = B = 1.0, N = 200, Iext = 1.8, g = −0.5, τ = 20
(a) ω = 0.001, (b) ω = 0.01, (c) ω = 0. 3, (d) ω = 0.05
Fig. 7 shows the ISI with the increase of angular frequency of high–low‐frequency electromagnetic radiation. The transformation of electrical mode on neurons can be observed clearly. The changes in the electrical mode are quit significant a phenomenon. When the value of angular frequency is small, the periodicity of the neuronal discharge mode is not obvious. When the angular frequency is >0.0012 and <0.037, the electric mode of neuron is in a spiking state. Moreover, the angular frequency is >0.095 and <0.113, the discharge mode of the neuron maintains a chaotic state. Therefore, the electrical pattern of neurons presents a spiking or bursting state with proper frequency of high–low‐frequency electromagnetic radiation.
Fig. 7.

Bifurcation diagram associated with different angular frequency ω of high–low‐frequency electromagnetic radiation: A = 1.0, B = 1.0, ω = 0.01, N = 200, g = −0.5, τ = 20. ISI denotes the inter‐spike interval in membrane potential series
Fig. 8 shows x and H as a function of time under different conditions (B, ω), respectively. The Hamilton energy and the Hamilton energy over time are calculated by using (15) and (16). The periodic high–low‐frequency electromagnetic radiation is exerted on neurons after 1000 time units. The results indicate that different parameters of angular frequency and amplitude of high–low‐frequency electromagnetic radiation give rise to the transformation of electrical modes of neurons; the changes of modes can lead to differences in Hamilton energy.
Fig. 8.

Evolution of action potential and energy function with time are calculated by changing the external high–low‐frequency electromagnetic radiation. The electromagnetic radiation is triggered at t = 1000 time units. For
(a1, b1) B = 0.1, ω = 0.01, (a2, b2) B = 1.0, ω = 0.001
Fig. 9 shows the electrical modes (or states) of neurons in the plane of the parameters (B, ω). It can be found that the regulated states depend on the parameters choice of high–low‐frequency electromagnetic radiation. The change is affected by the amplitude and angular frequency. Moreover, with the angular frequency of high–low‐frequency increase, the electrical mode of neurons changes from the quiescent state to spiking state. The spiking or bursting state will be presented by choosing suitable angular frequency and amplitude of high–low‐frequency electromagnetic radiation.
Fig. 9.

Distribution of the stable state by high–low‐frequency electromagnetic radiation: A = 1.0, N = 200, Iext = 1.8, g = −0.5, τ = 20
2.3 Autaptic regulation on neuronal discharge modes under Gaussian white noise
To study the effect of Gaussian white noise on the membrane potential of neurons, the dynamic equation (1) with Gaussian white noise can be rewritten as
| (17) |
where ξ(t) represents that the Gaussian white noise is added to the term that changes in membrane potential over time, and the membrane noise with mean and auto‐correlation function:
| (18) |
with the noise intensity D.
To discuss the effects of Gaussian white noise on the membrane potential, the dynamic equation (13) with Gaussian white noise is rewritten as follows:
| (19) |
where the term ξ(t) means that the Gaussian white noise is added to the term that changes in magnetic flux over time, and its mean and auto‐correlation function are given by (18).
In this subsection, the effects of membrane noise and stochastic magnetic flux on the membrane potential are, respectively, discussed by using numerical simulation. Fig. 10 shows the effects of membrane noise on the membrane potential, in which the periodic high–low‐frequency forcing current is added after 1000 time units, and the Gaussian white noise is exerted after 3000 time units. It is confirmed that the discharge of neurons can be enhanced by membrane noise. With the increasing of noise intensity (i.e. membrane noise), the electrical modes become more chaotic.
Fig. 10.

Time series of membrane potential of neurons under different noise intensity D of white Gaussian noise. The high–low‐frequency forcing current is triggered at t = 1000 time units and the white Gaussian noise is triggered at t = 3000 time units: A = B = 1.0, ω = 0.01, N = 200, g = −0.5, τ = 20
(a) D = 0.1, (b) D = 1.0, (c) D = 5.0, (d) D = 10.0
Fig. 11 shows the effects of stochastic magnetic flux on membrane potential, in which the periodic high–low‐frequency electromagnetic radiation is added after 1000 time units, and the Gaussian noise is exerted on neurons after 3000 time units. The results show that the neuronal electrical pattern is modulated by the stochastic magnetic flux, and the firing mode will become chaotic state with the increasing of noise intensity (i.e. the stochastic magnetic flux).
Fig. 11.

Time series of membrane potential of neurons under different noise intensity D with periodic high–low‐frequency electromagnetic radiation. The high–low‐frequency signal is triggered at t = 1000 time units and the white Gaussian noise is triggered at t = 3000 time units: A = B = 1.0, ω = 0.01, N = 200, I = 1.8, g = −0.5, τ = 20
(a) D = 0.1, (b) D = 1.0, (c) D = 5.0, (d) D = 15.0
Therefore, when we consider the magnetic flux affected by both the periodic high–low‐frequency forcing current and Gaussian white noise (i.e. membrane noise), the neuronal firing capacity can be enhanced by increasing the noise intensity. However, when we consider the magnetic flux affected by the high–low‐frequency electromagnetic radiation and the stochastic magnetic flux, the neuronal firing capacity can be inhibited by increasing the noise intensity.
3 Conclusion
In this paper, the autaptic regulation of electrical activities in neurons is observed under electromagnetic induction when different periodic high–low‐frequency forcing signals are applied on the neurons. The Hamilton energy and the Hamilton over time are calculated by the Helmholtz theory. Multiply mode of transitions in electrical patterns of neurons can be induced by changing the parameters of different high–low‐frequency forcing signals.
Our results confirm that the Hamilton energy increases when the neuronal electrical state is in a quiescent state, and the Hamilton energy decreases when the firing mode of neuron stays in a chaotic state. According to the distribution of the stable state with different high‐ and low‐frequency stimuli, the firing mode of neurons is regulated by the frequency and amplitude of high–low‐frequency forcing signal. The electrical modes of neurons keep a quiescent state by electing different amplitudes and angular frequencies of high–low‐frequency signals. The influences of high–low‐frequency signal on autaptic regulation of neuronal electrical activities are observed in these studies. However, it is found that the spiking state, bursting state, and even the quiescent state are induced by exerting proper angular frequency of different periodic high–low‐frequency signals.
The effects of membrane noise and stochastic magnetic flux on the membrane potential are, respectively, discussed by using numerical simulation. It is found that the firing capacity of neurons is enhanced by the membrane noise; however, the neuronal firing capacity is inhibited by the stochastic magnetic flux.
In previous researches [50, 51], the transformations of electrical modes in neurons were observed by exerting diverse high‐ and low‐frequency stimuli. Compared with the previous studies, when considering the autapstic regulation of negative feedback, the firing mode of neurons changes from the bursting or chaotic state to periodic spiking state at a suitable angular frequency of high–low‐frequency electromagnetic radiation. In this paper, the responses of autaptic regulation with diverse high–low‐frequency signals are studied during neuronic firing modes under electromagnetic induction. It gives possible orientation for the neuronal network and synchronisation modes.
There are various types of noise in biological systems, such as the Gaussian white noise with zero means, sine‐Wiener noises, channel noise, and so on. These types of noise had been explored in previous studies [54–58]. Moreover, the effects of field coupling and dependence of energy on the mode of electrical activity are researched in [59, 60]. Therefore, in our future works, it should be taken into account the multifarious types of noise, and apply the similar mechanism to other neuronal models, such as the Hodgkin–Huxley model, the Chay model, the FHN model, etc. Furthermore, it will be of great significance to further consider the field coupling and the dependence of energy on neuronal patterns on the basis of this paper.
4 Acknowledgments
This work was supported by the National Natural Science Foundation of China under 11775091 and 11474117. The authors acknowledge Prof. Jun Ma from the Lanzhou University of Technology for the constructive suggestions.
5 References
- 1. Izhikevich E.M.: ‘Neural excitability, spiking and bursting’, Int. J. Bifurcat. Chaos, 2000, 10, pp. 1171–1266 [Google Scholar]
- 2. Postnov D.E., Koreshkov R.N., and Brazhe N.A. et al.: ‘Dynamical patterns of calcium signaling in a functional model of neuron–astrocyte networks’, J. Biol. Phys., 2009, 35, pp. 425–445 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Wig G.S., Schlaggar B.L., and Petersen S.E.: ‘Concepts and principles in the analysis of brain networks’, Ann. N.Y. Acad. Sci., 2011, 1224, pp. 126–146 [DOI] [PubMed] [Google Scholar]
- 4. Ratté S., Hong S., and Schutter E.D. et al.: ‘Impact of neuronal properties on network coding: roles of spike initiation dynamics and robust synchrony transfer’, Neuron, 2013, 78, pp. 758–772 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Bean B.P.: ‘The action potential in mammalian central neurons’, Nat. Rev. Neurosci., 2007, 8, pp. 451–465 [DOI] [PubMed] [Google Scholar]
- 6. Hodgkin A.L., and Huxley A.F.: ‘Currents carried by sodium and potassium ions through the membrane of the giant axon of loligo’, J. Physiol., 1952, 116, pp. 449–472 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Ma J., Wu F.Q., and Hayat T. et al.: ‘Electromagnetic induction and radiation‐induced abnormality of wave propagation in excitable media’, Physica A, 2017, 486, pp. 508–516 [Google Scholar]
- 8. Jaeger J., Czobor P., and Berns S.M.: ‘Basic neuropsychological dimensions in schizophrenia’, Schizophr. Res., 2003, 65, pp. 105–116 [DOI] [PubMed] [Google Scholar]
- 9. Hermann B.P.: ‘Imaging epilepsy’, J. Int. Neuropsych. Soc., 2006, 12, pp. 154–155 [Google Scholar]
- 10. Jia B., Gu H.G., and Song S.L.: ‘Experimental researches on different complex bifurcation procedures of neural firing patterns’, Sci. China Phys. Mech., 2013, 43, pp. 518–523 [Google Scholar]
- 11. Hodgkin A.L., and Huxley A.F.: ‘A quantitative description of membrane current and its application to conduction and excitation in nerve’, J. Physiol., 1952, 117, pp. 500–544 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. FitzHugh R.A.: ‘Impulses and physiological states in theoretical models of nerve membrane’, Biophys. J., 1961, 1, pp. 445–466 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Hindmarsh J.L., and Rose R.M.: ‘A model of the nerve impulse using two first‐order differential equations’, Nature, 1982, 296, pp. 162–164 [DOI] [PubMed] [Google Scholar]
- 14. Hindmarsh J.L., and Rose R.M.: ‘A model of neuronal bursting using three coupled first order differential equations’, Proc. R. Soc. Lond. B. Biol. Sci., 1984, 221, pp. 87–102 [DOI] [PubMed] [Google Scholar]
- 15. Burkitt A.N.: ‘A review of the integrate‐and‐fire neuron model: I. Homogeneous synaptic input’, Biol. Cybern. 2006, 95, pp. 1–19 [DOI] [PubMed] [Google Scholar]
- 16. Burkitt A.N.: ‘A review of the integrate‐and‐fire neuron model: II. Inhomogeneous synaptic input and network properties’, Biol. Cybern., 2006, 95, pp. 97–122 [DOI] [PubMed] [Google Scholar]
- 17. Laing C.R., and Chow C.C.: ‘A spiking neuron model for binocular rivalry’, J. Comput. Neurosci., 2002, 12, pp. 39–53 [DOI] [PubMed] [Google Scholar]
- 18. Achard P., and Schutter E.D.: ‘Complex parameter landscape for a complex neuron model’, PLoS Comput. Biol., 2006, 2, pp. 0794–0804 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Tsumoto K., Kitajima H., and Yoshinaga T. et al.: ‘Bifurcations in Morris–Lecar neuron model’, Neurocomput, 2006, 69, pp. 293–316 [Google Scholar]
- 20. Gu H.G., Pan B.B., and Chen G.R. et al.: ‘Biological experimental demonstration of bifurcations from bursting to spiking predicted by theoretical models’, Nonlinear Dyn., 2014, 78, pp. 391–407 [Google Scholar]
- 21. Gu H.G., and Pan B.B.: ‘A four‐dimensional neuronal model to describe the complex nonlinear dynamics observed in the firing patterns of a sciatic nerve chronic constriction injury model’, Nonlinear Dyn., 2015, 81, pp. 2107–2126 [Google Scholar]
- 22. Ma J., and Tang J.: ‘A review for dynamics of collective behaviors of network of neurons’, Sci. China Tech. Sci., 2015, 58, pp. 2038–2045 [Google Scholar]
- 23. Wang Q.Y., and Aleksandra M.: ‘Perc M Taming desynchronized bursting with delays in the Macaque cortical network’, Chin. Phys. B, 2011, 20, p. 040504 [Google Scholar]
- 24. Dhamala M., Viktor K.J., and Ding M.Z.: ‘Transitions to synchrony in coupled bursting neurons’, Phys. Rev. Lett., 2004, 92, p. 028101 [DOI] [PubMed] [Google Scholar]
- 25. Ma J., Xu Y., and Ren G.D. et al.: ‘Prediction for breakup of spiral wave in a regular neuronal network’, Nonlinear Dyn., 2016, 84, pp. 497–509 [Google Scholar]
- 26. Djeundam S.R.D., Yamapi R., and Kofane T.C. et al.: ‘Deterministic and stochastic bifurcations in the Hindmarsh–Rose neuronal model’, Chaos, 2013, 23, p. 033125 [DOI] [PubMed] [Google Scholar]
- 27. Nian F.Z., Wang X.Y., and Niu Y.J. et al.: ‘Module‐phase synchronization in complex dynamic system’, Appl. Math. Comput., 2010, 217, pp. 2481–2489 [Google Scholar]
- 28. Storace M., Linaro D., and de Lange E.: ‘The Hindmarsh–Rose neuron model: bifurcation analysis and piecewise linear approximations’, Chaos, 2008, 18, p. 033128 [DOI] [PubMed] [Google Scholar]
- 29. Ma J., Lv M., and Zhou P. et al.: ‘Phase synchronization between two neurons induced by coupling of electromagnetic field’, Appl. Math. Comput., 2017, 307, pp. 321–328 [Google Scholar]
- 30. Song X.L., Jin W.Y., and Ma J.: ‘Energy dependence on the electric activities of a neuron’, Chin. Phys. B, 2015, 24, pp. 604–609 [Google Scholar]
- 31. Wang R.B., and Zhang Y.T.: ‘Can the activities of the large scale cortical network be expressed by neural energy? A brief review’, Cogn. Neurodyn., 2016, 10, pp. 1–5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Ma J., Wu F.Q., and Jin W.Y. et al.: ‘Calculation of Hamilton energy and control of dynamical systems with different types of attractors’, Chaos, 2017, 27, pp. 481–495 [DOI] [PubMed] [Google Scholar]
- 33. Ostojic S., Brunel N., and Hakim V.: ‘How connectivity, background activity, and synaptic properties shape the cross‐correlation between spike trains’, J. Neurosci., 2009, 29, pp. 10234–10253 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Straiker A., and Mackie K.: ‘Cannabinoid signaling in inhibitory autaptic hippocampal neurons’, Neuroscience, 2009, 163, pp. 190–201 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Yilmaz E., Baysal V., and Perc M. et al.: ‘Enhancement of pacemaker induced stochastic resonance by an autapse in a scale‐free neuronal network’, Sci. China Technol. Sci., 2016, 59, pp. 364–370 [Google Scholar]
- 36. Song X.L., Wang C.N., and Ma J. et al.: ‘Transition of electric activity of neurons induced by chemical and electric autapses’, Sci. China Technol. Sci., 2015, 58, pp. 1007–1014 [Google Scholar]
- 37. Uzun R.: ‘Influences of autapse and channel blockage on multiple coherence resonance in a single neuron’, Appl. Math. Comput., 2017, 315, pp. 203–210 [Google Scholar]
- 38. Guo D.Q., Wu S.D., and Chen M.M. et al.: ‘Regulation of irregular neuronal firing by autaptic transmission’, Sci. Rep., 2016, 6, p. 26096 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Yilmaz E., Baysal V., and Ozer M. et al.: ‘Autaptic pacemaker mediated propagation of weak rhythmic activity across small‐world neuronal networks’, Physica A, 2016, 444, pp. 538–546 [Google Scholar]
- 40. Wang L.F., Qiu K., and Jia Y.: ‘Effects of time delays in a mathematical bone model’, Chin. Phys. B, 2017, 26, p. 030503 [Google Scholar]
- 41. Xia P., Chen H.V., and Zhang D.X. et al.: ‘Memantine preferentially blocks extrasynaptic over synaptic NMDA receptor currents in hippocampal autapses’, J. Neurosci., 2010, 30, pp. 11246–11250 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Wang H.T., and Ma J. et al.: ‘Effect of an autapse on the firing pattern transition in a bursting neuron’, Commun. Nonlinear Sci., 2014, 19, pp. 3242–3254 [Google Scholar]
- 43. Qin H.X., and Wu Y. et al.: ‘Emitting waves from defects in network with autapses’, Commun. Nonlinear Sci., 2015, 23, pp. 164–174 [Google Scholar]
- 44. Wang C.N., and Guo S.L. et al.: ‘Formation of autapse connected to neuron and its biological function’, Complexity, 2017, 2017, p. 9, Article ID 5436737 [Google Scholar]
- 45. Lv M., Wang C.N., and Ren G.D. et al.: ‘Model of electrical activity in a neuron under magnetic flow effect’, Nonlinear Dyn., 2016, 85, pp. 1479–1490 [Google Scholar]
- 46. Lv M., and Ma J.: ‘Multiple modes of electrical activities in a new neuron model under electromagnetic radiation’, Neurocomputing, 2016, 205, pp. 375–381 [Google Scholar]
- 47. Zaikin A.A., López L.J., and Baltanás P. et al.: ‘Vibrational resonance in a noise‐induced structure’, Phys. Rev. E, 2002, 66, p. 011106 [DOI] [PubMed] [Google Scholar]
- 48. Yang L.J., Liu W.H., and Yi M. et al.: ‘Vibrational resonance induced by transition of phase‐locking modes in excitable system’, Phys. Rev. E, 2012, 86, p. 016209 [DOI] [PubMed] [Google Scholar]
- 49. Ullner E., Zaikin A., and García‐Ojalvo J. et al.: ‘Vibrational resonance and vibrational propagation in excitable systems’, Phys. Lett. A, 2003, 312, pp. 348–354 [Google Scholar]
- 50. Lu L.L., Jia Y., and Liu W.H. et al.: ‘Mixed stimulus‐induced model selection in neural activity driven by high and low frequency current under electromagnetic radiation’, Complexity, 2017, 2017, p. 11, Article ID 7628537, 10.1155/2017/7628537 [DOI] [Google Scholar]
- 51. Ge M.Y., Jia Y., and Xu Y. et al.: ‘Mode transition in electrical activities of neuron driven by high and low frequency stimulus in the presence of electromagnetic induction and radiation’, Nonlinear Dyn., 2018, 9, pp. 515–523 [Google Scholar]
- 52. Xu Y., Ying H.P., and Jia Y. et al.: ‘Autaptic regulation of electrical activities in neuron under electromagnetic’, Sci. Rep., 2017, 7, p. 43452 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Kobe D.H.: ‘Helmholtz's theorem revisited’, Am. J. Phys., 1986, 54, pp. 552–554 [Google Scholar]
- 54. Qiu K., Gao K.F., and Yang L.J. et al.: ‘A kinetic model of multiple phenotypic states for breast cancer cells’, Sci. Rep., 2017, 7, p. 9890 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Yao Y., Cao W., and Pei Q. et al.: ‘Breakup of spiral wave and order‐disorder spatial pattern transition induced by spatially uniform cross‐correlated sine‐Wiener noises in a regular network of Hodgkin–Huxley neurons’, Complexity 2018, 2018, p. 11, Article ID 8793298 [Google Scholar]
- 56. Yousif A.A.M., Lu L.L., and Ge M.Y. et al.: ‘Effects of intrinsic and extrinsic noises on transposons kinetics’, Chin. Phys. B, 2018, 27, p. 030501 [Google Scholar]
- 57. Yao Y.G., and Ma J.: ‘Weak periodic signal detection by sine‐Wiener‐noise‐induced resonance in the FitzHugh–Nagumo neuron’, Cogn. Neurodyn., 2018, 10.1007/s11571-018-9475-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Xu Y., Jia Y., and Ge M.Y. et al.: ‘Effects of ion channel blocks on electrical activity of stochastic Hodgkin–Huxley neural network under electromagnetic induction’, Neurocomputing, 2018, 283, pp. 196–204 [Google Scholar]
- 59. Xu Y., Jia Y., and Ma J. et al.: ‘Collective responses in electrical activities of neurons under field coupling’, Sci. Rep., 2018, 8, p. 1349 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Lu L.L., Jia Y., and Xu Y. et al.: ‘Energy dependence on modes of electric activities of neuron driven by different external mixed signals under electromagnetic induction’, Sci. China Tech. Sci., 2018, http://engine.scichina.com/doi/10.1007/s11431‐017‐9217‐x [Google Scholar]


