Abstract
Lung cancer is a leading cause of cancer‐related death worldwide. The early diagnosis of cancer has demonstrated to be greatly helpful for curing the disease effectively. Microarray technology provides a promising approach of exploiting gene profiles for cancer diagnosis. In this study, the authors propose a gene expression programming (GEP)‐based model to predict lung cancer from microarray data. The authors use two gene selection methods to extract the significant lung cancer related genes, and accordingly propose different GEP‐based prediction models. Prediction performance evaluations and comparisons between the authors’ GEP models and three representative machine learning methods, support vector machine, multi‐layer perceptron and radial basis function neural network, were conducted thoroughly on real microarray lung cancer datasets. Reliability was assessed by the cross‐data set validation. The experimental results show that the GEP model using fewer feature genes outperformed other models in terms of accuracy, sensitivity, specificity and area under the receiver operating characteristic curve. It is concluded that GEP model is a better solution to lung cancer prediction problems.
Inspec keywords: lung, cancer, medical diagnostic computing, patient diagnosis, genetic algorithms, feature selection, learning (artificial intelligence), support vector machines, multilayer perceptrons, radial basis function networks, reliability, sensitivity analysis
Other keywords: lung cancer prediction, cancer‐related death, cancer diagnosis, gene profiles, gene expression programming‐based model, gene selection, GEP‐based prediction models, prediction performance evaluations, representative machine learning methods, support vector machine, multilayer perceptron, radial basis function neural network, real microarray lung cancer datasets, cross‐data set validation, reliability, receiver operating characteristic curve
1 Introduction
Cancer is considered as a genetic disorder with unknown causes and mechanisms in most cases. Among the cancer types, lung cancer is a major killer disease around the world, especially in America and East Asia [1–3]. Lung cancer accounts for ∼25% of cancer related death worldwide, which is higher than other most prevalent cancers together, such as breast, prostate and colorectal cancers [4]. However, the genetic factors of lung cancer are still yet to be clearly understood because lung cancer is a complex genetic disease which is developed by the concurrence of many genetic changing events [5]. Lung cancer can be divided into two types: non‐small cell lung cancer (NSCLC) and small cell lung cancer (SCLC). The more common lung cancer type is NSCLC, which is found in ∼80% of lung cancer patients. NSCLC can also be sub‐categorised as squamous cell carcinoma, adenocarcinoma (AC) and large cell carcinoma (LCC) [6]. Traditionally, physical analyses of tissues are performed for lung cancer diagnosis and prognosis using chest X‐ray, computed tomography scan and magnetic resonance imaging [7, 8]. Unfortunately, these techniques can only detect the malignant cells in the late stage of lung cancer, which results in low survival rates (∼16% for NSCLC and 6% for SCLC) [9]. With the advances in molecular biology, unfortunately, these techniques can only detect the malignant cells in the late stage of lung cancer, which results in low survival rates (∼16% for NSCLC and 6% for SCLC) [9]. With the advances in molecular biology, especially the microarray technology, we can now acquire the information of DNA, RNA and proteins to detect the formation of tumours in earlier stages. This would result in an increase of cancer patient survival rate, especially for lung cancer patients. One application of microarray technology is for cancer classification analysis, in which microarray data are used to determine if genes are active, hyperactive or inactive in various tissues. Then, samples are classified into two or more groups especially the microarray technology, we can now acquire the information of DNA, RNA and proteins to detect the formation of tumours in earlier stages. This would result in an increase of cancer patient survival rate, especially for lung cancer patients. One application of microarray technology is for cancer classification analysis, in which microarray data are used to determine if genes are active, hyperactive or inactive in various tissues. Then, samples are classified into two or more groups [10]. There are many studies on the classification of lung cancer [1, 4, 11, 12]. To ensure the successful diagnosis and effective treatment for cancer diseases, the classification process has to be accurate and reliable.
Machine learning techniques have been widely used in the last two decades for cancer prediction and prognosis, especially the techniques of artificial neural networks (ANNs), support vector machines (SVMs), and Bayesian networks [13, 14]. For example, to identify SCLC and NSCLC cells, SVM method was used on lung cancer gene expression databases with prior knowledge [15]. ANNs have solved many problems related to classification and pattern recognition. ANNs use input variables to train the classifier and create the output by using multiple hidden layers which use mathematic processes to connect the neural nodes. ANN has become a standard method for different classification tasks [16]. However, it has some drawbacks. The structure of ANN causes many time‐consuming operations which lead to an inefficient performance. Furthermore, the generic layered structure of ANN known as a ‘black‐box’ makes it almost impossible to look into the working mechanism of the classification process or why an ANN does not work. Different from ANNs, SVM hardly has the over‐fitting problem, but when the dataset is large, the training process will be slow [13, 17]. In recent years, an innovative evolutionary algorithm called gene expression programming (GEP) was proposed by Ferreira [18, 19]. GEP provides a data visualisation model which can easily convert a classifier into a mathematic model. One study has shown the power of GEP in predicting essential proteins indispensable for cell survival [20]. Another success story of GEP is the prediction of adverse events of radical hysterectomy for cervical cancer patients with the accuracy of 71.96% [21]. For lung cancer classification, some GEP‐based models have been proposed. For example, Yu et al. [11] proposed an optimal biomarker joint model using a GEP algorithm to classify lung tumours. They also developed a GEP model for the auxiliary diagnosis of NSCLC lung cancer using serum biomarkers [17]. These research works show that GEP provides a promising approach to cancer prediction/diagnosis and prognosis because of its good performance of using simple coding to solve complex problems. However, to our knowledge, there is no research on using the GEP model to classify lung cancers from microarray data.
In this research, we propose a new GEP‐based classifier to classify lung cancers from microarray data. In fact, we use two models to select feature genes (attributes) from microarray data, one is the Relief Attribute Eval another is the Random Forest (RF). GEP models are then constructed based on the selected feature genes to classify lung cancers. We used three real lung cancer datasets to compare the prediction performance of our GEP‐based classifier and other three representative classifiers: SVM, multilayer perceptron (MLP) and radial basis function neural network (RBFNN) classifiers, in terms of accuracy, sensitivity, specificity and area under ROC curve (AUC). For the reliability evaluation, the k‐fold cross validation and the average of the results were used. The experimental results show that the proposed GEP model using fewer attributes outperforms the existing models in lung cancer prediction.
The paper is structured as follows. Section 2 briefly explains the GEP method followed by Section 3 which presents our GEP‐based approach for constructing a novel classifier and the settings of our experiments. The experimental results of our classifier in predicting lung cancer, as well as the comparison results of our classifier with other representative classifiers on the same datasets, are presented in Section 4. We discuss our experimental results in Section 5, and finally in Section 6 conclude our work with some directions for future work.
2 Gene expression programming
GEP is an algorithm that simulates biological evolutions to create and evolve computer programs. GEP was proposed by Ferreira [22] with the assumption of being, in some way, an extension of genetic programming (GP) [23] while preserving a small number of genetic algorithm (GA) properties [24]. The difference between GP and GEP is the chromosome representation. In GEP chromosomes are not represented as trees, but as linear strings with a fixed length. This feature is inherited from GA. In GEP, programmes (individuals) are encoded by chromosomes, and a chromosome consists of genes (can be one gene or more) which are structured with a head and a tail. The head consists of functional operators such as (+,−,×,/) and/or terminal elements such as symbols and conditions. The tail consists of terminal elements only and its size is calculated by t = h (n − 1) + 1, where h and n represent, respectively, the size of the head and the maximum number of parameters which is required by the functions in the function set [25]. There are no limitations on the size of a gene which is determined by the head size. Phenotype with an expression tree (ET) is a result of the conversion process from genotype, which is established when each gene representation is given.
A chromosome is constructed by a linking function (can be a mathematical function such as addition or a logical function such as AND) that links the genes to each other (i.e. the outcome of joining multiple trees together). Individual chromosomes form a sample population, which undergoes evolutions to produce new generations by performing genetic operations (mutation, transposition, root transposition, gene transcription and gene recombination), calculating the expression values for every chromosome/individual, judging the fitness of each chromosome based on its expression value, and then selecting those chromosomes with better fitness values as the next generation to continue the evolution. The evolution process will stop when a predefined termination criterion is satisfied, then the individual/chromosome with the best fitness value is selected as the classifier model. Depending on the problems considered, different fitness functions could be defined. More details of GEP can be found in [26].
3 Classification model and settings
3.1 GEP‐based classifier
In this work, we use GEP to construct a classifier for lung cancer prediction/classification. To do this, we need to follow the following major steps: defining chromosomes using the function and terminal sets, initialising a population with the defined group of chromosomes, defining a fitness function for evaluating chromosomes, selecting eugenic individual/chromosomes from the population, reproducing a group of chromosomes of the next generation via genetic operations on the selected eugenic chromosomes, and checking the termination condition of the evolution. Fig. 1 illustrates the flow chart of building a GEP classifier.
Fig. 1.
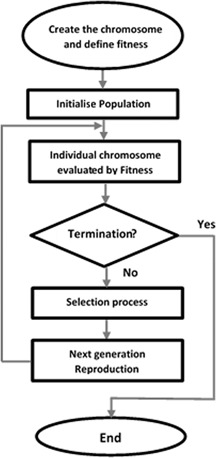
Flowchart of building a GEP classifier
Actually, to build a classifier from GEP for lung cancer prediction, we first build a set of functions and a set of terminals to define chromosomes that will be expressed as the non‐linear combinations of functions and terminals. The set of functions consists of mathematical operators which are +, −, ×, ÷, Exp, Sqrt, Log and Logi, while the set of terminals consists of extracting feature genes (attributes) from the microarray dataset and the relevant coefficients. Here Exp(x) is the exponential function, Sqrt(x) is the square root function, Log(x) is the logarithmic function, and Logi(x) is the function defined as Logi(x) = 1/(1 + exp(‐x)). After that, we define the chromosomal structure by setting the head length be 10, tail length is 11 and the number of genes in each chromosome be 4. For instance, if there are five attributes related to lung cancer (d 0,d 1,…,d 4), a single chromosome could be constructed as follows (the head is shown in bold, each line joined by the symbol ‘+’ represents a gene of GEP)
The chromosome notation used in the above example is called Karva notation, or K‐expression. A K‐expression can be converted into an ET. The conversion starts from the first position in the Karva notation, and expands as a binary tree by adding the elements of the Karva notation into the tree as the nodes one by one. At each tree layer, the elements are added from left to right. This tree expanding process continues layer‐by‐layer until all leaf nodes in the ET are the elements from the terminal set. The corresponding ET of the above chromosome is shown in Fig. 2.
Fig. 2.
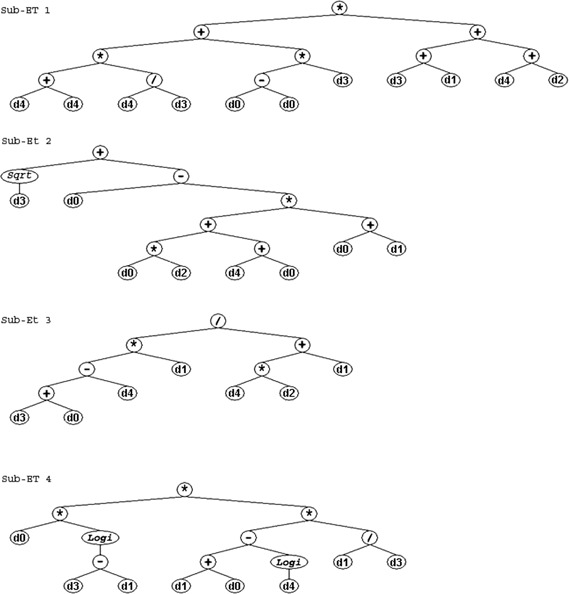
Example of GEP ETs. Four sub‐ETs
The second step is to initialise the population by randomly constructing individuals (i.e. chromosomes) from the defined function and terminal sets. The size of the population is set at 30 in our model.
The third step is to define a fitness function for evaluating each chromosome individually. The fitness function SSPN is defined as the product of sensitivity (SN), specificity (SP), positive predictive value (PPV), and negative predictive value (NPV). We select SSPN in this study as the fitness function, which is used to obtain optimal results [11, 23]. The mathematical formula of the fitness function is given by the following equation
| (1) |
where SN i , SP i , PPV i and NPV i are calculated by (2), (3), (4) and (5), respectively
| (2) |
| (3) |
| (4) |
| (5) |
where TN i , TP i , FN i and FP i are the numbers of true negatives, true positives, false negatives and false positives of classification/prediction, respectively, for chromosome i (a classifier) over the whole training dataset.
The above four possible outcomes TN, TP, FN and FP are for a single prediction of a binomial classification task with two classes ‘Yes’ (‘1’) and ‘No’ (‘0’). In fact, for each chromosome in an evolved generation has two steps. The first step is extracting the expression values of the training case from the microarray dataset with respect to the selected feature genes (attributes). The second step is calculating the value score by combining these extracted expression values according to the ET of the chromosome. Then, the classification score is converted into ‘1’ or ‘0’ using a 0/1 rounding threshold (e.g. 0.5), i.e. if the classification score is greater than the rounding threshold, then the result of the classification is ‘1’ (‘Yes’), otherwise ‘0’ (‘No’).
The fourth step is to rank all individuals (chromosomes) in the generation from the highest to the lowest fitness scores, and choose the top 20% of the population as the selected eugenic ones. The fifth step is to perform a set of genetic operations, including mutation, transposition and crossover, on the eugenic individuals to produce new chromosomes of the next generation that has the same size as the former one. Steps 4 and 5 are repeated until a predefined number of generations are achieved. Then, the individual (chromosome) with the highest fitness score in the last generation is selected as the final classifier. The settings of GEP method for building a classifier are presented in Table 1.
Table 1.
GEP parameters for building a lung cancer classifier from microarray datasets
| Parameter | Setting |
|---|---|
| number of chromosomes | 30 |
| number of genes | 4 |
| head size | 10 |
| tail size | 11 |
| gene size | 21 |
| number of generations | 700 |
| linking function | addition |
| function set | +, −, *, /, Exp, Sqrt, Log, Logi |
| mutation rate | 0.044 |
| IS transposition rate | 0.1 |
| RIS transposition rate | 0.1 |
| gene transposition rate | 0.1 |
| one‐point recombination rate | 0.3 |
| two‐point recombination rate | 0.3 |
| gene recombination rate | 0.1 |
3.2 Microarray datasets
In our experiments, we evaluated our GEP classification model on three public microarray datasets which are free to download and commonly used by researchers for lung cancer classifications. These three datasets and their main characteristics (e.g. the number of samples, the number of genes and class distribution) are shown in Table 2. These gene expression datasets were downloaded from the National Library of Medicine (http://www.ncbi.nlm.nih.gov/pubmed) and Kent Ridge Bio‐medical Dataset (http://datam.i2r.a‐star.edu.sg/datasets/krbd/index. html# cs4‐software), the details of these datasets are as follows.
Table 2.
Characteristics of microarray datasets
| Dataset | # Samples | # Genes | Class 1 | Class 2 |
|---|---|---|---|---|
| Michigan | 96 | 7129 | 86 | 10 |
| Harvard | 181 | 12 533 | 31 | 150 |
| GEO | 58 | 1700 | 40 | 18 |
Michigan dataset had 96 lung cancer cases and 7129 genes. Among these samples, 86 patients had cancer labelled as (‘Tumour’). The remaining ten patients were labelled as ‘Normal’ and they did not suffer from lung cancer.
Harvard dataset (Brigham and Women's Hospital and Harvard Medical School) had 181 lung cancer cases and 12,533 genes. Among these samples, 150 patients had cancer type AC. The remaining 31 patients suffer from malignant pleural mesothelioma.
GEO dataset (GSE10245) had 58 lung cancer cases and more than 1700 genes. Among these samples, 40 patients had cancer type (AC). The remaining 18 patients did not suffer from AC on both clinical and radiological tests.
3.3 Microarray attributes selection
Attribute or feature selection, is a technique of creating robust learning models by selecting the most relevant attributes from the original attributes. This technique is widely used in machine learning algorithms to improve learning model performance. Gene feature selection is essential to cancer classification, as we can use a small number of correctly selected genes to obtain accurate classification results [27]. The attributes in lung cancer microarray datasets are those genes informative for classification. We used two ways to extract the feature genes: n ‐top ranked genes selection and automatic gene selection.
3.3.1 n‐Top ranked genes selection
In our experiments, we used the attribute evaluator Relief Attribute Eval. Relief‐F method of this evaluator evaluates the feature F by selecting a random sample from F and samples of its nearest neighbours from the same class and other classes. F is scored depending on the differences between the different classes. If F has a different expression for samples from different classes, it will experience a higher score (or vice versa) [28, 29]. This ranking technique is provided by the software Weka [30], which is a collection of open access machine learning algorithms for data mining tasks. We selected 5, 10 and 20 top ranked informative genes (i.e. features to create three sub datasets for each original lung cancer microarray dataset. Each sub‐dataset of an original microarray dataset had the same number of samples (patients) as the original one, but a much less number of genes. We denoted a sub‐dataset with 5, 10 and 20 feature genes as GEP‐5, GEP‐10 and GEP‐20, respectively. The purpose of creating three sub datasets for each original dataset was to experimentally determine a proper number of features (genes) for the GEP algorithm to generate a better classifier and get better lung cancer prediction results. Reliability was assessed by cross‐data set validation. Using the ten‐fold cross‐validation, the dataset was randomly divided into ten equal subsets. For each run, nine subsets were used as a training dataset to construct the model while the remaining subset was used as a testing dataset for prediction. The average accuracy of ten iterations was recorded as the final measurement.
3.3.2 Automatic gene selection
To extract feature genes, we also used another feature selection technique RF [31] which can automatically determine the number of features. RF is one of the popular machine learning algorithms which can provide an accurate result with robustness and easy procedure [32]. It is an ensemble of decision trees and each node in the decision trees represents a condition of a single feature. Each decision tree is constructed by using a random subset of the training data. We first randomly divided the samples of each subset into two parts: training and testing. 80% of all patients (samples) were randomly selected as the training dataset for training the generated classifiers, while the remaining 20% of all patients formed a testing dataset which was used to test the predictive performance of the generated classifiers. To avoid the biased performance estimate, RF was trained on the training datasets only. The GEP classification method with this automatic feature gene selection is denoted as ‘GEP‐AS’. To ensure the reliability of the selected feature genes, we repeated the experiment ten times and used the average of the results to evaluate the performance of the classification models.
We used the software GeneXproServer 5.0 [22] to run GEP algorithm using the parameter set in Table 1.
3.4 Methods for comparison
We selected the representative classification methods to compare with our GEP‐based classifier in terms of classification performance. These methods were: SVM, MLP and RBFNN. These techniques are used by many studies for classification purposes [13, 14, 33]. GEP algorithm was performed using GeneXproServer 5.0 software [22] while SVM, MLP and RBFNN methods were simulated by DTREG software [34].
3.4.1 Support vector machine
SVM is a supervised learning method commonly used for data analysis and pattern recognition [35, 36]. SVM is becoming a public technique to deal with biological application problems and is popular for cancer microarray data classification and prediction [13, 14]. The main idea of SVM is to find the optimal hyperplane between two classes, which is working to separate the classes by placing a margin around each data point and maximising the margin between the classes. The parameters of the SVM classifier in our experiment were as follows:
Type of SVM model: C‐SVC.
Kernel function: radial basis function (RBF).
C search range: 0.1–5000
Gamma search range: 0.001–50.
Stopping criteria: 0.001000.
Cache size: 256.0.
3.4.2 Multi‐layer perceptron
MLP is one of neural network types that can process input variables through a group of layers [37]. Usually the MLP uses three layers. The first layer is the input layer which deals with features (attributes) of an input microarray or pattern. The second layer is a hidden layer (could be up to two hidden layers depending on the designer how many layers to use) which contains predefined number of nodes (neurons). The hidden layers work to add the whole variable values of the input data multiplied by weights. The weighted sum is used as the input for the activation function whose output is fed to the next layer. The output layer is the last layer which consists of neurons (nodes) and produces the final classification result of the model. The parameters of the MLP classifier selected in our experiment were as follows:
Number of layers: three (one hidden layer).
Hidden layer activation function: logistic.
Output layer activation function: logistic.
Automatic hidden layer neuron selection: Min = 2, max = 20, step = 1.
3.4.3 Radial basis function neural network
RBFNN has three layers. The first layer is an input layer; the second layer is a hidden layer where the radial basis function is used as an activation function. Each input vector in the input layer is used as an input to all neurons of a radial basis functions in the hidden layer. The number of neurons in the hidden layer is determined during the training process; the third layer is the output layer [38]. RBFNN is widely used in classification because it is simple to design, performs robustly and is tolerant of input noise [39]. The parameters of the RBFNN classifier selected in our experiment were as follows:
Number of layers: three (one hidden layer).
Hidden layer activation function: Logistic.
Output layer activation function: Logistic.
Automatic hidden layer neuron selection: Min = 2, max = 20, step = 1.
4 Experiment results
The experiments were designed to have two parts: we first evaluated the classification performance of our GEP‐based classifiers, then compared the GEP‐based classification performance with the performance of three selected classification methods on the experimental data sets. The performance was evaluated in terms of sensitivity, specificity, accuracy and area under the curve (AUC) [13]. Sensitivity and specificity have been defined in Section 2. The AUC and the accuracy were used to evaluate the overall performance of a classifier. Particularly, accuracy is used to measure the correct prediction, while AUC is to measure the prediction performance. AUC depends on the receiver operating characteristic (ROC) curve, which the graphical plot is showing the sensitivity (y ‐axis) versus its 1‐specificity (x ‐axis). The performance values were calculated on each subset which was created from every entire original dataset, i.e. GEP‐5, GEP‐10, GEP‐20 and GEP‐AS as indicated in Section 3.3. We applied GEP algorithm on the above sub datasets to generate different classifiers and evaluated the performance of these classifiers. For simplicity, in the following text without causing confusion, we also use GEP‐5, GEP‐10, GEP‐20 and GEP‐AS to represent the classifiers generated from these four sub datasets. Then, we compared the performance of these classifiers with the performance of the selected comparison methods (SVM, RBFNN and MLP). For reliability, we used the ten‐fold cross validation to obtain the predicted results of GEP‐5, GEP‐10 and GEP‐20. While in GEP‐AS model, the experiments were repeated ten times and the average performance evaluation results of GEP generated classifiers on the three evaluation datasets (GEO, Michigan and Harvard) were calculated.
For all experimental models the average results of the three datasets were calculated to show the overall performance of these models in terms of accuracy, sensitivity, specificity and AUC.
4.1 GEP models results
Among the GEP classifiers, the highest average accuracy from the three microarray datasets was 98.09% with standard deviation 2.32 which was achieved by GEP‐5, and the average accuracy achieved by GEP‐10 was 91.63% with standard deviation 1.75. The average accuracy achieved by GEP‐AS was 89.18% with standard deviation 3.52. The average accuracy achieved by GEP‐20 was 96.07% with standard deviation 3.42. While the average accuracy achieved by GEP Model with all attributes (genes) was 87.49% with standard deviation 5.89. The average results and the standard division of the five GEP models in terms of accuracy, sensitivity, specificity and AUC are presented in Figs. 3 and 4. The details of the results are shown in the appendix section of this paper.
Fig. 3.
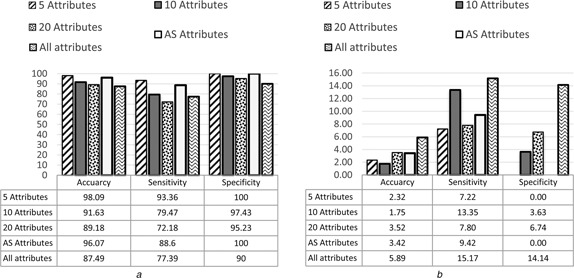
Average and standard deviation of GEP models for all datasets in term of accuracy, sensitivity and specificity
a Average results
b Standard deviation results
Fig. 4.
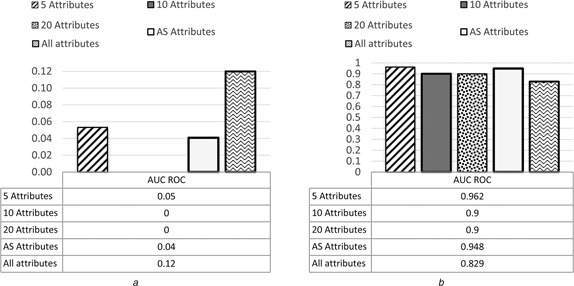
Average of AUC ROC with standard deviation of GEP models for all datasets
a Average results
b Standard deviation results
4.2 Comparisons of GEP with representative classifiers
The comparison results of classification performance among GEP classifiers, SVM, RBFNN and MLP classifiers in terms of accuracy, sensitivity, specificity and AUC are shown in Figs. 5, 6, 7–8, respectively. It can be seen from the results that the highest accuracy among the all models was 98.09% achieved by GEP‐5 model with the standard division of 2.32, while the highest accuracy with ten attributes was 97.74% achieved by MLP with the standard division of 2.07. The highest accuracy with 20 attributes was 97.37% achieved by MLP as well with the standard division of 1.82. The highest accuracy with all attributes was 91.72% achieved by MLP again with the standard division of 6.16. Finally, the highest accuracy with AS attributes was 96.29% achieved by both SVM and MLP with the standard division of 1.45.
Fig. 5.
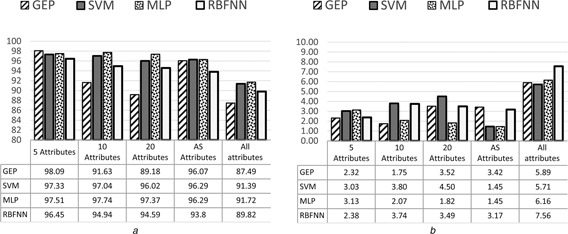
Average of accuracy with standard deviation of GEP classifiers for all datasets
a Average results
b Standard deviation results
Fig. 6.
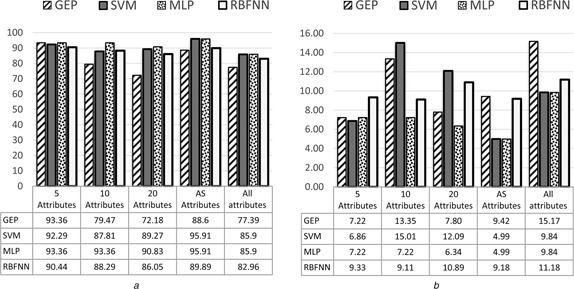
Average of sensitivity with standard deviation of GEP classifiers for all datasets
a Average results
b Standard deviation results
Fig. 7.
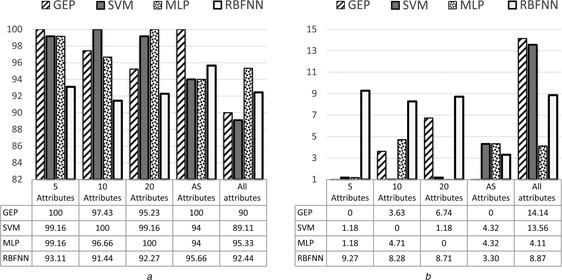
Average of specificity with standard deviation of GEP classifiers for all datasets
a Average results
b Standard deviation results
Fig. 8.
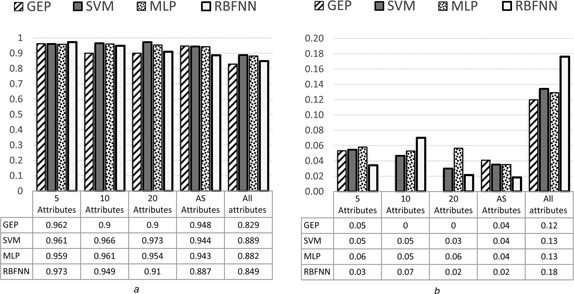
Average of AUC with standard deviation of GEP classifiers for all datasets
a Average results
b Standard deviation results
The detailed classification results on all datasets are shown in the appendix section (Tables 3, 4–5).
Table 3.
Geo microarray datasets performance comparison between GEP, SVM, MLP and RBF
| Training dataset | Testing dataset | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sub dataset | Classifier | Accuracy | TP | TN | FP | FN | Sensitivity | Specificity | AUC ROC | Sub dataset | Classifier | Accuracy | TP | TN | FP | FN | Sensitivity | Specificity | AUC ROC |
| 5 Attributes | GEP | 97.83 | 30.43 | 67.39 | 0 | 2.17 | 93.33 | 100 | 0.9 | 5 Attributes | GEP | 94.83 | 25.86 | 68.97 | 0 | 5.17 | 83.33 | 100 | 0.887 |
| SVM | 94.83 | 25.86 | 68.97 | 0 | 5.17 | 83.33 | 100 | 0.906 | SVM | 93.10 | 25.86 | 67.24 | 1.72 | 5.17 | 83.33 | 97.50 | 0.884 | ||
| MLP | 94.83 | 25.86 | 68.97 | 0 | 5.17 | 83.33 | 100 | 0.934 | MLP | 93.10 | 25.86 | 67.24 | 1.72 | 5.17 | 83.33 | 97.50 | 0.877 | ||
| RBF | 94.83 | 25.86 | 68.97 | 0 | 5.17 | 83.33 | 100 | 0.975 | RBF | 93.10 | 24.14 | 68.97 | 0 | 6.90 | 77.78 | 100 | 0.925 | ||
| 10 Attributes | GEP | 97.44 | 28.21 | 69.23 | 0 | 2.56 | 91.67 | 100 | 0.9 | 10 Attributes | GEP | 89.47 | 26.32 | 63.16 | 5.26 | 5.26 | 83.33 | 92.31 | 0.9 |
| SVM | 94.83 | 25.86 | 68.97 | 0 | 5.17 | 83.33 | 100 | 0.904 | SVM | 91.67 | 16.67 | 75 | 0 | 8.33 | 66.67 | 100 | 0.9 | ||
| MLP | 94.83 | 25.86 | 68.97 | 0 | 5.17 | 83.33 | 100 | 0.909 | MLP | 94.83 | 25.86 | 68.97 | 0 | 5.17 | 83.33 | 100 | 0.887 | ||
| RBF | 96.55 | 27.59 | 68.97 | 0 | 3.45 | 88.89 | 100 | 0.983 | RBF | 89.66 | 24.14 | 65.52 | 3.45 | 6.90 | 77.78 | 95.00 | 0.850 | ||
| 20 Attributes | GEP | 97.44 | 30.77 | 66.67 | 0 | 2.56 | 92.31 | 100 | 0.9 | 20 Attributes | GEP | 84.21 | 21.05 | 63.16 | 10.53 | 5.26 | 80 | 85.71 | 0.9 |
| SVM | 96.55 | 27.59 | 68.97 | 0 | 3.45 | 88.89 | 100 | 1 | SVM | 89.66 | 22.41 | 67.24 | 1.72 | 8.62 | 72.22 | 97.50 | 0.931 | ||
| MLP | 96.55 | 27.59 | 68.97 | 0 | 3.45 | 88.89 | 100 | 0.998 | MLP | 94.83 | 25.86 | 68.97 | 0 | 5.17 | 83.33 | 100 | 0.874 | ||
| RBF | 96.55 | 27.59 | 68.97 | 0 | 3.45 | 88.89 | 100 | 0.997 | RBF | 89.66 | 22.41 | 67.24 | 1.72 | 8.62 | 72.22 | 97.50 | 0.881 | ||
| AS | GEP | 97.83 | 23.91 | 73.91 | 0 | 2.17 | 91.67 | 100 | 0.9 | AS | GEP | 96.55 | 27.59 | 68.97 | 0 | 3.45 | 88.89 | 100 | 0.945 |
| SVM | 98.9 | 78.2 | 20.9 | 0 | 0.9 | 98 | 100 | 0.98 | SVM | 96.55 | 27.59 | 68.97 | 0 | 3.45 | 88.89 | 100 | 0.947 | ||
| MLP | 95.65 | 60 | 20 | 1.8 | 1.8 | 97.05 | 91.6 | 0.9 | MLP | 96.55 | 27.59 | 68.97 | 0 | 3.45 | 88.89 | 100 | 0.945 | ||
| RBF | 96.73 | 60.9 | 20 | 0.9 | 1.8 | 97.1 | 95.65 | 0.9 | RBF | 89.66 | 24.14 | 65.52 | 3.45 | 6.90 | 77.78 | 95 | 0.861 | ||
| All Dataset | GEP | 100 | 31.03 | 68.97 | 0 | 0 | 100 | 100 | 1 | All Dataset | GEP | 83.33 | 33.33 | 50 | 0 | 16.67 | 66.67 | 100 | 0.8 |
| SVM | 98.28 | 29.31 | 68.97 | 0 | 1.72 | 94.44 | 100 | 1 | SVM | 83.33 | 50 | 33.33 | 0 | 16.67 | 75 | 100 | 0.7 | ||
| MLP | 100 | 31.03 | 68.97 | 0 | 0 | 100 | 100 | 1 | MLP | 83.33 | 50 | 33.33 | 0 | 16.67 | 75 | 100 | 0.7 | ||
| RBF | 98.28 | 29.31 | 68.97 | 0 | 1.72 | 94.44 | 100 | 0.988 | RBF | 79.16 | 50 | 29.17 | 0 | 20.83 | 70.58 | 100 | 0.6 | ||
Table 4.
Michigan microarray datasets performance comparison between GEP, SVM, MLP and RBF
| Training dataset | Testing dataset | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sub dataset | Classifier | Accuracy | TP | TN | FP | FN | Sensitivity | Specificity | AUC ROC | Sub dataset | Classifier | Accuracy | TP | TN | FP | FN | Sensitivity | Specificity | AUC ROC |
| 5 Attributes | GEP | 100 | 90.63 | 9.38 | 0 | 0 | 100 | 100 | 1 | 5 Attributes | GEP | 100 | 87.5 | 12.5 | 0 | 0 | 100 | 100 | 1 |
| SVM | 100 | 89.58 | 10.42 | 0 | 0 | 100 | 100 | 1 | SVM | 100 | 89.58 | 10.42 | 0 | 0 | 100 | 100 | 1 | ||
| MLP | 100 | 89.58 | 10.42 | 0 | 0 | 100 | 100 | 1 | MLP | 100 | 89.58 | 10.42 | 0 | 0 | 100 | 100 | 1 | ||
| RBF | 100 | 89.58 | 10.42 | 0 | 0 | 100 | 100 | 1 | RBF | 97.92 | 89.58 | 8.33 | 2.08 | 0 | 100 | 80 | 0.997 | ||
| 10 Attributes | GEP | 98.44 | 87.5 | 10.94 | 0 | 1.56 | 98.25 | 100 | 0.9 | 10 Attributes | GEP | 93.75 | 90.63 | 3.13 | 0 | 6.25 | 93.55 | 100 | 0.9 |
| SVM | 100 | 89.58 | 10.42 | 0 | 0 | 100 | 100 | 1 | SVM | 100 | 89.58 | 10.42 | 0 | 0 | 100 | 100 | 1 | ||
| MLP | 100 | 89.58 | 10.42 | 0 | 0 | 100 | 100 | 1 | MLP | 98.96 | 89.58 | 9.38 | 1.04 | 0 | 100 | 90 | 1 | ||
| RBF | 100 | 89.58 | 10.42 | 0 | 0 | 100 | 100 | 1 | RBF | 97.92 | 89.58 | 8.33 | 2.08 | 0 | 100 | 80 | 1 | ||
| 20 Attributes | GEP | 98.44 | 84.38 | 14.06 | 0 | 1.56 | 98.18 | 100 | 0.9 | 20 Attributes | GEP | 91.67 | 25 | 66.67 | 0 | 8.33 | 75 | 100 | 0.9 |
| SVM | 100 | 89.58 | 10.42 | 0 | 0 | 100 | 100 | 1 | SVM | 98.96 | 88.54 | 10.42 | 0 | 1.40 | 98.84 | 100 | 0.991 | ||
| MLP | 100 | 89.58 | 10.42 | 0 | 0 | 100 | 100 | 1 | MLP | 98.96 | 88.54 | 10.42 | 0 | 1.04 | 98.84 | 100 | 0.997 | ||
| RBF | 100 | 89.58 | 10.42 | 0 | 0 | 100 | 100 | 1 | RBF | 96.88 | 88.54 | 8.33 | 2.08 | 1.04 | 98.84 | 80 | 0.931 | ||
| AS | GEP | 100 | 89.61 | 10.39 | 0 | 0 | 100 | 100 | 1 | AS | GEP | 100 | 89.47 | 10.53 | 0 | 0 | 100 | 100 | 1 |
| SVM | 100 | 89.6 | 10.39 | 0 | 0 | 100 | 100 | 1 | SVM | 97.92 | 88.54 | 9.38 | 1.04 | 1.04 | 98.84 | 90 | 0.986 | ||
| MLP | 100 | 89.6 | 10.39 | 0 | 0 | 100 | 100 | 1 | MLP | 97.92 | 88.54 | 9.38 | 1.04 | 1.04 | 98.84 | 90 | 0.986 | ||
| RBF | 100 | 89.6 | 10.39 | 0 | 0 | 100 | 100 | 1 | RBF | 97.35 | 89.47 | 7.89 | 0 | 2.63 | 91.89 | 100 | 0.9 | ||
| All Dataset | GEP | 96.88 | 88.54 | 8.33 | 2.08 | 1.04 | 98.84 | 80 | 0.995 | All Dataset | GEP | 95.83 | 88.54 | 7.29 | 3.13 | 1.04 | 98.84 | 70 | 0.989 |
| SVM | 96.88 | 88.54 | 8.33 | 2.08 | 1.04 | 98.84 | 80 | 0.995 | SVM | 95.83 | 88.54 | 7.29 | 3.13 | 1.04 | 98.84 | 70 | 0.989 | ||
| MLP | 100 | 89.58 | 10.42 | 0 | 0 | 100 | 100 | 1 | MLP | 97.92 | 88.54 | 9.38 | 1.04 | 1.04 | 98.84 | 90 | 0.986 | ||
| RBF | 100 | 89.58 | 10.42 | 0 | 0 | 100 | 100 | 1 | RBF | 95.83 | 87.50 | 8.33 | 2.08 | 2.08 | 97.67 | 80 | 0.966 | ||
Table 5.
Harvard microarray datasets performance comparison between GEP, SVM, MLP and RBF
| Training dataset | Testing dataset | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sub dataset | Classifier | Accuracy | TP | TN | FP | FN | Sensitivity | Specificity | AUC ROC | Sub dataset | Classifier | Accuracy | TP | TN | FP | FN | Sensitivity | Specificity | AUC ROC |
| 5 Attributes | GEP | 100 | 17.13 | 82.87 | 0 | 0 | 100 | 100 | 1 | 5 Attributes | GEP | 99.45 | 16.57 | 82.87 | 0 | 0.55 | 96.77 | 100 | 1 |
| SVM | 98.90 | 16.02 | 82.87 | 0 | 1.10 | 93.55 | 100 | 1 | SVM | 98.90 | 16.02 | 82.87 | 0 | 1.10 | 93.55 | 100 | 1 | ||
| MLP | 100 | 17.13 | 82.87 | 0 | 0 | 100 | 100 | 1 | MLP | 99.45 | 16.57 | 82.87 | 0 | 0.55 | 96.77 | 100 | 1 | ||
| RBF | 100 | 17.13 | 82.87 | 0 | 0 | 100 | 100 | 1 | RBF | 98.34 | 16.02 | 82.32 | 0.55 | 1.10 | 93.55 | 99.33 | 0.998 | ||
| 10 Attributes | GEP | 99.17 | 15.70 | 83.47 | 0 | 0.83 | 95 | 100 | 0.9 | 10 Attributes | GEP | 91.67 | 13.33 | 78.33 | 0 | 8.33 | 61.54 | 100 | 0.9 |
| SVM | 99.45 | 16.57 | 82.87 | 0 | 0.55 | 96.77 | 100 | 0.999 | SVM | 99.45 | 16.57 | 82.87 | 0 | 0.55 | 96.77 | 100 | 0.998 | ||
| MLP | 100 | 17.13 | 82.87 | 0 | 0 | 100 | 100 | 1 | MLP | 99.45 | 16.57 | 82.87 | 0 | 0.55 | 96.77 | 100 | 0.998 | ||
| RBF | 99.45 | 16.57 | 82.87 | 0 | 0.55 | 96.77 | 100 | 1 | RBF | 97.24 | 14.92 | 82.32 | 0.55 | 2.21 | 87.10 | 99.33 | 0.998 | ||
| 20 Attributes | GEP | 99.17 | 14.05 | 85.12 | 0 | 0.83 | 94.44 | 100 | 0.9 | 20 Attributes | GEP | 91.67 | 13.33 | 78.33 | 0 | 8.33 | 61.54 | 100 | 0.9 |
| SVM | 99.45 | 16.57 | 82.87 | 0 | 0.55 | 96.77 | 100 | 0.999 | SVM | 99.45 | 16.57 | 82.87 | 0 | 0.55 | 96.77 | 100 | 0.998 | ||
| MLP | 98.34 | 15.47 | 82.87 | 0 | 1.66 | 90.32 | 100 | 0.999 | MLP | 98.34 | 15.47 | 82.87 | 0 | 1.66 | 90.32 | 100 | 0.991 | ||
| RBF | 98.90 | 16.02 | 82.87 | 0 | 1.10 | 93.55 | 100 | 0.979 | RBF | 97.24 | 14.92 | 82.32 | 0.55 | 2.21 | 87.10 | 99.33 | 0.920 | ||
| AS | GEP | 99.31 | 11.72 | 87.59 | 0 | 0.69 | 94.44 | 100 | 0.9 | AS | GEP | 91.67 | 27.78 | 63.89 | 0 | 8.33 | 76.92 | 100 | 0.9 |
| SVM | 100 | 12.41 | 87.59 | 0 | 0 | 100 | 100 | 1 | SVM | 94.4 | 30.56 | 63.89 | 5.56 | 0 | 100 | 92 | 0.9 | ||
| MLP | 97.9 | 10.34 | 87.59 | 2.07 | 0 | 100 | 97.69 | 0.9 | MLP | 94.4 | 30.56 | 63.89 | 5.56 | 0 | 100 | 92 | 0.9 | ||
| RBF | 98.25 | 10.69 | 87.59 | 1.72 | 0 | 100 | 98 | 0.9 | RBF | 94.4 | 30.56 | 63.89 | 5.56 | 0 | 100 | 92 | 0.9 | ||
| All Dataset | GEP | 100 | 49.66 | 50.34 | 0 | 0 | 100 | 100 | 1 | All Dataset | GEP | 83.33 | 33.33 | 50 | 0 | 16.67 | 66.67 | 100 | 0.7 |
| SVM | 99.45 | 16.57 | 82.87 | 0 | 0.55 | 96.77 | 100 | 0.998 | SVM | 95.03 | 14.36 | 80.66 | 2.21 | 2.76 | 83.87 | 97.33 | 0.980 | ||
| MLP | 99.45 | 16.57 | 82.87 | 0 | 0.55 | 96.77 | 100 | 1 | MLP | 93.92 | 14.36 | 79.56 | 3.31 | 2.76 | 83.87 | 96 | 0.960 | ||
| RBF | 100 | 17.13 | 82.87 | 0 | 0 | 100 | 100 | 1 | RBF | 94.48 | 13.81 | 80.66 | 2.21 | 3.31 | 80.65 | 97.33 | 0.981 | ||
5 Discussion
The experimental results showed that the performance of the GEP model with fewer feature genes (i.e. 5 attributes) was better than the model with more attributes (i.e. 10, 20 and all attributes). The experimental results also showed that the lowest accuracy for the GEP classifiers was 87.49% with the standard division of 5.89 which were achieved by the classifier with all attributes, while the highest average accuracy of the GEP classifiers was 98.09% with the standard division of 2.32 when using 5 attributes. This is also the highest accuracy for all the experimental models (GEP, SVM, MLP and RBFNN). Actually the best accuracy the other three models (SVM, MLP and RBFNN) achieved was 97.74% which is lower than GEP model.
The results also indicated that the models using the automatically selected feature genes (performed by the RF method) could provide stable and convergent results. However, the classification performance was not the best across all the experimental models. This might be caused by the limitation of this feature selection method which is unable to select some informative genes for more effective classifications.
It was observed from the experimental results that GEP classifier was more efficient as it achieved the highest accuracy by using five feature genes only in the classification model. Of course, this five feature genes have to be properly selected and informative without missing microarray values.
6 Conclusions
In this paper, an innovative GEP‐based classifier is proposed to classify/predict lung cancer from microarray data. Compared with other representative machine learning‐based classifiers, the proposed classifier achieved higher accuracies in classifying/predicting lung cancers on the commonly used datasets (GEO, Michigan and Harvard). The evaluation results showed that GEP approach improved the lung cancer prediction.
The efficiency and effectiveness of the proposed GEP approach heavily depend on the proper selection of feature genes (attributes) that are informative without missing values for classification/prediction. Our future work is to propose innovative methods to more properly select features (attributes) from integrated lung cancer datasets and multiple sources of lung cancer data to improve the GEP‐based algorithm for lung cancer prediction.
Table 6.
The standard deviation for all microarray datasets performance comparison between GEP, SVM, MLP and RBF
| Accuracy | Sub dataset | GEP | SVM | MLP | RBF | TP | Sub dataset | GEP | SVM | MLP | RBF |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 2.318424 | 3.026916 | 3.131116 | 2.377356 | 5 | 31.47637 | 32.60562 | 32.44997 | 32.92989 | ||
| 10 | 1.747532 | 3.803796 | 2.072074 | 3.74383 | 10 | 33.79646 | 34.3937 | 32.44997 | 33.23572 | ||
| 20 | 3.516678 | 4.504001 | 1.818467 | 3.491488 | 20 | 4.846417 | 32.63768 | 32.27651 | 33.08101 | ||
| AS | 3.417371 | 1.448747 | 1.448747 | 3.167652 | AS | 29.12583 | 28.05828 | 28.05828 | 29.40071 | ||
| All attributes | 5.892557 | 5.713337 | 6.155541 | 7.560231 | All attributes | 26.02624 | 30.29157 | 30.29157 | 30.0854 | ||
| Sensitivity | Sub dataset | GEP | SVM | MLP | RBF | TN | Sub dataset | GEP | SVM | MLP | RBF |
| 5 | 7.218459 | 6.863266 | 7.218459 | 9.333475 | 5 | 30.43026 | 31.13021 | 31.13021 | 32.19723 | ||
| 10 | 13.34954 | 15.00863 | 7.218459 | 9.110438 | 10 | 32.47011 | 32.45769 | 31.87642 | 31.67098 | ||
| 20 | 7.795606 | 12.09045 | 6.342192 | 10.89274 | 20 | 6.484208 | 31.13021 | 31.39412 | 31.92407 | ||
| AS | 9.424551 | 4.986428 | 4.986428 | 9.180853 | AS | 26.433 | 26.97347 | 26.97347 | 26.79111 | ||
| All attributes | 15.16508 | 9.838267 | 9.838267 | 11.18011 | All attributes | 20.13369 | 30.37061 | 29.12816 | 30.39948 | ||
| Specificity | Sub dataset | GEP | SVM | MLP | RBF | FP | Sub dataset | GEP | SVM | MLP | RBF |
| 5 | 0 | 1.178511 | 1.178511 | 9.274204 | 5 | 0 | 0.810816 | 0.810816 | 0.880013 | ||
| 10 | 3.625101 | 0 | 4.714045 | 8.282497 | 10 | 2.479588 | 0 | 0.490261 | 1.184521 | ||
| 20 | 6.736371 | 1.178511 | 0 | 8.713003 | 20 | 4.96389 | 0.810816 | 0 | 0.653146 | ||
| AS | 0 | 4.320494 | 4.320494 | 3.299832 | AS | 0 | 2.413517 | 2.413517 | 2.291729 | ||
| All attributes | 14.14214 | 13.5567 | 4.109609 | 8.866026 | All attributes | 1.475496 | 1.313494 | 1.382052 | 1.012555 | ||
| AUC ROC | Sub dataset | GEP | SVM | MLP | RBF | FN | Sub dataset | GEP | SVM | MLP | RBF |
| 5 | 0.053269 | 0.054683 | 0.057983 | 0.034179 | 5 | 2.318424 | 2.223706 | 2.318424 | 3.026916 | ||
| 10 | 0 | 0.046676 | 0.052804 | 0.070244 | 10 | 1.279384 | 3.803796 | 2.318424 | 2.876924 | ||
| 20 | 0 | 0.03007 | 0.056622 | 0.021453 | 20 | 1.447212 | 3.620556 | 1.818467 | 3.33189 | ||
| AS | 0.040893 | 0.03516 | 0.035122 | 0.018385 | AS | 3.417371 | 1.444999 | 1.444999 | 2.843312 | ||
| All attributes | 0.119834 | 0.134165 | 0.12913 | 0.176176 | All attributes | 7.368053 | 6.997963 | 6.997963 | 8.563656 |
7 References
- 1. Engchuan W., and Chan J.H.: ‘Pathway activity transformation for multi‐class classification of lung cancer datasets’, Neurocomputing, 2015, 165, pp. 81–89 (doi: 10.1016/j.neucom.2014.08.096) [DOI] [Google Scholar]
- 2. Society A.C.: ‘Cancer facts & figures 2011’ (American Cancer Society Inc., 2011), vol. 1 [Google Scholar]
- 3. Laureen W., and Goh B.C.: ‘An overview of cancer trends in Asia’ (Innovationmagazine.com., 2012) [Google Scholar]
- 4. Mehta A. Dobersch S., and Romero‐Olmedo A.J. et al.: ‘Epigenetics in lung cancer diagnosis and therapy’, Cancer Metastasis Rev., 2015, 34, pp. 229–241 (doi: 10.1007/s10555-015-9563-3) [DOI] [PubMed] [Google Scholar]
- 5. Spitz M.R. Wei Q., and Dong Q. et al.: ‘Genetic susceptibility to lung cancer the role of DNA damage and repair’, Cancer Epidemiol. Biomarkers Prev., 2003, 12, pp. 689–698 [PubMed] [Google Scholar]
- 6. Melissa C.S.: ‘Lung cancer’ (Medicine.net, 2011) [Google Scholar]
- 7. Mountain C.F.: ‘Revisions in the international system for staging lung cancer FREE TO VIEW’, Chest, 1997, 111, pp. 1710–1717 (doi: 10.1378/chest.111.6.1710) [DOI] [PubMed] [Google Scholar]
- 8. Mountain C.F., and Dresler C.M.: ‘Regional lymph node classification for lung cancer staging’, Chesy J., 1997, 111, pp. 1718–1723 (doi: 10.1378/chest.111.6.1718) [DOI] [PubMed] [Google Scholar]
- 9. Tsou J.A. Hagen J.A., and Carpenter C.L. et al.: ‘DNA methylation analysis: a powerful new tool for lung cancer diagnosis’, Oncogene, 2002, 21, pp. 5450–5461 (doi: 10.1038/sj.onc.1205605) [DOI] [PubMed] [Google Scholar]
- 10. Diaz J.M. Pinon R.C., and Solano G.: ‘Lung cancer classification using genetic algorithm to optimize prediction models’. Fifth Int. Conf. on Information, Intelligence, Systems and Applications, IISA 2014, Chania, 2014, pp. 1–6
- 11. Yu Z. Chen X.Z., and Cui L.H. et al.: ‘Prediction of lung cancer based on serum biomarkers by gene expression programming methods’, Asian Pac. J. Cancer Prev., 2014, 15, pp. 9367–9373 (doi: 10.7314/APJCP.2014.15.21.9367) [DOI] [PubMed] [Google Scholar]
- 12. Rusch V.W. Asamura H., and Watanabe H. et al.: ‘The IASLC lung cancer staging project: a proposal for a new international lymph node map in the forthcoming seventh edition of the TNM classification for lung cancer’, J. Thorac. Oncol., 2009, 4, pp. 568–577 (doi: 10.1097/JTO.0b013e3181a0d82e) [DOI] [PubMed] [Google Scholar]
- 13. Kourou K. Exarchos T.P., and Exarchos K.P. et al.: ‘Machine learning applications in cancer prognosis and prediction’, Comput. Struct. Biotechnol. J., 2015, 13, pp. 8–17 (doi: 10.1016/j.csbj.2014.11.005) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Joseph A.C., and David S.W.: ‘Applications of machine learning in cancer prediction and prognosis’, Cancer Inf., 2006, 2, pp. 59–77 [PMC free article] [PubMed] [Google Scholar]
- 15. Guan P. Huang D., and He M. et al.: ‘Lung cancer gene expression database analysis incorporating prior knowledge with support vector machine‐based classification method’, J. Exp. Clin. Cancer Res., 2009, 28, pp. 1–7 (doi: 10.1186/1756-9966-28-1) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Ayer T. Alagoz O., and Chhatwal J. et al.: ‘Breast cancer risk estimation with artificial neural networks revisited: discrimination and calibration’. PMC, 2010, vol. 116, pp. 3310–3321 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Yu Z. Lu H., and Si H. et al.: ‘A highly efficient gene expression programming (GEP) model for auxiliary diagnosis of small cell lung cancer’, PLoS ONE, 2015, 10, pp. 1–19 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Ferreira C.: ‘Gene expression programming in problem solving’ 2002.
- 19. Ferreira C., and Gepsoft U.: ‘What is gene expression programming’, (Candida Ferreira, 2008) [Google Scholar]
- 20. Zhong J. Wang J., and Peng W. et al.: ‘Prediction of essential proteins based on gene expression programming’, BMC Genomics, 2013, 14, p. S7 (doi: 10.1186/1471-2164-14-S8-S7) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Kusy M. Obrzut B., and Kluska J.: ‘Application of gene expression programming and neural networks to predict adverse events of radical hysterectomy in cervical cancer patients’, Med. Biol. Eng. Comput., 2013, 51, pp. 1357–1365 (doi: 10.1007/s11517-013-1108-8) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Ferreira C.: ‘Gepsoft predictive modeling software’ (Candida Ferreira, 2001), vol. 2015 [Google Scholar]
- 23. Koza J.R.: ‘Genetic programming: on the programming of computers by means of natural selection’ (MIT Press, Cambridge, MA, 1992) [Google Scholar]
- 24. Ryan J.: ‘Genetic algorithms in search, optimization and machine learning (Book Review)’, ORSA J. Comput., 1991, 3, p. 176 (doi: 10.1287/ijoc.3.2.176) [DOI] [Google Scholar]
- 25. Han X.R. Li X.C., and Si H.Z. et al.: ‘QSAR study of the anti‐cancer activity of 38 compounds in different cancer cell lines based on gene expression programming’, Adv. Mater. Res., 2014, pp. 1291–1294 [Google Scholar]
- 26. Ferreira C.: ‘Gene expression programming: mathematical modeling by an artificial intelligence’ (Springer‐Verlag, Berlin, 2006), vol. 850 [Google Scholar]
- 27. Natarajan A., and Ravi T.: ‘A survey on gene feature selection using microarray data for cancer classification’. Int. J. Comput. Sci. Commun., 2014, 5, pp. 126–129 [Google Scholar]
- 28. Yildirim P.: ‘Filter based feature selection methods for prediction of risks in hepatitis disease’, Int. J. Mach. Learn. Comput., 2015, 5, p. 258 (doi: 10.7763/IJMLC.2015.V5.517) [DOI] [Google Scholar]
- 29. Wang X., and Gotoh O.: ‘A robust gene selection method for microarray‐based cancer classification’, Cancer Inf., 2010, 9, p. 15 (doi: 10.4137/CIN.S3794) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Mark H. Eibe F., and Geoffrey H. et al.: ‘The WEKA data mining software: An update’, SIGKDD Explorations, 2009, 11, (1), pp. 10–18 (doi: 10.1145/1656274.1656278) [DOI] [Google Scholar]
- 31. Breiman L.: ‘Random forests’, Mach. Learn., 2001, 45, (1), pp. 5–32 (doi: 10.1023/A:1010933404324) [DOI] [Google Scholar]
- 32. Touw W.G. Bayjanov J.R., and Overmars L. et al.: ‘Data mining in the life sciences with random forest: a walk in the park or lost in the jungle?’, Brief. Bioinf., 2012, 14, p. bbs034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Hosseinzadeh F. Kayvanjoo A.H., and Ebrahimi M.: ‘Prediction of lung tumor types based on protein attributes by machine learning algorithms’, SpringerPlus, 2013, 2, pp. 2–14 (doi: 10.1186/2193-1801-2-238) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Sherrod P.H.: DTREG predictive modelling software. Available at https://www.dtreg.com/, accessed 7 February 2015
- 35. George G.V.S., and Raj V.C.: ‘Review on feature selection techniques and the impact of SVM for cancer classification using gene expression profile’, Int. J. Comput. Sci. Eng. Surv., 2011, 2, p. 16 (doi: 10.5121/ijcses.2011.2302) [DOI] [Google Scholar]
- 36. Vanitha C.D.A. Devaraj D., and Venkatesulu M.: ‘Gene expression data classification using support vector machine and mutual information‐based gene selection’, Procedia Comput. Sci., 2015, 47, pp. 13–21 (doi: 10.1016/j.procs.2015.03.178) [DOI] [Google Scholar]
- 37. McClelland J.L. Rumelhart D.E., and Group P.R.: ‘Parallel distributed processing’, Explor. Microstruct. Cogn., 1986, 2, pp. 1–38 (doi: 10.1016/0749-6036(86)90143-6) [DOI] [Google Scholar]
- 38. Kubat M.: ‘Neural networks: a comprehensive foundation by Simon Haykin, Macmillan, 1994, ISBN 0–02‐352781‐7’ (Cambridge University Press, 1999) [Google Scholar]
- 39. Adetiba E., and Olugbara O.O.: ‘Improved classification of lung cancer using radial basis function neural network with affine transforms of voss representation’, PloS One, 2015, 10, p. e0143542 (doi: 10.1371/journal.pone.0143542) [DOI] [PMC free article] [PubMed] [Google Scholar]


