Abstract
Breast cancer is the second leading cause of death in the world. Breast cancer research is focused towards its early prediction, diagnosis, and prognosis. Breast cancer can be predicted on omics profiles, clinical tests, and pathological images. The omics profiles comprise of genomic, proteomic, and transcriptomic profiles that are available as high‐dimensional datasets. Survival prediction is carried out on omics data to predict early the onset of disease, relapse, reoccurrence of diseases, and biomarker identification. The early prediction of breast cancer is desired for the effective treatment of patients as delay can aggravate the staging of cancer. In this study, extreme learning machine (ELM) based model for breast cancer survival prediction named eBreCaP is proposed. It integrates the genomic (gene expression, copy number alteration, DNA methylation, protein expression) and pathological image datasets; and trains them using an ensemble of ELM with the six best‐chosen models suitable to be applied on integrated data. eBreCaP has been evaluated on nine performance parameters, namely sensitivity, specificity, precision, accuracy, Matthews correlation coefficient, area under curve, area under precision–recall, hazard ratio, and concordance Index. eBreCaP has achieved an accuracy of 85% for early breast cancer survival prediction using the ensemble of ELM with gradient boosting.
Inspec keywords: proteins, learning (artificial intelligence), patient treatment, proteomics, DNA, genetics, medical image processing, genomics, cancer, biochemistry
Other keywords: extreme learning‐based model, breast cancer research, omics profiles, genomic profiles, transcriptomic profiles, extreme learning machine based model, early breast cancer survival prediction, proteomic profiles, clinical tests, high‐dimensional datasets, diseases, gene expression, copy number alteration, DNA methylation, protein expression, pathological image datasets, Matthews correlation coefficient, area under curve, concordance Index, gradient boosting
1 Introduction
Healthcare in cancer research is inclined towards the recognition of some kind of cancer well in time and providing preventive actions to improve the health of a person [1]. Researchers and data scientists in the medical field are working together on healthcare for early prediction and preventions of one of the fatal diseases like breast cancer. Breast cancer is one of the most common kinds of cancers. It has attained huge attention due to its life‐threatening consequences. According to the National Cancer Institute (NCI) [2], around a hundred types of cancers are present in the human body, including breast, prostate, ovarian, liver, and bladder cancers. NCI shows that breast cancer is the most common type of cancer in the US and needs to be diagnosed early. Breast cancer is a common disease in both genders, surprisingly in males also but mostly found in women [3]. Every 1 in 1000, men have breast cancer. Breast cancer in males exists in smaller proportions [4]. However, in females, the percentage of women having breast cancer is 25% [5]. Globally, the survival rate of breast tumour patients is 50%, which is very low. The death rate of patients dying from malignancy is 58% [6]. The basic building blocks of the human body are cells. Breast cancer occurs as a result of abnormal growth in the cell of the body. The collection of these abnormal cells leads to tumours. From this collection, a cell detaches itself from other cells and move to other body parts through blood vessels. Genes present in the nucleus of the cells of the human body are responsible for the movement of cells. Sometimes anomalous changes may turn off or turn on these genes. This turns off and turns on may lead to breast cancer [7, 8]. Advanced computational intelligent [9] approaches in artificial intelligence (AI) are being exploited recently to predict breast cancer in its early stages. Omics datasets have been used recently for breast cancer prediction. Datasets like microarray datasets along with clinical and image datasets, are being used for early prediction. Healthcare data is very complex and working with such data requires various data mining, preprocessing and features extraction techniques for efficient results. Also, the size of the genomic profiles, which are being used is very large approaching to terabytes. Traditional relational databases failed to store such large databases using relational database systems [10]. For accurate data analysis, there is a need to develop an efficient framework for breast cancer survival prediction which can guide through preprocessing, feature extraction techniques and use highly accurate algorithms for early prediction in breast cancer.
In this paper, the Extreme Learning‐based model for Breast Cancer Survival Prediction named ‘eBreCaP’ is proposed.
It integrates different subtypes of genomic data [11] like gene expression [12], Copy Number Alteration (CNA) [13], deoxyribonucleic acid (DNA) methylation [14] and protein expression [15] with pathological images for efficient survival prediction of breast cancer.
It ensembles an ELM [16] with Buckley–James estimator, regularised cox model [16–17], likelihood boosting and gradient boosting [18] for survival prediction.
It optimises performance parameters for survival prediction such as accuracy, sensitivity, specificity, precision, area under curve (AUC), area under precision–recall (AUPR), Matthews correlation coefficient (MCC), concordance index (CI), and hazard ratio (HR).
The remaining of the paper is organised as follows. Motivation and related work are described in Section 2. In Section 3, eBreCaP is proposed. The experimental setup and results are given and elaborated in Section 4. In Section 5, the conclusion and future scope are presented.
2 Background
Breast cancer prediction is performed on various types of data with the help of machine learning (ML) [11] and deep learning (DL) algorithms [19]. Supervised ML [20] was used by Dai and co‐authors [21] for the prediction of breast cancer. The authors took DNA microarray data [22] of 117 young patients. The experiment was performed to accurately predict poor gene signature, which causes cancer. Zou and co‐authors [23] proposed unsupervised learning which consists of the integration of principle component analysis (PCA) [24] and autoencoder neural network (NN) [25] on gene expression dataset for breast cancer prediction. A total of 129,158 gene expressions profiles were taken and features were extracted with a DL approach. The model was trained and experimental results indicated that the proposed approach achieved 85% accuracy. Tabl et al. [26] made use of hierarchical ML algorithms to predict the survival of breast cancer patients. The method was trained with a support vector machine (SVM), Naïve‐Bayes classifier and random forest (RF) [27]. It is evident from the results that RF produces the best result by identifying all classes correctly and accurately. Huang et al. [19] anticipated a DL framework to identify for how much time the patient is going to survive after some treatment with Cox models [18]. Survival Analysis Learning with Multi‐Omics NN on a gene‐expression dataset for survival prediction was also carried out. Experimental results proved that the proposed approach attained an AUC value of 79%. Researchers also worked towards the integration of heterogeneous datasets as not to miss out on any related medical information hidden in various datasets which is important to be incorporated for prediction. Gevaert et al. [28] work on the integration of clinical and microarray data for early prediction of breast cancer with the help of Bayesian networks [29]. A sample of 78 patients was taken and preprocessing techniques were applied. Further, the clinical and microarray data were integrated with various techniques like full integration, decision integration, and partial integration. The trained and tested models made evident that Bayesian networks performed superior with a mean AUC value of 0.85. Sun et al. [30] carried out work on multimodal DL NN by integrating multi‐dimensional data (MDNNMD) for the detection of breast cancer patients. The experiment was implemented and compared with SVM, RF and logistic regression (LR) [31]. The end results accomplished 82% accuracy using the MDNNMD approach. Radiology images also play a crucial role in the identification of tumour cells. Li and co‐authors [32] presented a new strategy by integrating genomic and radiology images for breast cancer prognosis. The experimental study gave good results with a mean AUC value of 80% when integrated genomic and radiology images were taken. On the other side, Hung and Chui [33] used scored equation [34] which integrates gene expression and protein network datasets to identify subtypes of cancer correctly with the help of SVM [35] classifier. SVM attains 70% accuracy by accurately predicting three subtypes of the tumours. Han and co‐authors [36] proposed a more practical scheme called multiple kernel learning (MKL) [37] on omics data comprising micro Ribonucleic acid (miRNA) expression [22], copy number variation, and DNA methylation dataset. A sample of 10,000 patients was taken with 30 subtypes of cancers. The results indicated that MKL executed better as compared to RF and NN with a mean accuracy of 79%. Zhang and co‐authors [38] suggested a convolutional NN [25] comprising convolutional layer, small SE‐ResNet module and fully‐connected layer to work on histopathological images for the classification of breast cancer into benign, malignant and eight subtypes. The SE‐ResNet module [38] is a modification of the squeeze and excitation module. A sample of patients was taken and feature extraction techniques were applied. The end results achieved 98% accuracy for binary classification and 90% accuracy for multi‐class classification. Fan and co‐authors [39] use ML algorithms like logistic regression and Cox survival models to effectively classify breast cancer into different subtypes and to predict survival after no‐adjuvant chemotherapy. The model was trained and it is evidenced that the presented approach achieved an AUC value of 80%. Li and co‐authors [40] suggested a convolutional NN with an ELM algorithm for the detection of breast cancer. The experiments used a sample of 400 patients and attained 90% AUC value. Table 1 shows the comparison of work done on Breast Cancer Prediction with eBreCaP based on performance parameters.
Table 1.
Comparison of work done on breast cancer prediction on the basis of performance parameters with eBreCaP
| Authors | Sensitivity | Specificity | Precision | Accuracy | AUC | AUPR | CI | HR | MCC |
|---|---|---|---|---|---|---|---|---|---|
| Tabl et al. [26] | _ | _ | _ | ✓ | _ | _ | _ | _ | _ |
| Dai and co‐authors [21] | ✓ | _ | _ | ✓ | _ | _ | _ | _ | _ |
| Zou and co‐authors [23] | ✓ | _ | _ | ✓ | ✓ | _ | _ | _ | ✓ |
| Huang et al. [19] | _ | ✓ | _ | ✓ | _ | _ | ✓ | _ | _ |
| Gevaert et al. [28] | _ | ✓ | _ | ✓ | ✓ | _ | _ | _ | _ |
| Sun et al. [30] | ✓ | ✓ | ✓ | _ | _ | _ | _ | _ | _ |
| Li and co‐authors [32] | _ | ✓ | _ | _ | ✓ | _ | _ | _ | _ |
| Hung and Chui [33] | _ | _ | _ | ✓ | _ | _ | _ | _ | _ |
| Han and co‐authors [36] | _ | _ | _ | _ | ✓ | _ | _ | _ | _ |
| Zhang and co‐authors [38] | _ | ✓ | ✓ | _ | ✓ | _ | _ | _ | ✓ |
| Huang et al. [41] | ✓ | — | — | _ | ✓ | _ | _ | _ | ✓ |
| Li and co‐authors [40] | ✓ | ✓ | ✓ | ✓ | ✓ | _ | _ | _ | _ |
| eBreCaP | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
2.1 Motivation
Survivability of breast cancer patients can be predicted on omics data (Genomic, Transcriptomic, and Proteomic data) [42]. Apart from omics data, pathological images (tissue images features) can also be used in breast cancer research. Pathological images also give important information regarding the prognosis of breast cancer. Hence, they should also be considered while developing computational models/approaches for predicting the survivability of breast cancer patients. Existing computational approaches for the survivability analysis have not considered pathological images while predicting survivability of breast cancer patients [19, 21, 23, 26]. The extraction of features from omics data with pathological images and integrate information from both the datasets as mentioned above poses a huge challenge on how to efficiently extract the features from heterogeneous datasets to implement survival prediction for breast cancer patients [43]. Motivated by Sun et al. [44], an efficient model eBreCaP (extreme learning‐based Breast Cancer Prediction) for survival prediction of breast cancer is proposed and compared with different survival models considered in [44]. These existing models used to integrate genomic data and pathological image data. The results indicate that pathological images could contribute genuinely by uncovering hidden features important in the survival prediction of breast cancer patients.
2.2 Our contributions
The main contributions of this research work are
K‐means clustering and normalisation are used for pre‐processing the high‐dimensional genomic data for breast cancer survival prediction.
FSelector package is used for feature space reduction in genomic data.
Tiling for pathological images is used, which was further converted to textual data for more precise final evaluation.
The performance of eBreCaP is compared with five existing state‐of‐the‐art ML models using traditional performance parameters (sensitivity, precision, accuracy, AUC) and two new parameters (HR and AUPR).
eBreCaP: An Extreme Learning‐based Breast Cancer Survival Prediction model adds diversity in the classifier as it is capable of handling heterogeneous and high‐dimensional data simultaneously.
3 Proposed model: eBreCaP
eBreCaP exploits the concept of extreme learning‐based models. The underlying workflow of eBreCaP is shown diagrammatically in Fig. 1. eBreCaP follows three stages: Stage A: it selects the features from the genomic as well as pathological images dataset. Stage B: it integrates extracted features from genomic and pathological images dataset using ELM. It trains the selected candidate models namely ELM with Buckley–James estimator (ELMBJ), Ensemble of ELMBJ (ELMBJEN), ELM with Cox regularised models (ELMCOX), an ensemble of ELM with cox regularised (ELMCOX), ELM with likelihood boosting (ELMCOXBOOST) and ELM with gradient boosting (ELMBOOST) on integrated datasets. Stage C: it tests the performance of the selected models. Out of all other ensemble models taken in stage B, ELMBOOST outperforms with an accuracy of 85%.
Fig. 1.
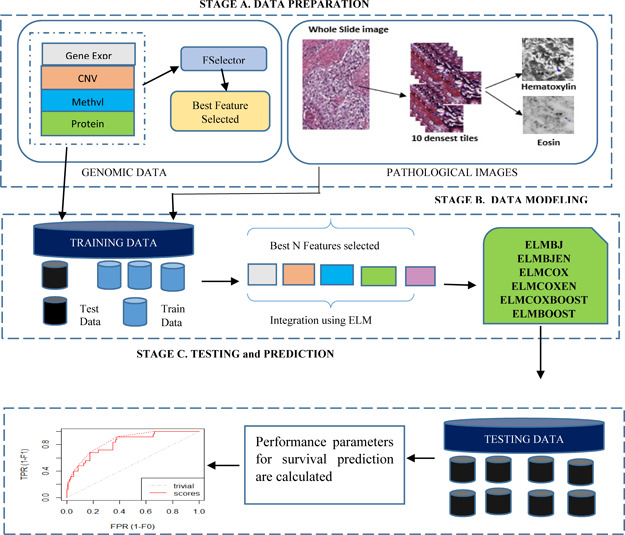
eBreCaP: the proposed model
3.1 Data preparation
The dataset for eBreCaP has been collected from The Cancer Genome Atlas portal (TCGA) [45]. This research considered four subtypes of genomic data comprising gene expression, CNA, DNA methylation, and protein expression data along with pathological images data. But each subtype contains a different number of patients. For example, for gene expression, 1250 samples and for pathological images, 1010 samples are available. Venn diagram was used to find common patients from genomic and pathological images. It gave 585 valid patients with 578 female patients and 7 male patients. As sufficient data is available for female patients, survival prediction is carried out on female breast cancer patients. Male patients were not taken into consideration due to the unavailability of sufficient data. For training, the threshold value of 5 years was taken and the patients were classified into low survival and high survival. The total number of patients with low survival was 445 and with high survival was 133.
3.2 Preprocessing of genomic data
Genomic Data consists of Gene Expression, CNA, DNA Methylation, and Protein Expression datasets. Bioconductor package [46] in the R language is used to download the data. A complete set of valid 578 patients is preprocessed and further divided into the training and testing sets in 70: 30 ratios. The whole preprocessing of the genomic and pathological image datasets is shown in Table 2.
Table 2.
Preprocessing and feature extraction steps for eBreCaP
| Steps used | Dataset | ||||
|---|---|---|---|---|---|
| Gene expression | CNA | DNA methylation | Protein expression | Pathological images | |
| Preprocessing (stage 1) | Removal of missing values using K‐mean algorithm | Removal of missing values using K‐mean algorithm | Removal of missing values using K‐mean algorithm | Removal of missing values using K‐mean algorithm | Image tiling using bftools |
| Preprocessing (stage 2) | Differential expressed genes with p‐value <0.5 | Directly take copy number values from SNP6 | Directly take the original beta values | Directly take the original values | Select ten denser tiles |
| Normalisation | Normalise them and set to under‐expression over‐expression baseline | Normalise them using z‐score normalisation | Normalise them using z‐score normalisation | Normalise them using min‐max normalisation | — |
| Feature selection package | FSelector information gain ratio | FSelector information gain ratio | FSelector information gain ratio | FSelector information gain ratio | Cell‐profiler |
| Extracted features | Best 50 features selected | Best 10 features selected | Best 40 features selected | Best 120 features selected | Best 130 features selected |
3.2.1 Gene expression
In gene expression data, information is produced by the gene, which is used to make a useful gene product [47]. The human body is comprised of a cell. Each cell contains miRNA data which is responsible for producing information [12]. The flow of information starts with DNA, which moves towards Ribonucleic acid (RNA) and then to protein. This conversion of DNA to RNA is known as transcriptomic data. Thousands of transcripts are produced every passing second by each cell [12]. These transcripts are responsible for affecting the activity of the body. First, 10% missing values (NA values) is removed using na.omit function in R language and remaining missing values are removed using the k‐means clustering algorithm [48]. The differentially expressed genes are calculated using p‐values which are divided into under‐expression, overexpression, and baseline [49], i.e.
3.2.2 Copy number alteration
CNA is a significant component of genomic data and is described as a DNA segment of one or more kilo‐base with certain variations [13]. This variation is because of several insertions, deletions, and modifications in the chromosome number, which leads to increased data size [13].
These variations get implicated in somatic cells that cause breast cancer. For copy number variation, removal of 10% NA values and missing values is performed with the k‐means clustering algorithm [48]. Linear copy number values from Affymetrix SNP6 are selected and used for further processing.
3.2.3 DNA methylation
In DNA methylation, the methyl group is converted to the cytosine ring of DNA at the fifth position [14], which modifies the function of genes and affects gene expression data [14]. For DNA methylation, removal of 10% NA values and missing values is done with a k‐means clustering algorithm [48]. Original beta values from the remaining dataset have been taken directly and normalised using z‐score normalisation [50].
3.2.4 Protein expression
Protein expression data defines how the proteins are modified in the cells of a human body. Blueprints of proteins are stored in DNA and further decoded to produce RNA [15]. RNA produces information in the form of proteins. Using the k‐means clustering algorithm [48], the 10% NA values and missing values are removed for protein expression, then the original values from the remaining dataset have been taken and normalised using min–max normalisation [50].
3.3 Preprocessing of pathological images
Pathological images are whole slide images in which a glass slide is converted into a digital image that can be managed or analysed on a computer screen [51]. Tissue slide of the affected area is taken, which can be seen in a microscopic environment to get the information. For pathological images, Hematoxylin and Eosin whole slide images were used. These images have been downloaded from TCGA and tiled into 1024 × 1024 pixels with the help of Bioconductor bftools [52]. This results in thousands of tiled images in gigabytes from which ten most denser tiles have been selected.
3.4 Feature selection
Feature selection is the process of selecting the relevant features and removing redundant and irrelevant features. Feature selection can be achieved using the filter method, wrapper method and embedded method [53]. The filter method is used to rank the most important features using the information gain ratio and Chi‐square method [54]. The wrapper method works by diving the features into different subsets. Each subset is trained and hence performance was evaluated [55]. The subset which performed the best out of all the subsets is selected. The embedded method is the same as the wrapper method but they use the learning model for selection purposes [56]. eBreCaP uses an FSelector [57] package for selecting the best features for the genomic dataset.
3.4.1 Feature extraction of genomic data
Genomic and Pathological image data is preprocessed in five steps, as shown in Table 2. Initial preprocessing is done in two stages and the data is normalised using z‐score and min–max normalisation. The normalisation process results in gene expression, copy number, DNA methylation, and protein expression with 15,000, 25,000, 16,000, 215 features, respectively. It is still a huge feature set to work with. Therefore, high‐dimensional data required an appropriate feature selection technique to extract the most important features in relevance to its domain. This research used the FSelector [57] package, which selects the most informative features using information gain ratio and avoids the problem of overfitting [41, 52] into model building. FSelector package used Algorithm 1 (Fig. 2) for selecting the most informative genes. This algorithm selects the top 50 features for gene expression, 10 most informative copy number values, 40 features for DNA methylation and 120 best features for protein expression data. The features are selected based on the rank given by the FSelector algorithm. CNA impact in our dataset is very less. Therefore, ten features from the whole feature set have been selected. Similarly, the impact of the protein expression dataset is extremely high. Therefore, more features have been selected for protein expression as compared to other subtypes. The values in range for each subtype are selected based upon the assigned weight. Genomic data is passed to FSelector package, which ranks the features from the highest to lowest and selects the top‐ranked features based on the cut‐off value [44].
Fig. 2.

Algorithm 1: FSelector package
3.4.2 Feature extraction of pathological images
Preprocessing of pathological images results in 1991 image features. It is still a huge feature set to work with. As a result, feature extraction is required. To extract important image features, Cell Profiler [58] is used which gives 130 images features including cell nuclei, cell nuclei, cell shape, cell size, no of tiles, no of cells in images tiles, and the texture of image tiles. The summary is shown in Table 3.
Table 3.
TCGA patients characteristics
| TCGA | |
|---|---|
| Characteristics | Summary |
| total patients | 585 |
| gender | male = 7, female = 578 |
| selected patients | 578 |
| short term survivor | 445 |
| long term survivor | 133 |
| average age of diagnosis | 30–78 (approx. avg = 58) |
| Data selected | |
| Genomic data | FSelector package |
| gene expression | 50 features |
| protein expression | 120 features |
| DNA methylation | 40 features |
| CNA | 10 features |
| pathological images | 196 features through cell profiler |
3.5 ML models
The models implemented in the present work consist of six models which are defined in a package called survELM and are described below.
3.5.1 Extreme learning machine
ELM is a single hidden layer feedforward NN that is used for survival analysis on high‐dimensional data [8, 59]. Earlier NNs have been used for survival analysis with the backpropagation algorithm. It worked well only for low‐dimensional datasets [60, 61]. For high‐dimensional datasets, ELM is a proven universal function approximator [41] which works by calculating the weights and bias randomly. The learning speed of ELM is faster than NN approaches, therefore it results in faster computations.
ELM works on a single‐hidden layer feed‐forward NN in which input weight value is chosen randomly and output is generated accordingly. It worked as follows:
For a given training sample, , if n defines total observations, p gives the dimension of covariates, defines the target, then ELM with n hidden layers is given as follows:
| (1) |
Here g defines the activation function, defines the input weights, defines the bias variable, defines the hidden layers, defines the output target variable. The hidden layer for ELM can be expressed as
| (2) |
and the target matrix is given by the following equation:
| (3) |
The output weights can be solved with the given equation as follows:
| (4) |
where I is an n*m matrix. Kernel ELM can be defined by the following equation:
| (5) |
Kernel ELM with L supporting vectors can be
| (6) |
where .
3.5.2 ELM with Buckley–James estimator
To perform survival analysis, we need to work with censored data [62]. Censored data is a particular kind of data in which some information is known but the exact information is unknown. ELM does not handle censored data. But, Buckley–James estimator, regularised Cox models and gradient boosting models works well with censored data and survival prediction. Therefore, the selection was made on the algorithms which work effectively on censored data. Hence, we combined ELM with Buckley–James estimator, regularised Cox models and gradient boosting models. To calculate survival time, Buckley–James estimator and Cox models are used which adopted the least square method for calculation. Buckley–James estimator is considered to be more superior to other least square methods [63] and gives efficient results. Buckley–James estimator was introduced in 1979, which makes use of the least square estimation method for censored data which is explained here.
Suppose a random variable Y forms a linear regression on some covariate X, then
| (7) |
where is a vector of 1 × p with a constant and having ɛ as a random variable with zero mean and finite variance [64], Y represents the survival time or an event. The survival time is estimated with Buckley–James estimator and then ELM is applied for survival analysis of patients. This whole process is named as ELMBJ. For more perfect results, an ensemble of ELM with Buckley–James estimator is performed, which is known as ELMBJEN. A unique feature for ELMBJ and ELMBJEN is the capability of giving correct predicted survival times instead of common relative risks.
3.5.3 Regularised Cox with ELM
In this, the linear version of the Cox model is replaced with a non‐linear ELM NN and as a result, the coefficient will be obtained [16]. Assume x is a variable set having a total number of p covariates on a dataset D with training samples , where D belongs to , i = 1, 2, … ,n. In the case of right‐censored data, , here is the true survival time, is the censored status, and is the censoring indicator [14]. The hazard of a patient is
| (8) |
Here is a function of the covariate , and for traditional Cox model, Also, an RF‐based ensemble is provided called ensemble of regularised Cox with ELM (ELMCOXEN) for its stable result. ELMCOXEN contains the advantages of both the Cox models and non‐linear properties of the ELM model [17].
3.5.4 ELM with gradient‐based boosting
In this, we apply the ELM model in boosting the environment to get the survival data. Two types of boosting named gradient boosting and likelihood‐based boosting have been used. Gradient and likelihood boosting help in minimising the loss function and give efficient results [65].
3.6 Models selected for comparison
The other models which are used as a comparison with this survELM are the regularised Cox model, random survival forest (RSF) [64], Boosting CI (BoostCI) [44] and supervised principal components regression (superPC) [59]. We use these models as a comparison because these models give efficient results, as proved by Sun et al. [44].
3.7 Ensembled modelling
eBreCaP consists of integrating genomic and pathological images dataset and used it for survival prediction. Due to the high dimensionality of data, kernel extreme learning machine (eBreCaP) has become a powerful choice for more efficient results. Therefore, the extracted features are integrated with the help of the kernel extreme learning machine. The kernel used in the whole process is of the linear type, which is given as follows:
| (9) |
Here (x, y) belongs to training data, b is a constant with adjustable parameter .
As eBreCaP consists of six models, firstly, ELMBJ was applied in which ELM integrates the data and the Buckley–James estimator will predict the survival outcome. In this, the kernel used is of linear type and the value of alpha used is 0.5. To improve the performance of ELMBJ, an ensemble version of this model, i.e. ELMBJEN was applied. This ensemble method uses 100 ELM base survival models for integrating the data and for predicting the performance. After, COXELM method is used for integration by taking linear kernel with an alpha value of 0.5. This method is enhanced with its ensemble version, which is an ELMCOXEN. ELMCOXEN used a linear kernel by taking an alpha value of 0 with 100 base models. After that, ELMBOOST and ELMCOXBOOST were used with an alpha value of 0.5 by taking a linear kernel. The whole process is iterated 20 times and the results obtained are compared with different baseline models given by various authors including SuperPC [59], RSF [64], survival regression (Survreg) and BoostCI [44].
3.8 Survival analysis
Survival analysis works by measuring the follow‐up time starting from a defined time to when the tumour occurs, i.e. measuring the time from the start of the event to end of the event or starting from the diagnosis of the tumour to the death of the patient [59]. Survival time uses the data, which is censored. Censored data is the one in which some information is known but the exact information is unknown. For example, when the follow‐up time for the patient has come but the event did not occur yet, when the patient dies before the event occurs, and when the patient leaves the study. These types of censoring are known as right censoring. For survival analysis, survival data is required, which includes the following attributes:
(i) Response time (RT i ), i.e. the time for a patient i at some specific event.
(ii) Censored time (CT i ) for the patient i.
- (iii) Event indicator is given as δi and its value is given as follows:
- (iv) The value to be observed is calculated using the following equation:
(10)
By using the above data, the survival function is
| (11) |
Here T is the response variable and is greater than 0.
This function tells the probability of a patient that he will survive the past time t. The range for t goes from 0 to ∞ and is non‐increasing.
- When t = 0, the probability of surviving time for the patient is 1 and is given by
- When t = ∞, the probability of surviving time for the patient is 0 and is given by
This is used in our research to calculate the response time for a patient.
4 Experiment analysis
A TCGA dataset from the cancer genome portal was used, which includes genomic data (gene expression, protein expression, DNA methylation, and CNA data) and pathological images dataset. The dataset is integrated and trained with the survELM model. The data is divided into 70 by 30 ratio and survival analysis is performed.
4.1 Experimental data
In our experiment, genomic and pathological image datasets available on the Cancer Genome Atlas portal has been used. Genomic Dataset consists of gene expression [12], CNA [13], DNA methylation [14], and protein expression [15] data. In the R source code, TCGA Bioconductor [46] package has been used for the downloading of datasets in which initially the datasets were available in a raw form consisting of 58,000 transcriptome values for gene expression, 40,000 copy number values with different duplicate chromosomes for CNA, 70,000 beta values for DNA methylation, and 20,000 protein values for protein expression. The size of the dataset is very large approaching to terabytes. Therefore, working with such data size is quite difficult and hence, preprocessing is required to reduce the size of the dataset. The preprocessing of data is explained in Section 3.1.1. The preprocessing stage results in 16,000, 25,000, 16,000, and 215 features of gene expression, CNA, DNA methylation, and protein expression, respectively. To further reduce the features, the FSelector [57] package has been used which will select the most informative features based on Information gain ratio function and gives 50, 10, 40, and 120 features of gene expression, CNA, DNA methylation, and protein expression, respectively. For pathological images, whole slide images have been taken and image tiling is performed to select the most denser slides. The preprocessing of images is defined in Section 3.1.2. The preprocessing of images results in 1991 features. Further, cell profiler [58] is used, which reduces the features space to 196 features having cell size, cell shape, cell perimeter, cell area, and nucleus.
4.2 Experimental setup
Once data is preprocessed, it is integrated and trained with the help of survELM package as described in Section 3.2. The dataset is divided into 70% training data and 30% testing data and is shown in Table 4.
Table 4.
Division of dataset
| Subtype | Percentage, % | No. of patients |
|---|---|---|
| training data | 70 | 404 |
| testing data | 30 | 174 |
Also, 10% of training data is used for the cross‐validation process. Then the trained model and validation process is used to predict the outcome of the result on the testing data. The tools used in the present work are (i) RStudio 3.5.1 for modelling purposes, (ii) bftools [52] for the tiling of images; (iii) cell profiler [58] for extracting important image features. Furthermore, the packages used in our research are Survelm, Survival, randomForestSRC, SuperPC, mboost, Survcomp, pROC, and Hmeasure.
4.3 Performance parameters
The parameters which we used to achieve the performance in our model are described below:
4.3.1 Concordance index
Concordance index is defined as a ranking variable whose value lies with 0 to 1, where 0 represents the worst value and 1 represents the best value. The higher values of the concordance index signify the better performance of the model. It is given as
| (12) |
Here n is total no of comparison, i represents the indicator and s represents the actual result.
4.3.2 Hazard ratio
The hazard ratio is the ratio of an event occurring in one group as compared to an event in another group. An event in one group means the treatment process and event in another group means the control process. The hazard ratio value should always be less than 1. When the value is close to 0, it means that there is an ∼100% reduction in risk in certain diseases and value close to 1 means there is a 0% risk reduction.
4.3.3 Area under precision–recall (AUPR)
The AUPR shows the relation between precision and recall at different threshold values. The higher values of AUPR signify the better performance of the model.
4.4 Results and discussion
The models given in eBreCaP are applied to predict the survival of breast cancer patients effectively. The obtained results are compared with recent studies [44]. We train the six models on high‐dimensional data by integrating genomic and pathological images. The desired results and performance was achieved in 20 epochs (training 20 times). The AUC value and other performance parameters are calculated for each model. The Receiver Operating Curve (ROC) for all the six models is shown in Figs. 3 and 4. The dark solid line in the curve shows the actual values which determine the curve between the true positive rate (TPR) and false‐positive rate (FPR). ELMBJ gives an AUC value of 0.83 and its ensemble method ELMBJEN gives an AUC value of 0.835 with slight increases of 0.5%. Similarly, ELMCOX produces an AUC value of 0.84 and its ensemble method ELMCOXEN gives an AUC value of 0.85. ELMCOXBOOST and ELMBOOST give an AUC value of 0.84 and 0.85, respectively. From the results, it is concluded that among all the six models, ELMBOOST performs the best with an AUC value of 0.85. The AUC value calculated using MKL [44] on the genomic and pathological images dataset was 0.80. eBreCaP when compared with MKL and other survival models comprising of survreg, RSF, SuperPC, BoostCI gives enhanced AUC value with 5% improvement. The results of eBreCap compared with the existing work [44] are shown in Table 5 and eBreCaP results are presented in bold. eBreCaP produces an accuracy of 83, 83.5, 84, 84, 85, and 84% for ELMBJ, ELMBJEN, ELMCOX, ELMCOXEN, ELMBOOST, and ELMCOXBOOST, respectively. Other parameters including sensitivity, specificity, precision, MCC, AUPR, HR, and CI are also calculated which shows an improvement in the results by 7, 2, 6, 7, 5, and 4%, respectively, when compared with other state‐of‐the‐art models [44]. eBreCaP is effective in predicting the survival time of breast cancer patients as it produces commendable results not only in accuracy but also in the case of the above‐mentioned parameters. Furthermore, the results are showcased graphically using line plots for AUC, accuracy, AUPR, and HR. The results of eBreCap are plotted using green coloured points whereas red coloured points are used to represent existing work results [44]. It is visible from the plot in Fig. 5 that eBreCaP accuracy is much more than the recent studies [44]. The decline in the line plot shows that eBreCaP is better with an accuracy of 85% predicted by ELMBOOST. Similarly, the line plot for the AUC is shown in Fig. 6. This plot shows an improvement of 5% than the traditional models [44]. Fig. 7 represents a line plot for AUPR in which ELMBOOST and ELMBJ give the highest AUPR value of 0.75 followed by ELMBJEN which gives the second‐highest value for AUPR in eBreCaP. The decline in line plot clearly shows an improvement of 5% compared with other state‐of‐the‐art models. Higher the value of AUPR, the better the model is. Additionally, the hazard ratio line plot is plotted as shown in Fig. 8. The value for hazard ratio must lies within 0 to 1. The value close to 0 shows that the risk introduced is very less and close to 1 or greater than 1 shows a higher risk. In eBreCaP, ELMBOOST shows a lower risk and survreg [44] produces a higher risk which shows the effectiveness of eBreCaP. Moving ahead, the bar plots for accuracy, sensitivity, precision, MCC, and CI are also plotted and shown in Fig. 9. It is visible from the plot that ELMBOOST gives efficient results having 85, 83, 64, 56, and 64% values for accuracy, sensitivity, precision, MCC, and CI, respectively. This shows an improvement of 5, 7, 2, 6, and 4%, respectively, for the above‐mentioned parameters when compared with the existing models [44]. The specificity is not calculated in the existing work [44] but eBreCaP achieved the specificity value >70% approximately for each model and is given in Table 5. The comparative analysis concludes that ELMBOOST is outperforming other algorithms consistently in breast cancer survival prediction.
Fig. 3.
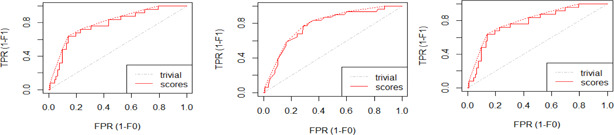
ROC value for ELMBJ, ELMNJEN, and ELMCOX
Fig. 4.
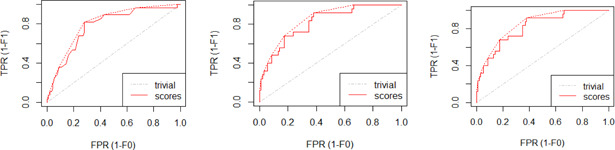
ROC for ELMCOXEN, ELMCOXBOOST, and ELMBOOST
Table 5.
Comparison of different models with eBreCaP
| Paper | Models | Sensitivity | Specificity | Precision | Accuracy | AUC | AUPR | MCC | HR | CI |
|---|---|---|---|---|---|---|---|---|---|---|
| Sun et al. [44] | SurvReg | 0.68 | — | 0.49 | 0.74 | 0.69 | 0.55 | 0.41 | 0.98 | 0.59 |
| RSF | 0.70 | — | 0.4 | 0.73 | 0.71 | 0.50 | 0.43 | 0.54 | 0.57 | |
| SuperPC | 0.72 | — | 0.46 | 0.76 | 0.72 | 0.42 | 0.42 | 0.65 | 0.53 | |
| BoostCI | 0.73 | — | 0.6 | 0.79 | 0.725 | 0.54 | 0.45 | 0.76 | 0.55 | |
| GPMKL | 0.76 | — | 0.62 | 0.80 | 0.80 | 0.68 | 0.50 | 0.44 | 0.60 | |
| our approach eBreCaP | ELMBJ | 0.78 | 0.70 | 0.63 | 0.83 | 0.83 | 0.75 | 0.52 | 0.14 | 0.63 |
| ELMBJEN | 0.79 | 0.72 | 0.635 | 0.835 | 0.835 | 0.73 | 0.54 | 0.09 | 0.64 | |
| ELMCOX | 0.80 | 0.71 | 0.63 | 0.846 | 0.84 | 0.71 | 0.55 | 0.32 | 0.63 | |
| ELMCOXEN | 0.805 | 0.715 | 0.64 | 0.84 | 0.85 | 0.72 | 0.54 | 0.07 | 0.635 | |
| ELMCOXBOOST | 0.82 | 0.74 | 0.63 | 0.84 | 0.84 | 0.71 | 0.53 | 0.33 | 0.63 | |
| ELMBOOST | 0.83 | 0.75 | 0.64 | 0.85 | 0.85 | 0.75 | 0.56 | 0.05 | 0.64 |
Bold values indicates the result of our proposed work eBreCaP. It is done to highlight the difference in results of proposed work and existing work.
Fig. 5.
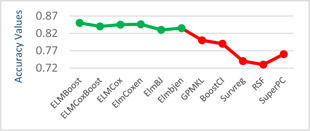
Line plot for accuracy
Fig. 6.
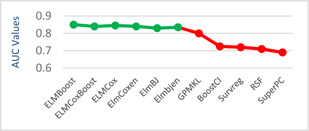
Line plot for AUC
Fig. 7.
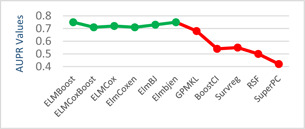
Line plot for AUPR
Fig. 8.
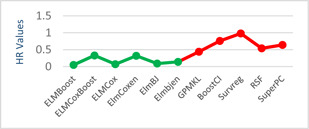
Line plot for HR
Fig. 9.
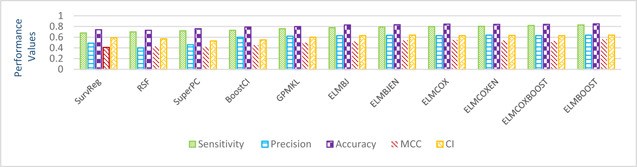
Bar graphs of precision, accuracy, sensitivity, CI and MCC for comparison of our results with recent studies [44]
5 Conclusions and future work
Breast cancer is one of the leading causes of death in females. Survival analysis is the statistical study of the different events like the onset of diseases, relapse, and re‐occurrence of the disease after treatment. In the present research, eBreCaP is proposed which effectively predicts the onset of breast cancer in females depending on real‐life integrated genomic and pathological profiles. The genomic data and pathological image data is available on TCGA which are integrated and used in eBreCaP for analysis. The high‐dimensional and heterogeneous data on and the most important and significant features were extracted contributing to the effective prediction of breast cancer in females. The effective application of preprocessing and feature extraction techniques on genomic as well as pathological images was eventually able to reduce 5‐digit feature space to 2‐digit feature space. The reduction in feature space is the most important contribution while handling high‐dimensional heterogeneous data like genomic and pathological data. eBreCaP is packaged with six models such as ELMBJ, ELMBJEN, ELMCOX, ELMCOXBOOST, ELMCOXEN, and ELMBOOST having accuracy 83, 83.5, 84.6, 84.5, 84, and 85%, respectively. It is experimentally analysed using six parameters like sensitivity, specificity, precision, accuracy, AUC, AUPR, MCC, HR, and CI. The results are also compared with the existing state‐of‐art‐work [44]. The observed results show improvement and increase in each performance parameter comprising sensitivity, precision, accuracy, AUC, AUPR, MCC, and CI by 4, 2, 5, 5, 7, 6, and 4%, respectively, in breast cancer survival prediction. ELMBOOST with 85% accuracy outperforms among all the six models. ELMBOOST also has high values for AUC, AUPR, CI, and HR which guarantees high accuracy and suitability of the model for the purpose. eBreCaP can also be applied to predict another type of cancers using clinical data, genomic data, images data as well as the integration of these data. DL algorithms can be applied for further improvement and the work can be extended on bio‐marker prediction.
6 References
- 1. Raheja K., Dubey A., and Chawda R.: ‘Data analysis and its importance in healthcare’, Int. J. Comput. Trends Technol., 2017, 48, pp. 2231–2803 [Google Scholar]
- 2. Stewart B. W., and Paul K., (Eds.): ‘World cancer report’ (IARC Press Lyon, France, 2003), pp. 181–188 [Google Scholar]
- 3. Bray F., Ferlay J., and Soerjomataram I. et al.: ‘Global cancer statistics 2018: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries’, CA Cancer J. Clin., 2018, 68, (6), pp. 394–424 [DOI] [PubMed] [Google Scholar]
- 4.‘Breastcancersymptoms’, Available at https://www.mayoclinic.org/diseases/conditions/breast‐cancer/symptoms‐causes/syc‐20352470, accessed September 2019
- 5.‘World‐wide cancer data’, Available at https://www.wcrf.org/dietandcancer/cancer‐trends/worldwide‐cancer‐data, accessed September 2019
- 6.‘Breast cancer in males and females’, Available at https://www.medicinenet.com/breast_cancer_in_males_and_females/ask.htm, accessed September 2019
- 7. Kaplan W.: ‘Priority Medicines for Europe and the World, A Public Health Approach to Innovation’. Ph.D. thesis, 2013.
- 8. Akay M.F.: ‘Support vector machines combined with feature selection for breast cancer diagnosis’, Expert Syst. Appl., 2009, 36, pp. 3240–3247 [Google Scholar]
- 9. Gill S.S., Tuli S., and Xu M. et al.: ‘Transformative effects of IoT, blockchain and artificial intelligence on cloud computing: evolution, vision, trends and open challenges’, Internet of Things, 2019, 8, p. 100118 [Google Scholar]
- 10. Han J., Haihong E., and Le G. et al.: ‘Survey on NoSQL database’. IEEE in Proc. Presented at 6th Int. Conf. Pervasive Computing and Applications, Port‐Elizabeth, South Africa, 26–28 October 2011, pp. 363–366 [Google Scholar]
- 11. Dhillon A., and Singh A.: ‘Machine learning in healthcare data analysis: a survey’, J. Biol. Today's World, 2018, 8, (2), pp. 1–10 [Google Scholar]
- 12. Shyamsundar R., Kim Y., and Higgins J.P. et al.: ‘A DNA microarray survey of gene expression in normal human tissues’, J. Genome Biol., 2005, 6, (3), p. 22 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Redon R., Ishikawa S., and Fitch K.: ‘Global variation in copy number in the human genome’, J. Nat., 2006, 444, pp. 444–454 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Jin B., Li Y., and Robertson K.: ‘DNA methylation superior or subordinate in the epigenetic hierarchy?’, Genes Cancer, 2011, 2, (6), pp. 607–6017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Cox B., Kislinger T., and Emili A.: ‘Integrating gene and protein expression data: pattern analysis and profile mining’, Methods, 2005, 35, (3), pp. 303–314 [DOI] [PubMed] [Google Scholar]
- 16. Wang H., and Gang L.: ‘Extreme learning machine Cox model for high‐dimensional survival analysis’, J. Stat. Med., 2019, 38, pp. 2139–2156 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Wang H., and Zhou L.: ‘SurvELM: an R package for high dimensional survival analysis with extreme learning machine’, J. Knowledge‐Based Syst. Sci., 2018, 160, pp. 28–33 [Google Scholar]
- 18. Ke G., Meng Q., and Finley T. et al.: ‘Lightgbm: a highly efficient gradient boosting decision tree’. Advances in Neural Information Processing Systems, Long Beach, CA, USA., 2017, pp. 3146–3154 [Google Scholar]
- 19. Huang Z., Zhan X., and Xiang S. et al.: ‘SALMON: survival analysis learning with multi‐omics neural networks on breast cancer’, J. Front. Genet., 2019, 10, p. 166 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Kotsiantis S.B., Zaharakis I., and Pintelas P.: ‘Supervised machine learning: a review of classification techniques’, Emerg. Artif. Intell. Appl. Comput. Eng., 2007, 160, pp. 3–24 [Google Scholar]
- 21. Van't Veer L.J., Dai H., and Van D. et al.: ‘Gene expression profiling predicts clinical outcome of breast cancer’, J. Nat., 2002, 415, pp. 530–536 [DOI] [PubMed] [Google Scholar]
- 22. Berrar D.P., Dubitzky W., and Granzow M. (Ed.): ‘A practical approach to microarray data analysis’ (Kluwer Academic Publishers, New York, 2013), pp. 15–19 [Google Scholar]
- 23. Zhang D., Zou L., and Zhou X. et al.: ‘Integrating feature selection and feature extraction methods with deep learning to predict clinical outcome of breast cancer’, IEEE Access, 2018, 6, pp. 28936–28944 [Google Scholar]
- 24. Jolliffe I.: ‘Principal component analysis’ (Springer, Berlin, Heidelberg, 2011), pp. 1094–1096 [Google Scholar]
- 25. Esteva A., Chou K., and Cui C. et al.: ‘A guide to deep learning in healthcare’, Nat. Med., 2019, 25, (1), p. 24 [DOI] [PubMed] [Google Scholar]
- 26. Tabl A.A., Rueda W., and Ngom A. et al.: ‘A machine learning approach for identifying gene biomarkers guiding the treatment of breast cancer’, J. Front. Genetics, 2019, 10, p. 256 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Manogaran G., and Lopez D.: ‘A survey of big data architectures and machine learning algorithms in healthcare’, Int. J. Biomed. Eng. Technol., 2017, 25, (2–4), pp. 182–211 [Google Scholar]
- 28. Gevaert O., Smet F., and Timmerman D. et al.: ‘Predicting the prognosis of breast cancer by integrating clinical and microarray data with Bayesian networks’, J. Bioinf., 2006, 22, pp. e184–e190 [DOI] [PubMed] [Google Scholar]
- 29. Friedman N., and Geiger D.: ‘Bayesian network classifiers’, Mach. Learn., 1997, 29, (2–3), pp. 131–163 [Google Scholar]
- 30. Sun D., Wang M., and Li A.: ‘A multimodal deep neural network for human breast cancer prognosis prediction by integrating multi‐dimensional data’, IEEE/ACM Trans. Comput. Biol. Bioinf., 2018, 16, pp. 841–850 [DOI] [PubMed] [Google Scholar]
- 31. Mitchell T.M.: ‘Logistic regression’, Mach. Learn., 2005, 10, p. 701 [Google Scholar]
- 32. Guo W., Li H., and Zhu Y. et al.: ‘Prediction of clinical phenotypes in invasive breast carcinomas from the integration of radiomics and genomics data’, J. Med. Imaging, 2015, 2, (4), p. 041007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Hung F., and Chiu H.: ‘Cancer subtype prediction from a pathway‐level perspective by using a SVM based on integrated gene expression and protein network’, J. Comput. Methods Prog. Biomed., 2017, 141, pp. 27–34 [DOI] [PubMed] [Google Scholar]
- 34.‘Statistics how To’, Available at https://www.statisticshowto.datasciencecentral.com/probability‐and‐statistics/z‐score/, accessed March 2020
- 35. Kaur P., Sharma N., and Singh A. et al.: ‘CI‐DPF: A cloud IoT based framework for diabetes prediction’. 2018 IEEE 9th Annual Information Technology, Electronics and Mobile Communication Conf. (IEMCON), Vancouver, BC, Canada, 2018, pp. 654–660 [Google Scholar]
- 36. Tao M., Song T., and Du W. et al.: ‘Classifying breast cancer subtypes using multiple kernel learning based on omics data’, J. Genes, 2019, 10, (3), p. 200 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Gönen M., and Alpaydın E.: ‘Multiple kernel learning algorithms’, J. Mac. Learning Res., 2011, 12, pp. 2211–2268 [Google Scholar]
- 38. Jiang Y., Chen L., and Zhang H. et al.: ‘Breast cancer histopathological image classification using convolutional neural networks with small SE‐ResNet module’, J. PLos One, 2019, 14, (3), p. e0214587 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Prat A., Fan C., and Fernández A. et al.: ‘Response and survival of breast cancer intrinsic subtypes neoadjuvant chemotherapy’, J. BMC Med., 2015, 13, p. 303 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Wang Z., Li Z., and Wang H. et al.: ‘Breast cancer detection using extreme learning machine based on feature fusion with CNN deep features’, IEEE Access, 2019, 7, pp. 105146–105158 [Google Scholar]
- 41. Huang G.B., Chen L., and Siew C.K.: ‘Universal approximation using incremental constructive feedforward networks with random hidden nodes’, IEEE Trans. Neural Netw., 2006, 17, (4), pp. 879–892 [DOI] [PubMed] [Google Scholar]
- 42. Vazquez A.I., Veturi Y., and Behring M. et al.: ‘Increased proportion of variance explained and prediction accuracy of survival of breast cancer patients with use of whole‐genome multiomic profiles’, Genetics, 2016, 203, (3), pp. 1425–1438 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Ching T., Do B.T., and Way G.P. et al.: ‘Opportunities and obstacles for deep learning in biology and medicine’, J. R. Soc., Interface, 2018, 15, (141), p. 20170387 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Sun D., Li A., and Tang B. et al.: ‘Integrating genomic data and pathological images to effectively predict breast cancer clinical outcome’, J. Comput. Methods Prog. Biomed., 2018, 161, pp. 45–53 [DOI] [PubMed] [Google Scholar]
- 45.‘GDC data portal’, Available at https://portal.gdc.cancer.gov/, accessed February 2019
- 46. Silva T.C., Colaprico A., and Olsen c. et al.: ‘TCGA workflow analyze cancer genomics and epigenomics data using bioconductor packages’ (Faculty of 1000 Ltd, UK: 2003) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.‘Geneexpression’, Available at https://en.wikipedia.org/wiki/Gene_expression, accessed June 2019
- 48. Rahman M.M., and Davis D.N.: ‘Machine learning‐based missing value imputation method for clinical datasets’, in ‘IAENG transactions on engineering technologies’ (Springer, Dordrecht, 2013), pp. 245–257 [Google Scholar]
- 49. He Y., Dai H., and Hart A. et al.: ‘A gene‐expression signature as a predictor of survival in breast cancer’, New England J. Med., 2002, 347, (25), pp. 1999–2009 [DOI] [PubMed] [Google Scholar]
- 50.‘Data normalization in data mining’, Available at https://www.geeksforgeeks.org/data‐normalization‐in‐data‐mining/, accessed March 2019
- 51.‘Digitalpathology’, Available at https://en.wikipedia.org/wiki/Digital_pathology, accessed September 2019
- 52. Linkert M., Rueden C., and Allan C. et al.: ‘Metadata matters: access to image data in the real world’, J. Cell Biol., 2010, 189, (5), pp. 777–782 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Guyon I., and Elisseeff A.: ‘An introduction to variable and feature selection’, J. Mach. Learn. Res., 2003, 3, pp. 1157–1182 [Google Scholar]
- 54.‘Information gain ratio’, Available at https://en.wikipedia.org/wiki/Information_gain_ratio, accessed September 2019
- 55.‘Featureselection’, Available at https://en.wikipedia.org/wiki/Feature_selection, accessed April 2019
- 56. Kohavi R., and John G.H.: ‘Wrappers for feature subset selection’, Artif. Intell., 1997, 97, (1–2), pp. 273–324 [Google Scholar]
- 57.‘FSelectorpackage’, Available at https://cran.rproject.org/web/packages/FSelector/FSelector.pdf, accessed September 2019
- 58.‘Cellprofiler’, Available at https://en.wikipedia.org/wiki/CellProfiler, accessed September 2019
- 59. Bair E., Hastie T., and Paul D. et al.: ‘Prediction by supervised principal components’, J. Am. Stat. Assoc., 2006, 101, p. 473 [Google Scholar]
- 60. Ravdin P.M., and Clark G.M.: ‘A practical application of neural network analysis for predicting outcome of individual breast cancer patients’, Breast Cancer Res. Treat., 1992, 22, (3), pp. 285–293 [DOI] [PubMed] [Google Scholar]
- 61. Biganzoli E., Mariani L., and Marubini E.: ‘Feedforward neural networks for the analysis of censored survival data: a partial logistic regression approach’, Stat. Med., 1998, 17, (10), pp. 1169–1186 [DOI] [PubMed] [Google Scholar]
- 62. Wang H., Wang J., and Zhou L.: ‘A survival ensemble of ELM’, Appl. Int., 2018, 48, (7), pp. 1846–1858 [Google Scholar]
- 63. Stare J., Heinzl H., and Harrell F.: ‘On the use of Buckley and James least squares regression for survival data’, New Approaches Appl. Stat., 2000, 16, pp. 125–134 [Google Scholar]
- 64. Ishwaran H., and Lu M.: ‘Random survival forests’ (Wiley StatsRef: Statistics Reference Online, USA., 2019), pp. 1–13 [Google Scholar]
- 65. Wang Z., and Wang C.Y.: ‘Buckley‐James boosting for survival analysis with high‐dimensional biomarker data’, Stat. Appl. Genet. Mole. Biol., 2010, 9, (1), pp. 1544–6115 [DOI] [PMC free article] [PubMed] [Google Scholar]


