Ubiquitin chain specific auto‐ubiquitination triggers sustained oscillation, bistable switches and excitable firing

Abstract

Ubiquitin modification of cellular proteins commonly targets them for proteosomal degradation, but can also convey non‐proteolytic functions. Over the past years, advances in experimental approaches have helped uncover the extensive involvement of ubiquitination in protein regulation. However, our understanding of the dynamics of the ubiquitination‐related networks have lagged behind. A common regulatory theme for many E3 ligases is the ability to self‐catalyse their own ubiquitination without involving external E3 ligating enzymes. Here, the authors have explored computational models of both proteolytic and non‐proteolytic auto‐ubiquitination of E3 ligases and characterised the dynamic properties of these regulatory motifs. Remarkably, in both cases auto‐ubiquitination coupled with multi‐step de‐ubiquitination process can bring about sustained oscillatory behaviour. In addition, the same basic wiring structures can trigger bistable switches of activity and excitable firing of the dynamic responses of the ubiquitinated E3 ligase. Bifurcation analysis allows one to derive parametric conditions that govern these dynamics. They also show that these complex non‐linear behaviours persist for a more detailed mechanistic description that involves the E1 and E2 enzymes. Their work therefore provides new insights into the dynamic features of auto‐ubiquitination in different cellular contexts.

1 Introduction

Protein modification by ubiquitination has emerged as a dynamic and versatile post‐translational modification that controls not only protein degradation but also a variety of non‐proteolytic functions [1–4]. Ubiquitination is involved in a broad spectrum of cellular processes including protein trafficking, cell cycle progression, DNA damage and immune response [5–9]. Deregulation of the ubiquitination pathway is associated with many human diseases, including neuronal disorders and cancers [10–12]. Recent evidence from proteomic studies demonstrated the sheer size of the ubiquitome where extensive numbers of proteins, if not all, are modified with ubiquitin at certain times, suggesting key functional roles of different types of ubiquitination in cellular processes [13–15].

The first step of ubiquitination, the covalent conjugation of an ubiquitin molecule to the target protein substrate, is catalysed by one of at least two ubiquitin‐activating enzymes (E1) that are coded by the human genome. This initiation step generates a high‐energy thiol‐ester intermediate. In the second step, this intermediate is transferred to one of about 50 available ubiquitin conjugating enzymes (E2) [1]. The third step exhibits significant substrate specificity and is catalysed by one of over 500 ubiquitin ligating enzymes, E3 ligases. In this final step, ubiquitin is tagged to the substrate. Ubiquitination is a reversible protein modification where the E3 ligase is opposed by the action of a large family of de‐ubiquitinating enzymes (DUBs), with almost 100 DUBs encoded in the human genome [16, 17]. The three‐step reaction cascade is repeated, and additional ubiquitin moieties are sequentially conjugated to the growing chain of an iso‐peptide bond through one of seven internal Lys residues (Lys6, Lys11, Lys27, Lys29, Lys33, Lys48 or Lys63) on ubiquitin. As a result, a bewildering repertoire of poly‐ubiquitin chains with various linkage configurations can be generated [4, 18, 19]. Usually, K48‐linked chains mark target substrates for degradation by the proteasome machinery, while K63‐ or K11‐linked chains can trigger non‐degradative events, often involving modulation of the substrate protein's catalytic activities [17].

E3 ligases display a strong diversity of their mechanistic and functional properties. A common regulatory theme that emerges among many E3 ligases is the ability to self‐catalyse their own ubiquitination without the need of external E3 ligating enzyme [3, 18]. Auto‐ubiquitination of E3 ligases are primarily found to mediate either (i) their own degradation, or (ii) their E3 ligase activity and the recruitment of substrates, depending on the linkage configuration of the self‐generated ubiquitin chain [18]. Table 1 provides a list of selected E3 ligases that undergo auto‐ubiquitination and their implications for cell signalling. For example, Ring1B‐mediated ubiquitination of histone H2A is crucial in gene silencing controlled by the Polycomb Repressive Complex 1. Ubiquitination of H2A relies on Ring1B ability to undergo self‐catalysed ubiquitination, resulting in generation of mixed and branched K6‐, K27‐ and K48‐ linked ubiquitin chains [4]. Similarly, the BRCA1 (breast cancer 1) E3 ligase is subject to auto‐ubiquitination producing K6‐linked chains, which enhances the ligase catalytic potential to ubiquitinate histones in vitro [20, 21]. Auto‐ubiquitination can improve the recruitment of substrates able to bind ubiquitin, as has been shown for TRAF6 and NEDD4 [3, 22, 23]. Multiple E3 ligases including E6‐AP (E6‐associated protein), RING ligase SIAH1 (seven in absentia 1) and even TRAF6 have been reported to self‐catalyse their own ubiquitination in an intermolecular manner to promote their own degradation [18]. Table 1 illustrates auto‐ubiquitination as a widespread mechanism for self‐control by the E3 ligases.

Table 1.

Selected E3 ligases capable of undergoing auto‐ubiquitination and the corresponding consequences for cell signalling

E3 ligase	E3 ligase type	Chain type	Interaction type	Function	Known roles
TRAF6	RING	K63	likely intermolecular as homodimers found essential for self‐Ubi	enhanced activity	TNF receptor superfamily signalling, NF‐kB and JNK signalling
ITCH	HECT	K63	intermolecular	enhanced activity	erythroid and lymphoid cell differentiation, immune responses regulation. Mutations cause syndromic multisystem autoimmune disease
RING1B	RING	K6/K27	intermolecular	enhanced activity	repression of gene expression via histone modification. Implicated in occult macular dystrophy, and embryonal cancer
BRCA1	RING	K6	na	enhanced activity	DNA damage repair. Implicated in breast cancer
Diap1	RING	K63	na	repressed activity	blocking caspases‐mediated apoptosis
E6‐AP	HECT	K48	intermolecular	self‐degradation	mutations within the E6‐AP gene are responsible for some cases of Angelman syndrome
SIAH1	RING	K48	intermolecular	self‐degradation	implicated in the development of certain forms of Parkinson's disease, regulation of the cellular response to hypoxia and induction of apoptosis
Mdm2	RING	K48	likely intermolecular	self‐degradation	p53 signalling, apoptosis
CBL	RING	K48	na	self‐degradation	RTKs signalling. Mutations implicated in cancers, particularly acute myeloid leukaemia
Rsp5	HECT	K48	intramolecular	self‐degradation	protein degradation, protein trafficking. VB sorting, heat shock response, transcription, endocytosis, and ribosome stability; human homolog is involved in Liddle syndrome; mutant tolerates aneuploidy;
Grr1p	F‐box	K48	intramolecular	self‐degradation	cell cycle regulation, glucose sensing
NEDD4	HECT	mono‐ubiquitination	na	enhanced activity	Clathrin‐mediated endocytosis, degradation pathway
NEDD4‐1, NEDD4‐2	HECT	K48	intramolecular, modulated by phos	self‐degradation	endocytosis, degradation pathway
SMURF2	HECT	K48	intramolecular, modulated by phos	self‐degradation	degradation pathway. Implicated in diseases like cerebral cavernous malformations‐2, and ureteral obstruction
WWP1	HECT	K48	intramolecular, modulated by phos	self‐degradation	protein degradation, transcription, and RNA splicing. Implicated in liddle syndrome, and human t‐cell leukemia virus type 1
Nrdp1	RING	K48	na	self‐degradation	ErbB3 degradation
TRAF3	RING	K63	na	modified activity	TNF receptor superfamily signalling NF‐kB signalling

Although auto‐ubiquitination has been uncovered experimentally as a common regulatory mechanism, we have limited understanding how this process may affect the dynamic properties of E3 ligases and the ubiquitination network in which they operate. We have previously shown that the process of generating a poly‐ubiquitin chain via sequential reversible attachments of single ubiquitin moieties can bring about intricate dynamic features including sustained oscillation and bistable switches [24]. We have also shown that the interplay between ubiquitination and phosphorylation and associated feedback regulation can confer rich dynamics of the harbouring network [3].

In this study, we analyse an ensemble of dynamic computational models, which include auto‐ubiquitination of E3 ligases within varying topological circuitries, to explore the dynamic properties of these regulatory motifs. We found that for both categories of E3 ligases where auto‐ubiquitination can promote self‐degradation or catalytic activity, these regulatory mechanisms can bring about sustained oscillatory behaviour. Interestingly, the oscillatory dynamics are mediated by a positive feedback and no explicit negative feedback regulation is required. We found that auto‐ubiquitination can also enable the system to generate bistable switches, and mixed modes of oscillation‐bistability regimes where excitable overshoot of the E3 activity can emerge. Using modelling, simulation and bifurcation analysis we derived parametric conditions governing the emergence of the identified dynamics. Furthermore, we confirmed our results with more mechanistically detailed models that explicitly account for the action of the E1 and E2 enzymes. This study extends our current understanding of the complex dynamics of E3 ligases and ubiquitin‐related regulation. It reveals the ability to generate additional layers of rich and complex temporal behaviour by ubiquitination enzymes. Our results also suggest novel design principles for constructing biological oscillators and excitable devices that are inspired by the ubiquitination related circuits, which could be of particular interest to the emerging field of synthetic biology.

2 Results

2.1 Core models of E3 ligase auto‐ubiquitination predict complex non‐linear dynamics

2.1.1 Development of core kinetic models of auto‐ubiquitination

We first constructed core models of E3 ligase auto‐ubiquitination where the E1 and E2 enzymes were not explicitly incorporated. This simplifying assumption is supported by the observations suggesting that E2, such as Cdc34, is mostly pre‐loaded with ubiquitin under steady‐state conditions [25]. The simplest reaction scheme of auto‐ubiquitination is displayed as model NP1 in Fig. 1 a. The prefix ‘NP’ means ‘non‐proteolytic’ and labels all models of non‐proteolytic auto‐ubiquitination, whereas models of proteolytic auto‐ubiquitination are labelled with the prefix ‘P’, used hereafter. In model NP1, the E3 ligase is initially converted into the ubiquitinated form (E3_Ub), and E3_Ub further promotes ubiquitination of new E3 molecules, forming a positive feedback regulation. The ubiquitinated E3 is de‐ubiquitinated by external DUBs, implying the reversibility of ubiquitination. Based on this mechanistic reaction scheme, we constructed the model using ordinary differential equations (ODEs). Model reactions and derivation of ODEs can be found in the Supplementary Information (SI). This simple motif did not produce sustained oscillation, when we extensively explored the model dynamic behaviours over wide ranges of parameters. Indeed, similar motifs previously described for auto‐phosphorylation kinases have never been reported to produce oscillation.

Fig. 1.

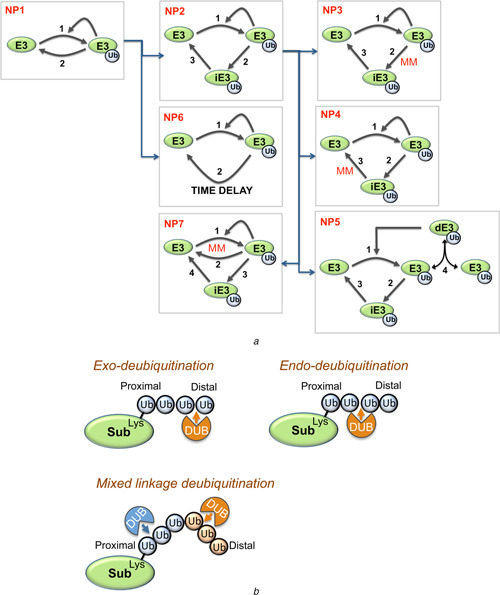
Simplest reaction scheme of auto‐ubiquitination is displayed as model NP1

a Simplified schematic diagrams of non‐proteolytic auto‐ubiquitination models

Different models NP1‐NP7 and the relations between them

MM indicates the MM kinetics of the respective reactions

In model NP5, dE3 is the dimerised form of the ubiquitinated E3 ligase (E3_Ub)

b Schematic diagram of various modes of de‐ubiquitination

Different ubiquitin (Ub) linkages are indicated by different colours of the Ub molecule

Similarly, different DUBs are indicated by different colours

Recent structural and biochemical analysis of DUBs showed that rather than occurring in a single step (as depicted in model NP1), de‐ubiquitination is a multi‐step process. DUBs can display specificity at multiple levels, distinguishing different types of ubiquitin linkages and chain configuration [16, 17]. Ubiquitin chains can be cleaved by two main mechanisms: (i) exo‐deubiquitination where cleavage occurs from the end or (ii) endo‐de‐ubiquitination where cleavage occurs internally within the chain (Fig. 1 b). USP14, for instance, has exo‐activity as it removes K48‐linked chains only from the distal end, producing exclusively mono‐ubiquitin moieties [26]; whereas other DUBs including CYLD, USP9X, AMSH‐LP and A30 were shown to possess endo‐activity, cleaving longer ubiquitin chains from their substrates [17, 27]. Moreover, the fact that auto‐ubiquitination can generate mixed linkages (e.g. Ring1B) and the demonstrated ability of DUBs to discriminate particular linkages highlights that de‐ubiquitination of mixed linkage chain can be accomplished by coordination of multiple DUBs with distinct specificity: a mechanism we term mixed linkage de‐ubiquitination (Fig. 1 b). It is important to realise that in all these cases, de‐ubiquitination of poly‐ubiquitin chains is a multi‐step process with sequential removal of ubiquitin either as a single molecule or as longer chains of ubiquitin moieties.

2.1.2 Non‐proteolytic auto‐ubiquitination generates sustained oscillation

In light of experimental evidence discussed above, we now assume that the de‐ubiquitination occurs via (at least) one intermediate ubiquitinated E3 form (iE3_Ub). Consequently, the simple scheme of model NP1 is modified to render model NP2 (Fig. 1 a). We found that this system circuitry becomes capable of generating sustained oscillations, a feature that was not observed for model NP1. To characterise the kinetic requirement for oscillations, we considered a number of variant models derived from NP2: models NP3–NP5 with different kinetic structures, shown in Fig. 1 a.

Assuming simple first‐order kinetics, self‐catalysed ubiquitination of E3 can be described by the following reactions [3, 4]:

• (1) E3 → E3_Ub (rate constant k ₁).

• (2) E3 + E3_Ub → E3_Ub + E3_Ub (rate constant k _1a ) which results in the self‐catalysed ubiquitination rate

  $$v_1=[\mathrm{E}3]\left(k_1+k_{1a}[\mathrm{E}{3}_{\text{Ub}}]\right)$$ (1)

  where [X] denotes the concentration of protein X.

The rate expression (1) together with an assumption that at least one reaction of the multi‐step de‐ubiquitination process follows the Michaelis‐Menten (MM) kinetics [reaction (2) or (3) in models NP3 and NP4] are sufficient for the existence of oscillations. Fig. 2 a shows the temporal oscillatory behaviour for all model NP3 species. The level of E3 total strongly influences the shape of oscillations. Increasing this level initially enlarges the oscillation amplitude, but as the E3 total is further increased, the amplitude becomes diminished, indicating a biphasic dependence of the oscillation amplitude on the E3 abundance (Figs. 2 b and d). The oscillatory dynamics pattern ranges from sinusoid‐like to pulse‐like as the E3 abundance decreases (Fig. 2 b). Parameter sensitivity analysis further shows that while lowering the rates k ₁, k _1a or V ₂ leads to slower oscillation and thus results in the longer period, the opposite is true for lowering k ₃ of reaction (3) (Fig. S1). Global bifurcation analysis revealed that oscillation occurs as a stable limit cycle through the Hopf bifurcation (HB). A one‐dimensional (1D) bifurcation diagram in Fig. 2 d shows two HB points, as the E3 total (E3_tot) is varied. 2D bifurcation diagrams show the oscillation region when the parameter space is projected onto two‐parameter planes, in this case the E3 total against the ubiquitination rate (k ₁) or de‐ubiquitination rate (V ₂) (Figs. 2 e and f). Interestingly, while only a defined range of the E3 total or the de‐ubiquitination rate can support oscillations, the permissive rate of ubiquitination reaction (1) does not have a lower bound but only an upper bound, suggesting that extremely slow ubiquitination can still give rise to oscillations.

Fig. 2.

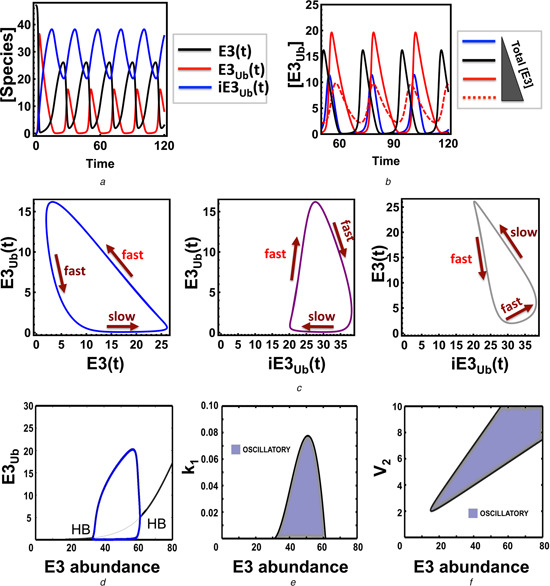
Sustained oscillations in the core non‐proteolytic auto‐ubiquitination models

a Temporal oscillatory dynamics for all species of model NP3

Corresponding ODEs and parameter values are given in Table S3a and b

b Influence of the E3 abundance on oscillations (time unit is in seconds in A and B)

c 2D phase plots showing trajectories of the model species over time, overlaid with temporal timescales

d 1D bifurcation plot showing the dependence of the steady‐state ubiquitinated E3 level in response to changes in the E3 abundance

Thick and thin black lines indicate stable and unstable fixed point steady states, respectively; blue lines indicate the low and high branches of the limit cycle (oscillation)

e and f 2D bifurcation plots partitioning the parameter space into oscillatory and non‐oscillatory regions projected onto the (e) k ₁ ‐E3_tot and (f) V ₂ ‐E3_tot planes

To provide an intuitive explanation of how oscillation may arise in the model NP3 without explicit presence of negative feedback, we analysed the phase diagrams where the time trajectories of model species were plotted against each other. Fig. 2 c overlays the temporal timescale on the trajectories of oscillations. Intuitively, assuming the system starts at a high level of un‐ubiquitinated E3, E3 will be slowly converted to its ubiquitinated form (E3_Ub). When E3_Ub crosses a threshold, the E3_Ub level suddenly and quickly surges up because of the positive feedback, accompanied by a fast depletion of E3. While this happens, the intermediate species iE3_Ub level is not significantly affected. After the sudden build‐up of E3_Ub, it is quickly converted to iE3_Ub leading to an increase in iE3_Ub followed by its slow depletion and thus slow replenishing of E3. During this time, E3_Ub does not substantially change, but mainly the conversion of iE3_Ub into E3 (or the opposite conversion) takes place. E3 then slowly increases until it crosses the threshold and the cycle starts again, leading to sustained oscillations.

2.1.3 Oscillation requires sufficient level of combined network non‐linearity

It is reasonable to assume that the de‐ubiquitination reactions (2) and/or (3) in models NP3 and NP4 follow the MM kinetics, as a consequence of the DUB‐mediated catalysis (Fig. 1 a). The MM kinetics is required to enable oscillation, since it brings sufficient non‐linearity to the system. The NP2 reaction circuitry where both de‐ubiquitination reactions follow linear first‐order kinetics and the reaction rate is given by (1) is indeed incapable of exhibiting oscillation. However, since it is currently unknown if the assumptions underlying MM regime are valid for these reaction, we also analysed what alternative kinetics for models NP3–NP4 can produce oscillation. Assuming both reactions (2) and (3) follow the first‐order kinetics, we found that the system can still oscillate, if the auto‐ubiquitination reactions bring about additional nonlinearity, for example, the reaction rate v ₁ has the following form

$$v_1=[\mathrm{E}3]\left(k_1+k_{1a}[\mathrm{E}{3}_{\text{Ub}}]{}^n\right),\text{with}n\ge 2$$ (2)

In addition to numerical analysis, an analytical examination of this model to derive analytical conditions under which oscillation may occur is given in Section 4 of the SI. One wiring topology, in which the rate in expression (2) could be obtained, is given by model NP5 in Fig. 1 a. As derived below, n = 2 is brought about by assuming the ubiquitinated E3 undergoes dimerisation and that the dimerised, active form catalyses its own ubiquitination. In this case, the reactions involving auto‐ubiquitination are

• (1) $\mathrm{E}3\stackrel{k}{\to }\mathrm{E}{3}_{\text{Ub}}$

• (2) $\mathrm{E}{3}_{\text{Ub}}+\mathrm{E}{3}_{\text{Ub}}\stackrel{k_{f1},k_{r1}}{\leftrightarrow }d\mathrm{E}{3}_{\text{Ub}}$

• (3) $\mathrm{E}3+\text{dE}{3}_{\text{Ub}}\stackrel{k_{f2},k_{r2}}{\leftrightarrow }\mathrm{E}3\_d\mathrm{E}{3}_{\text{Ub}}\stackrel{k_{c2}}{\to }d\mathrm{E}{3}_{\text{Ub}}+\mathrm{E}{3}_{\text{Ub}}$

Assuming the binding reactions that form the intermediate complexes (d E3_Ub and E 3_d E3_Ub) operate at much faster rates and approach steady‐state quicker than the catalytic steps, the quasi‐steady‐state (QSS) assumption results in

$$[d\mathrm{E}{3}_{\text{Ub}}]=\frac{k_{f1}}{k_{r1}}[\mathrm{E}{3}_{\text{Ub}}]{}^2$$

$$[\mathrm{E}3\_d\mathrm{E}{3}_{\text{Ub}}]=\frac{k_{f2}}{k_{r2}+k_{c2}}\frac{k_{f1}}{k_{r1}}[\mathrm{E}3][\mathrm{E}{3}_{\text{Ub}}]{}^2$$

The composite reaction rate v ₁ can then be written as

$$\begin{array}{rl}{v}_1& =k\left[\mathrm{E}3\right]+k_{c2}\frac{k_{f2}}{k_{r2}+k_{c2}}\frac{k_{f1}}{k_{r1}}[\mathrm{E}3][\mathrm{E}{3}_{\text{Ub}}]{}^2\\ & =\left[\mathrm{E}3\right]\left(k_1+k_{1a}{\left[\mathrm{E}{3}_{\text{Ub}}\right]}^2\right)\end{array}$$ (3)

where

$$k_1=k\text{and}{k}_{1a}=k_{c2}\frac{k_{f2}}{k_{r2}+k_{c2}}\frac{k_{f1}}{k_{r1}}$$

Model NP5 with dimerised ubiquitinated E3 can generate sustained oscillation even with linear kinetics of both de‐ubiquitination reactions. This analysis indicates that the level of non‐linearity required for the existence of oscillation can be distributed between different parts (reactions) of the network. Moreover, we found that given the sufficient non‐linearity generated by the new rate v ₁ above, the sequential de‐ubiquitination reactions (i.e. via the intermediate iE3_Ub) simply serve to introduce a time‐delay necessary for the emergence of oscillation. This is corroborated by a variant of model NP2 that explicitly includes de‐ubiquitination step with a delay (model NP6, Fig. 1 a). Simulations of these delayed differential equations robustly produce sustained oscillatory dynamics (see SI).

2.1.4 Self‐promoted degradation by auto‐ubiquitination generates sustained oscillation

Auto‐ubiquitination that generates K48‐linked ubiquitin chains is a recurring theme among many E3 ligases to self‐promote its degradative process via the 26S proteasome [18]. We thus asked if such regulatory motif on its own would be able to produce oscillations. We first examined the simplest scheme, depicted as model P1 in Fig. 3, where the attachment and removal of the ubiquitin chain signalling degradation occurs in single steps [and the reaction rate v ₁ follows (3)]. Note that we denote all models of proteolytic auto‐ubiquitination with the prefix ‘P’. The ubiquitinated E3 ligase in model P1 is subjected to rapid proteasome‐mediated degradation, and this degradation is balanced by a constant synthesis of unmodified E3 ligase.

Fig. 3.

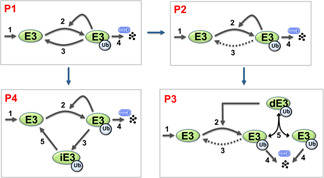
Simplified schematic diagrams of proteolytic (degradative) auto‐ubiquitination models

Different models P1–P4 and the relations between them

Recall that a single‐step de‐ubiquitination renders model NP1 incapable of displaying oscillation. Importantly, when the synthesis and degradation reactions are incorporated (model P1), robust sustained oscillation is observed (Fig. 4 a). Similar to models NP2–NP5, oscillations emerge through the HB. Two HB points characterise the emergence of oscillation, as the positive feedback parameter k _2a is varied. This is shown in the 1D‐bifurcation plot in Fig. 4 c. Interestingly, while the limit cycle oscillation arises in a gradual fashion with increasing amplitude through the higher HB point as k _2a decreases, it terminates more abruptly at the lower HB point, with the amplitude suddenly collapsing to a stable fixed point. This is in contrast to the existence of only a single HB point observed for k ₂ variation (Fig. 4 d). Further, 2D bifurcation analysis showed that oscillation occurs only within a defined range of the synthesis rate (k ₁) whereas the permissive range for the degradation rate (k ₄) is less restricted (Fig. 4 e). The ubiquitination rate constant k ₂ is the most sensitive parameter for the oscillation period, and k ₂ also strongly controls the shape of the oscillatory dynamics. Lowering k ₂ makes oscillated much more pulse‐like (Fig. 4 b). In the extreme case of exceedingly small k ₂ values, the period of these pulses can be very large, which is consistent with the bifurcation plot in Fig. 4 d.

Fig. 4.

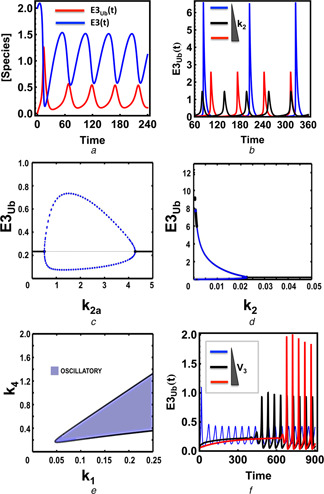
Sustained oscillations in the core proteolytic auto‐ubiquitination models

a Temporal oscillatory dynamics for all species of model P1

Corresponding ODEs and parameter values are given in Table S7a and b

b Influence of the ubiquitination rate constant k ₂ on oscillation

Values used: k ₂ = 0.001, 0.005, 0.01 (time unit is in seconds in A and B)

c and d 1D bifurcation plot showing dependence of the steady‐state ubiquitinated E3 level in response to change in k _2a (strength of the positive feedback) and k ₂

e 2D bifurcation plots partitioning the parameter space into oscillatory and non‐oscillatory regions projected onto the k ₁ –k ₄ plane

f Dependence of oscillatory dynamics in model P4 on change of the rate of the (delayed) de‐ubiquitination reaction, V ₃ (0, 0.5 and 1 for low, medium and high), time unit is in seconds

ODEs and parameter values are given in the SI, Table S9a and b

Interestingly, we found that the de‐ubiquitination step is dispensable for the existence of oscillation, as indicated by the dashed line in model P2 (Fig. 3). In this case, the reversible inter‐conversion of the ubiquitinated E3 is not required, but rather synthesis and degradation serve as source and sink respectively which allow oscillation to arise. The presence of increasingly stronger direct de‐ubiquitination does not affect the occurrence of oscillation but affects the oscillation pattern in the opposite manner to the ubiquitination rate, conferring pulse‐like dynamics at high value.

Similar to model NP5, model P3 presents a possible mechanistic scenario where the higher degree of non‐linearity is brought about by dimerisation, which is necessary and sufficient for oscillation when the synthesis and degradation reactions are assumed to follow linear kinetics. If we assume the degradation reaction to follow the MM kinetics, then oscillations do not require E3 dimerisation or n > 1 in expression (1) (Fig. S2). These observations suggest that the distributed non‐linearity control mechanism could be a common property of biological oscillators.

Since a K48‐linked chain can be de‐ubiquitinated in multiple steps (models NP2–NP5), we examined the scenario where multistep de‐ubiquitination occurs in the degradation (model P4, Fig. 3). We found that oscillation is affected in the same way by the de‐ubiquitination rates as observed in the models NP2–NP5, suggesting that the two oscillation‐generating mechanisms operate independently. Interestingly, increasing the de‐ubiquitination reaction rate V ₄ appears to lengthen the onset of the oscillation dynamics (Fig. 4 f).

2.1.5 Non‐proteolytic auto‐ubiquitination induces mixed modes of dynamics

Biological processes can be graded or digital. Examples of graded processes include cardiac output during exercise, or the secretion of insulin from pancreatic beta cells in response to increasing blood glucose levels. In other biological processes, cells and organisms show all‐or‐none, ‘digital’ responses to stimuli, such as differentiation, cell division and apoptosis. Bistability is a hallmark of biochemical signalling networks underlying digital decision making mechanisms in cells. A bistable network can switch between two distinct stable states (often a low and a high activity level), but cannot rest in intermediate states (where the activity level is in‐between). Bistability typically results from mutually activating or repressing regulations, such as positive or double‐negative feedback loops [28]. However, intermolecular auto‐phosphorylation has also been reported to induce bistability without a need for an explicit positive feedback loop [29]. Based on similar topological structure between auto‐phosphorylation and non‐proteolytic auto‐ubiquitination, we hypothesised that bistability could also arise in the self‐ubiquitinated E3 models given in Fig. 1 a.

Using model NP3 as the representative system for analysis, we indeed found that bistability is a robust feature induced by self‐ubiquitination. Fig. 5 a displays a typical hysteresis curve (a characteristic feature of bistability) for the steady‐state dependence of the ubiquitinated E3 level on the abundance of E3 ligase. Increasing the E3 abundance of small initial values, initially maintains the ubiquitinated E3 form at low levels (on the low level branch). When the E3 abundance crosses a threshold value, the ubiquitinated E3 concentration [E3_Ub] abruptly jumps up to a substantially higher value and then continues traversing the high level branch. Decreasing the E3 abundance when [E3_Ub] has already resided on the high branch switches [E3_Ub] down at the low branch in a similarly abrupt fashion, but at a different, lower threshold values. Likewise, bistable switches and hysteresis can be observed for the ubiquitinated E3 ligase level in response to the variation of other model parameters such as the (de)ubiquitination rates. Fig. 5 b shows how the bistable range depends on k _2a (the rate of auto‐ubiquitination that serves as positive feedback).

Fig. 5.

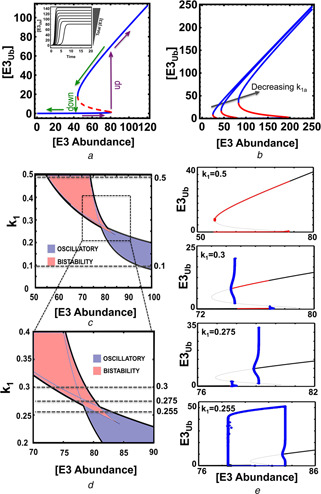
Separation of the parameter space into regions of qualitatively different behaviours in the non‐proteolytic auto‐ubiquitination

a Bistable, ‘all‐or‐none’ response and hysteresis curve of the system: the dependence of steady‐state levels of ubiquitinated E3 on the increasing abundance of the E3 ligase

Inbox shows the abrupt change in the temporal systems dynamics with a gradual increase of E3 total, which is characteristic of a bistable system

Parameter values for plotting: E3_tot = 5.56, k ₃ = 5.55, k ₁ = 0.01, k _1a = 0.035, V ₂ = 18 and K_{m 2} = 4.236

b Effects of the auto‐ubiquitination rate constant on bistability (parameter k _1a = 0.01, 0.035 and 0.1)

c 2D bifurcation and its zoomed‐out plot

d Which partitions the parameter space into complex dynamic regions, projected onto the E3_tot –k ₁ plane

For the indicated values of k ₁ (dashed lines, k ₁), the corresponding 1D bifurcation plot against E3_tot is presented in panel

e In these plots, thick and thin black lines indicate stable and unstable fixed point steady state; blue lines indicate the low and high branches of the limit cycle (oscillation), red thick lines indicate region of bistability

In these plots, the representative model NP3 was used for plotting with the parameter values given in Table S3a and b

When the difference between the activation and deactivation thresholds is large, the decision to switch to a different ubiquitinated level is difficult to reverse. Once a commitment is made, small fluctuations in the initiating stimulus are insufficient to cause a significant change in the output. Such property can be particularly useful in scenarios where the ubiquitinated ligase activates downstream signalling to trigger irreversible cell‐fate decisions, such as differentiation or apoptosis.

2.1.6 Bifurcation analysis reveals mixed complex dynamics

Auto‐ubiquitination wiring design does not necessarily guarantee that a particular network will be bistable or oscillatory, since the observed dynamics depends on specific parameter values. To examine how the model parameters control emergence of these dynamics, we carried out extensive bifurcation analysis using numerical continuation algorithms in XPPAUT (www.math.pitt.edu/~bard/xpp/xpp.html). A two‐parameter bifurcation diagram reveals a complex picture of different dynamic regimes on the plane of E3 abundance (E3_tot) and the de‐ubiquitination kinetic rate (k ₁), including oscillatory and bistable responses (Fig. 5 c). This partitioning of the parameter space allows us to perceive how changes in the model kinetic parameters and the E3 ligase abundance affect the ubiquitinated state of E3 and bring about regions of oscillations, bistable switches and potentially other dynamics. These regions are separated by so‐called bifurcation boundaries, where abrupt, dramatic changes in the steady‐state and dynamic behaviour of the E3 ubiquitination cycle occur. In Fig. 5 c, these boundaries are determined by two types of bifurcation, a saddle‐node (SN) and a HB. In the former, an unstable steady state (termed saddle) merges with another steady state (node), whereas in the latter, a steady state changes its stability and is accompanied by the appearance or disappearance of a limit cycle, where stable limit cycle corresponds to an oscillatory pattern of ubiquitinated E3 form.

Fixing the de‐ubiquitination kinetic constant k ₁ at different values and plotting the corresponding 1D bifurcation diagram for E3_Ub, while varying E3_tot illustrates diverse patterns of dynamic transitions of this E3 ligase system (Fig. 5 e). At high k ₁, the system exhibits only bistability which emerges from the two SN bifurcation points at distinct thresholds of E3_tot (Fig. 5 e). At low k ₁, the system exhibits only oscillation emerging from the two HB points for E3_tot within which oscillation is realised (Fig. 5 e). However, at an intermediate k ₁, the system first passes through a SN bifurcation traversing the stable lower steady‐state branch and becomes unstable until it encounters a turning point. When the system traverses the high steady‐state branch in the opposite direction, it passes a SN and then a turning point. Consequently, as E3_tot increases the system has one stable state, then one stable + two unstable states, then shows bistability, followed by one stable + two unstable states and finally by one stable state. At a slightly higher k ₁, the system displays sub‐critical HBs with an unstable hysteresis‐like curve connecting the HB points (Fig. 5 e). The rate constant k ₁ thus plays a substantial role in determining the dynamics of the system where high k ₁ values correspond to bistability, while low k ₁ values favour oscillation. Interestingly, exploring the parameter space by sampling model parameters within biologically feasible ranges (see SI) and assessing the system local stability by the corresponding eigenvalues when each parameter is sampled (which informs whether the system may oscillate or display bistability) revealed k ₃ to be the most sensitive parameter for system dynamics (Fig. S3). Thus, considering noise that affects the parameter values, perturbing k ₃ is the most straight forward option to alter the system dynamics, while changing other parameters alone does not guarantee a dynamics shift.

2.1.7 Emergence of excitable behaviour

The excitable behaviour is also exhibited by the self‐ubiquitinated E3 ligase system. To demonstrate this behaviour, we perturbed the system by different means and observed the corresponding responses. We found that under restricted parametric conditions, a single‐stable‐steady state with low ubiquitinated E3 level can become excitable. The E3 ligase thus acts as an excitable device with a built‐in excitability threshold, which is the perturbation magnitude or its duration. Fig. 6 shows that if the magnitude of a step‐like perturbation to the abundance of the E3 ligase is below a threshold value, the ubiquitinated E3 only slightly changes before returning to its basal level before the perturbation. However, when the perturbation magnitude is even slightly over the threshold, this perturbation triggers a dramatic transient response with a large overshoot in the level of ubiquitinated E3 level, which returns to the basal level after a significantly longer time compared to the sub‐threshold perturbations (Figs. 6 a and b). Similarly, introducing pulse‐like perturbations with variable durations but fixed magnitude, we observed excitable behaviour when the duration crosses a critical threshold (Fig. 6 c). Fig. 6 d displays the region where excitable behaviour is detected.

Fig. 6.

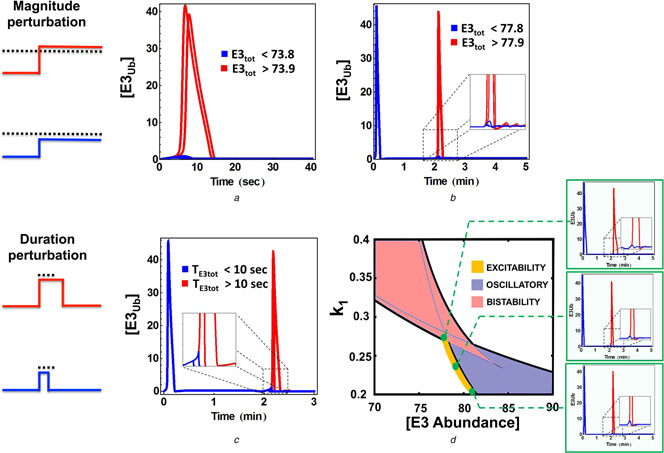
Excitable firing in response to various perturbations

a Qualitatively different responses of the ubiquitinated E3 level to perturbations in the E3 abundance under and over a threshold at starting point of the system

b Similar excitable firing of the ubiquitinated E3 level when the E3 abundance is slightly perturbed (step‐like change) when the system initially resides at steady state

c Excitable firing when the duration of a pulse‐like perturbation in the E3 abundance crosses a critical threshold level

d 2D bifurcation plot showing region where excitability is detected

Parameters values used for plotting are the same as in Fig. 5 d

2.2 Complex dynamics persist in the extended models with E1 and E2 enzymes

Simplified models of self‐ubiquitinated E3 ligase systems considered so far capture key regulatory interactions and greatly facilitate a comprehensive analysis of the systems dynamics. Yet, ubiquitination is a complex, multi‐step process involving not only the E3 ligases, but also the E1 activating and the E2 conjugating enzymes. Therefore, we asked if our core E3 mediated interaction circuits, after being extended to include these additional layers of regulation, could exhibit the complex dynamics that was predicted for simplified models. We thus extended model NP3 to incorporate the E1 and E2 enzymes and a detailed mechanistic description of auto‐ubiquitination of the E3 ligase (see the kinetic scheme in Fig. 7 a). Following well‐known sequential reactions catalysed by E1, E3 and E3, we assumed that ubiquitin (Ub) becomes activated when it has bound to E1. The interaction of the E1–Ub complexes with E2 results in ubiquitins being loaded onto the E2 enzyme in pre‐assembled blocks. Subsequently, the E2–Ub complex binds to the pre‐assembled substrate‐E3 complex (where the substrate is the E3 ligase itself) and then ubiquitins are transferred to the substrate E3–E3, releasing free E2. The ubiquitinated E3 ligase then dissociates from the complex E3_Ub –E3 yielding the catalytically active, ubiquitinated E3 form as the product. This form then acts as a catalysing E3 enzyme to ubiquitinate available unmodified E3 molecules.

Fig. 7.

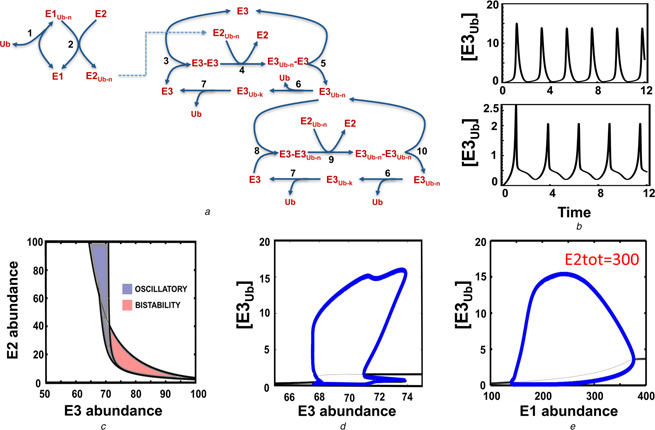
Complex dynamics persist in the extended E1/E2/E3 model

a Kinetic diagram showing the detailed auto‐ubiquitination model that explicitly incorporates the E1 and E2 enzymes

The reactions, ODEs and parameter values of this model are given in Table S12a and b. Ub–n indicates ubiquitin chain of length n

b Dependence of the oscillatory pattern on the abundance of the regulatory enzymes (time is in minutes)

The upper panel shows the simple and the lower panel a more complex dynamic pattern

For the lower panel, [E1_tot] = [E2_tot] = 145 and [E3_tot] = 77

c Partition of the parameter space into complex qualitatively different dynamic regions, including oscillation, bistability and excitability, projected onto the E3_tot –E2_tot plane

d and e 1D bifurcation plots showing the steady‐state ubiquitinated E3 levels, while varying the E3 abundance (d) or the E1 abundance (e) is

In panel (e), we used [E2_tot] = 300 for plotting

The ubiquitinated E3 products are continuously de‐ubiquitinated via multi‐step reactions catalysed by DUBs, recycling free Ub molecules. Since under the normal conditions, the intracellular pool of ubiquitin is likely to be maintained at homeostasis, we assumed the ubiquitin abundance to be constant and thus considered it as a parameter in the extended model for simplification. The model reactions, ODEs and parameter values are given in the SI, Tables S12.

We found that oscillations persist for this elaborate mechanistic model of self‐catalysed ubiquitination under specific conditions. Bifurcation analysis show that the existence of oscillation is sensitive to changes in the abundance of E1, E2 and E3 enzymes (Figs. 7 c –e). Similar to the previous observations for a core model, oscillation arises only within bounded ranges of the E3 abundance, and now also within defined concentration ranges of the E1 and E2 enzymes. This suggests that oscillation requires proper tuning of these regulatory enzyme abundances. In addition, we found that for certain values of the enzyme levels, oscillation can display complex oscillatory patterns, as illustrated in Fig. 7 b. As expected, we also found bistable behaviours in the extended models due to the auto‐ubiquitination mediated positive feedback. Taken together, these results indicate that oscillations and bistability are inherent to the system of auto‐ubiquitination, when the effects of additional regulatory enzymes such as E1 and E2 are explicitly accounted for.

3 Discussion and conclusion

3.1 Sufficient non‐linearity and delayed de‐ubiquitination are critical for sustained oscillation

Our analysis of the E3 ligase self‐catalysed ubiquitination models has shown the emergence of sustained oscillations. In the case of non‐proteolytic auto‐ubiquitination, multi‐step conversion of the ubiquitinated E3 into its un‐ubiquitinated form is the first key requirement. Essentially, this multi‐step de‐ubiquitination creates a time delay. We argue that this is a typical in vivo scenario that occurs through the sequential removal of either single or small blocks of ubiquitin molecules by de‐ubiquitinase enzymes. Moreover, poly‐ubiquitin chains can consist of mixed, branched linkages that may necessitate the involvement of different types of DUBs whose coordinated action also confers a time delay. Strikingly, the degradative E3 auto‐ubiquitination system does not require an explicit de‐ubiquitination reaction, as the presence of degradation balanced by protein synthesis can already trigger oscillations. The second key requirement involves the level of non‐linearity in both non‐proteolytic and proteolytic systems. We found that non‐linearity generated either by protein dimerisation or enzymatic reactions can be distributed throughout and compensated by different parts of the system. When the combined non‐linearity is sufficient, oscillations arise. Specifically, the dimerisation of the E3 ligase makes the assumption of MM kinetics for de‐ubiquitination dispensable. Similarly, a nonlinear kinetics of the degradation reaction can spare the need of the dimerisation assumption. These results are in line with similar requirements reported for oscillations in negative feedback systems [28, 30], constituting unifying principles that underlie this dynamic behaviour.

3.2 Novel designs of biological oscillator and excitable device

Oscillations are ubiquitously observed in cells and have been shown to play important roles in a broad array of cellular processes, including glycolysis [31], circadian rhythms [32] and cell cycles [33]. Our current study shows the potential existence of oscillatory dynamics in the novel context of cellular ubiquitination, driven not by negative feedback but self‐mediated positive feedback of the E3 ligases. Since ubiquitination is a major posttranslational modification implicated in many systems where oscillation has been observed, such as the cell cycle and NF‐kB signalling [6–8], our theoretical prediction that oscillations can arise solely from self‐catalysed ubiquitination adds a new aspect to the existing landscape of mechanisms that induce biological oscillations. Consequently, the question of how the ubiquitination dependent and independent mechanisms that generate oscillations cooperate within specific systems is an intriguing avenue for future research. Importantly, our results put forward novel minimal regulatory motif designs in a general context, based on which new synthetic oscillators can be constructed. In addition, the possible co‐existence of bistability and oscillation in these designs enables excitability, which could serve as foundation for constructing novel excitable devices.

3.3 Concluding remarks

Recent advancement in experimental – omics technologies have shown the widespread involvement of ubiquitination, illuminating its important roles in the regulation of protein activation and degradation. However, this rapid development was not followed by the analysis of the dynamic properties of ubiquitination related networks at the mechanistic level and how various regulatory mechanisms specific to ubiquitination control the network behaviour. The current work fills this knowledge gap by providing a comprehensive investigation into the dynamic features of auto‐ubiquitination in different contexts. Our results also inspire novel design principles for construction of simple but functional oscillator and excitable device.