Ensembled machine learning framework for drug sensitivity prediction

Abstract

Drug sensitivity prediction is one of the critical tasks involved in drug designing and discovery. Recently several online databases and consortiums have contributed to providing open access to pharmacogenomic data. These databases have helped in developing computational approaches for drug sensitivity prediction. Cancer is a complex disease involving the heterogeneous behaviour of same tumour‐type patients towards the same kind of drug therapy. Several methods have been proposed in the literature to predict drug sensitivity. However, these methods are not efficient enough to predict drug sensitivity. The present study has proposed an ensemble learning framework for drug‐response prediction using a modified rotation forest. The proposed framework is further compared with three state‐of‐the‐art algorithms and two baseline methods using Genomics of Drug Sensitivity in Cancer (GDSC) and Cancer Cell Line Encyclopedia (CCLE) drug screens. The authors have also predicted missing drug response values in the data set using the proposed approach. The proposed approach outperforms other counterparts even though gene mutation data is not incorporated while designing the approach. An average mean square error of 3.14 and 0.404 is achieved using GDSC and CCLE drug screens, respectively. The obtained results show that the proposed framework has considerable potential to improve anti‐cancer drug response prediction.

1 Introduction

In recent years, drug sensitivity prediction using computational approaches has gained a lot of attention due to increased interest among researchers in personalised drug therapies. Moreover, the availability of large‐scale pharmacogenomics data sets has further encouraged researchers to develop predictive models. Predicting the sensitivity of drug for an individual is one of the challenging tasks in personalised medicine. Personalised therapies out rule the concept of one size fits all, rather they emphasise tailored drug therapy for individuals [1]. The main concept of personalised drug therapy is to suggest drugs based on individual genomic profiles. Earlier most of the drug therapies are based on an anatomical origin of the disease, but later molecular analysis clarified that genomic characterisation of the patient plays an important role in designing drug therapy. Cancer is one of the genetic diseases caused due to mutation and variation in genes. Complexity in the tumour microenvironment makes cancer complex disease from the treatment perspective. Patients with the same type of cancer show heterogeneous treatment responses toward the same type of targeted therapies. Such differences in responses are because of genetic variations among individuals. Although providing personalised treatment for cancer patients is a challenging task, still researchers are trying hard to design personalised therapies. Various large‐scale throughput drug screenings have been performed to reveal the relationships between genomic profiles and drug responses. These screens provide pharmacogenomics data sets, including a large number of human cancer cell lines and their corresponding drug responses. Genomics of Drug Sensitivity in Cancer (GDSC) [2], Cancer Cell Line Encyclopedia (CCLE) [3] and NCI‐Dream Challenge [4] are few such large‐scale databases that aim to promote oncological research. This data‐sets help in predicting drug (responses/combinations/repositioning) and play a critical role in modern‐day drug discovery. There is a need to develop computational methods which could utilise these large‐scale screening data‐sets and build effective predictive models. One of the important tasks is to predict potential drugs for a given cell line by exploiting the relationships between existing cancerous genomic profiles and their drug responses.

Various machine learning approaches such as regularised regression [3, 5], kernel‐based method [4, 6] and ensemble learning [7, 8] have been proposed in the literature for predicting drug sensitivity [9–11] or drug combination synergy in cancer treatment. Most of these approaches rely on genetic measurements for predicting drug sensitivity. These approaches are based on the common assumption that similar drugs (similarity in chemical structure) will have similar drug targets. Most of the methods proposed in the literature exploit the drugs structure similarity and similarity in cell lines (genomic characterisation). Random forest and Elastic‐net regularisation are the most frequently used machine learning algorithms to predict drug sensitivity (response) in cancerous cell lines. Most of the computational methods for drug response methods are based on traditional machine learning algorithms such as Random Forest, Support Vector Machine and Neural Network (NN). However, these methods do not perform well always because of issues related to high dimensionality and imbalanced nature of data. Hence, ensemble methods are thought to provide better prediction results. In ensemble learning, multiple base classifiers are trained and their output is combined to obtain final output. Performance of an ensemble classifier is greatly affected by the accuracy of the base classifier but also depends on the diversity of the group of classifiers. Diverse classifiers help to minimise errors and make more accurate decisions [12].

There are several other ensemble classifiers proposed in the literature based on bagging and boosting [13]. Rotation forest (RF) is one of the recently proposed ensemble classifiers which has the underlying mechanism similar to random forest [14]. It has shown promising results in comparison to other ensemble classifiers. Randomised heuristics are used to provide diversity in bagging based ensembles as in case of RF. RF uses decision trees (DTs) as base learner which are separately trained on bootstrap samples from the training data set and further add diversity in ensemble classifier by randomised feature selection.

2 Related work

Recently various studies have been proposed in the literature on drug response prediction. Wan and Pal [7] developed in silico method based on random forest regression. Their proposed method was validated using the single agent and multi‐agent anti‐cancer drug screen. Zhang et al. [15] developed the network‐based approach using dual‐layer integrated network consisting of drug–drug and tissue–tissue similarity network. They validated their proposed approach using benchmark data set obtained from CCLE and GDSC databases. Turki and Wei [16] proposed a novel algorithm for drug response prediction using link‐prediction approaches. Their results show that link‐prediction algorithm has great potential in designing in silico method for anti‐cancer drug discovery. Apart from these approaches, multi‐task learning is also exploited for predicting the anti‐cancer drug responses. Gonen and Margolin [6] proposed kernelised Bayesian multi‐task learning using the Gaussian kernel and multi‐task learning and demonstrated potentially high performance. In 2014, Ammad‐ud‐din et al. [17] have proposed QSAR analysis approach using kernelised Bayesian matrix factorisation.

In 2016, Tan [18] presented drug sensitivity prediction algorithm using trace‐norm multi‐task learning. Their proposed approach converts the input gene expression data into kernelised expression data. This kernel trick helps them to achieve better performance as compared to other algorithms. Similarly, Yuan et al. [19] proposed drug sensitivity prediction algorithm using regularised multi‐task learning. Later in 2017, Wang et al. [20] proposed a Pearson correlation‐based drug response prediction algorithm. Their study emphasises on the fact that similar drugs show similar drug responses. Recently ensemble learning is also used in various research domains. It has shown promising results due to low‐variance models and diverse base learners. In this paper, we have proposed the ensembled framework for drug‐response prediction using RF.

2.1 Our contribution

• (i) Tissue sensitivity signatures (TSSs) and drug activity signatures (DASs) are prepared using LINCS database.

• (ii) Dimensionality reduction is used to deal with high dimensional nature of data.

• (iii) RF is modified to improve the prediction performance.

• (iv) Diverse base learners are used to introduce diversity in the prediction model.

3 Background and preliminaries

3.1 Rotation forest

RF is highly efficient ensemble classifiers proposed by Rodriguez et al. [14] in 2006. They perform well as an ensemble classifier because of principal component analysis (PCA) transformation and feature disturbance. It is based on bootstrap sampling with axis rotation of training data set. RF algorithm is designed to train multiple DTs. Before training original feature data is randomly divided into various feature subsets. Then, the new training subsets are obtained, the linear transformation is performed using PCA. Now, all the transformed feature subsets are integrated to reconstruct the original feature set. Finally, base learners are used to obtain the learned classifiers using transformed feature set. The rotational forest provides diversity in classifier using PCA and it is used for axis rotation of subset features. The steps for RF algorithm can be described as follows.

Consider a training set $T=(a_i,b_i){}_{i=1}^N$, where N is the number of training samples in which $a_i$ denotes the input feature vector and $b_i$ denotes class labels. Assume that feature set F is divided into P subsets and there are K DTs in RF such as $P_1$, $P_2$, $P_3$. ………. $P_K$ denotes K subsets.

• Step 1: Divide feature set F into P disjoint subsets with m  = n /P features.

• Step 2: Let $F_{ij}$ be the j th subset of features for training classifiers $P_i$ and $A_{ij}$ be the corresponding data set from A for feature subset $A_{ij}$.

• Step 3: Randomly selects the non‐empty subset of classes from $A_{ij}$.

• Step 4: Bootstrapping of subsets is performed from 75% of the data set to obtain training set denoted by $T^{\prime }$.

• Step 5: Further, PCA is performed on $T^{\prime }$ for generating the coefficient matrix $C_{ij}$.

• Step 6: Sparse rotation matrix $R_i$ is obtained from $C_{ij}$.

  $$R_i=\left[\begin{array}{cccccccc}{r}_{i1}^{(1)},& .....& r_{i1}^{(m_1)},& & 0& .....& 0& \\ & 0& r_{i2}^{(1)},& & 0& .....& 0& \\ & .....& & & .....& .....& .....& \\ 0& & & 0& & & .....& r_{iK}^{(1)}\end{array}\right]$$ (1)

• Step 7: Rearrangement of $R_i$ should be performed to obtain $R_i^{\prime }$. The training set obtained after transformation is $X{R}_i^a$.

• Step 8: Parallel classification is performed.

• Step 9: To classify new samples say r, let $p_{ij}$ ($X{R}_i^{\prime }$) denote the probability of classifier $P_i$ that r $\epsilon$ i. Then the average combination method is used to compute class confidence

  $$C_j(r)=\frac{1}{K}\sum _{i=1}^K{p}_{ij}(x{R}_i^{\prime })$$ (2)

3.2 Decision tree

DTs are one of the most effective graphical approaches to represent the classification or evaluation process of an object. It helps to define the rules to take the particular decision regarding a given problem domain. These are built using the bottom‐up approach with the inclusion of recursion. Internal nodes of the DT represent the test cases for attributes and branches represent the output of those test cases. Each leaf node is a representation of different class label. Various versions of the DT are available such as ID3, C4.5, and CART. However, the DT is not scalable and are prone to the issue of overfitting.

3.3 Extreme learning machine (ELM)

Huang et al. [21] proposed ELMs in 2004 as a modified version of the NN. ELM is considered to be more accurate, fast and has better generalisation ability. It uses a single hidden layer feedforward NN, which reduces the computational time. It is a three‐layer network structure with the first layer as the input layer, the second layer as the hidden layer and the third layer as the output layer. Random assignment of input weights and hidden layer threshold is done in ELM. It is considered as one of the simple machine learning algorithms with fast learning and generalisation performance.

3.4 Neural network

The artificial NN is one of the most extensively used machine learning models. Due to an increase in computational power and data storage capabilities, recently it has gained much attention. It is used widely in various domains such as image processing, speech recognition, and natural language processing. In this paper, we are using the multi‐layer feed‐forward NN with multi‐task abilities.

3.5 Data set

In this study, we have used open‐source data sets from the GDSC [2] and CCLE [3]. GDSC is a curated database consisting of drug screening response data of thousands of tumour cell lines. Their main contribution is to boost oncological research and help to identify potential cancer biomarkers. The cell line information is provided in the form of copy number variation, gene expression and coding variants. However, gene expression data is considered an optimal choice among researchers for computational modelling. Hence, we are also using gene expression profiles of cancer cell lines in our present study. We are using the CCLE data set. It is also an open‐source data set consisting of the perturbated cell line database obtained using Affymetrix U133 + 2 arrays. It consists of data of 504 cancer cell lines perturbed with 24‐anticancer drugs. More than 15,000 genes are obtained in drug screening assays from GDSC and CCLE databases. Gene expression data from such data sources is high dimensional in nature.

We have also used the LINCS database to generate signatures which can represent the activity and sensitivity of the drugs and cell lines. The database currently holds perturbation profiles of tens of thousands of cell lines treated with tens of thousands of drugs (small molecules). The profiles are given in terms of 978 landmark genes that can help to explain the variance in gene expression profiles of cell lines. We have used top 50 landmark genes which have shown highest variation as key descriptors for DASs and TSSs. Therefore, modelling is done on this data which will help to predict whether a given drug is active on a given cell line or not.

4 Proposed framework

Fig. 1 shows a detailed overview of the proposed drug sensitivity prediction framework. First, the original data set is sub‐sampled into smaller data sets for training sub‐samples using modified RF. Traditionally, RF is proposed using DT as base learners but in the modified version of RF, we have used two more diverse base learners – NN and ELMs. RF is one of the recently developed and effective ensemble learning method. One of the most intriguing features of RF its ability to transform feature space into new feature space using PCA transformation. RF train multiple DTs.

Fig. 1.

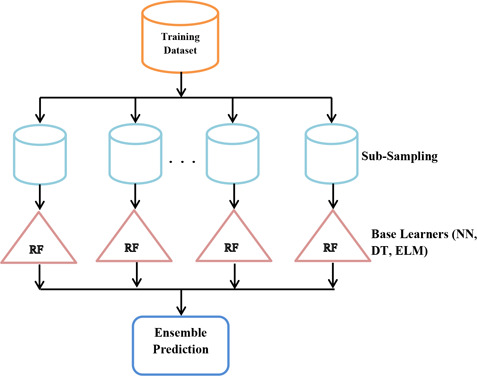
Proposed framework for drug response prediction

In the proposed technique, the first original feature data is divided into sub‐samples to obtain feature subsets. Second, the linear transformation is performed on all the subsets of feature data. Third, the integration of transformed feature sub‐sets is performed and finally, base learners are used for training and model building. Linear transformation helps to attain feature rotation along the feature axis. The diversity of base learners helps to build better generalisation ensemble models. To add more diversity to trained classifier rather than using single base learner, we are using multiple base learners. The inclusion of multiple base learners add diversity and remove overfitting in DTs. In the proposed RF we use the NN, ELMs and DTs as base learners. Ensemble classifier is developed with better performance and generalisation as a result of a modified RF.

4.1 $I{C}_{50}$ data normalisation

$I{C}_{50}$ value is the drug response value which signifies the drug concentration required to inhibit 50% of the diseased cells. If the obtained $I{C}_{50}$ value is more than the drug maximum concentration then, that cell line is considered resistant to the given drug. In order to normalise the drug response data, we divide the data with maximum drug concentration and further perform log‐normalisation. If obtained $I{C}_{50}$ is greater than zero then, cell lines are considered resistant else they are sensitive to the particular drug. After normalisation drug responses are in the range [−1, 1]. Normalisation helps to deal with skewed data and improves data interpretability.

4.2 Drug activity signatures

DASs are the way to know the drug effects on a given cell line at the genetic level. When a drug is given to a cell line some of the genes are upregulated and downregulated

$$\text{ES}(D,C)=⟨g_1\uparrow ,g_2,\downarrow ,g_3,\uparrow ,...,g_k\uparrow ⟩$$ (3)

where experimental signatures (ES) represent the genetic variation on a cell line C with the application of drug D. LINCS (http://www.lincsproject.org/) database and cloud service provide access to calculate this vector for each drug‐cell line (D‐C) pair. It provides top 50 genes which show the highest regulation. Using these experimental signatures we can define DASs

$$\text{DAS}(D)={\cup }_{\mathrm{c}}\text{ES}(D,C)$$ (4)

where ${\cup }_{\mathrm{c}}$ represents the combined effect of all the cell lines for a particular drug. To sum up, now we have identified descriptor which shows the combined variation induced on all cell lines as a result of drug application (see Fig. 2).

Fig. 2.

Algorithm 1: drug sensitivity prediction using modified ensembled RF

4.3 Tissue sensitivity signatures

TSSs represent the genetic variation occurred in the tissue as a result of different drugs perturbation. However, drugs considered to calculate TS should be active with cell line. First, we need to find sensitivity signatures for each D‐C pair by querying with LINCS database. Querying may result in three possibilities:

• DC pair is present in LINCS database.

• D‐C for a given drug‐cell line, the experiment may not be present.

• If target protein for a given drug is used in experiments and their interaction information is present in the database then by using similarity mapping we can use that target protein. The mathematical representation of all the three cases can be done as mentioned below

  $$\text{SS}(D,C)=\left\{\begin{array}{cc}\text{ES}(D,C),& (D,C)\in \text{LINCS}.\\ \text{DAS}(D),& D\in \text{LINCS}\\ & (D,C)\notin \text{LINCS}.\\ \text{TS}(\text{Target}{\mathrm{s}}_{\mathrm{D}}),& D\notin \text{LINCS}.\end{array}\right.$$ (5)

  where TS is target similarity signature for a given drug. Using above sensitivity signatures one can define tissue similarity signatures for a particular cell line as

  $$\text{TSS}(C)={\cup }_{\mathrm{D}}\text{SS}(D,C)$$ (6)

4.4 Signature similarity

The sensitivity signature defines the key descriptor at the genetic level which can cause cell death. Similarly, DASs define the key descriptors that cause cell death on the application of given drug. Intuitively if we could compare the key descriptors of drugs and cell lines then, we will be able to establish a relationship between drug response and genetic variation. Although the huge amount of drug‐response data is available still we are not able to represent the drug‐response of each individual drug. In such a scenario ensembled model helps to integrate the diversity among different models and to build a better prediction model. We have proposed an ensemble modelling strategy which exploits drug and tissue similarity signatures for building drug response prediction model. Sub‐sampling of training data is also done to train a diverse set of base models and finally integrating results from different learners.

5 Experimental analysis

This section presents detailed explanation of the experimental evaluation of the proposed drug‐response prediction framework using GDSC and CCLE data sets. Multiple iterations (≃200) of the proposed technique is performed and results are obtained after averaging the mean square error (MSE) of ten‐fold cross‐validation. MSE is computed using (7). Dimentionality reduction is performed using partial least square [22]. Figs. 3 and 4 show the boxplot comparison of the per drug MSE of proposed approach and other methods using CCLE and GDSC data sets, respectively. Boxplot comparison shows that for most of the drugs it is narrower and MSE is converging at lesser value as compared to other competing methods

$$\text{MSE}(d)=\frac{1}{N_{\mathrm{d}}}({\hat{y}}_{\mathrm{d}}-y_{\mathrm{d}}){}^{\mathrm{T}}({\hat{y}}_{\mathrm{d}}-y_{\mathrm{d}})$$ (7)

Proposed technique is compared with three existing state‐of‐the‐art techniques namely: KBMTL [17], Elastic‐net [2] and Scalable‐Time Ridge Estimator by Averaging of Models (STREAM) [23] and two baseline methods NN and Vanilla RF (VRF) [14]. and NN using two publicly available data sets GDSC and CCLE.

Fig. 3.

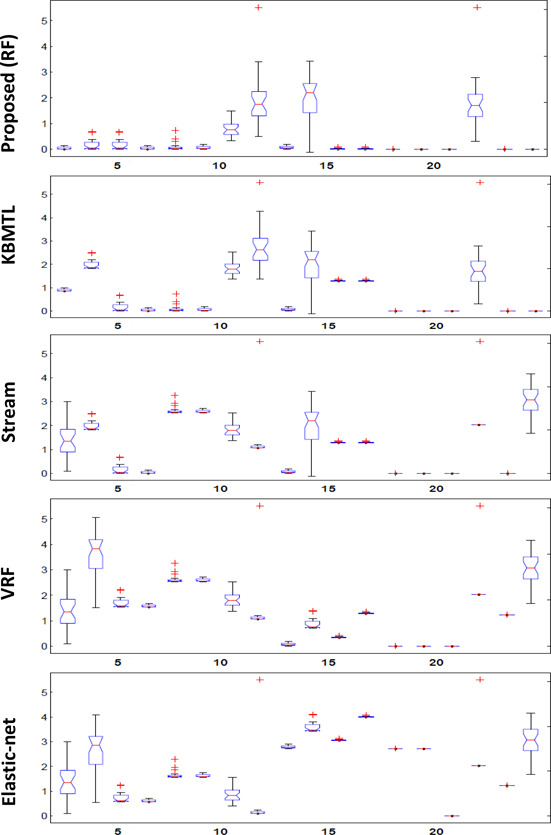
Boxplot comparison of the per drug MSE of the proposed approach and other methods using CCLE data set (X‐axis: drugs, Y‐axis: MSE)

Fig. 4.

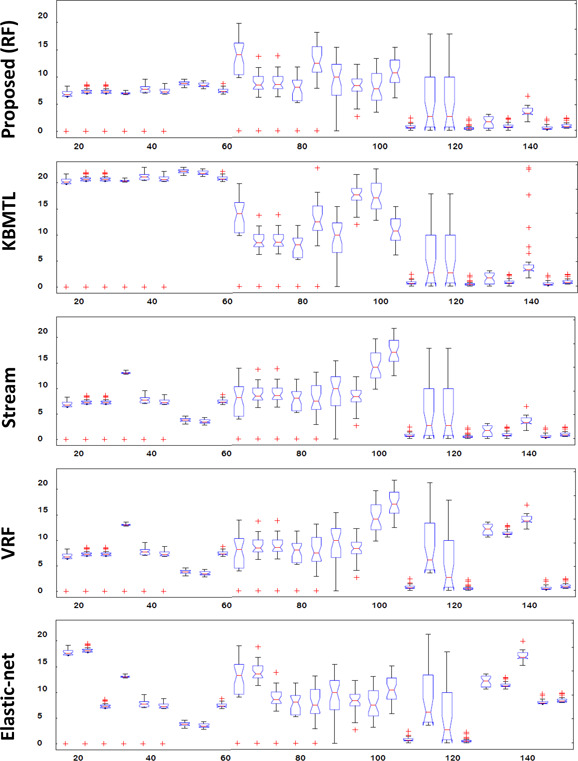
Boxplot comparison of the per drug MSE of the proposed approach and other methods using GDSC data set (X‐axis: drugs, Y‐axis: MSE)

Fine‐tuning of parameters of all the techniques are performed using grid search approach. There are two parameters used with Elastic‐net ($\alpha =0.01$ and $\gamma =1$) which corresponds to lasso regression. Scikit learn is used for implementing Elastic‐net. Parameters for KBMTL are set to their default values as suggested in the paper [17]. KBMTL needs parameter optimisation, so we have selected eight different parameter sets determined from the suggestions of the different authors. In a NN implementation, two hidden layers are used with rectified linear activation function. STREAM performs Bayesian model averaging over regularisation parameters, so does not require parameter optimisation. In the case of RF for our proposed approach the value of K (number of subsets) is set to 10 as it further helps in ten‐fold cross‐validation. The value of B (number of base learners) is set to 50 as with the further increase in the number of base learners no significant gain is achieved. Similarly, sensitivity analysis of r (dimensionality reduction parameter) revealed that it is quite robust when 0.1 ≤ r  ≤ 0.2. The drug averaged MSE is used as a comparative metric for analysing the performance of different techniques. Table 1. represents the comparison of average MSE results for different algorithms.

Table 1.

Performance comparison of proposed algorithm with existing algorithms for all the drugs using average MSE. Best results are highlighted if there is significant difference in performance according to paired t ‐test with p  < 0.05

	GDSC	CCLE
STREAM	3.414 ± 0.607	0.5 ± 0.702
NN	3.368 ± 0.9	0.556 ± 0.29
VRF	3.351 ± 0.72	0.521 ± 0.31
KBMTL	3.34 ± 0.2	0.505 ± 0.81
Elastic‐net	3.319 ± 0.64	0.503 ± 0.25
RF	3.14 ± 0.36	0.404 ± 0.66

In order to get more insights into per drug performance of all the algorithms, we computed the number of statistically significant wins using the paired t ‐test. Table 2 represents the statistical comparison results of different algorithms. Each row gives the comparison of statistically significant win count with a number of wins when an algorithm is directly compared to another algorithm. An algorithm is said to win as compared to other algorithms if it has lower MSE for a given drug t. In the majority of the cases, RF wins as compared to other algorithms representing the lesser error in prediction results. Robustness of the proposed technique is checked using a ten‐fold cross‐validation technique. In a ten‐fold cross‐validation, we split the data set into 10 equal parts and each time using one part for testing and rest other parts for training. We have also validated the proposed approach by using the CCLE data set. The CCLE data set contains the activity area as drug response parameters. As already discussed above, Table 1 contains averaged prediction results obtained after ten‐fold cross‐validation.

Table 2.

Count of statistically significant wins versus count of wins when algorithm is directly compared to another algorithm

Data set		KBMTL	STREAM	Elastic‐net	NN	VRF	RF
GDSC	KBMTL	—	10/54	15/50	14/74	11/64	3/31
	STREAM	26/90	—	39/62	26/80	40/47	7/29
	Elastic‐net	25/84	23/56	—	16/78	35/63	4/37
	NN	23/81	59/21	20/59	—	34/19	2/26
	VRF	76/41	69/32	31/20	15/39	—	6/21
	RF	58/110	43/101	36/105	42/113	34/103	—

Cytotoxicity prediction for missing drug response values in the original data set is also performed to further check the performance of RF. The drug response prediction model is trained using existing data values and further used to predict missing drug responses in the GDSC data set. Lapatinib is an EGFR inhibitor for which most (≃60%) of the drug response values are missing. Similarly, PD‐0332991 is a CDK 4 inhibitor with almost 10% of the drug responses missing. We predicted drug responses for unassayed cell lines corresponding to such drugs. Table 3 shows results for some of such D‐C pairs. Results are presented in terms of natural logμM and only values <−4 ($\simeq 0.05\mu \mathrm{M}$) are listed in the table. Standard error while cross‐validation for each drug‐cell line pair is also calculated and summed up in Table 3. The smaller value of standard error and predicted cytotoxicity for given D‐C pair suggest their high potential in personalised drug therapy. Some of our results can also be inferred from in vivo studies performed in literature. We are listing few such potential pairs from our results that also contains literature evidence. The results suggest that lapatinib is sensitive to EGFR mutated cell lines and PD‐0332991 is more sensitive to CDK mutated cell lines. Our results are consistent with already published studies using assayed cell lines [24].

Table 3.

Pairwise prediction results from GDSC data set

GEO Id	Cell line	Drug	Predicted $\mathrm{I}{\mathrm{C}}_{50}$, μM	CV std. error
GSM1669764	EMC‐BAC‐2	Vinorelbine	−6.124	0.365
GSM136261	VMCUB‐1	Etoposide	−5.946	0.351
GSM887330	MOLM‐16	Midostaurin	−5.46	0.483
GSM887525	RCH‐ACV	AP‐24534	−4.67	0.124
GSM851918	HEYA8	PD0325901	−4.54	0.197
GSM50202	MALME3M	AZD6244	−4.96	0.201
GSM62330	NCIH2122	Nilotinib	−4.92	0.649
GSM274702	FUOV1	Tk 1258	−4.18	0.476
GSM50202	MALME3M	PLX4720	−4.23	0.123
GSM887493	P3HR1	L685458	−4.08	0.145

Vinorelbine is a cytotoxic drug used for the treatment of various types of cancer. The first pair in Table 3. (EMC‐BAC‐2, Vinorelbine) suggests that vinorelbine is sensitive to EMC‐BAC‐2 cell line(non‐small lung cancer). The same observation is found in the in vivo research outcomes of Buhl et al. [25]. Their study suggests that response outcome is more effective when vinorelbine is given in combination with cisplatin. If we analyse another pair (NCIH2122 and Nilotinib), cross‐validation error is maximum suggesting Nilotinib not suitable for NCIH2122 (lung cancer cell line). Nilotinib is a Bcr‐Abl kinase inhibitor, used in Parkinson and Alzheimer disease [26]. Although gene mutation is not considered while modelling drug response data, still RF correctly predicts drug responses for unassayed cell lines.

5.1 Application of the proposed approach to human cancer data set

The proposed approach is a drug sensitivity prediction framework, developed using gene expression and drug sensitivity data. The proposed approach has the potential in preliminary analysis of tumour patients towards various drugs. To further evaluate the performance of the proposed framework, we have downloaded the data set of ovarian cancer patients from gene expression Omnibus (GEO) [https://www.ncbi.nlm.nih.gov/gds] database (GSE30161). The proposed approach is then used to predict the responses of 53 ovarian cancer cell lines to cisplatin, doxorubicin, paclitaxel, gemcitabine, carboplatin. We have randomly selected two patients with ID (GSM746865, GSM746873). The patient with GEO ID GSM746865 is predicted to be responsive to carboplatin, gemcitabine, and paclitaxel and non‐responsive to other drugs. On the other hand the patient with GEO ID GSM746873 is not responsive to gemcitabine, paclitaxel but responsive to other drugs. Overall our analysis suggests that the majority of the cell lines are responsive to carboplatin and gemcitabine.

6 Non‐Parametric statistical analysis

For further statistical analysis, the non‐parametric statistical test, Wilcoxon signed‐rank test has been conducted. The difference between each pair of average results for each problem is computed. These differences are sorted in ascending order and assigned a rank from smallest to the largest difference. In case, if more than one difference is equal, then the average rank is assigned to each of them. Thereafter, the ranks are converted to signed ranks. It is used to compare the proposed approach with other algorithms in a pair‐wise manner. The positive rank is given to the proposed algorithm if it is better than the competitor algorithms with respect to a particular data set. Otherwise, the negative rank is assigned. For comparison, a significance level is set to 0.10 and summed up all the positive and negative rank. The results of the Wilcoxon test are tabulated in Table 4 where +, −, and = indicate that the performance of the proposed approach is superior, inferior, and equal to competitor algorithms, respectively. It is observed from Table 4 that the proposed method outperforms over all the competitor algorithms on CCLE and GDSC data sets.

Table 4.

Wilcoxon signed‐rank test results between proposed and other algorithms

Algorithms	GDSC	CCLE
KBMTL	=	+
STREAM	+	+
Elastic‐net	+	−
VRF	+	+

7 Conclusion and future work

Cancer is a complex ailment involving diverse responses to the same targeted therapies among distinct patients of alike cancer type. There is a great need to develop advanced drugs and personalised treatment alternatives. Unfortunately, the drug designing cost and time‐consuming clinical trials act as a major overhead for cancer treatment. There is a critical need to devise a protocol which can assist in the prediction of drug responses to provide customised treatment at the given instant. We propose to apply the modified RF ensemble method for the prediction of anti‐cancer drug responses. The performance of the prediction algorithm is usually degraded attributing to noisy features and the overfitting of models. However, these two aspects are critically considered and taken into consideration by the proposed technique. Ensemble learning helps in avoiding overfitting and adding diversity. Dimensionality reduction is used to avoid noisy and redundant features. The proposed framework is compared with three state‐of‐the‐art methods and two baseline techniques using two distinct data sets namely: GDSC and CCLE. Further, for checking the performance of RF for prediction of cytotoxicity of new drug‐cell line pair, we implemented RF to detect missing response values. Results clearly depict that the proposed method outperforms the other existing algorithms. In the proposed work, the performance gain is not just attributed to ensemble method used but, also due to the inclusion of TSSs and DASs. Additionally, the proposed work can be put into the application for the prediction of drug synergism and can be extended using the large pharmacogenomic database to achieve better and efficient prediction results.