Improvement in prediction of antigenic epitopes using stacked generalisation: an ensemble approach

Abstract

The major intent of peptide vaccine designs, immunodiagnosis and antibody productions is to accurately identify linear B‐cell epitopes. The determination of epitopes through experimental analysis is highly expensive. Therefore, it is desirable to develop a reliable model with significant improvement in prediction models. In this study, a hybrid model has been designed by using stacked generalisation ensemble technique for prediction of linear B‐cell epitopes. The goal of using stacked generalisation ensemble approach is to refine predictions of base classifiers and to get rid of the worse predictions. In this study, six machine learning models are fused to predict variable length epitopes (6–49 mers). The proposed ensemble model achieves 76.6% accuracy and average accuracy of repeated 10‐fold cross‐validation is 73.14%. The trained ensemble model has been tested on the benchmark dataset and compared with existing sequential B‐cell epitope prediction techniques including APCpred, ABCpred, BCpred and $\text{AA}{\mathrm{P}}_{\text{BCPred}}$.

1 Introduction

Interaction between antigen and antibody plays a vital role in the humoral immune response. Antigenic determinants (epitopes) are the specific region of antigens where antibodies bind. B‐cell epitopes can be categorised into two parts: sequential and discontinuous epitopes. Sequential epitopes are the ones which have amino acids lying linearly in the polypeptide chain. The discontinuous epitopes are generated by using amino acids which are located in different segments of the polypeptide chain. 10% of epitopes are sequential and the rest are discontinuous. Disclosure of sequential epitopes plays an important role in experimental designs, immunodiagnostic tests and vaccine production [1] where most of the B‐cell epitopes are discontinuous.

The propensity scales such as hydrophilicity [2], antigenicity [3] and surface accessibility [4] were used to predict sequential B‐cell epitopes. Traditionally, single property of amino acid was used to describe the information of sequence. Later on, more than one physicochemical properties had been employed in the methods like PREDITOP [5], PEOPLE [6], BEPITOPE [7] and BcePred [8]. The performance of models was enhanced by using physicochemical properties in contrast to the techniques those used single property. ABCPred [9] used recurrent artificial neural systems for predicting linear B‐cell epitopes and attained accuracy of 65.93%. Chen et al. [10] used epitopes of 20‐mers to prepare SVM with 400 features and their model achieved accuracy of 71.09%. BCPred used SVM and a string kernel [11] to predict linear epitopes. It scored AUC (area under the curve) value 0.758. BEST [12] used dataset of 20‐mers epitopes to train SVM model for prediction and attained AUC value 0.81 and 0.85. The SVM model [13] predicted antigenic epitopes by using tri‐peptide similarity and propensity of amino acid. It attained AUC value 0.702. Huang et al. [14] used random forest model to predict the linear B‐cell epitopes and scored accuracy of 78.31%. Lian Yao et al. [15] utilised a sequence‐based linear B‐cell epitope predictor which used deep maxout network and dropout training approaches. To minimise the training time of the classifier, graphics processing unit was used. It achieved accuracy of 68.33% with AUC 0.743. For linear B‐cell epitope prediction, Weike Shen et al. [16] had proposed APCpred method, which used amino acid anchoring pair composition (APC). The SVM model of 20‐mers epitopes achieved accuracy of 68.43%.

Biologists recognise B‐cell epitopes to generate peptide‐based vaccines, epitope‐based antibodies and diagnostic tools. Without computer interference, biologists identify B‐cell epitopes by doing experiments in the wet labs. While doing experiments, they have to test all the peptides individually to get B‐cell epitope. This makes their task tedious in terms of efforts, cost and time. To make biologist's task easy, an accurate statistical model is required which can predict whether a peptide is an epitope or a non‐epitope. Therefore, machine learning techniques are used to generate predictions which reduce the human efforts, time, cost and wet lab experiments. Machine learning technique is beneficial because it facilitates the computer to understand the hidden patterns within the dataset and produces predictions on the unknown data without human interference. Therefore, with the help of machine learning techniques only those samples which are filtered by these techniques are used in the wet labs for further analysis like in experiments, peptide‐based vaccines, epitope‐based antibodies and diagnostic tools. In the present study, the large number of peptides are given to the machine learning models and they predict whether that peptide is an epitope or a non‐epitope. The filtered peptides which are epitopes according to the models are used for further analysis rather than using all the peptides. This makes biologist's job easy by reducing time, cost and efforts for identifying B‐cell epitopes.

Inspired from the performance of machine learning models and need to find a reliable model which can predict antigenic epitopes and reduces the expense on the experimental testing of epitopes, a hybrid method has been proposed by using stacked generalisation ensemble technique. To train the models, physicochemical properties of amino acids are used which in turn classify the sequential B‐cell epitopes as described in Section 3. From literature survey, some shortcomings of B‐cell epitope prediction methods have been found which includes feature selection phase [9, 10, 11, 13], fixed length of amino acid sequences [9, 10, 12, 13], small dataset and basic models (random forest, SVM, neural network). Feature selection phase is essential because it reduces complexity of dataset and enhances the performance of model. Model trained with fixed length of epitopes is used to predict fixed length of epitopes. Nowadays, flexible model is required which can predict any length of epitope. The effectiveness of model is dependent on the size of the training dataset. The datasets used in existing methods [9, 10, 11, 12, 13, 14, 16] contain ∼700, 2479, 701, 4925, 2479, 727, 727, 1573 antigenic epitopes, respectively.

In order to overcome the above‐stated flaws, the contributions of the proposed ensemble model are stated below:

• The proposed ensemble model is a combination of six models which includes blackboost [17], regularised random forest [18], SVM [19, 20], random forest [21, 22], GBM (generalised boosted regression modelling) [23] and avNNet [24, 25]. The proposed ensemble model has been explained in Section 3.2. It is different from existing sequential B‐cell prediction techniques because such techniques are based on single model (mostly used models RF, SVM and NN), which may produce false predictions.

• In the proposed work, variable length epitopes (6–49 mers) are used to train the models. 45,320 epitopes are taken out of which 21,999 are positive and rest are negative.

• The features of amino acids have been filtered by using boruta [26] as mentioned in Section 2.3. Boruta feature selection algorithm is based on wrapper technique which uses random forest model to eliminate the least important features and gives important features to train the models.

• There are many approaches like bagging, boosting and stacked generalisation to create an ensemble model. In the proposed work, stacked generalisation ensemble technique has been used. One of the benefits, for selecting stacked generalisation technique is to refine the output of the base classifier. The models are then linked with each other in such a way that wrong prediction by one model may be corrected by the other model which produces stable and effective results.

• There exist many sequential B‐cell epitope prediction techniques. The comparison between some targeted techniques and the proposed ensemble model is performed. It describes that the proposed ensemble model enhances the accuracy of prediction model which is shown in Table 1.

• The proposed model will be beneficial for the biologists because of its predictability. Only filtered epitopes will be available to them which decreases the expenditure cost to do the experiments in wet lab.

The paper is structured as follows: the brief of the dataset, feature extraction, feature importance, the models of machine learning and the benchmark dataset are mentioned in Section 2. The proposed methodology and ensemble model are narrated in Section 3. Section 4 consists of model evaluation process. Section 5 contains result analysis, comparison and discussion. In the end, the conclusion and future work are mentioned in Section 6.

Table 1.

Performance comparison of existing and the proposed ensemble model

Models	Acc, %	Sen, %	Spe, %	MCC	AUC	TOPSIS score	Rank
proposed model	69.2	62.82	79.6	0.375	0.692	0.84	1
APCpred [16]	67.96	56.15	79	0.362	0.748	0.78	2
ABCpred [9]	66.41	71.66	61.5	0.333	0.736	0.24	4
Bcpred [11]	65.89	66.31	65.5	0.318	0.699	0.27	3
$\text{AA}{\mathrm{P}}_{\text{BCPred}}$ [10]	64.6	64.17	65	0.292	0.689	0.21	5

MCC, Matthews correlation coefficient.

2 Materials and methods

2.1 Dataset and its features

Normally, 10% epitopes are sequential and the rest are discontinuous. In this work, continuous epitopes have been considered. The dataset of sequential B‐cell epitopes which contains positive and negative epitopes is accessed from LBtope server [27, 28]. The extracted dataset is imbalanced thus to handle this issue, fixed length of epitopes are added to the dataset. Fixed length epitopes are extracted from the same source. After removing duplicate sequences and imbalanced class handling, 45,320 sequences are obtained which are of variable length ranging from 6 to 49 mers. There are 21,999 positive and rest are negative sequences. An example of the dataset is presented in Table 2.

Table 2.

Sample dataset containing the sequence length, physicochemical properties of amino acid and class of epitopes

SL	$F_a$	$F_b$	$F_c$	$F_d$	——	$F_z$	$F_{aa}$	$F_{ab}$	$F_{ac}$	CL
12	57.67	4.08	1.46	−1.00	——	34.33	9.33	26.00	5	0
15	131.0	0.80	1.38	1.09	——	21.00	14.33	7.67	3	0
8	49.75	3.62	1.50	4.09	——	51.00	51.00	1.00	8	0
20	84.00	1.91	1.25	−1.00	——	21.00	6.00	16.00	4	1
6	82.67	2.35	1.35	1.09	——	17.67	17.67	1.00	6	1
49	98.35	3.70	1.62	2.95	——	45.90	25.49	21.41	540	1

SL represents sequence length; CL represents class label, i.e. 1 means antigenic epitope and 0 means non‐antigenic epitope.

2.2 Feature extraction

In feature extraction phase, a set of features is defined which represents meaningful information about the area of interest and that set is important for the further analysis. To increase the accuracy and effectiveness of supervised learning, feature extraction phase is essential. In this study, 29 different physicochemical properties of amino acids including aliphatic index ($F_a$), potential protein interaction index ($F_b$), hydrophobic moment ($F_c$), instability index (${\mathrm{F}}_d$), probability of detection of peptides ($F_e$), number of possible neighbours $F_f$, tiny ($F_g$), small ($F_h$), aliphatic ($F_i$), Aromatic ($F_j$), non‐polar ($F_k$), polar ($F_l$), charged ($F_m$), basic ($F_n$), acidic ($F_o$), percentage of tiny ($F_p$), percentage of small ($F_q$), percentage of aliphatic ($F_r$), percentage of aromatic ($F_s$), percentage of non‐polar ($F_t$), percentage of polar ($F_u$), percentage of charged ($F_v$), percentage of basic ($F_w$), percentage of acidic ($F_x$), charge of protein sequence ($F_y$), hydrophobicity ($F_z$), Kidera factor ($F_{aa}$), molecular weight ($F_{ab}$), isoelectric point ($F_{ac}$) are used and described in our previous work [29]. All these properties have been extracted by using R which is an open source software licensed under GNU GPL and calculated with default parameters of all the functions.

2.3 Boruta for feature importance

In the feature importance phase, those features are removed which are highly correlated with other feature, biases and noise from the data. It filters the required features which improves the performance of model. Huang et al. [14] use random forest model's inbuilt property to select important features in which mean decrease in accuracy is used to get important features. Three different sets of features are then created based on their importance values larger than 0.05, 0.1 and 0.15, respectively. Now, a model is trained multiple times depending on the sets of features.

Motivated from this property of random forest model and to reduce the overhead of training the model with different set of features, boruta [26] algorithm has been used which gives a list of important, unimportant and tentative features.

In the proposed work, feature selection task has been done by boruta [30–32], because it uses random forest results and z ‐score to find out the importance of a feature. The boruta feature selection algorithm is based on wrapper technique which uses random forest to eliminate the less important features. The random forest [21] has been selected because it uses an ensemble approach and has low‐cost calculations. It gathers votes from all decision trees which are based on weak classifiers. The z ‐score is calculated by dividing mean loss of accuracy by its standard deviation. In boruta, the dataset is shuffled by creating random copies of all the features which are known as the shadow features. It trains the random forest model on the huge dataset and applies a feature significance measure to know the importance of every feature. It repeatedly checks in each run that a real feature has a high significance than the best of its shadow features and constantly removes insignificant features. At final stage, the stopping criteria of algorithm is when all the elements get accepted or rejected or it achieves a predefined breaking point of random forest runs.

Boruta can be executed in Python [33–35], R [36–38] and does tedious work in a simple way [39]. To filter out the features, boruta gives a list of important, unimportant and tentative features. In this study, there is not any tentative feature. The important features are filtered out which are used to train the models. According to the boruta algorithm, features $F_e$ and $F_{ab}$ are least important. So, these are discarded and rest are considered to train the model. Fig. 1 represents the importance of features in which green represents the important features, red represents the unimportant features and blue represents shadow min, shadow mean and shadow max. Variables having z ‐score less than shadow variables are marked as unimportant and hence discarded.

Fig. 1.

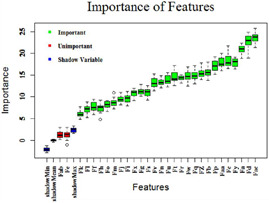
Plot representing the importance of each feature calculated by using boruta algorithm

2.4 Machine learning methods

Table 3 shows the models which are used in this study. It describes required packages and default tuning parameters which are used in execution of the models. To get better results, models can be tuned but in this study default values of parameters are considered.

Table 3.

Machine learning models considered for ensembling; their respective R packages, methods and tuning parameters

Machine learning model	Function	Package	Tuning parameter
BlackBoost [40]	blackboost	mboost	none
Avnnet [41]	avNNet	caret	size = 5, linout = TRUE, trace = FALSE
regularised random forest (RRF) [42]	RRF	RRF	none
support vector machine (SVM) [43]	ksvm	kernlab	kernel = ‘rbfdot’, prob.model = TRUE
random forest [44]	randomForest	randomForest	ntree = 500, mtry = 3
GBM [45]	gbm	gbm	var.monotone, distribution = ‘gaussian’, n.trees = 1000

2.5 Benchmark of the proposed ensemble model correctness

For the benchmark of the proposed ensemble model correctness, benchmark dataset is collected from Shen et al. [16] and he has provided the comparison of ABCpred, BCpred, $\text{AA}{\mathrm{P}}_{\text{BCPred}}$ with APCpred. The benchmark dataset is composed of 187 epitopes and 200 non‐epitopes of length 16‐mers [9]. The benchmark dataset is used to test the proposed ensemble model and compared with APCpred, ABCpred, BCpred, $\text{AA}{\mathrm{P}}_{\text{BCPred}}$ techniques. There is no overlapping between training peptide data and benchmark peptide data. The proposed ensemble model and existing models have been evaluated on different parameters including accuracy, MCC, AUC, sensitivity and specificity as mentioned in Table 1. Results reveal that the proposed ensemble model is performing well in comparison to the existing techniques which is discussed in Section 5.1.

3 Methodology

The proposed methodology is presented in Fig. 2. Initially, the peptide sequences are extracted from LBtope server [27]. The dataset contains negative and positive epitopes having variable length ranging from 6 to 49 mers. The dataset is imbalanced thus to handle this issue, fixed length of epitopes are added to the dataset. Fixed length epitopes are extracted from the same source. In next step, the feature extraction is performed, as mentioned in Section 2.2. Duplicate and missing entries are eliminated from the dataset in the third step. In the fourth step, boruta algorithm [26] has been used to extract the important features. After these steps, the dataset is generated which is used to train the models. Table 3 represents the models which have been used in this study. By using stacked generalisation ensemble technique, six models have been combined as detailed in Section 3.2. The control flow of the proposed scheme has been represented in Fig. 3 and discussed in Section 3.1. Finally, performances of the models have been evaluated on different parameters including specificity, AUC, accuracy, gini and sensitivity. To rank the models on the basis of their evaluation parameters, TOPSIS (technique for order preference by similarity to an ideal solution) has been used. Section 5.1 describes the benchmark dataset which is used to validate the proposed ensemble model. Repeated k ‐fold cross‐validation has been used to measure the robustness of its predictability.

Fig. 2.

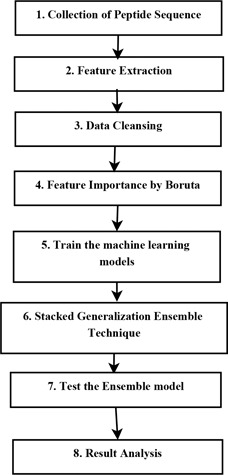
Methodology: step‐by‐step procedure of the proposed work

Fig. 3.

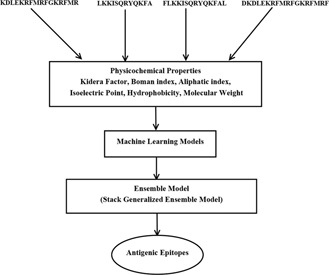
Workflow of the proposed ensemble model

3.1 Flow of the proposed scheme

Fig. 3 shows the proposed ensemble model for prediction of antigenic epitopes. To train the models, a dataset which consists of B‐cell epitopes with their 29 physicochemical properties (Section 2) has been used. An ensemble model has been obtained by fusing six models as described in Section 3.2. The proposed ensemble model gives final prediction regarding the fact that whether an epitope is antigenic or non‐antigenic.

3.2 Proposed stacked generalised ensemble model

Ensembling has been performed to get rid of the worst prediction of the model. In this study, major focus is on the refinement of predictions made by the base classifiers which has been dealt with stacked generalisation ensemble technique. The combination of six models including blackboost, RRF, SVM, random forest, avNNet and GBM are used to improve the accuracy as described in Fig. 4. 70% of dataset is used to train all these models and the rest of the dataset is used as testing dataset. The proposed ensemble model has been partitioned in three phases which are detailed below:

• Phase I: Base classifiers in Tier 1 include random forest, SVM and RRF which have been trained on the training dataset. To check whether the models have learned the training data properly or not, the trained models are also tested with training dataset.

  Fig. 4.

  

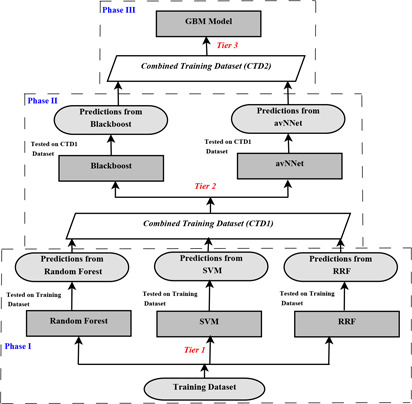  Procedural steps to build the proposed ensemble model

• Phase II: The predictions on training dataset from Phase I are used to create CTD1 dataset which is a combination of training dataset and predictions from random forest, SVM and RRF. CTD1 (combined training dataset 1) dataset have been used to train the Tier 2 classifiers which includes blackboost and avNNet. These models are then tested by using CTD1 dataset. If a base classifier of Tier 1 incorrectly learned some particular instances, the second tier (Tier 2) classifiers can detect this undesired behaviour.

• Phase III: The predictions on CTD1 dataset from Phase II are used to create CTD2 dataset which is a combination of CTD1 dataset and predictions from blackboost and avNNet models. Along with the learned behaviours of base classifiers, it can correct improper training. CTD2 dataset has been used to train GBM model which is Tier 3 meta classifier.

Final predictions on testing dataset are obtained by taking the average of minimum and maximum prediction probabilities of each instance. Here, minimum and maximum predicted probability of each instance has been obtained from six above described trained models. In this study, instead of considering a class (0 or 1), prediction probability of each class has been used and hence it increases the impact of the proposed ensemble model.

4 Model evaluation

Model evaluation is an essential phase in developing the models. It suggests the model which efficiently represents the data and produces accurate predictions. While training the models, overfitting/underfitting/biasness problems may occur. Such issues are resolved by cross‐validation and benchmark dataset. Different parameters like gini, accuracy, AUC, specificity and sensitivity are used to evaluate the performance of the model as mentioned in Section 4.1. TOPSIS a multiple criteria decision‐making method is used to rank the individual and proposed ensemble models on the basis of evaluation parameters. To analyse the consistency of the proposed ensemble model, repeated k ‐fold cross‐validation is performed.

After applying boruta algorithm on the dataset, two features ($F_e$ and $F_{ab}$) are discarded and rest are considered as important which has been discussed in Section 2.3. In the proposed work, (1) is formulated by using important features and target class to train the models

$$\begin{array}{cc}& CL\sim f(F_a,F_b,F_c,F_d,F_f,F_g,F_h,F_i,F_j,F_k,F_l,\\ & F_m,F_n,F_o,F_p,F_q,F_r,F_s,F_t,F_u,F_v,\\ & F_w,F_x,F_y,F_z,F_{aa},F_{ac})\end{array}$$ (1)

4.1 Performance evaluation

There are different parameters like gini, accuracy, AUC, specificity and sensitivity which are used to check the performance of models. To get an optimised result which is based on the combination of these evaluation parameters, TOPSIS a multiple criteria decision‐making method has been used. It generates score by using these evaluation parameters and rank each model according to this score. In this study, models are evaluated on all these parameters which are explained in upcoming section.

4.1.1 Gini coefficient

Gini coefficient is measured to calculate inequality in the distribution. The gini value lies between 0 and 1. Value 1 means inequality and value 0 means equality. For example, if a model scores gini value 60% then it is considered as a good model.

4.1.2 Area under the curve

To check the quality of the model, AUC is calculated. The region below receiver operating characteristics curve is known as AUC. A model is better than others if model has highest AUC value. Its value lies between 0 and 1. The model has AUC value near to 1 means its quality is good.

4.1.3 Accuracy

Accuracy tells the correctness of the model predictions and calculated as follows:

$$\text{Accuracy}=\frac{\text{TP}+\text{TN}}{\text{Total}\text{data}}\times 100$$ (2)

4.1.4 Sensitivity

Sensitivity (Sens) is the fraction of true positives which are accurately predicted as positives by model and is calculated as follows:

$$\text{Sensitivity}=\frac{\text{TP}}{\text{TP}+\text{FN}}$$ (3)

4.1.5 Specificity

Specificity (Spec) measures the fraction of true negatives which are accurately predicted as negative and is calculated as follows:

$$\text{Specificity}=\frac{\text{TN}}{\text{TN}+\text{FP}}$$ (4)

TN is true negative, FP is false positive, TP is true positive and FN is false negative.

4.1.6 Technique for order preference by similarity to an ideal solution

TOPSIS [46, 47] is one of the multiple criteria decision‐making methods. This technique is useful for decision makers to structure the problems to be solved, conduct analyses, comparisons and ranking of the alternatives. In other words, it is used to find out the combined solution which involves multiple criteria. In this study, a R package named TOPSIS is used to get optimised result by using evaluation parameters. Rather giving importance to one evaluation parameter, all the evaluation parameters are considered to generate the TOPSIS score which is used to rank all the individual and proposed ensemble models.

4.2 Repeated k ‐fold cross‐validation

Number of iterations are beneficial for reliability comparison of model performance. Repeated k ‐fold cross‐validation has been used to increase the number of iterations or rerun the k ‐fold cross‐validation multiple times. On the other hand, in k ‐fold cross‐validation, it runs only k times. The data has been shuffled in each fold to do the comparisons. In this study, 10‐fold cross‐validation has been repeated for five times.

5 Result analysis, comparison and discussion

In this study, sequential B‐cell epitopes have been considered because they are important for antibody production, experimental designs, immunodiagnostic tests and vaccine productions. There are some shortfalls in existing sequential B‐cell epitopes prediction techniques which are discussed in Section 1. The proposed ensemble model has been used to overcome those shortfalls.

While training the models, problems like overfitting and underfitting can occur. An overfitted model learns too much and an underfitted model learns too less. In both the cases, results get fluctuated during every run. Solutions for such problems are cross‐validation and testing with unknown data. In the cross‐validation process, model runs n times and the accuracy is noted. If there is high fluctuation in the accuracy then it means the model is overfitted/underfitted/biased. In this study, repeated k ‐fold cross‐validation has been performed and the accuracy is consistent. It shows that the proposed ensemble model is not affected from any issues as described above. For validation of the proposed ensemble model, benchmark dataset has been used. The output represents the two factors: former is, the proposed ensemble model is not overfitted/underfitted/biased and another one is, outcome of the proposed ensemble model is better than the existing techniques.

In the present work, boruta algorithm is used to select the important features. The impact of feature selection phase is demonstrated in Table 4. Evaluation parameters like accuracy, gini, sensitively and AUC are boosted up by using feature selection phase. Therefore, for training the models, only important features are considered and rest are discarded.

Table 4.

Performance evaluation of machine learning models and the proposed ensemble model

Model name	Spec	Sens	ACC%	Gini	AUC	TOPSIS score	Rank
random forest	0.66	0.83	75	0.51	0.75	0.74	4
SVM	0.57	0.85	71.25	0.47	0.73	0.18	6
RRF	0.67	0.83	75.01	0.51	0.75	0.81	2
Blackboost	0.57	0.86	72.1	0.48	0.74	0.19	5
avNNet	0.54	0.87	71	0.47	0.73	0.06	7
GBM	0.67	0.82	75.05	0.51	0.75	0.80	3
proposed model	0.70	0.82	76.6	0.52	0.76	0.94	1

The stacked generalised ensemble approach is used to train the machine learning models as explained in Section 3.2. To create the proposed ensemble model, six models are used as mentioned in Table 3. 70% of the dataset is used to train these models and 30% is used as testing dataset. The performance of above individual models and the proposed ensemble model is shown in Table 4.

In the present work, multiple criteria decision‐making method TOPSIS is used to get the ranking of models on the basis of their evaluation parameters. The benefit of this technique is that the decision of selecting best model is based on all the five evaluation parameters rather than any one or two parameters. The evaluation parameters get increased by using the proposed ensemble model. According to TOPSIS technique, the proposed ensemble model is at first rank which suggests that the proposed ensemble model is better than individual models.

The proposed ensemble model is compared with the existing techniques as mentioned in Section 5.1. Table 1 shows the performance of the proposed ensemble model and existing techniques on the benchmark dataset. TOPSIS and other evaluation parameters have suggested that the proposed ensemble model is outperforming the existing techniques.

To analyse the robustness of the proposed ensemble model, 10‐fold cross‐validation is performed five times which scores mean accuracy of 73.13%. In cross‐validation process, dataset is divided into two sets: 70% for training and 30% for testing. Fig. 5 shows the accuracy of the proposed ensemble model for ten runs executed five times each which in turn represents the consistency in accuracy.

Fig. 5.

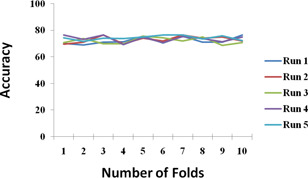
Repeated k‐fold cross‐validation of the proposed ensemble model for ten runs executed five times

From the results and comparison, it is concluded that predictability of the proposed ensemble model has been improved significantly as compared to the individual models.

5.1 Performance comparison on benchmark dataset

The proposed technique has been compared with existing sequential B‐cell epitopes prediction techniques on the benchmark dataset. The results conclude that the proposed ensemble model outperforms current techniques which is shown in Table 1. Accuracy scored by APCpred, ABCpred, BCpred, $\text{AA}{\mathrm{P}}_{\text{BCPred}}$ and the proposed ensemble model is 67.96, 66.41, 65.89, 64.60 and 69.2%, respectively. The proposed ensemble model has boosted the accuracy as well as the other parameters and scores at first rank according to the TOPSIS technique which is shown in Table 1. The increased results and TOPSIS ranking suggest that the proposed ensemble model is more accurate and effective than that of the existing techniques.

6 Conclusion

The present work contributes in peptide vaccine designs, immunodiagnosis, antibody productions and experimental determination by predicting sequential B‐cell epitopes. The proposed ensemble model works well on large dataset and produces improved results for variable length epitopes (6–49 mers). Length of the epitopes is important for better performance of the model as well as for prediction of antigenic epitopes. In this study, six models blackboost, avNNet, random forest, SVM, GBM and RRF have been used to create an ensemble model by using stack generalised ensemble technique which improves the predictability of the proposed ensemble model. Different parameters like gini, AUC, specificity, sensitivity and accuracy have been used to evaluate six models individually. The evaluation process is repeated for the proposed ensemble model. TOPSIS, a multiple criteria decision‐making method is used to rank the models on the basis of their evaluation parameters. The benefit of this technique is that the decision of selecting best model is based on all the five evaluation parameters rather than any one or two parameters. The comparison and ranking by TOPSIS show that an ensemble model performs better than that of the individual models. For validation, comparison between APCpred, ABCpred, BCpred, $\text{AA}{\mathrm{P}}_{\text{BCPred}}$ and the proposed ensemble model is performed, which demonstrates that the proposed ensemble model is more efficient. To analyse the robustness of the proposed ensemble model, repeated k ‐fold cross‐validation has been performed. It is a crucial task to identify sequential B‐cell epitopes. Although different techniques already exist for the same, the proposed technique is better as shown by comparative analysis.

The proposed ensemble approach can be expanded to perform beneficial role in the different areas of the biology including drug designing, prediction of chronic diseases, prediction of T‐cell epitopes, protein structure prediction, allergy and infection predictions and many more. The results may be further enhanced by using emerging machine learning models, optimising the tuning parameters of the models, extracting more peptides of variable length and adding more physicochemical properties.

7 Supplement data

The dataset used in this study is available at https://bit.ly/2PeOlvf. There are three files:

• ‘Positive_Negative_epitopes.csv’ contains all the positive and negative epitopes.

• ‘Complete_Dataset.csv’ contains complete dataset with all features.

• ‘Blind_Dataset.csv’ contains the benchmark dataset with all features.