Competitive numerical analysis for stochastic HIV/AIDS epidemic model in a two‐sex population

Abstract

This study is an attempt to explain a reliable numerical analysis of a stochastic HIV/AIDS model in a two‐sex population considering counselling and antiretroviral therapy (ART). The authors are comparing the solutions of the stochastic and deterministic HIV/AIDS epidemic model. Here, an endeavour has been made to explain the stochastic HIV/AIDS epidemic model is comparatively more pragmatic in contrast with the deterministic HIV/AIDS epidemic model. The effect of threshold number H ^* holds on the stochastic HIV/AIDS epidemic model. If H ^*  < 1 then condition helps us to control disease in a two‐sex human population while H ^*  > 1 explains the persistence of disease in the two‐sex human population. Lamentably, numerical methods such as Euler–Maruyama, stochastic Euler, and stochastic Runge–Kutta do not work for large time step sizes. The recommended structure preserving framework of the stochastic non‐standard finite difference (SNSFD) scheme conserve all vital characteristics such as positivity, boundedness, and dynamical consistency defined by Mickens. The effectiveness of counselling and ART may control HIV/AIDS in a two‐sex population.

1 Introduction

When the first time the Centre for Disease Control (CDC) in 1981 reported for AIDS, the universal spread of the disease has beyond reaching. Early cases of AIDS were limited to lesbians in Africa and Europe, there were influencing indicators that HIV has the greatest damage for the emerging countries. The continents of Asia, South America, and Africa are the largest projected areas of the disease in 1991, where a few sources were available to overcome the pandemic economically. Most cases of infection in the developed nations were due to homosexuality and blood transmission. Therefore, it was critical to develop particular models for displaying the spread of pandemic with new attributes in mind. Bus Enberg proposed a model to study the character of prostitutes in the spread of the pandemic in the locality. A simple symmetry was supposed in early models of heterosexual transmission that the male to female and female to male diffusion rates were same to lessen models into sale population model. A heterosexual model lessens corresponds to the one‐sex model. The preservation of relations between females and males have more generality then the symmetry supposition and may give a better model for the HIV transmission in Africa was proposed by Castillo‐Chavez and Bus Enberg. For the two‐sex model, we prefer to read the article published by Castillo‐Chavez and Bus Enberg. In order to fight the disease, a joined effort to build medication and oversight measures such as cure and screening of HIV patients is much needed. It is not known until now that this programme will diminish the pandemic in Cuba. Hsieh proposed theoretical models to overcome this disease. Velasco‐Hernandez and Hsieh studied the impact of cure and behaviour changes. All these models supposed the pandemic spread in the locality with a steady employment rate. This supposition implies clearly that population size remains limited, which is more beneficial to implement the controlling measures in a specific locality with limited population size, as for the gay community. In developing models, we must consider all individuals who will be able to spread the epidemic in the area. In developing countries, the size of the population is fluctuating. That is why supposing the proportional deployment into the population, we study the impact of community cure on the heterosexual diffusion of HIV under the supposition of fluctuating population size. Accordingly, we assume analogous recruitments in the population [1, 2].

It is strongly deduced that HIV emerged in Kinshasa the Republic of Congo near 1920 when HIV interweave genre from chimpanzees into humans. Until in the 1980s, we were not sure how many peoples are infected by HIV/AIDS. HIV was not escorted by signs, symptoms, and transmission. While various cases of AIDS were reported in 1970, convenient data proposed that the disease was originated in mid of the 1970s. HIV spread to five continents (Australia, South America, Europe, North America, and Africa) and about 100,000–300,000 peoples were already infected during this period. A lungs infection known as Pneumocystis carinii pneumonia (PCP) originated in five young peoples. In the meanwhile, a group of males in California was infected by a cancer Kaposi's Sarcoma. The very first infections of PCP were found in peoples injecting drugs in December 1981. About 270 cases of HIV were reported by the end of 1981 among gays and 121 had died. A group of victims among gays were reported in California that the cause of HIV was sexual relations and a syndrome called gay‐related HIV in June 1982. At the end of this month, the pandemic was found in Haitians ruling to assume that HIV had begun in Haiti. Firstly, the CDC used the term AIDS in September, describing the pandemic as a defect of cells immunity due to which a person loses the power to fight against diseases. AIDS was reported in several countries of Europe. Doctors reported a new disastrous pandemic known as slim in Uganda. A number of organisations such as san Francisco AIDS foundation was set up in the USA by this point. AIDS cases were reported in January 1983 in females having male partners who are infected by the disease and suggested that it can transfer through heterosexual sex. In France, doctors at Pasteur Institute discovered a new virus named lymphadenopathy, the associated virus that can be the origin of AIDS. The first report about children showed that it can transfer through usual contact, but later concluded that they personally got AIDS from their mothers before or after birth. The CDC reported all the causes of transmission and negated the transmission through food, air, usual contact or surfaces. The CDC published the first report on precautions for the healthcare subordinates and doctors to prevent the transmission of AIDS. WHO called a meeting in November to see the worldwide AIDS situation and began worldwide observations? AIDS cases in the USA risen to 3064 and 1292 of them had died by the end of 1983 [3].

National Institute of Cancer announced in April 1984 that they found the causes of AIDS. In collaboration with the Pasteur Institute, they declared that human T‐lymphotropic virus type III (HTLV‐III) and lymphadenopathy associated virus (LAV) are similar and probably the cause of AIDS. A blood test designed to detect the virus with the expectation to develop a vaccine in two years. CDC states that keeping away from injecting drugs and dispensing needles could be effective in the transmission of HIV. Sex clubs and bath houses were banned in San Francisco in October due to high risk of AIDS. Almost 7699 cases of AIDS were found and 3665 deaths recorded in the USA. First needle and syringe plan were made for more regards about HTLV. First blood test enzyme‐linked immunosorbent assay was approved by the Food and Drug Administration (FDA) in March 1985 to diagnose antitoxin virus. Health and human services department of USA and WHO in April organised an international seminar on AIDS in Atlanta Georgia. A teenager Rayan White from Indiana banned from school getting AIDS through polluted blood product used for haemophilia treatment. An actor Rock Hudson died from AIDS in October and left $250,000 to build AIDS research foundation. The first endorsement for averting mother‐to‐child transformation of the virus was issued by the U.S. in December. Every part of the world reported minimum one case of AIDS and 20,303 died in total at the end of 1985. An international organisation on the classification of viruses announced in May 1986, the virus that causes AIDS will be called HIV rather than human T‐lymphotrophic virus type III–V (HTL III–V). Almost 85 countries reported 38,401 cases to WHO by the end of 1986. In Africa 2323, America 31,741, Asia 84, Europe 3858 and Oceania 395 died because of AIDS. The WHO initiated the worldwide programme on AIDS to enhance the awareness; generate affirmation base strategies, by providing technological and economic support for under developed countries, organising research, promoting non‐governmental organisation's contribution and boosts the rights of HIV infected peoples in February 1987. AZT was the first antiretroviral medicine approved by the FDA as a cure for HIV in April 1987. The WHO affirmed that HIV can transfer from mother‐to‐child by breastfeeding in July 1987. AIDS was the first pandemic discussed in the General Assembly of United Nations in October 1987. According to the report of WHO ∼5–10 million people were infected by HIV/AIDS globally. The WHO announced 1st December, first AIDS day in 1988. In the start of 1989, 145 nations reported 142,000 AIDS cases. Nonetheless, the WHO reported 400,000 cases globally. The CDC emancipates the first suggestion to prevent PCP, an expedient infection that causes death among peoples living with AIDS. Almost 100,000 cases of AIDS were reported in the USA by the end of 1989. Ryan White died because of an AIDS related disease at the age of 18, on 8 April 1990. A protest was recorded in an international AIDS conference held in San Francisco opposing the USA immigration policies which stops HIV infected peoples to enter the country. The USA passed the Americans disabilities act in July, which stops differentiation against peoples living with HIV. The FDA approved AZT for the treatment of children with AIDS in October. Over 307,000 cases of AIDS were reported officially by the end of 1990. Approximately 8–10 million were believed to be living with AIDS globally. The red ribbon flattered as an international sign of AIDS awareness. A basketball player Earvin Johnson disclosed that he had HIV and gets retirement from sports with the aim to enlighten young people about the virus. Freddie Mercury a leading singer of rock group queen announced that he had AIDS and died a few days later. In 1992, an international AIDS symposium that was planned to be clench in Boston, USA was shifted to Amsterdam because of USA immigration policies for the HIV infected peoples. Arthur Ashe a tennis star in 1983 disclosed that he was infected by HIV because of blood transmission. The FDA, in May, authorised ten minutes diagnosing kit for the detection of HIV by the healthcare units. USA congress voted massively to continue the ban on countries entry for HIV infected peoples in March 1993. In Asia and the Pacific, over 700,000 peoples were infected by HIV. Approximately 2.5 million cases of AIDS were seen globally at the end of 1993 [4, 5]. The USA Health care services permit to apply AZT to avert the mother‐to‐child imparting of HIV in August 1994. An oral HIV test (first non‐blood test) was permitted by the FDA in December. The FDA authorised the first protease cramp originating the latest span of extremely dynamic antiretroviral treatment [highly active antiretroviral therapy (HAART)] in 1995. After the consolidation of HAART into medical practice, 60 and 80% death rates reduce immediately in the countries which afford it. Approximately 4.7 million new peoples were infected by HIV at the end of 1995, 2.5 million in south Asia and 1.9 million in sub‐Saharan Africa. United Nations programme (UNAIDS) was initiated to promote the global efforts on the scourge and correlate the HIV responses to the United Nations (UN) in 1996. An international AIDS conference held in Vancouver spotlighted the potency of HAART ruling to a span of optimism. First home testing device for measuring the HIV level in the blood was approved by the FDA. New HIV epidemics were identified in Eastern Europe, India, Cambodia, Vietnam, China, and the Soviet Union among others. Almost 23 million peoples were living with HIV at the end of 1996. By estimation of UNAIDS 30 million people were infected by HIV at the end of 1997. HIV is increasing at the rate of 16,000 per day. The fourth largest cause of death worldwide was AIDS announced by WHO in 1999. Almost 33 million people were infected by HIV by the end of 1999 and 14 million died because of AIDS since the beginning of this epidemic. Negotiations with five medication companies were made by UNAIDS to reduce the prices of antiretroviral drugs for the under‐developed countries in July 1999. United Nations acquire the millennium development targets including a particular intent to minimise the spread of HIV, malaria, and tuberculosis. A global funding scheme was formulated by the UN General Assembly in June 2001 for supporting the countries and organisations who are confronting the increase of HIV by preventing, treatments and caring to comprise the buying of medications. India started to produce discounted HIV drugs for the under developed countries, some other pharmaceutical companies also sympathise for the reduction of HIV drugs prices. Developing countries are allowed to formulate inclusive medicines to fight against health crises such as HIV World Trade Organisation in November [6, 7].

The first grant total of $600 million was approved by global funds in April 2002. AIDS was the leading cause of death in Africa reported by UNAIDS in July 2002. Also, a constitutional court instructs the government in Africa to formulate the nevirapine, HIV medicine, and make available to HIV‐positive pregnant females and to their new‐born child that was a legal challenge for the remedy action campaigns. The first most rapid HIV test that gives results in 20 min with an accuracy of 99.6% was approved by the FDA in November. Unites States president George W. Bush offered $15 billion for the five years under president's AIDS relief programme to fight against HIV especially in the countries with a high rate of HIV infected peoples, in January 2003. WHO declared to lead HIV treatment of 3 million victims in December 2005? Male circumcision found to be the greatest risk reducer for a female to male HIV scattering by 60% in 2006. WHO and UNAIDS furnished a new guideline in May 2007 for the recommendation of supplier initiated, examine HIV in health‐care units? The aim was to spread the knowledge of HIV and increase the access to cure and prevention. The travelling outlaw for HIV‐infected peoples from entering the USA was uplifted in January 2010. IPEX revealed 85 results which show a reduction of HIV accession in males who have sex with males by 44%. HPTL 52 appraisal results in 2011 manifest that the antiretroviral treatment minimises the hazard of HIV transmission among Siro‐divergent couples by 96%. Prep approved by FDA in July 2012 which obstructs HIV transmission among HIV‐negative peoples during sex. The first time, most of the peoples about 54% having eligibility for treatment were acquiring it. Death rate because of AIDS has fallen down 30% that was at a peak in 2005, reported by UNAIDS in 2013. Approximately 35 million peoples worldwide were existing with HIV. UNAIDS fast track programme was started in September 2014 for the consequential increase in HIV precautions and treat 28 million people to eradicate this disease by the end of 2030 as a health care issue. An ambitious 90 programme was launched by UNAIDS with the aim to diagnose, 90% of them identified to be acquiring antiretroviral therapy (ART) and 90% of them acquiring this treatment will attain viral suppression by the end of 2020. HIV and AIDS related millennium development goals had reached 6 months ahead from the schedule, announced by UNAIDS in July 2015. The millenium development goals (MDG) target was stumbling and invalidating the escalation of HIV. New treatment policy was recommended by WHO in September that every HIV infected patient will receive antiretroviral treatment, unless the CD4 count, immediately after diagnosing. A new sustainable development goals programme was launched by UNAIDS in October for 2016–2021 with the aim to accelerate the worldwide HIV reactions to gain critical HIV prevention goals and to attain zero distinction [8, 9]. One million people were living with HIV in Russia by the end of 2016. A newly published report announced that 64% of new HIV diagnosing in Europe happen in Russia. 18.2 million were receiving ART announced by UNAIDS including 910,000 children's and the number is double than the five years preliminarily. By increasing access to ART means enhancing the drug resistance. The WHO published a report for fighting against this issue. AVERT manifest at 30th anniversary for providing HIV information from the beginning of the disease and will continue to emancipate people via awareness to prevent HIV. In 2017, the first time in the history 19.5 million peoples were acquiring ART worldwide that was greater than half of the total living with HIV, federations around the world super scribe’ undetectable = untransmutable’ (U = U). This anti‐sigma trademark was introduced by averting access crusade based on the vigorous scientific affirmation that the people who are cohered to therapy and attain an undetectable viral load cannot transfer the virus. In developed countries, ‘U = U’ became explicate for the HIV response, but it fails in the lower resource countries, where virus detection is much difficult. New cases of HIV have fallen down in Asia and Africa, especially among girls and young women. It is considered that this success is because of dreams commencement with the aim to minimise HIV in girls and young women of Africa by giving economic treatments along with better services and education. A deep understanding of widespread diseases has been made possible by the application of various mathematical frameworks. The composition of the model and the feasible imitation enable us to analyse the vulnerability and juxtaposition of conjuncture models. Consequently, the forecasting of moderator, host and environmental conditions affecting the health of people at large is possible and those who are entrusted with the task of policy making on health can draw scientifically accurate conclusions and then transform them into reality in health services [4]. Different models of the transmission of the epidemic disease have been studied. [2]. It is an established fact that non‐linear initial value problems are devoid of any perpetual analytical solutions. The obtainable traditional explicit finite‐difference schemes such as Runge–Kutta and Euler methods are capable of injecting misguiding anarchy and deceptive fluctuations for some intensity of the discretisation frameworks [10–13]. All these causes coupled with a few other schemes which are numerically unstable make such methods less attractive and less‐reliable.

Generally, the elasticity of stochastic differential equations (SDEs) are difficult and the solutions of SDEs do not exist explicitly. Different numerical schemes will be utilised to solve non‐linear models and remain consistent with their biological nature [14–17]. An obvious question can be raised on numerical schemes despite the convergence analysis: are the dynamical characteristics of the original system protected by the numerical scheme [18]?

In the case of deterministic modelling, Euler and Runge–Kutta usual pragmatic numerical schemes neither protect the dynamical characteristics of the initial system nor is it protected by stochastic Euler and stochastic Runge–Kutta which begs the question: is there any stochastic numerical method that can provide protection to all dynamical properties?

Our main purpose in this study is to propose a method, which we call SNSFD scheme. It is based on the model proposed by Mickens in the deterministic case [14–17].

This paper is further divided into the following sections: in Section 2, we give all the basic details of SDEs. Section 3 deals with the invention of stochastic epidemic models. Section 4 is dedicated to the discussion of deterministic HIV/AIDS epidemic models and the points of equilibrium. Finally, in Section 5, we conclude with future work.

2 Preliminaries

Einstein gave the idea of SDEs in 1905 [17, 19, 20]. These days the SDEs are drawing a lot of attention because of their growth in systems of our daily life. One of the reasons for their growth is that the ordinary differential equations (ODEs) do not support randomness and stochastic inputs. A stochastic calculus distributes mathematical constituents in SDEs. Generally, a SDE with continuous time t and variable $V_t$ can be written as

$$\mathrm{d}{V}_t=u(t,V_t)\mathrm{d}t+v(t,V_t)\text{dB}\left(t\right)$$ (1)

and the integral form is

$$V\left(t\right)=c+{\int }_{t_{\mathrm{o}}}^{t}u\left(s,V_{\mathrm{s}}\right)\mathrm{d}s+{\int }_{t_{\mathrm{o}}}^{t}v\left(s,V_{\mathrm{s}}\right)\mathrm{d}{\mathrm{B}}_{\mathrm{s}}.$$ (2)

The differential equation (1) is termed as the Ito SDE. Here $u(t,V_t)\text{and}v(t,V_t)$ are the drift coefficient and diffusion coefficient. The casual variable c at instant $t_{\mathrm{o}}$ is utilised as the initial value. An outcome $V_t$ of (1) and (2) is known as a stochastic process.

3 Stochastic epidemic models

Epidemics are usually twisted by non‐linear systems pragmatic through patchy noisy data. The epidemic models can be divided into two main types such as deterministic epidemic models and stochastic epidemic models. The deterministic epidemic models do not preserve the natural uncertainty of disease dynamics but the idea of stochastic epidemic models preserves all types of uncertainty of disease dynamics. Deterministic epidemic models can be diffused to stochastic epidemic models by numerous conducts [21, 22]. Discrete and continuous time Markov chains along with Ito SDEs are involved in stochastic epidemic modelling. Consequently, the theme of Ito SDEs gives a more opportune way to move from deterministic epidemic models to stochastic epidemic models. The idea of Ito SDE can be used by parametric and non‐parametric perturbation methods. In the former method, we select a parameter from the model and transform it into the model's random variables. In the latter, we propose the Brownian motion in each differential equation (or propose the extra stochasticity parameter). In comparison, non‐parametric perturbation is more convenient than those proposed by the authors of [23, 24]. We will simulate non‐parametric perturbation in deterministic epidemic models and check its efficacy by using different numerical models in stochastic epidemic models. Here, the idea is to examine the relation between deterministic and stochastic epidemic models.

4 Deterministic HIV/AIDS model

In this segment, we consider the deterministic HIV/AIDS model in a two‐sex population considering counselling and ART [25]. Let at any arbitrary time t, the variables are stated as follows: $H_{{\mathrm{m}}_1}\left(t\right)$ represents the number of susceptible males, $H_{{\mathrm{m}}_2}\left(t\right)$ represents the number of infected males, $H_{{\mathrm{m}}_3}\left(t\right)$ represents the number of infected males who recovered by getting ART, $C_{\mathrm{m}}\left(t\right)$ represents the average number of sexual cohorts of infected males with females, $C_{\mathrm{m}}^{\ast }\left(t\right)$ represents the average number of sexual cohorts of infected males receiving ART with females whereas $H_{{\mathrm{f}}_1}\left(t\right)$ represents the number of susceptible females, $H_{{\mathrm{f}}_2}\left(t\right)$ represents the number of infected females and $H_{{\mathrm{f}}_3}\left(t\right)$ represents the number of infected females who recovered by getting ART, $C_{\mathrm{f}}\left(t\right)$ represents the average number of sexual cohorts of infected females with males, $C_{\mathrm{f}}^{\ast }\left(t\right)$ represents the average number of sexual cohorts of infected females receiving ART with males. The communication dynamics of the HIV/AIDS model in a two‐sex population is shown in Fig. 1.

Fig. 1.

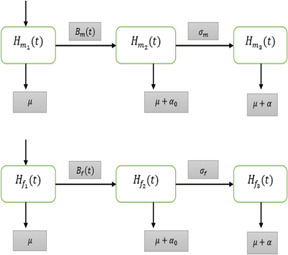
Flow diagram of the HIV/AIDS model in two sex populations

The parameters of the model are described as follows: ${\beta }_{\mathrm{m}}$ (symbolises the chance of transmission by an infected male), ${\beta }_{\mathrm{m}}^{\ast }$ (symbolises the chance of transmission by an infected male getting ART, ${\sigma }_{\mathrm{m}}$ (symbolises the part of infected males getting ART), ${\beta }_{\mathrm{f}}$ (symbolises the chance of transmission by an infected female), ${\beta }_{\mathrm{f}}^{\ast }$ (symbolises the chance of transmission by an infected female getting ART), ${\sigma }_{\mathrm{f}}$ (symbolises the part of infected females getting ART), T (symbolises the extreme life‐span of genders after infection), K (symbolises the worth of ART for genders), b (symbolises the birth rate genders), $\mu$ (symbolises the death rate of both genders), ${\alpha }_0$ (symbolises the death rate of infected genders not getting ART) and $\alpha$ (symbolises the death rate of infected genders getting ART).

The governing differential equations of the HIV/AIDS model are given below:

$$\left.\begin{array}{rl}& \frac{\mathrm{d}{H}_{{\mathrm{m}}_1}\left(t\right)}{\mathrm{d}t}=b{N}_{\mathrm{m}}-B_{\mathrm{m}}{H}_{{\mathrm{m}}_1}\left(t\right)-\mu H_{{\mathrm{m}}_1}\left(t\right)\\ & \frac{\mathrm{d}{H}_{{\mathrm{m}}_2}\left(t\right)}{\mathrm{d}t}=B_{\mathrm{m}}{H}_{{\mathrm{m}}_1}\left(t\right)-\left(\mu +{\alpha }_0+{\sigma }_{\mathrm{m}}\right)H_{{\mathrm{m}}_2}\left(t\right)\\ & \frac{\mathrm{d}{H}_{{\mathrm{m}}_3}\left(t\right)}{\mathrm{d}t}={\sigma }_{\mathrm{m}}{H}_{{\mathrm{m}}_2}\left(t\right)-\left(\mu +\alpha \right)H_{{\mathrm{m}}_3}\left(t\right)\\ & \frac{\mathrm{d}{H}_{{\mathrm{f}}_1}\left(t\right)}{\mathrm{d}t}=b{N}_{\mathrm{f}}-B_{\mathrm{f}}{H}_{{\mathrm{f}}_1}\left(t\right)-\mu H_{{\mathrm{f}}_1}\left(t\right)\\ & \frac{\mathrm{d}{H}_{{\mathrm{f}}_2}\left(t\right)}{\mathrm{d}t}=B_{\mathrm{f}}{H}_{{\mathrm{f}}_1}\left(t\right)-\left(\mu +{\alpha }_0+{\sigma }_{\mathrm{f}}\right)H_{{\mathrm{f}}_2}\left(t\right)\\ & \frac{\mathrm{d}{H}_{{\mathrm{f}}_3}\left(t\right)}{\mathrm{d}t}={\sigma }_{\mathrm{f}}{H}_{{\mathrm{f}}_2}\left(t\right)-\left(\mu +\alpha \right)H_{{\mathrm{f}}_3}\left(t\right)\end{array}\right\}$$ (3)

where $N_{\mathrm{m}}$ and $N_{\mathrm{f}}$ are the total population of males and females, respectively, i.e.

$$N_{\mathrm{m}}=H_{{\mathrm{m}}_1}\left(t\right)+H_{{\mathrm{m}}_2}\left(t\right)+H_{{\mathrm{m}}_3}\left(t\right)$$ (4)

$$N_{\mathrm{f}}=H_{{\mathrm{f}}_1}\left(t\right)+H_{{\mathrm{f}}_2}\left(t\right)+H_{{\mathrm{f}}_3}\left(t\right)$$ (5)

$B_{\mathrm{m}}(t)$ and $B_{\mathrm{f}}(t)$ are frequency rates of infections of both males and females, respectively, and is as follows:

$$B_{\mathrm{m}}\left(t\right)=\frac{c_{\mathrm{m}}\left(t\right){\beta }_{\mathrm{f}}{H}_{{\mathrm{f}}_2}\left(t\right)-c_{\mathrm{m}}^{\ast }\left(t\right){\beta }_{\mathrm{f}}^{\ast }{H}_{{\mathrm{f}}_3}\left(t\right)}{N_{\mathrm{f}}}$$ (6)

$$B_{\mathrm{f}}\left(t\right)=\frac{c_{\mathrm{f}}\left(t\right){\beta }_{\mathrm{m}}{H}_{{\mathrm{m}}_2}\left(t\right)-c_{\mathrm{f}}^{\ast }\left(t\right){\beta }_{\mathrm{m}}^{\ast }{H}_{{\mathrm{m}}_3}\left(t\right)}{N_{\mathrm{m}}}$$ (7)

The normalised and reduced form of the HIV/AIDS model (3) is

$$\begin{array}{rl}\frac{\mathrm{d}{h}_{{\mathrm{m}}_2}\left(t\right)}{\mathrm{d}t}& =\left(c_{\mathrm{m}}{\beta }_{\mathrm{f}}{h}_{{\mathrm{f}}_2}\left(t\right)-c_{\mathrm{m}}^{\ast }{B}_{\mathrm{f}}^{\ast }{H}_{{\mathrm{f}}_3}\left(t\right)\right)\left(1-h_{{\mathrm{m}}_2}\left(t\right)-h_{{\mathrm{m}}_3}\left(t\right)\right)\\ & -\left(b_0+{\sigma }_{\mathrm{m}}\right)h_{{\mathrm{m}}_2}\left(t\right)+\alpha h_{{\mathrm{m}}_3}\left(t\right)h_{{\mathrm{m}}_2}\left(t\right)+{\alpha }_0{h}_{{\mathrm{m}}_2}^2\left(t\right),\end{array}$$ (8)

$$\begin{array}{rl}\frac{\mathrm{d}{h}_{{\mathrm{m}}_3}\left(t\right)}{\mathrm{d}t}& ={\sigma }_{\mathrm{m}}{h}_{{\mathrm{m}}_2}\left(t\right)-\left(b+\alpha \right)h_{{\mathrm{m}}_3}\left(t\right)\\ & +{\alpha }_0{h}_{{\mathrm{m}}_2}\left(t\right)h_{{\mathrm{m}}_3}\left(t\right)+\alpha h_{{\mathrm{m}}_3}^2\left(t\right),\end{array}$$ (9)

$$\begin{array}{rl}\frac{\mathrm{d}{h}_{{\mathrm{f}}_2}\left(t\right)}{\mathrm{d}t}& =\left(c_{\mathrm{f}}{\beta }_{\mathrm{m}}{h}_{{\mathrm{m}}_2}\left(t\right)-c_{\mathrm{f}}^{\ast }{\beta }_{\mathrm{m}}^{\ast }{h}_{{\mathrm{m}}_3}\left(t\right)\right)\left(1-h_{{\mathrm{f}}_2}\left(t\right)-h_{{\mathrm{f}}_3}\left(t\right)\right)\\ & -\left(b_0+{\sigma }_{\mathrm{f}}\right)h_{{\mathrm{f}}_2}\left(t\right)+\alpha h_{{\mathrm{f}}_3}\left(t\right)h_{{\mathrm{f}}_2}\left(t\right)+{\alpha }_0{h}_{{\mathrm{f}}_2}^2\left(t\right),\end{array}$$ (10)

$$\begin{array}{rl}\frac{\mathrm{d}{h}_{{\mathrm{f}}_3}\left(t\right)}{\mathrm{d}t}& ={\sigma }_{\mathrm{f}}{h}_{{\mathrm{f}}_2}\left(t\right)-\left(b+\alpha \right)h_{{\mathrm{f}}_3}\left(t\right)\\ & +{\alpha }_0{h}_{{\mathrm{f}}_2}\left(t\right)h_{{\mathrm{f}}_3}\left(t\right)+\alpha h_{{\mathrm{f}}_3}^2\left(t\right),\end{array}$$ (11)

where

$$\begin{array}{rl}{h}_{{\mathrm{m}}_1}\left(t\right)& =\frac{H_{{\mathrm{m}}_1}\left(t\right)}{N_{\mathrm{m}}},h_{{\mathrm{m}}_2}\left(t\right)=\frac{H_{{\mathrm{m}}_2}\left(t\right)}{N_{\mathrm{m}}},h_{{\mathrm{m}}_3}\left(t\right)=\frac{H_{{\mathrm{m}}_3}\left(t\right)}{N_{\mathrm{m}}},\\ h_{{\mathrm{f}}_1}\left(t\right)& =\frac{H_{{\mathrm{f}}_1}\left(t\right)}{N_{\mathrm{f}}},h_{{\mathrm{f}}_2}\left(t\right)=\frac{H_{{\mathrm{f}}_2}\left(t\right)}{N_{\mathrm{f}}},h_{{\mathrm{f}}_3}\left(t\right)=\frac{H_{{\mathrm{f}}_3}\left(t\right)}{N_{\mathrm{f}}}\end{array}$$

with conditions

$h_{{\mathrm{m}}_1}\left(t\right)+h_{{\mathrm{m}}_2}\left(t\right)+h_{{\mathrm{m}}_3}\left(t\right)=1$ and $h_{{\mathrm{f}}_1}\left(t\right)+h_{{\mathrm{f}}_2}\left(t\right)+h_{{\mathrm{f}}_3}\left(t\right)=1.$

4.1 Steady states of the HIV/AIDS model

The transmission dynamics of models (8)–(11) is only infected females receiving ART. For this, we place ${\sigma }_{\mathrm{f}}>0,{\sigma }_{\mathrm{m}}=0$ in the given models (8)–(11) as follows:

$$\frac{\mathrm{d}{h}_{{\mathrm{m}}_2}\left(t\right)}{\mathrm{d}t}=c_{\mathrm{m}}{\beta }_{\mathrm{f}}{h}_{{\mathrm{f}}_2}\left(t\right)\left(1-h_{{\mathrm{m}}_2}\left(t\right)\right)-b_0{h}_{{\mathrm{m}}_2}\left(t\right)+{\alpha }_0{h}_{{\mathrm{m}}_2}^2\left(t\right)$$ (12)

$$\begin{array}{rl}\frac{\mathrm{d}{h}_{{\mathrm{f}}_2}\left(t\right)}{\mathrm{d}t}& =c_{\mathrm{f}}{\beta }_{\mathrm{m}}{h}_{{\mathrm{m}}_2}\left(t\right)\left(1-h_{{\mathrm{f}}_2}\left(t\right)-h_{{\mathrm{f}}_3}\left(t\right)\right)\\ & -\left(b_0+{\sigma }_{\mathrm{f}}\right)h_{{\mathrm{f}}_2}\left(t\right)+\alpha h_{{\mathrm{f}}_2}\left(t\right)h_{{\mathrm{f}}_3}\left(t\right)+{\alpha }_0{h}_{{\mathrm{f}}_2}^2\left(t\right)\end{array}$$ (13)

$$\begin{array}{rl}\frac{\mathrm{d}{h}_{{\mathrm{f}}_3}\left(t\right)}{\mathrm{d}t}& ={\sigma }_{\mathrm{f}}{h}_{{\mathrm{f}}_2}\left(t\right)-\left(b+\alpha \right)h_{{\mathrm{f}}_3}\left(t\right)\\ & +{\alpha }_0{h}_{{\mathrm{f}}_2}\left(t\right)h_{{\mathrm{f}}_3}\left(t\right)+\alpha h_{{\mathrm{f}}_3}^2\left(t\right)\end{array}$$ (14)

Disease‐free equilibrium is $D_1=\left(0,0,0\right).$ Endemic equilibrium is $E_1=\left(0.2667,0.1568,0.2676\right)$.

$H^{\ast }=\left(\left(c_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}-b_0^2\right)/\left({\sigma }_{\mathrm{f}}{b}_0\right)\right)$. Note that $H^{\ast }$ is the reproduction number.

4.2 Stochastic HIV/AIDS model

The stochastic HIV/AIDS models corresponding to deterministic models (12)–(14) are as follows [26, 27]:

$$\begin{array}{rl}{h}_{{\mathrm{m}}_2}\left(t\right)& =\left(c_{\mathrm{m}}{\beta }_{\mathrm{f}}{h}_{{\mathrm{f}}_2}\left(t\right)\left(1-h_{{\mathrm{m}}_2}\left(t\right)\right)-b_0{h}_{{\mathrm{m}}_2}\left(t\right)\right.\\ & \left.+{\alpha }_0{h}_{{\mathrm{m}}_2}^2\left(t\right)\right)\mathrm{d}t+{\sigma }_1\mathrm{d}{\mathrm{B}}_1\left(t\right)h_{{\mathrm{m}}_2}\left(t\right)\end{array}$$ (15)

$$\begin{array}{rl}{h}_{{\mathrm{f}}_2}\left(t\right)& =\left(c_{\mathrm{f}}{\beta }_{\mathrm{m}}{h}_{{\mathrm{m}}_2}\left(t\right)\left(1-h_{{\mathrm{f}}_2}\left(t\right)-h_{{\mathrm{f}}_3}\left(t\right)\right)-\left(b_0+{\sigma }_{\mathrm{f}}\right)h_{{\mathrm{f}}_2}\left(t\right)\right.\\ & \left.+\alpha h_{{\mathrm{f}}_2}\left(t\right)h_{{\mathrm{f}}_3}\left(t\right)+{\alpha }_0{h}_{{\mathrm{f}}_2}^2\left(t\right)\right)\mathrm{d}t+{\sigma }_2\mathrm{d}{\mathrm{B}}_2\left(t\right)h_{{\mathrm{f}}_2}\left(t\right)\end{array}$$ (16)

$$\begin{array}{rl}{h}_{{\mathrm{f}}_3}\left(t\right)& =\left({\sigma }_{\mathrm{f}}{h}_{{\mathrm{f}}_2}\left(t\right)-\left(b+\alpha \right)h_{{\mathrm{f}}_3}\left(t\right)+{\alpha }_0{h}_{{\mathrm{f}}_2}\left(t\right)h_{{\mathrm{f}}_3}\left(t\right)\right.\\ & \left.+\alpha h_{{\mathrm{f}}_3}^2\left(t\right)\right)\mathrm{d}t+{\sigma }_3\mathrm{d}{\mathrm{B}}_3\left(t\right)h_{{\mathrm{f}}_3}\left(t\right)\end{array}$$ (17)

The Brownian motion is denoted by $B_k\left(t\right),\left(k=1,2,3\right)$, ${\sigma }_1,{\sigma }_2,\text{and}{\sigma }_3$ are the randomness of each equation of systems (12)–(14) (Table 1).

Table 1.

Parameter values of HIV/AIDS model [25]

Parameters	Values
	DFE	EE
α o	0.2	0.2
σ m	0.15	0.15
σ f	0.15	0.15
β *m	0	0
β *f	0	0
c m	3	10
C f	3	10
c *m	1	1
c *f	1	1
σ m	0	0
σ f	0.8	0.8
T	10	10
K	1	1
B	0.5	0.5
b o	0.7	0.7
σ 1	0.4	0.4
σ 2	0.3	0.3
σ 3	0.2	0.2

DFE: disease free equilibrium

EE: endemic equilibrium

4.3 Stochastic Euler method

The stochastic Euler method (15)–(17) is as follows [26, 27]:

$$\begin{array}{rl}{h}_{{\mathrm{m}}_2}^{n+1}\left(t\right)& =h_{{\mathrm{m}}_2}^n\left(t\right)+h[h_{{\mathrm{m}}_2}^n\left(t\right)+h\left[c_{\mathrm{m}}{\beta }_{\mathrm{f}}{h}_{{\mathrm{f}}_2}^n\left(t\right)\left(1-h_{{\mathrm{m}}_2}^n\right)-b_0{h}_{{\mathrm{m}}_2}^n\left(t\right)\right.\\ & \left.+{\alpha }_0{h}_{{\mathrm{m}}_2}^{2n}\left(t\right)+{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}{h}_{{\mathrm{m}}_2}^n\left(t\right)\right]\end{array}$$ (18)

$$\begin{array}{rl}& h_{f_2}^{n+1}\left(t\right)=h_{{\mathrm{f}}_2}^n\left(t\right)+h\left[c_{\mathrm{f}}{\beta }_{\mathrm{m}}{h}_{{\mathrm{m}}_2}^n\left(t\right)\left(1-h_{{\mathrm{f}}_2}^n\left(t\right)-h_{{\mathrm{f}}_3}^n\left(t\right)\right)-\left(b_0+{\sigma }_{\mathrm{f}}\right)h_{{\mathrm{f}}_2}^n\left(t\right)\right.\\ & \left.+\alpha h_{{\mathrm{f}}_2}^n\left(t\right)h_{{\mathrm{f}}_3}^n\left(t\right)+{\alpha }_0{h}_{{\mathrm{f}}_2}^{2n}\left(t\right)+{\sigma }_2\mathrm{\Delta }{B}_n{h}_{{\mathrm{f}}_2}^n\left(t\right)\right]\end{array}$$ (19)

$$\begin{array}{rl}{h}_{{\mathrm{f}}_3}^{n+1}\left(t\right)& =h_{{\mathrm{f}}_3}^n\left(t\right)+h\left[{\sigma }_{\mathrm{f}}{h}_{{\mathrm{f}}_2}^n\left(t\right)-\left(b+\alpha \right)h_{{\mathrm{f}}_3}^n\left(t\right)+{\alpha }_0{h}_{{\mathrm{f}}_2}^n\left(t\right)h_{{\mathrm{f}}_3}^n\left(t\right)\right.\\ & \left.+\alpha h_{{\mathrm{f}}_3}^{2n}\left(t\right)+{\sigma }_3\mathrm{\Delta }{B}_{\mathrm{n}}{h}_{{\mathrm{f}}_3}^n\left(t\right)\right]\end{array}$$ (20)

where the time step size is denoted by ‘h’ and $\mathrm{\Delta }{B}_{\mathrm{n}}$ is normally distributed in between drift and diffusion coefficients, i.e. $\mathrm{\Delta }{B}_{\mathrm{n}}\sim N\left(0,1\right)$.

4.4 Stochastic Runge–Kutta method

The stochastic Runge–Kutta method (15)–(17) is as follows [26, 27]:

Stage 1.

$$\begin{array}{rl}& K_1=h\left[c_{\mathrm{m}}{\beta }_{\mathrm{f}}{h}_{{\mathrm{f}}_2}^n\left(t\right)\left(1-h_{{\mathrm{m}}_2}^n\left(t\right)\right)-b_0{h}_{{\mathrm{m}}_2}^n\left(t\right)\right.\\ & \left.+{\alpha }_0{h}_{{\mathrm{m}}_2}^{2n}\left(t\right)+{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}{h}_{{\mathrm{m}}_2}^n\left(t\right)\right]\\ & M_1=h\left[c_{\mathrm{f}}{\beta }_{\mathrm{m}}{h}_{{\mathrm{m}}_2}^n\left(t\right)\left(1-h_{{\mathrm{f}}_2}^n\left(t\right)-h_{{\mathrm{f}}_3}^n\left(t\right)\right)-\left(b_0+{\sigma }_{\mathrm{f}}\right)h_{{\mathrm{f}}_2}^n\left(t\right)\right.\\ & \left.+\alpha h_{{\mathrm{f}}_2}^n\left(t\right)h_{{\mathrm{f}}_3}^n\left(t\right)+{\alpha }_0{h}_{{\mathrm{f}}_2}^{2n}\left(t\right)+{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}{h}_{{\mathrm{f}}_2}^n\left(t\right)\right]\\ & N_1=h\left[{\sigma }_{\mathrm{f}}{h}_{{\mathrm{f}}_2}^n\left(t\right)-\left(b+\alpha \right)h_{{\mathrm{f}}_3}^n\left(t\right)+{\alpha }_0{h}_{{\mathrm{f}}_2}^n\left(t\right)h_{{\mathrm{f}}_3}^n\left(t\right)\right.\\ & \left.+\alpha h_{{\mathrm{f}}_3}^{2n}\left(t\right)+{\sigma }_3\mathrm{\Delta }{B}_{\mathrm{n}}{h}_{{\mathrm{f}}_3}^n\left(t\right)\right]\end{array}$$

Stage 2.

$$\begin{array}{rl}& K_2=h\left[c_{\mathrm{m}}{\beta }_{\mathrm{f}}\left(h_{{\mathrm{f}}_2}^n\left(t\right)+\frac{M_1}{2}\right)\left(1-\left(h_{{\mathrm{m}}_2}^n\left(t\right)+\frac{K_1}{2}\right)\right)-b_0\left(h_{{\mathrm{m}}_2}^n\left(t\right)+\frac{K_1}{2}\right)\right.\\ & +{\alpha }_0{\left(h_{{\mathrm{m}}_2}^n\left(t\right)+\frac{K_1}{2}\right)}^2+{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}\left(h_{{\mathrm{m}}_2}^n\left(t\right)+\frac{K_1}{2}\right)\\ & M_2=h[c_{\mathrm{f}}{\beta }_{\mathrm{m}}\left(h_{{\mathrm{m}}_2}^n\left(t\right)+\frac{K_1}{2}\right)\\ & \left(1-\left(h_{{\mathrm{f}}_2}^n\left(t\right)+\frac{M_1}{2}\right)-\left(h_{{\mathrm{f}}_3}^n\left(t\right)+\frac{N_1}{2}\right)\right)\\ & -\left(b_0+{\sigma }_{\mathrm{f}}\right)\left(h_{{\mathrm{f}}_2}^n\left(t\right)+\frac{M_1}{2}\right)+\alpha (h_{{\mathrm{f}}_2}^n\left(t\right)\\ & \left.+\frac{M_1}{2}\right)\left(h_{{\mathrm{f}}_3}^n\left(t\right)+\frac{N_1}{2}\right)+{\alpha }_0{\left(h_{{\mathrm{f}}_2}^n\left(t\right)+\frac{M_1}{2}\right)}^2\\ & \left.+{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\left(h_{{\mathrm{f}}_2}^n\left(t\right)+\frac{M_1}{2}\right)\right]\\ & N_2=h\left[{\sigma }_{\mathrm{f}}\left(h_{{\mathrm{f}}_2\left(t\right)}^n+\frac{N_1}{2}\right)-\left(b+\alpha \right)\left(h_{{\mathrm{f}}_3}^n\left(t\right)+\frac{N_1}{2}\right)+{\alpha }_0\left(h_{{\mathrm{f}}_2}^n\left(t\right)+\frac{N_1}{2}\right)\left(h_{{\mathrm{f}}_3}^n\left(t\right)+\frac{N_1}{2}\right)\right.\\ & \left.+\alpha {\left(h_{{\mathrm{f}}_3}^n\left(t\right)+\frac{N_1}{2}\right)}^2+{\sigma }_3\mathrm{\Delta }{B}_{\mathrm{n}}\left(h_{{\mathrm{f}}_3}^n\left(t\right)+\frac{N_1}{2}\right)\right]\end{array}$$ (21)

Stage 3.

$$\begin{array}{rl}& K_3=h\left[c_{\mathrm{m}}{\beta }_{\mathrm{f}}\left(h_{{\mathrm{f}}_2}^n\left(t\right)+\frac{M_2}{2}\right)\left(1-h_{{\mathrm{m}}_2}^n\left(t\right)+\frac{K_2}{2}\right)-b_0\left(h_{{\mathrm{m}}_2}^n\left(t\right)+\frac{K_2}{2}\right)\right.\\ & \left.+{\alpha }_0{\left(h_{{\mathrm{m}}_2}^n\left(t\right)+\frac{K_2}{2}\right)}^2+{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}\left(h_{{\mathrm{m}}_2}^n\left(t\right)+\frac{K_2}{2}\right)\right]\\ & M_3=h[c_{\mathrm{f}}{\beta }_{\mathrm{m}}\left(h_{{\mathrm{m}}_2}^n\left(t\right)+\frac{K_2}{2}\right)\\ & \left(1-\left(h_{{\mathrm{f}}_2}^n\left(t\right)+\frac{M_2}{2}\right)-\left(h_{{\mathrm{f}}_3}^n\left(t\right)+\frac{N_2}{2}\right)\right)\\ & -\left(b_0+{\sigma }_{\mathrm{f}}\right)\left(h_{{\mathrm{f}}_2}^n\left(t\right)+\frac{M_2}{2}\right)+\alpha (h_{{\mathrm{f}}_2}^n\left(t\right)\\ & +\frac{M_2}{2})\left(h_{{\mathrm{f}}_3}^n\left(t\right)+\frac{N_2}{2}\right)+{\alpha }_0{\left(h_{{\mathrm{f}}_2}^n\left(t\right)+\frac{M_2}{2}\right)}^2\\ & +\left.{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\left(h_{{\mathrm{f}}_2}^n\left(t\right)+\frac{M_2}{2}\right)\right]\\ & N_3=h\left[{\sigma }_{\mathrm{f}}\left(h_{{\mathrm{f}}_2\left(t\right)}^n+\frac{M_2}{2}\right)-\left(b+\alpha \right)\left(h_{{\mathrm{f}}_3}^n\left(t\right)+\frac{N_2}{2}\right)\right.\\ & +{\alpha }_0\left(h_{{\mathrm{f}}_2}^n\left(t\right)+\frac{M_2}{2}\right)\left(h_{{\mathrm{f}}_3}^n\left(t\right)+\frac{N_2}{2}\right)\\ & \left.+\alpha {\left(h_{{\mathrm{f}}_3}^n\left(t\right)+\frac{N_2}{2}\right)}^2+{\sigma }_3\mathrm{\Delta }{B}_{\mathrm{n}}\left(h_{{\mathrm{f}}_3}^n\left(t\right)+\frac{N_2}{2}\right)\right]\end{array}$$

Stage 4

$$\begin{array}{rl}& K_4=h\left[c_{\mathrm{m}}{\beta }_{\mathrm{f}}\left(h_{{\mathrm{f}}_2}^n\left(t\right)+M_3\right)\left(1-(h_{{\mathrm{m}}_2}^n\left(t\right)+K_3)\right)-b_0\left(h_{{\mathrm{m}}_2}^n\left(t\right)+K_3\right)\right.\\ & +{\alpha }_0{\left(h_{{\mathrm{m}}_2}^n\left(t\right)+K_3\right)}^2+{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}\left(h_{{\mathrm{m}}_2}^n\left(t\right)+K_3\right)\\ & M_4=h\left[c_{\mathrm{f}}{\beta }_{\mathrm{m}}\left(h_{{\mathrm{m}}_2}^n\left(t\right)+K_3\right)\right.\\ & \left(1-\left(h_{{\mathrm{f}}_2}^n\left(t\right)+M_3\right)-\left(h_{{\mathrm{f}}_3}^n\left(t\right)+N_3\right)\right)\\ & -\left(b_0+{\sigma }_{\mathrm{f}}\right)\left(h_{{\mathrm{f}}_2}^n\left(t\right)+M_3\right)+\alpha (h_{{\mathrm{f}}_2}^n\left(t\right)\\ & +M_3)\left(h_{{\mathrm{f}}_3}^n\left(t\right)+N_3\right)+{\alpha }_0{\left(h_{{\mathrm{f}}_2}^n\left(t\right)+M_3\right)}^2\\ & +\left.{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\left(h_{{\mathrm{f}}_2}^n\left(t\right)+M_3\right)\right]\\ & N_4=h\left[{\sigma }_{\mathrm{f}}\left(h_{{\mathrm{f}}_2\left(t\right)}^n+M_3\right)-\left(b+\alpha \right)\left(h_{{\mathrm{f}}_3}^n\left(t\right)+N_3\right)\right.\\ & +{\alpha }_0\left(h_{{\mathrm{f}}_2}^n\left(t\right)+M_3\right)\left(h_{{\mathrm{f}}_3}^n\left(t\right)+N_3\right)\\ & \left.+\alpha {\left(h_{{\mathrm{f}}_3}^n\left(t\right)+N_3\right)}^2+{\sigma }_3\mathrm{\Delta }{B}_{\mathrm{n}}\left(h_{{\mathrm{f}}_3}^n\left(t\right)+N_3\right)\right]\end{array}$$

Final stage

$$\left.\begin{array}{c}{h}_{{\mathrm{m}}_2}^{n+1}\left(t\right)=h_{{\mathrm{m}}_2}^n\left(t\right)+\frac{1}{6}\left[K_1+2K_2+2K_3+K_4\right]\\ h_{{\mathrm{f}}_2}^{n+1}\left(t\right)=h_{{\mathrm{f}}_2}^n\left(t\right)+\frac{1}{6}\left[M_1+2M_2+2M_3+M_4\right]\\ h_{{\mathrm{f}}_3}^{n+1}\left(t\right)=h_{{\mathrm{f}}_3}^n\left(t\right)+\frac{1}{6}\left[N_1+2N_2+2N_3+N_4\right]\end{array}\right\}$$ (22)

Where the time step size is denoted by ‘h’ and i.e. $\mathrm{\Delta }{B}_n\sim N\left(0,1\right)$.

4.5 SNSFD method

The SNSFD method (15)–(17) is as follows [26, 27]:

$$h_{{\mathrm{m}}_2}^{n+1}\left(t\right)=\frac{h_{{\mathrm{m}}_2}^n\left(t\right)+\varphi \left(h\right)\left[c_{\mathrm{m}}{\beta }_{\mathrm{f}}{h}_{{\mathrm{f}}_2}^n\left(t\right)+{\alpha }_0{h}_{{\mathrm{m}}_2}^n\left(t\right)h_{{\mathrm{m}}_2}^n\left(t\right)+{\sigma }_1{h}_{{\mathrm{m}}_2}^n\left(t\right)\mathrm{\Delta }{B}_{\mathrm{n}}\right]}{1+\varphi \left(h\right)\left[1+c_{\mathrm{m}}{\beta }_{\mathrm{f}}{h}_{{\mathrm{f}}_2}^n\left(t\right)+b_0\right]}$$ (23)

$$h_{{\mathrm{f}}_2}^{n+1}\left(t\right)=\frac{h_{{\mathrm{f}}_2}^n\left(t\right)+\varphi \left(h\right)\left[c_{\mathrm{f}}{\beta }_{\mathrm{m}}{h}_{{\mathrm{m}}_2}^{n+1}\left(1-h_{{\mathrm{f}}_2}^{n+1}\right)+\alpha h_{{\mathrm{f}}_2}^n{h}_{{\mathrm{f}}_3}^n+{\alpha }_0{h}_{{\mathrm{f}}_2}^n{h}_{{\mathrm{f}}_2}^n\right]+\varphi \left(h\right){\sigma }_2{h}_{{\mathrm{f}}_2}^n\left(t\right)\mathrm{\Delta }{B}_{\mathrm{n}}}{\left(1+\varphi \left(h\right)c_{\mathrm{f}}{\beta }_{\mathrm{m}}{h}_{{\mathrm{m}}_2}^{n+1}+\varphi \left(h\right)\left(b_0+{\sigma }_{\mathrm{f}}\right)\right)}$$ (24)

$$h_{{\mathrm{f}}_3}^{n+1}\left(t\right)=\frac{h_{{\mathrm{f}}_3}^n\left(t\right)+\varphi \left(h\right)\left[{\sigma }_{\mathrm{f}}{h}_{{\mathrm{f}}_2}^{n+1}\left(t\right)+{\alpha }_0{h}_{{\mathrm{f}}_2}^{n+1}\left(t\right)h_{{\mathrm{f}}_3}^n\left(t\right)+\alpha h_{{\mathrm{f}}_3}^n\left(t\right)h_{{\mathrm{f}}_3}^n\left(t\right)+{\sigma }_3{h}_{{\mathrm{f}}_3}^n\left(t\right)\mathrm{\Delta }{B}_{\mathrm{n}}\right]}{\left[1+\varphi \left(h\right)\left(b+\alpha \right)\right]}$$ (25)

4.6 Stability of stochastic NSFD method

We consider F, G, and H as follows:

$$\begin{array}{rl}& F=h_{{\mathrm{m}}_2}\left(t\right)+h\left[c_{\mathrm{m}}{\beta }_{\mathrm{f}}{h}_{{\mathrm{f}}_2}\left(t\right)+{\alpha }_{\mathrm{o}}{h}_{{\mathrm{m}}_2}^2\left(t\right)\right.\\ & \left.+{\sigma }_1{h}_{{\mathrm{m}}_2}\left(t\right)\mathrm{\Delta }{B}_{\mathrm{n}}\right]/\left(1+h{c}_{\mathrm{m}}{\beta }_{\mathrm{f}}{h}_{{\mathrm{f}}_2}\left(t\right)+h{b}_{\mathrm{o}}\right)\\ & G=h_{{\mathrm{f}}_2}\left(t\right)+h\left[c_{\mathrm{f}}{\beta }_{\mathrm{m}}{h}_{{\mathrm{m}}_2}\left(t\right)\left(1-h_{{\mathrm{f}}_3}\left(t\right)\right)+\alpha h_{{\mathrm{f}}_2}\left(t\right)h_{{\mathrm{f}}_3}\left(t\right)+{\alpha }_{\mathrm{o}}{h}_{{\mathrm{f}}_2}^2\left(t\right)\right.\\ & \left.+{\sigma }_1{h}_{{\mathrm{f}}_2}\left(t\right)\mathrm{\Delta }{B}_{\mathrm{n}}\right]/\left[1+h{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{h}_{{\mathrm{m}}_2}\left(t\right)+h\left(b_{\mathrm{o}}+{\sigma }_{\mathrm{f}}\right)\right]\\ & H=h_{{\mathrm{f}}_3}\left(t\right)+h\left[{\sigma }_{\mathrm{f}}{h}_{{\mathrm{f}}_2}\left(t\right)+{\alpha }_{\mathrm{o}}{h}_{{\mathrm{f}}_2}\left(t\right)h_{{\mathrm{f}}_3}\left(t\right)+\alpha h_{{\mathrm{f}}_3}^2\left(t\right)\right.\\ & \left.+{\sigma }_3{h}_{{\mathrm{f}}_3}\left(t\right)\mathrm{\Delta }{B}_{\mathrm{n}}\right]/\left[1+h\left(b+\alpha \right)\right]\end{array}$$

The Jacobian matrix as

$$\mathit{J}=\left[\begin{array}{ccc}\frac{\partial F}{\partial h_{{\mathrm{m}}_2}}& \frac{\partial F}{\partial h_{{\mathrm{f}}_2}\left(t\right)}& \frac{\partial F}{\partial h_{{\mathrm{f}}_3}\left(t\right)}\\ \frac{\partial G}{\partial h_{{\mathrm{m}}_2}}& \frac{\partial G}{\partial h_{{\mathrm{f}}_2}\left(t\right)}& \frac{\partial G}{\partial h_{{\mathrm{f}}_3}\left(t\right)}\\ \frac{\partial H}{\partial h_{{\mathrm{m}}_2}}& \frac{\partial H}{\partial h_{{\mathrm{f}}_2}\left(t\right)}& \frac{\partial H}{\partial h_{{\mathrm{f}}_3}\left(t\right)}\end{array}\right]$$

For disease‐free equilibrium, we get the Jacobean matrix as follows:

$$(h_{{\mathrm{m}}_2}\left(t\right),h_{{\mathrm{f}}_2}\left(t\right),h_{{\mathrm{f}}_3}\left(t\right)=\left(0,0,0\right)$$

$$\begin{array}{rl}\Rightarrow J\left(0,0,0\right)& =\left[\begin{array}{ccc}\frac{1+h{\sigma }_3\mathrm{\Delta }{B}_{\mathrm{n}}}{1+h{b}_{\mathrm{o}}}& \frac{\left(1+h{b}_{\mathrm{o}}\right)\left(h{c}_{\mathrm{m}}{\beta }_{\mathrm{f}}\right)}{{\left[1+h{b}_{\mathrm{o}}\right]}^2}& 0\\ \frac{\left(1+h\left(b_{\mathrm{o}}+{\sigma }_{\mathrm{f}}\right)\right)\left(h{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}\right)}{{\left[1+h\left(b_{\mathrm{o}}+{\sigma }_{\mathrm{f}}\right)\right]}^2}& \frac{1+h{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}}{1+h\left(b_{\mathrm{o}}+{\sigma }_{\mathrm{f}}\right)}& 0\\ 0& \frac{h{\sigma }_{\mathrm{f}}}{1+hb+h\alpha }& \frac{1+h{\sigma }_3\mathrm{\Delta }{B}_{\mathrm{n}}}{1+hb+h\alpha }\end{array}\right]\\ \Rightarrow J\left(0,0,0\right)& =\frac{1+h{\sigma }_3\mathrm{\Delta }{B}_{\mathrm{n}}}{1+hb+h\alpha }\left[\begin{array}{cc}\frac{1+h{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}}{1+h{b}_{\mathrm{o}}}& \frac{\left(h{c}_{\mathrm{m}}{\beta }_{\mathrm{f}}\right)}{\left(1+h{b}_{\mathrm{o}}\right)}\\ \frac{\left(h{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}\right)}{1+h\left(b_{\mathrm{o}}+{\sigma }_{\mathrm{f}}\right)}& \frac{1+h{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}}{1+h\left(b_{\mathrm{o}}+{\sigma }_{\mathrm{f}}\right)}\end{array}\right].\end{array}$$ (26)

The eigen value of the Jacobian matrix as follows:

$$\lambda =\frac{1+h{\sigma }_3\mathrm{\Delta }{B}_{\mathrm{n}}}{1+h\left(b+\alpha \right)}<1$$

because the stochasticity's such as ${\sigma }_1,{\sigma }_2,\text{and}{\sigma }_3$ is small noise disturbance with Brownian motions $B_k\left(t\right),\left(k=1,2,3\right)$ in each compartment of the HIV/AIDS model. So, each stochastic term ${\sigma }_j.\left(j=1,2,3\right)<b\text{and}\alpha ,$ where parameter b is the natural birth rate of humans and $\alpha$ is the death rate of humans [25].

A  = trace of the Jacobian matrix.

B  = Determinant of a Jacobian matrix.

$$\begin{array}{rl}A& =\frac{2+h{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+h{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}+h^2{b}_{\mathrm{o}}{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+h^2{\sigma }_1{\sigma }_{\mathrm{f}}\mathrm{\Delta }{B}_{\mathrm{n}}+h^2{b}_{\mathrm{o}}{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}+2h{b}_{\mathrm{o}}+h{\sigma }_{\mathrm{f}}}{\left(1+h{b}_{\mathrm{o}}\right)\left(1+h\left(b_{\mathrm{o}}+{\sigma }_{\mathrm{f}}\right)\right)}\\ B& =\frac{1+h{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+h{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}+h^2{\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}}-h^2{c}_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}}{\left(1+h{b}_{\mathrm{o}}\right)\left(1+h\left(b_{\mathrm{o}}+{\sigma }_{\mathrm{f}}\right)\right)}.\end{array}$$ (27)

For the quadratic equation ${\lambda }^2-A\lambda +B=0$, $\left|{\lambda }_i\right|<1,i=1,2$; if and only if succeeding conditions are satisfied [28]:

$$\begin{array}{rl}& \left(\mathrm{i}\right)1+A+B>0\\ & \left(\text{ii}\right)1-A+B>0\\ & \left(\text{iii}\right)B<1.\end{array}$$

For proof see the Appendix.

4.7 Comparison section

In this section, we shall draw a comparison of existing stochastic explicit methods and proposed a stochastic non‐standard finite difference method as follows:

4.8 Covariance of sub‐populations

In this section, we shall discuss the covariance of different sub‐populations for the HIV/AIDS epidemic model in a two‐sex population. To examine the covariance among various sub‐populations, we calculated the correlation coefficients and results are reported in Table 2.

Table 2.

Correlation coefficient

Sub‐populations	Correlation coefficient (ρ)	Relationship
(h m2, h f2)	0.8872	direct
(h f2, h f2)	−0.7241	inverse
(h m2, h f2)	−0.3319	inverse

The results in Table 2 show a direct relationship between HIV/AIDS infected males and infected females. This means that HIV/AIDS infected males will increase with the increase in HIV/AIDS infected females. The inverse relationship between females receiving ART and remaining two sub‐populations. This means that the females receiving ART will increase with the decrease in remaining sub‐populations and eventually the system will attain disease‐free equilibrium.

4.9 Results and discussions

Figs. 2 and 3 depict that the stochastic Euler scheme converges the factual steady states equilibrium whereas the mean of the stochastic Euler solution is the deterministic outcome for descretisation h  = 0.001 at different sub‐sections of the model. In Figs. 4 and 5, if we enlarge time step size, the stochastic Euler scheme is unable to maintain positivity for steady states at different subsections of the model as well. Ultimately for obtaining the solutions of stochastic HIV/AIDS model the stochastic Euler scheme is not a reliable method.

Fig. 2.

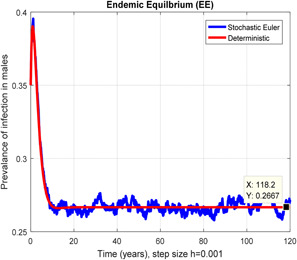
In the prevalence of infection in males stochastic Euler converges for h = 0.001

Fig. 3.

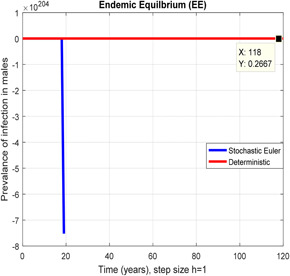
In the prevalence of infection in males, stochastic Euler shows negativity for h = 1

Fig. 4.

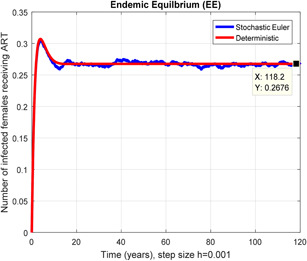
In a number of females receiving ART stochastic Euler converges for h = 0.001

Fig. 5.

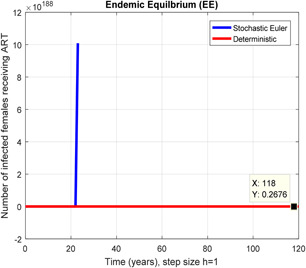
In a number of females receiving ART stochastic Euler shows unboundedness for h = 1

Figs. 6 and 7 represent that the stochastic Runge–Kutta scheme converges the endemic equilibrium whereas the mean of the stochastic Runge–Kutta solution is the deterministic outcome for descretisation h  = 0.01 at different subsections of the model, respectively. In Figs. 8 and 9, if we enlarge the time step size, the stochastic Runge–Kutta scheme is unable to maintain boundeness for steady states at different subsections of the model. Finally, the above‐mentioned method fails for any time step size. Hence aforasaid stochastic schemes do not support all dynamical properties. [15, 16].

Fig. 6.

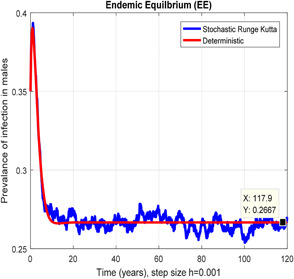
In the prevalence of infection in males stochastic Runge Kutta converges for h = 0.001

Fig. 7.

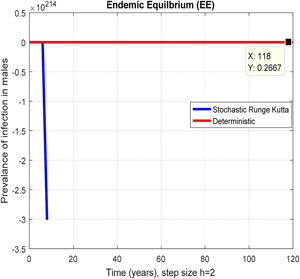
In the prevalence of infection in males, stochastic Runge Kutta shows negativity for h = 2

Fig. 8.

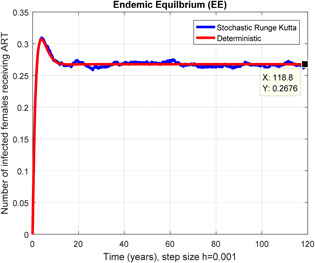
In a number of females receiving ART stochastic Runge Kutta shows converges for h = 0.001

Fig. 9.

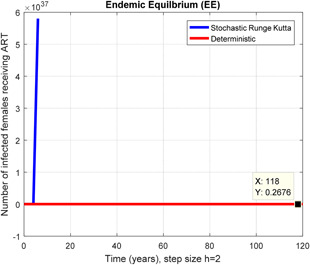
In a number of females receiving ART stochastic Runge Kutta shows unboundedness for h = 2

In Figs. 10, 11, 12–13, we have concluded that the stochastic NSFD method converges the endemic equilbrium whereas the mean of stochastic NSFD solution is the deterministic outcome for any descretisation like h  = 0.1 and 100 at different subsections of the model, respectively. Hence the stochastic NSFD method supports all dynamical properties characterised by Mickens in a stochastic context. The proposed framework stochastic NSFD method has successfully worked for any time step size.

Fig. 10.

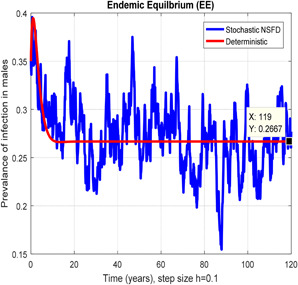
In the prevalence of infection in males stochastic NSFD converges for h = 0.01

Fig. 11.

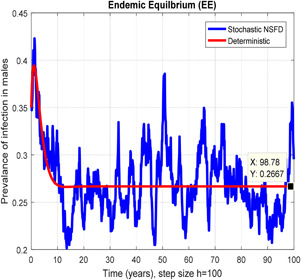
In the prevalence of infection in males, stochastic NSFD converges for h = 100

Fig. 12.

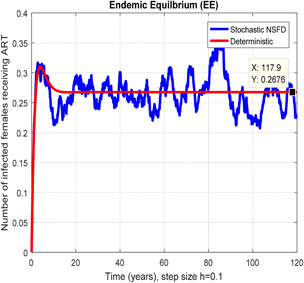
In a number of females receiving ART stochastic NSFD converges for h = 0.1

Fig. 13.

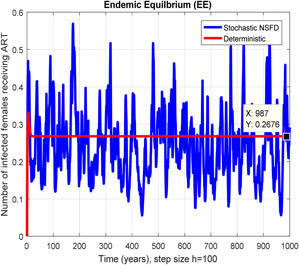
In a number of females receiving ART stochastic NSFD converges for h = 100

In Figs. 14, 15, 16–17, we have drawn the comparison of stochastic explicit methods with stochastic NSFD. Also, the averages of stochastic simulations have the solution of ODEs (deterministic) system.

Fig. 14.

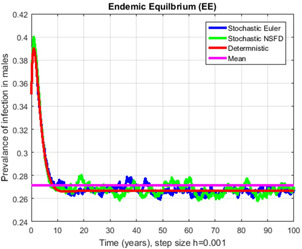
Contrast of stochastic Euler, stochastic NSFD, deterministic and mean for h = 0.001

Fig. 15.

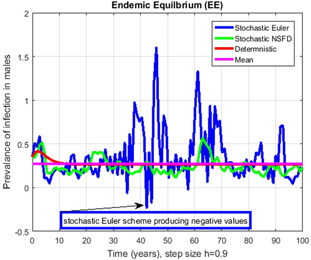
Contrast of stochastic Euler, stochastic NSFD, deterministic and mean for h = 0.9, but stochastic Euler shows negative values

Fig. 16.

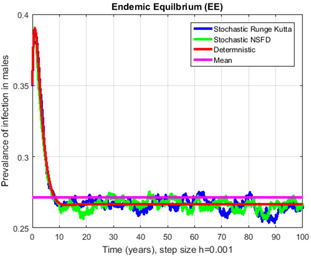
Contrast of stochastic Runge–Kutta, stochastic NSFD, deterministic and mean for h = 0.001

Fig. 17.

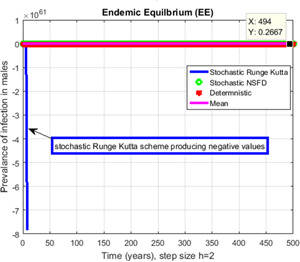
Contrast of stochastic Runge–Kutta, stochastic NSFD, deterministic and mean for h = 2 but stochastic Runge Kutta shows negative values

5 Conclusion and future frame work

For comprehending HIV/AIDS epidemic model dynamics, the stochastic epidemic model is a more beneficial approach in contrast to the deterministic epidemic model in terms of numerical analysis. The above‐mentioned stochastic numerical method converges to true equilibrium points, but for very little time step size. These aforesaid stochastic numerical methods diverge and lose dynamical properties. However, as we increase the time, these schemes diverge and fail to obey the above‐mentioned dynamical properties. The suggested structure of SNSFD of the HIV/AIDS epidemic model performs for any time step size defined by Mickens [15, 16] in the stochastic framework. This frame work (SNSFD) is appropriate for all non‐linear and complex stochastic epidemic models. The deterministic ODE outcomes and stochastic outcomes are quite close to each other. The stochastic epidemic models study shows an important role in disease dynamics. We have observed that stochastic epidemic models are more practical rather than deterministic epidemic models. For future work, the proposed SNSFD can be executed to the complicated stochastic diffusion and stochastic delay epidemic models. Moreover, in the extension of the stochastic fractional order dynamical system [7, 29–32], the proposed numerical analysis of this work might also be used. Our future plan is to construct an authentic numerical scheme for the fractional order stochastic epidemic model for different diseases model.

$$\begin{array}{rl}& 1-A+B>0\\ & \Rightarrow \left(1+h{b}_{\mathrm{o}}\right)\left(1+h\left(b_{\mathrm{o}}+{\sigma }_{\mathrm{f}}\right)\right)-2-h{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}\\ & -h{\sigma }_2\mathrm{\Delta }{B}_n-h^2{b}_{\mathrm{o}}{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}-h^2{\sigma }_1{\sigma }_{\mathrm{f}}\mathrm{\Delta }{B}_{\mathrm{n}}-h^2{b}_{\mathrm{o}}{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\\ & -2h{b}_{\mathrm{o}}-h{\sigma }_{\mathrm{f}}+1+h{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+h{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\\ & +h^2{\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}}-h^2{c}_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}>0\\ & \Rightarrow h^2\left[b_{\mathrm{o}}^2-b_{\mathrm{o}}({\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}-{\sigma }_{\mathrm{f}})\right.\\ & \left.-{\sigma }_1{\sigma }_{\mathrm{f}}\mathrm{\Delta }{B}_{\mathrm{n}}+{\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}}-c_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}]>0\right]\\ & \Rightarrow h^2>0\end{array}$$

$\Rightarrow h>0$, where h is any time step size

$$\left(1+A+B\right)>0$$

Since $1>0$ and $A>0$ so it is enough to show $B>0$

$$\begin{array}{rl}\Rightarrow & \frac{1+h{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+h{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}+h^2{\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}}-h^2{c}_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}}{\left(1+h{b}_{\mathrm{o}}\right)\left(1+h\left(b_{\mathrm{o}}+{\sigma }_{\mathrm{f}}\right)\right)}>0\\ \Rightarrow & 1+h{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+h{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}+h^2{\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}}\\ & -h^2{c}_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}>0\\ \Rightarrow & h^2\left[c_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}-{\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}}\right]<1\\ & +h[{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}]\\ \Rightarrow & h^2\left[c_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_m{\beta }_{\mathrm{f}}-{\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}}\right]\\ & -1-h[{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}]<0\\ \Rightarrow & h^2-\frac{h[{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}]}{c_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}-{\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}}}\\ & -\frac{1}{c_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}-{\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}}}<0\\ \Rightarrow & h^2-2h\left(\frac{[{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}]}{2(c_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}-{\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}})}\right)\\ & +{\left(\frac{[{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}]}{2(c_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}-{\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}})}\right)}^2\\ & >{\left(\frac{[{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}]}{2(c_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}-{\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}})}\right)}^2\\ & +\frac{1}{c_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}-{\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}}}\\ \Rightarrow & {\left(\frac{[{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}]}{2(c_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}-{\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}})}-h\right)}^2\\ & >{\left(\frac{[{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}]}{2(c_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}-{\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}})}\right)}^2+\frac{1}{c_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}-{\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}}}\end{array}$$

Satisfied

$$B<1$$

$$\begin{array}{rl}\Rightarrow & \frac{1+h{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+h{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}+h^2{\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}}-h^2{c}_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_f}{\left(1+h{b}_{\mathrm{o}}\right)\left(1+h\left(b_{\mathrm{o}}+{\sigma }_{\mathrm{f}}\right)\right)}<1\\ \Rightarrow & 1+h{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+h{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}+h^2{\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}}\\ & -h^2{c}_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}<\left(1+h{b}_{\mathrm{o}}\right)\left(1+h\left(b_{\mathrm{o}}+{\sigma }_{\mathrm{f}}\right)\right)\\ \Rightarrow & h^2\left({\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}}+c_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}-b_{\mathrm{o}}^2-{\sigma }_{\mathrm{f}}{b}_{\mathrm{o}}\right)\\ & +h\left[{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}-2b_{\mathrm{o}}-{\sigma }_{\mathrm{f}}\right]>0\\ \Rightarrow & h^2+h\left(\frac{{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}-2b_{\mathrm{o}}-{\sigma }_{\mathrm{f}}}{{\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}}+c_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}-b_{\mathrm{o}}^2-{\sigma }_{\mathrm{f}}{b}_{\mathrm{o}}}\right)>0\\ \Rightarrow & h^2+2h\left[\frac{{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}-2b_{\mathrm{o}}-{\sigma }_{\mathrm{f}}}{2({\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}}+c_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}-b_{\mathrm{o}}^2-{\sigma }_{\mathrm{f}}{b}_{\mathrm{o}})}\right]\\ & +{\left[\frac{{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}-2b_{\mathrm{o}}-{\sigma }_{\mathrm{f}}}{2({\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}}+c_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}-b_{\mathrm{o}}^2-{\sigma }_{\mathrm{f}}{b}_{\mathrm{o}})}\right]}^2\\ & >{\left[\frac{{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}-2b_{\mathrm{o}}-{\sigma }_{\mathrm{f}}}{2({\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}}+c_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}-b_{\mathrm{o}}^2-{\sigma }_{\mathrm{f}}{b}_{\mathrm{o}})}\right]}^2\\ \Rightarrow & {\left[h+\frac{{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}-2b_{\mathrm{o}}-{\sigma }_{\mathrm{f}}}{2({\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}}+c_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}-b_{\mathrm{o}}^2-{\sigma }_{\mathrm{f}}{b}_{\mathrm{o}})}\right]}^2\\ & >{\left[\frac{{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}-2b_{\mathrm{o}}-{\sigma }_{\mathrm{f}}}{2({\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}}+c_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}-b_{\mathrm{o}}^2-{\sigma }_{\mathrm{f}}{b}_{\mathrm{o}})}\right]}^2\\ \Rightarrow & h+\frac{{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}-2b_{\mathrm{o}}-{\sigma }_{\mathrm{f}}}{2({\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}}+c_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}-b_{\mathrm{o}}^2-{\sigma }_{\mathrm{f}}{b}_{\mathrm{o}})}\\ & >\frac{{\sigma }_1\mathrm{\Delta }{B}_{\mathrm{n}}+{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}-2b_{\mathrm{o}}-{\sigma }_{\mathrm{f}}}{2({\sigma }_1{\sigma }_2\mathrm{\Delta }{B}_{\mathrm{n}}\mathrm{\Delta }{B}_{\mathrm{n}}+c_{\mathrm{m}}{c}_{\mathrm{f}}{\beta }_{\mathrm{m}}{\beta }_{\mathrm{f}}-b_{\mathrm{o}}^2-{\sigma }_{\mathrm{f}}{b}_{\mathrm{o}})}\end{array}$$

$\Rightarrow h>0$, where h is any time step size.