Abstract
Green houses play a vital role in modern agriculture. Artificial light illumination is very important in a green house. While light is necessary for plant growth, excessive light in a green house may not bring more profit and even damages plants. Developing a plant‐physiology‐based light control strategy in a green house is important, which implies that a state‐space model on photosynthetic activities is very useful because modern control theories and techniques are usually developed according to model structures in the state space. In this work, a simplified model structure on photosystem II activities was developed with seven state variables and chlorophyll fluorescence (ChlF) as the observable variable. Experiments on ChlF were performed. The Levenberg–Marquardt algorithm was used to estimate model parameters from experimental data. The model structure can fit experimental data with a small relative error (<2%). ChlF under different light intensities were simulated to show the effect of light intensity on ChlF emission. A simplified model structure with fewer state variables and model parameters will be more robust to perturbations and model parameter estimation. The model structure is thus expected useful in future green‐house light control strategy development.
Inspec keywords: parameter estimation, fluorescence, lighting control, photosynthesis, agriculture, state‐space methods, greenhouses
Other keywords: Levenberg–Marquardt algorithm, ChlF emission, state variables, green‐house light control strategy development, model parameter estimation, light intensity, model parameters, photosystem II activities, simplified model structure, state‐space model, plant‐physiology‐based light control strategy, plant growth, artificial light illumination, light‐adapted state, dark‐adapted state, photosystem II chlorophyll fluorescence transition
1 Introduction
In photosynthetic organisms (higher plants, algae, and cyanobacteria), large numbers of chlorophyll molecules are bounded to increase the area of light absorption by light‐harvesting complexes, which provide an antenna for reaction centres (RC) [1]. Photosystem II (PSII) works efficiently to absorb photons and then the absorbed energy is transferred to RCs to reduce water to form hydrogen ions and molecular oxygen [2]. Light is the driving force of photosynthesis. Green houses play a vital role in modern agriculture. Artificial light illumination is very important in green house light control. There are three pathways for the light absorbed by plant leaves: photochemical reaction, heat loss, and fluorescence emission [3]. While light is necessary for plant growth, excessive light in a green house may not bring more profit and even damages plants. Due to the photo protection mechanism, the surplus energy which is not involved in photochemistry will be reemitted as fluorescence or dissipated as heat [4]. Unavoidable risks may be taken by photosynthetic apparatus if too much light is absorbed [5, 6].
Traditionally, the light control strategy in a green house is usually based on experience without considering the real‐time photosynthetic need of plants. This makes the light control strategy not optimal. Modern control theories and techniques are usually based on state space model structures [7]. A state space photosynthetic model structure is thus very useful in developing into control strategy by using modern control theory directly. There are two photosystems in plants, photosystem I (PSI) and PSII. PSII is very vulnerable to environmental stress and thus only PSII activities are considered in this work. In literature, PSII activities were modelled with different levels of complexity, but there is a lack of state space PSII model structure that can cover PSII activities under both the dark‐adapted and light‐adapted conditions with moderate complexity. The non‐photochemical quenching (NPQ) process has been simulated by varieties of models. However, few models have been fit to experiment data [8]. Furthermore, most models involve complex structures. For instance, 19 differential equations make up the model in Chernev et al. [8]. Lazár [9] made an essential contribution to simplifying model structures, which still consist of over ten state variables. To enhance green house light strategy development, a simplified PSII model structure with an observable variable that can be easily measured is desirable because the observable variable can serve as the feedback and make the control as a feedback control.
Chlorophyll a fluorescence induction (ChlF) from PSII can be easily measured and is very popular in photosynthesis research [9]. ChlF couples with photosynthetic activities and can be used to sense plant physiological status and environmental changes. For a dark‐adapted leaf, the ChlF induction has a quickly increasing phase named as OJIP and a slowly declining phase named as PS(M)T. The meaning of the abbreviation is as follows: O is for origin minimum fluorescence level, J and I are for immediate levels, P is for peak, S is for a semi‐steady state, M is for a maximum, and T is for the terminal steady‐state level [10]. ChlF has the potential to serve as an observable variable in a PSII model structure. Previous research is mostly focused on the OJIP phase and great contributions have been made to the mechanism of OJIP phase, while the dynamics of PSM phase has not been well studied [11, 12]. In this work, a simplified PSII photosynthesis model structure was built in order to simulate the whole process and study PSII behaviour under strong light.
In the fluorescence induction, the photoreaction stage includes three basic processes [13]. (i) The Kok cycle describes the oxygen evolving complex in the S states. Guo and Tan [24] neglected the Kok cycle but could simulate the OJIP curve successfully. In the proposed model structure, the decomposition of water in the Kok cycle was considered with simplification of the detailed S state transitions. (ii) Electron transfer cycle in two electron acceptors, Q A and Q B, was included because the yield of fluorescence is closely related to the speed of the electron transfer. (iii) The reversible radical pair, which involves the absorption of light, the initial electron transfer from excited photons, was considered. In this work, the focus is to simulate the system dynamics in the time range of 2 s. This period of time allows the electron transition in PSII systems and accumulation of hydrogen ions in the lumen. Subsequent steps such as the consumption of hydrogen ion, the generation of adenosine triphosphate (ATP) and so on occur on the timescale of seconds to minutes, so these steps were neglected in this work. Readers may refer to Zhu et al. [18] to find the reaction of these three basic processes in details.
2 Model development
For a dark‐adapted leaf, the leaf will reach light adapted status with continuous light illumination. In the process, NPQ will happen. NPQ has a close relationship with PSII activities. The NPQ, as a photoprotection mechanism, can be divided into three parts: energy dependent (qE), state transition (qT), photo‐inhibitory quenching (qI) [14–16]. The qI, slowing‐forming NPQ because of photo‐damage [10], was neglected in the proposed model structure. PSI contributes little to the variable fluorescence quantum yield compared to PSII system, so only PSII was considered. qT, only around 5% of the total quenching, is mainly related to adjustment of the relative absorption cross sections of PSI and PSII [10] and thus was also neglected. Quenching dynamics process occurs on the timescale of seconds to minutes. Oxygen evolution and charge separation processes occur on the order of milliseconds and even faster. Consequently, it will not lose significant accuracy if the fast processes were omitted and simplified.
In photosynthesis, antenna (A, original state of antenna) obtains energy from the light and becomes A* (excited state of antenna). The step of absorbing light can thus be represented as
| (1) |
where k 1 is a reaction constant related to light absorption and u stands for light intensity.
There are two pathways in NPQ when A* becomes A. One is the process of emitting chlorophyll fluorescence (ChlF); the other is the process of emitting heat. The qE quenching is related to the xanthophyll cycle. The zeaxanthin (denoted as N) is considered a direct quencher in the cycle, which is formed from the de‐epoxidation of violaxanthin under the H+ gradient [14]. Therefore, the H+ concentration indirectly determines the NPQ efficiency, and when H+ concentration in the lumen is higher, the NPQ efficiency is higher. The process can be described as follows:
| (2) |
where N is concentration or probability of zeaxanthin, the active state of quencher. k 2 is a reaction constant relating to ChlF dissipation, and k 3 is reaction constant. The product of k 3 and (1 + N) represents energy dissipation through heat.
The absorbed light energy on A* may also quickly pass to P680 and elevated P680 to its excited state (P680*) [17]. The electron in the stated state on P680* may quickly transfer to plastoquinone A (QA) via pheophytin. Electron transport rate to plastoquinones is much slower than that between P680* and pheophytin [18]. As a result, pheophytin is omitted in reaction kinetics for simplification [19]. It is deserved to mention that reaction rate will become effective state because of the simplification. PSII work efficiently to absorb photons and then energy is transferred to reaction centre to reduce water to form hydrogen ions and oxygen molecules [2]. All the process can thus be represented by (3) if they are lumped together
| (3) |
| (4) |
k 4 and k 5 are the forward or backward reaction constants, and Q A − is the reduced state of Q A, and H+ stands for hydrogen ions in the lumen. The H+ in the stroma was to be constant, and it had no effect on NPQ [14]. So it was not considered in this work.
Oxidised and reduced states of the molecule are marked by the + and – superscript, respectively. One electron on Q A − is likely to be transferred to plastoquinone B (Q B), which can take two negative charges [3, 19, 20, 21]. Then the next step of electron transport can be represented as
| (5) |
or
| (6) |
where k 6 through k 9 are reaction constants, and Q B − and Q B 2− are, respectively, the single‐ and double‐reduced forms of Q B.
After receiving two electrons, two protons from the stroma will combine with Q B 2− to form plastoquinol (Q H2). Then Q H2 will diffuse to the thylakoid lumen and be oxidised to become Q B again [3, 19, 20, 21], which make a contribution to the irreversible oxidation of Q B 2−. To describe the plastoquinone activities, these reactions may be together represented as
| (7) |
or
| (8) |
In the xanthophyll cycle that is associated with NPQ process, violaxanthin is deeply oxidised to zeaxanthin in two steps. The reverse epoxidation is catalysed by a stromal epoxidase. Epoxy groups are removed from xanthophylls (e.g. violaxanthin, antheraxanthin, diadinoxanthin) to create de‐epoxidised xanthophylls (e.g. diatoxanthin, zeaxanthin) in the xanthophyll cycle, which play a vital role in stimulating energy dissipation within light‐harvesting antenna proteins. In higher plants, violaxanthin, antheraxanthin, and zeaxanthin are active in the xanthophyll cycle. Under light stress conditions, violaxanthin becomes zeaxanthin through the intermediate antheraxanthin, which serves as a lipid‐protective anti‐oxidant. The luminal pH extremely affects the deep oxidation reaction [22]. Photosynthetic electron flow is directly regulated by lumen acidification through lowering the plastoquinol oxidation rate [23]. We consider the total amount of quencher as constant and it is normalised to unity, N + N 0 = 1
| (9) |
where N 0 is the concentration or probability of violaxanthin.
There is one Q A site and one Q B site in an active PSII reaction centre. The concentration or probability of presence for the total Q A (including Q A and Q A −) or total Q B (including Q B, Q B −, and Q B 2−) or total quencher (N and N 0) can be set to unity. The reactions represented by expressions (1)–(9) can then be described by the following nine differential equations:
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
A0 stands for the conserved quantities of A and A* and PQ0 is the conserved quantities of PQ and PQH2. The denotations of the state variables are shown in Table 1
Table 1.
State variables
| Parameter | Value |
|---|---|
| A* | y 1 |
| Q A − | y 2 |
| Q B − | y 3 |
| Q B 2– | y 4 |
| PQ | y 5 |
| N | y 6 |
| H+ | y 7 |
3 Experiments and setup
Two types of tree leaves (Camellia japonica and Pittosporum tobira) used in the experiments were collected from the campus of Jiangnan University (Wuxi, China). The leaves were picked in the morning between 6 a.m. and 7 a.m. in July, when the environment temperature was around 28°C. The picked leaves were transported to the laboratory for experiments rapidly. The laboratory temperature was controlled at 25°C.
Twenty‐six leaves were measured for each variety of plant in the experiments. Evaporation and moisture conditions can have an impact on ChlF emission. To reduce the effect of water loss, all the sample leaves were floated in water for at least 2 h. The leaves were dark‐adapted for at least 15 min in dark‐adaption clips before ChlF measurement. ChlF was measured with a FluorPen PSI (Photon Systems Instruments, Czech Republic) by selecting its OJIP protocol. The illumination light intensity was set as 3000 µmol photons m−2 s−1.
4 Results and discussion
4.1 Model fitting
To verify the flexibility of the developed model structure representing ChlF kinetics, the model structure was fit the experimental data. The Levenberg–Marquardt algorithm was used to estimate the model parameters in (10)–(17). Matlab (Version 8.5, The Mathworks, Natick, MA, USA) was used to carry out the optimisation algorithm and numerical calculations. The experiment data and fitting curves were shown in Figs. 1 a and b. The plots with both linear time coordinate and logarithmic time coordinate were provided. The model predictions can match experimental data very well with average relative error <2% for the total 52 leaf sample.
Fig. 1.
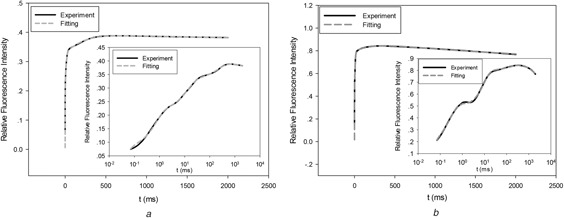
Experimental data fitting
(a) Experiment and fitting for a leaf from C. Japonica, (b) Experiment and fitting for a leaf from P. tobira
4.2 Species concentration dynamics
The concentration dynamics of reactants are illustrated in Fig. 2. As the previous literatures explained [18, 24], the J phase in OJIP curve means the moment when Q B quickly convert to Q B −. Consequently, the Q B − curve (in Fig. 2 a) rise sharply in J phase. I phase means the moment that the maximum of Q B −, the first plateau of Q B 2−, and the moment that PQ begin moving to the Q B site. From Fig. 2, it can be seen that the simulation agrees with literature very well. The relative concentration of PQ on Fig. 2 begins to decrease at the point of I phase. The P phase often implies the maximum value of fluorescence. As is shown in Fig. 2, the hydrogen ions begin to accumulate rapidly after the P phase, accompanied with the increase of zeaxanthin. Then the NPQ starts to play a role in the photosynthesis with the decrease fluorescence.
Fig. 2.
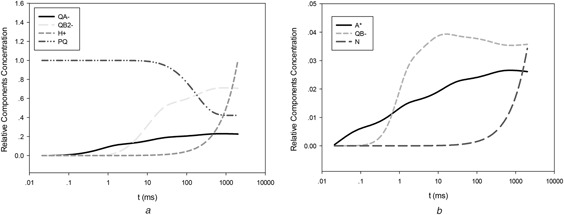
Components concentration dynamics
(a) Concentration dynamics of QA −, QB 2–, PQ and H+, (b) Concentration dynamics of A*, QB − and N
4.3 Simulations of ChlF under different light intensities
Fig. 3 shows the simulation results of the relative fluorescence values under different light intensities. It can be seen that under strong light, the fluorescence value is higher due to the faster electronic transmission in PSII, and the NPQ trend is more obvious because of the self‐protection mechanism of photosystems under strong light.
Fig. 3.
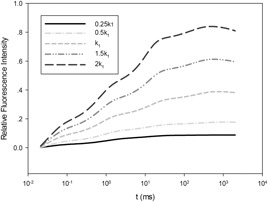
Simulation of chlorophyll fluorescence under different light intensities
In previous work, the models about ChlF induction are complicated and have too many parameters involving NPQ [10, 19]. In this work, a simplified mathematical model was built, aiming at providing a model structure for OJIP curve and the main NPQ mechanism. Experiments have proved that the simplified model structure not only fits the OJIP curve very well, but also reflects the non‐photochemical mechanism well. Through simulation in different light intensities, the fluorescence induction curves can be predicted.
5 Conclusion
In this work, a simplified model structure in the state space was built to describe PSII major reaction activities. The model structure considers the NPQ effect and can fit experiment data from the dark‐adapted state to the initial stage of light‐adapted state with a small relative fitting error (<2%). Species concentration dynamics and light intensity on ChlF emission can be obtained by simulations through the model structure. The estimated model parameter values correctly reflected the expected changes induced by continuous light. Modern control theories and techniques are often built based on models in the state space. A simplified model structure with fewer state variables and model parameters will be more robust to perturbations and model parameter estimation. The developed simplified model structure can thus be further developed into useful artificial light controlling strategy for green house applications in future. In future research, optimal plant growth controlling strategy will be built based on the developed model structure to achieve maximal profit.
6 Acknowledgments
This project was partially supported by National Natural Science Foundation of China (grant no. 31771680), Fundamental Research Funds for the Central Universities of China (grant no. JUSRP51730A), the Modern Agriculture Funds of Jiangsu Province (grant no. BE2015310), the New Agricultural Engineering of Jiangsu Province (grant no. SXGC[2016]106 and grant no. SXGC[2017]210), the 111 Project (grant no. B1208), and the Research Funds for New Faculty of Jiangnan University.
7 References
- 1. Horton P.: ‘Optimization of light harvesting and photoprotection: molecular mechanisms and physiological consequences’, Phil. Trans. R. Soc. B, 2012, 367, (1608), pp. 3455–3465 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Zaks J. Amarnath K., and Kramer D.M. et al.: ‘A kinetic model of rapidly reversible nonphotochemical quenching’, Proc. Natl. Acad. Sci. USA, 2012, 109, (39), pp. 15757–15762 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Taiz L., and Zeiger E.: ‘Plant physiology’ (Sinauer Associates Press, Sunderland, MA, 1998, 2nd edn.), pp. 428–429 [Google Scholar]
- 4. Latimer P. Bannister T.T., and Rabinowitch E.: ‘Quantum yields of fluorescence of plant pigments’, Science, 1956, 124, (3222), pp. 585–586 [DOI] [PubMed] [Google Scholar]
- 5. Osmond B. Badger M., and Maxwell K. et al.: ‘Too many photons: photorespiration, photoinhibition and photooxidation’, Trends Plant Sci., 1997, 2, (4), pp. 119–121 [Google Scholar]
- 6. Demming‐Adams B., and Adams W.W.: ‘Photoprotection in an ecological context: the remarkable complexity of thermal energy dissipation’, New Phytol., 2006, 172, (1), pp. 11–21 [DOI] [PubMed] [Google Scholar]
- 7. Csaki F. Bars R., and Higgins T.J.: ‘Modern control theories: nonlinear, optimal and adaptive systems’, IEEE Trans. Syst. Man Cybern., 1973, SMC‐3, (5), pp. 530–531 [Google Scholar]
- 8. Chernev P. Goltsev V., and Zaharieva I. et al.: ‘A highly restricted model approach quantifying structural and functional parameters of photosystem II probed by the chlorophyll a fluorescence rise’, Ecol. Eng. Environ. Protect., 2006, 5, (2), pp. 19–29 [Google Scholar]
- 9. Lazár D.: ‘Modelling of light‐induced chlorophyll a fluorescence rise (O‐JI‐P transient) and changes in 820 nm‐transmittance signal of photosynthesis’, Photosynthetica, 2009, 47, (4), pp. 483–498 [Google Scholar]
- 10. Stirbet A., and Govindjee.: ‘The slow phase of chlorophyll a fluorescence induction in silico: origin of the S–M fluorescence rise’, Photosynth. Res., 2016, 130, (1–3), pp. 193–213 [DOI] [PubMed] [Google Scholar]
- 11. Ebenhoh O. Fucile G., and Finazzi G. et al.: ‘Short‐term acclimation of the photosynthetic electron transfer chain to changing light: a mathematical model’, Phil. Trans. R. Soc. B, 2014, 369, (1604), p. 20130223 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Matuszynska A. Heidari S., and Jahns P. et al.: ‘A mathematical model of non‐photochemical quenching to study short‐term light memory in plants’, Biochim. Biophys. Acta, 2016, 1857, (12), pp. 1860–1869 [DOI] [PubMed] [Google Scholar]
- 13. Xin C., and Zhu X.: ‘A model of chlorophyll a fluorescence induction kinetics with explicit description of structural constraints of individual photosystem II units’, Photosynth. Res., 2013, 117, (1–3), pp. 339–354 [DOI] [PubMed] [Google Scholar]
- 14. Oliver E., and Torsten H.: ‘A minimal mathematical model of nonphotochemical quenching of chlorophyll fluorescence’, BioSystems, 2011, 103, (2), pp. 196–204 [DOI] [PubMed] [Google Scholar]
- 15. Horton P., and Johnson M.P.: ‘Photosynthetic acclimation: does the dynamic structure and macro‐organisation of photosystem ll in higher plant grana membranes regulate light harvesting states’, FEBS J., 2008, 275, (6), pp. 1069–1079 [DOI] [PubMed] [Google Scholar]
- 16. Quick W., and Stitt M.: ‘An examination of factors contributing to non‐photochemical quenching of chlorophyll fluorescence in barley leaves’, Biochim. Biophys. Acta, 1989, 977, (3), pp. 287–296 [Google Scholar]
- 17. Goltsev V. Zaharieva I., and Lambrev P. et al.: ‘Simultaneous analysis of prompt and delayed chlorophyll a fluorescence in leaves during the induction period of dark to light adaptation’, Theoretical Biol., 2003, 225, (2), pp. 171–183 [DOI] [PubMed] [Google Scholar]
- 18. Zhu X., Govindjee., Baker N.R. et al.: ‘Chlorophyll a fluorescence induction kinetics in leaves predicted from a model describing each discrete step of excitation energy and electron transfer associated with photosystem II’, Planta, 2005, 223, (1), pp. 114–133 [DOI] [PubMed] [Google Scholar]
- 19. Goltsev V., and Yordanov I.: ‘Mathematical model of prompt and delayed chlorophyll fluorescence induction kinetics’, Photosynthetica, 1997, 33, (4), pp. 571–586 [Google Scholar]
- 20. Blankenship R.E.: ‘Molecular mechanisms of photosynthesis’, Blackwell Sci., 2002, 256, (2), pp. 85–123 [Google Scholar]
- 21. Govindjee.: ‘A bit of basics and history’, in: Govindjee. (Ed.): ‘Chlorophyll a fluorescence’ (Springer Press, Netherlands, 2004, 1st edn.), pp. 1–42 [Google Scholar]
- 22. Gilmore A.M. Mohanty N., and Yamamoto H.Y.: ‘Epoxidation of zeaxanthinand antheraxanthin reverses non‐photochemical quenching of photosystem IIchlorophyll a fluorescence in the presence of trans‐thylakoid delta pH’, FEBS Lett., 1994, 350, (2–3), pp. 271–274 [DOI] [PubMed] [Google Scholar]
- 23. Hope A.B..: ‘The chloroplast cytochrome b6f complex A critical focus on function’, Biochim. Biophys. Acta, 1993, 1143, (1), pp. 1–22 [DOI] [PubMed] [Google Scholar]
- 24. Guo Y., and Tan J.: ‘Modeling and simulation of the initial phases of chlorophyll fluorescence from photosystem ll’, BioSystems, 2011, 103, (2), pp. 152–157 [DOI] [PubMed] [Google Scholar]


