Abstract
The identification of hot spots, a small subset of protein interfaces that accounts for the majority of binding free energy, is becoming increasingly important for the research on protein–protein interaction and drug design. For each interface residue or target residue to be predicted, the authors extract hybrid features which incorporate a wide range of information of the target residue and its spatial neighbor residues, that is, the nearest contact residue in the other face (mirror‐contact residue) and the nearest contact residue in the same face (intra‐contact residue). Here, feature selection is performed using random forests to avoid over‐fitting. Thereafter, the extreme learning machine is employed to effectively integrate these hybrid features for predicting hot spots in protein interfaces. By the 5‐fold cross validation in the training set, their method can achieve accuracy (ACC) of 82.1% and Matthew's correlation coefficient (MCC) of 0.459, and outperforms some alternative machine learning methods in the comparison study. Furthermore, their method achieves ACC of 76.8% and MCC of 0.401 in the independent test set, and is more effective than the major existing hot spot predictors. Their prediction method offers a powerful tool for uncovering candidate residues in the studies of alanine scanning mutagenesis for functional protein interaction sites.
Inspec keywords: biochemistry, bioinformatics, correlation methods, drugs, free energy, learning (artificial intelligence), molecular biophysics, proteins, feature selection
Other keywords: hot spot prediction, protein interfaces, extreme learning machines, spatial neighbour residue information, binding free energy, protein‐protein interaction, drug design, interface residue, spatial neighbor residues, nearest contact residue, random forests, alanine scanning energetics database, independent test set, binding interface database, 5‐fold cross validation, correlation coefflcient, alternative machine learning methods, alanine scanning mutagenesis, functional protein interaction sites, feature selection
1 Introduction
Protein–protein interactions play a critical role in almost all biological processes. The study of residues at protein–protein interfaces has shown that only a small portion of all interface residues is actually essential for recognition or binding [1]. These residues are termed as hot spots which contribute most binding free energy in protein interfaces. The identification of hot spots is a first step towards understanding the function of proteins and studying their interactions. Furthermore, several studies discovered small molecules bound to hot spots in protein interfaces that can disrupt protein–protein interactions [2]. Uncovering hot spots and revealing their mechanisms may provide promising prospect for medicinal chemistry and drug design [3, 4].
Alanine scanning mutagenesis is a popular technique to identify hot spots by evaluating the change in binding free energy when substituting interface residues with alanine. However, this traditional experimental approach is expensive and time‐consuming, and only a limited number of complexes are deposited in public databases of experimental results such as the Alanine Scanning Energetics Database (ASEdb [5]) and the Binding Interface Database (BID [6]).
Quest for the characteristics of hot spot has been carried out by several works. Studies on the composition of hot spots and non‐hot spots show that Trp, Arg and Tyr rank the top three, whereas Leu, Ser, Thr and Val are often disfavoured [7]. Structural analysis of the protein–protein surface shows that structurally conserved residues tend to be hot spots, and distinguish between binding sites and exposed surface residues [8]. The O‐ring theory reveals that the hot spot at a protein interface is surrounded by a ring of residues that are energetically less important for binding, whose role is to occlude water molecules from the hot spot (‘water exclusion’ hypothesis [9]). Furthermore, ‘double water exclusion’ hypothesis refines the O‐ring theory by assuming the hot spot itself is water‐free [10].
Based on the existing studies on the characteristics of hot spots, several methods have been developed for the prediction of hot spots. These methods can be roughly categorised into four groups: molecular dynamics (MD) simulations, energy‐based methods, knowledge‐based methods and the other methods of predicting hot spots.
MD simulations [11] simulate alanine substitutions and estimate the corresponding changes in binding free energy. These molecular simulation methods have good performance on identifying hot spots from protein interfaces, however, they suffer from enormous computational cost. Energy‐based methods make a hot spot prediction based on an estimate of the energetic contribution to binding for every interface residue. Robetta [1] used a free energy function to calculate the binding free energy of alanine mutation in a protein–protein complex. FOLDEF [12] provided a fast and quantitative estimation of the importance of the interactions contributing to the stability of proteins and protein complexes. Knowledge‐based methods try to learn the complex relationship between hot spots and various residue features in training data and predict new hot spots. Ofran and Rost [13] proposed neural networks based on sequence to predict hot spots. Darnell et al. [14] applied decision trees to predict hot spots with features such as atomic contacts, physicochemical properties, shape specificity and computational alanine scanning. Tuncbag et al. [15] presented an intuitive efficient method to determine computational hot spots based on conservation, solvent accessibility and statistical pairwise residue potentials of the interface residues. Cho et al. [16], Xia et al. [17], Zhu and Mitchell [18] and Xu et al. [19] proposed support vector machines (SVMs) to predict hot spots with features of both sequence and structure. Assi et al. [20] predicted hot spots by Bayesian networks with features incorporating structural, evolutionary and energetic information. Recently, we proposed random forests (RFs) to predict hot spots with focus on using structural neighbourhood properties [21].
In recent years, other methods of hot spot prediction have also been developed. Shulman‐Peleg et al. [22] performed spatial comparisons of physicochemical interactions common to different types of protein–protein complexes, and showed that major of these interactions correspond to known hot spots. del Sol and O'Meara [23] used small‐world network representation of protein complexes, and showed that the central residues correlate with experimental hot spots. Li and Liu [10] represented protein complexes as bipartite graphs. Maximal biclique subgraphs were subsequently identified from the bipartite graphs to locate biclique patterns which are rich of hot spots. Tuncbag et al. [24] analysed residue contact networks of protein interfaces as minimum cut trees where the highest degree nodes tend to be hot spots.
Although a variety of methods, especially machine learning‐based methods, have obtained relatively good performance on the prediction of hot spots. There are still some problems waiting to be solved in this area. For each interface residue (target residue), existing machine learning methods mainly extract features only from the target residue. However, hot spots were found to be clustered within locally and tightly packed regions [8]. How to effectively utilise the information of spatial neighbour residues should be considered. Moreover, although many features have been generated and used in the previous studies, effective feature selection methods and useful feature subsets have not been proposed yet. To deal with the problems mentioned above, in this work, we extract various features from the target residue and its two neighbouring residues, that is, the nearest contact residue in the other face (mirror‐contact residue) and the nearest contact residue in the same face (intra‐contact residue), and employ RFs to generate an effective feature subset. Then, we propose an extreme learning machine (ELM)‐based approach to effectively integrate these hybrid features for hot spot prediction. Finally, we evaluate the proposed method by 5‐fold cross validation and an independent test set, which demonstrate the performance advantage of our approach over several existing hot spot predictors, such as Robetta, FOLDEF, KFC [14], HotPoint [15], MINERVA [16] and KFC2 [18], and some alternative machine learning methods, such as SVM, naive Bayes (NB) and RF.
2 Materials and methods
2.1 Datasets
Interface residues (contact residues across the interface) are defined as in Wang et al. [21]. Briefly, two residues are considered to be in contact across the interface if there is at least a pair of contact atoms, one from each residue. Here we describe the atomic contacts between residues by using CSU program [25], which is based on inter‐atomic distances and the extent of crowding in the environment. Alanine mutated complexes were extracted from ASEdb and the published data by Kortemme and Baker [1]. To eliminate redundancy, we used the PISCES sequence culling server [26] with the sequence identity less than 35%. As a result, the training set consists of 318 alanine‐mutated interface residues derived from 20 protein complexes. The interface residues with binding free energy (ΔΔG) ≥ 2.0 kcal/mol are defined as hot spots [14, 15, 21]. Thus these interface residues were divided into 77 hot spots and 241 non‐hot spots. In addition, the dataset from BID was used as an independent test set. We ensured that these proteins in the test set are not homologous to those in the training set in the similar fashion to the training set. BID categorises the effect of mutations as strong, intermediate, weak or insignificant. The residues having strong interaction strengths are considered as hot spots in this study. This test set consists of 18 protein complexes containing 125 interface residues, of which 38 residues are hot spots and 87 residues are non‐hot spots. Details of training set and independent test set are listed in Tables 1 and 2, respectively.
Table 1.
Details of training set
| PDB | First molecule | Second molecule | H | NH |
|---|---|---|---|---|
| 1a22 | human growth hormone | human growth hormone binding protein | 7 | 46 |
| 1a4y | angiogenin | ribonuclease inhibitor | 3 | 21 |
| 1ahw | immunoglobulin Fab 5G9 | tissue factor | 1 | 7 |
| 1brs | barnase | barstar | 9 | 3 |
| 1bxi | colicin E9 immunity Im9 | colicin E9 DNase | 6 | 11 |
| 1cbw | BPTI trypsin inhibitor | chymotrypsin | 1 | 5 |
| 1dn2 | engineered peptide | Fc fragment of human immunoglobulin G | 2 | 0 |
| 1dvf | idiotopic antibody FV D1.3 | anti‐idiotopic antibody FV E5.2 | 7 | 7 |
| 1f47 | bacterial cell‐division protein zipA | FtsZ fragment | 3 | 5 |
| 1fc2 | Fc fragment | fragment B of protein A | 1 | 2 |
| 1fcc | Fc (IGG1) | protein G | 4 | 4 |
| 1jck | T‐cell receptor beta‐chain | superantigen | 5 | 13 |
| 1jrh | antibody A6 | interferon‐gamma receptor | 8 | 18 |
| 1vfb | mouse monoclonal antibody D1.3 | hen egg lysozyme | 3 | 22 |
| 2ptc | BPTI | trypsin | 1 | 0 |
| 3hfm | hen egg lysozyme | lg FAB fragment HyHEL‐10 | 11 | 12 |
| 1gc1 | envelope protein GP120 | CD4 | 0 | 17 |
| 1jtg | beta‐lactamase inhibitor protein‐II | TEM‐1 beta‐lactamase | 2 | 8 |
| 1nmb | NC10 antibody | influenza virus neuraminidase | 1 | 1 |
| 1dan | blood coagulation factor VIIA | tissue factor | 2 | 39 |
H – hot spot; NH – non‐hot spot
Table 2.
Details of independent test set
| PDB | First molecule | Second molecule | H | NH |
|---|---|---|---|---|
| 1cdl | calcium‐bound calmodulin | peptide of the kinase | 6 | 6 |
| 1dva | coagulation Factor VIIA | peptide exosite inhibitor E‐76 | 5 | 18 |
| 1dx5 | serine proteinase alpha‐thrombin | thrombomodulin | 3 | 13 |
| 1ebp | EPO receptor | EPO mimetics peptide 1 | 4 | 5 |
| 1es7 | bone morphogenetic protein‐2 | bone morphogenetic protein receptor IA | 1 | 3 |
| 1fak | soluble tissue factor | blood coagulation factor VIIa | 2 | 19 |
| 1fe8 | von willebrand factor | immunoglobulin IGG RU5 | 0 | 5 |
| 1foe | Rac1 | tiam1 protein | 1 | 1 |
| 1g3i | HslV protease | HslU ATPase | 5 | 0 |
| 1gl4 | nidogen‐1 | immunoglobulin‐like domain 3 of perlecan | 5 | 2 |
| 1ihb | p18INK4C | p18INK4C | 0 | 4 |
| 1jat | Mms2 | Ubc13 | 2 | 0 |
| 1jpp | beta‐catenin | adenomatous polyposis coli | 2 | 5 |
| 1mq8 | intercellular adhesion molecule‐1 | integrin alpha‐L | 1 | 0 |
| 2hhb | hemoglobin (alpha chain) | hemoglobin (beta chain) | 0 | 1 |
| 1nfi | NF‐KAPPA‐B | I‐KAPPA‐B‐ALPHA | 1 | 1 |
| 1nun | FGF10 | FGFR2b | 0 | 3 |
| 1ub4 | MazF protein | MazE protein | 0 | 1 |
H – hot spot; NH – non‐hot spot
2.2 Features of description
In our experiment, a wide variety of descriptors for interface residues were designed for the hot spots classification, and they were combined into five groups based on their sources and properties.
2.2.1 Atom contacts and atom contact areas
Two atoms α and β are defined to be in contact using CSU program [25]. Furthermore, we filtered out the non‐attractive contact such as hydrophobic–hydrophilic contact, and the remaining types of atom contacts were used in the following calculation. Atom contacts of a residue i were calculated by summing these atom contacts between the residue i and any other residue j in the protein–protein interface, that is,
| (1) |
where atom_contact (α, β) is equal to 1 if atoms α and β are in contact, otherwise, it is equal to 0. Atom contact areas between the residue i and its neighbour residues in the other face of the interface were computed by summing these atom contact areas across the interface, that is,
| (2) |
where atom_ contact_ area (α, β) is the contact area between two contact atoms α and β, and was obtained by CSU program.
2.2.2 Residue contacts and physicochemical features
The contact between two residues is defined when at least one atom contact exists between the two residues. Residue contacts of a residue i were computed by summing these residue contacts between the residue i and other residues in the interface, that is,
| (3) |
where residue_ contact (i, j) is equal to 1 if residues i and j are in contact, otherwise, it is equal to 0.
Thereafter, six physicochemical features of a residue were also generated as the descriptors, including hydrophobicity, hydrophilicity, mass, isoelectric point, polarity and polarisability. The parameters of hydrophobicity were referred from Fauchere and Pliska [27], whereas the parameters of other properties were referred from the AAindex database [28]. Here, the physicochemical features of a residue are defined by itself and its contact residues. For example, the hydrophobicity of the residue i is defined as
| (4) |
where hydrophobicity_param (i) and hydrophobicity_param (j) are the hydrophobicity parameters of the two contact residues i and j, respectively.
2.2.3 Depth index
The depth of an atom α is defined as the distance between atom α and the closest solvent accessible atom β. Local interactions formed in protein interfaces are usually created by the deeply buried hot spots [7]. For an interface residue i, based on depth index four descriptors can be derived by PSAIA program [29], including average depth index (ave_ dpx, mean value of all atom values), standard deviation of depth index (sd_ dpx, standard deviation of all atom values), side‐chain average depth index (s‐ch_ ave_ dpx, mean value of all side‐chain atom values) and standard deviation of side‐chain depth index (sd_ s‐ch_ dpx, standard deviation of all side‐chain atom values). We also calculated relative depth index (rel_ dpx) and relative side‐chain depth index (rel_ s‐ch_ dpx) of the residue i upon binding as
| (5) |
| (6) |
2.2.4 Relative accessible surface area (ASA) and relative side‐chain ASA
The ASA is the surface area of a biomolecule that is accessible to a solvent. Key functional properties of proteins and active amino acid sites strongly correlate with the ASA of residues. The relative change of ASA between the unbound and bound states of the residues was found to be crucial for the hot spot prediction [16]. Here, we computed the relative ASA (rel_ ASA) and relative side‐chain ASA (rel_ s‐ch_ ASA) of an interface residue i by the equations as follows
| (7) |
| (8) |
2.2.5 Secondary structure and category of residues
We used residue secondary structure (including three types, that is, helix, strand and loop) as a descriptor, and it was obtained by DSSP [30]. In addition, the categorical attribute of a residue was used as another descriptor. Based on their dipoles and volumes of the side chains, 20 amino acids were clustered into six classes, that is, Class 1: D, E; Class 2: R, K; Class 3: A, G, V; Class 4: Y, M, T, S, C; Class 5: I, L, F, P and Class 6: H, N, Q, W. For the above categorical descriptors, that is, secondary structure and category of residues, we assigned numeric indices such as 1 through K (i.e. the number of possible enumerated types) for them, respectively.
Totally, 19 descriptors were generated for each interface residue. For every target residue that we were predicting, the features were encoded from its descriptors and those of its two spatially neighbouring residues, that is, the nearest contact residue in the other face (mirror‐contact residue) and the nearest contact residue in the same face (intra‐contact residue). Here we define the distance between two residues by the shortest Euclidean distance between their atoms. Consequently, we extracted 57 features for every target residue. Furthermore, we normalised these features into the range [−1, 1].
2.3 Feature selection
Feature selection is an important step in training classifiers and is often utilised to improve the performance of a classifier by removing redundant and irrelevant features. In this work, 57 features were generated initially. Such a feature set may cause over‐fitting of the model. Therefore, we employed RFs [31] to find important features, with which to obtain better discrimination of hot spot residues and non‐hot spot residues.
A RF is an ensemble classifier that operates by constructing a multitude of decision trees to reduce the output variance of individual trees and thus improves the stability and accuracy of classification [31]. Typically, each tree is created in the following way: from the original sample a bootstrap sample is drawn, and an unpruned tree is fitted to the bootstrap sample. For each split in the tree, RF randomly chooses a constant number of features and the one with the maximum decrease in Gini index is selected. A RF model is generally made up of tens or hundreds of trees. After training, the RF prediction is determined by a majority voting scheme of individual trees. RF returns several measures of variable importance. The most reliable measure is based on the decrease in classification accuracy when the values of a particular feature are randomly permuted on these out‐of‐bag (OOB) samples. We used this measure to evaluate the importance of various features. In this work, the randomForest R package [32] was used for feature selection.
2.4 Classification algorithm
ELM for single‐hidden layer feedforward neural networks (SLFNs) randomly chooses hidden nodes and analytically determines the output weights of SLFNs [33]. Fig. 1 presents the SLFN architecture adopted by ELM algorithm. Compared with conventional machine learning methods, ELM has the advantages of short learning time and high accuracy.
Fig. 1.
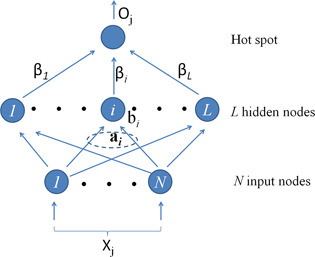
Feedforward network architecture adopted by ELM algorithm
Given a training set ℵ = {( xj , tj )| xj ∈ Rn , tj ∈ Rm , j = 1, …, N }, hidden node output function G ( a , b, x ) = F ( a T x + b), where F () is an activation function, and the number of hidden nodes L, the ELM algorithm consists of the following steps:
Assign randomly hidden node parameters ( ai , bi ), i = 1, …, L, where ai and bi are input weight and bias of hidden node i, respectively.
- Calculate the hidden layer output matrix H , where
where G ( ai , bi , xj ) is the output of hidden node i for input vector xj under hidden node parameter ( ai , bi ).
Calculate the output weight β :β = H † T.
where H † is the Moore–Penrose generalised inverse of hidden layer output matrix H , and T = [t 1, …, tN ]T.
The output of SLFNs for input vector x is . In our work, for EML the activation function was taken as sigmoid function, and the number of hidden nodes was set as 5. To select the proper hidden node parameters ( ai , bi ), i = 1, …, L, to obtain the better prediction performance, we repeated the 5‐fold cross validation in the training set for 1000 times with different hidden node parameters. The hidden node parameters that obtain the best prediction result were used as the final parameters for further analysis and prediction.
2.5 Measurements of prediction performance
To evaluate the classification performance of the ELM method proposed in this study, we adopted some widely used measures, including prediction accuracy (ACC), sensitivity (SE), precision (PR), specificity (SP) and Matthew's correlation coefficient (MCC). These measurements are defined as
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
where TP, FP, TN and FN denote the number of true positives (correctly predicted hot spot residues), false positives (non‐hot spot residues incorrectly predicted as hot spots), true negatives (correctly predicted non‐hot spot residues) and false negatives (hot spot residues incorrectly predicted as non‐hot spot residues), respectively.
3 Results and discussions
3.1 Evaluating the feature importance
The RF was implemented to estimate the importance of a specific feature. It was evaluated by calculating the average decrease of classification accuracy on the OOB samples when the values of a particular feature are randomly permutated. Fig. 2 shows the mean decrease of accuracy of these particular features when it is greater than 15%. We found that the features extracted from target residues and their mirror‐contact residues play an important role in the prediction of hot spots. This finding is consistent with previous studies that revealed hot spots contributing most of the conserved physicochemical interactions across the interfaces [22]. In the following, we selected the top‐20 features whose values of importance are significantly higher than those of the others, and then tested the prediction performance using ELM algorithm.
Fig. 2.
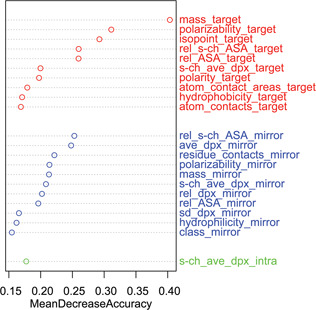
Feature importance generated by RFs
The top‐20 features were picked out and used for the hot spot prediction
3.2 Cross validation in the training set
We tested the ELM classifier by 5‐fold cross validation in the training set. The dataset was divided into 5‐folds randomly with almost the same size. The 4‐fold was used as a training set and the remaining 1‐fold was used as a test set. The process was repeated five times for each fold as a test set. It predicted these hot spots with ACC of 82.1% and MCC of 0.459. The overall prediction performance is listed in Table 3. Furthermore, the performance of our ELM method was compared with three existing machine learning methods, including SVM, NB and RF, using the same selected features. The ACC values are 80.8, 77.0 and 80.5% for SVM, NB and RF, respectively. The MCC values are 0.408, 0.439 and 0.446 for SVM, NB and RF, respectively. These results indicate the effectiveness of the proposed ELM method of predicting hot spots with selected features.
Table 3.
Results of 5‐fold cross validation by various machine learning methods
| Method | PR, % | SE, % | SP, % | ACC, % | MCC |
|---|---|---|---|---|---|
| ELM | 70.8 | 44.2 | 94.2 | 82.1 | 0.459 |
| RF | 61.2 | 53.3 | 89.2 | 80.5 | 0.446 |
| NB | 52.0 | 67.5 | 80.1 | 77.0 | 0.439 |
| SVM | 69.1 | 37.7 | 94.6 | 80.8 | 0.408 |
To further analyse the importance of these selected features for the prediction of hot spots, we categorised them into four groups (listed in Table 4) according to their sources, and estimated prediction performance of the 5‐fold cross validation by subtracting one of the groups individually. The results are presented in Table 5. After subtracting each group in describing these interface residues, we found that the MCC of prediction was decreased than that of using all groups.
Table 4.
Four feature groups clustered from the top‐20 features
| No. | Features |
|---|---|
| 1 | atom_contact_areas_target, atom_contacts_target |
| 2 | mass_target, polarisability_target, isopoint_target, polarity_target, hydrophobicity_target, residue_contacts_mirror, polarisability_mirror, mass_mirror |
| 3 | s‐ch_ave_dpx_target, ave_dpx_mirror, s‐ch_ave_dpx_mirror, rel_dpx_mirror, sd_dpx_mirror, s‐ch_ave_dpx_intra |
| 4 | rel_s‐ch_ASA_target, rel_ASA_target, rel_s‐ch_ASA_mirror, rel_ASA_mirror |
Table 5.
Predictive results by subtracting each feature group
| Without the following group | PR, % | SE, % | SP, % | ACC, % | MCC |
|---|---|---|---|---|---|
| group 1 | 70.7 | 37.7 | 95.0 | 81.1 | 0.418 |
| group 2 | 62.2 | 36.4 | 93.0 | 79.3 | 0.360 |
| group 3 | 68.3 | 36.4 | 94.6 | 80.5 | 0.396 |
| group 4 | 69.6 | 41.6 | 94.2 | 81.5 | 0.435 |
| with all groups | 70.8 | 44.2 | 94.2 | 82.1 | 0.459 |
3.3 Prediction in the independent test set
We compared our ELM method with several related works that include alanine scanning methods such as Robetta [1] and FOLDEF [12], decision tree methods such as KFC [14], SVM methods such as MINERVA [16] and KFC2 [18] and empirical methods such as HotPoint [15]. The detailed measures of these different predictors are listed in Table 6. Performance results of the compared methods were obtained from their corresponding web servers. The trained ELM achieved the ACC of 76.8% and MCC of 0.401, and presents the best prediction performance compared with other methods in the independent test set.
Table 6.
Comparison of different hot spot prediction methods in the independent test set
| Method | PR, % | SE, % | SP, % | ACC, % | MCC |
|---|---|---|---|---|---|
| Our method | 71.4 | 39.5 | 93.1 | 76.8 | 0.401 |
| MINERVA | 65.4 | 44.7 | 89.7 | 76.2 | 0.390 |
| KFC2 | 58.1 | 47.4 | 85.1 | 73.6 | 0.345 |
| HotPoint | 49.0 | 63.2 | 71.3 | 68.8 | 0.324 |
| Robetta | 52.0 | 34.2 | 86.2 | 70.4 | 0.235 |
| KFC | 48.0 | 31.6 | 85.1 | 68.8 | 0.191 |
| FOLDEF | 47.6 | 26.3 | 87.4 | 68.8 | 0.168 |
3.4 Case studies
3.4.1 Complex between the peptide exosite inhibitor E‐76 and coagulation factor VIIa.
The peptide E‐76 (PDBID:1dva, chain X) binds to an exosite on the factor VIIa (PDBID:1dva, chain H) protease domain, and non‐competitively inhibit activation of factor X and amidolytic activity [34]. Five hot spots (HIS76:H, LEU2:X, TRP11:X, TYR12:X and PHE15:X, indicated in Fig. 3) and 18 non‐hot spots have experimentally been determined in the 1dvaHX interface. In these 23 alanine‐mutated residues, our method identified three residues (TRP11:X, TYR12:X and PHE15:X) as hot spots and the rest as non‐hot spots. Three of the five hot spots and all the non‐hot spots were correctly predicted. In contrast, MINERVA predicted four residues (LEU73:H, LEU2:X, ASP9:X and PHE15:X) as hot spots and the others as non‐hot spots. MINERVA can correctly predict 2 of the 5 hot spots and 16 of the 18 non‐hot spots.
Fig. 3.
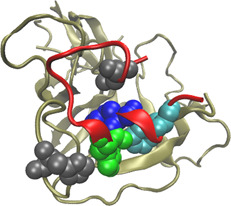
Interaction between peptide E‐76 (PDBID:1dva, chain X, coloured by red) and coagulation factor VIIa (PDBID:1dva, chain H, colored by tan)
HIS76:H, LEU2:X, TRP11:X, TYR12:X and PHE15:X (represented by VDW spheres) are experimentally determined hot spots in the 1dvaHX interface. In these five residues, TRP11:X, TYR12:X and PHE15:X (coloured by green, blue and cyan, respectively) were correctly predicted by our method
3.4.2 Complex between calmodulin and a peptide of smooth muscle myosin light chain kinase
Calcium‐bound calmodulin (Ca2+ ‐CaM) (PDBID:1cdl, chain A) binds to a peptide analogue of the CaM‐binding region of chicken smooth muscle myosin light chain kinase (PDBID:1cdl, chain E), and can relieve the autoinhibition of smooth muscle myosin light chain kinase [35]. Experimentally found hot spot residues at 1cdlAE interface are PHE92:A, TRP800:E, GLY804:E, ILE810:E, ARG812:E and LEU813:E (indicated in Fig. 4). Furthermore, PHE12:A, PHE19:A, LYS799:E, LYS802:E, ARG808:E and GLY811:E were found experimentally to be non‐hot spots. Our method correctly predicted four out of the six hot spot residues, that is, PHE92:A, TRP800:E, ILE810:E and LEU813:E, and five out of the six non‐hot spots, that is, PHE12:A, PHE19:A, LYS802:E, ARG808:E and GLY811:E. As a comparison, MINERVA correctly predicted four out of the six hot spots and four out of the six non‐hot spots.
Fig. 4.
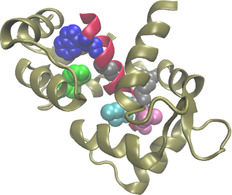
Interaction between calcium‐bound calmodulin (PDBID:1cdl, chain A, coloured by tan) and a peptide of smooth‐muscle myosin light chain kinase (PDBID:1cdl, chain E, coloured by red)
The defined hot spot residues are PHE92:A, TRP800:E, GLY804:E, ILE810:E, ARG812:E and LEU813:E (represented by VDW spheres) in the 1cdlAE interface. PHE92:A, TRP800:E, ILE810:E and LEU813:E (coloured by green, blue, cyan and purple, respectively) are the hot spots which were correctly predicted by our method
4 Conclusion
In this study, we proposed a new effective computational method to identify hot spots in the protein interfaces. We extracted various features from target residues, mirror‐contact residues and intra‐contact residues, and selected the most important features by RFs. Then we employ the ELM algorithm to effectively integrate these features for predicting interaction hot spots at the protein interfaces. Experimental results indicate that our ELM method is more effective than the alternative machine learning methods and the major existing hot spot prediction methods. Owing to the time consumption and labor intensity in experimental determination of binding free energy for alanine‐mutated residues, hot spots are available only for a very limited number of complexes. Our prediction model can help to uncover candidate residues for further alanine‐scanning mutagenesis.
5 Acknowledgments
This work was supported by the Tianjin Municipal High School Science and Technology Development Fund Program (Grant no. 20120803), National Natural Science Foundation of China (NSFC) (Grant nos. 31370075, 31200106, 61272509 and 11301382), Tianjin University of Science and Technology (Grant no. 20120101), Tianjin Technological SME Technology Innovation Fund Program (Grant no. 12ZXCXGX33500).
6 References
- 1. Kortemme T., and Baker D.: ‘A simple physical model for binding energy hot spots in protein–protein complexes’, Proc. Natl. Acad. Sci., 2002, 99, pp. 14116–14121 (doi: 10.1073/pnas.202485799) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Wells J., and McClendon C.: ‘Reaching for high‐hanging fruit in drug discovery at protein–protein interfaces’, Nature, 2007, 450, pp. 1001–1009 (doi: 10.1038/nature06526) [DOI] [PubMed] [Google Scholar]
- 3. Liu Q. Hoi S.C., and Su C.T. et al.: ‘Structural analysis of the hot spots in the binding between H1N1 HA and the 2D1 antibody: do mutations of H1N1 from 1918 to 2009 affect much on this binding?’, Bioinformatics, 2011, 27, pp. 2529–2536 [DOI] [PubMed] [Google Scholar]
- 4. Liu Z.P. Wu L.Y. Wang Y. Zhang X.S., and Chen L.: ‘Bridging protein local structures and protein functions’, Amino Acids, 2008, 35, pp. 627–650 (doi: 10.1007/s00726-008-0088-8) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Thorn K.S., and Bogan A.A.: ‘ASEdb: a database of alanine mutations and their effects on the free energy of binding in protein interactions’, Bioinformatics, 2001, 17, pp. 284–285 (doi: 10.1093/bioinformatics/17.3.284) [DOI] [PubMed] [Google Scholar]
- 6. Fischer T.B. Arunachalam K.V., and Bailey D. et al.: ‘The binding interface database (BID): a compilation of amino acid hot spots in protein interfaces’, Bioinformatics, 2003, 19, pp. 1453–1454 (doi: 10.1093/bioinformatics/btg163) [DOI] [PubMed] [Google Scholar]
- 7. Moreira I.S. Femandes P., and Ramos M.: ‘Hot spots – a review of the protein–protein interface determinant amino‐acid residues’, Proteins, 2007, 68, pp. 803–812 (doi: 10.1002/prot.21396) [DOI] [PubMed] [Google Scholar]
- 8. Keskin O. Ma B., and Nussinov R.: ‘Hot regions in protein–protein interactions: the organization and contribution of structurally conserved hot spot residues’, J. Mol. Biol., 2005, 345, pp. 1281–1294 (doi: 10.1016/j.jmb.2004.10.077) [DOI] [PubMed] [Google Scholar]
- 9. Li X. Keskin O. Ma B. Nussinov R., and Liang J.: ‘Protein–protein interactions: hot spots and structurally conserved residues often locate in complemented pockets that pre‐organized in the unbound states: implications for docking’, J. Mol. Biol., 2004, 344, pp. 781–795 (doi: 10.1016/j.jmb.2004.09.051) [DOI] [PubMed] [Google Scholar]
- 10. Li J., and Liu Q.: ‘Double water exclusion: a hypothesis refining the O‐ring theory for the hot spots at protein interfaces’, Bioinformatics, 2009, 25, pp. 743–750 (doi: 10.1093/bioinformatics/btp058) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Huo S. Massova I., and Kollman P.A.: ‘Computational alanine scanning of the 1:1 human growth hormone‐receptor complex’, J. Comput Chem., 2002, 23, pp. 15–27 (doi: 10.1002/jcc.1153) [DOI] [PubMed] [Google Scholar]
- 12. Guerois R. Nielsen J., and Serrano L.: ‘Predicting changes in the stability of proteins and protein complexes: a study of more than 1000 mutations’, J. Mol. Biol., 2002, 320, pp. 369–387 (doi: 10.1016/S0022-2836(02)00442-4) [DOI] [PubMed] [Google Scholar]
- 13. Ofran Y., and Rost B.: ‘Protein–protein interaction hotspots carved into sequences’, PLoS Comput. Biol., 2007, 3, p. e119 (doi: 10.1371/journal.pcbi.0030119) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Darnell S. LeGault L., and Mitchell J.: ‘PAn automated decision‐tree approach to predicting protein interaction hot spots’, Proteins, 2007, 68, pp. 813–823 (doi: 10.1002/prot.21474) [DOI] [PubMed] [Google Scholar]
- 15. Tuncbag N. Gursoy A., and Keskin O.: ‘Identification of computational hot spots in protein interfaces: combining solvent accessibility and inter‐residue potentials improves the accuracy’, Bioinformatics, 2009, 25, pp. 1513–1520 (doi: 10.1093/bioinformatics/btp240) [DOI] [PubMed] [Google Scholar]
- 16. Cho K.I. Kim D., and Lee D.: ‘A feature‐based approach to modeling protein–protein interaction hot spots’, Nucleic Acids Res., 2009, 37, pp. 2672–2687 (doi: 10.1093/nar/gkp132) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Xia J.F. Zhao X.M. Song J., and Huang D.S.: ‘APIS: accurate prediction of hot spots in protein interfaces by combining protrusion index with solvent accessibility’, BMC Bioinformatics, 2009, 11, p. 174 (doi: 10.1186/1471-2105-11-174) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Zhu X., and Mitchell J.: ‘KFC2: a knowledge‐based hot spot prediction method based on interface solvation, atomic density, and plasticity features’, Proteins, 2011, 79, pp. 2671–2683 (doi: 10.1002/prot.23094) [DOI] [PubMed] [Google Scholar]
- 19. Xu B. Wei X. Deng L. Guan J., and Zhou S.: ‘A semi‐supervised boosting SVM for predicting hot spots at protein–protein interfaces’, BMC Syst. Biol., 2012, 6, (Suppl 2), p. S6 (doi: 10.1186/1752-0509-6-S2-S6) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Assi S.A. Tanaka T. Rabbitts T.H., and Fernandez‐Fuentes N.: ‘PCRPi: presaging critical residues in protein interfaces, a new computational tool to chart hot spots in protein interfaces’, Nucleic Acids Res., 2010, 38, p. e86 (doi: 10.1093/nar/gkp1158) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Wang L. Liu Z.P. Zhang X.S., and Chen L.: ‘Prediction of hot spots in protein interfaces using a random forest model with hybrid features’, Protein Eng. Des. Sel., 2012, 25, pp. 119–126 (doi: 10.1093/protein/gzr066) [DOI] [PubMed] [Google Scholar]
- 22. Shulman‐Peleg A. Shatsky M. Nussinov R., and Wolfson H.J.: ‘Spatial chemical conservation of hot spot interactions in protein–protein complexes’, BMC Biol., 2007, 5, p. 43 (doi: 10.1186/1741-7007-5-43) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. del Sol A., and O'Meara P.: ‘Small‐world network approach to identify key residues in protein‐protein interaction’, Proteins, 2005, 58, pp. 672–682 (doi: 10.1002/prot.20348) [DOI] [PubMed] [Google Scholar]
- 24. Tuncbag N. Salman F.S. Keskin O., and Gursoy A.: ‘Analysis and network representation of hotspots in protein interfaces using minimum cut trees’, Proteins, 2010, 78, pp. 2283–2294 (doi: 10.1002/prot.22741) [DOI] [PubMed] [Google Scholar]
- 25. Sobolev V. Sorokine A. Prilusky J. Abola E.E., and Edelman M.: ‘Automated analysis of interatomic contacts in proteins’, Bioinformatics, 1999, 15, pp. 327–332 (doi: 10.1093/bioinformatics/15.4.327) [DOI] [PubMed] [Google Scholar]
- 26. Wang G., and Dunbrack R.L.: ‘PISCES: a protein sequence culling server’, Bioinformatics, 2003, 19, pp. 1589–1591 (doi: 10.1093/bioinformatics/btg224) [DOI] [PubMed] [Google Scholar]
- 27. Fauchere J.L., and Pliska V.: ‘Hydrophobic parameters pi of amino‐acid side chains from the partitioning of N‐acetyl‐amino‐acid amides’, Eur. J. Med. Chem., 1983, 18, pp. 369–375 [Google Scholar]
- 28. Kawashima S. Ogata H., and Kanehisa M.: ‘AAindex: amino acid index database’, Nucleic Acids Res., 1999, 27, pp. 368–369 (doi: 10.1093/nar/27.1.368) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Mihel J. Sikić M. Tomić S. Jeren B., and Vlahovicek K.: ‘PSAIA – protein structure and interaction analyzer’, BMC Struct. Biol., 2008, 8, p. 21 (doi: 10.1186/1472-6807-8-21) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Kabsch W., and Sander C.: ‘Dictionary of protein secondary structure: pattern recognition of hydrogen‐bonded and geometrical features’, Biopolymers, 1983, 22, pp. 2577–2637 (doi: 10.1002/bip.360221211) [DOI] [PubMed] [Google Scholar]
- 31. Breiman L.: ‘Random Forests’, Mach. Learn., 2001, 45, pp. 5–32 (doi: 10.1023/A:1010933404324) [DOI] [Google Scholar]
- 32. Liaw A., and Wiener M.: ‘Classification and regression by random forest’, R. News, 2002, 2, pp. 18–22 [Google Scholar]
- 33. Huang G.B. Zhu Q.Y., and Siew C.K.: ‘Extreme learning machine: theory and applications’, Neurocomputing, 2006, 70, pp. 489–501 (doi: 10.1016/j.neucom.2005.12.126) [DOI] [Google Scholar]
- 34. Dennis M.S. Eigenbrot C., and Skelton N.J. et al.: ‘Peptide exosite inhibitors of factor VIIa as anticoagulants’, Nature, 2000, 404, pp. 465–470 (doi: 10.1038/35006574) [DOI] [PubMed] [Google Scholar]
- 35. Meador W.E. Means A.R., and Quiocho F.A.: ‘Target enzyme recognition by calmodulin: 2.4 A structure of a calmodulin‐peptide complex’, Science, 1992, 257, pp. 1251–1255 (doi: 10.1126/science.1519061) [DOI] [PubMed] [Google Scholar]


