Modular bond‐graph modelling and analysis of biomolecular systems

Abstract

Bond graphs can be used to build thermodynamically‐compliant hierarchical models of biomolecular systems. As bond graphs have been widely used to model, analyse and synthesise engineering systems, this study suggests that they can play the same rôle in the modelling, analysis and synthesis of biomolecular systems. The particular structure of bond graphs arising from biomolecular systems is established and used to elucidate the relation between thermodynamically closed and open systems. Block diagram representations of the dynamics implied by these bond graphs are used to reveal implicit feedback structures and are linearised to allow the application of control‐theoretical methods. Two concepts of modularity are examined: computational modularity where physical correctness is retained and behavioural modularity where module behaviour (such as ultrasensitivity) is retained. As well as providing computational modularity, bond graphs provide a natural formulation of behavioural modularity and reveal the sources of retroactivity. A bond graph approach to reducing retroactivity, and thus inter‐module interaction, is shown to require a power supply such as that provided by the ATP ⇌ ADP + Pi reaction. The mitogen‐activated protein kinase cascade (Raf–MEK–ERK pathway) is used as an illustrative example.

1 Introduction

In their review paper, The rôle of control and system theory in systems biology, Wellstead et al. [1] suggest that ‘systems biology is an area where systematic methods for model development and analysis, such as bond graphs, could make useful new contributions as they have done in the physical world’. The purpose of this paper is to show that bond graphs not only provide a systematic method for model development and analysis of biomolecular systems, but also provide a bridge allowing application of control engineering methodology, in particular feedback concepts, to systems biology.

Bond graphs were introduced by Paynter [2] and their engineering application is described in number of text books [3–6] and a tutorial for control engineers [7]. Bond graphs were first used to model chemical reaction networks by Oster et al. [8] and a detailed account is given by Oster et al. [9]. Subsequent to this, the bond graph approach to chemical reactions has been extended by Cellier [10], Thoma and Mocellin [11] and Greifeneder and Cellier [12]. More recently, the bond graph approach has been used to analyse biochemical cycles by Gawthrop and Crampin [13] and has been shown to provide a modular approach to building hierarchical biomolecular system models which are robustly thermodynamically compliant [14]; combining thermodynamically compliant modules gives a thermodynamically compliant system. In this paper, we will call this concept, computational modularity.

Computational modularity is a necessary condition for building physically correct computational models of biomolecular systems. However, computational modularity does not imply that module properties (such as ultrasensitivity) are retained when a module is incorporated into a larger system. In the context of engineering, modules often have buffer amplifiers at the interface so that they have unidirectional connections and may thus be represented and analysed on a block diagram or signal flow graph where the properties of each module are retained. This will be called behavioural modularity in this paper. However, biological networks do not usually have this unidirectional property, but rather display retroactivity [15–20]; retroactivity modifies the properties of the interacting modules. As will be shown, the property of retroactivity is naturally captured by bond graphs. In particular, a bond graph approach to reducing retroactivity, and thus inter‐module interaction, is discussed and shown to require a power supply such as that provided by the $\text{ATP}\rightleftharpoons \text{ADP}+\text{Pi}$ reaction.

Early attempts at modelling the mitogen‐activated protein kinase (MAPK) cascade [21, 22], used modules which displayed behavioural modularity. However, because they use the Michaelis–Menten approximation, the modules do not have the property of computational modularity and thus the results were based on a non‐physical model. This was noted in later work which examined the neglected interactions: in particular, Ortega et al. [23] show that ‘product dependence and bifunctionality compromise the ultrasensitivity of signal transduction cascades’ and the ‘effects of sequestration on signal transduction cascades’ are considered by Bluthgen et al. [24]. In this paper, the MAPK cascade is used as an illustrative example which illustrates how a computationally modular approach based on bond graphs avoids the errors associated with assuming irreversible Michaelis–Menten kinetics. Moreover, the bond graph approach to reducing retroactivity is used to make the modules approximately modular in the behavioural sense. This emphasises the necessity for a power supply to support signalling networks in biology as well as in engineering.

The bond graph approach gives the set of non‐linear ordinary differential equations describing the biomolecular system being modelled. Linearisation of non‐linear systems is a standard technique in control engineering: as discussed by Goodwin et al. [25], ‘The incentive to try to approximate a non‐linear system by a linear model is that the science and art of linear control is vastly more complete and simpler than they are for the nonlinear case’. Nevertheless, it is important to realise that conclusions drawn from linearisation can only be verified using the full non‐linear equations. In the context of bond graphs, linearisation (and the associated concept of sensitivity) has been treated by the authors [26–28]. This paper builds on this work to explicitly derive the bond graph corresponding to the linearised non‐linear system and thus provide a method to analyse behavioural modularity.

Section 2 briefly shows how biomolecular systems can be modelled using bond graphs. Section 3 shows how thermodynamically closed systems can be converted to thermodynamically open systems using the twin notions of chemostats and flowstats. Linearisation is required to understand module behaviour, and this is developed in Section 4. Section 5 looks at modularity, retroactivity and feedback and Section 6 illustrates the main results using the MAPK cascade example. Section 7 concludes the paper and suggests future research directions.

2 Bond graph modelling of biomolecular systems

As discussed by Maxwell [29], the use of ‘mathematical or formal analogy’ enables us to avail ‘ourselves of the mathematical labours of those who had already solved problems essentially the same.’ The bond graph approach provides a systematic approach to the use of analogy in the modelling of systems across different physical domains; in the context of this paper, this allows engineering concepts to be carried across to biomolecular systems.

A number of text books about bond graphs [3–6] and a tutorial for control engineers [7] are available. Briefly, bond graphs focus on a pair of variables generically termed effort e and flow f whose product is power p = ef. In the electrical domain, effort is identified with voltage V (V) and flow with current i (C·s^–1) and in the mechanical domain effort is identified with force F (N) and flow with velocity v (m·s^–1). Thus voltage and force are effort analogies and current and velocity are flow analogies. Although the effort (and the flow) variables have different units in each domain, their product (power) has the same units (W or J·s^–1); power is the common currency of disparate physical domains. The pair e f is represented on the bond graph by the harpoon symbol: $\rightharpoondown$ which can be optionally annotated with specific effort and flow variables, for example $\underset{f}{\overset{e}{\rightharpoondown }}$. Sign convention is handled by the harpoon direction: thus if e and f are positive, the flow f is in the harpoon direction.

As well as analogous variables, bond graphs deal in analogous components. Thus the bond graph C component models both the ideal electrical capacitor (with capacitance c _c ) and the ideal mechanical spring (with stiffness K _s). In both cases, the C component physically accumulates flow to give the integrated flow q corresponding to electrical charge or mechanical displacement. In the linear case, this gives an effort proportional to q. To summarise

$$\begin{array}{rl}\dot{Q}& =i,V=\frac{Q}{c_c}(\text{electrical})\\ \dot{x}& =v,F=K_{\mathrm{s}}x(\text{mechanical})\\ \dot{q}& =f,e=Kq(\text{generic})\end{array}$$ (1)

Similarly, electrical resistors and mechanical dampers are represented by bond graph R components where

$$V=ri(\text{electrical})$$ (2)

$$F=rv(\text{mechanical})$$ (3)

$$e=rf(\text{generic})$$ (4)

where r represents the (linear) electrical resistance and mechanical damping factor.

Bonds are connected by 0 and 1 junctions, which again conserve energy; the 0 junction gives the same effort on each impinging bond and the 1 junction gives the same flow on each impinging bond.

Fig. 1 shows a simple electrical circuit connecting two capacitors with capacitance c ₁ and c ₂ by a resistor with resistance r ₁. Fig. 1 a gives the electrical schematic diagram and Fig. 1 b gives the corresponding bond graph which uses the C , R , 0 and 1 components connected by bonds.

Fig. 1.

Simple example. (a) An RC circuit schematic. (b) As discussed in the text, capacitors (c₁ & c₂) are represented by bond graph C components, resistors (r₁) by bond graph R components and connections by 0 and 1 junctions; the bonds ($\rightharpoondown$) carry the effort (voltage) and flow (current) variables. (c) Reaction $A\stackrel{1}{\rightleftharpoons }B$. As discussed in Section 2.1, the 1 and R components are replaced by a single two port Re component representing the reaction and the C components correspond to the reactants A and B

a Electrical Circuit

b Bond graph

c Bond graph for $A\stackrel{1}{\rightleftharpoons }B$

The bond graph TF component represents both an electrical transformer and a mechanical lever with ratio ρ. In generic terms, the bond graph fragment: $\underset{f_1}{\overset{e_1}{\rightharpoondown }}\mathit{T}\mathit{F}:\rho \underset{f_2}{\overset{e_2}{\rightharpoondown }}$ represents the two equations

$$f_2=\rho f_1,e_1=\rho e_2$$ (5)

Note that energy is conserved as

$$p_2=e_2{f}_2=\frac{e_1}{\rho }\rho f_1=e_1{f}_1=p_1$$ (6)

2.1 Biomolecular bond graph components

It is assumed that biochemical reactions occur under conditions of constant pressure (isobaric) and constant temperature (isothermal). Under these conditions, the chemical potential μ _A of substance A is given [30] in terms of its mole fraction χ _A as

$${\mu }_A={\mu }_A^{\star }+RT\ln {\chi }_A(\mathrm{J}\cdot \text{mo}{\mathrm{l}}^{-1})$$ (7)

where the standard chemical potential ${\mu }_A^{\star }$ is the value of μ _A when A is pure (χ _A = 1), R = 8.314 JK⁻¹ mol⁻¹ is the universal gas constant, T (K) is the absolute temperature and ln is the natural (or Napierian) logarithm [Unlike voltage and force (which could be dimensioned as J·C^–1 and J·m^–1, respectively) chemical potential does not have its own unit. Job and Herrmann [31] suggest Gibbs (G) as the unit of chemical potential.]. It is convenient to define a normalised chemical potential ${\stackrel{⌣}{\mu }}_A$ as

$${\stackrel{⌣}{\mu }}_A=\frac{{\mu }_A}{RT}$$ (8)

The key to modelling chemical reactions by bond graphs is to determine the appropriate effort and flow variables. As discussed by Oster et al. [8, 9], the appropriate effort variable is chemical potential μ and the appropriate flow variable is molar flow rate v.

In the context of chemical reactions, the bond graph C component of (1) is defined by (7) as

$$\begin{array}{rl}& {\dot{x}}_A=v_A(\text{mol}\cdot {\mathrm{s}}^{-1}){\mu }_A=RT\ln K_A{x}_A(\mathrm{J}\cdot \text{mo}{\mathrm{l}}^{-1})\\ & (\text{chemical})\end{array}$$ (9)

where x _A is the molar amount of A and the thermodynamic constant K _A is given by

$$K_A=\frac{1}{n_{\text{total}}}\exp \frac{{\mu }_A^{\star }}{RT}=\frac{1}{n_{\text{total}}}\exp {\stackrel{⌣}{\mu }}_A{}^{\star }(\text{mo}{\mathrm{l}}^{-1})$$ (10)

where n _total is the total number of moles in the mixture. Alternatively, (9) can be written more simply in terms of the normalised chemical potential $\stackrel{⌣}{\mu }$ of (8)

$${\dot{x}}_A=v_A(\text{mol}\cdot {\mathrm{s}}^{-1}){\stackrel{⌣}{\mu }}_A=\ln K_A{x}_A$$ (11)

We follow Oster et al. [9] in describing chemical reactions in terms of the Marcelin–de Donder formulae as discussed by Van Rysselberghe [32] and Gawthrop and Crampin [13]. In particular, given the i th reaction [9, (5.9)]

$$\begin{array}{rl}& {\nu }_A^{\mathrm{f}}A+{\nu }_B^{\mathrm{f}}B+{\nu }_C^{\mathrm{f}}C+{\nu }_D^{\mathrm{f}}D\cdots \\ & \stackrel{i}{\rightleftharpoons }{\nu }_A^{\mathrm{r}}A+{\nu }_B^{\mathrm{r}}B+{\nu }_C^{\mathrm{r}}C+{\nu }_D^{\mathrm{r}}D\cdots \end{array}$$ (12)

where the stoichiometric coefficients ν are either zero or positive integers, the forward affinity $A_i^{\mathrm{f}}$ and the reverse affinity $A_i^{\mathrm{r}}$ are defined as

$$A_i^{\mathrm{f}}={\nu }_A^{\mathrm{f}}{\mu }_A+{\nu }_B^{\mathrm{f}}{\mu }_B+{\nu }_C^{\mathrm{f}}{\mu }_C+{\nu }_D^{\mathrm{f}}{\mu }_D\cdots$$ (13)

$$A_i^{\mathrm{r}}={\nu }_A^{\mathrm{r}}{\mu }_A+{\nu }_B^{\mathrm{r}}{\mu }_B+{\nu }_C^{\mathrm{r}}{\mu }_C+{\nu }_D^{\mathrm{r}}{\mu }_D\cdots$$ (14)

The units of affinity are the same as those of chemical potential: J · mol⁻¹. Again, normalised affinities are useful

$${\stackrel{⌣}{A}}_i^{\mathrm{f}}=\frac{A_i^{\mathrm{f}}}{RT},{\stackrel{⌣}{A}}_i^{\mathrm{r}}=\frac{A_i^{\mathrm{r}}}{RT}$$ (15)

The i th reaction flow v _i is then given by

$$\begin{array}{rl}{v}_i& ={\kappa }_i\left(v_0^{+}-v_0^{-}\right)\text{where}{v}_0^{+}={\mathrm{e}}^{(A_i^{\mathrm{f}}/RT)}={\mathrm{e}}^{{\stackrel{⌣}{A}}_i^{\mathrm{f}}}\\ & \text{and}{v}_0^{-}={\mathrm{e}}^{(A_i^{\mathrm{r}}/RT)}={\mathrm{e}}^{{\stackrel{⌣}{A}}_i^{\mathrm{r}}}\end{array}$$ (16)

Note that the arguments of the exponential terms are dimensionless as are $v_0^{+}$ and $v_0^{-}$. The units of the reaction rate constant κ _i are those of molar flow rate: mol · s⁻¹.

The i th reaction flow v _i depends on the forward and reverse affinities $A_i^{\mathrm{f}}$ and $A_i^{\mathrm{r}}$, but cannot be written as the difference between the affinities. Unlike the electrical R component (see Fig. 1), it cannot be written as a one port component with the flow dependent on the difference between the efforts. However, as discussed by Gawthrop and Crampin [13], a two port resistive component, the Re component, can be used to model the reaction (16).

The fact that the capacitive C and resistive Re components are intrinsically non‐linear is one factor distinguishing biochemical systems from the electrical and mechanical systems of (1).

The TF component is used in this context to account for any non‐unity and non‐zero stoichiometric coefficients ν in (12) [8, 9, 13]. Moreover, as will be discussed in the following section, the TF component can be used to abstract the entire network of bonds, 0 and 1 junctions connecting the C and Re components.

2.2 Examples

Consider the simple reaction $A\stackrel{1}{\rightleftharpoons }B$. In this case, ${\stackrel{⌣}{A}}^{\mathrm{f}}={\stackrel{⌣}{\mu }}_A$ and ${\stackrel{⌣}{A}}^{\mathrm{r}}={\stackrel{⌣}{\mu }}_B$. With reference to Fig. 1 c, substance A is modelled by C : A , substance B is modelled by C : B and the reaction by $\mathit{R}\mathit{e}:\mathit{r}\mathbf{1}$. The equations of the C components correspond to (9) and that of the Re component to (16). The equations are

$${\stackrel{⌣}{A}}^{\mathrm{f}}={\stackrel{⌣}{\mu }}_A=\ln K_A{x}_A,{\stackrel{⌣}{A}}^{\mathrm{r}}={\stackrel{⌣}{\mu }}_B=\ln K_B{x}_B$$ (17)

$$v_0^{+}={\mathrm{e}}^{{\stackrel{⌣}{A}}^{\mathrm{f}}}=K_A{x}_A,v_0^{-}={\mathrm{e}}^{{\stackrel{⌣}{A}}^{\mathrm{r}}}=K_B{x}_B$$ (18)

$$\begin{array}{rl}& v=\kappa \left(K_A{x}_A-K_B{x}_A\right)=k^{+}{x}_A-k^{-}{x}_B\\ & \text{where}{k}^{+}=\kappa K_A\text{and}{k}^{-}=\kappa K_B\end{array}$$ (19)

In this simple case, the equations are linear and the rate constants k ⁺ and k ⁻ are given in terms of the reaction rate‐constant κ and the thermodynamic constants K _A and K _B . The equilibrium constant K ^eq is given by

$$K^{\text{eq}}=\frac{k^{+}}{k^{-}}=\frac{K_A}{K_B}$$ (20)

and is thus a function of the thermodynamic constants K _A and K _B , but not the reaction rate‐constant κ. A general formula relating all the equilibrium constants in a biomolecular network to the rate constants is given by Gawthrop et al. [14, §3].

The enzyme catalysed reaction

$$A+E\stackrel{1}{\rightleftharpoons }C\stackrel{2}{\rightleftharpoons }B+E$$ (21)

where A is the reactant, B is the product, C is the intermediate complex and E is the enzyme, is ubiquitous in biochemical systems. Reaction (21) was first modelled using bond graphs by Oster et al. [9, Fig. 5. 9].

Fig. 5.

Modularity, retroactivity and feedback

a Series connection: bond graph

b Series connection: linearised block diagram

Fig. 9.

MAPK cascade: modular model

a Phosphorylation/dephosphorylation

b MAPK cascade

c Time courses

d Effect of ATP

Fig. 2 a shows the bond graph corresponding to (21). The components $\mathit{R}\mathit{e}:\mathit{r}\mathbf{1}$ and $\mathit{R}\mathit{e}:\mathit{r}\mathbf{2}$ represent the reactions $\stackrel{1}{\rightleftharpoons }$ and $\stackrel{2}{\rightleftharpoons }$ and the four C components C : A , C : B , C : C and C : E represent the four species A, B, C and E, respectively. The left‐hand 1 junction ensures that the flow out of C : A and C : E is the reaction flow v ₁ and the right‐hand 1 junction ensures that the flow into C : B and C : E is the reaction flow v ₂. The net flow into C : E is thus v ₁ − v ₂.

Fig. 2.

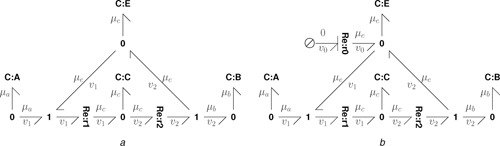
Example: Enzyme catalysed reaction. (a) Bond graph of the enzyme catalysed reaction $A+E\stackrel{1}{\rightleftharpoons }C\stackrel{2}{\rightleftharpoons }B+E$. A is the reactant, B the product, C the intermediate complex and E the enzyme. (A and B are used as chemostats given in Section 3). (b) An enzyme degradation reaction $\mathit{R}\mathit{e}:\mathit{r}\mathbf{0}$ is added. ($\mathit{R}\mathit{e}:\mathit{r}\mathbf{0}$ is used as a flowstat given in Section 3)

a Bond graph

b Bond graph with enzyme degradation

The additional reaction $\mathit{R}\mathit{e}:\mathit{r}\mathbf{0}$ has been added in Fig. 2 b together with the zero‐potential source $\oslash$; this can be used to model enzyme degradation. C : A and C : B are used in Section 3 as an example of a chemostat and $\mathit{R}\mathit{e}:\mathit{r}\mathbf{0}$ as an example of a flowstat. The enzyme catalysed reaction is analysed further in Section 5.2.

3 Closed systems and open systems: chemostats and flowstats

Specific bond graphs (such as Figs. 1 c and 2 a) model specific sets of chemical reactions. It is convenient to generalise such bond graphs to allow generic statements to be made and generic equations to be written. The molar amounts of the n _X species x _A , x _B , …, the corresponding chemical potentials μ _A , μ _B , … and the corresponding thermodynamic constants K _A , K _B , … are collected into column vectors

$$\mathit{X}=\left(\begin{array}{c}{x}_A\\ x_B\\ ⋮\end{array}\right),\mathit{\mu }=\left(\begin{array}{c}{\mu }_A\\ {\mu }_B\\ ⋮\end{array}\right),\mathit{K}=\left(\begin{array}{c}{K}_A\\ K_B\\ ⋮\end{array}\right)$$ (22)

Similarly, the n _V reaction flows v ₁, v ₂, …, affinities (forward and reverse) A ₁, A ₂, … and the corresponding reaction constants κ ₁, κ ₂, … are collected into column vectors

$$\mathit{V}=\left(\begin{array}{c}{v}_1\\ v_2\\ ⋮\end{array}\right),\mathit{A}=\left(\begin{array}{c}{A}_1\\ A_2\\ ⋮\end{array}\right),\mathit{\kappa }=\left(\begin{array}{c}{\kappa }_1\\ {\kappa }_2\\ ⋮\end{array}\right)$$ (23)

As discussed by Karnopp et al. [6], the C components can be subsumed into a single C ‐field, the Re components (as two‐port R components) subsumed into an R‐field and the connecting bonds, 0 and 1 junctions subsumed into a junction structure. Moreover, as this junction structure transmits, but does not store or dissipate energy, it can be modelled as the two multiport transformers $\mathcal{T}\mathcal{F}:{\mathit{N}}^{\mathrm{f}}$ and $\mathcal{T}\mathcal{F}:{\mathit{N}}^{\mathrm{r}}$ as shown in Fig. 3 a. These two multiport transformers are defined to transform flows as

$${\dot{\mathit{X}}}^{\mathrm{r}}={\mathit{N}}^{\mathrm{r}}\mathit{V},{\dot{\mathit{X}}}^{\mathrm{f}}={\mathit{N}}^{\mathrm{f}}\mathit{V}$$ (24)

Fig. 3.

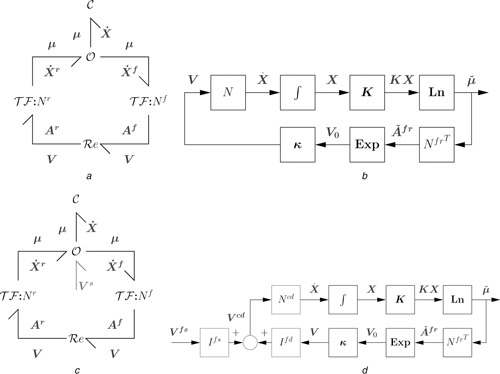
Closed and open systems: (a) General closed system. Bond symbols $\rightharpoondown$ correspond to vectors of bonds; $\mathcal{C}$, $\mathcal{R}e$ and $\mathcal{O}$ correspond to arrays of C, Re and 0 components; the two $\mathcal{T}\mathcal{F}$ components represent the intervening junction structure comprising bonds, 0 and 1 junctions and TF components. N ^f and N ^r are the forward and reverse stoichiometric matrices. (b) Corresponding block diagram. (c) Addition of the chemostat and flowstat flows V^s to the closed system of Fig. 3 a gives an open system. (d) Corresponding block diagram

a Closed system bond graph

b Closed system block‐diagram

c Open system bond graph

d Open system block diagram

As they do not store or dissipate energy, it follows that the affinities are given by

$${\mathit{A}}^{\mathrm{r}}={{\mathit{N}}^{\mathrm{r}}}^{\mathrm{T}}\mathit{\mu },{\mathit{A}}^{\mathrm{f}}={{\mathit{N}}^{\mathrm{f}}}^{\mathrm{T}}\mathit{\mu }$$ (25)

As discussed by Gawthrop and Crampin [13], and with reference to Fig. 3 a, the system states X correspond to the molar amounts of each species stored in each C component and are given in terms of the reaction flows V as

$$\dot{\mathit{X}}={\dot{\mathit{X}}}^{\mathrm{r}}-{\dot{\mathit{X}}}^{\mathrm{f}}=\mathit{N}\mathit{V}\text{where}\mathit{N}={\mathit{N}}^{\mathrm{r}}-{\mathit{N}}^{\mathrm{f}}$$ (26)

N is the stoichiometric matrix [33]; N ^f and N ^r are referred to as the forward and backward stoichiometric matrices.

From (9), the composite chemical potential μ is given by the non‐linear equation [Following [34], we use the convenient notation Exp X to denote the vector whose i th element is the exponential of the i th element of X and Ln X to denote the vector whose i th element is the natural logarithm of the i th element of X .]

$$\frac{\mathit{\mu }}{RT}=\stackrel{⌣}{\mathit{\mu }}=\text{Ln}\mathit{K}\mathit{X}\text{where}\mathit{K}=\text{diag}K$$ (27)

and from (16), the composite reaction flow V is given by the non‐linear equations

$${\mathit{V}}_0^{+}=\text{Exp}\left(\frac{{\mathit{A}}^{\mathrm{f}}}{RT}\right)=\text{Exp}{\stackrel{⌣}{\mathit{A}}}^{\mathrm{f}},{\mathit{V}}_0^{-}=\text{Exp}\left(\frac{{\mathit{A}}^{\mathrm{r}}}{RT}\right)=\text{Exp}{\stackrel{⌣}{\mathit{A}}}^{\mathrm{r}}$$ (28)

$$\mathit{V}=\kappa \left({\mathit{V}}_0^{+}-{\mathit{V}}_0^{-}\right)\text{where}\kappa =\text{diag}\kappa$$ (29)

Defining the composite stoichiometric and composite reaction constant matrices N ^fr and κ ^fr as

$${\mathit{N}}^{\text{fr}}=\left(\begin{array}{cc}{\mathit{N}}^{\mathrm{f}}& {\mathit{N}}^{\mathrm{r}}\end{array}\right)\text{and}{\mathit{\kappa }}^{\text{fr}}=\left(\begin{array}{cc}\mathit{\kappa }& -\mathit{\kappa }\end{array}\right)$$ (30)

Equations (25), (28) and (29) can be rewritten in a more compact form as

$${\stackrel{⌣}{\mathit{A}}}^{\text{fr}}={{\mathit{N}}^{\text{fr}}}^{\mathrm{T}}\stackrel{⌣}{\mathit{\mu }},{\mathit{V}}_0=\text{Exp}{\stackrel{⌣}{\mathit{A}}}^{\text{fr}},\mathit{V}={\mathit{\kappa }}^{\text{fr}}{\mathit{V}}_0$$ (31)

which can be combined to give a compact expression for the flows V in terms of the state X

$$\mathit{V}={\mathit{\kappa }}^{\text{fr}}\text{Exp}\left({{\mathit{N}}^{\text{fr}}}^{\mathrm{T}}\text{Ln}\mathit{K}\mathit{X}\right)$$ (32)

3.1 Block diagrams

Block diagrams are the conventional way of describing systems in the context of control design [25]. However, as discussed by Gawthrop and Bevan [7], bond graphs are superior to block diagrams in the context of system modelling. Nevertheless, block diagrams have advantages when analysing the system dynamics arising from the bond graph model; in particular, block diagrams expose the underlying feedback structure of the equations arising from the bond graph model. Fig. 3 b shows the block diagram corresponding to the closed system bond graph of Fig. 3 a; it is a diagrammatic way of writing down (26), (27) and (31). Each arrow corresponds to a vector of signals corresponding to: the n _X species concentrations X and normalised chemical potentials $\stackrel{⌣}{\mathit{\mu }}$, the n _V reaction flows V and the 2n _V normalised forward and reverse affinities ${\stackrel{⌣}{\mathit{A}}}^{\text{fr}}$. $\int$ represents the integration of $\dot{\mathit{X}}$ to give X implied by (26). Ln and Exp represent the non‐linear functions in (27) and (29), respectively.

3.2 Examples

For example, in the case of the simple reaction $A\stackrel{1}{\rightleftharpoons }B$ of Fig. 1 c

$$\begin{array}{rl}& \mathit{X}=\left(\begin{array}{c}{x}_A\\ x_B\end{array}\right),\mathit{V}=\left(\begin{array}{c}{v}_1\end{array}\right),{\mathit{N}}^{\mathrm{f}}=\left(\begin{array}{c}1\\ 0\end{array}\right),{\mathit{N}}^{\mathrm{r}}=\left(\begin{array}{c}0\\ 1\end{array}\right),\\ & {\mathit{N}}^{\text{fr}}=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right),\mathit{N}=\left(\begin{array}{c}-1\\ 1\end{array}\right)\end{array}$$ (33)

As N ^fr is a unit matrix, the ODE is

$$-{\dot{x}}_A={\dot{x}}_B=v_1=\kappa \left(K_A{x}_A-K_B{x}_B\right)$$ (34)

In the case of the enzyme‐catalysed reaction $A+E\stackrel{1}{\rightleftharpoons }C\stackrel{2}{\rightleftharpoons }B+E$ of Fig. 2 b

$$\begin{array}{rl}& \mathit{X}=\left(\begin{array}{c}{x}_A\\ x_B\\ x_C\\ x_E\end{array}\right),\mathit{V}=\left(\begin{array}{c}{v}_1\\ v_2\end{array}\right),N_{\mathrm{f}}=\left(\begin{array}{cc}1& 0\\ 0& 0\\ 0& 1\\ 1& 0\end{array}\right),\\ & N_{\mathrm{r}}=\left(\begin{array}{cc}0& 0\\ 0& 1\\ 1& 0\\ 0& 1\end{array}\right),\mathit{N}=\left(\begin{array}{cc}-1& 0\\ 0& 1\\ 1& -1\\ -1& 1\end{array}\right)\end{array}$$ (35)

Substituting into (29) gives

$$\begin{array}{rl}& v_1={\kappa }_1\left(K_A{K}_E{x}_A{x}_E-K_C{x}_C\right),\\ & v_2={\kappa }_2\left(K_C{x}_C-K_B{K}_E{x}_B{x}_E\right)\end{array}$$ (36)

and substituting into (26) gives

$${\dot{x}}_A=-v_1,{\dot{x}}_B=v_2,{\dot{x}}_C=-{\dot{x}}_E=\left(v_1-v_2\right)$$ (37)

3.3 Chemostats

As discussed by Polettini and Esposito [35], the notion of a chemostat is useful in creating an open system from a closed system; a similar approach is used by Qian and Beard [36] who use the phrase ‘concentration clamping’. The chemostat has three interpretations:

1. One or more species is fixed to give a constant concentration [14]; this implies that an appropriate external flow is applied to balance the internal flow of the species.

2. An ideal feedback controller is applied to species to be fixed with setpoint as the fixed concentration and control signal an external flow.

3. As a C component with a fixed state.

Define ${\mathcal{I}}^{\text{cs}}$ as the set containing the indices of the species corresponding to the chemostats. Then the n _X × n _X diagonal matrices I ^cs and I ^cd are defined as

$$I_{ii}^{\text{cs}}=\left\{\begin{array}{cc}1& \text{if}i\in {\mathcal{I}}^{\text{cs}}\\ 0& \text{if}i\notin {\mathcal{I}}^{\text{cs}}\end{array}\right.,I_{ii}^{\text{cd}}=\left\{\begin{array}{cc}0& \text{if}i\in {\mathcal{I}}^{\text{cs}}\\ 1& \text{if}i\notin {\mathcal{I}}^{\text{cs}}\end{array}\right.$$ (38)

It follows that I _X = I ^cs + I ^cd where I _X is the n _X × n _X unit matrix. The stoichiometric matrix N can then be expressed as the sum of two matrices: the chemostatic stoichiometric matrix N ^cs and the chemodynamic stoichiometric matrix N ^cd as

$$\mathit{N}={\mathit{N}}^{\text{cs}}+{\mathit{N}}^{\text{cd}}$$ (39)

where

$${\mathit{N}}^{\text{cs}}={\mathit{I}}^{\text{cs}}\mathit{N}\text{and}{\mathit{N}}^{\text{cd}}={\mathit{I}}^{\text{cd}}\mathit{N}$$ (40)

Note that N ^cd is the same as N except that the rows corresponding to the chemostat variables are set to zero. The stoichiometric properties of N ^cd, rather than N , determine system properties when chemostats are present. When chemostats are used, the state (26) is replaced by

$$\dot{\mathit{X}}={\mathit{N}}^{\text{cd}}\mathit{V}=\mathit{N}\mathit{V}-{\mathit{V}}^{\text{cs}}\text{where}{\mathit{V}}^{\text{cs}}={\mathit{N}}^{\text{cs}}\mathit{V}$$ (41)

and thus the fixed states are held constant by the external flow V ^s = − V ^cs = − N ^cs V acting at the C components. Thus the closed‐system bond graph of Fig. 3 a is replaced by the open‐system bond graph of Fig. 3 c where the external flows V ^s have been added.

3.4 Flowstats

In addition to ‘concentration clamping’ (identified with chemostats in Section 3.3), Qian and Beard [36] also use ‘boundary flux injection’ to convert closed to open systems. Here we ‘fix’ flows though Re components to create flowstats. Although Polettini and Esposito [35] ‘focus on chemostats for thermodynamic modelling’ and note that chemostats can be used to create fixed currents, it is argued that flowstats provide a useful complement to chemostats.

In a similar way to Section 3.3, define ${\mathcal{I}}^{\text{fs}}$ as the set containing the indices of the reactions corresponding to the flowstats. Then the n _V × n _V diagonal matrices I ^fs and I ^fd are defined as

$$I_{ii}^{\text{fs}}=\left\{\begin{array}{cc}1& \text{if}i\in {\mathcal{I}}^{\text{fs}}\\ 0& \text{if}i\notin {\mathcal{I}}^{\text{fs}}\end{array}\right.,I_{ii}^{\text{fd}}=\left\{\begin{array}{cc}0& \text{if}i\in {\mathcal{I}}^{\text{fs}}\\ 1& \text{if}i\notin {\mathcal{I}}^{\text{fs}}\end{array}\right.$$ (42)

It follows that I _V = I ^fs + I ^fd where I _V is the n _V × n _V unit matrix. Thus the flows V are replaced by V ^cd where

$${\mathit{V}}^{\text{cd}}={\mathit{I}}^{\text{fd}}\mathit{V}+{\mathit{I}}^{\text{fs}}{\mathit{V}}^{\text{fs}}$$ (43)

Assuming that chemostats are also present, (41) is replaced by

$$\dot{\mathit{X}}={\mathit{N}}^{\text{cd}}{\mathit{V}}^{\text{cd}}={\mathit{N}}^{\text{cd}}\left({\mathit{I}}^{\text{fd}}\mathit{V}+{\mathit{I}}^{\text{fs}}{\mathit{V}}^{\text{fs}}\right)$$ (44)

If V ^fs ≠ 0, the stoichiometric properties of N ^cd (i.e. determined by the chemostats) determine system properties. However, if V ^fs = 0 then the stoichiometric properties of

$${\mathit{N}}^d={\mathit{N}}^{\text{cd}}{\mathit{I}}^{\text{fd}}={\mathit{I}}^{\text{cd}}\mathit{N}{\mathit{I}}^{\text{fd}}$$ (45)

(i.e. both chemostats and flowstats) determine system properties. Note that N ^d is the same as N ^cd except that the columns corresponding to the flowstat variables are set to zero.

Fig. 3 d shows the block diagram corresponding to the open‐system bond graph of Fig. 3 c. It differs from Fig. 3 a in that N of (27) is replaced by N ^cd of (41) to reflect the fact that the chemostat states are not affected by V and thus correspond to the zero rows of N ^cd. Moreover, the matrices I ^fd and I ^fds, and the flows V ^fs are added to reflect the effect of the flowstats.

3.5 Reduced‐order equations

As discussed by the authors [37, 38], the presence of conserved moieties leads to potential numerical difficulties with the solution of (26). As chemostats introduce further conserved moieties it is important to resolve this issue. The following outline uses the notation and approach of Gawthrop and Crampin [13, §3(c)].

Defining G ^cd as the left null‐space matrix of N ^cd it follows that

$${\mathit{G}}^{\text{cd}}\dot{\mathit{X}}={\mathit{G}}^{\text{cd}}{\mathit{N}}^{\text{cd}}\mathit{V}=0$$ (46)

Hence, each of the n _G rows of G ^cd defines an algebraic relationship between the states contained in X . Thus the number of independent states n _x is given in terms of the total number of states n _X by

$$n_x=n_X-n_G$$ (47)

The derivative of the independent states x is given in terms of the derivative of state X by the n _x × n _X transformation matrix ${\mathit{L}}_{xX}^{\text{cd}}$

$$\dot{\mathit{x}}={\mathit{L}}_{xX}^{\text{cd}}\dot{\mathit{X}}$$ (48)

Similarly

$$\dot{\mathit{X}}={\mathit{L}}_{Xx}^{\text{cd}}\dot{\mathit{x}}$$ (49)

where ${\mathit{L}}_{Xx}^{\text{cd}}$ is an n _X × n _x matrix. Integrating (49)

$$\mathit{X}={\mathit{L}}_{Xx}^{\text{cd}}\mathit{x}+{\mathit{X}}_0-{\mathit{L}}_{Xx}^{\text{cd}}{\mathit{x}}_0={\mathit{L}}_{Xx}^{\text{cd}}\mathit{x}+G_X^{\text{cd}}{\mathit{X}}_0$$ (50)

where

$$G_X^{\text{cd}}={\mathit{I}}_{n_X\times n_X}-{\mathit{L}}_{Xx}^{\text{cd}}{\mathit{L}}_{xX}^{\text{cd}}$$ (51)

and x ₀ and X ₀ are the values of x and X at time t = 0, respectively.

Fig. 4 a corresponds to the open‐system bond graph and block diagram of Fig. 3, but the reduced‐order (48) and (50) have been incorporated. The block ${\mathit{L}}_{xX}^{\text{cd}}$ contracts the state dimension from n _X to n _x and the block ${\mathit{L}}_{Xx}^{\text{cd}}$ expands it again. The initial condition term G _X X (0) becomes an exogenous signal analogous to the setpoint term of feedback control; note that this includes the states of all of the chemostats.

Fig. 4.

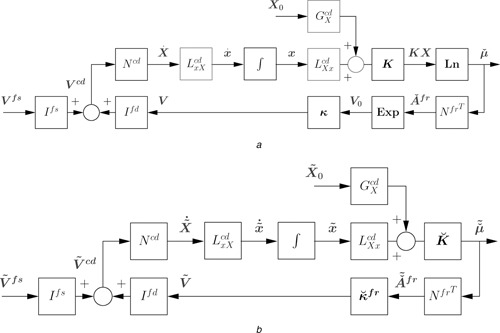
Reduced‐order system block diagrams

a Reduced‐order system

b Linearised reduced‐order system

3.6 Examples

The simple reaction $A\stackrel{1}{\rightleftharpoons }B$ of Fig. 1 c has a single conserved moiety represented by

$$x_A+x_B=x_{AB}$$ (52)

where x _AB is a constant. One possibility is

$$\begin{array}{rl}& \mathit{x}=\left(\begin{array}{c}{x}_A\end{array}\right),L_{xX}=\left(\begin{array}{cc}1& 0\end{array}\right),\\ & L_{Xx}=\left(\begin{array}{c}1\\ -1\end{array}\right),G_X=\left(\begin{array}{cc}0& 0\\ 1& 1\end{array}\right)\end{array}$$ (53)

The enzyme‐catalysed reaction $A+E\stackrel{1}{\rightleftharpoons }C\stackrel{2}{\rightleftharpoons }B+E$ of Fig. 2 b has a number of possible representations depending on which C components are chemostats and which Re components are flowstats. Two of these are examined here.

First, consider the case where both C : A and C : B are chemostats and Re : r 0 is a flowstat with zero flow. The relevant stoichiometric matrix is thus N ^d of (45) that determines system properties and

$${\mathit{N}}^d=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 1& -1\\ 0& -1& 1\end{array}\right),{\mathit{G}}^d=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 1\end{array}\right)$$ (54)

G ^d has three rows corresponding to the three conserved moieties x _A , x _B and x _C + x _E . The first correspond to the two chemostats, the third to the well‐known conserved moiety for enzyme‐catalysed reactions: the total enzyme amount is conserved. There is only one independent state which is chosen as x _C . With this choice

$$\begin{array}{rl}& L_{xX}=\left(\begin{array}{cccc}0& 0& 1& 0\end{array}\right),L_{Xx}=\left(\begin{array}{c}0\\ 0\\ 1\\ -1\end{array}\right),\\ & G_X=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 1& 1\end{array}\right)\end{array}$$ (55)

Second, consider the case where both C :A and C :B are chemostats and Re :r 0 is a flowstat with non‐zero flow. The relevant stoichiometric matrix is thus N ^cd of (39) that determines system properties and

$${\mathit{N}}^{\text{cd}}=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 1& -1\\ 1& -1& 1\end{array}\right),{\mathit{G}}^{\text{cd}}=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\end{array}\right)$$ (56)

The effect of the variable flowstat is to remove the third conserved moiety leaving only the chemostat states x _A and x _B . There are now two independent states x _C and x _E . This gives

$$\begin{array}{rl}& L_{xX}=\left(\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right),L_{Xx}=\left(\begin{array}{cc}0& 0\\ 0& 0\\ 1& 0\\ 0& 1\end{array}\right),\\ & G_X=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right)\end{array}$$ (57)

4 Linearisation

As discussed in Section 1, linearisation of non‐linear systems is a standard technique in control engineering. In Section 5, linearisation is used to analyse the properties of modules.

Assuming that the system reaches a steady‐state $\overline{\mathit{X}}$, i.e. $\dot{\mathit{X}}=0$ when $\mathit{X}=\overline{\mathit{X}}$, the system can be linearised about that steady state by introducing perturbation variables $\tilde{\mathit{X}}$ so that $\mathit{X}=\tilde{\mathit{X}}+\overline{\mathit{X}}$. These can be defined for each relevant variable; e.g.

$$\begin{array}{rl}& x=\overline{x}+\tilde{x},\mu =\overline{\mu }+\tilde{\mu },A^{\mathrm{f}}={\overline{A}}^{\mathrm{f}}+{\tilde{A}}^{\mathrm{f}},\\ & A^{\mathrm{r}}={\overline{A}}^{\mathrm{r}}+{\tilde{A}}^{\mathrm{r}},v=\overline{v}+\tilde{v}\end{array}$$ (58)

If the perturbation is small, each variable can be approximated using a first‐order Taylor series; thus, e.g. $\tilde{\mu }\simeq (\partial \mu /\partial x)\tilde{x}$.

4.1 Component linearisation: C and Re

The non‐linear C component is defined by (11). In particular, for substance A

$${\stackrel{⌣}{\mu }}_A=\ln K_A{x}_A,{\dot{x}}_A=v_A$$ (59)

Using the perturbation approach, it follows that the linearised C component is defined by the equations

$${\widetilde{\stackrel{⌣}{\mu }}}_A={\stackrel{⌣}{K}}_A{\tilde{x}}_A,{\stackrel{⌣}{K}}_A=\frac{\partial {\stackrel{⌣}{\mu }}_A}{\partial x_A}=\frac{1}{{\overline{x}}_A},{\dot{\tilde{x}}}_A={\tilde{v}}_A$$ (60)

The non‐linear Re component representing the i th reaction (12) is defined by (16), in particular

$$v_i={\kappa }_i\left(v_0^{+}-v_0^{-}\right),v_0^{+}={\mathrm{e}}^{{\stackrel{⌣}{A}}_i^{\mathrm{f}}},v_0^{-}={\mathrm{e}}^{{\stackrel{⌣}{A}}_i^{\mathrm{r}}}$$ (61)

Hence the linearised Re component is defined by the following equations

$$\begin{array}{rl}& {\tilde{v}}_i={\stackrel{⌣}{\kappa }}_i^{\mathrm{f}}{\widetilde{\stackrel{⌣}{A}}}_i^{\mathrm{f}}-{\stackrel{⌣}{\kappa }}_i^{\mathrm{r}}{\widetilde{\stackrel{⌣}{A}}}_i^{\mathrm{r}},\\ & {\stackrel{⌣}{\kappa }}_i^{\mathrm{f}}=\frac{\partial v_i}{\partial {\stackrel{⌣}{\mathit{A}}}_i^{\mathrm{f}}}={\kappa }_i{\overline{v}}_0^{+},{\stackrel{⌣}{\kappa }}_i^{\mathrm{r}}=-\frac{\partial v_i}{\partial {\stackrel{⌣}{\mathit{A}}}_i^{\mathrm{r}}}={\kappa }_i{\overline{v}}_0^{-}\end{array}$$ (62)

4.2 Linearised system equations

Section 4.1 shows how the bond graph components are linearised; essentially the non‐linear exp and ln functions are replaced by linear gains dependent on the steady‐state flows and steady‐state states, respectively. The n _X constants ${\stackrel{⌣}{K}}_A,{\stackrel{⌣}{K}}_B,\dots$ of the linearised C components, and the n _V constants ${\stackrel{⌣}{\kappa }}_1^{\mathrm{f}},{\stackrel{⌣}{\kappa }}_2^{\mathrm{f}},\dots$ and ${\stackrel{⌣}{\kappa }}_1^{\mathrm{r}},{\stackrel{⌣}{\kappa }}_2^{\mathrm{r}},\dots$ are collected into column vectors

$$\stackrel{⌣}{\mathit{K}}=\left(\begin{array}{c}{\stackrel{⌣}{K}}_A\\ {\stackrel{⌣}{K}}_B\\ ⋮\end{array}\right),{\stackrel{⌣}{\mathit{\kappa }}}^{\mathrm{f}}=\left(\begin{array}{c}{\stackrel{⌣}{\kappa }}_1^{\mathrm{f}}\\ {\stackrel{⌣}{\kappa }}_2^{\mathrm{f}}\\ ⋮\end{array}\right),{\stackrel{⌣}{\mathit{\kappa }}}^{\mathrm{r}}=\left(\begin{array}{c}{\stackrel{⌣}{\kappa }}_1^{\mathrm{r}}\\ {\stackrel{⌣}{\kappa }}_1^{\mathrm{r}}\\ ⋮\end{array}\right)$$ (63)

Fig. 4 b shows the block diagram corresponding to the linearisation of the reduced‐order system depicted in Fig. 4 a where

$$\stackrel{⌣}{\mathit{K}}=\text{diag}\stackrel{⌣}{\mathit{K}},\stackrel{⌣}{\mathit{\kappa }}=\text{diag}{\stackrel{⌣}{\mathit{\kappa }}}^{\text{fr}},\text{where}{\stackrel{⌣}{\mathit{\kappa }}}^{\text{fr}}=\left(\begin{array}{c}{\stackrel{⌣}{\mathit{\kappa }}}^{\mathrm{f}}\\ {\stackrel{⌣}{\mathit{\kappa }}}^{\mathrm{r}}\end{array}\right)$$ (64)

The block diagram of the linearised version of the full system of Fig. 3 d gives the following linear state‐space equations

$$\tilde{\mathit{V}}=\mathit{C}\tilde{\mathit{X}},{\tilde{\mathit{V}}}^{\text{cd}}={\mathit{I}}^{\text{fd}}\tilde{\mathit{V}}+{\mathit{I}}^{\text{fs}}{\tilde{\mathit{V}}}^{\text{fs}},\dot{\tilde{\mathit{X}}}=\mathit{A}\tilde{\mathit{X}}+\mathit{B}{\tilde{\mathit{V}}}^{\text{fs}}$$ (65)

where

$$\mathit{A}={\mathit{N}}^{\text{cd}}{\mathit{I}}^{\text{fd}}\mathit{C}={\mathit{N}}^d\mathit{C},\mathit{B}={\mathit{N}}^{\text{cd}}{\mathit{I}}^{\text{fs}},\mathit{C}={\stackrel{⌣}{\mathit{\kappa }}}^{\text{fr}}{N^{\text{fr}}}^{\mathrm{T}}\stackrel{⌣}{\mathit{K}}$$ (66)

The block diagram of the reduced system shown in Fig. 4 b gives the following linear state‐space equations

$$\tilde{\mathit{V}}=\mathit{c}\tilde{\mathit{x}}+\mathit{d}{\tilde{\mathit{X}}}_0,\dot{\tilde{\mathit{x}}}=\mathit{a}\tilde{\mathit{x}}+{\mathit{b}}_v{\tilde{\mathit{V}}}^{\text{fs}}+{\mathit{b}}_x{\tilde{\mathit{X}}}_0$$ (67)

where

$$\begin{array}{rl}& \mathit{a}={\mathit{L}}_{xX}^{\text{cd}}{\mathit{A}\mathit{L}}_{Xx}^{\text{cd}},{\mathit{b}}_v={\mathit{L}}_{xX}^{\text{cd}}\mathit{B}\mathbf{,}{\mathit{b}}_x={\mathit{L}}_{xX}^{\text{cd}}\mathit{A}{G}_X^{\text{cd}},\\ & \mathit{c}={\mathit{C}\mathit{L}}_{Xx}^{\text{cd}},\mathit{d}=\mathit{C}{G}_X^{\text{cd}}\end{array}$$ (68)

Equations (67) can be written more compactly as

$$\tilde{\mathit{V}}=\mathit{c}\tilde{\mathit{x}}+\mathit{d}\tilde{\mathit{U}}$$ (69)

$$\dot{\tilde{\mathit{x}}}=\mathit{a}\tilde{\mathit{x}}+\mathit{b}\tilde{\mathit{U}}$$ (70)

where

$$\mathit{U}=\left(\begin{array}{c}{\tilde{\mathit{X}}}_0\\ {\tilde{\mathit{V}}}^{\text{fs}}\end{array}\right)$$ (71)

$$\mathit{b}=\left(\begin{array}{cc}{\mathit{b}}_x& {\mathit{b}}_v\end{array}\right)$$ (72)

and

$$\mathit{d}=\left(\begin{array}{cc}{\mathit{d}}_x& {\mathbf{0}}_{n_x\times n_V}\end{array}\right)$$ (73)

where ${\mathbf{0}}_{n_x\times n_V}$ is the zero matrix with indicated dimensions.

As the state‐space systems (65) and (67) are linear, they can also be represented as transfer functions in the Laplace variable s. In particular, the reduced‐order system (67) has the transfer function G (s) given by

$$\begin{array}{rl}& \mathit{G}(s)=\mathit{c}{\left(s{\mathit{I}}_{n_x\times n_x}-\mathit{a}\right)}^{-1}\mathit{b}+\mathit{d}\\ & \text{where}\mathit{V}(s)=\mathit{G}(s)\mathit{U}(s)\end{array}$$ (74)

${\mathit{I}}_{n_x\times n_x}$ is the unit matrix with indicated dimensions.

4.3 Examples

The simple reaction $A\stackrel{1}{\rightleftharpoons }B$ of Fig. 1 c has a flow given by (19). As both state derivatives are proportional to v, it follows that the steady‐state is defined by: v = κ (K _A x _A − K _B x _A ) = 0. As noted in (52), x _A + x _B = x _AB where x _AB is a constant. It follows that the steady‐state values of x _A and x _B are

$${\overline{x}}_A=\frac{K_B}{K_A+K_B}{x}_{AB},{\overline{x}}_B=\frac{K_A}{K_A+K_B}{x}_{AB}$$ (75)

From (18), $v_0^{+}=K_A{x}_A$ and $v_0^{-}=K_B{x}_B$. Hence

$${\overline{v}}_0^{+}={\overline{v}}_0^{-}=\frac{K_A{K}_B}{K_A+K_B}{x}_{AB}$$ (76)

Using formulae (60) and (62), it follows that the coefficients of the linearised C components are

$${\stackrel{⌣}{K}}_A=\frac{1}{{\overline{x}}_A}=\frac{K_A+K_B}{K_B{\overline{x}}_{AB}},{\stackrel{⌣}{K}}_B=\frac{1}{{\overline{x}}_B}=\frac{K_A+K_B}{K_A{\overline{x}}_{AB}}$$ (77)

and that the coefficients of the linearised Re component are

$${\stackrel{⌣}{\mathit{\kappa }}}^{\mathrm{f}}={\stackrel{⌣}{\mathit{\kappa }}}^{\mathrm{r}}=\kappa \frac{K_A{K}_B}{K_A+K_B}{x}_{AB}$$ (78)

Hence the linearised equations for the flow are

$$\tilde{v}={\stackrel{⌣}{\mathit{\kappa }}}^{\mathrm{f}}{\stackrel{⌣}{K}}_A{\tilde{x}}_A-{\stackrel{⌣}{\mathit{\kappa }}}^{\mathrm{r}}{\stackrel{⌣}{K}}_B{\tilde{x}}_B=\kappa \left(K_A{\tilde{x}}_A-K_B{\tilde{x}}_B\right)$$ (79)

As expected, the linearisation of a linear equation is the same as the linear equation.

5 Modularity, retroactivity and feedback

Modularity provides one approach to understanding the complex systems associated with biochemical systems [39–44]. However, as discussed by Kaltenbach and Stelling [45] there are many possible concepts of modularity. These include structure deduced from the stoichiometric matrix [46, 47]; modular construction of in silico models [48]; and modular structure designed to minimise the retroactivity between modules [19, 20, 45].

This paper focuses on two overlapping, but conceptually different concepts of modularity:

• Computation modularity: modules retain physically correct results when connected together to form a system.

• Behavioural modularity: modules retain their behaviour (such as ultrasensitivity) when connected together.

Gawthrop et al. [14] have shown that bond graphs provide an effective foundation for modular construction of computer models of biochemical systems. This paper focuses on the second interpretation of modularity and shows that bond graphs provide a natural interpretation of inter‐module retroactivity [15–17, 19, 20, 49, 50]. Retroactivity has been illustrated experimentally in the context of ‘signalling properties of a covalent modification cycle’ [51], ‘load‐induced modulation of signal transduction networks’ [52] and the ‘temporal dynamics of gene transcription’ [53]. Retroactivity can be removed using ‘insulation’ Vecchio and Murray [20], Sontag [49], Vecchio and Sontag [54]; however, this may come at an energetic cost [55].

As discussed in Section 1, feedback is another concept crucial to the understanding of complex systems. Kholodenko [22], Brightman and Fell [56], Asthagiri and Lauffenburger [57], Kolch et al. [58], Hornberg et al. [59] and Sauro and Ingalls [60] investigate the feedback in the context of MAPK cascades. As will be shown in this paper, retroactivity and feedback are closely related concepts. As will be seen, feedback arises in a number of ways including:

• Intrinsic feedback: due to the interaction of reactions and species within and between modules

• Conserved moieties: implicitly generate feedback loops

• Feedback inhibition: explicitly uses negative feedback.

As discussed in Section 4, linearisation of a non‐linear system allows a wide range of control engineering techniques to be applied. In this section, linearisation is used to investigate behavioural modularity using transfer functions and frequency‐domain methods.

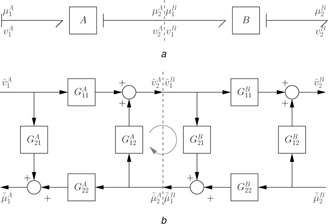
Fig. 5 a shows the series interconnection of two bond graph modules labelled A and B. In this example, each module has two ports labelled 1 and 2 and the modules are interconnected to form a composite module AB with two ports. To create a block diagram from a bond graph, the concept of causality is required. This concept is discussed in detail in [3–6], but here it suffices to know that causality determines which variable on a bond impinging on a system is the input, and which the output. For example, in this case the causality is such that flow v is the input (and effort μ the output) on port 1 and that effort μ is the input (and flow v the output) on port 2.

As discussed by Gawthrop et al. [14], the bond graph approach can be used to build arbitrarily complex systems out of such modules. However, to delve more deeply into the power of the bond graph approach and to understand how modules interact, it is instructive to look at the block diagram equivalents following linearisation as discussed in Section 4. With the assumed causality, each module can be represented by four transfer functions G ₁₁, G ₁₂, G ₂₁ and G ₂₂ which can be combined into a 2 × 2 matrix

$$\left(\begin{array}{c}{\tilde{v}}_2\\ {\widetilde{\stackrel{⌣}{\mu }}}_1\end{array}\right)=\left(\begin{array}{cc}{G}_{11}& G_{12}\\ G_{21}& G_{22}\end{array}\right)\left(\begin{array}{c}{\tilde{v}}_1\\ {\widetilde{\stackrel{⌣}{\mu }}}_2\end{array}\right)$$ (80)

Using the superscripts A and B to refer to the two modules, the four transfer functions of (80) can be represented for each of the interconnected modules as Fig. 5 b. Connecting port 2 of A to port 1 of B shown in Fig. 5 a is equivalent to connecting the corresponding signals shown in Fig. 5 b

$${\tilde{v}}_2^A={\tilde{v}}_1^B\text{and}{\widetilde{\stackrel{⌣}{\mu }}}_1^A={\widetilde{\stackrel{⌣}{\mu }}}_1^B$$ (81)

This connection induces a feedback loop involving $G_{12}^A$ and $G_{21}^B$ thus the properties of the composite system are dependent on the loop gain L _I of this feedback loop.

In particular, using (80) for A and B and substituting (81) gives the transfer function G ^AB for the composite module as

$$G_{11}^{AB}=\frac{G_{11}^A{G}_{11}^B}{1+L_I}$$ (82)

$$G_{12}^{AB}=G_{12}^B+\frac{G_{11}^B{G}_{12}^A{G}_{22}^B}{1+L_I}$$ (83)

$$G_{21}^{AB}=G_{21}^A+\frac{G_{22}^A{G}_{21}^B{G}_{11}^A}{1+L_I}$$ (84)

$$G_{22}^{AB}=\frac{G_{22}^B{G}_{22}^A}{1+L_I}$$ (85)

$$L_I=-G_{12}^A{G}_{21}^B$$ (86)

L _I will be called the interaction loop‐gain. In linear systems, feedback shifts system poles and therefore changes the behaviour of the interacting systems. In particular, each of the transfer functions $G_{ij}^{AB}$ of (82)–(85) is modified by the interaction loop‐gain. Thus the feedback loop comprising $G_{12}^A$ and $G_{21}^B$ is the source of behaviour alteration when two modules are connected. It follows that approximate behavioural modularity is achieved by making the interaction loop‐gain as small as possible. Indeed, in the special case that $G_{12}^A=G_{21}^B=0$ and so L _I = 0 then

$$\begin{array}{rl}& G_{11}^{AB}=G_{11}^A{G}_{11}^B,G_{21}^{AB}=G_{21}^A,\\ & G_{12}^{AB}=G_{12}^B,G_{22}^{AB}=G_{22}^B{G}_{22}^A\end{array}$$ (87)

5.1 Example module: simple reaction

Fig. 6 a shows a simple reaction system comprising a species represented by the C component C :C and the reaction component Re :r . This closed system is converted to an open system by appending a flowstat Re :r 0 with flow v ₀ and a chemostat C :S with state x _s . This system is linear and the reaction flow (though Re :r ) is given by

$$v=\kappa \left(K_c{x}_c-K_{\mathrm{s}}{x}_s\right)$$ (88)

and the rate of change of x _c is

$${\dot{x}}_c=v_0-v$$ (89)

Fig. 6.

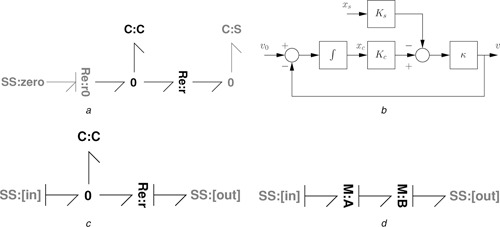
Example module: simple reaction

a With flowstat and chemostat

b Block diagram

c With ports

d Example series connection

Equations (88) and (89) can be visualised using the block diagram of Fig. 6 b, which clearly shows the implicit feedback structure with loop gain

$$L=\frac{\kappa K_c}{s}$$ (90)

It follows from the block diagram of Fig. 6 b that

$$\begin{array}{rl}& \left(\begin{array}{c}v\\ x_c\end{array}\right)=\frac{1}{1+L}\left(\begin{array}{cc}L& \kappa K_{\mathrm{s}}\\ \frac{1}{s}& \frac{\kappa K_{\mathrm{s}}}{s}\end{array}\right)\\ & \left(\begin{array}{c}{v}_0\\ x_s\end{array}\right)=\frac{1}{s+\kappa K_c}\left(\begin{array}{cc}\kappa K_c& -s\kappa K_{\mathrm{s}}\\ 1& \kappa K_{\mathrm{s}}\end{array}\right)\left(\begin{array}{c}{v}_0\\ x_s\end{array}\right)\end{array}$$ (91)

In the particular case, that κ = K _c = K _s = 1

$$G_{11}=G_{22}=G_{21}=\frac{1}{s+1},G_{12}=\frac{-s}{s+1}$$ (92)

If two identical copies of this module are placed in series as shown in Fig. 6 d

$$L_I=\frac{s}{{(s+1)}^2},\frac{1}{1+L_I}=\frac{{(s+1)}^2}{s^2+3s+1}$$ (93)

and the resulting overall transfer function is

$$\begin{array}{rl}& G_{11}^{AB}=G_{22}=\frac{1}{s^2+3s+1},G_{21}^{AB}=\frac{-s(s+2)}{s^2+3s+1},\\ & G_{12}^{AB}=\frac{s+2}{s^2+3s+1}\end{array}$$ (94)

The isolated modules each have a single pole at s = −1; the series modules have a pole at s = −0.38 and at s = −2.62. This shift in pole location is due to non‐zero interaction loop‐gain L _I (86).

Such reaction systems are often incorrectly modelled using an irreversible reaction where the flow is independent of μ ₂. This would imply that G ₁₂ = G ₂₂ = L = 0 and thus the overall transfer function would be

$$\begin{array}{rl}& G_{11}^{AB}=\frac{1}{{(s+1)}^2}=\frac{1}{s^2+2s+1},\\ & G_{21}^{AB}=\frac{-s}{s+1},G_{12}^{AB}=G_{22}^{AB}=0\end{array}$$ (95)

This thermodynamically incorrect system has zero retroactivity. As will be shown in the sequel, approximate irreversibility, and thus approximate zero retroactivity, can be achieved, but at the metabolic cost of using a power supply such as that provided by the $\text{ATP}\rightleftharpoons \text{ADP}+\text{Pi}$ reaction.

5.2 Example module: enzyme‐catalysed reaction

As an example, the enzyme‐catalysed reaction of Fig. 2 b is considered as a two‐port module (as illustrated in Fig. 5). In particular, the flowstat corresponding to Re :r 0 is replaced by port 1 and the chemostat corresponding to C :B is replaced by port 2. Thus (80) becomes

$$\left(\begin{array}{c}{\tilde{v}}_2\\ {\widetilde{\stackrel{⌣}{\mu }}}_E\end{array}\right)=\left(\begin{array}{cc}{G}_{11}& G_{12}\\ G_{21}& G_{22}\end{array}\right)\left(\begin{array}{c}{\tilde{v}}_0\\ {\widetilde{\stackrel{⌣}{\mu }}}_B\end{array}\right)$$ (96)

The system parameters were K _B = K _C = K _E = 1, κ ₁ = 10 and κ ₂ = 1. Three alternative values were used for K _A : 2, 10 and 100. Using an initial state ${\mathit{X}}_0=(\begin{array}{cccc}100& 1& 0& 1\end{array}){}^{\mathrm{T}}$, the steady states were found for each value of K _A and the system was linearised using the method of Section 4. The transfer functions for the three cases were found to be

$$G_2=\left(\begin{array}{cc}\frac{-s+10}{s^2+32s}& \frac{-0.34s-10.31}{s+32}\\ \frac{2.91s+32}{s^2+32s}& \frac{-1}{s+32}\end{array}\right)$$ (97)

$$G_{10}=\left(\begin{array}{cc}\frac{-s+90}{s^2+112s}& \frac{-0.10s-10.80}{s+112}\\ \frac{10.18s+112}{s^2+112s}& \frac{-1}{s+112}\end{array}\right)$$ (98)

$$G_{100}=\left(\begin{array}{cc}\frac{-s+990}{s^2+1012s}& \frac{-0.01s-10.98}{s+1012}\\ \frac{92s+1012}{s^2+1012s}& \frac{-1}{s+1012}\end{array}\right)$$ (99)

Although these transfer functions are simple enough to analyse directly, in more complex cases it is useful to look at the transfer function frequency responses obtained by replacing the Laplace variable s by jω where $\mathrm{j}=\sqrt{-1}$ and ω is a frequency in rad · s⁻¹. Fig. 7 gives the frequency response magnitude of the three transfer functions: G ₁₁ relating ${\tilde{v}}_0$ to ${\tilde{v}}_2$, G ₂₂ relating ${\widetilde{\stackrel{⌣}{\mu }}}_B$ to ${\widetilde{\stackrel{⌣}{\mu }}}_E$ and the loop‐interaction L _I = −G ₁₂ G ₂₁ for each of the three cases.

Fig. 7.

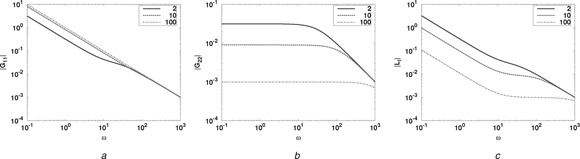
Example module: enzyme‐catalysed reaction. Three frequency responses are plotted for K_A = 210, 100 against frequency ω (rad · s⁻¹)

a |G ₁₁ (jω)|

b |G ₂₂ (jω)|

c |L _I (jω)| = |G ₁₂ (jω)G ₂₁ (jω)|

The forward transfer function G ₁₁ approaches 1/s as K _A increases, the transfer functions G ₂₂ and L _I decrease as K _A increases. Thus larger values of K _A give approximate behavioural modularity. However, this comes at an energetic cost measured by the external flow associated with the chemostat C :A .

5.3 Example module: phosphorylation/dephosphorylation

A bond graph model of the thermodynamically correct formulation of the phosphorylation/dephosphorylation cycle of Beard and Qian [61] was presented by Gawthrop and Crampin [13]. Fig. 9 a shows a modular version where the two ports are given by flowstat Re :r 0 and the chemostat C :MP . The three components representing ATP, ADP and Pi ( C :ATP, C :ADP and C :P) are also chemostats and provide the power source for the module.

As shown in Section 5.2, this module can be analysed by plotting the frequency response of the three transfer functions. The parameters (which are illustrative and do not correspond to a specific biological instance) are

$$\begin{array}{rl}& \mathit{X}=\left(\begin{array}{c}{x}_{E1}\\ x_{C1}\\ x_{E2}\\ x_{C2}\\ x_{\text{ATP}}\\ x_{\text{ADP}}\\ x_{\mathrm{P}}\\ x_M\\ x_{\text{MP}}\end{array}\right),{\mathit{X}}_0=\left(\begin{array}{c}0\\ 0\\ 0.001\\ 0\\ 110,100\\ 1\\ 0.01\\ 10\\ 0\end{array}\right),\\ & K=\left(\begin{array}{c}100\\ 1\\ 100\\ 1\\ 0.1\\ 0.001\\ 0.001\\ 1\\ 1\end{array}\right),\kappa =\left(\begin{array}{c}10\\ 1000\\ 10\\ 1000\end{array}\right)\end{array}$$ (100)

The (fixed) amount of ATP was set at three alternative values: x _ATP = 110, 100. As shown in Section 5.2, larger values give reduced loop interaction at the expense of more power needed to drive the module.

5.4 Example module: feedback inhibition

The idea that a product can inhibit an enzyme and thus give negative feedback is a well‐established concept in biology [62–65]. This section focuses on one possible mechanism, competitive inhibition [66, §1.4.3]. The basic idea is that the product P binds to the enzyme E to form a complex C (thus partially sequestering E) via the reaction

$$P+E\rightleftharpoons C$$ (101)

Together with an additional flow of enzyme modelled by Re :r 0, this reaction is modelled by the bond graph of Fig. 10 a. This can be represented as a two‐port module if C : P , Re :r 0 and associated junctions are replaced by ports. This module will be used in the sequel to apply feedback inhibition to the MAPK cascade.

Fig. 10.

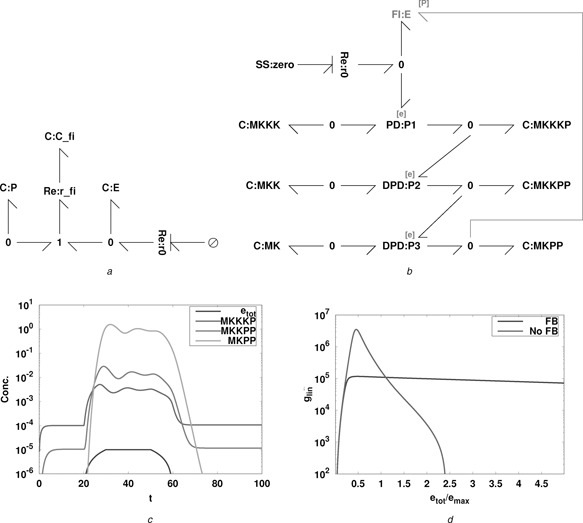
MAPK cascade with feedback inhibition

a Feedback inhibition

b MAPK cascade with feedback inhibition

c Time courses

d Incremental gains

6 MAPK cascades

The MAPK cascade is a well‐studied signalling pathway with ultrasensitive components [21, 22, 58]. However, the use of the Michaelis–Menten approximation to enzyme‐catalysed reactions can be misleading in this context. In particular, as discussed by Voit [67, §9.5], ‘It is tempting to set up the two phosphorylation steps with Michaelis–Menten rate functions, but such a strategy is not the best option, because (i) the enzyme concentration is not constant, (ii) the enzyme concentration is not necessarily smaller than the substrate concentration and (iii) the two reaction steps are competing for the same enzyme’.

This section shows that the bond graph property of computational modularity can be used to build a computational model of the MAPK cascade which is thermodynamically correct and thus avoids the pitfalls associated with inappropriate use of the Michaelis–Menten approximation. Moreover, having seen in Section 5.3 that that the bond graph module corresponding to phosphorylation/dephosphorylation can be designed to give approximate behavioural modularity, the MAPK cascade can be built with approximate behavioural modularity.

Fig. 9 b shows the bond graph of the MAPK cascade based on the phosphorylation/dephosphorylation module PD of Fig. 8 and the double phosphorylation/dephosphorylation module DPD the Re :r 0 component is used as a flowstat generating a flow v ₀ as discussed in Section 5.2. The non‐linear system of ODEs corresponding to Fig. 9 b was simulated for 100 time units with an input v ₀ given by

$$v_0=\left\{\begin{array}{cc}{10}^{-6}& 20\ge t\ge 30\\ -{10}^{-6}& 50\ge t\ge 60\\ 0& \text{otherwise}\end{array}\right.$$ (102)

This gives a maximum value of the total enzyme of e _max = 10⁻⁵. The system parameters are those used in Section 5.3.

Fig. 8.

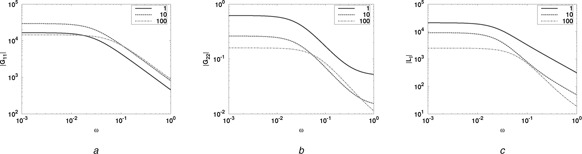
Example module: phosphorylation/dephosphorylation

a |G ₁₁ (jω)|

b |G ₂₂ (jω)|

c |L _I (jω)| = |G ₁₂ (jω)G ₂₁ (jω)|

Fig. 9 c shows the corresponding time courses for the total amount of enzyme e _tot, and the amounts of MKKKP, MKKPP and MKPP. A logarithmic scale is used to account for the large range of values. Note that the gain between e _tot and the concentration x _MKPP is of the order of 10⁶.

The steady‐state value of x _MKPP was computed for a range of values of e _tot and the incremental values (dx _MKPP /de _tot) were computed numerically for three values of ATP: $x_{\text{ATP}}=2.5,5,10$. Fig. 9 d shows the incremental gain plotted against e _tot. The high gain due to the ultrasensitivity of the phosphorylation/dephosphorylation modules vanishes between ATP amounts of 2 and 5.

In his seminal paper Black [68] points out that ‘by building an amplifier whose gain is deliberately made, say 40 dB higher than necessary …, and then feeding the output back on the input in such a way as to throw away the excess gain, it has been found possible to effect extraordinary improvement in constancy of amplification and freedom from non‐linearity.’ In this context, Fig. 10 b is the same as shown in Fig. 9 b except that the feedback inhibition module of Section 5.4 is incorporated into the bond graph and the system is re‐simulated with K _fi = 4 and κ _fi = 1.

The steady‐state value of x _MKPP was computed for a range of values of e _tot and the incremental values (dx _MKPP /de _tot) were computed numerically both with and without feedback and plotted in Fig. 10 d. The gain of the system is reduced by a factor of about 20, but the system is now more linear: the gain is approximately constant over a wider range of e _tot than was the case without feedback.

7 Conclusions

Building on its inherent computational modularity; it has been shown that the bond graph approach can be used to explain and adjust behavioural modularity. The MAPK cascade was used as an example to illustrate this point. It would be interesting to repeat the MAPK examples with parameter values taken from the literature [69, 70]. This may provide insight into the evolutionary trade‐off between energy consumption and signalling performance [71–73].

Control‐theoretic concepts based on linearisation were shown to provide a quantitative analysis of behavioural modularity. However, non‐linear systems can be approximated in other ways apart from linearisation. In the context of metabolic network modelling, Heijnen [74] discusses and compares a number of approximations including: logarithmic‐linear, power law generalised mass action, S‐systems [63, 67] and linear logarithmic [75, 76]. It would be interesting to see whether such approximations provide an alternative to linearisation in analysing behavioural modularity.

It has been suggested that metabolism and its dysfunctions may relate to certain diseases including Parkinson's disease [77, 78], heart disease [79], cancer [80, 81] and chronic fatigue [82]. It is envisaged the energy‐based approach used in this paper will help to understand such energy‐related diseases.

The example in this paper examines a signalling network as an analogy to an electronic amplifier. Gene regulatory networks have been analysed and synthesised as amplifiers [83–85]. Future work will examine the bond graph‐based analysis and synthesis of gene regulatory networks.