Observer‐based resilient finite‐time control of blood gases model during extra‐corporeal circulation

Abstract

This study aims at designing an observer‐based resilient controller to regulate the amount of oxygen and carbon dioxide in the blood of patients during the extra‐corporeal blood circulation process. More precisely, in this study, a suitable observer‐based resilient controller is constructed to regulate the levels of patient blood gases in a finite interval of time. The finite‐time boundedness with the prescribed $H_{\mathrm{\infty }}$ performance index of the considered blood gases control system against modelling uncertainty and external disturbances is ensured by using Lyapunov stability analysis. Moreover, a set of sufficient conditions for obtaining the controller gain is developed in the form of linear matrix inequalities (LMIs). Finally, the effectiveness of the proposed robust finite‐time control scheme is verified through simulation results. The result reveals that the blood gases are maintained in their physiological ranges during a stable extra‐corporeal circulation process via the proposed observer‐based resilient controller.

1 Introduction

In recent decades, extra‐corporeal blood circulation (ECC) process is one of the most important requirements during the cardiac surgeries such as coronary bypass or heart transplantation [1–3]. Since, during the cardiac operation, the heart is opened and temporarily stopped, so the external machine is required to pump and maintain the blood with proper oxygen and carbon dioxide concentrations [4]. More precisely, ECC process is used to maintain the patient's blood circulation and lung function outside the body and also it gives a life support for the persons whose heart and lungs are unable to regulate an adequate amount of oxygen and carbon dioxide in the blood to sustain life [5]. In particular, the machine cannot function the same way as the heart, so it is necessary and significant to do research on the enhancement and better performance of ECC process for the safety of patient. On the other hand, continuous information about flow rate and arterial partial pressure of blood gases are significant as a measure of the cardiopulmonary state of a patient in operation theaters. Currently, several methods are used for finding flow rate and arterial partial pressure of blood gas measurements; however, most of the techniques are too sensitive to interference from external noise events. On another research front, many real‐time control systems states are successfully estimated by constructing state observer [6–9]. In observer‐based problems, the unavailable states are estimated from the knowledge of inputs and outputs of the system. A new LMI‐based approach is developed in [10] for designing an observer‐based controller for stochastic time‐delay system without imposing any constraints on the system matrices.

Additionally, in practical point of view, an ECC process commonly exists as a possibility for the occurrence of perturbations in the controller as well as observer gains. This phenomenon may lead to poor performance of the system, and hence it is significant to design a controller which can tolerate certain level of gain variations in the circulation process. Therefore, resilient‐based control scheme has received much attention in the study of dynamical control systems [11–13]. For instance, the conditions for the existence of resilient controllers are derived in [14] for the Markovian jump non‐linear systems with gain variations. Sakthivel et al. [15] investigated the non‐fragile control synthesis problem for uncertain structural systems by using Lyapunov–Krasovskii functional and LMI technique. On the other hand, the $H_{\mathrm{\infty }}$ control problem has gained much attention due to its application in control systems [16, 17]. It was proposed to reduce the effect of disturbance input on regulated output within a prescribed level [17–19]. In [20], the problem of non‐fragile $H_{\mathrm{\infty }}$ control has been discussed for a class of discrete‐time systems with randomly occurring gain variations, channel fading as well as infinite‐distributed delays.

During cardiac operations, informations about flow rate and arterial partial pressure of blood gases have to be monitored and the optimal or adequate rate of these factors has to be maintained throughout the process. The trajectories of these components should be controlled from an initial to a fixed value during a prescribed time interval or in other words it can be stated that the trajectories flow rate and arterial pressure of blood gases should be bounded over a finite‐time interval. Unless otherwise it may result in serious complications which may even put the patients’ life in risk. Hence, the transient performance of an ECC process is crucial. These requirements can be accomplished by using the notion of finite‐time stability. Finite‐time stability is a concept which admits that the state does not exceed a certain boundary for a fixed finite‐time interval [21, 22]. The issue of finite‐time $H_{\mathrm{\infty }}$ control for Markovian jump non‐linear system has been discussed in [23]. Mahmoud [24] obtained two distinct control design schemes for controlling the patient blood gases in their physiological ranges during a stable extra‐corporeal circulation process. Moreover, most of the existing works on the feedback control problem for ECC process have been carried out over an infinite‐time interval (see [24] and references therein). However, up to now, no work has been reported in connection with the finite‐time $H_{\mathrm{\infty }}$ resilient control for blood gases control system. Motivated by this fact, in this paper, we discuss the problem of observer‐based resilient $H_{\mathrm{\infty }}$ finite‐time boundedness for controlling the patient blood gases with aim of maintaining them in the physiological ranges during ECC process. The main contributions of this paper can be summarised as follows:

• The proposed observer‐based resilient controller estimates the exact states of the considered blood gases control system, namely flow rates and arterial partial pressure of the blood gases, for regulating the levels of patient blood gases in a finite interval of time.

• By employing Lyapunov technique, sufficient conditions in the form of LMIs are presented to ensure the finite‐time boundedness of the patient blood gas control system with a desired $H_{\mathrm{\infty }}$ performance index.

• Moreover, the proposed non‐fragile feedback controller design is more general since it contains the perturbations in the controller and observer structure.

The main difficulty in dealing with this problem is how to obtain finite‐time boundedness for blood gases model during ECC process, when the issues such as unmeasurable flow rates of blood gases and perturbations in commanded flow rates of blood gases occurs simultaneously. Another complication in handling this problem is that the unacceptable responses of the states have to be avoided even in the presence of external disturbances.

Finally, a numerical example is provided with simulation results to illustrate the effectiveness of the proposed control design.

2 Problem formulation

In this section, we first consider the state‐space representation of the blood gases control system in the following form [24]:

$$\left\{\begin{array}{rl}& \dot{x}(t)=\mathit{A}x(t)+\mathit{B}u(t)+\mathbf{\Gamma }w(t)\\ & z(t)=\mathit{G}x(t)+\mathit{D}u(t)+\mathbf{\Phi }w(t)\\ & y(t)=\mathit{C}x(t)+\mathbf{\Psi }w(t),\end{array}\right.$$ (1)

where $x(t)={\left[\begin{array}{cccc}{x}_1^{\mathrm{T}}(t)& x_2^{\mathrm{T}}(t)& x_3^{\mathrm{T}}(t)& x_4^{\mathrm{T}}(t)\end{array}\right]}^{\mathrm{T}}$, $x_1(t)$ is the flow rate of oxygen, $x_2(t)$ is the flow rate of carbon dioxide, $x_3(t)$ is the arterial partial pressure of oxygen, $x_4(t)$ is the arterial partial pressure of carbon dioxide, $u(t)={\left[\begin{array}{cc}{u}_1^{\mathrm{T}}(t)& u_2^{\mathrm{T}}(t)\end{array}\right]}^{\mathrm{T}}$, $u_1(t)$ is the commanded oxygen flow rate and $u_2(t)$ is the commanded carbon dioxide flow rate; $\mathit{w}(t)$ is the external disturbance vector with ${\int }_0^{\mathcal{T}}{w}^{\mathrm{T}}(t)\mathit{w}(t)\mathrm{d}t\le d^2,d>0$. Furthermore $\mathit{A}\in {\mathbb{R}}^{4\times 4}$, $\mathit{B}\in {\mathbb{R}}^{4\times 2}$, $\mathit{C}\in {\mathbb{R}}^{2\times 4}$, $\mathit{G}\in {\mathbb{R}}^{2\times 4}$, $\mathit{D}\in {\mathbb{R}}^{2\times 2}$, $\mathit{F}\in {\mathbb{R}}^{2\times 4}$, $\mathbf{\Gamma }\in {\mathbb{R}}^{4\times 2}$, $\mathbf{\Phi }\in {\mathbb{R}}^{2\times 2}$ and $\mathbf{\Psi }\in {\mathbb{R}}^{2\times 2}$ are given real constant matrices that describe the dynamics of blood gases.

In many practical control systems, when all state variables are not measurable, an observer is required. In this paper, in order to estimate the flow rate and arterial pressure of blood gases, we construct the following state observer:

$$\left\{\begin{array}{rl}& \dot{\hat{x}}(t)=\mathit{A}\hat{x}(t)+\mathit{B}u(t)+\mathit{L}[y(t)-\hat{y}(t)],\\ & \hat{y}(t)=\mathit{C}\hat{x}(t),\\ & u(t)=\mathit{K}\hat{x}(t),\end{array}\right.$$ (2)

where $\hat{x}(t)$ is the estimation of $x(t)$; $\hat{y}(t)$ is the observer output; $\mathit{K}$ and $\mathit{L}$ are the controller and observer gains, respectively, which have to be designed. By defining the estimated error as $e(t)=x(t)-\hat{x}(t)$, and combining (1) and (2), the closed‐loop augmented system can be expressed as follows:

$$\left\{\begin{array}{c}{\dot{x}}_c(t)={\mathit{A}}_c{x}_c(t)+{\mathit{B}}_c\mathit{w}(t)\\ z(t)=\mathit{C}{x}_c(t)+{\mathit{D}}_c\mathit{w}(t),\end{array}\right.$$ (3)

$$\left.\begin{array}{c}\text{where}{x}_c(t)=\left[\begin{array}{c}\hat{x}(t)\\ e(t)\end{array}\right],{\mathit{A}}_c=\left[\begin{array}{cc}\mathit{A}+\mathit{B}\mathit{K}& \mathit{L}\mathit{C}\\ 0& \mathit{A}-\mathit{L}\mathit{C}\end{array}\right],\\ {\mathit{B}}_c=\left[\begin{array}{c}\mathit{L}\mathrm{\Psi }\\ \mathrm{\Gamma }-\mathit{L}\mathrm{\Psi }\end{array}\right],{\mathit{C}}_c=\left[\begin{array}{cc}\mathit{G}+\mathit{D}\mathit{K}& \mathit{G}\end{array}\right]\text{and}{\mathit{D}}_c=\mathrm{\Phi }.\end{array}\right\}$$ (4)

Before proceeding further, we consider the following definitions and lemma, which are needed to obtain our main results.

[25] The closed‐loop system (3) is finite‐time bounded (FTB) with respect to ($c_1$ , $c_2$, $\mathcal{T}$, $\mathit{R}$, d ), where $0<c_1<c_2$ and $\mathit{R}>0$ if

$$\begin{array}{rl}& x_c^{\mathrm{T}}(0)\mathit{R}{x}_c(0)\le c_1^2\Rightarrow x_c^{\mathrm{T}}(t)\mathit{R}{x}_c(t)<c_2^2\\ & \mathrm{\forall }{\int }_0^{\mathcal{T}}{w}^{\mathrm{T}}(t)w(t)\mathrm{d}t\le d^2\text{and}\mathrm{\forall }t\in [0,\mathcal{T}].\end{array}$$ (5)

[25] The closed‐loop system (3) is $H_{\mathrm{\infty }}$ FTB with respect to ( $c_1$ , $c_2$, $\mathcal{T}$, $\mathit{R}$, $\gamma$ , d ), where $0<c_1<c_2$ and $\mathit{R}>0$ if the closed‐loop system ( 3) is FTB with respect to ( $c_1$ , $c_2$, $\mathcal{T}$, $\mathit{R}$, d) and under zero initial condition, the controlled output $z(t)$ satisfies the following constrained condition:

$${\int }_0^{\mathcal{T}}{z}^{\mathrm{T}}(t)z(t)\mathrm{d}t<{\gamma }^2{\int }_0^{\mathcal{T}}{w}^{\mathrm{T}}(t)w(t)\mathrm{d}t$$ (6)

for any non‐zero $\mathit{w}(t)$, where $\gamma$ is a prescribed positive scalar.

[10] For a real scalar $\rho >0$ and real matrices $\mathbf{\Lambda }$, ${\mathit{U}}_i$ , ${\mathit{V}}_i$ and ${\mathit{W}}_i$ ( $i=1,\dots ,N$ ), if the condition $\left[\begin{array}{c}\mathcal{A}\end{array}\right]<0$ holds where matrix $\mathcal{A}$ is given by

$$\left[\begin{array}{ccccc}\mathbf{\Lambda }& {\mathit{U}}_1+\rho {\mathit{V}}_1& {\mathit{U}}_2+\rho {\mathit{V}}_2& \cdots & {\mathit{U}}_N+\rho {\mathit{V}}_N\\ & -\rho {\mathit{W}}_1-\rho {\mathit{W}}_1^{\mathrm{T}}& 0& \cdots & 0\\ & \ast & -\rho {\mathit{W}}_2-\rho {\mathit{W}}_2^{\mathrm{T}}& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ & \ast & \ast & \ast & -\rho {\mathit{W}}_N-\rho {\mathit{W}}_N^{\mathrm{T}}\end{array}\right]$$

then, we have

$$\mathbf{\Lambda }+\sum _{i=1}^N[({\mathit{U}}_i{\mathit{W}}_i^{-1}{\mathit{V}}_i^{\mathrm{T}})+({\mathit{U}}_i{\mathit{W}}_i^{-1}{\mathit{V}}_i^{\mathrm{T}}){}^{\mathrm{T}}]<0.$$

3 Main results

In this section, first, we will investigate the finite‐time boundedness and $H_{\mathrm{\infty }}$ performance analysis for the blood gases control system (1). Next, a resilient controller design will be designed with the $H_{\mathrm{\infty }}$ performance criterion.

Given positive scalars $\alpha$, $\mathcal{T}$, $c_1$ , d and matrices $\mathit{R}>0$, $\mathit{K}$, $\mathit{L}$, system (1) under the observer‐based feedback controller is FTB with respect to $(c_1,c_2,\mathcal{T},\mathit{R},d)$ if there exist symmetric matrices $\mathit{P}>0$ , ${\mathit{Q}}_1>0$ , ${\mathit{Q}}_2>0$ and positive scalars ${\eta }_1$ , ${\eta }_2$ and $c_2$ such that

$$\left[\begin{array}{cc}\text{sym}(\mathit{P}{\mathit{A}}_c)-\alpha \mathit{P}& \mathit{P}{\mathit{B}}_c\\ & -{\mathit{Q}}_2\end{array}\right]<0,$$ (7)

$${\eta }_{1}I<{\mathit{Q}}_1^{-1}<\mathit{I},$$ (8)

$$0<{\mathit{Q}}_2<{\eta }_2\mathit{I},$$ (9)

$${\eta }_1^{-1}{c}_1^2+{\eta }_2{d}^2<{\mathrm{e}}^{-\alpha \mathcal{T}}{c}_2^2,$$ (10)

where $\mathit{P}=R^{(1/2)}{\mathit{Q}}_1{R}^{(1/2)}$ and $\text{sym}(\mathit{P}{\mathit{A}}_c)$ denotes $\mathit{P}{\mathit{A}}_c+{\mathit{A}}_c^{\mathrm{T}}{\mathit{P}}^{\mathrm{T}}$ .

To prove the required result, we consider the following Lyapunov function candidate:

$$V(x_c(t))=x_c^{\mathrm{T}}(t)\mathit{P}{x}_c(t).$$ (11)

Then, we take the time derivative along the trajectories of the closed‐loop system (3), we obtain

$$\begin{array}{rl}\dot{V}(x_c(t))& ={\dot{x}}_c^{\mathrm{T}}(t)\mathit{P}{x}_c(t)+x_c^{\mathrm{T}}(t)\mathit{P}{\dot{x}}_c(t)\\ & ={\left[\begin{array}{c}{x}_c(t)\\ \mathit{w}(t)\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{cc}\text{sym}(\mathit{P}{\mathit{A}}_c)& \mathit{P}{\mathit{B}}_c\\ \ast & 0\end{array}\right]\left[\begin{array}{c}{x}_c(t)\\ \mathit{w}(t)\end{array}\right].\end{array}$$ (12)

From (7), (9) and (12) we have

$$\begin{array}{rl}\dot{V}(x_c(t))& <\alpha V(x_c(t))+w^{\mathrm{T}}(t){\mathit{Q}}_{2}w(t),\\ & <\alpha V(x_c(t))+{\eta }_2{w}^{\mathrm{T}}(t)w(t).\end{array}$$ (13)

Multiplying both sides of (13) by ${\mathrm{e}}^{-\alpha t}$, we can obtain

$${\mathrm{e}}^{-\alpha t}\dot{V}(x_c(t))-\alpha {\mathrm{e}}^{-\alpha t}V(x_c(t))<v^{-\alpha t}{\eta }_2{w}^{\mathrm{T}}(t)w(t),$$ (14)

which can be equivalently written as

$$\frac{\mathrm{d}}{\mathrm{d}t}({\mathrm{e}}^{-\alpha t}V(x_c(t))<{\mathrm{e}}^{-\alpha t}{\eta }_2{w}^{\mathrm{T}}(t)w(t).$$ (15)

Integrating (15) from $0$ to t with $t\in [0,\mathcal{T}]$, we can obtain

$${\mathrm{e}}^{-\alpha t}V(x_c(t))-V(x_c(0))<{\eta }_2{\int }_0^t{\mathrm{e}}^{-\alpha \tau }{w}^{\mathrm{T}}(\tau )w(\tau )\mathrm{d}\tau .$$ (16)

In view of $\alpha >0$, ${\mathrm{e}}^{-\alpha \tau }<1$, from (8), (11) and (16) and it follows that:

$$\begin{array}{rl}V(x_c(t))& <{\mathrm{e}}^{\alpha t}V(x_c(0))+{\eta }_2{\int }_0^t{\mathrm{e}}^{\alpha (t-\tau )}{w}^{\mathrm{T}}(\tau )w(\tau )\mathrm{d}\tau \\ & <{\mathrm{e}}^{\alpha t}(x_c^{\mathrm{T}}(0)\mathit{P}{x}_c(0))+{\eta }_2{\int }_0^t{\mathrm{e}}^{\alpha (t-\tau )}{w}^{\mathrm{T}}(\tau )w(\tau )\mathrm{d}\tau \\ & \le {\mathrm{e}}^{\alpha \mathcal{T}}({\eta }_1^{-1}{c}_1^2+{\eta }_2{d}^2),\end{array}$$ (17)

$$V(x_c(t))=x_c^{\mathrm{T}}(t)\mathit{P}{x}_c(t)>x_c^{\mathrm{T}}(t)\mathit{R}{x}_c(t).$$ (18)

From (17) and (18), it guarantees that

$$x_c^{\mathrm{T}}(t)\mathit{R}{x}_c(t)<{\mathrm{e}}^{\alpha \mathcal{T}}({\eta }_1^{-1}{c}_1^2+{\eta }_2{d}^2)<c_2^2.$$ (19)

Hence, by Definition 1, system (1) is FTB. This completes the proof. □

The following theorem provides sufficient conditions for finite‐time boundedness with $H_{\mathrm{\infty }}$ performance index for the blood gases control system (1).

The blood gases control system (1) with external disturbance is FTB under the $H_{\mathrm{\infty }}$ controller $u(t)=\mathit{K}\hat{x}(t)$ if for any given positive scalars $\alpha$, $\mathcal{T}$, $c_1$ , d and matrices $\mathit{R}>0$, $\mathit{K}$, $\mathit{L}$, there exist symmetric positive definite matrices $\mathit{P}$ and ${\mathit{Q}}_1$ , and positive scalars ${\eta }_1$ , $c_2$ and $\gamma$ such that the following constraints hold:

$$\left[\begin{array}{ccc}\text{sym}(\mathit{P}{\mathit{A}}_c)-\alpha \mathit{P}& \mathit{P}{\mathit{B}}_c& {\mathit{C}}_c^{\mathrm{T}}\\ & -{\gamma }^2{\mathrm{e}}^{-\alpha \mathcal{T}}& {\mathit{D}}_c^{\mathrm{T}}\\ & \ast & -\mathit{I}\end{array}\right]<0,$$ (20)

$${\eta }_1\mathit{I}<{\mathit{Q}}_1^{-1}<\mathit{I},$$ (21)

$${\eta }_1^{-1}{c}_1^2+{\gamma }^2{\mathrm{e}}^{-\alpha \mathcal{T}}{d}^2<{\mathrm{e}}^{-\alpha \mathcal{T}}{c}_2^2.$$ (22)

The matrix inequality (20) implies necessarily the following equation:

$$\left[\begin{array}{cc}\text{sym}(\mathit{P}{\mathit{A}}_c)-\alpha \mathit{P}& \mathit{P}{\mathit{B}}_c\\ & -{\gamma }^2{\mathrm{e}}^{-\alpha \mathcal{T}}\end{array}\right]<0.$$ (23)

Letting ${\mathit{Q}}_2={\gamma }^2{\mathrm{e}}^{-\alpha \mathcal{T}}\mathit{I}$, by Theorem 1, conditions (22) and (23) guarantee that system (1) is FTB. Furthermore, considering (11) and noting (12) and (23), we have

$$\dot{V}(x_c(t))<\alpha V(x_c(t))+{\gamma }^2{\mathrm{e}}^{-\alpha \mathcal{T}}{w}^{\mathrm{T}}(t)w(t)-z^{\mathrm{T}}(t)z(t).$$ (24)

Multiplying (24) by ${\mathrm{e}}^{-\alpha t}$

$${\mathrm{e}}^{-\alpha t}\dot{V}(x_c(t))-\alpha {\mathrm{e}}^{-\alpha t}V(x_c(t))<{\mathrm{e}}^{-\alpha t}[{\gamma }^2{\mathrm{e}}^{-\alpha \mathcal{T}}{w}^{\mathrm{T}}(t)w(t)-z^{\mathrm{T}}(t)z(t)]$$ (25)

and under zero initial condition, by integrating $0$ to $\mathcal{T}$, we obtain

$${\mathrm{e}}^{-\alpha \mathcal{T}}V(x_c(\mathcal{T}))<{\int }_0^{\mathcal{T}}{\mathrm{e}}^{-\alpha t}[{\gamma }^2{\mathrm{e}}^{-\alpha \mathcal{T}}{w}^{\mathrm{T}}(t)w(t)-z^{\mathrm{T}}(t)z(t)]\mathrm{d}t.$$ (26)

From the fact that ${\mathrm{e}}^{-\alpha \mathcal{T}}V(x_c(\mathcal{T}))>0$, it implies that

$${\int }_0^{\mathcal{T}}{\mathrm{e}}^{-\alpha t}{z}^{\mathrm{T}}(t)z(t)\mathrm{d}t<{\gamma }^2{\mathrm{e}}^{-\alpha \mathcal{T}}{\int }_0^{\mathcal{T}}{\mathrm{e}}^{-\alpha t}{w}^{\mathrm{T}}(t)w(t)\mathrm{d}t.$$ (27)

In view of ${\mathrm{e}}^{-\alpha \mathcal{T}}\le {\mathrm{e}}^{-\alpha t}\le 1$ for all $t\in [0,\mathcal{T}]$, we have

$${\int }_0^{\mathcal{T}}{z}^{\mathrm{T}}(t)z(t)\mathrm{d}t<{\gamma }^2{\int }_0^{\mathcal{T}}{w}^{\mathrm{T}}(t)w(t)\mathrm{d}t.$$

Thus, the condition (6) is satisfied and hence, by Definition 2, the blood gases control system (1) is FTB under the proposed $H_{\mathrm{\infty }}$ observer‐based feedback controller. This completes the proof. □

Most of the existing works on state‐space models of ECC process have been carried out over an infinite‐time interval, but it is not always appropriate since it possesses undesirable transient performance. To study the transient performance of the system, the concept of finite‐time stability has to be implemented. Despite various improvements in the area of ECC process, since it supports human life, there requires higher degrees of the ability of an entire study to be duplicated and to reduce the risks which demand the use of various controls. Furthermore, though there are some studies on robust control for blood gases model during extra‐corporeal circulation in the presence of system parameter uncertainties, the possibility of deviations or vagueness arising in the commanded flow rates of blood gases has not yet been reported which is a serious problem to be resolved since human life is involved with the system.

Although there has been investigations done on control of blood gases during ECC process, all of them are based on the assumption that the states can be measured. In practise, the full measurement of the system states is not always available, but it is required for diagnosis and control of the system. This motivated us to develop an observer‐based control with occurrence of deviations in the estimated blood gases model during extra‐corporeal circulation. Usually, in the literature, observer‐based control is proposed using singular value decomposition technique and by imposing extra constraints on the system matrices. However, different from usual way, by introducing slack matrix variables and without imposing extra constraints on the system matrices, sufficient conditions for the finite‐time stability via observer‐based resilient are derived in the next section.

3.1 Resilient finite‐time observer‐based $H_{\mathrm{\infty }}$ controller

In this section, we design a resilient observer‐based controller for the blood gases control system (1) to ensure the regulations of the blood gases with a prescribed $H_{\mathrm{\infty }}$ performance index in a finite interval of time. In this connection, we consider the controller and observer gains are in the forms $\mathit{K}+\mathrm{\Delta }\mathit{K}(t)$ and $\mathit{L}+\mathrm{\Delta }\mathit{L}(t)$, respectively, where $\mathrm{\Delta }\mathit{K}(t)$ and $\mathrm{\Delta }\mathit{L}(t)$ represent gain perturbations, which have the following form:

$$\begin{array}{c}\mathrm{\Delta }\mathit{K}(t)={\mathit{M}}_{\mathit{K}}{\mathbf{\Sigma }}_{\mathit{K}}(t){\mathit{N}}_K,\mathrm{\Delta }\mathit{L}(t)={\mathit{M}}_{\mathit{L}}{\mathbf{\Sigma }}_{\mathit{L}}(t){\mathit{N}}_{\mathit{L}},\end{array}$$ (28)

where ${\mathit{M}}_{\mathit{K}}$, ${\mathit{M}}_{\mathit{L}}$, ${\mathit{N}}_{\mathit{K}}$ and ${\mathit{N}}_{\mathit{L}}$ are known constant matrices, and ${\mathbf{\Sigma }}_{\mathit{K}}(t)$ and ${\mathbf{\Sigma }}_{\mathit{L}}(t)$ are unknown matrices satisfying ${\mathbf{\Sigma }}_{\mathit{K}}^{\mathrm{T}}(t){\mathbf{\Sigma }}_{\mathit{K}}(t)\le \mathit{I}$ and ${\mathbf{\Sigma }}_{\mathit{L}}^{\mathrm{T}}(t){\mathbf{\Sigma }}_{\mathit{L}}(t)\le \mathit{I}$. Then, the state observer (2) can be rewritten as

$$\left\{\begin{array}{rl}& \dot{\hat{x}}(t)=\mathit{A}\hat{x}(t)+\mathit{B}u(t)+(\mathit{L}+\mathrm{\Delta }\mathit{L}(t))[y(t)-\hat{y}(t)]\\ & \hat{y}(t)=\mathit{C}\hat{x}(t)\\ & u(t)=(\mathit{K}+\mathrm{\Delta }\mathit{K}(t))\hat{x}(t).\end{array}\right.$$ (29)

Now, the matrices in (4) can be rewritten as

$$\left\{\begin{array}{rl}& {\mathit{A}}_c={\mathit{A}}_1+{\mathit{B}}_1(\mathit{K}+\mathrm{\Delta }\mathit{K}(t)){\mathit{I}}_1+{\mathit{I}}_2(\mathit{L}+\mathrm{\Delta }\mathit{L}(t)){\mathit{C}}_2\\ & {\mathit{B}}_c={\mathbf{\Gamma }}_1+{\mathit{I}}_2(\mathit{L}+\mathrm{\Delta }\mathit{L}(t))\mathbf{\Psi }\\ & {\mathit{C}}_c={\mathit{G}}_1+\mathit{D}(\mathit{K}+\mathrm{\Delta }\mathit{K}(t)){\mathit{I}}_1,{\mathit{D}}_c=\mathbf{\Phi },\end{array}\right.$$ (30)

where ${\mathit{A}}_1=\left[\begin{array}{cc}\mathit{A}& 0\\ 0& \mathit{A}\end{array}\right]$, ${\mathit{B}}_1=\left[\begin{array}{c}\mathit{B}\\ 0\end{array}\right]$, ${\mathit{I}}_1=\left[\begin{array}{cc}\mathit{I}& 0\end{array}\right]$, ${\mathit{I}}_2={\left[\begin{array}{cc}\mathit{I}& -\mathit{I}\end{array}\right]}^{\mathrm{T}}$, ${\mathit{C}}_1=\left[\begin{array}{cc}0& \mathit{C}\end{array}\right]$, ${\mathit{G}}_1=\left[\begin{array}{cc}\mathit{G}& \mathit{G}\end{array}\right]$ and ${\mathbf{\Gamma }}_1={\left[\begin{array}{cc}0& {\mathbf{\Gamma }}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}}$.

Consider the blood gases control system (1) with the observer‐based non‐fragile controller $u(t)=(\mathit{K}+\mathrm{\Delta }\mathit{K}(t))\hat{x}(t)$ with gain perturbations satisfying ( 28 ). For given positive scalars $\rho$ , $\alpha$, $\mathcal{T}$, $c_1$ , d and matrix $\mathit{R}>0$ if there exist matrices $\mathit{P}>0$ , ${\mathit{Q}}_1>0$ , ${\mathit{X}}_K$ , ${\mathit{X}}_L$ , ${\mathit{Y}}_K$ , ${\mathit{Y}}_L$ and positive scalars ${\eta }_1$ , $c_2$ , $\gamma$ , ${\epsilon }_1$ and ${\epsilon }_2$ such that the following constraints hold:

$$\left[\begin{array}{cc}{\mathbf{\Pi }}_1& {\mathbf{\Pi }}_2\\ \ast & {\mathbf{\Pi }}_3\end{array}\right]<0,$$ (31)

$${\eta }_{1}I<{\mathit{Q}}_1^{-1}<I,$$ (32)

$$\left[\begin{array}{cc}{\gamma }^2{d}^2{\mathrm{e}}^{-\alpha \mathcal{T}}-c_2^2{\mathrm{e}}^{-\alpha \mathcal{T}}& c_1\\ \ast & -{\eta }_1\end{array}\right]<0,$$ (33)

where

$$\begin{array}{rl}{\mathbf{\Pi }}_1& =\left[\begin{array}{ccc}{a}_1-\alpha \mathit{P}& \mathit{P}{\mathbf{\Gamma }}_1+{\mathit{I}}_2{\mathit{Y}}_{\mathit{L}}\mathbf{\Psi }& {\mathit{G}}_1^{\mathrm{T}}\\ \ast & -{\gamma }^2{\mathrm{e}}^{-\alpha \mathcal{T}}& {\mathrm{\Phi }}^{\mathrm{T}}\\ \ast & \ast & -I\end{array}\right],\\ {\mathbf{\Pi }}_2& =\left[\begin{array}{cccccc}{a}_2& a_3& a_4& a_5& \mathit{P}{\mathit{I}}_2{\mathit{M}}_{\mathit{L}}& {ϵ}_2{\mathit{C}}_1^{\mathrm{T}}{\mathit{N}}_L^{\mathrm{T}}\\ 0& \rho {\mathbf{\Psi }}^{\mathrm{T}}{\mathit{Y}}_L^{\mathrm{T}}& 0& 0& 0& {ϵ}_2{\mathrm{\Psi }}^{\mathrm{T}}{N}_L^{\mathrm{T}}\\ \mathit{D}& 0& \mathit{D}{\mathit{M}}_{\mathit{K}}& 0& 0& 0\end{array}\right],\end{array}$$

${\mathrm{\Pi }}_3=\text{diag}\{-\rho {\mathit{X}}_K-\rho {\mathit{X}}_K^{\mathrm{T}},-\rho {\mathit{X}}_L-\rho {\mathit{X}}_L^{\mathrm{T}},-{ϵ}_{1}I,-{ϵ}_{1}I,-{ϵ}_{2}I,-{ϵ}_{2}I\}$, $a_1=\text{sym}(\mathit{P}{\mathit{A}}_1+{\mathit{B}}_1{\mathit{Y}}_{\mathit{K}}{\mathit{I}}_1+{\mathit{I}}_2{\mathit{Y}}_L{\mathit{C}}_1)$ , $a_2=-{\mathit{B}}_1{\mathit{X}}_K+\mathit{P}{\mathit{B}}_1+\rho {\mathit{I}}_1^{\mathrm{T}}{\mathit{Y}}_K^{\mathrm{T}}$ , $a_3=-{\mathit{I}}_2{\mathit{X}}_L+\mathit{P}{\mathit{I}}_2+\rho {\mathit{C}}_1^{\mathrm{T}}{\mathit{Y}}_L^{\mathrm{T}}$ , $a_4=\mathit{P}{\mathit{B}}_1{M}_K$ and $a_5={ϵ}_1{\mathit{I}}_1^{\mathrm{T}}{\mathit{N}}_K^{\mathrm{T}}$ , then the blood gases control system ( 1) is $H_{\mathrm{\infty }}$ FTB with disturbance attenuation $\gamma >0$ via the proposed non‐fragile observer‐based controller, where the controller and observer gains are given by $\mathit{K}={\mathit{X}}_K^{-1}{\mathit{Y}}_K$ and $\mathit{L}={\mathit{X}}_L^{-1}{\mathit{Y}}_L$ , respectively.

By following a similar procedure as in the proof of Theorem 2, we can easily obtain the $H_{\mathrm{\infty }}$ FTB criterion. By using the relations in (30), it can be established that:

$$\mathit{P}{\mathit{B}}_1\mathit{K}{\mathit{S}}_1={\mathit{B}}_1{\mathit{Y}}_K{\mathit{S}}_1+(-{\mathit{B}}_1{\mathit{X}}_K+\mathit{P}{\mathit{B}}_1){\mathit{X}}_K^{-1}{\mathit{Y}}_K{\mathit{S}}_1,$$ (34)

$$\mathit{P}{\mathit{I}}_2\mathit{L}{\mathit{S}}_2={\mathit{I}}_2{\mathit{Y}}_L{\mathit{S}}_2+(-{\mathit{I}}_2{\mathit{X}}_L+\mathit{P}{\mathit{I}}_2){\mathit{X}}_L^{-1}{\mathit{Y}}_L{\mathit{S}}_2,$$ (35)

with ${\mathit{S}}_1=\left[\begin{array}{ccc}{\mathit{I}}_1& 0& 0\end{array}\right]$ and ${\mathit{S}}_2=\left[\begin{array}{ccc}{\mathit{C}}_1& \mathbf{\Psi }& 0\end{array}\right].$ Then, using (30), (34) and (35), (20) can be written as

$${\mathbf{\Pi }}_1+\text{sym}(E_1{\mathit{X}}_K^{-1}{F}_1^{\mathrm{T}}+E_2{\mathit{X}}_L^{-1}{F}_2^{\mathrm{T}}+E_3{\mathrm{\Sigma }}_K{F}_3^{\mathrm{T}}+E_4{\mathrm{\Sigma }}_L{F}_4^{\mathrm{T}})<0,$$ (36)

where $E_1={\left[\begin{array}{ccc}-{\mathit{X}}_K^{\mathrm{T}}{B}_1^{\mathrm{T}}+B_1^{\mathrm{T}}P& 0& D_1^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}}$, $F_1=S_1^{\mathrm{T}}{\mathit{Y}}_K^{\mathrm{T}}$, $E_2={\left[\begin{array}{ccc}-{\mathit{X}}_L^{\mathrm{T}}{I}_2^{\mathrm{T}}+I_2^{\mathrm{T}}P& 0& 0\end{array}\right]}^{\mathrm{T}}$, $F_2=S_2^{\mathrm{T}}{\mathit{Y}}_L^{\mathrm{T}}$, $E_3={\left[\begin{array}{ccc}{M}_K^{\mathrm{T}}{B}_1^{\mathrm{T}}P& 0& M_K^{\mathrm{T}}{D}_1^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}}$, $F_3=S_1^{\mathrm{T}}{N}_K^{\mathrm{T}}$, $E_4={\left[\begin{array}{ccc}{M}_L^{\mathrm{T}}{I}_2\mathit{P}& 0& 0\end{array}\right]}^{\mathrm{T}}$ and $F_4=S_2^{\mathrm{T}}{N}_L^{\mathrm{T}}$. By using Lemma 1 and Lemma 2.7 in [15], (36) guarantees (31). Therefore, the considered blood gases control system (1) is $H_{\mathrm{\infty }}$ FTB via the non‐fragile observer‐based controller in (29). □

A reconstruction in (4) is done to obtain (30) which will bring the gain matrices $\mathit{K}$ and $\mathit{L}$ apart in $A_c$. This will pay way for convenient synthesis of controller. By introducing (34), (35) and by using Lemma 1, the pairing of $\mathit{K}$ and $\mathit{L}$ with $\mathit{P}$ is successfully avoided which made it easy to proceed with the design of observer‐based finite‐time $H_{\mathrm{\infty }}$ controller for the system.

When the gain perturbation are absent, that is, when $\mathrm{\Delta }K=\mathrm{\Delta }L=0$, the matrices in (30) will take the form $A_c=A_1+B_1\mathit{K}{I}_1+I_2\mathit{L}{C}_2,B_c={\mathrm{\Gamma }}_1+I_2\mathit{L}\mathrm{\Psi },C_c=G_1+\mathit{D}\mathit{K}{I}_1,D_c=\mathrm{\Phi }.$In this case, the $H_{\mathrm{\infty }}$ FTB observer‐based controller can be designed through the following corollary.

The blood gases control system (1) is $H_{\mathrm{\infty }}$ FTB under the feedback controller ( 2) with respect to $(c_1,c_2,\mathcal{T},\mathit{R},\gamma ,d)$ if for any given positive scalars $\rho$ , $\alpha$, $\mathcal{T}$, $c_1$ , d and matrix $\mathit{R}>0$ , there exist matrices $\mathit{P}>0$ , ${\mathit{Q}}_1>0$ , ${\mathit{X}}_K$ , ${\mathit{X}}_L$ , ${\mathit{Y}}_K$ , ${\mathit{Y}}_L$ and positive scalars ${\eta }_1$ , $c_2$ and $\gamma$ such that the following constraints hold:

$$\left[\begin{array}{cc}{\overline{\mathbf{\Pi }}}_1& {\overline{\mathbf{\Pi }}}_2\\ \ast & {\overline{\mathbf{\Pi }}}_3\end{array}\right]<0,$$ (37)

$${\eta }_{1}I<{\mathit{Q}}_1^{-1}<I,$$ (38)

$$\left[\begin{array}{cc}{\gamma }^2{d}^2{\mathrm{e}}^{-\alpha \mathcal{T}}-c_2^2{\mathrm{e}}^{-\alpha \mathcal{T}}& c_1\\ \ast & -{\eta }_1\end{array}\right]<0,$$ (39)

where

$$\begin{array}{rl}{\overline{\mathbf{\Pi }}}_1& =\left[\begin{array}{ccc}{b}_1-\alpha \mathit{P}& \mathit{P}{\mathbf{\Gamma }}_1+{\mathit{I}}_2{\mathit{Y}}_L\mathbf{\Psi }& {\mathit{G}}_1^{\mathrm{T}}\\ \ast & -{\gamma }^2{\mathrm{e}}^{-\alpha \mathcal{T}}& {\mathrm{\Phi }}^{\mathrm{T}}\\ \ast & \ast & -I\end{array}\right],\\ {\overline{\mathbf{\Pi }}}_2& =\left[\begin{array}{cc}{b}_2+\rho {\mathit{I}}_1^{\mathrm{T}}{\mathit{Y}}_K^{\mathrm{T}}& b_3+\rho {\mathit{C}}_1^{\mathrm{T}}{\mathit{Y}}_L^{\mathrm{T}}\\ 0& \rho {\mathbf{\Psi }}^{\mathrm{T}}{\mathit{Y}}_L^{\mathrm{T}}\\ \mathit{D}& 0\end{array}\right],\\ {\overline{\mathbf{\Pi }}}_3& =\text{diag}\{-\rho {\mathit{X}}_K-\rho {\mathit{X}}_K^{\mathrm{T}}-\rho {\mathit{X}}_L-\rho {\mathit{X}}_L^{\mathrm{T}}\},\end{array}$$

$b_1=\text{sym}(\mathit{P}{\mathit{A}}_1+{\mathit{B}}_1{\mathit{Y}}_K{\mathit{I}}_1+{\mathit{I}}_2{\mathit{Y}}_L{\mathit{C}}_1)$, $b_2=-{\mathit{B}}_1{\mathit{X}}_K+\mathit{P}{\mathit{B}}_1$ and $b_3=-{\mathit{I}}_2{\mathit{X}}_L+\mathit{P}{\mathit{I}}_2$. Then, the controller and observer gains are given by $\mathit{K}={\mathit{X}}_K^{-1}{\mathit{Y}}_K$ and $\mathit{L}={\mathit{X}}_L^{-1}{\mathit{Y}}_L$ , respectively.

Proof of this corollary immediately follows from the proof of Theorem 3. □

4 Numerical example

In this section, a simulation is conducted to illustrate the effectiveness and usefulness of the FTB criteria and controller design developed in this paper. For the simulation purposes, consider system (1) with the following system matrices as given in [24]:

$$\begin{array}{rl}\mathit{A}& =\left[\begin{array}{cccc}-10.045& 0.002& 0.003& 0.001\\ 0.001& -9.989& 0.001& 0.001\\ 6.045& -3.002& -4.997& 0.001\\ 0.002& 0.505& 0.001& -5.002\end{array}\right],\\ \mathit{B}& =\left[\begin{array}{cc}10& 0\\ 0& 10\\ 0& 0\\ 0& 0\end{array}\right],{\mathit{C}}^{\mathrm{T}}=\left[\begin{array}{cc}0& 0\\ 0& 0\\ 0& 1\\ 1& 0\end{array}\right],\mathbf{\Gamma }=\left[\begin{array}{cc}0.1& 0\\ 0.1& 0\\ 0& 1\\ 0& 1\end{array}\right],{\mathit{G}}^{\mathrm{T}}=\left[\begin{array}{cc}0.2& 0\\ 0.3& 0\\ 0& 1\\ 0& 1\end{array}\right]\\ \mathit{D}& =\left[\begin{array}{cc}0.2& 0.1\\ 0.1& 0.3\end{array}\right],\mathbf{\Phi }=\left[\begin{array}{cc}0.2& 0.1\\ 0.1& 0.3\end{array}\right]\text{and}\mathbf{\Psi }=\left[\begin{array}{cc}0.2& 0\\ 0& 0.2\end{array}\right].\end{array}$$

The main aim of the proposed control design is to accurately estimate the arterial partial pressure of oxygen and carbon dioxide in the blood to regulate the flow rates of theirs. Also, we have to determine the controller that makes system (1) FTB with a prescribed $H_{\mathrm{\infty }}$ performance. Let $\alpha =0.6$, $\rho =0.8$ and the finite‐time parameters as $c_1=5$, $\mathcal{T}=1$, $\mathit{R}=\mathit{I}$ and $d=2$. The exogenous disturbance is assumed to be $[0.01\sin (t)0.01\sin (t)]{}^{\mathrm{T}}$. Assume that the controller and observer gains with perturbations $\mathrm{\Delta }\mathit{K}(t)$ and $\mathrm{\Delta }\mathit{L}(t)$ having structure (28). In this connection, the gain fluctuation matrices are chosen as ${\mathit{M}}_K={\left[\begin{array}{cc}0.1& 0.3\end{array}\right]}^{\mathrm{T}}$, ${\mathit{M}}_L={\left[\begin{array}{cccc}0.8& 0.9& 0.3& 0.9\end{array}\right]}^{\mathrm{T}}$, ${\mathit{N}}_K=\left[\begin{array}{cccc}0.5& 0.7& 0.3& 0.3\end{array}\right]$ and ${\mathit{N}}_L=\left[\begin{array}{cc}0.4& 0.4\end{array}\right]$. Then by solving the LMI constraints of Theorem 3, we can obtain the optimum $H_{\mathrm{\infty }}$ performance index $\gamma =2.2783$ and optimum finite‐time bound value as $c_2=7.5568$ with the controller and observer gains as

$$\begin{array}{rl}\mathit{K}& =\left[\begin{array}{cccc}-11.8896& -0.9332& -0.0333& 0.0065\\ 1.9914& -2.8619& -0.0794& -0.00062\end{array}\right]\text{and}\\ \mathit{L}& ={\left[\begin{array}{cccc}0.1673& -0.0710& 0.1396& -0.7152\\ 0.0449& -0.0048& -0.3619& 0.4284\end{array}\right]}^{\mathrm{T}},\text{respectively}.\end{array}$$

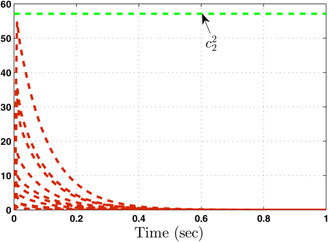
The system performance under finite‐time observer‐based controller is presented in Figs. 1–8. Figs. 1–4 depict the trajectories of flow rates of oxygen and carbon dioxide, arterial pressure of oxygen and carbon dioxide along with their estimations. It can be clearly seen from Figs. 1–4 that the estimated states closely track the exact states from which it is evident that the observer performs well. We can also see that the system stability is maintained despite the variations in controller and observer designs. The disturbance vector $\mathit{w}(t)$ is shown in Fig. 5. The corresponding control and output trajectories are plotted in Figs. 6 and 7, respectively. From Figs. 6 and 7, it can be seen that the proposed control effectively regulates the blood gases even in the presence of gain fluctuation in the control design, which shows the practical significance of the developed controller. Fig. 8 depicts the evolution of $x_c^{\mathrm{T}}(t)\mathit{R}{x}_c(t)$ for different initial conditions over the time interval [0, 1 s]. It can be seen from Fig. 8 that the value of $x_c^{\mathrm{T}}(t)\mathit{R}{x}_c(t)$ does not exceed $c_2^2$ during [0, 1 s]. Hence, it is concluded that the system is finite‐time stable with respect to $(5,7.5568,1,\mathit{I},2)$ even when disturbance and gain fluctuations exist.

Fig. 1.

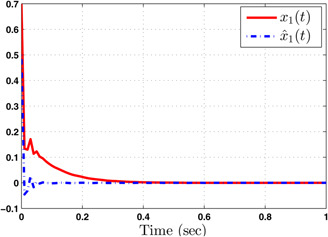
Responses of flow rate of oxygen ( $x_1(t)$) and its estimate ( ${\hat{x}}_1(t)$ )

Fig. 8.

Response of

$x_c^T(t)\mathit{R}{x}_c(t)$

Fig. 4.

Responses of arterial partial pressure of carbon dioxide ( $x_4(t)$) and its estimate ( ${\hat{x}}_4(t)$ )

Fig. 5.

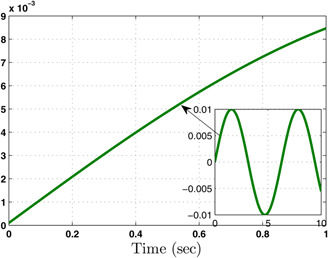
Disturbance

Fig. 6.

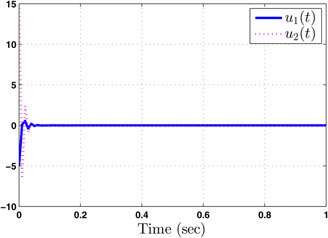
Commanded flow rates

Fig. 7.

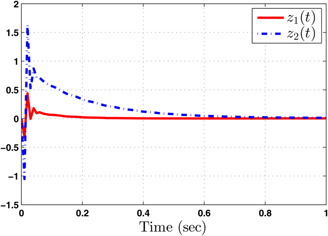
Controlled output trajectories

Fig. 2.

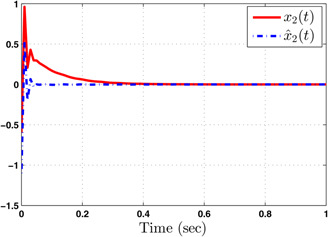
Responses of flow rate of carbon dioxide ( $x_2(t)$) and its estimate ( ${\hat{x}}_2(t)$ )

Fig. 3.

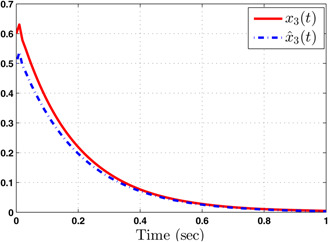
Responses of arterial partial pressure of oxygen ( $x_3(t)$) and its estimate ( ${\hat{x}}_3(t)$ )

Furthermore, for the above‐assumed designing parameter values with $\mathrm{\Delta }\mathit{K}(t)=\mathrm{\Delta }\mathit{L}(t)=0$, solving the LMIs in Corollary 1, we can obtain the optimal values $\gamma =2.1952$ and $c_2=7.3556$. It should be noted that the optimum $H_{\mathrm{\infty }}$ performance index $\gamma$ and optimal finite‐time bound $c_2$ based on Theorem 3 are obtained as $2.2783$ and $7.5568$, respectively, whereas based on Corollary 1, the optimal values are obtained as $2.1952$ and $7.3556$. This variation is due to the presence and absence of uncertainties in the control gain. Therefore, from the analysis of simulation results, it is concluded that blood gases are maintained in their physiological ranges during a stable extra‐corporeal circulation process even in the presence of fluctuation in control inputs and external disturbances, which demonstrate the robustness of the proposed controller.

5 Conclusion

In this paper, we have studied the problem of regulating the patient blood gases during ECC by using an observer‐based finite‐time $H_{\mathrm{\infty }}$ control with gain fluctuations. To estimate the unmeasurable flow rates of blood gases, Luenberger full state observer has been constructed. Moreover, based on the Lyapunov stability theory, a resilient controller has been designed in terms of LMIs, which ensures the finite‐time stability of the closed‐loop system with a prescribed $H_{\mathrm{\infty }}$ performance index level. Finally, a numerical example has been provided to demonstrate the effectiveness of the proposed control design technique.