From synapse to network: Models of information storage and retrieval in neural circuits

Abstract

The mechanisms of information storage and retrieval in brain circuits are still the subject of debate. It is widely believed that information is stored at least in part through changes in synaptic connectivity in networks that encode this information, and that these changes lead in turn to modifications of network dynamics, such that the stored information can be retrieved at a later time. Here, we review recent progress in deriving synaptic plasticity rules from experimental data, and in understanding how plasticity rules affect the dynamics of recurrent networks. We show that the dynamics generated by such networks exhibit a large degree of diversity, depending on parameters, similar to experimental observations in vivo during delayed response tasks.

1. Introduction

Brain networks have a remarkable ability to store information in memory, on time scales ranging from seconds to years. Over the last decades, a theoretical scenario has progressively emerged that describes qualitatively the process of information storage and retrieval. In this scenario, sensory stimuli to be memorized drive specific patterns of neuronal activity in relevant neural circuits. These patterns of neuronal activity lead in turn to changes in synaptic connectivity, thanks to synaptic or structural plasticity mechanisms. These changes in synaptic connectivity allow the network to stabilize a specific pattern of activity associated with the sensory stimulus, and they can also allow the network to retrieve this specific pattern, based on partial or noisy cues. This scenario has led to two complementary trends of research, on both the experimental and theoretical sides: The first has focused on rules and mechanisms of synaptic plasticity; The second has focused on how activity-dependent synaptic modifications lead to changes in network dynamics.

Theoretical models have played a major role in bridging the gap between synaptic and network levels. These models have been constrained by two types of data. Data at the synaptic level constrain plasticity rules that can be implemented in network models. This data typically come from in vitro studies, but recent work, discussed in this review, has also sought to constrain synaptic plasticity models using in vivo data. Data at the network level yield information about the types of dynamics that can be generated by networks that maintain information about past sensory stimuli, and/or future actions to be executed. Experiments in vivo in animals performing delayed response tasks have shown two types of dynamics in the delay periods of such tasks (see e.g. [1]): (i) Persistent activity, where neuronal firing rates are approximately constant during the delay period, consistent with attractor dynamics; (ii) Dynamic patterns of activity, where neuronal firing rates have significant temporal modulations during the delay period. Theoretical models that have sought to reproduce such dynamics have followed two different paths. The first has been to use networks whose connectivity matrix is built using biophysically plausible learning rules. The second has been to ignore experimental data on synaptic plasticity, and rather use supervised learning approaches that teach the network to perform a given task, a set of tasks, or neuronal recordings.

In this review, we will first describe recent progress in deriving synaptic plasticity rules from experimental data. In particular, we review recent approaches to infer plasticity rules in vivo. We will then describe recent theoretical work that has explored the dynamics of networks with connectivity matrices built using biophysically realistic plasticity rules. We will also discuss the storage capacity of such networks.

2. Synaptic plasticity rules

Studies of synaptic plasticity in vitro (reviewed in [11, 12, 13]) have shown that synaptic modifications (Δw) depend on spike-patterns of pre- and postsynaptic neurons through relative timing, firing rates, the location of the synapse along the dendritic tree, and on the extracellular conditions of the preparation. Diverse types of STDP (Spike Timing Dependent Plasticity) curves have been characterized, in different preparations, or sometimes in the same preparation but different experimental conditions (Fig. 1A). Furthermore, synaptic modifications are often weight-dependent. For example, plasticity can be multiplicative (i.e.,Δw ∝ w), and some plasticity experiments are consistent with discrete synapses [14] (i.e., synapses that are stable only in one of a discrete number of efficacy levels). Such complex dependencies are typically simplified in mathematical models to reduce the number of parameters fit to data, and facilitate analytical treatment of plasticity at the network level. Models can be divided into classes which differ in the identity of the intermediate biophysical quantities which trigger plasticity: Firing-rate-based rules, which assume that changes to synaptic efficacy depend on the spike-trains only through their temporal average [9] (Fig. 1B,C); Spike-timing-based models [15, 16]; Spike and voltage-based rules [17]; Calcium-based models [18, 8, 4^•]; And finally, more detailed models based on biochemical networks involved in synaptic plasticity [19].

Figure 1: Synaptic plasticity.

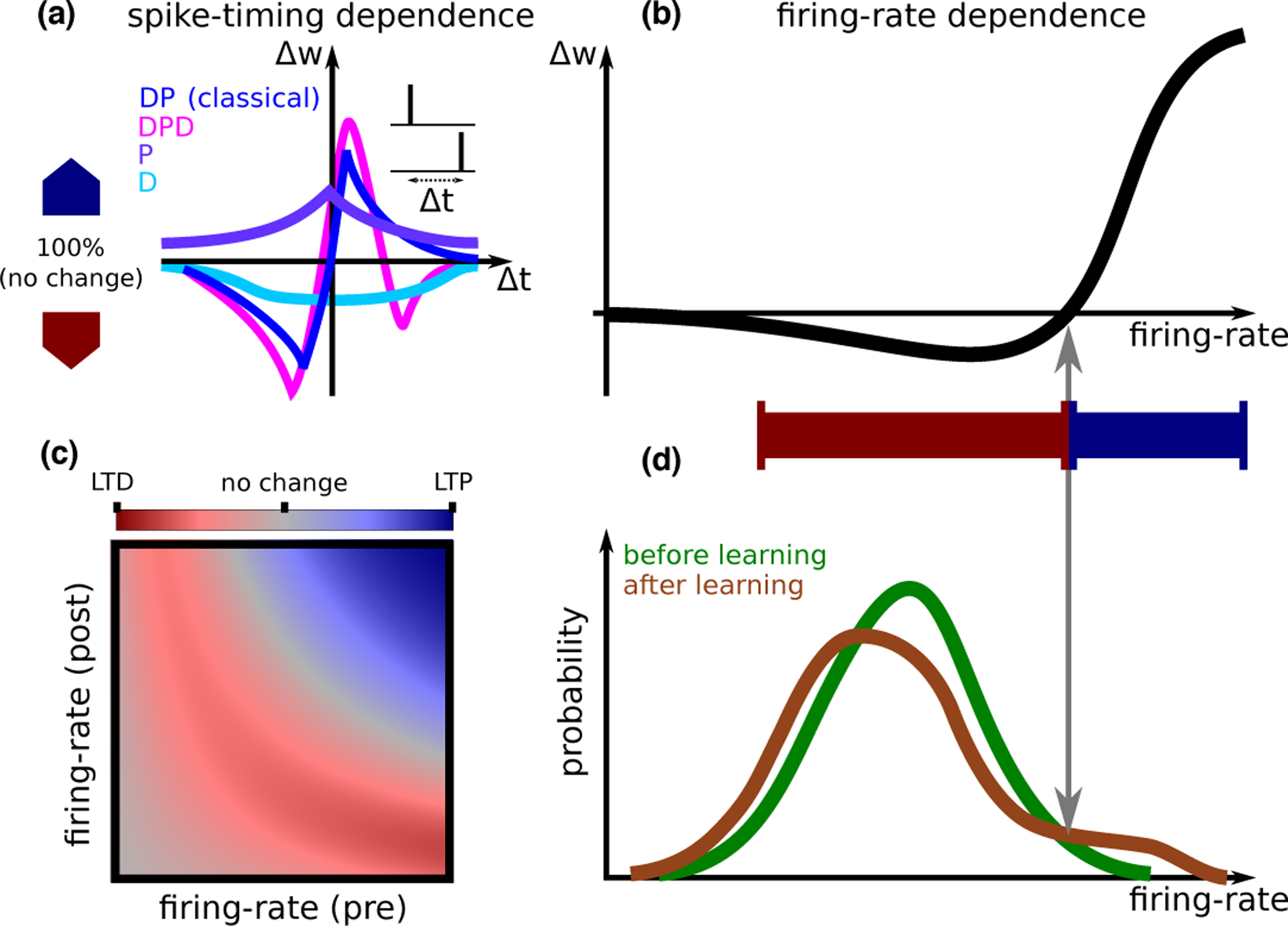
A. STDP (spike timing dependent plasticity) curves (i.e., dependence of synaptic plasticity on the timing difference between pre- and postsynaptic spikes Δt) observed experimentally. A number of qualitatively distinct STDP curve shapes have been reported experimentally: The classical curve (dark blue, seen e.g., in hippocampal cultures [2] and cortical slices [3]) exhibits a depression window $(\mathcal{D})$ followed by a potentiation window $(\mathcal{P})$; A curve with a second depression window ($\mathcal{D}\mathcal{P}\mathcal{D}$, magenta, seen in CA3 to CA1 connections at high calcium concentration[4^•]); A curve with only potentiation ($\mathcal{P}$, purple, seen in area CA3 [5], in hippocampal cultures in the presence of dopamine[6]); and finally a curve with only depression ($\mathcal{D}$, light blue, in CA3 to CA1 connections at low extra-cellular calcium concentrations[7, 4^•]).A calcium based model can account for all curve shapes with different choices of parameters [8], and for the transition between different curves as a function of the extracellular calcium concentration [4^•]. B. Models from each of the classes discussed in the text are typically fit to in vitro data based on plasticity protocols where the same pre-post pattern of activity is repeated. These models all give qualitatively similar firing rate dependence, which is similar to the BCM rule [9]. The specific shape of the non-linearity, and in particular the threshold separating LTD and LTP, depends on the model and its parameters, and on whether pre/postsynaptic (or both) firing-rate(s) are varied. A learning rule inferred from in vivo data [10^•] gives a similar dependence on firing rate. C. Models can also be used to predict synaptic plasticity for independent pre- and postsynaptic firing-rates. Shown here qualitatively is the magnitude of LTD (red) and LTP (blue), in a scenario where synaptic modifications are well approximated by the form Δw = g(r_pre)f(r_post) [10^•]. The dependence of plasticity on both pre- and postsynaptic firing rate, varying as two independent variables, has not yet been characterized experimentally. D. Inferring plasticity rules from in vivo data. The firing-rate distribution of a single neuron in response to sensory stimuli exhibits significant differences between novel and familiar stimuli. These differences can be used to reverse-engineer a learning rule that causes such differences. This learning rule has a dependence on the postsynaptic firing rate that is qualitatively similar to the curve in panel B. Such a learning rule sparsens the representation of sensory stimuli, decreasing the response of most neurons (those that respond with a firing rate that is smaller than the threshold between LTD and LTP), but leading to an increased response for a small subset of neurons that have initially the strongest response [10^•].

While some of these models have had success in reproducing multiple in vitro synaptic plasticity protocols [18, 16, 17, 8], it remains unclear whether plasticity rules fit to in vitro experiments apply to in vivo conditions. Indeed, recent work shows that setting the extracellular calcium concentration to physiological levels, instead of the higher concentrations typically used in in vitro studies, leads to profoundly altered plasticity rules [4^•]: No significant plasticity was reported for pairs of single pre- and postsynaptic spikes, independent of timing, at physiological low calcium concentrations. Significant plasticity could be recovered using either high-frequency stimulation, or bursts of spikes. A calcium-based rule was found to describe this data well quantitatively, provided interactions between calcium transients triggered by pre- and postsynaptic spikes are sufficiently non-linear [4^•].

An alternative approach to bridge plasticity rules and changes to network structure as an animal learns, is to infer rules of synaptic plasticity directly from in vivo data (Fig. 1D). A difficulty in obtaining information about synaptic plasticity in vivo is that it is not yet possible to simultaneously measure synaptic efficacy together with pre- and postsynaptic activity. However, Lim et al. [10^•] noticed that changes in neuronal responses to repeated presentations of sensory stimuli can provide information on the putative plasticity rule that is responsible for these changes. In particular, they used distributions of visual responses of neurons in the inferior temporal cortex (ITC) to two different sets of stimuli (one novel, the other familiar). Assuming the plasticity rule depends on firing rates of pre- and postsynaptic neurons as Δw = f(r_post)g(r_pre), one can use these distributions to infer f, i.e., the dependence of the plasticity rule on postsynaptic firing rate (Fig. 1B,D). The function g cannot be fully determined, but can be shown to be positively correlated with presynaptic firing rate. Interestingly, the inferred function f exhibits depression at low rates and potentiation at high rates, consistent with multiple plasticity rules inferred from in vitro data. In a subsequent study, Lim found that the analysis of changes in temporal patterns of activity with familiarity makes it possible to disentangle recurrent and feedforward synaptic plasticity [20]. More recently, machine-learning approaches have been developed to infer plasticity rules from data, by training a neural network to classify the presumed plasticity rule into one of a number of categories [21, 22]. So far, these approaches have been applied to synthetic data with known ground-truth, but not to real data.

Another major recent advance in our understanding of synaptic plasticity in vivo is the demonstration that plasticity can be induced by pairing presynaptic spikes with postsynaptic ‘plateau potentials’ [23^•]. Crucially, this form of plasticity is far less sensitive to the relative timing of events than classical STDP (~ 1s relative to ~ 20–50ms), thus providing a new mechanism connecting synaptic modifications and behavior. Voltage- and calcium-based plasticity rules mentioned above could potentially be modified to account for this mechanism through the introduction of a long time-scale. In the future, experiments that combine whole-cell patch clamp of postsynaptic neurons or imaging of dendritic spines, together with (sensory and/or optogenetic) manipulations of activity, are likely to provide essential information on synaptic plasticity in vivo (e.g., [24, 25, 26]). Another approach that will become more powerful with tool development is to track the strength of synaptic connections based on inference from large scale longitudinal electrophysiological recordings using silicon probes or fast voltage indicators [27].

3. Network dynamics

What type of dynamics emerge in networks endowed with the biologically plausible learning rules described above? Are such dynamics consistent with neural recordings? Theoretical studies tackling these questions can be divided into two learning scenarios. In the first scenario, learning and retrieval occur in two distinct phases. In the learning phase, input patterns to the network are imprinted in the connectivity by synaptic plasticity rules. After learning, the network connectivity is held fixed during retrieval of memory items. This scenario implicitly assumes a separation of time scales between learning and retrieval, or alternatively, that learning is gated by a third factor, such as neuromodulators. In the second scenario, the synaptic connectivity is dynamic, and synaptic plasticity is always ongoing, during both the learning of new memories and their successive retrieval. In this section, we describe recent progress in addressing the above questions in these two scenarios.

Networks with fixed learned connectivity.

In classic attractor network models, memories are represented as fixed-point attractors of the network dynamics [30, 31] (see Fig. 3A). In attractor states, subsets of neurons maintain an elevated persistent activity after the presentation of an item that is stored in memory, while other neurons remain at low activity levels (Fig. 3B). Such dynamics can be generated when synaptic connectivity is structured using a temporally symmetric plasticity rule (associating pre- and postsynaptic activity occuring at the same time t) in order to learn new memories (Fig. 2A). Attractor network models reproduce qualitatively the phenomenon of persistent activity that has been widely observed in delayed response tasks. However, learning rules used in these models have until recently been unconstrained by data. Furthermore, neuronal activity observed during delay periods in the prefrontal cortex is often characterized by a strong temporal variability, that seems hard to reconcile with fixed-point attractor retrieval states [32^•, 33]. Recently, a network endowed with a temporally symmetric learning rule and transfer functions inferred from in vivo recordings in ITC (see Fig. 1D,[10^•]) was shown to exhibit attractor dynamics (Fig. 3A–C) [28^•]. Firing rate distributions in retrieval states are close to log-normal and qualitatively match experimental data [34, 35]. When the strength of the recurrent connections increases, the network undergoes a transition in which retrieval states become chaotic [28^•, 36] (Fig. 3D). In this state, firing rates strongly fluctuate in time while the overlap remains constant (Fig. 3E–F). This activity strongly resembles neural activity in the prefrontal cortex during delayed response tasks, where dynamics are confined to a stable subspace despite large temporal fluctuations among individual neurons [32^•].

Figure 3:

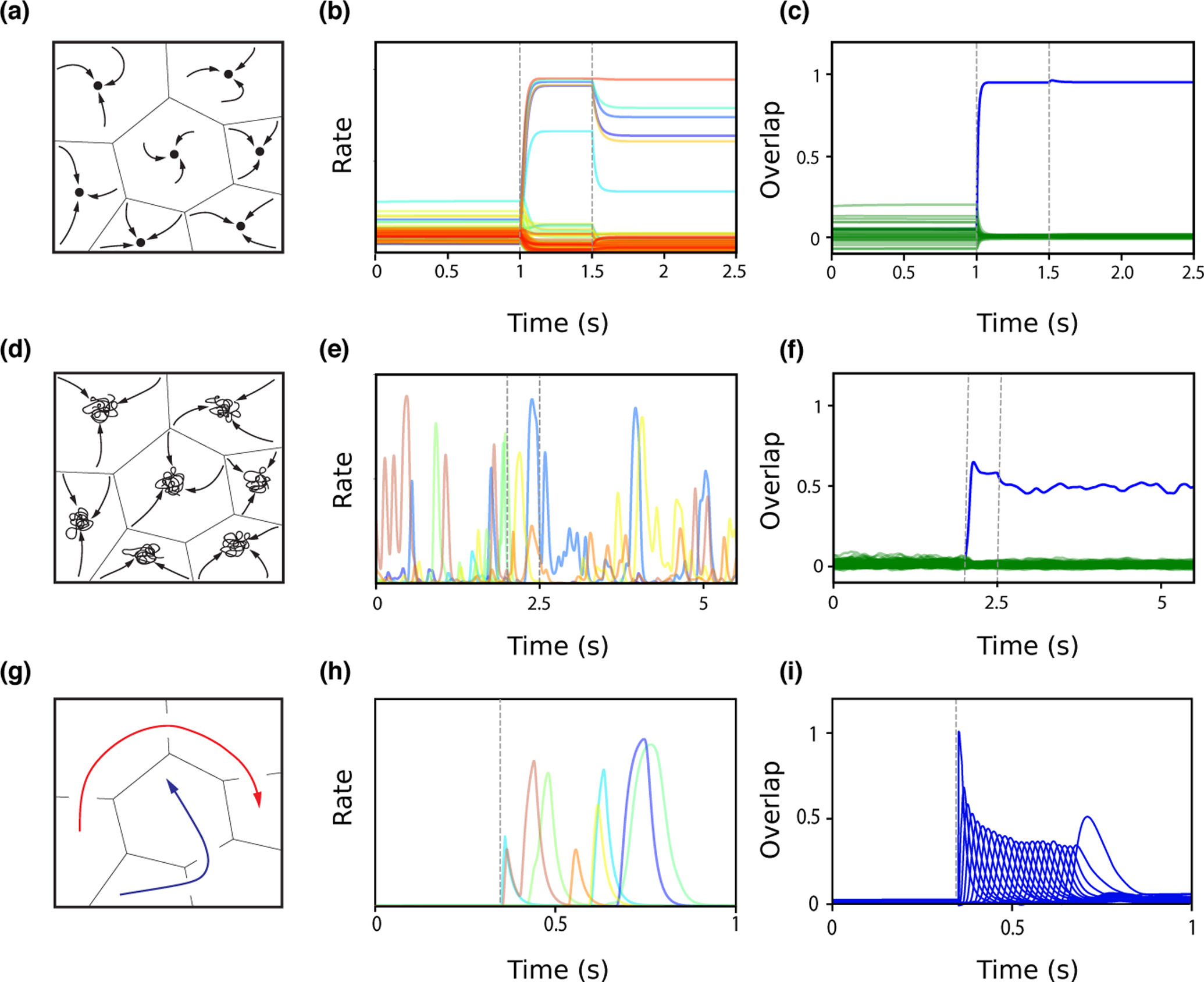
Network dynamics following learning. A. Schematic of fixed point attractor retrieval states occupying discrete subspaces. The space of network states is divided into basins of attraction, within which network activity will converge to a fixed point (black circle), representing a learned item. B. Single unit firing rates during background (0–1s), presentation of a pattern stored in memory (between dashed lines, 1–1.5s), and ‘delay’ period following stimulus presentation (1.5–2.5s), in a network in which distributions of stored patterns and learning rule have been inferred from data [28^•]. In the background state, single neurons fire with a wide (~ log-normal) distribution of rates. During the stimulus presentation, a small fraction of neurons are driven to high rates, while most neurons are suppressed. After the stimulus is removed, the network converges to a selective attractor states, in which a small fraction of neurons exhibits persistent activity. C. Overlap between network state and the presented pattern (blue) increases during stimulus presentation, and remains high following removal of external input, while overlaps between network state and other stored patterns (green) remains small. D. Schematic of chaotic attractor retrieval states. Network activity is confined to a subspace, but does not converge to a stable fixed point. E–F. Similar as in panel B–C, except the network has stronger recurrent connections and stimulus presentation is between 2 and 2.5s [28^•]. The network is in a chaotic state before stimulus presentation, with all single neuron firing rates fluctuating widely. After stimulus presentation, the network switches to a different chaotic state that is strongly correlated with the stored pattern (see blue overlap in F). G. Schematic of sequential pattern retrieval for two separate stored sequences (red and blue). Activity transitions from one subspace to the next. H–I. Similar as in panels B–C, except the network stores sequences, and is initialized close to the first stored pattern in a sequence of 24 patterns at 0.35s [29^•]. Single neurons are transiently activated at different times, and the network successively visits the neighborhoods of the different patterns composing the sequence as shown by transient overlap activations in I.

Figure 2:

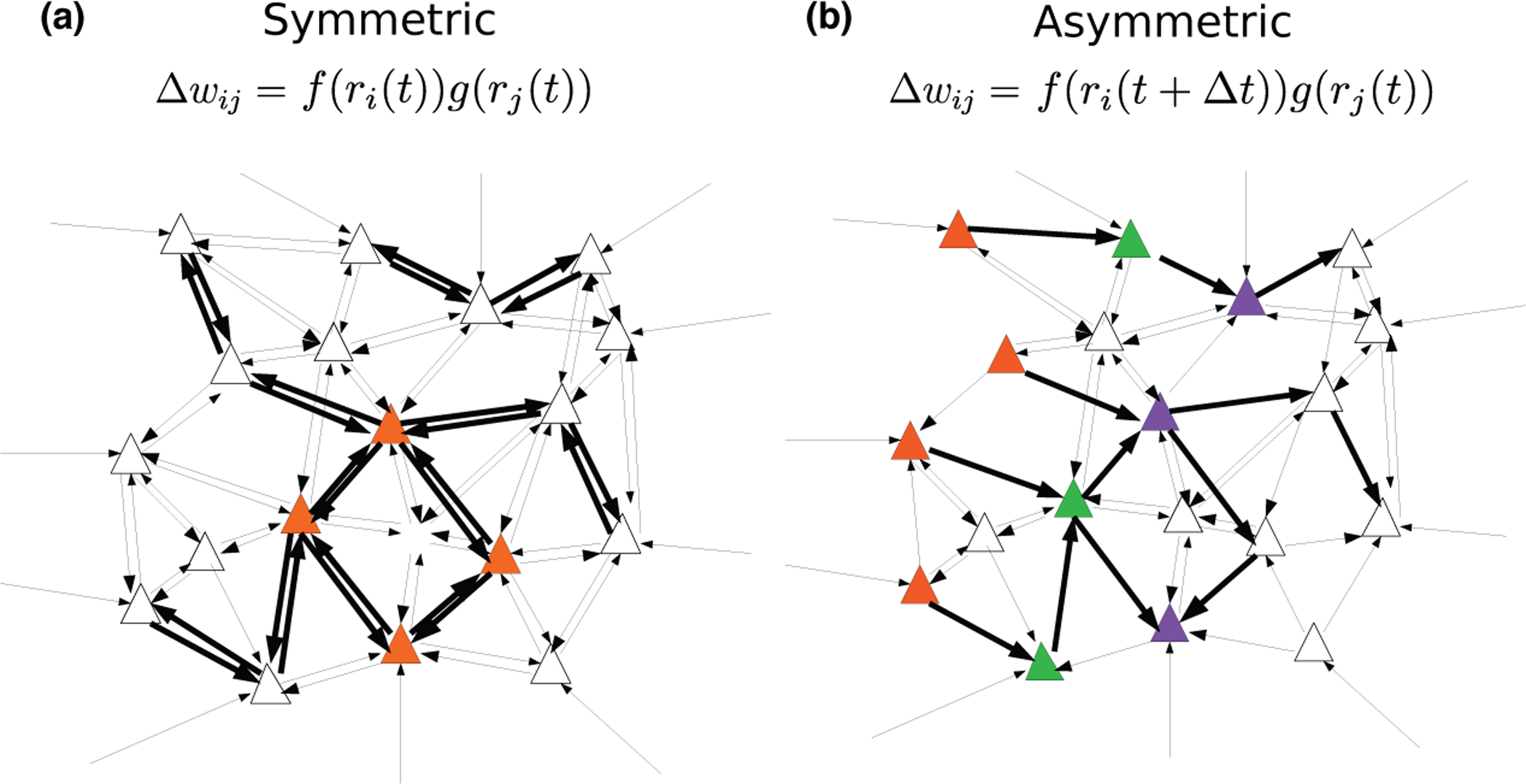
Network connectivity after learning with temporally symmetric (A) and asymmetric (B) plasticity rules. A. An external input leads to increased activity of the set of orange neurons. With a temporally symmetric plasticity rule, this activity leads in turn to strengthening of synapses connecting these neurons in a bidirectional fashion, leading to strongly symmetric synaptic connectivity. B. Temporally varying external inputs lead to successive activation of the orange, green and purple sets of neurons. With a temporally asymmetric plasticity rule, connectivity is strengthened in a unidirectional fashion, leading to an asymmetric, effectivety feedforward connectivity between these sets of neurons.

When the learning rule is temporally asymmetric, network connectivity storing sequences of input patterns is strongly asymmetric (Fig. 2B) [37, 38, 29^•].The network dynamics no longer converges to fixed points, but rather exhibits sequential activity, in which neurons are active at particular points in time that are reproducible across multiple trials (Fig. 3H–I). The dynamics of these networks display several features that are consistent with experimentally observed activity [29^•]. These include non-uniform temporal statistics, such as an overrepresentation of activity at the beginning of a sequence, and a broadening of ‘time fields’ with elapsed time, similar to observations in time cells during delay period activity [39, 40]. Other studies have explored how the interplay between symmetric and asymmetric connectivity shapes network dynamics, leading to ‘Hebbian assemblies’ for predominantly symmetric connectivity while sequential activity is generated for predominantly asymmetric connectivity [41].

Networks with dynamic connectivity.

Multiple theoretical studies have explored scenarios of online learning, in which learning is continuously active [42, 43, 44, 45, 46, 47, 48, 49, 50]. These networks typically begin with random, unstructured connectivity, and organize through time as a function of network activity. One of the main challenges in this learning scenario is the stability of information encoded in the weights and of network activity. In particular, Hebbian synaptic plasticity is well known to produce instabilities, due to the positive feedback loop between neuronal activity and synaptic strength inherent in this form of plasticity. Thus, additional stabilization mechanisms must be added, such as homeostatic plasticity [51], constraints on total incoming [52] and/or outgoing [42] synaptic weights, metaplasticity [9] and inhibitory plasticity [12].

To generate persistent activity from structured inputs, specific assemblies can be repeatedly activated through targeted external inputs. Spike-based plasticity among excitatory neurons, in combination with homeostatic and inhibitory plasticity, selectively strengthens the (symmetric) recurrent connections necessary to sustain activity within a given active assembly [53, 43, 44, 49]. To generate sequential activity from structured inputs, assemblies can be activated with a repeated temporal order to drive the formation of asymmetric feedforward connectivity [54, 46, 49]. It has also been shown that oscillatory external input can interact with Hebbian plasticity to favor the emergence of a connectivity structure supporting sequential activity [55]. Both assemblies and feedforward structure can also self-organize from spatially unstructured Poisson input. In this scenario, constraints on the total incoming/outgoing synaptic weights are critical to both the initial development of this structure and its long-term stability [42, 56].

In general, whether feedforward or assembly connectivity structure in these models develops over the course of learning depends on specific features of the plasticity rule that favor different local network motifs [57, 45, 47], as well as the timing of stimuli presentations in the case of structured input [49].

4. Storage capacity

A long-standing theoretical question about information storage in recurrent networks is the question of storage capacity: How many memories can be stored in a network with a given architecture? Theorists have used two types of approaches to address this question. The first consists in computing the storage capacity of networks with specific learning rules - the paradigmatic example being the computation of the storage capacity of the fully connected Hopfield model [58]. Storage capacity, defined as the number of retrievable memory items divided by number of plastic input connections per neuron, was subsequently shown to increase when connectivity is sparse [59], and with sparse coding of memories [60]. The second approach consists in computing the optimal storage capacity, in the space of all possible connectivity matrices [61]. This last approach therefore gives an upper bound, referred to as the Gardner bound, on what can be achieved by any plasticity rule (but see below). However, though this optimal capacity can be achieved using a supervised learning rule such as the perceptron learning rule or its variants, it is unclear whether biologically plausible unsupervised learning rules can reach this bound, and if not, how close to capacity they can get.

Recent studies have revisited the issue of storage capacity using models constrained by data. A sparsely connected network with a learning rule constrained by ITC data was shown to have a remarkably large capacity, similar to the capacity of sparsely connected networks of binary neurons [28^•]. Furthermore, it was shown that learning rules fitted to data are close to the optimal capacity, in the space of unsupervised Hebbian plasticity rules, parameterized by a sigmoidal dependence on pre- and postsynaptic rates. The optimal capacity in this space is given by a learning rule that stores a covariance of binarized input patterns [60]. The storage capacity of networks storing sequences have also been computed recently in a special case of a learning rule storing the time-delayed covariance of Gaussian input patterns [29^•], but the optimal capacity in the space of unsupervised rules remains an open question in this case.

While capacity has traditionally been studied exclusively in networks with unconstrained weights, or in networks with plasticity restricted to excitatory-to-excitatory weights, Mongillo et al [62^•] have recently studied the impact of inhibitory plasticity on capacity. They used a network of excitatory and inhibitory neurons and constrained connectivity parameters to ensure average firing rates and spiking variability were at physiologically observed values. These constraints lead in their model to a variance of inhibitory inputs that is much larger than the variance of excitatory inputs. They then studied the storage capacity of the network, using Hebbian/anti-Hebbian plasticity in excitatory/inhibitory connections, and showed plasticity in inhibitory connections can provide a very large boost to capacity, increasing it several fold.

A longstanding open question is how close are networks with unsupervised Hebbian rules to theoretical bounds. Work from the 1980s had shown that in the sparse coding limit, the storage capacity of networks with a covariance rule gets asymptotically close to the Gardner bound [60, 61]. Recently, Schonberg et al [63^•] showed that networks of neurons with threshold-linear units that store memories through a Hebbian rule can have a storage capacity that reaches and even exceeds the Gardner bound, for sparse enough memories. This apparent discrepancy can be understood by the fact that the Gardner bound is computed assuming attractors are exactly identical to stored memories. In networks with Hebbian rules, attractors are in general correlated, but distinct from the patterns that are stored in the connectivity matrix. In the network studied in [63^•], attractors turn out to be sparser than the stored patterns, which leads to a higher capacity than the Gardner capacity, computed for the sparseness level of the stored patterns. Intriguingly, theoretical work on the properties of synaptic connectivity in networks optimizing information storage has shown that many non-trivial experimentally observed properties of synaptic connectivity in cortex can be reproduced by such optimal networks, including low connection probability and over-representation of bidirectionnally connected pairs of excitatory neurons [64^•], high connection probability of inhibitory connections [65] and balance between excitation and inhibition [66].

5. Discussion

We have reviewed here recent progress on the characterization of Hebbian synaptic plasticity rules in in vivo conditions, on the dynamics of recurrent networks endowed with Hebbian synaptic plasticity rules, and on the storage capacity of such networks. On the synaptic plasticity front, the emerging picture is that isolated pairs of pre- and postsynaptic spikes are insufficient to elicit significant plasticity in physiological conditions. Rather, more prominent activity patterns, involving bursts of spikes, plateau potentials and/or sufficiently high firing rates, seem to be necessary to induce lasting changes in synaptic connectivity. Calcium-based models have been shown to fit well a broad range of data, and are a good starting point for extensions and generalizations, including bridging plasticity to behavioral timescales, studying plasticity in spatially extended neurons, and disentangling effects of plasticity induced by pre- and postsynaptic activity from additional factors such as neuromodulators.

On the network dynamics front, recent studies have shown that simple Hebbian plasticity rules can lead to a wide diversity of retrieval dynamics, from convergence to a fixed point (leading to persistent activity), to chaos (leading to highly irregular persistent activity), or sequential dynamics, depending on coupling strength and the degree of asymmetry in the synaptic plasticity rule. An important question is whether a given network, with a given learning rule is able to produce diverse types of dynamics, depending on the statistics of inputs received during learning and/or the delay period. The study of ref. [49] provides a proof of principle that a network with a temporally asymmetric Hebbian rule can generate both persistent activity and sequential activity, depending on the input temporal statistics during learning.

The diversity of the types of dynamics that are observed in networks with simple unsupervised Hebbian plasticity rules is reminiscent of the diversity of experimentally observed dynamics in delay periods in delayed response tasks in mammalian cortices. The phenomenon of persistent activity, which has been widely observed in multiple types of delayed response tasks [67], has long been thought to be a manifestation of recurrent dynamics in cortical circuits [68]. Perturbation studies have shown that the dynamics in the ellipsoid body of flies [69] and area ALM of mice [70^•], are consistent with attractor dynamics. However, a number of challenges to the persistent activity/attractor dynamics hypothesis have been identified (see e.g. [33]): (1) even when persistent activity is seen after trial averaging, the dynamics in single trials shows a high degree of irregularity, with activity often occurring in sparse, transient bursts; (2) the trial-averaged activity is often dynamic, with ramping or sequential activity patterns. While ramping activity could be reconciled with a fixed point attractor scenario in the presence of time-dependent input encoding elapsed time [70^•], sequential activity requires a different conceptual framework than attractor dynamics. As described in Section 3, the diversity of dynamics observed in networks with Hebbian plasticity can recapitulate the experimentally observed diversity: Classic persistent activity could correspond to the fixed point attractor scenario (Fig.3A–C), while persistent activity with highly irregular/bursty single trial activity could correspond to the chaotic attractor scenario (Fig.3D–F), both of which can be generated using temporally symmetric synaptic plasticity. Finally, sequential activity can be generated using temporally asymmetric synaptic plasticity, as shown in Fig.3G–I.

The networks discussed in Section 3 also reproduce a number of non-trivial features of experimentally observed activity. For instance, when parameters of neuronal transfer functions and learning rule are inferred from data, the distributions of firing rates in the delay period do not exhibit a strong bimodality, similar to what is seen in delay match to sample tasks [34, 35, 28^•]. In the case of sequences, the temporal characteristics of retrieved sequences display a number of striking similarities with data, such as the broadening of time fields with elapsed time, and the non-uniformity of the distribution of time field centers [29^•].

In the theoretical framework we have described here, memories stored in the network correspond to fixed network states (or sets of network states in the case of sequences). Recent longitudinal recordings of population activity on the time scale of weeks have shown that, far from being fixed, these network states constantly reorganize on these long time scales (a phenomenon that has been termed representational drift) [71]. In a recent paper, we have shown that this phenomenon is compatible with the storage of fixed memories, in the presence of slow synaptic dynamics, either due to random fluctuations, or to storage of new memories [29^•].

The approach we have outlined in this review (i.e., using unsupervised, biophysically motivated synaptic plasticity rules) can be contrasted with recent studies that have used supervised learning approaches, either to reproduce a given task or set of tasks [72, 73, 74, 75], or to reproduce the observed sequential activity [76]. This approach has had success in reproducing some of the diversity of observed dynamics, but has the drawback that the plasticity rules do not satisfy locality constraints and are therefore not biologically plausible. Several steps have been taken towards making these rules more biologically realistic, either by imposing by hand a locality constraint [77], or by using a three-factor plasticity rule that include a delayed reward information [78]. Integrating unsupervised and reward-based learning remain an important subject for future work.

Much work remains to extend of the results described in this review to more biophysically realistic learning settings, in which recurrent synaptic inputs interact with external inputs in non-trivial ways. In addition, the storage capacity of online plasticity rules remain an open question. On the experimental side, an outstanding open question is demonstrating that the types of dynamics seen during delayed response tasks depend on Hebbian synaptic plasticity. The ongoing parallel progress in experimental and computational techniques makes us hopeful that answers to these questions might become available in the next few years.