Highlights
-
•
Precision agriculture for pest control in organic banana.
-
•
Prediction of Pest incidence with machine learning techniques.
-
•
Machine learning modeling applied to organic banana cultivation.
-
•
IOT sensor network and cloud-based data logging system in banana plantation.
Keywords: Multi-class classification, Machine learning, Organic banana pest, Support vector machine, Red rust thrips, Twin Support Vector Machine
Abstract
The organic banana is one of the most popular products worldwide and its popularity is mainly due to its excellent nutritional properties and tasty flavor. Peru is considered one of the major producers and exporters of this product, being the city of Piura the main region with most of the national agro-producers. It is also considered a key factor in the development of the economy of this region as it creates job opportunities because of the productive chain required in the process (harvest, post-harvest, and export). The main problem faced by producers is the existence of pests such as Red spot thrips, Black Sigatoka, and others, which affect the production and the quality of the final product. Therefore, this article aims to propose an alternative solution, using the 4.0 Industry technology as well as the installation of an IoT sensor network in banana plantations in order to develop a model which estimates the classification of the pest incidence level based on Machine learning techniques, making use of the atmospheric variables measured with the IoT sensor network as input data. In the research, we have used The Support Vector Machine techniques, which have successfully achieved models with a high level of accuracy. The implementation of this system aims to help producers improve the management of pest control by scheduling spraying dates more effectively, optimizing not only the quality of the product but also reducing costs.
Multi-class classification; Machine learning; Organic banana pest; Support vector machine; Red rust thrips; Twin Support Vector Machine
1. Introduction
The organic banana is a product in great demand worldwide for its nutritional properties and exquisite flavor [1]. This product is considered the fifth most important crop worldwide, representing a caloric source for more than 500 million people in tropical countries [2], its main producers are located in Asia and America [3].
Peru has an area of 197,837 hectares which are used for agriculture [4], and is one of the main suppliers of this product in the American market [5], accounting for approximately 3% of the world's organic banana production. As with other organic products, one of the main problems to be faced is the poor management of pests and diseases associated with climatic conditions [6], [7], which impair the productivity and quality of the product.
To face this type of problem precision agriculture has appeared as an alternative that promises to improve the efficiency and quality of agricultural production [8], transforming manual work into a technological one [9].
Precision agriculture can be defined as the combination of information and communication technologies, also known as 4.0 technologies, which allows obtaining information from numerous sources, allowing more efficient decision-making based on the analysis of this information [10], [11].
The 4.0 technologies applied in the agricultural sector are Big Data [12], [13], Cloud Computing [14], [15], Cyber-Physical System [16], [17], Internet of Things (IoT) [18], [19], and Artificial Intelligence (AI) [20], [21]. The interpretation of information with Machine Learning (ML) techniques allows the development of mathematical models with high estimation accuracy [22].
In [23], itś been used a multi-sensor network system and the Support Vector Machine technique to work on an early warning model of pests in vegetables based on the information collected in a multidimensional way: the number of pests, soil, environment, climate, and meteorological factors in real-time, to have a Big Data system.
In [24], we introduce a description of current trends for crop pest prediction using machine learning techniques such as Support Vector Machine. In [25], a high-resolution spatial image is used to determine the extent of Yellow Sigatoka infection in a banana crop being able to predict phenotypic phenomena from a Support Vector Machine model. In [26], a system for early prediction of Black Sigatoka outbreak in banana plantations is developed through the use of techniques such as linear regression, multivariate regression, regression tree, and additive regression.
In [27], a multiple logistic regression model was used to find the relationship between the level of infection in the fungus commonly found in the fly larvae of the Mediterranean fruit. In [28], we have detailed the multiple regression model for crop pest risk prediction as well as we have evaluated the performances of multiple regression models and neural networks. In [29], the cereal loss rate in the harvesting phase has been estimated by designing a model based on logistic regression. In [30], the model based on the multiple logistic regression shows the factors that determine the level at which the IPM (Integrated Pest Management) system is adopted by a producer. In [31], itś been introduced a model based on the Decision Trees model to be able to predict the behavior of nutrients in the soil of banana plantations, facilitating decision-making and optimizing resources. In [32], itś been developed a pest prediction model for banana crops using linear regression and Support Vector Machine techniques, evaluating and comparing both alternatives.
Thus this work proposes a mathematical model to predict the level of pest incidence in banana crops, using Support Vector Machine (SVM). By comparing its performance and accuracy, this new tool would facilitate the decision-making for farmers in the region of Piura, Peru.
The methodology to develop these models includes data collection in the field with a data recording system, description of the binary classification for pest incidence, protocol and parameters of the experiment management, selection of the input variable, design of the SVM prediction models, comparison of the metrics and discussion of the results.
2. Information gathering
A data logging system has been installed in a banana plantation located in the district of Buenos Aires, province of Morropón, department of Piura, Peru, with geographical coordinates 5° 16' 13.4" S 79° 57' 10.1" W, this plot has an area of 1 Ha.
2.1. Data logging system
The installed system consists of a network of IoT (Internet of Things) sensors to measure climatic and soil variables. The sensors were installed at 3 levels: the soil (subway level), below the banana leaves (microclimate level), and above the banana leaves (climate level).
The sensor network is composed of two nodes and a weather station as shown in Fig. 1, due to the seasonal behavior of the pest these variables are strongly related to the development of pests in banana crops as detailed in [33], [34].
Figure 1.

Data recording system for banana crop distribution (1 Ha).
Table 1 shows the variables measured by the data recording system at all levels. It is important to note that not all variables were relevant to the mathematical model design.
Table 1.
System for recording data on measurement variables
| Variables | ||
|---|---|---|
| Weather station | Node 1 | Node 2 |
| Climate |
Micro-climate |
|
| -Temperature | -Temperature | |
| -Relative humidity | -Humidity |
|
| -Solar radiation | Soil |
|
| -Atmospheric pressure | -Temperature | |
| -Wind Speed | -Relative humidity | |
| -Precipitation | -Electrical conductivity | |
3. Pest control
The procedure followed to determine the incidence of the pest in the plot starts by choosing 25 plants at random; afterward, a detailed inspection is carried out for which it is necessary to cut leaves from the plant and perform a visual inspection to count the number of insects found. This information is recorded because it will allow us to decide when to carry out the pest control process. The diagnosis of the crop plot is carried out using the pest incidence level “α”, which is defined as:
| (1) |
The application of the control action will depend on the classification of the level of incidence of thrips, as indicated in Table 3. So, considering the level of pest incidence, farmers apply products such as Sulphocalcic Broth, which is a combination of Sulphocalcic Broth with agricultural oil or Entrust SC. Crop rotation is relevant in the use of these products to avoid creating resistance in the plants to be sprayed. In addition, one of the main challenges is to avoid the excessive use of these products in the plantations.
Table 3.
Thrips incidence level classification.
| Low Incidence | 0 ≤ IT < 0.64 |
| Medium Incidence | 0.64 ≤ IT < 1.56 |
| High Incidence | 1.56 ≤ IT |
4. Experiment management
Data has been systematically stored since the installation of the statics collection system in the organic banana plantation in November 2019. Likewise, 112 samples were taken for the development of this research until March 2021.
4.1. Limitations
Considering the geographic location detailed in section 2, the results of this research were developed in a region with a desert climate, low rainfall during the year, an annual temperature ranging between 20 °C and 31 °C, low wind speed, and high solar radiation.
Itś also been modeled the behavior of the growing population of the red spot Thrips (Chaetanaphothrips signipennis), which affects plants of the Musaceae family.
4.2. Thrips incidence behavior analysis
The incidence prediction model was designed for the pest called Red spot thrips (Chaetanaphothrips signipennis) since it has the most severe impact on organic banana crops in the region of Piura, Peru. The behavior of this pest is seasonal and its increase is due to the high temperatures during the summer months, from December to March.
By analyzing the level of incidence, it was possible to identify that the behavior of the frequency of the Red spot thrips resembles an exponential function since it can be used to describe the growth of the population of this pest. (See Fig. 2.) Thus, the following can be written:
| (2) |
Figure 2.

Red rust thrips incidence behavior.
Considering that represents the incidence of Red rust thrips, is the initial population, r is the effective population growth rate and t is the time represented in days, the population can be calculated for time from a previous population at time .
| (3) |
It has been determined that the most relevant meteorological variables measured by data logging systems are micro-climate temperature (°C), rain rate (mm), and wind speed () [26], [34], [35]. These variables vary their behavior cyclically throughout the year. In order to explain the relationship between pest and atmospheric variables, it was decided to write r as follows:
| (4) |
T is representing the average temperature, is the average wind speed and R is the average rainfall incidence. The meteorological variables are averaged over the time interval . is the Cumulative Effect of Fumigation for the red rust thrips, is the Cumulative Effect of Fumigation for other pests, CEC is the Cumulative Effect for the Cleaning and the following sections are showing how they are calculated considering the fumigation and cleaning dates. The coefficients , , , , , , are expected to be estimated with mathematical modeling.
It is possible to linearize (3) by applying a natural logarithm to the expression. By linearizing the function, we can apply a regression method on the incidence of Red rust thrips.
| (5) |
It is possible to replace with Δt.
| (6) |
It is possible to determine the variables for machine learning algorithms by applying equation (6).
An analysis has been performed in section 5.2 in order to select the variables to be used in the mathematical model training.
4.2.1. Thrips incidence level classification
The incidence in the red rust thrips can be determined by using the values shown in Table 3. So, taking these levels into account, the control strategies can be applied as recommended in [36].
Ranking the values of thrips incidence together with the criteria described above gives the following results, see Fig. 3.
Figure 3.

Red rust thrips distribution class.
At present, farmers from the region of Morropon spend $861/ha, without including labor and scheduled plot cleaning which is done every 20 days. This is because 12 leaf fumigations, 12 stem fumigations, and 4 stem fumigations with cleaning must be applied during the year considering the costs in Table 4.
Table 4.
Control action and cost by level of incidence.
| Incidence level | Control action | Cost |
|---|---|---|
| Low | Leaf fumigation | 18.64 $/ha |
| Medium | Stem fumigation | 35.13 $/ha |
| High | Stem fumigation and cleaning | 54.04 $/ha |
5. Prediction model design
The objective of the mathematical model designed in this research is to predict the incidence level classification based on input variables relevant to Thrips reproduction and death behavior.
5.1. Cumulative effect of fumigation and cleaning
It is important to consider the causes of mortality of the species in order to calculate the incidence of red rust thrips, including strategies such as spraying and plot cleaning applied to control the pest.
These variables have a behavior that can be described as an exponential function with a negative rate, which is called degradation rate, and describes the speed with which the chemical used or the cleaning in the plot decreases until it converges to a value close to 0.
| (7) |
In equation (7), represents the time in days since the last fumigation, this variable can be calculated from the recorded dates of fumigation. But only describes the effect on a day, so in order to describe the Cumulative Effect of Fumigation () between the inspection days, it is necessary an integral one.
| (8) |
represents the days since the last fumigation according to the last inspection and represents the day since the last fumigation was made. This can be applied to red rust thrips fumigations, other pest fumigations as well as to the cleaning (weeding) of the plot.
5.2. Features selection
It is possible to determine the mathematical importance through numerical weighting by applying sensitivity analysis of the characteristics in the variables described in Table 2.
Table 2.
Features variables.
| Nomenclature | Expression | Description |
|---|---|---|
| x0 | Δt | Days since the previous Thrips incidence |
| x1 | TΔt | Average temperature by time delta |
| x2 | SwΔt | Average Wind speed by time delta |
| x3 | RΔt | Average rain incidence by time delta |
| x4 | CEF1Δt | Cumulative Effect Fumigation for Red rust thrips by time delta |
| x5 | CEF2Δt | Cumulative Effect Fumigation for other pest by time delta |
| x6 | CECΔt | Cumulative Effect Cleaning for other pest by time delta |
| x7 | Natural logarithm of the previous thrips incidence multiplied by time delta |
Previously, all variables were multiplied by Delta T between plot inspections, in order to resemble the mathematical model to the linearization shown in equation (6).
The results of the analysis have been shown in Fig. 4, specifically in the graphs showing sensitivity to shuffled values (“shuffle”) and sensitivity to the omitted values (“missing”), the variable with the highest sensitivity for predicting thrips incidence is the logarithm of the previous incidence, then the cumulative effect of spraying for red spot thrips (), followed by mean microclimate temperature and mean wind speed.
Figure 4.
Feature sensitivity analysis.
The variables with lower sensitivity are rain rate, the cumulative effect of plot cleaning, Δt, and the cumulative effect of spraying for other pests.
The variables Δt and rain rate have been eliminated since they did not have a significant effect on the output variable; however, it was decided to leave the cumulative effects of spraying other pests and cleaning as they are the cause of death.
5.3. Data pre-processing
Since the characteristics are worked with different units and scales, we have considered applying a scaling method, so for this research, we have chosen the standard normalization described in equation (9).
| (9) |
5.4. Support Vector Machine
The Support Vector Machine is a supervised machine learning algorithm that allows solving classification problems as in [23], [24], [25].
5.4.1. Support vector regression
Support vector regression (SVR) allows predefining the acceptable error for the model and, consequently, to find a hyperplane that fits the data.
Unlike linear regression, the objective function of SVR is to minimize the norm of the coefficient vector and not the squared error. This is handled in the constraints of the problem, where the absolute error can be less than or equal to a specified margin, also called the maximum error (ϵ). ϵ can be adjusted to the desired accuracy of the model. There are scenarios in which the model can't fit all points, for this reason, it is necessary to include slack variables, which are defined as the deviation of the data that are not within the margin. These deviations are assumed to exist, but the objective is to minimize them as much as possible. So the objective function is modified to:
| (10) |
represents the vector containing the input data of the mathematical model, is the vector containing the weighting corresponding to each input variable and the value of the bias. C can be defined as the tolerance of the points outside the margin. The tolerance increases with C, so C should be as close to 0 as possible. (See Fig. 5.)
Figure 5.

SVR with slack variables example.
The Kernel function is an additional tool that allows fitting the mathematical model to data with non-linear behavior by adding a higher dimension to the space generated by the input variables.
| (11) |
The equation describing the hyperplane is , the objective function results in:
| (12) |
5.4.2. Support vector classifier
The Support vector classifier (SVC) tries to separate different classes by optimizing the location of a plane and maximizing the margin. But it is also necessary that the hyperplane has the maximum possible margin concerning the data it is separating; the margin is the distance between the points closest to the hyperplane (which are known as support vectors). Thus, the condition expressed in equation (13) must be fulfilled.
| (13) |
Thus, the distance or margin (d) is related to the vector modulus ω and can be calculated with equation (14).
| (14) |
An example of the optimal placement of a hyperplane is illustrated in Fig. 6.
Figure 6.

SVC example (A, B, C and D are support vectors).
The objective of the SVC consists of finding the highest margin which satisfies the separation between two classes, so it becomes an optimization problem described in equation (15).
| (15) |
It is not always possible to find a hyperplane which satisfies the conditions posed by this problem, so it is necessary to include a slack variant () whose value must satisfy the condition of always being positive. Then the new function to be optimized is:
| (16) |
It is possible to solve this problem if the points can be separated linearly, however, it is not necessarily feasible, so it is recommended to apply a transformation (Kernel function) [37] to the input data to create a higher dimension so that a linear separation can be applied in this new division.
| (17) |
5.4.3. Twin support vector classifier
The Twin support vector machine (TSVM) differs from the previous approach because it uses two non-parallel hyperplanes to separate classes. Therefore, it tries to solve a pair of small problems instead of a much more complex problem as it would be the conventional SVC. (See Figure 7, Figure 8.)
Figure 7.

SVC with kernel function.
Figure 8.

Twin SVM example.
Having two hyperplanes, the objective function of the Twin Support Vector Machine is composed of two equations:
| (18) |
| (19) |
Adding the Kernel function, the result is:
| (20) |
| (21) |
6. Results and discussion
For the results, we have used the GridCVSearch algorithm of Sci-Kit Learn for the different combinations of SVM parameter values, with 20-fold cross-validations.
6.1. SVR results
Several models were run with SVR to numerically estimate the incidence of red spot thrips. The metrics of the models in which the cumulative effects of spraying and cleaning have not been considered are at least 20% lower than those shown below, Table 5 shows the results of the models that include the cumulative effects of spraying and cleaning.
Table 5.
SVR results.
| Kernel | R2 | RMSE | Parameters | ||
|---|---|---|---|---|---|
| Linear | 67.49% | 3.7698 | C: 0.0625 | ||
| RBF | 82.92% | 1.9806 |
|
||
| Sigmoid | 8.92% | 10.5634 |
|
We can observe that the results with RBF were better even by dividing the preciseness by seasons, so the accuracy of the SVR Linear Kernel does not exceed the accuracy of the RBF SVR Kernel. When analyzing the yield by season, it is found that in summer a more accurate prediction is possible, since a more differentiated behavior of the pest is noticed, and this is aligned with the information collected in the field, since the agro-producers informed us that the pest has a higher incidence in summer months as there is a higher average daily temperature and a greater amount of rainfall per week.
For the autumn and winter seasons, low goodness-of-fit values were obtained, the SVR RBF kernel manages to follow a trend in the real behavior but does not manage to adjust itself, this may be because these are the seasons when the population reaches the lowest values. (See Fig. 9.)
Figure 9.

Real data vs SVR prediction models.
None of the SVR alternatives can predict the spring season. At the end of spring, there is an increase in the thrips population, which prepares the conditions for much more rapid development of the pest in the summer season. Therefore, it is not easy to adjust the model to the behavior during this season.
Finally, the numerical value obtained from the SVR model prediction was converted into classes as shown in Table 2. We were also able to obtain metrics of 82% in F1-score as well as in its precision with the SVR RBF kernel transformation. The rest of the models did not exceed 73% in any of the aforementioned metrics.
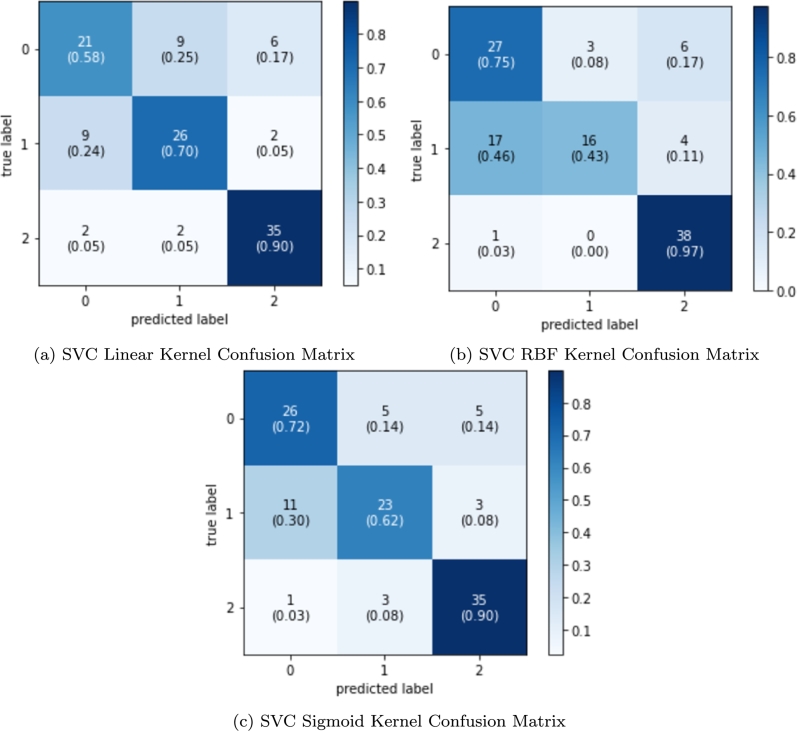
6.2. SVC results
The confusion matrix was used to analyze the results of the classification, the correct as well as the incorrect classifications are accounted [38].
As it can be seen in Table 6, better results were obtained taking into account the total points of the year, however, in the analysis done considering the season, it is possible to observe that during summer the SVC Linear Kernel has the highest metrics. On the other hand, in winter, the highest metrics were obtained by the SVC RBF Kernel and during the other two seasons, the SVC Sigmoid Kernel excels.
Table 6.
SVC Results.
| F1-Score | Accuracy | |
|---|---|---|
| SVC Linear Kernel | 73% | 73% |
| SVC RBF Kernel | 70% | 72% |
| SVC Sigmoid Kernel | 74% | 75% |
These models did not improve the accuracy and F1-score metrics obtained by converting the SVR RBF Kernel SVR model results into classes. (See Fig. 10.)
Figure 10.
SVC Results.
Considering the classifiers these were able to improve the predictions during the fall and winter seasons, which was not possible to achieve with the SVR. Spring is the season with the worst accuracy performance, which is reflected in the behavior observed in the SVR results.
6.3. Twin SVC results
Finally, we trained a One-versus-One multiclass Twin SVC model. The results were as follows, see Fig. 11 and Table 8.
Figure 11.
TSVC Results.
Table 8.
TSVC results.
| Accuracy | F1-Score | |
|---|---|---|
| TSVC Linear Kernel | 73% | 72% |
| TSVC RBF Kernel | 83% | 82% |
When comparing TSVC and SVC with Linear Kernel, we realize that both have similar performance if metrics for the whole year are taken into account. However, if the analysis is seasonal we find that the values of the TSVC metric fall in summer while it increases during the rest of the seasons, so it is required a model which allows better monitoring of the population growth.
The highest metrics are those of the TSVC RBF kernel, which outperforms the ranking of the SVR model prediction. In addition, it has a very stable behavior in summer, autumn, and spring, with metrics above 87%, that is, it is superior to all the proposed models in all the circumstances under which they have been evaluated.
6.4. Discussion
It can be observed from the implemented models that the behavior during summer differs from the rest of the seasons, so it is possible to model it using linear regressions with a high level of adjustment; during the rest of the seasons the adjustment drops considerably, this may be because, during the time interval it has been sampled, two summers correspond to the years 2020 and 2021, which allows identifying more precisely the behavior of the pest during this season.
Any alternative studied is not able to model the behavior of population growth during spring. Spring can be considered as the transition season since during the winter and autumn months the average temperature is lower than the rest of the year, however, during spring the temperature begins to increase preparing the circumstances for the considerable increase of the population that occurs in summer taking into account that during the first months there are still no adequate temperature values for an uncontrolled growth of the pest, which are found at the end of December due to the fact that in this month there are values that promote considerable increases.
It is important to point out that the seasonal performance of TSVC RBF Kernel significantly outperforms the other alternatives analyzed for the fall and winter seasons. From a practical point of view, it can be used for 9 months of the year as it has the potential to be implemented as a monitoring system that can not only be adapted with little work but also does not require much time.
7. Conclusions
This research has an important value for the development of precision agriculture in Peru, considering that the agricultural sector has had a growth trend in the last 10 years, due to the development of tools such as the one based on industry 4.0. It would open possibilities to apply new technologies to this sector, and thus allow small and medium agro-producers to be more competitive nationally and internationally.
The possibility of developing a seasonally differentiated alarm system has been determined taking the seasonal results into account. It can be affirmed that the predictions in the winter season are less reliable if we consider the results shown in Tables 7 and 9, so it would be convenient to resume specific modeling of this season as soon as enough points have been collected. This could take approximately 4 years.
Table 7.
SVC Results per season.
|
|
|
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Summer |
Accuracy |
89% |
80% |
83% |
||||||
| F1-Score | 88% | 81% | 82% | |||||||
| Autumn |
Accuracy |
65% |
70% |
74% |
||||||
| F1-Score | 66% | 73% | 74% | |||||||
| Winter |
Accuracy |
85% |
88% |
85% |
||||||
| F1-Score | 85% | 88% | 86% | |||||||
| Spring | Accuracy |
50% |
50% |
57% |
||||||
| F1-Score | 51% | 39% | 56% | |||||||
Table 9.
TSVC Results per season.
|
|
||||||
|---|---|---|---|---|---|---|---|
| Summer |
Accuracy |
86% |
91% |
||||
| F1-Score | 86% | 91% | |||||
| Autumn |
Accuracy |
70% |
96% |
||||
| F1-Score | 69% | 96% | |||||
| Winter |
Accuracy |
88% |
88% |
||||
| F1-Score | 88% | 90% | |||||
| Spring | Accuracy |
46% |
57% |
||||
| F1-Score | 38% | 56% | |||||
Determining that the growing population of pests has an exponential behavior has permitted us to propose mechanistic mathematical modeling alternatives, with the possibility of developing new alternatives and with greater precision, based on a deeper understanding of the principles of the process. Presently, the inclusion of the logarithm of the previously measured incidence allows the model to linearize the exponential behavior of reproduction in pest species.
If we consider the costs shown in Table 4, it is possible to analyze the economic impact of implementing a pest early warning system with a high level of reliability. It is estimated that low-class spraying would no longer be necessary and stem spraying with cleaning would be reduced by half its costs. We came to this conclusion as a result of the interviews we had with the farmers who reported that they could only perform one pest inspection per plot, that most of the spraying they do is not properly programmed and in many opportunities, they must spray stems during the month; considering that the tool can be identified at intervals decided by the user, it would be possible to program the spraying when the incidence level is projected to increase. This would result in an annual cost of $529.73/ha, i.e. a saving of 39% of the total cost.
Finally, it is proposed to develop new pest alert systems focused on red spot thrips, the use of tools to optimize the decision making as well as include optimization for the scheduling of cleaning and fumigation taking into account the quality of the agro-product, the costs of production, fumigation, and cleaning, thus achieving greater efficiency in the process and the competitiveness of small farmers in the international market.
Declarations
Author contribution statement
Jose Manrique-Silupu: Conceived and designed the experiments; Contributed reagents, materials, analysis tools or data; Wrote the paper. Jean C. Campos: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper. Ernesto Paiva: Conceived and designed the experiments; Analyzed and interpreted the data. William Ipanaqué: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data.
Funding statement
The authors acknowledge the financial support of the Project Concytec-Banco Mundial “Mejoramiento y ampliación de los Servicios del Sistema Nacional de Ciencia Tecnología e Innovación Tecnológica” 8682-PE, through its executing unit Prociencia [contrato número 165-2018-FONDECYT-BM-IADTAV – Project: “Transformación Digital del sector Agro-Industrial aplicado al Banano Orgánico”.]
Data availability statement
The data that has been used is confidential.
Declaration of interests statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
References
- 1.Someya S., Yoshiki Y., Okubo K. Antioxidant compounds from bananas (musa cavendish) Food Chem. 2002;79(3):351–354. [Google Scholar]
- 2.Aurore G., Parfait B., Fahrasmane L. Bananas, raw materials for making processed food products. Trends Food Sci. Technol. 2009;20(2):78–91. [Google Scholar]
- 3.Potts J., Lynch M., Wilkings A., Huppé G.A., Cunningham M., Voora V.A. International Institute for Sustainable Development Manitoba; Canada: 2014. The state of sustainability initiatives review 2014: Standards and the green economy. [Google Scholar]
- 4.Sánchez Castañeda J. Mercado de productos agrícolas ecológicos en colombia. Suma de Negocios. 2017;8(18):156–163. [Google Scholar]
- 5.Machovina B., Feeley K.J. Climate change driven shifts in the extent and location of areas suitable for export banana production. Ecol. Econ. 2013;95:83–95. [Google Scholar]
- 6.Dadrasnia A., Usman M.M., Omar R., Ismail S., Abdullah R. Potential use of bacillus genus to control of bananas diseases: approaches toward high yield production and sustainable management. J. King Saud Univ., Sci. 2020;32(4):2336–2342. [Google Scholar]
- 7.Gaitán C.F. In: Climate Extremes and Their Implications for Impact and Risk Assessment. Sillmann J., Sippel S., Russo S., editors. Elsevier; 2020. Chapter 7 - machine learning applications for agricultural impacts under extreme events; pp. 119–138. [Google Scholar]
- 8.Annosi M.C., Brunetta F., Monti A., Nati F. Is the trend your friend? An analysis of technology 4.0 investment decisions in agricultural smes. Comput. Ind. 2019;109:59–71. [Google Scholar]
- 9.Gurney T., Hanafi S. 2016. Digging into data to support the sustainable agriculture revolution. [Google Scholar]
- 10.Li M., Chung S.-O. Special issue on precision agriculture. Comput. Electron. Agric. 2015;112:1. Precision Agriculture. [Google Scholar]
- 11.Mazon-Olivo B., Hernández-Rojas D., Maza-Salinas J., Pan A. Rules engine and complex event processor in the context of Internet of things for precision agriculture. Comput. Electron. Agric. 2018;154:347–360. [Google Scholar]
- 12.Kamilaris A., Kartakoullis A., Prenafeta-Boldú F.X. A review on the practice of big data analysis in agriculture. Comput. Electron. Agric. 2017;143:23–37. [Google Scholar]
- 13.Huang Y., Chen Z. xin, Yu T., Huang X. zhi, Gu X. fa. Agricultural remote sensing big data: management and applications. J. Integr. Agric. 2018;17(9):1915–1931. [Google Scholar]
- 14.Ojha T., Misra S., Raghuwanshi N.S. Sensing-cloud: leveraging the benefits for agricultural applications. Comput. Electron. Agric. 2017;135:96–107. [Google Scholar]
- 15.Hsu T.-C., Yang H., Chung Y.-C., Hsu C.-H. A creative iot agriculture platform for cloud fog computing. Sustain. Comput., Inform. Syst. 2020;28 [Google Scholar]
- 16.An W., Wu D., Ci S., Luo H., Adamchuk V., Xu Z. In: Cyber-Physical Systems. Song H., Rawat D.B., Jeschke S., Brecher C., editors. Academic Press; Boston: 2017. Chapter 25 - agriculture cyber-physical systems; pp. 399–417. (Intelligent Data-Centric Systems). [Google Scholar]
- 17.Guo P., Dusadeerungsikul P.O., Nof S.Y. Agricultural cyber physical system collaboration for greenhouse stress management. Comput. Electron. Agric. 2018;150:439–454. [Google Scholar]
- 18.Colizzi L., Caivano D., Ardito C., Desolda G., Castrignanò A., Matera M., Khosla R., Moshou D., Hou K.-M., Pinet F., Chanet J.-P., Hui G., Shi H. In: Agricultural Internet of Things and Decision Support for Precision Smart Farming. Castrignanò A., Buttafuoco G., Khosla R., Mouazen A.M., Moshou D., Naud O., editors. Academic Press; 2020. Chapter 1 - introduction to agricultural iot; pp. 1–33. [Google Scholar]
- 19.Khanna A., Kaur S. Evolution of Internet of things (iot) and its significant impact in the field of precision agriculture. Comput. Electron. Agric. 2019;157:218–231. [Google Scholar]
- 20.Jha K., Doshi A., Patel P., Shah M. A comprehensive review on automation in agriculture using artificial intelligence. Artif. Intell. Agric. 2019;2:1–12. [Google Scholar]
- 21.Pantazi X.E., Moshou D., Bochtis D. In: Intelligent Data Mining and Fusion Systems in Agriculture. Pantazi X.E., Moshou D., Bochtis D., editors. Academic Press; 2020. Chapter 2 - artificial intelligence in agriculture; pp. 17–101. [Google Scholar]
- 22.Pantazi X.E., Moshou D., Bochtis D. In: Intelligent Data Mining and Fusion Systems in Agriculture. Pantazi X.E., Moshou D., Bochtis D., editors. Academic Press; 2020. Chapter 3 - utilization of multisensors and data fusion in precision agriculture; pp. 103–173. [Google Scholar]
- 23.Cai J., Xiao D., Lv L., Ye Y. An early warning model for vegetable pests based on multidimensional data. Comput. Electron. Agric. 2019;156:217–226. [Google Scholar]
- 24.Kim Y.H., Yoo S.J., Gu Y.H., Lim J.H., Han D., Baik S.W. 2013 International Conference on Future Software Engineering and Multimedia Engineering (ICFM 2013) vol. 6. 2014. Crop pests prediction method using regression and machine learning technology: survey; pp. 52–56. (IERI Procedia). [Google Scholar]
- 25.Calou V.B.C., dos Santos Teixeira A., Moreira L.C.J., Lima C.S., de Oliveira J.B., de Oliveira M.R.R. The use of uavs in monitoring yellow sigatoka in banana. Biosyst. Eng. 2020;193:115–125. [Google Scholar]
- 26.Freitez J., Ablan M., Gómez-Cárdenas C. Propuesta de modelos predictivos del brote de la Sigatoka Negra para las plantaciones de plátano al sur del Lago de Maracaibo, Venezuela. Revista Científica UDO Agrícola. 2009;9:191–198. [Google Scholar]
- 27.Garrido-Jurado I., Valverde-García P., Quesada-Moraga E. Use of a multiple logistic regression model to determine the effects of soil moisture and temperature on the virulence of entomopathogenic fungi against pre-imaginal Mediterranean fruit fly ceratitis capitata. Biol. Control. 2011;59(3):366–372. [Google Scholar]
- 28.Yan Y., Feng C.-C., Wan M.P.-H., Chang K.T.-T. vol. 233. 2015. Multiple Regression and Artificial Neural Network for the Prediction of Crop Pest Risks; pp. 73–84. (Lecture Notes in Business Information Processing). [Google Scholar]
- 29.Huang T., Li B., Shen D., Cao J., Mao B. Analysis of the grain loss in harvest based on logistic regression. 5th International Conference on Information Technology and Quantitative Management; ITQM 2017; 2017. pp. 698–705. [Google Scholar]
- 30.Talukder A., Sakib M., Islam M. Determination of influencing factors for integrated pest management adoption: a logistic regression analysis. Agrotechnology. 2017;6(163):2. [Google Scholar]
- 31.Vite Cevallos H., Carvajal Romero H., Barrezueta Unda S. Aplicación de algoritmos de aprendizaje automático para clasificar la fertilidad de un suelo bananero. Conrado. 2020;16(72):15–19. [Google Scholar]
- 32.Almeyda E., Paiva J., Ipanaqué W. 2020 IEEE Engineering International Research Conference (EIRCON) IEEE; 2020. Pest incidence prediction in organic banana crops with machine learning techniques; pp. 1–4. [Google Scholar]
- 33.Elbehri A., Calberto G., Staver C., Hospido A., Skully D., Ignacio Sotomayor L., Bustamante A. Organización de las Naciones Unidas para la Alimentación y la Agricultura (FAO); 2015. Cambio climático y sostenibilidad del banano en el Ecuador: Evaluación de impacto y directrices de política. [Google Scholar]
- 34.Zhang J., Huang Y., Pu R., Gonzalez-Moreno P., Yuan L., Wu K., Huang W. Monitoring plant diseases and pests through remote sensing technology: a review. Comput. Electron. Agric. 2019;165 [Google Scholar]
- 35.Elavarasan D., Vincent D.R., Sharma V., Zomaya A.Y., Srinivasan K. Forecasting yield by integrating agrarian factors and machine learning models: a survey. Comput. Electron. Agric. 2018;155:257–282. [Google Scholar]
- 36.Hayduk D. Organización de las Naciones Unidas para la Alimentación y la Agricultura (FAO); 2017. Manejo de Pesticidas en la industria bananera. [Google Scholar]
- 37.Yang X.-S. In: Introduction to Algorithms for Data Mining and Machine Learning. Yang X.-S., editor. Academic Press; 2019. 7 - support vector machine and regression; pp. 129–138. [Google Scholar]
- 38.Binkhonain M., Zhao L. A review of machine learning algorithms for identification and classification of non-functional requirements. Expert Syst. Appl., X. 2019;1 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that has been used is confidential.