Genetic Influences on the Interactionist Model of Socioeconomic Development: Incorporating Polygenic Scores for Educational Attainment into Developmental Research Using the Family Transitions Project (FTP)

Abstract

Genetic and environmental factors account for variability in a range of developmental outcomes including socioeconomic status (SES). The challenge is to find ways to incorporate genetic information based on studies using biologically-related family members (i.e., studies not involving twins). To address this issue, we computed polygenic scores associated with educational attainment (Lee et al., 2018) for the Family Transitions Project (e.g., R. Conger & Conger, 2002) and incorporated them into the model tested by R. Conger et al. (this issue). Polygenic scores correlated with observed educational attainment for all relevant members of the Family Transitions Project. Moreover, polygenic scores were correlated with many of the other constructs in the R. Conger et al. (in press) model pointing to the relevance of genetic factors for process-models of SES attainment. At the same time, the primary pathways described in R. Conger et al. (this issue) remained viable when polygenic scores were included in the analyses suggesting that the environmental pathways predicted by the Interactionist Model (e.g., R. Conger et al., 2010) are still tenable. The current study thereby illustrates how genetic information can be included in tests of developmental models to clarify SES attainment across generations.

The study by Conger, Martin and Masarik (in press) in this special section involved a test of a theoretical model whereby which family processes and economic history contributed to the development of adolescent conscientiousness, which in turn, predicted socio-economic characteristics during adulthood. The present investigation extends that work by considering possible genetic influences on key aspects of their theoretical model, the interactionist model (IM). To accomplish this task, we capitalize on genetic information collected from study participants during the course of the longitudinal study. This is an important extension because research consistently indicates that genetic differences between people contribute to differences in complex phenotypic variables like personality, the quality of social interactions, and educational attainment (e.g., Ayorech, Krapol, Plomin, & von Stumm, 2017; Belsky et al., 2016; Belsky et al., 2018; Cesarini & Visscher, 2017; Conley et al., 2015; Lee et al., 2018; Okbay e al., 2016; Reitveld et al. 2013; Reitveld et al. 2014; Selzam et al. 2016). Indeed, classic twin studies have pointed to the relevance of genetic factors for psychological attributes for over fifty years (Polderman et al., 2015; see Plomin, DeFries, Knopik, & Neiderhiser, 2015) as these studies almost always report that the identical twins are more similar than dizygotic twins for a range of psychological and cognitive attributes (Turkheimer & Waldron, 2000). Researchers have only started to incorporate molecular genetic information into developmental studies but the results of such work suggest that genetic factors are relevant for the development of SES (e.g., Bates et al., 2018; Belsky et al., 2016; Belsky et al., 2018; Kong et al., 2018). The current paper extends these recent developments using data from the Family Transitions Project.

A recent genome-wide association study (GWAS; for an accessible introduction see Bush & Moore, 2012) involving DNA samples from over 1.1 million participants identified a set of genetic variants associated with educational attainment (Lee et al., 2018). This work extended earlier GWAS studies of this same phenotype (Okbay et al., 2016; Reitveld et al., 2013; Reitveld et al. 2014). We expected that these genetic variants would be especially important for the present study inasmuch as a key construct in the Conger et al. (in press) developmental model is educational attainment during the transition from adolescence to adulthood. Indeed, we expected that the genetic characteristics would be associated with educational attainment and with the antecedents and consequences of such attainment as proposed by the interactionist model from Conger and his colleagues (e.g., Conger & Donnellan, 2007; Conger et al., 2010; R. Conger et al., in press). Fortunately, there are procedures that can make use of summary GWAS findings to create composite variables (polygenic scores) that reflect, in part, the genetic propensity for educational attainment and correlated attributes (see also Ayorech et al. 2017; Belsky et al., 2016; Chambris, Lee, Cesarini, Benjamin, & Laibson, 2015; Conley et al., 2015). In the following sections, we consider the nature of polygenic scores, how they can be embedded in a developmental model like the IM, and the specific hypotheses guiding the current analysis.

What is a Polygenic Score?

Polygenic scores can be computed from the summary output generated by a GWAS. Briefly, a GWAS makes use of genetic variants called single nucleotide polymorphisms (SNPs). A SNP is a base pair location (locus) on the DNA sequence that shows variability among individuals. The less common allele or genetic variant in the population is called the minor allele. For example, the rs1537415 SNP found on chromosome 9 in humans has two alleles – either a C or G. The C allele is the most common variant whereas the G is the minor allele. Common variants are typically defined as having minor allele frequencies greater than 1% in the population.

A standard GWAS is basically a huge set of regression analyses in which a quantitative trait (e.g., educational attainment) is regressed on each SNP. Each SNP genotype is coded 0, 1, 2, where the values refer to the number of reference alleles. For example, assuming an additive model and a C-G SNP where the reference allele is the G allele, genotype C/C would be coded 0 (no G alleles), genotype C/G would be coded 1 and the G/G genotype coded 2. The regression coefficient represents the allelic effect: the change in educational attainment for an allele change from C to G (e.g., C/C to C/G, a change from 0 to 1 reference allele; or C/G to G/G, a change from 1 to 2 G alleles). Such an analysis is repeated for each SNP, typically a million or more markers. The SNP name or location, reference allele, allelic effect, and sometimes the p-value make up the summary GWAS data that is used to construct genome-wide polygenic scores.

The results of multiple GWAS studies of psychological variables prompted Chambris et al. (2015) to propose a Fourth Law of Behavioral Genetics to amend Turkheimer’s (2000) existing three laws: “A typical human behavioral trait is associated with very many genetic variants, each of which accounts for a very small percentage of the behavioral variability” (p. 305). This Fourth Law, hypothesized by R. A. Fisher 100 years ago (Fisher, 1918), is that a large number of variants contribute to complex phenotypes in line with the infinitesimal model from theoretical biology (e.g., Barton, Etheridge, Véber, 2017; Hu, Wang, & Zu, 2012). In other words, there appears to be no single gene entirely responsible for differences in complex human characteristics like intelligence or self-control or propensity to smoke cigarettes. Many genetic variants each with quite small effects seem to statistically account (at least, partially) for the differences between people for complicated phenotypes studied by psychological and behavioral scientists.

A polygenic score reflects the Fourth Law of Behavioral Genetics because the score is a summation of the many individual effects estimated from a GWAS, often based on some statistical threshold for selecting variants associated with the phenotype of interest (see Dudbridge, 2013). The scoring algorithm derived from an initial GWAS can be used with a new genetically informed dataset to compute a genetic propensity score in that sample (e.g., Ayorech et al. 2017; Belsky et al. 2016; Conley et al. 2015). This process is analogous to deriving a regression model on a large set of training data that is subsequently used with a second dataset containing the same predictor variables to generate new predicted scores. An important caveat is that the sample sizes for an initial GWAS needs to be quite large to produce a scoring procedure that is predictive of the phenotype of interest in subsequent datasets (see Dudbridge, 2013). This reflects the well-known phenomenon of overfitting whereby statistical models often capture sample-specific idiosyncrasies that do not generalize to other datasets (see Yarkoni & Westfall, 2017). It appears that using large datasets for GWAS yields viable scoring procedures.

Belsky et al. (2016) used the GWAS results from Rietveld et al. (2013) to create a polygenic score for educational attainment for the 918 non-Maori members of the Dunedin Study (see Poulton, Moffitt, & Silva, 2015). This polygenic score was positively associated with a phenotypic measure of educational attainment by age 38 (r = .15) and some of its correlates including greater socioeconomic attainment (i.e. SES; r = .13). This approach was extended using data from the Environmental Risk Longitudinal Twin Study (E-Risk) and four other longitudinal studies including the Add Health Dataset and the Health and Retirement Study (Belsky et al., 2018). The E-Risk results showed that polygenic educational scores were associated with educational achievement scores at age 18. This association also held controlling for parental educational attainment. Conley et al. (2015) conducted similar analyses correlating polygenic scores and SES using members of the Framington Heart Study (r = .16). Collectively, these results indicate that polygenic scores for educational attainment have viability. A caveat is that the observed correlations between polygenic scores and years of education is modest. Nonetheless, Reitveld et al. (2014) noted that “polygenic scores can have large enough effects to be usable even in relatively small samples” (p. 1984).

Incorporating a Polygenic Score into a Test of the Interactionist Model (IM)

The Interactionist Model (IM) described by Conger and his colleagues (e.g., Conger & Donnellan, 2007; Conger et al., 2010; R. Conger et al., in press) outlines intergenerational processes that connect socioeconomic conditions, family processes, and individual development. This model posits that both social influence and social selection mechanisms are relevant to these connections. According to the terminology commonly associated with the model, social influence processes reflect environmental causes of developmental outcomes whereas social selection mechanisms typically involve genetically influenced characteristics that act on environments through processes such as evoking predictable responses from the environment or actively seeking out social contexts (see Scarr & McCartney, 1983).

In the original presentation of the model in Conger and Donnellan (2007), personal characteristics evident in childhood and adolescence such as personality traits and scholastic aptitude are thought to contribute to socioeconomic attainment, interpersonal processes, and subsequent parenting practices. These pathways reflect, in part, person-environment transactions that are likely to be driven, in part, by genetic factors given that personality traits and cognitive aptitude are heritable following Turkheimer’s (2000) First Law of Behavioral Genetics – virtually all human attributes show genetic influence.

Indeed, personality traits have been implicated in educational attainment (see Damian, Su, Shanahan, Trautwein, & Roberts, 2015; Mõttus, Realo, Vainik, Allik, & Esko, 2017; Roberts, Kuncel, Shiner, Caspi, & Goldberg, 2007) and Roberts et al. (2007) reported that the typical effect sizes for personality-adult SES associations were comparable to the effect sizes for the association between intelligence and adult SES. In the present analysis, we focus on the personality trait of conscientiousness because Conger et al. (in press) suggested it was mediating variable (in the statistical sense) between family history and later social and economic attainment, presumably because conscientious individuals tend to work hard, persist in the face of difficulty, and set high goals for conventional success. Conscientiousness related attributes like perseverance, achievement striving, and planfulness are associated with educational success in numerous studies (e.g., Corker, Donnellan, & Oswald, 2012; Damian et al., 2015; Mõttus et al., 2017; Noftle & Robins, 2007; Poropat, 2009). Especially important, a recent meta-analysis of 16 twin studies found significant evidence of genetic contributions to differences between people in their level of conscientiousness (Vukasović & Bratko, 2015) and a recent report found the polygenic scores for education were associated with personality traits (Mõttus et al., 2017), albeit the effect sizes were modest (range from −.09 to .12 in terms of correlations). Thus, we propose that genetic effects on educational attainment are explained, in part, by genetic influences on personality traits (see also Mõttus et al., 2017). Jocklin, McGue, and Lykken (1996) made a similar point with respect to the idea that genetic influences on divorce (another complex phenotype like educational attainment) are mediated, in part, by personality traits.

Social influence pathways are specified in the IM by positing that socioeconomic conditions contribute to family stress processes and parental investments because of environmental causation. Likewise, the IM posits that family stress processes and parental investments in children influence physical, cognitive, and social/emotional development via environmentally-mediated processes. The basic idea of social influence is that some aspects of socioeconomic conditions and family environments have causal impact on developmental outcomes net of genetic influences passed from parents to children.

Genetic factors, at least the sort described in this paper, are relevant to understanding the social selection pathways in the IM. In particular, certain genotypes may elicit particular environmental responses or motivate individuals to niche pick environments that are consistent with their genotypes (Scarr & McCartney, 1983). These are known as evocative gene-environment correlations and active gene-environment correlations (see Jaffee & Price, 2007; Plomin, DeFries, & Loehlin, 1977). For example, evocative gene-environment correlations or elicitation processes would occur if children and adolescents with a higher genetic propensity for educational attainment draw out greater parental investments in their education because of their initial interest, success, and motivation in school-related areas. Parents might be more likely to buy extra books and pay for enriching summer school activities for children who are especially interested in reading and academic pursuits. Active gene-environmental correlations or niche picking might occur as individuals with a greater genetic propensity for educational attainment end up affiliating with higher achieving peers or selecting into more academically challenging courses thereby promoting greater school attainment. Simply put, genetic differences may help youth to create social environments that promote certain types of developmental outcomes (see also Ayoub et al., 2019).

It is also the case that parental genetic factors might influence their offspring’s SES above and beyond direct genetic transmission. Parental genotypes may influence parental SES, parental investments in the education of their offspring, and parenting practices. Two recent studies using sophisticated methods for isolating genes passed to offspring from parental genes not transmitted to offspring, support this contention (Bates et al., 2018; Kong et al., 2018). This work suggests that parental genetic factors contribute to the rearing environments of children, a phenomenon also known as a passive gene-environment correlation (Plomin et al., 1977). We conduct some ancillary analyses to investigate this issue as well but our sample sizes are reduced.

The Current Study

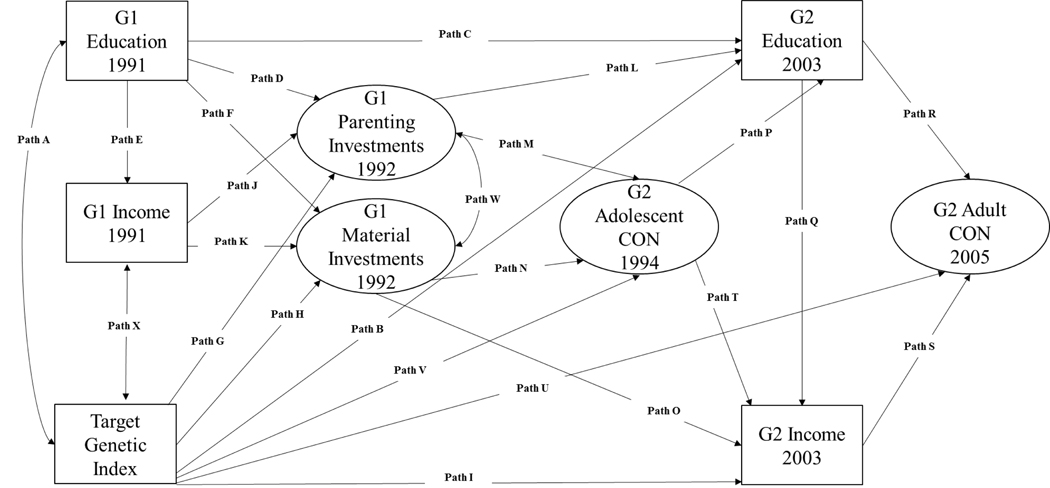
As noted earlier, the current study builds on the R. Conger et al. (this issue) tests of the IM (see Figure 1) by incorporating polygenic scores for educational attainment into their model. The contribution of our work is that we illustrate how polygenic scores can be incorporated into existing developmental models tested on samples like the Family Transitions Project described in this special section. We hope this approach provides a template for future studies that could also embed genetically informed variables into existing models using data from biologically-related families (see also Belsky et al., 2016). Four predictions guided this study.

Figure 1.

Interactionist Model with a Genetic Index

H1: Polygenic scores will be associated with years of education for both the G1 and G2 generations. This prediction is a test of the validity of the polygenic scores and is an important prerequisite for subsequent analyses using polygenic scores in the developmental model.

H2: Polygenic scores for G2 adolescents will be associated with G1 material and parenting investments in the adolescent. This is an extension of the earlier arguments that genetic propensities may be related to person-environment transactions.

H3: Polygenic scores for G2 adolescents will be associated with adolescent conscientiousness. We posit that some of the genetic variants implicated in educational attainment will also contribute to the development of personality attributes linked to the domain of conscientiousness.

H4: Polygenic scores for G2 adolescents will be associated with higher incomes. This prediction is consistent with Belsky et al. (2016) and stems from the close connection between educational attainment and income in contemporary society.

Method

Participants and Procedures

Data used in this report were drawn from the Family Transitions Project (FTP) which is described in the introductory paper for this special section (see K. Conger, Neppl, & Scaramella, in press). Data collection for the most recent waves was approved by the University of California, Davis IRB (#21946–11 “Family Transitions Project”). The IRB protocol was officially closed in 2013 but the closure allows for the analysis of data. De-identified data were analyzed for this project. This long-term longitudinal study involves three generations of participants. For the present analyses we focused on the first two generations including the G1 parents of the G2 cohort of early adolescents, the G2 target adolescents, and close-aged siblings of the target adolescents who also participated in the study. This group of participants provided the best configuration of subjects for genetic analyses in terms of sample size and the availability of data on educational attainment (i.e. using the G3 offspring of G2 targets would not be justified as the vast majority are still in the process of completing their schooling). Tests of Hypothesis 1 use all available genetic data from the G1 parents, G2 targets, and siblings in the sample whereas tests of Hypotheses 2 to 4 use the subsample of the FTP used in the Conger et al. (in press) investigation. Readers interested in extensive detail about the measures should consult Conger et al. (in press). DNA was extracted from saliva samples taken with Oragene kits (DNA Genotek, Ontario, Canada). Samples were collected between November 2007 and August 2012. Polygenic scores were available for 326 G1 fathers, 391 G1 mothers, 405 G2 targets, and 372 siblings in the entire FTP sample. A technical report describing the quality control efforts for genotyping is included as a supplemental material.

Measures

G1, G2, and sibling educational attainment.

Educational attainment for all participants was coded on a 6-point scale (1= less than high school; 2 = high school degree/GED; 3 = degree from junior, vocational, or community college, or attended college but did not earn a 4-year degree; 4 = degree from 4-year college; 5 = Master’s degree; and 6 = PhD or professional degree). The average of G1 father and mother educational attainment was used in the current analyses.

G1 and G2 income.

G1 and G2 income were measured as an income-to-needs ratio by dividing the total family income for the past year by the U.S. Department of Health and Human Services poverty guidelines by family size. Family income included all wages, salaries, and other sources of income (e.g., self-employment income, farm net income, child support, and supplemental security income).

G1 parenting investments in G2.

The same observational variables used in R. Conger et al. (in press) were used in this report. Parenting investments captured the degree to which the G1 parents provided emotionally supportive and appropriate managerial behaviors in their child. This was a latent variable with three indicators – warm parenting, low hostile parenting, and low harsh and inconsistent discipline.

G1 material investments in G2.

A cumulative index measured material investments as reported in R. Conger et al. (in press). This index was created by dichotomizing seven variables related to parental investments (extracurricular activities, parental aid during the transition to adulthood, parental aid with talents and skills, and four interviewer reported items assessing the family’s living environment) so that higher scores represent greater investments. The underlying logic for cumulative indexes is explained in Rauer et al. (2008).

G2 Conscientiousness in adolescence and adulthood.

The achievement and control lower-order scales from the Multidimensional Personality Questionnaire Scale (MPQ; e.g., Harkness, Tellegen, & Waller, 1995) were the indicators of a latent Conscientiousness variable during adolescence and adulthood. These scales were selected based on previous work suggesting these scales are substantially correlated with NEO domain scores for Conscientiousness (Church, 1994; Tellegen & Waller, 2008). The G1 parents of the G2 targets served as informants in adolescence whereas romantic partners of G2 targets served as informants in adulthood. Parents completed an informant report of the MPQ and romantic partners completed the informant report of the Iowa Personality Questionnaire (Donnellan, Conger, & Burzette, 2005), a measure intended to measure the same dimensions as the MPQ.

Genotyping.

Approximately half the FTP participants were genotyped using the Illumina HumanOmni1-Quad v1 platform (Omni-Quad) and half were genotyped using the Illumina HumanOmniExpressExome v1 platform (Express-Exome). The Illumina HumanOmni1-Quad genotyping platform was discontinued midway through our genotyping efforts. Quality control (QC) analyses were conducted within platform, and across platforms using a common set of markers. The Omni-Quad chip included 1,134,514 genetic variants—including single-nucleotide polymorphisms (SNPs), copy number variants (CNVs) and insertion/deletion variants (INDELS). The Express-Exome chip included 958,179 genetic and structural variants. Only SNPs were used for the current analyses; other structural variants were removed.

Marker map locations and annotations were based on the Human Genome Reference Consortium GenomeBuild 37.1. SNP markers that did not have a reliable chromosome or base-pair location using Build 37.1 were not used, and markers with minor allele frequencies (MAF) < .01 and call rates less than 95% were also removed. Markers included in the HapMap Project and 1000 Genomes Project have been extensively validated in independent samples. Thus, we further limited our SNPs to those validated in these databases (960,445 Omni-Quad SNPs and 952,624 Express-Exome SNPs).

The final SNP marker set included 582,624 markers common to both genotyping platforms that met all QC filters. Using these SNPs the average missing genotype rate (per individual) was 0.0115 (SD=0.0739). Plotting heterozygosity rate against the proportion of missing genotypes suggested .03 as an appropriate missing data threshold. Consequently, we removed 82 individuals with greater than 3% missing genotypes. No individuals were removed for excess (or less than expected) heterozygosity (or X chromosome homozygosity). Relationship (kinship) status among family members was verified using PLINK (Chang et al., 2015; Purcell, S. & Chang, C., PLINK 1.9, url: www.cog-genomics.org/plink/1.9/). Identity-by-descent (IBD) estimates for duplicate control samples indicate excellent genotyping quality (average mean IBD > 0.999; range 0.9995 to 1.0). (Additional details are available in the supplementary material).

Final genotypes were imputed, separately by platform, from this common set of SNPs using the 1000 Genomes phase 3 (1000 Genomes Project, 2015; (www.ncbi.nlm.nih.gov/bioproject/28889) reference panel (via the Michigan Imputation Server; (https://imputationserver.sph.umich.edu). Imputation yielded approximately 48 million SNPs; SNPs with MAF > 0.01 were used in the current analyses (~9 million SNPs).

Genome-wide Polygenic Scores.

We used summary results from a meta-GWAS of educational attainment, obtained from the Social Science Genetic Association Consortium (SSGAC; url: https://www.thessgac.org/), to generate polygenic scores from Lee et al. (2018). However, due to IRB restrictions the 23andMe cohort was not available through the SSGAC. Thus, summary data (file: GWAS_EA_excl23andMe.txt)were based on a meta-GWAS of 766,345 individuals (combined discovery and replication samples). Polygenic scores (PS) were generated using PLINK (www.cog-genomics.org/plink/1.9/; Chang et al., 2015). PSs were constructed from 7,187,581 SNPs available in both the FTP sample and the SSGAC summary data (for details see Donnellan and Martin, this issue). Using various p-value thresholds to select subsets of SNPs (e.g., selecting only SNPs with p-values less than 0.50, 0.25, 0.1, 0.05) did not yield markedly different correlations. Thus, the PSs were scored using all 7,187,581 common SNPs. Results using the earlier Okbay et al. (2016) GWAS scoring procedure were nearly identical to those reported here in terms of statistical significance and effect size estimates.

Results

Preliminary Analyses: Correlations among Polygenic Scores and Educational Attainment in the FTP

Table 1 provides correlations between polygenic scores and reported educational attainment for G1 Fathers, G1 Mothers, G2 Targets, and siblings. As seen in Table 1, the polygenic score was related to the phenotype of interest across all four roles (rs range from .19 to .22, all ps < .01). These results provide support for H1 in the current study. In other words, polygenic scores computed in this sample appear to have validity. Our effect size estimates were consistent with findings in the literature. For example, Mõttus et al., 2017 reported a correlation of .18 between educational attainment and corresponding polygenic scores.

Table 1.

Correlations between Polygenic Scores and Observed Educational Attainment in the Family Transitions Project

Person	Correlation	p-value
G1 Fathers (n = 321)	.189	.001
G1 Mothers (n = 388)	.191	<.001
G2 Siblings (n = 364)	.220	<.001
G2 Targets (n = 395)	.219	<.001

Note: G1 and G2 refer to generations in the FTP.

To further evaluate the validity of the polygenic scores, we estimated correlations between family members. Conley et al. (2015) reported correlations between polygenic scores for mothers, fathers, and target respondents in the Framingham Heart Study (r = .59 for targets and mothers, r = .60 for targets and fathers, and r = .22 for mothers and fathers). Results for the FTP are reported in Table 2. As shown in column 2 of Table 2, the correlation between biologically related 1^st degree relatives in the FTP were about .50 on average (rs ranged from .440 to .586), consistent with Conley et al. (2015) and with expectations of biological theory.

Table 2:

Family Pair Correlations for Polygenic Scores and for Observed Educational Attainment in the Family Transitions Project

Pairs	Polygenic Scores	Observed Scores	Partial Correlations
Fathers and Mothers	.029 (p = .633, n = 272)	.318 (p< .001, n = 422)	.335 (p< .001, df = 264)
Fathers and Siblings	.586 (p< .001, n = 238)	.280 (p< .001, n = 390)	.243 (p< .001, df = 229)
Fathers and Targets	.440 (p< .001, n = 249)	.315 (p< .001, n = 393)	.258 (p< .001, df = 237)
Mothers and Siblings	.513 (p < .001, n = 277)	.304 (p< .001, n = 435)	.226 (p< .001, df = 270)
Mothers and Targets	.522 (p< .001, n = 297)	.260 (p< .001, n = 442)	.186 (p = .002, df = 285)
Siblings and Targets	.488 (p< .001, n = 287)	.356 (p < .001, n = 432)	.313 (p< .001, df = 276)

Note: The Partial Correlation column reports correlations between observed educational attainment score controlling for the polygenic scores of both family members.

There was little indication of assortative mating for polygenic scores for G1 mothers and fathers in the FTP (r = .029), counter to Conley et al. (2015). The third column of Table 2 provides correlations between family members’ educational attainment, which ranged from .260 (mothers and targets) to .356 (siblings and targets). To determine the degree to which these correlations might result from genetic relatedness, column 4 in Table 2 provides partial correlations for educational attainment for FTP pairs controlling for polygenic scores. As seen in Table 2, the partial correlations were still statistically distinguishable from zero, although the effect size estimates were reduced from column 3 for biological relatives. The average reduction was .06 in Cohen’s q metric (i.e., the difference between r-to-z transformed correlations). Thus, polygenic scores did not substantially account for the phenotypic correlations between family members for educational attainment.

Table 2 also shows that the maximum sample size for an analysis that would include polygenic scores from mothers and targets would by 297. That is, there were 297 cases with polygenic scores from both the targets and their mothers. This figure was 238 cases for targets and dads. This limited the statistical power for analyses that would focus on genetic information from targets and at least one parent.

Incorporating Target Polygenic Scores into a Developmental Model

The structural equation model (SEM) depicted in Figure 1 was estimated with MPlus 8.0 (Muthén & Muthén, 1998–2018) using full information maximum likelihood (FIML) procedures. As noted previously, this model is an extension of the model reported by R. Conger et al. (this issue) adding polygenic scores. The model fit the data reasonably well (RMSEA = .048, CFI = .958; see note for Table 4). Prior to considering the path coefficients, we first examined the estimated correlations for the latent variables specified in Figure 1. These are reported in Table 3 and replicate correlations reported in R. Conger et al. (in press). The additional row with the polygenic scores is new to this report. Consistent with the broad theorizing in this paper, polygenic scores were correlated with all constructs in the analyses (all ps < .05) except G1 income. Of note, polygenic scores were correlated with G1 material and parenting investments in G2, results consistent with the predictions in Hypothesis 2. Likewise, polygenic scores were associated with conscientiousness during both adolescence and adulthood, consistent with Hypothesis 3, and with subsequent G2 income, consistent with Hypothesis 4. These zero-order correlations provide an important foundation for helping to interpret the path coefficients in the SEM.

Table 4.

Standardized Path Coefficients for Figure 1

Path	Label	Standardized Coefficient	SE	p	Polygenic Score
A	Correlation: G2 Polygenic Scores and G1 Educational Attainment	0.200	0.059	0.001	Yes
B	G2 Educational Attainment on G2 Polygenic Scores	0.107	0.049	0.028	Yes
C	G2 Educational Attainment on G1 Educational Attainment	0.175	0.061	0.004
D	G1 Parenting on G1 Educational Attainment	0.475	0.066	0.000
E	G1 Income on G1 Educational Attainment	0.255	0.052	0.000
F	G1 Material Investments on G1 Educational Attainment	0.229	0.054	0.000
G	G1 Parenting Investments on Polygenic Scores	0.111	0.077	0.153	Yes
H	G1 Material Investments on Polygenic Scores	0.099	0.059	0.093	Yes
I	G2 Income on G2 Polygenic Scores	0.061	0.056	0.277	Yes
J	G1 Parenting Investments on G1 Income	0.176	0.067	0.008
K	G1 Material Investments on G1 Income	0.158	0.054	0.003
L	G2 Educational Attainment on G1 Parenting Investments	0.215	0.086	0.012
M	G2 Adolescent Conscientiousness on G1 Parenting Investments	0.337	0.087	0.000
N	G2 Adolescent Conscientiousness on G1 Material Investments	0.209	0.071	0.003
O	G2 Income on G1 Material Investments	0.143	0.054	0.008
P	G2 Educational Attainment on G2 Adolescent Conscientiousness	0.399	0.058	0.000
Q	G2 Income on G2 Educational Attainment	0.312	0.061	0.000
R	G2 Adult Conscientiousness on G2 Educational Attainment	0.244	0.090	0.007
S	G2 Adult Conscientiousness on G2 Income	0.215	0.080	0.007
T	G2 Income on G2 Adolescent Conscientiousness	0.180	0.072	0.012
U	G2 Adult Conscientiousness on G2 Polygenic Scores	0.055	0.070	0.432	Yes
V	G2 Adolescent Conscientiousness on G2 Polygenic Scores	0.072	0.067	0.278	Yes
W	Correlation: G1 Material Investments and G1 Parenting Investments	0.327	0.078	0.000
X	Correlation: G2 Polygenic Scores and G1 Income	−0.045	0.066	0.501	Yes

Note: Polygenic Score = Path involves Polygenic Scores. SE = Standard Error. Model Fit: Chi-Square: 81.606, df = 45; CFI = .958, TLI = .928, RMSEA = .048 (90% CI: .031 to .065), SRMR = .039. Sample Size = 346.

Table 3.

Correlations between Study Variables (N = 346)

		1	2	3	4	5	6	7	8	9
1	G1 Income	1.000
2	G1 Educational Attainment	0.255	1.000
3	G1 Material Investments	0.217	0.289	1.000
4	G1 Parenting Investments	0.298	0.542	0.443	1.000
5	G2 Adolescent Conscientiousness	0.146	0.257	0.368	0.444	1.000
6	G2 Income	0.110	0.230	0.314	0.315	0.417	1.000
7	G2 Educational Attainment	0.168	0.416	0.309	0.510	0.558	0.472	1.000
8	G2 Adult Conscientiousness	0.065	0.162	0.151	0.204	0.236	0.341	0.360	1.000
9	G2 Polygenic Index	0.008	0.200	0.145	0.207	0.172	0.192	0.255	0.158	1.000

Note. All correlations significant (p < 05; two-tailed) except for G1 Income and the G2 Polygenic Index (p = .908).

Standardized path coefficients for the model depicted in Figure 1 are reported in Table 4. Paths involving the polygenic score are indicated in the last column of Table 4 for easier identification. Several results are worth discussing. First, not all paths involving polygenic scores were statistically significant in the multivariate path analysis. For example, there was no evidence that the path coefficient from G2 polygenic scores to G2 income was distinguishable from zero (i.e., path I in the model). The same was true of the path coefficient from G2 polygenic scores to G2 adult Conscientiousness (path U in the model), and from G2 polygenic scores to G2 adolescent Conscientiousness (path V in the model). Other statistical effects in the model appear to account for any effect from G2 polygenic scores to these seemingly downstream correlates.

Second, evidence for genetic and environmental correlations on parenting and material investments are not as strongly evident in Table 4 (Hypothesis #2). There was no evidence that G2 polygenic scores predicted G1 material investments (path H) or G1 parenting investments (path G) using the p < .05 threshold for statistical significance. This likely means that the shared variance between polygenic scores, G1 education, and G1 income account for the zero-order associations between polygenic scores and these variables. Third, the direct path from the G2 polygenic score to G2 educational attainment was .11 (path B) compared to the correlation of .25. The model depicted in Figure 1 therefore appears to cut the effect size of the polygenic score on observed attainment by more than 50%. Such a result suggests that the model has some promise in helping to explain (at least statistically) how the genetic variants captured by the polygenic scores are associated with the complex developmental phenotype of educational attainment, a point we elaborate upon in the next section.

Last, we note that all of the social influence pathways reported in Conger et al. (in press) remained statistically distinguishable from zero in the analyses reported in Table 4 and the effect size estimates (i.e., the standardized betas) were largely unchanged from those reported in the earlier analysis. For example, G1 educational attainment was still related to G2 educational attainment (path C) taking polygenic scores and the other variables in Figure 1 into account. This finding suggests that the major conclusions of Conger et al. (in press) hold after taking polygenic scores into account. We emphasize again, however, that our polygenic scores were “only” correlated with educational attainment around .25 (see Table 3), leaving a substantial proportion of the genetic variance in educational attainment unexplained.

Ancillary Analyses Incorporating Parental and Target Genetic Information into the Model

As displayed in Tables 1 and 2 and discussed earlier, information about parental DNA is available in the FTP. A limiting factor, however, is the reduced sample size available for analyses using parents and targets. Nonetheless, we averaged the maternal and paternal polygenic scores and included that variable in an additional test of the model depicted in Figure 1. We estimated the model by regressing all 9 key variables in Figure 1 on the parental polygenic variable. The model fit the data reasonably well (RMSEA = .045, CFI = .967) based on 293 families.

The estimated zero-order correlations between the Parental Polygenic index and variables in Figure 1 pointed to associations between parental genetic factors and the constructs in the IM. This variable was associated with G1 Parenting Investments (r = .20, p < .05), G1 Educational Attainment (r = .22, p < .05), G2 income (r = .16, p < .05), G2 educational attainment (r = .25, p < .05), G2 adult Conscientiousness (r = .18, p < .05), and G2 Polygenic Scores (r = .60, p < .05). However, this variable did not have statistically detectable associations with G1 Income (r = .08, p = .19), G1 Material Investments (r = .10 p = .07), or Adolescent Conscientiousness (r = .10, p = .13). The complete correlation matrix and reporting of coefficients from this structural equation model are contained in the supplemental materials.

Other than the coefficients described in this paragraph, none of the other statistically significant effects in Table 4 were altered. The correlation in Figure 1 between G2 Polygenic Scores and G1 Educational Attainment was reduced from the value in Table 4 (r = .08, p = .26 versus r = .20, p < .05). This suggests that the significant correlation reported in Table 4 between G2 Polygenic Scores and G1 Educational Attainment was likely driven by parental genes (i.e., variance in G1 Educational Attainment that is unique from G1 Polygenic scores is unrelated to G2 Polygenic Scores). G2 polygenic scores no longer predicted G2 attainment (β = .08, p = .21) while including a pathway for G1 polygenic scores (β = .09, p =.162). This is likely a result of the correlation between polygenic scores for parents and children described above. As expected, G1 average polygenic score statistically predicted G1 Educational attainment (β = .22, p < .05) and G2 polygenic scores (β = .60, p < .05). We also repeated analyses placing just a correlation between G2 polygenic scores and G1 polygenic scores given how missing data are handled in Mplus version 8 as this increases sample size because parental polygenic scores are no longer treated as the sole exogenous variable. The same pattern of results occurred. Collectively, these results suggest that the statistically significant focal pathways in the Conger et al. (in press) paper are not eliminated when including information about polygenic scores from parents.

Discussion

The objective of this paper was to incorporate polygenic scores associated with educational attainment into the Interactionist Model (IM) described by Conger and his colleagues (e.g., Conger & Donnellan, 2007; Conger et al., 2010). The IM depicts intergenerational processes that connect socio-emotional development with socioeconomic conditions and parenting processes by invoking both social influence and social selection processes. We posited that genetic factors captured by polygenic scores would be relevant to constructs involved in the IM. Likewise, we posited that genetic factors are relevant to the person-environment transactions depicted in the model and related theorizing. We view the current results as an illustration of the value of embedding polygenic variables into existing developmental models that are typically evaluated using family-based longitudinal designs. We think there is value in using information about DNA extracted from saliva collected from participants to incorporate genetic information into tests of the IM.

We first replicated previous results by showing that polygenic scores computed using weights developed from summary data from large GWAS studies (Lee et al., 2018) predicted educational attainment in the Family Transitions Project. This was the foundation for our subsequent analyses. The effect sizes, although they would probably be considered “small” by typical conventions (rs between .15 and .21; e.g., Cohen, 1988; McCartney & Rosenthal, 2000), were consistent across FTP members (e.g., mothers and fathers) and with previous studies. Thus, we found evidence consistent with the first hypothesis tested in this paper and with the general idea that genetic factors are relevant to SES attainment. Moreover, small effect sizes are often quite common in individual difference research (Gignac & Szodorai, 2016).

We then used the polygenic scores for G2 targets in subsequent analyses designed to extend tests of the R. Conger et al. (in press) model described elsewhere in this special section. Consistent with the predictions that genetic-related variability is associated with the processes outlined in the IM, G2 polygenic scores were correlated with the eight other latent constructs in the model (see Table 3). Of note, polygenic scores were correlated with G1 educational attainment and G2 educational attainment. Polygenic scores were also associated with adolescent conscientiousness (Hypothesis 3) and the two parenting variables (Hypothesis 2, at least at the zero-order level). The correlations with parenting are consistent with the idea that genetic factors partially underlie evocative child to parent processes (e.g., Scarr & McCartney, 1983).

The evaluation of the SEM depicted in Figure 1 provided additional tests of our hypotheses. The deviations from the correlational results involving polygenic scores were noteworthy, at least when considering statistical significance and effect sizes: the paths involving income and personality attributes. Broadly speaking, these results suggest that the processes in the IM are a plausible way to account (in statistical terms) for the associations between polygenic scores and the phenotypes of primary interest in this special issue. Likewise, the correlation of approximately .25 between polygenic scores and G2 attainment in Table 3 was reduced to roughly .11 in the multivariate analyses reported in Table 4. This suggests that a genetically informed IM is a useful way to conceptualize some of the processes that account for associations between polygenic scores and educational attainment. In other words, the modified IM may help to explain why polygenic scores are associated with educational attainment.

Table 4 is also potentially noteworthy because the key pathways reported in Conger et al. (in press) remain viable. For example, G2 educational attainment is still associated with G1 parenting investments while accounting for polygenic scores. The same is true for the association between G2 educational attainment and G1 educational attainment. Such results suggest that many of the key pathways posited by the IM are not eliminated by taking polygenic scores for educational attainment into account. This is a one way to begin to incorporate genetic information into longitudinal studies not involving twins. Thus, the current results are promising in showing how genetic information can be a part of traditional family-based longitudinal studies common in developmental psychology. Although educational attainment is one of the better-characterized variables of interest to developmental researchers in the GWAS literature, that literature is expanding rapidly to cover variables related to psychopathology, physical health problems, and personality attributes. Although exceptionally large sample sizes are often required to generate polygenic scores, such large samples do not seem necessary to profitably use polygenic scores (Reitveld et al., 2014) in subsequent studies, as shown here (see also Belsky et al., 2016).

Limitations and Future Directions

The standard limitations noted by R. Conger et al. (this issue) also apply here. An additional issue is that we did not have measures of G2 personality in childhood (the project started when the G2s were in 7^th grade). This means that we are missing the data necessary to fully evaluate evocative child-to-parent effects that quite likely start prior to adolescence (e.g., Anderson, Lytton, & Romney, 1986; Ayoub et al., 2019; Bell, 1968). This is an important limitation that we might eventually be able to address with data from the Family Transitions Project given that we have measures of temperament and personality of the children of the G2s (e.g. Neppl et al., 2010). The caveat is that we need to wait until the G2 are sufficiently old enough to have had enough time to fulfill their educational potential. We suspect that other datasets could evaluate these processes sooner and hope this happens.

In addition, we are obligated to discuss additional limitations involving polygenic scores in the current report. As noted earlier, the association between polygenic scores and a complex phenotype like educational attainment is modest (at best). This finding was replicated in the current results and could be considered a limitation for the utility of polygenic scores. This concern is especially notable when the polygenic scores are used to justify strong claims about social influence processes. The size of the association between polygenic scores and the phenotypes of interest illustrates the so-called missing heritability problem (Manolio et al. 2009).

Researchers have noted gaps in the estimated size of genetic influences on complex traits from twin studies and more direct estimates from genetic variants associated with complex phenotypes in GWAS studies. This heritability gap has led to a large number of theories involving genetic heterogeneity, complex interactions, and epigenetic mechanisms. On a practical level, it might be possible to adjust polygenic scores for measurement error but we are not confident we have good estimates of how much error is involved in these scores. However, this is an important future direction and will likely increase the correlation between polygenic scores and phenotypes of interest.

We regard this an important limitation of the current study but we have a few thoughts on this issue. Foremost, we hope we are appropriately cautious about the strength of the evidence in the current report given the design strengths and limitations. True experiments would permit strong inferences but are difficult to conduct with the constructs in question (e.g., Conger & Donnellan, 2007). Quasi-experiments are often more practical (see e.g., Constello, Compton, Keelerm & Angold, 2003) and they seem to suggest that socioeconomic factors are related to developmental outcomes in ways consistent with the IM. Thus, we think there are additional reasons to consider the social influence pathways viable in the model besides the current results. Second, the old adage that perfect is the enemy of the good is relevant. Polygenic scores are evolving and using them in tests of models strikes us as a useful alternative strategy to not accounting for genetic factors in developmental research. This is why we have framed the current study as a useful illustration of how developmental researchers can begin to account for genetic factors in existing longitudinal studies like the FTP. We anticipate that future GWAS studies will refine the computation of polygenic scores so that correlations between scores and phenotypes of interest increase.

In light of this issue, future studies should incorporate newer approaches for computing polygenic scores for educational attainment as well as other constructs used in the IM. Right now, educational attainment is probably one of the better-characterized phenotypes (see e.g., Belsky et al., 2016) but this literature is changing rapidly as sample sizes increase with more data pooling and greater harmonization of measures across studies. Likewise, we anticipate that GWAS studies of personality and psychopathology will become increasing more powerful so that scoring algorithms improve thus potentially increasing the correlation between polygenic scores and phenotypes of interest. We anticipate that the GWAS literature will become increasingly more relevant to the kinds of variables that are the focus of many developmental studies.

In closing, we have illustrated how polygenic scores can be incorporated into a widely used developmental model to more directly test hypotheses about the roles that genetic factors play in social selection and evocative child-parent processes related to the attainment of SES. This is a valuable proof of concept about the evolution of the tools used to test theories about human development. The costs of genotyping developmental samples are decreasing while the information available to construct useful polygenic scores is increasing. These two trends point to new opportunities for understanding how genetic and environmental factors contribute to important developmental outcomes like SES. Such technological advances can help to keep existing resources like the FTP relevant as social scientists work to better understand how genetic factors are translated into complex phenotypes.