A deep learning approach for the blind logP prediction in SAMPL6 challenge

Abstract

Water octanol partition coefficient serves as a measure for the lipophilicity of a molecule and is important in the field of drug discovery. A novel method for computational prediction of logarithm of partition coefficient (logP) has been developed using molecular fingerprints and a deep neural network. The machine learning model was trained on a dataset of 12,000 molecules and tested on 2000 molecules. In this article, we present our results for the blind prediction of logP for the SAMPL6 challenge. While the best submission achieved a RMSE of 0.41 logP units, our submission had a RMSE of 0.61 logP units. Overall, we ranked in the top quarter out of the 92 submissions that were made. Our results show that the deep learning model can be used as a fast, accurate and robust method for high throughput prediction of logP of small molecules.

Introduction

Computational prediction of logP values of molecules is important in several fields including drug design [1-7], agriculture [8-11], environment [12, 13], consumer-chemicals [14-17] etc as it serves as a measure of lipophilicity (or hydrophobicity) of the molecule. In the field of drug design, lipophilicity of a drug molecule is directly related to the absorption and membrane penetration, solubility, partitioning into tissues and the final excretion. It is considered as one of the most important properties of a drug and is a part of the Lipinski’s rule of five [18, 19]. A drug molecule has to be soluble enough in lipid to be absorbed in the tissues and organs [20, 21]. However, it should not be too soluble to prohibit its excretion [22]. In agriculture and environment science, it is related to the toxicity of the fertilizers and pesticides used. In the field of cosmetics and skin care products, it measures the propensity of the product being absorbed by the skin [23-25].

LogP is related to the partition coefficient of a molecule between water and the lipid phase. Typically, the lipid phase is n-octanol and logP is given by:

$$logP=log\frac{[Solute{]}_{oct}}{[Solute{]}_{water}}$$ (1)

Given the importance of logP prediction, the Drug Design and Data Resources (D3R) consortium organized the sixth iteration of Statistical Assessment of the Modeling of Proteins and Ligands (SAMPL) competition to compare different methods in this field [26]. Previously, SAMPL competitions involved solvation free energy [27, 28], logD [29, 30] and pK_a [31-33] prediction. Specifically, in the first iteration of the SAMPL6 competition, pK_a prediction challenge involved charged microstates of a set of 24 drug-like molecules . A subset of these molecules, where the neutral species was the most abundant microstate, were used in part II of the SAMPL6 competition for logP prediction [26].

Many different approaches were employed by a large number of groups. These can be seen in the other submissions to the SAMPL6 competition available in this special issue. These methods span both physical and empirical approaches. The quantum level approaches calculate the solvation free energy of the molecule separately in two solvent phases—water and octanol—and use it to estimate the partition coefficient. Specifically, Andreas Klamt’s group at COSMOlogic generated relevant conformations of the molecule and for each conformation calculated the chemical potential difference between the two phases. Among the empirical approaches, another group used quantitative structure–activity relationship (QSAR) model based on molecular descriptor based on properties and trained a random forest model to predict pK_a values.

Several cheminformatics-based methods have been developed over the years for logP prediction [34-36]. These methods are generally based on creating a set of molecular descriptors to represent the molecules and using a statistical method to model the contributions of the fragments [22]. Schroeter et al. [37] used Gaussian processes(GP), support vector machines and ridge regression for the prediction and found GP to perform the best. Ognichenko et al. [38] used a random forest approach for the prediction and showed the importance of non-additive character of the contribution from the fragments.

Deep neural network is a promising choice for generating a model for logP prediction. It has recently been used in a number of fields including QSAR studies for IC50 prediction for 15 datasets in the Kaggle competition [39]. Popova et al. [40] used reinforcement learning to design a library of molecules with specific properties like melting point, hydrophobicity and JAK2 inhibition. Lusci et al. [41] used deep architectures to predict aqueous solubility of drug like molecules. Mayr et al. [42] compared deep neural network performance to other machine learning algorithms (Support vector Machines, Random Forest etc) on the ChEMBL database for drug target prediction and found the former to outperform the other methods. Hughes et al. [43] used deep convolutional neural networks to build a model for the site of epoxidation using a database of epoxidation reactions and achieved close to 95% area under curve (AUC) performance.

In this work, we have developed a novel deep learning model for the computational prediction of logP values. The results presented in the article correspond to the submissions tc4xa and g6dwz. We have used fingerprinting to generate features for the molecule. A large database of more than 14,000 molecules was used to train and test the model. Our goal for the project was to develop a model which can utilize this large database and generalize over a large test set. We explored the usage of deep neural networks with two different models with five and three hidden layers respectively.

The paper is organized as follows. In section “Computational details”, we describe the computational details of the method, including the description of the data set used and the architecture of the neural networks that were designed. Section “Results and discussion” covers our major results, comparison to other methods and a discussion on prospects for further improvement on the work. Finally, in section “Conclusion”, a brief conclusion of the study is provided.

Computational details

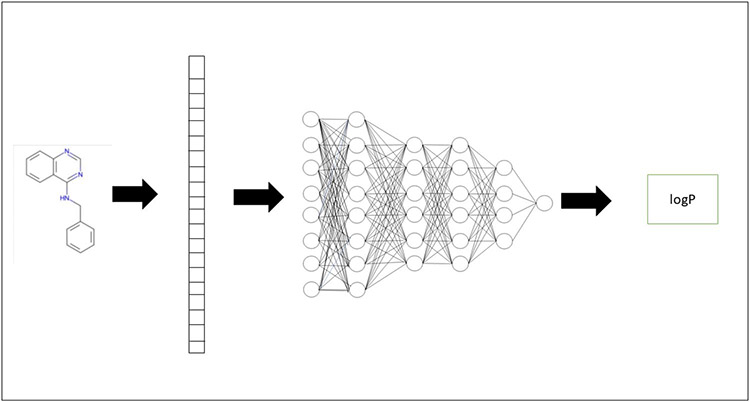
We carried out this study to perform a blind prediction in the SAMPL6 logP challenge. A schematic representation of the approach is given in Fig. 1. SAMPL6 organizers provided a set of 11 drug-like molecules in the SMILES string format. In order to use a machine learning approach for prediction, we first made a vector-space representation of the molecule. We trained a number of deep neural network models on a previous dataset of logP predictions. The models which provided the least error in our validation and test sets were used further to make the final prediction for the challenge molecules. In the next subsections, we provide a detailed description of the approach used including the vector space representation, training and testing of our models.

Fig. 1.

Schematic representation of the deep learning approach. In the first stage, a molecule is transformed to its feature (vector) space representation using Extended Connectivity Fingerprinting. This serves as the input to the neural network. Neural network is trained on a large set of such molecules and corresponding logP. At the inference stage, output of the neural network is the predicted logP

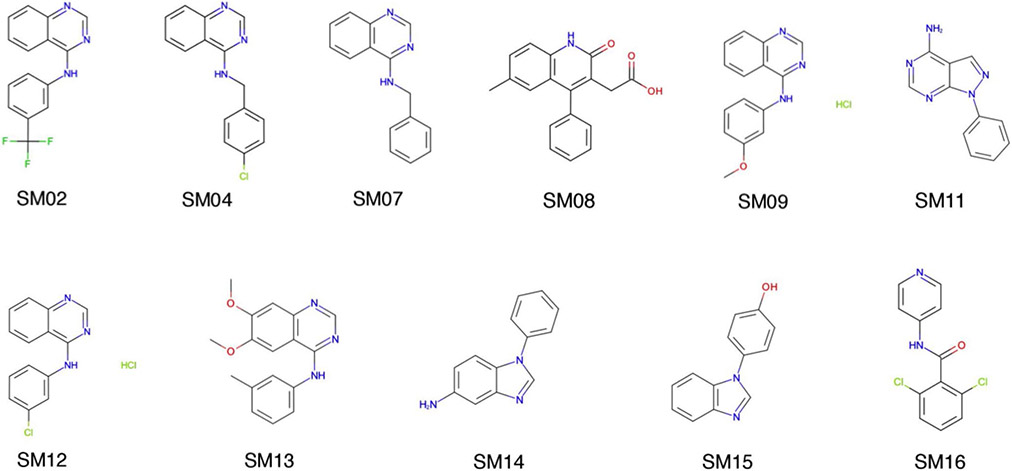
SAMPL6 logP prediction challenge molecules

The logP prediction challenge consisted of making blind prediction of the octanol–water partition coefficients of 11 small molecules that are similar to small molecule protein kinase inhibitors. Figure 2 shows the two dimensional structure of the molecules. An ASCII formatted notation for the molecules, named Simplified Molecular-Input Line-Entry System (SMILES), is used for the initial representation of the molecule. SMILES string provides a unique way for naming a molecule. Atoms are represented by their symbol with the option of including the charge if any. Bonds are represented by symbols: single (−), double (=), triple (#) and aromatic (:). Branches are depicted with brackets. Cycles are broken at one bond and labels are attached on the atoms in the broken bond. More details about the representation scheme for SMILES can be obtained from the Daylight manual for SMILES [44].

Fig. 2.

Two-dimensional structure of the SAMPLE6 logP challenge molecules. All the 11 molecules in this challenge were a subset of the previous pK_a challenge

Extended-connectivity fingerprinting

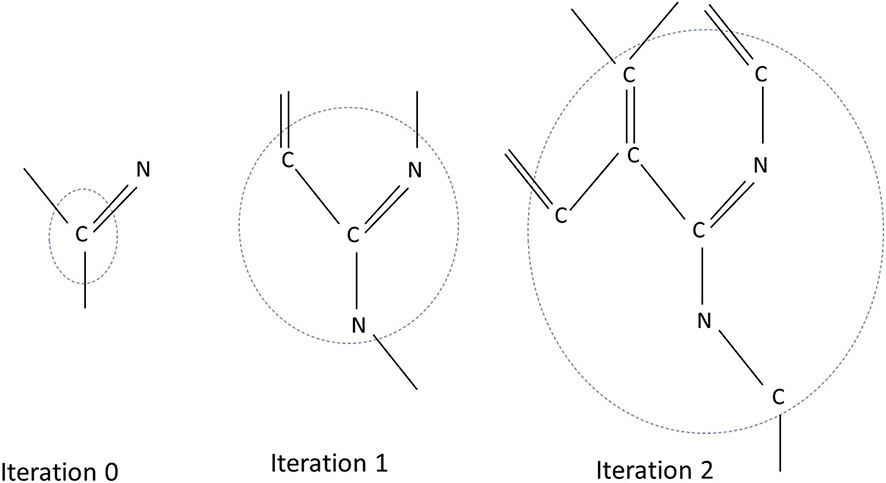
We used the approach formulated by Rogers and Hahn [45] to make a vector space representation of the molecule. This method, termed Extended-Connectivity Finger Printing (ECFP), has been used extensively in the QSAR field for structure-function modeling. A schematic representation of the method is shown in Fig. 3. It models the atoms and its bonded neighborhood iteratively at longer bond distances.

Fig. 3.

Schematic representation of the process of ECFP for three iterations for the identifier associated with the atom C represented above. After the zeroth iteration, the identifier associated with C is only about the atom and its bonds in the molecule. After the first iteration, the identifier also contains information about the atoms which are one bond away from atom C. The identifiers calculated after zeroth iteration for the neighboring atoms are used for creating the identifier for C at this iteration. After the second iteration, atoms within two bond distances from the center atom are included in the identifier. This iteration continues until a user specified iteration threshold is reached. In the present study four iterations are used

In the first iteration, seven features of each non-hydrogen atom in the molecule are calculated:

1. number of heavy neighbors

2. valence of the atom subtracted by the number of hydrogen atoms attached

3. atomic number

4. Atomic charge

5. Atomic mass

6. Number of attached hydrogens

7. Whether the atom is contained in a ring

These identifiers are hashed into a 32-bit integer. At the end of the first iteration, we have an array of 32-bit integers, one for each heavy atom.

In the next set of iterations, we try to model the bonded environment of each atom. The identifier array is appended by a tuple for each bond. The first entry for the tuple is bond order and the second entry are the identifier calculated at the first iteration. The full array for each atom is again hashed to create a new 32-bit integer. Thus, at the end of this iteration, we have an array of integers—one for each atom and one for each bond centered at the respective atom. Any duplicate entries, if present, are removed from the array.

The same process is repeated for another iteration to get the identifiers for atoms separated by 2 bonds. These iterations can be seen as adding features representing atom-centered substructures of larger radii [45]. In this study we have used ECFPs up to the fourth order. The array of integers at the last iteration is hashed to create a 1024-bit vector. This vector serves as the final vector space representation for a molecule. We used rdkit python library to create the fingerprint for each molecule [46].

Training and testing data set

Training data was obtained from [40]. It contains a set of 14,176 data points with SMILES string as the molecule and the corresponding logP values. Of these, a 12,000/2000 split of randomly selected data points were used as the training and test set, respectively. The database is accessible through the EPI suite and contains various physical properties, including partition coefficient, vapor pressure, boiling point etc, for more than 41,000 chemicals [47].

Architecture of neural network

We trained a number of different models which varied in the size and number of hidden layers in their architecture [48]. We searched over these hyperprameter space using the five-fold cross validation error and error over the 2000 molecules in the test set. Here, we report of two of those architectures that we submitted in the SAMPL6 challenge. The first neural network has 5 hidden layers: 3 layers of 512 units and 2 layers of 256 units. The second neural network is much simpler and has 3 hidden layers with 512, 256 and 128 units in the hidden layers. All the models have one output layer. A total of 150 epochs of training was done on the dataset with 5-fold cross validation within the training data. Tensforflow version 1.14 was used for training and inference [49].

Results and discussion

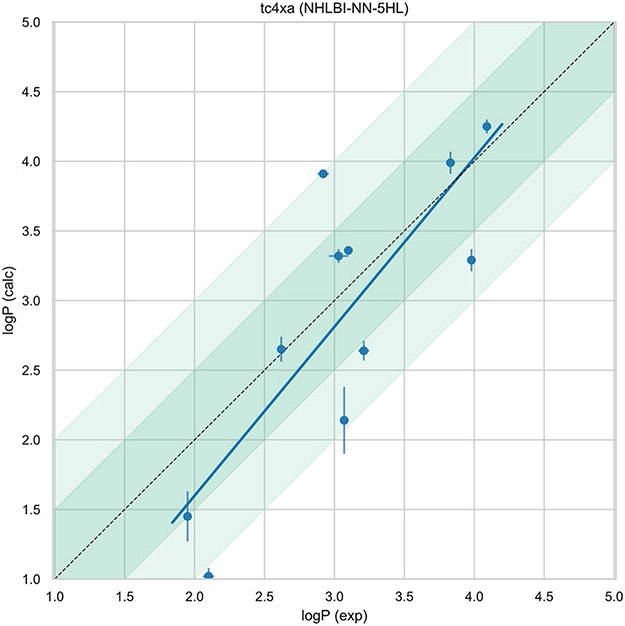
Our results show very good agreement with the experimental data. Results are presented in Table 1 . With the 5 hidden layers model (Fig. 4), we obtained a root mean squared error (RMSE) of 0.62 logP units while the Mean absolute error (MAE) was 0.51 logP units. Correlation with the experimental data was 0.66 and the slope of the regression line was 1.21. With the 3 hidden layers model (Fig. 5), we obtained a root mean squared error (RMSE) of 0.84 logP units while the mean absolute error (MAE) was 0.71 logP units. With the 3 hidden layers model, we obtained a RMSE of 0.85 logP units. Correlation coefficient for this model was 0.52 and slope of the regression line was 1.18.

Table 1.

Table of the logP experimental and predicted values

Molecule Id	Isomeric SMILES	Experimental	5 Hidden layers	3 Hidden layers
SM02	c1ccc2c(c1)c(ncn2)Nc3cccc(c3)C(F)(F)F	4.09 ± 0.03	4.25 ± 0.05	4.39 ± 0.05
SM04	c1ccc2c(c1)c(ncn2)NCc3ccc(cc3)Cl	3.98 ± 0.03	3.29 ± 0.08	2.86 ± 0.12
SM07	c1ccc(cc1)CNc2c3ccccc3ncn2	3.21 ± 0.04	2.64 ± 0.07	2.09 ± 0.11
SM08	Cc1ccc2c(c1)c(c(c(=O)[nH]2)CC(=O)O)c3ccccc3	3.10 ± 0.03	3.36 ± 0.03	3.41 ± 0.09
SM09	COc1cccc(c1)Nc2c3ccccc3ncn2	3.03 ± 0.07	3.32 ± 0.05	3.27 ± 0.03
SM11	c1ccc(cc1)n2c3c(cn2)c(ncn3)N	2.10 ± 0.04	1.02 ± 0.06	0.96 ± 0.10
SM12	c1ccc2c(c1)c(ncn2)Nc3cccc(c3)Cl	3.83 ± 0.03	3.99 ± 0.08	3.96 ± 0.04
SM13	Cc1cccc(c1)Nc2c3cc(c(cc3ncn2)OC)OC	2.92 ± 0.04	3.91 ± 0.03	3.97 ± 0.11
SM14	c1ccc(cc1)n2cnc3c2ccc(c3)N	1.95 ± 0.03	1.45 ± 0.18	1.60 ± 0.07
SM15	c1ccc2c(c1)ncn2c3ccc(cc3)O	3.07 ± 0.03	2.14 ± 0.24	1.58 ± 0.05
SM16	c1cc(c(c(c1)Cl)C(=O)Nc2ccncc2)Cl	2.62 ± 0.01	2.65 ± 0.09	2.00 ± 0.06

Fig. 4.

Experimental vs. prediction for the 5 hidden layers model. The darker shaded region is a 0.5 logP units while the lighter shaded region is the 1 logP units. These results are also available at [50]

Fig. 5.

Experimental vs. prediction for the 3 hidden layer model. The darker shaded region is a 0.5 logP units while the lighter shaded region is the 1 logP units. These results are also available at [50]

As expected, our 5 hidden layers model performs better than the one with 3 hidden layers (Table 2). As seen in Supplementary table 1, the number of tunable parameters in this model is more than 1.2 million. This model is able to approximate an “arbitrary” function much better than a model with less number of parameters. Since we have a large dataset of 12,000 training set representing a wide variety of chemical moieties (substructures), the bias in the model is expected to be low.

Table 2.

Metrics for the two submissions

Method	RMSE	MAE	R2	m
5 hidden layers	0.62	0.51	0.66	1.21
3 hidden layers	0.85	0.72	0.52	1.18

We also tested the model of a larger dataset of 2000 molecules and the results are shown in Fig. 6. MAE in this set was 0.68 logP units. This shows that the model is robust over a larger number of molecules with a variety of substructures and is expected to perform well in other studies as well with non-kinase targeting drug-like fragments.

Fig. 6.

Plot of the predicted vs. true logP values for 2000 molecules chosen randomly from the dataset

Radius of ECFP affects the feature space representation of the molecule. A larger radius creates identifiers which correspond to bigger interaction regions in the molecule. This also leads to a dramatic increase in the size of the features space and would give a sparser distribution over the bits of the feature space. As noted by Liu et al. [22], ECFP2 serve as a good compromise for feature representation and performs well for database searching and QSPR studies.

One limitation of informatics-based approach for property prediction should be realized. The machine learning model learns the distribution of the data that it is used for its training [51]. If the test data is drawn from a different distribution, the model is not expected to be robust enough to make the correct predictions. In other words, machine learning models are good at interpolating within the distribution but not reliable for extrapolation. In terms of logP prediction, if the test molecules contain substructures that are absent in the training data, the trained model will give high errors. However, the SAMPL6 competition involved prediction for kinase-fragment molecules which are very well represented in our training set. Hence the errors in our predictions are within 1.5 logP units for all the molecules. This dataset was recently used by [40] for reinforcement learning based drug-design.

Although the distribution of chemical moieties in our training dataset includes kinase-fragment molecules, the exact molecules from SAMPL6 were not present i.e. the model doesn’t simply reiterate the data memorized from the training set. We used Tanimoto distance to compute the similarity of each SAMPL6 molecule to all the molecules in the training dataset. The results are shown in Supplementary Figure 3. The SAMPL6 molecule with the closest similar molecule in the dataset is SM13 in which case the molecule in the training dataset has an extra Bromine atom. However, the error in prediction from our model for SM13 is 0.99 pK_a units for 5 hidden layer model, which is higher than our mean absolute error of 0.51 pK_a units. As the model is trained on the entire dataset, the learned parameters are more global in nature.

A clear advantage of the present approach is the speed of calculation. Although collection of training data and training the model can take appreciable time, inference is very fast. In our tests performed on a Volta Nvidia GPU, each molecule takes less than a second for prediction. This makes the approach amenable to deployment for high-throughput prediction in the industrial setup where a large number of molecules need to be tested. Physical approaches, based on QM and/or MM approaches take several hours in contrast for prediction for one molecule. Several physical models have some level of empirical parametrization as well. For example, QM models are parametrized to calculate implicit solvent solvation free energy in a number of solvents [52-54]. Similarly, there are ongoing efforts in the field of MM to improve the parameterization of the force field [55-57].

There are several avenues to build up on the work presented in this article. One criticism of the machine learning approaches is the requirement of large amount of data needed to train a model. Small sample size gives high bias and the model is not expected to perform well. However, large training size might not be available for different physical properties. Transfer learning can be used to handle this issue [58-61]. For example, a related problem to transfer free energy prediction between water and octanol is that of prediction of transfer free energy prediction between water and cyclohexane [62-64]. The architecture of the present model, trained on a large water-octanol logP, can be modified at the outer layer to make a prediction for water-cyclohexane logP and training it further on a smaller set of data for the second property. These approaches have been used in the field of computer vision [65].

Our results show that deep neural networks can be used to predict logP values. The features space representation is easy to build and the model trains very fast on the modern GPUs even with a large number of tunable parameters. Results on 2000 molecules show that the model is robust over a large variety of substructures.

Conclusion

We have developed a novel method for prediction of logP for the SAMPL6 physical properties challenge organized by Drug, Design, Data and Research Consortium. The method uses structure-based fingerprints to represent a molecule in a vector space. Several deep neural architectures were trained on a dataset of 14,000 known logP values. The submitted models (tc4xa and g6dwz) gave good results on a blind set of 11 kinase-inhibitors drug like molecules. The method is fast, accurate and robust over a variety of molecules.