Abstract

Genetic design automation methods for combinational circuits often rely on standard algorithms from electronic design automation in their circuit synthesis and technology mapping. However, those algorithms are domain-specific and are hence often not directly suitable for the biological context. In this work we identify aspects of those algorithms that require domain-adaptation. We first demonstrate that enumerating structural variants for a given Boolean specification allows us to find better performing circuits and that stochastic gate assignment methods need to be properly adjusted in order to find the best assignment. Second, we present a general circuit scoring scheme that accounts for the limited accuracy of biological device models including the variability across cells and show that circuits selected according to this score exhibit higher robustness with respect to parametric variations. If gate characteristics in a library are just given in terms of intervals, we provide means to efficiently propagate signals through such a circuit and compute corresponding scores. We demonstrate the novel design approach using the Cello gate library and 33 logic functions that were synthesized and implemented in vivo recently (Nielsen, A., et al., Science, 2016, 352 (6281), DOI: 10.1126/science.aac7341). Across this set of functions, 32 of them can be improved by simply considering structural variants yielding performance gains of up to 7.9-fold, whereas 22 of them can be improved with gains up to 26-fold when selecting circuits according to the novel robustness score. We furthermore report on the synergistic combination of the two proposed improvements.
Keywords: genetic design automation, synthetic biology, circuit synthesis, structural variants, cell-to-cell variability, robust genetic circuit
1. Introduction
Genetic design automation (GDA) parallels early efforts in electronic design automation (EDA) and recently also got to use state-of-the-art EDA tools to generate gene-regulatory circuits realizing combinational logic1,2 as well as sequential logic.3 While historically EDA quickly ran into unmanageable computational complexity and hence devised clever approximate methods, current GDA problems are yet too small to require such approximations. In contrast to EDA’s scalability, GDA suffers from our limited understanding of what parameters fully characterize a genetic part or device,4−6 reflecting itself in GDA libraries with models of insufficient accuracy and scope. In particular, the context-dependency of circuit components7 represents a central problem. That is, components behave differently depending on their adjacent up and downstream DNA sequences,8,9 on the specific resource allocation of the host organism,10,11 on the cross-talk from native regulatory factors,12,13 and on adjacent components that are biochemically up and downstream of the circuit.14,15 Cell-to-cell variability—referring to the fact that even within an isogenic cell population a synthetic circuit will behave differently from cell to cell—can also be understood as another context effect, i.e., the circuit functioning depends on the specific intracellular conditions realized within a particular cell. Cells may differ in their cell-cycle stage, their plasmid copy number, and inevitably they will differ due to the random nature of biomolecular events, introducing copy number fluctuations in involved molecules.16,17 Such intrinsic noise will especially be important when the circuit is realized through lower abundant molecules, for instance through RNA regulators,18,19 when compared to transcription factor based implementations.
As a consequence of cell-to-cell variability, the individual on and off expression levels for a genetic logic circuit may easily span 1 order of magnitude across a cell population (see, e.g., ref (1)). For biomedical applications, such as disease detection and therapeutic circuits,20,21 stringent specifications are needed that guarantee the proper functioning of a circuit on the single-cell level and not just on bulk averages. As long as the on and off output levels cannot be assessed for each cell individually, such specifications translate to the requirement that the two distributions corresponding to the circuit’s on and off levels across the cell population, accessible for instance through flow-cytometry, do not show any overlap.22 In other applications such as biotechnology these requirements may be overly stringent, and one is more concerned with just the fold-change between on and off bulk levels.
Taken together, current GDA tools such as Cello1,2 require further domain specific adaptation in order to cope with context-dependency, the under-specification of part and device models and the intracellular variations encountered at the single-cell level. For instance, considering host energetics, GDA should find the circuit topology with the minimal number of components and should select the specific component realizations from the library that lead to robust circuits functioning under varying conditions. Existing tools for genetic circuit design23 either use standard EDA methods and tools to determine the circuit topology, including Cello1 and GeneTech,24 or leave the specification of the topology to the user and optimize inside its boundaries, like SBROME25 does. iBioSim26 uses an elaborate technology mapping algorithm that structurally matches library gates on a subject graph using branch-and-bound, but also constructs only one topology with minimal size in base pairs. Furthermore, Cello scores circuits based on the on and off levels corresponding to their median parametrization without incorporating variance information during the optimization process but provides predicting output distributions of the synthesized circuit. GeneTech does not provide simulation capabilities, SBROME uses a deterministic gene expression model for single level output prediction only, and iBioSim—while being very flexible in integrating simulation capabilities—could not be found to incorporate simulation results in the synthesis and technology mapping process.
To this end, we propose the following extensions to the state-of-the-art GDA workflow. First, we demonstrate that better circuit topologies can be found compared to the ones obtained through generic EDA tools, exemplified by the 33 circuits reported in ref (1). We efficiently enumerate all structural circuit variants,27 which remains undoubtedly feasible for circuit sizes currently encountered in synthetic biology. Second, we improve the simulated annealing (SA) based gate assignment by employing neighborhood relation among all possible assignments.28−30 Since prominent placement tools for field programmable gate arrays31 also utilize such neighborhood relation, we adopted schemes from them. Third, we introduce parametric uncertainty in device models to mimic cell-to-cell variability, context-dependency, or under-specification and extend the circuit scoring function to account for the incurred variability. We modify the traditional Wasserstein metric32,33 to obtain a score that scales with the distance of the on and off levels and also reflects the degree of overlap among the corresponding distributions. Accordingly, two realizations of the same logic circuit showing the same output medians across the complementary input assignments, and hence leading to identical scores in the traditional setting, could now be scored differently due to their possibly different output variability. Moreover, we develop a framework for robust design in the absence of probability distributions for specifying parametric uncertainty. In particular, if uncertainty is only given in terms of upper and lower bounds on the device parameters or gate characteristics, we present a worst-case design approach based on envelope transfer function (see Figure 1 for an overview).
Figure 1.
Different circuit design approaches. (A) Traditional design and scoring approach with a nominal parametrization without uncertainty, as used by Cello.1 Cello does allow the prediction of output distributions but performs circuit synthesis only on median parametrizations. (B) Robust design approach accounting for cell-to-cell variability when probability distributions for device parameters are available, presented in this article. (C) Robust design solely based on interval specifications of transfer characteristics, presented in this article.
2. Results and Discussion
2.1. General Problem Statement
This work
deals with the particular problems of circuit synthesis and technology
mapping in an automated generation of genetic logic circuits. It therefore
focuses on jointly finding an optimal circuit topology γ in
a set of topologies Γ and an optimal gate assignment a in a set of possible assignments 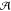 —which
varies with the topology γ—given
a library of gates
—which
varies with the topology γ—given
a library of gates  and
a Boolean function specification
and
a Boolean function specification 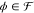 . To formulate an optimization problem,
we need a measure of compliance of a circuit (γ, a) with the functional requirement ϕ. This measure S(γ, a), which we call the circuit score, will
be the optimization objective, and we state the optimization problem
as
. To formulate an optimization problem,
we need a measure of compliance of a circuit (γ, a) with the functional requirement ϕ. This measure S(γ, a), which we call the circuit score, will
be the optimization objective, and we state the optimization problem
as
| 1 |
with the optimal topology γ* and assignment a*. It is now crucial for the quality of the resulting logic
circuit to take great care in specifying the set of possible topologies
Γ on the one hand and the circuit score S(γ, a) on the other. In the following, we will discuss possible
approaches to find and characterize application-optimal Γ and S(γ, a), which are compared with the approaches being part of the
Cello framework1, used as benchmark. These
benchmark approaches encompass the circuit topologies from the original
article* and gate assignments obtained from our own re-implementation
of the technology mapping procedure as detailed in the supporting
information document on cellocad.org*, which includes everything detailed
in section V.D., 'repressor assignment'. Besides the core
gate assignment
optimization, this includes toxicity constraints and the avoidance
of illegal promoter combinations which we required both for our own
results as well. The results from the benchmark are collectively referred
to by "Cello''. Since the dependence of 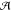 on the topology
γ reflects the natural
hierarchy of the problem, we will first address the synthesis problem
and then proceed with the discussion on technology mapping and the
score.
on the topology
γ reflects the natural
hierarchy of the problem, we will first address the synthesis problem
and then proceed with the discussion on technology mapping and the
score.
2.2. Circuit Synthesis Involving Structural Variants
Prominent EDA tools, like ABC used in Cello, apply the cost functions area and delay,34 which are not directly suitable for genetic circuits, where fold-change and robustness pose the main challenges of design. We therefore enumerate circuits of all different topologies available from a given library of logic gates, which satisfy the logic function of the circuit. Since this structural enumeration is a combinatorial problem and quickly becomes infeasible, we optimize this procedure by following a hierarchical approach by considering only equivalent fan-out free circuits and performing pruning by isomorphism checking and the application of synthesis and library constraints online during enumeration (see Figure 2A and also Section 4.2). After all fan-out free circuits have been found, we remove redundant gates inherent to this specific type of circuit topology to obtain the final set of circuits as generally structured Directed Acyclical Graphs (DAGs).
Figure 2.
(A) Synthesis flow for genetic circuits involving the enumeration of structural variants (also see Section 4.2). (B) Synthesis results for the 33 Boolean functions using Cello’s and our proposed synthesis approach with the number of excess gates allowed denoted in parentheses. Every function is represented by one line and its color codes the size of its minimal circuit implementation. The monotonically ascending lines clearly show that the majority of circuits perform better using the proposed synthesis approach, while no circuit performs worse. (C) Resulting circuits and their scores using Cello’s scoring metric for function 0x4D using Cello’s synthesis (with SA and optimal gate assignment) and our proposed synthesis approach. Given optimal gate assignments, the improved topology leads to a 3.8-fold improvement in the circuit score. Both circuit topologies feature the same number of genetic gates, as for the implicit output OR no physical realization is needed. (D) Plot showing the output histograms of the circuits for function 0x4D. The proposed design features a higher output in the ON case, thus increasing the separation between the complementary outputs and the Cello score.
In order to measure the benefit of including structural variety in genetic circuit synthesis, we synthesized all 33 functions provided in1 using Cello’s library of genetic logic gates. In total, we carried out three runs of our proposed synthesis approach, constraining the search space differently. We only included circuits of minimum size in the first run and then relaxed this criterion to include one and two excess gates in the second and final run, respectively. At this point, we still used Cello’s circuit score metric to rate the separation of complementary Boolean outputs of the synthesized circuits. Finally, we compared our results to the circuits synthesized by Cello. To prevent fairness issues coming from Cello’s stochastic gate assignment optimization, we simulated all possible assignments exhaustively for both Cello’s and our circuit structures.
We found that in the first run we were able to improve the circuit score of 22 of the examined 33 functions, while no circuit performed worse than the corresponding circuit synthesized by Cello and exactly the same number of logic gates was used (Figure 2B). A 3.8-fold improvement in the score could be achieved maximally (Figure 2C), while on average the scores improved by 29%. Relaxing the considered circuit size to include up to one excess gate, the circuit score for 30 of the 33 functions could be improved up to 7.9-fold, leading to an overall improvement of 111% on average compared to Cello. Relaxing the size by two excess gates, this trend continued (improvement for 32 of 33 functions up to 7.9-fold, 133% on average). Thus, our synthesis approach not only improves on Cello for many of the considered functions using exactly the same number of logic gates, it also enables the designer to trade off circuit size against circuit performance deliberately (Figure 2B). It also shows that genetic circuit synthesis profits from the additional degree of freedom of circuit topology. While the gate libraries are constricted and feature gates with heterogeneous transfer functions, it allows for placing well performing combinations of genetic gates in the circuit. For function 0x4D, for example, the proposed synthesis approach generated a circuit topology in which the output is driven by a NOR gate instead of the implicit OR gate while keeping the total number of genetic gates minimal (see Figure 2C). Figure 2D depicts the increased separation of the complementary output states that leads to the improved Cello score of the proposed design.
2.3. Technology Mapping of Genetic Circuits Using Neighborhood Heuristics
In EDA, the process of choosing logic
gates from a library to implement a given circuit is called technology
mapping.35 This process tries to find an
assignment of gate realizations 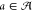 from the library
from the library  of real
logic gates to the abstract logic
gates in the circuit topology γ that optimizes a given score
on the circuit. With regard to the presented circuit synthesis approach
and the following statistical circuit evaluation method, an elaborate
heuristic for technology mapping can contribute to alleviate the increased
complexity in the synthesis process.
of real
logic gates to the abstract logic
gates in the circuit topology γ that optimizes a given score
on the circuit. With regard to the presented circuit synthesis approach
and the following statistical circuit evaluation method, an elaborate
heuristic for technology mapping can contribute to alleviate the increased
complexity in the synthesis process.
Cello already addresses the technology mapping problem with a generic Simulated Annealing (SA) heuristic to find the optimal gate assignment. However, since no problem specific knowledge is used during the generation of neighboring assignments by drawing gates from the library, their implementation can exhibit a far from optimal solution quality (see Figure 2C). To alleviate this problem and obtain a more traversable assignment scoring landscape, we design a Markov policy for the random draws, which uses a metric that defines a distance between library gates on the space of analytical characteristics of the gates’ steady-state transfer functions (see Figure 3A and also Section 4.3). Then a weighted euclidean distance in this space is used to allow drawing gates from an adaptive radius during SA (Figure 3B, 3C).
Figure 3.
(A) Parametrization of a general repressor Hill transfer function with offset and distribution of the considered genetic gates in the defined space of characteristics xm, ym, and y′(xm). (B) Radius based informed move of SA. The realization of one randomly selected gate of the circuit is swapped for a realization in the library based on the current radius r. (C) Exemplary SA trace illustrating the adaptive radius. (D) Number of simulations needed for mapping the set of benchmark circuits with SA applying 66 different weight configurations.
To evaluate our technology mapping approach, we first compiled a set of 32 circuits by synthesizing multiple circuit variants for the Boolean functions examined in ref (1) and selecting circuits with 5 or more logic gates, thus sorting out circuits that are well assignable exhaustively. The problem sizes ranged from ∼1 × 106 to ∼7.3 × 107 possible gate assignments given the usage of Cello’s gate library. We then mapped the circuits using our basic SA and SA with proximity based neighborhood generation with different ratios of the distance weights. To account for SA’s stochastic run time, we repeated the mapping process 10 times and determined the mean run time of all runs.
Table 1 shows the mean score and number of simulations needed for different SA configurations compared to exhaustive search. Independently from the chosen weights, all SA runs yielded near-optimal scores. The base SA algorithm (no metric) reduced the number of simulations needed compared to exhaustive search by 97.5%. Enabling the proximity based neighborhood generation with equally weighted dimensions, a further 1.61-fold speedup over basic SA is provided. For finding the best ratio of the weights given Cello’s gate library, we repeated the evaluation for the 66 different configurations depicted in Figure 3D. Using the best configuration found, we were able to speed up the mapping process 2.23-fold across the set of 32 circuits and 5.8-fold for single circuits maximally over basic SA while still yielding near optimal technology mapping results. Mapping the benchmark set on a standard desktop PC, we measured a run time of 14.96 h for basic SA and 7.19 h using the best weight configuration.
Table 1. Mean Number of Simulations Needed and Mean Score for Different Simulated Annealing Configurations Across 32 Circuits.
| mapping algorithm | weight config. | wym | wxm | wy′(xm) | score | simulations | speedup |
|---|---|---|---|---|---|---|---|
| exhaustive | – | – | – | – | 439.27 | 820 029 600 | 0.02 |
| SA | none | 0.0 | 0.0 | 0.0 | 439.18 | 20 475 365 | 1.0 |
| SA | equal | 1.0 | 1.0 | 1.0 | 439.00 | 12 696 430 | 1.61 |
| SA | best | 0.1 | 0.9 | 0.0 | 439.10 | 8 987 015 | 2.23 |
2.4. Robust Circuit Scoring
Signal propagation in genetic circuits varies significantly across members of a cell population due to context effects including those collectively termed cell-to-cell-variability. Therefore, a population-wide examination of such a circuit must naturally encompass a range of possible realizations of this circuit. We present two approaches to achieve such an inclusion. The first is based on a stochastic description of the circuit, which uses statistics of gate parametrizations and scores whole distributions of circuit outputs. The other is based on interval representations of transfer functions and signals to bound ranges of possible signal outputs of the circuit. Both approaches enter problem eq 1 by an appropriate choice of the score S(γ, a), which defines how we identify an optimal circuit and how much effort is needed to do so.
2.4.1. Expectation-Based Score (E-score)
The score used by Cello is calculated using median realizations of the mapped gates’ known transfer function statistics, which are obtained empirically using flow cytometry measurements of isolated gates. Although this approach ignores the cell-to-cell variability of the circuit function, it results in a fast scoring procedure. While calculating any single circuit realization demands a similar runtime, the median realization is presumed to pose as what is deemed a typical realization of the respective circuit. However, this circumstance does not allow the user to trade computation time for scoring detail. To allow such a trade-off, we propose a sampling-based approach as an adjustable, parallelizable alternative, which—given an assignment—calculates output samples based on randomly drawn transfer function realizations from the known statistics and scores the resulting empirical distributions as a whole with a score, which roots in the Wasserstein distance.32 We can show that the Wasserstein distance of the logarithmic output distributions emerges as a natural measure of separation corresponding to the population-wide expected on–off difference (see Methods 4.4.3). While the distance alone is a suitable candidate for comparing possibly overlapping output distributions in the sense of obtaining a functionally robust circuit, it is agnostic to variances in symmetric distributions. Although the obtained output distributions were often found to be skewed (in the direction of the complementary Boolean output), this insensitivity to variance is not suitable for a general score. We therefore chose to evaluate the distance partially in the sense depicted in Figure 4B. We name the so obtained new score the E-score, and it allows us to score the negative impact of larger variance compared to an optimal output under a given median distance as shown in Figure 4A and detailed in Methods 4.4.3. For the calculation in particular consider eq 8 in 4.4.3. Note that as a consequence, the E-score generally has a different absolute scale and a circuit scored by the E-score is not necessarily comparable to one scored by the Cello score.
Figure 4.
(A) Proposed E-score and Cello score of the two output distributions plotted over their standard deviation σ. The medians stay constant for all σ. Although intuitively the distributions with higher variance would be considered worse, Cello’s score does not take this into account. (B) Illustration of the two scores. The CDF’s of the two distributions representing Boolean on and off are plotted. An optimal output would concentrate all probability mass at specific points, which are considered to be at the median locations in accordance to Cello. Our score tries to capture the area enclosed by the inner tails of the output distributions within the optimal boundaries in the way hatched in gold, while Cello only builds the difference between two points. Choosing the Wasserstein-equivalent (cf. eq 7 in Methods 4.4.3) scores the area between the two blue lines, which would equal Cello’s score.
The sample realizations of the gate transfer functions themselves are obtained from sampled points of “noisy” Hill functions. These sampled points are obtained from Cello’s median realization processed together with histograms generated from flow cytometry data, which are sourced from Cello’s user constraint files (UCFs). Processing these has been done in accordance to the instructions from Cello’s supplementary material. The points are sampled, such that they represent equal quantiles on the so obtained empirical CDFs. We fitted Hill functions to these points, so that Cello’s median realization becomes a special case of a set of quantile realizations leading to empirical output distributions, which as a whole score the circuit (Figure 4A and B). If we speak of quantile realizations, we mean these fitted gate transfer functions, which match specific quantiles on the empirical CDFs from Cello’s data. A more detailed description on how the samples have been obtained is given in Methods 4.4.2. To generate the circuit’s output distributions, first a sample circuit input is chosen. Then, an individual sample quantile realization is taken for each of the circuit’s gates and a circuit output sample is obtained from calculation of the circuit’s transfer function. This is done multiples times with new samples each time, until a desired refinement of the so obtained empirical output distribution is achieved. Details on the calculation are found in Methods 4.4.1.
To test the procedure, we first rescored all circuits with ≤6 gates with their previous optimal assignments obtained from the exhaustive search using Cello’s original score described above, but this time drawing 5000 quantile realizations and using the E-score. Unsurprisingly, since our score is stricter than the Cello score, the scores have been significantly lower (Figure 4A). We kept the same circuit topologies obtained originally by Cello to retain comparability and only changed the gate assignment based on the new score. We found the best gate assignments for these topologies exhaustively while incorporating all sample realizations and the E-score instead of only the median realizations and the original score. We could improve 20 of 31 assignments. The median improvement (only the improved assignments) was by 71.08% in score, while the mean improvement was at 198.82% (we will come back to this in a few sentences). If the circuit could be improved, on average 30.02% of the gates have been exchanged in comparison to the assignment obtained using Cello's score. The mean number of gates in improved circuits has been 5.2, while in kept circuits it has been 3.45. The reason for the large mean improvement is that the E-score naturally detects and punishes error prone circuits, which occur in the exhaustive results obtained from Cello's score, as long as these are not being ruled out by additional constraints. We use the term “error prone” circuit here as a simplifying term for circuits, which result in a large fraction of inverted Boolean outputs using the sampled circuit realizations (see Figure 5D). Since Cello’s score cannot detect such circuits, an assignment might lead to inverted outputs in a real circuit where cell-to-cell variability is present. The original Cello framework offers circuit performance evaluation tools, which detect the worst of such assignments. However, these tools work on the median circuit realization alone as well and thus oversimplify the dependency of a gate's input variance on the preceding gate cascade in a circuit (c.f. Figure 5A), resulting in unnecessarily accepted or rejected assignments. Our scoring approach avoids such error prone assignments by construction. This circumstance lead in the extreme to a 26-fold improvement in score in circuit 0x1C. The target output levels of 0x1C stayed unchanged, since the final gate has been kept. Additionally, to demonstrate the practicability of the SA heuristic, we mapped the two largest circuits 0x41 and 0x81 with ∼7.3 × 107 possible assignments using SA and compared the results with the (exhaustively obtained) best possible assignments from Cello's score while still not modifying the circuit topology. Despite the stochastic optimization, both circuits could be improved (0x41 significantly and 0x81 slightly by 125.57% and 10.14%). Exemplary output histograms for circuit 0x41 and the restored nonfunctional circuit 0x1C are given in Figure 5C and D. We can conclude that, especially for strong cell-to-cell variability, a higher confidence in the functionality of the so obtained circuit w.r.t. a whole population can be achieved incorporating known statistics in the technology mapping process. To give an overview of the experiments, we provide statistical results in Table 2, where we compare sample scoring runs utilizing 5000, 500, 100, and 50 samples with the result obtained using Cello’s score. While excluding error-prone assignments by default (cf. Figure 5D), our score was able to reduce the variance of the logarithmic output distributions significantly (cf. Table 2, column 3). Note, that the broad availability of efficient low-level array computation tools allows for a competitive calculation of our score, leading to the comparably small performance decrease shown in Table 2. Another interesting phenomenon is, that since our calculated median gate outputs are of higher accuracy compared to those obtained from Cello's median circuit realization, we find some circuits to pass the (median) toxicity constraints, which would have been rejected by Cello. This can lead to assignments obtained via E-score which also exhibit larger Cello scores than those obtained using the Cello score directly as an optimizer (e.g. circuit 0x41 in the supplement).
Figure 5.
(A) Input, output and joint histograms for a sample gate I/O scenario. The gate corresponds to promoter “BM3R1” with ribosome binding site “B3”. The gate's transfer statistics are reconstructed using the flow cytometry data from the Cello UCF “Eco1C1G1T1.pAN1201.UCF.json”. If only the medians of input distributions and gate transfer functions are considered like in Cello, the blue output would be considered a preferred result compared to the yellow one. (B) Illustration of the sampling procedure. N parametrizations are predrawn for each gate for the respective environment and combined under independence assumption to yield the circuit output. (C,D) Plot showing the two histograms generated for the best assignments chosen by the respective scoring scheme. (C) 0x41 and (D) 0x1C. The optimal assignment of circuit 0x1C under Cello score results in many inverted Boolean outputs with given cell-to-cell variability and under the independence assumption made for the sampling.
Table 2. Exhaustive Runs (31 Circuits) Giving an Impression of Different Scoring Schemesa.
Cello score, E-score (5000 samples; used as a reference), E-score (500 samples), E-score (100 samples), E-score (50 samples), I-score (uniform), I-score (maximin). The median reference E-score was roughly the same ≈73 for all. Besides the reference score with 5000 samples, which incorporates the most detail of the output distributions among all scores presented, we used the maximum variance of the logarithmic output distributions as another measure of fitness for the resulting assignment.
2.4.2. Interval-Based Score (I-score)
The E-score uses inverse transform sampling to draw samples representing random quantiles on the histograms obtained from flow cytometry. While for an acceptable amount of samples and under correct assumptions this approach is versatile and guaranteed to provide a consistent result, it might be useful to think about efficient alternatives with a stronger focus on robustness. We present two such efficient alternatives based on interval estimation. We call these variants I-score. One of the two variants implements the maximin principle fundamental to robust optimization36 the other is based on inscribed distributions. Though by construction not able to express output separation tendencies in proportions of the population, the score is able to identify assignments, which shift at least one individual to wrong outputs or in proximity to possible decision boundaries. Details can be found in Methods 4.5, but we give a short summary in the following. The basis of this score are bounding envelopes derived from our set of estimated context parameters, which enclose all or almost all of the known gate transfer function realizations. We then create a modified circuit double in size to the original, which is able to propagate (interval bounded) signals through the enveloped circuit and generate output intervals, which bound the output signals of the whole population, see Figure 6A. Scoring by the maximin principle on these intervals is then performed by taking the distance of the smallest lower interval boundary corresponding to Boolean 1 and the largest upper boundary corresponding to Boolean 0 (cf. eq 11 in Methods 4.5). An illustration of this idea is given in Figure 6. Having obtained the output intervals, scoring by the maximin approach is just one among a variety of possibilities. As an example, we could as well suspect these output intervals to support distributions of output values again like in Section 2.4.1. By having no additional information, a maximum entropy assumption—and therefore uniform distributions on the support enclosed by the output intervals—would be a reasonable choice, which we briefly refer to by uniform I-score.
Figure 6.
(A) Overview of the designs considered within this work. The black arrows illustrate the direction of increasingly refined modeling. (A.1) Cello scoring: model representing median parametrization without considering uncertainty. (A.2) Expectation-based scoring (E-score, eq 8): distributional information provided by parameter statistics taken into account. (A.3) Interval-based scoring (I-score, eq 11): enveloped model of transfer functions, consisting of a lower and upper envelope. (A.4) Modified envelope-free circuit equivalent to the one shown in A.3. (B) Exemplary illustration of an enveloped circuit and its envelope-free version below. Note that the wires in the enveloped circuit carry intervals and not scalar values, which is alleviated in the equivalent envelope-free circuit.
To evaluate the maximin approach, we again mapped all circuits with ≤6 gates using this score as a maximizer. We then rescored all circuits and their worst-case optimal assignments obtained with the maximin I-score again using the expectation-based E-score with 5000 quantile realizations. In comparison to Cello, of the 31 circuits, 9 have been improved, 4 have been kept, and 18 have been worsened w.r.t. the E-score. The mean E-score was the lowest of all tested scoring schemes, and as expected, the very bad E-scores assumed by the Cello solutions have been avoided. Remarkable is the maximal variance of the logarithmic outputs. Their maximum has with 0.99 been significantly lower compared to Cello and also to some degree compared to the expectation-based scoring schemes. The mean maximal variance at 0.57 has been the lowest throughout. We then did the same experiment again with the only difference being that we did not use the maximin I-score on the output intervals but inscribed uniform distributions into these intervals and scored them using the E-score. In comparison to Cello, of the 31 circuits, 15 have been improved, 5 have been kept, and 11 have been worsened. The mean uniform I-score has been around 4 points larger than that of Cello, while a very good minimum could be reached comparable to that of the full sampling E-Scoring. The maximal variance of the logarithmic outputs has been low overall as well. Its maximum has been the lowest throughout and its mean lies only a small portion above that of the stricter maximin approach.
Both schemes avoid erroneous circuits (large fraction of inverted Boolean outputs) and reduce output distribution overlap. Since the focus of the approach with inscribed uniform distributions on population-wide output separation is stronger, its minimal score has been almost as large as that of the baseline. Both interval-based approaches take less than two times the runtime of the Cello score, which has been the fastest overall. Unsurprisingly, the two interval-based scoring approaches also lead to output distributions with minimal log-variance. Like above, an overview can be found in Table 2.
3. Conclusions
This work provides improvements to the emerging domain of genetic design automation, in particular for the synthesis of combinational logic circuits. We show that there is currently little need to make aggressive approximations in the circuit synthesis and the technology mapping step when compared to electronic design automation. Neither the implementable logic circuits nor the device libraries reach sizes that would require them. Using 33 example circuits from ref (1), we demonstrate that enumerating structural variants for a given Boolean specification and having an optimized stochastic search strategy in the technology mapping yield significantly better circuit realizations with an up to 40-fold improvement, all based on the traditional Cello library and scoring scheme (see Figure 2). Under optimal gate assignments a 7.9-fold improvement can be achieved just due to structural variants, whereas for a given circuit structure one can find better gate assignments through a fast stochastic search that reliably finds the best assignment with a 2.2-fold speed-up (Table 1). Compared to the invested experimental time to actually implement and test genetic circuits, the incurred higher runtime for enumerating structural variants is negligible.
Going beyond those direct improvements of the established design process, the work presents a more general design approach that takes into account unavoidable underspecifications within biological device libraries, context-effects, and cell-to-cell variability of circuit function. We show that accounting for them in the simplest way through parametric uncertainty, the design process yields more robust circuits, quantified in terms of a novel scoring metric that penalizes variance and overlap of the complementary circuit output distributions. We use random parametric families of Hill curves, learned directly from flow-cytometry data as gate models in the library and establish a fast Monte Carlo based scoring scheme. If uncertainty is only specified in terms of interval boundary, we provide another robust scoring scheme that just works with envelopes of gate characteristics and does not require any sampling step. The general methodology developed in this paper is not bound to a particular gate library. For libraries involving gates other than NOT and NOR gates, the neighborhood heuristic in the gate assignment can be adapted using correspondingly other features of the gate response curves. The proposed interval propagation method (Figure 6) works for all monotone gate characteristics.
The proposed usage of structural variants and the robustness score can also be combined. To demonstrate the power of this combination, Figure 7 compares the synthesis of circuit function 0xF6 according to an optimal Cello run (complete enumeration is used instead of SA) and according to our approaches with a near-optimal assignment obtained from neighborhood-based SA. Compared to using only the new logic synthesis, the combination reduces the log-output variance by four-fifths, and compared to using only the new scoring, it doubles the output fold-change. When compared to an optimal Cello run for this circuit, with a 2-fold- increase for each isolated method, the combination achieves a synergistic 4-fold increase in E-score. We also performed the evaluation of our methods without the constraints on toxicity levels and promoter combinations. Compared to the constrained case, the results, and in particular the performance gain achieved by the novel approach, stayed qualitatively the same.
Figure 7.
Synthesis results for function 0xF6. (A) Circuit structure synthesized by Cello with optimal gate assignment found by exhaustive search separately with respect to Cello’s score. (B) Circuit structure synthesized using structural variants with gate assignment optimized with respect to the E-score using the neighborhood based SA. (C) Repressor legend. (D) Plot showing the output histograms of both circuits. The proposed synthesis methods lead to a circuit that features a higher output fold-change and a lower variance in the ON state.
We see the work as a first step toward the use of more fine grained device models and the development of domain-adapted logic synthesis and technology mapping tools. There are several more extensions that we foresee in order for computer-based design methods to reach the necessary predictive power to be routinely used in the lab. Context-effects such as host energetics will require a more detailed biophysical model for how gate characteristics change under different conditions. Even if a random parametrization can account for that to a zeroth order, it will require the incorporation of a correlation structure among parameters that will be induced by cellular confounders like the cell’s energy state. Another aspect that also generates interdependence among gates is cross-talk due to, for instance, off-target binding of involved regulators or polymerase readthroughs for adjacent expression units. Such interdependency asks for enriched device models in libraries but will open up new interesting computational challenges for the circuit synthesis. Methods that account for intrinsic noise and for temporal aspects even for combinational logic,37 such as rise times or simple reversibility of circuit responses, are also yet to be developed. Integrating the temporal properties of genetic circuits that are central for designing sequential logic circuits3 into a consistent robust design and scoring framework is another challenge ahead.
4. Methods
4.1. Robust Circuit Synthesis and Technology Mapping
In the following, we introduce the optimization problem formally
in more detail compared to Section 2 and then dedicate separate sections to circuit synthesis
and technology mapping/scoring. Let thus 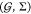 be the set of all labeled
DAGs where
be the set of all labeled
DAGs where 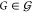 is a DAG with G = (V, E), E ⊆ V × V, and labeling
is a DAG with G = (V, E), E ⊆ V × V, and labeling  , with
, with 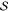 denoting
the set of available types of
functions (i.e., gate types) in that technology. Circuit synthesis
returns a finite set of circuit topologies
denoting
the set of available types of
functions (i.e., gate types) in that technology. Circuit synthesis
returns a finite set of circuit topologies 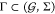 based on the synthesis
map from the space
of specifications in terms of Boolean formulas
based on the synthesis
map from the space
of specifications in terms of Boolean formulas 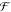 and an available
library
and an available
library 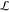 , i.e.,
, i.e., 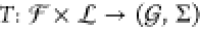 . The technology mapping
is the injective
function M that takes each vertex of a topology γ
in Γ and assigns it one element of library
. The technology mapping
is the injective
function M that takes each vertex of a topology γ
in Γ and assigns it one element of library 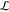 , i.e.,
, i.e., 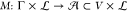 . Both processes jointly result in a circuit
(γ, a) with γ ∈ Γ and
. Both processes jointly result in a circuit
(γ, a) with γ ∈ Γ and 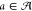 . Rating such a circuit is then done using
a circuit score function
. Rating such a circuit is then done using
a circuit score function 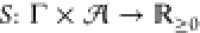 with the
choice S(γ, a) = exp(s(γ, a)),
which we conveniently define to be the exponential of the log-score
function
with the
choice S(γ, a) = exp(s(γ, a)),
which we conveniently define to be the exponential of the log-score
function 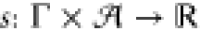 . The definition of S as
an exponential allows us to tackle the scoring in the logarithmic
domain, which is more amenable with respect to the biological application.
The score S is then quantifying the compliance of
the circuit outputs with the Boolean functional requirement
. The definition of S as
an exponential allows us to tackle the scoring in the logarithmic
domain, which is more amenable with respect to the biological application.
The score S is then quantifying the compliance of
the circuit outputs with the Boolean functional requirement  . Proceeding from here, we can formulate
the process of synthesis and technology mapping as an optimization
problem of the form
. Proceeding from here, we can formulate
the process of synthesis and technology mapping as an optimization
problem of the form
using the monotonicity of the logarithm for the last equality, with (γ*, a*) being the optimal structure and assignment combination w.r.t. the score S. The efficient construction of the set Γ and the proposed functional forms of s will be detailed in the following sections.
4.2. Circuit Synthesis involving Structural Variants
The problem of finding all structurally
different implementations
of a Boolean function is a DAG-enumeration problem. Thus, we intermediately
enumerate all fan-out free circuit structures C =
{γ ∈ Γ : ∀v ∈ V : |{u ∈ V : (v, u) ∈ E}| = 1},
simplifying enumeration and pruning (see Figure 2A). During the systematic construction of C from the given set of gate types S in
a library of genetic logic gates 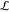 , the found
topologies are pruned according
to the optional synthesis constraints maximum circuit weight ω
and depth δ, i.e., ∀γ ∈ C : |γ| ≤ ω ∧ l ≤
δ, with l being the longest path of γ.
Furthermore, let ϕ be the n-ary Boolean target
function and Iγ = {i0, i1, ...} be the set of
unconnected gate inputs of γ, then ∀γ ∈ C : |Iγ| ≥ n. If the enumeration leads to isomorphism between the newly
found topology γ′ and any existing topology γ,
i.e., ∃γ ∈ C : γ ≃
γ′, γ′ is also discarded. The intermediate
result is the complete set of unique fan-out free circuits consisting
of gates of types S with a sufficient number of unconnected
gate inputs to implement ϕ.
, the found
topologies are pruned according
to the optional synthesis constraints maximum circuit weight ω
and depth δ, i.e., ∀γ ∈ C : |γ| ≤ ω ∧ l ≤
δ, with l being the longest path of γ.
Furthermore, let ϕ be the n-ary Boolean target
function and Iγ = {i0, i1, ...} be the set of
unconnected gate inputs of γ, then ∀γ ∈ C : |Iγ| ≥ n. If the enumeration leads to isomorphism between the newly
found topology γ′ and any existing topology γ,
i.e., ∃γ ∈ C : γ ≃
γ′, γ′ is also discarded. The intermediate
result is the complete set of unique fan-out free circuits consisting
of gates of types S with a sufficient number of unconnected
gate inputs to implement ϕ.
Then, a set of primary inputs  with
with 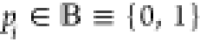 is instantiated, and all possible assignments
of unconnected gate inputs and primary inputs are generated, i.e.,
is instantiated, and all possible assignments
of unconnected gate inputs and primary inputs are generated, i.e.,  . For each fully specified circuit the Boolean
function is evaluated, and thus the set of circuits Cϕ implementing ϕ is obtained, i.e.,
. For each fully specified circuit the Boolean
function is evaluated, and thus the set of circuits Cϕ implementing ϕ is obtained, i.e.,
 |
99 |
Redundant
logic gates inherent to fan-out
free circuits are then eliminated by evaluating their function w.r.t.
to the primary inputs and merging functionally equivalent gates, thus
returning to a general DAG structure. This allows an application of
final library constraints, i.e., checking whether the total number
of genetic realizations in  and the number
of realizations per gate
type
and the number
of realizations per gate
type 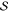 is sufficient
to implement each circuit.
is sufficient
to implement each circuit.
4.3. Technology Mapping of Genetic Circuits Using Neighborhood Heuristics
The smallest possible change that can be performed to generate a neighbor from a given solution is the substitution of one gate realization by another realization of the same logic type. Given that the gates, e.g., used in Cello differ greatly in their signal transfer behavior, a random substitution of one gate leads to an arbitrarily big change in the gate’s transfer function and thus in the circuit’s performance. Thus, we determine characteristic features of the gate realizations’ transfer functions and combine them into a proximity measure, enabling heuristic search algorithms to deliberately control the severity of changes to a solution during neighborhood generation.
The elementary transfer behavior of Cello’s genetic logic gates is characterized by a Hill repressor function
| 2 |
where x and y denote the input and output promoter activity, ymin and ymax define the output interval, K is the repression coefficient, and n the Hill coefficient. This transfer function gives the gates a NOT or a NOR characteristic, depending on how many signals it is sensitive to. A feature used for characterizing electronic NOT gates is the switching threshold Vm. It is defined as the point on the transfer function where Vin = Vout and impacts the device’s noise margins.38 Because of the global voltage levels VDD and VGND used commonly for input and output signals and thus symmetrical input and output intervals, Vm can be found near the inverter curves inflection point for well built devices. Genetic logic gates lack a common reference value for input and output levels. Thus, we redefined the switching threshold for the considered genetic gates to be the point on the Hill curve, where an output concentration halfway between the minimum and maximum output concentrations is reached (see Figure 3A). Let ym be that output concentration and xm the corresponding input concentration. We choose these characteristic features to be the first two dimensions of our proximity measure, i.e.,
| 3 |
| 4 |
Further examination of the given gate library showed that the gates transfer functions differ greatly in the gradient at y(xm). Thus, we define the gradient y′(xm) at the switching threshold to be another characteristic feature
| 5 |
Denote by di the three-dimensional
feature vector of gate i and define the diagonal
weighting matrix  with entries Wnm = wn/δn for n = m, where wn ∈ [0, 1] is the adjustable
weight for feature n (see Figure 3D) and
δn the maximal absolute difference
in the n-th feature between two gates across the
whole library, then we can quantify the similarity between any two
gates i and j in library by the W-norm
with entries Wnm = wn/δn for n = m, where wn ∈ [0, 1] is the adjustable
weight for feature n (see Figure 3D) and
δn the maximal absolute difference
in the n-th feature between two gates across the
whole library, then we can quantify the similarity between any two
gates i and j in library by the W-norm
In order to evaluate if local search heuristics for the technology mapping of genetic circuits can benefit from the proposed proximity measure, we integrated it into the neighborhood generation of SA that has been shown to profit from a well structured, problem specific neighborhood.28−30
A major challenge when implementing SA is to specify central parameters like initial temperature and annealing schedule that lead to the desired solution quality and a reasonable run time. For the base implementation of the algorithm, we adopted these specifications from VPR, a tool for FPGA logic synthesis that uses SA for FPGA placement.31 Then, we adapted the algorithm to yield near-optimal results for the given technology mapping problem by slowing down the annealing schedule and conditioning the number of iterations per temperature level on the problem size. Here, the problem size is the number of possible gate assignments resulting combinatorially from the composition of gates in the circuit and in the library.
For every iteration k, VPR determines a radius rk in which logic cells on the chip are considered to be swapped in the search process. The ratio of the number of accepted solutions to the number of total evaluations α is calculated continuously during the annealing process, and r is controlled to keep α near the empirically determined sweet spot of 0.44, i.e., rk = rk–1(1 – 0.44 + α). When, caused by the decreasing temperature, α drops below 0.44, the search radius r is decreased. This leads to a more local search for neighboring solutions in the late phase of the annealing process that are likely to have similar score values, thus leading to an increase of α. This ultimately results in the evaluation of less solutions with low scores that would be rejected anyway. We adapted this approach to our proximity based neighborhood generation. In our case, the radius controls which two gate realizations i and j in the library are considered for a swap, based on their distance Dij. The radius is initialized with the maximum distance of gates in the library, thus allowing for a global search in the search space in the early, high temperature phase. During the annealing process, r is decreased, progressively excluding gates with strongly differing transfer characteristics from the neighborhood generation. Further implementation details can be learned from the code available in a public repository.
4.4. Expectation-Based Score (E-score)
Like mentioned in Section 2.4.1, to better represent the variability of the gates over different cellular contexts, considering statistical descriptions of the circuits and their outputs is one possible way. This improves the representation of population-wide circuit behavior in the score function S(γ, a) (and therefore s(γ, a), which is used as a proxy). However, before we focus on the scoring in detail, we need a stochastic description of a genetic circuit. Therefore, we first introduce such a description, then we talk about how to generate sample realizations from this circuit, and finally, we talk about the score.
4.4.1. Circuit Description Respecting Cell-to-Cell Variability
Let thus 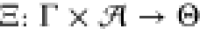 denote
the parametrization of a circuit
(γ, a). To represent the cellular context in
terms of known statistics, we understand Ξ(γ, a) as a random variable characterized by a distribution
Ξ(γ, a) ∼ P(θ) associated with circuit (γ, a). In the following, if we speak of a circuit parametrization, a
circuit realization or a specific context, we mean a particular realization
Ξ(γ, a) = θ, which
we assume to be constant for each member in a population. Our goal
will be to not only calculate the circuit output based on the median
realization of the parameters, like Cello, but also a set of sample
outputs consistent with realizations based on the measured data, which
jointly represent output distributions associated with a whole cell
population. Since the circuit function under a fixed parametrization
is—at this scale—assumed to be sufficiently deterministic,
the output distributions depend on a vector of realizations representing
the M circuit inputs
denote
the parametrization of a circuit
(γ, a). To represent the cellular context in
terms of known statistics, we understand Ξ(γ, a) as a random variable characterized by a distribution
Ξ(γ, a) ∼ P(θ) associated with circuit (γ, a). In the following, if we speak of a circuit parametrization, a
circuit realization or a specific context, we mean a particular realization
Ξ(γ, a) = θ, which
we assume to be constant for each member in a population. Our goal
will be to not only calculate the circuit output based on the median
realization of the parameters, like Cello, but also a set of sample
outputs consistent with realizations based on the measured data, which
jointly represent output distributions associated with a whole cell
population. Since the circuit function under a fixed parametrization
is—at this scale—assumed to be sufficiently deterministic,
the output distributions depend on a vector of realizations representing
the M circuit inputs 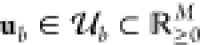 and the vector
of realizations θ ∈ Θ representing the (cellular) context.
Let further the realization of the random variable representing the
1-bit output be denoted by v. A Boolean label
and the vector
of realizations θ ∈ Θ representing the (cellular) context.
Let further the realization of the random variable representing the
1-bit output be denoted by v. A Boolean label 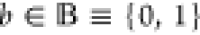 is attached to each set of input configurations
is attached to each set of input configurations 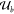 and its elements ub to indicate which output v is associated
with a Boolean value 0 or 1 from the truth-table ϕ. If we just
write u, we usually mean an arbitrary input without caring
about any underlying logic function. The output density p(v) can be found by marginalization
and its elements ub to indicate which output v is associated
with a Boolean value 0 or 1 from the truth-table ϕ. If we just
write u, we usually mean an arbitrary input without caring
about any underlying logic function. The output density p(v) can be found by marginalization
| 6 |
with p(v|ub, θ) being the density
of the circuit output conditioned on a particular
input and context realization. Given a gate library 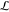 containing L context-dependent
gate quasi-steady-state transfer functions {g1, ..., gL}, of
which all are of a type
containing L context-dependent
gate quasi-steady-state transfer functions {g1, ..., gL}, of
which all are of a type 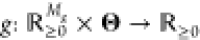 , where Mg is the number of gate inputs.
Then, the circuit output can
be calculated from a circuit transfer function f(ub, θ) ≡ f(ub, θ, g′, g″, ...) ≡ f (ub, θ, γ, a) depending on the set of gates in the
circuit
, where Mg is the number of gate inputs.
Then, the circuit output can
be calculated from a circuit transfer function f(ub, θ) ≡ f(ub, θ, g′, g″, ...) ≡ f (ub, θ, γ, a) depending on the set of gates in the
circuit 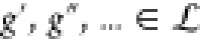 . This circuit transfer function can be
evaluated from subsequently calculating gate outputs. Therefore, the
output conditional p(v|u, θ) can be calculated directly from f, since for a specific context θ and input realization u the circuits transfer function f is deterministic
(as are all gates g). Consequently, p(v|u, θ) = δ(v – f (u, θ)) is given by a degenerate distribution, where δ is the Dirac
delta function. As a simplifying assumption, we require the factorizations p(u, θ) ≡ p(u)p(θ) and
. This circuit transfer function can be
evaluated from subsequently calculating gate outputs. Therefore, the
output conditional p(v|u, θ) can be calculated directly from f, since for a specific context θ and input realization u the circuits transfer function f is deterministic
(as are all gates g). Consequently, p(v|u, θ) = δ(v – f (u, θ)) is given by a degenerate distribution, where δ is the Dirac
delta function. As a simplifying assumption, we require the factorizations p(u, θ) ≡ p(u)p(θ) and 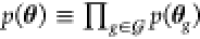 . The first assumes input distributions
independent of the cellular context and circuit chosen and the second
that the cellular context is acting independently on the gates in
the circuit. This allows us to equip every gate with an individual
set of sample realizations independent of which other gates are in
the circuit. The latter enables initial sample generation for all
gates in the library to allow a fast simulation in a technology mapping
process. We require further that gl(x, θ) ≡ gl(x, θl) for all
. The first assumes input distributions
independent of the cellular context and circuit chosen and the second
that the cellular context is acting independently on the gates in
the circuit. This allows us to equip every gate with an individual
set of sample realizations independent of which other gates are in
the circuit. The latter enables initial sample generation for all
gates in the library to allow a fast simulation in a technology mapping
process. We require further that gl(x, θ) ≡ gl(x, θl) for all 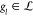 to allow
learning the gate parameters from
Cello’s isolated gate measurements.
to allow
learning the gate parameters from
Cello’s isolated gate measurements.
Cello’s gate library has some properties we need to address briefly. It consists only of NOT and NOR gates, where the latter combine multiple inputs to a single input via implicit summation. This means, if we write g(x, θ), this also includes gates with Mg > 1 by g(x, θ) ≡ g(x0 + x1 + ... + xMg, θ), cf. ref (1).
4.4.2. Collecting Samples
We built our set of samples by taking the cytometry data from Cello’s UCFs. For each binned data set in the UCF file associated with an input concentration from the discrete set x ≡ (x0, x1, ..., xk), we define the empirical distribution P̃k represented by the random variable ξk ∼ P̃k, so that P̃k is represented by the binned data set with its median logarithmically shifted to 0 (if not already). We multiplied these ξk with the Hill functions representing median realizations g(x, θ̃) also present in the UCF file to obtain “noisy” Hill function values g(xk, θ̃)ξk for each k (we added log ξk in the logarithmic domain). We did this in accordance to the instructions from the Cello supplementary material. We thus obtain a new distribution P̃′k for each k with support logarithmically shifted by the constant logg(xk, θ̃). Employing inverse transform sampling, we drew a set of N i.i.d. standard uniform random variates q = (q0, q1, ..., qN) representing quantiles and—using these and the inverses of the empirical CDFs—obtained N sets of k samples yn = (y0(n), y1, ..., yk(n)) from the P̃′k representing similar quantile locations for all the k. The relation between qn and yk is then given by qn = P̃k(yk(n)). Let g (θ) ≡ (g(x0, θ), ..., g(xk, θ)) be the vector of gate outputs for each of the xk under realization θ. We then solved the Tikhonov-regularized least-squares regression problems θn = minθ∥g(θ)– yn∥2 + λ∥θ – θ̃∥22 to obtain N sets of environment parameter samples θn (we use Hill function parameters as a proxy) representing the variability captured by the cytometry measurements. Under the independence assumptions outlined in the previous Section 4.4.1, we can generate the samples offline and store them in an extended gate library.
4.4.3. The Score
Equipped with our definitions from above, we are now able to specify a suitable s(γ, a), which we use to score a context-dependent circuit. Like Cello, we use the logarithmic on–off difference as a basis for our score, which seems to be a suitable quantification of the separation of two values in the positive reals. However, in contrast to Cello, which calculates logf(u1, θ̃) – logf(u0, θ̃) with the median realization θ̃, we have probability distributions to score if Ξ(γ, a) is a random variable. As a consequence logf(u1, Ξ(γ, a)) – logf(u0, Ξ(γ, a)) is a random variable as well. Therefore, we first chose its expectation as a scoring candidate, which manifests in the log-score
| 7 |
where 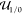 is the set of all real valued circuit input
vectors associated with Boolean output 1/0 from the circuit’s
truth-table ϕ. Let logf(u0, Ξ(γ, a)) ∼ P0 and logf(u1, Ξ(γ, a)) ∼ P1 for a specific (u0, u1). So, P0 and P1 are the CDF’s of population-wide individual log-outputs
associated with Boolean 1 and 0 for specific circuit inputs u0 and u1. Then, interestingly,
the expectation in eq 7 is equal to the Wasserstein distance of P0 and P1 if P0(v) – P1(v) never changes sign. This means that looking at any arbitrary
circuit log-output v′, there must lie more
probability mass below this value associated with Boolean 0 than with
Boolean 1, so P0(v′)
> P1(v′). The
Wasserstein distance, which is meant here, is defined on the metric
space
is the set of all real valued circuit input
vectors associated with Boolean output 1/0 from the circuit’s
truth-table ϕ. Let logf(u0, Ξ(γ, a)) ∼ P0 and logf(u1, Ξ(γ, a)) ∼ P1 for a specific (u0, u1). So, P0 and P1 are the CDF’s of population-wide individual log-outputs
associated with Boolean 1 and 0 for specific circuit inputs u0 and u1. Then, interestingly,
the expectation in eq 7 is equal to the Wasserstein distance of P0 and P1 if P0(v) – P1(v) never changes sign. This means that looking at any arbitrary
circuit log-output v′, there must lie more
probability mass below this value associated with Boolean 0 than with
Boolean 1, so P0(v′)
> P1(v′). The
Wasserstein distance, which is meant here, is defined on the metric
space  by
by
 |
where 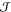 is the
set of all joint probability measures F on
is the
set of all joint probability measures F on 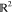 , which have marginals P0 and P1. Note that
the last
equality holds unconditionally. In our case, where we have two empirical
distributions P̃0 with samples
, which have marginals P0 and P1. Note that
the last
equality holds unconditionally. In our case, where we have two empirical
distributions P̃0 with samples 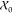 =
= 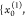
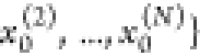 and P̃1 with samples
and P̃1 with samples  =
= 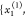
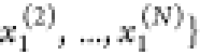 (ordered by increasing
magnitude), the
calculation reduces to (cf. the analogy for
(ordered by increasing
magnitude), the
calculation reduces to (cf. the analogy for 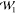 in ref (33))
in ref (33))
 |
where x0(n) is the n-th order statistic (n-th smallest sample)
in 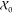 . The same holds for x1 and
. The same holds for x1 and 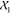 . We discussed
in Section 2.4.1 that, however, this score is agnostic
to variance in symmetric distributions. Therefore, if the output distributions
are symmetric, an overlap could not be detected. We therefore modify
the score in the sense depicted in Figure 4B to only score the negative deviation from
a per-median optimal output window caused by the distributions’
variances. This formalizes in the log-score
. We discussed
in Section 2.4.1 that, however, this score is agnostic
to variance in symmetric distributions. Therefore, if the output distributions
are symmetric, an overlap could not be detected. We therefore modify
the score in the sense depicted in Figure 4B to only score the negative deviation from
a per-median optimal output window caused by the distributions’
variances. This formalizes in the log-score
| 8 |
where f̃(u) ≡ f̃(u, Ξ(γ, a)) is the median circuit output for input u over Ξ(γ, a). We call the exponential S(γ, a) = exp(s(γ, a))
with s(γ, a)
from (eq 8) the E-score.
Note that this modification does not reduce the computational effort
in comparison to 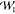 (P̃0, P̃1) but does not increase it notably either.
The expectation in the score (eq 8) can be calculated on the empirical output distributions
by
(P̃0, P̃1) but does not increase it notably either.
The expectation in the score (eq 8) can be calculated on the empirical output distributions
by
 |
9 |
where x̃0 and x̃1 are the medians of P̃0 and P̃1. Note that these are not equal to logf(u0, θ̃) or logf(u1, θ̃), since the output of the median circuit realization does not guarantee to yield the median circuit output. Note that the resulting score S(γ, a) generalizes Cello’s score. For degenerate distributions (two “samples”), it is simply given by S(γ, a) = exp(x1 – x0). In the case of Cello, the x0, x1 are the logarithms of the circuit outputs produced by the median realization θ̃ for two corresponding inputs u0 and u1.
4.5. Interval-Based Score (I-score)
Like mentioned in 2.4.2, we propose another approach, which is stricter and concentrates more on robust optimization.39 It is an implementation of the maximin principle in the sense that it does not seek to negotiate the diversity of a population, like an expectation does, but to find just the weakest element. This can also be the case if we do not want to calculate samples to approximate an output distribution or do not have sufficient data to derive distributions of parameters. In this case, the circuit parametrization Ξ(γ, a) is not understood to be random anymore, but becomes a set-valued map, returning a set containing all known parameter realizations Θ ∈ Ξ(γ, a) ⊂ Θ in circuit (γ, a). The associated maximin-score is then
 |
10 |
with an additional minimizer over the range
of possible parameters. We now, without knowledge of existence, choose
two parameter sets θ and θ̅, for which we demand the conditions that for
any  with
with 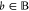 we have f(ub, θ̅) ≥
maxθ∈Ξ(γ,a)fb(ub, θ) and f(ub, θ) ≤ minθ∈Ξ(γ,a)fb(ub, θ) so that we obtain the following lower
bound s(γ, a) ≤ s̃(γ, a)
we have f(ub, θ̅) ≥
maxθ∈Ξ(γ,a)fb(ub, θ) and f(ub, θ) ≤ minθ∈Ξ(γ,a)fb(ub, θ) so that we obtain the following lower
bound s(γ, a) ≤ s̃(γ, a)
| 11 |
which we use as an interval-based
score and
call its exponential S(γ, a) = exp(s(γ, a)) the I-score.
We can show that if all gates in the circuit (γ, a) have transfer functions  that are monotonous (either decreasing
or increasing) for any fixed parametrization θ and
that are monotonous (either decreasing
or increasing) for any fixed parametrization θ and 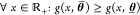 , then θ and θ̅ exist
and the output intervals
, then θ and θ̅ exist
and the output intervals 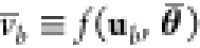 ≥
≥ 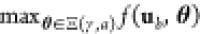 and
and 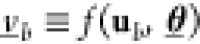 ≤
≤ 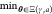
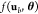 for
for 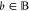 can be calculated only from the bounds θ and θ̅.
Since, like explained in 4.4.1, we use Cello’s
gate library, which consists only of NOT gates and NOR gates with
implicit summation, the monotonicity condition for all g is satisfied. Additionally, because we derived all available samples
from Cello’s cytometry data and the bounds have been chosen
appropriately, the inequality is very strict given the knowledge.
To calculate the output intervals [vb, v̅b] for
can be calculated only from the bounds θ and θ̅.
Since, like explained in 4.4.1, we use Cello’s
gate library, which consists only of NOT gates and NOR gates with
implicit summation, the monotonicity condition for all g is satisfied. Additionally, because we derived all available samples
from Cello’s cytometry data and the bounds have been chosen
appropriately, the inequality is very strict given the knowledge.
To calculate the output intervals [vb, v̅b] for 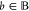 , we can generate a modified circuit, which
consists of 2K gates (if the circuit consists of K). This is done by generating two gates g̅, g from one
, we can generate a modified circuit, which
consists of 2K gates (if the circuit consists of K). This is done by generating two gates g̅, g from one  in the circuit, which contain the upper θ̅
and lower θ parametrizations.
Then, for all following adjacent gates g′,
we wire the output g̅ into g′ and g into g̅′. This resulting
circuit then propagates input intervals [ub, u̅b] to output intervals [vb, v̅b]. Once the output interval is calculated
by standard signal propagation (see 4.4.1)
through the modified circuit, the score (eq 10) can be approximated by eq 11, taking the smallest difference v1 – v̅0. The generation of g̅ and g can thereby be done offline in advance,
and the new information can be gathered in an extended gate library.
in the circuit, which contain the upper θ̅
and lower θ parametrizations.
Then, for all following adjacent gates g′,
we wire the output g̅ into g′ and g into g̅′. This resulting
circuit then propagates input intervals [ub, u̅b] to output intervals [vb, v̅b]. Once the output interval is calculated
by standard signal propagation (see 4.4.1)
through the modified circuit, the score (eq 10) can be approximated by eq 11, taking the smallest difference v1 – v̅0. The generation of g̅ and g can thereby be done offline in advance,
and the new information can be gathered in an extended gate library.
As a small addition, and to give an idea of possible further considerations, we also propose a relaxed, less strict version of this score. Since it is easy to calculate output interval bounds [v1, v̅1] associated with Boolean 1 and [v0, v̅0] associated with Boolean 0, we can again think of these intervals as supporting output distributions. We could, e.g., use this as a starting point for approximations of eq 8. Doing so, a reasonable assumption—if nothing else than the interval boundaries were known—would be assuming maximum entropy and therefore two uniform distributions with support within the interval boundaries. These can then again be scored using, e.g., the E-score (eq 8).
The source code of the proposed synthesis and scoring methods is available at https://www.rs.tu-darmstadt.de/ARCTIC.
Acknowledgments
Nicolai Engelmann and Heinz Koeppl acknowledge support from the European Research Council (ERC) within the CONSYN project, grant agreement number 773196.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acssynbio.1c00193.
(A) Pseudo-code algorithms of the enumeration of structural circuit variants and the generation of equivalent envelope-free circuits; (B) Circuit diagrams of designs synthesized using structural variants and uncertainty-aware assignment optimization (PDF)
Special Issue
Invited contribution from the 12th International Workshop on Bio-Design Automation.
Author Contributions
§ T.S., N.E., and E.K. contributed equally to this research.
Author Contributions
H.K. and C.H. provided the research idea and contributed methodology. T.S., N.E., and E.K. conceived novel synthesis and scoring schemes and carried out mathematical analysis and software development. All authors contributed to the writing of the paper.
The authors declare no competing financial interest.
Supplementary Material
References
- Nielsen A. A. K.; Der B. S.; Shin J.; Vaidyanathan P.; Paralanov V.; Strychalski E. A.; Ross D.; Densmore D.; Voigt C. A. Genetic circuit design automation. Science 2016, 352, aac7341. 10.1126/science.aac7341. [DOI] [PubMed] [Google Scholar]
- Chen Y.; Zhang S.; Young E. M.; Jones T. S.; Densmore D.; Voigt C. A. Genetic circuit design automation for yeast. Nature Microbiology 2020, 5, 1349–1360. 10.1038/s41564-020-0757-2. [DOI] [PubMed] [Google Scholar]
- Andrews L. B.; Nielsen A. A.; Voigt C. A. Cellular checkpoint control using programmable sequential logic. Science 2018, 361, eaap8987. 10.1126/science.aap8987. [DOI] [PubMed] [Google Scholar]
- Mutalik V. K.; Guimaraes J. C.; Cambray G.; Mai Q.-A.; Christoffersen M. J.; Martin L.; Yu A.; Lam C.; Rodriguez C.; Bennett G.; et al. Quantitative estimation of activity and quality for collections of functional genetic elements. Nat. Methods 2013, 10, 347. 10.1038/nmeth.2403. [DOI] [PubMed] [Google Scholar]
- Decoene T.; De Paepe B.; Maertens J.; Coussement P.; Peters G.; De Maeseneire S. L.; De Mey M. Standardization in synthetic biology: an engineering discipline coming of age. Crit. Rev. Biotechnol. 2018, 38, 647–656. 10.1080/07388551.2017.1380600. [DOI] [PubMed] [Google Scholar]
- Gómez-Schiavon M.; Dods G.; El-Samad H.; Ng A. H. Multidimensional Characterization of Parts Enhances Modeling Accuracy in Genetic Circuits. ACS Synth. Biol. 2020, 9, 2917–2926. 10.1021/acssynbio.0c00288. [DOI] [PubMed] [Google Scholar]
- Cardinale S.; Arkin A. P. Contextualizing context for synthetic biology - identifying causes of failure of synthetic biological systems. Biotechnol. J. 2012, 7, 856. 10.1002/biot.201200085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagy-Staron A.; Tomasek K.; Carter C. C.; Sonnleitner E.; Kavčič B.; Paixão T.; Guet C. C. Local genetic context shapes the function of a gene regulatory network. eLife 2021, 10, e65993. 10.7554/eLife.65993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeung E.; Dy A. J.; Martin K. B.; Ng A. H.; Del Vecchio D.; Beck J. L.; Collins J. J.; Murray R. M. Biophysical constraints arising from compositional context in synthetic gene networks. Cell Systems 2017, 5, 11–24. 10.1016/j.cels.2017.06.001. [DOI] [PubMed] [Google Scholar]
- Liao C.; Blanchard A. E.; Lu T. An integrative circuit-host modelling framework for predicting synthetic gene network behaviours. Nature Microbiology 2017, 2, 1658–1666. 10.1038/s41564-017-0022-5. [DOI] [PubMed] [Google Scholar]
- Ceroni F.; Algar R.; Stan G.-B.; Ellis T. Quantifying cellular capacity identifies gene expression designs with reduced burden. Nat. Methods 2015, 12, 415–418. 10.1038/nmeth.3339. [DOI] [PubMed] [Google Scholar]
- Brewster R. C.; Weinert F. M.; Garcia H. G.; Song D.; Rydenfelt M.; Phillips R. The transcription factor titration effect dictates level of gene expression. Cell 2014, 156, 1312–1323. 10.1016/j.cell.2014.02.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedlander T.; Prizak R.; Guet C. C.; Barton N. H.; Tkačik G. Intrinsic limits to gene regulation by global crosstalk. Nat. Commun. 2016, 7, 1–12. 10.1038/ncomms12307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jayanthi S.; Nilgiriwala K. S.; Del Vecchio D. Retroactivity controls the temporal dynamics of gene transcription. ACS Synth. Biol. 2013, 2, 431–441. 10.1021/sb300098w. [DOI] [PubMed] [Google Scholar]
- Falk J.; Bronstein L.; Hanst M.; Drossel B.; Koeppl H. Context in synthetic biology: Memory effects of environments with mono-molecular reactions. J. Chem. Phys. 2019, 150, 024106. 10.1063/1.5053816. [DOI] [PubMed] [Google Scholar]
- Bowsher C. G.; Swain P. S. Identifying sources of variation and the flow of information in biochemical networks. Proc. Natl. Acad. Sci. U. S. A. 2012, 109, E1320–E1328. 10.1073/pnas.1119407109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zechner C.; Koeppl H. Uncoupled analysis of stochastic reaction networks in fluctuating environments. PLoS Comput. Biol. 2014, 10, e1003942. 10.1371/journal.pcbi.1003942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green A. A.; Kim J.; Ma D.; Silver P. A.; Collins J. J.; Yin P. Complex cellular logic computation using ribocomputing devices. Nature 2017, 548, 117–121. 10.1038/nature23271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehr F.-X.; Hanst M.; Vogel M.; Kremer J.; Göringer H. U.; Suess B.; Koeppl H. Cell-free prototyping of AND-logic gates based on heterogeneous RNA activators. ACS Synth. Biol. 2019, 8, 2163–2173. 10.1021/acssynbio.9b00238. [DOI] [PubMed] [Google Scholar]
- Kitada T.; DiAndreth B.; Teague B.; Weiss R. Programming gene and engineered-cell therapies with synthetic biology. Science 2018, 359, eaad1067. 10.1126/science.aad1067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie Z.; Wroblewska L.; Prochazka L.; Weiss R.; Benenson Y. Multi-input RNAi-based logic circuit for identification of specific cancer cells. Science 2011, 333, 1307–1311. 10.1126/science.1205527. [DOI] [PubMed] [Google Scholar]
- Schneider C.; Bronstein L.; Diemer J.; Koeppl H.; Suess B. ROC’n’Ribo: characterizing a riboswitching expression system by modeling Single-Cell data. ACS Synth. Biol. 2017, 6, 1211–1224. 10.1021/acssynbio.6b00322. [DOI] [PubMed] [Google Scholar]
- Appleton E.; Madsen C.; Roehner N.; Densmore D. Design Automation in Synthetic Biology. Cold Spring Harbor Perspect. Biol. 2017, 9, a023978. 10.1101/cshperspect.a023978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baig H.; Madsen J.. Genetic Design Automation: A Practical Approach for the Analysis, Verification and Synthesis of Genetic Logic Circuits; Springer, 2020. [Google Scholar]
- Huynh L.; Tsoukalas A.; Koeppe M.; Tagkopoulos I. SBROME: A Scalable Optimization and Module Matching Framework for Automated Biosystems Design. ACS Synth. Biol. 2013, 2, 263. 10.1021/sb300095m. [DOI] [PubMed] [Google Scholar]
- Roehner N.; Myers C. J. Directed Acyclic Graph-Based Technology Mapping of Genetic Circuit Models. ACS Synth. Biol. 2014, 3, 543–555. 10.1021/sb400135t. [DOI] [PubMed] [Google Scholar]
- Lee S.; R. Jiang J.; Mishchenko A.; Brayton R.. Enumeration of Minimum Fanout-Free Circuit Structures. In IWLS-2019. International Workshop on Logic & Synthesis; 2019.
- Alizamir S.; Rebennack S.; Pardalos P. In Global Optimization: Focus on Simulated Annealing; Tan C. M., Ed.; I-Tech Education and Publication, 2008; pp 363–382. [Google Scholar]
- Goldstein L.; Waterman M. Neighborhood Size in the Simulated Annealing Algorithm. American Journal of Mathematical and Management Sciences 1988, 8, 409–423. 10.1080/01966324.1988.10737247. [DOI] [Google Scholar]
- Yuan J.; Wang L.; Zhou X.; Xia Y.; Hu J.. RBSA: Range-based simulated annealing for FPGA placement. In 2017 International Conference on Field Programmable Technology (ICFPT); 2017; pp 1–8.
- Betz V.; Rose J.. VPR: A New Packing, Placement and Routing Tool for FPGA Research; Field-Programmable Logic and Applications: Berlin, Heidelberg, 1997; pp 213–222.
- Gibbs A. L.; Su F. E. On Choosing and Bounding Probability Metrics. Int. Stat. Rev. 2002, 70, 419. 10.1111/j.1751-5823.2002.tb00178.x. [DOI] [Google Scholar]
- Villani C.Topics in Optimal Transportation; Graduate Studies in Mathematics; American Mathematical Society, 2003. [Google Scholar]
- Brayton R.; Mishchenko A.. ABC: An Academic Industrial-Strength Verification Tool; Computer Aided Verification: Berlin, Heidelberg, 2010; pp 24–40.
- Keutzer K.; Ravindran K. In Encyclopedia of Algorithms; Kao M.-Y., Ed.; Springer US: Boston, MA, 2008; pp 944–947. [Google Scholar]
- Ben-Tal A.; Ghaoui L. E.; Nemirovski A.. Robust Optimization; Princeton University Press, 2009. [Google Scholar]
- Fontanarrosa P.; Doosthosseini H.; Borujeni A. E.; Dorfan Y.; Voigt C. A.; Myers C. Genetic circuit dynamics: Hazard and Glitch analysis. ACS Synth. Biol. 2020, 9, 2324–2338. 10.1021/acssynbio.0c00055. [DOI] [PubMed] [Google Scholar]
- Abbas K.Handbook of Digital CMOS Technology, Circuits, and Systems, 1st ed.; Springer International Publishing, 2020. [Google Scholar]
- Ben-Tal A.; El Ghaoui L.; Nemirovski A.. Robust Optimization; Princeton Series in Applied Mathematics; Princeton University Press, 2009. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.










