Fast calculation of nanodosimetric quantities in treatment planning of proton and ion therapy

Abstract

Details of the pattern of ionization formed by particle tracks extends knowledge of dose effects on the nanometer scale. Ionization detail (ID), frequently characterized by ionization cluster size distributions (ICSD), is obtained through time-consuming Monte Carlo (MC) track-structure simulations. In this work, TOPAS-nBio was used to generate a highly precise database of biologically significant ID quantities, sampled with randomly oriented 2.3 nm diameter cylinders, 3.4 nm (10 base pairs) long, inside a chromatin-size cylinder, irradiated by 1–1000 MeV/u ions of Z=1–8. A macroscopic method developed to utilize the database using condensed-history MC was used to calculate distributions of the ICSD first moment $M_1^{C_2}$ and cumulative probability $F_3^{C_2}$ in a 20×20×40 cm³ water phantom irradiated with proton and carbon spread-out Bragg peak (SOBP) of 10.5 cm range, 2 cm width. Results were verified against detailed MC track-structure simulations using phase space scored at several depths. ID distributions were then obtained for intensity modulated proton and carbon radiotherapy plans in a digitized anthropomorphic phantom of a base of skull tumor to demonstrate clinical application of this approach.

The database statistical uncertainties were 0.5% (3 standard deviations). Fluence-averaged ID as implemented proved unsuitable for macroscopic calculation. E_dep-averaged ID agreed with track-structure results within 0.8% for protons. For carbon, maximum absolute differences of 2.9%±1.6% and 5.6%±1.9% for $M_1^{C_2}$, 1.7%±0.8% and 1.9%±0.4% (1 standard deviation) for $F_3^{C_2}$, were found in the plateau and SOBP, respectively, up to 11.5%±5.6% in the tail region. Macroscopic ID calculation was demonstrated for a realistic treatment plan. Computation times with or without ID calculation were comparable in all cases.

Pre-calculated nanodosimetric data may be used for condensed-history MC for nanodosimetric ID-based treatment planning in ion radiotherapy in the future. The macroscopic approach developed has the calculation speed of condensed-history MC while approaching the accuracy of full track structure simulations.

1. Introduction

The detailed spatial distribution of ionization events from a particle track passing through tissue or water is closely correlated with the distribution and complexity of DNA damage in cells exposed to ionizing radiation (Goodhead 1994). Parameters used to quantify a detail of ionization distributions are henceforth referred to as an ionization detail (ID). ID provides information on ionization patterns on the scale of the DNA molecules, adding biologically relevant information to the knowledge of macroscopic dose distributions.

Monte Carlo (MC) track structure codes are commonly used to provide information of the spatial ionization pattern in irradiated matter by simulating the transport of particles interaction by interaction (Nikjoo et al 2006). In the complementary field of nanodosimetry, ID is typically evaluated by measuring or simulating probability distributions of ionization cluster sizes in nanodosimetric volumes, i.e., the number of ionizations occurring in a closely packed cluster, which can be quantified in terms of statistical moments (e.g. the first moment, M₁) or cumulative probabilities (e.g. the probability to have a cluster size larger than 2, F₂). These are commonly referred to as nanodosimetric quantities (Grosswendt et al 2007, Palmans et al 2015). Of special interest for radiotherapy is the evaluation of the distribution of clusters of ionizations in volumes of the size comparable to DNA segments (Palmans et al 2015). It has been suggested that the formation of biologically relevant damage, e.g., complex strand breaks resulting from more than two individual breaks within 10 base-pairs, increases with increasing the ionization cluster size (see, for example, Nikjoo and Lindborg 2010). In addition, the chromatin structure affects the repair kinetics, e.g., repair of damage in heterochromatin is not as straightforward as repair in euchromatin (Goodarzi et al 2010, Watts 2016). Thus, complexity of DNA damage and local chromatin structure together influencing repair dictate radiobiological effectiveness. Therefore, it is of potential clinical interest to provide this type of information when creating radiation treatment plans. However, the long execution time of MC track structure codes to calculate ID in nanoscale geometries limits the use of ID in clinical applications, which calls for an alternative approach to calculate ID distributions in patient geometries.

Monte Carlo simulations of particle transport through patient geometries employ techniques that account for the accumulated effect of a large number of interactions in a segment of the particle track, a technique known as condensed history Monte Carlo. Table 1 shows the difference in performance (CPU time) between Monte Carlo track structure and condensed history simulations to simulate all ionization events along a single electron tracked through water using the Geant4-DNA track structure code (Incerti et al 2010, Bernal et al 2015) and the Livermore condensed history models of the Geant4 toolkit (Agostinelli et al 2003). The detailed transport of electrons requires several orders of magnitude more CPU time.

Table 1.

Execution time of simulation of electron transport in liquid water calculated with Geant4 version 10.2 patch 03. Simulations were performed using either the condensed history MC with the Livermore physics list with 1 μm production cut for electrons or using detailed track simulation with Geant4-DNA. The primary and secondary electrons were simulated down to zero kinetic energy. The simulations were run on a 2.8 GHz Intel Core i7 processor. Uncertainty is 1 standard deviation. The continuous-slowing-down approximation (CSDA) range is interpolated from ESTAR database from National Institute of Standards and Technology (Berger et al 2018).

Primary e– energy (keV)	CSDA range in water (mm)	Average CPU time per history
		Livermore	Geant4-DNA
100	0.143	0.53 ± 0.01 ms	5.7 ± 0.1 s
200	0.449	0.63 ± 0.01 ms	19.2 ± 0.2 s
300	0.842	0.73 ± 0.02 ms	42.6 ± 0.6 s
500	1.766	0.90 ± 0.01 ms	103.5 ± 2.1 s
700	2.778	1.03 ± 0.01 ms	204.8 ± 5.1 s
1000	4.367	1.30 ± 0.04 ms	436.9 ± 16.9 s

To reduce the very long computation time of nanodosimetric quantities, Alexander and coauthors (Alexander et al. 2015a, 2015b) devised an efficient method for protons, which links M₁ and F₂ with microscopic scale scenarios in a cell nucleus. Pre-calculated with Geant4-DNA, M₁ and F₂ quantities as a function of the primary energy for protons were used to obtain stopping-power-weighted values to describe the radiation track in a cell-size volume. Comparison with full Monte Carlo track structure simulations showed good agreement of 3.4%. However, the authors did not extend these calculations to the ~millimeter voxel-size volumes commonly used in patient treatment planning. The latter was suggested by Casigari and Schulte (2015) who combined condensed-history and track structure simulations to directly calculate averaged nanodosimetric quantities in nanoscopic volumes enclosed in a simple linear array of five macroscopic cubic voxels of 5 mm width that were irradiated by a spread-out Bragg peak (SOBP) of protons or carbon ions. The authors showed that weighting of individual pencil beams could be used to create uniform distributions of nanodosimetric quantities in the voxel array, which may imply uniform biological effectiveness. However, the calculation time for the case of carbon ions was reported to be prohibitively long to be practical in clinical applications.

The purpose of this work was several fold. First, we introduce the concept of ID on the nanometer scale as a physical quantity describing a specific aspect of the detailed spatial pattern of ionization interactions produced by ionizing radiation in matter. The ionization cluster size distribution (ICSD), ICSD density, and ICSD moments are all special cases of this ID. Second, we provide an extensive, highly precise database of several ID quantities of biological significance to ion radiotherapy. Since ion fragments are created in the plateau and travel beyond the Bragg peak in proton and carbon-ion therapy, the database included eight different stable ions ranging from protons to oxygen with energies covering the energy range observed in ion radiotherapy. Third, in a similar fashion to the method reported by Alexander et al (Alexander et al. 2015a) for microscopic volumes, we implemented a fast calculation method to score average nanodosimetric quantities in patient size geometries to be used in proton and ion beam radiotherapy. Finally, to demonstrate clinical usefulness, we presented the calculations of ID distributions for two RBE-weighted dose optimized treatment plans for a digitized head and neck phantom irradiated with protons and carbon-ion beams.

2. Materials and method

2.1. Track structure simulations for nanodosimetric quantities (ID) of protons and ions in water

The TOPAS-nBio (McNamara et al 2017, Ramos-Méndez et al 2018) extension of the TOPAS tool (Perl et al 2012), layered on top of Geant4-DNA (version 10.2.p03) (Incerti et al 2010, Bernal et al 2015), was used for detailed Monte Carlo track structure simulations used here to generate an ID database for ions of therapeutic energies. Geant4-DNA has been shown to satisfactorily reproduce experimental measurements of ionization cluster size distributions for protons and ion beams (see Burigo et al 2016). To physically characterize ion tracks, a simplified discrete geometry of a DNA’s chromatin fiber described in (Bueno et al. 2015) was used in the current work. It consisted of a cylinder of 161 nm length and 30.4 nm diameter, approximating a chromatin fiber, which enclosed 1800 cylinders, each one of 2.3 nm diameter and 3.4 nm length, approximating DNA segments of 10 base pairs. The small cylinders were uniformly randomly positioned and oriented in the larger cylinder without volume overlaps. The larger cylinder was embedded in either a cubic box of 200 × 200 × 200 nm³ or a sphere (see below). The chemical composition of this structure was liquid water. This simplified DNA geometry allowed the sampling of ion tracks with small energy loss (<1.5%) through the large cylinder. Thus, it provided look-up tables of nanodosimetric quantities for incoming protons and ions for a defined energy.

To aid in the selection of source geometry, we tested three different irradiation configurations for both proton and carbon ions as follows (see figure 1): a) The particle source was placed on the surface of the large cylinder, with the primary particles directed to points randomly located inside this cylinder as in (Bueno et al. 2015); b) The particle source was randomly distributed on the surface of a spherical shell of radius larger than the length of the large cylinder and equal to the range of the most energetic secondary electrons to ensure charged particle equilibrium, as suggested in (Pater et al. 2014), with primary particles directed to points randomly located inside the cylinder; c) The particle source was normally incident at the center of one of the end caps of the large cylinder (referred to as “normally incident at a point” in the remainder of this paper).

Figure 1.

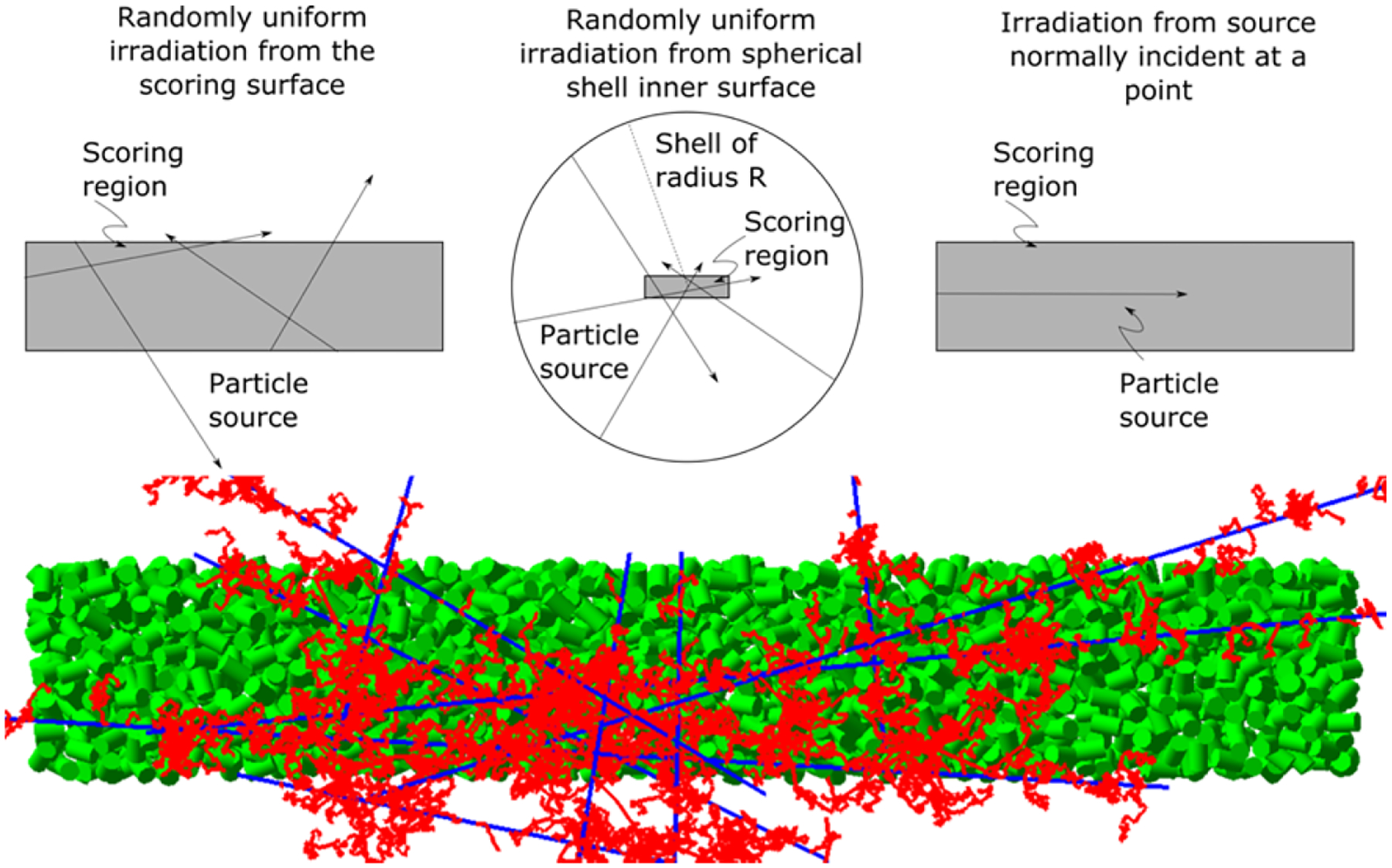
The three different source geometries simulated in this work, in grey, each embedded in a water phantom. Top left: The particle source is spread randomly across the surface of the large cylinder. Top center: The particle source is spread randomly across the surface of a spherical shell with radius equal to the range of the most energetic secondary electrons from the primary particles. Top right: The particle source is normally incident on the center of one of the end caps of the large cylinder (referred to as “normally incident at a point”). For the first two cases, the particle direction is chosen as the line from the source to a randomly chosen point inside the scoring region (in grey). Bottom: Illustration of tracks arising from several randomly chosen 1 MeV source protons incident on the top left source geometry. Tracks of protons (blue lines) and secondary electrons (red lines) through the large cylinder; also shown are the small cylinders (green).

The particles simulated in this work were protons with energies ranging from 0.5–100 MeV, ⁴He ions with energies from 1–100 MeV/u and ⁷Li, ⁹Be, ¹¹B, ¹²C, ¹⁴N, ¹⁶O ions with energies from 1–1000 MeV/u. All of the ionization events that occurred in the small cylinders were scored per primary history. To improve computational efficiency, we used the flagged uniform particle split variance reduction technique (Ramos-Mendez et al 2017). Briefly, this technique reduces the variance of the quantity of interest by means of population control. In this work, the number of secondary electrons produced in ionization events in the small cylinders was artificially increased (i.e. split) by the split number, N_s, then the number of histories required to achieve a desired statistical uncertainty was reduced. The statistical weight of the split electrons was multiplied by 1/N_s, and a flag was assigned to each split electron and inherited by all their progeny in future interactions. The flag was then used to reclassify these electrons as if they were created by independent histories, avoiding biasing the cluster sizes (Ramos-Mendez et al 2017). The selection of the number of split N_s is problem dependent. For this work, N_s was set to 50, as described later in the discussion section.

The cluster size ionization distribution P(v|Q), defined as the probability per primary history that a cluster with ν ionizations is produced within the scoring region (small cylinders) by a beam of quality Q (Grosswendt et al 2007) was obtained; in addition, the conditional distribution with ionization cluster sizes of ν ≥ 2, $P^{C_2}(\nu |Q)$ (in notation from Hilgers et al, 2017), was obtained. The conditional distribution with ν ≥ 2 was selected. The reason for this choice was to display the local ID in terms of moments and cumulative probabilities for events that are more likely to create double-strand breaks (DSB). Therefore, events with ν = 0 and ν = 1 included in P(ν | Q) have been excluded by using the conditional $P^{C_2}(\nu |Q)$. While this assumption needs to be supported by radiobiological data, a method for faster calculation of ID using condensed history Monte Carlo was first developed, in this work, to facilitate experimental investigation. Then, a set of nanodosimetric quantities, summarized in Table 2, was obtained as a function of particle type and energy.

Table 2.

Nanodosimetric quantities (ID) parameterized in this work. The reference and a short description is also included.

Quantity	Reference	Description
$M_1\left(Q\right)={\sum }_{\nu =0}^{\infty }\nu P(\nu |Q)$	(Grosswendt et al 2007)	First moment of the ionization probability distribution.
$F_2\left(Q\right)={\sum }_{\nu =2}^{\infty }P(\nu |Q)$	(Grosswendt et al 2007)	Cumulative probability of having ν ≥ 2.
$M_1^{C_2}\left(Q\right)={\sum }_{\nu =2}^{\infty }\nu P^{C_2}(\nu |Q)$	(Bueno et al 2015)	First moment of the conditional probability ν ≥ 2 ionization distribution.
$F_3^{C_2}\left(Q\right)={\sum }_{\nu =3}^{\infty }{P}^{C_2}(\nu |Q)$	(Bueno et al 2015)	Cumulative probability of having ν ≥ 3.

P(ν|Q) probability that a cluster with ν ionizations is produced within the scoring region

$P^{C_2}(\nu |Q)$ conditional distribution with ionization cluster sizes of ν ≥ 2 in notation from (Hilgers et al 2017)

2.2. Fast computation of nanodosimetric quantities for mixed radiation field

For a given mixed radiation field comprised of different particles with different energies, the exact solution to quantify an ID when using the unconditional distribution P(ν|Q) is simply the sum of the individual probability distributions for each particle weighted by the relative particle number. This is due to the additive property of independent probability distributions. However, the use of conditional distributions (justified at the end of section 2.1) does not allow us to exploit this additive property. A different approach is needed.

For a radiation field interacting in a given macroscopic volume (e.g. a millimeter sized voxel), the averaged nanodosimetric quantity (using conditional distributions) in that volume can be estimated by the weighted sum of the ID of each particle in the field with a known track-related physical quantity. For treatment planning systems the track-related physical quantities available are the fluence and stopping power, and hence, track length and energy deposited. Thus, it is a natural starting point to select these quantities as candidates for weighting the ID in macroscopic voxels, although it was not clear to us whether either quantity would result in a sufficiently accurate estimate of ID. In this work, two averaging approaches were considered, namely:

$${\overline{ID}}_{\Phi }\left(Q\right)=\frac{{\sum }_{j,p}{q}_j^p\left(E_j\right)\Delta T_j}{{\sum }_j\Delta T_j},\text{ fluence-averaged ID}$$ (3)

$${\overline{ID}}_E\left(Q\right)=\frac{{\sum }_{j,p}{q}_j^p\left(E_j\right)\Delta E_j}{{\sum }_j\Delta E_j},{\text{E}}_{\text{dep}}\text{-averaged ID}$$ (4)

where ΔT_j and ΔE_j are respectively the track-length and energy deposited, respectively, between successive interactions (j-1)th and jth in the volume. The sum extended over all histories intersecting the volume and their respective energies. The nanodosimetric quantity q^p_i(E_j) (see table 2) for the particle type p with incoming kinetic energy E_j is obtained via linear interpolation from the pre-calculated ID database. The extent to which the fluence and energy deposited weighting factors provided the true ID value was evaluated by comparing the macroscopically calculated $\overline{ID}$ to the ID calculated with Monte Carlo track-structure simulations of the mixed radiation field, as described in section 2.3.

We used equations (3) and (4) to calculate the depth-$\overline{ID}$ curve in a water box of 200 × 200 × 400 mm³. The traversal dimensions of the phantom ensured full containment of the beam in the water box. The proton and carbon-ion source particles were normally incident on a slab of air, 4 cm upstream of the water phantom surface, with the following energy distributions:

1. A set of proton pencil beams incident at a single point at the center of the water phantom. The energies and weights were those of an SOBP from a commissioned beam line at the Northwestern Medicine Chicago Proton Center (Piersimoni et al 2017). The SOBP had a range of 105 mm and width of 17.9 mm. The dose and ID were scored in voxels with large lateral widths of 200 × 200 mm², extending through the whole phantom, and 0.8 mm in the depth (beam) direction. This variance-reduction approach is based on the geometry equivalence theorem and is commonly used to achieve a much higher calculation efficiency than scoring quantities on the central axis in millimeter-sized voxels (see, e.g., Bielajew and Rogers 1988).

2. An RBE-weighted carbon SOBP of 105 mm range and 20 mm width was generated with a research version of the matRad toolkit (Wieser et al 2017) with generic carbon-ion beam data, giving the energies and weights used in both the TOPAS and matRad calculations. The carbon ion pencil beams had 7 mm full-width half maximum Gaussian-shaped spots and 3 mm spacing covering a 40 × 40 mm² field. The dose and ID were scored in cubic voxels of 1 mm³ volume. The physical dose calculated with matRad and TOPAS was sufficiently close to justify the use of the spatial and energy distributions of fluence calculated with matRad in the TOPAS simulations. For example, in the case of the SOBP Bragg curve with peak at 8.44 cm depth, dose differences between matRad and TOPAS at 4 cm depth and at peak, with dose normalized at the surface, were −0.14±0.84% and 0.13±0.94%, respectively.

2.3. Comparison of macroscopic ID calculation with track structure simulations

The averaged ID quantities defined in table 2 resulting from fast calculations according to equations (3) and (4) are referred to here as macroscopic $\overline{ID}$ and the calculation approach as macroscopic simulation. To verify the accuracy of these calculations, they were compared against the exact results from track structure simulations at different depths of the water phantom described in section 2.2. For the track structure simulations, several volumetric phase space files were first scored on slices of 1 mm thickness at different depths along the SOBP for the proton and carbon-ion source. For the carbon-ion source, the central 40 × 40 mm² region was used. The volumetric phase space scoring included primary particle type, energy, angle of incidence and position at the point of entry into the scoring volume. Secondary ions created in the volume that would not reach the next boundary surface were scored at the point of creation. Otherwise, phase space information was scored at the entrance surface of the scoring volume. All secondary particles were scored with the exception of neutral particles, since these are sparsely ionizing and contribute negligibly to the ID, and electrons and positrons, since these are accounted for in the pre-calculated database. The ID distributions were calculated from the particles in the phase space using the track structure simulation geometry described in section 2.1, with the particle incident on the center of one of the end caps of the large cylinder (rights side of figure 1) with the incident angle from the phase space data. Each history was independent from all other histories. In the macroscopic simulations, the lateral extent of the beam was fully contained by the phantom, allowing the coordinates of all particles in the phase space to be collapsed to the same point in the track structure simulations. Flagged uniform particle split variance reduction was used in the track structure simulations with a split number of 50 for both protons and carbon ions (Ramos-Méndez et al 2017).

2.4. Calculation of macroscopic $\overline{ID}$ distributions for clinical proton and carbon ion treatment plans

To demonstrate the potential clinical application of fast $\overline{ID}$ calculations, spatial distributions of these quantities were calculated in a digitized anthropomorphic phantom using optimized treatment plans for scanned IMPT. Two optimized RBE-weighted plans, one for protons and one for carbon ions, were created for a hypothetical chordoma case of the base of skull with a target volume defined by one of the authors (RS). The two were obtained using the head of a digitized phantom of a 30 year old female (Lee et al 2010), with 2 mm wide cubic voxels. The proton plan was generated with a research version of RayStation (version 4.6.102), commissioned with beam data from the Northwestern Medicine Chicago Proton Center (Piersimoni et al 2017). The carbon-ion plan was generated using matRad. In both cases, the IMPT plans were optimized to deliver 72 Gy-RBE uniform RBE-weighted dose to the tumor target. A constant RBE of 1.1 was used for the proton plan, while the original version of the Local Effect Model (now called LEM I) (Scholz et al 1997) was used to calculate RBE-weighted dose for the optimized carbon-ion plan (Krämer and Scholz 2000). The constant RBE and the LEM I models were available for optimizing IMPT plans in the research versions of RayStation and matRAD, respectively, and these were perfectly adequate for our purposes. While the use of a constant RBE for protons has been criticized by different studies (see revision paper (Paganetti 2014)) and the LEM model has been modified over the years (e.g. LEM IV in (Grün et al 2012)), it remains common practice to assume a constant RBE in proton planning and to use LEM I for treatment planning at the Heidelberg Ion-Beam Therapy Center (HIT). Regardless, the methodology proposed in this work is independent of radiobiological model.

Three coplanar fields were calculated for each plan, one anterior-posterior field, one right-posterior-oblique field and one left-posterior-oblique field. The plans, including the fluence distributions for each field, were exported to TOPAS. Condensed history MC was then used to calculate the trajectories of primary and secondary particles throughout the phantom. The energy, track length and energy deposition of each and every particle in each voxel was used to calculate average $\overline{ID}$ using equations (3) and (4).

3. Results

3.1. Ionization clusters size distributions for 1 MeV/u ions.

Probability distributions of ionization cluster sizes equal or larger than 1, calculated with TOPAS, are shown for ions of 1 MeV/u in figure 2. The geometrical setup was that described in section 2.1 consisting on the large cylinder filled with 1800 small cylinders randomly positioned and oriented. The particle source was that randomly uniform distributed from the large cylinder surface and only the ionizations occurred in the small cylinders were scored. As shown, the larger the charge of the ion, the larger the probability of large ionization cluster size in the tail of the distribution. All distributions exhibited an initial exponential drop. For heavier ions, this was followed by a region of fairly constant probability of ionization cluster size. A similar pattern was obtained experimentally in (Hilgers et al 2017) who reported the measured cluster size distribution of 88 MeV carbon ions irradiating a gas volume equivalent to a water target of 2.3 nm diameter and 6.1 nm length using a broad beam with an effective diameter of 17.1 nm. The primary particle produced most of the large ionization clusters, while secondary electrons produced most of the small ionization clusters, as demonstrated in top right of figure 2 for 1 MeV/u carbon ions. Note that the distribution for all the ionizations is not equal to the sum of the distributions from primary and secondary ionizations. The distribution for all the ionizations needs to be calculated separately, since combining primary and secondary ionizations results in a greater probability of larger cluster sizes.

Figure 2.

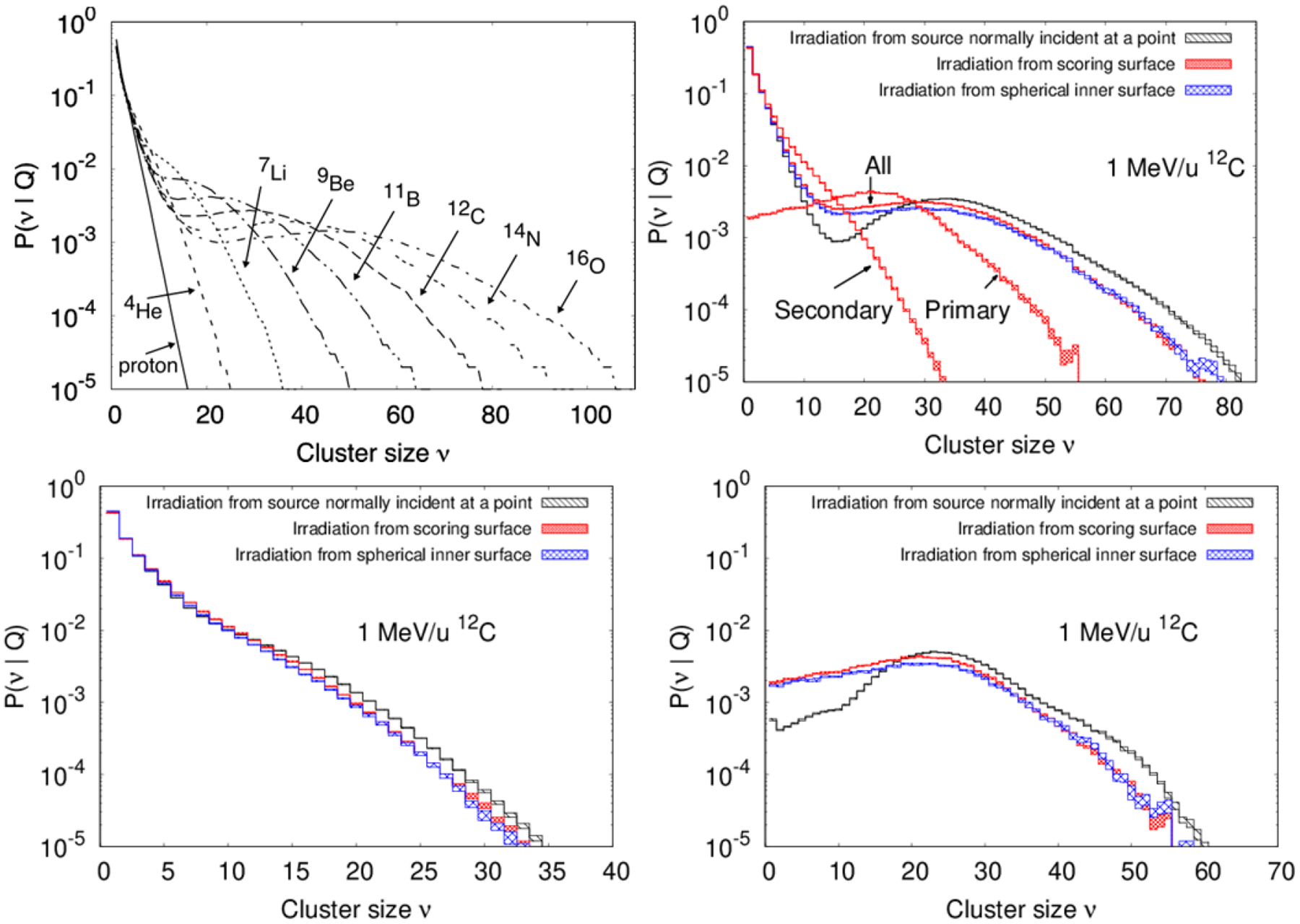
Ionization cluster size probability distributions at 1 MeV/u for proton and ions as indicated. Top right: results for ¹²C ions for the three different source shapes from Figure 1 shown with different pattern-filled lines, the thickness represents 1 standard deviation of statistical uncertainty. Bottom: Ionization cluster size probability distributions restricted to secondary ionizations only (left) and restricted to primary ionizations only (right). In all cases zero clusters sizes were not produced as the source used to irradiate the geometry of figure 1 ensures at least one cylinder has at least one ionization event.

3.2. Effect of source geometry

The probability distribution of ionization cluster sizes for all the ionizations, restricted to secondary ionizations only and restricted to primary ionizations only when using the different source geometries displayed in figure 1, are shown in figure 2. As shown, using the source normally incident at a point, larger clusters sizes are more likely produced from primary ionizations, whereas small clusters are produced with lower probability. As probability distributions from secondary ionization are similar for the three sources, the main difference is from sampling primary ionizations. Figure 3 shows M₁(Q) as a function of the primary particle energy for protons and carbon ions. The results generated with the source on the surface of the sphere that encompasses the large cylinder are within 0.5% of those with the source on the surface of the large cylinder, nearly indistinguishable in the figure. Simulations using the source on the surface of the cylinder instead of the sphere were on average 30% faster in execution time for both protons and carbon ions because the mean track length for the primaries were shorter. Compared to uniform irradiation, the use of a source normally incident at a point for protons resulted in higher M₁(Q) values with decreasing energy below 10 MeV, a 5% discrepancy at 0.5 MeV, the lowest energy simulated. Differences for this source with carbon ions becomes evident below 100 MeV/u, with the maximum difference of 12% occurring at 1 MeV/u, the lowest energy simulated.

Figure 3.

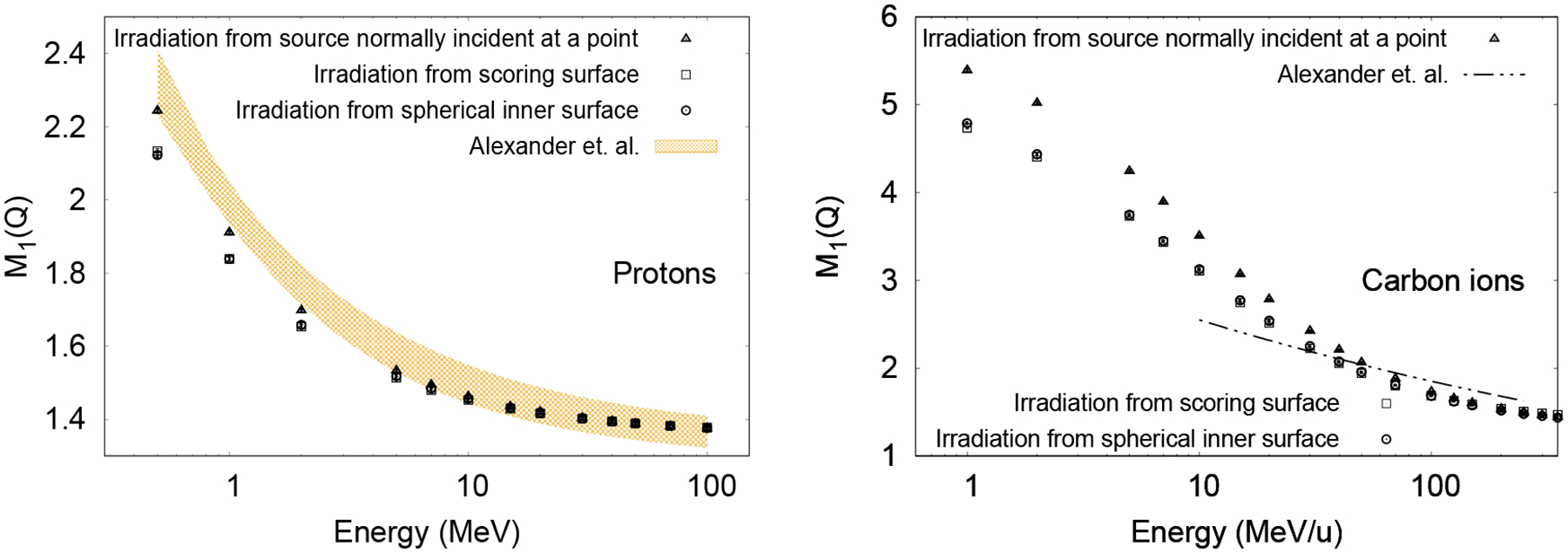
Effect of source geometry on the mean ionization cluster size for protons (left) and carbon ions (right). Data from the literature (Alexander et al. 2015a) for a source with particles normally incident at a point (see figure 1) is also shown as the shaded region for protons (left), the thickness corresponding to the uncertainty in the fitting parameters of a power law function with three parameters, and with the double-dotted dashed lines for carbon ions (right). The large fitting uncertainty (~50% and 100% for the amplitude and power parameters, respectively) of the power law function for carbon ions from Alexander et al. (2015b) is not shown in this case.

The results from Alexander et al (2015a; 2015b) for a source inside an essentially infinite geometry, with randomly placed small cylinders of the same dimensions used in the present work, are also shown in figure 3. Proton and carbon ion results from the present work for the source normally incident at a point agree with the published results within the fitting errors, where the authors used an older version of Geant4-DNA.

Given that the spherical source is more realistic than a point source and the results for the cylindrical source were comparable to those from the spherical source but faster to calculate, the source in the following simulations was randomly distributed over the surface of the large cylinder for the generation of ID databases.

3.3. Database of ID quantities

Figure 4 shows M₁(Q) and $M_1^{C_2}\left(Q\right)$ as a function of ion type and primary particle energy. The dependence on energy for each ion was fitted to the following empirical formula:

$$M_1\left(Q\right)=\frac{P_1}{1+exp\left(\frac{ln\left(P_3\right)-ln\left(E\right)}{P_4}\right)}+P_2,$$ (5)

with the fitting parameters P₁, P₂, P₃ and P₄ given in tables 3 and 4. The errors listed in the tables include statistical uncertainties and fitting errors. The ID quantities F₂(Q) and $F_3^{C_2}\left(Q\right)$ are also shown in figure 4 as a function of ion type and kinetic energy. For these quantities, their more complex response as a function of energy was incompatible for fitting to an analytical expression. The statistical uncertainties (3 standard deviations) from 36 simulations, the available number of CPUs, in the ID shown in figure 4 were all below 0.5%. From the parameters in table 3 and 4 for M₁(Q) and $M_1^{C_2}\left(Q\right)$ for ions, the amplitude P₁ of the sigmoid function (Eq. 5) was correlated with the increasing charge of the particle. Parameter P₂, the y-intercept, closely described the minimum M₁(Q) and $M_1^{C_2}\left(Q\right)$ values achieved at the highest energy values. In that region, the data converged to the same M₁(Q) or $M_1^{C_2}\left(Q\right)$ values, indicating a constant P₂. The parameter P₃ represents the midpoint of the sigmoid function and it also increased with the charge of the particle. Finally, the slope given by the parameter P₄ remained almost constant. M₁(Q) and $M_1^{C_2}\left(Q\right)$ are insensitive to this parameter. The fitted parameters for protons exhibited abrupt changes and were left out of the analysis of fitting parameters for ions. Care should be taken in interpretation of the physics behind the parameters fitted to this arbitrary function.

Figure 4.

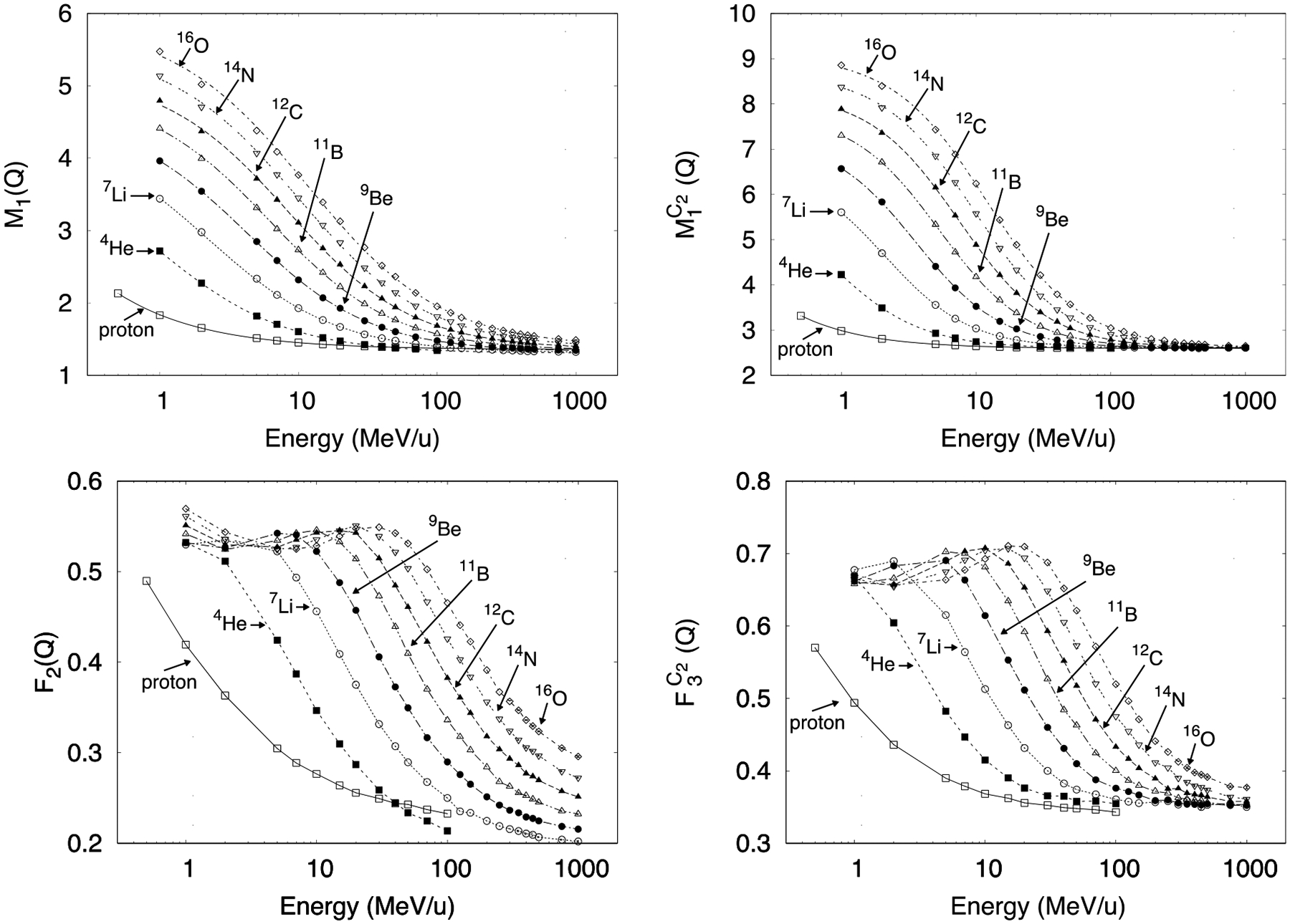
ID as a function of ion type and kinetic energy. Top: First moment of the ionization probability distribution for ν ≥ 1 (left) and for ν ≥ 2 (right). Only for these two panels the lines shown are fitted curves using Equation 5. Bottom: Cumulative probability of having ν ≥ 2 (left) and for ν ≥ 3 (right). The lines shown are only as guideline for the eye. Error bars (3 standard deviations) are mostly smaller than the symbols.

Table 3.

Fitting parameters from equation (5) for M₁(Q) (figure 3). Uncertainties are 1 standard deviation.

Particle	Fitting parameters
	P1	P2	P3	P4
Proton	17.36 ± 0.77	1.359 ± 0.001	0.007 ± 0.001	−1.393 ± 0.006
4 He	2.93 ± 0.07	1.308 ± 0.003	0.919 ± 0.039	−1.094 ± 0.012
7 Li	3.13 ± 0.02	1.317 ± 0.001	2.239 ± 0.036	−1.063 ± 0.005
9 Be	3.27 ± 0.01	1.331 ± 0.001	4.267 ± 0.040	−1.027 ± 0.004
11 B	3.57 ± 0.01	1.346 ± 0.001	6.230 ± 0.053	−1.031 ± 0.003
12 C	3.80 ± 0.01	1.367 ± 0.001	8.391 ± 0.069	−1.035 ± 0.003
14 N	4.15 ± 0.01	1.382 ± 0.001	9.899 ± 0.065	−1.074 ± 0.003
16 O	4.47 ± 0.01	1.396 ± 0.001	11.510 ± 0.081	−1.116 ± 0.004

Table 4.

Fitting parameters for $M_1^{C_2}\left(Q\right)$ from equation (5) (figure 4). Uncertainties are 1 standard deviation.

Particle	Fitting parameters
	P1	P2	P3	P4
Proton	12.38 ± 0.56	2.599 ± 0.002	0.025 ± 0.002	−1.079 ± 0.009
4 He	3.87 ± 0.14	2.602 ±0.004	0.776 ± 0.037	−0.784 ± 0.012
7 Li	4.07 ± 0.04	2.608 ±0.001	2.101 ± 0.036	−0.728 ± 0.005
9 Be	4.68 ± 0.02	2.605 ± 0.001	3.569 ± 0.025	−0.738 ± 0.003
11 B	5.21 ± 0.02	2.603 ± 0.001	5.341 ±0.036	−0.752 ± 0.003
12 C	5.64 ± 0.02	2.605 ± 0.001	7.443 ± 0.054	−0.767 ± 0.003
14 N	6.08 ± 0.01	2.608 ± 0.001	9.628 ± 0.046	−0.788 ± 0.002
16 O	6.46 ± 0.01	2.618 ± 0.002	12.035 ± 0.058	−0.806 ± 0.002

3.4. Verification of depth-dependent ${\overline{ID}}_{\Phi }$ and ${\overline{ID}}_E$ for proton and carbon ion beams

Fluence-averaged $\left({\overline{ID}}_{\Phi }\right)$ and E_dep-averaged $\left({\overline{ID}}_E\right)$ ID were calculated as a function of depth in water in the macroscopic simulations of the SOBP’s using equations (3) and (4) and are shown in figure 5 for the quantities $M_1^{C_2}\left(Q\right)$ and $F_3^{C_2}\left(Q\right)$ represented by the following notation ${\overline{M_1^{C_2}}}_{\Phi }$, ${\overline{F_3^{C_2}}}_{\Phi }$, ${\overline{M_1^{C_2}}}_{\text{E}}$ and ${\overline{F_3^{C_2}}}_{\text{E}}$. The results from track structure simulations using the corresponding volumetric phase space data generated with the macroscopic simulations are also shown for comparison and depth-dose curves are shown to delimit the region covered by the SOBPs. The SOBPs need not correlate with the ID since these are different physical quantities. The agreement described below would be better for a pristine Bragg peak.

Figure 5.

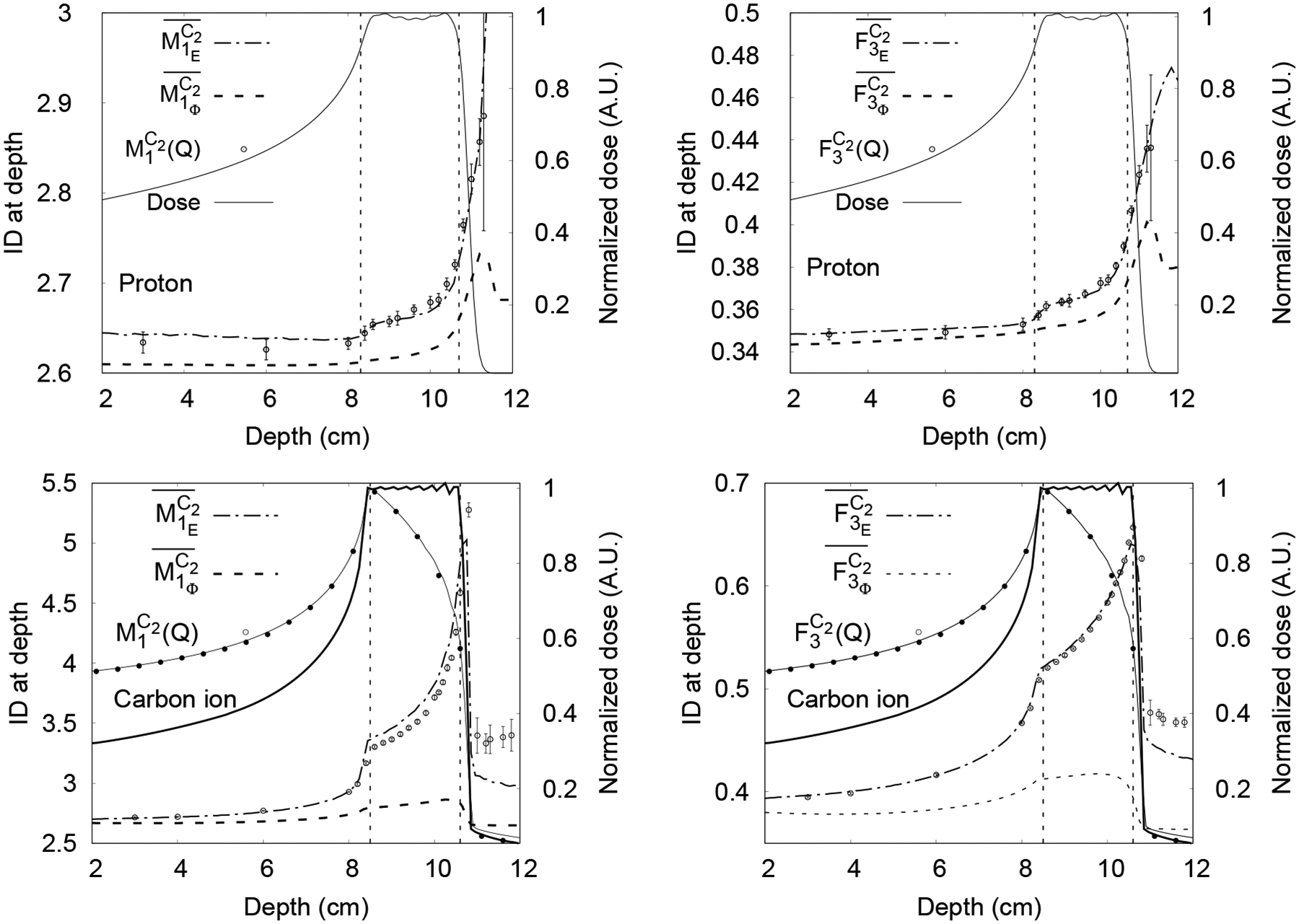
Macroscopic unnormalized E_dep -averaged ${\overline{\text{ID}}}_{\text{E}}$ (dot-dashed line) and fluence-averaged ${\overline{\text{ID}}}_{\Phi }$ (broken line) calculated with TOPAS for proton SOBP (top row) and carbon-ion SOBP (bottom row). Results from Geant4-DNA track structure simulations calculated with TOPAS-nBio shown as points with error bars of 1 standard deviation, with a different scale for each graph. The central axis depth-dose curves are plotted (solid lines) to show the depth of the plateau and SOBP regions, with the scale shown on the right. The vertical dotted lines indicate 90% dose for protons, 100% RBE-weighted dose for carbon ions. In the case of carbon, the physical dose calculated with TOPAS (thin line) and matRAD (points with 0.5 cm spacing) are shown along with the RBE-weighted dose calculated with matRad (thick line).

For the proton beam, the fluence-averaged quantities ${\overline{M_1^{C_2}}}_{\Phi }$ and ${\overline{F_3^{C_2}}}_{\Phi }$ did not agree with the values obtained with track structure simulations, showing differences of 2.3% ± 0.24% and 4.6% ± 0.4% at the depth of 10.5 cm, respectively. Conversely, the E_dep-averaged quantities ${\overline{M_1^{C_2}}}_{\text{E}}$ and ${\overline{F_3^{C_2}}}_{\text{E}}$ agreed with the results from track structure simulations within the statistical uncertainties, namely 0.4% and 0.8% (1 standard deviation), respectively.

The fluence-averaged ID calculated for the carbon-ion beam showed much higher differences than the proton case; for example, −17.6% ± 0.5% and −21.9% ± 0.3% at 9 cm depth for ${\overline{M_1^{C_2}}}_{\Phi }$ and ${\overline{F_3^{C_2}}}_{\Phi }$, respectively. Conversely, the E_dep-averaged ${\overline{M_1^{C_2}}}_{\text{E}}$ agreed with results from track structure simulations within −2.9% ± 1.6% (1 standard deviation) in the plateau and from 3.3% ± 0.3% to 5.6% ± 1.9% (1 standard deviation) in the SOBP. For ${\overline{F_3^{C_2}}}_{\text{E}}$ differences as high as 1.7% ± 0.8% (1 standard deviation) in the plateau and from 1.3% ± 0.3 to 1.9% ± 0.4% (1 standard deviation) in the SOBP were found. For both ID quantities downstream of the SOBP, the highest differences were found, e.g., −11.5% ± 5.6% and −6.7% ± 2.3% at 11 cm depth for ${\overline{M_1^{C_2}}}_{\text{E}}$ and ${\overline{F_3^{C_2}}}_{\text{E}}$, respectively.

3.5. Clinical treatment plan calculations

Figure 6 shows the RBE-weighted dose distribution, see section 2.4, in the central axial plane and the dose-volume histograms for the contoured organs and target volume. Results were calculated with TOPAS for the proton plan and matRad for the carbon ion plan. Figures 7 and 8 show the corresponding spatial distributions of ${\overline{M_1^{C_2}}}_{\text{E}}$ and ${\overline{F_3^{C_2}}}_{\text{E}}$ for the proton and carbon-ion plans, respectively. For reference, normalized iso-dose lines from Figure 6 are shown in each image. For the proton plan, ${\overline{M_1^{C_2}}}_{\text{E}}$ was fairly uniformly distributed along the beam path. For the carbon-ion plan, both ID quantities were higher at points distal to the target in the beam direction. For ${\overline{F_3^{C_2}}}_{\text{E}}$, on the other hand, higher gradients are present for both protons and carbon ions in regions around the target and distal regions. In general, uniform ID was obtained in the tumor region but higher values were obtained in other structures, with ${\overline{F_3^{C_2}}}_{\text{E}}$ showing more pronounced gradients.

Figure 6.

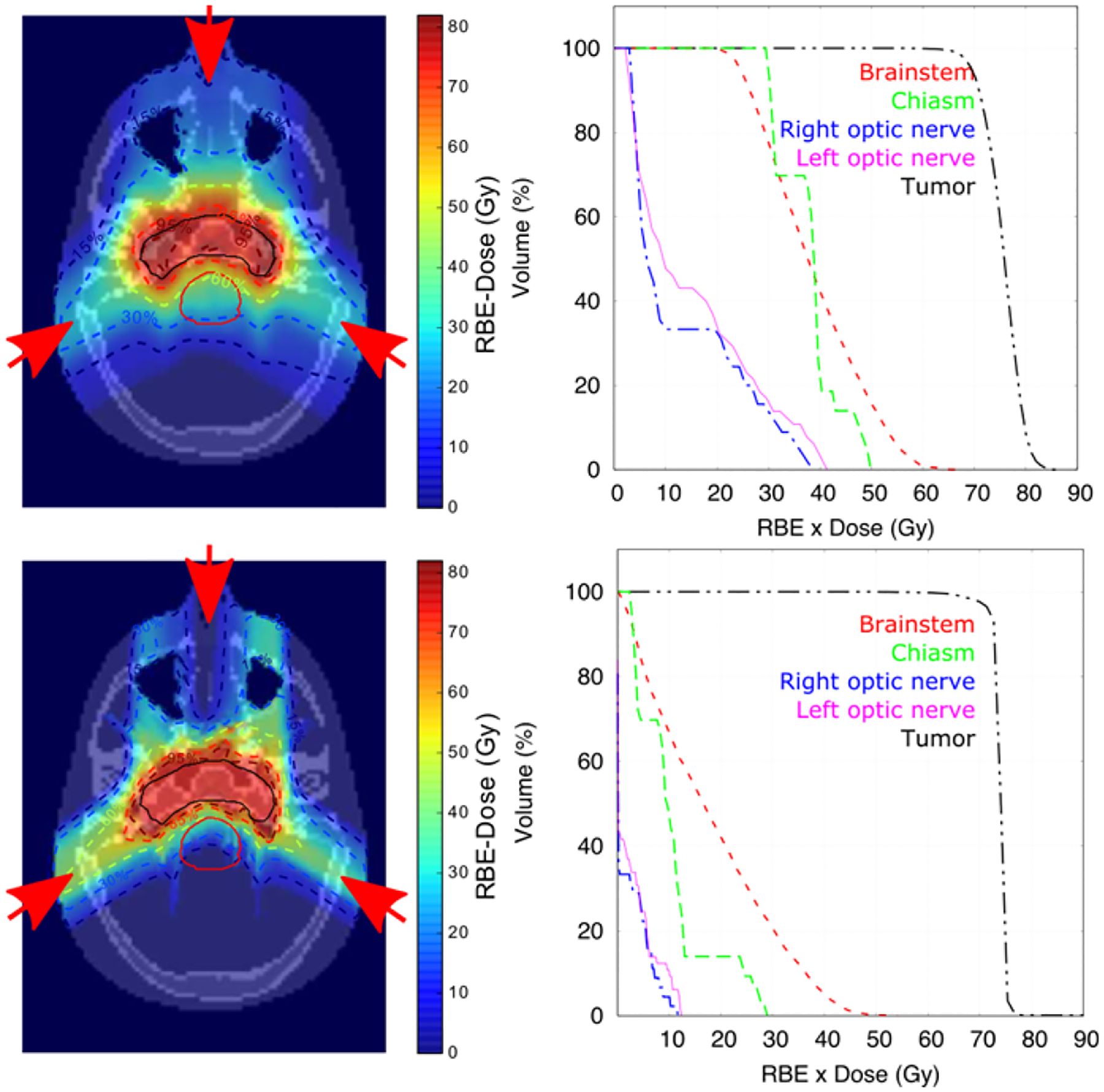
RBE-weighted dose distributions in central axial plane and dose volume histograms for a head IMPT plan for protons from TOPAS (top row) and carbon ions from MatRad (bottom row). Beam directions are shown by red arrows. Isodose lines are at 95%, 85%, 60%, 30% and 15% of the prescribed dose (dashed lines). Contours (solid lines) are drawn for the tumor (black) and brainstem (red).

Figure 7.

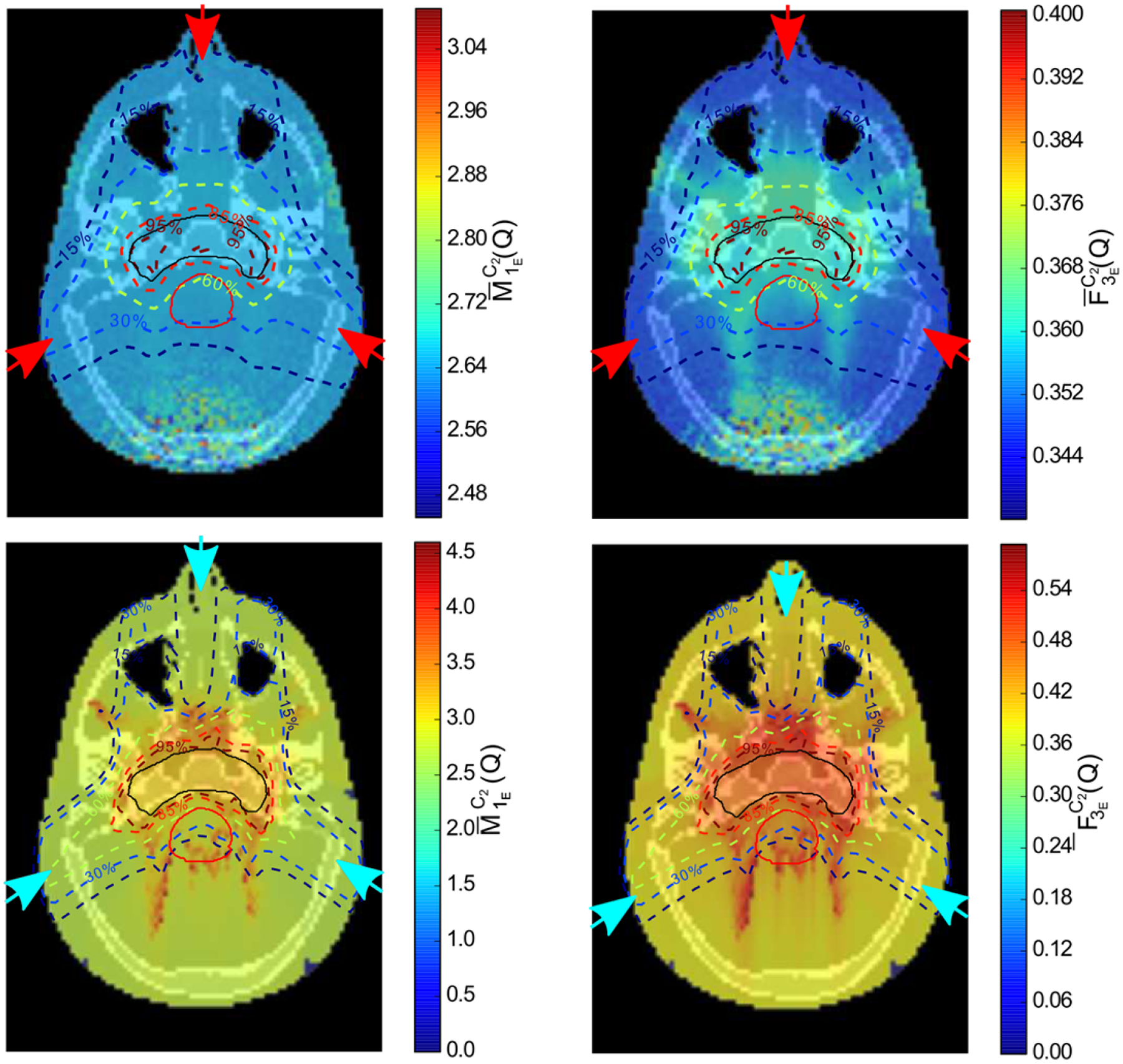
ID distributions of the proton plan (top row) and carbon ion plan (bottom row) through the central axial plane shown in figure 6 for ${\overline{M_1^{C_2}}}_{\text{E}}$ (left column) and ${\overline{F_3^{C_2}}}_{\text{E}}$ (right column). Isodose lines and contours are from figure 6.

Figure 8.

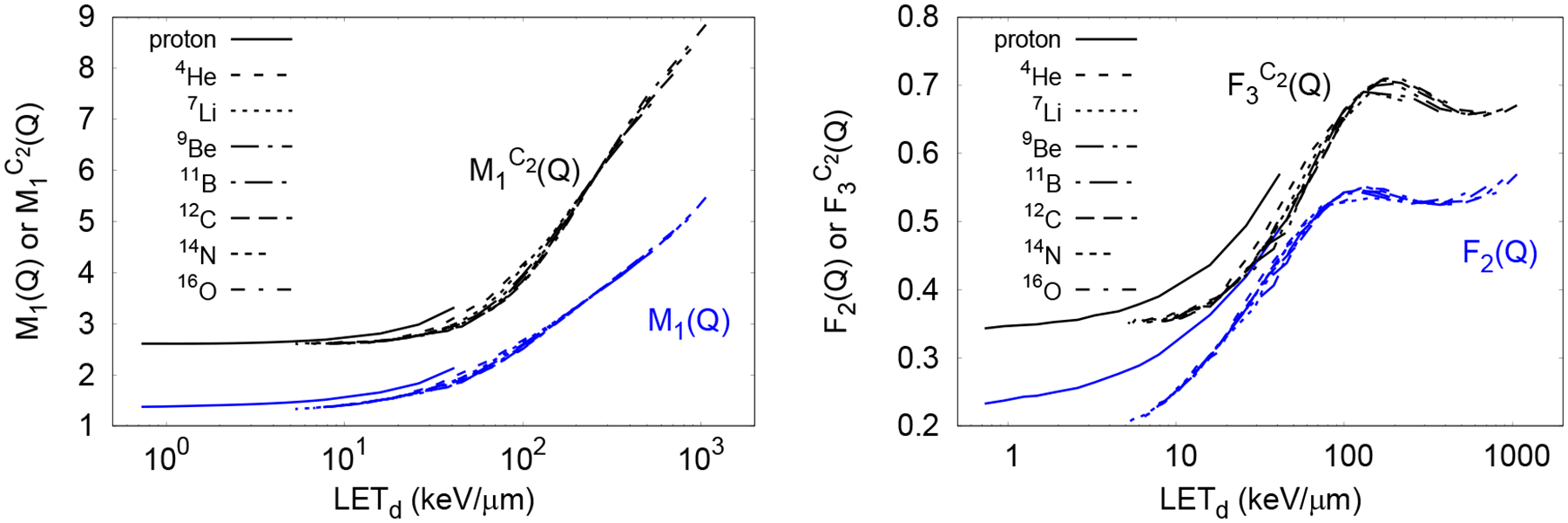
Nanodosimetric quantities M₁(Q), $M_1^{C_2}\left(Q\right)$ (left) and F₂(Q), $F_3^{C_2}\left(Q\right)$ (right) as a function of LET_d for ions up to ¹⁶O.

4. Discussion

In this work, variance reduction was used to generate an ID database with high precision for a variety of ions at a wide energy range of interest suitable for ID calculation in ion radiotherapy. The database for all energies and particles was calculated in a week of CPU time using 36 cores on 2.7–2.9 GHz Xeon CPUs. The ID database was used in simulations using the much faster condensed history MC method to obtain the spatial distribution of ID in patient-size geometries at millimeter voxel resolution typically used in radiotherapy. The fast technique developed in this work to estimate nanodosimetric quantities in patient geometries, offers an approach to facilitate the study of biological endpoints correlated with nanodosimetric quantities at the macroscopic level.

The method for fast calculation of E_dep-averaged ID approached the accuracy of full track structure simulations for the 2 test cases of clinical SOBP for proton and carbon ion beams, within statistical uncertainty for the proton case, and within the least restrictive of 3% and 3 standard deviations statistical uncertainty for the carbon ion case. In this way the calculation of ID distributions for particle radiotherapy in patients treated with clinical beams of protons and carbon ions was successfully demonstrated. The ID distributions can be performed in conjunction with the dose calculation using the condensed history MC method with negligible increase to calculation time. The success of this approach relied on limiting the energy loss along the step by limiting the maximum step size, such that the number of ionization along the step was approximately proportional to the energy loss in the step.

For the calculation of the ID database, the different sampling methods and geometries considered in this work had little impact on the methodology used for fast ID calculation in macroscopic volumes. Nonetheless, improvements in efficiency and accuracy were explored. In this work, the sampling process based on 1800 non-overlapping cylindrical volumes, which differs from the sampling process used in previous work where several million overlapping cylinders were overlaid on pre-calculated tracks (Alexander et al. 2015b). The use of overlap allows homogeneous sampling of the track segments, whereas the fixed discontinuous small-cylinder geometry used in this work (Figure 1), may lead to underscoring of larger ionization clusters, as shown in left side of Figure 3, where the data from (Alexander et al 2015a) whom used overlapping cylinders, has higher values of M₁(Q) that those calculated in this work with the source normal incident at a point. Nonetheless, being representative of a DNA structure (chromatin fiber) filled with randomly oriented non-overlapping DNA segments, was considered the preferred scoring geometry.

The source geometry influenced the mean cluster size of ionizations. Simulations with the source normally incident at a point produced clusters of larger mean ionization cluster size (M₁) than simulations with a spatially uniform source (figure 3). This can be explained as follows: with source particles normally incident at the endcap center, the length of the primary tracks within the cylindrical envelope were constant and equal to the length of the large cylinder. Whereas in spatially uniform irradiation, the cord length of primary tracks was randomly distributed and those tracks traversing relatively close to the edge of the cylindrical envelope had bias towards sampling the periphery of the track. The larger clusters of ionizations produced near the track core or produced by the primary tracks were thus sampled more frequently when the source was incident at the center of the endcap (see figure 2). Thus, the final averaged mean ionization cluster size was smaller with a spatially uniform source. A spatially uniform source was preferred as it is a more realistic representation of the irradiation of DNA structures in the cell.

The mean ionization cluster size increased monotonically with LET_D, as shown in figure 9. This previously reported performance, (see, for example, Alexander et al. 2015a; Bueno et al. 2015) was expected due to two factors: First, within the energy range of protons and ions considered in this work from Geant4-DNA (Incerti et al 2010, Francis et al 2011), the stopping power cross section increases with LET_D, producing more ionizations; Second, for a given ion type, at higher LET_D the maximum energy transferred to secondary electrons decreases (Francis et al 2011), producing more densely ionizing lower energy electrons. Therefore, the number of local ionizations density increases, resulting in larger ionization clusters.

Figure 9.

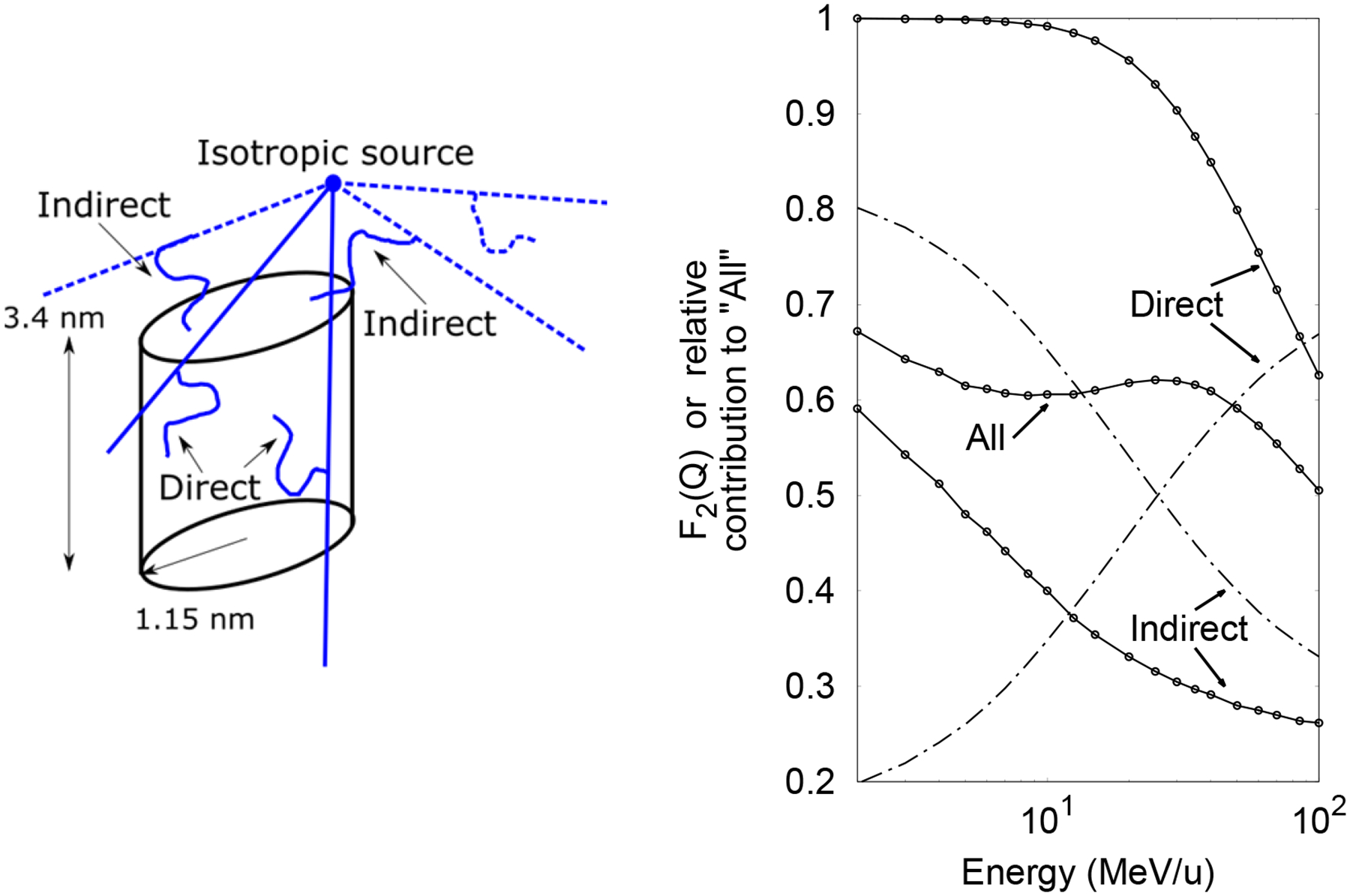
Left: Diagram of a cylinder of 1.15 nm radius and 3.4 nm length irradiated by an isotropic ion source 1 nm above the edge of the cylinder. Ionizations in the cylinder from delta-rays produced by ions that interacted in the cylinder (solid lines) constitute “Direct” interactions, whereas those produced by ions that missed the cylinder (dashed lines) constitute “Indirect” interactions. Right: Cumulative probability F₂(Q) as a function of the energy of “All”, “Direct” and “Indirect” interactions in the cylinder (points connected with solid lines). Relative contribution of the different interactions is also shown (dotted dashed lines).

The cumulative probabilities F₂(Q) and $F_3^{C_2}\left(Q\right)$ increased monotonically with the LET_D up to ~100 keV/μm and ~200 keV/μm, respectively, where they reached a broad, local peak before increasing again (see figure 9). Similar response of the yield of DSB as a function of the LET has been obtained with track-structure calculations (Friedland et al 2017). However, we believe that more simulated and measured data is required to reliably relate ID to any biological endpoint. Further investigation showed that this peak resulted from the combined contribution of primary ionizations and ionizations produced by secondary electrons in the small cylinders when the source particles did not intersect directly into the small scoring cylinders. To illustrate this phenomenon, a single small cylinder was irradiated by an isotropic oxygen-ion source positioned outside as shown in figure 9. In the following, “Direct” interactions correspond to all ionizations within the cylinder scored only if the primary ion traversed the cylinder. “Indirect” interactions correspond to all ionizations produced by secondary electrons only if the primary ion did not intersect the cylinder. ”All” interactions correspond to any event occurring in the cylinder. As seen in figure 9, F₂(Q) for the Direct interaction increases as the energy decreases (i.e. as LET increases) down to the saturation region at 10 MeV/u, whereas at high energies, F₂(Q) for the Indirect interaction increases slowly as the energy decreases and more rapidly at low energies. At high energies, the relative contribution of Direct interactions to All interactions is much higher than Indirect interactions as shown in figure 9 with dotted-dashed lines. Then the dependence of F₂(Q) on energy for All interactions is similar to that for the Direct interactions. As energy decreases, the relative contribution of Indirect interactions increases, exceeding the contribution of the Direct interactions at low energies. Then the dependence of F₂(Q) on energy in this region for All interactions is similar to that from Indirect interactions. The transition between the relative contributions of Direct and Indirect interaction produces the maximum in All at 25 MeV/u.

In this work, two weighting approaches using quantities commonly found in treatment planning systems were explored for fast calculation of averaged ID in mixing radiation fields. The approach used to retrieve ID distributions as a function of depth for normally incident SOBP beams is in much better agreement with full track structure simulations when computing E_dep-averaged ID, than fluence-averaged ID (figure 5). The difference, seen in both the plateau and SOBP for both protons and carbon ions, is most prominent in the carbon ion SOBP. This is explained as follows. Fluence is independent of the kinetic energy of the particle, unlike energy deposition. Thus two secondary particles having the same fluence are likely to have different kinetic energies (hence a different energy deposition), yet these two particles will have equal relative contribution using the fluence-averaged ID approach. Conversely, the energy loss along one condensed history step is proportional to the number of ionizations events through the mean energy to create an ion pair. Thus E_dep averaging correctly accounts for the relative contribution of each particle to $\overline{\text{ID}}$. In both cases, the averaged IDs distributions were independent of the range for production cuts for secondary electrons in the condensed history simulations with values ranging from 20 μm to 1 mm (results not shown). For the carbon ion results shown in figure 5, the macroscopic calculation of E_dep-averaged ID underestimated ID calculated from track structure simulations in the region distal to the SOBP. In the scoring with condensed history simulations, at the end of the SOBP and on the distal edge where the dose falls off steeply, the energy of track-end carbon ions and fragments changed significantly along the macroscopic (millimeter-sized) voxel. In this region large variations in ID (see figure 4) are expected to occur. However, in the track-structure simulations the scoring geometry is small enough to consider energy changes of ions negligible. Then, a better approach to track-length averaging may involve an integration of ID from the energy in the entrance to the energy at the exit of each voxel.

The computation of $\overline{ID}$ distributions in the patient geometry when using the condensed history Monte Carlo method for dose calculation only results in a small overhead. As the weighting approach folds the fluence with ID, most of the extra 8% CPU time was expended retrieving interpolated data from the ID database.

The calculated $\overline{ID}$ distributions of ${\overline{M_1^{C_2}}}_{\text{E}}$ and ${\overline{F_3^{C_2}}}_{\text{E}}$ for the clinical case considered here were fairly uniform across the tumor target but with higher inhomogeneity outside the target volume, for both proton and carbon-ion IMPT plans. This result is specific for the location and beam arrangement and does not preclude the possibility of larger variations in alternative plans for similar cases and plans for other treatment sites. Variations in $\overline{ID}$ across the target and normal tissue open the possibility of using $\overline{ID}$ distributions obtained with the technique developed in this work, with conventional dose calculation approaches to quickly calculate nanodosimetric quantities with sufficient accuracy to improve understanding of the relationship between the initial distribution of ionization and biological effect in clinical treatment fields, including the estimation of RBE or analogous quantities. An important clinical application may be in nanodosimetric-based IMPT optimization, for example, where nanodosimetric quantities are calculated as part of the dose calculation with minimal impact on computation time.

5. Conclusions

A highly precise database of nanodosimetric quantities has been calculated with MC track structure simulations for stable ions from proton to oxygen covering the energy range of importance for ion-beam radiotherapy. It was demonstrated that this ID database can be used for computation of nanodosimetric quantities using condensed-history MC simulations to calculate the spatial distributions of these quantities in patient treatment plans, with only minor increases of computation time for dose calculations and with an accuracy comparable to detailed track structure simulations. This approach allows for fast calculation of ID distributions in patients in routine treatment planning, which can potentially be used for optimization of biologically weighted dose in ion-beam radiotherapy without inferring RBE values.