Some (Fish Might) Like It Hot: Habitat Quality and Fish Growth from Past to Future Climates

Abstract

Current expectation is that projected climate change may have adverse effects on fish habitats and survival. The analysis leading to these concerns is typically done at large scale with limited possibility to quantify the local biological response and compare with previous conditions. Our research investigated the effects of recorded climate conditions on Chinook salmon (Oncorhynchus tshawytscha) spawning and rearing habitats and growth responses to the local climate and compared those conditions to predicted responses to a climate change. The study site was a 7 km long reach of Bear Valley Creek, an important spawning stream for this US Endangered Species Act listed species, in the Pacific Northwest of United States. We used 2D numerical modeling supported by accurate, high-resolution survey data to calculate flow hydraulics at various discharges from base to bankfull flows. For past and future conditions, computed flow hydraulics were combined with habitat suitability indices (SI) to compute spawning and rearing habitat suitability. Information on habitat suitability along with fish density and stream water temperature informed a growth model to quantify the potential fish size, an index of survival rates and fitness. Our results indicate that yearly-averaged rearing habitat quality remains similar to historic, but the timing of high- and low-quality habitat periods shift within the calendar year. Future spawning habitat quality may be significantly reduced during the seasonal period to which Chinook have currently adapted their spawning behavior. The growth model indicates an increase in anticipated size of Chinook salmon for predicted future climate conditions due to water temperature increase. Consequently, future climate conditions may have a substantial negative impact on spawning and limited impact on rearing conditions due to flow reduction and thus quality and extent of available habitat. However, the expected warmer stream water temperatures may benefit rearing, because of increased fish size in these high elevation streams.

INTRODUCTION

Current projections for climate change indicate that, over the next century, the Earth’s atmosphere will experience a warming trend (IPCC, 2014). In the Pacific Northwest (USA), air temperatures are predicted to rise 2 to 5 °C in th enext century from current temperatures (IPCC, 2014). Within the scientific community, it is accepted that at global and regional scales, this rise in air temperature has broad implications for seasonal and annual weather patterns, particularly precipitation and stream temperature (Isaak et al., 2018; Luce et al., 2013). By extension, climate change will also impact the ongoing habitat quality for a variety of stream species, both plant and animal (Isaak et al., 2010; Muñoz-Mas et al., 2016; Rieman et al., 2007; Santiago et al., 2017), because changes in hydrology will impact stream hydraulics, morphology and thermal regimes (Goode et al., 2013; Hamlet and Lettenmaier, 2007). What is less well understood are the biophysical responses to climate change by the various physical and habitat systems and by the species that reside within them. This is especially true when considering these responses at sub-region and local scales, because previous investigations have focused mainly on regional scales with stream segment and watershed resolutions at hundreds of meters and square kilometer (Battin et al., 2007; Rieman et al., 2007). For aquatic systems, the specific responses, both physical and biotic, depend substantially upon the local environment (Huntsman et al., 2018). High mountain headwater streams, for example, are highly morphologically heterogeneous (Montgomery and Buffington, 1998) and will almost certainly have a different physical response and biotic adaptation to regional climate change than would a low altitude river within the same geographic region.

The expected air temperature increases may have profound impact on the precipitation regime, which may result in changes in snowmelt peak intensity and timing, transition from snow-dominated to rain-snow systems, and more variable spring discharges (Barnett et al., 2005; Stewart, 2009). Change in precipitation and temperature patterns may impact hillslope processes, including wildfire and sediment delivered to streams (Goode et al., 2012). Large winter and extended spring discharges may increase scouring events of redds, the egg nest of salmonids placed within the streambed gravel, during the incubation period, which may disrupt egg survival. Similarly, these large spring discharges may mobilize fine sediments and clog or entomb salmon redds, potentially threatening the embryonic development (Maturana et al., 2013). Conversely lower summer flows may reduce spawning habitat, which could be further impaired by reduced fine flushing flows, by habitat fragmentation and shrinking and reduce stream-floodplain interaction.

Flow regime changes are expected to impact stream thermal regime, food availability and fish density. All these variables impact fish development and growth especially for rearing salmonids before migrating to the ocean (Crozier et al., 2010). It is expected that body size may have a significant effect on fish fitness as larger fish may have higher reproductive success, and lower mortality (Kingsolver and Huey, 2008; Sogard, 1997) than smaller conspecifics, although not necessarily higher potential of ocean migration success as shown from a large population study of Chinook salmon (Oncorhynchus tshawytscha) along the dam-regulated Columbia river basin (Zabel and Achord, 2004). Consequently, modeling the effects of flow hydraulics on fish habitat distribution and fish biological response is crucial for predicting the effect of climate change on fish habitat quality. Analysis of past climate change’s effect on fish could be an attractive approach to understand fish response. However, it requires past monitored data at a spatial and temporal resolutions that are difficult to attain if we aim to include variability at micro-habitat scale (meter or sub-meter scale). Since, in most cases, direct experimentation on climate change scenarios and the responses to those changes is virtually impossible, the primary tool for climate change research is numerical and statistical modeling (Rieman et al., 2007; Wenger et al., 2011). Aquatic habitat (suitability) models combine hydraulic and biological information (Tonina and Jorde, 2013) at different levels, from the popular correlative statistical models or suitability index based models (SI-based), like the instream flow incremental methodology, IFIM, (Bovee, 1978; Noack et al., 2013), bioenergetic (Fausch, 1984; Hayes et al., 2007; Wall et al., 2017, 2016) to individual-based models, IBM (Railsback et al., 2014, 2013, 1999; Railsback and Rose, 1999). Correlative statical models (Naman et al., 2019) relate hydraulic variables to habitat suitability indices (SI), mainly depth, velocity and substrate (Tonina and Jorde, 2013), but also temperature (Benjankar et al., 2019), scour and other variables, typically expressed as univariate curves or fuzzy logic derived indices, to quantify a species-life-stage-specific weighted usable areas (WUA) (Jorde et al., 2000; Noack et al., 2013). Although this approach has been widely criticized because of its lack of predictivity with fish abundance, WUA is actually an index of suitable habitat availability and not an index of fish abundance expect when fish are only limited by space, namely they are at carrying capacity (Hayes et al., 2016). Thus it cannot be related to fish fitness, although it has been reported to be effective in defining the habitat use when supported by accurate hydraulic information at the fish scale (Brown and Pasternack, 2009; Ghanem et al., 1996; Kammel et al., 2016; Le Pichon et al., 2009; Leclerc et al., 1995; Noack et al., 2013) with hydromorphological information predicted with two or three dimensional models (Tonina and Jorde, 2013). A key limitation of SI-based approach is WUA sensitivity to the suitability indices whose transferability among streams and seasons has been questioned because fish presence-absence depend also on food availability, intra- and inter-specific interactions, seasonality, and time of the survey and population and its site adaptation (Naman et al., 2020).

To address some of the limitation of SI-approach and account for the impact of food availability and thermal regime on fish growth, bioenergetic models have been proposed based on foraging models (Fausch, 1984). They estimate net rate of energy intake (NREI) as the difference between gross rate of energy intake, adjusted for losses to waste products and swimming costs (Fausch, 1984; Naman et al., 2020). Their key limitation is information on food availability, especially for drift-feeding salmonids, as drift may change spatially and temporally (Hayes et al., 2007). Whereas bioenergetic assessments resolve the problem of food and thermal regimes, they do not account for fish interaction and their dynamic behavior, which is addressed with individual-based salmon models (Railsback et al., 2013). An alternative approach to these behavioral models is the use of statistical growth models supported by information of habitat availability (Crozier et al., 2010). The statistical growth model is based on regression analysis of past information on fish size and environmental variables which may include habitat extent, population size stream water temperature to predict fish growth. The advantage of this latter approach is that it would not require information on food availability, which may be indirectly accounted into the regression model.

A common thread of all these approaches is their dependence on accurate morphological and hydraulic information, which should describe the fish environment at its micro-scale on reaches long enough to capture the natural variability of their habitat. Hydraulic information is typically predicted from numerical modeling. 1D modeling is insufficient to this task due to its limited ability to provide detailed flow and topographic information. (Ghanem et al., 1996) The situation has significantly improved with 2D or 3D flow models, whose hydraulic simulations can be used to provide spatially explicit habitat maps (e.g., Brown and Pasternack, 2009; Ghanem et al., 1996; Kammel et al., 2016; Leclerc et al., 1995). However, to take full advantage of 2D and 3D models, which can then represent usable habitat as geographically explicit patches, high-resolution bathymetric data is needed over longer reaches than it can be reasonably obtained using conventional surveying techniques (McKean et al., 2009). Past studies have limited in their extent, reach lengths that were on the order of 100 meters, by difficulties associated with obtaining detailed bathymetric data (Boavida et al., 2012; Brown and Pasternack, 2009; Crowder and Diplas, 2000; Leclerc et al., 1995; Li et al., 2015). Advances in surveying techniques has recently allowed segment (several km) and full (tens of km) river length habitat quality modeling (Carnie et al., 2015; Kammel et al., 2016; Tonina and McKean, 2010).

Despite the availability of these different ecohydraulic methods, previous research on climate change effects on fish habitat tended to be exclusively focused on either habitat hydraulics or on biological responses, with little crossover between the disciplines. Some notable studies, though, have incorporated both ecohydraulics and bioenergetics in their research methodologies. Jager et al. (1999) used a 1D flow supported PHABSIM model (SI-based approach) that was sub-divided into individual habitat units to create a quasi-2D model. This was coupled with an individual-based trout population model to simulate the effects of climate change driven temperature and flow fluctuations on population mortality and persistence in the North Middle-Fork of the Tule River, a Sierra Nevada stream in California. Van De Wolfshaar et al. (2010) used a 2D hydrodynamic model and a spatially explicit habitat model, combined in a GIS-type analysis, to investigate the effect of stream temperatures on the spawning behaviors and young-of-year (YOY) densities of roach (Rutilus rutilus), pikeperch (Sander lucioperca), bream (Abramis brama) and bleak (Alburnus alburnus) fish species in floodplain areas of the River Waal, Netherlands. Their study considered only the floodplains and not the main channel of the river. Habitat areas were defined from biological surveys and not from the hydraulic modeling itself. Yates et al. (2008) used the WEP21 water resource management program to investigate the effects of climate change induced stream temperature increases and dam operation on the Sacramento River in California’s Central Valley on the spawning and rearing productivity of Chinook salmon. Thompson et al. (2012) used climate projections from six General Circulation Models (GCM), for the period 2010 – 2099, as input into the WEAP model to project steam flows and temperatures in Butte Creek, California. These projected values were then used as inputs to SALMOD (Bartholow et al., 1997), a spatially explicit salmon population-dynamics model to predict the survivability of spring-run Chinook salmon populations. Because the hydraulics models used in the Yates and Thompson studies were one-dimensional, neither study incorporated spatially explicit hydraulics in their projections.

In the present study, we leveraged the advances in remote sensing and numerical hydraulic modeling to investigate the seasonal aquatic habitat quality variability for spawning and rearing activities of Chinook salmon under historic and future climate conditions. Our goal was to understand the impact of climate variability on fish fitness, which is approximated by fish size (Crozier et al., 2010; Lomnicki, 1988), to better constrain and interpret the prediction of aquatic habitat changes. To address our goal, we developed a scalable approach that combines ecohydraulic modeling, supported by high resolution topobathymetric information, with a statistical growth model to quantify future fish fitness. We applied it to an important Chinook salmon spawning and rearing stream, Bear Valley Creek (Idaho, USA), to model fish growth from the early 1900 to the end of the current century. We used a spatially explicit, high-resolution, SI-based, 2D ecohydraulic model supported by a meter scale bathymetry, to predict spawning and rearing habitat availability for past and future hydrological and thermal conditions predicted through several scenarios downscaled with the Variable Infiltration Capacity (VIC) climate change model (Liang et al., 1994). We then coupled the ecohydraulic model with the statistical growth model, which accounted for redd productivity with respect to fry survival to predict growth potential from past to future climate.

MATERIAL AND METHODS

STUDY SITE

Bear Valley Creek is a tributary to the Middle Fork of the Salmon River (Idaho, USA) with mean watershed elevation of 2,152 m (Figure 1) (Carnie et al., 2015; Gariglio et al., 2013; McKean and Tonina, 2013). It is a highly sinuous stream (sinuosity index: 1.5) that meanders across glacially carved valley floors connected by narrow canyons. The 7.4 km study reach (same as Carnie et al. (2015)) has a mean bankfull width of approximately 15 m and a mean streambed slope of approximately 0.0035 m m⁻¹ (Gariglio et al., 2013). Streambed material is characterized primarily by gravel with median grain size, D₅₀, of 0.052 m with patches of sand distributed throughout (Maturana et al., 2013; McKean and Tonina, 2013).

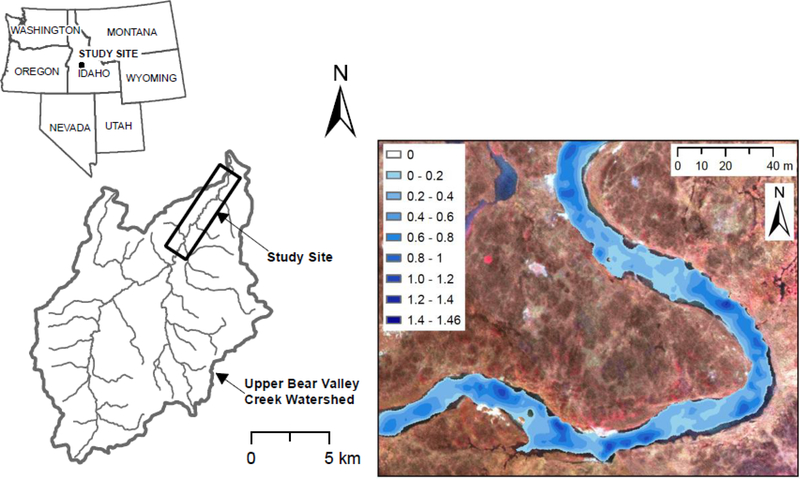
Figure 1:

(Left) The Bear Valley Creek study site encompassing approximately 7.4 km of relatively pristine, high mountain meadow, gravel bed spawning and rear habitat for Chinook salmon and other salmonid species, in Central Idaho. (Right) The 2D hydrodynamic model predicts hydraulic and habit characteristics with a high degree of spatial and geographic specificity. In this view, water depth profiles at a 1-meter spatial resolution are shown geolocated for a small portion of the Bear Valley study site. Predictions, at the same resolution, were also created for flow velocity, water surface elevation, shear stress and hydraulic habitat suitability.

The hydrograph is typical of a snowmelt dominated system with peak flow occurring during the melt season (April to June). Base flows occur for the remainder of the year (McKean and Tonina, 2013). The current base flows for Bear Valley Creek are observed in the late summer or early fall (August to September) and average approximately 1 m³ s⁻¹. Snowmelt bankfull flows for Bear Valley Creek average approximately 7.0 m³ s⁻¹.

Spring-run Chinook salmon spawn in Bear Valley Creek each year between late July and early September. Salmonid species lay and incubate their eggs in the streambed sediment in egg nests called redds (Tonina and Buffington, 2009). The rearing life cycle stage begins the following spring as fry emerge from their redds. The hatchling Chinook rear in the relatively still waters of side channels and main channel margins for 1 to 2 years before migrating to the Pacific Ocean (Isaak et al., 2007).

Although the system appears natural, as for many meadow systems in the Pacific Northwest, it had mining operation in its headwaters between 1956 and 1959, which may have impaired sediment transport, and livestock grazing, from sheep bands till 1920 and cattle afterwards. Cattle management started to be regulated for protecting aquatic habitat as early as the 1960, till it was entirely closed in 2001 (Platts and Nelson, 1975; Stone, 2015). Past timber harvest practice, grazing and recreational activities, mainly hunting, camping, canoeing, and kayaking, along with grazing supported the development of forest roads along the stream from its confluence with Elk Creek, downstream of the study site, to its headwaters.

METHODS

We downscaled 3 future climate scenarios, A1B, B1 and Ensemble Mean (EM) climate, predicted by the Global Climate Models (GCMs) in the Fourth Assessment Report AR4 of IPCC (IPCC, 2007) with VIC macro-scale hydrologic model (Liang et al., 1994). Hydrological and air temperature data along with spawning and rearing suitability indices were used as input variables for 2D hydraulic, aquatic habitat and fish growth modeling for Chinook salmon to study the change in aquatic habitat quality and fish size (as a surrogate for fitness) under observed past and predicted future climate conditions. Each numerical model, VIC, 2D hydraulic and aquatic habitat model, was validated with measured data.

Historical hydrograph reconstruction

We used more than one gage station for hydrograph reconstruction because there is no permanent gage station at the study site. The nearest gauge is approximately 12 km downstream of the study site (USGS gauge 13309000: Bear Valley Creek near Cape Horn, Idaho), which was decommissioned in 1960. The additional gauge (USGS 13295000: Valley Creek at Stanley, Idaho) was used to reconstruct flows at the Bear Valley Creek gauge and to extend its period of record (Carnie et al., 2015). These two gauges are close to each other (36 km) and their watershed characteristics are similar (Table 1). Following previous works in the same study site (McKean and Tonina, 2013), we used linear regression analysis between Bear Valley Creek and Valley Creek mean monthly discharges for the overlapping period of record (WY 1929 through WY 1960). To improved predictions instead of one liner model, we quantified monthly correlation coefficients, whose time series analysis did not show any trend, and which were used to estimate the Bear Valley Creek discharge for the ungaged historic period from Valley Creek discharges. These coefficients were kept constant through the historic period, with the assumption that changes in climate between 1960 and 2010 would have similar effects in both watersheds.

Table 1:

Bear Valley Creek and Valley Creek USGS gauge summary information.

Gauge ID	Gauge Name	Period of Record	Watershed Area (km2)	Mean Basin Elevation (m)
13309000	Bear Valley Creek near Cape Horn, Idaho	1921 – 1928 (summer months) WY 1929 – WY 1960	443	2,146
13295000	Valley Creek near Stanley, Idaho	June 1911 – October 1913 May 1921 – November 1971 May 1972 – September 1972 WY 1993 – WY 2010	381	2,256

After reconstructing the Bear Valley Creek gauge, a basin-area scaling factor was used to compute the monthly discharge at the study site. The same basin-area scaling factor was applied to future hydrograph predictions from the VIC modeling. Verification of the method with several measured daily discharges between 2006 and 2011 showed error within 10% of the measured discharge (Figure S1 supporting material) (McKean and Tonina, 2013). We used monthly and not daily discharges because monthly values should be more robust values than daily in future climate.

Future hydrograph reconstruction

Climate change modeling:

To evaluate the impacts of climate changes on hydrology and air temperature, statistically downscaled meteorological data from Global Climate Models (GCMs) in the Fourth Assessment Report AR4 of IPCC (IPCC, 2007) was used. IPCC Data Distribution Center provides simulation results from 24 GCMs for the 21st Century divided into six emission groups (A1F, A1B, A1T, A2, B1, and B2) drawn from four families of alternative energy technology development, one group each in A2, B1, B2, and three groups within the A1 family. Additionally, they provide the ensemble mean, EM, scenario, which is the predictions based on the mean of all 24 scenarios. Among the 24 GCMs, the A1B and B1 are those typically modeled because considered the most likely to occur. The A1B scenario represents a medium emissions scenario associated with increasing greenhouse gases through the end of the 21st century. The B1 scenario reflects significant greenhouse gas mitigation, which begins to stabilize greenhouse gas concentrations by the end of the 21st century (Mote and Salathé, 2010). Thus, the A1B and B1 emissions scenarios were selected for use in this study along with the ensemble mean scenario EM, which weights the effect of all 24 scenarios.

VIC model

The comprehensive hydrologic databases (historical and future) produced for the study area are based upon simulations using the VIC macro-scale hydrologic model (Liang et al., 1994) implemented at 1/16th degree resolution. The VIC model is a macro scale, grid-based water and energy balance model, which has been successfully applied to many large river basins with practical results (Abdulla et al., 1996; Maurer et al., 2002; Tang and Piechota, 2009). Distinguishing features of the VIC model include the sub grid variability in soil moisture, land surface vegetation, precipitation, and topography in use of the elevation bands. Surface runoff was generated in the upper two layers by a variable infiltration curve, and base flow was produced from the bottom layer (Todini, 1996).

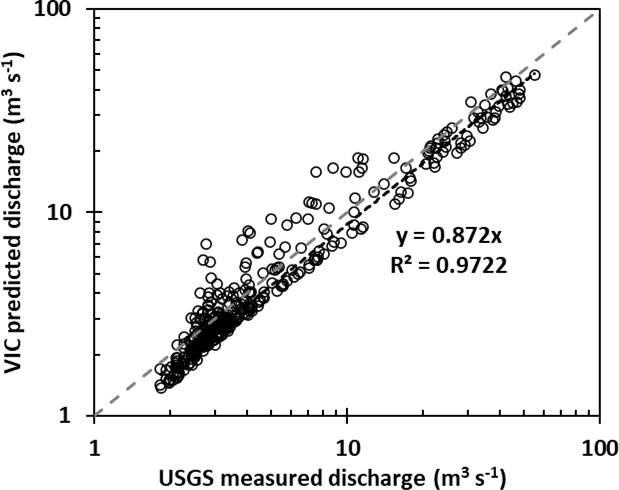
VIC model was validated by comparing observed and simulated monthly average flows for the Bear Valley Creek near Cape Horn USGS gauge (13309000). Model results for January 1931 through December 1959 (n = 348) have good performance with a high R² value and the near unit regression slope (Figure 2). The VIC hydrology model slightly under predicted flow magnitude, but the overall fit between modeled and observed flows is good over the range of flows experienced in Bear Valley Creek.

Figure 2:

Observed (USGS) v. predicted (VIC) monthly discharge for Bear Valley Creek. Dashed 1:1 line represents line of perfect agreement. Trend line fit to data demonstrates slight under prediction of flows using VIC model, although across the range of flows the system behavior is represented quite well.

Data Collection

To obtain the detailed topographic data needed for a 2D hydraulic model of the study site, the terrestrial-bathymetric Experimental Advanced Airborne Research LiDAR (EAARL) was flown over Bear Valley Creek in October 2007 (Carnie et al., 2015). The EAARL is a low power, narrow beam, high pulse frequency, green laser that record reflected energy from both terrestrial and submerged streambed topography (McKean et al., 2009). It is a topobathymetric LiDAR which simultaneously maps submerged (e.g., streambeds) and emerged (e.g., floodplain) topographies. The horizontal spacing of the EAARL points collected for Bear Valley Creek was approximately 2 m with a vertical uncertainty of ±13 cm RMSE (McKean et al., 2014). Sensitivity analysis on the effects of this uncertainty on 2D numerical modeling showed that they have negligible effects on hydraulic modeling results (McKean et al., 2014).

Field data also include a map of 249 surveyed patches of homogenous substrate size and sand percent cover for the entire study site (Carnie et al., 2015). The observed substrate grain sizes range from 2 to 305 mm with sand fraction ranging from 0 to 100%. Sand percentages were grouped into four categories that include: greater than 75% (A), 50–75% (B), 30–50% (C) and less than 30% (D) (Table 2). Patch boundaries for grain size and sand coverage were used for the habitat modeling and to define spatially variable streambed roughness (Legleiter et al., 2011). Previous research demonstrated that river morphology is stable (McKean and Tonina, 2013) as are grain size patch locations (Maturana et al., 2013), we also analyzed sediment mobility based on predicted shear stresses between low and bankfull discharges (supporting information).

Table 2:

Parameter estimates and summary statistics for multiple regression models of Chinook salmon juvenile growth.

Model	Predictors	b (SE)	p-value	t	r2
1	Intercept	−73.56 (58.89)	0.24	−1.24	0.84
	T	5.22 (5.34)	0.35	0.98
	D	−21.21 (33.80)	0.54	−0.63
	T × D	1.41 (2.50)	0.58	0.56
	J	0.29 (0.17)	0.12	1.66
2	Intercept	−47.34 (34.91)	0.20	−1.35	0.83
	T	2.31 (1.20)	0.10	1.77
	D	−2.19 (0.84)	0.02	−2.61
	J	0.36 (0.13)	0.02	2.69
3	Intercept	−5.22 (27.7)	0.85	−0.40	0.78
	D	−2.37 (0.9)	0.02	−2.67
	J	0.30 (0.139)	0.05	2.15
4	Intercept	−101 (34.39)	0.012	−2.94	0.72
	T	2.73 (1.58)	0.11	1.73
	J	0.61 (0.10)	< 0.01	5.57
5	Intercept	−18.09 (403.6)	0.96	−0.045	0.84
	T2	0.31 (2.27)	0.89	0.13
	T	−314 (60.47)	0.89	−0.05
	D	−20.84 (35.69)	0.57	−0.58
	T × D	1.38 (2.64)	0.61	0.52
	J	0.29 (0.18)	0.15	1.57
6	Intercept	−23.85 (380.8)	0.95	0.063	0.83
	T2	0.41 (2.18)	0.85	0.18
	T	−8.46 (57.39)	0.88	−0.14
	D	−2.21 (0.89)	0.03	−2.49
	J	0.35 (0.13)	0.029	2.54

Hydraulic modeling

The USGS Multi-Dimensional Surface Water Modeling Systems, MD-SWMS (now iRIC), was selected to perform 2D hydraulic modeling and to quantify the habitat quality at each cell (Nelson et al., 2016). MD-SWMS uses the Flow and Sediment Transport Morphological Evolution of Channels (FaSTMECH) model, which solves the Reynolds Averaged Navier-Stokes (RANS) equations on a curvilinear grid (with s and n the longitudinal and transverse coordinates) with a finite element difference method (McDonald et al., 2005). The model requires selection of two parameters, which may be spatially and discharge dependent: the lateral eddy viscosity, v_t, and a drag coefficient (roughness coefficient), C_d. We used the validated model of Carnie et al. (2015), who adopted a spatially varying C_d (s, n) as a function of the local median grain size, d₅₀, and mean depth h, $C_d(s,n)={\int }_{z_0\left(s,n\right)}^{h\left(s,n\right)}f(z,z_o)dz$, with z₀ = a d₅₀, z the vertical coordinate and f the logarithmic velocity vertical profile. Carnie et al. (2015) calibrated the model on a 1.6 km long sub-reach of our study site selecting v_t = 0.05m²/s and a=0.15 for a low discharge of Q=1 m³/s. Sensitivity analysis showed negligible change in velocity and water surface elevation distribution by varying v_t ± 50%, so this parameter was kept spatially and discharge constant (McKean et al., 2014). Then the model was validated by comparing its predictions with water surface elevation surveyed over the entire study site at a discharge of 1.6 m³ s⁻¹ and velocity measured at 2 cross-sections in the middle of the study site for a discharge of 1 m³ s⁻¹. This comparison reported water surface elevation (RMSE=0.054 m and regression line with slope of 1 and R²=0.99) and velocity (RMSE=0.06 m s⁻¹ and regression line with slope of 0.92 and R²=0.84) root mean square errors and R² within the range reported in literature (Tonina and Jorde, 2013). Flow conditions for the calibration and validation discharges were highly spatially heterogeneous in this meandering pool-riffle system (Figure 1) with depths and velocities ranging between as 0.01 – 1.62 m (mean = 0.32 m) and velocities 0 – 1.4 m s⁻¹ (mean = 0.25 m s⁻¹) at Q=1 m³ s⁻¹ and 0.01 – 1.73 m (mean = 0.35 m) and velocities 0.0 – 1.73 m s⁻¹ (mean = 0.35 m s⁻¹) at Q=1.6 m³ s⁻¹. The hydraulic modeling results provided a detailed mosaic of depth, velocity, shear stress, and other hydraulic parameters on a scale that delineated within-channel habitat suitability for Chinook salmon spawning and rearing activities, as exemplified in Figure 1.

Habitat modeling

Hydraulic habitat quality was modeled for both spawning and rearing life stages of Chinook salmon with suitability indices (Bjornn and Reiser, 1991; Hampton, 1988; Tonina and McKean, 2010) (Figure S1). We used the SI-based approach to constrain the available habitat expressed as streambed wetted area to its spatial extent with physical conditions, e.g., substrate, velocity, and depth, within those used by Chinook salmon, so not as an index of fish abundance or fitness. This use may minimize the limitations reported by others on food availability, among and intra species dynamic (Orth, 1987). Spawning habitat quality was modeled with univariate suitability indices for water depth, flow velocity, sand coverage and substrate grain size and rearing habitat quality with suitability indices for depth and velocity (Figure S1). The geometric mean method was used to define a cell habitat quality, CSI, as a combined value from each single suitability index (Vadas and Orth, 2001):

$${CSI}_i={\left(\prod _l{SI}_i\right)}^{1/l}$$ (1)

where SI indicates the suitability index of the i-th predictor and l the number of predictors; l is equal of 4 and 2 for spawning and rearing habitats. The habitat quality for the entire study site was then estimated using two parameters: Weighted Usable Area (WUA) and Hydraulic Habitat Suitability (HHS) as follows (Bovee, 1982):

$$\begin{gathered} WUA=\sum _{i=1}^{NC}{\mathit{CSI}}_i{A}_i \\ HHS=\frac{WUA}{A_W} \end{gathered}$$ (2)

where NC is the number of cells within the wetted area A_w of the stream and A_i is the area of the i-th cell. Both parameters, which are function of discharge, provide information on the global quality of the habitat at the reach scale. Whereas WUA depends on the size of the stream its normalized value, HHS, is expected to be used to compare aquatic habitat quality among reaches of different sizes. Rating curves for WUA and HHS values for both Chinook spawning and rearing life stages were derived for flow rates between 0.5 and 7 m³/s using regression analysis of simultated flows from 1 to 7 m³/s at 1 m³/s increments. Flow greater than the bankfull condition of 7 m³/s were not included because the scope of this study is limited to hydraulic conditions within the channel.

Carnie et al. (2015) tested the performance of the aquatic habitat model by comparing habitat quality patch prediction with 29 surveyed redd locations mapped in Bear Valley Creek in fall 2005 along our study site. Redd locations have horizontal precision of approximately 0.3–0.5 m, which is comparable to our spatial resolution. Comparison between model predicted spawning habitat patches and redd location showed that 24 of the surveyed redds were located within the model-predicted, high-quality patches (CSI>0.8) and the rest of the surveyed redds in the second-best quality (CSI>0.6) class. This suggests that our biological model accurately predicts habitat quality used by spawning salmonids.

Fish growth model

Data on aquatic habitat quality for juvenile Chinook rearing estimates were used in a multiple regression model that predicted inter-annual variation in juvenile Chinook salmon length (Figure 3). We based our model on a form used previously by Crozier et al. (2010) in which modal fish length for a summer was predicted as:

$$Y=b_0+b_{1}D+b_{2}T+b_{3}J+b_{4}DxT+\epsilon$$ (3)

where: Y = fish length, b₀ = Y-intercept, b₁ = parameter estimate associated with fish density (D, expressed as ln (parr density)), b₂ = parameter estimate associated with stream temperature (T), b₃ = parameter estimate associated with Julian Day (J), b₄ = parameter estimate associated with the interaction between density and temperature (DxT) and ε = residual error (Table 2). In this high elevation meadows, it is unlikely that historic stream water temperatures even in warm years exceeded the optimum range (as shown in Crozier et al., 2010) and stream water temperature are sufficiently high (higher than 17.8 C) to reduce growth and survival in this systems (Maret et al., 2005). To explore this possibility, we added two additional models with a quadratic temperature term, one with the interaction term T x D,

$$Y=b_0+b_{1}D+b_{2}T+b_{2,2}{T}^2+b_{3}J+b_{4}DxT+\epsilon$$ (4)

and without.

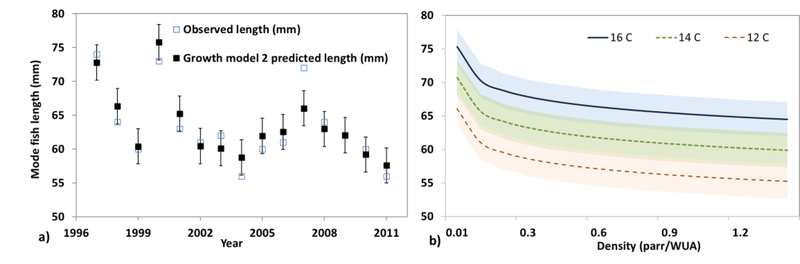
Figure 3:

(a) Observed and predicted Chinook salmon juvenile length from 1997 – 2011 based on growth model 2 with density, temperature, and Julian day as predictors and with bars showing standard error on predictions. (b) Response curves from regression model 2 for Chinook mode length with bands of standard errors for 3 mean summer stream water temperatures as a function of parr density.

Length of juvenile salmon in this reach of Bear Valley from 1997 – 2011 were obtained from a long-term monitoring program (Achord et al., 2007). Fish collection and PIT-tagging began in late July and ended in early August for each year. Thus, Julian day was included as a predictor in the model to adjust for nuisance variation associated with interannual differences in dates that fish lengths were recorded (Crozier et al., 2010). We quantified juvenile density by dividing the number of Chinook salmon redds from the previous fall (n_redds) (redds are counted each year in this reach (Isaak et al., 2007)) by the WUA estimate the following summer, WUA_s. We assumed that each redd contained 5,594 eggs, n_e, (expressing female fecundity) and that survival was s_h= 3.9% from eggs to parr, such the density is quantified as D= ln (s_h s_e n_r/WUA_s) (noticed that D as the natural log). Conversely from Crozier et al. (2010) who used the mean temperatures from April (hatching period) until September, we used mean summer temperature between July 15^th to September 15^th because of their availability from the NorWeST website (Isaak et al., 2017), which hosts a regional stream temperature database and climate scenarios for historical summer periods for streams across the Northwest U.S. (Isaak et al., 2017). Stream water temperatures were recorded between July 15th and September 15th (summer period) for 46 years at 18 unique sites (some sites sampled more than one summer) on this reach of Bear Valley Creek. These data were used to calibrate the NorWeST model and derive historical scenarios (for years when measurements are not available). We used this collected data along with daily mean air temperature, T_air, information and stream discharge to develop a linear regression equation to predict daily mean stream water temperature, T_stream, during the summer from air temperature and flow discharge:

$$T_{stream}=0.4166T_{air}-0.0598Q+7.449(r^2=0.79;p<0.05)$$ (5)

with unit of degree Celsius for temperature and discharge in m³ s⁻¹. We also used this equation to predict stream water temperature from climate change modeled air temperature predictions and in-stream flows from the VIC model.

The fully parameterized form, model 1 (equation 3), of the fish growth model was compared to 3 additional forms with reduced sets of predictors (Table 2) as some parameters may not be important. The relative performance among models was assessed based on Akaike’s Information Criterion (AIC) corrected for small sample size (Table 3). The final model was used to develop response curves showing fish length relative to temperature and density and to compare fish lengths between the historical and future scenarios.

Table 3:

Model selection results for multiple regressions predicting juvenile Chinook salmon modal length each August from 1997–2011 in Bear Valley Creek, Idaho.

Model	Predictor Variables	p	ΔAICc	AIC weight (wi)	Evidence ratio (wI/wi)	r2
1	T + D + T*D +J	5	1.53	0.1910	0.46	0.84
2	T + D + J	4	0	0.4005	1	0.83
3	D + J	3	1.75	0.1712	0.41	0.78
4	T + J	3	5.23	0.0366	0.07	0.72
5	T2 + T + D + D*T + J	6	3.49	0.0693	0.17	0.84
6	T2 + T + D + J	5	1.95	0.1507	0.37	0.83

Notes: 1) models are ranked from most plausible to least plausible based ΔAIC_c. (0.00 = most plausible model).

2) p = number of parameters in model.

3) Ratio of Akaike weights (wI/wi) indicates the plausibility of the best fitting model (wI) compared to other models (wi). So, for example, the best model is x times more plausible than the worst model in this set.

4) All models include a parameter for Julian day to control for inter-annual differences in fish tagging date that caused variation in fish length.

Habitat conditions for the historical scenario were quantified by applying the climate change and hydrological models during the historic period from 1929– 2010. Habitat conditions in the future scenario came from the global recirculation climate change and VIC models for the scenario A1, A1B and EM. For the response curves and scenarios, fish densities were calculated over a range of redd numbers (10 – 500) and assuming the same female fecundity n_e, and survival rates as described above for 3 mean stream water summer temperatures. The fecundity, n_e, and survival rates, s_h, may change with spawning fitness, e.g., n_e may increase with spawner size, and embryonic development, depending on interstitial flow conditions (Martin et al., 2017), which we assume remain constant. However, clogging by fines or scouring of redds by high winter discharges may reduce s_h value.

RESULTS

Climate modeling and hydrology

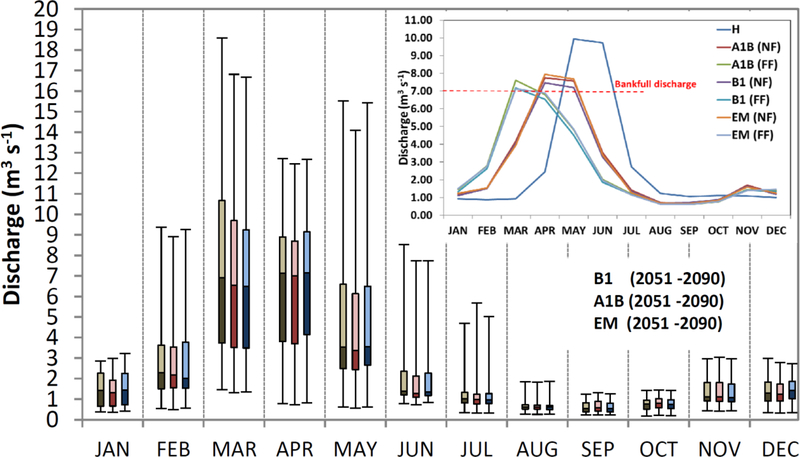
During the near future period (NF, 2011–2050), mean monthly discharge is predicted to increase for all months from November through the following April, for all climate scenarios (A1B Table S1, B1 Table S2, EM Table S3) compared to historic stream hydrology (Table S4). Decreases in mean monthly discharge are predicted during the May – October months for all scenarios. Peak snowmelt flows for all climate scenarios are predicted to occur in April or May, as opposed to the historical peak discharges observed during May or June (c.f., Table S4 with Table S1, Table S2, and Table S3). The magnitude of peak discharges is predicted to decrease for all climate scenarios (average monthly peak discharges ranging from 7.5 m³ s⁻¹ for B1 in April to 7.9 m³ s⁻¹ for EM in April) compared to the historical observations (average monthly peak discharge of 9.9 m³ s⁻¹ in May). Far Future (FF, 2051–2090) climate scenarios also predict lower base flows during the August to October months (minimum average monthly flow of 0.67 m³ s⁻¹ for A1B in September) compared to historical observations (minimum average monthly flow of 1.1 m³ s⁻¹ in September). Variability in mean monthly flows is predicted to be greater during the months of November – May for all climate scenarios compared to the historical flow observations. Decreased variability in mean monthly flows is predicted during the months of June – August for all climate scenarios compared to historical flow observations. Variability during September and October is similar between the climate scenarios and historical observations.

During the FF period, mean monthly discharge is predicted to increase during the November – April months for all climate scenarios (Tables S1–S4). Decreases in mean monthly discharge are predicted during the May – October months for all climate scenarios, matching the pattern observed for the NF time window. Peak snowmelt flows are shifted earlier in the year when compared to the NF predictions and historical observations. Peak snowmelt flows are predicted to occur in March or April, which is much earlier than the historical observation of peak flows occurring in May or June. Similar to the NF time window, mean peak discharges are predicted to decrease for all climate scenarios (average monthly peak discharges ranging from 7.1 m³ s⁻¹ for EM and B1 in March to 7.6 m³ s⁻¹ for A1B in March) compared to the historical observations (average monthly peak discharge of 9.9 m³ s⁻¹ in May). Lower base flows during August to October were again predicted during the FF time window and match the pattern that was observed for the NF predictions. Variability in mean monthly flows is predicted to be greater during the months of November – April for all climate scenarios compared to the historical flow observations. Decreased variability in mean monthly discharges is predicted during the months of June – August, again matching the pattern observed for the NF time window when comparing to historical observations. Variability during the May and September – October months was similar for the FF time window compared to historical observations.

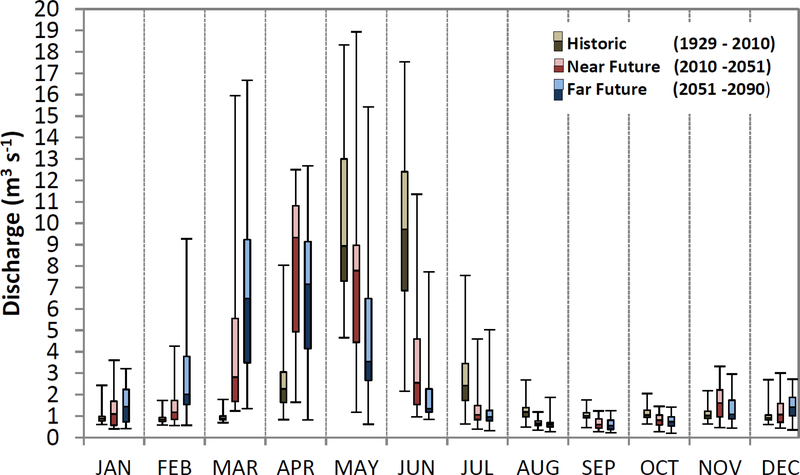
Compared to the historical hydrograph, all climate scenarios predict increased mean flows during the months of January, February, March, April, November, and December for both the NF and FF periods as exemplified by Figure 5 for the EM case. The reduction of high flows near bankfull discharge, 7 m³ s⁻¹, indicates that flooding of the meadow plain will be much reduced spatially in extent and water depths and nearly 50% temporally, from 2 months of current conditions to 1 month in FF.

Figure 5:

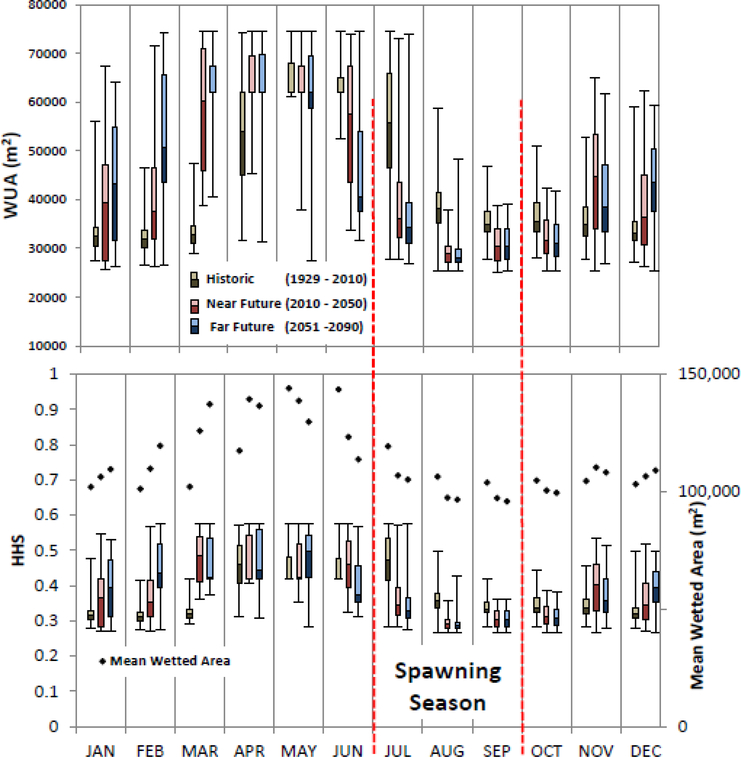
Box-and-whiskers plot of monthly discharges for historical (H; 1929–2010, left whisker in each month, brown hues), near future (NF; 2011–2050, center whisker, red hues), and far future (FF; 2051–2090, right whisker, blue hues). Future scenarios are for the ensemble climate, EM, scenario. Box gradations represent the 25, 50 and 75^th percentiles. Whisker extents represent the maximum and minimum observed values.

Habitat modeling results

All of the examined climate change scenarios have similar effects on rearing HHS and wetted areas and consequently on WUA for the entire water years (Supplementary Information Figure S4). Consequently, we focus only on the EM climate scenario to compare aquatic habitat quality changes between historic and future climatic conditions.

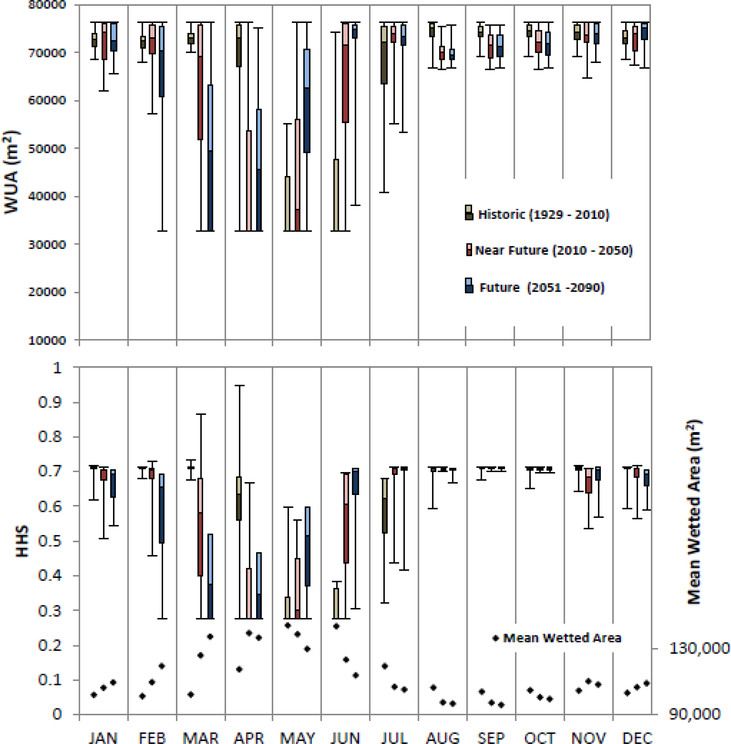
Climate change models indicate that peak runoff in the Bear Valley Creek is likely to occur at least one month earlier and convey approximately 30 percent less runoff at that peak as compared to the past 80 years. We calculated WUA and HHS parameters for the spawning and rearing life stages for past and future conditions. Assuming that the timing of spawning activity will not change over the period of interest, a comparison of the spawning WUA values for past monthly averages and future monthly averages suggest some downward pressure on Chinook spawning productivity (Figure 6). Monthly averages for spawning WUA drop approximately 32% during the beginning of spawning season between the past and future conditions (Table 4). Monthly averages for spawning WUA drop approximately 23% at the end of the spawning season between past and future conditions. As such, the future condition spawning season starts with significantly less spawning area and drops to the baseline a full month earlier than in past conditions. Monthly averages for rearing WUA drop approximately 23% at the beginning of the spring emergence and remained low until the end of the spring increasing by 37%, 70% and 7% in May, June, and July, respectively (Table 4). However, besides May, June and July, all other months show a decrease in rearing habitat in future compared to historic scenarios (Figure 7). Spawning and rearing HHS show similar percentage changes to the WUA values (Table 4). The future condition graph (Figure 6) indicates that the peak annual HHS values occur approximately one month earlier in the future conditions and the time span of peak value will decline by approximately one month. Intra annual variability of spawning WUA and HHS decreases in the predicted future scenario compared to historic data. Shorter box plots in the future scenario as compared to historic suggests that the low spawning habitat extent and quality will persist among years (Figure 6). Conversely for rearing habitat, the data show a potentially larger monthly variability for all months but similar to historic in the months from July to October (Figure 7).

Figure 6:

Box-and-whiskers plot of monthly weighted usable areas, WUA, (top) and hydraulic habitat suitability, HHS (bottom) of spawning habitat for historical (H; 1929–2010, left whisker in each month, brown hues), near future (NF; 2011–2050, center whisker, red hues), and far future (FF; 2051–2090, right whisker, blue hues) for the ensemble case scenario.

Table 4:

WUA and HHS for Chinook salmon juvenile rearing and spawning habitat.

		Past Avg. (1929 – 2010)		Future Avg. (2011 – 2090)		Percent Change
		WUA (m2)	HHS (-)	WUA (m2)	HHS (-)	WUA %	HHS %
Spawning	July	55300	0.47	37700	0.35	−32%	−24%
	August	38560	0.36	29350	0.29	−23%	−18%
Rearing	January	72583	0.71	72359	0.68	−0.3%	−4.8%
	February	72313	0.71	69716	0.63	−3.6%	−10.9%
	March	72960	0.71	56276	0.48	−22.9%	−33.0%
	April	70516	0.62	45513	0.38	−35.5%	−39.1%
	May	38038	0.31	52105	0.44	37.0%	41.4%
	June	40158	0.33	68561	0.61	70.7%	84.9%
	July	68599	0.59	73026	0.69	6.5%	16.6%
	August	74324	0.70	70019	0.71	−5.8%	−1.4%
	September	74011	0.71	71332	0.71	−3.6%	−0.2%
	October	74163	0.71	72014	0.71	−2.9%	−0.3%
	November	73988	0.71	73390	0.68	−0.8%	−4.0%
	December	73041	0.71	73512	0.68	0.6%	−3.3%

Figure 7:

Box-and-whiskers plot of monthly weighted usable areas, WUA, (top) and hydraulic habitat suitability, HHS (bottom) of rearing habitat for historical (H; 1929–2010, left whisker in each month, brown hues), near future (NF; 2011–2050, center whisker, red hues), and far future (FF; 2051–2090, right whisker, blue hues) for the ensemble case scenario.

Fish growth model

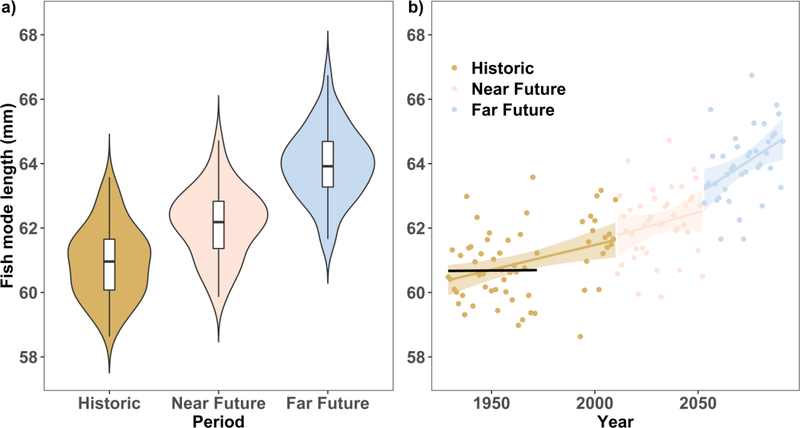
The fish growth models were developed based on 15 available years of data and their statistical analysis indicated that model 2 is the most likely based on lowest ΔAIC and R² similar to the full model (Table 2 and 3). The models with the quadratic term (model 5 and 6) had large ΔAIC, uncertainty on the coefficients and p-values with similar R² of the simpler model 2. Model 2 accounts for stream water temperature, density and Julian day and predicts an increase in fish mode length of 5 %, for the FF scenario, assuming 100 redds density in the stream reach and setting the same Julian day at 210 (Figure 8a). This is an average increase of nearly 5 mm, which is larger than the estimated standard error (2.6 mm) of model 2. Fish length shows no trend until 1980 but then a statistically significant increase of 0.04 mm per year (Y =0.04*N_Year+61.4, r²=0.45, p<0.01, with N_year the number of years from the 1990) after that. Whereas the interannual variability remained similar (fish length variance in both periods was 1.2 mm²).

Figure 8:

Predicted Chinook salmon mode lengths based on model 2 as violin and box plots for historic (1929–2010), near future (2011–2050) and far future (2051–2090) scenarios (a) and their yearly trends with linear regression line and shaded area show standard error (b). The black line is the regression line for years earlier than 1990 and it is virtually horizontal with slope not statistically significant (p>0.01). Inter annual variation in temperature and flow hydraulics results in model fish length variability, which is larger than the 2.6 mm standard error of the model. Results were standardized at 100 redds per year and at the same Julian day of 210.

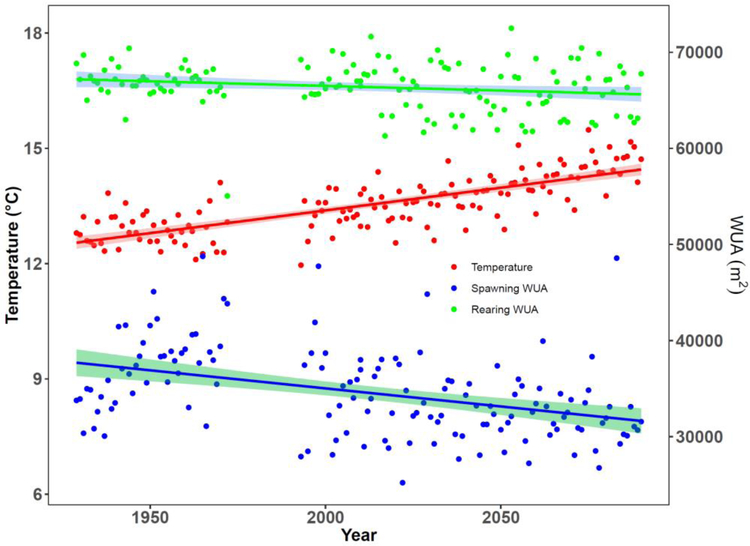
Fish size increase is due to the increase of summer stream water temperature, whose mean values are expected to increase almost 2 °C degree by the end of the century (Figure 9). Application of model 3, which is based only on density and Julian day, results in a negligible decrease in length of 0.3% due to reduce rearing habitat (Figure 9). Temperature are projected to be always below critical values even in the predicted warmest years.

Figure 9:

Predicted yearly mean spawning and rearing weighted usable areas (WUA) and yearly mean stream water summer temperatures from historic to EM predicted future climate conditions.

DISCUSSION

The general trends for all climate scenario A1B, B1 and EM are similar, which suggests that the conditions imposed on Bear Valley Creek should follow a well-defined trajectory under various climate scenarios. The air temperature projections also align with trend in measured air temperatures in the region (Isaak et al., 2012; Mantua et al., 2010). All climate change scenarios predict reduced mean peak flows, earlier timing of snowmelt, increased duration of the runoff event, reduced base flows, and an overall increase in flow variability during the year. This hydrologic pattern is broadly similar to those predicted in other watersheds within the Pacific Northwest (Hamlet et al., 2005; Leppi et al., 2012; Luce and Holden, 2009; Mantua et al., 2010; Mote et al., 2005; Mote and Salathé, 2010). Although, the specifics can vary from stream to stream depending on watershed morphology and geology, the general pattern is that streams are running off sooner as accumulated snowpacks melt earlier with each successive decade, for peak flows to be smaller because a larger proportion of precipitation falls as rain rather than snow, and for summer flows to be lower. The timing and duration of spring runoff is likely to be highly variable from year-to-year with the largest flow near bankfull rather than higher as in historic conditions. The river-floodplain interaction will be drastically reduced to shorter periods and smaller extent with important implication for floodplain and riparian vegetation growth. Conversely, discharges are generally predicted to be higher during winter months and lower during summer flows as compared to the historic record, following the trend observed by others (Luce and Holden, 2009).

In many stream systems, the influence of higher spring flows and the transition from a snow dominated system to a rain-snow system would likely increase scouring events, which could disrupt Chinook salmon redd productivity (Hassan et al., 2015). However, Bear Valley Creek, like many other meadow systems, runs through a broad valley with an extensive floodplain system. Because over-bank flows have access to this large floodplain, large magnitude floods are unlikely to produce scouring shear stresses sufficient to mobilize salmonid spawning gravel (McKean and Tonina, 2013; Tonina and McKean, 2010). Sediment mobility analysis (supplemental information) based on Andrews’ shielding method and d₅₀ ranging between 0.03 and 0.054 m to cover the most likely range of median grain sizes observed in the patches along the study site supports this observation and shows limited mobility of coarse (d₅₀ and higher) grains less than 10 and 3% of the streambed with d₅₀=0.03 and 0.054 m respectively for the highest future scenario flow of 7 m³/s. In contrast to other sites where gravel and d₅₀ are mobile at bankfull discharge (e.g., Mueller et al., 2005), this analysis confirmed what was reported by McKean and Tonina (2013) on a shorter reach, that even at flows near bankfull, coarse particle in the range of the median grain size are mostly immobile, indicating that scour would not be a critical issue in this stream (Figure S2a shows the case of d₅₀=0.04m). With this coarse-particle low mobility, an armor layer of coarser surface grain size distribution would most likely form through removal of fine grains (Wilcock and DeTemple, 2005). Thus, high spring discharges may provide flushing flows to clean sand from the pore structure of gravel, potentially enhancing redd productivity (Kondolf and Wilcock, 1996; Wu, 2000; Wu and Chou, 2003).

However, depending on fine sediment inputs, larger and more extended winter flows may mobilize fine sediments and clog or entomb salmon redds (Maturana et al., 2013), potentially threatening the embryonic development by reducing the delivery of oxygen-rich surface water to the eggs via hyporheic fluxes (Stuart, 1954; Tonina and Buffington, 2009). In future (NF and FF) climate scenarios, flows that may transport sand are likely to occur during the egg gestation period (April and May). These flows may fully or partially clog the redds although embryos from some redds will potentially hatch prior to the sediment peak flows. This clogging scenario is less likely under current sand input conditions and most likely cleaning of coarse sediment may occur. However, changes in hillslope processes with increased potential for wildfires and fine sediment delivered to the stream may potentially increase this risk (Sankey et al., 2017) and consequently reduce embryos survival to parr, s_h.

Changes to the WUA can be used as a metric to gage the impact of an environmental change on a stream’s habitat quality. For example, Boavida, et. al. (2012) used cumulative time below preassigned WUA thresholds (WUA in the condition under examination as a percent of the peak WUA for a reference area) to evaluate the impact of restoration of a degraded stream on habitat quality for Mediterranean freshwater fish species. For the present study, we make a quantitative comparison of the available WUA under the different climate scenarios. Our results indicate that, during the spawning season, the WUA values in the future condition range from 68% of historic (July) to 76% of historic (August). For rearing, WUA values are only significantly below the historic rearing WUA values in March (77%) and April (64%). May and June have significantly higher WUA value in the future conditions, 137% and 170% respectively. These results suggest a significant negative impact on spawning habitat with a modest and possibly positive impact on rearing habitat. The average future condition for rearing WUA values may not be too different from present in future scenarios. However, fragmentation of rearing habitat due to the lower summer flows may be a significant component, which has not yet been quantified due to lack of information on fish spatial distribution. Rearing habitat, which is in slow moving water, is mainly in marginal areas, backwater zones and in lateral channels. Lateral channels may disconnect from the main channel during very low flows reducing access and or stranding fish.

Carnie et al. (2015) investigate habitat patch size and patch connectivity on spawning habitat for the same river for different discharge scenarios and found that low discharges (1 m³ s⁻¹) during spawning period would increase the fragmentation of high-quality habitat from the historic conditions (above 2 m³ s⁻¹). However, connectivity was found to be a secondary effect compared to patch size. Future scenarios project even lower discharges that may results in more fragmentation which may potentially exacerbate the reduction in available spawning habitat.

Conversely to other regions (Muñoz-Mas et al., 2018), the projected increase in stream water temperature for these high elevation meadow systems may have a positive effect on fish growth. The impact of future climate on fish size is approximately a 5 % increase in their mode length from the historic to the far future scenario. This increase is about 5 mm in the FF and is at least 5 times the standard deviation (about 1.1 mm) of natural intra annual variability quantified for the historic scenario. It is unknown, if this increase is sufficient to increase the potential for fish to reach the ocean significantly but, in general, any increase in size has been thought to increase success. However, a Chinook multi-population, including Bear Valley Creek, study on juvenile downstream migration survival showed that mean length was a poor predictor of passing lower Granite Dam, a major migratory bottleneck (Zabel and Achord, 2004). The same study also noticed that size might significantly impact success of the next life stages, because longer fish start migration earlier and they might have advantages during the ocean phase. Consequently, longer fish may have overall better fitness. Thus, although future population of Chinook salmon may find reduced spawning habitat, which may lead to lower redd density from historic condition, the warmer waters may in turn help to have larger fish migrating to the ocean.

Our fish growth model is based on only 15 years of data and may not capture the entire variability of fish densities and stream water temperatures. Another limitation could be the use of summer mean water temperatures instead of the entire period after hatching, March-August, which was shown to be a better predictor of fish size than summer temperature (Crozier et al., 2010). This may potentially explain the high p-value and uncertainty of the temperature term, which may indicate that it is less significant than the other terms. The predicted future fish size increase is due to increase in stream water temperatures accounted through the temperature term in model 2. Typically models within 2 or 3 ΔAICc are considered similar candidates, which indicated that growth models 1, 3, and 6 could be plausible predictors based on our sample data. Growth models with temperature (models 1, 2, 6) all predict increase in fish size only based on the effect of temperature, whose terms, however, are not statistically significant (p>0.05) in all models. Conversely, Model 3, which has similar r² but slightly higher AIC (ΔAICc=1.75) value than model 2, predicts a negligible decrease in fish size, −0.3% for the FF scenario, due to reduction in rearing habitat. However, temperature has such an important effect on fish growth due to fish physiology, that warrants its inclusion. Conversely, the inclusion of the quadratic term for temperature is not supported by the ranges of summer temperatures experienced by fish during the sampling period and thus does not improve prediction. The problem is also further complicated by the low number of fish spawners returning, much lower than historic conditions, which may potentially add more weight on the density.

While our results suggest that climate change will cause negative pressure on spawning habitat and a modest decrease in rearing habitat, the overall outlook for Bear Valley Creek is that it will continue to host a substantially usable environment for salmon spawning and growth especially for the current densities. In recent decades, the number of fish returning to and spawning in Bear Valley Creek are quite low as compared to historical numbers such that redd density are orders of magnitude smaller than what they used to be historically. Consequently, future salmonids’ success may be more dependent on habitat accessibility (e.g., keeping adequate migration corridors) than from natal stream habitat quality. The increase of stream water temperature may provide some benefits (from model 2 analysis) at these high elevation cold-water streams, but it may have far more detrimental impact during upstream migration, when anadromous fish may exhaust their stored energy before reaching their spawning grounds (Connor et al., 2019; Crossin et al., 2008). This effect could be exacerbated by the expected lower discharges during summer further increasing stream water temperature along the entire river network, not just its headwaters.

Thus, inclusion of fine scale resolution analysis similar to that applied in this work within life cycle models may better constrain the impact of climate change on population adaptation and survival. These models will pass the condition of one life stage to the next one, accounting for local conditions and thus better quantify the impact of stream water temperature and flows changes on fish population besides fish size. Results could be also better constrained by bioenergetic or individual-based model approaches, because they would take advantage of the fish-scale high-resolution spatial and temporal distribution of the hydromorphological quantities. A key limitation in these approaches, though, is the quantification of food availability (e.g., drifts) and intra and among species dynamics. Our statistical growth approach is parsimonious, and it associates energy and cospecies dynamics with stream water temperature and fish density, respectively. It is based on regression analysis that requires historic information on fish length and stream discharge, which underlines the importance of continuous monitoring companies (Achord et al., 2003; Crozier et al., 2010). However, our key assumption is that fish length is a proxy for fish survival and fitness, but fish size may not always be an indicator of better survival as documented by Carlson et al. (2008) nor of better migration success as shown by Zabel and Achord (2004). Thus incorporation of fine scale microhabitat analysis along river networks within fish population models may provide a more effect approach to address questions like those asked in the work.

Bear Valley Creek is not a unique meadow system within the tributaries of the Salmon River or of the Columbia River at large. Many meadow systems in the region have similar characteristics, snowmelt dominated, meandering and cold-water streams. Our results would be broadly representative of many other streams in the Pacific Northwest region (Hamlet et al., 2005; Hamlet and Lettenmaier, 2007; Leppi et al., 2012; Mote and Salathé, 2010). Salmon and several other closely related cold-water species occupy many streams and rivers across a range of elevations where hydrology is similarly being affected by climate change (Isaak et al., 2018). Moreover, numerous hydrologic studies in this region have documented past and future predicted transitions from snow to rain/snow hydrology (Hamlet et al., 2005; Hamlet and Lettenmaier, 2007; Leppi et al., 2012; Luce et al., 2013; Luce and Holden, 2009; Mote and Salathé, 2010), but our study is one of the few that translates those effects to locally specific habitat changes.

CONCLUSION

With the use of fine-resolution and large-scale modeling this work quantifies that future climate conditions will likely reduce spawning suitability of Chinook salmon by about 30 %. Rearing habitat quality may also reduce for most of the year but within the range of historic values. Future inter-annual variability of habitat quality is similar to that observed in the past for spawning but exhibits larger fluctuations for rearing habitat. As the climate warms, the watershed will transition from a snowmelt dominated water supply regime to a rain/snow scenario. This will result in a broadening of the spring flow peak in the annual hydrograph in which the rising and falling limbs of the spring flow are shallower than in the past and the peak flow is lower. The major effect on the watershed, between past and future scenarios, is a change in timing of peak flows and their reductions. The future high discharges are around the historic bankfull discharge, while historic high discharges were larger than bankfull during the snowmelt period (May-June) flooding the surrounding meadow floodplain for almost 2 months. These lower peak flows will strongly spatially and temporally reduce the river-floodplain interaction.

The altered flow regime mostly impacts spawning conditions rather than rearing because, presently, low flows occur during the spawning period. The increase of stream water temperature for the future scenarios may potentially improve the biological response of the fish population, due to fish length predicted increase, although its benefits on counterbalancing the reduction in both spawning and rearing habitats are still unclear and potentially limited. Young fish size increase has been suggested as an indication of potential increase fitness. This suggests that for Bear Valley Creek and in extension for other high elevation meadow systems, increases in stream water temperature may be beneficial but our analysis could not demonstrate if this may compensate for the reduction in spawning and rearing areas. Our modeling approach and local results at the spawning and rearing life stage could be incorporated in a life-cycle model to better constrain our analysis at the population level.

To constrain our analysis and better answer our questions, this micro-habitat approach should be used within a life cycle model to understand the potential impact at the population scale. Similarly, whereas rearing habitat quantified as WUA or HHS decreased for most part of the year, the impact of its fragmentation is less constrained than the spawning habitat and consequently more research should focus on this aspect. This investigation shows that numerical modeling and remote sensing surveying tools allow analyzing physical and biological processes that occur at the microscale over kilometers of stream network. This approach can be scaled to the river network as hydrological and topographical information are available and its results improved by use of bio-energetic or individual-based modeling approaches.

Figure 4:

Box-and-whiskers plot of monthly discharges for B1 (brown hues), A1B (red hues) and ensemble mean, EM, (blue hues) climate change scenario for far future prediction (FF; 2051–2090). Box gradations represent the 25, 50 and 75^th percentiles. Whisker extents represent the maximum and minimum predicted values. The inset shows the averaged historic (H) and predicted near future (NF, 2011–2051) and far future (FF, 2051–2090) monthly discharges for three climate models (A1B, B1 and EM) and the horizontal red dashed line indicates the current bankfull discharge.