Multiple Sclerosis Lesion Segmentation with Tiramisu and 2.5D Stacked Slices

Abstract

In this paper, we present a fully convolutional densely connected network (Tiramisu) for multiple sclerosis (MS) lesion segmentation. Different from existing methods, we use stacked slices from all three anatomical planes to achieve a 2.5D method. Individual slices from a given orientation provide global context along the plane and the stack of adjacent slices adds local context. By taking stacked data from three orientations, the network has access to more samples for training and can make more accurate segmentation by combining information of different forms. The conducted experiments demonstrated the competitive performance of our method. For an ablation study, we simulated lesions on healthy controls to generate images with ground truth lesion masks. This experiment confirmed that the use of 2.5D patches, stacked data and the Tiramisu model improve the MS lesion segmentation performance. In addition, we evaluated our approach on the Longitudinal MS Lesion Segmentation Challenge. The overall score of 93.1 places the L₂-loss variant of our method in the first position on the leaderboard, while the focal-loss variant has obtained the best Dice coefficient and lesion-wise true positive rate with 69.3% and 60.2%, respectively.

1. Introduction

Multiple Sclerosis (MS) is a demyelinating disease of the central nervous system. Magnetic resonance imaging (MRI) is commonly used for monitoring the disease course. Automated quantification of focal MS lesions in the white matter (WM) is a desirable goal, but this task is complicated by the vast variability in lesion appearance, shape and location, as well as sensitivity to scanning protocols and patient populations. Even manual segmentation of lesions is highly challenging; in addition to being time-consuming, this process is prone to notoriously high inter- and intra-observer variability [3]. Many novel automated algorithms have been proposed to improve the segmentation results over the past years.

Among the automated methods, supervised techniques have dominated this field by their strong ability to detect MS lesions [3]. In recent years, machine learning techniques, especially convolutional neural networks (CNNs), have shown better performance than other methods. The deep neural networks create features directly from the training data without any manual feature engineering. With the growth of computing power and the development of deep learning, the CNN-based models have provided state-of-the-art results in MS lesion segmentation [1,5]. Among the variety of network architectures, the U-Net [10] is currently widely used in medical image segmentation.

Contributions.

In this work, we adapted the fully convolutional densely connected networks (Tiramisu [6]) for MS lesion segmentation. We introduced the use of 2.5D stacked slices (Sect. 2.2) to improve the network performance. We conducted experiments on our in-house dataset and the ISBI 2015 Longitudinal MS Lesion Segmentation Challenge dataset (Challenge). For the in-house dataset (Sect. 4.1), we performed realistic lesion simulation on healthy controls. The simulated dataset allows us to perform an ablation study without the complexities of intra-rater and inter-rater variabilities that often plague manual lesion segmentations [3]. The ablation experiments show that the introduction of 2.5D stacked slices is helpful for the segmentation performance and the Tiramisu model performs better than U-Net. While valuable for running experiments in a controlled environment, all simulations inevitably have limitations; thus, we also conducted experiments on a real dataset. For the Challenge (Sect. 4.2), as of March 2019, the score of our proposed method places us in the first position on the leaderboard with a score substantially higher than the previously reported results.

2. Materials and Methods

2.1. Datasets and Pre-processing

In-house Dataset.

This dataset consists of 15 healthy controls. For each subject, 3T T1-w MPRAGE and FLAIR images were acquired at Brigham and Women’s Hospital [9]. We use a publicly available lesion simulation tool to generate a dataset with ground truth lesion masks.¹ The unambiguous ground truth definition allows us to precisely measure performance in the ablation study presented in Sect. 4.1. The number of simulation time-points for each healthy control is normally distributed with N(4, 1) so that we get on average 4 time-points for each subject. The lesion load follows the log-normal distribution Log − N(log(15), $\frac{\mathit{log}(3)}{3}$) and is forced into the range [5, 50]. This yields an approximate average lesion load of 15ml, which is a plausible lesion load.

ISBI Longitudinal MS Lesion Segmentation Challenge Dataset.

This dataset contains 5 training and 14 testing subjects, with 4 to 5 time-points per subject [3]. T1-w MPRAGE, FLAIR, T2-w and PD images were acquired at 3T. Lesions were manually delineated by two expert raters.

Pre-processing.

For the in-house dataset, T1-w and FLAIR images were co-registered to the T1-w space using ANTs [2] and skull-stripped using BET [13]. Next, bias correction was performed by N4ITK [14]. For the Challenge dataset, we used the pre-processed data as provided [3]. This includes N4 bias correction, skull-stripping, dura-stripping, followed by a second N4 bias correction and a rigid registration to the MNI template. Afterward, all images were registered to the baseline image. Finally, for both datasets, we performed an intensity normalization for each image with kernel density estimation.

2.2. 2.5D Stacked Slices

A stack of 3 slices is defined as a center slice and its 2 adjacent slices. We only consider the stacks whose corresponding lesion mask has at least one voxel of lesion in the center slice. While the central slice is the most important one, the neighboring slices provide contextual information about possible lesions. Due to limited data and computational resources, current 3D methods use small patches to train the network, which leads to a lack of global structure information. In contrast, a stack of adjacent slices from any plane provides global information along two axes (e.g., x, y) and local information from the third axis (e.g., z).

The term 2.5D is defined as stacked slices along three orthogonal planes (axial, coronal and sagittal). Although this term is previously used in [11] for fusing three orthogonal views of a region into a training sample, we define it here referring to using 2D slices from the three orientations independently. For a multi-modal dataset of N modalities (e.g., N = 4 for the Challenge dataset which contains T1-w, T2-w, FLAIR and PD images), the input would be the concatenation of N stacked slices of the same location from different modalities.

The 2.5D stacked slices exploit the 3D nature of MRI but are still 2D, providing efficient training. This enables the network to learn the global structure from all three orientations. The inference results along the different orientations are combined via majority vote to output the final segmentation. To force the stacks from different orientations have the same size, they are randomly cropped to 128 × 128.

2.3. Network Structure and Loss Functions

Our network is a 2D fully convolutional densely connected network adopted from the Tiramisu model [6]. The network takes the 2.5D stacked slices from all the available modalities (T1-w, FLAIR, etc.) as the input and outputs the lesion segmentation binary mask (Fig. 1). The loss function has to be carefully chosen for training the deep neural network. In this work, we used L₂ loss, Dice loss and focal loss [8] and compared their performance.

Fig. 1.

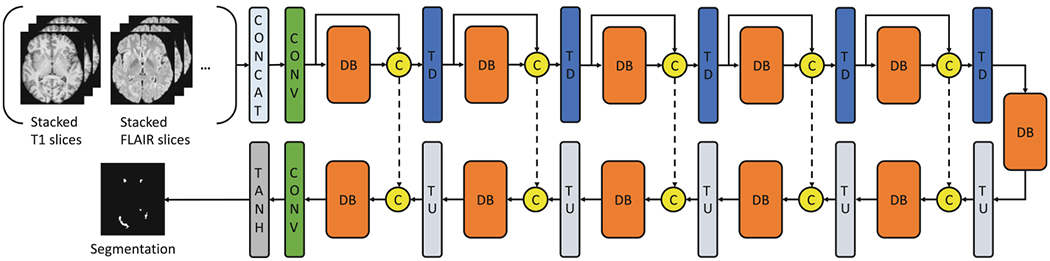
The network architecture of our proposed method. The downsampling path consists of a convolutional layer (CONV), 5 dense blocks (DB) and the transition down (TD) blocks. The upsampling path is symmetrical to the downsampling path, but for the input of each block, it concatenates the output from the Transition Up (TU) block and the output from the corresponding downsampling block. The final Tanh layer brings the output values to the [−1, 1] range. Within each DB, the input of each layer is the concatenation of all the previous layers. Each DB consists of 4 layers.

The L₂ loss is defined as: ${\mathcal{L}}_{L_2}=|F(X)-Y{|}_2$ where X represents the inputs of all available modalities and F(·) is the function of the neural network. Y is the training lesion mask which can be ground truth or gold standard.

The Dice loss (${\mathcal{L}}_{\mathit{Dice}}$) and Dice Similarity Coefficient (DSC) are defined as: ${\mathcal{L}}_{\mathit{Dice}}=1-DSC(F(X),Y)$ and $DSC(F(X),Y)=2\frac{|F(X)\cap Y|}{|F(X)|+\left|Y\right|}$.

The focal loss is defined as ${\mathcal{L}}_{\mathit{focal}}=-\alpha Y\cdot {(1-F(X))}^{\gamma }\log (F(X))-(1-\alpha )(1-Y)\cdot F{(X)}^{\gamma }\log (1-F(X))$ where α is the weighting factor and γ is the modulating factor. α balances the importance of positive and negative examples whereas γ is used to give more focus on potentially mislabeled examples.

3. Experimental Methods

Evaluation Metrics and Compared Methods.

We evaluated our method following the metrics described in [3]. The metrics include: Dice Similarity Coefficient (DSC), Positive Predictive Value (PPV, or precision), True Positive Rate (TPR, or recall), Lesion-wise False Positive Rate (LFPR), Lesion-wise True Positive Rate (LTPR) and Volume difference (VD). For both datasets, in addition to experiment-specific comparisons, we also compared our results with two established methods, FLEXCONN [12] and MIMoSA [15].

Implementation Details.

For our simulated in-house dataset, we split 4/5 of the simulated data into the training set, and 1/5 into the test set. For the Challenge, we trained 5 models based on 5-fold cross-validation and then use majority voting to get the segmentation output of the Challenge test set.

Our networks were trained using the Adam optimizer [7] with the initial learning rate (lr) of 0.0002 and momentum term of 0.5. The initial lr was used for 100 epochs and then it linearly decayed to 0 within the chosen epoch number. For the network trained with focal loss, we use the setting γ = 2, α = 0.25, following the findings of [8].

4. Results

4.1. Simulated In-House Dataset

Since manual lesion segmentation is notorious for inter-rater and intra-rater variations [3], we first evaluated our method on the simulated in-house dataset to momentarily avoid the ambiguities introduced by human raters. Figure 2(A–D) illustrates that the simulation is visually realistic. Figure 2(E–G) demonstrates that our method is able to segment the lesions on this simulated dataset.

Fig. 2.

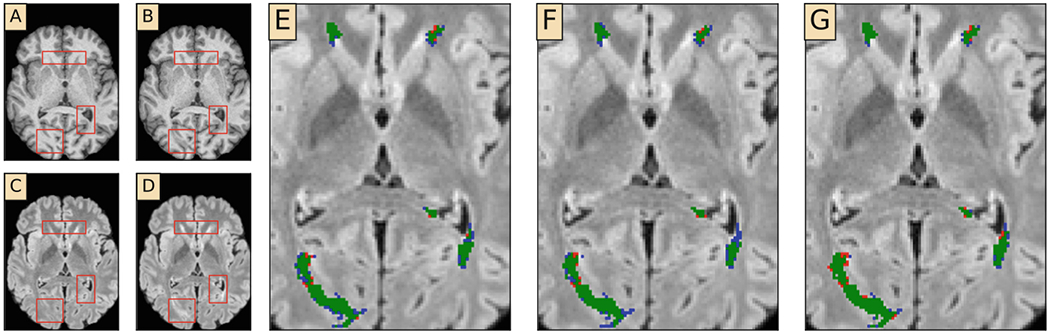
Qualitative results from the simulated in-house dataset. (A) Original T1-w image (B) Simulated T1-w image (C) Original FLAIR image (D) Simulated FLAIR image (E–G) Zoomed-in segmentation results with L₂ loss, Dice loss and focal loss, respectively. Green: true positive. Red: false positives. Blue: false negatives. Red boxes in (A)–(D) highlight lesions (Colour figure online).

We trained our network with three different loss functions to assess performance. In Table 1, the results of these three variants are shown in the first three rows. The focal-loss variant achieved the highest DSC and TPR while the L₂ variant achieved the best PPV and LFPR. The former showed stronger ability to recall lesions but the latter achieved a better balance between LFPR and LTPR. The L₂ variant outperformed the Dice variant in most metrics.

Table 1.

Results on the simulated in-house dataset. The first 3 rows are our proposed methods trained with different losses. The following 4 rows each show the effect of changing one component of the baseline (Ours (${\mathcal{L}}_{\mathit{Focal}}$)). The last two rows are the results obtained with FLEXCONN and MIMoSA based on the same dataset.

	DSC	PPV	TPR	LFPR	LTPR	VD
Ours (${\mathcal{L}}_{L_2}$)	0.861	0.919	0.810	0.104	0.603	0.119
Ours (${\mathcal{L}}_{\mathit{Dice}}$)	0.847	0.904	0.798	0.150	0.597	0.118
Ours (${\mathcal{L}}_{\mathit{Focal}}$)	0.865	0.850	0.880	0.209	0.636	0.045
Only 2.5D	0.859	0.866	0.853	0.278	0.620	0.028
Stacked 2D	0.828	0.801	0.858	0.584	0.640	0.088	Ablation Study
Smaller Patch	0.858	0.850	0.868	0.236	0.644	0.040
U-Net	0.835	0.803	0.871	0.597	0.694	0.087
FLEXCONN [12]	0.707	0.624	0.832	0.667	0.546	0.393
MIMoSA [15]	0.424	0.530	0.370	0.851	0.544	0.316

Since we have the ground truth for the simulated dataset, it is well-suited for an ablation study to illustrate the role of the introduced techniques. We used the network trained with the focal loss as the baseline and removed individual components to assess the resulting difference in performance. We considered the following settings: (1) using only 2.5D (i.e., along 3 different orientations) without stacking; (2) only 2D stacked data along a single orientation; (3) smaller patch sizes (64 × 64 instead of 128 × 128, with stacking and 2.5D); (4) a U-net architecture rather than Tiramisu. The results are shown in Table 1. When we only use 2.5D slices without stacking, we observe that all the metrics, except PPV and VD, get worse. Similarly, when we only use stacked 2D data or use U-Net, the performance is not as good as the baseline. Moreover, using smaller patches (64 × 64) to train the network cannot reach the same performance as large patches (128 × 128) since they contain less structural information.

We next consider the Precision-Recall (PR) curves by controlling the threshold (between −1 and 1) of membership predictions (Fig. 3(a)). The curve of L₂-loss network is closest to the upper right corner which means it has the best performance. The baseline (the focal loss network) performed better than its variations, as expected. An interesting observation of the Dice-loss network is that most of its predictions are exactly −1 (Non-lesion) or 1 (Lesion). Because of this, most data points on the PR curve lie in a small range for this variant, unlike the other networks. For lesion-wise comparison, the lesion-wise Receiver Operating Characteristic (ROC) curves are plotted in Fig. 3(b). The L₂ variant had higher LTPR when LFPR is smaller than 0.20, whereas the focal loss variant performed best when the LFPR is allowed to be higher. With respect to lesion-wise metrics, the baseline method also showed better performance than the networks in the ablation study.

Fig. 3.

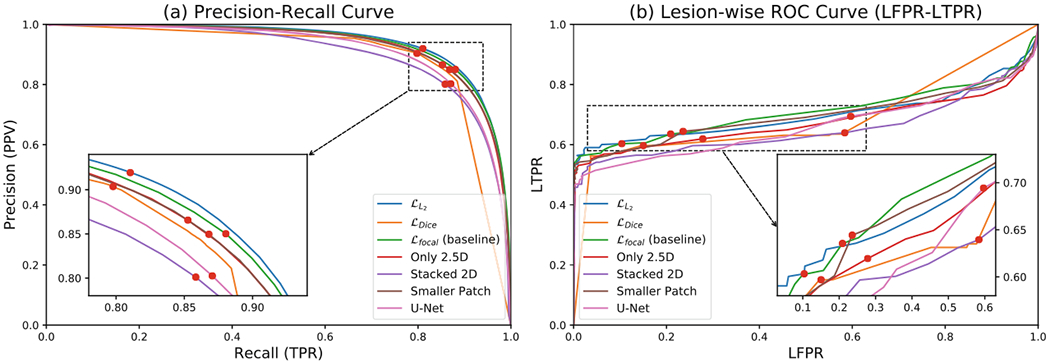
Precision-Recall and Lesion-wise ROC (LFPR-LTPR) curves for the ablation study. The in-set figures provide zoomed-in views. The red dots indicate when the threshold is set to 0 (the membership function values are in the range [−1, 1]).

4.2. The Longitudinal MS Lesion Segmentation Challenge

The results on the public Challenge dataset are shown in Table 2. In this table, we also compare our results to the three top-ranking methods on the leaderboard prior to our method, Hashemi et al. [5], Feng et al. [4], Aslani et al. [1]. For each metric, the best two scores are emphasized because the values are very close. An overall score (SC) of 90 indicates segmentation accuracy similar to the human raters [3]. The scores of our proposed methods are substantially higher than the previous best-reported score (92.486). Similar to our results on the simulated dataset, among the networks, the L₂ variant has the best overall performance (the highest score). It made a good trade-off between LFPR and LTPR. The focal loss variant achieved the best DSC, the best LTPR and the second-best TPR (recall) which mean it is very sensitive to the lesions. The Dice variant’s performance is close to that of the L₂ variant, but the latter is better in most metrics. These are consistent with our findings on the simulated in-house dataset.

Table 2.

Results on the ISBI challenge test set. For each metric, the bold values mean the best result and the underlined values are the second-best result. The first three rows are our proposed methods trained with different losses. The following three rows are the reported state-of-the-art methods. The last two rows are other established methods.

	SC	DSC	PPV	TPR	LFPR	LTPR	VD
Ours (${\mathcal{L}}_2$)	93.21	0.643	0.908	0.533	0.124	0.520	0.428
Ours (${\mathcal{L}}_{\mathit{Dice}}$)	93.11	0.642	0.902	0.533	0.155	0.540	0.425
Ours (${\mathcal{L}}_{\mathit{focal}}$)	92.85	0.693	0.818	0.644	0.236	0.602	0.340
Hashemi et al. [5]	92.49	0.584	0.921	0.456	0.087	0.414	0.497
Feng et al. [4]	92.41	0.682	0.782	0.645	0.270	0.600	0.326
Aslani et al. [1]	92.12	0.611	0.899	0.490	0.139	0.410	0.454
FLEXCONN [12]	90.48	0.524	0.866	N/A	0.110	N/A	0.521
MIMoSA [15]	87.72	0.568	0.611	0.570	0.474	0.353	0.343

Among the top-ranking methods, [5] implemented the 3D Tiramisu and used Dice/focal loss. [4] uses a 3D U-Net and weighted binary cross entropy. [1] used 2D U-Net and 2.5D patches. Compared to the leading 3D approaches in the Challenge [4,5], our networks have more samples for training and are less susceptible to training data size. Compared to the leading 2D approach [1], our 2.5D stacked representation gives a glimpse of the 3D context without causing a substantial reduction in training set size. On the challenge leaderboard, a recent submission achieved a higher score than these three methods (but lower than our scores). However, we are unable to include it since, to the best of our knowledge, this approach has not yet been published. We note that there is an overall performance drop between the in-house dataset and the Challenge dataset, which we believe is due to imperfections in the manually created labels of the Challenge dataset.

5. Conclusion

We proposed a novel pipeline using fully convolutional DenseNets and 2.5D stacked slices for automated MS lesion segmentation. We trained our network with L₂ loss, Dice loss and focal loss. The network trained with L₂/Dice loss shows the good trade-off between true positives and false positives. The network trained with focal loss has a strong ability to recall lesions. On the simulated in-house dataset, we developed our method and the ablation study showed the 2.5D stacked data and Tiramisu model are the main reasons for the improvements. On the ISBI Challenge, our method outperformed the state-of-the-art methods. We achieved the best overall score with the use of L₂ loss and the highest DSC/LTPR with the focal loss. The excellent performance achieved on the ISBI challenge suggest fully convolutional DenseNets and stacked 2.5D data as a highly promising approach for medical image segmentation.