Voltammetric and galvanostatic methods for measuring hydrogen crossover in fuel cell

Summary

Hydrogen crossover rate is an important indicator for characterizing the membrane degradation and failure in proton exchange membrane fuel cell. Several electrochemical methods have been applied to quantify it. But most of established methods are too rough to support follow-up applications. In this paper, a systematic and consistent theoretical foundation for electrochemical measurements of hydrogen crossover is established for the first time. Different electrochemical processes occurring throughout the courses of applying potentiostatic or galvanostatic excitations on fuel cell are clarified, and the linear current-voltage behavior observed in the steady-state voltammogram is reinterpreted. On this basis, we propose a modified galvanostatic charging method with high practicality to achieve accurate electrochemical measurement of hydrogen crossover, and the validity of this method is fully verified. This research provides an explicit framework for implementation of galvanostatic charging method and offers deeper insights into the principles of electrochemical methods for measuring hydrogen crossover.

Graphical abstract

Highlights

• •Analysis of fuel cell electrode processes under potentiostatic/galvanostatic conditions
• •Reinterpretation of the linear current-voltage behavior of fuel cell in voltammograms
• •Galvanostatic method with high accuracy for measuring hydrogen crossover

Catalysis; Electrochemical energy production; Energy systems; Energy materials

Introduction

Proton exchange membrane (PEM) fuel cell vehicle has become one of the development targets of next-generation electric vehicles owing to its advantages of low operating temperature, high conversion efficiency, long driving range, and zero pollution emissions (Yuan et al., 2020, 2021a, 2021b). As its name suggests, PEM fuel cell is the heart of power system in this type of electric drive vehicle. In a PEM fuel cell, the PEM is sandwiched between an anode electrode and a cathode electrode. To function, the membrane must conduct hydrogen ions (protons) and also act as a non-permeable gas barrier between the cathode that typically receives air and the anode to which hydrogen is fed. Ideally, either gas is not allowed to pass to the other side of the cell. However, as a consequence of the small size of hydrogen molecule and the porosity of the membrane (Castelino et al., 2021), a small amount of hydrogen will inevitably penetrate the PEM from anode to cathode, which is known to be hydrogen crossover. Hydrogen permeation across the membrane is closely related with membrane degradation. The direct reaction between the fuel and the oxidant at the cathode surface (Kim et al., 2011) can result in the production of hydrogen peroxide (Liu and Zuckerbrod, 2005). Such an intermediate of oxygen reduction reaction subsequently decays to radical species, such as hydroxyl radicals, which continuously attack the membrane and promote chemical degradation of electrolyte material (Curtin et al., 2004; Inaba et al., 2006; Yuan et al., 2012). The decomposition of PEM is then a direct reason for membrane thinning or pinhole formation (De Moor et al., 2012; Lim et al., 2014). When membrane deterioration proceeds with the increase in loss of the polymer units, more hydrogen will pass through weak areas or voids, which further worsens the situation (Tang et al., 2007; Yuan et al., 2010). It is manifestly a positive feedback process. Previous studies (Inaba et al., 2006; Liu and Case, 2006; Wu et al., 2010; Yu et al., 2005) have reported that during the fuel cell degradation experiments, hydrogen crossover rate slightly increases in the initial period but then rises in an accelerated manner at a later stage, which conforms with the effect of the aforementioned membrane degradation mechanisms. Hence, hydrogen crossover rate is a key indicator to assess the aging degree of PEM, and accurate measurements of hydrogen crossover will be of critical help to the lifespan evaluation and failure diagnosis of fuel cells.

Various methods have been developed to measure the hydrogen permeation rate of PEM, mainly including the direct detection method and electrochemical method. The former method is usually carried out with a high-resolution analytical instrument, such as gas chromatograph (Broka and Ekdunge, 1997; Cleghorn et al., 2003; Endoh et al., 2004; Hwang et al., 2018; Takaichi et al., 2007) or mass spectrometer (Baik et al., 2011, 2013a, 2013b; Jung et al., 2016, 2017; Kreitmeier et al., 2012), which has the ability to detect directly the hydrogen in the cathode exhaust at a trace level and present quantitative results regarding hydrogen content. As a general rule, hydrogen crossover is characterized by a constant flow rate under a given operating condition, and when measurements are taken, the permeate-side is commonly fed with inert gas to exclude the interference of oxidants. Thus, by combining the mole fraction of hydrogen in inert gas and the measured value of inert gas flow rate, the hydrogen crossover rate can be figured out. The direct detection method has a major advantage of providing more authentic results. However, such trace analytical techniques require not only extremely expensive equipment but also cumbersome test procedures, which only adapts to research work in a well-equipped laboratory. Compared with the direct detection method, the electrochemical method is more convenient to implement, which points to potential on-board application. This type of method can be further classified as voltammetric method and galvanostatic charging method (GCM). Under the former method, a specific voltage profile is applied between two opposite electrodes as a function of time and the current produced by the system is measured. In this manner, all the hydrogen permeating through PEM is converted into a limiting hydrogen oxidation current (i.e., hydrogen crossover current), which is equivalent to the hydrogen crossover rate, and the key to the measurement is to isolate this component from the total current. Linear sweep voltammetry (LSV) is the most commonly used potential sweep technique in measuring hydrogen crossover (Brooker et al., 2012; Giner-Sanz et al., 2014; Huang et al., 2013; Hwang et al., 2018; Kocha et al., 2006; Niroumand et al., 2015; Wasterlain et al., 2011), but different scan rates always give rise to inconsistent results. Another electroanalytical method as a derivative of LSV is staircase voltammetry (also called as potential step method [PSM]), in which the potential sweep is a series of stair steps, and it has been employed in electrochemical measurements of hydrogen crossover (Schoemaker et al., 2014). Despite its time-consuming nature, this potentiostatic method did minimize the impact of capacitive charging current and is easy to operate and analyze. The potential weakness of their study is that no attempt was made to adequately verify the obtained results using non-electrochemical data. As regards the measuring principle of GCM, galvanostatic excitation with several charging currents is applied to the fuel cell, and the voltage response between two electrodes is recorded and analyzed, from which helpful information on hydrogen crossover current can be distilled. Although a few previous researchers have made sporadic progress in developing the galvanostatic analysis technique as an in situ diagnostic tool for hydrogen crossover (Chatillon et al., 2013; Hu et al., 2018; Lee et al., 2012; Pei et al., 2014, 2018), there are still many important details to be worked out. The characteristics of voltage response curves were not sufficiently analyzed yet, and there is a lack of a unified and unambiguous strategy that can guide data processing and selection. Moreover, most researchers failed to use non-electrochemical methods as validation tools to fully confirm the validity of the GCMs proposed in their literature. Collectively, previous studies employed very different philosophies in analyzing the raw data, and corresponding methods are too rough to support follow-up applications.

Our study seeks to provide, for the first time, a deep insight into the heterogeneous electrode reactions of fuel cell occurring under different excitations of external electrical signals and explore reliable methods to achieve accurate measurement of hydrogen crossover. This is the first study trying to sufficiently verify the validity of the PSM by comparing it with a non-electrochemical method. Furthermore, our research attempts to propose an explicit data processing scheme for GCM to essentially enhance its practicality and accuracy.

Results and discussion

Measurement by direct detection method

The direct detection method was first experimentally performed to establish a reliable reference value of hydrogen crossover rate for electrochemical methods. In the fuel cell, a certain amount of hydrogen gas from the anode can permeate through the membrane and blend into the exit stream with high purity nitrogen at cathode (Figure 1). When the whole system reaches a steady state, it is safely assumed that the molar flow rate of hydrogen gas within the exhaust of nitrogen is equal to the hydrogen crossover rate because the hydrogen at the cathode has only one source. With the help of trace analytical technique, the mole fraction of trace hydrogen gas in the sample gas was determined, which turned out to be 850 ± 16 ppm. Combining the measured value of nitrogen gas flow rate, hydrogen crossover rate is then calculated to be (1.848 ± 0.034) ×10⁻⁷ mol·s⁻¹. For straight comparisons of measurement results between the direct detection method and electrochemical methods, this flow rate is finally converted into an equivalent current with the value of (35.66 ± 0.66) ×10⁻³ A (see STAR Methods for details).

Figure 1.

Schematic Diagram of Direct Detection Method

CL, catalyst layer; GDL, gas diffusion layer; BP, bipolar plates; EP, endplates.

Measurement by potential step method

Steady electrochemical processes during staircase voltammetric experiments

In staircase voltammetric experiments, different potentials are kept constant until capacitive processes have finished and the total current at the end of each step is measured as the steady-state response. Figure 2 provides a diagram of steady-state electrochemical processes occurring in this measurement. When crossovered hydrogen approaches the catalyst layer at the nitrogen side, the hydrogen molecule is dissociatively adsorbed onto the surface of platinum catalyst to form Pt-H species (Gennero de Chialvo and Chialvo, 1999; Varela and Krischer, 2001) as written:

$${\text{H}}_2+2\text{Pt}\to 2\text{Pt}-\text{H}$$ (Equation 1)

where Pt-H is the adsorption of hydrogen on platinum. The Pt-H bond is very relaxed allowing the hydrogen to participate in secondary reactions easily with other neighboring substances, which is the final purpose of Pt catalysts (Poulain et al., 1986, 1997). Consequently, a portion of the adsorbed hydrogen is apt to be purged away by the continuous nitrogen flow at the cathode side and this desorption process can be explained by Tafel reaction (Murthy et al., 2018), as described in Equation 2.

$$\text{Pt}-\text{H}+\text{Pt}-\text{H}\to {\text{H}}_2+2\text{Pt}$$ (Equation 2)

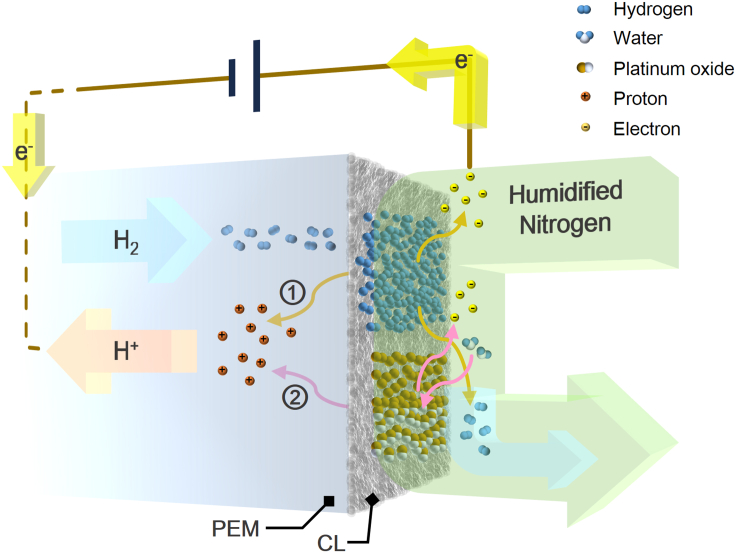
Figure 2.

Schematic Representation of Steady-state Electrochemical Processes

Process ①: oxidation of crossovered hydrogen. Process ②: platinum oxidation.

When the whole system reaches a stable equilibrium state, the rates of these two opposite reactions shown in Equations 1 and 2 tend to reach an equal level and the amount of adsorbed hydrogen on Pt will stay almost constant if there is no external voltage or current imposed on the fuel cell, which is the case in measurement by the direct detection method. As a low and constant voltage is applied in staircase voltammetric experiments, another portion of the adsorbed hydrogen on Pt catalyst at nitrogen side loses electrons and will be oxidized to hydrogen ions, which is presented by Process ① in Figure 2. It is generally believed that the electrochemical oxidation of adsorbed hydrogen atoms accompanied by hydration proceeds via the Volmer reaction (Murthy et al., 2018; Varela and Krischer, 2001):

$$\text{Pt}-\text{H}+{\text{H}}_2\text{O}\to {\text{H}}_3{\text{O}}^{+}+{\text{e}}^{-}+\text{Pt}$$ (Equation 3)

where H3O⁺ is the hydronium ion. The produced hydrogen ions pass through PEM by binding to water molecules, which have been omitted in Figure 2 for a clear display, and react with electrons to generate hydrogen molecules on catalyst layer of the hydrogen side. In the meantime, released electrons flow toward the positive terminal of the voltage source to complete the circuit. In such a case, the amount of hydrogen flowing onto the Pt surfaces of the nitrogen side must be equal to the amount flowing away from it. It means that the sum of the amount of hydrogen purged away by nitrogen flow and the amount consumed for electrochemical oxidation in unit time should balance with the hydrogen crossover rate. If the applied voltage exceeds a certain value, all hydrogen that permeates through PEM will be oxidized to generate electrical current, and there is no more hydrogen carried away by the nitrogen flow. This limiting current equivalent to the hydrogen crossover rate that has been measured by the direct detection method is the so-called hydrogen crossover current.

Besides oxidation of hydrogen crossing the membrane, we consider that the other part of the overall response current results from platinum oxidation, as presented by Process ② in Figure 2. A small amount of platinum is oxidized into platinum oxide at a constant voltage. At the nitrogen side, platinum is positively charged and the oxidation half-reaction represented by Equation 4 takes place.

$$\text{Pt}+{\text{H}}_2\text{O}\to \text{PtO}+2{\text{H}}^{+}+2{\text{e}}^{-}$$ (Equation 4)

As for the pathway for hydrogen ions and the reduction reaction on the hydrogen side, they are the same as described in the previous paragraph. Through electrochemical impedance spectroscopy, it was revealed that the ohmic resistance of the single cell used in our experiments was not more than 3 milliohm and the charge transfer resistance on the hydrogen side turned out to be below 1 milliohm. That is, the ohmic overvoltage across the membrane and the activation overvoltage on the hydrogen side are both negligible. Therefore, it is reasonable to approximate the applied cell voltage as the overvoltage of electrode reactions at the nitrogen side, and the measured current is the sum of two contributions: platinum oxidation and hydrogen oxidation.

In the general case, the current-overpotential characteristic in an electrode reaction can be expressed as:

$$\frac{i}{i_0}=\left(1-\frac{i}{i_{l,c}}\right)e^{-\alpha f\eta }-\left(1-\frac{i}{i_{l,a}}\right)e^{(1-\alpha )f\eta }$$ (Equation 5)

where i is the net current, i₀ is the exchange current, i_l,c is the cathodic limiting current, i_l,a is the anodic limiting current, α is the transfer coefficient, f is a coefficient related to the temperature, and η is the overpotential (overvoltage). This general equation is capable of interpreting the electrode kinetics of the two reactions described in Equations 3 and 4. A simple representation of the current-overpotential curve corresponding to Equation 5 is shown in Figure 3. For sufficiently small η, the approximate form of Equation 5 can be written as:

$$i=-i_{0}f\eta$$ (Equation 6)

which shows that the net current is linearly related to overpotential in a narrow potential range near equilibrium position, as marked in Figure 3. Detailed derivations of Equations 5 and 6 are given in the book (Allen and Larry, 2001). In general, the platinum oxidation reaction can take place continuously at an appreciable rate only when cell voltage exceeds 0.8 V (Génevé et al., 2017), where the reaction has reached ohmic polarization stage. In this experiment, the maximal cell voltage is around 0.45 V, at which the platinum oxidation reaction at the nitrogen side may still stay in the initial stage of activation polarization, and its current change is likely to exhibit linear characteristic in a certain potential range.

Figure 3.

Simple Representation of Stationary Current-overpotential Curve for a General Electrode Reaction

Although two parallel electrode reactions at the nitrogen side have a common overvoltage, the oxidation current of crossovered hydrogen is mainly controlled by mass transfer effect. A higher oxidation current than that determined by the hydrogen crossover rate will never be sustained even if the applied voltage continues to be raised. Owing to the pretty small value of hydrogen crossover rate, the hydrogen oxidation reaction under low voltage excitation can easily enter the limiting current region, which is also circled in Figure 3.

It is then predicted that the limited crossover current is superimposed by a linearly increasing current of platinum oxidation in a certain potential range, and then a linearized relationship between the total response current and applied voltages can be established using the following formula:

$$I=I_{H_2}+K_{Pt}\cdot U$$ (Equation 7)

where I is the total current (A), $I_{H_2}$ is the hydrogen crossover current (A), U is the applied voltage(V), and K_Pt is the slope resulting from platinum oxidation (A·V⁻¹). In dependency of a I−U plot, the values of $I_{H_2}$ and K_Pt can be quantitatively evaluated.

Measured result by PSM

According to the complete signals of current response and voltage excitation in the staircase voltammetric experiment (Figure S3), the steady-state response current is plotted as a function of potential to yield a totally steady-state voltammogram (Figure 4).

Figure 4.

Estimation of Hydrogen Crossover Current by Steady-state Voltammetric Measurements

It can be discovered from Figure 4 that the measured current rises linearly with the voltage in the range of 0.25–0.45 V, which agrees with the prediction in the previous section. The data points in the linear region are selected to fit the first-order linear model given by Equation 7. The result indicates that this simple linear regression fitting is conducted highly successfully using the least squares approach. According to Figure 4, the parameter K_Pt that corresponds to the slope is 87.25 × 10⁻³ A·V⁻¹ and the hydrogen crossover current $I_{H_2}$ represented by the intercept of the fitted line on vertical axis is 35.19 × 10⁻³ A. After repeated experiments (Table S2), PSM is confirmed to have excellent repeatability, and the resulting values of K_Pt and $I_{H_2}$ are, respectively, (87.07 ± 0.48) ×10⁻³ A·V⁻¹ and (35.20 ± 0.29) ×10⁻³ A, which quite coincides with the measurement result from direct detection method with a relative error lower than 2%.

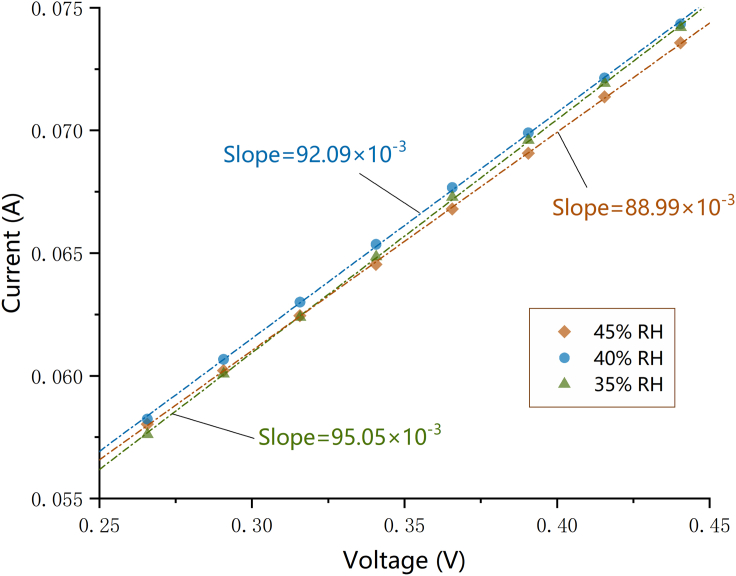
In the past, it was a widely held view that the linear current-voltage characteristics observed in voltammetry were caused by the short-circuit resistance of PEM (Génevé et al., 2017; Giner-Sanz et al., 2014; Huang et al., 2013; Kocha et al., 2006; Pei et al., 2018; Schoemaker et al., 2014; Sugawara et al., 2009). However, there has been no reliable evidence for this view until recently. In this paper, the linear region in the voltammogram has been associated with platinum oxidation reaction as discussed above. To strengthen our argument further, additional experiments were conducted under conditions in which the relative humidity of the gas feed was successively fixed at 45%, 40%, and 35%. The results obtained under different humidity conditions can be compared in Figure 5. It is notable that reducing the water content of the fuel cell leads to a pronounced increase in the slope of the measured data. If the linear current-voltage behavior was a consequence of electronic short circuits, the slope reflecting the electronic conductivity of PEM would not be significantly affected by humidity change, and the short-circuit resistance that restricts the flow of electrons through the membrane was unlikely to be barely 10.52 Ω, which is calculated from reciprocal of the maximal slope in Figure 5. All in all, the evidence presented in this section suggests that the linear current-voltage behavior is not linked to short circuits of PEM.

Figure 5.

Influence of Humidity on Steady-state Voltammetry

Measurement by modified galvanostatic charging method

Analysis of dynamic electrochemical processes with experimental data accompanied

In galvanostatic charging experiments, 11 charging currents are successively applied to the fuel cell. Figure 6 displays the dynamic variations of response voltage with respect to time under different charging currents. It is apparent from this figure that the cell voltage at each current level keeps rising over time, but its increasing rate varies distinctly in different time segments. In addition, it will take more time to reach the cutoff voltage when the charging current is smaller. It is almost certain that the shape of the voltage profile is greatly affected by capacitive processes (Chatillon et al., 2013; Hu et al., 2018; Lee et al., 2012; Pei et al., 2014, 2018), which must be included in the subsequent analysis on dynamic electrochemical processes occurring during galvanostatic charging.

Figure 6.

Dynamic Variations of Response Voltage with Respect to Time under Different Charging Currents

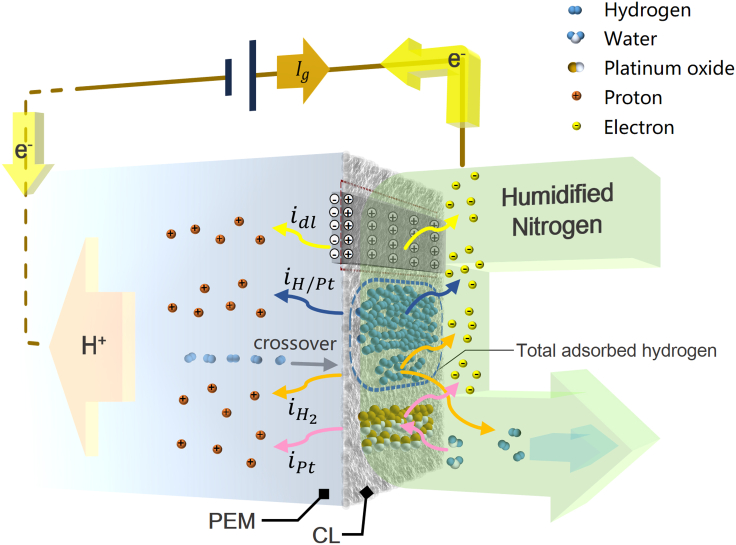
It could conceivably be hypothesized that the constant current supplied by electrochemical workstation is consumed in four ways at the nitrogen side: electrical double-layer charging, hydrogen electro-desorption, oxidation of crossovered hydrogen, and platinum oxidation. The diagram describing these four processes is presented in Figure 7. The electrical double layer is formed at the interface between the catalysts (electrodes) and the PEM (electrolyte). This structure behaves essentially as a capacitor, and the amount of electric charge stored in it is closely linked to the applied voltage. Thus the double-layer charging current i_dl can be given by the product of the capacitance C_dl and the rate of change in voltage $\frac{du}{dt}$, as shown below.

$$i_{dl}=C_{dl}\cdot \frac{du}{dt}$$ (Equation 8)

Figure 7.

Schematic Representation of Four Electrochemical Processes Occurring During Galvanostatic Charging

In general, the double-layer capacitance depending on catalyst loading can be regarded as a constant value (Pei et al., 2018).

In addition to double-layer charging, the hydrogen electro-desorption process behaves also like a capacitive component. It was reported that the quantity of adsorbed hydrogen on platinum is potential dependent in the sense that increase of the applied potential drives hydrogen desorption (Jerkiewicz, 2010). Therefore, the hydrogen desorption reaction, which has been expressed by Equation 3, can be triggered by a change in voltage. With electrons and hydrogen ions liberated, this faradaic charge transfer takes place between electrolyte and electrode. If dQ_H/Pt and du denote, respectively, the charge of oxidative desorption and the change of voltage during elementary time period dt, then the ratio of these two quantities $\frac{d{Q}_{H/Pt}}{du}$ arises that has the properties of a capacitance:

$$\frac{d{Q}_{H/Pt}}{du}=\frac{d{Q}_{H/Pt}/dt}{du/dt}=\frac{i_{H/Pt}}{du/dt}=C_p$$ (Equation 9)

where i_H/Pt is faradaic current generated by the oxidation of adsorbed hydrogen and C_p is differential capacitance value shown by the hydrogen electro-desorption process. C_p is known as hydrogen adsorption pseudocapacitance, which can be treated as some continuous function of potential (Yoo et al., 2009). In other words, this pseudocapacitance is intimately related to the storage quantity of hydrogen on platinum surfaces. Although the electrochemical reaction for the oxidation of crossovered hydrogen and that for the hydrogen electro-desorption have the same nature, for the sake of our analysis, these two current components are considered separately in our study. The former is accountable for the balance of hydrogen flow at each instant, whereas the latter is responsible for the variation of the adsorbed amount between two different potential states. Given that double-layer capacitance and pseudocapacitance both contribute to the total capacitance value, the total capacitive current i_C can be expressed as:

$$i_C=i_{dl}+i_{H/Pt}=(C_{dl}+C_p)\frac{du}{dt}=C_{tot}\cdot \frac{du}{dt}$$ (Equation 10)

where C_tot is the total capacitance. With regard to oxidation of crossovered hydrogen and platinum oxidation, the detailed processes have been discussed in the previous analysis on PSM. Taken together, the total charging current I_g can be written as:

$$I_g=i_C+i_{H_2}+i_{Pt}$$ (Equation 11)

where $i_{H_2}$ is the current resulting from oxidation of crossovered hydrogen, i_Pt is the current component used to oxidize platinum, and all terms on the right side of the equal sign are instantaneous variables. In the next paragraphs, the composition changes of the total current during charging will be discussed in combination with experimental data.

Since shapes of the response curves shown in Figure 6 are quite similar at different charging currents, the measured data at the constant current of 100 mA is picked out as a sample to dissect the charging process (Figure 8A). According to the above theoretical analysis, it is clear that the instantaneous rate of voltage change $\frac{du}{dt}$ has emerged as an important variable for the determination of the relative changes in magnitude between different current components. For this reason, the $\frac{du}{dt}-t$ curve derived from the raw data with a charging current of 100 mA is plotted (Figure 8B). Data obtained by PSM have revealed that the current component for oxidation of crossovered hydrogen under low voltage excitation is much larger than that for platinum oxidation. Therefore, platinum oxidation current is ignored here for the sake of analysis simplicity, as the approximation showed below.

$$I_g\approx i_C+i_{H_2}$$ (Equation 12)

Figure 8.

Data Obtained from Galvanostatic Measurement with a Charging Current of 100 mA

(A) u−t curve.

(B) $\frac{du}{dt}-t$ curve.

This relationship suggests that when one current component is falling, the other is rising.

At the initial moment of the charging process (i.e., Point A marked in Figure 8B), the capacitive effect dominates (Allen and Larry, 2001) so that the vast majority of total current contributes to charging C_tot. Based on this, the initial value of C_tot can be calculated as:

$$C_{tot-init}=\frac{I_g}{{\frac{du}{dt}}^A}$$ (Equation 13)

where C_tot−init is the total capacitance before charging and ${\frac{du}{dt}}^A$ is the voltage variation rate at the initial time point. To avoid error from smoothed data, the value of ${\frac{du}{dt}}^A$ is determined from the slope of the tangent to the voltage-time curve at Point A, which is obtained by plotting a line of best fit through the nearby data points (Figure 8A). It can be inferred that almost all of crossovered hydrogen is blown away by nitrogen gas stream at this instant, which is the same as the equilibrium situation where no current has been applied, as described in Figure 9A. Then, after this point, i_C gradually decays (Allen and Larry, 2001) and in contrast, $i_{H_2}$ starts to increase. In line with the downward trend in i_C, $\frac{du}{dt}$ is observed to steadily decline and exhibit low values between Point A and Point B (Figure 8B). During this time period, the system can be assumed to operate in a quasi-steady state, where the quantity of adsorbed hydrogen on catalyst layer is changing slowly enough and the amount of hydrogen flowing onto the Pt surfaces in unit time can be considered equal to the amount flowing away from it. Here, we believe that there are two paths for crossovered hydrogen to leave the catalyst layer of nitrogen side: one is being converted into protons to produce the current $i_{H_2}$, and the other is getting carried away by the continuous nitrogen flow (Figure 9B). On the background that the hydrogen crossover rate remains virtually constant throughout the entire charging process, as $i_{H_2}$ progressively increases, the amount of hydrogen streaming into the gas flow channel of the nitrogen side will be reduced accordingly. It is worth noting in Figure 8B that $\frac{du}{dt}$ hits its minimum at Point B and then begins to rise dramatically. A viable explanation for this phenomenon can be that $i_{H_2}$ exactly balances out the hydrogen crossover rate at Point B (Figure 9C). After this brief moment, $i_{H_2}$ continues to experience an upward trend, and consequently the hydrogen permeation flow is no longer able to compensate for oxidative consumption of hydrogen, resulting in a massive loss of adsorbed hydrogen over a short time (Figure 9D). On the one hand, when the adsorbed hydrogen participating in the electrode reaction described by Equation 3 is in short supply, the polarization overpotential becomes quite elevated, which is similar to reactant starvation in PEM fuel cells. On the other hand, according to Equation 10, depletion of adsorbed hydrogen on the electrode surface causes a rapid reduction in the total capacitance, thereby driving $\frac{du}{dt}$ sharply higher. Under the joint action of the above two factors, $\frac{du}{dt}$ exhibits a steep increase between Point B and Point C (Figure 8B). Nevertheless, it is impossible for C_tot to fall without any limit owing to the presence of double-layer capacitance. So, as $\frac{du}{dt}$ increases to a certain extent, i_C will reverse its declining tendency and thus suppress $i_{H_2}$ back to lower levels (Figure 9E). In that case, hydrogen crossover can replenish adsorbate for the catalyst layer, enabling the reactant starvation to be alleviated and the aberrant overvoltage to recover. Furthermore, the partly restored total capacitance will substantially curb the fast variations of voltage again. It is this series of coupled processes that brings on a drop-off in $\frac{du}{dt}$ after Point C (Figure 8B). In summary, the data from Point B, where $i_{H_2}$ matches the hydrogen crossover current, are especially crucial for the measurement of hydrogen crossover.

Figure 9.

Variations of Electrochemical Processes Throughout the Entire Charging Process

(A) At Point A.

(B) Between Point A and Point B.

(C) At Point B.

(D) Between Point B and Point C.

(E) After Point C.

Charging model and results of modified GCM

To build a theoretical model with high accuracy, the platinum oxidation reaction should be again taken into consideration. In this way, the charging model, which only applies to the point where $\frac{du}{dt}$ achieves the minimum value, is mathematically described as:

$$I_g=C_{tot}^B\cdot {\frac{du}{dt}}^B+K_{Pt}\cdot U^B+I_{H_2}$$ (Equation 14)

where $C_{tot}^B$, ${\frac{du}{dt}}^B$, and U^B represent the total capacitance, voltage variation rate, and voltage value at Point B, respectively. The approach of obtaining ${\frac{du}{dt}}^B$ is identical with that of obtaining ${\frac{du}{dt}}^A$ (Figure 8A). For different charging currents, data processing and selection were conducted under the same procedures, and the obtained values of ${\frac{du}{dt}}^B$ and U^B from u−t curves are listed in Table 1. It is interesting to note that there is a significant positive correlation between ${\frac{du}{dt}}^B$ and I_g, but values of U^B throughout the dataset only fluctuate within a small range. It can therefore be assumed that the total capacitance $C_{tot}^B$ at Point B in our study shares a common value under each charging condition, which is based on the tight connection between potential and adsorption amount, as mentioned earlier. Likewise, owing to the stable operating conditions in our experiments, $I_{H_2}$ and K_Pt can be considered to be unchanged as well. Hence, $C_{tot}^B$, K_Pt, and $I_{H_2}$ can be regarded as three parameters in the multivariate model (Equation 14), where ${\frac{du}{dt}}^B$ and U^B are input variables and I_g is deemed to be the single outcome variable. Then the trust region algorithm is adopted to fit the charging model to the data in Table 1. As can be seen from the fitted result (Figure 10), the orange plane, representing the well fit model, matches these data points nicely. Evidently, this linear model can be trusted to provide a reasonable description of relationships between multiple variables. The best-fit values for the parameters are K_Pt = 89.35 × 10⁻³ A·V⁻¹ and $I_{H_2}=34.49\times {10}^{-3}$ A (Figure 10). After repeated experiments (Table S2), GCM is confirmed to have satisfactory repeatability, and the resulting values of K_Pt and $I_{H_2}$ are, respectively, (90.64 ± 1.09) ×10⁻³ A·V⁻¹ and (34.43 ± 0.13) ×10⁻³ A. Compared with the result obtained by PSM, the estimation of K_Pt with GCM produced a relative error around 4%, and with the direct detection method designated as the reference method, the relative error on measurement of hydrogen crossover is only 3.449%, demonstrating that the GCM implemented in our study possesses a high degree of accuracy.

Table 1.

Values of ${\frac{\mathit{du}}{\mathit{dt}}}^{\mathit{B}}$ and U^B under all applied charging currents

Ig	${\frac{\mathit{du}}{\mathit{dt}}}^{\mathit{B}}$	UB
0.0900	0.00674	0.2500
0.0917	0.00740	0.2503
0.0936	0.00776	0.2509
0.0956	0.00805	0.2507
0.0978	0.00843	0.2501
0.1015	0.00921	0.2516
0.1036	0.00964	0.2513
0.1053	0.01006	0.2514
0.1073	0.01044	0.2522
0.1093	0.01087	0.2520
0.1116	0.01136	0.2528

Figure 10.

Fitting the Multivariate Linear Model (Orange Plane) to Data Points (Gray Spheres)

Although the galvanostatic technique has been introduced to measure hydrogen crossover in a few previous studies, there is still no unified strategy for the extraction of appropriate data. Lee et al. utilized the information of experiment data over an appropriate voltage range, where the u−t curves show a large slope, for the evaluation of hydrogen crossover current (Lee et al., 2012), but how to determine the boundary of this voltage range was not specified. By contrast, Chatillon et al. merely picked out a single data point in each curve, which corresponds to Point C (Figure 8B), to carry out model fitting (Chatillon et al., 2013). However, the uniqueness in data selection has not been fully rationalized by the author, and similar imperfections also existed in the studies by Pei et al. (2014, 2018) and by Hu et al. (2018). Among the five published studies mentioned above, only Pei et al. used the results measured by trace analytical technique to examine the effectiveness of measured results and proposed the most complete charging model to date (Pei et al., 2018). Nonetheless, the measurements in their paper could only attain sufficient precision when the selected data points lay in the middle of the whole voltage range, which was hard to pre-delimit without enough experiments.

In our work, the GCM is modified by proposing a novel scheme for data processing, and the corresponding theoretical support for it is also provided. Meanwhile, in the charging model employed in our study, the short-circuit resistance dependent term that was considered in previous research (Pei et al., 2018) is replaced with a term proportional to voltage, which stems from platinum oxidation reaction. In an attempt to measure hydrogen crossover current by this modified method, we just need to convert the potential versus time data obtained from galvanostatic measurements with various charging currents into $\frac{du}{dt}-t$ curves rather than $\frac{dQ}{du}-u$ curves or $\frac{du}{dt}-u$ curves, as was the case in earlier studies (Chatillon et al., 2013; Lee et al., 2012; Pei et al., 2014, 2018), and then extract the lowest point in each curve for further model fitting. Therefore, besides high estimation accuracy, the modified GCM also has the advantage of efficient data extraction.

Further verification of the validity of modified GCM

To assess the rationality of fitted result for the parameter $C_{tot}^B$, the initial values of total capacitance under all applied charging currents are calculated according to Equation 13. Based on the tangential slope at the initial point of the u−t curve, C_tot−init is calculated to be 6.513 ± 0.055 F, which turns out to be larger, as expected, than the resulting value of the fitted parameter $C_{tot}^B$ (4.811 F) in Figure 10, and this difference between two values may be due to the hydrogen desorption between Point A and Point B. Hence, in addition to K_Pt and $I_{H_2}$, the fitted result for $C_{tot}^B$ can also be considered acceptable to some extent.

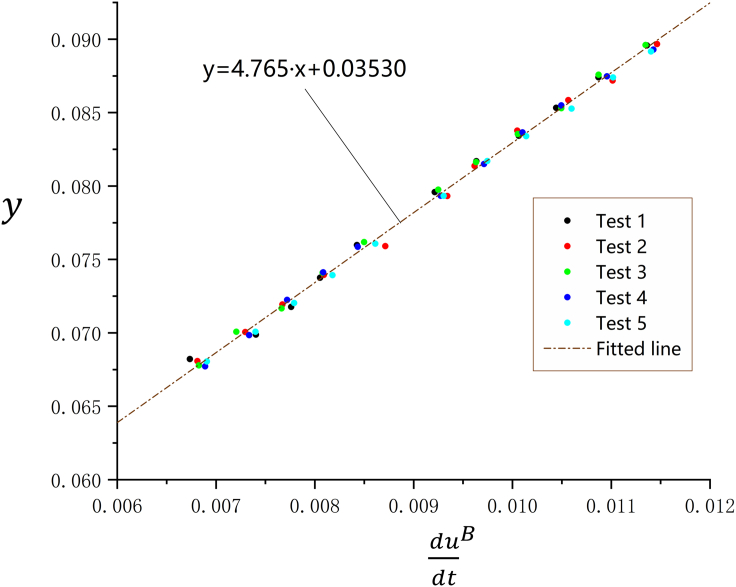
In order to further verify the validity of modified GCM, the estimated parameter K_Pt obtained from PSM is introduced for dimension reduction of charging model. In this way, the multivariate model (Equation 14) can be simplified as:

$$y=I_g-K_{Pt}\cdot U^B=C_{tot}^B\cdot {\frac{du}{dt}}^B+I_{H_2}$$ (Equation 15)

where K_Pt is the fitted slope of the I−U plot obtained by PSM and y is the newly introduced auxiliary variable, whose value is determined by I_g and U^B. Here, K_Pt becomes a constant, and then a linear relationship between the single input variable ${\frac{du}{dt}}^B$ and the single output variable y can be assumed by this simple linear regression model, in which $C_{tot}^B$ and $I_{H_2}$ represent the two model parameters to be estimated. Based on the data from repetitive experiments, five new sets of data that contain both input and output data can be constituted for the linear regression. The 55 data points are then plotted in a two-dimensional coordinate system with ${\frac{du}{dt}}^B$ on the abscissa and y on the ordinate, and the method of least squares is used to find the best-fitting line. As evidenced in Figure 11, the data points are tightly distributed around the fitted line, which reflects an excellent fitting degree, and this fitted line has a slope of $C_{tot}^B=4.765$ F and a y-intercept of $I_{H_2}=35.30\times {10}^{-3}$ A. It is surprising to note that the fitted result for $C_{tot}^B$ is quite close to that obtained by modified GCM, and the estimated value of $I_{H_2}$ is still basically consistent with the result measured by the direct detection method, which further proves that the charging model (Equation 14) is suitable to describe the relations among variables quantitatively. Collectively, we can conclude that the modified GCM and the exposition on electrochemical processes occurring during its implementation are valid.

Figure 11.

Fitting the Simple Linear Regression Model (Brown Line) to All Data Points

Conclusions

• (1)The linear region existing in steady-state voltammograms is considered to be caused by platinum oxidation rather than short-circuit resistance mainly due to the fact that the resulting slope can be remarkably affected by humidity change, and the current component linked to this linear feature is also reflected in the galvanostatic tests.
• (2)Both the PSM and the modified GCM can accurately measure the hydrogen crossover current of PEM fuel cell and have excellent repeatability. Besides owning high accuracy, the modified GCM also enables more explicit and efficient data extraction compared with previous methods. In addition, this galvanostatic analysis technique is capable of determining the initial total capacitance of fuel cell, which consists of double-layer capacitance and pseudocapacitance.
• (3)The analysis for the electrode processes throughout implementation of electrochemical methods is valid and the theoretical model employed in this study can satisfyingly describe the relationship among multiple variables.

This study represents a significant advance in the development of in situ, low-cost, high-accuracy, and quantitative analytic tools for lifespan evaluation and failure diagnosis of PEM fuel cells. The modified GCM proposed in our study provides a powerful tool allowing accurate measurements of the hydrogen crossover in fuel cell, which will serve as an important basis for the development of a new aging characterization technique for fuel cell stack. Meanwhile, this research verifies the PSM as another valid tool for measuring hydrogen crossover. This work also enhances our understanding on the principles of electrochemical methods for measuring hydrogen crossover by providing systematic analysis of corresponding electrode processes, which may help to guide the optimization of electrochemical measurement methods for fuel cells.

Limitations of the study

On the premise that the stability of model fit is guaranteed and simultaneously the application condition of charging model is not violated, the number of charging times and the magnitude of charging currents in the galvanostatic charging method need to be further optimized so as to shorten the data acquisition time.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and algorithms
Origin 2018	OriginLab	https://www.originlab.com/
MATLAB R2014b	MathWorks	https://www.mathworks.com/
Other
MEA	Yangtze Energy Technologies	http://www.fc-mea.com/
850e Fuel Cell Test System	Scribner Associates	https://www.scribner.com/
Agilent 5977B GC/MSD	Agilent Technologies	https://www.agilent.com.cn/
Electrochemical workstation, DH7000	Donghua Test	http://www.dhtest.com/

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Haifeng Dai (tongjidai@tongji.edu.cn).

Materials availability

This study did not generate new unique reagents.

Experimental model and subject details

The experimental subject in this study is a single PEM fuel cell with an active area of 25 cm² for the membrane electrode assembly (MEA). The MEA, which is composed of PEM, catalyst layer (CL) and gas diffusion layer (GDL), with platinum loadings of 0.3 mg·cm⁻² at the cathode and 0.1 mg·cm⁻² at the anode was commercially produced by Yangtze Energy Technologies. The PEM from Gore-Select®, which uses expanded polytetrafluoroethylene (ePTFE) as a reinforcing material, has a thickness of 18 μm. The end plates, the graphitic bipolar plates and the MEA were uniformly assembled by a torque wrench whose clamping pressure was 10 N·m, which was possibly a suitable clamping pressure for this MEA to avoid reactant leakages on the premise of not destroying the porous layer.

Method details

Fuel cell test bench

All tests were performed on the Scribner 850e fuel cell test bench. Figure S1 displays the photograph of the fuel cell and test bench. Hydrogen, nitrogen or air are supplied by volumetric flow controllers of high accuracy and inlet gas pressure is regulated through the back-pressure module. As the supplied gas passes through humidifier, it will be saturated with moisture at a set dew point temperature. Generally, the relative humidity of inlet gas is obtained by calculating the percentage of the saturated vapor pressure at the dew-point against the saturated vapor pressure at the cell temperature. So the relative humidity of inlet gas could be adjusted by changing the humidifier temperature and fuel cell temperature. A thermocouple is placed at the anode to monitor the cell temperature and two heating rods producing heat are inserted into the holes in both end plates. According to real-time feedback, the test bench stabilizes the cell temperature at a given value by controlling the heating power automatically. This test bench also contains an electronic load which makes the fuel cell operate at certain currents. Variable conditions can be controlled by specifying desired parameters on the host computer connected to the test bench.

For all measurements, humidified hydrogen was supplied to anode while humidified nitrogen was supplied to cathode. The relative humidity of gases at both sides was set at 50%. The flow rates of hydrogen and nitrogen were both set at 300 standard cubic centimeter per minute (SCCM) and gas pressures of both anode and cathode sides were always atmospheric. To reach the expected relative humidity condition, the dew point of humidified gases at both sides was stabilized at 46°C and the cell temperature was maintained at 60°C. Unless otherwise specified, all the measurements described in this study were carried out at the same operation conditions.

Experimental details of direct detection method

The trace analytical technique, which combines gas chromatograph with mass spectrometer (GC-MS) to identify trace substances within a test sample, has been adopted to establish a reliable reference value of hydrogen crossover rate for electrochemical methods. Given that the GC-MS is not easily available in our lab, we collected the exhaust gases at nitrogen side in sampling bags and entrusted a third party testing laboratory with appropriate qualifications to conduct corresponding tests. The schematic diagram of this method is given in Figure 1. Nitrogen containing a small amount of hydrogen flowed first through the moisture trap, which was used to eliminate the interference of water in the exhaust. The sampling bag was installed in a bypass line near outlet to collect the dehydrated gas mixture, and this process took at least 20 min to achieve a steady-state gas distribution in the sampling bag, which was soon afterwards sent to be analyzed. Finally the detecting results were given in mole fraction of hydrogen in the gas mixture.

Experimental details of electrochemical methods

The electrochemical workstation DH7000, which served as a power source to apply staircase potentials or constant currents to the single cell, was utilized in electrochemical experiments. In this case, the fuel cell could be regarded as a load and its anode and cathode collectors were connected to negative and positive of the external power source, respectively. The schematic diagram of experimental setups for two electrochemical methods is depicted in Figure S2. Reference electrode (blue) and counter electrode (red) were connected to the collector plate at hydrogen side, and working electrode (green) and sensing electrode (yellow) were connected to the collector plate at nitrogen side. All control signals and measured data were transmitted between the host computer and electrochemical workstation via Ethernet cable, and the sampling frequency was set to 10 Hz.

In the measurement by employing the potential step method, a staircase potential signal was applied, i.e., the potential of the working electrode was stepped through a series of increasing steps from the initial potential to approximately 0.45 V, at which all hydrogen that has crossed over from the anode to the cathode should be completely oxidized. In order to strike a balance between accuracy and efficiency of this measurement, the amplitude and duration time of each successive step were set to 0.025 V and 30 s, respectively. Figure S3 presents the complete signals of current response and voltage excitation in the staircase voltammetric experiment. As is exhibited in the zoomed view, the current response drops exponentially as a result of the capacitive charging effect and finally tends towards a constant at the end of step period, where the ultimate data is acquired. The steady-state value of response current under each applied potential was acquired by averaging the sampled values in the last 1 s of each step. Then the response current was plotted as a function of potential to yield a totally steady-state voltammogram, as shown in Figure 4.

During the galvanostatic tests, the electrochemical workstation was switched to constant current mode and the fuel cell was successively charged with 11 different constant currents in the range of 90 mA to 110 mA. The response voltage signals were collected from the initial potential up to 0.55 V for each charging process and then the power source was automatically disconnected from the single cell to avoid the irreversible platinum or carbon oxidation at high potentials. When the end voltage of fuel cell returned to a steady level around the initial value, the same operation was applied to the next charging current, until all 11 galvanostatic charging tests were completed. The response voltages with respect to time under different charging currents are shown in Figure 6. The tangents to the voltage-time curve, whose slopes represent ${\frac{du}{dt}}^A$ and ${\frac{du}{dt}}^B$, are obtained by plotting a line of best fit through five points nearest to Point A and Point B.

Calculation procedure of direct detection method

Through the GC-MS testing, the mole fraction of trace hydrogen gas in the gas mixture at nitrogen side was successfully determined, which turned out to be 850±16 ppm (parts-per-million). In general, the hydrogen crossover can be calculated by the following equation:

$$J_{H_2}=x_{H_2}\cdot J_{total}$$ (Equation 16)

where $J_{H_2}$ is hydrogen crossover rate (mol·s⁻¹), $x_{H_2}$ is mole fraction of hydrogen gas in the gas mixture, and J_total is total molar flow rate of gas mixture (mol·s⁻¹). Obviously, the $x_{H_2}$ and J_total in Equation 16 can be approximated as:

$$x_{H_2}\approx \frac{J_{H_2}}{J_{N_2}}$$ (Equation 17)

$$J_{total}\approx J_{N_2}$$ (Equation 18)

where $J_{N_2}$ is molar flow rate of nitrogen gas (mol·s⁻¹). Since the volumetric flow controller for nitrogen gas is designed to control the volumetric flow rate to a given setpoint, the volumetric flow rate of nitrogen with units of cubic centimeter per minute at standard temperature and pressure (STP) needs to be converted into the form of molar flow rate with units of mol·s⁻¹:

$$J_{N_2}=\frac{Q_{N_2}}{60}\cdot \frac{{\rho }_{N_2}}{M_{N_2}}$$ (Equation 19)

where $Q_{N_2}$ is volumetric flow rate of nitrogen gas at STP (SCCM), ${\rho }_{N_2}$ is density of nitrogen gas at STP (g·cm⁻³), and $M_{N_2}$ is molecular weight of nitrogen gas (g·mol⁻¹). According to the above equations, Equation 16 can be rewritten as:

$$J_{H_2}=x_{H_2}\cdot \frac{Q_{N_2}}{60}\cdot \frac{{\rho }_{N_2}}{M_{N_2}}$$ (Equation 20)

with this simple equation, the value of hydrogen crossover rate is calculated to be (1.848±0.034) ×10⁻⁷ mol·s⁻¹.

For straight comparisons of measurement results between the direct detection method and electrochemical methods, the hydrogen crossover rate is converted into an equivalent current of hydrogen crossover using Faraday's law:

$$I_{H_2}=n\cdot F\cdot J_{H_2}$$ (Equation 21)

where $I_{H_2}$ is hydrogen crossover current (A), n is number of electrons transferred in hydrogen oxidation reaction (HOR) per hydrogen molecule, and F is Faraday constant (C·mol⁻¹). Values of parameters and constants used in above calculations are listed in Table S1 and the calculated hydrogen crossover current is 35.66±0.66 mA.

Published: January 21, 2022

Data and code availability

• •All data reported in this paper will be shared by the lead contact upon request.
• •This paper does not report original code.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.