Differential analysis of binarized single-cell RNA sequencing data captures biological variation

Abstract

Single-cell RNA sequencing data is characterized by a large number of zero counts, yet there is growing evidence that these zeros reflect biological variation rather than technical artifacts. We propose to use binarized expression profiles to identify the effects of biological variation in single-cell RNA sequencing data. Using 16 publicly available and simulated datasets, we show that a binarized representation of single-cell expression data accurately represents biological variation and reveals the relative abundance of transcripts more robustly than counts.

INTRODUCTION

Single cell RNA sequencing (scRNAseq) data are highly sparse, and the common belief is that the zero values are primarily caused by technical artifacts (often referred to as dropouts). Although more zeros are observed in scRNAseq data than expected, these can largely be explained by biological rather than technical factors (1). Also, the amount of zeros in scRNAseq is in line with distributional models of molecule sampling counts (2,3). These distributional models show that a zero observation is not simply a missing-value, as a missing-value would provide no information. On the contrary, a zero observation for a gene reveals that the respective gene is unlikely to be highly expressed (3). Methods that utilize zero observations for feature selection (4,5) and cell type clustering (6) have recently been developed and perform better or comparable with methods relying on the continuous expression values of highly variable genes. For instance, Qiu (6) binarized scRNAseq count data, where each zero remains zero and every non-zero value was assigned a one. With this binary representation, cell type clusters were identified based on co-occurrence of transcripts. Yet, it is not clear whether differences in the number of zeros for a gene also reflect differences across distinct biological cell populations. Therefore, we investigated whether biological differences across cell population can be identified using Binary Differential Analysis (BDA) rather than the commonly used differential expression analysis (DEA). Instead of relying on changes in the expression value of genes across cell populations, which can be sparse and are subject to pre-processing steps, we analyzed the binary expression patterns across biological distinct cell populations, i.e. are there more (or less) zeros for a gene in condition A compared to condition B. Taken together the main contribution of our work is that we show that the binarization of gene expression is biologically relevant and can be used to test for differences between a wide variety of groupings, and that this holds across different datasets, as well as different single-cell protocols.

MATERIALS AND METHODS

Single-cell RNA-seq datasets

In total, 16 scRNAseq dataset (14 human and 2 mouse) were used to investigate the utility and biological relevance of binarized expression profiles of genes (Table 1). All datasets had pre-annotated cell types and conditions. From the corresponding references, un-normalized count matrices were acquired, and only annotated cells were kept for further analysis. For each dataset, we extracted the annotated cell type, patient ID, and to which of contrasting cell population the cell belonged from the included meta data. This was slightly different for the aging mouse atlases and cancer atlas. For the aging mouse atlases (7), instead of annotated cell types we retrieved the tissue names. For the cancer atlas (8), the contrasting cell populations were defined by cell type, so we retrieved the tissue and the cancer-type for each cell. Each dataset was separately pre-processed. For BDA, the count matrices were transformed to a binary representation, where each zero remain zero and every non-zero value was assigned a one. For the DEA, each count matrix was log-normalized using Seurat 3.2.2 (9), such that , where 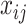and are the raw and normalized values for every gene in every cell 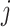, respectively. This normalizes the feature expression measurements for each cell by the total expression, multiplies this by a scale factor (10 000 by default), and log-transforms the result. The cancer atlas was already normalized, as it was a merger of multiple datasets.

Table 1.

Single cell datasets included in this study.

Dataset	No. of unique individuals	No. of cells	No. of genes	Contrasting subpopulation defined by:	Description	Protocol	Reference
Alzheimer’s Disease (AD)	14	13 214	10 850	Control versus AD	Entorhinal cortex	10x Chromium	(21)
Major Depressive Disorder (MDD)	34	78 886	30 062	Control versus MDD	Prefrontal cortex	10x Chromium	(31)
Type 2 Diabetes (T2D)	10	3514	26 271	Control versus T2D	Pancreas	Smart-seq2	(32)
Coronavirus Disease 2019 (COVID19)	13	44 721	26 361	Control versus COVID19	PBMCs	Seq-Well	(33)
Lung adenocarcinoma (LUAD, Lung)	22	88 144	29 634	Normal tissue versus cancerous tissue	Lung	10x Chromium	(34)
Lung adenocarcinoma (LUAD, Lymph node)	17	54 577	29 634	Normal tissue versus cancerous tissue	Lymph node	10x Chromium	(34)
Four cancers (T-cells)	14	132 549	22 815	Normal tissue versus cancerous tissue	Colon, Endo, Lung, Renal	10x Chromium	(35)
Aging Mouse Atlas FACS	14	74 157	22 966	3m versus 24m	Aging mouse	Smart-seq2	(7)
Aging Mouse Atlas Droplet	11	83 262	20 138	3m versus 24m	Aging mouse	10x Chromium	(7)
Allen Brain Atlas (Medialis temporalis Gyrus)	8	14 689	48 304	Inhibitory neurons versus excitatory neurons	Medialis temporalis Gyrus	Smart-Seq v4	(36)
Colorectal Cancer	23	63 502	27 946	Normal tissue versus cancerous tissue	Colon CRC cells	10x Chromium	(37)
Cortex Neurons	5	9451	28 985	Inhibitory neurons versus excitatory neurons	Cortex	10x Chromium	(25)
Cortex Oligodendrocytes	5	307	28 985	OPC versus ODC	Cortex	10x chromium	(25)
Substantia Nigra	7	4711	28 985	OPC versus ODC	Substantia Nigra	10x chromium	(25)
Cancer Atlas (1)	171	33 346	50 705	Regulatory T cells versus T helper cells	Cancer atlas	Multiple	(8)
Cancer Atlas (2)	162	30 105	48 942	Naive-memory CD4 T cells versus Transitional memory CD4 T cells	Cancer atlas	Multiple	(8)

Statistical analysis

P-values were corrected for multiple tests with the Benjamini–Hochberg procedure and significance was assumed at an adjusted P-value of P_FDR ≤ 0.05. Spearman’s rank correlation coefficient and the associated P-values were calculated using the cor.test function in R v4.0.2.

Differential expression analysis

DEA was performed using the Wilcoxon Rank Sum test using the FindMarkers function in Seurat 3.2.2 (9). Note that the Wilcoxon Rank Sum test from Seurat takes into account zero measurements and handles them as ties between contrasting cell populations. Genes coding for ribosomal proteins were excluded and we only tested genes that were expressed in at least 10% of the cells in either of the respective groups of interest. This is the default option in the FindMarkers function and speeds up testing by ignoring infrequently expressed genes. P-values were corrected for multiple tests.

Binary differential analysis (BDA)

As the sampling process of biomolecules is the main cause for generating zeros, as illustrated by Svensson (2) and Sarkar and Stephens (3). The probability of measuring a gene is dependent on the relative abundance; more abundant genes are less likely to result in a zero observation. Extrapolating this to a population of cells, the number of zeros for a gene is representative of the abundance within the respective cell population, and differences in the number of zeros between two groups of cells are representative of differential abundance. Lastly, we assume that within a single-cell experiment zeros induced by stochastic processes are not confounded by the groupings. In other words, a stochastically induced zero is equally likely to happen in either cell population, as such, in this setting can be ignored.

Implementation

In the main analyses, to statistically test for significant differences of zero observations between pre-defined groups in scRNAseq data, we used a logistic regression (BDA-LR). Specifically, the glm(family = ‘binomial’) function in R v4.0.2, with the binarized expression pattern of the genes as outcome variables and the grouping (i.e. healthy versus diseased) as predictor variable. We have used logistic regression because it allows to add covariates to correct for potential confounding factors. Moreover, predictor variables as well as covariates can be continuous, allowing for complex study designs. All genes that were tested with DEA were also tested with BDA. The resulting association P-values were corrected for multiple tests (see Statistical analysis). In addition to logistic regression, we used the Chi-squared test (BDA-chisq), the Fisher’s exact test (BDA-fisher) and binary Pearson's correlation (BDA-Phi) on the simulated data. The Chi-squared test and the Fisher’s exact tests were performed with the chisq.test() and fisher.test() R functions, respectively. These tests were performed for each gene on the contingency table representing the binarized gene expression against the pre-defined groupings. The binary Pearson’s correlation was calculated between each binarized gene and the pre-defined groupings and performed with the cor.test() R function, where one group was defined as 0 and the other group as 1. In a binary setting the outcome statistic of Pearson’s correlation is called Phi (φ).

BDA–DEA comparison

For the comparison between BDA and DEA, we investigated agreement and disagreement between detected genes and the linear association between the logOR and logFC. Agreement was calculated by the Jaccard index, i.e. number of genes that both tests commonly detected, divided by the total number of genes that were detected. Agreement was calculated on the combination of all datasets and for each individual dataset. The disagreement was investigated by means of inspecting characteristics of BDGs-only and DEGs-only. BDGs-only were defined as genes that were detected (P_FDR ≤ 0.05) by BDA and were not detected (P_FDR > 0.05) by DEA. Conversely, DEGs-only were defined as genes that were detected (P_FDR ≤ 0.05) by DEA and were not detected (P_FDR > 0.05) by BDA. The Spearman’s rank correlation coefficients between the logOR and logFC were calculated with the estimates of all tested genes of the respective datasets. The scale differences for every dataset, between logOR and logFC, were calculated with a linear model on the estimates of all tested genes of the respective datasets, using the lm function in R v4.0.2. The logOR was specified as outcome variable and the logFC as predictor variable. The resulting slopes were interpreted as scale differences between the logOR and logFC

Simulation

Data were simulated with muscat 1.2.1 (10). The provided PBMC dataset (11) was used as reference. In total, 100 simulated datasets were generated with varying sample sizes (1000 cells, 2000 cells, 5000 cells and 10 000 cells), 25 simulations per sample size. For each simulation 1000 genes were generated of which 25% were differently expressed between two groups of equal size. For all tests we calculated the False Positive Rate (FPR), Positive Predictive Value (PVV) and accuracy (F1-score) per simulation. Performance was evaluated of 12 DEA methods. Eight methods implemented in Seurat (wilcox, bimod, t, negbinom, poisson, LR, MAST (12), DESeq2 (13)), 4 additional methods (DEsingle (14), BPSC (15), monocle (16), limmaVoom (17)) and 4 BDA methods (logistic regression, chi squared test, Fisher’s exact test and binary Pearson’s correlation). For the runtime benchmark, each run of the simulation of every tests was also timed with proc.time()function in R. Tests requiring >20 min computational time on one simulated dataset were excluded.

Validation with existing bulk RNA-seq data

The AD bulk RNA-seq datasets were acquired from Gemma (18). The first dataset from Friedman et al. (19) consisted of 33 controls (CT) and 84 samples from individuals diagnosed with Alzheimer’s Disease (AD) collected from the fusiform gyrus. This dataset was reprocessed by Gemma and no batch effects were present. For the differential expression analysis in bulk we used the Wilcoxon Rank Sum test from limma v3.44.3 (20). In total, 2228 genes were tested for differential expression, as these genes were also included in the scRNAseq AD dataset (21) analysis. The second dataset from Hokama et al. (22) consisted of 47 controls and 32 AD samples. The samples originated from the frontal cortex (N_CT = 18, N_AD = 15), temporal cortex (N_CT = 19, N_AD = 10) and hippocampal formation (N_CT = 10, N_AD = 7). The data was reprocessed and batch corrected by Gemma. For the differential expression analysis no distinction was made between brain regions. In total, 2001 genes were tested for differential expression. All resulting association P-values were corrected for multiple tests. For validation, the significant BDGs and DEGs from the scRNAseq AD dataset analyses were compared with the significantly differentially expressed genes from the bulk analyses. Venn diagrams were plotted with ggVennDiagram(v0.3) (23). Correlations were calculated between the logOR and logFC of the single-cell analysis with the bulk logFC.

RESULTS

BDA competitive with Wilcoxon Rank Sum test

As proof of concept, we performed BDA with a simple logistic regression on binarized expression profiles from 16 scRNAseq datasets (662 825 cells in total, Table 1). We compared the results of BDA-LR with those of differently expressed genes (DEGs) detected using the commonly used Wilcoxon Rank Sum test, which is also top ranked for single cell analyses (9,24). We tested each gene using both BDA-LR and DEA for differences between conditions (6 datasets), cell types (6 datasets) and normal versus cancerous tissues (4 datasets, Figure 1A). Across all datasets, a total of 96 275 significant genes (P_FDR ≤ 0.05) were identified with either BDA-LR (92 381 genes) or DEA (91 521 genes). Of these, 87 627 were identified by both tests, resulting in a Jaccard index of 0.91. This high degree of agreement is also reflected in each individual dataset (median = 0.92, minimum = 0.76, and maximum = 0.99). We did not use a log fold-change (logFC) or log odds-ratio (logOR) threshold, as for each dataset and comparison different thresholds are appropriate. In all datasets, the logFC and logOR were significantly (spearman) correlated (median (ρ) = 0.90, minimum (ρ) = 0.49 and maximum (ρ) = 0.98, P ≤ 5 × 10^–100). The three datasets with the lowest correlation coefficient between logOR and logFC (ρ ≤ 0.62) were datasets generated using the Smart-seq protocol (Table 1). Across the datasets, we observed an average increase of 1.80 in logOR (median = 1.70, Q₁ = 1.59, Q₃ = 2.10), for every increase in logFC (see Figure 1B for the cancer atlas (2) dataset (8)). The high degree of agreement of detected genes shows that BDA-LR performs on par with the Wilcoxon Rank Sum test, and the strong correlation of the logFC and logOR across all datasets shows that the results can be interpreted in a similar way.

Figure 1.

(A) Heatmap of the dataset characteristics, general overview of the results of both BDA-LR and DEA per dataset, and a comparison of the results. The rows represent the datasets, the first column shows the cell populations that were used as contrast for testing. (B) Plot of the logOR and logFC of the Cancer Atlas (2) dataset. The x-axis represent the logFCs of each tested gene, and the y-axis represent the logORs for the same genes. The blue lines shows the linear association between the logFC and logOR. The Spearman’s rank correlation coefficient (ρ) is also shown in the plot. (C) Barplots of the F-score of four BDA methods and 12 DEA methods on simulated data. Numbers above the barplots show the number of cells that were generated within the simulation. Height of bar defines the median value from 25 simulations, error bars are the first and third quartile. (D) Two density plots of MTUS2 from cortex neuron dataset. The top plot shows the density of MTUS2 in inhibitory neurons and the bottom plot shows the density of MTUS2 in excitatory neurons. (E) Two density plots of Gnb2I1 from the aging mouse atlas droplet dataset. The top plot shows the density of Gnb2I1 in 3-month-old mice and the bottom plot shows the density of Gnb2I1 in 24-month-old mice. Both (D and E) are supported with fraction of zeros and variance of each cell population.

BDA among the best performing tests on simulated data

To compare the performance of binary methods with methods relying on counts in a controlled manner, we simulated scRNAseq data with muscat (10) using the provided dataset as reference (11). We generated scRNAseq data with varying number of cells and 25% of differentially expressed genes. With 1000 and 2000 simulated cells, DEsingle (14) performed the best as the F1-score (Figure 1C) and positive predictive value (PPV, Supplementary Figure S1) were the highest and the false positive rate (FPR, Supplementary Figure S2) was the lowest. However, this performance comes at a cost in terms of considerably required computational time (Supplementary Figure S3a). For that reason, we excluded DEsingle when simulating 5000 and 10 000 cells (running time >20 min). All binary-based methods performed consistently good, with 1000 and 2000 cells ranking tightly together. BDA-fisher and BDA-Phi had decreased relative performance with 5000 and 10 000 cells, while the performances of BDA-chisq and BDA-LR were also among the best with 5000 and 10 000 cells. Taken together, this shows that differences in the frequency of zeros between groups can represent biological variation and can most accurately be detected with BDA-chisq and BDA-LR in a time efficient manner.

Differences in test outcomes explained by differences in variance between contrasting cell populations

Despite the observed association between mean expression and number of zeros, which has been previously described (2), and similar performance of the two tests, there were 4754 and 3894 genes uniquely identified using BDA and DEA, respectively, across all datasets. To better understand these differences, we highlighted two extreme exemplar cases that were not significant differentially expressed (P_FDR ≥ 0.05), while they were binary differential genes (BDGs, P_FDR ≤ 5.27 × 10^–115). In the cortex dataset (25), MTUS2 had significantly less zeros in excitatory neurons (logOR = 1.30, P_FDR|BDA = 5.27 × 10^–115, Figure 1D) compared to inhibitory neurons, while the expression levels were not significantly different (logFC = -1.70 × 10^–3, P_FDR|DEA = 5.70 × 10^–2), implying additional high ranked expressions for every additional zero. In the aging mouse atlas droplet dataset (7), Gnb2l1 had significantly less zeros in the 3-month-old mice (logOR = -0.67, P_FDR|BDA = 1.81 × 10^–122, Figure 1E) compared to the 24-month-old mice, while again the expression levels were not significantly different (logFC = 3.15 × 10^–3, P_FDR|DEA = 6.97 × 10^–1). These examples show that differences in variance between contrasting cell populations can interfere with the association between observed zeros and mean expression, resulting in disparities between BDA and DEA. Of note, most BDGs-only and DEGs-only had small differences in P-values between the two tests i.e. a borderline significant difference in frequency of zeros while not having a significant difference in median expression (Supplementary Figure S4). The mean P_FDR for the 4754 genes uniquely identified using BDA was 9.57 × 10^–3, while the mean P_FDR of the same genes using DEA was 3.18 × 10^–1. As for the 3894 genes uniquely identified using DEA the mean P_FDR of BDA was 3.45× 10^–1 and mean P_FDR of DEA was 8.56 × 10^–3.

Binary differential genes are not driven by technological or biological process

To exclude that the differentially behaving genes between BDA and DEA associate with a specific technological or biological process, we investigated whether there were genes repeatedly detected by a one of the two methods. In most cases, genes that were identified as BDG-only (or DEG-only) were found within a single dataset (Supplementary Figure S5a, Supplementary Figure S5b), suggesting the absence of a driving process for them.

Binary differential genes validated with bulk RNA sequencing data

To provide additional insight that differences in zero observations are indeed biologically relevant and represent differential abundance we compared the results of the Alzheimer’s disease (AD) dataset (21) (entorhinal cortex) with DEA analysis performed on a bulk RNAseq AD dataset (19), an approach followed by others (26). The bulk RNAseq datatset was comprised of samples from the fusiform gyrus. For genes measured in both, the scRNAseq dataset and the bulk dataset (N = 2177), the majority of BDG-only (59.4%) were also differentially expressed in bulk (Figure 2A). The logOR of the single cell analysis was also significantly correlated with the logFC of the bulk analysis (ρ = 0.39, P = 9.70 × 10^–79, Figure 2B). Similarly, in a second dataset (22), 65.9% of the BDG-only genes were differentially expressed in bulk samples from the frontal cortex, temporal cortex and hippocampal formation (Supplementary Figure S6). Given that the differences in zero observations for genes between the tested groups (expressed in logOR) highly correlates with the differences in median expression in bulk RNAseq data (expressed in logFC), and that the majority of BDG-only were still detected in bulk, further emphasizes that binarized scRNAseq expression data can be used to detect differentially abundant genes.

Figure 2.

(A) Venn diagram of genes detected (P_FDR ≤ 0.05) in a bulk AD dataset (Friedman et al.), in the single cell AD dataset with BDA-LR (BDGs) and with DEA (DEGs). Each section shows the number and percentage of genes belonging to that section. (B) Plot of the logFC from the AD bulk dataset (x-axis) and the logOR from the single cell AD dataset (y-axis). The red line represents the linear association between the bulk logFC and logOR. The Spearman's rank correlation coefficient (ρ) and corresponding association P-value are also shown. Outlier genes (n = 9, B) were removed from the plots.

Binarization with a threshold of one most appropriate for BDA

To test the binarization scheme, we performed a BDA on the AD dataset for binary profiles generated with different thresholds for binarization (thresholds ranging from one to ten counts). Naturally, for every increase in the threshold, the number of genes with zero measurements across all cells increased, resulting in a decreasing number of tested and significant genes (Supplementary Figure S7a,b). With higher thresholds, we found a decrease in correlation of the logORs from BDA with the logFC from DEA (Supplementary Figure S7c). These results show that the default binarization scheme where zeros remain zero and every non-zero value is assigned a one, is indeed appropriate.

DISCUSSION

Altogether, our results show that binarized expression patterns across cell populations represent biological variation and can be used as measure of relative abundance of transcripts. Across 16 datasets and a variety of contrasting cell populations (disease versus healthy, cell types and cancer status), BDA detected biologically relevant genes that were missed by DEA. While the performance of BDA and DEA on real data is largely comparable, with a known ground truth, BDA performed better than DEA on simulated data. Additionally, BDA benefits reproducibility and is more robust than DEA, since the only pre-processing step required for BDA is the binarization of counts. In contrast, DEA requires normalization and transformation of counts, where an analyst can choose from an excess of equally valid methods (27). Performing BDA on datasets generated using the Smart-seq protocol should be approached with more caution: although the agreement of detected genes between BDA and DEA was high, we observed the lowest correlation between the logOR and logFC for these datasets.

With six of the sixteen datasets we performed the differential analyses between cell types that were based on clusters that were determined with the expression data itself, opposed to a case–control setting. We should note that this is a circular analysis (double dipping) and that the resulting P-values in these comparisons are thus not guaranteed to be controlled for false discoveries. This is, however, still common practice in single-cell differential analyses, as this setup is used to identify cell type markers. For the other ten dataset, the results are not compromised statistically as the case–control definitions are not based on the single-cell data itself.

In our main approach to test for BDA, we have used logistic regression. A logistic regressor for differential expression has been used before (12,28,29). These previous applications, however, use continuous expression values of genes as input, while we propose to use the binary expression value. As for MAST (12), a logistic regression on binarized expression values is implemented to take into account the zeros (expressed versus not expressed) and is combined in a hurdle model with a linear Gaussian model for the continuous values. In contrast to the previously described methods, we show that the frequencies of zeros alone are sufficient to capture biological variation and to identify differential expression of genes between biologically distinct groups in single-cell data.

A commonly used term for observed zeros in single-cell data is dropouts. As zeros in single-cell data can largely be explained by distributional models of molecule sampling counts (2,3), the use of the term dropout can be misleading, as indicated by Sarkar and Stephens (3). This work contributes to clarifying the origin of zeros in single-cell RNAseq data, by showing that the frequency of zeros can actually be used to identify biological differences.

Performing BDA is normalization-free, time efficient and an accurate alternative for DEA for which we see three potential use cases. First, BDA could be performed in isolation as a fast and accurate alternative to DEA. For different use cases, different BDA tests can be used. For more complex study designs BDA-LR could be used as it allows to adjust for covariates, allowing to take into account biological replicates, which decreases false discoveries (30). More straightforward designs could be performed with BDA-chisq. Second, BDA could be performed in addition to DEA to identify more genes. Finally, BDA could be used to validate pre-processing, normalization and DEA as a big discrepancy between the BDGs and DEGs could indicate an aberration in the DEA results.

DATA AVAILABILITY

The datasets used and prepared for this study can be downloaded from Zenodo (http://doi.org/10.5281/zenodo.4487320). The results are also made available in an interactive shiny dashboard: http://insyprojects.ewi.tudelft.nl:5000/BinaryDifferentialAnalysis/. The scripts, functions and source data for the figures are available at the Github repository: https://github.com/gbouland/binary-differential-analysis, including two vignettes describing a BDA starting from a Seurat object and a raw count matrix. BDA is also implemented in an R-package and is available at: https://github.com/gbouland/BDA.

SUPPLEMENTARY DATA

Supplementary Data are available at NARGAB Online.

FUNDING

This research received funding by an NWO Gravitation project: BRAINSCAPES: A Roadmap from Neurogenetics to Neurobiology (NWO: 024.004.012).

Conflict of interest statement. None declared.