Photobleaching step analysis for robust determination of protein complex stoichiometries

Abstract

The counting of discrete photobleaching steps in fluorescence microscopy is ideally suited to study protein complex stoichiometry in situ. The counting range of photobleaching step analysis has been significantly improved with more-sophisticated algorithms for step detection, albeit at an increasing computational cost and with the necessity for high-quality data. Here, we address concerns regarding robustness, automation, and experimental validation, optimizing both data acquisition and analysis. To make full use of the potential of photobleaching step analysis, we evaluate various labeling strategies with respect to their molecular brightness, photostability, and photoblinking. The developed analysis algorithm focuses on automation and computational efficiency. Moreover, we validate the developed methods with experimental data acquired on DNA origami labeled with defined fluorophore numbers, demonstrating counting of up to 35 fluorophores. Finally, we show the power of the combination of optimized trace acquisition and automated data analysis by counting labeled nucleoporin 107 in nuclear pore complexes of intact U2OS cells. The successful in situ application promotes this framework as a new resource enabling cell biologists to robustly determine the stoichiometries of molecular assemblies at the single-molecule level in an automated manner.

INTRODUCTION

The fundamental functions of living cells are carried out by protein assemblies at the molecular level. Precise quantitative knowledge on the composition of these protein complexes in the cellular environment is crucial to deepen our understanding of their cellular functions (Matthews, 2012). In many cases these protein assemblies contain not only a variety of different components, but also several copies of each component (Ahnert et al., 2015).

To investigate the stoichiometry of a particular protein of interest in a molecular assembly, fluorescence microscopy offers several advantages. It is highly specific, live-cell compatible, and single-molecule sensitive and therefore capable of resolving heterogeneities within ensembles in situ. In the past two decades, different fluorescence-based molecular counting methods have been developed (Gruβmayer et al., 2019). Among them are methods relying on brightness calibration (Wu and Pollard, 2005), counting of photobleaching steps (Ulbrich and Isacoff, 2007), single-molecule localization microscopy (Lee et al., 2012; Puchner et al., 2013; Rollins et al., 2015; Jungmann et al., 2016), and photon antibunching (Ta et al., 2010; Grußmayer and Herten, 2017). To date, photobleaching step analysis (PBSA) and brightness estimation are most widely used in biological applications of molecular counting, due to their simplicity in data acquisition and the relatively straightforward interpretation (Arant and Ulbrich, 2014). PBSA has the advantage that counting of fluorophores requires no calibration and that it is relatively robust to variations in molecular brightness. Importantly, any molecular counting approach based on fluorescence microscopy requires additional calibration of the degree of labeling, that is, the number of fluorophores attached per target to relate measured fluorophore numbers to the underlying number of target proteins (Gruβmayer et al., 2019; Hummert et al., 2021).

While the idea of counting photobleaching steps is straightforward, numerous approaches exist for data analysis. Often the number of steps is classified by visual inspection (Ulbrich and Isacoff, 2007; Engel et al., 2009; Dixon et al., 2015), which is not only time-consuming but also highly subjective. The exclusion of traces that cannot reliably be classified upon visual inspection will inevitably lead to a biased estimate, because traces with a higher number of fluorophores tend to exhibit a higher complexity. More reliable is the determination of the unitary step height by pairwise frequency analysis (Leake et al., 2006). Thereby, however, differences in step height over the field of view will broaden the measured emitter number distribution. Chung–Kennedy (Das et al., 2007) or median rank (Dixon et al., 2015) filters are often applied to photobleaching traces to improve step detection. Measuring ensemble photobleaching against density allows fast determination of mean fluorophore numbers but lacks single-complex resolution (Liesche et al., 2015). Recently, molecular counting via photobleaching has attracted renewed attention due to the development of novel analysis modalities based on Bayesian statistics (Tsekouras et al., 2016; Garry et al., 2020) and machine learning (Xu et al., 2019).

However, these novel methods are demanding in terms of data quality, which in turn leads to new requirements regarding fluorophore properties. In the trade-off between signal-to-noise ratio (SNR) of the individual bleaching steps and the rate of photobleaching, bright and stable fluorophores are advantageous. Thus, buffer systems (Aitken et al., 2008; Vogelsang et al., 2008) to increase photostability and reduce complex photophysical behavior could help to improve data quality. This motivates an investigation into which labeling approaches and buffer systems are most suited to generate data compatible with automated and robust photobleaching step analysis at an increased counting range. Additionally, Bayesian methods are computationally costly and therefore limit the number of photobleaching traces that can be processed in a given experiment. Therefore, we see the necessity for an approach to bridge the gap between simple methods such as visual inspection and the novel Bayesian methods. Finally, the experimental validation with standard samples is often not the focus of theoretical methods development although calibration samples are readily available (Schmied et al., 2014; Thevathasan et al., 2019).

Here, we address these hurdles to make photobleaching step analysis a more robust and thoroughly validated tool in the biophysics toolbox. We describe a comprehensive framework for PBSA that provides guidelines for the choice of fluorescent label and acquisition conditions as well as a new photobleaching trace analysis algorithm. The quickPBSA package was developed with a focus on automation and speed, providing the high throughput necessary to meet the demands for in situ protein counting. We then validate the method with molecular counting experiments on DNA origami carrying defined label numbers. Finally, we show that quickPBSA, in conjunction with optimized trace data acquisition, is well suited to characterize protein structures in cells by determining the copy number of nucleoporin 107 (NUP107) in the nuclear pore complex (NPC).

RESULTS

The reliability of automated photobleaching trace evaluation strongly depends on the quality of the input data, that is, individual photobleaching traces. Historically, PBSA has mostly been performed using fluorescent proteins as labels (Arant and Ulbrich, 2014). However, fluorescent proteins tend to be less photostable than small organic fluorophores and are known to exhibit complex photophysics, complicating trace interpretation (Ha and Tinnefeld, 2012). To identify fluorophores suited for generating photobleaching traces with high SNR, we therefore compared the fluorescent proteins EGFP, mCherry, and mNeonGreen, as well as the organic fluorophores tetramethylrhodamine (TMR) and silicon rhodamine (SiR) conjugated to the self-labeling protein tags SNAP-tag and HaloTag with respect to their photostability, brightness, and propensity for photoinduced blinking. In addition, we tested to which degree photostabilizing buffers composed of reducing and oxidizing systems (ROXSs) and an oxygen scavenger could be used to increase photostability, suppress photoblinking, and thereby improve trace quality.

Both the molecular brightness of a fluorescent label and its photostability contribute to the overall photon budget and thereby directly influence the SNR. Because the molecular brightness is a well-studied property of fluorophores, it can be readily compared across different fluorophores based on reported values in the literature (Supplemental Table S1). For organic fluorophores conjugated to protein tags, a strong influence of the tag on the fluorophore was observed and has to be taken into account when comparing the brightness of different fluorophores after conjugation to protein tags (Erdmann et al., 2019). In contrast, the photostability of a fluorophore can strongly depend on its environment and on the applied measurement conditions. For this reason, we performed systematic photobleaching measurements under comparable conditions with the selected fluorophores. For this, we expressed each label as fusion protein in U2OS or COS-7 cell lines (Supplemental Figure S1) and imaged them after chemical fixation. We determined the photostability of each fluorophore in phosphate-buffered saline (PBS; pH 7.4) and three photostabilizing buffers, each containing methyl viologen and ascorbic acid as ROXS and an oxygen scavenger system consisting of either glucose oxidase and catalase (GodCat) (Harada et al., 1990), protocatechuate-3,4-dioxygenase (PCD) (Aitken et al., 2008), or sodium sulfite (NaSO₃) (Hartwich et al., 2018).

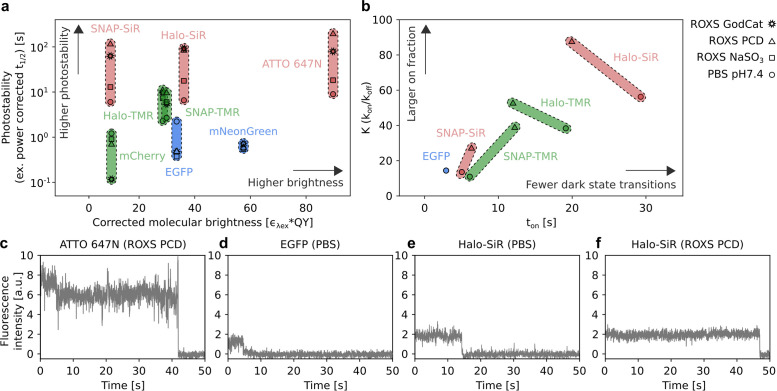
Upon high-intensity illumination, we observed biexponential intensity decay patterns for all tested fluorophores (Supplemental Figure S2). Such behavior has been reported before for both organic fluorophore and fluorescent proteins (Song et al., 1995; Bakker and Swain, 2019). We therefore decided to use the time to reach half maximum (t_1/2 ) as a model-independent metric to compare conditions and fluorophores. Across all tested conditions, t_1/2 varied considerably, covering three orders of magnitude (0.5–200 s). Overall, fluorescent proteins were less photostable than organic fluorophores and far-red organic fluorophores exhibited the highest photostability. Differences between fluorophores were less pronounced in conventional buffers without photostabilizing additives. Addition of ROXS and oxygen scavengers resulted in strongly increased photostability for organic fluorophores, particularly for the red-absorbing fluorophores ATTO 647N and SiR (Figure 1a). For ATTO 647N, photostability was improved twofold with ROXS buffer supplemented with NaSO₃ as oxygen scavenger. Replacing NaSO₃ with the enzymatic oxygen scavengers GodCat or PCD resulted in further improvements of ∼10- and 20-fold, respectively. Similar trends were observed for both TMR and SiR conjugated to SNAP-tag or HaloTag. Here, SiR conjugated to SNAP-tag in ROXS PCD showed the highest stability, with a t_1/2 of 120 s (20-fold improvement over PBS) and a 60-fold improvement over EGFP, but still 50% lower stability compared with ATTO 647N in the same buffer. In contrast, a decrease in photostability for EGFP and mCherry in the methyl viologen and ascorbic acid–based ROXS buffer was observed for all three oxygen scavenging systems, possibly due to pH changes of the buffers during imaging (Swoboda et al., 2012). Interestingly, no such decrease in photostability was observed for mNeonGreen, which could be due to improved stability of the protein structure of mNeonGreen (Shaner et al., 2013).

FIGURE 1:

Fluorophore and image acquisition buffer selection for PBSA. (a) Comparison of photostability and molecular brightness for different fluorescent proteins and organic fluorophores conjugated to protein tags. Symbols indicate mean t_1/2 and molecular brightness under indicated conditions. Color coding according to excitation wavelength used in this study: blue: 488 nm, green: 561 nm, red: 640 nm. t_1/2 was normalized to 1 kW/cm² excitation power density. The molecular brightness of fluorophores was corrected for mismatches between excitation wavelength and absorption maximum (Supplemental Table S1). The full data set is shown in Supplemental Figure S2. (b) Comparison of mean equilibrium constant K (k_on/k_off) between fluorescent and nonfluorescent states and mean on-time t_on obtained from image correlation experiments for the indicated conditions. Color coding as in a. See Supplemental Figure S5 for full set of rate values. (c–f) Representative single-fluorophore intensity traces for the indicated fluorophores and buffer recorded via TIRF microscopy of surface immobilized ATTO 647N (c) or plasma membrane–localized EGFP and labeled HaloTag constructs in chemically fixed HeLa cells (d–f).

In addition to the increased photostability of organic fluorophores, ROXS buffers were also reported to reduce emission intensity fluctuations on the millisecond to second timescale, also known as photoblinking, which complicates trace interpretation in PBSA (Vogelsang et al., 2008). For a quantitative characterization of photoblinking, we performed on- and off-rate measurements for a selection of fluorophores and buffer conditions using an image correlation approach that robustly determines photoblinking rates across a range of blinking regimes without requiring traces of individual fluorophores (Sehayek et al., 2019). For these measurements, we recorded image series on chemically fixed cells with the labels EGFP, SNAP-tag, or HaloTag localized at the plasma membrane. These image series were then used to compute the temporal autocorrelation function (ACF), which we fitted with a three-state fluorophore model (Supplemental Figure S3). Of note, such a three-state fluorophore model does not necessarily reflect the underlying photophysical processes for the evaluated fluorophores, but rather serves to facilitate a quantitative comparison of fluorophores and conditions. The degree of photoblinking observed in this assay varied strongly between the tested fluorophores and was apparent both by visual inspection of intensity traces from individual fluorophores (Figure 1, c–f) and in the corresponding ACFs (Supplemental Figure S4). Fitting the ACFs obtained from image correlation then allowed us to determine on- and off-rates for photoblinking across the different conditions (Supplemental Figure S5).

In PBS, the on-time (t_on, 1/k_off) and the equilibrium constant K (k_on/k_off) of EGFP and TMR or SiR conjugated to SNAP-tag were comparable (Figure 1b). In contrast, fluorophores conjugated to HaloTag exhibited a much lower degree of photoblinking, evidenced by higher K and t_on even without addition of ROXS or oxygen removal. For EGFP, the strong decrease in photostability described above prevented a photoblinking analysis in ROXS PCD. For TMR and SiR conjugated to both tags, we observed an increased on-fraction K upon switching to ROXS PCD buffer. Interestingly, the effect on the on-time was less consistent. While fluorophores conjugated to SNAP-tag showed increased t_on in ROXS PCD as compared with PBS, fluorophores conjugated to HaloTag exhibited lower t_on after ROXS addition and oxygen removal. In the case of TMR, this resulted in very similar photoblinking behaviors in ROXS PCD for both tags. For SiR, conjugation to HaloTag resulted in ∼3× larger K and t_on in ROXS PCD compared with SNAP-tag in the same buffer. It was recently reported that fluorophores conjugated to HaloTag are tightly associated to the protein surface, while fluorophores conjugated to SNAP-tag protrude away from the protein surface (Wilhelm et al., 2021). We speculate that this could result in differences in accessibility for soluble factor, which could explain the different propensity for photoblinking and the different effect of ROXS components. Based on these observations, the trace quality and counting range of PBSA-based quantification can be improved by using self-labeling protein tags in combination with longer-wavelength organic fluorophores and ROXS buffers supplemented with enzymatic oxygen scavenger systems.

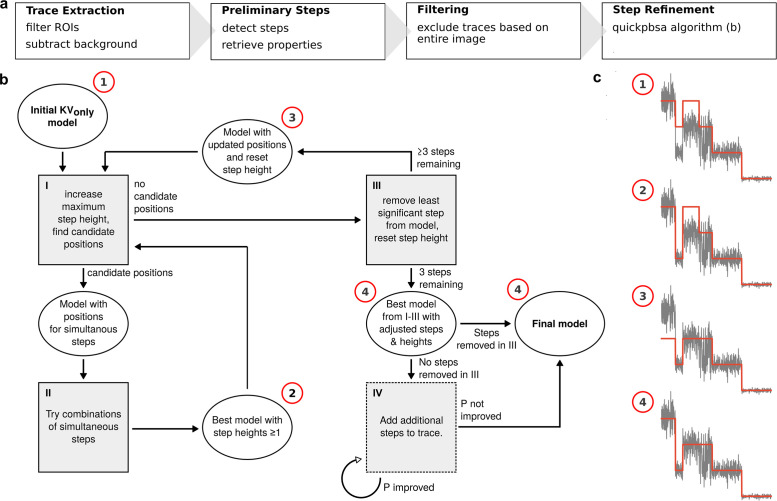
Turning from the data acquisition to the data analysis, we set out to develop a routine capable of estimating fluorophore number distributions directly from the experimental data (i.e., image stacks) with minimal user input. To that end, apart from the novel quickPBSA algorithm for trace interpretation, the framework includes modules for automated trace extraction from raw time-lapse image stacks and filtering. The underlying principle of the framework is to perform a preliminary step detection for each trace and then refine the results iteratively. The final refinement step makes use of a Bayesian posterior from Pressé and coworkers (Tsekouras et al., 2016), thus incorporating prior knowledge about the photobleaching process. In contrast to the previously published approach, the Bayesian posterior is not used to detect step positions but only to determine step significance and find simultaneous bleaching events. The full data analysis workflow is made up of four major parts (Figure 2a), which are described in the following.

FIGURE 2:

Framework concept and quickPBSA algorithm. (a) The four parts of the framework as detailed in the text. (b) Flowchart of the quickPBSA step refinement algorithm. (c) Example to illustrate how a simulated trace propagates through the algorithm, starting from the result of the preliminary step detection. Note that step IV is skipped for the example trace because steps were removed in step III.

Trace extraction

The first step is the identification of regions of interest (ROIs) and the automated extraction of photobleaching traces from image stacks. Here, the ROIs can be provided as pixel coordinates (for instance, generated by a localization algorithm) or via a segmentation mask image (for instance, generated by thresholding). As the photobleaching trace is extracted from the ROI, a ring-shaped region with variable offset from the ROI is used to extract a background bleaching trace (Supplemental Figure S6). Other ROIs are automatically excluded from the background region. Especially for measurements in cells, we found that background bleaching due to autofluorescence and out-of-focus fluorescence occurred on similar timescales as that of the fluorophore bleaching. Therefore, background subtraction proved to be essential to recover traces with discernible photobleaching steps. Additionally, background subtraction also facilitates identifying and excluding ROIs that are not fully bleached at the end of the measurement.

Preliminary step detection

After trace extraction, a preliminary step detection is performed on all extracted traces. This is accomplished by successively placing steps and evaluating each added step using the Schwarz Information Criterion (SIC) as first demonstrated by Kalafut and Visscher (2008, see supplementary text). In our implementation of this algorithm, a user-defined threshold to ignore minor changes in the mean intensity reduces the detection of spurious steps, rendering the preliminary step detection more robust.

Filtering

Traces are excluded based on the result of the preliminary step detection. The model selection in the quickPBSA algorithm critically depends on the correct detection of the last and the penultimate bleaching steps in each trace because the period where only one fluorophore is active is used to retrieve the properties of an individual fluorophore. Therefore, traces that are not fully bleached at the end of an acquisition or where the last step potentially corresponds to a double bleaching event need to be excluded. Assuming that the last two steps are correctly identified in most traces from the image stack, the distribution of single-fluorophore signal means across all traces can be used to filter out traces. Using this information from the entire image stack, we exclude traces where the single-fluorophore or background signal are out of bounds.

quickPBSA algorithm

Ultimately, the result is refined by evaluating the entire trace according to the full marginal posterior from Pressé and coworkers (Tsekouras et al., 2016). This posterior incorporates the possibility of simultaneous bleaching events as well as a penalty for too many bleaching events and thus is a far more content-aware evaluation of step placement than the information criterion used in the preliminary step detection. The quickPBSA algorithm iteratively minimizes the negative logarithm of the posterior (–log(P), see supplemetary text, Table S2), starting from the result of the preliminary step placement with all steps considered to be single events. Figure 2b shows a flowchart of the iterative optimization procedure, together with a simulated trace showing how the algorithm removes steps and optimizes step heights from the preliminary result. The iterative procedure is as follows:

• I. Find candidate positions for simultaneous steps. In the first iteration (double steps) these are all positions. For more fluorophores bleaching simultaneously, only the locations from the last iteration are considered. For example, triple steps are considered only where double steps yielded an improvement. If there are candidate positions, proceed with II, otherwise go to III.

• II. Try all possible combinations with step heights up to the current occupancy. The result of this process is accepted and considered the new optimum if a lower value of –log(P) is found at any point. Step heights from 1 to the maximum step height are considered, so that, for instance, [2,2,2] can be replaced by [1,3,2]. Return to step I to find new candidate positions.

• III. Remove the least significant step found during preliminary step detection. The final two steps in a trace are always kept in place because they are required for posterior calculation. If there are only three steps left, proceed with step IV, else reset all steps to single occupancy and return to step I.

• IV. If no steps could be removed to yield an improved posterior, that is, the current optimum contains the same number of steps as the preliminary result, the algorithm proceeds to add single-fluorophore steps. This is accomplished by calculating –log(P) for additional positive or negative steps at all positions before the penultimate step. Repeat step IV until the last two added steps yielded no improved posterior or a specified maximum number of added steps is reached.

• V. Return the step/event combination with the minimal value for –log(P) found at any point in I–IV.

In the quickPBSA algorithm, the evaluation of simultaneous step arrangements is computationally most expensive. Especially for traces with many steps in the preliminary result, the number of possible combinations is excessive. We therefore implemented several strategies to reduce the computational cost at this point, as detailed in the documentation of the software package.

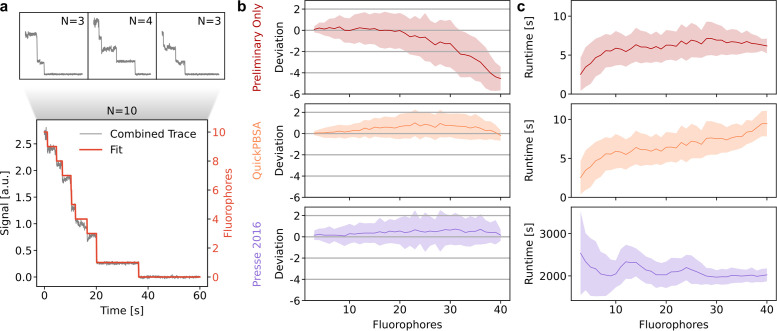
We benchmarked the quickPBSA trace analysis algorithm using semisynthetic data generated from experimental data. For this, we acquired experimental data from an in vitro sample with few fluorophores per diffraction-limited spot, namely immobilized DNA oligonucleotides labeled with four ATTO 647N fluorophores. We selected traces where the quickPBSA result could be confirmed by visual inspection, obtaining a set of traces with known ground truth. We then generated increasingly complex semisynthetic traces with known ground truth by combining several of these traces (Figure 3a). Using this approach, benchmarking traces with fluorophore numbers up to 40 were generated and used to evaluate the accuracy of the quickPBSA trace analysis.

FIGURE 3:

Benchmark with semisynthetic traces. (a) Semisynthetic traces for benchmarking are generated by combining manually classified traces. (b) Deviation from ground truth for semisynthetic traces analyzed without quickPBSA step refinement, including step refinement, and with the algorithm from Pressé and coworkers (Tsekouras et al., 2016). (c) Runtime per trace for the three algorithms. Mean (line) and SD (shaded region) are shown.

For each fluorophore number, ∼100 semisynthetic traces with 3000 time points per trace were included in the analysis (Supplemental Figure S7). To compare the performance of the algorithm with that of a state-of-the-art Bayesian algorithm, we analyzed the benchmarking data set with the algorithm previously published by Pressé and coworkers (Tsekouras et al., 2016), hereafter called Pressé 2016. Figure 3b shows the results of the benchmark data set after the filtering step (Preliminary Only), including the quickPBSA refinement algorithm, and from the Pressé 2016 algorithm. For the benchmarking data set, the result of the preliminary step detection starts to deviate systematically from the ground truth for fluorophore numbers beyond 20, most likely due to missed bleaching events, which occurred in close temporal succession. The results after quickPBSA step refinement and from the Pressé 2016 algorithm, on the other hand, show a slight overestimation. But in both algorithms the mean estimated fluorophore number never deviates by more than one fluorophore from the expected value. Additionally, the overestimation is likely caused by the selection of ground truth traces, because a simple ruler method shows an even larger overestimation for the benchmarking data set (Supplemental Figure S7). Overall, the results from the quickPBSA algorithm and Pressé 2016 are very similar. A two-sample t test shows that the means obtained from the two algorithms never differ significantly (p > 0.01; Supplemental Figure S7).

We also used the semisynthetic traces to benchmark the runtime of the analyses in dependence on the number of fluorophores (Figure 3c). We observed that for up to 20 fluorophores, the quickPBSA total runtime was dominated by the preliminary step detection. For higher fluorophore numbers, the runtime increases due to the quickPBSA refinement and increases further for higher fluorophore numbers. Nonetheless, the mean runtime remained below 10 s per trace (3000 data points) for the entire benchmarking data set containing traces with up to 40 fluorophores. In contrast, the runtime of the Pressé 2016 algorithm is more than 30 min per trace for the entire benchmarking data set. Thus, using the quickPBSA algorithm, we were able to analyze the data set with comparable results and a greater than100-fold lower computation time. The mean analysis times for all data sets included in this publication are below 3 min per trace even for complex experimental traces with up to 15,000 data points (Table 1).

TABLE 1:

Mean and SDs extracted from Gaussian modeling of measured emitter number distributions from DNA origami experiments.

Sample	Mean	Mean expected	SD	SD expected	Sample size	Runtime/trace (s)
R09	6.7 (0.1)	6.3	1.9 (0.1)	1.4	197;13;1	25
R20	14.2 (0.2)	14	6.1 (0.2)	2.1	636;43;2	53
R35	22.6 (0.5)	24.5	8.6 (0.5)	2.7	499;25;2	168
R09*	6.0 (0.1)	6.3	2.2 (0.1)	1.4	1667;5;1	19
Y09	7.9 (0.1)	6.3	1.6 (0.1)	1.4	853;12;1	88

SEs in parentheses as extracted from least-squares fitting. The expected values are calculated assuming a 70% labeling efficiency. *Measurement on alternative microscope setup with sCMOS detector. Sample size: number of traces; measurements; independent experiments.

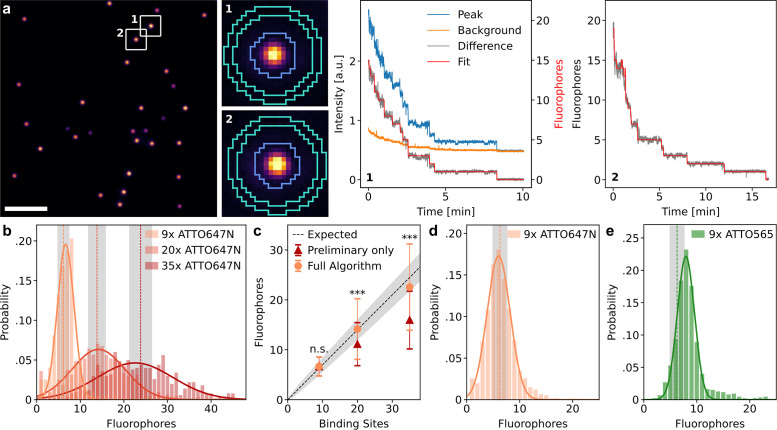
To fully validate the developed framework with experimental data, we used DNA origami carrying a well-defined number of fluorophores. DNA origami with 9, 20, and 35 binding sites for labeling strands carrying a single ATTO 647N fluorophore (R09, R20, and R35) were sparsely immobilized on coverslips to ensure that stochastically overlapping origami structures did not significantly influence the measurement (Figure 4a). The labeling efficiency specified by Gattaquant for the DNA origami is 70%, which we independently validated for the R20 origami using counting by photon statistics (Grußmayer and Herten, 2017) (Supplemental Figure S8). Photobleaching traces from individual DNA origami structures were then extracted using the trace extraction module described above, using the software thunderSTORM (Ovesný et al., 2014) for ROI localization and removing origami with close nearest neighbors (Supplemental Figure S6). Because the extracted traces exhibited only weak background bleaching, the background subtraction step for this sample mainly removed a constant offset caused by excitation bleed-through and readout noise (Figure 4a, center).

FIGURE 4:

Validation with DNA origami samples. (a) Representative image and traces from the origami experiment with 20 binding sites for ATTO 647N. Scale bar: 10 µm. (b) Fluorophore number distributions for origami with 9, 20, and 35 binding sites. The histograms are modeled with a Gaussian to extract means and SDs (results and sample sizes in Table 1). Vertical dashed lines and areas shaded in gray indicate the expected mean and SD obtained from binomial distributions. (c) Fit results from b compared with the expected mean of the label number distribution, which is a binomial distribution with a labeling efficiency of 70%. Error bars and shaded region show the SD. The quickPBSA result differs significantly from the result without quickPBSA refinement for 20 and 35 binding sites (two sample t test, ***: p < 0.001, n.s.: not significant). (d) Measured label number distribution of origami with nine binding sites for ATTO 647N on a different microscope setup with a larger field of view and sCMOS detector. (e) Measured label number distribution for origami with nine binding sites for ATTO 565.

Processing the background-corrected traces using the full quickPBSA algorithm resulted in good agreement between intensity and predicted fluorophore numbers over time (Figure 4a). The obtained fluorophore number distributions were symmetrical, indicating no systematic deviation and an unbiased measurement error (Figure 4b). The means obtained from fitting a normal distribution to the quickPBSA fluorophore number estimates agreed with the expected values for a labeling efficiency of 70%. In contrast, the means of distributions obtained without quickPBSA refinement (preliminary only), while similar for origami with nine binding sites, exhibited a significant underestimation for origami with 20 and 35 binding sites (Figure 4c). This underestimation for larger fluorophore numbers is in line with the benchmarking results with semisynthetic traces.

A full comparison of all parameters from the fits and a comparison to the mean and SD of a binomial distribution with the known number of binding sites and the expected labeling efficiency are shown in Table 1. We observed that the measured distributions broadened with increasing fluorophore number, stronger than would be expected from the binomial distribution of label numbers alone. For instance, while broadening of the measured data was negligible for R09 origami, the SD increased by a factor of 3 for R20 origami (Table 1). This suggests that experimental data contain additional sources of uncertainty that are not fully reproduced using semisynthetic data and therefore highlights the importance of additional benchmarking with standardized samples.

To validate that the quickPBSA algorithm performed robustly upon variation of experimental parameters, we performed additional measurements with the R09 origami samples on a different wide-field microscope setup with homogeneous illumination power and a sCMOS instead of an emCCD camera for detection. As in the first experiment with the R09 origami, the expected mean and width of the fluorophore number distribution were well reproduced (Figure 4d; Table 1). A large field of view is advantageous for the acquisition of photobleaching data because the overall measurement time is decreased and the potential impact of degrading buffer performance can be minimized.

We further explored the sensitivity of the quickPBSA algorithm to fluorophore properties by measuring a fluorophore number distribution for origami with nine binding sites labeled with ATTO 565 (Y09). Here, the measured distribution showed a peak at 7.9 fluorophores, significantly above the expected mean fluorophore number of 6.3 (Figure 4e; Table 1). A likely explanation for this deviation is that ATTO 565 exhibited two distinct brightness states as frequently observed in individual photobleaching traces (Supplemental Figure S9). If the last photobleaching step occurs from a lower brightness state in a significant number of traces, the mean signal of a single fluorophore is underestimated for these traces, leading to an overestimation of the total number of fluorophores. This again highlights how important label selection is in photobleaching experiments, even for organic fluorophores. Additionally, taking the complex photochemical behavior into account can extend the counting range of photobleaching analysis even further (Bryan et al., 2020).

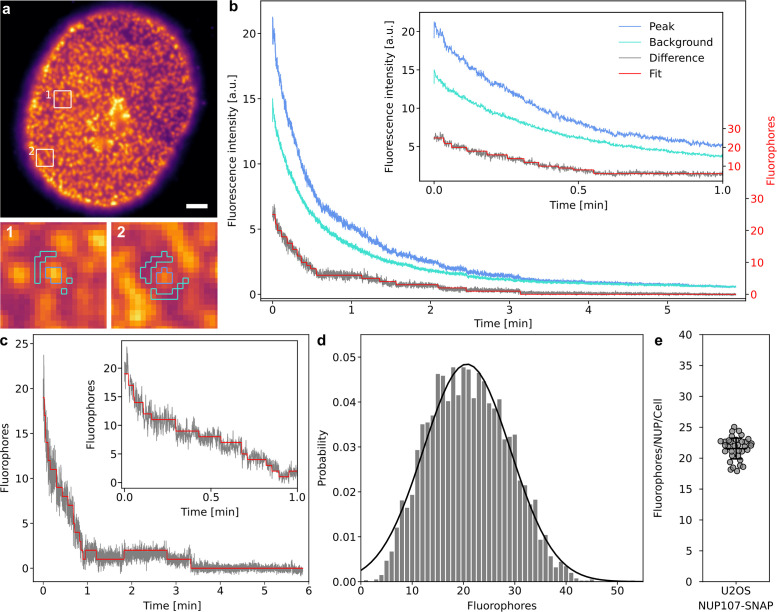
While DNA origami samples are ideally suited for determining the accessible counting range of a novel method, the application to biological targets within the complex cellular environment is subject to additional challenges that are not captured in simplified in vitro experiments. Background (auto)fluorescence, density of structures, and biological variation cannot readily be controlled in a biological sample and will impact data quality. To assess how the quickPBSA framework coped with a more complex in situ sample, we decided to determine the number of NUP107 protein copies contained in individual NPCs. To minimize the influence of protein expression and labeling efficiency, we used a genome-edited U2OS cell line expressing NUP107-SNAP from its native genomic context (Li et al., 2018). Labeling of SNAP-tag conjugated NUP107 was performed with the corresponding SiR substrate BG-SiR. From epifluorescence images of chemically fixed and labeled cells, it is immediately evident that fluorescent background is much more pronounced in situ than in the origami experiments described above (Figure 5a). Additionally, the high density of NPCs resulted in regions where it was no longer possible to identify individual NPCs. As for the in vitro samples, individual NPCs were localized with thunderSTORM (Ovesný et al., 2014). The trace extraction routine in the quickPBSA framework automatically excludes NPCs based on localization parameters such as width of the fitted Gaussian or nearest-neighbor distance. Thus, only sufficiently isolated and diffraction-limited structures are considered for further analysis (Supplemental Figures S6 and S10). Despite this prefiltering, raw traces from individual ROIs did not exhibit clear bleaching steps and the decay in the background region occurred on a similar timescale as the fluorescence signal of the ROI (Figure 5b). Background fluorescence can therefore be mainly attributed to out-of-focus fluorescence rather than autofluorescence. After subtraction of the background signal, photobleaching steps could be observed toward the end of photobleaching traces (Figure 5b). Despite the substantially lower SNR compared with the previously successfully evaluated traces recorded using ATTO 647N as fluorophore, we subjected the extracted traces to analysis with the quickPBSA algorithm (Figure 5, b and c). The resulting fluorophore number distribution cumulated across 32 cells from two independent experiments (Supplemental Figure S10) was well described by a normal distribution with a mean of 20.7 ± 0.2 fluorophores per NPC and a SD of 8.5 ± 0.2 (Figure 5d). The mean fluorophore number per NPC per cell was 21.6 ± 1.7, indicating that quickPBSA yielded robust estimates across the entire population of cells (Figure 5e). The width of the cumulated distribution is comparable to that of the distribution obtained from R35 DNA origami, indicating that background subtraction and spot prefiltering successfully reduced the complexity of obtained traces and did not result in reduced precision. NUP107 has been reported previously to be present in NPCs at 32 copies per pore (Bui et al., 2013; Ori et al., 2013). Based on the mean fluorophore number of 20.7 ± 0.2 per NPC, this translates into a labeling efficiency of ∼65% for SNAP-tag labeling with BG-SiR, which is in excellent agreement with recent reports (Thevathasan et al., 2019). This indicates that quickPBSA is able to correctly measure fluorophore numbers even for less-bright fluorophore labels in the complex environment of a eukaryotic cell and with precision comparable to that of localization microscopy–based methods (Thevathasan et al., 2019).

FIGURE 5:

Protein counting of NUP107 in U2OS cells. (a) Representative image of U2OS cell stably expressing NUP107-SNAP-tag labeled with BG-SiR. Scale bar: 5 µm. (b) Traces extracted from the segmented ROI and background regions and evaluated difference trace from example trace b. (c) Evaluated background-corrected trace extracted from ROI c (scaled to overlap). (d) Measured fluorophore number distribution and Gaussian model fit (black line, mean 20.7 ± 0.2, SD 8.5 ± 0.2). Four thousand traces from 32 cells, two independent experiments. (e) Mean fluorophore number per NPC per cell. Bars show mean ± SD across cells (21.6 ± 1.7).

DISCUSSION

The presented framework for photobleaching step analysis offers a robust, fast, and well-validated approach for molecular counting in situ. The evaluation of various fluorophores along with different buffer conditions with respect to the precision of photobleaching step analysis may serve as a practical guide for robust counting of proteins and other biomolecules. Additionally, it may serve as a blueprint for extended screening of other fluorescent labels and experimental conditions. The high photostability and low degree of photoblinking of organic fluorophores imaged in ROXS buffer with enzymatic oxygen removal enabled the generation of high-quality input data for automated trace interpretation. Despite the lower brightness compared with HaloTag, the high photostability of SiR conjugated to SNAP-tag in ROXS PCD buffer was found to be suitable for PBSA protein counting. Clearly, fluorophore characteristics strongly depend on the specific environment, as is especially evident by the influence of protein tags on photoblinking of TMR and SiR and the effect of SNAP-tag conjugation on SiR brightness. Therefore, evaluating fluorophore properties should always be considered when using alternative labeling approaches. Fluorophores with improved molecular brightness and photostability (Grimm et al., 2015; Scott et al., 2018), as well as recently reported self-healing fluorophores (van der Velde et al., 2018; Henrikus et al., 2021), might allow the extension of the accessible counting range of photobleaching step analysis. Approaches to improve the SNR during image acquisition such as confocalized detection or single-plane illumination could help to improve trace quality and thereby further extend the accessible counting range of quickPBSA (Mi et al., 2015).

On the analysis side, we found it beneficial to make use of information from the entire field of view during trace selection, combining features from pairwise frequency methods with features from Bayesian approaches. In this spirit, the methodology for trace analysis is a combination and extension of two previous approaches to photobleaching step analysis. The combined method has only a few user-defined parameters, simplifying automation and improving robustness. The high degree of automation together with the more than 100-fold improved computational efficiency of the combined method provides the significantly increased throughput required for biological applications. We believe that the developed method of testing algorithms with semisynthetic data will be highly useful not only for benchmarking other PBSA algorithms but also to generate training data for machine learning–based approaches (Xu et al., 2019).

Using ATTO 647N-labeled structures with a known stoichiometry in vitro, we showed that quickPBSA yields highly accurate (<10% deviation across all samples) estimates of mean fluorophore numbers for structures containing up to 35 fluorophores. We furthermore demonstrated the robustness of the quickPBSA workflow by successfully analyzing data acquired on different experimental setups. We also demonstrated that the complex photochemical behavior of fluorophores can skew fluorophore number estimates, highlighting the importance of careful fluorophore characterization before experiments.

To show that quickPBSA performs well in biological applications, we determine the number of NUP107 protein copies in NPCs of U2OS cells. At this point, the background subtraction and trace filtering modules of quickPBSA proved to be crucial for obtaining traces from complex samples. Factoring in the expected labeling efficiency for SNAP-tag labeling, the previously reported number of 32 protein copies was well reproduced. This constitutes, to our knowledge, the highest stoichiometry successfully measured with photobleaching step analysis in a biological sample so far and demonstrates the robustness of the outlined approach in biological samples.

Future developments of alternative algorithms for PBSA to further improve the precision of fluorophore counting, such as novel Bayesian approaches (Bryan et al., 2020), will be of high interest for moving beyond measuring mean complex stoichiometries and toward characterizing stoichiometry distributions across ensembles of individual complexes. At this point, however, advances in data analysis will need to go hand in hand with the development of novel labeling schemes with improved labeling efficiency to reduce the variation in fluorophore numbers caused merely by incomplete labeling of target proteins.

Overall, the combination of improved data acquisition and the novel analysis routines contained in the quickPBSA framework provide a reliable way to determine protein stoichiometries in cellulo and will enable the use of automated PBSA as a routine tool for cell biology in future applications.

MATERIALS AND METHODS

Request a protocol through Bio-protocol.

Preparation of DNA in vitro samples

Custom brightness DNA origami with 9, 20, or 35 nominal binding sites labeled with ATTO 647N or ATTO 565 at approximate labeling efficiencies of 70% (Gattaquant DNA Nanotechnologies, Germany) were dissolved in 0.5 × TBE (Tris-borate-ethylenediaminetetraacetic acid) buffer supplemented with 11 mM MgCl₂ and stored at –20°C until use. DNA oligonucleotides labeled with 4 ATTO 647N (tetraATTO 647N) as previously described (Liesche et al., 2015) (biomers.net, Germany) were dissolved in PBS (10 mM phosphate buffer, 2.7 mM KCl, 137 mM NaCl, pH 7.4; Sigma Aldrich, Germany) and stored at –20°C until use. Both DNA origami and DNA oligonucleotides were immobilized in eight-well LabTek (Nunc/Thermo Fisher, USA) chambered coverslips via biotin–streptavidin linkage as previously described (Grußmayer and Herten, 2017). Prepared samples were kept in PBS (DNA oligonucleotides) or PBS supplemented with 20 mM MgCl₂ (DNA origami) unless stated otherwise.

Cell culture

COS-7, U2OS, and HeLa cells (all American Type Culture Collection) were cultured in DMEM supplemented with GlutaMax and 1 mM sodium pyruvate (all Life Technologies Technologies, USA). Cells were grown at 37°C, 5% CO₂ in a humidified atmosphere and routinely subcultured every 3 d or upon reaching 80% confluency. Cultures were kept in culture for up to 30 passages and were not routinely tested for mycoplasma contamination. For wide-field imaging, cells were seeded into eight-well LabTek chambered coverslips. Before the cells were seeded, LabTek coverslips were cleaned with 0.1 M hydrofluoric acid for 2 × 30 s and extensively washed with PBS. Transfection of COS-7 cells was performed with TransIT-X2 transfection reagent (Mirus Bio, USA) according to the manufacturer’s instructions 24 h after cell seeding and at least 22 h before fixation. Fixation of cells was performed with 3.7% (wt/vol) prewarmed paraformaldehyde (PFA; EM grade; Electron Microscopy Sciences, USA) freshly diluted in PBS for 20 min at room temperature. All samples were washed repeatedly with PBS after fixation and imaged directly after or kept in PBS at 4°C until being imaged.

Preparation of cells expressing SNAP-tag or HaloTag

HeLa cells stably expressing Escherichia coli glutamine synthetase GlnA-HaloTag (Finan et al., 2015) were a gift of Florian Salopiata (DKFZ Heidelberg). U2OS cells stably expressing NUP107-SNAP-tag were a gift of Jan Ellenberg (EMBL Heidelberg) (Otsuka and Ellenberg, 2017). Both cell lines were labeled with corresponding tag substrates directly before fixation. GlnA-HaloTag–expressing cells were labeled with TMR HaloTag ligand (HTL-TMR; Promega, USA) or SiR HaloTag ligand (SiR-HTL; Spirochrome, Switzerland) at 100 nM in growth medium for 120 min at 37°C. NUP107-SNAP-tag–expressing cells were labeled with benzylguanine-functionalized TMR (BG-TMR; NEB, USA) or SiR (BG-SiR; Spirochrome) at 200 nM in growth medium for 120 min at 37°C. After labeling, cells were washed repeatedly with growth medium and fixed as described above.

Imaging buffers

Samples were imaged either in PBS or in buffers containing different ROXSs. ROXS buffers were prepared from a base solution (50 mM phosphate buffer, 13.5 mM KCl, 0.685 M NaCl, and 10 mM MgCl₂, 12.5% [vol/vol] glycerol, pH 7.4; all Sigma-Aldrich) that was degassed by flowing argon through the buffers for at least 20 min before mixing or addition of buffers to samples. Paraquat dichloride (1 mM) and 1 mM ascorbic acid were added as reducing/oxidizing agents. Oxygen was depleted from the buffer by the addition of 10 mM NaSO₃, 50 nM PCD (>3 U/mg), and 2.5 mM protocatechuic acid (ROXS PCD) or 0.66 M d-glucose, 5000 U catalase, and 40–80 U glucose oxidase (ROXS GodCat). The ROXS GodCat buffer was additionally supplemented with 1 mM Tris(2-carboxyethyl)phosphine. All buffer components were obtained from Sigma Aldrich (Germany).

Wide-field fluorescence microscopy

If not stated otherwise, single-molecule fluorescence microscopy was performed on a custom-built inverted microscope (Nikon Eclipse Ti; Nikon, Japan) with epifluorescence and total internal reflection fluorescence (TIRF) illumination. The microscope setup included an autofocus system (PFS2) and a 100× 1.49 NA oil immersion objective (Apo TIRF; both Nikon). Images were recorded using a back-illuminated emCCD camera (iXon Ultra 897; Andor, UK) at 96 nm pixel size in the sample plane. A fiber-coupled multilaser engine (MLE-LFA; TOPTICA Photonics, Germany) equipped with 488, 561, and 640 nm laser lines was used for illumination. The excitation light was filtered by a quadband notch filter. A quadband dichroic mirror separated the emission and excitation beam paths. Emitted signal was further filtered using 525/50, 605/70, and 690/70 nm bandpass filters (all AHF Analysetechnik, Germany) mounted in a motorized filter wheel (FW102C; Thorlabs, USA) placed before the camera. All microscope components were controlled using µManager (Edelstein et al., 2014). Exposure times and electron-multiplying gain and illumination intensities were optimized for each sample individually to ensure maximum signals at the start of measurements while avoiding saturation of individual pixels.

Wide-field fluorescence microscopy with extended field of view and homogeneous illumination

Single-molecule trace acquisition with improved throughput was performed on a custom-built wide-field fluorescence microscope built around an inverted Axiovert 200 stand (Zeiss, Germany). A 647 nm fiber laser with Gaussian-shaped emission profile (MPB Communications, Canada) was expanded to 6.0 mm and converted into a flattop beam using a beamshaper (πShaper AdlOptica Optical Systems GmbH, Germany) and further expanded to a diameter of 47 mm. The expanded beam was then guided into the microscope stand and focused on the back focal plane of a 100× 1.49 NA oil immersion objective (Apo TIRF; Nikon, Japan) objective. The variation in irradiance was below 15% across the entire illuminated area. Emitted signal was collected through the same objective, separated from excitation light using a quad-band dichroic filter (R405/488/561/635; Semrock, USA), and further filtered using a 405/488/532/635 nm notch filter (Semrock) and a 700/50 nm bandpass filter (Chroma, USA). Images were projected onto a back-illuminated sCMOS camera with a 130 × 130 µm field of view (Prime95B; Photometrics, UK). Samples were placed on a motorized stage (MS2000) and kept in focus using an autofocus system (CRISP; both Applied Scientific Instrumentation, USA). Camera and laser were synchronized using an Arduino Mega microcontroller board. All microscope components were controlled using µManager.

Fluorophore stability measurements

The photostability of different fluorophores and the influence of ROXS buffers on the blinking and photostability of fluorophores were evaluated by recording time-lapse data from samples labeled with the corresponding fluorophore upon high-intensity excitation. The stability of ATTO 647N was evaluated using DNA oligonucleotides labeled with ATTO 647N immobilized as described above. TMR and SiR substrates for SNAP-tag and HaloTag were evaluated in fixed cells using cell lines expressing NUP107-SNAP-tag or GlnA-HaloTag as described above. The stability of EGFP, mCherry, and mNeonGreen was evaluated in COS-7 cells transiently expressing H2A-EGFP-HaloTag (kind gift of Richard Wombacher, Max-Planck Institute for Medical Research, Heidelberg, Germany), TOMM20-mCherry-HaloTag (Werther et al., 2020), or TOMM20-mNeonGreen (Allele Biotechnology, USA) fixed 24 h after transfection. For each fluorophore, the stability in PBS, pH 7.4, and the NaSO₃, ROXS PCD, and ROXS GodCat buffer systems was tested with buffer compositions as described above. Before imaging, samples were washed once with PBS, pH 7.4, and sample chambers were filled with the respective buffer and sealed with Parafilm to minimize gas exchange during experiments.

Bleaching curves were acquired on an epifluorescence setup for all buffer–fluorophore combinations described above. EGFP- and mNeonGreen-labeled structures were bleached at 0.58 kW/cm² average irradiance, mCherry- and TMR-labeled samples were bleached at 0.84 kW/cm² average irradiance, and ATTO 647N- and SiR-labeled samples were bleached at 2.42 kW/cm² average irradiance. Image series were acquired with constant illumination until samples were fully bleached and the signal reached a plateau.

All data were background corrected by subtracting a constant offset from acquired image series to account for camera offset and excitation light bleedthrough. Offsets were manually determined for each sample and were found to be well reproducible within one condition, but variable across conditions. Bleach curves were then extracted from image series by extracting the frame-wise average intensity within a masked region. Masks were obtained from a Gaussian-filtered average projection of the first 10 images in the series and local thresholding following the Bernsen method. Mask segmentation and intensity extraction were performed using custom-written code in Fiji/ImageJ. Bleach curves were normalized to the maximum intensity in the respective trace, and the raw half bleach time (t_1/2,raw), defined as the time at which the intensity traces had decayed to <50% of the maximum intensity, was extracted using custom-written Matlab code. To facilitate comparison between fluorophores excited at different wavelengths, t_1/2,raw were normalized against the applied illumination power density (IPD) to obtain the excitation power–corrected t_1/2 = t_1/2,raw/IPD at an illumination power density of 1 kW/cm².

Fluorophore photoblinking characterization

For characterization of fluorophore blinking, an EGFP-HaloTag-SNAP-tag fusion protein targeted to the plasma membrane via fusion to the N-myristoylation sequence MGCIKSKRKDNLNDDE was stably expressed in HeLa cells. Cells expressing this construct were grown in LabTek chambered coverslips and labeled with TMR or SiR for HaloTag or SNAP-tag as described above. After labeling, cells were fixed in prewarmed PBS supplemented with 4% PFA and 0.05% glutaraldehyde for 30 min at room temperature. Cells were then repeatedly washed in PBS and imaged directly after or kept in PBS at 4°C until being imaged. For recording of image time series, samples were prepared in either PBS or ROXS PCD buffer and individual cells were randomly selected for imaging. Image stacks of 1000 frames were acquired with TIRF at an illumination power density of 50 W/cm² and with an exposure time of 25 ms on the alternative setup with homogenized illumination. Images were correlated following the approach developed in Sehayek et al. (2019) using Matlab code provided by the authors available at https://github.com/ssehayek/blink-project.git. ACFs were computed using the first 1000 frames of each image stack and a maximum lag time of 600 frames. The initial decay (lag times 2–125 frames) of obtained ACFs containing information about photoblinking was fitted to a three-state model (equalBleach) developed by Sehayek et al. (2019).

Counting by photon statistics measurements

Counting by photon statistics (CoPS) measurements were performed on a custom-built confocal microscope constructed around an inverted microscope stand (Axiovert 100; Zeiss, Germany). Linearly polarized light emitted by a ps-pulsed laser diode emitting at 640 nm (LDH P-C-640B; PicoQuant, Germany) operated at a repetition rate of 20 MHz diode was circularized using a quarter wave plate and coupled into a single-mode polarization maintaining fiber (Schäfter Kirchhof, Germany). The excitation light was directed toward a 100× NA 1.45 objective (Alpha Plan-Fluar; Zeiss) using a dichroic mirror (z532/640; CHROMA). Light emitted by the sample was collected by the same objective and passed through the dichroic filter. Scattered excitation light was removed using a quad-band notch filter (488/532/631–640 nm; AHF Analysetechnik). The remaining emitted light was then spatially filtered with a pinhole (100 µm diameter) placed in the focal plane between two achromatic doublet lenses (f = 75 mm; Thorlabs). All remaining light was split into four equal paths using three 50:50 beamsplitters (Thorlabs) and focused on four avalanche photo diode (APD) detectors (SPCM AQR-13; Perkin-Elmer, USA) using achromatic doublet lenses (f = 200 mm; Thorlabs). Bandpass filters (685/70 nm) were placed in front of each APD. Signals detected by the APDs were processed using a HydraHarp400 multichannel time-correlated single photon counting system and the SymPhoTime 64 software platform (both PicoQuant). The positions of objective and sample were controlled by a one-axis piezo scanner (P-721 PIFOC) and a two-axis piezo stage (7332CD; both Physik Instrumente, Germany). The two-axis piezo stage was also used for stage scanning during image acquisition.

DNA origami samples were prepared for CoPS measurements as described above and imaged ∼30 min after sealing of LabTek sample chambers. Measurements were initiated by acquisition of an overview scan to identify immobilized, diffraction-limited signals from individual DNA origami. Time-correlated single-photon counting (TCSPC) data were then recorded by focusing on individual origami with 10 µW excitation as measured before the objective.

CoPS coincidence data were analyzed by computing coincident photon histograms from the first 1 × 10⁷ laser cycles (=0.5 s) of acquired TCSPC data for each origami. The histogram is then modeled with the analytical equation for coincidence probabilities (Ta et al., 2010) using the Python scipy optimization model (Levenberg–Marquardt algorithm). Traces with a modeled molecular brightness of <5 × 10⁻³ were excluded.

Photobleaching step analysis

Data acquisition.

Data for photobleaching step analysis were acquired in ROXS PCD buffer for all samples. DNA origami data were acquired with 2.4 kW/cm² average laser power at 640 nm for R09, R20, and R35 and with 0.84 kW/cm² average laser power at 561 nm for Y09 origami. NUP107 data were acquired with 1.2 kW/cm² average laser power at 640 nm. Exposure times were 50 or 200 ms for all measurements.

Data analysis.

The first five images from the measured image sequence were averaged and used to locate fluorophore clusters. The localization was performed with Fiji 1.52p (Schindelin et al., 2012; Schneider et al., 2012) using the plug-in thunderSTORM (Ovesný et al., 2014). Trace extraction was done with the trace extraction submodule of the quickPBSA package, as detailed in the package documentation. In short, the average signal from circular regions around the localizations was extracted with typical diameters of 950 nm for the in vitro samples and 150 nm for the NUP107 experiment. For background correction, the average signal from ring-shaped regions was subtracted (inner diameter 1.7 µm for origami, 0.6 µm for NUP107, outer diameter 2.0 µm for origami, 0.9 µm for NUP107). Regions around neighboring localizations were excluded from the background region. Additionally, ROIs with nearest neighbors at a distance below 950 nm for DNA origami and 475 nm for NUP107 were excluded.

Photobleaching step analysis was performed using the quickPBSA package, as detailed in the main text and in the documentation of the quickPBSA package. Typically, the threshold parameter for preliminary step detection was set at 0.03 and maxiter at 200. Other analysis parameters were kept at their default values, except for the mult_threshold parameter in step refinement, which was typically set to 1.5 to decrease runtime.

Semisynthetic data sets were generated by manual annotation of traces obtained from tetraATTO 647N DNA oligonucleotides measured in NaSO₃ ROXS buffer. The analysis according to Tsekouras et al. (2016) was performed with the Python code from https://github.com/lavrys/Photobleach. The analysis of the benchmarking data set was performed on the University of Birmingham’s High Performance Computing Service BlueBEAR (Intel CascadeLake; 40 cores). All other analyses were carried out on a workstation with an eight-core CPU at 3.4 GHz (Intel(R) Core(TM) i7-3770) and 12 GB DDR3 memory.

Code availability

The quickPBSA package, example data, and documentation are available at https://github.com/JohnDieSchere/quickpbsa.

Abbreviations used:

ACF

autocorrelation function

APD

avalanche photo diode

BG

benzylguanine

CoPS

counting by photon statistics

EGFP

enhanced green fluorescent protein

emCCD

electron multiplying charge-coupled device

GodCat

glucose oxidase and catalase

IPD

illumination power density

KV

kalafut-visscher

NPC

nuclear pore complex

NUP107

Nucleoporin 107

PBS

phosphate buffered saline

PBSA

photobleaching step analysis

PCD

protocatechuate-3,4-dioxygenase

PFA

paraformaldehyde

quickPBSA

quick photobleaching step analysis

ROI

region of interest

ROXS

reducing and oxidizing system

sCMOS

scientific complementary metal–oxide–semiconductor

SD

standard deviation

SE

standard error of mean

SIC

schwarz information criterion

SiR

Silicon rhodamine

SNR

Signal-to-noise ratio

TBE

Tris-borate-ethylenediaminetetraacetic acid

TCSPC

time-correlated single-photon counting

TMR

tetramethylrhodamine.