Abstract
In this study, the nonlinear optical (NLO) response of alkali metal atom (Li, Na and K) and their corresponding superalkali (Li3O, Na3O and K3O) doped six membered cyclic thiophene (6CT) has been explored. The optimized geometries of complexes; Li@6CT, Na@6CT, K@6CT, Li3O@6CT, Na3O@6CT and K3O@6CT depict that the superalkalis and alkali metals interact through the active cavity of 6CT. Interaction energies reveal that superalkalis have higher interaction with 6CT than alkali metals. The nonlinear optical (NLO) response of the reported complexes is estimated via both static and dynamic hyperpolarizabilities which are further rationalized by the HOMO–LUMO gap, natural bond orbital (NBO) charge transfer, dipole moment, polarizabilities and βvec. A remarkably high NLO response is computed for Na3O@6CT among all of the complexes. The static hyperpolarizability of the Na3O@6CT complex is 5 × 104 au along with the highest βvec value (2.5 × 104 au). High charge transfer (1.53e−) and small EH–L gap (2.96 eV) is responsible for such a large NLO response. For dynamic NLO responses, electro-optic Pockel's effect (EOPE) and second-harmonic generation (SHG) are explored. A very large quadratic nonlinear optical response (3.8 × 10−12 au) is observed for the Na3O@6CT complex. Moreover, the absorption spectrum of the Na3O@6CT complex shows ultra-high transparency in the ultraviolet and visible regions unlike any other of its counterparts.
In this study, the nonlinear optical (NLO) response of alkali metal atom (Li, Na and K) and their corresponding superalkali (Li3O, Na3O and K3O) doped six membered cyclic thiophene (6CT) has been explored.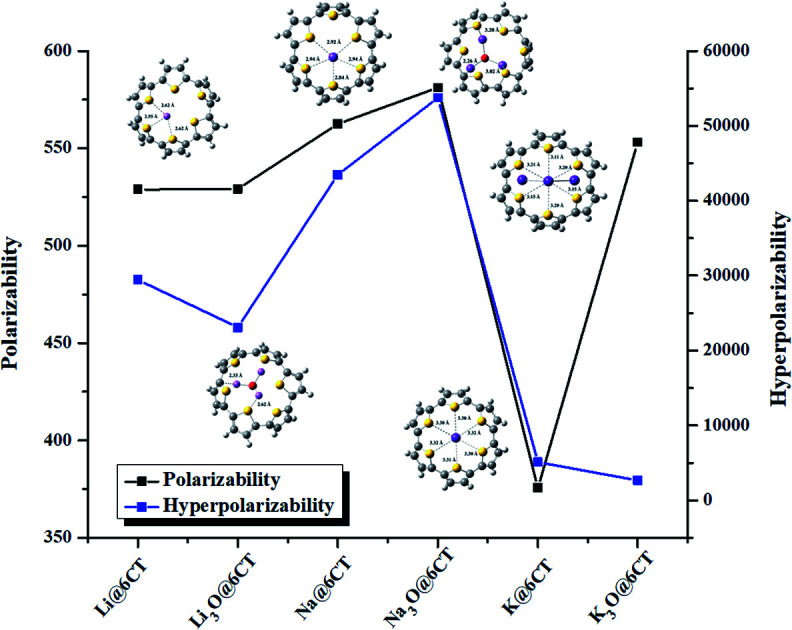
1. Introduction
To date, significant consideration has been devoted to the fabrication of high performance nonlinear optical (NLO) materials,1–4 due to their utility in electro-optic devices.5–7 To fulfil this demand, various kinds of novel NLO materials with excess electrons have been designed.8,9 It is very well documented that the excess electrons play a pivotal role in the large NLO response.10,11 Excess electrons can be generated by capping a material with alkali metal atoms.12 Thus alkali metal doping leads to large first and second hyperpolarizabilities of the systems.13,14 Munsif et al.,15 reported the exceptionally high NLO response of inorganic nanocages upon doping with alkali metal atoms. In their study, the authors claimed that the hyperpolarizability of potassium doped boron phosphide (inorganic nanocage) was the highest (7.9 × 105 au) ever reported. Maria and co-workers illustrated the exceptional increase in the hyperpolarizability of inorganic systems to 1.3 × 104 au from 0.00 au (pure material) upon doping with potassium metal.16 In another similar report, Maria et al.,17 studied the nonlinear optical behaviour of inorganic nanocages. Their results suggested the hyperpolarizability of such systems was greatly enhanced upon capping with alkali metal atoms. Like inorganic systems, the NLO behaviour of organic systems is equally enhanced on complexation with alkali metals. For example, Li et al.,8 theoretically designed a novel electride by adsorbing lithium metal on calix[4]pyrrole. The resulting electride molecule showed a large hyperpolarizability value (7326 au) which was twenty times larger than that of isolated calix[4]pyrrole systems. Based on the above discussion, it can be concluded that the doping of alkali metals remarkably enhance the opto-electronic properties of inorganic as well as organic systems.
In the recent decades, superalkalis, a kind of superatom clusters are attaining more interest as compared to alkali metal atoms. The superalkalis have greater affinity of donating valance electrons due to the lower vertical ionization potential.18 Therefore, their usage in nonlinear optics advocated significant interest of experimental and theoretical researchers. It has been observed that the superalkalis doping increases the hyperpolarizability of the inorganic materials such as aluminium phosphide,19 boron phosphide20 and silicon carbide nanocages.21 Apart from the inorganic systems, the NLO response of organic materials doped with superalkalis is also investigated. The organic molecules are expected to have giant NLO response because of their extended π-conjugation.22–24 In this regard, the nonlinear behaviour of graphdiyne was measured upon doping with superalkalis. Shehzadi et al.,25 reported the dramatic increase in the first hyperpolarizability of superalkalis doped graphdiyne to 7.7 × 104 au. In another similar report, the remarkable enhancement in the NLO response of graphdiyne sheet upon complexation with superalkalis is demonstrated by Kosar et al.26 The authors compared the NLO response of M3O and M3S (M = Li, Na & K) complexed graphdiyne and observed that both showed equal effect. In our previous report, we have presented that superalkalis (M3O) doping in cyclic oligofuran remarkably enhances the NLO response. We reported that the cyclic conjugated ring systems can effectively be used as high NLO material due to their electron dense active cavity.27
The area of alkali and superalkalis doped cyclic thiophene ring system needs to be further explored. Thus, here we intend to compare the NLO response of macrocyclic hexathiophene ring (6CT) upon complexation with alkali metal atom (Li, Na, K) and their superalkalis analogues (Li3O, Na3O and K3O). The geometric, electronic and nonlinear optical properties of alkali and superalkalis doped 6CT i.e., Li@6CT, Na@6CT, K@6CT, Li3O@6CT, Na3O@6CT and K3O@6CT complexes are studied computationally. The NLO behaviour of said complexes are investigated via first hyperpolarizability (βo), electro-optical Pockels effect (EOPE), second harmonic generation (SHG), and nonlinear refractive index (n2) calculations.
2. Computational methods
Geometry optimizations of complexes are performed with two high level Minnesota functionals including M05-2X and M06-2X along with 6-31G(d,p), 6-31+G(d,p) and 6-311+G(d,p) basis sets. All calculations are performed with Gaussian09 software.28 The interaction energies of complexes are defined by the expression below (eqn (1)).
| Eint = Ecomplex − E6CT − ESA/AA | 1 |
where Ecomplex, E6CT and ESA/AA are the energies of alkali atoms/superalkalis@6CT complex, cyclic hexathiophene and superalkalis/alkali atoms, respectively. Frontier molecular orbital (FMO) and NBO analysis are performed for the estimation of HOMO–LUMO (H–L) gap and amount of charge transfer of 6CT, respectively, upon complexation with alkali/superalkalis. To confirm the charge transfer and variation of H–L gaps, density of state (DOS) spectra are plotted through GaussSum software.29 The polarizability, first hyperpolarizability calculations are benchmarked at M05-2X, M06-2X and LC-BLYP functionals with 6-31+G(d,p) basis set. However, the dynamic NLO responses of complexes are calculated at LC-BLYP because it is reported as a best functional for the estimation of nonlinear optical properties due to the full range separation with 1.00 correct fraction of nonlocal exchange functional.15,30 The polarizability (αo), first hyperpolarizability (βo) and second order hyperpolarizability βvec are defined as:
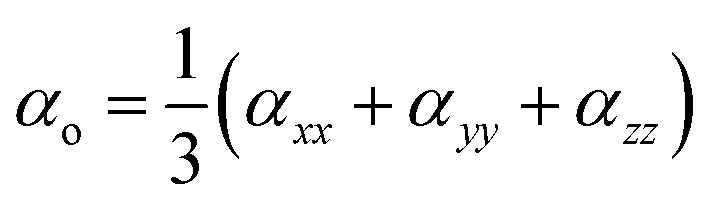 |
2 |
| βo = (βx2 + βy2 + βz2)1/2 | 3 |
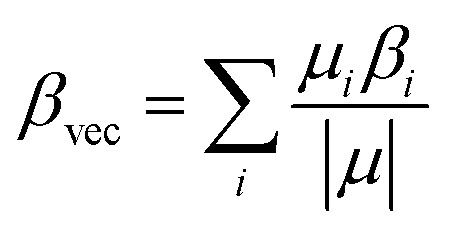 |
4 |
where βx = βxxx + βxyy + βxzz, βy = βyyy + βxzz + βyxx, βz = βzzz + βzxx + βzyy
| βi = ∑(βijj + βjji + βjij)i, j = {x, y, z} | 5 |
The second hyperpolarizability (γo) is estimated as:
The frequency dependent NLO response in terms of the second harmonic generation (SHG) β(−2ω, ω, ω), the electro-optical Pockels effect (EOPE) β(−ω, ω, 0), electro-optic Kerr effect (EOKE) form γ(−ω, ω, 0, 0) and SHG form γ(−2ω, ω, ω, 0) are estimated at two standard Nd:Yag laser frequencies: ω = 0.0428 au (1064 nm) and ω = 0.0856 au (532 nm).
The frequency dependent/dynamic NLO response is computed through Coupled Perturbed Kohn–Sham (CPKS) method31 and results are analyzed through Multiwfn software.32 The dynamic first hyperpolarizability can be represented using the following equation:β(ω) = [βx2(ω) + βy2(ω) + βz2(ω)]1/2where the coefficients of second harmonic generation (SHG) are obtained usingβi = βiii(−2ω, ω, ω) + βijj(−2ω, ω, ω) + βikk(−2ω, ω, ω)
And the coefficients of electro-optical Pockels effect (EOPE) are obtained fromβi = βiii(−ω, ω, 0) + βijj(−ω, ω, 0) + βikk(−ω, ω, 0).
3. Results and discussion
3.1. Optimized geometries and stabilities
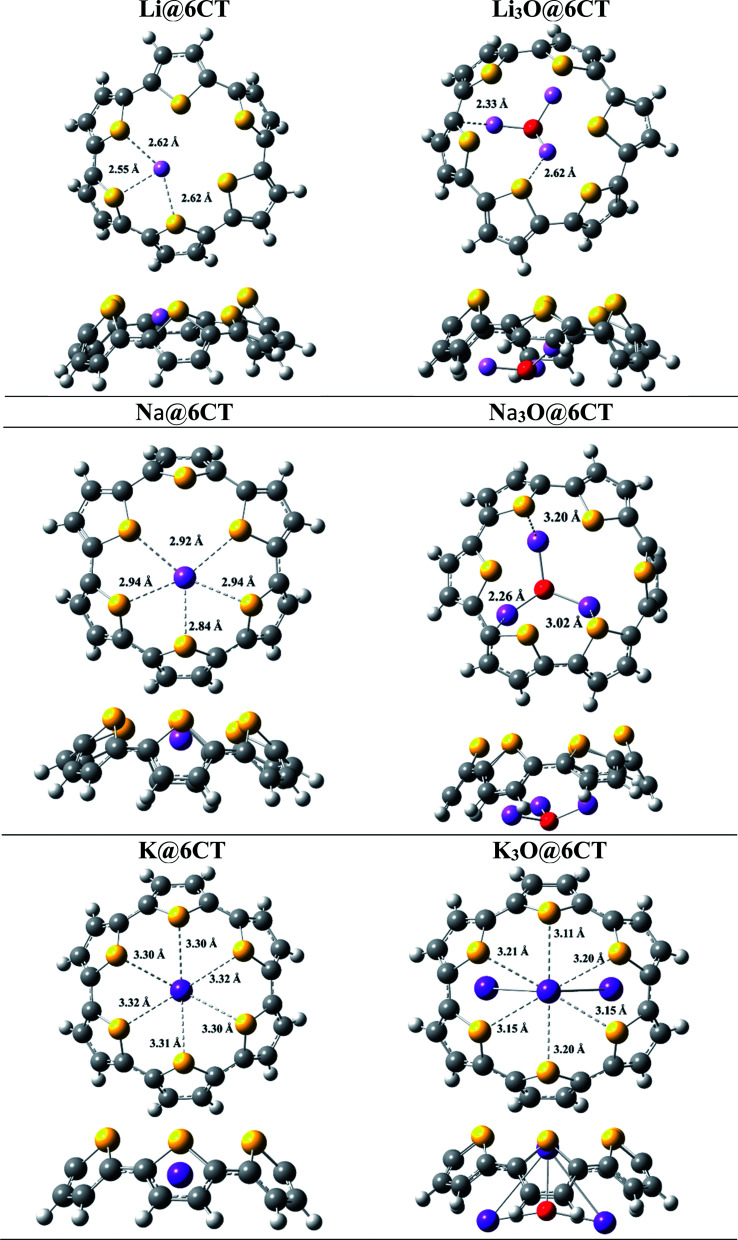
The six membered cyclic thiophene ring (6CT) is doped with three alkali metal atoms (Li, Na, K) and superalkalis (Li3O, Na3O and K3O) to form AA@6CT (alkali metal doped) and SA@6CT (superalkalis doped) complexes. The different orientations of interactions are possible due to the various sensitive positions of 6CT. All these orientations are studies and their geometries are given in ESI (Fig. S1–S3).† Among all possibilities, the most stable geometries are considered for detailed analysis and their structures are displayed in Fig. 1. The interaction energies of AA@6CT and SA@6CT complexes are calculated at two Minnesota functionals i.e., M05-2X & M06-2X. The selection here is based on the previous reports, revealing the higher accuracy of Minnesota functionals to estimate the noncovalent interactions. For even better analysis, calculations are performed by using 6-31G (d,p), 6-31+G(d,p) and 6-311+G(d,p) basis sets. The interaction energies of complexes are listed in Table 1. Broadly, the interaction energies of SA@6CT complexes are higher at all methods as compared to AA@6CT complexes which might be due to the higher electron density on superalkalis than alkali atom. Among all the complexes, the highest interaction energies are computed for Li3O@6CT complex at M05-2X functional. The interaction energies of Li3O@6CT complex are −76.60, −71.86 and −70.34 kcal mol−1 at M05-2X/6-31G(d,p), M05-2X/6-31+G(d,p) and M05-2X/6-311+G(d,p) level of theory, respectively.
Fig. 1. Top and side view of most stable optimized geometries of AA@6CT and SA@6CT complexes.
Benchmark interaction energies (in kcal mol−1) of SA@6CT and AA@6CT complexes at different level of density functional theory.
| Complexes | M052X | M062X | |||||
|---|---|---|---|---|---|---|---|
| 6-31G (d,p) | 6-31+G (d,p) | 6-311+G (d,p) | 6-31G (d,p) | 6-31+G (d,p) | 6-311+G (d,p) | ||
| Li@6CT | −41.07 | −40.29 | −41.90 | −39.54 | −38.85 | −40.44 | |
| Li3O@6CT | −76.60 | −71.86 | −70.34 | −72.76 | −67.66 | −67.37 | |
| Na@6CT | −35.59 | −35.10 | −36.58 | −33.41 | −32.94 | −34.53 | |
| Na3O@6CT | −64.41 | −59.67 | −61.95 | −60.90 | −56.18 | −58.54 | |
| K@6CT | −40.51 | −39.83 | −42.19 | −39.34 | −38.72 | −41.11 | |
| K3O@6CT | −71.19 | −61.45 | −60.82 | −73.76 | −64.29 | −66.06 | |
Similarly, in case of AA@6CT complexes, lithium doped complex also shows higher stability with the interaction energies of −41.07, −40.26 and −41.90 kcal mol−1 at 6-31G (d,p), 6-31+G(d,p) and 6-311+G(d,p) basis sets, respectively. Quite similar to M05-2X, Li and Li3O doped complexes also exhibit higher stability at M06-2X with a small exception at 6-31G(d,p) basis set. The interaction energies of Li3O@6CT complexes are −72.76, −67.66 and −67.37 kcal mol−1 while Li@6CT complex are −39.54, −38.85 and −40.44 kcal mol−1 at M06-2X/6-31G(d,p), /6-31+G(d,p) and /6-311+G(d,p), respectively. Owing to the smallest atomic size, the lithium atom interacts more closely to the 6CT which is further evident by the least interaction distance (Id) among all SA@6CT and AA@6CT complexes. The interaction distances of Li3O@6CT and Li@6CT complexes are 2.62 and 2.55 Å, respectively (see Table 2) which are least among all the other complexes.
Interaction parameters of optimized geometries of SA@6CT and AA@6CT complexes.
| Complexes | Sym | Int bond | Int distance (Å) | HOMO (eV) | LUMO (eV) | E H–L (eV) | Q (e−) |
|---|---|---|---|---|---|---|---|
| 6CT | C 1 | — | — | −6.43 | −0.24 | 5.02 | — |
| Li@6CT | C 1 | Li⋯S | 2.55 | −4.58 | −1.31 | 3.27 | 0.60 |
| Li3O@6CT | C 1 | Li⋯S | 2.62 | −4.59 | −1.44 | 3.15 | 1.69 |
| Na@6CT | C 1 | Na⋯S | 2.84 | −4.54 | −1.00 | 3.14 | 0.76 |
| Na3O@6CT | C 1 | Na⋯S | 3.02 | −4.50 | −1.54 | 2.96 | 1.53 |
| K@6CT | C 1 | K⋯S | 3.30 | −4.01 | −1.48 | 2.93 | 0.75 |
| K3O@6CT | C 1 | K⋯S | 3.11 | −4.54 | −1.24 | 3.29 | 0.91 |
The stability of the lithium-based complexes is followed by the potassium doped complexes. The high stability of K3O@6CT complex can be explained by examining the geometry. Fig. 1 reveals that only a single K atom equally interacts with all the sulfur atoms of 6CT unlike Na doped complexes where interaction of sodium is with some sulfur atoms. The interaction distances (K⋯S) of K or K3O and 6CT are 3.30 and 3.11 Å, respectively. The average interaction distances between sodium atom of Na and Na3O with sulfur atoms of 6CT are 2.84 and 3.02 Å, respectively. The interaction energies of K3O@6CT and K@6CT complexes are higher at all methods than Na3O@6CT and Na@6CT complexes, respectively (see Table 1). It can be seen from the results, the basis set 6-31G(d,p) (without polarization) overestimates the energy values while 6-31+G(d,p) basis set predicts higher accuracy in the results.
3.2. Electronic properties
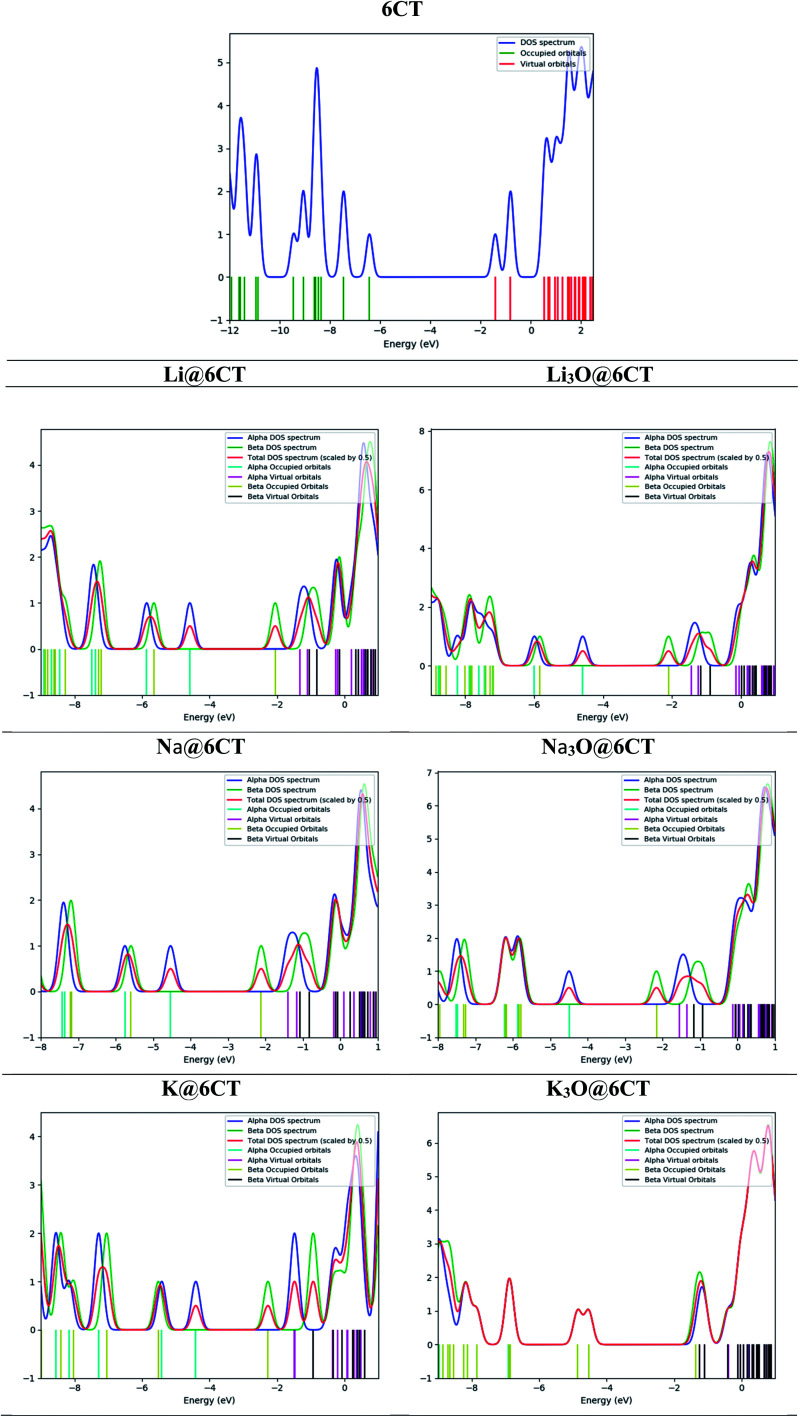
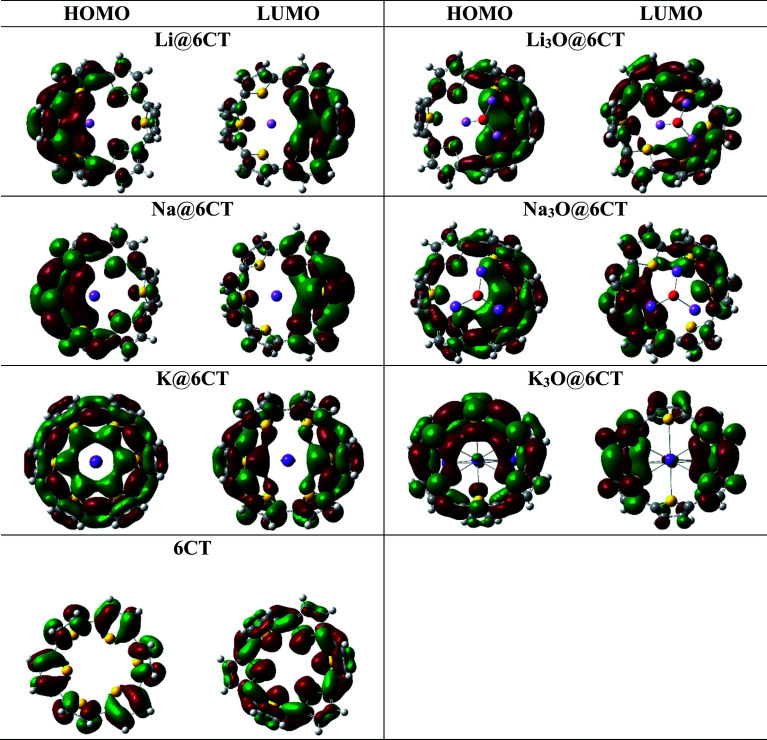
Molecular orbital analysis is performed to examine and compare the variation of electronic parameters of 6CT upon complexation with alkali atoms and superalkalis. The energies of HOMO and LUMO orbitals and their differences (EH–L) in eV are given in Table 2. The EH-L of isolated 6CT is 5.02 eV where the energies of HOMO and LUMO are −6.43 and −0.24 eV, respectively. The EH–L of 6CT decreases upon complexation due to the formation of new energy levels.33 In comparison with alkali metals, the superalkalis doping widely reduces the H–L gaps which reflects the large availability of excess electrons in SA@6CT complexes. The EH–L of 6CT is reduced to 3.15, 2.96 and 3.29 eV in Li3O@6CT, Na3O@6CT and K3O@6CT complexes, respectively. On the other hand, the EH–L of Li@6CT, Na@6CT and K@6CT complexes are 3.27, 3.14 and 2.93 eV, respectively. The decrease in the H–L gaps of complexes is due to the variation in the energies of HOMO and LUMO orbitals upon complexation with alkali metals and superalkalis. For instant, the LUMO energy of 6CT (−0.24 eV) reduces to −1.31, −1.00 and −1.48 eV on interaction with Li, Na, and K atoms, respectively. Similarly, the LUMO energies of Li3O@6CT, Na3O@6CT and K3O@6CT complexes are shifted to −1.44, −1.54 and −1.24 eV, respectively. The decreasing trends of LUMO energies of AA@6CT and SA@6CT complexes are as follow; K > Li > Na and Na3O > Li3O > K3O, respectively. Moreover, the trend of increasing energies of HOMO orbital for AA@6CT and SA@6CT complexes are; K > Na > Li and Na3O > K3O > Li3O, respectively. The effects of K and Na3O in H–L gaps of AA@6CT and SA@6CT complexes, respectively are more pronounced. Therefore, the K@6CT and Na3O@6CT complexes show the lowest H–L gap among in their series. Furthermore, DOS spectra reveal (Fig. 3) that the generation of new HOMO/occupied energy levels on interaction plays pivotal role to lower the EH–L gaps of complexes. It is clearly seen in Fig. 2 that the HOMO orbitals of the systems mainly reside near the doped alkali atoms or superalkalis, indicating the generation of new HOMO orbitals which are further responsible of producing excess electrons in the system. The DOS spectrum in Fig. 3 reveals that the occupied and virtual orbitals of isolated 6CT are located at −6.43 and −0.24 eV, respectively. Upon complexation with alkali atoms and superalkalis, the spin state has been changed from singlet (in 6CT) to doublet (in AA@6CT and SA@6Ct complexes) due to the involvement of unpaired electrons from doped metal atoms. Moreover, the occupied orbitals of the 6CT are shifted closer to the Fermi level on interaction. The occupied orbitals appear at −4.58, −4.54, −4.01 eV (light blue colour) in Li@6CT, Na@6CT and K@6CT complexes, respectively. However, the occupied orbitals peaks of Li3O@6CT, Na3O@6CT and K3O@6CT complexes appear at −4.59, −4.50 and −4.54 eV, respectively. Moreover, the peaks (red colour) in the DOS spectrum of 6CT are also shifted toward Fermi level upon complexation with alkali and superalkalis (light brown peaks). From DOS analysis, it can be concluded that the HOMO and LUMO energy gaps of AA@6CT and SA@6CT complexes decrease due to the shift or generation of new orbitals close to the Fermi level.
Fig. 3. DOS spectra of 6CT, AA@6CT and SA@6CT complexes.
Fig. 2. HOMO and LUMO orbitals of 6CT, AA@6CT and SA@6CT complexes.
NBO analysis is performed to examine the charge transfer between 6CT and AA or SA. Expectedly, the charge transfer in SA@6CT complexes is higher than AA@6CT complexes due to the large electronic density on superalkalis. The NBO charge transferred (Q) in Li3O@6CT, Na3O@6CT and K3O@6CT complexes is 1.69, 1.53 and 0.91e−, respectively. Probably, some of the electronic density is shifted from alkali atoms toward the covalently bonded electronegative oxygen atom of superalkalis. This charge transfer increases with decreasing the electronegativity of alkali atoms from Li to Na. Due to the increasing charge transfer between the atoms of superalkalis, the charge transfer decreases between superalkalis and 6CT from Li3O to Na3O. On the other side, the amount of charge transfer increases upon increasing atomic number of alkali atoms. The amounts of charge transfer is 0.60, 0.76 and 0.75e− in Li@6CT, Na@6CT and K@6CT complexes, respectively.
3.3. UV-vis analysis
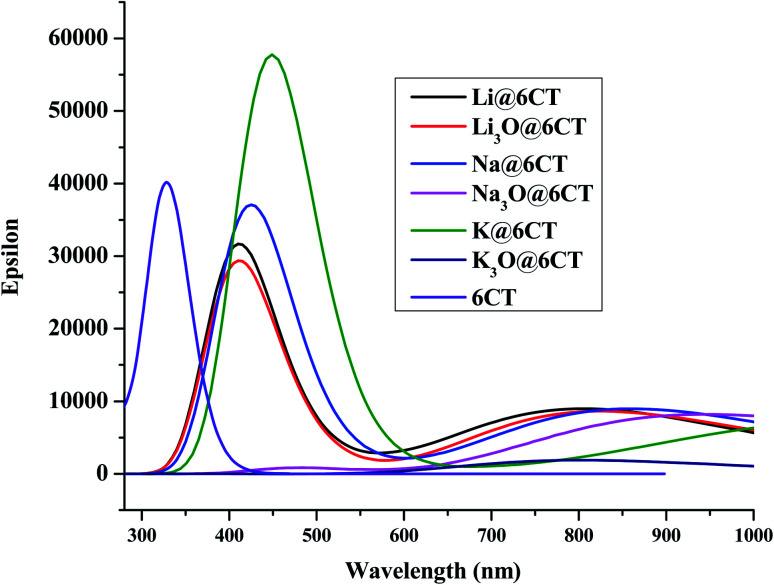
It is postulated that NLO active material should be transparent in the interested region of EMR spectrum.34 In order to find the adsorption wavelength of 6CT before and after doping, the UV-vis analysis is performed at TD/M05-2X/6-31+G(d,p). It is cleared from the results (Table 3 & Fig. 4) that the maximum absorption of isolated 6CT appears at 328 nm. The absorption spectrum of 6CT splits into two red shifted peaks in visible region upon complexation especially with Li, Na, K and Li3O. Firstly, the red shift in the UV-vis spectra of AA@6CT and SA@6CT complexes articulates the increasing π–π* transitions. Results reveal that all the reported materials are transparent in ultraviolet region. However, the Na3O@6CT and K3O@6CT complexes show good transparency in both ultraviolet and visible regions due to the absence of peak maxima between 200 to 800 nm. In comparison, Na3O@6CT and K3O@6CT complexes indicate adequate transparency for laser applications in both UV and vis regions.
NLO parameters: dipole moment (μo), polarizability (αo), first hyperpolarizability (βo), projection of β on dipole moment vector (βvec), hyper-Rayleigh (βHRS), second hyperpolarizability (γo), crucial excitation energies (Eex), change in dipole moment (Δμ), vertical ionization energy (VIE), maximum absorbance (λmax) and oscillator strength (fo) of isolated 6CT and AA@6CT & SA@6CT complexes.
| LC-BLYP | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Complexes units | μ o D | α o au | β o au | β vec au | β HRS au | γ o au | ΔEex eV | Δμ D | V IE eV | λ max nm | f o au |
| 6CT | 4.85 | 384.56 | 2 × 102 | — | — | — | 0.85 | 1.19 | 6.96 | 328 | 0.49 |
| Li@6CT | 6.00 | 528.90 | 3 × 104 | 1.5 × 104 | 1.5 × 104 | 2.0 × 106 | 3.10 | 1.76 | 5.02 | 424 | 0.38 |
| Li3O@6CT | 6.50 | 529.20 | 2 × 104 | 9.8 × 103 | 1.1 × 104 | 1.7 × 106 | 3.10 | 1.38 | 5.03 | 425 | 0.28 |
| Na@6CT | 6.93 | 562.53 | 4 × 104 | 2.3 × 104 | 2.4 × 104 | 4.1 × 106 | 3.06 | 2.31 | 4.98 | 443 | 0.21 |
| Na3O@6CT | 6.89 | 581.13 | 5 × 104 | 2.5 × 104 | 2.7 × 104 | 2.6 × 106 | 1.66 | 6.19 | 4.94 | 883 | 0.09 |
| K@6CT | 7.27 | 375.62 | 5 × 103 | 3.9 × 103 | 2.3 × 103 | 5.6 × 106 | 2.96 | 1.34 | 4.92 | 448 | 0.71 |
| K3O@6CT | 13.17 | 553.15 | 3 × 103 | 2.5 × 103 | 1.3 × 103 | 3.6 × 105 | 2.39 | 2.95 | 6.33 | 809 | 0.04 |
Fig. 4. UV-vis spectra of 6CT, AA@6CT and SA@6CT complexes.
4. Nonlinear optical properties
4.1. Static NLO responses
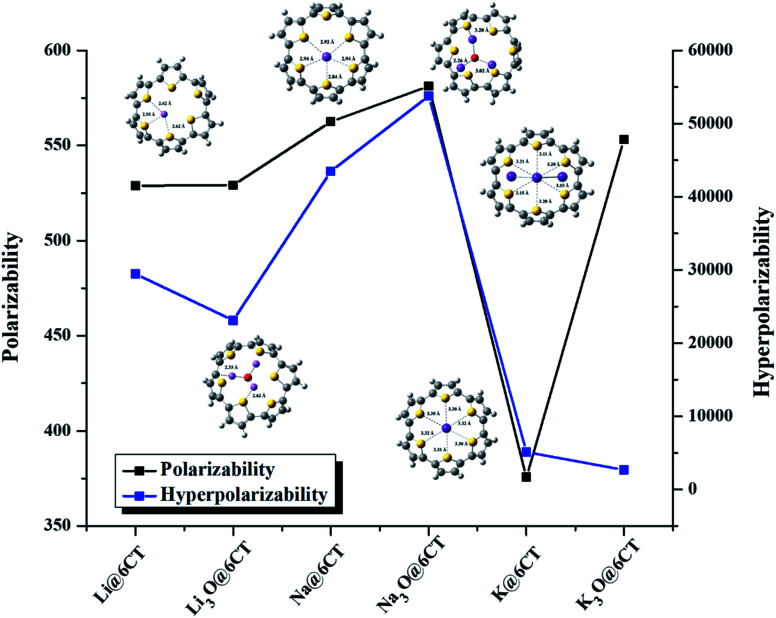
The values of dipole moment (μo) and polarizabilities (αo) of isolated and complexed 6CT are given in Table 3. The dipole moment of 6CT is 4.85 D due to its C1 symmetry (Table 2). However, the dipole moment of 6CT increases upon complexation with alkali metals and superalkalis due to the distortion of symmetry. The dipole moments are ranging from 6.00 to 7.27 D and 6.50 to 13.17 D in AA@6CT and SA@6CT series, respectively. Similarly, the static polarizabilities of SA@6CT complexes are higher than AA@6CT complexes due to the greater electronic contribution of superalkalis. The polarizabilities of Na@6CT and Na3O@6CT complexes are the highest among all complexes which is well consistent with the hyperpolarizabilities (vide infra). The αo of AA@6CT complexes is ranging from 375.62 au (K@6CT) to 562.53 au (Na@6CT) whereas, these values range from 528.90 to 553.15 au for SA@6CT complexes.
The static hyperpolarizabilities of the designed complexes have been computed to explore their NLO responses and the results are listed in Table 3 & Fig. 5. The static hyperpolarizability (βo) of isolated 6CT is 2 × 104 au. The complexation of alkali metal and superalkalis remarkably boost the βo of 6CT to lie in the range of 2 × 104–5 × 104 au. Surprisingly, the NLO responses of Li and K doped 6CT is higher than their corresponding superalkalis complexes. The lower NLO responses of Li3O@6CT and K3O@6CT complexes are probably due to the higher vertical ionization energy (VIE) values33 which reflects the removal of electron is difficult from these systems. On the hand, Na3O@6CT complex exhibits lower VIE (4.94 eV) than corresponding Na@6CT complex, therefore, the βo of former is far higher than the later complexes. Furthermore, βo results reveal that the Na3O@6CT complex is highly NLO active among other designed complexes.
Fig. 5. Graphical representation of polarizability and hyperpolarizability of AA@6CT and SA@6CT complexes.
To support these findings, the projection of static hyperpolarizability on the dipole moment vector (βvec) is also computed. The trend of βvec is exactly consistent to the βo of complexes which reveals that Na3O@6CT complex is highly NLO sensitive while K3O@6CT complex shows least sensitivity. These findings are well comparable to the above-mentioned electronic parameters especially HOMO–LUMO gap and NBO charge transfer analysis. The hyperpolarizability of superalkalis doped complex agrees well with the previously reported similar superalkalis doped cyclic conjugated ring systems. In our previous study, we have reported that the βo of superalkalis doped cyclic oligofuran systems was appreciably high and ranges from 1 × 104 to 2 × 104 au especially in Li3O doped complexes.27 In another similar study, the reported βo of lithium doped cyclic conjugated ring system was 7.3 × 103 au33 and 3 × 104 au.34 In this study, we found that the NLO responses of alkali and superalkalis doped 6CT complexes have shown good agreement with the previously reported similar systems.35,36
Two level model is performed to interpret the effects of change in dipole moment (Δμ), oscillator strength (fo) and crucial excited energy (ΔEex) on the hyperpolarizability of complexes. The two-level model can be defined by the expression below;37βo ∝ fo × Δμ/ΔEex3
Based on the above equation, the βo increases with increasing values of oscillator strength or the change in dipole moment. On the other side, the value of βo is lower if a complex exhibits high crucial excited energy. The results illustrate that the Na3O@6CT complex shows the highest βo which might be due to the largest value of Δμ (6.19 D). The lowest value of crucial excited energy (1.66 eV) is also contributing to the higher hyperpolarizability of Na3O@6CT complex. Similarly, the smallest oscillator strength (fo) (0.04 au) of K3O@6CT complex plays a vital role of exhibiting small NLO response.
The static second hyperpolarizability (γo) values are also estimated and the results revealed that γo values have trend similar to that of βo but the γo values are significantly larger. The γo values of the designed complexes are in the range of 3.6 × 105 to 5.6 × 106 au. According to previous results,38 the giant NLO response in the alkali and superalkalis doped cyclic thiophene may be caused by the excess electrons of doped alkali/superalkalis.
Due to the lack of experimental results, the hyperpolarizability of complexes are also calculated at M05-2X and M06-2X with different basis sets including 6-31G(d,p), 6-31+G(d,p) and 6-311+G(d,p) (Table 4). The trend of hyperpolarizability of AA@6CT and SA@6CT complexes at Minnesota functional is quite comparable with LC-BLYP. Like LC-BLYP, the βo of Na3O@6CT complex is the highest in all the cases with little exception at 6-31G(d,p) and 6-311+G(d,p) basis sets. The βo of Na@6CT and Na3O@6CT are 2.3 × 104 and 2.9 × 104 au, respectively at M05-2X/6-31+G(d,p) level of theory, the highest compared to other AA@6CT and SA@6CT complexes. At M06-2X, the βo values of Na@6CT and Na3O@6CT complexes are 2.2 × 104 and 2.6 × 104 au which is quite consistent with the results of competing M05-2X method. Though the trend is same with LC-BLYP but the values of βo for complexes are appreciably lower at Minnesota functionals. Moreover, LC-BLYP is a full range separated functional with 1.00 fraction for nonlocal exchange at asymptotic distance.39,40 Therefore, the nonlinear optical results of material are more reliable at LC-BLYP15 thus, the dynamic hyperpolarizability has been calculated at widely accepted LC-BLYP.
Hyperpolarizability (βo in au) of SA@6CT and AA@6CT complexes at M052X and M062X methods.
| Complexes | M052X | M062X | ||||
|---|---|---|---|---|---|---|
| 6-31G (d,p) | 6-31+G (d,p) | 6-311+G (d,p) | 6-31G (d,p) | 6-31+G (d,p) | 6-311+G (d,p) | |
| 6CT | 7.0 × 101 | 2.1 × 102 | 2.4 × 102 | 6.6 × 100 | 2.3 × 102 | 2.2 × 102 |
| Li@6CT | 1.6 × 104 | 1.8 × 102 | 1.8 × 104 | 1.6 × 104 | 1.8 × 104 | 1.8 × 104 |
| Li3O@6CT | 1.6 × 104 | 1.8 × 104 | 1.9 × 104 | 1.6 × 104 | 1.9 × 104 | 1.9 × 104 |
| Na@6CT | 2.0 × 104 | 2.3 × 104 | 3.5 × 103 | 1.9 × 104 | 2.2 × 104 | 2.1 × 104 |
| Na3O@6CT | 2.6 × 104 | 2.9 × 104 | 3.1 × 104 | 1.1 × 105 | 2.6 × 104 | 2.5 × 104 |
| K@6CT | 3.0 × 102 | 3.8 × 102 | 4.6 × 102 | 4.1 × 102 | 1.9 × 102 | 2.6 × 102 |
| K3O@6CT | 6.1 × 104 | 5.9 × 103 | 2.5 × 103 | 4.0 × 104 | 3.3 × 103 | 9.7 × 103 |
4.2. Dynamic NLO responses
The dynamic first hyperpolarizability coefficients i.e. electro-optic Pockel's effect (EOPE) with β(−ω, ω, 0) and the second-harmonic generation (SHG) with β(−2ω, ω, ω) of the designed complexes are calculated and the values are given in Table 5. The frequency dispersion analysis was performed with the wavelengths of 532 nm (0.0856 au) and 1064 nm (0.0428 au) in order to provide a frequency dependent NLO response at the routinely utilized Nd:YAG laser frequencies. The calculated results revealed that the first hyperpolarizability β(ω) coefficients are dependent on the wavelengths. One can see that the static first hyperpolarizability of the designed complexes are in the range of 3 × 103 to 5 × 104 au while the frequency dependent response are largely enhanced. The EOPE values at 1064 nm are in the range of 3.1 × 103 to 1.9 × 106 au. The EOPE values are further enhanced to the range of 3.6 × 104 to 7.2 × 107 au at shorter wavelength of 532 nm. This indicates that EOPE values are more susceptible to shorter wavelength (532 nm). The second-harmonic generation (SHG) coefficient β(−2ω, ω, ω) values of the designed complexes lie in the range of 8.8 × 103 to 2.0 × 108 au at 1064 nm and decreases to the range of 2.5 × 104 to 2.2 × 107 au which indicates that the resonant enhancement for SHG process takes place at higher wavelength (1064 nm). Overall SHG process has stronger NLO response than EOPE at wavelength of 1064 nm for all designed complexes however, shorter wavelength 532 nm induces slightly stronger EOPE response than SHG process for Li3O@6CT, Na@6CT, Na3O@6CT, and K@6CT complexes.
Estimated values of β(−ω, ω, 0), β(−2ω, ω, ω), γ(−ω, ω, 0, 0), γ(−2ω, ω, ω, 0), γDFWM, and n2 (cm2 W−1) in au.
| Parameters | Frequency ω | Li@6CT | Li3O@6CT | Na@6CT | Na3O@6CT | K@6CT | K3O@6CT |
|---|---|---|---|---|---|---|---|
| β(−ω, ω, 0) | 1064 nm | 4.4 × 105 | 1.7 × 105 | 9.8 × 104 | 1.9 × 106 | 3.1 × 103 | 5.6 × 103 |
| 532 nm | 4.8 × 104 | 3.6 × 104 | 2.7 × 105 | 7.2 × 107 | 8.2 × 104 | 8.8 × 104 | |
| β(−2ω, ω, ω) | 1064 nm | 7.7 × 105 | 2.7 × 105 | 5.6 × 105 | 2.0 × 108 | 8.8 × 103 | 1.6 × 105 |
| 532 nm | 9.2 × 104 | 2.5 × 104 | 5.8 × 104 | 2.2 × 107 | 4.9 × 104 | 1.7 × 105 | |
| γ(−ω, ω, 0,0) | 1064 nm | 5.1 × 107 | 7.8 × 106 | 1.4 × 108 | 1.5 × 109 | 8.1 × 105 | 1.0 × 106 |
| 532 nm | 4.0 × 106 | 4.6 × 106 | 3.5 × 107 | 3.7 × 1010 | 2.2 × 108 | 4.4 × 107 | |
| γ(−2ω, ω, ω, 0) | 1064 nm | 2.1 × 108 | 7.4 × 107 | 9.4 × 107 | 1.3 × 1011 | 5.5 × 106 | 1.4 × 107 |
| 532 nm | 1.5 × 107 | 1.0 × 107 | 3.2 × 106 | 2.9 × 1010 | 2.4 × 107 | 6.7 × 108 | |
| γ DFWM | 1064 nm | 1.2 × 108 | 3.2 × 107 | 1.7 × 108 | 4.6 × 1010 | 7.9 × 105 | 5.7 × 106 |
| 532 nm | 8.2 × 106 | 7.4 × 106 | 3.5 × 107 | 4.6 × 1010 | 2.3 × 108 | 2.7 × 108 | |
| n 2 (cm2 W−1) | 1064 nm | 1.0 × 10−14 | 2.7 × 10−15 | 1.4 × 10−14 | 3.8 × 10−12 | 6.6 × 10−17 | 4.7 × 10−16 |
| 532 nm | 6.9 × 10−16 | 6.2 × 10−16 | 2.9 × 10−15 | 3.8 × 10−12 | 1.9 × 10−14 | 2.2 × 10−14 |
The dynamic second hyperpolarizability coefficients including dc-Kerr effect γ(−ω, ω, 0, 0) and the electric field-induced second harmonic generation (ESHG) γ(−2ω, ω, ω, 0) are also computed and the results are listed in the Table 5. Like dynamic first hyperpolarizability analysis, the frequency dispersion analysis was performed with the same wavelengths of 532 nm (0.0856 au) and 1064 nm (0.0428 au). From Table 5, one can see that the designed complexes have remarkably large dc-Kerr effect (up to 3.7 × 1010 au) and ESHG (up to 1.3 × 1011 au). The largest dc-Kerr effect and ESHG response was shown by Na3O@6CT complex. From static, dc-Kerr and ESHG second hyperpolarizability coefficients, degenerate four-wave mixing (DFWM), γDFWM(ω) = γ(−ω, ω, −ω, ω) was calculated using the following equation:41γDFWM(−ω, ω, −ω, ω) ≈ (1/3)γ(−2ω, ω, ω, 0) + γ(−ω, ω, 0, 0) − (1/3)γ(0, 0, 0, 0)
Then from DFWM values we can evaluate the quadratic nonlinear refractive index (n2) using the following equation:42n2 (cm2 W−1) = 8.28 × 10−23γDFWM (au)
The values of quadratic nonlinear refractive index (n2) are significantly large for all complexes. At wavelength of 1064 nm, the n2 values ranges from 6.6 × 10−17 to 3.8 × 10−12 au and at 532 nm, the n2 values are in the range of 6.9 × 10−16 to 3.8 × 10−12 au. The n2 values as a function of wavelength confirm that the amplitude of the second order nonlinear optical response is expected to vary with changes in wavelength as well as different alkali metal.
5. Conclusions
In this research, a series of complexes have been designed by doping alkali metal atoms (Li, Na and K) and superalkalis (Li3O, Na3O & K3O) for nonlinear optical applications. The interaction energies at M05-2X and M06-2X with 6-31G(d,p), 6-31+G(d,p) and 6-311+G(d,p) basis sets reveal that the reported complexes are thermodynamically stable. In comparison, the interaction stabilities of superalkalis@6CT complexes are far higher than alkali atoms@6CT complexes. Furthermore, the doping of alkali metals and their corresponding superalkalis leads to remarkably high NLO responses. Among all the complexes, Na3O@6CT complex exhibits highest NLO response. The static hyperpolarizability of Na3O@6CT complex is 5 × 104 au along with pronounced βvec value (2.5 × 104 au) and significantly large quadratic nonlinear optical response (3.8 × 10−12 au). The electronic properties provide evidence of high NLO response of Na3O@6CT complex. For example, Na3O@6CT complex shows an appreciable amount of NBO charge transfer (1.53e−) along with the considerably low EH–L gap (2.96 eV). The absorption spectrum also illustrates the ultra-high transparency of Na3O@6CT complex in UV-vis region. Finally, the improved second-harmonic generation, electro-optic Pockel's effect and nonlinear refractive index of our alkali/superalkali doped 6CT complexes open new prospective for the designing of new NLO material, especially Na3O@6CT, for opto-electronic applications.
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
We acknowledge this work to the Higher Education Commission of Pakistan and COMSATS University Islamabad, Abbottabad Campus.
Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra08099c
References
- Eaton D. F. Science. 1991;253:281–287. doi: 10.1126/science.253.5017.281. [DOI] [PubMed] [Google Scholar]
- Cheng W.-D. Xiang K.-H. Pandey R. Pernisz U. C. J. Phys. Chem. B. 2000;104:6737–6742. doi: 10.1021/jp000016b. [DOI] [Google Scholar]
- Geskin V. M. Lambert C. Brédas J.-L. J. Am. Chem. Soc. 2003;125:15651–15658. doi: 10.1021/ja035862p. [DOI] [PubMed] [Google Scholar]
- Ichida M. Sohda T. Nakamura A. J. Phys. Chem. B. 2000;104:7082–7084. doi: 10.1021/jp0009453. [DOI] [Google Scholar]
- Kirtman B. Champagne B. Bishop D. M. J. Am. Chem. Soc. 2000;122:8007–8012. doi: 10.1021/ja993226e. [DOI] [Google Scholar]
- Muhammad S. Xu H.-L. Zhong R.-L. Su Z.-M. Al-Sehemi A. G. Irfan A. J. Mater. Chem. C. 2013;1:5439. doi: 10.1039/C3TC31183J. [DOI] [Google Scholar]
- Wu C.-L. Lin Y.-H. Su S.-P. Huang B.-J. Tsai C.-T. Wang H.-Y. Chi Y.-C. Wu C.-I. Lin G.-R. ACS Photonics. 2015;2:1141–1154. doi: 10.1021/acsphotonics.5b00192. [DOI] [Google Scholar]
- Chen W. Li Z.-R. Wu D. Li Y. Sun C.-C. Gu F. L. J. Am. Chem. Soc. 2005;127:10977–10981. doi: 10.1021/ja050601w. [DOI] [PubMed] [Google Scholar]
- Zhong R.-L. Xu H.-L. Sun S.-L. Qiu Y.-Q. Su Z.-M. Chem.–Eur. J. 2012;18:11350–11355. doi: 10.1002/chem.201201570. [DOI] [PubMed] [Google Scholar]
- Chen W. Li Z.-R. Wu D. Li R.-Y. Sun C.-C. J. Phys. Chem. B. 2005;109:601–608. doi: 10.1021/jp0480394. [DOI] [PubMed] [Google Scholar]
- Jing Y.-Q. Li Z.-R. Wu D. Li Y. Wang B.-Q. Gu F. L. Aoki Y. ChemPhysChem. 2006;7:1759–1763. doi: 10.1002/cphc.200600157. [DOI] [PubMed] [Google Scholar]
- Ichimura A. S. Dye J. L. Camblor M. A. Villaescusa L. A. J. Am. Chem. Soc. 2002;124:1170–1171. doi: 10.1021/ja016554z. [DOI] [PubMed] [Google Scholar]
- Champagne B. Spassova M. Jadin J.-B. Kirtman B. J. Chem. Phys. 2002;116:3935–3946. doi: 10.1063/1.1446046. [DOI] [Google Scholar]
- Spassova M. Champagne B. Kirtman B. Chem. Phys. Lett. 2005;412:217–222. doi: 10.1016/j.cplett.2005.06.106. [DOI] [Google Scholar]
- Munsif S. Maria Khan S. Ali A. Gilani M. A. Iqbal J. Ludwig R. Ayub K. J. Mol. Liq. 2018;271:51–64. doi: 10.1016/j.molliq.2018.08.121. [DOI] [Google Scholar]
- Maria Iqbal J. Ayub K. J. Alloys Compd. 2016;687:976–983. doi: 10.1016/j.jallcom.2016.06.121. [DOI] [Google Scholar]
- Maria Iqbal J. Ludwig R. Ayub K. Mater. Res. Bull. 2017;92:113–122. doi: 10.1016/j.materresbull.2017.03.065. [DOI] [Google Scholar]
- Gutsev G. L. Boldyrev A. I. Chem. Phys. Lett. 1982;92:262–266. doi: 10.1016/0009-2614(82)80272-8. [DOI] [Google Scholar]
- Ullah F. Kosar N. Ayub K. Mahmood T. Appl. Surf. Sci. 2019;483:1118–1128. doi: 10.1016/j.apsusc.2019.04.042. [DOI] [Google Scholar]
- Ullah F. Kosar N. Ayub K. Gilani M. A. Mahmood T. New J. Chem. 2019;43:5727–5736. doi: 10.1039/C9NJ00225A. [DOI] [Google Scholar]
- Ullah F. Kosar N. Arshad M. N. Gilani M. A. Ayub K. Mahmood T. Opt. Laser Technol. 2020;122:105855. doi: 10.1016/j.optlastec.2019.105855. [DOI] [Google Scholar]
- Hu C. Chen Z. Xiao H. Zhen Z. Liu X. Bo S. J. Mater. Chem. C. 2017;5:5111–5118. doi: 10.1039/C7TC00735C. [DOI] [Google Scholar]
- Liu F. Yang Y. Cong S. Wang H. Zhang M. Bo S. Liu J. Zhen Z. Liu X. Qiu L. RSC Adv. 2014;4:52991–52999. doi: 10.1039/C4RA08951K. [DOI] [Google Scholar]
- Sajid H. Ullah F. Yar M. Ayub K. Mahmood T. New J. Chem. 2020;44:16358–16369. doi: 10.1039/D0NJ02291H. [DOI] [Google Scholar]
- Shehzadi K. Ayub K. Mahmood T. Appl. Surf. Sci. 2019;492:255–263. doi: 10.1016/j.apsusc.2019.06.221. [DOI] [Google Scholar]
- Kosar N. Shehzadi K. Ayub K. Mahmood T. J. Mol. Graphics Modell. 2020;97:107573. doi: 10.1016/j.jmgm.2020.107573. [DOI] [PubMed] [Google Scholar]
- Sajid H. Ayub K. Mahmood T. New J. Chem. 2020;44:2609–2618. doi: 10.1039/C9NJ05065E. [DOI] [Google Scholar]
- Frisch M. J., Trucks G. W., Schlegel H. B., Scuseria G. E., Robb M. A., Cheeseman J. R., Scalmani G., Barone V., Mennucci B., Petersson G. A., Nakatsuji H., Caricato M., Li X., Hratchian H. P., Izmaylov A. F., Bloino J., Zheng G., Sonnenberg J. L., Hada M., Ehara M., Toyota K., Fukuda R., Hasegawa J., Ishida M., Nakajima T., Honda Y., Kitao O., Nakai H., Vreven T., Montgomery Jr J. A., Peralta J. E., Ogliaro F., Bearpark M. J., Heyd J., Brothers E. N., Kudin K. N., Staroverov V. N., Kobayashi R., Normand J., Raghavachari K., Rendell A. P., Burant J. C., Iyengar S. S., Tomasi J., Cossi M., Rega N., Millam N. J., Klene M., Knox J. E., Cross J. B., Bakken V., Adamo C., Jaramillo J., Gomperts R., Stratmann R. E., Yazyev O., Austin A. J., Cammi R., Pomelli C., Ochterski J. W., Martin R. L., Morokuma K., Zakrzewski V. G., Voth G. A., Salvador P., Dannenberg J. J., Dapprich S., Daniels A. D., Farkas Ö., Foresman J. B., Ortiz J. V., Cioslowski J. and Fox D. J., Gaussian 09, Rev. C. 01, Wallingford CT, 2009 [Google Scholar]
- O'boyle N. M. Tenderholt A. L. Langner K. M. J. Comput. Chem. 2008;29:839–845. doi: 10.1002/jcc.20823. [DOI] [PubMed] [Google Scholar]
- Shokuhi A. Ayub K. Mater. Res. Bull. 2018;97:399–404. doi: 10.1016/j.materresbull.2017.09.036. [DOI] [Google Scholar]
- Gu F. L., Aoki Y., Springborg M. and Kirtman B., Calculations on nonlinear optical properties for large systems, 2015, pp. 67–83 [Google Scholar]
- Lu T. Chen F. J. Comput. Chem. 2012;33:580–592. doi: 10.1002/jcc.22885. [DOI] [PubMed] [Google Scholar]
- Ullah F. Ayub K. Mahmood T. New J. Chem. 2020;44:9822–9829. doi: 10.1039/D0NJ01670E. [DOI] [Google Scholar]
- Sun W.-M. Chen C.-Y. Li C.-Y. Wu D. Kang J. Li Y. Li Z.-R. ChemPhysChem. 2018;19:2518–2524. doi: 10.1002/cphc.201800466. [DOI] [PubMed] [Google Scholar]
- Zhong R.-L. Xu H.-L. Li Z.-R. Su Z.-M. J. Phys. Chem. Lett. 2015;6:612–619. doi: 10.1021/jz502588x. [DOI] [PubMed] [Google Scholar]
- Sun W.-M. Fan L.-T. Li Y. Liu J.-Y. Wu D. Li Z.-R. Inorg. Chem. 2014;53:6170–6178. doi: 10.1021/ic500655s. [DOI] [PubMed] [Google Scholar]
- Oudar J. L. Chemla D. S. J. Chem. Phys. 1976;66:2664–2668. doi: 10.1063/1.434213. [DOI] [Google Scholar]
- Li X. Zhang Y. Lu J. Appl. Surf. Sci. 2020;512:145544. doi: 10.1016/j.apsusc.2020.145544. [DOI] [Google Scholar]
- Maria M. Iqbal J. Ayub K. RSC Adv. 2016;6:94228–94235. doi: 10.1039/C6RA21797D. [DOI] [Google Scholar]
- Oviedo M. B. Ilawe N. V. Wong B. M. J. Chem. Theory Comput. 2016;12:3593–3602. doi: 10.1021/acs.jctc.6b00360. [DOI] [PubMed] [Google Scholar]
- Tarazkar M. Romanov D. A. Levis R. J. J. Chem. Phys. 2014;140:214316. doi: 10.1063/1.4880716. [DOI] [PubMed] [Google Scholar]
- Brée C. Demircan A. Steinmeyer G. IEEE J. Quantum Electron. 2010;46:433–437. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.