Quantum conformance test

A practical quantum scheme is shown to have a performance beyond the classical limits in monitoring a manufacturing process.

Abstract

We introduce a protocol addressing the conformance test problem, which consists in determining whether a process under test conforms to a reference one. We consider a process to be characterized by the set of end products it produces, which is generated according to a given probability distribution. We formulate the problem in the context of hypothesis testing and consider the specific case in which the objects can be modeled as pure loss channels. We demonstrate theoretically that a simple quantum strategy, using readily available resources and measurement schemes in the form of two-mode squeezed vacuum and photon counting, can outperform any classical strategy. We experimentally implement this protocol, exploiting optical twin beams, validating our theoretical results, and demonstrating that, in this task, there is a quantum advantage in a realistic setting.

INTRODUCTION

Substantial progress has been made in recent years in the field of quantum sensing (1, 2) both for continuous parameter estimation (3–5) and for discrimination tasks in the case of discrete variables (6–8). The use of quantum states and resources brings an advantage that has been demonstrated in various specific tasks: both phase (9–13) and loss (14–20) estimation, quantum imaging (21–23), and discrimination protocols such as target detection (24–27) and quantum reading (28, 29).

In this class of problems, a parameter of interest is encoded in some quantum states, or channels, and the values it can take can belong to either discrete or continuous sets. The estimation of this parameter requires the choice of a probe, as well as a measurement scheme, i.e., a measurement strategy. Here, we consider an important discrimination problem that can find various important applications, the quantum conformance test (QCT). In this problem, one wants to assess whether a process is conform to a reference, or if it is defective. In the general case, the process is characterized by a physical parameter distributed according to some continuous probability density distribution. We experimentally have access to the end products of this process, which we can perform measurements on. Accordingly, the measurement outcomes belong to a continuous set of possible values. However, the expected output of the procedure should be binary: conform or not conform. Such conformity tests appear frequently in many applications (30), one example being product safety testing.

Under energy constraints for the probe, quantum mechanical fluctuations set lower bounds to the probability of error that depend on the decision strategy. It is important to investigate whether, and to what extent, the use of certain quantum resources can reduce the probability of error below what is possible in the classical domain.

In this work, we introduce a formal description of the conformance test problem in the context of quantum information (31) and consider the paradigmatic example of bosonic pure loss channels probed with light. We demonstrate that, under the same energy constraints, i.e., fixing the photon number, a quantum strategy making use of entangled photons as probe states, and photon counting (PC) as a measurement strategy, can deliver better results than any classical strategy. Last, we present an experimental optical implementation of our proposed quantum protocol, which validates our theoretical model and shows that a genuine quantum advantage persists even in the presence of experimental inefficiencies.

Quantum conformance test

The QCT can be modeled as follows. We define the binary random variable x ∈ {0,1}, which corresponds to the process from which the physical system under test (SUT) was generated, 0 being the reference and 1 being the defective one. We consider the monitoring of a physical process P_x, producing a quantum object (the SUT), ℰ_θ, which depends on a parameter θ. The process P_x can be described by the ensemble {g_x(θ), ℰ_θ}: The parameter θ is extracted from a set A, according to the probability distribution g_x(θ), and it defines the physical object ℰ_θ. The set A can be either discrete or continuous. The conformance test consists in ruling whether an unknown process is conform to a “reference” process, P₀, or if it should be labeled “defective,” P₁, using measurements on the set of objects it produces {ℰ_θ}.

A QCT is performed using a probe in a generic quantum state ρ. After the probe has interacted with the SUT, the final state is measured by a positive-operator-valued measure (POVM) Π and, after classical postprocessing of the measurement results, the outcome of the procedure is a final guess on the nature of the production process, expressed by the binary variable y ∈ {0,1}.

The test is successful when y = x, i.e., when the guess is correct. On the other hand, if y ≠ x, the test fails. Two cases can be distinguished:

● False negative: In this scenario, a SUT produced by a conform process (x = 0) is labeled as defective (y = 1). In an industrial context, this kind of outcome can be seen as an economic loss for a manufacturer, as a conform process is considered defective. We will denote the probability of false negatives as p₁₀.

● False positive: A SUT produced by a defective process (x = 1) is labeled as conform (y = 0). This outcome represents a risk since possibly unsafe products are released. The false-positive probability will be referred to as p₀₁.

The analysis of false positives and negatives plays a central part in conformity testing, and the specific choice, if required, of the tolerance on either one of those errors vastly depends on the situation considered. In a general scenario, a relevant figure of merit—when the energy of the probe is considered a limited resource and, therefore, one compares the results at fixed energy—that can be used to assess the effectiveness of the test is the total probability of error, defined as

$${\mathit{p}}_{\text{err}}=\frac{1}{2}({\mathit{p}}_{01}+{\mathit{p}}_{10})$$ (1)

In Fig. 1, we present some examples of error probabilities for the conformance test. In Fig. 1 (A and B), two possible scenarios for the conform and defective processes are shown. In Fig. 1A, we consider two distributions whose overlap is negligible, whereas, in Fig. 1B, we consider significantly overlapping distributions. In Fig. 1 (C to F), we show the probability distributions for the parameter, convoluted with the noise emerging from both the measurement process and the probe state, either classical (Fig. 1, C and D) or quantum (Fig. 1, E and F). From these distributions, the outcome y must be decided. One can observe that the noise present in the state, which probes the SUT, translates into an error in the discrimination.

Fig. 1. Examples of error probabilities for the conformance test.

(A and B) Distributions of the reference process (red) P₀, and defective one (blue) P₁: the two rows present opposite and archetypal situations. The graphics (C to F) are obtained considering a pure loss channel of parameter θ = τ as the SUT, and a PC measurement. (C and D) Resulting photon number distributions p(n), in the case where a classical state is used as a probe. The overlaps between the two distributions, highlighted in green and blue, the two colors distinguishing the cases where the reference or the defective process is most likely, are visualizations of the conditional error probabilities, at a given value of τ, while their weighted sum gives an appreciation of the total error probability. (E and F) Case in which quantum probes are used: Quantum correlations enhance the performance of the discrimination task.

In the subsequent parts of this work, we focus on a specific class of SUTs: the bosonic pure loss channels. We show how, in this case, quantum resources can be used to notably mitigate the spurious effect of the noise and can improve the discrimination performance—evaluated in terms of total probability of error—over any classical strategy. Subsequently, we analyze the case in which a constraint is imposed on either the false-positive or false-negative probabilities. We note that the quantum reading problem, originally proposed in (28) and experimentally tested in (29), can be considered to be a special case of the conformance test (i.e., in the case where g₀ and g₁ are both Dirac delta functions).

RESULTS

Pure loss channels

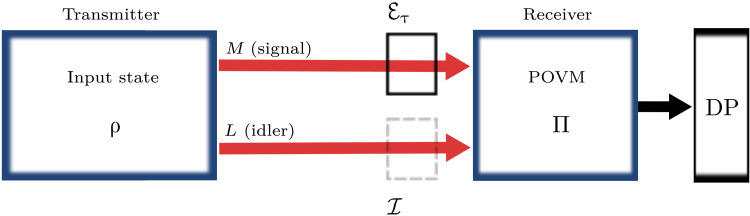
A bosonic loss channel ℰ_τ is characterized by its transmittance τ ∈ [0,1]. The input-output relation for such a channel is $\widehat{\mathit{a}}\to \sqrt{\mathrm{\tau }} \widehat{\mathit{a}}+\mathit{i}\sqrt{1-\mathrm{\tau }} \widehat{\mathit{v}}$, where $\widehat{\mathit{a}}$ is the annihilation operator of the input mode (32). The annihilation operator of the mode on the second port, $\widehat{\mathit{v}}$, acts on the vacuum, as we are considering pure losses. The configuration for a conformance test over a pure loss channel is described in Fig. 2. A transmitter irradiates an optical probe state ρ on the SUT. In a general case, the state is bipartite, having a number M of signal modes interacting with the SUT and a number L of idler ones that represent the ancillary modes. The state is measured at the receiver by a joint measurement, and its outputs are processed to obtain the final outcome.

Fig. 2. Quantum conformance test.

A probe ρ sends M signal modes through the loss channel ℰ_τ, representing the SUT, while L idler modes directly reach the receiver—I represents the identity operator. A POVM Π is applied to the output state. Using the result of this measurement and data processing (DP), a decision y is taken: The process generating ℰ_τ is identified as conform (y = 0) or defective (y = 1).

After the interaction with the SUT, an input state ρ will be mapped into either ρ₀ or ρ₁, with

$$\begin{array}{c}{\mathrm{\rho }}_0={\mathbb{E}}_{{\mathcal{P}}_0}[({\mathcal{E}}_{\mathrm{\tau }}\otimes \mathcal{I})\mathrm{\rho }]\to \text{reference process}\\ {\mathrm{\rho }}_1={\mathbb{E}}_{{\mathcal{P}}_1}[({\mathcal{E}}_{\mathrm{\tau }}\otimes \mathcal{I})\mathrm{\rho }]\to \text{defective process}\end{array}$$ (2)

and where ${\mathbb{E}}_{\mathcal{P}}[·]$ represents the expectation value over the ensemble P and I is the identity operator.

In general, the output states of the reference and defective processes, ρ₀ or ρ₁, will overlap. Accordingly, the discrimination between the processes will be affected by an error probability $p_{\text{err}}^{\mathrm{\rho },\mathrm{\Pi }}({\mathcal{P}}_0,{\mathcal{P}}_1)$, which is a function of the processes considered, the input state, and the POVM—as well as the decision procedure applied to the measurement result. The optimization of the QCT protocol is achieved by a minimization of $p_{\text{err}}^{\mathrm{\rho },\mathrm{\Pi }}({\mathcal{P}}_0,{\mathcal{P}}_1)$ over all possible input states ρ and POVMs Π

$$p_{\text{err}}({\mathcal{P}}_0,{\mathcal{P}}_1)={\text{min}}_{\mathrm{\Pi }}\left[{\text{min}}_{\mathrm{\rho }}\right[p_{\text{err}}^{\mathrm{\rho },\mathrm{\Pi }}({\mathcal{P}}_0,{\mathcal{P}}_1)\left]\right]$$ (3)

Without constraints on the energy, a trivial strategy is to let the energy of the probe system go to infinity, which, given a suitable measurement, would nullify the quantum noise and lead to the minimum possible p_err permitted by the problem, i.e., the overlap between the two initial distributions g₀ and g₁ (see Fig. 1). Nevertheless, in several relevant cases, one cannot dispose of, or use, states of arbitrarily large energy (e.g., in order not to damage the SUT). In the case we are considering, we fix the total energy of the probe, and the optimization problem is not easily solved directly—this is particularly true when experimental imperfections are taken into account. Moreover, any theoretical bound that could be found would not necessarily correspond to a viable experimental implementation (feasible input state and output measurement). Our goal is more practical: Following the approaches used, for example, in (28, 33), we find the minimum probability of error that can be achieved with any classical transmitter. Then, we show that a class of quantum transmitters, namely, multimode two-mode squeezed vacuum (TMSV) states, achieves probabilities of error below the classical bound, demonstrating a quantum advantage.

Classical limit

First, we turn our attention to the derivation of the minimum error probability which can be achieved using classical input states. In the context of quantum optics, classical states can be defined as the states having a positive P-representation (34). A generic classical bipartite state can be represented as

$${\mathrm{\rho }}^{\text{cla}}=\int {\mathit{d}}^{2\mathrm{M}}\mathbf{\alpha } {\mathit{d}}^{2\mathrm{L}}\mathbf{\beta } \mathit{P}(\mathbf{\alpha },\mathbf{\beta })\mid \mathbf{\alpha }\rangle \langle \mathbf{\alpha }\mid \otimes \mid \mathbf{\beta }\rangle \langle \mathbf{\beta }\mid$$ (4)

where ∣α⟩ and ∣β⟩ are M- and L-mode coherent states, respectively (corresponding to the signal and idler channels), and P(α, β) ≥ 0 is a probability density. The energy constraint for the signal system is expressed, in terms of mean signal photon number ${\overline{\mathit{n}}}_{\mathit{S}}$, as

$$\int {\mathit{d}}^{2\mathrm{M}}\mathbf{\alpha } {\mathit{d}}^{2\mathrm{L}}\mathbf{\beta } \mathit{P}(\mathbf{\alpha },\mathbf{\beta }){\mid \mathbf{\alpha }\mid }^2={\overline{\mathit{n}}}_{\mathit{S}}$$ (5)

While the choice of imposing the energy constraint only on the signal system is arbitrary—the alternative being, for example, a constraint on the total energy—it is a natural choice for real applications, where the energy irradiated over the SUT should be limited.

Given an input state ρ^cla, the output states, after interaction with the SUT, are ${\mathrm{\rho }}_0^{\text{cla}}$ and ${\mathrm{\rho }}_1^{\text{cla}}$, calculated according to Eq. 2. In this context, the minimum probability of error for the QCT protocol with classical states is equal to the minimum probability of error in the discrimination of ${\mathrm{\rho }}_0^{\text{cla}}$ and ${\mathrm{\rho }}_1^{\text{cla}}$. The best performance in this task is achieved by using a POVM measurement which assumes the Helstrom projectors as elements (6). This optimal discrimination procedure yields a probability of error given by

$${\mathit{p}}_{\text{err}}=\frac{1}{2}(1-\mathit{D}({\mathrm{\rho }}_0,{\mathrm{\rho }}_1))$$ (6)

where D(ρ₀, ρ₁) = ‖ρ₀ − ρ₁‖/2 is the trace distance with $\Vert \mathrm{\rho }\Vert =\sqrt{{\mathrm{\rho }}^{†}\mathrm{\rho }}$. A lower limit for ${\mathit{p}}_{\text{err}}^{\text{cla}}$ can be found by upper bounding D(ρ₀, ρ₁). By exploiting the convexity of the trace distance (see the Supplementary Materials for details), the minimum error probability for classical states in the QCT protocol is bounded by

$$\mathcal{C}≔p_{\text{err}}^{\text{cla}}\ge \frac{1-{\mathbb{E}}_{{\mathcal{P}}_0}\left[{\mathbb{E}}_{{\mathcal{P}}_1}\right[\sqrt{1-e^{-{\bar{n}}_S{(\sqrt{{\mathrm{\tau }}_0}-\sqrt{{\mathrm{\tau }}_1})}^2}}\left]\right]}{2}$$ (7)

The quantity C establishes a lower bound for the discrimination error probability when considering classical resources and an optimal measurement strategy. We note that this bound is not tight, which means that it may not be reached by any classical receiver.

Quantum strategy

In the following, we analyze the particular strategy, involving quantum states, that is able to surpass the best classical performance C. It uses a transmitter ρ constituted of K replicas of a TMSV state and a PC receiver (29), whose output is processed by a maximum likelihood decision.

The TMSV state (35) admits the following expression in the photon number basis: $\mid \mathrm{\psi }⟩={\sum }_{\mathit{n}=0}^{\infty }\sqrt{{\mathit{P}}_{\overline{\mathit{n}}}(\mathit{n})}\mid {\mathit{n}⟩}_{\mathit{S}}\mid {\mathit{n}⟩}_{\mathit{I}}$, where ${\mathit{P}}_{\overline{\mathit{n}}}(\mathit{n})$ is a thermal distribution, $\overline{\mathit{n}}$ is the mean photon number, and ∣n⟩_i is the n-photon state in the i = S signal, or i = I idler mode. TMSV states can easily be produced experimentally by spontaneous parametric down-conversion (SPDC) (36–38) or four-wave mixing (39, 40, 41). A multimode TMSV state is a tensor product of K TMSV states ⊗^K ∣ψ⟩. It admits a multithermal distribution for the total photon number in both the signal and idler modes ${\mathit{n}}_{\mathit{i}}={\sum }_{\mathit{k}=1}^{\mathit{K}}{\mathit{n}}_{\mathit{i}}^{(\mathit{k})}$, denoted as ${\mathit{P}}_{\overline{\mathit{n}},\mathit{K}}({\mathit{n}}_{\mathit{i}})$ (the same notation $\overline{\mathit{n}}$ is used for the mean photon number) and preserves perfect photon number correlation between the channels, i.e., ${\mathit{P}}_{\overline{\mathit{n}},\mathit{K}}({\mathit{n}}_{\mathit{S}},{\mathit{n}}_{\mathit{I}})={\mathit{P}}_{\overline{\mathit{n}},\mathit{K}}({\mathit{n}}_{\mathit{I}}){\mathrm{\delta }}_{{\mathit{n}}_{\mathit{S}},{\mathit{n}}_{\mathit{I}}}$. The result of the PC measurement is the classical random variable n = (n_S, n_I), whose distribution p(n∣P_x) = ⟨n_S, n_I∣ρ_x∣n_S, n_I⟩ is conditioned on the nature x of the process, where ρ_x is defined in Eq. 2. Using Bayes theorem and assuming the defective and reference processes to be equiprobable, p(P_x = P₀) = p(P_x = P₁) = 1/2, we can write the a posteriori probability p(P_x∣n) as

$$p({\mathcal{P}}_x\mid \mathit{n})=\frac{p(\mathit{n}\mid {\mathcal{P}}_x)p({\mathcal{P}}_x)}{p(\mathit{n})}=\frac{p(\mathit{n}\mid {\mathcal{P}}_x)}{p(\mathit{n}\mid {\mathcal{P}}_0)+p(\mathit{n}\mid {\mathcal{P}}_1)}$$ (8)

Let us first consider the action of a pure loss channel on the photon number distribution of a state. The distribution p(n∣τ) after the interaction is the composition of the joint distribution ${\mathit{P}}_{\overline{\mathit{n}},\mathit{K}}({\mathit{n}}_{\mathit{S}},{\mathit{n}}_{\mathit{I}})$ with a binomial distribution

$$\mathit{p}(\mathit{n}\mid \mathrm{\tau })={\displaystyle {\sum }_{\mathit{m}={\mathit{n}}_{\mathit{S}}}^{\infty }}{\mathit{P}}_{\overline{\mathit{n}},\mathit{K}}(\mathit{m},{\mathit{n}}_{\mathit{I}})\mathrm{ℬ}({\mathit{n}}_{\mathit{S}}\mid \mathit{m},\mathrm{\tau })$$ (9)

since the m signal photons can be seen as undergoing a Bernoulli trial each, with probability of success τ, resulting in the binomial distribution ℬ(n_S∣m, τ). Using the linearity of quantum operations, we can evaluate the effect of a loss channel with transmittance τ, p(n∣P_x), as

$$p(\mathit{n}\mid {\mathcal{P}}_x)={\int }_{{\mathrm{A}}_x}p(\mathit{n}\mid \mathrm{\tau })g_x(\mathrm{\tau })d\mathrm{\tau }$$ (10)

After the measurement, the decision is made by choosing the outcome that maximizes the conditional probability: y is chosen such that $y=\underset{x\in \{0,1\}}{\text{arg} \text{max}}p({\mathcal{P}}_x\mid \mathit{n})$. We note that this condition for the choice of y is equivalent, due the constant prior, to a maximum likelihood decision, i.e., choosing y such that p(n∣P_y) ≥ p(n∣P_1−y). The probability of error for the quantum strategy, Q, is given by

$$\begin{array}{cc}\hfill \mathcal{Q}& ≔p_{\text{err}}^{\text{QCT}}=\sum _n\underset{x}{\text{min}}p({\mathcal{P}}_x\mid \mathit{n})p(\mathit{n})\hfill \\ & =\frac{1}{2}\sum _n\underset{x}{\text{min}}p(\mathit{n}\mid {\mathcal{P}}_x)\hfill \end{array}$$ (11)

Classical states and PC

We have derived a limit C on the performance that can be achieved with an optimal classical strategy, i.e., optimal classical input states and an unspecified optimal receiver. We also defined the performance, Q, of a quantum strategy using TMSV and PC. In this section, we consider the case in which classical states are paired with a PC receiver. The bound found in Eq. 7 is not tight, meaning that it may not be possible to reach it. Moreover, in the case where a POVM could be found that saturates the bound, its implementation may be of difficult practical realization. The analysis of the best classical performance achievable with the PC receiver will give a second classical benchmark, whose performance can be experimentally validated.

The analysis is analogous to the one performed for the quantum strategy. However, since the input states considered are limited to classical ones, the use of idler modes cannot improve the performance. Classical states are statistical mixtures of coherent states that are Poisson distributed in the photon number: Their variance is lower bounded by the Poisson one (34). In this scenario, the best performance is achieved using signal states having a Poisson photon number distribution. The error probability p_err is proportional to the overlap of the measurement outcomes, as shown in Fig. 1, which, in the case of a PC measurement, are the photon number distributions. Using a state with a narrower photon number distribution will lead to better discrimination performances. We denote the best performance that can be achieved using classical states and PC as C^pc and write it in the form

$${\mathcal{C}}^{\text{pc}}≔p_{\text{err}}^{\text{cla},\text{pc}}=\frac{1}{2}(1-q_p)$$ (12)

where 0 ≤ q_p ≤ 1. The form of the function q_p depends on the distributions of the considered processes, g₀ and g₁. In the following, we report on the case where both the reference and defective processes have Gaussian distributions ${\mathit{G}}_{\overline{\mathrm{\tau }},\mathrm{\sigma }}$ (where $\overline{\mathrm{\tau }}$ and σ² are the mean and the variance). The distributions that we consider are thus ${\mathit{g}}_0={\mathit{G}}_{{\overline{\mathrm{\tau }}}_0,{\mathrm{\sigma }}_0}$ and ${\mathit{g}}_1={\mathit{G}}_{{\overline{\mathrm{\tau }}}_1,{\mathrm{\sigma }}_1}$ for the reference and defective processes, respectively. For more general solutions and a more in-depth analysis, we refer the reader to the Supplementary Materials.

As pointed out in previous sections, the probability of error depends on the overlap of the two measurement distributions p(P₀∣n_S) and p(P₁∣n_S). Under the assumption of Gaussian distributions for both processes, and of a large photon number in the initial probe state ${\overline{\mathit{n}}}_{\mathit{s}}\gg 1$, the photon number distribution at the outcome can be well approximated by a Gaussian: $p({\mathcal{P}}_x\mid n)\approx G_{{\overline{\mathrm{\tau }}}_x{\overline{n}}_s,{\mathrm{\sigma }}_{G^{(x)}}}$, with ${({\mathrm{\sigma }}_{\mathit{G}}^{(\mathit{x})})}^2={\overline{\mathit{n}}}_{\mathit{s}}{\overline{\mathrm{\tau }}}_{\mathit{x}}+{\overline{\mathit{n}}}_{\mathit{s}}^2{\mathrm{\sigma }}_{\mathit{x}}^2$ (details can be found in the Supplementary Materials). An expression for the overlap can be found after the determination of the solutions of the equality p(P₀∣n) = p(P₁∣n). In general, this equation admits two solutions in the case where the distributions are Gaussian. If we can assume the variances ${\mathrm{\sigma }}_{\mathit{G}}^{(\mathit{x})}$ to be of the same order, and ${\overline{\mathrm{\tau }}}_0<{\overline{\mathrm{\tau }}}_1$, often only one of the solutions, labeled n_th, will be in a range where p(P₀∣n) and p(P₁∣n) are not negligible. Under these conditions, we can derive a closed form for the function q_p in Eq. 12 as

$${\mathit{q}}_{\mathit{b}}=\frac{1}{2}\left(\text{erf}\right[\frac{{\mathit{n}}_{\mathrm{th}}-{\overline{\mathit{n}}}_{\mathit{s}}{\overline{\mathrm{\tau }}}_0}{\sqrt{2}{\mathrm{\sigma }}_{\mathit{G}}^{(0)}}]-\text{erf}[\frac{{\mathit{n}}_{\mathrm{th}}-{\overline{\mathit{n}}}_{\mathit{s}}{\overline{\mathrm{\tau }}}_1}{\sqrt{2}{\mathrm{\sigma }}_{\mathit{G}}^{(1)}}\left]\right)$$ (13)

As indicated before, the expression in Eq. 13 holds for certain regimes, and a more general solution, as well as an explicit expression for n_th, is reported in the Supplementary Materials.

Numerical study

In the strategies described in the previous sections, the performance of the QCT is a function of the mean photon number ${\overline{\mathit{n}}}_{\mathit{S}}$, as well as the form of the distributions of the processes considered, g₀ and g₁.

A visualization of the discrimination problem is depicted in Fig. 1, where the measurement strategy considered at the receiver is PC. In Fig. 1A, the distributions of the processes to be discriminated are shown, g₀ in red and g₁ in blue. In the first row, the two distributions barely overlap. Nonetheless, when a probe with finite energy is used to perform the discrimination, the intrinsic noise of the state on the photon number distribution results in a substantial amplification of the overlap of the measurement outcome distributions. This is shown in Fig. 1C, where the two possible photon number distributions, after the interaction with the SUT, and for the classical input state discussed in the previous sections, are plotted. The overlap area, highlighted in blue-green, is a visual representation of the probability of error: p_err is equal to half that area. This overlap cannot be reduced using classical states without an increment to the total energy used. However, using the same signal energy, an improvement can be achieved using quantum correlations. If we consider as input a TMSV state, as described earlier in the text, we can analyze the photon number distribution for the signal system, conditioned to having measured a given photon number in the idler branch. This analysis is shown in Fig. 1E, where the overlap between the two distributions is markedly reduced, leading to much more efficient discrimination. The nature of the advantage resides in the photon number correlations, which are used to greatly reduce the photon number noise of the initial state. In the second row, is depicted a situation in which the overlap of the parameter distributions is high. In Fig. 1B, the considered distributions have the same mean value but different variances. In this case, using a classical discrimination strategy performs very poorly, as shown in Fig. 1D, where the two processes are almost indistinguishable. Figure 1F shows how, once again, quantum correlation can be used to greatly improve the performance. We note that the best performances (shown in Fig. 1, E and F) are achieved in the limit of large K so that ${\overline{\mathit{n}}}_{\mathit{S}}/\mathit{K}\ll 1$.

From this point on, to reduce the number of considered parameters, we assume the reference process P₀ to be strongly peaked around τ₀ so that we can approximate it as ${\mathit{g}}_0(\mathrm{\tau })\approx \mathrm{\delta }(\mathrm{\tau }-{\mathrm{\tau }}_0)$, where δ(τ) is the Dirac delta distribution. We also consider two different noteworthy forms for g₁: the Gaussian distribution $\mathit{g}={\mathit{G}}_{\overline{\mathrm{\tau }},\mathrm{\sigma }}$, and the uniform one $g={\mathcal{U}}_{\overline{\mathrm{\tau }},\mathrm{\delta }}$. Using a Gaussian probability distribution for the transmittance τ is justified by the wide range of physical phenomena it can describe. In this case, the processes are fully characterized by their mean value $\overline{\mathrm{\tau }}$ and variance σ². On the other hand, the uniform distribution, ${\mathcal{U}}_{\overline{\mathrm{\tau }},\mathrm{\delta }}$, is well suited to describe situations in which there is a complete lack of knowledge of the nature of the process, whose range can be limited by the physical constraints of the apparatus. Once more, the processes are characterized by two parameters only: their mean $\overline{\mathrm{\tau }}$ and half-width δ. To make a fair comparison of the error probabilities for Gaussian and uniform distributions, we choose their parameters such that the resulting variances are equal. In particular, we will use $\mathrm{\delta }=\sqrt{3}\mathrm{\sigma }$, since Var$\left[{\mathcal{U}}_{\overline{\mathrm{\tau }},\mathrm{\delta }}\right]={\mathrm{\delta }}^2/3$.

In Fig. 3, we show how, for each of the three strategies studied—the classical optimal, C, the classical strategy with PC, C^pc, and the quantum strategy Q—the error probability depends on the reference process transmittance τ₀. The number of signal photons is fixed to n_s = 10⁵, as well as the mean value of the transmittance of the defective process ${\overline{\mathrm{\tau }}}_1=0.997$. In Fig. 3A, the performances of the different strategies are plotted in the case of a uniformly distributed defect, while in Fig. 3B the case of a Gaussian distributed one is reported. In both cases, the results for different values of the variance of the process (denoted by different colors) are shown. In the range studied, it can be seen that the quantum strategy (solid lines) outperforms both the classical lower bound (dashed lines) and the strategy using a classical probe and PC (dotted lines). Both classical and quantum strategies have a maximum error probability when ${\mathrm{\tau }}_0=\overline{\mathrm{\tau }}$. This shared feature does not depend on the noise but on the nature of the problem. In this configuration, the overlap between the initial distributions is maximum and, as a result, the error probability is maximum as well. In both panels, we see how, in this high overlap region, the effect of the probe state’s noise is such that, when using a classical strategy, the process results are completely (p_err = 0.5), or almost completely, indistinguishable, while distinguishability is recovered when quantum states with reduced noise are used.

Fig. 3. Error probabilities.

The error probabilities as functions of the mean value of the reference process ${\overline{\mathrm{\tau }}}_0$ are displayed, for different values of standard deviation of the defective process σ (the numerical values are reported in the legend), and for the different discrimination strategies described in the main text: the quantum strategy (solid line), the classical strategy with PC (dotted line), and the optimal classical strategy (dash-dotted line). The reference distribution is considered strongly peaked: ${\mathit{g}}_0\approx \mathrm{\delta }(\mathrm{\tau }-{\overline{\mathrm{\tau }}}_0)$. In (A), the defect distribution, g₁(τ), is uniform; in (B), it is Gaussian. The distributions g₁(τ) for different values of variance are plotted on the first row panels. In both bottom panels, the mean number of signal photons is fixed to n_s = 10⁵ and the mean value of the defective process is ${\overline{\mathrm{\tau }}}_1=0.997$.

Experimental results

To validate the presence of a quantum advantage for the conformance test, we experimentally implemented the protocol described in the “Quantum strategy” section—with the substantial difference that we operate with a nonideal detection efficiency η. The detection efficiency encompasses different processes: the nonunit quantum efficiency of the detectors, the losses due to the different optical elements, and, in the case of correlated photon sources, the imperfect efficiency affecting the measurement of the correlated photons. These losses cannot be distinguished from those caused by a pure loss channel. Hence, the fit with theoretical curves must be made using the substitution τ → ητ. In general, the effect is equivalent to a reduction of the probe energy of the same factor τ. For the quantum strategy, however, another effect is the reduction of the degree of correlation of the state. Because of this, in general, it is expected that the quantum advantage will be reduced as η becomes lower. The setup used is thoroughly described in Materials and Methods.

Our results are presented in Fig. 4. Using a sample presenting a varying spatial transmittance, we acquired data for different values of τ. We used this experimental dataset to realize different defect distributions: In Fig. 4, we plot p_err (see Eq. 1) when uniform distributions are considered with $\mathit{A}:\{\mathrm{\delta }=0.001,\overline{\mathrm{\tau }}=0.999\}$, $\mathit{B}:\{\mathrm{\delta }=0.002,\overline{\mathrm{\tau }}=0.994\}$, and $\mathit{C}:\{\mathrm{\delta }=0.003,\overline{\mathrm{\tau }}=0.997\}$. For each acquisition, the mean numbers of photons n_S and n_I, and the efficiencies η_S and η_I of the signal and idler channels, are estimated, as well as the electronic noise ν of the camera. These values are used to draw the theoretical curves: the quantum and classical error probabilities with PC, Q, and C^pc, as well as the classical optimal bound C, defined in Eq. 7. We display the results in Fig. 4 (D to F). As a comparison, we also plot the ideal case η_S = η_I = 1 in Fig. 4 (A to C). For the quantum error probability, we also report the confidence region at two standard deviations as a colored band around the curve. The two sets of experimental data reported in Fig. 4 correspond to the quantum and classical PC strategies, respectively. More details on the elaboration of these results and data analysis can be found in Materials and Methods.

Fig. 4. Error probabilities for the QCT.

(A to F) Error probabilities are plotted as a function of the reference parameter τ₀, for different values of the defective process’s mean value $\overline{\mathrm{\tau }}$ and half-width δ: $\mathit{A}:\{\mathrm{\delta }=0.001,\overline{\mathrm{\tau }}=0.999\}$, $\mathit{B}:\{\mathrm{\delta }=0.002,\overline{\mathrm{\tau }}=0.994\}$, and $\mathit{C}:\{\mathrm{\delta }=0.003,\overline{\mathrm{\tau }}=0.997\}$. On the left-hand side, we show the theoretical curves (quantum and classical probability of error with PC Q and C^pc, as well as classical bound C) in the ideal case of unitary detection efficiency (η_S = η_I = 1) for different sets of parameters σ and $\overline{\mathrm{\tau }}$. In the right column, we show the experimental error probabilities obtained using the quantum PC protocol (black dots—Exp Q) and the classical PC one (black circles—Exp C). The efficiencies of the channels in the experimental realization are η_S ≃ η_I ≈ 0.76, while the mean number of signal photons is n_S ≈ 10⁵. The theoretical error probabilities using the estimated experimental parameters (black and light green solid lines—Q and C^pc) are plotted for both protocols, as well as the confidence interval for the quantum case (green shaded areas—± one SD). The classical bound C is also displayed as a comparison.

For the three regimes considered, most points fall within the confidence interval. These results show that, even in the case of degraded detection efficiency, the quantum strategy always brings an advantage with respect to the classical one based on PC. However, within the range of the defect distribution, the optimal classical bound C on the error probability becomes smaller than the quantum strategy error probability in some regions. To bring this point into perspective, we point to Fig. 4 (A to C), which are constructed with the same experimental parameters but unit detection efficiency. In this case, the quantum strategy overcomes any classical one. We note that, as expected, while the classical error probabilities are little modified by the change in efficiency η, the quantum one improves substantially in case of η = 1. This effect stems from the fact that, as mentioned, spurious losses η reduce the photon number correlations between signal and idler channels.

Constrained probability of error

Up until now, the figure of merit considered was the total probability of error p_err (Eq. 1). However, this quantity may not be the most relevant one to optimize, depending on the nature of the process under test. In some instances, it can be required to impose a constraint in either one of the conditional probabilities p₀₁ or p₁₀, instead of their sum. These two types of errors represent different outcomes, and the minimization of one can be deemed more important than that of the other. To proceed further, we use the notion of cost, which quantifies the fact that, in the mislabeling of a process, the false positives and false negatives may not be equivalent for the operator making the decision: One type of error may be more “costly” than the other. We introduce the coefficient 0 < S < 1 and define the total cost C of the conformance test as

$$\mathit{C}={\mathit{Sp}}_{10}+(1-\mathit{S}){\mathit{p}}_{01}$$ (14)

From Eq. 14, it follows that, if we use the cost C as the figure of merit for the evaluation of the QCT, the minimum probability of error is achieved for S = 1/2. If S ≠ 1/2, the minimization of the cost will, in general, not minimize the total error probability p_err.

In the following, we analyze how the strategies presented in the previous sections, consisting of PC and a maximum likelihood decision, for both classical and quantum probes, can be modified to minimize the cost C. In the formalism of the previous sections, we write the general term for the probabilities p_ij as

$$p_{01}=\sum _{\mathit{n}}p(\mathit{n}\mid {\mathcal{P}}_1)\mathrm{\Theta }[p(\mathit{n}\mid {\mathcal{P}}_0)-p(\mathit{n}\mid {\mathcal{P}}_1)]$$

$$p_{10}={\sum }_{\mathit{n}}p(\mathit{n}\mid {\mathcal{P}}_0)\mathrm{\Theta }[p(\mathit{n}\mid {\mathcal{P}}_1)-p(\mathit{n}\mid {\mathcal{P}}_0)]$$ (15)

where Θ is the step function.

The false-positive and false-negative probabilities are plotted as functions of the number of signal photons in Fig. 5A for the previous section’s strategies, in the case where p_err is the optimized quantity. In both the classical (red lines) and quantum (blue lines) cases, the false-negative probability tends to be smaller than the false-positive one, meaning that the procedure is more likely to select the reference process. This unbalance comes from the fact that we consider as a reference process a distribution strongly peaked around τ₀, while, for the defective process, we consider a uniform distribution. In terms of photon count probability, this results in the fact that, when an overlap is present, the most peaked process, P₀, is chosen, while the defective one is selected in a range that is larger, but also less likely to be measured. This results in a bias toward P₀.

Fig. 5. Cost analysis in QCT.

(A) Dependence on the signal photon number n_S of the total error probability (p_err), false positive (p₀₁), and false negative (p₁₀). The maximum likelihood postprocessing used in this case minimizes p_err. The reference process is considered strongly peaked around the value τ₀ = 0.8, while the defective one is chosen uniformly distributed with mean $\overline{\mathrm{\tau }}=0.9$ and half-width δ = 0.09. (B) A situation similar to that of (A) is considered, but we use a biased maximum likelihood postprocessing with bias coefficient b = 0.6 (see the main text for details). (C) We fix photon number to n_S = 500 and analyze the dependence of the cost C on b. All the other parameters are equal to those of the previous panels. (D) Optimum value of b as a function of S.

The maximum likelihood postprocessing used up until now minimizes the probability of error by construction. To minimize the cost C, a different postprocessing is needed. We can modify the maximum likelihood condition used for the decision, p(n∣P_y) ≥ p(n∣P_{1 − y}), to make it more likely that one specific process is selected according to some parameters. We select y when

$$B^{(y)}p(\mathit{n}\mid {\mathcal{P}}_y)\ge B^{(1-y)}p(\mathit{n}\mid {\mathcal{P}}_{1-y})$$ (16)

where

$${\mathit{B}}^{(0)}=\frac{1-\mathit{b}}{2}$$

$${\mathit{B}}^{(1)}=\frac{1+\mathit{b}}{2}$$ (17)

and where b ∈ [ − 1,1] is a real constant. We call this modified postprocessing biased maximum likelihood. Selecting a positive b results in the defective process being chosen more often, while a negative b results in a more likely selection of the reference one. In other words, the value of b can be varied to shift p₀₁ and p₁₀, reducing the cost function C at the cost of the increase of the total error probability. This is shown in Fig. 5B: p₀₁ and p₁₀ have been brought closer to each other and the total error probability slightly increased, in both the quantum and classical cases. It is worth highlighting how the quantum advantage that we had with maximum likelihood processing is well preserved when the biased maximum likelihood one is used. The optimization of C is performed by varying the coefficient b. As an example, we consider the particular situation in which S = 1/4, meaning that each false positive is considered three times as costly as a false negative. In this situation, it is convenient to use a positive value for b, whose effect is to reduce the number of times the reference process P₀ is selected overall, thus reducing the false-positive probability p₀₁. The dependence of C on b is shown in Fig. 5C. In both the quantum and classical cases, as expected, there is a single optimum value for b, for which one has a minimum cost. The dependence of the optimum value of b on S, with respect to the cost C, is shown in Fig. 5D.

The false-positive and false-negative probabilities of the classical and quantum strategies with a PC receiver can be evaluated experimentally with the same procedure as the one described in Materials and Methods for the total probability of error. The experimental points, along with the theoretical curves, are reported in Fig. 6.

Fig. 6. Theoretical and experimental conditional probabilities of error for the quantum and classical strategies with PC receiver.

The distribution is taken such that $\overline{\mathrm{\tau }}=0.999$ and δ = 0.001. The mean number of signal photons is n_s ≈ 10⁵, and the channel efficiencies are η_S ≃ η_I ≈ 0.76. In the legend, the quantum case is denoted as q ij and the classical as c ij, with i,j = 0,1.

DISCUSSION

In this work, we proposed a protocol addressing the conformance test task, exploiting specific probe states and measurement strategies. We investigated the specific scenario in which the systems under test, representing possible outputs of the unknown process, can be modeled by pure loss channels.

In this context, we found a lower bound on the error probability that can be achieved in the discrimination task, using any classical source paired with an optimal measurement. We then showed that a particular class of quantum states, namely TMSV states, can be used in conjunction with a simple receiver consisting of a PC measurement and a maximum likelihood decision to improve the performances over those of any classical strategy. This enhancement is due to the high degree of correlation (entanglement) of TMSV states, whose nature is fundamentally quantum. We also analyzed the particular case of a classical source paired with PC measurements at the receiver.

We demonstrated that the quantum advantage persists for a wide range of parameters, even in the presence of losses due to possible experimental imperfections, and we validated our results by performing an experimental realization of the protocol. We showed an experimental advantage in a realistic scenario where experimental losses amounted to more than 20%, highlighting the robustness of the proposed protocol.

We emphasize the fact that these results are particularly important because they are achieved using states that are easily produced, as well as a receiver design of simple implementation, allowing practical applications of the protocol with present technology. We found an advantage, although the bound C on the performance of classical states is not tight, meaning that the actual quantum advantage could effectively be higher. For a thorough study, one can consider a scenario in which a set of objects is tested instead of one. In this scenario, we find an informational limit using the Holevo bound and we showed how our proposed quantum strategy, relying on an independent measurement over individual systems, surpasses a more general classical strategy, where joint measurements over a collection of systems are allowed. A detailed description of this result will be presented in a forthcoming paper. The proposed QCT protocol could be used in the foreseeable future in notable problems concerning the monitoring of production processes of any object probed with quantum states. For example, our results on loss channel QCT can be used to boost the accuracy in the identifications of issues in concentration and composition of chemical production by transmittance measurement.

MATERIALS AND METHODS

Experimental setup

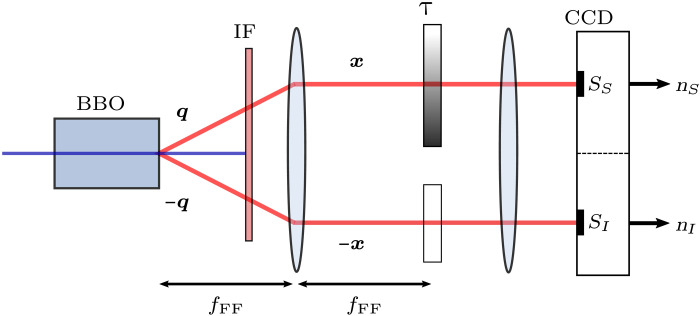
The experiment is based on SPDC and is depicted in Fig. 7. A multimode TMSV state ⊗^K∣ψ⟩ is generated using a 1-cm³ type II β-barium borate crystal and a continuous-wave laser at λ_p = 405 nm, delivering a power of 100 mW. The down-converted photons are correlated in momentum. This correlation is mapped into spatial correlations using a lens in f-f configuration: The “far-field” lens (f_FF = 1 cm) is positioned at one focal length of the output plane of the crystal. The absorption sample is positioned in the conjugated plane, which corresponds to the far field of the source. It consists of a coated glass plate, which presents different transmittance regions, realized with depositions of varying density. A blank coated glass is inserted in the idler beam’s path to match the optical paths of both beams. The sample is imaged using a second “imaging” lens onto a charge-coupled device camera (Princeton Instruments PIXIS:400BR eXcelon), working in linear mode with high quantum efficiency (>95% at 810 nm) and low (few electrons per pixel per frame) electronic noise. Individual pixels of the camera are binned together in 12 × 12 macropixels to increase the readout signal-to-noise ratio and the acquisition speed.

Fig. 7. Schematic of the experimental setup.

Pumping a β-barium borate (BBO) crystal with a laser at 405 nm, a multimode TMSV is generated. Using a lens of focal f_FF, the correlation in momentum is converted into correlation in position in the sample plane, which is then imaged on the camera using a second lens. The signal beam passes through the sample of transmittance τ and is then detected in the S_S region of the charge-coupled device (CCD). The idler beam goes directly to S_I without interacting with the sample, although its optical path is matched with the sample’s one using a nonabsorbing glass. Integrating the signals over the two detection regions, n_S and n_I are collected.

The photon counts n_S and n_I of the signal and idler beams are obtained by integrating over two spatially correlated detection areas S_S and S_I, which are subparts of the “full” correlated areas. The two full correlated areas are schematically defined by the two illuminated regions on the camera, i.e., the spatial extent of the idler and signal beams. Their precise definition is made using a procedure described in (22). The total number of spatial modes collected is K_s ∼ 10³, and that of temporal mode is K_t ∼ 10¹⁰ [see (42) for more details on the estimation]. The mean photon number measured in one region S_i is ${\overline{\mathit{n}}}_{\mathit{i}}\sim 10^5$. Hence, the mean occupation number per mode is very small ${\overline{\mathit{n}}}_{\mathit{i}}/({\mathit{K}}_{\mathit{s}} \times {\mathit{K}}_{\mathit{t}})\sim 10^{-8}$. Under these conditions, the multithermal marginal photon number distributions can be well approximated by Poisson distributions (34). When the absorptive sample is replaced with an equivalent coated glass plate without any deposition, we estimate, for each pair of regions S_S and S_I, the corresponding detection efficiencies η_S and η_I, by exploiting the correlations of the SPDC process (43, 44). The phase matching conditions, the interference filter, the quality of the optical alignment, and the pixels’ properties on the camera all introduce small differences in the photon number correlations that need to be accounted for. With the absorptive sample, for each pair of regions, i.e., for all the different values of τ, N_Dτ = 2 · 10⁴ frames are recorded (D_τ designates the experimental dataset for transmittance τ).

Data analysis

Using the experimental data, two error probabilities, p₀₁ and p₁₀, must be evaluated to access to the total error probability

$${\mathit{p}}_{\text{err}}=\frac{1}{2}({\mathit{p}}_{01}+{\mathit{p}}_{10})$$ (18)

In our analysis, the reference process P₀ is strongly peaked around τ₀. Hence, the evaluation of p₁₀ with experimental data is rather straightforward. We use the dataset D_τ0, composed of M measurement outcome (n_s; n_i), when the transmittance τ₀ is inserted in the signal branch to compute the experimental frequency of error f₁₀. In particular, for each data pair (n_s; n_i) ∈ D_τ0, a label y ∈ {0,1} is assigned according to the maximum likelihood strategy described in the main text. In the evaluation, experimental parameters such as the mean photon number of the source and the detection efficiencies are used, estimated in a calibration phase. f₁₀ is then defined as the number of wrong decisions, which, in this case, is simply the number of occurrences of y = 1 over M. f₁₀ will converge to the real probability of error p₁₀ as the number of experimental points in the dataset M becomes large.

On the other hand, the evaluation of p₀₁ requires a more careful approach. One has to construct an ensemble of experimental data D_P1, whose data are taken with parameters τ distributed in a way that is representative of the true probability density g₁(τ). Experimentally, we acquire $\overline{\mathit{M}}$ photon number pairs for each of the transmittance τ_i, i ∈ {1, …, L}, i.e., $\overline{\mathit{M}}·\mathit{L}$ data points in total. The transmittance values τ_i are selected in an interval [τ_min, τ_max]. They may not be distributed uniformly in this interval because of a nonperfect experimental control of the position of the absorption layer, and the uncertainty on the estimation of τ_i. Starting from the experimental dataset, and binning the interval [τ_min, τ_max] in K equal subintervals of size 2l (2l = (τ_max − τ_min)/K), we define the experimental distribution for the transmittance, g, as the normalized histogram

$$\mathit{g}(\mathrm{\tau })={\displaystyle \sum _{\mathit{k}=1}^{\mathit{K}}}\frac{{\mathit{d}}_{\mathit{k}}}{2\mathit{lL}}{\mathrm{\Theta }}_{\mathit{k}}(\mathrm{\tau })$$ (19)

where d_k is the number of experimental transmittance values τ_i that fall in the kth bin so that the relative number of pairs (n_s; n_i)_k is ${\mathit{d}}_{\mathit{k}}\overline{\mathit{M}}$. Θ_k(τ) is a step function, equal to unity in the kth bin and 0 elsewhere. In an ideal case, the experimental distribution g in Eq. 19 should be a uniform distribution in the interval [τ_min, τ_max], but, in practice, because of the experimental issues mentioned above, it can present substantial discrepancies with respect to it.

To approximate a general probability distribution f(t), we can multiply the coefficients in Eq. 19, by proper weights w_k, with k ∈ {1, …, K}. Once the weights are determined by a proper optimization procedure, described in the Supplementary Materials, they are used to modulate the number of experimental data in each bin according to the substitution ${\mathit{d}}_{\mathit{k}}\overline{\mathit{M}}⟼{\mathit{d}}_{\mathit{k}}{\mathit{w}}_{\mathit{k}}\overline{\mathit{M}}$, where w_k represents the fraction of data kept in bin k. The ensemble of data randomly picked from the initial set, according to the weights, will define the final set D_P1. We refer to the distribution of D_P1 after the reweighting procedure, as g_w(τ), where w = [w₁, …, w_K]. Since the experimental set cannot be increased, the constraint 0 ≤ w_k ≤ 1 must be imposed. The procedure will, in general, reduce the number of points in the dataset: An increase of the statistical uncertainty can arise. Thus, it may be useful to introduce a second constraint on the size of the final dataset, ${\mathit{M}}_{\mathit{T}}={\sum }_{\mathit{k}=1}^{\mathit{K}}{\mathit{d}}_{\mathit{k}}{\mathit{w}}_{\mathit{k}}\overline{\mathit{M}}$, in the optimization procedure to put a lower bound on how much data are discarded.

For the optimization process, we define the objective function to be maximized as the Bhattacharyya coefficient between the distributions f and g_w

$$\mathit{T}(\mathbf{w})={\displaystyle {\int }_{{\mathrm{\tau }}_{\text{min}}}^{{\mathrm{\tau }}_{\text{max}}}}\sqrt{\mathit{f}(\mathrm{\tau }){\mathit{g}}_{\mathbf{w}}(\mathrm{\tau })}\mathit{d}\mathrm{\tau }$$ (20)

This quantity measures their similarity and ranges between 0 and 1. T(w) gives a quantitative measure of how close the experimental dataset can be arranged to resemble the objective distribution. We define a threshold value 0 ≤ T_th ≤ 1, above which the approximation of f ≈ g_w is deemed “good enough,” i.e., T(w) ≥ T_th. In general, the optimal w and the corresponding T(w) depend on the interval [τ_min; τ_max], which should be chosen so that ${\int }_{{\mathrm{\tau }}_{\text{min}}}^{{\mathrm{\tau }}_{\text{max}}}\mathit{f}(\mathit{t})$ dt is close to unity. We note that the minimum number of data points M_T and the initial distribution of the experimental data can affect the results of the optimization algorithm. For this reason, in our realization of this algorithm, we sampled the interval [τ_min, τ_max] with a dense array of values τ_i, taken equispaced within the experimental uncertainty, and we took a very large total number of data points with respect to the target M_T. The approximated distribution for the data, reported in Results, had a coefficient T ∼ 1. A more formal description, as well as further details on the procedure, is reported in the Supplementary Materials.

Supplementary Materials

This PDF file includes:

Supplementary Materials

Figs. S1 to S3